الحفاظ على الكربون العضوي في الرواسب البحرية المدعوم بعمليات الامتزاز والتحول Preservation of organic carbon in marine sediments sustained by sorption and transformation processes

المجلة: Nature Geoscience، المجلد: 18، العدد: 1
DOI: https://doi.org/10.1038/s41561-024-01606-y
PMID: https://pubmed.ncbi.nlm.nih.gov/39822308
تاريخ النشر: 2025-01-01

الحفاظ على الكربون العضوي في الرواسب البحرية المدعوم بعمليات الامتزاز والتحول

تاريخ الاستلام: 2 مايو 2023
تاريخ القبول: 29 أكتوبر 2024
تاريخ النشر على الإنترنت: 3 يناير 2025
تحقق من التحديثات

بيمان باباخاني , أندرو و. ديل , كلير وودز , أوليفر و. مور , كي-تشينغ شياو® , ليزا كيرتي (1) & كارولين ل. بيكوك (1)

تظل الضوابط على الحفاظ على الكربون العضوي في الرواسب البحرية مثيرة للجدل ولكنها حاسمة لفهم الديناميات المناخية الماضية والمستقبلية. هنا نطور نموذجًا رياضيًا مفاهيميًا لتحديد العمليات الرئيسية للحفاظ على الكربون العضوي. يأخذ النموذج في الاعتبار العمليات الرئيسية المعنية في تحلل الكربون العضوي، بما في ذلك التحلل المائي للكربون العضوي المذاب، والخلط، وإعادة التمعدن، وامتصاص المعادن، والتحول الجزيئي. وهذا يسمح بإعادة تعريف كفاءة الدفن ككفاءة الحفاظ، والتي تأخذ في الاعتبار كل من الكربون العضوي الجزيئي وكربون المرحلة المعدنية. نوضح أن كفاءة الحفاظ أعلى تقريبًا بثلاث مرات من كفاءة الدفن المعرفة تقليديًا وتتناسب التنبؤات مع بيانات الحقل العالمية. تعتبر الامتصاص الديناميكي والتحول الضوابط السائدة على الحفاظ على الكربون العضوي. نستنتج أن تأثيرًا تآزريًا بين الامتصاص الديناميكي والتحول الجزيئي (الجيوبوليمرization) يخلق ناقلًا معدنيًا حيث يتم حماية كربون المرحلة المعدنية العضوية من إعادة التمعدن في الرواسب السطحية ويتم إطلاقه في العمق. تفسر النتائج لماذا يستمر الكربون العضوي المتحول على مدى فترات زمنية طويلة ويزداد مع العمق.
يعد الحفاظ على الكربون العضوي (OC) في الرواسب البحرية أمرًا حيويًا لدورات الكربون والأكسجين العالمية، وبالتالي، لمناخ الأرض وتركيب الغلاف الجوي , توزيع موارد الطاقة وإيجاد استراتيجيات تخفيف محتملة قائمة على المحيط لإزالة ثاني أكسيد الكربون الجوي الزائد الذي يدفع تغير المناخ . ومع ذلك، فإن الضوابط على الحفاظ على الكربون غير واضحة حاليًا . في المحيط السطحي، تقوم المنتجون الأساسيون أو العوالق النباتية بامتصاص ثاني أكسيد الكربون الجوي لتوليد الكتلة الحيوية، والتي تصل نسبة منها إلى الرواسب ككربون عضوي جزيئي (POC) وتخضع لسلسلة من مسارات التحلل المعقدة، والتي قد تؤدي في النهاية إلى إما إعادة تمعدن الكربون أو دفنه . ومع ذلك، فإن هذا النموذج يتجاهل دور الكربون العضوي المذاب (DOC) في
الحفاظ على الكربون . يعتبر DOC، الذي يتم إنتاجه من التحلل المائي لـ POC، وسيطًا رئيسيًا في دورة الكربون قبل أن يتم إعادة تمعدن OC إلى كربون غير عضوي، على سبيل المثال، ثاني أكسيد الكربون. ومع ذلك، قد تبدو التركيزات الحالية لـ DOC في مياه مسام الرواسب البحرية منخفضة , مما يؤدي إلى نقص المعرفة حول دوره في الحفاظ على OC ودورته. ومع ذلك، تشير التحقيقات التجريبية والقياسات الميدانية إلى أن DOC قد يتراكم مع مرور الوقت نتيجة لامتصاصه إلى المعادن لتشكيل كربون المرحلة المعدنية (MOC) و/أو تحوله الجزيئي داخل الرواسب المعروف باسم الجيوبوليمرization , أو تخفيفه في عمود الماء بعد الانتشار من الرواسب , وبالتالي قد يؤثر بشكل كبير على دورة الكربون على الأرض .
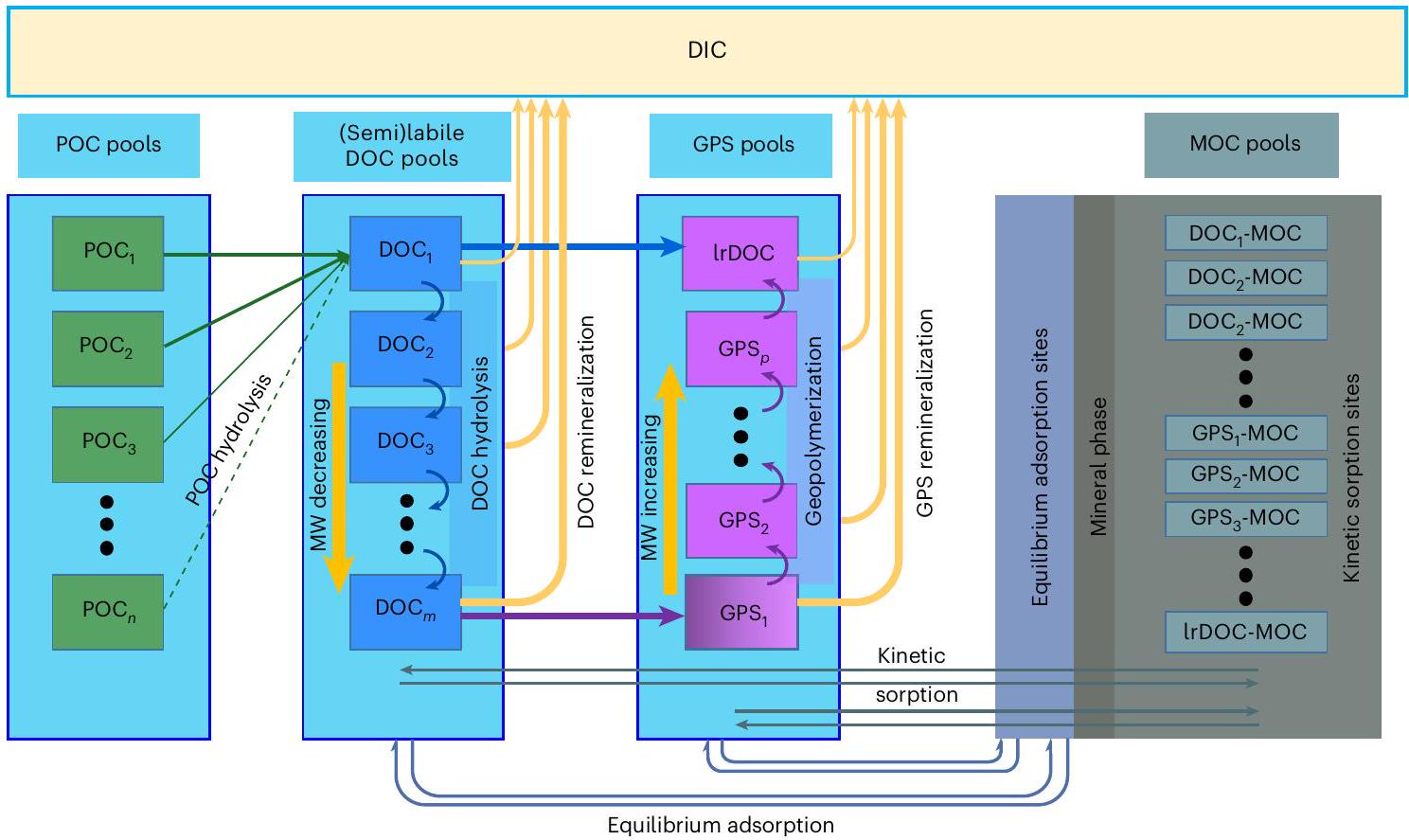
الشكل 1| نموذج مفاهيمي لدورة DOC في الرواسب. يتضمن النموذج المفاهيمي المقترح آليات الجيوبوليمرization، وامتصاص التوازن، والامتصاص الديناميكي ومفهومًا معدلًا للتحلل المائي الذي يتبع دورة DOC في عمود الماء . تشمل تسميات النموذج المخطط POC، GPS، lrDOC، DOC المذاب الممتص بالمعادن المختلفة ((نصف) قابل للتحلل DOC-MOC، GPS-MOC وIrDOC-MOC)، DIC وMW. يمكن لجميع تجمعات DOC وGPS وIrDOC التفاعل مع المعادن من خلال امتصاص التوازن والامتصاص الديناميكي. بشكل عام، يمكن أن يتم تحلل تجمعات POC التي تنشأ من عمود الماء
على أي عمق في الرواسب أو تبقى غير متحللة. يتم نقلها في الرواسب بشكل مشابه للمعادن الصلبة في الرواسب. يتم نقل تجمعات MOC بشكل مشابه للمعادن الصلبة في الرواسب وPOC، ولكنها تنشأ من صافي امتصاص DOC وGPS وIrDOC إلى المعادن ويفترض أنها غير تفاعلية ما لم يتم إزالة الكربون من المعادن. يعتبر جزء من POC، الذي لم يتم تحلله عند عمق معين، وجزء من MOC، الذي لم يتم إزالته عند ذلك العمق، مدفونًا بشكل دائم.
حتى الآن، لم تحظَ مساهمات هذه العمليات في الحفاظ على OC، وبالتالي، دورة الكربون باهتمام كبير وتظل غير معروفة بشكل سيء. علاوة على ذلك، فإن المفهوم التقليدي لكفاءة دفن OC (BE) في الرواسب – مؤشر على القدرة على الحفاظ على الكربون وقياس الميزانيات العالمية للكربون في الرواسب الحديثة والقديمة – غير صحيح من الناحية المفاهيمية إذا كان الحفاظ على OC عبر امتصاص DOC والتحول كبيرًا ومهملًا. نعيد تعريف BE ككفاءة الحفاظ (PE)، والتي تشمل كل من دفن POC الذي يعتبر تقليديًا وحفاظ MOC.
هنا، نطور نموذجًا ميكانيكيًا للتفاعل والنقل (RTM) يأخذ في الاعتبار العمليات الرئيسية للحفاظ على OC في الرواسب البحرية عبر دورة DOC. بعد التحقق الشامل، يتم استخدام النموذج جنبًا إلى جنب مع تحليلات مونت كارلو والشبكات العصبية الاصطناعية (ANN) لتوفير رؤى عالمية حول دور العمليات التي تتحكم في الحفاظ على الكربون في الرواسب البحرية وتظهر أين وكيف يحدث الحفاظ.

تصور دورة الكربون والحفاظ عليها في الرواسب

يبدأ نموذجنا المفاهيمي لدورة الكربون والحفاظ عليها في الرواسب مع التحلل المائي لعدة كسور POC منفصلة ( وما إلى ذلك) إلى تجمع DOC واحد ( ) ذو وزن جزيئي مرتفع (MW) (الشكل 1). يستمر التحلل المائي المتسلسل لـ في إنتاج DOC بوزن جزيئي أقل بشكل متزايد ( وما إلى ذلك) وتفاعل أعلى (معدل إعادة التمعدن)، وهو مشابه للنموذج الحديث لدورة DOC في عمود الماء . يختلف نهج التحلل المائي المتسلسل بشكل ملحوظ عن الفرضية السابقة (الشكل 1)، حيث ينتج كل كسر POC منفصل تجمع DOC المقابل له بتفاعل مشابه لوالده . لتمثيل إنتاج DOC الأقل تفاعلاً (lrDOC)، ندرج التراكم المباشر لـ DOC الذي تم تحلله حديثًا ولكنه غير قابل للتحلل بشكل جوهري
عبر نقل مباشر لـ إلى IrDOC (الشكل 1). نعتبر أيضًا الجيوبوليمرization لـ DOC منخفض الوزن الجزيئي ( ) إلى جزيئات ذات وزن جزيئي أعلى يُشار إليها هنا بالمواد الجيوبوليمرized (GPS-DOC أو ببساطة GPS) مع تفاعل أقل بشكل متزايد (GPS وما إلى ذلك)، والتي تساهم في النهاية في تجمع IrDOC (الشكل 1). وبالتالي، يتكون تجمع IrDOC لدينا من كل من DOC غير القابل للتحلل جوهريًا وGPS المتحول جزيئيًا. يتم اختيار تفاعلات تجمعات DOC بناءً على أعمارها في عمود الماء وتصنيفها على أنها قابلة للتحلل ونصف قابلة للتحلل ( وما إلى ذلك، مجمعة كـ (نصف) قابل للتحلل-DOC، مع عمر يتراوح من إلى سنوات)، ومتوسطة التفاعل ( وما إلى ذلك، مع عمر سنوات) وأقل تفاعلًا (lrDOC، مع عمر سنوات) . لتمثيل امتصاص DOC إلى المعادن، ندرج وصفًا بموقعين لـ ‘امتصاص التوازن و’الامتصاص/الإزالة الديناميكية’. يهدف الامتصاص/الإزالة الديناميكية، وهو وصف عام لعمليات الامتصاص/الإزالة التي ليست في حالة توازن، في الغالب إلى تمثيل الانسداد داخل المعادن، والترسيب المشترك و/أو التجمع مع المعادن، والعمليات العكسية التي تؤدي إلى إزالة الكربون من مصفوفة المعادن . تؤدي النتيجة الصافية للامتصاص-الإزالة الديناميكية إلى تشكيل تجمعات، بما في ذلك (نصف) قابل للتحلل DOC-MOC، GPS-MOC وIrDOC-MOC (الشكل 1). يتم نقل هذه التجمعات MOC بعد ذلك مع المعادن بشكل مشابه لتجمعات POC التي يتم خلطها مع المعادن، على الرغم من أن MOC تختلف عن POC من حيث الأصل، أي أن POC تنشأ من عمود الماء بينما يتم تشكيل MOC في الرواسب عبر الامتصاص الديناميكي لـ DOC إلى المعادن.
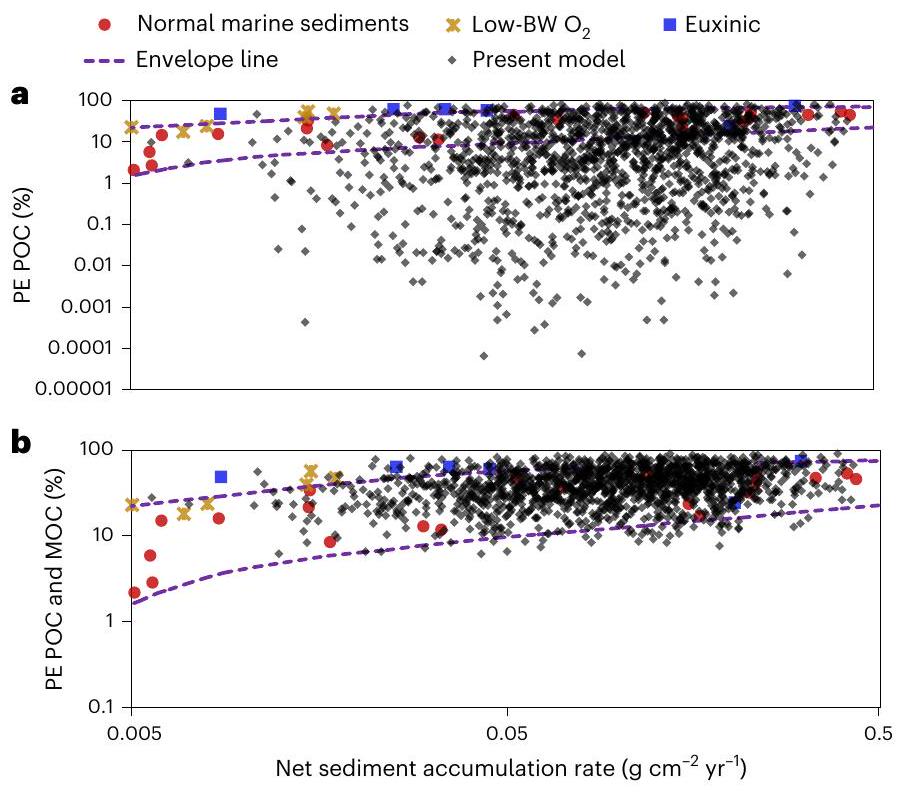
نقوم بإدماج نموذجنا المفاهيمي (الشكل 1) في RTM تم حله عموديًا للرواسب البحرية الذي يربط بين عمليات النقل (على سبيل المثال، سرعة دفن الرواسب قبل الضغط، والخلط الناتج عن الكائنات الحية) والتفاعلات البيوجيوكيميائية (على سبيل المثال، إعادة تمعدن DOC). نقوم بتنفيذ RTM الذي تم التحقق منه باستخدام نهج مونت كارلو ( محاكاة) باستخدام معلمات الإدخال التي تتغير عشوائيًا
الشكل 2 | مقارنة PE الناتج عن النموذج مع بيانات الأدبيات. أ، ب، البيانات الناتجة عن 1450 تشغيل نموذج في نهج مونت كارلو (نقاط سوداء شفافة) للطريقة التقليدية لحساب PE لـ POC التي تأخذ في الاعتبار فقط POC (أ) ولـ PE المحدد حديثًا الذي يأخذ في الاعتبار كل من POC و MOC (ب). يتم مقارنتها مع بيانات الحقل من دراسات سابقة . يتم اشتقاق انتشار بيانات النموذج من توزيع طبيعي لمعدل تراكم الرواسب الصافية الملاحظ في مجموعات بيانات الشبكة العالمية (الأشكال التكميلية 1 و 2). تمثل خط الغلاف (الخط المنقط) الحدود العامة لانتشار البيانات المحددة في الدراسات السابقة . منخفضة تشير إلى تركيز الأكسجين في المياه القاعية المنخفض.
ضمن نطاقات ذات صلة عالمياً (الجدول التكميلية 1) بناءً على التوزيعات الإحصائية المأخوذة من ست مجموعات بيانات نمذجة ميدانية (الأشكال التكميلية 1 و 2) وعشر دراسات سابقة (الجدول التكميلية 2) لفحص الدور الأوسع لعمليات الحفاظ على OC المختلفة (الشكل التكميلية 3، المرحلة 1).
ثم نستخدم مجموعة البيانات الناتجة عن RTM لتدريب وتحديد أهمية العمليات التي تتحكم في الحفاظ على OC (الشكل التكميلية 3، المرحلة 2). يسمح نموذجنا بتضمين كل من تشكيل MOC في OC الصلب ودفن POC في العمق في تعريف PE على عكس الطريقة التقليدية حيث يتم اعتبار دفن POC فقط في النموذج . المعادلات الخاصة بـ PE التقليدي و PE المحدد حديثًا (المعادلات (6) و (7)) وغيرها من تفاصيل تطوير نموذجنا واختباره وتنفيذه موضحة في الأقسام التكميلية 1 و 2. نستخدم PE لتقييم الأداء العام للنموذج مقابل البيانات العالمية. نحن نتحقق أيضًا من صحة نموذجنا الرياضي وجوانب أخرى من نموذجنا كما هو ملخص في الطرق ومفصل بالكامل في القسم التكميلية 2، الأشكال التكميلية 4-12 والجدول التكميلية 3-7.

تقييم النموذج

تمت مقارنة دمج MOC في نماذج PE مع النهج الكلاسيكي الذي يأخذ في الاعتبار فقط POC في الشكل 2 (المراجع 12، 36). لا يمكن أن يفسر PE لـ POC وحده الاتجاه الملحوظ وغلاف قيم PE مقابل معدل تراكم الرواسب (الشكل 2 أ، الخطوط المنقطة) . فقط عندما يتم اعتبار الحفاظ على MOC جنبًا إلى جنب مع POC يقع الغالبية العظمى من بيانات مخرجات النموذج داخل الغلاف (الشكل 2 ب).
تم اقتراح العديد من العوامل المختلفة لشرح الحفاظ على OC في الرواسب البحرية . تشير قدرة نموذجنا على التنبؤ ببيانات PE العالمية المتاحة إلى أن اعتبار دورة DOC والعمليات ذات الصلة، وخاصة الامتصاص والجيوبوليمرization، أمر حاسم للتنبؤ بـ PE. وهذا ملحوظ لأنه لم يتم ضبط أي معلمات نموذجية في هذه المحاكاة (الشكل 2). يسمح نهجنا في دمج RTM و ANN ومونت كارلو بفهم قائم على العمليات لـ
الشكل 3 | الأهمية النسبية لعمليات مختلفة. أ، ب، الأهمية النسبية (%) لست عمليات لـ PE عندما يتم اعتبار MOC بالإضافة إلى POC (أ) ومعدلات الحفاظ على MOC (ب). العمليات الست هي تحلل DOC، إعادة معدنة DOC، الخلط، الامتصاص التوازني، الامتصاص الحركي والجيوبوليمرization. يتم إعطاء PE المحدد حديثًا بواسطة المعادلة (7). يتم عرض معدلات الحفاظ على MOC كمعدل لتشكيل MOC، وهو مجموع معدلات الامتصاص الحركي الصافية المدمجة عند عمق لـ DOC و GPS و IrDOC. يتم الحصول على أهمية كل عملية بناءً على أقصى حساسية للمعلمات المصنفة لكل عملية. يتم تقديم التصنيف في الجدول التكميلية 9. كل عمود هو متوسط 1000 تنفيذ لتحليل أهمية العملية، وتمثل أشرطة الخطأ فترة الثقة. تفاصيل أخذ العينات في طريقة مونت كارلو لتحليل أهمية العملية موضحة في الأقسام التكميلية 1.3-1.5 وفي الدراسات السابقة .
ديناميات الكربون ليتم ترجمتها إلى فهم عالمي دون الحاجة إلى ضبط النموذج لمواقع محددة قد تقدم عدم اليقين المرتبط بالظروف المحددة للموقع.
تعريف نموذجنا لتحلل POC مشابه لذلك الذي يعتبر إعادة معدنة POC في أماكن أخرى , وبالتالي، فإن تقديرنا لـ PE لـ POC مشابه للطريقة التقليدية , والتي تقدر أيضًا PE الميدانية بقيم عالمية مقدرة تقل عن (المراجع 28). ومع ذلك، يتتبع نموذجنا أيضًا DOC المتحلل من POC وامتصاصه للمعادن، مما يؤدي في النهاية إلى توقع أفضل بكثير لبيانات PE الميدانية مقارنة بالطريقة التقليدية. القيم المتوسطة لجميع تشغيلات نموذج مونت كارلو ( ) هي و لـ PE لـ POC و POC + MOC، على التوالي.

دور العمليات المختلفة في الحفاظ على الكربون

نحن نقوم بتحديد أهمية ست عمليات نموذجية في التحكم في المؤشرات الرئيسية للحفاظ على الكربون، بما في ذلك PE ومعدلات تشكيل MOC (أو معدلات امتصاص DOC). يُفهم تقليديًا أن ثلاث عمليات مهمة للحفاظ على الكربون , وهي، تحلل DOC إلى DOC منخفض الوزن الجزيئي بشكل متزايد، إعادة معدنة DOC وخلط الرواسب بواسطة الحيوانات. أهمية العمليات الثلاث الأخرى متنازع عليها أو غير مفهومة جيدًا، وهي، الامتصاص الحركي، الامتصاص التوازني والجيوبوليمرization (الجدول التكميلية 8 و 9).
تكشف النتائج أن الامتصاص الحركي هو العملية الأكثر أهمية لـ PE مع أهمية نسبية قدرها بين العمليات الست، تليها الخلط ( )، إعادة المعدنة ( )، الجيوبوليمرization ( )، تحلل DOC ( ) والامتصاص التوازني (الشكل 3 أ). بشكل عام، العمليات التي تتحكم في تدفق دفن POC ودوران الكربون في العمق، مثل الخلط وإعادة المعدنة، هي أكثر أهمية لـ PE من الجيوبوليمرization وتحلل DOC. نحن أيضًا نحقق في أهم العمليات لمعدل الحفاظ على أنواع DOC-MOC (الشكل التكميلية 13) التي تم متوسطها في الشكل 3 ب. تظهر هذه أن الجيوبوليمرization (نسبياً لجميع العمليات الست) هي العملية الأكثر أهمية للحفاظ على DOC-MOC، تليها الامتصاص الحركي , تحلل DOC ( )، إعادة المعدنة ( )، الخلط ( ) والامتصاص التوازني (الشكل 3 ب). تضيف الأهمية العالية لعملية الجيوبوليمرization في التحكم في الحفاظ على DOC-MOC وزنًا لوجود تأثير تآزري للجيوبوليمرization مع امتصاص DOC، حيث تجعل الجيوبوليمرization DOC أقل تفاعلاً ويوفر الامتصاص حماية إضافية من إعادة المعدنة الميكروبية .
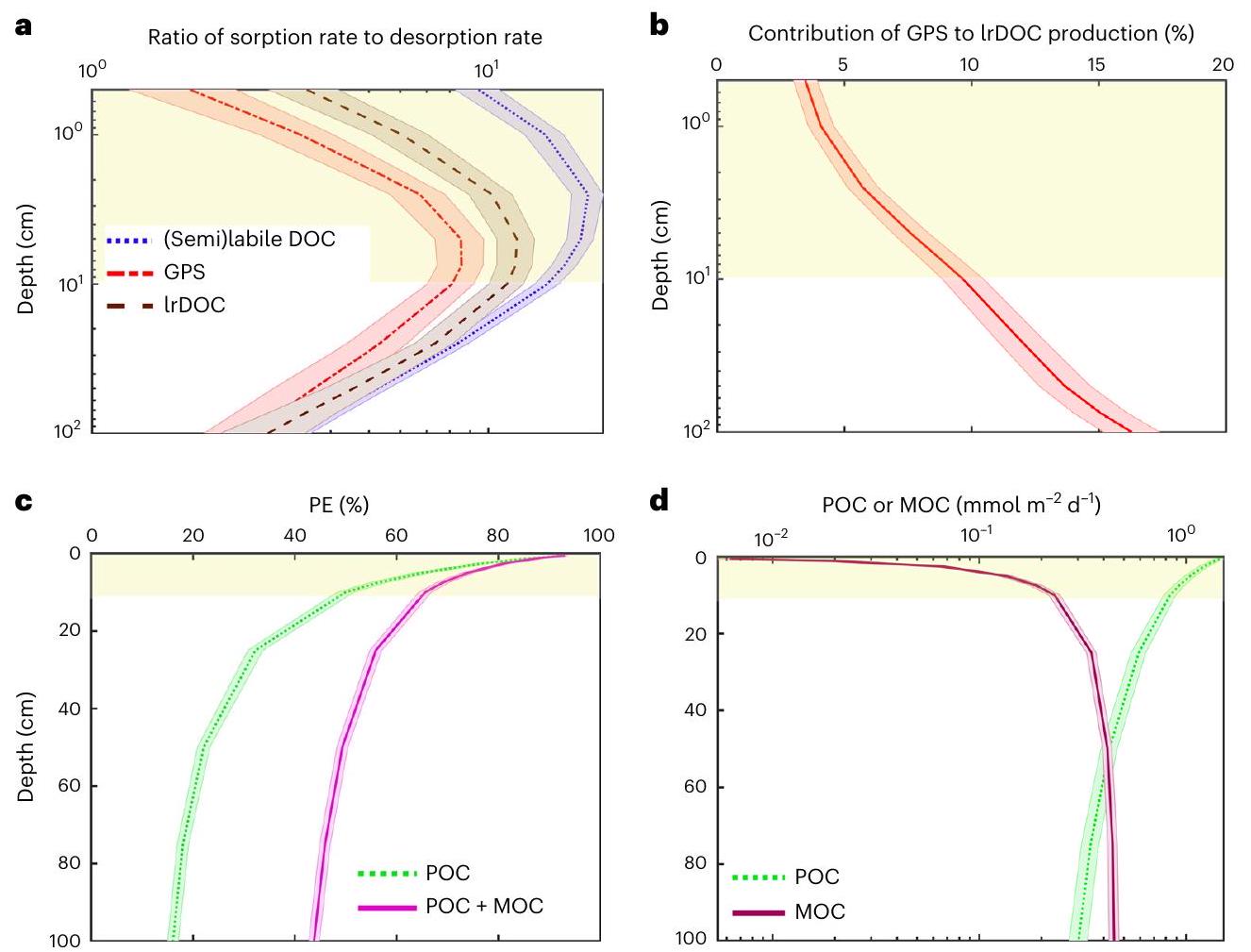
الشكل 4 | ملفات العمق التي تم الحصول عليها من نمذجة مونت كارلو. أ، نسبة معدلات الامتصاص الحركي المتوسطة لـ 1450 تشغيلًا من نمذجة مونت كارلو إلى معدلات الإزالة المتوسطة أيضًا لـ 1450 تشغيلًا نموذجية عند أعماق مختلفة. ب، النسبة المئوية لمساهمة مجموعة GPS النهائية في إجمالي إنتاج IrDOC (الشكل 1) عند أعماق مختلفة. تم متوسط هذه المساهمات لـ 1450 تشغيلًا من نمذجة مونت كارلو. المعادلات الرياضية المستخدمة لإنتاج هذه الرسوم البيانية موضحة في القسم التكميلية 3. ج، PE (%) لـ POC فقط ولـ POC و MOC معًا، مما يوضح أن MOC يزيد
PE المحسوبة بمقدار 2.7 عند عمق 1 متر مقارنة بالطريقة التقليدية التي تأخذ في الاعتبار فقط POC. د، تدفقات POC ومعدل الحفاظ على MOC. يتجاوز محتوى MOC POC عند عمق ولا يزال يستمر في الارتفاع تحت هذا العمق. تم متوسط جميع القيم لـ 1450 تشغيلًا من نموذج مونت كارلو. تمثل المناطق المظللة من المنحنيات فترات الثقة التي تم الحصول عليها من تشغيلات نموذج مونت كارلو. تمثل المنطقة المظللة باللون الأصفر الفاتح عمق الطبقة المختلطة (أعلى 10 سم).
كانت الاعتبارات السابقة لامتصاص DOC في الرواسب البحرية محدودة بعملية امتصاص سطح توازني بسيطة معبر عنها باستخدام معامل تقسيم ( )، سواء في إطار نمذجة أو في التحقيقات الميدانية والتجريبية . جادل آخرون بأن الامتصاص التوازني لا يمكن أن يكون مسؤولاً عن الحفاظ على المركبات العضوية القابلة للتحلل بطبيعتها وأن بعض أنواع الامتصاص غير القابلة للعكس و/أو التغير في تفاعلية OC قد تكون مسؤولة . الأنماط المقترحة، مثل امتصاص طبقة أحادية من DOC على الأسطح المعدنية , لا تزال تعتمد على افتراض الامتصاص السطحي البسيط وقد تم انتقادها لعدم قدرتها على وصف الحفظ الملحوظ في بيئات المحيطات المختلفة . إن اعتبارنا لعدة عمليات متزامنة يظهر أنه، بينما لا تزال مؤشرات حفظ الكربون غير حساسة لعملية الامتصاص التوازني، فإن تحكمها من قبل هذه العملية هو الأقل بين العمليات الستة المدروسة (الشكل 3أ، ب). بينما يمكن أن يقلل الامتصاص التوازني من تركيز DOC القابل للاستخدام البيولوجي في سوائل المسام، مما يبطئ من تحلل DOC , يمكن أن يتم امتصاص DOC في المواقع التوازنية على الفور إذا انخفضت تركيزات DOC في مياه المسام (على سبيل المثال، نتيجة للتحلل الميكروبي أو الامتصاص الحركي) . ومع ذلك، يمكن لآليات حماية DOC المعدنية التي تتحكم فيها الحركية مثل الترسيب المشترك، والانغلاق والتجمع، أن تحمي DOC على مدى فترات زمنية أطول بكثير . تكشف تحليلاتنا أن عملية الامتصاص الحركي هي العامل الأكثر أهمية في التحكم في PE (الشكل 3أ) والثاني الأكثر أهمية في التحكم في معدلات حفظ MOC المتوسطة (الشكل 3ب).
مؤخراً، تم إظهار أن الجيوبوليمرية في شكل تفاعل تكثيف من نوع ميلارد من خلال التحفيز بواسطة الحديد والمغنيسيوم المذاب أو الجزيئي هي عملية حاسمة لـ DOC القاعية
دورة . ومع ذلك، فإن قياس عملية الجيوبوليمرية وأهميتها مقارنةً بالعمليات الأخرى لحفظ الكربون لا يزال صعباً حتى الآن . يظهر تحليلنا أن الجيوبوليمرية مهمة بنفس القدر، أو أكثر، لـ PE مقارنةً بالتحلل المائي لـ DOC (الشكل 3أ). علاوة على ذلك، في المتوسط، تعتبر الجيوبوليمرية العامل الأكثر أهمية لمعدل حفظ أنواع DOC بين جميع العمليات الستة المدروسة (الشكل 3ب).

كيف تتحكم الامتصاص والجيبوليمرية في حفظ OC

نستخدم ملفات عمق الرواسب (الشكل 4 والقسم التكميلي 3) المستمدة من محاكاة مونت كارلو لتوفير رؤية أوسع حول كيفية تحكم العمليات المختلفة في حفظ OC. نلاحظ أن الطبقة المختلطة تعمل كوسيلة نقل لمجموعات DOC المختلفة من خلال حمايتها من التعرض للأكسجين والمواد المغذية والإنزيمات الميكروبية، وبالتالي، تحد من إعادة التمعدن السريع لها في الطبقة المختلطة وتوصيلها إلى أعماق أكبر (الشكل 4أ). كما نحقق في مسارات إنتاج IrDOC، التي تظهر أن الجيوبوليمرية تساهم في تشكيل lrDOC (الشكل 4ب). يتم مناقشة هذه الأمور بالكامل في القسم التكميلي 4.
نلاحظ أيضاً أن PE يمكن أن يتغير مع أفق عمق الرواسب أو أفق العمر . تتفق ملفات PE النموذجية مقابل العمق في الرواسب التي تأخذ في الاعتبار POC فقط بالإضافة إلى POC و MOC (الشكل 4ج) مع المرجع 28 على أنه يوجد تغيير في PE مع العمق. ومع ذلك، يبدو أن هذا التغيير يصبح أقل وضوحًا تحت 75 سم. والأهم من ذلك، أن تشكيل MOC ينمو بشكل كبير ضمن أعلى 10 سم ويستمر في الزيادة تحت هذا العمق (الشكل 4د) إلى النقطة التي يتجاوز فيها MOC محتوى POC تحت 50 سم (يتم مناقشته بشكل أكبر في القسم التكميلي 4).
في الختام، تكشف نتائجنا أنه، بخلاف العمليات المعروفة تقليديًا (التحلل المائي، والخلط وإعادة التمعدن)، فإن الامتصاص الحركي والجيبوليمرية ربما تلعب دورًا رئيسيًا في حفظ OC. يخلق الامتصاص الحركي وسيلة نقل معدنية تزيل DOC بفعالية من الطبقة السطحية النشطة وتطلقه في العمق، بينما تجعل الجيوبوليمرية كعملية تعتمد على العمر OC أقل تفاعلاً. يؤدي الامتصاص الحركي إلى تشكيل جزء مرتبط بالمعادن يصبح أكبر من مجموعة POC تحت , على الرغم من أن ملف POC العالمي المتوسط (الشكل 4د، المنحنى الأخضر) و PE لـ POC يبقيان مشابهين لتلك التي تم التنبؤ بها من قبل النموذج التقليدي. وبالتالي، فإن حفظ OC في الرواسب البحرية، الذي تم تصوره حتى الآن على أنه نتيجة لدفن POC، هو نتيجة لعدة عمليات مرتبطة بـ DOC، بما في ذلك التحلل المائي، والجيبوليمرية والامتصاص الصافي لـ DOC إلى المعادن. إن اعتبار هذه العمليات في نموذج واحد يتصالح مع عدم تطابق PE النموذجي مع بيانات الحقل ويسلط الضوء على الأدوار المتزامنة والمعقدة للعمليات المختلفة. نقترح أن يتم اعتبار تصوراتنا في نماذج دورة الكربون وقد تؤدي إلى قياس أفضل وفهم لميزانيات الكربون العالمية، وديناميات المناخ الحالية والماضية، والآثار طويلة الأجل لتقنيات إزالة ثاني أكسيد الكربون المحتملة المستندة إلى المحيط . نعترف أنه، على الرغم من أننا اتبعنا أفضل ممارسات النمذجة ويقدم نموذجنا تقدمًا في عدة جوانب، قد لا تزال نماذج أخرى تتطور في المستقبل تصف دورة الكربون في الرواسب البحرية بشكل أفضل.

المحتوى عبر الإنترنت

أي طرق، مراجع إضافية، ملخصات تقارير Nature Portfolio، بيانات المصدر، بيانات موسعة، معلومات تكملية، شكر وتقدير، معلومات مراجعة الأقران؛ تفاصيل مساهمات المؤلفين والمصالح المتنافسة؛ وبيانات توفر البيانات والرموز متاحة على https://doi.org/10.1038/s41561-024-01606-y.

References

  1. Alcott, L. J., Mills, B. J. W. & Poulton, S. W. Stepwise Earth oxygenation is an inherent property of global biogeochemical cycling. Science 366, 1333-1337 (2019).
  2. Berner, R. A. Biogeochemical cycles of carbon and sulfur and their effect on atmospheric oxygen over Phanerozoic time. Glob. Planet. Change 1, 97-122 (1989).
  3. Amon, R. M. W. & Benner, R. Rapid cycling of high-molecular-weight dissolved organic matter in the ocean. Nature 369, 549-552 (1994).
  4. Li, Z., Zhang, Y. G., Torres, M. & Mills, B. J. W. Neogene burial of organic carbon in the global ocean. Nature 613, 90-95 (2023).
  5. Abelson, P. H. Organic matter in the Earth’s crust. Annu. Rev. Earth Planet. Sci. 6, 325-351 (1978).
  6. Hatcher, P. G., Spiker, E. C., Szeverenyi, N. M. & Maciel, G. E. Selective preservation and origin of petroleum-forming aquatic kerogen. Nature 305, 498-501 (1983).
  7. Smetacek, V. et al. Deep carbon export from a Southern Ocean iron-fertilized diatom bloom. Nature 487, 313-319 (2012).
  8. Babakhani, P. et al. Potential use of engineered nanoparticles in ocean fertilization for large-scale atmospheric carbon dioxide removal. Nat. Nanotechnol. 17, 1342-1351 (2022).
  9. Arndt, S. et al. Quantifying the degradation of organic matter in marine sediments: a review and synthesis. Earth Sci. Rev. 123, 53-86 (2013).
  10. Kleber, M. et al. Dynamic interactions at the mineral-organic matter interface. Nat. Rev. Earth Environ. 2, 402-421 (2021).
  11. Burd, A. B. et al. Assessing the apparent imbalance between geochemical and biochemical indicators of meso-and bathypelagic biological activity: what the @$#! is wrong with present calculations of carbon budgets? Deep Sea Res. Part II 57, 1557-1571 (2010).
  12. Burdige, D. J. Preservation of organic matter in marine sediments: controls, mechanisms, and an imbalance in sediment organic carbon budgets? Chem. Rev. 107, 467-485 (2007).
  13. Burdige, D. J. & Komada, T. in Biogeochemistry of Marine Dissolved Organic Matter (eds Hansell, D. A. & Carlson, C. A.) 535-577 (Elsevier, 2015).
  14. Burdige, D. J., Komada, T., Magen, C. & Chanton, J. P. Modeling studies of dissolved organic matter cycling in Santa Barbara Basin (CA, USA) sediments. Geochim. Cosmochim. Acta 195, 100-119 (2016).
  15. Burdige, D. J., Berelson, W. M., Coale, K. H., McManus, J. & Johnson, K. S. Fluxes of dissolved organic carbon from California continental margin sediments. Geochim. Cosmochim. Acta 63, 1507-1515 (1999).
  16. Keil, R. G., Montluçon, D. B., Prahl, F. G. & Hedges, J. I. Sorptive preservation of labile organic matter in marine sediments. Nature 370, 549-552 (1994).
  17. Lalonde, K., Mucci, A., Ouellet, A. & Gélinas, Y. Preservation of organic matter in sediments promoted by iron. Nature 483, 198-200 (2012).
  18. Hemingway, J. D. et al. Mineral protection regulates long-term global preservation of natural organic carbon. Nature 570, 228-231 (2019).
  19. Hedges, J. I. & Keil, R. G. Sedimentary organic matter preservation: an assessment and speculative synthesis. Mar. Chem. 49, 81-115 (1995).
  20. Dittmar, T. et al. Enigmatic persistence of dissolved organic matter in the ocean. Nat. Rev. Earth Environ. 2, 570-583 (2021).
  21. Moore, O. W. et al. Long-term organic carbon preservation enhanced by iron and manganese. Nature 621, 312-317 (2023).
  22. Arrieta, J. M. et al. Dilution limits dissolved organic carbon utilization in the deep ocean. Science 348, 331-333 (2015).
  23. Middelburg, J. J. Escape by dilution. Science 348, 290-290 (2015).
  24. Hansell, D. A. Recalcitrant dissolved organic carbon fractions. Annu. Rev. Mar. Sci. 5, 421-445 (2013).
  25. Sexton, P. F. et al. Eocene global warming events driven by ventilation of oceanic dissolved organic carbon. Nature 471, 349-352 (2011).
  26. Lenton, T. M., Daines, S. J. & Mills, B. J. W. COPSE reloaded: an improved model of biogeochemical cycling over Phanerozoic time. Earth Sci. Rev. 178, 1-28 (2018).
  27. Katsev, S. & Crowe, S. A. Organic carbon burial efficiencies in sediments: the power law of mineralization revisited. Geology 43, 607-610 (2015).
  28. Bradley, J. A., Hülse, D., LaRowe, D. E. & Arndt, S. Transfer efficiency of organic carbon in marine sediments. Nat. Commun. 13, 7297 (2022).
  29. Hedges, J. I. The formation and clay mineral reactions of melanoidins. Geochim. Cosmochim. Acta 42, 69-76 (1978).
  30. Schrumpf, M. et al. Storage and stability of organic carbon in soils as related to depth, occlusion within aggregates, and attachment to minerals. Biogeosciences 10, 1675-1691 (2013).
  31. Mayer, L. M. The inertness of being organic. Mar. Chem. 92, 135-140 (2004).
  32. Henrichs, S. M. & Sugai, S. F. Adsorption of amino acids and glucose by sediments of Resurrection Bay, Alaska, USA: functional group effects. Geochim. Cosmochim. Acta 57, 823-835 (1993).
  33. Henrichs, S. M. Sedimentary organic matter preservation: an assessment and speculative synthesis-a comment. Mar. Chem. 49, 127-136 (1995).
  34. Dale, A. W. et al. A revised global estimate of dissolved iron fluxes from marine sediments. Glob. Biogeochem. Cycles 29, 691-707 (2015).
  35. Babakhani, P., Bridge, J., Doong, R. A. & Phenrat, T. Parameterization and prediction of nanoparticle transport in porous media: a reanalysis using artificial neural network. Water Resour. Res. 53, 4564-4585 (2017).
  36. Canfield, D. E. Factors influencing organic carbon preservation in marine sediments. Chem. Geol. 114, 315-329 (1994).
  37. Boudreau, B. P. Diagenetic Models and Their Implementation Vol. 410 (Springer, 1997).
  38. Berner, R. A. Inclusion of adsorption in the modelling of early diagenesis. Earth Planet. Sci. Lett. 29, 333-340 (1976).
  39. Sohma, A., Sekiguchi, Y. & Nakata, K. Modeling and evaluating the ecosystem of sea-grass beds, shallow waters without sea-grass, and an oxygen-depleted offshore area. J. Mar. Syst. 45, 105-142 (2004).
  40. Mayer, L. M. Surface area control of organic carbon accumulation in continental shelf sediments. Geochim. Cosmochim. Acta 58, 1271-1284 (1994).
  41. Lee, C. Kitty litter for carbon control. Nature 370, 503-504 (1994).
  42. Mayer, L. M. Relationships between mineral surfaces and organic carbon concentrations in soils and sediments. Chem. Geol. 114, 347-363 (1993).
  43. Keil, R. G. & Mayer, L. M. in Treatise on Geochemistry 2nd edn (eds Holland H. D. & Turekian K. K.) 337-359 (Elsevier, 2014).
  44. Rothman, D. H. & Forney, D. C. Physical model for the decay and preservation of marine organic carbon. Science 316, 1325-1328 (2007).
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons. org/licenses/by/4.0/.
(c) The Author(s) 2025

طرق

المنهجية

نظرة عامة على إجراء النمذجة. تم تطوير RTM للنظر في دورة وحفظ DOC في الرواسب البحرية. ثم يتم محاكاة هذا RTM باستخدام الذكاء الاصطناعي، الذي يستخدم كأداة لإجراء تحليل قوي لأهمية العمليات. يتم عرض مخطط سير نشر النموذج في الشكل التكميلي 3. التقنية الذكاء الاصطناعي التي نستخدمها في هذه الدراسة هي ANN، ويتم محاكاة RTM باستخدام ANN من خلال نهج مونت كارلو (الشكل التكميلي 3، المرحلة 1)، حيث يتم تنفيذ RTM عدة مرات (على سبيل المثال، ) باستخدام معلمات إدخال متغيرة عشوائيًا للحصول على مخرجات النموذج (على سبيل المثال، معدلات الحفظ لمختلف أجزاء MOC). ثم تُستخدم هذه المجموعات من بيانات الإدخال والإخراج لتدريب ANN (الشكل التكميلي 3، المرحلة 2) , مما يسمح بتقييم حساسية كل مخرج لمختلف معلمات الإدخال المجمعة في عدد من العمليات.
من بين 68 معلمة إدخال غير معروفة للنموذج، نحصل على النطاقات والتوزيعات الإحصائية لـ 6 من معلمات الإدخال، بما في ذلك عمق المياه , ومعدل تراكم الرواسب , ومسامية سطح الرواسب وتركيزات واجهة الرواسب والمياه لـ POC، والتي يُفترض أن تكون هي نفسها الإجمالي (المراجع 48،49) و (المراجع 48،49) (الجداول التكملية 1 و 8 والأشكال التكملية 1 و 2) من بيانات مصفوفة عالمية. بالنسبة للمعلمات غير المعروفة الأخرى النموذجية، قمنا بتجميع بيانات من عشر دراسات سابقة أجرت نمذجة النقل التفاعلي على بيانات الحقل (ملخصة في الجداول التكملية 1 و 2). تم أيضًا أخذ النطاقات للمعلمات الجديدة إما من الأدبيات أو من ملاءمة نموذجنا لبيانات النمذجة الحقلية من الأدبيات (Burdige et al. ). على الرغم من أننا اختبرنا RTM ضد مجموعات بيانات الحقل واخترنا النطاقات لبعض من المعلمات الجديدة للنموذج من خلال النظر في قيم المعلمات المعايرة (القسم التكميلي 2.2)، فإن مثل هذه الملاءمات للنموذج لمجموعات بيانات الحقل مفيدة ولكنها ليست ضرورية. وذلك لأن RTM، الذي يعتمد على مفاهيم راسخة أو افتراضية، يجسد بالفعل المعرفة المستندة إلى العمليات في النهج، ويسمح التطبيق الإضافي لـ ANN ومونت كارلو باستخدام نطاقات المعلمات بدلاً من القيم المحددة. يتم تقديم وصف أكثر تفصيلاً لإجراء النمذجة الشامل في القسم التكميلي 1.1.
صياغة RTM. يأخذ RTM في الاعتبار جميع تفاعلات الدياجينيس المبكرة الشائعة لمركبات مختلفة بما في ذلك الأنواع المذابة ( , الكربون غير العضوي المذاب (DIC)، , إلى إلى , و IrDOC، حيث يمثل الحرف الفرعي الحد الأقصى لعدد مجموعات DOC ويمثل الحرف الفرعي الحد الأقصى لعدد مجموعات GPS) والأنواع الجزيئية (أكسيد الحديد عالي التفاعل، , أكسيد الحديد متوسط التفاعل، , أكسيد الحديد غير التفاعلي، , و إلى , حيث يمثل الحرف الفرعي يمثل العدد الأقصى لبرك POC) كما هو مدرج في الجدول التكميلي 10. هنا، اعتبرنا سبعة أنواع لـ POC، وأربعة أنواع لـ DOC، ونوعين لـ GPS بالإضافة إلى IrDOC. يتم اختيار عدد الأنواع الكربونية المختلفة بشكل أساسي بناءً على التوافق مع الأدبيات السابقة. ومع الأخذ في الاعتبار جوانب أخرى من النمذجة، بما في ذلك التوافق مع النموذج المفاهيمي، والانتقال السلس لمعدلات الأنواع المختلفة لأغراض الحل العددي وتقليل عدد معلمات النموذج غير المعروفة. يجب ملاحظة أنه، كما هو موضح في القسم التكميلية 1.2.2، فإن اختيار عدد هذه الأنواع، على سبيل المثال، خزانات DOC، بحد ذاتها، لا يؤثر بشكل ملحوظ على مخرجات النموذج.
المعادلات الثلاثة الحاكمة لنموذج RTM للأنواع المذابة، والأنواع الجزيئية، والأنواع الممتصة، على التوالي، هي كما يلي، بينما يتم تقديم التفاصيل الكاملة لتطوير النموذج والتحقق من صحته
في الأقسام التكميلية 1 و 2:
(1) المعادلة الحاكمة للأنواع المذابة:
(2) المعادلة الحاكمة للأنواع الجسيمية:
(3) المعادلة الحاكمة لمرحلة المعادن، MOC، الناتجة عن الكمية الممتصة حركياً من الأنواع المذابة:
أين هو تركيز الأنواع المذابة أو “مياه المسام”، هو تركيز الأنواع الجسيمية ، هو تركيز الأنواع المذابة ممتص حركيًا على معادن الرواسب “الرواسب الصلبة”، هو المسامية، هو الكسر الصلب من الرواسب، والذي يساوي و هي سرعات دفن مياه المسام والأنواع الجسيمية ) ، هو الكثافة الجافة للرواسب ) ، هو معامل الانتشار الظاهر للأنواع المذابة ، هو معامل الري الحيوي ( ) ، هو معامل التخلخل البيولوجي ( ) ، هو عمق الرواسب بالنسبة لنظام الإحداثيات الموجود عند واجهة الرواسب والماء (سم)، و تمثل معدلات التفاعل للأنواع الجزيئية والمذابة والممتصة حركيًا و )، على التوالي، والتي تتغير زمنياً ومكانياً، هو معدل نقل الكتلة بين الأطوار المذابة والممتصة حركياً إلى المعادن (مجموعات MOC) ، و هو ما يُعرف بمعامل التوزيع في تعبير نقل الكتلة الحركي ( ).
تعتبر المرحلة الأولى من التحلل المائي مشابهة لنموذج الانحلال التقليدي من الدرجة الأولى متعدد نقاط التحلل المعروف باسم نموذج متعدد الجوانب. مع سلسلة من برك POC تتحول إلى بركة DOC واحدة، DOC ، بالتوازي:
أين هو ثابت معدل التحلل المائي، الذي تم اعتباره بطريقة مشابهة لثوابت معدل التحلل للمواد العضوية القابلة للذوبان في نموذج الاستمرارية وفقًا للدراسات السابقة. .
تم وصف المرحلة المتسلسلة من التحلل المائي باستخدام تعبير تفاعل من الدرجة الأولى المتتالي. :
أين هو معدل التحويل لـ إلى ، و هو معدل التحويل لـ إلى في .
نفس المعادلة الرياضية تُستخدم لوصف الجيوبوليمرة كما هو موضح في القسم التكميلي 1 مع التفاصيل الأخرى.
حساب PE. يُعرف PE، المعروف أيضًا باسم BE، تقليديًا بـ يتم تعريفه على النحو التالي:
أين يتم اعتبار العمق المعطى هنا كـ 1 م. في الدراسة الحالية، وبفضل الاعتبار الكامل لمصير DOC في نموذجنا، نحن قادرون على تقديم اعتبار أكثر دقة لـ PE يتضمن جزءًا من OC في الطور الصلب الذي خضع للتحلل المائي والامتزاز على المعادن:
معدل الامتصاص هو معدل الامتصاص الديناميكي الصافي لمادة الكربون العضوي الذائب (معدل الامتصاص ناقص معدل الإزالة أو معدل تكوين المادة العضوية الصافية). تم تقديم مزيد من الشروحات حول المعدلات في الأقسام التكميلية 2.4 و3. على الرغم من أن اعتبار آفاق العمق مقابل العمر في نمذجة التحلل المبكر يمكن أن يكون مهمًا للتنبؤات العالمية، كما تم تسليط الضوء عليه مؤخرًا. في الدراسة الحالية، اعتبرنا فقط أفق عمق ثابت حيث أن الهدف هو الحصول على فهم للعمليات التي تتحكم في حفظ الكربون العضوي بدلاً من إجراء توقعات عالمية.
الشبكة العصبية الاصطناعية لتحليل أهمية العمليات. تعتبر الشبكة العصبية الاصطناعية أداة متعددة الاستخدامات وعالمية لمشاكل تقريب الدوال وتتميز بتطبيقها على الأنظمة المعقدة وغير الخطية. الهيكل الشائع الاستخدام للشبكات العصبية الاصطناعية هو تكوين مكون من ثلاث طبقات تشمل طبقات الإدخال والطبقات المخفية وطبقات الإخراج. . يتكون كل من هذه الطبقات من سلسلة من العقد (الخلايا العصبية) حيث يتوافق عددها في طبقات الإدخال والإخراج مع عدد متغيرات الإدخال والإخراج، على التوالي. يجب تحسين عدد الخلايا العصبية في الطبقات المخفية أو الوسطى عند البحث عن أفضل ملاءمة خلال عملية التدريب. المعادلة الرئيسية المستخدمة لمعالجة المعلومات (أو الإشارة) في هيكل الشبكة العصبية الاصطناعية هي معادلة جبرية بسيطة على شكل ، والذي ينطبق على كل خلية عصبية في الطبقة المخفية. ثم يتم جمع المعلومات لجميع العقد؛ وتُستخدم وظائف إضافية تُسمى وظائف النقل (أو وظائف التنشيط) التي تُطبق على المعلومات المدخلة والمخرجة والتي تم تفصيلها في أماكن أخرى. . هنا، يمثل المعلومات (أو الإشارة) المدخلة، يمثل معلومات الإخراج، هو الأوزان و هو التحيزات. الأوزان والتحيزات هي المعلمات الفائقة للشبكة العصبية الاصطناعية، والتي يتم تحديدها بعد ملاءمة الشبكة العصبية للبيانات، ومتى ما تم تحديدها، تشكل شبكة تجريبية يمكن استخدامها للتنبؤات الجديدة. في نطاق الدراسة الحالية، نستخدم الشبكة العصبية فقط لتحليل أهمية العمليات، وليس للتنبؤ. هنا، نستخدم طريقة المشتق الجزئي. لتحليل أهمية العمليات. باختصار، في هذه الطريقة، يتم استخدام مشتقات المعادلات المستخدمة في هيكل الشبكة العصبية الاصطناعية لتمثيل دور كل مدخل من مدخلات الشبكة في التحكم في مخرجات الشبكة؛ على سبيل المثال، بالنسبة للمعادلة الرئيسية المشتق يساوي . بهذه الطريقة، الـ تمثل القيمة لكل خلية عصبية قوة الإشارات التي تمر عبر تلك الخلية العصبية . وهذا يعني أنه في تحليل أهمية العملية، لا تلعب قيم معلمات الإدخال دورًا بارزًا؛ بل إن التغيرات فيها هي المهمة والتي تنعكس في هيكل الشبكة العصبية الاصطناعية. تم اختيار تفاصيل نموذج الشبكة العصبية الاصطناعية المستخدمة هنا بناءً على المرجع 35 وتم وصفها في القسم التكميلية 1.5.
تحقق النموذج. نحن نتحقق من نموذجنا بعدة طرق. نحن نتحقق من المعادلات الحاكمة التي طورناها لنموذج RTM بناءً على نهج تحليلي. في هذا النهج، للحالة التي يُتوقع فيها أن يتصرف الامتصاص التوازني والامتصاص الحركي بشكل مشابه، أي عند معدلات تبادل عالية، نقوم أولاً بتشغيل النموذج بعد إيقاف الامتصاص التوازني ثم نقوم بتشغيل النموذج مرة أخرى بعد إيقاف تعبير الامتصاص الحركي. بعد ذلك، تتم مقارنة مخرجات النموذج لهذين النوعين من المحاكاة. استخدمنا بيانات النمذجة الميدانية الموجودة (بشكل رئيسي من حوض سانتا باربرا، نظرًا للتفاصيل الشاملة)
تتوفر مجموعة البيانات كما هو موضح في الأشكال التكميلية 5-11 والجدول التكميلية 6. لقد قمنا أيضًا بالتحقق من صحة النموذج بناءً على ميزانيات الكتلة. تم التحقق من استخدام الشبكة العصبية الاصطناعية بناءً على قدرتها على وصف البيانات (المقاسة باستخدام معايير جودة الملاءمة الموضحة في القسم التكميلية 2.2) واستخدام عدم اليقين الذي تنتجه في تحليل أهمية العمليات. أخيرًا، تم إجراء التحقق من عملية نمذجة RTM العامة باستخدام ميزانيات الكتلة لمخرجات النموذج المتوسطة على مدار عدة جولات من مونت كارلو. تم ذلك باستخدام مفهوم تدفق الكتلة في النموذج الموضح في الشكل التكميلية 14.
تظهر نتائج مقارنة مخرجات النموذج بين الحالات التي تكون فيها الامتصاص الحركي فعالاً وتلك التي يكون فيها الامتصاص في حالة توازن عند معدل نقل كتلة مرتفع تطابقاً ممتازاً. ; الشكل التوضيحي الإضافي 4) يؤكد نهجنا نحو تطوير وتنفيذ صيغة الامتصاص في المعادلات الحاكمة.
نتائج النموذج الملائم لعدة مجموعات بيانات ميدانية أو نمذجة، بما في ذلك دراسة ميسمان وآخرون. (الشكل التوضيحي التكميلي 5)، كراال وآخرون. (الأشكال التكميلية 6 و 8 والجداول التكميلية 3-5) وبورديج وآخرون. (الأشكال التكميلية 9-11 والجداول التكميلية 6) تظهر تطابقات ممتازة بين نموذجنا ومجموعات بيانات النماذج الميدانية الموجودة لمعظم ملفات التركيز مقابل العمق. الاستثناءات عمومًا هي و الملفات، التي تظهر توافق نموذج أقل بسبب نقص الأنواع الكربونية في نموذجنا. يتم التحقق من التعقيد المضاف لنموذجنا (المزيد من المعلمات غير المعروفة) في ثمانية خطوات مقابل مجموعة بيانات حوض سانتا باربرا. (الجدول التكميلي 6)، مما يظهر أن كل خطوة مبررة من حيث التحسينات في ملاءمة النموذج للبيانات مقابل تكلفة التعقيد، وفقًا لمعايير اختيار النموذج. زيادة من 0.626 في الخطوة 2 إلى 0.843 في الخطوة 7. برديج وآخرون. تمت المراجعة بشكل أعمق ونسب الكربون إلى النيتروجين في نموذجهم وقارنوها مع القياسات الميدانية التي لم تُجرَ هنا.
نموذج الشبكة العصبية الاصطناعية يمكن أن يتناسب مع البيانات في جميع الحالات مع أفضل ملاءمة تنبؤية وفقًا لمعيار كفاءة نموذج ناش-سوتكليف. تتراوح من 0.923 إلى 0.944 (الجدول التكميلي 7 والشكل التكميلي 12). تم تحديد عدم اليقين في تحليل أهمية عملية الشبكة العصبية الاصطناعية على أنه كانت فترات الثقة نسبياً صغيرة (انظر أشرطة الخطأ في الشكل 3). تتراوح هذه الشكوك من إلى ( في المتوسط) للقيم المتوسطة للحالات التي تم التحقيق فيها والم shown في الشكل 3 والشكل التكميلي 13.
تم حساب ميزانيات الكتلة لمقاطع العرض المختلفة للنموذج المفاهيمي المبسط الموضح في الشكل التوضيحي 14 بناءً على النتائج المتوسطة لجميع جولات نموذج مونت كارلو. في المرحلة 1. وفقًا لهذه النتائج، فإن ميزانية الكتلة في المقطع العرضي هو ، في ب-بيس وفي C-C هو ، مما يدل على خطأ في توازن الكتلة بشكل عام ، وهو أقل من خطأ توازن الكتلة المقبول تم النظر في ذلك في عملية النمذجة العامة لدينا. يجب أن نلاحظ أنه، على الرغم من عملية التحقق الواسعة لنموذجنا، في الدراسة الحالية، نستخدم النموذج فقط لتحليل أهمية العمليات والعثور على رؤى حول العمليات الأساسية المسؤولة عن الحفاظ على OC، وليس لإجراء توقعات عالمية، وهو موضوع الدراسة المستقبلية. أخيرًا، استنادًا إلى عدم اليقين المقبول ( فترة الثقة) المتعلقة بمجموع كل تشغيل RTM، الموضح كمنطقة مظللة حول المنحنيات في الشكل 4 والشكل التكميلي 16، وعدم اليقين في تحليل أهمية العملية المستمد من مرحلة ANN الموضحة في الشكل 3، تشير إلى أن نهجنا العام في التغيير العشوائي للمعلمات المدخلة مناسب.
يجب ملاحظة أن هناك حدًا في سعة مواقع الامتصاص، على سبيل المثال، امتصاص طبقة أحادية. عادةً لا ينطبق على الامتصاص الحركي لأن نموذج الامتصاص الحركي في الدراسة الحالية يمثل بشكل رئيسي العمليات التي تقوم بإدخال المواد العضوية الذائبة في المصفوفة المعدنية، مثل الانسداد، والترسيب المشترك، والتجمع، وبالتالي فإن الامتصاص ذو السعة المحدودة الذي تم النظر فيه في الأدبيات غالبًا من خلال فرضية امتصاص السطح الأحادي ليس
ينطبق على إنتاج MOC لدينا. علاوة على ذلك، فإن الامتصاص الحركي أبطأ من الامتصاص في حالة التوازن، المعروف بأنه فوري. وبالتالي، فإن الامتصاص الحركي، الذي يحده تركيزات المياه في المسام التي تتحكم فيها أيضًا التحلل المائي، والتحلل، وما إلى ذلك، من غير المرجح أن يواجه قيدًا ثانيًا من سعة مواقع الامتصاص مقارنةً بالامتصاص الفوري في حالة التوازن، الذي تم تعريف أنواع مختلفة من الإيزوثرم له، مثل الخطية، ولانغموير، وفرويدليتش. إضافة معلمة إضافية لفرض نسبة من OC يتم استيعابها بواسطة مواقع الامتصاص الحركية والتوازنية ستضيف المزيد من المعلمات غير المعروفة وتعتبر غير ضرورية في هذه الحالة.

توفر البيانات

البيانات المرتبطة بالأشكال 2-4 متاحة عبر figshare علىhttps://doi. org/10.6084/m9.figshare. 27273006 (مرجع 68). البيانات المتعلقة بالأشكال التكميلية 13 و 15 و 16 ومجموعات البيانات الرئيسية (مثل تلك التي تم إنشاؤها بواسطة RTM من خلال عملية مونت كارلو (المرحلة 1) والتي تم استخدامها في تحليل أهمية عملية ANN (المرحلة 2)) متاحة عبر figshare علىhttps://doi.org/10.6084/m9.figshare. 27273030 (مرجع 69).

توفر الشيفرة

رموز الكمبيوتر متاحة من المؤلفين عند الطلب.

References

  1. Burwicz, E. B., Rüpke, L. H. & Wallmann, K. Estimation of the global amount of submarine gas hydrates formed via microbial methane formation based on numerical reaction-transport modeling and a novel parameterization of Holocene sedimentation. Geochim. Cosmochim. Acta 75, 4562-4576 (2011).
  2. Restreppo, G. A., Wood, W. T. & Phrampus, B. J. Oceanic sediment accumulation rates predicted via machine learning algorithm: towards sediment characterization on a global scale. Geo-Mar. Lett. 40, 755-763 (2020).
  3. Lee, T. R., Wood, W. T. & Phrampus, B. J. A machine learning (kNN) approach to predicting global seafloor total organic carbon. Glob. Biogeochem. Cycles 33, 37-46 (2019).
  4. WOA18 Data Access (National Centers for Environmental Information, 2018); https://www.nodc.noaa.gov/OC5/woa18/woa18data.html
  5. Bohlen, L., Dale, A. W. & Wallmann, K. Simple transfer functions for calculating benthic fixed nitrogen losses and C:N:P regeneration ratios in global biogeochemical models. Global Biogeochem. Cycles 26, GB3029 (2012).
  6. Burdige, D. J., Komada, T., Magen, C. & Chanton, J. P. Methane dynamics in Santa Barbara Basin (USA) sediments as examined with a reaction-transport model. J. Mar. Res. 74, 277-313 (2016).
  7. Jørgensen, B. B. A comparison of methods for the quantification of bacterial sulfate reduction in coastal marine sediments: I. Measurement with radiotracer techniques. Geomicrobiol. J. 1, 11-27 (1978).
  8. Bradley, J. A. et al. Widespread energy limitation to life in global subseafloor sediments. Sci. Adv. 6, eaba0697 (2020).
  9. Rogalinski, T., Liu, K., Albrecht, T. & Brunner, G. Hydrolysis kinetics of biopolymers in subcritical water. J. Supercrit. Fluids 46, 335-341 (2008).
  10. Leong, L. P. & Wedzicha, B. L. A critical appraisal of the kinetic model for the Maillard browning of glucose with glycine. Food Chem. 68, 21-28 (2000).
  11. Babakhani, P. et al. Comparison of a new mass-concentration, chain-reaction model with the population-balance model for early-and late-stage aggregation of shattered graphene oxide nanoparticles. Colloids Surf. A 582, 123862 (2019).
  12. McCulloch, W. S. & Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5, 115-133 (1943).
  13. Yu, H. et al. Prediction of the particle size distribution parameters in a high shear granulation process using a key parameter definition combined artificial neural network model. Ind. Eng. Chem. Res. 54, 10825-10834 (2015).
  14. Nourani, V. & Sayyah-Fard, M. Sensitivity analysis of the artificial neural network outputs in simulation of the evaporation process at different climatologic regimes. Adv. Eng. Softw. 47, 127-146 (2012).
  15. Gevrey, M., Dimopoulos, I. & Lek, S. Two-way interaction of input variables in the sensitivity analysis of neural network models. Ecol. Modell. 195, 43-50 (2006).
  16. Yerramareddy, S., Lu, S. C. Y. & Arnold, K. F. Developing empirical models from observational data using artificial neural networks. J. Intell. Manuf. 4, 33-41 (1993).
  17. Gevrey, M., Dimopoulos, I. & Lek, S. Review and comparison of methods to study the contribution of variables in artificial neural network models. Ecol. Modell. 160, 249-264 (2003).
  18. Meysman, F. J. R., Middelburg, J. J., Herman, P. M. J. & Heip, C. H. R. Reactive transport in surface sediments. II. Media: an object-oriented problem-solving environment for early diagenesis. Comput. Geosci. 29, 301-318 (2003).
  19. Kraal, P., Slomp, C. P., Reed, D. C., Reichart, G. J. & Poulton, S. W. Sedimentary phosphorus and iron cycling in and below the oxygen minimum zone of the northern Arabian Sea. Biogeosciences 9, 2603-2624 (2012).
  20. Akaike, H. A new look at the statistical model identification. Autom. Control IEEE Trans. 19, 716-723 (1974).
  21. Nash, J. E. & Sutcliffe, J. V. River flow forecasting through conceptual models part I—a discussion of principles. J. Hydrol. 10, 282-290 (1970).
  22. Clark, M. M. Transport Modeling for Environmental Engineers and Scientists (Wiley, 2011).
  23. Langmuir, D. Aqueous Environmental Geochemistry (Prentice Hall, 1997).
  24. Babakhani, P. et al. Babakhani_etal_main_text_figure_source_ data. figshare https://doi.org/10.6084/m9.figshare. 27273006 (2024).
  25. Babakhani, P. et al. Babakhani_etal_supplementary_data. figshare https://doi.org/10.6084/m9.figshare. 27273030 (2024).

شكر وتقدير

نحن نشكر D. Burdige على إرسال بيانات الميدان و B. Mills على المناقشة المفيدة ومراجعة النسخة السابقة من ورقتنا. يتم الاعتراف باستخدام مرافق الحوسبة عالية الأداء (ARC) في جامعة ليدز. نحن نشكر التمويل من المجلس الأوروبي للبحث (ERC) بموجب برنامج الأبحاث والابتكار Horizon 2020 التابع للاتحاد الأوروبي (رقم اتفاقية المنحة 725613 MinOrg). C.L.P. تعبر عن امتنانها لجائزة البحث من الجمعية الملكية Wolfson (WRM/FT/170005) وزمالة Leverhulme للبحث (RF-2023-395\4).

مساهمات المؤلفين

تصور: ب.ب، س.ل.ب. و أ.و.د. تنسيق البيانات: ب.ب، س.ل.ب. و أ.و.د. التحليل الرسمي: ب.ب. التحقيق: ب.ب. المنهجية: ب.ب، أ.و.د. و س.ل.ب. التصور: ب.ب. الحصول على التمويل: س.ل.ب. إدارة المشروع: س.ل.ب. الموارد: س.ل.ب. البرمجيات: ب.ب. و أ.و.د. الإشراف: س.ل.ب، أ.و.د. و ج.و. التحقق: ب.ب، أ.و.د، س.ل.ب. و ك.-ك.س. الكتابة – المسودة الأصلية: ب.ب. الكتابة – المراجعة والتحرير: ب.ب، س.ل.ب، أ.و.د، ج.و، أ.و.م، ك.-ك.س. و ل.س.

المصالح المتنافسة

يعلن المؤلفون عدم وجود مصالح متنافسة.
معلومات مراجعة الأقران تشكر مجلة Nature Geoscience المراجعين المجهولين على مساهمتهم في مراجعة هذا العمل. المحرر الرئيسي: شوجيا جيانغ، بالتعاون مع فريق Nature Geoscience.
معلومات إعادة الطباعة والتصاريح متاحة علىwww.nature.com/reprints.

معلومات إضافية

معلومات إضافية النسخة الإلكترونية تحتوي على مواد إضافية متاحة علىhttps://doi.org/10.1038/s41561-024-01606-y.
يجب توجيه المراسلات والطلبات للحصول على المواد إلى بييمان باباخاني.
  1. مدرسة الأرض والبيئة، جامعة ليدز، ليدز، المملكة المتحدة. قسم الهندسة المدنية والإدارة، جامعة مانشستر، مانشستر، المملكة المتحدة. مركز جيومار هيلمهولتز لأبحاث المحيطات كيل، كيل، ألمانيا. مدرسة الجغرافيا، جامعة ليدز، ليدز، المملكة المتحدة. قسم البيئة والجغرافيا، جامعة يورك، يورك، المملكة المتحدة. مركز أبحاث العلوم البيئية والإيكولوجية، الأكاديمية الصينية للعلوم، بكين، الصين. البريد الإلكتروني:peyman.babakhani@manchester.ac.uk

Journal: Nature Geoscience, Volume: 18, Issue: 1
DOI: https://doi.org/10.1038/s41561-024-01606-y
PMID: https://pubmed.ncbi.nlm.nih.gov/39822308
Publication Date: 2025-01-01

Preservation of organic carbon in marine sediments sustained by sorption and transformation processes

Received: 2 May 2023
Accepted: 29 October 2024
Published online: 3 January 2025
Check for updates

Peyman Babakhani , Andrew W. Dale , Clare Woulds , Oliver W. Moore , Ke-Qing Xiao® , Lisa Curti (1) & Caroline L. Peacock (1)

Controls on organic carbon preservation in marine sediments remain controversial but crucial for understanding past and future climate dynamics. Here we develop a conceptual-mathematical model to determine the key processes for the preservation of organic carbon. The model considers the major processes involved in the breakdown of organic carbon, including dissolved organic carbon hydrolysis, mixing, remineralization, mineral sorption and molecular transformation. This allows redefining of burial efficiency as preservation efficiency, which considers both particulate organic carbon and mineral-phase organic carbon. We show that preservation efficiency is almost three times higher than the conventionally defined burial efficiency and reconciles predictions with global field data. Kinetic sorption and transformation are the dominant controls on organic carbon preservation. We conclude that a synergistic effect between kinetic sorption and molecular transformation (geopolymerization) creates a mineral shuttle in which mineral-phase organic carbon is protected from remineralization in the surface sediment and released at depth. The results explain why transformed organic carbon persists over long timescales and increases with depth.
The preservation of organic carbon (OC) in marine sediments is critical to the global carbon and oxygen cycles and, thus, to Earth’s climate and atmospheric composition , the distribution of energy resources and finding potential ocean-based mitigation strategies for the removal of excess atmospheric carbon dioxide that drives climate change . The controls on carbon preservation, however, are currently unclear . In the surface ocean, primary producers or phytoplankton take up atmospheric carbon dioxide to generate biomass, a fraction of which reaches the sediment as particulate OC (POC) and undergoes a series of complex degradation pathways, which may ultimately lead to either carbon remineralization or burial . However, this paradigm neglects the role of dissolved OC (DOC) in
carbon preservation . DOC, which is produced from the hydrolysis of POC, is a key intermediary in carbon cycling before OC is remineralized to inorganic carbon, for example, carbon dioxide. Present concentrations of DOC in marine sediment pore waters, however, may seem low , leading to a lack of knowledge on its role in OC preservation and cycling. Nevertheless, experimental investigations and field measurements suggest that DOC may accumulate over time as a result of its sorption to minerals forming mineral-phase OC (MOC) and/or its molecular transformation within sediments known as geopolymerization , or its dilution in the water column after diffusing out from sediments , and may thus substantially impact the carbon cycle on Earth .
Fig. 1| Conceptual model for DOC cycling in sediments. The proposed conceptual model incorporates mechanisms of geopolymerization, equilibrium adsorption and kinetic sorption and a modified concept of hydrolysis that follows DOC cycling in the water column . Model schematic nomenclature includes POC, GPS, lrDOC, various mineral-sorbed DOC ((semi)labile DOC-MOC, GPS-MOC and IrDOC-MOC), DIC and MW. All DOC, GPS and IrDOC pools can interact with minerals through equilibrium adsorption and kinetic sorption. In general, POC pools that originate from the water column can be hydrolysed
at any depth in the sediment or remain unhydrolysed. Their transport in the sediment is similar to the sediment solid minerals. MOC pools are transported similarly to sediment solid minerals and POC, but they originate from the net sorption of DOC, GPS and IrDOC to minerals and are further assumed to be unreactive unless the carbon is desorbed from minerals. Part of the POC, which is not hydrolysed at a given depth, and part of the MOC, which is not desorbed at that depth, are considered to be permanently buried.
So far, the contributions of these processes to OC preservation and, thus, carbon cycling have received relatively little attention and are poorly known. Moreover, the conventional concept of OC burial efficiency (BE) in sediments-an indicator of the potential to preserve carbon and quantify global budgets of carbon in modern and ancient sediments -is conceptually incorrect if preservation of OC via DOC sorption and transformation is considerable and ignored. We redefine BE as preservation efficiency (PE), which includes both conventionally considered POC burial and MOC preservation.
Here, we develop a mechanistic reaction-transport model (RTM) that considers the key processes of OC preservation in marine sediments via DOC cycling. After extensive validation, the model is used alongside Monte Carlo and artificial neural network (ANN) analyses to provide global insights into the role of the processes controlling carbon preservation in marine sediments and show where and how preservation occurs.

Conceptualizing carbon cycling and preservation in sediments

Our conceptual model for carbon cycling and preservation in sediments begins with the hydrolysis of several discrete POC fractions ( and so on) to a single DOC pool ( ) of high molecular weight (MW) (Fig. 1). Continuing sequential hydrolysis of produces DOC with increasingly lower MW ( and so on) and higher reactivity (remineralization rate), analogous to the recent paradigm for DOC cycling in the water column . The sequential hydrolysis approach is markedly different from the previous hypothesis (Fig. 1), where each discrete POC fraction produces a corresponding DOC pool with similar reactivity to its parent . To represent the production of least-reactive DOC (lrDOC), we include the direct accumulation of freshly hydrolysed but intrinsically undegradable DOC
via a direct transfer of to IrDOC (Fig. 1). We further consider the geopolymerization of low-MW DOC ( ) to higher-MW molecules herein referred to as geopolymerized substances (GPS-DOC or simply GPS) with increasingly lower reactivity (GPS and so on), which eventually contribute to the IrDOC pool (Fig. 1). Our IrDOC pool, thus, comprises both intrinsically undegradable DOC and aged molecularly transformed GPS. Reactivities of DOC pools are selected on the basis of their lifetimes in the water column and are categorized as labile and semi-labile ( and so on, grouped as (semi)labile-DOC, with a lifetime of to years), mid-reactive ( and so on, with a lifetime of years) and least-reactive (lrDOC, with a lifetime of years) . To represent the sorption of DOC to minerals, we include a two-site description of ‘equilibrium adsorption and ‘kinetic sorption/desorption’. Kinetic sorption/ desorption, which is a general description of sorption/desorption processes that are not in equilibrium, mostly aims to represent occlusion within minerals, co-precipitation and/or aggregation with minerals, and reverse processes that result in the desorption of carbon from the mineral matrix . The net result of the kinetic sorption-desorption leads to the formation of pools, including (semi)labile DOC-MOC, GPS-MOC and IrDOC-MOC (Fig. 1). These MOC pools are then transported with minerals similar to POC pools that are mixed with minerals, although MOC is different from POC by origin, that is, POC originates from the water column whereas MOC is formed in the sediments via kinetic sorption of DOC to minerals.
We incorporate our conceptual model (Fig. 1) into a vertically resolved RTM for marine sediments that couples transport processes (for example, sediment burial velocity before compaction, and bioturbation mixing) and biogeochemical reactions (for example, DOC remineralization). We execute the validated RTM in a Monte Carlo approach ( simulations) using input parameters that are varied randomly
Fig. 2 | Comparing model-generated PE with literature data. a,b, Data generated for 1,450 model runs in a Monte Carlo approach (transparent black dots) for the conventional approach to calculate PE of POC that considers only POC (a) and for the newly defined PE that considers both POC and MOC (b). These are compared with field data from previous studies . The spread of model data is derived from a normal distribution of the net sediment accumulation rate data observed in the global grid datasets (Supplementary Figs. 1 and 2). The envelope line (dashed line) represents the general boundaries of the spread of data identified in previous studies . Low stands for low bottom water oxygen concentration.
within globally relevant ranges (Supplementary Table 1) based on statistical distributions taken from six field-modelling datasets (Supplementary Figs. 1 and 2) and ten previous studies (Supplementary Table 2) to examine the broader role of different OC preservation processes (Supplementary Fig. 3, stage 1).
We then use the RTM-generated dataset to train an and determine the importance of processes that control OC preservation (Supplementary Fig. 3, stage 2). Our model allows both MOC formation in the solid-phase OC and POC burial at depth to be included in the definition of PE in contrast to the conventional approach where only POC burial is considered in the model . The equations for the conventional and the newly defined PE (equations (6) and (7)) and other details of our model development, testing and execution are given in Supplementary Sections 1 and 2. We use PE to evaluate the overall model performance against global data. We further validate our mathematical model and other aspects of our model as summarized in Methods and fully described in Supplementary Section2, Supplementary Figs. 4-12 and Supplementary Tables 3-7.

Model evaluation

The incorporation of MOC into models of PE is compared with the classical approach that considers only POC in Fig. 2 (refs. 12,36). The PE of POC alone cannot explain the observed trend and envelope of PE values versus sediment accumulation rate (Fig. 2a, dashed lines) . Only when the preservation of MOC is considered along with POC does the vast majority of model output data fall inside the envelope (Fig. 2b).
Many different factors have been proposed to explain OC preservation in marine sediments . The ability of our model to predict available global PE data indicates that consideration of DOC cycling and related processes, especially sorption and geopolymerization, is critical to predicting PE. This is remarkable because no model parameters were tuned in these simulations (Fig. 2). Our approach of combining RTM, ANN and Monte Carlo allows the process-based understanding of
Fig. 3 | The relative importance of different processes. a,b, The relative importance (%) of six processes to PE when MOC is considered in addition to POC (a) and to preservation rates for MOC (b). The six processes are DOC hydrolysis, DOC remineralization, mixing, equilibrium adsorption, kinetic sorption and geopolymerization. The newly defined PE is given by equation (7). The preservation rates for MOC are shown as the rate of MOC formation, which is the sum of net kinetic sorption rates integrated at the depth of for DOC, GPS and IrDOC. The importance of each process is obtained on the basis of the maximum sensitivity of the parameters categorized for each process. The categorization is presented in Supplementary Table 9. Each bar is the mean of 1,000 executions of the process importance analysis, and the error bars represent the confidence interval. Details of sampling in the Monte Carlo method for process importance analysis are provided in Supplementary Sections 1.3-1.5 and in previous studies .
carbon dynamics to be translated into global understanding without the necessity for model fitting to specific sites that may introduce uncertainties related to site-specific conditions.
Our model definition of POC hydrolysis is similar to that considered as POC remineralization elsewhere , and thus, our estimation for PE of POC is similar to the conventional approach , which also underestimates field PE with estimated global values that are less than (ref. 28). Our model, however, additionally tracks DOC hydrolysed from POC and its sorption to minerals, which eventually leads to a much better prediction of PE field data compared with the conventional approach. The mean values for all Monte Carlo model runs ( ) are and for PE of POC and POC + MOC, respectively.

The role of different processes in carbon preservation

We quantify the importance of six model processes in controlling key indicators of carbon preservation, including PE and MOC formation rates (or DOC sorption rates). Three processes are traditionally understood to be important for carbon preservation , namely, DOC hydrolysis to increasingly lower-MW DOC, DOC remineralization and sediment mixing by fauna. The importance of the other three processes is disputed or poorly understood, namely, kinetic sorption, equilibrium adsorption and geopolymerization (Supplementary Tables 8 and 9).
The results reveal that kinetic sorption is the most important process for PE with a relative importance of among the six processes, followed by mixing ( ), remineralization ( ), geopolymerization ( ), DOC hydrolysis ( ) and equilibrium adsorption (Fig. 3a). In general, processes that control POC burial flux and carbon turnover at depth, such as mixing and remineralization, are more important for PE than geopolymerization and DOC hydrolysis. We also investigate the most important processes for the preservation rate of DOC-MOC species (Supplementary Fig. 13) that are averaged in Fig. 3b. These show that geopolymerization relative to all six processes) is the most important process for DOC-MOC preservation, followed by kinetic sorption , DOC hydrolysis ( ), remineralization ( ), mixing ( ) and equilibrium adsorption (Fig. 3b). The highest importance of the geopolymerization process in controlling DOC-MOC preservation adds weight to the existence of a synergic effect of geopolymerization with DOC sorption, in which geopolymerization renders DOC less reactive and sorption provides extra protection from microbial remineralization .
Fig. 4 | Depth profiles obtained from Monte Carlo modelling. a, The ratio of the kinetic sorption rates averaged for 1,450 runs of the Monte Carlo modelling to the desorption rates also averaged for 1,450 model runs at different depths. b, The percentage contribution of the final GPS pool to the total IrDOC production (Fig.1) at different depths. These contributions are averaged for 1,450 runs of the Monte Carlo modelling. The mathematical equations used to produce these plots are presented in Supplementary Section 3. c, The PE (%) for only POC and for both POC and MOC together, demonstrating that MOC increases
calculated PE by a factor of 2.7 at 1 m depth compared with the conventional approach considering only POC. d, POC fluxes and MOC preservation rate. MOC content exceeds POC at a depth of and still continues to rise below this depth. All values have been averaged for 1,450 Monte Carlo model runs. The shaded areas of the curves represent confidence intervals obtained from Monte Carlo model runs. The light-yellow-shaded region represents the mixed layer depth (top 10 cm ).
Previous considerations of DOC sorption in marine sediments have been limited to a simple equilibrium surface adsorption process expressed using a partition coefficient ( ), whether in a modelling framework or in field and experimental investigations . Others have argued that equilibrium adsorption cannot be responsible for the preservation of intrinsically labile organic compounds and some type of irreversible sorption and/or change in OC reactivity might be responsible . Proposed patterns, such as monolayer adsorption of DOC onto mineral surfaces , still rely on the assumption of mere surface-mediated adsorption and have been criticized for not being able to describe the observed preservation in various ocean settings . Our consideration of several concurrent processes shows that, while carbon preservation indicators are still not insensitive to the equilibrium adsorption process, their control by this process is the least among the six processes considered (Fig. 3a,b). While equilibrium adsorption can reduce the DOC concentration that is bioavailable in pore fluids, thereby retarding DOC degradation , DOC at equilibrium sites can be instantaneously desorbed if the DOC concentrations in the pore water decrease (for example, as a result of microbial degradation or kinetic sorption) . Kinetically controlled mineral DOC protection mechanisms such as co-precipitation, occlusion and aggregation, however, can protect DOC over much longer timescales . Our analysis reveals that the kinetic sorption process is the most important factor in controlling PE (Fig. 3a) and the second most important in controlling averaged MOC preservation rates (Fig. 3b).
Recently, it has been shown that geopolymerization in the form of a Maillard-type condensation reaction through catalysis by dissolved or particulate iron and manganese is a crucial process for benthic DOC
cycling . Yet, quantification of the geopolymerization process and its importance compared with other processes of carbon preservation has so far remained difficult . Our analysis shows that geopolymerization is equally, or more, important for PE compared with DOC hydrolysis (Fig. 3a). Furthermore, on average, geopolymerization is the most important factor for the preservation rate of DOC species among all six processes considered (Fig. 3b).

How sorption and geopolymerization control OC preservation

We use sediment depth profiles (Fig. 4 and Supplementary Section 3) obtained from the Monte Carlo simulations to provide a broader insight into how different processes control OC preservation. We observe that the mixed layer acts as a shuttle for different DOC pools by protecting them from exposure to oxygen, nutrients and microbial enzymes and, consequently, limiting their rapid remineralization in the mixed layer and delivering them to greater depths (Fig. 4a). We also investigate the pathways of IrDOC production, which show that geopolymerization contributes to lrDOC formation (Fig. 4b). These are fully discussed in Supplementary Section 4.
We further observe that PE can vary with the sediment depth horizon or age horizon . The modelled profiles of PE versus depth in sediment considering only POC as well as POC plus MOC (Fig. 4c) agree with ref. 28 that there is a change in PE with depth. However, it appears that this change becomes less discernible below 75 cm . More importantly, MOC formation grows substantially within the top 10 cm and continues to increase below this depth (Fig. 4d) to the point where MOC exceeds the POC content below 50 cm (further discussed in Supplementary Section 4).
In conclusion, our results reveal that, aside from conventionally known processes (hydrolysis, mixing and remineralization), kinetic sorption and geopolymerization probably play a major role in OC preservation. Kinetic sorption creates a mineral shuttle that effectively removes DOC from the active surface layer and releases it at depth, while geopolymerization as an age-dependent process renders OC less reactive. Kinetic sorption leads to the formation of a mineral-associated fraction that becomes larger than the POC pool below , even though the globally averaged POC profile (Fig. 4d, green curve) and PE of POC remain similar to those predicted by the conventional paradigm. Thus, the preservation of OC in marine sediments, hitherto conceived to be due to the burial of POC, is a result of several DOC-related processes, including hydrolysis, geopolymerization and net sorption of DOC to minerals. Consideration of these processes in a single model reconciles the otherwise mismatch of modelled PE with field data and sheds light on the concurrent and complex roles of different processes. We suggest that our conceptualization should be considered in models of carbon cycling and may lead to better quantification and understanding of global carbon budgets, present and past climate dynamics and long-term implications for potential ocean-based carbon dioxide removal technologies . We acknowledge that, although we have followed the best modelling practice and our model presents advancement in several facets, other models may still be developed in the future that better describe the carbon cycle in marine sediments.

Online content

Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41561-024-01606-y.

References

  1. Alcott, L. J., Mills, B. J. W. & Poulton, S. W. Stepwise Earth oxygenation is an inherent property of global biogeochemical cycling. Science 366, 1333-1337 (2019).
  2. Berner, R. A. Biogeochemical cycles of carbon and sulfur and their effect on atmospheric oxygen over Phanerozoic time. Glob. Planet. Change 1, 97-122 (1989).
  3. Amon, R. M. W. & Benner, R. Rapid cycling of high-molecular-weight dissolved organic matter in the ocean. Nature 369, 549-552 (1994).
  4. Li, Z., Zhang, Y. G., Torres, M. & Mills, B. J. W. Neogene burial of organic carbon in the global ocean. Nature 613, 90-95 (2023).
  5. Abelson, P. H. Organic matter in the Earth’s crust. Annu. Rev. Earth Planet. Sci. 6, 325-351 (1978).
  6. Hatcher, P. G., Spiker, E. C., Szeverenyi, N. M. & Maciel, G. E. Selective preservation and origin of petroleum-forming aquatic kerogen. Nature 305, 498-501 (1983).
  7. Smetacek, V. et al. Deep carbon export from a Southern Ocean iron-fertilized diatom bloom. Nature 487, 313-319 (2012).
  8. Babakhani, P. et al. Potential use of engineered nanoparticles in ocean fertilization for large-scale atmospheric carbon dioxide removal. Nat. Nanotechnol. 17, 1342-1351 (2022).
  9. Arndt, S. et al. Quantifying the degradation of organic matter in marine sediments: a review and synthesis. Earth Sci. Rev. 123, 53-86 (2013).
  10. Kleber, M. et al. Dynamic interactions at the mineral-organic matter interface. Nat. Rev. Earth Environ. 2, 402-421 (2021).
  11. Burd, A. B. et al. Assessing the apparent imbalance between geochemical and biochemical indicators of meso-and bathypelagic biological activity: what the @$#! is wrong with present calculations of carbon budgets? Deep Sea Res. Part II 57, 1557-1571 (2010).
  12. Burdige, D. J. Preservation of organic matter in marine sediments: controls, mechanisms, and an imbalance in sediment organic carbon budgets? Chem. Rev. 107, 467-485 (2007).
  13. Burdige, D. J. & Komada, T. in Biogeochemistry of Marine Dissolved Organic Matter (eds Hansell, D. A. & Carlson, C. A.) 535-577 (Elsevier, 2015).
  14. Burdige, D. J., Komada, T., Magen, C. & Chanton, J. P. Modeling studies of dissolved organic matter cycling in Santa Barbara Basin (CA, USA) sediments. Geochim. Cosmochim. Acta 195, 100-119 (2016).
  15. Burdige, D. J., Berelson, W. M., Coale, K. H., McManus, J. & Johnson, K. S. Fluxes of dissolved organic carbon from California continental margin sediments. Geochim. Cosmochim. Acta 63, 1507-1515 (1999).
  16. Keil, R. G., Montluçon, D. B., Prahl, F. G. & Hedges, J. I. Sorptive preservation of labile organic matter in marine sediments. Nature 370, 549-552 (1994).
  17. Lalonde, K., Mucci, A., Ouellet, A. & Gélinas, Y. Preservation of organic matter in sediments promoted by iron. Nature 483, 198-200 (2012).
  18. Hemingway, J. D. et al. Mineral protection regulates long-term global preservation of natural organic carbon. Nature 570, 228-231 (2019).
  19. Hedges, J. I. & Keil, R. G. Sedimentary organic matter preservation: an assessment and speculative synthesis. Mar. Chem. 49, 81-115 (1995).
  20. Dittmar, T. et al. Enigmatic persistence of dissolved organic matter in the ocean. Nat. Rev. Earth Environ. 2, 570-583 (2021).
  21. Moore, O. W. et al. Long-term organic carbon preservation enhanced by iron and manganese. Nature 621, 312-317 (2023).
  22. Arrieta, J. M. et al. Dilution limits dissolved organic carbon utilization in the deep ocean. Science 348, 331-333 (2015).
  23. Middelburg, J. J. Escape by dilution. Science 348, 290-290 (2015).
  24. Hansell, D. A. Recalcitrant dissolved organic carbon fractions. Annu. Rev. Mar. Sci. 5, 421-445 (2013).
  25. Sexton, P. F. et al. Eocene global warming events driven by ventilation of oceanic dissolved organic carbon. Nature 471, 349-352 (2011).
  26. Lenton, T. M., Daines, S. J. & Mills, B. J. W. COPSE reloaded: an improved model of biogeochemical cycling over Phanerozoic time. Earth Sci. Rev. 178, 1-28 (2018).
  27. Katsev, S. & Crowe, S. A. Organic carbon burial efficiencies in sediments: the power law of mineralization revisited. Geology 43, 607-610 (2015).
  28. Bradley, J. A., Hülse, D., LaRowe, D. E. & Arndt, S. Transfer efficiency of organic carbon in marine sediments. Nat. Commun. 13, 7297 (2022).
  29. Hedges, J. I. The formation and clay mineral reactions of melanoidins. Geochim. Cosmochim. Acta 42, 69-76 (1978).
  30. Schrumpf, M. et al. Storage and stability of organic carbon in soils as related to depth, occlusion within aggregates, and attachment to minerals. Biogeosciences 10, 1675-1691 (2013).
  31. Mayer, L. M. The inertness of being organic. Mar. Chem. 92, 135-140 (2004).
  32. Henrichs, S. M. & Sugai, S. F. Adsorption of amino acids and glucose by sediments of Resurrection Bay, Alaska, USA: functional group effects. Geochim. Cosmochim. Acta 57, 823-835 (1993).
  33. Henrichs, S. M. Sedimentary organic matter preservation: an assessment and speculative synthesis-a comment. Mar. Chem. 49, 127-136 (1995).
  34. Dale, A. W. et al. A revised global estimate of dissolved iron fluxes from marine sediments. Glob. Biogeochem. Cycles 29, 691-707 (2015).
  35. Babakhani, P., Bridge, J., Doong, R. A. & Phenrat, T. Parameterization and prediction of nanoparticle transport in porous media: a reanalysis using artificial neural network. Water Resour. Res. 53, 4564-4585 (2017).
  36. Canfield, D. E. Factors influencing organic carbon preservation in marine sediments. Chem. Geol. 114, 315-329 (1994).
  37. Boudreau, B. P. Diagenetic Models and Their Implementation Vol. 410 (Springer, 1997).
  38. Berner, R. A. Inclusion of adsorption in the modelling of early diagenesis. Earth Planet. Sci. Lett. 29, 333-340 (1976).
  39. Sohma, A., Sekiguchi, Y. & Nakata, K. Modeling and evaluating the ecosystem of sea-grass beds, shallow waters without sea-grass, and an oxygen-depleted offshore area. J. Mar. Syst. 45, 105-142 (2004).
  40. Mayer, L. M. Surface area control of organic carbon accumulation in continental shelf sediments. Geochim. Cosmochim. Acta 58, 1271-1284 (1994).
  41. Lee, C. Kitty litter for carbon control. Nature 370, 503-504 (1994).
  42. Mayer, L. M. Relationships between mineral surfaces and organic carbon concentrations in soils and sediments. Chem. Geol. 114, 347-363 (1993).
  43. Keil, R. G. & Mayer, L. M. in Treatise on Geochemistry 2nd edn (eds Holland H. D. & Turekian K. K.) 337-359 (Elsevier, 2014).
  44. Rothman, D. H. & Forney, D. C. Physical model for the decay and preservation of marine organic carbon. Science 316, 1325-1328 (2007).
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons. org/licenses/by/4.0/.
(c) The Author(s) 2025

Methods

Methodology

Overview of the modelling procedure. A RTM is developed to consider the cycling and preservation of DOC in marine sediment. This RTM is then emulated with artificial intelligence, which is used as a tool for conducting a robust process importance analysis. The flowchart of the model deployment is shown in Supplementary Fig. 3. The artificial intelligence technique we use in this study is an ANN, and the RTM is emulated with ANN through a Monte Carlo approach (Supplementary Fig. 3, stage 1), whereby the RTM is executed multiple times (for example, ) using randomly varied input parameters to obtain the model outputs (for example, the preservation rates for different MOC fractions). These inputoutput datasets are then used to train an ANN (Supplementary Fig. 3, stage 2) , which allows assessment of the sensitivities of each output to different input parameters grouped into a number of processes.
Among the 68 unknown input parameters of the model, we obtain the ranges and statistical distributions for 6 of the input parameters, including water depth , sediment accumulation rate , sediment surface porosity and sediment-water interface concentrations of POC, which are assumed to be the same as total (refs. 48,49 ) and (refs. 48,49) (Supplementary Tables 1 and 8 and Supplementary Figs. 1 and 2) from globally gridded data. For other typical unknown parameters, we compiled data from ten previous studies that had conducted reactive transport modelling on field data (summarized in Supplementary Tables 1 and 2). The ranges for new parameters were also taken either from the literature or from fitting our model to the field-modelling data from the literature (Burdige et al. ). Although we have tested the RTM against field datasets and have selected the ranges for some of the new model parameters by considering the calibrated parameter values (Supplementary Section 2.2), such model fittings to field datasets are useful but not necessary. This is because the RTM, which is based on established or hypothetical concepts, already embodies process-based knowledge in the approach, and the additional application of ANN and Monte Carlo allows the use of parameter ranges instead of set values. A more detailed description of the overall modelling procedure is provided in Supplementary Section 1.1.
Formulation of the RTM. The RTM considers all common early diagenesis reactions for different compounds including dissolved species ( , dissolved inorganic carbon (DIC), , to to , and IrDOC, where subscript represents the maximum number of DOC pools and subscript represents the maximum number of GPS pools) and particulate species (highly reactive iron oxide, , moderately reactive iron oxide, , non-reactive iron oxide, , and to , where subscript represents the maximum number of POC pools) as listed in Supplementary Table 10. Here, we considered seven species for POC, four species for DOC and two species for GPS in addition to IrDOC. The number of different carbon species are selected mainly on the basis of consistency with previous literature and with consideration of other aspects of modelling, including alignment with the conceptual model, smooth transition of rates across different species for numerical solution considerations and minimizing the number of unknown model parameters. It should be noted that, as demonstrated in the Supplementary Section 1.2.2, the selection of the number of these species, for example, DOC pools, per se, does not affect the model outputs noticeably.
The three governing equations of RTM for dissolved species, particulate species and sorbed species, respectively, are as follows, while the full details of the model development and validation are provided
in Supplementary Sections 1 and 2:
(1) The governing equation for dissolved species:
(2) The governing equation for particulate species:
(3) The governing equation for mineral phase, MOC , resulting from the kinetically sorbed fraction of dissolved species:
where is the concentration of dissolved species or of pore water), is the concentration of particulate species , is the concentration of dissolved species kinetically sorbed to sediment minerals ( of solid sediments), is porosity, is the solid fraction of sediments, which is equal to and are the burial velocities of pore water and particulate species ( ), is the dry density of sediments ( ), is the apparent diffusion coefficient of dissolved species , is the bio-irrigation coefficient ( ), is the bioturbation coefficient ( ), is the sediment depth with respect to the coordinate system located at the sediment-water interface (cm), and stand for reaction rates of particulate, dissolved and kinetically sorbed species ( and ), respectively, which are temporally and spatially variable, is the mass transfer rate between the dissolved and kinetically sorbed phases to minerals (MOC pools) , and is the so-called distribution coefficient in the kinetic mass transfer expression ( ).
The first stage of the hydrolysis is considered similar to the conventional first-order multi-POC degradation model known as the multi-G model with a series of POC pools converting to a single DOC pool, DOC , in parallel:
where is the hydrolysis rate constant, which was considered in a similar way to the degradation rate constants of POC in the continuum model following previous studies .
The sequential stage of the hydrolysis has been described using a consecutive first-order reaction expression :
where is the conversion rate of to , and is the conversion rate of to in .
The same mathematical formula is used to describe geopolymerization as provided in Supplementary Section 1 along with the other details.
Calculation of PE. PE, elsewhere known as BE, conventionally considered for is defined as follows:
where is a given depth herein considered as 1 m . In the present study, owing to the full consideration of the fate of DOC in our model, we are able to present a more accurate consideration of PE that includes the fraction of solid phase OC that has undergone hydrolysis and sorption to minerals:
The sorption rate is the net DOC kinetic sorption rate (sorption rate minus desorption rate or the net MOC formation rate). Further explanations about the rates are provided in Supplementary Sections 2.4 and 3. Although the consideration of depth-versus-age horizons in early digenesis modelling can be important for global predictions, as was recently highlighted , in the present study, we considered only a constant depth horizon as the aim is to obtain insight into the processes that control OC preservation rather than making global predictions.
ANN for process importance analysis. The ANN is a versatile and universal tool for function approximation problems and is notable for its application to complex, nonlinear systems . The commonly used ANN structure is a three-layer configuration comprising input, hidden and output layers . Each of these layers is composed of a series of nodes (neurons) with their numbers in the input and output layers corresponding to the number of input and output variables, respectively. The number of neurons on the hidden or middle layers should be optimized when finding the best fit during the training process . The main equation used for processing the information (or signal) in the structure of the ANN is a simple algebraic equation in the form of , which applies to each neuron in the hidden layer. The information is then summed up for all nodes; additional functions called transfer (or activation) functions that are exerted on the input and output information that are detailed elsewhere . Here, stands for the input information (or signal), stands for output information, is weights and is biases. Weights and biases are the hyperparameters of the ANN, which are determined after fitting ANN to data, and once they are determined, they form an empirical network that can be used for new predictions. In the scope of the present study, we use ANN only for process importance analysis, not for prediction. Here, we use the partial derivative method for process importance analysis. In brief, in this method, the derivatives of the equations used in the structure of ANN are used to represent the role of each ANN input in controlling the ANN output; for example, for the main equation , the derivative is equal to . In this way, the value for each neuron represents the strength of the signals passing through that neuron . This implies that in the process importance analysis, the input parameter values do not play a marked role; rather, it is their variations that are important and reflected in the structure of the ANN. Details of the ANN model used here have been selected following ref. 35 and are described in Supplementary Section 1.5.
Model validation. We validate our model in a number of ways. We validate our developed governing equations of the RTM on the basis of an analytical approach. In this approach, for the condition where equilibrium adsorption and kinetic sorption are expected to behave similarly, that is, at high exchange rates, we first run the model after turning off equilibrium adsorption and then run the model again turning off the kinetic sorption expression. Then, the model outputs for these two types of simulation are compared. We used existing field-modelling data (principally from Santa Barbara Basin, given the comprehensive
dataset available) as shown in Supplementary Figs. 5-11 and Supplementary Table 6. We also validated the model on the basis of mass budgets. The use of the ANN is validated on the basis of its ability to describe the data (measured using goodness-of-fit criteria described in Supplementary Section 2.2) and using the uncertainties it yields in the process importance analysis. Finally, validation of the overall RTM modelling process was carried out using mass budgets of the averaged model outputs over the multiple runs of the Monte Carlo. This was done using the concept of mass flow in the model illustrated in Supplementary Fig. 14.
The results of the model output comparison between the cases when kinetic sorption is operative and when the equilibrium adsorption is operative at a high mass transfer rate show an excellent match ( ; Supplementary Fig. 4) verifying our approach towards development and implementation of sorption formulation in the governing equations.
The results of the model fit to several field or modelling datasets, including Meysman et al. (Supplementary Fig. 5), Kraal et al. (Supplementary Figs. 6 and 8 and Supplementary Tables 3-5) and Burdige et al. (Supplementary Figs. 9-11 and Supplementary Tables 6) show excellent matches between our model and existing field-model datasets for most of the concentration-versus-depth profiles. The exceptions are generally and profiles, which show poorer model fit due to the lack of carbonate species in our model. The added complexity of our model (more unknown parameters) is validated in eight steps against the Santa Barbara Basin dataset (Supplementary Table 6), showing that each step is justifiable in terms of improvements in model fits to the data for the cost of complexity, according to model selection criteria increasing from 0.626 in step 2 to 0.843 in step 7. Burdige et al. further considered and carbon-to-nitrogen ratios in their model and matched them with field measurements that are not conducted here.
The ANN model could fit the data in all cases with the best predictive fit Nash-Sutcliffe model efficiency criterion ranging from 0.923 to 0.944 (Supplementary Table 7 and Supplementary Fig. 12). The uncertainties in the ANN process importance analysis determined as a confidence interval were relatively minor (see error bars in Fig. 3). These uncertainties range from to ( on average) of the mean values for the cases investigated and shown in Fig. 3 and Supplementary Fig. 13.
The mass budgets for different cross-sections of the simplified conceptual model shown in Supplementary Fig. 14 were calculated on the basis of averaged results of all Monte Carlo model runs at stage 1. According to these results, the mass budget in cross-section is , in B-Bis and in C-C is , demonstrating an overall mass balance error of , which is less than the acceptable mass balance error of considered in our general modelling process. It should be noted that, despite our extensive model validation process, in the present study, we use the model only for process importance analysis and finding insight into the underlying processes responsible for OC preservation, not for making global predictions, which is the subject of future study. Finally, based on acceptable uncertainties ( confidence interval) related to the sum of all RTM runs, shown as the shaded area around the curves in Fig. 4 and Supplementary Fig. 16, and the uncertainties of process importance analysis obtained from the ANN stage shown in Fig. 3, our general approach of random variation of input parameters is appropriate.
It should be noted that limitation in the capacity of sorption sites, for example, monolayer sorption , typically does not apply to kinetic sorption because the kinetic sorption model in the present study mainly represents the processes that internalize DOC into the mineral matrix, such as occlusion, co-precipitation and aggregation, and thus, limited-capacity sorption considered in the literature mostly through the monolayer surface adsorption hypothesis is not
applicable to our MOC production. Furthermore, kinetic sorption is slower than equilibrium adsorption, which is known to be instantaneous. Thus, kinetic sorption, which is limited by pore water concentrations that are also controlled by hydrolysis, degradation and so on, is less likely to face a second limitation by the capacity of sorption sites compared with instantaneous equilibrium adsorption for which different types of isotherm, such as linear, Langmuir and Freundlich, have been defined . Adding an additional parameter to force a proportion of the OC to be taken up by the kinetic and equilibrium sorption sites would add more unknown parameters and is deemed unnecessary in this case.

Data availability

Data associated with Figs. 2-4 are available via figshare at https://doi. org/10.6084/m9.figshare. 27273006 (ref. 68). Data related to Supplementary Figs.13,15 and 16 and the main datasets (such as those generated by RTM through the Monte Carlo process (stage1) and used in the ANN process importance analysis (stage 2)) are available via figshare at https://doi.org/10.6084/m9.figshare. 27273030 (ref. 69).

Code availability

Computer codes are available from the authors upon request.

References

  1. Burwicz, E. B., Rüpke, L. H. & Wallmann, K. Estimation of the global amount of submarine gas hydrates formed via microbial methane formation based on numerical reaction-transport modeling and a novel parameterization of Holocene sedimentation. Geochim. Cosmochim. Acta 75, 4562-4576 (2011).
  2. Restreppo, G. A., Wood, W. T. & Phrampus, B. J. Oceanic sediment accumulation rates predicted via machine learning algorithm: towards sediment characterization on a global scale. Geo-Mar. Lett. 40, 755-763 (2020).
  3. Lee, T. R., Wood, W. T. & Phrampus, B. J. A machine learning (kNN) approach to predicting global seafloor total organic carbon. Glob. Biogeochem. Cycles 33, 37-46 (2019).
  4. WOA18 Data Access (National Centers for Environmental Information, 2018); https://www.nodc.noaa.gov/OC5/woa18/woa18data.html
  5. Bohlen, L., Dale, A. W. & Wallmann, K. Simple transfer functions for calculating benthic fixed nitrogen losses and C:N:P regeneration ratios in global biogeochemical models. Global Biogeochem. Cycles 26, GB3029 (2012).
  6. Burdige, D. J., Komada, T., Magen, C. & Chanton, J. P. Methane dynamics in Santa Barbara Basin (USA) sediments as examined with a reaction-transport model. J. Mar. Res. 74, 277-313 (2016).
  7. Jørgensen, B. B. A comparison of methods for the quantification of bacterial sulfate reduction in coastal marine sediments: I. Measurement with radiotracer techniques. Geomicrobiol. J. 1, 11-27 (1978).
  8. Bradley, J. A. et al. Widespread energy limitation to life in global subseafloor sediments. Sci. Adv. 6, eaba0697 (2020).
  9. Rogalinski, T., Liu, K., Albrecht, T. & Brunner, G. Hydrolysis kinetics of biopolymers in subcritical water. J. Supercrit. Fluids 46, 335-341 (2008).
  10. Leong, L. P. & Wedzicha, B. L. A critical appraisal of the kinetic model for the Maillard browning of glucose with glycine. Food Chem. 68, 21-28 (2000).
  11. Babakhani, P. et al. Comparison of a new mass-concentration, chain-reaction model with the population-balance model for early-and late-stage aggregation of shattered graphene oxide nanoparticles. Colloids Surf. A 582, 123862 (2019).
  12. McCulloch, W. S. & Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5, 115-133 (1943).
  13. Yu, H. et al. Prediction of the particle size distribution parameters in a high shear granulation process using a key parameter definition combined artificial neural network model. Ind. Eng. Chem. Res. 54, 10825-10834 (2015).
  14. Nourani, V. & Sayyah-Fard, M. Sensitivity analysis of the artificial neural network outputs in simulation of the evaporation process at different climatologic regimes. Adv. Eng. Softw. 47, 127-146 (2012).
  15. Gevrey, M., Dimopoulos, I. & Lek, S. Two-way interaction of input variables in the sensitivity analysis of neural network models. Ecol. Modell. 195, 43-50 (2006).
  16. Yerramareddy, S., Lu, S. C. Y. & Arnold, K. F. Developing empirical models from observational data using artificial neural networks. J. Intell. Manuf. 4, 33-41 (1993).
  17. Gevrey, M., Dimopoulos, I. & Lek, S. Review and comparison of methods to study the contribution of variables in artificial neural network models. Ecol. Modell. 160, 249-264 (2003).
  18. Meysman, F. J. R., Middelburg, J. J., Herman, P. M. J. & Heip, C. H. R. Reactive transport in surface sediments. II. Media: an object-oriented problem-solving environment for early diagenesis. Comput. Geosci. 29, 301-318 (2003).
  19. Kraal, P., Slomp, C. P., Reed, D. C., Reichart, G. J. & Poulton, S. W. Sedimentary phosphorus and iron cycling in and below the oxygen minimum zone of the northern Arabian Sea. Biogeosciences 9, 2603-2624 (2012).
  20. Akaike, H. A new look at the statistical model identification. Autom. Control IEEE Trans. 19, 716-723 (1974).
  21. Nash, J. E. & Sutcliffe, J. V. River flow forecasting through conceptual models part I—a discussion of principles. J. Hydrol. 10, 282-290 (1970).
  22. Clark, M. M. Transport Modeling for Environmental Engineers and Scientists (Wiley, 2011).
  23. Langmuir, D. Aqueous Environmental Geochemistry (Prentice Hall, 1997).
  24. Babakhani, P. et al. Babakhani_etal_main_text_figure_source_ data. figshare https://doi.org/10.6084/m9.figshare. 27273006 (2024).
  25. Babakhani, P. et al. Babakhani_etal_supplementary_data. figshare https://doi.org/10.6084/m9.figshare. 27273030 (2024).

Acknowledgements

We acknowledge D. Burdige for sending field data and B. Mills for helpful discussion and review of an earlier version of our paper. The use of High-Performance Computing (ARC) facilities at the University of Leeds is acknowledged. We acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 725613 MinOrg). C.L.P. gratefully acknowledges the Royal Society Wolfson Research Merit Award (WRM/FT/170005) and Leverhulme Research Fellowship (RF-2023-3954).

Author contributions

Conceptualization: P.B., C.L.P. and A.W.D. Data curation: P.B., C.L.P. and A.W.D. Formal analysis: P.B. Investigation: P.B. Methodology: P.B., A.W.D. and C.L.P. Visualization: P.B. Funding acquisition: C.L.P. Project administration: C.L.P. Resources: C.L.P. Software: P.B. and A.W.D. Supervision: C.L.P., A.W.D. and C.W. Validation: P.B., A.W.D., C.L.P. and K.-Q.X. Writing—original draft: P.B. Writing—review and editing: P.B., C.L.P., A.W.D., C.W., O.W.M., K.-Q.X. and L.C.

Competing interests

The authors declare no competing interests.
Peer review information Nature Geoscience thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editor: Xujia Jiang, in collaboration with the Nature Geoscience team.
Reprints and permissions information is available at www.nature.com/reprints.

Additional information

Supplementary information The online version contains supplementary material available at https://doi.org/10.1038/s41561-024-01606-y.
Correspondence and requests for materials should be addressed to Peyman Babakhani.
  1. School of Earth and Environment, University of Leeds, Leeds, UK. Department of Civil Engineering and Management, University of Manchester, Manchester, UK. GEOMAR Helmholtz Centre for Ocean Research Kiel, Kiel, Germany. School of Geography, University of Leeds, Leeds, UK. Department of Environment and Geography, University of York, York, UK. Research Center for Eco-Environmental Sciences, Chinese Academy of Sciences, Beijing, China. e-mail: peyman.babakhani@manchester.ac.uk