DOI: https://doi.org/10.1016/j.apmt.2024.102094
تاريخ النشر: 2024-02-10
تحليل فجوة الطاقة في مواد MOF: تمييز الانتقالات المباشرة وغير المباشرة باستخدام مطيافية الأشعة فوق البنفسجية والمرئية
للاستشهاد بهذه النسخة:
تحليل فجوة النطاق في مواد MOF: تمييز الانتقالات المباشرة وغير المباشرة باستخدام طيف الأشعة فوق البنفسجية والمرئية
معلومات المقال
الكلمات المفتاحية:
وزارة المالية
انحدار بولتزمان
كرامر-كرونيغ
UV-مرئي
الملخص
إطارات المعادن العضوية (MOFs) قد حظيت باهتمام كبير بسبب تطبيقاتها المحتملة في تخزين الغاز، والفصل، والحفز. هذه المواد المسامية تظهر خصائص تهم في فيزياء أشباه الموصلات والحفز الضوئي المتجانس، حيث يتم غالبًا مزج المفاهيم من كيمياء التنسيق وفيزياء أشباه الموصلات. في مجال الحفز الضوئي، يعتبر فجوة الطاقة البصرية لأشباه الموصلات معلمة حاسمة تحدد وظيفتها. على الرغم من كل الاهتمام بـ MOFs، لا يزال هناك نقص كبير في المعلومات حول تقييم فجوة الطاقة الخاصة بها (خاصة إذا كانت الفجوة مباشرة أو غير مباشرة) باستخدام مطيافية الأشعة فوق البنفسجية والمرئية، وهناك تباين كبير في هذه القيم. تُستخدم طريقة مخطط تاوك بشكل متكرر للوصول إلى فجوات الطاقة، على الرغم من أنها ليست دقيقة دائمًا، خاصة في تمييز الفجوات المباشرة وغير المباشرة. يمكن الوصول إلى تحليل أكثر اكتمالاً ودقة من خلال استخدام تقنيات تجريبية إضافية (مطيافية XPS وUPS وIPES)، التي ليست دائمًا سهلة الوصول. تتناول هذه الدراسة عدة طرق لتحديد فجوة الطاقة لمواد MOF وتقترح منهجيات لتفسير البيانات بشكل صحيح، مما يؤدي إلى توافق أفضل بين الفجوات التجريبية والنظرية. تم تحليل عدة طرق للوصول إلى فجوة الطاقة لمواد MOF المختلفة – UiO-66(Zr)، UiO-66(Hf)، UiO-66(Zr/Ti)، UiO-66(Hf/Ti)، UiO-67(Zr)_NH2، UiO-67(Zr/Hf)_NH2، UiO67(Hf)_NH2، MIL-125(Ti)، وMIL-125(Ti)_NH2 – فقط من بيانات الانعكاس المنتشر للأشعة فوق البنفسجية والمرئية (DR-UV-vis). طريقة كوبيلكا-مونك و
1. المقدمة
وهندسة الكيمياء [2،3]. بعد عرض تحليل الماء الضوئي في وجود
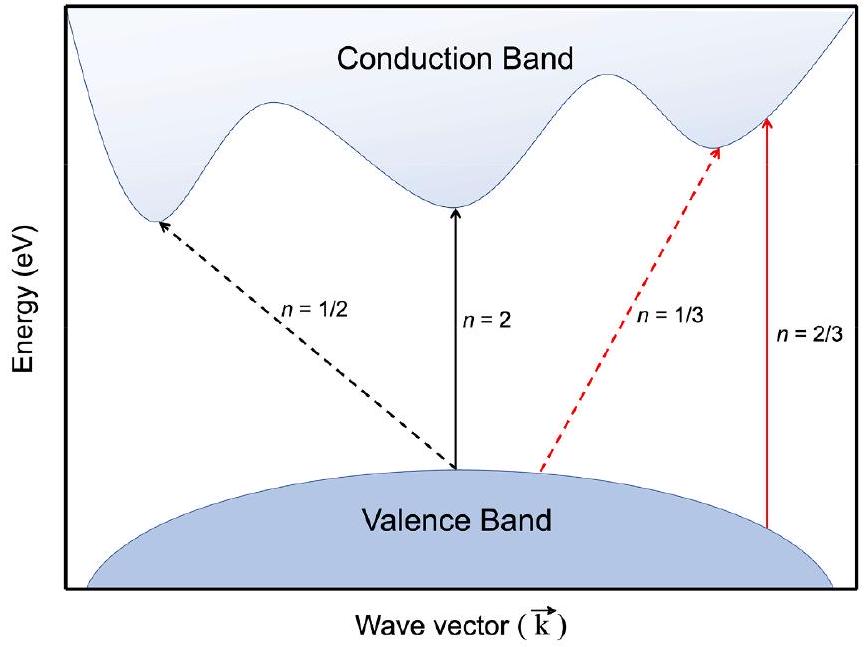
1.1. نظرية فجوة النطاق في مطيافية UV-vis
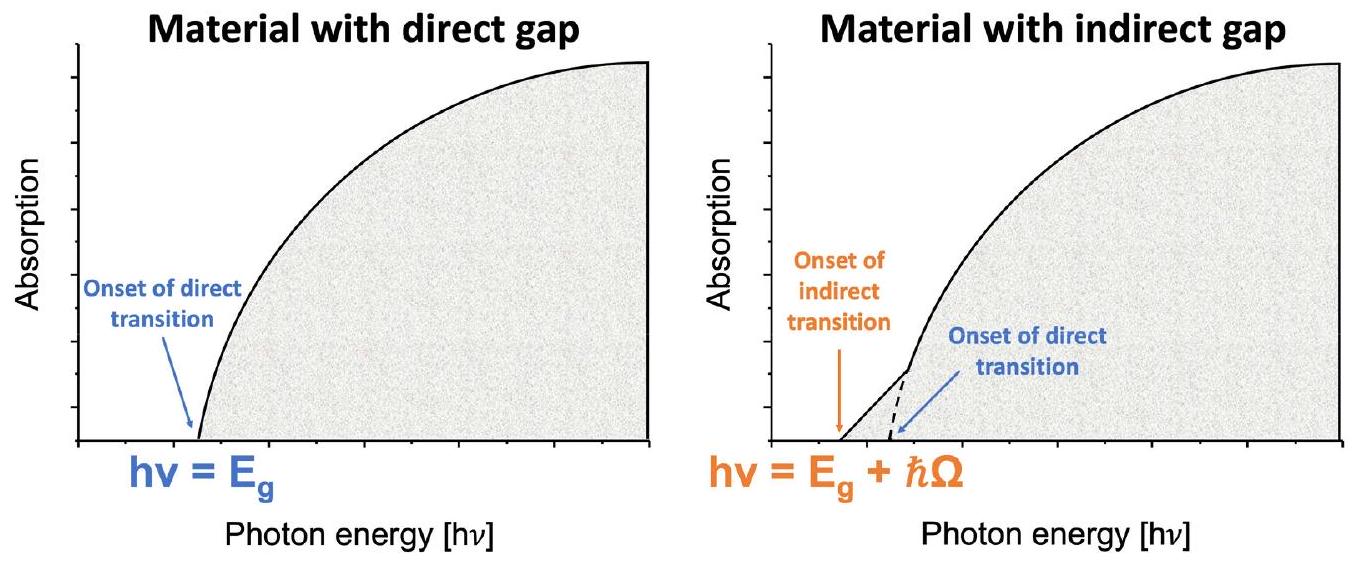
مثل درجة الحرارة المحلية [39]، والحقول الكهربائية أو المغناطيسية الخارجية القوية [40،41]، وتأثيرات التخصيب-السبائك في الاعتبار لأنها يمكن أن تؤثر على
طرق متاحة للحصول على معامل الامتصاص (
| طريقة | صيغة | اعتبارات |
| بوجر-لامبرت-بير [52-54] |
|
لا تأخذ في الاعتبار الانعكاسية |
| بانكوف [55] |
|
يعتبر أن المنتج
|
| بانكوف-فاهالوفا [55، |
|
يشمل الانعكاسات الداخلية للقيم الصغيرة من
|
| 56] |
|
|
| كابلكا-مونك [57] |
|
يعتبر نموذج إشعاع ذو تدفقين |
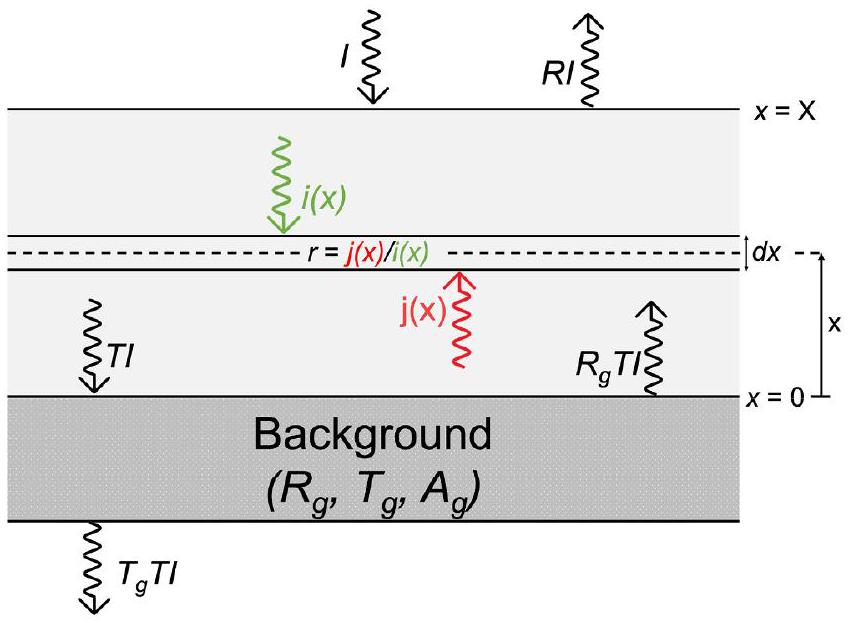
1.2. الرابط بين الامتصاص والانعكاسية المنتشرة
1.3. تقييم طاقة فجوة النطاق في مواد MOF
2. المواد والطرق
الخصائص التركيبية والفيزيائية الكيميائية للمركبات التي تم تخليقها في هذا العمل والتي تعرض النسبة الذرية، حجم البلورات،
| MOF | محتوى المعدن ICP-OES | حجم البلورة
|
SSA
|
حجم المسام الدقيقة (
|
| UiO-66(Zr) |
|
0.10 0.25 |
|
0.60(3) |
| UiO-66(Hf) |
|
0.18 3.33 |
|
0.41(3) |
| UiO-66(Zr/Ti) |
|
0.10 – |
|
0.47(5) |
|
|
0.25 | 28 | ||
| UiO-66(Hf/Ti) |
|
0.20 – |
|
0.30(9) |
|
|
0.34 | |||
| UiO-67(Zr)_NH2 |
|
32-51 |
|
0.68(4) |
| UiO-67(Zr/Hf) |
|
105-140 |
|
0.65(7) |
|
|
|
34 | ||
| UiO-67(Hf)_NH2 |
|
24-44 |
|
0.48(4) |
| MIL-125(Ti) |
|
0.76 – |
|
0.60(4) |
| 1.32 | 34 | |||
| MIL-125(Ti) |
|
3.2-5.3 |
|
0.51(4) |
| _NH2 | 26 |
التحليل الطيفي للانبعاث الضوئي – البلازما المقترنة: تم إجراء تجارب التحليل الطيفي للانبعاث الضوئي – البلازما المقترنة (ICP-OES) باستخدام جهاز طيفي Agilent 5110 ICP-OES في وضع الرؤية الشعاعية. تم إجراء تحلل العينات باستخدام 100 ملغ من مركبات UiO-66 المنشطة. أولاً، تم هضم العينات المسحوقة باستخدام محلول يحتوي على 10 مل من HF و5 مل من
طرق، ومن الجدير بالذكر استقراء منحنى الانعكاس المنتشر R [34]، واستقراء منحنى K-M
3. النتائج والمناقشة
3.1. توصيف المواد النقية
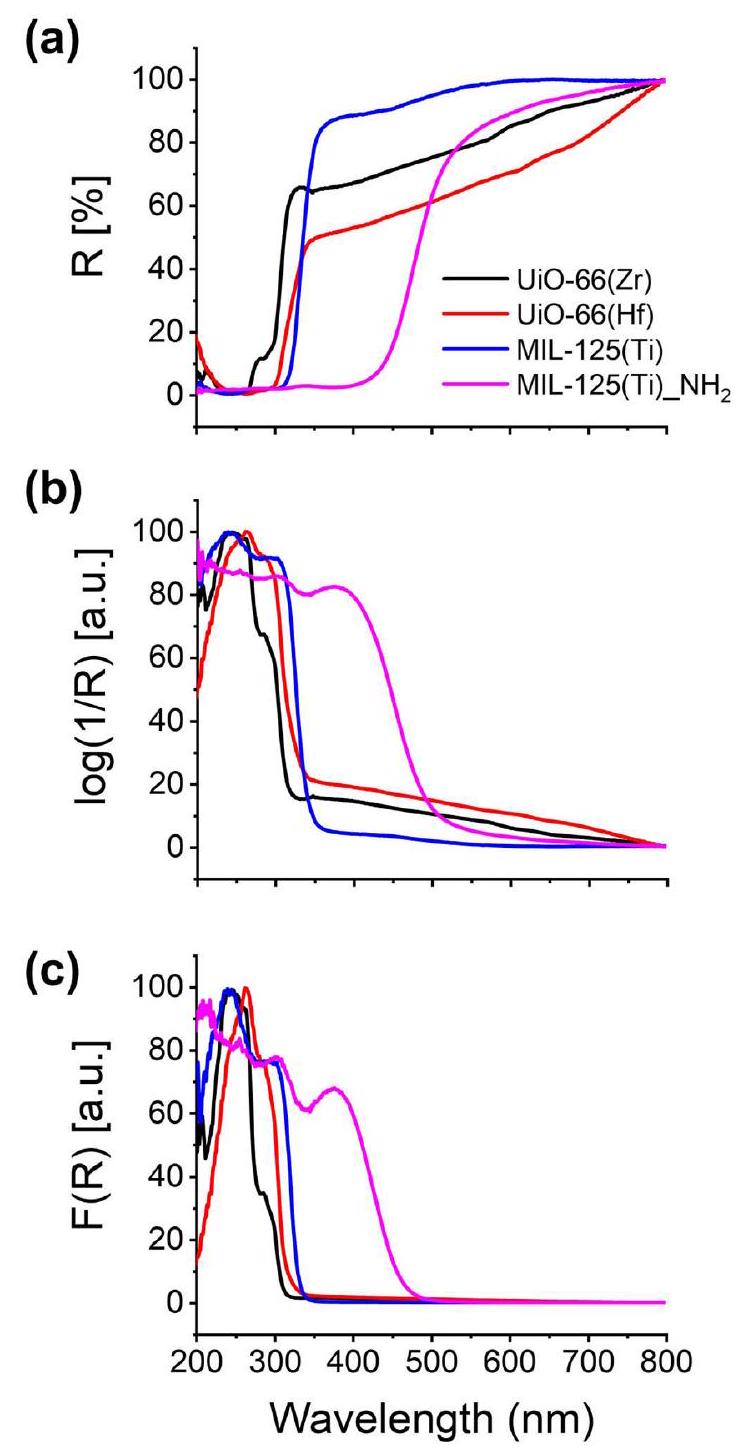
3.2. طيف الامتصاص الضوئي المرئي فوق البنفسجي بالانعكاس المنتشر
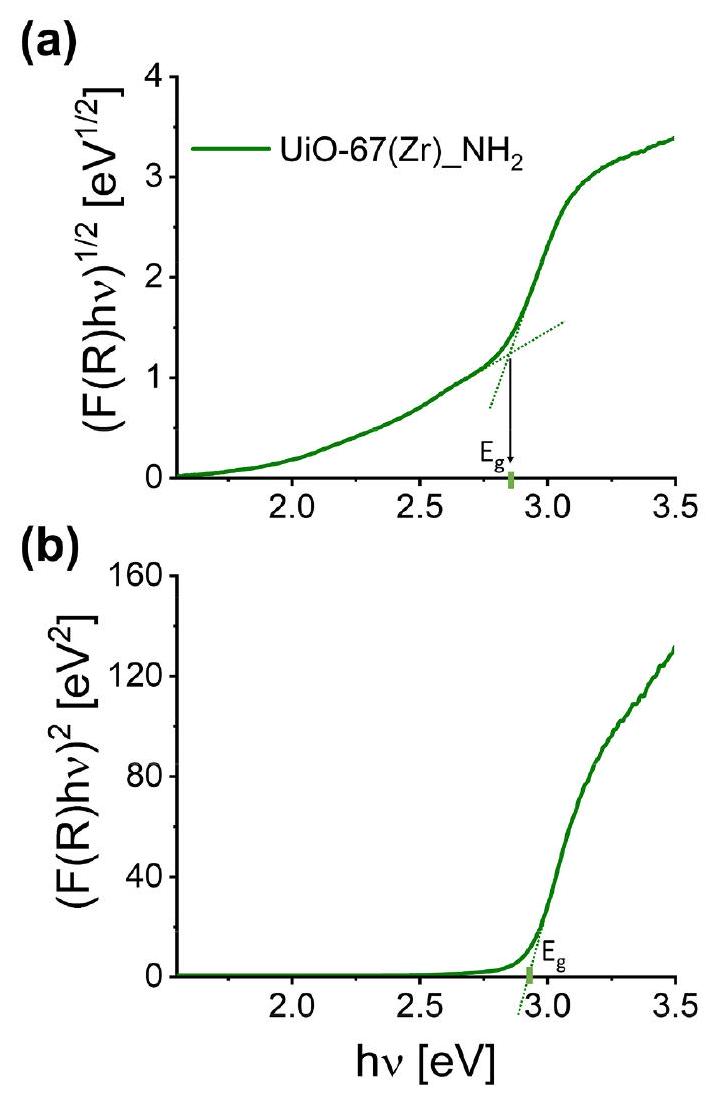
3.3. تقييم فجوة الطاقة: طرق كودي، تاوك، والمباشرة/غير المباشرة

قيم فجوة النطاق (eV) التي تم تقييمها من خلال الرسم لـ
| طريقة | UiO-66 | UiO-67_NH2 | MIL-125 | ||||||
| زر | Hf | زركونيوم/تيتانيوم | Hf/Ti | زر | زركونيوم/هفنيوم | Hf | H |
|
|
| ر | ٤.٢٠ | ٤.١٤ | ٤.٠٩ | 3.97 | 3.08 | 3.04 | 3.08 | 3.88 | ٣.٠٠ |
| ف(ر) | 3.98 | 3.93 | 3.89 | 3.94 | 2.83 | 2.88 | ٢.٩٠ | 3.75 | 2.69 |
| (F(R)/h
|
3.95 | 3.88 | 3.74 | 3.74 | 2.84 | 2.89 | 2.92 | 3.67 | 2.54 |
|
|
3.96 | 3.89 | 3.78 | 3.79 | 2.85 | 2.92 | ٢.٩٠ | 3.67 | 2.52 |
|
|
3.96 | 3.90 | 3.79 | 3.82 | 2.85 | 2.91 | 2.92 | 3.67 | 2.53 |
|
|
٤.٠٥ | ٤.٠٤ | ٤.٠٠ | ٤.٠٤ | 2.92 | 2.95 | 2.98 | 3.82 | 2.80 |
|
|
٤.٠٦ | ٤.٠٣ | ٤.٠٢ | ٤.٠٥ | 2.93 | 2.96 | 2.98 | 3.81 | 2.80 |
أن تكون غير مباشر بسبب القرب بين
الطيف الذي يتم تحليله بشكل إضافي للحصول على فجوة الطاقة للعينات. كما أنه من الواضح أن حواف نطاقات الامتصاص محددة بشكل أفضل باستخدام طريقة K-M من
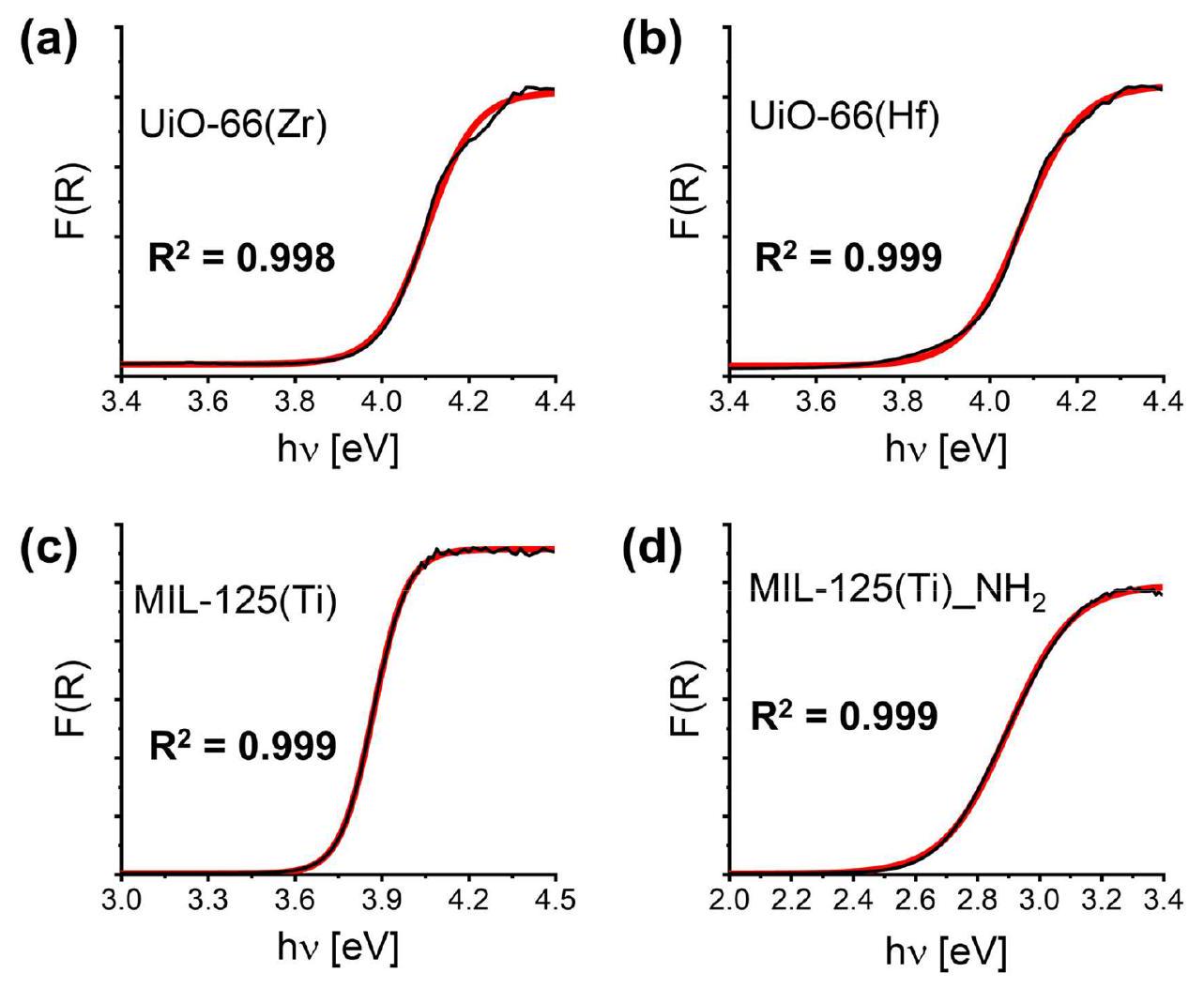
3.4. تقييم فجوة الطاقة: انحدار بولتزمان
طاقات فجوة النطاق (eV) المحسوبة من المعادلة (9) مع الأخذ في الاعتبار
| طريقة | UiO-66 | UiO-67_NH2 | MIL-125 | ||||||
| زر | Hf | زركونيوم/تيتانيوم | Hf/Ti | زر | زركونيوم/هفنيوم | Hf | H |
|
|
|
|
٤.١١ | ٤.٠٧ | ٤.١٨ | ٤.٤٩ | ٢.٩٩ | 2.98 | 3.01 | 3.87 | ٢.٩٠ |
|
|
0.056 | 0.067 | 0.171 | 0.215 | 0.111 | 0.061 | 0.065 | 0.058 | 0.١٠٣ |
|
|
٤.٠٦ | ٤.٠١ | ٤.٠٣ | ٤.٣٠ | 2.89 | 2.93 | 2.95 | 3.82 | 2.81 |
|
|
3.91 | 3.84 | 3.58 | 3.74 | 2.61 | 2.77 | 2.78 | 3.67 | 2.54 |
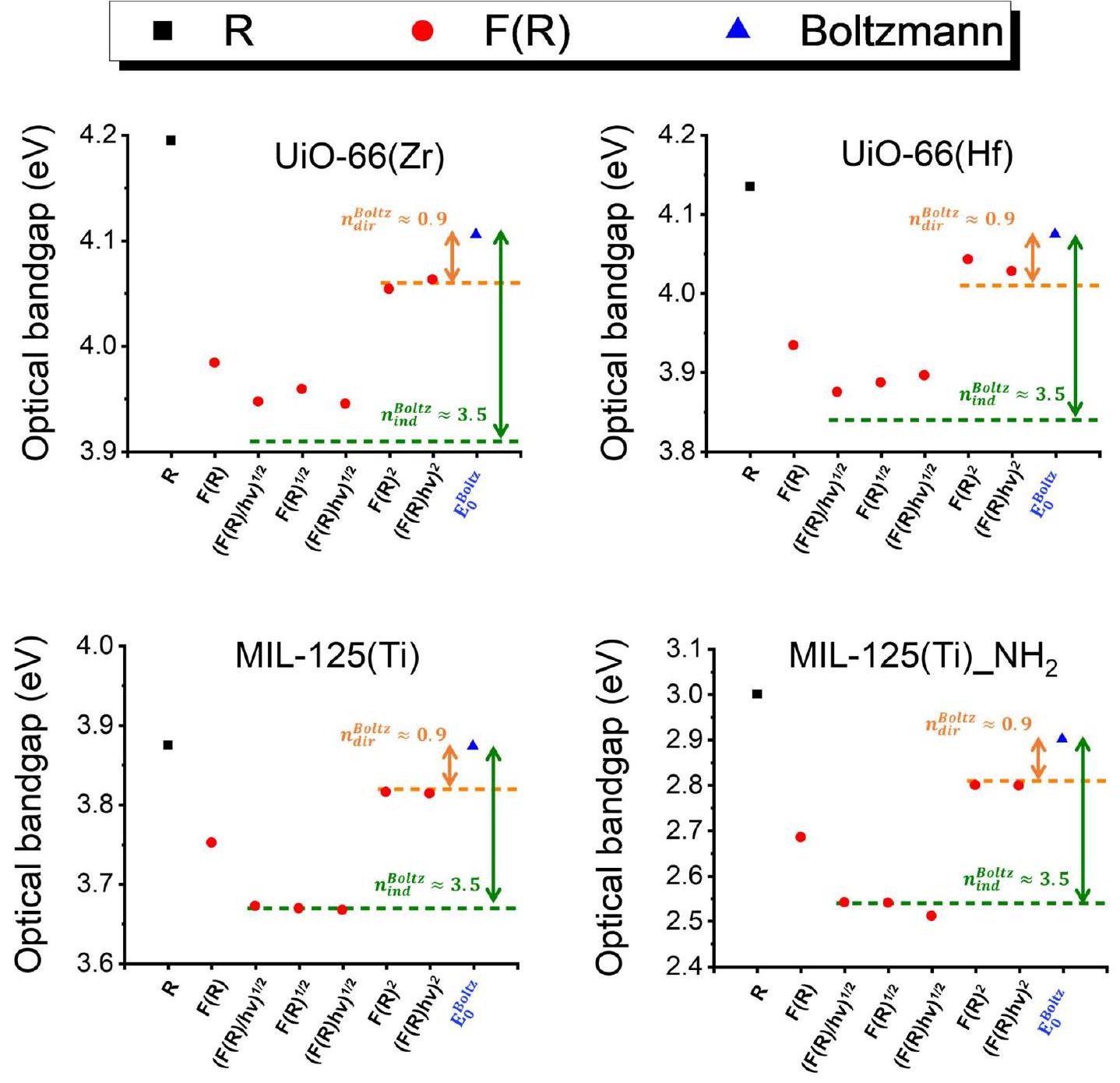
المركبات، التي تُنسب إلى الدقة المنخفضة لهذه الطريقة عند التعامل مع بيانات الانعكاس المنتشر للأشعة فوق البنفسجية والمرئية.
أن تكون غير دقيقة في حالة MOFs، حيث أن
3.67 إلكترون فولت؛ بينما قدم MIL-125(Ti)_NH2
3.5. تقييم فجوة الطاقة: الدالة العزلية المعقدة وتحويل كرامرز-كرونيغ
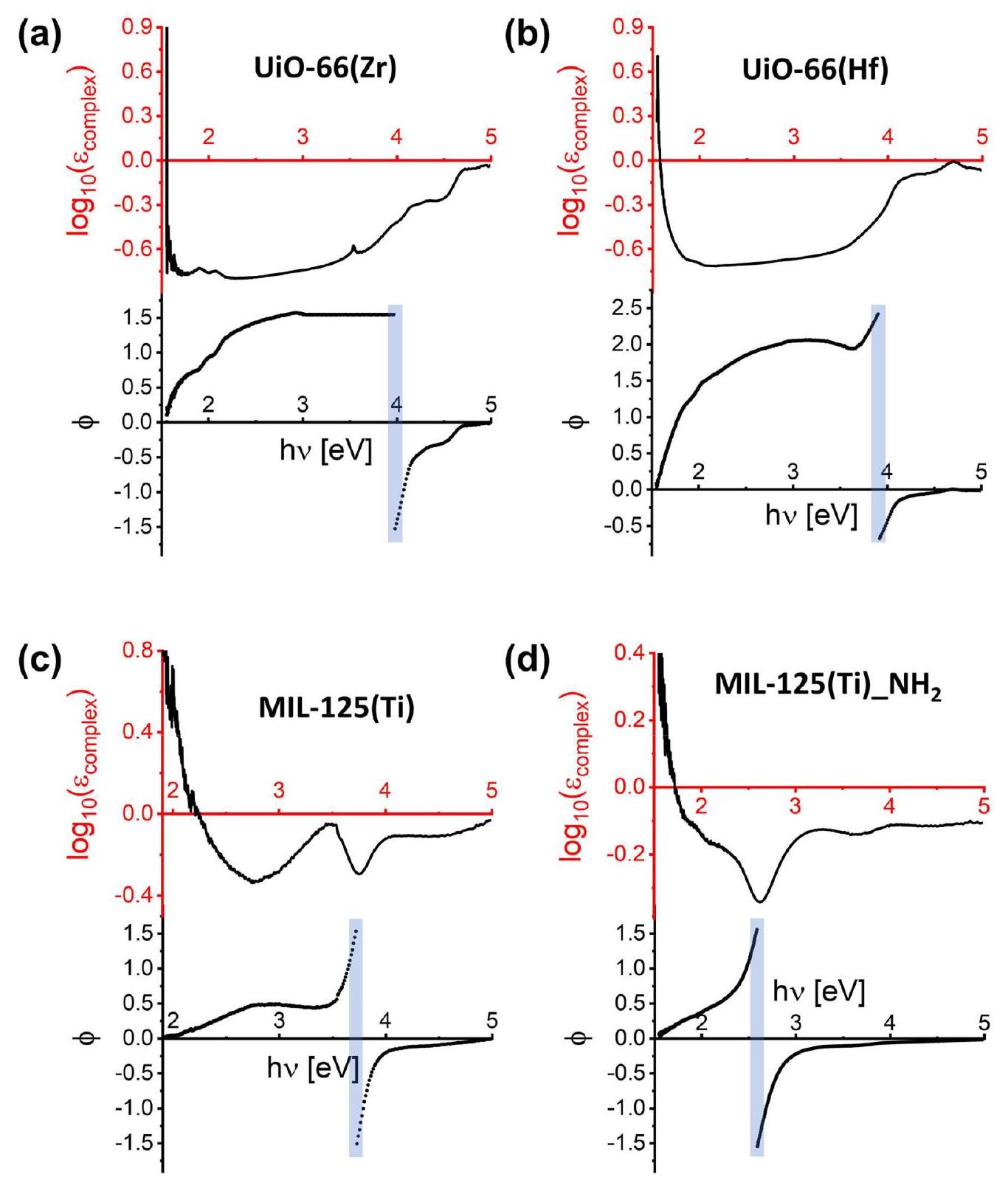
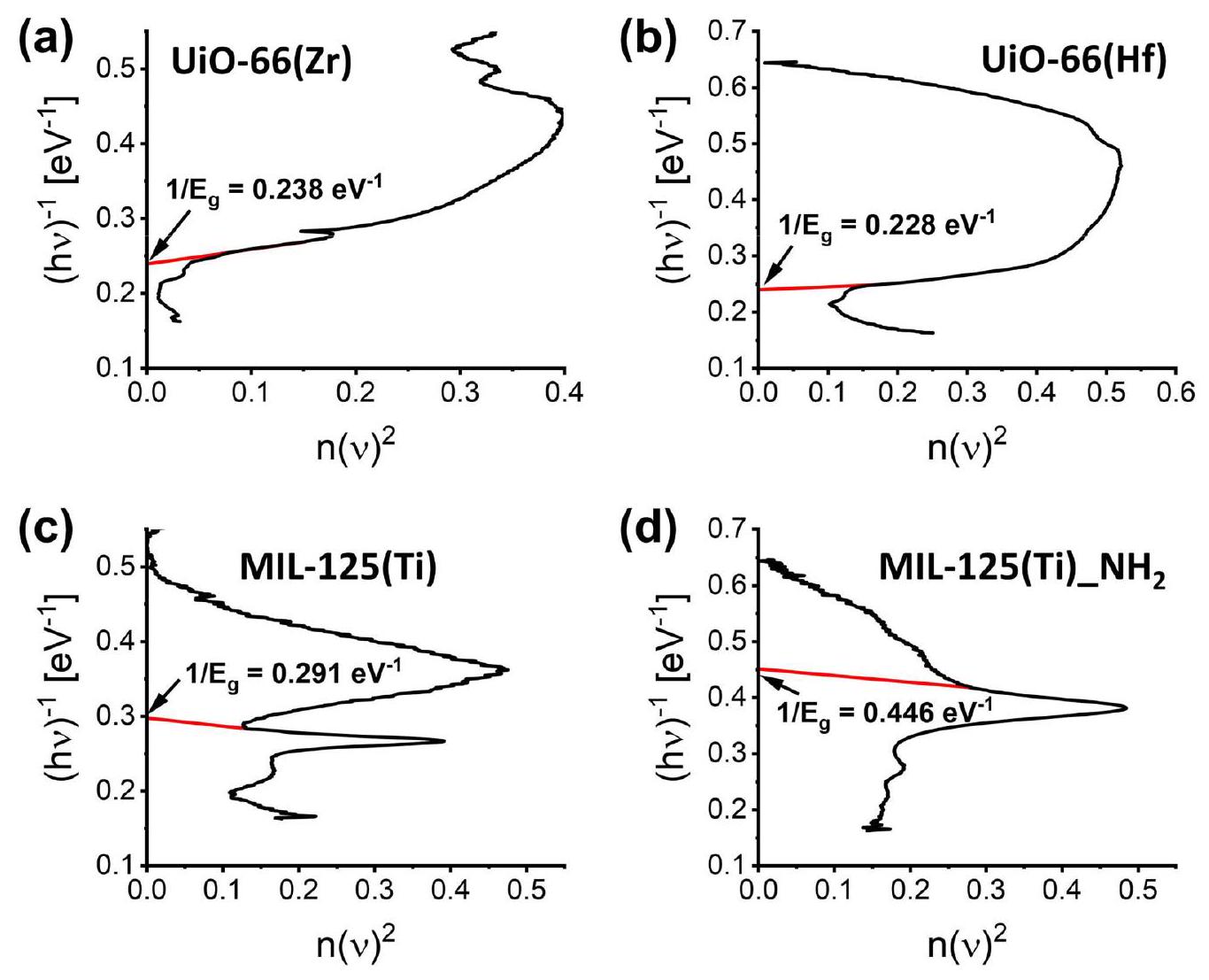
طاقات فجوة النطاق المحسوبة باستخدام تحويل كرامرز-كرونيغ، مقارنة مع المتوسط للقيم المباشرة وغير المباشرة
| وزارة المالية |
|
|
|
||
| مباشر [eV] | غير مباشر [eV] |
|
|
||
| [eV] | |||||
| UiO-66(Zr) | ٤.٢٠ | ٤.٠٧ | 3.94 | 3.2 | 6.6 |
| UiO-66(Hf) | ٤.٣٩ | ٤.٠٤ | 3.86 | ٨.٦ | 13.7 |
| UiO-66(Zr/Ti) | ٤.٣٥ | ٤.٠٥ | 3.69 | ٧.٤ | 17.9 |
| UiO-66(Hf/Ti) | ٤.٤١ | ٤.١٧ | 3.73 | 5.8 | 18.2 |
| UiO-67(Zr)_NH2 | 3.22 | 2.93 | 2.76 | 9.9 | ١٦.٧ |
| UiO-67(Zr/Hf)_NH2 | 3.13 | ٢.٩٦ | 2.86 | 5.7 | 9.4 |
| UiO-67(Hf)_NH2 | 3.13 | 2.98 | 2.87 | 5.0 | 9.1 |
| ميل-125(تي) | 3.44 | 3.83 | 3.66 | 10.2 | 6.0 |
| MIL-125(Ti)_NH2 | ٢.٢٤ | 2.82 | 2.51 | ٢٠.٦ | 10.8 |
- تم الحصول على القيم المباشرة من خلال اعتبار المتوسط بين فجوات النطاق المباشرة لتوك، والفجوات المباشرة النقية، وفجوات النطاق المباشرة لبولتزمان. وتم الحصول على القيم غير المباشرة من خلال اعتبار المتوسط بين فجوات النطاق غير المباشرة لكودي، وتوك غير المباشرة، والفجوات غير المباشرة النقية، وفجوات النطاق غير المباشرة لبولتزمان.
طرق، وخطأ بين
نسب انتقال فجوة النطاق البصري (مباشر أو غير مباشر) مع الأخذ في الاعتبار القيم الطاقية المتوسطة المحسوبة من طيف الأشعة فوق البنفسجية والمرئية المحول بواسطة كوبيلكا-مونك. تم اعتبار الانتقالات المباشرة للمتوسط: “مباشر” نقي و”مباشر” تاوك. تم اعتبار الانتقالات غير المباشرة للمتوسط: “غير مباشر” نقي، “غير مباشر” تاوك، وفجوة نطاق كودي. تمت مقارنة القيم بالطاقة المحسوبة باستخدام انحدار بولتزمان.
| وزارة المالية |
|
|
|
|
نسبة بولتزمان |
|
نسبة K-K | استنتاج |
| [eV] | [eV] | [eV] | [eV] | [eV] | ||||
| UiO-66(Zr) | ٤.٠٦ | 3.96 | ٤.٠٦ | 3.91 | مباشر | ٤.٢٠ | مباشر | مباشر |
| UiO-66(Hf) | ٤.٠٤ | 3.89 | ٤.٠١ | 3.84 | مباشر | ٤.٣٩ | مباشر | مباشر |
| UiO-66(Zr/Ti) | ٤.٠١ | 3.77 | ٤.٠٣ | 3.58 | مباشر | ٤.٣٥ | مباشر | مباشر |
| UiO-66(Hf/Ti) | ٤.٠٥ | 3.78 | ٤.٣٠ | 3.74 | غير مباشر | ٤.٤١ | مباشر | غير حاسم |
| UiO-67(Zr)_NH2 | 2.93 | 2.85 | 2.89 | 2.61 | مباشر | 3.22 | مباشر | مباشر |
| UiO-67(Zr/Hf)_NH
|
2.96 | 2.91 | 2.93 | 2.77 | مباشر | 3.13 | مباشر | مباشر |
| UiO-67(Hf)_NH2 | 2.98 | 2.91 | ٢.٩٥ | 2.78 | مباشر | 3.13 | مباشر | مباشر |
| ميل-125(تي) | 3.82 | ٣.٦٧ | 3.82 | ٣.٦٧ | مباشر/غير مباشر | 3.44 | غير مباشر | غير مباشر |
| MIL-125(Ti)_NH
|
2.80 | 2.53 | 2.81 | 2.54 | مباشر/غير مباشر | ٢.٢٤ | غير مباشر | غير مباشر |
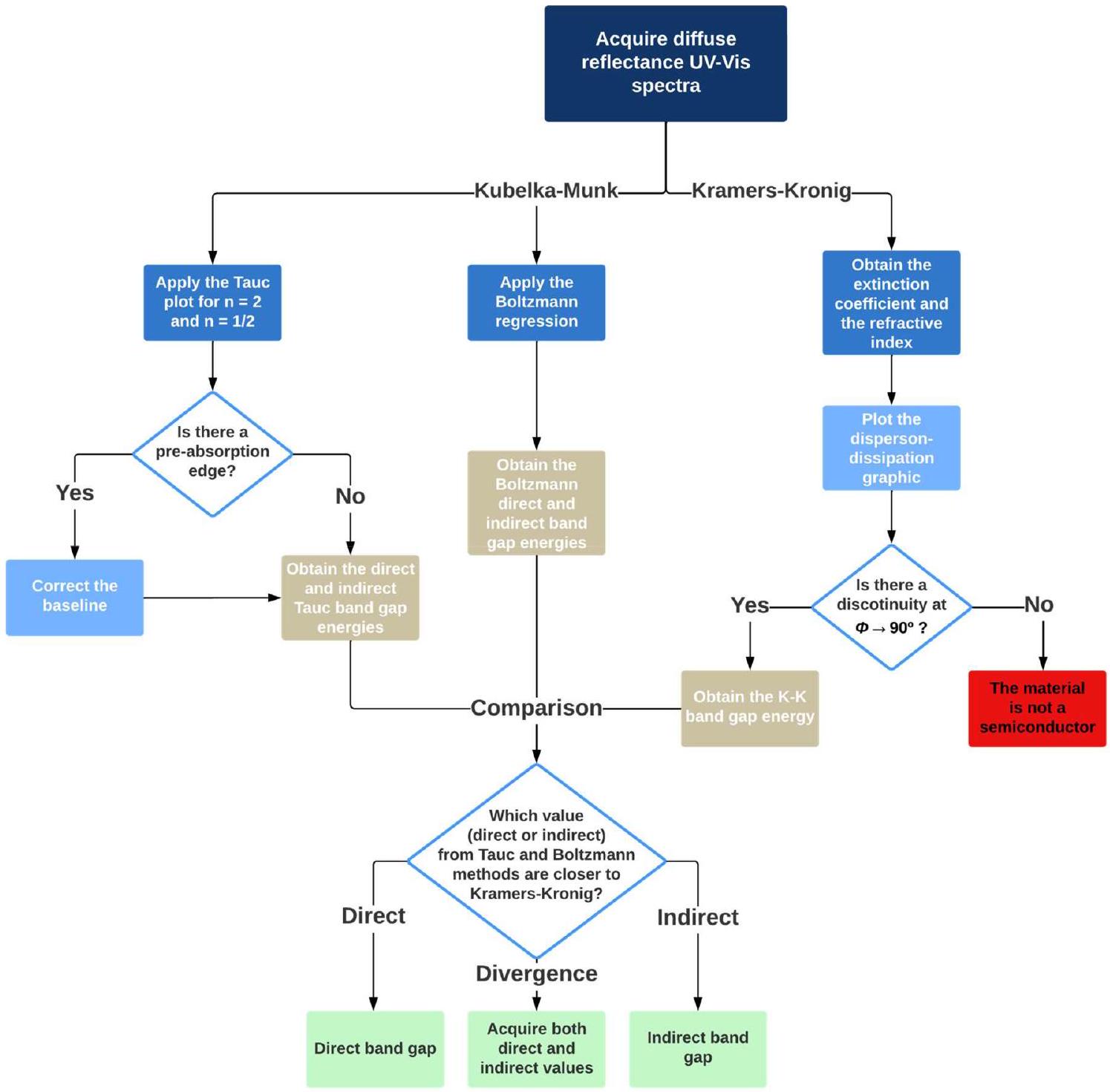
معظم المواد. في الواقع، فإن UiO بالكامل-
4. الاستنتاجات
بيان مساهمة مؤلفي CRediT
إعلان عن تضارب المصالح
توفر البيانات
شكر وتقدير
References
[2] M.A. Fox, M.T. Dulay, Heterogeneous photocatalysis, Chem. Rev. 93 (1993) 341-357, https://doi.org/10.1021/cr00017a016.
[3] A. Chatterjee, L. Wang, P. Van Der Voort, Metal-organic frameworks in photocatalytic Z-scheme heterojunctions: an emerging technology, Chem. Commun. 59 (2023) 3627-3654, https://doi.org/10.1039/D2CC05819G.
[4] F. Fischer, Photoelectrode, photovoltaic and photosynthetic microbial fuel cells, Renew. Sustain. Energy Rev. 90 (2018) 16-27, https://doi.org/10.1016/j. rser.2018.03.053.
[5] S. Chu, Y. Wang, Y. Guo, J. Feng, C. Wang, W. Luo, X. Fan, Z. Zou, Band structure engineering of carbon nitride: in search of a polymer photocatalyst with high photooxidation property, ACS Catal. 3 (2013) 912-919, https://doi.org/ 10.1021/cs4000624.
[6] L. Jiao, Y. Wang, H.L. Jiang, Q. Xu, Metal-organic frameworks as platforms for catalytic applications, Adv. Mater. 30 (2018) 1-23, https://doi.org/10.1002/ adma. 201703663.
[7] P.H.M. Andrade, A.L.M. Gomes, H.G. Palhares, C. Volkringer, Post-synthetic modification of aluminum trimesate and copper trimesate with TiO2 nanoparticles for photocatalytic applications, J. Mater. Sci. 57 (2022) 4481-4503, https://doi.org/10.1007/s10853-021-06842-w.
[8] M.R. Hoffmann, S.T. Martin, W. Choi, D.W. Bahnemann, Environmental applications of semiconductor photocatalysis, Chem. Rev. 95 (1995) 69-96, https://doi.org/10.1021/cr00033a004.
[9] X. Deng, Z. Li, H. García, Visible light induced organic transformations using metal-organic-frameworks (MOFs), Chem. Eur. J. 23 (2017) 11189-11209, https://doi.org/10.1002/chem. 201701460.
[10] R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki, Y. Taga, Visible-light photocatalysis in nitrogen-doped titanium oxides, Science 293 (2001) 269-271, https://doi.org/ 10.1126/science. 1061051 (80.).
[11] C.W. Jones, Metal-organic frameworks and covalent organic frameworks: emerging advances and applications, JACS Au 2 (2022) 1504-1505, https://doi. org/10.1021/jacsau.2c00376.
[12] S.M. Moosavi, A. Nandy, K.M. Jablonka, D. Ongari, J.P. Janet, P.G. Boyd, Y. Lee, B. Smit, H.J. Kulik, Understanding the diversity of the metal-organic framework ecosystem, Nat. Commun. 11 (2020) 1-10, https://doi.org/10.1038/s41467-020-17755-8.
[13] J.L. Mancuso, A.M. Mroz, K.N. Le, C.H. Hendon, Electronic structure modeling of metal-organic frameworks, Chem. Rev. 120 (2020) 8641-8715, https://doi.org/ 10.1021/acs.chemrev.0c00148.
[14] N. Kolobov, M.G. Goesten, J. Gascon, Metal-organic frameworks: molecules or semiconductors in photocatalysis? Angew. Chem. Int. Ed. 60 (2021) 26038-26052, https://doi.org/10.1002/anie. 202106342.
[15] S. Wang, L. Pan, J.J. Song, W. Mi, J.J. Zou, L. Wang, X. Zhang, Titanium-defected undoped anatase TiO2 with p-type conductivity, room-temperature ferromagnetism, and remarkable photocatalytic performance, J. Am. Chem. Soc. 137 (2015) 2975-2983, https://doi.org/10.1021/ja512047k.
[16] J.P. Kleider, Y.M. Soro, R. Chouffot, A.S. Gudovskikh, P. Roca i Cabarrocas, J. Damon-Lacoste, D. Eon, P.J. Ribeyron, High interfacial conductivity at amorphous silicon/crystalline silicon heterojunctions, J. Non-Cryst. Solids 354 (2008) 2641-2645, https://doi.org/10.1016/j.jnoncrysol.2007.09.087.
[17] K. Lu, D. Erb, M. Liu, Thermal stability and electrical conductivity of carbonenriched silicon oxycarbide, J. Mater. Chem. C. 4 (2016) 1829-1837, https://doi. org/10.1039/c6tc00069j.
[18] V. Somjit, P. Thinsoongnoen, S. Waiprasoet, T. Pila, P. Pattanasattayavong, S. Horike, K. Kongpatpanich, Processable UiO-66 metal-organic framework fluid gel and electrical conductivity of its nanofilm with sub-100 nm thickness, ACS Appl. Mater. Interfaces 13 (2021) 30844-30852, https://doi.org/10.1021/ acsami.1c07262.
[19] P. Salcedo-Abraira, A. Santiago-Portillo, P. Atienzar, P. Bordet, F. Salles, N. Guillou, E. Elkaim, H. Garcia, S. Navalon, P. Horcajada, A highly conductive nanostructured PEDOT polymer confined into the mesoporous MIL-100(Fe), Dalton Trans. 48 (2019) 9807-9817, https://doi.org/10.1039/C9DT00917E.
[20] P.H.M. Andrade, H. Palhares, C. Volkringer, T. Loiseau, M. Hureau, E. Nunes, A. Moissette, State of the art in visible-light photocatalysis of aqueous pollutants using metal-organic frameworks, J. Photochem. Photobiol. C Photochem. Rev. 57 (2023) 100635, https://doi.org/10.1016/j.jphotochemrev.2023.100635.
[21] L.D. Yuan, H.X. Deng, S.S. Li, S.H. Wei, J.W. Luo, Unified theory of direct or indirect band-gap nature of conventional semiconductors, Phys. Rev. B 98 (2018) 1-10, https://doi.org/10.1103/PhysRevB.98.245203.
[22] X. Guo, L. Liu, Y. Xiao, Y. Qi, C. Duan, F. Zhang, Band gap engineering of metalorganic frameworks for solar fuel productions, Coord. Chem. Rev. 435 (2021), https://doi.org/10.1016/j.ccr.2021.213785.
[23] R. Elzein, C.M. Chang, I. Ponomareva, W.Y. Gao, S. Ma, R. Schlaf, Advanced photoemission spectroscopy investigations correlated with DFT calculations on the self-assembly of 2D metal organic frameworks nano thin films, ACS Appl. Mater. Interfaces 8 (2016) 31403-31412, https://doi.org/10.1021/ acsami.6b10340.
[24] A.H. Wilson, The theory of electronic semi-conductors, Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 133 (1931) 458-491, https://doi.org/10.1098/rspa.1931.0162.
[25] A.H. Wilson, The theory of electronic semi-conductors II, Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 134 (1931) 277-287, https://doi.org/10.1098/ rspa.1931.0196.
[26] C.A. Mead, W.G. Spitzer, Fermi level position at semiconductor surfaces, Phys. Rev. Lett. 10 (1963) 471-472, https://doi.org/10.1103/PhysRevLett.10.471.
[27] Z. Huang, M. Lee Tang, Semiconductor nanocrystal light absorbers for photon upconversion, J. Phys. Chem. Lett. 9 (2018) 6198-6206, https://doi.org/ 10.1021/acs.jpclett.8b02154.
[28] C. Dette, M.A. Pérez-Osorio, C.S. Kley, P. Punke, C.E. Patrick, P. Jacobson, F. Giustino, S.J. Jung, K. Kern, TiO2 anatase with a bandgap in the visible region, Nano Lett. 14 (2014) 6533-6538, https://doi.org/10.1021/nl503131s.
[29] L.M. Yang, G.Y. Fang, J. Ma, E. Ganz, S.S. Han, Band gap engineering of paradigm MOF-5, Cryst. Growth Des. 14 (2014) 2532-2541, https://doi.org/10.1021/ cg500243s.
[30] C.H. Hendon, D. Tiana, M. Fontecave, C. Sanchez, L. D’Arras, C. Sassoye, L. Rozes, C. Mellot-Draznieks, A. Walsh, Engineering the optical response of the titanium-MIL-125 metal-organic framework through ligand functionalization, J. Am. Chem. Soc. 135 (2013) 10942-10945, https://doi.org/10.1021/ja405350u.
[31] L.M. Yang, G.Y. Fang, J. Ma, R. Pushpa, E. Ganz, Halogenated MOF-5 variants show new configuration, tunable band gaps and enhanced optical response in the visible and near infrared, Phys. Chem. Chem. Phys. 18 (2016) 32319-32330, https://doi.org/10.1039/c6cp06981a.
[32] Q. Wang, Q. Gao, A.M. Al-Enizi, A. Nafady, S. Ma, Recent advances in MOF-based photocatalysis: environmental remediation under visible light, Inorg. Chem. Front. 7 (2020) 300-339, https://doi.org/10.1039/c9qi01120j.
[33] C.J.H. Wort, R.S. Balmer, Diamond as an electronic material, Mater. Today 11 (2008) 22-28, https://doi.org/10.1016/S1369-7021(07)70349-8.
[34] A.R. Zanatta, Revisiting the optical bandgap of semiconductors and the proposal of a unified methodology to its determination, Sci. Rep. 9 (2019) 11225, https:// doi.org/10.1038/s41598-019-47670-y.
[35] V. Sarritzu, N. Sestu, D. Marongiu, X. Chang, Q. Wang, S. Masi, S. Colella, A. Rizzo, A. Gocalinska, E. Pelucchi, M.L. Mercuri, F. Quochi, M. Saba, A. Mura, G. Bongiovanni, Direct or indirect bandgap in hybrid lead halide perovskites? Adv. Opt. Mater. 6 (2018) 1-8, https://doi.org/10.1002/adom. 201701254.
[36] G. Wang, C. Robert, M.M. Glazov, F. Cadiz, E. Courtade, T. Amand, D. Lagarde, T. Taniguchi, K. Watanabe, B. Urbaszek, X. Marie, In-plane propagation of light in transition metal dichalcogenide monolayers: optical selection rules, Phys. Rev. Lett. 119 (2017) 1-7, https://doi.org/10.1103/PhysRevLett.119.047401.
[37] W. Eberhardt, F.J. Himpsel, Dipole selection rules for optical transitions in the fcc and bcc lattices, Phys. Rev. B 21 (1980) 5572-5576, https://doi.org/10.1103/ PhysRevB.21.5572.
[38] C. Kittel, Introduction to Solid State Physics, Wiley, 2005, pp. 185-219.
[39] Y.P. Varshni, Band-to-band radiative recombination in groups IV, VI, and III-V semiconductors (I), Phys. Status Solidi 19 (1967) 459-514, https://doi.org/ 10.1002/pssb. 19670190202.
[40] R. Soref, B. Bennett, Electrooptical effects in silicon, IEEE J. Quantum Electron. 23 (1987) 123-129, https://doi.org/10.1109/JQE.1987.1073206.
[41] S. Zwerdling, B. Lax, L.M. Roth, Oscillatory magneto-absorption in semiconductors, Phys. Rev. 108 (1957) 1402-1408, https://doi.org/10.1103/ PhysRev.108.1402.
[42] J. Tauc, R. Grigorovici, A. Vancu, Optical properties and electronic structure of amorphous germanium, Phys. Status Solidi 15 (1966) 627-637, https://doi.org/ 10.1002/pssb. 19660150224.
[43] N.F. Mott, E.A. Davis, Conduction in non-crystalline systems V. Conductivity, optical absorption and photoconductivity in amorphous semiconductors, Philos. Mag. 22 (1970) 903-922, https://doi.org/10.1080/14786437008221061.
[44] J.B. Coulter, D.P. Birnie, Assessing tauc plot slope quantification: ZnO thin films as a model system, Phys. Status Solidi Basic Res. 255 (2018) 1-7, https://doi.org/ 10.1002/pssb. 201700393.
[45] Y. Feng, S. Lin, S. Huang, S. Shrestha, G. Conibeer, Can Tauc plot extrapolation be used for direct-band-gap semiconductor nanocrystals? J. Appl. Phys. 117 (2015) https://doi.org/10.1063/1.4916090.
[46] B.D. Viezbicke, S. Patel, B.E. Davis, D.P. Birnie, Evaluation of the Tauc method for optical absorption edge determination: ZnO thin films as a model system, Phys. Status Solidi Basic Res. 252 (2015) 1700-1710, https://doi.org/10.1002/ pssb. 201552007.
[47] R. López, R. Gómez, Band-gap energy estimation from diffuse reflectance measurements on sol-gel and commercial TiO2: a comparative study, J. Sol-Gel Sci. Technol. 61 (2012) 1-7, https://doi.org/10.1007/s10971-011-2582-9.
[48] A. Dolgonos, T.O. Mason, K.R. Poeppelmeier, Direct optical band gap measurement in polycrystalline semiconductors: a critical look at the Tauc method, J. Solid State Chem. 240 (2016) 43-48, https://doi.org/10.1016/j. jssc.2016.05.010.
[49] M. Meinert, G. Reiss, Electronic structure and optical band gap determination of NiFe2O4, J. Phys. Condens. Matter 26 (2014) 115503, https://doi.org/10.1088/ 0953-8984/26/11/115503.
[50] P. Makuła, M. Pacia, W. Macyk, How to correctly determine the band gap energy of modified semiconductor photocatalysts based on UV-vis spectra, J. Phys. Chem. Lett. 9 (2018) 6814-6817, https://doi.org/10.1021/acs.jpclett.8b02892.
[51] G.D. Cody, B.G. Brooks, B. Abeles, Optical absorption above the optical gap of amorphous silicon hydride, Sol. Energy Mater. 8 (1982) 231-240, https://doi. org/10.1016/0165-1633(82)90065-X.
[52] P. Bouguer, Traité d’optique sur la gradation de la lumière, Guerin and Delatour, Paris, 1852. https://gallica.bnf.fr/ark:/12148/bpt6k948469/f2.item.
[53] J.H. Lambert, Photometria, Sive de Mensura et Gradibus Luminis, Colorum et Umbrae, Leipzig : W. Engelmann, 1760. https://archive.org/details/lambertsph otome00lambgoog.
[54] Beer, Bestimmung der Absorption des rothen Lichts in farbigen Flüssigkeiten, Ann. Phys. 162 (1852) 78-88, https://doi.org/10.1002/andp. 18521620505.
[55] J.I. Pankove, Optical Processes in Semiconductors, Dover Publications, New York, 1971. I. 0-486-60275-3.
[56] R. Vahalová, L. Tichý, M. Vlček, H. Tichá, Far infrared spectra and bonding arrangement in some Ge-Sb-S glasses, Phys. Status Solidi 181 (2000) 199-209, https://doi.org/10.1002/1521-396X(200009), 181:1<199::AID-PSSA199>3.0. CO;2-X.
[57] P. Kubelka, F. Munk, An article on optics of paint layers, Z. Tech. Phys. 12 (1931) 593-601.
[58] Y. Lee, S. Kim, J.K. Kang, S.M. Cohen, Photocatalytic CO2 reduction by a mixed metal (
[59] D. Yamashita, Y. Nakajima, A. Ishizaki, M. Uda, Photoelectron spectrometer equipped with open counter for electronic structures of organic materials, J. Surf. Anal. 14 (2008) 433-436. http://www.sasj.jp/JSA/CONTENTS. /vol.14_4/Vol. 14 No.4/Vol. 14 No. 4 433-436.pdf.
[60] R.J. Davis, M.T. Lloyd, S.R. Ferreira, M.J. Bruzek, S.E. Watkins, L. Lindell, P. Sehati, M. Fahlman, J.E. Anthony, J.W.P. Hsu, Determination of energy level alignment at interfaces of hybrid and organic solar cells under ambient environment, J. Mater. Chem. 21 (2011) 1721-1729, https://doi.org/10.1039/ C0JM02349C.
[61] J. Jasieniak, M. Califano, S.E. Watkins, Size-dependent valence and conduction band-edge energies of semiconductor nanocrystals, ACS Nano 5 (2011) 5888-5902, https://doi.org/10.1021/nn201681s.
[62] P. Kubelka, New contributions to the optics of intensely light-scattering materials. Part I, J. Opt. Soc. Am. 44 (1948) 330, https://doi.org/10.1364/josa.44.000330.
[63] D.R. Duncan, The colour of pigment mixtures, Proc. Phys. Soc. 52 (1940) 390-401, https://doi.org/10.1088/0959-5309/52/3/310.
[64] T. Burger, J. Kuhn, R. Caps, J. Fricke, Quantitative determination of the scattering and absorption coefficients from diffuse reflectance and transmittance measurements: application to pharmaceutical powders, Appl. Spectrosc. 51 (1997) 309-317, https://doi.org/10.1366/0003702971940404.
[65] D.J. Dahm, K.D. Dahm, Representative layer theory for diffuse reflectance, Appl. Spectrosc. 53 (1999) 647-654, https://doi.org/10.1366/0003702991947298.
[66] T. Burger, H.J. Ploss, J. Kuhn, S. Ebel, J. Fricke, Diffuse reflectance and transmittance spectroscopy for the quantitative determination of scattering and absorption coefficients in quantitative powder analysis, Appl. Spectrosc. 51 (1997) 1323-1329, https://doi.org/10.1366/0003702971941999.
[67] S. Landi, I.R. Segundo, E. Freitas, M. Vasilevskiy, J. Carneiro, C.J. Tavares, Use and misuse of the Kubelka-Munk function to obtain the band gap energy from diffuse reflectance measurements, Solid State Commun. 341 (2022) 1-7, https:// doi.org/10.1016/j.ssc.2021.114573.
[68] G. Férey, Hybrid porous solids: past, present, future, Chem. Soc. Rev. 37 (2008) 191-214, https://doi.org/10.1039/b618320b.
[69] M.A. Nasalevich, C.H. Hendon, J.G. Santaclara, K. Svane, B. Van Der Linden, S. L. Veber, M.V. Fedin, A.J. Houtepen, M.A. Van Der Veen, F. Kapteijn, A. Walsh, J. Gascon, Electronic origins of photocatalytic activity in d0 metal organic frameworks, Sci. Rep. 6 (2016) 1-9, https://doi.org/10.1038/srep23676.
[70] P.H.M. Andrade, N. Henry, C. Volkringer, T. Loiseau, H. Vezin, M. Hureau, A. Moissette, Iodine uptake by Zr -/Hf-Based UiO-66 materials: the influence of
metal substitution on iodine evolution, ACS Appl. Mater. Interfaces (2022), https://doi.org/10.1021/acsami.2c07288.
[71] J. Heine, K. Müller-Buschbaum, Engineering metal-based luminescence in coordination polymers and metal-organic frameworks, Chem. Soc. Rev. 42 (2013) 9232-9242, https://doi.org/10.1039/c3cs60232j.
[72] P. Huo, T. Chen, J. Le Hou, L. Yu, Q.Y. Zhu, J. Dai, Ligand-to-ligand charge transfer within metal-organic frameworks based on manganese coordination polymers with tetrathiafulvalene-bicarboxylate and bipyridine ligands, Inorg. Chem. 55 (2016) 6496-6503, https://doi.org/10.1021/acs.inorgchem.6b00571.
[73] C. Xu, Y. Pan, G. Wan, H. Liu, L. Wang, H. Zhou, S.H. Yu, H.L. Jiang, Turning on visible-light photocatalytic C-H oxidation over metal-organic frameworks by introducing metal-to-cluster charge transfer, J. Am. Chem. Soc. 141 (2019) 19110-19117, https://doi.org/10.1021/jacs.9b09954.
[74] C.A. Kent, D. Liu, L. Ma, J.M. Papanikolas, T.J. Meyer, W. Lin, Light harvesting in microscale metal-organic frameworks by energy migration and interfacial electron transfer quenching, J. Am. Chem. Soc. 133 (2011) 12940-12943, https://doi.org/10.1021/ja204214t.
[75] M.A. Nasalevich, M.G. Goesten, T.J. Savenije, F. Kapteijn, J. Gascon, Enhancing optical absorption of metal-organic frameworks for improved visible light photocatalysis, Chem. Commun. 49 (2013) 10575-10577, https://doi.org/ 10.1039/c3cc46398b.
[76] P.H.M. Andrade, M. Moreau, N. Henry, M.T. Bakouche, S. Duval, C. Volkringer, T. Loiseau, M. Hureau, A. Moissette, Raman mapping as a tool for evaluating I2 and I3- diffusion over single-crystal UiO-67_NH2(M) (
[77] P.H.M. Andrade, H. Ahouari, C. Volkringer, T. Loiseau, H. Vezin, M. Hureau, A. Moissette, Electron-donor functional groups, band gap tailoring, and efficient charge separation: three keys to improve the gaseous iodine uptake in MOF materials, ACS Appl. Mater. Interfaces 15 (2023) 31032-31048, https://doi.org/ 10.1021/acsami.3c04955.
[78] T. Ahnfeldt, N. Guillou, D. Gunzelmann, I. Margiolaki, T. Loiseau, G. Férey, J. Senker, N. Stock,
[79] J.H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga, K. P. Lillerud, A new zirconium inorganic building brick forming metal organic frameworks with exceptional stability, J. Am. Chem. Soc. 130 (2008) 13850-13851, https://doi.org/10.1021/ja8057953.
[80] M. Dan-Hardi, C. Serre, T. Frot, L. Rozes, G. Maurin, C. Sanchez, G. Férey, A new photoactive crystalline highly porous titanium(IV) dicarboxylate, J. Am. Chem. Soc. 131 (2009) 10857-10859, https://doi.org/10.1021/ja903726m.
[81] S. Jakobsen, D. Gianolio, D.S. Wragg, M.H. Nilsen, H. Emerich, S. Bordiga, C. Lamberti, U. Olsbye, M. Tilset, K.P. Lillerud, Structural determination of a highly stable metal-organic framework with possible application to interim radioactive waste scavenging: Hf-UiO-66, Phys. Rev. B Condens. Matter Mater. Phys. 86 (2012) 1-11, https://doi.org/10.1103/PhysRevB.86.125429.
[82] M.J. Katz, Z.J. Brown, Y.J. Colón, P.W. Siu, K.A. Scheidt, R.Q. Snurr, J.T. Hupp, O.K. Farha, A facile synthesis of UiO-66, UiO-67 and their derivatives, Chem. Commun. 49 (2013) 9449-9451, https://doi.org/10.1039/C3CC46105J.
[83] M. Leloire, C. Walshe, P. Devaux, R. Giovine, S. Duval, T. Bousquet, S. Chibani, J. Paul, A. Moissette, H. Vezin, P. Nerisson, L. Cantrel, C. Volkringer, T. Loiseau, Capture of gaseous iodine in isoreticular zirconium-based UiO-n metal-organic frameworks: influence of amino functionalization, DFT calculations, Raman and EPR spectroscopic investigation, Chem. Eur. J 28 (2022), https://doi.org/ 10.1002/chem. 202104437 e202104437.
[84] S. Hu, M. Liu, K. Li, Y. Zuo, A. Zhang, C. Song, G. Zhang, X. Guo, Solvothermal synthesis of NH2-MIL-125(Ti) from circular plate to octahedron, CrystEngComm 16 (2014) 9645-9650, https://doi.org/10.1039/c4ce01545b.
[85] A.Y. Galashev, A.S. Vorob’ev, Physical properties of silicene electrodes for Li -,
[86] K. Hendrickx, D.E.P. Vanpoucke, K. Leus, K. Lejaeghere, A. Van Yperen-De Deyne, V. Van Speybroeck, P. Van Der Voort, K. Hemelsoet, Understanding intrinsic light absorption properties of UiO-66 frameworks: a combined theoretical and experimental study, Inorg. Chem. 54 (2015) 10701-10710, https://doi.org/ 10.1021/acs.inorgchem.5b01593.
[87] L.M. Yang, E. Ganz, S. Svelle, M. Tilset, Computational exploration of newly synthesized zirconium metal-organic frameworks UiO-66, -67, -68 and analogues, J. Mater. Chem. C 2 (2014) 7111-7125, https://doi.org/10.1039/c4tc00902a.
[88] A.S. Yasin, J. Li, N. Wu, T. Musho, Study of the inorganic substitution in a functionalized UiO-66 metal-organic framework, Phys. Chem. Chem. Phys. 18 (2016) 12748-12754, https://doi.org/10.1039/c5cp08070c.
[89] A. Wang, Y. Zhou, Z. Wang, M. Chen, L. Sun, X. Liu, Titanium incorporated with UiO-66(Zr)-type metal-organic framework (MOF) for photocatalytic application, RSC Adv. 6 (2016) 3671-3679, https://doi.org/10.1039/c5ra24135a.
[90] J. Tu, X. Zeng, F. Xu, X. Wu, Y. Tian, X. Hou, Z. Long, Microwave-induced fast incorporation of titanium into UiO-66 metal-organic frameworks for enhanced photocatalytic properties, Chem. Commun. 53 (2017) 3361-3364, https://doi. org/10.1039/c7cc00076f.
[91] S. Liu, Z. Ren, H. Xu, Y. Xing, X. Jin, G. Ni, Z. Wang, Visible-light-responsive
[92] X. Zhao, M. Xu, X. Song, X. Liu, W. Zhou, H. Wang, P. Huo, Tailored linker defects in UiO-67 with high ligand-to-metal charge transfer toward efficient photoreduction of CO2, Inorg. Chem. 61 (2022) 1765-1777, https://doi.org/ 10.1021/acs.inorgchem.1c03690.
[93] E. Flage-Larsen, A. Røyset, J.H. Cavka, K. Thorshaug, Band gap modulations in UiO metal-organic frameworks, J. Phys. Chem. C 117 (2013) 20610-20616, https://doi.org/10.1021/jp405335q.
[94] S. Chavan, J.G. Vitillo, D. Gianolio, O. Zavorotynska, B. Civalleri, S. Jakobsen, M. H. Nilsen, L. Valenzano, C. Lamberti, K.P. Lillerud, S. Bordiga, H2 storage in isostructural UiO-67 and UiO-66 MOFs, Phys. Chem. Chem. Phys. 14 (2012) 1614-1626, https://doi.org/10.1039/c1cp23434j.
[95] S.Q. Wang, X. Wang, X.Y. Zhang, X.M. Cheng, J. Ma, W.Y. Sun, Effect of the defect modulator and ligand length of metal-organic frameworks on carbon dioxide photoreduction, ACS Appl. Mater. Interfaces 13 (2021) 61578-61586, https:// doi.org/10.1021/acsami.1c21663.
[96] R. Raciti, R. Bahariqushchi, C. Summonte, A. Aydinli, A. Terrasi, S. Mirabella, Optical bandgap of semiconductor nanostructures: methods for experimental data analysis, J. Appl. Phys. 121 (2017) 234304, https://doi.org/10.1063/1.4986436.
[97] C. Rotaru, S. Nastase, N. Tomozeiu, Amorphous phase influence on the optical bandgap of polysilicon, Phys. Status Solidi 171 (1999) 365-370, https://doi.org/ 10.1002/(SICI)1521-396X(199901)171. :1<365::AID-PSSA365>3.0.CO;2-M.
[98] B. Gu, N.H. Kwong, R. Binder, Relation between the interband dipole and momentum matrix elements in semiconductors, Phys. Rev. B 87 (2013) 125301, https://doi.org/10.1103/PhysRevB.87.125301.
[99] B. Jensen, Quantum theory of the complex dielectric constant of free carriers in polar semiconductors, IEEE J. Quantum Electron. 18 (1982) 1361-1370, https:// doi.org/10.1109/JQE.1982.1071713.
[100] P. Hervé, L.K.J. Vandamme, General relation between refractive index and energy gap in semiconductors, Infrared Phys. Technol. 35 (1994) 609-615, https://doi. org/10.1016/1350-4495(94)90026-4.
[101] H. Finkenrath, The Moss rule and the influence of doping on the optical dielectric constant of semiconductors-I, Infrared Phys. 28 (1988) 327-332, https://doi.org/ 10.1016/0020-0891(88)90054-1.
[102] T.S. Moss, Relations between the refractive index and energy gap of semiconductors, Phys. Status Solidi 131 (1985) 415-427, https://doi.org/ 10.1002/pssb. 2221310202.
[103] N.M. Ravindra, P. Ganapathy, J. Choi, Energy gap-refractive index relations in semiconductors-an overview, Infrared Phys. Technol. 50 (2007) 21-29, https:// doi.org/10.1016/j.infrared.2006.04.001.
[104] D.R. Penn, Wave-number-dependent dielectric function of semiconductors, Phys. Rev. 128 (1962) 2093-2097, https://doi.org/10.1103/PhysRev.128.2093.
[105] S.H. Wemple, Optical oscillator strengths and excitation energies in solids, liquids, and molecules, J. Chem. Phys. 67 (1977) 2151-2168, https://doi.org/ 10.1063/1.435102.
[106] P. George, P. Chowdhury, Complex dielectric transformation of UV-vis diffuse reflectance spectra for estimating optical band-gap energies and materials classification, Analyst 144 (2019) 3005-3012, https://doi.org/10.1039/ c8an02257g.
[107] H.A. Kramers, The quantum theory of dispersion, Nature 114 (1924) 310-311, https://doi.org/10.1038/114310b0.
[108] R. de L. Kronig, On the theory of dispersion of X-rays, J. Opt. Soc. Am. 12 (1926) 547-557, https://doi.org/10.1364/JOSA.12.000547.
[109] A.B. Kuzmenko, Kramers-Kronig constrained variational analysis of optical spectra, Rev. Sci. Instrum. 76 (2005) 83108, https://doi.org/10.1063/1.1979470.
[110] E. Yablonovitch, Photonic band-gap structures, J. Opt. Soc. Am. B 10 (1993) 283-295, https://doi.org/10.1364/JOSAB.10.000283.
- Corresponding author.
E-mail address: pedro.moraisandrade@univ-lille.fr (P.H.M. Andrade).
DOI: https://doi.org/10.1016/j.apmt.2024.102094
Publication Date: 2024-02-10
Band gap analysis in MOF materials: Distinguishing direct and indirect transitions using UV-vis spectroscopy
To cite this version:
Band gap analysis in MOF materials: Distinguishing direct and indirect transitions using UV-vis spectroscopy
A R T I C L E I N F O
Keywords:
MOF
Boltzmann regression
Kramers-Kronig
UV-vis
Abstract
Metal-Organic Frameworks (MOFs) have gained considerable attention due to their potential applications in gas storage, separation, and catalysis. These porous materials exhibit properties of interest for semiconductor physics and homogeneous photocatalysis, in which concepts from coordination chemistry and semiconductor physics are often mixed. In the photocatalysis field, the optical band gap of the semiconductors is a crucial parameter that determine their functionality. Despite all the interest of MOFs, there is still a considerable lack of information about their band gap evaluation (especially if the gap is direct or indirect) using UV-Vis spectroscopy, and there is a considerable scattering in these values. The Tauc plot method is frequently used to access band gaps, even though it is not always accurate, especially for distinguishing direct and indirect band gaps. A more complete and precise analysis can be reached by using additional experimental techniques (XPS, UPS, and IPES spectroscopies), that are not always of easy access. This work examines several approaches for determining the band gap of MOF materials and proposes methodologies for a correct data interpretation, which leads to a better agreement between experimental and theoretical gaps. Several methods were analyzed to access the band gap of different MOF materials – UiO-66(Zr), UiO-66(Hf), UiO-66(Zr/Ti), UiO-66(Hf/Ti), UiO-67(Zr)_NH2, UiO-67(Zr/Hf)_NH2, UiO67(Hf)_NH2, MIL-125(Ti), and MIL-125(Ti)_NH2 – purely from diffuse reflectance UV-vis (DR-UV-vis) data. The Kubelka-Munk and
1. Introduction
and chemical engineering [2,3]. After the demonstration of the water photolysis in the presence of

1.1. The band gap theory in UV-vis spectroscopy

effects such as local temperature [39], external strong electric or magnetic fields [40,41], and doping-alloying effects should be considered as they can influence the
Available methods for obtaining the absorption coefficient (
| Method | Formula | Considerations |
| Bouger-LambertBeer [52-54] |
|
Does not consider the reflectance |
| Pankove [55] |
|
Considers that the product
|
| PankoveVahalová [55, |
|
Includes internal reflections for small values of
|
| 56] |
|
|
| Kubelka-Munk [57] |
|
Considers a two-flux radiation model |

1.2. The link between absorption and diffuse reflectance
1.3. Assessment of the band gap energy in MOF materials
2. Materials and methods
Textural and physical chemical properties of the compounds synthesized in this work displaying the atomic ratio, the crystallite size, the
| MOF | Metal content ICP-OES | Crystal size
|
SSA
|
Microporous volume (
|
| UiO-66(Zr) |
|
0.10 0.25 |
|
0.60(3) |
| UiO-66(Hf) |
|
0.18 3.33 |
|
0.41(3) |
| UiO-66(Zr/Ti) |
|
0.10 – |
|
0.47(5) |
|
|
0.25 | 28 | ||
| UiO-66(Hf/Ti) |
|
0.20 – |
|
0.30(9) |
|
|
0.34 | |||
| UiO-67(Zr)_NH2 |
|
32-51 |
|
0.68(4) |
| UiO-67(Zr/Hf) |
|
105-140 |
|
0.65(7) |
|
|
|
34 | ||
| UiO-67(Hf)_NH2 |
|
24-44 |
|
0.48(4) |
| MIL-125(Ti) |
|
0.76 – |
|
0.60(4) |
| 1.32 | 34 | |||
| MIL-125(Ti) |
|
3.2-5.3 |
|
0.51(4) |
| _NH2 | 26 |
Inductively coupled plasma – optical emission spectrometry: Inductively coupled plasma – optical emission spectrometry (ICP-OES) experiments were conducted using an Agilent 5110 ICP-OES spectrometer in radial sighting mode. The mineralization of the samples was performed using 100 mg of the activated UiO-66 compounds. First, the powdered samples were digested using a solution containing 10 mL of HF and 5 mL of
methods, worth mentioning the extrapolation of the diffuse reflectance curve R [34], the extrapolation of the K-M curve
3. Results and discussion
3.1. Characterization of the pristine materials

3.2. Diffuse reflectance UV-vis spectroscopy

3.3. Band gap evaluation: Cody, Tauc, and direct/indirect methods

Band gap values (eV) assessed through the plot of
| Method | UiO-66 | UiO-67_NH2 | MIL-125 | ||||||
| Zr | Hf | Zr/Ti | Hf/Ti | Zr | Zr/Hf | Hf | H |
|
|
| R | 4.20 | 4.14 | 4.09 | 3.97 | 3.08 | 3.04 | 3.08 | 3.88 | 3.00 |
| F(R) | 3.98 | 3.93 | 3.89 | 3.94 | 2.83 | 2.88 | 2.90 | 3.75 | 2.69 |
| (F(R)/h
|
3.95 | 3.88 | 3.74 | 3.74 | 2.84 | 2.89 | 2.92 | 3.67 | 2.54 |
|
|
3.96 | 3.89 | 3.78 | 3.79 | 2.85 | 2.92 | 2.90 | 3.67 | 2.52 |
|
|
3.96 | 3.90 | 3.79 | 3.82 | 2.85 | 2.91 | 2.92 | 3.67 | 2.53 |
|
|
4.05 | 4.04 | 4.00 | 4.04 | 2.92 | 2.95 | 2.98 | 3.82 | 2.80 |
|
|
4.06 | 4.03 | 4.02 | 4.05 | 2.93 | 2.96 | 2.98 | 3.81 | 2.80 |
to be indirect due to the proximity between the

spectra that is further analyzed to obtain the band gap of the samples. Also, it is clear that the edges of the absorption bands are better defined using the K-M approach than the
3.4. Band gap evaluation: the Boltzmann regression
Band gap energies (eV) calculated from Eq. (9) considering the
| Method | UiO-66 | UiO-67_NH2 | MIL-125 | ||||||
| Zr | Hf | Zr/Ti | Hf/Ti | Zr | Zr/Hf | Hf | H |
|
|
|
|
4.11 | 4.07 | 4.18 | 4.49 | 2.99 | 2.98 | 3.01 | 3.87 | 2.90 |
|
|
0.056 | 0.067 | 0.171 | 0.215 | 0.111 | 0.061 | 0.065 | 0.058 | 0.103 |
|
|
4.06 | 4.01 | 4.03 | 4.30 | 2.89 | 2.93 | 2.95 | 3.82 | 2.81 |
|
|
3.91 | 3.84 | 3.58 | 3.74 | 2.61 | 2.77 | 2.78 | 3.67 | 2.54 |

compounds, which is ascribed to the inferior accuracy of this approach when dealing with diffuse reflectance UV-vis data.
to be inaccurate in the case of MOFs, as the
3.67 eV ; whereas MIL-125(Ti)_NH2 presented an
3.5. Band gap evaluation: complex dielectric function and the KramersKronig transformation


Band gap energies calculated using the Kramers-Kronig transformation, comparison with the average for direct and indirect values
| MOF |
|
|
|
||
| Direct [eV] | Indirect [eV] |
|
|
||
| [eV] | |||||
| UiO-66(Zr) | 4.20 | 4.07 | 3.94 | 3.2 | 6.6 |
| UiO-66(Hf) | 4.39 | 4.04 | 3.86 | 8.6 | 13.7 |
| UiO-66(Zr/Ti) | 4.35 | 4.05 | 3.69 | 7.4 | 17.9 |
| UiO-66(Hf/Ti) | 4.41 | 4.17 | 3.73 | 5.8 | 18.2 |
| UiO-67(Zr)_NH2 | 3.22 | 2.93 | 2.76 | 9.9 | 16.7 |
| UiO-67(Zr/Hf)_NH2 | 3.13 | 2.96 | 2.86 | 5.7 | 9.4 |
| UiO-67(Hf)_NH2 | 3.13 | 2.98 | 2.87 | 5.0 | 9.1 |
| MIL-125(Ti) | 3.44 | 3.83 | 3.66 | 10.2 | 6.0 |
| MIL-125(Ti)_NH2 | 2.24 | 2.82 | 2.51 | 20.6 | 10.8 |
- direct values were obtained considering the average between the Tauc direct, the pure direct, and the Boltzmann direct band gaps. Indirect values were obtained considering the average between the Cody, Tauc indirect, pure indirect, and Boltzmann indirect band gaps.
methods, and an error between the
Optical band gap transitions attributions (direct or indirect) considering the average energy values calculated from the Kubelka-Munk transformed UV-vis spectra. Direct transitions considered for the average: “pure” direct and Tauc direct. Indirect transitions considered for the average: “pure” indirect, Tauc indirect, and Cody band gap. The values were compared to the energies calculated using the Boltzmann regression (
| MOF |
|
|
|
|
Boltzmann attribution |
|
K-K attribution | Conclusion |
| [eV] | [eV] | [eV] | [eV] | [eV] | ||||
| UiO-66(Zr) | 4.06 | 3.96 | 4.06 | 3.91 | Direct | 4.20 | Direct | Direct |
| UiO-66(Hf) | 4.04 | 3.89 | 4.01 | 3.84 | Direct | 4.39 | Direct | Direct |
| UiO-66(Zr/Ti) | 4.01 | 3.77 | 4.03 | 3.58 | Direct | 4.35 | Direct | Direct |
| UiO-66(Hf/Ti) | 4.05 | 3.78 | 4.30 | 3.74 | Indirect | 4.41 | Direct | Inconclusive |
| UiO-67(Zr)_NH2 | 2.93 | 2.85 | 2.89 | 2.61 | Direct | 3.22 | Direct | Direct |
| UiO-67(Zr/Hf)_NH
|
2.96 | 2.91 | 2.93 | 2.77 | Direct | 3.13 | Direct | Direct |
| UiO-67(Hf)_NH2 | 2.98 | 2.91 | 2.95 | 2.78 | Direct | 3.13 | Direct | Direct |
| MIL-125(Ti) | 3.82 | 3.67 | 3.82 | 3.67 | Direct/indirect | 3.44 | Indirect | Indirect |
| MIL-125(Ti)_NH
|
2.80 | 2.53 | 2.81 | 2.54 | Direct/indirect | 2.24 | Indirect | Indirect |

most materials. In fact, the entire UiO-
4. Conclusions
CRediT authorship contribution statement
Declaration of competing interest
Data availability
Acknowledgements
References
[2] M.A. Fox, M.T. Dulay, Heterogeneous photocatalysis, Chem. Rev. 93 (1993) 341-357, https://doi.org/10.1021/cr00017a016.
[3] A. Chatterjee, L. Wang, P. Van Der Voort, Metal-organic frameworks in photocatalytic Z-scheme heterojunctions: an emerging technology, Chem. Commun. 59 (2023) 3627-3654, https://doi.org/10.1039/D2CC05819G.
[4] F. Fischer, Photoelectrode, photovoltaic and photosynthetic microbial fuel cells, Renew. Sustain. Energy Rev. 90 (2018) 16-27, https://doi.org/10.1016/j. rser.2018.03.053.
[5] S. Chu, Y. Wang, Y. Guo, J. Feng, C. Wang, W. Luo, X. Fan, Z. Zou, Band structure engineering of carbon nitride: in search of a polymer photocatalyst with high photooxidation property, ACS Catal. 3 (2013) 912-919, https://doi.org/ 10.1021/cs4000624.
[6] L. Jiao, Y. Wang, H.L. Jiang, Q. Xu, Metal-organic frameworks as platforms for catalytic applications, Adv. Mater. 30 (2018) 1-23, https://doi.org/10.1002/ adma. 201703663.
[7] P.H.M. Andrade, A.L.M. Gomes, H.G. Palhares, C. Volkringer, Post-synthetic modification of aluminum trimesate and copper trimesate with TiO2 nanoparticles for photocatalytic applications, J. Mater. Sci. 57 (2022) 4481-4503, https://doi.org/10.1007/s10853-021-06842-w.
[8] M.R. Hoffmann, S.T. Martin, W. Choi, D.W. Bahnemann, Environmental applications of semiconductor photocatalysis, Chem. Rev. 95 (1995) 69-96, https://doi.org/10.1021/cr00033a004.
[9] X. Deng, Z. Li, H. García, Visible light induced organic transformations using metal-organic-frameworks (MOFs), Chem. Eur. J. 23 (2017) 11189-11209, https://doi.org/10.1002/chem. 201701460.
[10] R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki, Y. Taga, Visible-light photocatalysis in nitrogen-doped titanium oxides, Science 293 (2001) 269-271, https://doi.org/ 10.1126/science. 1061051 (80.).
[11] C.W. Jones, Metal-organic frameworks and covalent organic frameworks: emerging advances and applications, JACS Au 2 (2022) 1504-1505, https://doi. org/10.1021/jacsau.2c00376.
[12] S.M. Moosavi, A. Nandy, K.M. Jablonka, D. Ongari, J.P. Janet, P.G. Boyd, Y. Lee, B. Smit, H.J. Kulik, Understanding the diversity of the metal-organic framework ecosystem, Nat. Commun. 11 (2020) 1-10, https://doi.org/10.1038/s41467-020-17755-8.
[13] J.L. Mancuso, A.M. Mroz, K.N. Le, C.H. Hendon, Electronic structure modeling of metal-organic frameworks, Chem. Rev. 120 (2020) 8641-8715, https://doi.org/ 10.1021/acs.chemrev.0c00148.
[14] N. Kolobov, M.G. Goesten, J. Gascon, Metal-organic frameworks: molecules or semiconductors in photocatalysis? Angew. Chem. Int. Ed. 60 (2021) 26038-26052, https://doi.org/10.1002/anie. 202106342.
[15] S. Wang, L. Pan, J.J. Song, W. Mi, J.J. Zou, L. Wang, X. Zhang, Titanium-defected undoped anatase TiO2 with p-type conductivity, room-temperature ferromagnetism, and remarkable photocatalytic performance, J. Am. Chem. Soc. 137 (2015) 2975-2983, https://doi.org/10.1021/ja512047k.
[16] J.P. Kleider, Y.M. Soro, R. Chouffot, A.S. Gudovskikh, P. Roca i Cabarrocas, J. Damon-Lacoste, D. Eon, P.J. Ribeyron, High interfacial conductivity at amorphous silicon/crystalline silicon heterojunctions, J. Non-Cryst. Solids 354 (2008) 2641-2645, https://doi.org/10.1016/j.jnoncrysol.2007.09.087.
[17] K. Lu, D. Erb, M. Liu, Thermal stability and electrical conductivity of carbonenriched silicon oxycarbide, J. Mater. Chem. C. 4 (2016) 1829-1837, https://doi. org/10.1039/c6tc00069j.
[18] V. Somjit, P. Thinsoongnoen, S. Waiprasoet, T. Pila, P. Pattanasattayavong, S. Horike, K. Kongpatpanich, Processable UiO-66 metal-organic framework fluid gel and electrical conductivity of its nanofilm with sub-100 nm thickness, ACS Appl. Mater. Interfaces 13 (2021) 30844-30852, https://doi.org/10.1021/ acsami.1c07262.
[19] P. Salcedo-Abraira, A. Santiago-Portillo, P. Atienzar, P. Bordet, F. Salles, N. Guillou, E. Elkaim, H. Garcia, S. Navalon, P. Horcajada, A highly conductive nanostructured PEDOT polymer confined into the mesoporous MIL-100(Fe), Dalton Trans. 48 (2019) 9807-9817, https://doi.org/10.1039/C9DT00917E.
[20] P.H.M. Andrade, H. Palhares, C. Volkringer, T. Loiseau, M. Hureau, E. Nunes, A. Moissette, State of the art in visible-light photocatalysis of aqueous pollutants using metal-organic frameworks, J. Photochem. Photobiol. C Photochem. Rev. 57 (2023) 100635, https://doi.org/10.1016/j.jphotochemrev.2023.100635.
[21] L.D. Yuan, H.X. Deng, S.S. Li, S.H. Wei, J.W. Luo, Unified theory of direct or indirect band-gap nature of conventional semiconductors, Phys. Rev. B 98 (2018) 1-10, https://doi.org/10.1103/PhysRevB.98.245203.
[22] X. Guo, L. Liu, Y. Xiao, Y. Qi, C. Duan, F. Zhang, Band gap engineering of metalorganic frameworks for solar fuel productions, Coord. Chem. Rev. 435 (2021), https://doi.org/10.1016/j.ccr.2021.213785.
[23] R. Elzein, C.M. Chang, I. Ponomareva, W.Y. Gao, S. Ma, R. Schlaf, Advanced photoemission spectroscopy investigations correlated with DFT calculations on the self-assembly of 2D metal organic frameworks nano thin films, ACS Appl. Mater. Interfaces 8 (2016) 31403-31412, https://doi.org/10.1021/ acsami.6b10340.
[24] A.H. Wilson, The theory of electronic semi-conductors, Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 133 (1931) 458-491, https://doi.org/10.1098/rspa.1931.0162.
[25] A.H. Wilson, The theory of electronic semi-conductors II, Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 134 (1931) 277-287, https://doi.org/10.1098/ rspa.1931.0196.
[26] C.A. Mead, W.G. Spitzer, Fermi level position at semiconductor surfaces, Phys. Rev. Lett. 10 (1963) 471-472, https://doi.org/10.1103/PhysRevLett.10.471.
[27] Z. Huang, M. Lee Tang, Semiconductor nanocrystal light absorbers for photon upconversion, J. Phys. Chem. Lett. 9 (2018) 6198-6206, https://doi.org/ 10.1021/acs.jpclett.8b02154.
[28] C. Dette, M.A. Pérez-Osorio, C.S. Kley, P. Punke, C.E. Patrick, P. Jacobson, F. Giustino, S.J. Jung, K. Kern, TiO2 anatase with a bandgap in the visible region, Nano Lett. 14 (2014) 6533-6538, https://doi.org/10.1021/nl503131s.
[29] L.M. Yang, G.Y. Fang, J. Ma, E. Ganz, S.S. Han, Band gap engineering of paradigm MOF-5, Cryst. Growth Des. 14 (2014) 2532-2541, https://doi.org/10.1021/ cg500243s.
[30] C.H. Hendon, D. Tiana, M. Fontecave, C. Sanchez, L. D’Arras, C. Sassoye, L. Rozes, C. Mellot-Draznieks, A. Walsh, Engineering the optical response of the titanium-MIL-125 metal-organic framework through ligand functionalization, J. Am. Chem. Soc. 135 (2013) 10942-10945, https://doi.org/10.1021/ja405350u.
[31] L.M. Yang, G.Y. Fang, J. Ma, R. Pushpa, E. Ganz, Halogenated MOF-5 variants show new configuration, tunable band gaps and enhanced optical response in the visible and near infrared, Phys. Chem. Chem. Phys. 18 (2016) 32319-32330, https://doi.org/10.1039/c6cp06981a.
[32] Q. Wang, Q. Gao, A.M. Al-Enizi, A. Nafady, S. Ma, Recent advances in MOF-based photocatalysis: environmental remediation under visible light, Inorg. Chem. Front. 7 (2020) 300-339, https://doi.org/10.1039/c9qi01120j.
[33] C.J.H. Wort, R.S. Balmer, Diamond as an electronic material, Mater. Today 11 (2008) 22-28, https://doi.org/10.1016/S1369-7021(07)70349-8.
[34] A.R. Zanatta, Revisiting the optical bandgap of semiconductors and the proposal of a unified methodology to its determination, Sci. Rep. 9 (2019) 11225, https:// doi.org/10.1038/s41598-019-47670-y.
[35] V. Sarritzu, N. Sestu, D. Marongiu, X. Chang, Q. Wang, S. Masi, S. Colella, A. Rizzo, A. Gocalinska, E. Pelucchi, M.L. Mercuri, F. Quochi, M. Saba, A. Mura, G. Bongiovanni, Direct or indirect bandgap in hybrid lead halide perovskites? Adv. Opt. Mater. 6 (2018) 1-8, https://doi.org/10.1002/adom. 201701254.
[36] G. Wang, C. Robert, M.M. Glazov, F. Cadiz, E. Courtade, T. Amand, D. Lagarde, T. Taniguchi, K. Watanabe, B. Urbaszek, X. Marie, In-plane propagation of light in transition metal dichalcogenide monolayers: optical selection rules, Phys. Rev. Lett. 119 (2017) 1-7, https://doi.org/10.1103/PhysRevLett.119.047401.
[37] W. Eberhardt, F.J. Himpsel, Dipole selection rules for optical transitions in the fcc and bcc lattices, Phys. Rev. B 21 (1980) 5572-5576, https://doi.org/10.1103/ PhysRevB.21.5572.
[38] C. Kittel, Introduction to Solid State Physics, Wiley, 2005, pp. 185-219.
[39] Y.P. Varshni, Band-to-band radiative recombination in groups IV, VI, and III-V semiconductors (I), Phys. Status Solidi 19 (1967) 459-514, https://doi.org/ 10.1002/pssb. 19670190202.
[40] R. Soref, B. Bennett, Electrooptical effects in silicon, IEEE J. Quantum Electron. 23 (1987) 123-129, https://doi.org/10.1109/JQE.1987.1073206.
[41] S. Zwerdling, B. Lax, L.M. Roth, Oscillatory magneto-absorption in semiconductors, Phys. Rev. 108 (1957) 1402-1408, https://doi.org/10.1103/ PhysRev.108.1402.
[42] J. Tauc, R. Grigorovici, A. Vancu, Optical properties and electronic structure of amorphous germanium, Phys. Status Solidi 15 (1966) 627-637, https://doi.org/ 10.1002/pssb. 19660150224.
[43] N.F. Mott, E.A. Davis, Conduction in non-crystalline systems V. Conductivity, optical absorption and photoconductivity in amorphous semiconductors, Philos. Mag. 22 (1970) 903-922, https://doi.org/10.1080/14786437008221061.
[44] J.B. Coulter, D.P. Birnie, Assessing tauc plot slope quantification: ZnO thin films as a model system, Phys. Status Solidi Basic Res. 255 (2018) 1-7, https://doi.org/ 10.1002/pssb. 201700393.
[45] Y. Feng, S. Lin, S. Huang, S. Shrestha, G. Conibeer, Can Tauc plot extrapolation be used for direct-band-gap semiconductor nanocrystals? J. Appl. Phys. 117 (2015) https://doi.org/10.1063/1.4916090.
[46] B.D. Viezbicke, S. Patel, B.E. Davis, D.P. Birnie, Evaluation of the Tauc method for optical absorption edge determination: ZnO thin films as a model system, Phys. Status Solidi Basic Res. 252 (2015) 1700-1710, https://doi.org/10.1002/ pssb. 201552007.
[47] R. López, R. Gómez, Band-gap energy estimation from diffuse reflectance measurements on sol-gel and commercial TiO2: a comparative study, J. Sol-Gel Sci. Technol. 61 (2012) 1-7, https://doi.org/10.1007/s10971-011-2582-9.
[48] A. Dolgonos, T.O. Mason, K.R. Poeppelmeier, Direct optical band gap measurement in polycrystalline semiconductors: a critical look at the Tauc method, J. Solid State Chem. 240 (2016) 43-48, https://doi.org/10.1016/j. jssc.2016.05.010.
[49] M. Meinert, G. Reiss, Electronic structure and optical band gap determination of NiFe2O4, J. Phys. Condens. Matter 26 (2014) 115503, https://doi.org/10.1088/ 0953-8984/26/11/115503.
[50] P. Makuła, M. Pacia, W. Macyk, How to correctly determine the band gap energy of modified semiconductor photocatalysts based on UV-vis spectra, J. Phys. Chem. Lett. 9 (2018) 6814-6817, https://doi.org/10.1021/acs.jpclett.8b02892.
[51] G.D. Cody, B.G. Brooks, B. Abeles, Optical absorption above the optical gap of amorphous silicon hydride, Sol. Energy Mater. 8 (1982) 231-240, https://doi. org/10.1016/0165-1633(82)90065-X.
[52] P. Bouguer, Traité d’optique sur la gradation de la lumière, Guerin and Delatour, Paris, 1852. https://gallica.bnf.fr/ark:/12148/bpt6k948469/f2.item.
[53] J.H. Lambert, Photometria, Sive de Mensura et Gradibus Luminis, Colorum et Umbrae, Leipzig : W. Engelmann, 1760. https://archive.org/details/lambertsph otome00lambgoog.
[54] Beer, Bestimmung der Absorption des rothen Lichts in farbigen Flüssigkeiten, Ann. Phys. 162 (1852) 78-88, https://doi.org/10.1002/andp. 18521620505.
[55] J.I. Pankove, Optical Processes in Semiconductors, Dover Publications, New York, 1971. I. 0-486-60275-3.
[56] R. Vahalová, L. Tichý, M. Vlček, H. Tichá, Far infrared spectra and bonding arrangement in some Ge-Sb-S glasses, Phys. Status Solidi 181 (2000) 199-209, https://doi.org/10.1002/1521-396X(200009), 181:1<199::AID-PSSA199>3.0. CO;2-X.
[57] P. Kubelka, F. Munk, An article on optics of paint layers, Z. Tech. Phys. 12 (1931) 593-601.
[58] Y. Lee, S. Kim, J.K. Kang, S.M. Cohen, Photocatalytic CO2 reduction by a mixed metal (
[59] D. Yamashita, Y. Nakajima, A. Ishizaki, M. Uda, Photoelectron spectrometer equipped with open counter for electronic structures of organic materials, J. Surf. Anal. 14 (2008) 433-436. http://www.sasj.jp/JSA/CONTENTS. /vol.14_4/Vol. 14 No.4/Vol. 14 No. 4 433-436.pdf.
[60] R.J. Davis, M.T. Lloyd, S.R. Ferreira, M.J. Bruzek, S.E. Watkins, L. Lindell, P. Sehati, M. Fahlman, J.E. Anthony, J.W.P. Hsu, Determination of energy level alignment at interfaces of hybrid and organic solar cells under ambient environment, J. Mater. Chem. 21 (2011) 1721-1729, https://doi.org/10.1039/ C0JM02349C.
[61] J. Jasieniak, M. Califano, S.E. Watkins, Size-dependent valence and conduction band-edge energies of semiconductor nanocrystals, ACS Nano 5 (2011) 5888-5902, https://doi.org/10.1021/nn201681s.
[62] P. Kubelka, New contributions to the optics of intensely light-scattering materials. Part I, J. Opt. Soc. Am. 44 (1948) 330, https://doi.org/10.1364/josa.44.000330.
[63] D.R. Duncan, The colour of pigment mixtures, Proc. Phys. Soc. 52 (1940) 390-401, https://doi.org/10.1088/0959-5309/52/3/310.
[64] T. Burger, J. Kuhn, R. Caps, J. Fricke, Quantitative determination of the scattering and absorption coefficients from diffuse reflectance and transmittance measurements: application to pharmaceutical powders, Appl. Spectrosc. 51 (1997) 309-317, https://doi.org/10.1366/0003702971940404.
[65] D.J. Dahm, K.D. Dahm, Representative layer theory for diffuse reflectance, Appl. Spectrosc. 53 (1999) 647-654, https://doi.org/10.1366/0003702991947298.
[66] T. Burger, H.J. Ploss, J. Kuhn, S. Ebel, J. Fricke, Diffuse reflectance and transmittance spectroscopy for the quantitative determination of scattering and absorption coefficients in quantitative powder analysis, Appl. Spectrosc. 51 (1997) 1323-1329, https://doi.org/10.1366/0003702971941999.
[67] S. Landi, I.R. Segundo, E. Freitas, M. Vasilevskiy, J. Carneiro, C.J. Tavares, Use and misuse of the Kubelka-Munk function to obtain the band gap energy from diffuse reflectance measurements, Solid State Commun. 341 (2022) 1-7, https:// doi.org/10.1016/j.ssc.2021.114573.
[68] G. Férey, Hybrid porous solids: past, present, future, Chem. Soc. Rev. 37 (2008) 191-214, https://doi.org/10.1039/b618320b.
[69] M.A. Nasalevich, C.H. Hendon, J.G. Santaclara, K. Svane, B. Van Der Linden, S. L. Veber, M.V. Fedin, A.J. Houtepen, M.A. Van Der Veen, F. Kapteijn, A. Walsh, J. Gascon, Electronic origins of photocatalytic activity in d0 metal organic frameworks, Sci. Rep. 6 (2016) 1-9, https://doi.org/10.1038/srep23676.
[70] P.H.M. Andrade, N. Henry, C. Volkringer, T. Loiseau, H. Vezin, M. Hureau, A. Moissette, Iodine uptake by Zr -/Hf-Based UiO-66 materials: the influence of
metal substitution on iodine evolution, ACS Appl. Mater. Interfaces (2022), https://doi.org/10.1021/acsami.2c07288.
[71] J. Heine, K. Müller-Buschbaum, Engineering metal-based luminescence in coordination polymers and metal-organic frameworks, Chem. Soc. Rev. 42 (2013) 9232-9242, https://doi.org/10.1039/c3cs60232j.
[72] P. Huo, T. Chen, J. Le Hou, L. Yu, Q.Y. Zhu, J. Dai, Ligand-to-ligand charge transfer within metal-organic frameworks based on manganese coordination polymers with tetrathiafulvalene-bicarboxylate and bipyridine ligands, Inorg. Chem. 55 (2016) 6496-6503, https://doi.org/10.1021/acs.inorgchem.6b00571.
[73] C. Xu, Y. Pan, G. Wan, H. Liu, L. Wang, H. Zhou, S.H. Yu, H.L. Jiang, Turning on visible-light photocatalytic C-H oxidation over metal-organic frameworks by introducing metal-to-cluster charge transfer, J. Am. Chem. Soc. 141 (2019) 19110-19117, https://doi.org/10.1021/jacs.9b09954.
[74] C.A. Kent, D. Liu, L. Ma, J.M. Papanikolas, T.J. Meyer, W. Lin, Light harvesting in microscale metal-organic frameworks by energy migration and interfacial electron transfer quenching, J. Am. Chem. Soc. 133 (2011) 12940-12943, https://doi.org/10.1021/ja204214t.
[75] M.A. Nasalevich, M.G. Goesten, T.J. Savenije, F. Kapteijn, J. Gascon, Enhancing optical absorption of metal-organic frameworks for improved visible light photocatalysis, Chem. Commun. 49 (2013) 10575-10577, https://doi.org/ 10.1039/c3cc46398b.
[76] P.H.M. Andrade, M. Moreau, N. Henry, M.T. Bakouche, S. Duval, C. Volkringer, T. Loiseau, M. Hureau, A. Moissette, Raman mapping as a tool for evaluating I2 and I3- diffusion over single-crystal UiO-67_NH2(M) (
[77] P.H.M. Andrade, H. Ahouari, C. Volkringer, T. Loiseau, H. Vezin, M. Hureau, A. Moissette, Electron-donor functional groups, band gap tailoring, and efficient charge separation: three keys to improve the gaseous iodine uptake in MOF materials, ACS Appl. Mater. Interfaces 15 (2023) 31032-31048, https://doi.org/ 10.1021/acsami.3c04955.
[78] T. Ahnfeldt, N. Guillou, D. Gunzelmann, I. Margiolaki, T. Loiseau, G. Férey, J. Senker, N. Stock,
[79] J.H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga, K. P. Lillerud, A new zirconium inorganic building brick forming metal organic frameworks with exceptional stability, J. Am. Chem. Soc. 130 (2008) 13850-13851, https://doi.org/10.1021/ja8057953.
[80] M. Dan-Hardi, C. Serre, T. Frot, L. Rozes, G. Maurin, C. Sanchez, G. Férey, A new photoactive crystalline highly porous titanium(IV) dicarboxylate, J. Am. Chem. Soc. 131 (2009) 10857-10859, https://doi.org/10.1021/ja903726m.
[81] S. Jakobsen, D. Gianolio, D.S. Wragg, M.H. Nilsen, H. Emerich, S. Bordiga, C. Lamberti, U. Olsbye, M. Tilset, K.P. Lillerud, Structural determination of a highly stable metal-organic framework with possible application to interim radioactive waste scavenging: Hf-UiO-66, Phys. Rev. B Condens. Matter Mater. Phys. 86 (2012) 1-11, https://doi.org/10.1103/PhysRevB.86.125429.
[82] M.J. Katz, Z.J. Brown, Y.J. Colón, P.W. Siu, K.A. Scheidt, R.Q. Snurr, J.T. Hupp, O.K. Farha, A facile synthesis of UiO-66, UiO-67 and their derivatives, Chem. Commun. 49 (2013) 9449-9451, https://doi.org/10.1039/C3CC46105J.
[83] M. Leloire, C. Walshe, P. Devaux, R. Giovine, S. Duval, T. Bousquet, S. Chibani, J. Paul, A. Moissette, H. Vezin, P. Nerisson, L. Cantrel, C. Volkringer, T. Loiseau, Capture of gaseous iodine in isoreticular zirconium-based UiO-n metal-organic frameworks: influence of amino functionalization, DFT calculations, Raman and EPR spectroscopic investigation, Chem. Eur. J 28 (2022), https://doi.org/ 10.1002/chem. 202104437 e202104437.
[84] S. Hu, M. Liu, K. Li, Y. Zuo, A. Zhang, C. Song, G. Zhang, X. Guo, Solvothermal synthesis of NH2-MIL-125(Ti) from circular plate to octahedron, CrystEngComm 16 (2014) 9645-9650, https://doi.org/10.1039/c4ce01545b.
[85] A.Y. Galashev, A.S. Vorob’ev, Physical properties of silicene electrodes for Li -,
[86] K. Hendrickx, D.E.P. Vanpoucke, K. Leus, K. Lejaeghere, A. Van Yperen-De Deyne, V. Van Speybroeck, P. Van Der Voort, K. Hemelsoet, Understanding intrinsic light absorption properties of UiO-66 frameworks: a combined theoretical and experimental study, Inorg. Chem. 54 (2015) 10701-10710, https://doi.org/ 10.1021/acs.inorgchem.5b01593.
[87] L.M. Yang, E. Ganz, S. Svelle, M. Tilset, Computational exploration of newly synthesized zirconium metal-organic frameworks UiO-66, -67, -68 and analogues, J. Mater. Chem. C 2 (2014) 7111-7125, https://doi.org/10.1039/c4tc00902a.
[88] A.S. Yasin, J. Li, N. Wu, T. Musho, Study of the inorganic substitution in a functionalized UiO-66 metal-organic framework, Phys. Chem. Chem. Phys. 18 (2016) 12748-12754, https://doi.org/10.1039/c5cp08070c.
[89] A. Wang, Y. Zhou, Z. Wang, M. Chen, L. Sun, X. Liu, Titanium incorporated with UiO-66(Zr)-type metal-organic framework (MOF) for photocatalytic application, RSC Adv. 6 (2016) 3671-3679, https://doi.org/10.1039/c5ra24135a.
[90] J. Tu, X. Zeng, F. Xu, X. Wu, Y. Tian, X. Hou, Z. Long, Microwave-induced fast incorporation of titanium into UiO-66 metal-organic frameworks for enhanced photocatalytic properties, Chem. Commun. 53 (2017) 3361-3364, https://doi. org/10.1039/c7cc00076f.
[91] S. Liu, Z. Ren, H. Xu, Y. Xing, X. Jin, G. Ni, Z. Wang, Visible-light-responsive
[92] X. Zhao, M. Xu, X. Song, X. Liu, W. Zhou, H. Wang, P. Huo, Tailored linker defects in UiO-67 with high ligand-to-metal charge transfer toward efficient photoreduction of CO2, Inorg. Chem. 61 (2022) 1765-1777, https://doi.org/ 10.1021/acs.inorgchem.1c03690.
[93] E. Flage-Larsen, A. Røyset, J.H. Cavka, K. Thorshaug, Band gap modulations in UiO metal-organic frameworks, J. Phys. Chem. C 117 (2013) 20610-20616, https://doi.org/10.1021/jp405335q.
[94] S. Chavan, J.G. Vitillo, D. Gianolio, O. Zavorotynska, B. Civalleri, S. Jakobsen, M. H. Nilsen, L. Valenzano, C. Lamberti, K.P. Lillerud, S. Bordiga, H2 storage in isostructural UiO-67 and UiO-66 MOFs, Phys. Chem. Chem. Phys. 14 (2012) 1614-1626, https://doi.org/10.1039/c1cp23434j.
[95] S.Q. Wang, X. Wang, X.Y. Zhang, X.M. Cheng, J. Ma, W.Y. Sun, Effect of the defect modulator and ligand length of metal-organic frameworks on carbon dioxide photoreduction, ACS Appl. Mater. Interfaces 13 (2021) 61578-61586, https:// doi.org/10.1021/acsami.1c21663.
[96] R. Raciti, R. Bahariqushchi, C. Summonte, A. Aydinli, A. Terrasi, S. Mirabella, Optical bandgap of semiconductor nanostructures: methods for experimental data analysis, J. Appl. Phys. 121 (2017) 234304, https://doi.org/10.1063/1.4986436.
[97] C. Rotaru, S. Nastase, N. Tomozeiu, Amorphous phase influence on the optical bandgap of polysilicon, Phys. Status Solidi 171 (1999) 365-370, https://doi.org/ 10.1002/(SICI)1521-396X(199901)171. :1<365::AID-PSSA365>3.0.CO;2-M.
[98] B. Gu, N.H. Kwong, R. Binder, Relation between the interband dipole and momentum matrix elements in semiconductors, Phys. Rev. B 87 (2013) 125301, https://doi.org/10.1103/PhysRevB.87.125301.
[99] B. Jensen, Quantum theory of the complex dielectric constant of free carriers in polar semiconductors, IEEE J. Quantum Electron. 18 (1982) 1361-1370, https:// doi.org/10.1109/JQE.1982.1071713.
[100] P. Hervé, L.K.J. Vandamme, General relation between refractive index and energy gap in semiconductors, Infrared Phys. Technol. 35 (1994) 609-615, https://doi. org/10.1016/1350-4495(94)90026-4.
[101] H. Finkenrath, The Moss rule and the influence of doping on the optical dielectric constant of semiconductors-I, Infrared Phys. 28 (1988) 327-332, https://doi.org/ 10.1016/0020-0891(88)90054-1.
[102] T.S. Moss, Relations between the refractive index and energy gap of semiconductors, Phys. Status Solidi 131 (1985) 415-427, https://doi.org/ 10.1002/pssb. 2221310202.
[103] N.M. Ravindra, P. Ganapathy, J. Choi, Energy gap-refractive index relations in semiconductors-an overview, Infrared Phys. Technol. 50 (2007) 21-29, https:// doi.org/10.1016/j.infrared.2006.04.001.
[104] D.R. Penn, Wave-number-dependent dielectric function of semiconductors, Phys. Rev. 128 (1962) 2093-2097, https://doi.org/10.1103/PhysRev.128.2093.
[105] S.H. Wemple, Optical oscillator strengths and excitation energies in solids, liquids, and molecules, J. Chem. Phys. 67 (1977) 2151-2168, https://doi.org/ 10.1063/1.435102.
[106] P. George, P. Chowdhury, Complex dielectric transformation of UV-vis diffuse reflectance spectra for estimating optical band-gap energies and materials classification, Analyst 144 (2019) 3005-3012, https://doi.org/10.1039/ c8an02257g.
[107] H.A. Kramers, The quantum theory of dispersion, Nature 114 (1924) 310-311, https://doi.org/10.1038/114310b0.
[108] R. de L. Kronig, On the theory of dispersion of X-rays, J. Opt. Soc. Am. 12 (1926) 547-557, https://doi.org/10.1364/JOSA.12.000547.
[109] A.B. Kuzmenko, Kramers-Kronig constrained variational analysis of optical spectra, Rev. Sci. Instrum. 76 (2005) 83108, https://doi.org/10.1063/1.1979470.
[110] E. Yablonovitch, Photonic band-gap structures, J. Opt. Soc. Am. B 10 (1993) 283-295, https://doi.org/10.1364/JOSAB.10.000283.
- Corresponding author.
E-mail address: pedro.moraisandrade@univ-lille.fr (P.H.M. Andrade).
