DOI: https://doi.org/10.1016/j.ijcard.2025.133443
PMID: https://pubmed.ncbi.nlm.nih.gov/40456317
تاريخ النشر: 2025-05-31
المؤلف: David B. Olawade وآخرون
الموضوع الرئيسي: الذكاء الاصطناعي في الرعاية الصحية
نظرة عامة
تستكشف هذه الدراسة تطبيق تقنيات التعلم الآلي (ML) للتنبؤ بمرض الشريان التاجي (CAD) باستخدام مجموعتين من البيانات: مجموعة بيانات فرامينغهام ومجموعة بيانات ز-علي زاده ساني. من خلال اعتماد منهجية منظمة تشمل معالجة البيانات، واختيار الميزات عبر خوارزمية تحسين بحث النسر الأصلع (BESO)، وتقييم نماذج التصنيف المتعددة، تحدد الأبحاث أن الغابة العشوائية (RF) هي الأكثر فعالية كتصنيف. حققت RF أعلى دقة، ودقة، واسترجاع، ودرجة F1 عبر كلا مجموعتي البيانات، متفوقة بشكل كبير على درجات المخاطر السريرية التقليدية ونماذج ML الأخرى مثل الانحدار اللوجستي (LR)، وآلات الدعم الناقل (SVM)، وجيران الأقرب (KNN).
تسلط الدراسة الضوء على فعالية BESO في تحسين اختيار الميزات، مما يعزز كفاءة النموذج ويزيد من قابليته للتفسير من خلال تقليل أبعاد مجموعات البيانات. ومن الجدير بالذكر أن أداء النماذج الخطية اختلف بشكل كبير بين مجموعتي البيانات، مما يشير إلى أن خصائص مجموعة البيانات تلعب دورًا حاسمًا في فعالية المصنف. تشير النتائج إلى أن تحسين الدقة التنبؤية يمكن أن يؤدي إلى تحسين تصنيف المخاطر والتدخلات المستهدفة في البيئات السريرية. ومع ذلك، فإن الفائدة السريرية لهذه النماذج ستعتمد على قابليتها للتفسير ودمجها في سير العمل الحالي. يجب أن تركز الأبحاث المستقبلية على التحقق من صحة التوقعات، وتأثيرها على اتخاذ القرار السريري، وتطوير واجهات سهلة الاستخدام لتسهيل اعتمادها من قبل مقدمي الرعاية الصحية.
مقدمة
تسلط مقدمة هذه الورقة البحثية الضوء على التحدي الصحي العالمي الكبير الذي يمثله مرض الشريان التاجي (CAD)، وهو أحد الأسباب الرئيسية للمراضة والوفيات المرتبطة بتضيق الشرايين التاجية بسبب تصلب الشرايين. يعد الكشف المبكر أمرًا حيويًا لمنع المضاعفات الشديدة مثل احتشاء عضلة القلب وفشل القلب، ومع ذلك، فإن طرق التشخيص التقليدية غالبًا ما تكون غازية ومكلفة. وقد أدى ذلك إلى زيادة الاهتمام بتقنيات التعلم الآلي (ML) كبدائل غير غازية للتنبؤ بمخاطر CAD باستخدام بيانات المرضى المتاحة بسهولة.
تناقش الورقة تطبيق مجموعة متنوعة من خوارزميات التعلم تحت الإشراف، بما في ذلك الانحدار اللوجستي (LR)، وآلات الدعم الناقل (SVM)، وجيران الأقرب (KNN)، والغابات العشوائية (RF)، في تصنيف مرضى CAD بناءً على عوامل الخطر. ومع ذلك، يمكن أن تعيق التحديات مثل الميزات الزائدة أو غير ذات الصلة في مجموعات البيانات الطبية أداء النموذج. لمعالجة هذه القضايا، يتم التأكيد على اختيار الميزات كاستراتيجية حاسمة، حيث غالبًا ما تفشل الطرق التقليدية مثل تحليل المكونات الرئيسية (PCA) في مجموعات البيانات المعقدة. تم تقديم خوارزمية تحسين بحث النسر الأصلع (BESO) كنهج واعد مستوحى من الطبيعة لاختيار الميزات، حيث توازن بين الاستكشاف والاستغلال لتعزيز تعميم النموذج. تهدف الدراسة إلى تطوير خط أنابيب ML محسن لتنبؤ CAD من خلال دمج BESO مع خوارزميات التصنيف المختلفة، مع التركيز على تقييم تأثير BESO على اختيار الميزات، ومقارنة الدقة التنبؤية عبر نماذج مختلفة، وتحديد النموذج الأكثر فعالية للكشف المبكر عن CAD.
طرق
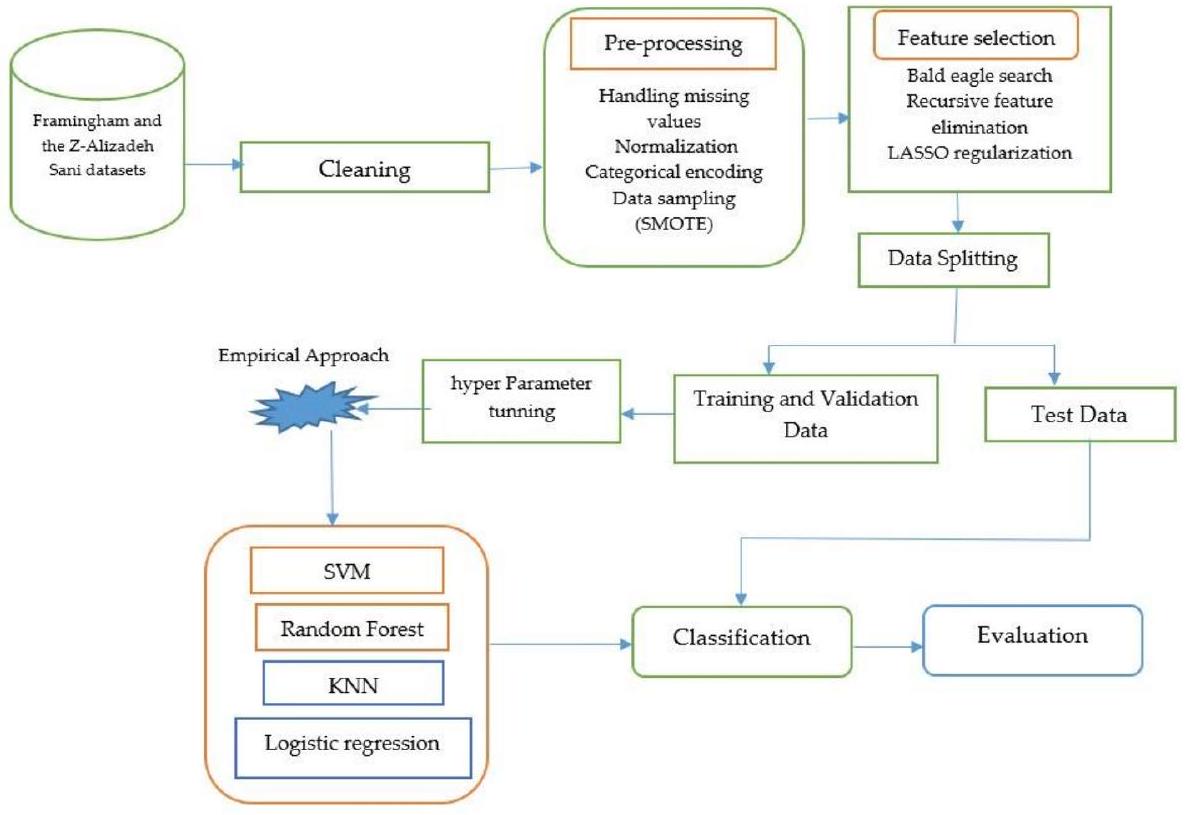
شملت منهجية هذه الدراسة خط أنابيب تعلم آلي منظم يهدف إلى التنبؤ بمرض الشريان التاجي (CAD). تضمنت هذه الخطوط أنشطة مثل الحصول على البيانات، والمعالجة المسبقة، واختيار الميزات عبر خوارزمية تحسين مستوحاة من الطبيعة، وتدريب النموذج مع التقييم. استخدمت عملية اختيار الميزات خوارزمية BESO، التي حددت 10 ميزات مثالية من مجموعة بيانات فرامينغهام، بما في ذلك معدل ضربات القلب، والعمر، ومؤشر كتلة الجسم، بينما تم التخلص من خمسة أخرى. تم تقييم أداء نماذج التعلم الآلي المختلفة، حيث حققت الغابة العشوائية (RF) أعلى دقة، ودقة، واسترجاع، ودرجة F1، مما يدل على قوتها في التقاط الأنماط المعقدة وتقليل أخطاء التصنيف الخاطئ. بالمقابل، كانت النماذج الخطية مثل آلة الدعم الناقل (SVM) مع نواة خطية والانحدار اللوجستي أداؤها ضعيفًا، مما يبرز العلاقات غير الخطية الموجودة في البيانات. أظهرت SVM مع نواة RBF نتائج محسنة، لكنها لا تزال متأخرة عن RF، بينما أظهرت جيران الأقرب (KNN) أداءً مستقرًا، وإن كان أقل من RF.
للمزيد من التحقق من صحة طريقة اختيار الميزات، تم تحليل مجموعة بيانات ز-علي زاده ساني، حيث حددت BESO مرة أخرى 10 ميزات مثالية. حافظت RF على أدائها المتفوق عبر هذه المجموعة من البيانات، بينما حقق الانحدار اللوجستي أداءً أفضل بكثير مما كان عليه في مجموعة بيانات فرامينغهام، مما يشير إلى مساحة ميزات أكثر قابلية للفصل خطيًا. كما أظهرت SVM مع كل من النوى الخطية وRBF أداءً قويًا، مما يدل على أن الميزات المختارة كانت مؤشرات ذات صلة. ومع ذلك، كانت SVM مع نواة متعددة الحدود أداؤها ضعيفًا، مما يشير إلى أن فعاليتها تعتمد على توزيعات الميزات. بشكل عام، تؤكد النتائج على أهمية اختيار الميزات واختيار النموذج في تعزيز الدقة التنبؤية لـ CAD عبر مجموعات بيانات مختلفة.
نتائج
في هذه الدراسة، استخدم المؤلفون مجموعتي بيانات فرامينغهام وز-علي زاده ساني للتنبؤ بمرض الشريان التاجي (CAD) من خلال خط أنابيب تعلم آلي منظم يتضمن اختيار مجموعة فرعية من الميزات عبر خوارزمية تحسين بحث النسر الأصلع (BESO). تشير النتائج إلى أن هذه المنهجية تعزز بشكل كبير اختيار مجموعات الميزات المثلى، مما يحسن الدقة التنبؤية لـ CAD.
تم إجراء تحليل مقارن لمجموعة متنوعة من نماذج التعلم الآلي، بما في ذلك جيران الأقرب (KNN)، وآلة الدعم الناقل (SVM) مع نوى خطية ومتعددة الحدود ووظيفة الأساس الشعاعي (RBF)، والانحدار اللوجستي (LR)، والغابة العشوائية (RF). تم تقييم أداء هذه النماذج باستخدام مقاييس مثل الدقة، والدقة، والاسترجاع، ودرجة F1. تؤكد النتائج على التأثير الإيجابي لـ BESO على كل من اختيار الميزات والأداء التنبؤي العام للنماذج المستخدمة.
مناقشة
تسلط قسم المناقشة في الورقة البحثية الضوء على فعالية نماذج التعلم الآلي، وخاصة الغابة العشوائية (RF)، في التنبؤ بمرض الشريان التاجي (CAD) عند دمجها مع طرق اختيار الميزات المحسنة مثل تحسين بحث النسر الأصلع (BESO). استخدمت الدراسة مجموعتين متميزتين من البيانات – مجموعة بيانات فرامينغهام، التي تركز على التنبؤ بمخاطر القلب والأوعية الدموية على المدى الطويل، ومجموعة بيانات ز-علي زاده ساني، التي تقيم الحالة الحالية لـ CAD. تشير النتائج إلى أن RF تفوقت باستمرار على النماذج الأخرى عبر كلا مجموعتي البيانات، مما يظهر قوتها في التعامل مع البيانات عالية الأبعاد والتقاط التفاعلات المعقدة للميزات، وهو أمر حاسم في التشخيص الطبي.
كشفت التحليلات عن تفاوتات كبيرة في الأداء بين النماذج الخطية، مثل الانحدار اللوجستي (LR) وآلات الدعم الناقل (SVM)، عبر مجموعتي البيانات. بينما واجهت هذه النماذج صعوبة مع مجموعة بيانات فرامينغهام، إلا أنها أدت بشكل أفضل على مجموعة بيانات ز-علي زاده ساني، مما يشير إلى أن طبيعة مجموعة الميزات وهدف التنبؤ تؤثر بشكل كبير على فعالية النموذج. تؤكد الدراسة على أهمية اختيار النموذج المناسب بناءً على خصائص مجموعة البيانات، بالإضافة إلى مزايا BESO في تعزيز أداء النموذج من خلال اختيار الميزات الفعال. لم يحسن BESO الدقة فحسب، بل حافظ أيضًا على الكفاءة الحسابية، مما يبرز إمكانياته في التطبيقات الطبية حيث تكون مجموعات البيانات عالية الأبعاد شائعة. بشكل عام، تدعو النتائج إلى دمج تقنيات التعلم الآلي المتقدمة في تقييم المخاطر السريرية، مما يوفر قدرات تنبؤية محسنة مقارنة بالطرق التقليدية.
القيود
تقدم الدراسة نقاط قوة ملحوظة ولكن أيضًا عدة قيود تستدعي الاعتبار. تتمثل إحدى القيود الرئيسية في الفجوة الكبيرة في الحجم بين مجموعات البيانات المستخدمة؛ حيث تتكون مجموعة بيانات فرامينغهام من أكثر من 4,200 حالة، بينما تحتوي مجموعة بيانات ز-علي زاده ساني على 304 فقط. قد تعيق هذه الفجوة تعميم النموذج، حيث تتطلب نماذج التعلم الآلي عادةً مجموعات بيانات تدريب أكبر لتحقيق الأداء الأمثل. على الرغم من أن تقنيات اختيار الميزات حسنت من فعالية النموذج، إلا أن حجم العينة الصغيرة لمجموعة بيانات ز-علي زاده ساني قد يؤدي إلى إدخال تباين، مما يؤثر على قابلية تعميم النتائج على السكان الأوسع.
بالإضافة إلى ذلك، فإن نقص التحقق الخارجي باستخدام بيانات سريرية من العالم الحقيقي يعد قيدًا حاسمًا. مجموعات البيانات المستخدمة معالجة مسبقًا ومنظمة، مما قد لا يعكس بدقة تعقيدات البيئات السريرية الحقيقية حيث يمكن أن تكون البيانات أكثر ضوضاءً وعرضة للأخطاء. يجب أن تعطي الأبحاث المستقبلية الأولوية لتطبيق المنهجية المقترحة على بيانات المرضى الفعلية لتقييم أهميتها السريرية. علاوة على ذلك، لا تقارن الدراسة خوارزمية اختيار الميزات BESO مع طرق أخرى معروفة، مثل الإزالة التكرارية للميزات (RFE) أو تحليل المكونات الرئيسية (PCA)، والتي يمكن أن توفر رؤى قيمة حول فعاليتها النسبية. أخيرًا، قد تؤثر التحيزات المحتملة الموجودة في مجموعات البيانات، الناجمة عن عوامل ديموغرافية أو مؤسسية، على الأداء التنبؤي للنماذج. سيكون من الضروري معالجة هذه التحيزات والتحقق من صحة النماذج على مجموعات بيانات أكبر وأكثر تنوعًا لتعزيز العدالة وقابلية تطبيق نماذج التنبؤ بمرض الشريان التاجي (CAD) في الممارسة السريرية.
DOI: https://doi.org/10.1016/j.ijcard.2025.133443
PMID: https://pubmed.ncbi.nlm.nih.gov/40456317
Publication Date: 2025-05-31
Author(s): David B. Olawade et al.
Primary Topic: Artificial Intelligence in Healthcare
Overview
This study investigates the application of machine learning (ML) techniques for predicting coronary artery disease (CAD) using two datasets: the Framingham dataset and the Z-Alizadeh Sani dataset. By employing a structured methodology that includes data preprocessing, feature selection via the Bald Eagle Search Optimization (BESO) algorithm, and evaluation of multiple classification models, the research identifies Random Forest (RF) as the most effective classifier. RF achieved the highest accuracy, precision, recall, and F1-score across both datasets, significantly outperforming traditional clinical risk scores and other ML models such as Logistic Regression (LR), Support Vector Machines (SVM), and K-Nearest Neighbors (KNN).
The study highlights the effectiveness of BESO in optimizing feature selection, which not only enhances model efficiency but also improves interpretability by reducing the dimensionality of the datasets. Notably, the performance of linear models varied significantly between the two datasets, indicating that dataset characteristics play a crucial role in classifier efficacy. The findings suggest that improved predictive accuracy could lead to better risk stratification and targeted interventions in clinical settings. However, the clinical utility of these models will depend on their interpretability and integration into existing workflows. Future research should focus on prospective validation, the impact on clinical decision-making, and the development of user-friendly interfaces to facilitate adoption by healthcare providers.
Introduction
The introduction of this research paper highlights the significant global health challenge posed by coronary artery disease (CAD), a leading cause of morbidity and mortality linked to the narrowing of coronary arteries due to atherosclerosis. Early detection is crucial for preventing severe complications such as myocardial infarction and heart failure, yet traditional diagnostic methods are often invasive and costly. This has led to an increasing interest in machine learning (ML) techniques as non-invasive alternatives for predicting CAD risk using readily available patient data.
The paper discusses the application of various supervised learning algorithms, including logistic regression (LR), support vector machines (SVM), K-nearest neighbors (KNN), and random forests (RF), in classifying CAD patients based on risk factors. However, challenges such as redundant or irrelevant features in medical datasets can hinder model performance. To address these issues, feature selection is emphasized as a critical strategy, with traditional methods like Principal Component Analysis (PCA) often falling short in complex datasets. The Bald Eagle Search Optimization (BESO) algorithm is introduced as a promising nature-inspired approach for feature selection, balancing exploration and exploitation to enhance model generalization. The study aims to develop an optimized ML pipeline for CAD prediction by integrating BESO with various classification algorithms, focusing on assessing the impact of BESO on feature selection, comparing predictive accuracy across different models, and identifying the most effective model for early CAD detection.
Methods
The methodology of this study involved a structured machine learning pipeline aimed at predicting coronary artery disease (CAD). This pipeline included data acquisition, preprocessing, feature selection via a nature-inspired optimization algorithm, and model training with evaluation. The feature selection process utilized the BESO algorithm, which identified 10 optimal features from the Framingham dataset, including heart rate, age, and BMI, while discarding five others. The performance of various machine learning models was assessed, with Random Forest (RF) achieving the highest accuracy, precision, recall, and F1-score, indicating its robustness in capturing complex patterns and minimizing misclassification errors. In contrast, linear models such as Support Vector Machine (SVM) with a linear kernel and Logistic Regression performed poorly, highlighting the non-linear relationships present in the data. SVM with an RBF kernel showed improved results, but still lagged behind RF, while K-Nearest Neighbors (KNN) demonstrated stable performance, albeit lower than RF.
To further validate the feature selection method, the Z-Alizadeh Sani dataset was analyzed, where BESO again identified 10 optimal features. RF maintained its superior performance across this dataset, while Logistic Regression performed significantly better than in the Framingham dataset, suggesting a more linearly separable feature space. SVM with both linear and RBF kernels also exhibited strong performance, indicating that the selected features were relevant predictors. However, SVM with a polynomial kernel underperformed, suggesting its effectiveness is contingent on the feature distributions. Overall, the results underscore the importance of feature selection and model choice in enhancing the predictive accuracy for CAD across different datasets.
Results
In this study, the authors utilized the Framingham and Z-Alizadeh Sani datasets to predict coronary artery disease (CAD) through a structured machine learning pipeline that incorporated feature subset selection via the Bald Eagle Search Optimization (BESO) algorithm. The results indicate that this methodology significantly enhances the selection of optimal feature subsets, thereby improving predictive accuracy for CAD.
A comparative analysis of various machine learning models, including K-Nearest Neighbors (KNN), Support Vector Machine (SVM) with linear, polynomial, and radial basis function (RBF) kernels, Logistic Regression (LR), and Random Forest (RF), was conducted. The performance of these models was evaluated using metrics such as accuracy, precision, recall, and F1-score. The findings underscore the positive impact of BESO on both feature selection and the overall predictive performance of the models employed.
Discussion
The discussion section of the research paper highlights the effectiveness of machine learning models, particularly Random Forest (RF), in predicting coronary artery disease (CAD) when combined with optimized feature selection methods like Bald Eagle Search Optimization (BESO). The study utilized two distinct datasets—the Framingham dataset, which focuses on long-term cardiovascular risk prediction, and the Z-Alizadeh Sani dataset, which assesses current CAD status. The results indicate that RF consistently outperformed other models across both datasets, demonstrating its robustness in handling high-dimensional data and capturing complex feature interactions, which is crucial in medical diagnostics.
The analysis revealed significant performance disparities between linear models, such as Logistic Regression (LR) and Support Vector Machines (SVM), across the two datasets. While these models struggled with the Framingham dataset, they performed better on the Z-Alizadeh Sani dataset, suggesting that the nature of the feature set and the prediction target significantly influence model efficacy. The study emphasizes the importance of tailored model selection based on dataset characteristics, as well as the advantages of BESO in enhancing model performance through effective feature selection. BESO not only improved accuracy but also maintained computational efficiency, underscoring its potential in medical applications where high-dimensional datasets are common. Overall, the findings advocate for the integration of advanced machine learning techniques in clinical risk assessment, offering improved predictive capabilities over traditional methods.
Limitations
The study presents notable strengths but also several limitations that warrant consideration. A primary limitation is the significant size discrepancy between the datasets used; the Framingham dataset comprises over 4,200 instances, while the Z-Alizadeh Sani dataset contains only 304. This disparity may hinder model generalization, as machine learning models typically require larger training datasets for optimal performance. Although feature selection techniques improved model efficacy, the small sample size of the Z-Alizadeh Sani dataset could introduce variability, affecting the generalizability of the findings to broader populations.
Additionally, the lack of external validation using real-world clinical data is a critical limitation. The datasets employed are pre-processed and structured, which may not accurately reflect the complexities of real-time clinical environments where data can be noisier and more prone to errors. Future research should prioritize the application of the proposed methodology to actual patient data to evaluate its clinical relevance. Furthermore, the study does not compare the BESO feature selection algorithm with other established methods, such as Recursive Feature Elimination (RFE) or Principal Component Analysis (PCA), which could provide valuable insights into its relative effectiveness. Lastly, potential biases inherent in the datasets, stemming from demographic or institutional factors, may influence the predictive performance of the models. Addressing these biases and validating the models on larger, more diverse datasets will be essential for enhancing the fairness and applicability of coronary artery disease (CAD) prediction models in clinical practice.