DOI: https://doi.org/10.1021/jacs.4c02018
PMID: https://pubmed.ncbi.nlm.nih.gov/38538570
تاريخ النشر: 2024-03-27
تعزيز أداء تطور الهيدروجين الكهروكيميائي من خلال ديناميات الفقاعات الناتجة عن التلاحم
الملخص
تطور فقاعات الغاز الناتجة عن الكهرباء أثناء التحليل الكهربائي للماء يمكن أن يعيق بشكل كبير كفاءة العملية العامة. لذلك، فإن تعزيز مغادرة الفقاعات الناتجة عن الكهرباء أثناء (التحليل الكهربائي للماء) يعد مفيدًا. بالنسبة لفقاعة واحدة، تحدث مغادرة من سطح القطب عندما تنتصر القوة الطافية على القوى المؤثرة لأسفل (مثل قوى التلامس، وقوى مارانغوني، والقوى الكهربائية). في هذا العمل، يتم دراسة ديناميات زوج من
مقدمة
الموجات الصوتية، القوى الطرد المركزي، الحمل الميكانيكي، تعديل الضغط، المجالات المغناطيسية الخارجية) والطرق السلبية.
لا يزال هناك نقص في كيفية استغلال الديناميات الناتجة عن التلاحم لتحسين أداء الأقطاب الكهربائية التي تطلق الغاز. وينطبق هذا أيضًا على تحسين المعلمات، نظرًا للتعقيدات مثل احتمال عودة الفقاعات إلى سطح القطب الكهربائي.
طرق
كوبية زجاجية (هيلما) بأبعاد
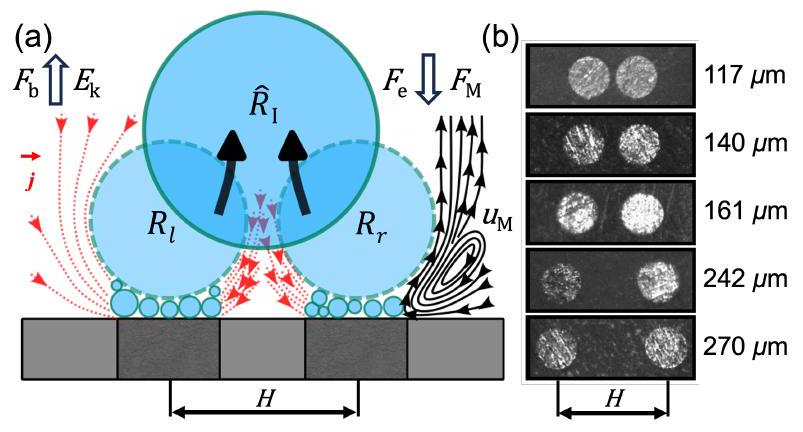
تمت معالجتها بواسطة برنامج DaViS 10، الذي يستخدم خوارزمية تتبع الجسيمات (PTV) لتتبع كل جزيء على مدى 25 مللي ثانية قبل المغادرة. بسبب العدد المحدود من الجزيئات القريبة من أو عند واجهة الفقاعة-الإلكتروليت، تم جمع المسارات الناتجة للجزيئات لـ 60 فقاعة. بعد ذلك، تم تحويل المسارات إلى حقل متجه باستخدام دالة تجميع تقوم بترتيب المسارات المحلية على شبكة دقيقة محددة.
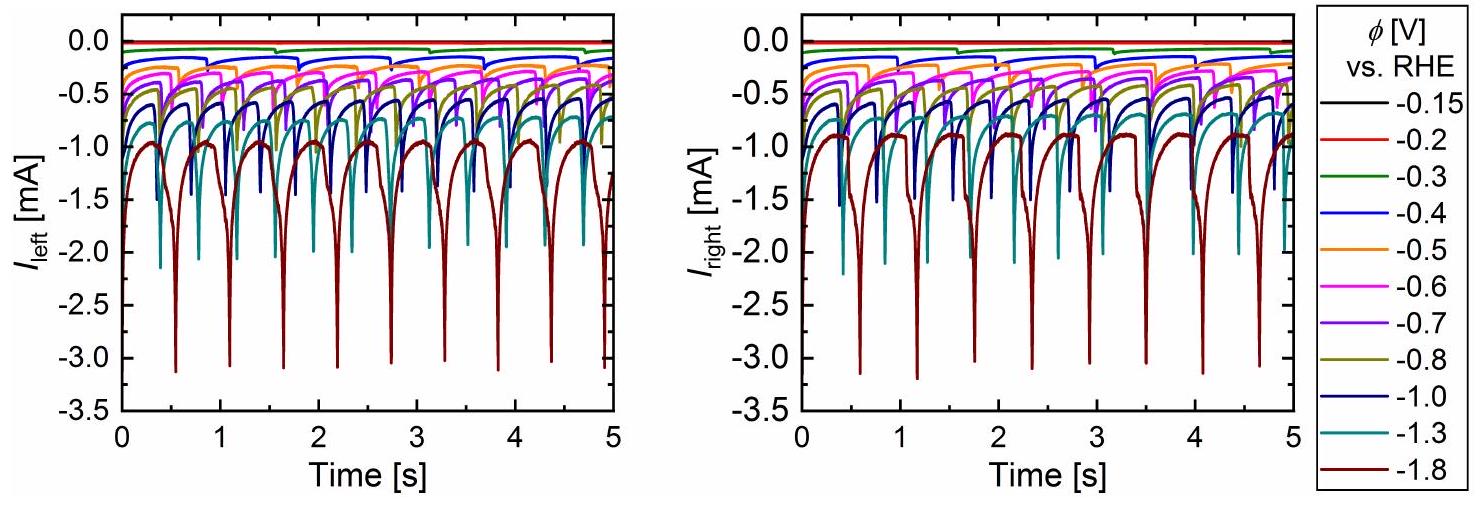
قطب واحد
قطب مزدوج
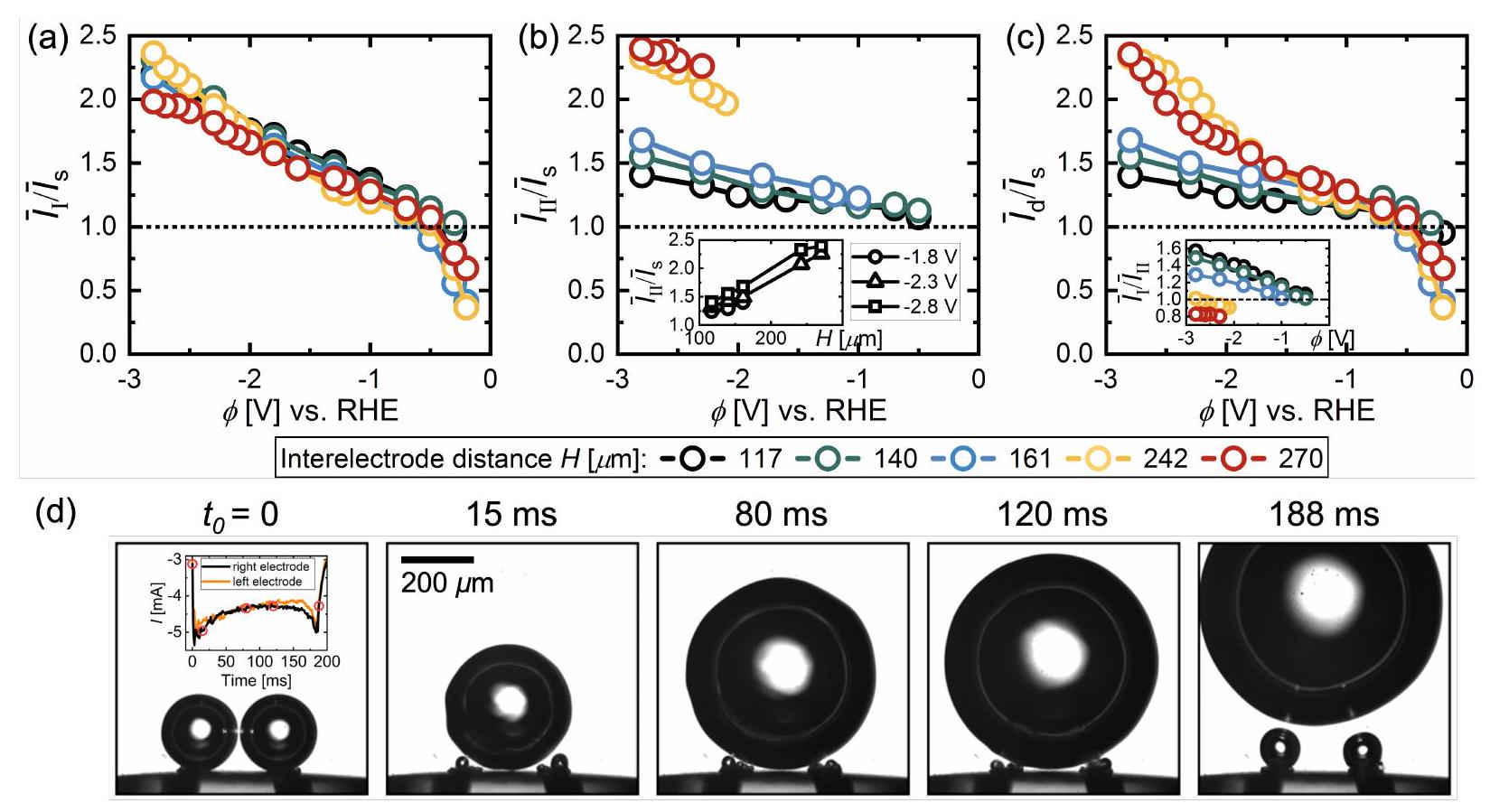
أنماط تطور الفقاعات
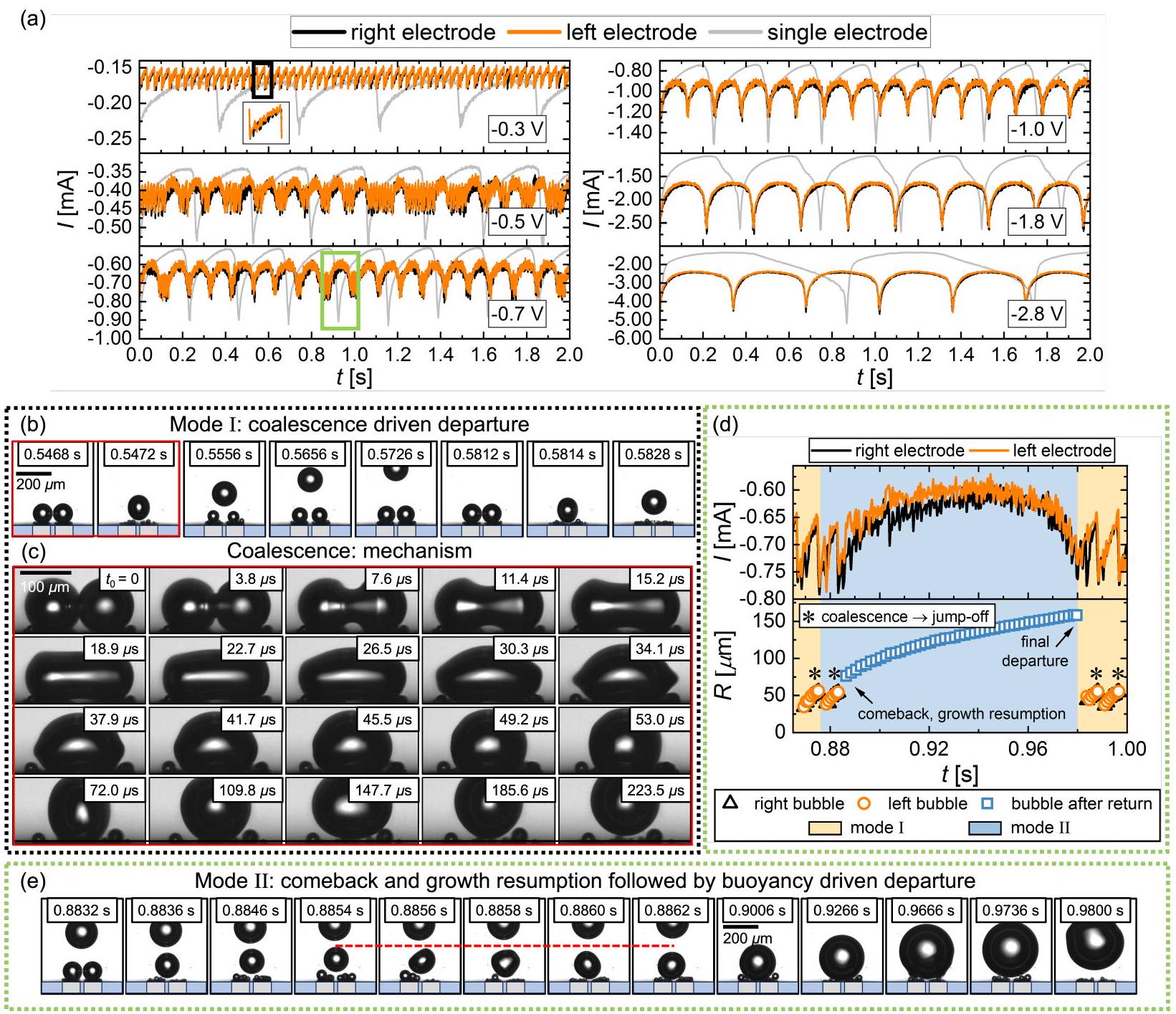
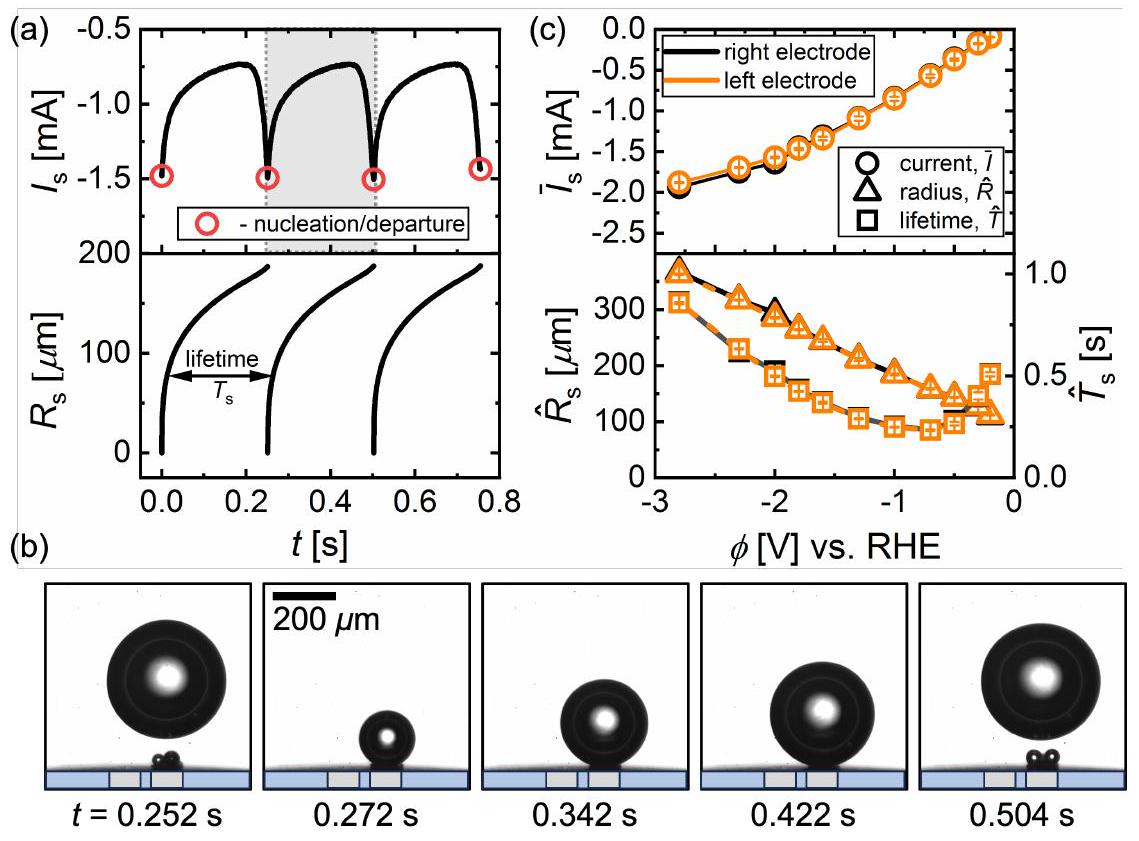
الشكل 3d مع تطور حجم الفقاعات. كانت مغادرة الفقاعة الأولى المضمنة في الشكل 3d تسير بشكل مشابه لتلك المعروضة في الشكل 3b، وتستمر الفقاعة في الارتفاع بعيدًا عن القطب بعد الإقلاع الناتج عن التلاحم. سنشير إلى هذا باسم ‘الوضع I’ من الآن فصاعدًا. ومع ذلك، كما تظهر الظلال المقابلة في الشكل 3e، على الرغم من أن الفقاعة تقفز أيضًا بعد حدث التلاحم الثاني، إلا أنها تُعاد في النهاية إلى السطح من خلال التلاحم المتكرر مع فقاعات جديدة تتشكل عند كلا القطبين (انظر الفترة بين
مخطط الطور
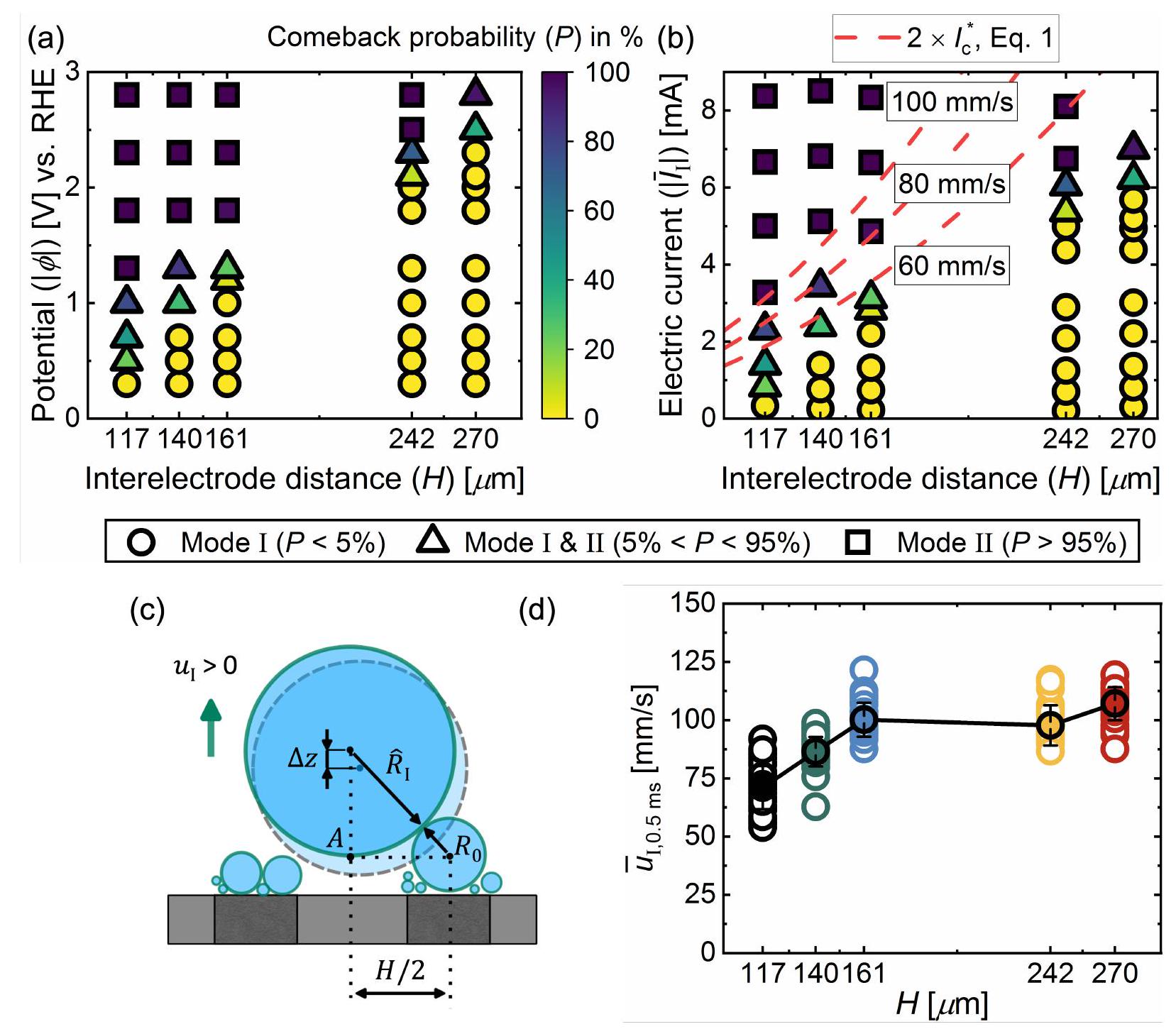
بين الوضع I والوضع II يتم التحكم فيهما بالتالي من خلال تنافس بين سرعة مغادرة أو ‘قفز’ الفقاعة بعد الاندماج ومعدل نمو الفقاعات عند القطب. إن مقدار التيار الكهربائي الأكبر، الذي يزداد تقريبًا بشكل خطي مع
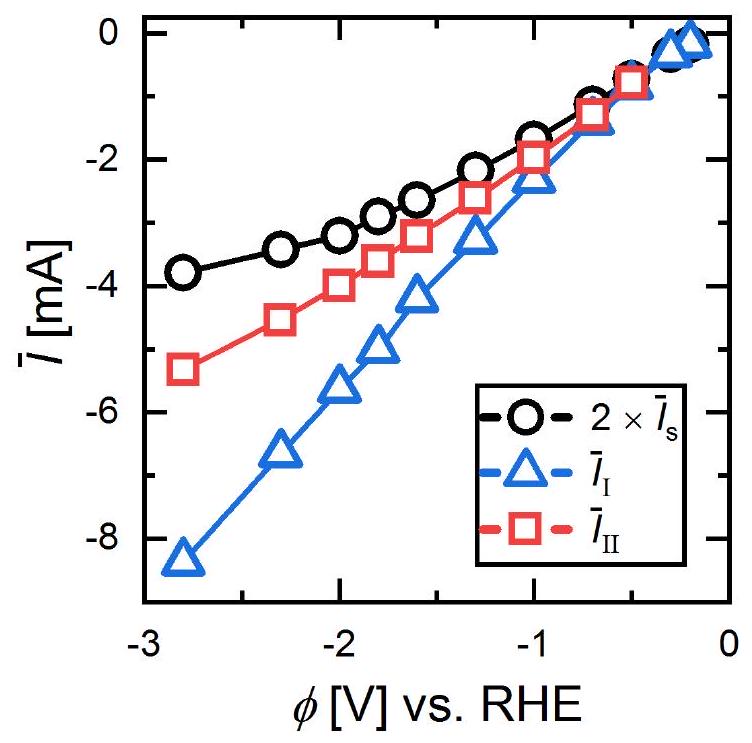
الأداء مقابل مسافة بين الأقطاب
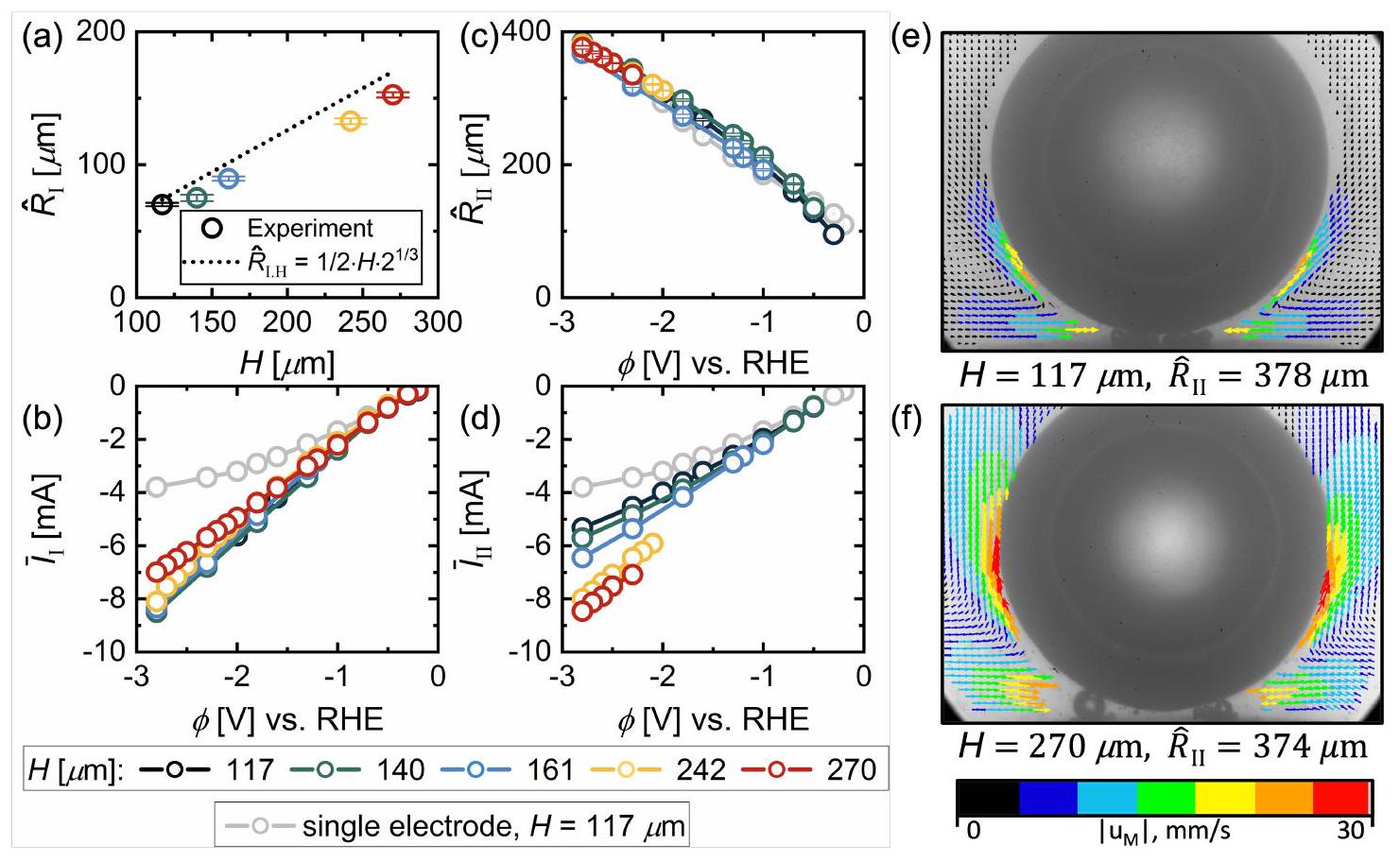
لا تمارس قوة ظاهرة كبيرة على الفقاعة (انظر المعلومات الداعمة للتفاصيل).
في
الاستنتاجات
تعارض المصالح
شكر وتقدير
تلقى D.K. و D.L. و M.T.M.K. تمويلاً من المجلس الأوروبي للبحث (ERC) (رقم اتفاق منحة BU-PACT 950111، رقم منحة متقدمة ERC 740479-DDD ورقم منحة متقدمة ERC ‘FRUMKIN’ 101019998، على التوالي). نشكر V. Sanjay على المناقشات المثمرة حول هذا الموضوع.
References
(2) Staffell, I.; Scamman, D.; Abad, A. V.; Balcombe, P.; Dodds, P. E.; Ekins, P.; Shah, N.; Ward, K. R. The role of hydrogen and fuel cells in the global energy system. Energy
(3) Dawood, F.; Anda, M.; Shafiullah, G. Hydrogen production for energy: An overview. International Journal of Hydrogen Energy 2020, 45, 3847-3869.
(4) Lee, J. K.; Lee, C.; Fahy, K. F.; Kim, P. J.; Krause, K.; LaManna, J. M.; Baltic, E.; Jacobson, D. L.; Hussey, D. S.; Bazylak, A. Accelerating bubble detachment in porous transport layers with patterned through-pores. ACS Applied Energy Materials 2020, 3, 9676-9684.
(5) Swiegers, G. F.; Terrett, R. N.; Tsekouras, G.; Tsuzuki, T.; Pace, R. J.; Stranger, R. The prospects of developing a highly energy-efficient water electrolyser by eliminating or mitigating bubble effects. Sustainable Energy & Fuels 2021, 5, 1280-1310.
(6) Yu, S.; Li, K.; Wang, W.; Xie, Z.; Ding, L.; Kang, Z.; Wrubel, J.; Ma, Z.; Bender, G.; Yu, H.; others Tuning Catalyst Activation and Utilization Via Controlled Electrode Patterning for Low-Loading and High-Efficiency Water Electrolyzers. Small 2022, 18, 2107745.
(7) Yuan, S.; Zhao, C.; Cai, X.; An, L.; Shen, S.; Yan, X.; Zhang, J. Bubble evolution and transport in PEM water electrolysis: Mechanism, impact, and management. Progress in Energy and Combustion Science 2023, 96, 101075.
(8) Zhao, X.; Ren, H.; Luo, L. Gas bubbles in electrochemical gas evolution reactions. Langmuir 2019, 35, 5392-5408.
(9) Angulo, A.; van der Linde, P.; Gardeniers, H.; Modestino, M.; Rivas, D. F. Influence of bubbles on the energy conversion efficiency of electrochemical reactors. Joule 2020, 4, 555-579.
(10) Angulo, A. E.; Frey, D.; Modestino, M. A. Understanding bubble-induced overpotential losses in multiphase flow electrochemical reactors. Energy & Fuels 2022, 36, 7908-7914.
(11) Shih, A. J.; Monteiro, M. C.; Dattila, F.; Pavesi, D.; Philips, M.; da Silva, A. H.; Vos, R. E.; Ojha, K.; Park, S.; van der Heijden, O.; others Water electrolysis. Nature Reviews Methods Primers 2022, 2, 84.
(12) He, Y.; Cui, Y.; Zhao, Z.; Chen, Y.; Shang, W.; Tan, P. Strategies for bubble removal in electrochemical systems. Energy Reviews 2023, 100015.
(13) Gross, S. J.; McDevitt, K. M.; Mumm, D. R.; Mohraz, A. Mitigating bubble traffic in
gas-evolving electrodes via spinodally derived architectures. ACS Applied Materials
(14) Tang, Z.; Wang, P.; Xu, B.; Meng, L.; Jiang, L.; Liu, H. Bioinspired Robust Water Repellency in High Humidity by Micro-meter-Scaled Conical Fibers: Toward a LongTime Underwater Aerobic Reaction. Journal of the American Chemical Society 2022, 144, 10950-10957.
(15) Krause, L.; Skibińska, K.; Rox, H.; Baumann, R.; Marzec, M. M.; Yang, X.; Mutschke, G.; Żabiński, P.; Lasagni, A. F.; Eckert, K. Hydrogen Bubble Size Distribution on Nanostructured Ni Surfaces: Electrochemically Active Surface Area Versus Wettability. ACS Applied Materials & Interfaces 2023, 15, 18290-18299.
(16) Nam, Y.; Aktinol, E.; Dhir, V. K.; Ju, Y. S. Single bubble dynamics on a superhydrophilic surface with artificial nucleation sites. International Journal of Heat and Mass Transfer 2011, 54, 1572-1577.
(17) Lu, Z.; Zhu, W.; Yu, X.; Zhang, H.; Li, Y.; Sun, X.; Wang, X.; Wang, H.; Wang, J.; Luo, J.; others Ultrahigh hydrogen evolution performance of under-water “superaerophobic”
(18) Li, Y.; Zhang, H.; Xu, T.; Lu, Z.; Wu, X.; Wan, P.; Sun, X.; Jiang, L. Under-water superaerophobic pine-shaped Pt nanoarray electrode for ultrahigh-performance hydrogen evolution. Advanced Functional Materials 2015, 25, 1737-1744.
(19) Hao, J.; Yang, W.; Huang, Z.; Zhang, C. Superhydrophilic and superaerophobic copper phosphide microsheets for efficient electrocatalytic hydrogen and oxygen evolution. Advanced Materials Interfaces 2016, 3, 1600236.
(20) Iwata, R.; Zhang, L.; Wilke, K. L.; Gong, S.; He, M.; Gallant, B. M.; Wang, E. N. Bubble growth and departure modes on wettable/non-wettable porous foams in alkaline water splitting. Joule 2021, 5, 887-900.
(21) Andaveh, R.; Darband, G. B.; Maleki, M.; Rouhaghdam, A. S. Superaerophobic/superhydrophilic surfaces as advanced electrocatalysts for the hydrogen evolution reaction: a comprehensive review. Journal of Materials Chemistry A 2022, 10, 51475173.
(22) Cheng, X.; Du, Z.-d.; Ding, Y.; Li, F.-y.; Hua, Z.-s.; Liu, H. Bubble Management for Electrolytic Water Splitting by Surface Engineering: A Review. Langmuir 2023,
(23) Winther-Jensen, O.; Chatjaroenporn, K.; Winther-Jensen, B.; MacFarlane, D. R. Towards hydrogen production using a breathable electrode structure to directly separate gases in the water splitting reaction. International Journal of Hydrogen Energy 2012, 37, 8185-8189.
(24) Tiwari, P.; Tsekouras, G.; Wagner, K.; Swiegers, G. F.; Wallace, G. G. A new class of bubble-free water electrolyzer that is intrinsically highly efficient. International Journal of Hydrogen Energy 2019, 44, 23568-23579.
(25) Tsekouras, G.; Terrett, R.; Yu, Z.; Cheng, Z.; Swiegers, G. F.; Tsuzuki, T.; Stranger, R.; Pace, R. J. Insights into the phenomenon of ‘bubble-free’ electrocatalytic oxygen evolution from water. Sustainable Energy & Fuels 2021, 5, 808-819.
(26) Hodges, A.; Hoang, A. L.; Tsekouras, G.; Wagner, K.; Lee, C.-Y.; Swiegers, G. F.; Wallace, G. G. A high-performance capillary-fed electrolysis cell promises more costcompetitive renewable hydrogen. Nature Communications 2022, 13, 1304.
(27) Kadyk, T.; Bruce, D.; Eikerling, M. How to Enhance Gas Removal from Porous Electrodes? Scientific Reports 2016, 6.
(28) Teschke, O.; Galembeck, F. A New Type of Separator for High Temperature Water Electrolyzers. Journal of The Electrochemical Society 1983, 130, 33-36.
(29) Teschke, O.; Galembeck, F. Effect of PTFE Coverage on the Performance of Gas Evolving Electrodes. Journal of The Electrochemical Society 1984, 131, 1095-1097.
(30) Brussieux, C.; Viers, P.; Roustan, H.; Rakib, M. Controlled electrochemical gas bubble release from electrodes entirely and partially covered with hydrophobic materials. Electrochimica Acta 2011, 56, 7194-7201.
(31) Lake, J. R.; Soto, Á. M.; Varanasi, K. K. Impact of Bubbles on Electrochemically Active Surface Area of Microtextured Gas-Evolving Electrodes. Langmuir 2022, 38, 3276-3283.
(32) Matsushima, H.; Nishida, T.; Konishi, Y.; Fukunaka, Y.; Ito, Y.; Kuribayashi, K. Water electrolysis under microgravity: Part 1. Experimental technique. Electrochimica Acta 2003, 48, 4119-4125.
(33) Zhou, J.; Zhang, Y.; Wei, J. A modified bubble dynamics model for predicting bubble departure diameter on micro-pin-finned surfaces under microgravity. Applied Thermal Engineering 2018, 132, 450-462.
(34) Brinkert, K.; Richter, M. H.; Akay, Ö.; Liedtke, J.; Giersig, M.; Fountaine, K. T.; Lewerenz, H.-J. Efficient solar hydrogen generation in microgravity environment. Nature Communications 2018, 9, 2527.
(35) Akay, Ö.; Bashkatov, A.; Coy, E.; Eckert, K.; Einarsrud, K. E.; Friedrich, A.; Kimmel, B.; Loos, S.; Mutschke, G.; Röntzsch, L.; others Electrolysis in reduced gravitational environments: current research perspectives and future applications. npj Microgravity 2022, 8, 56.
(36) Akay, Ö.; Poon, J.; Robertson, C.; Abdi, F. F.; Cuenya, B. R.; Giersig, M.; Brinkert, K. Releasing the bubbles: nanotopographical electrocatalyst design for efficient photoelectrochemical hydrogen production in microgravity environment. Advanced Science 2022, 9, 2105380.
(37) Raza, M. Q.; Köckritz, M. v.; Sebilleau, J.; Colin, C.; Zupancic, M.; Bucci, M.; Troha, T.; Golobic, I. Coalescence-induced jumping of bubbles in shear flow in microgravity. Physics of Fluids 2023, 35.
(38) Bashkatov, A.; Yang, X.; Mutschke, G.; Fritzsche, B.; Hossain, S. S.; Eckert, K. Dynamics of single hydrogen bubbles at Pt microelectrodes in microgravity. Physical Chemistry Chemical Physics 2021, 23, 11818-11830.
(39) Janssen, L. J.; Hoogland, J. The effect of electrolytically evolved gas bubbles on the thickness of the diffusion layer. Electrochimica Acta 1970, 15, 1013-1023.
(40) Sides, P. J.; Tobias, C. W. A close view of gas evolution from the back side of a transparent electrode. Journal of the Electrochemical Society 1985, 132, 583.
(41) Hashemi, S. M. H.; Karnakov, P.; Hadikhani, P.; Chinello, E.; Litvinov, S.; Moser, C.; Koumoutsakos, P.; Psaltis, D. A versatile and membrane-less electrochemical reactor for the electrolysis of water and brine. Energy & Environmental Science 2019, 12, 1592-1604.
(42) Ikeda, H.; Misumi, R.; Nishiki, Y.; Kuroda, Y.; Mitsushima, S. tert-Butyl-alcoholinduced breakage of the rigid bubble layer that causes overpotential in the oxygen evolution reaction during alkaline water electrolysis. Electrochimica Acta 2023, 452, 142283.
(43) Westerheide, D. E.; Westwater, J. Isothermal growth of hydrogen bubbles during electrolysis. AIChE Journal 1961, 7, 357-362.
(44) Bashkatov, A.; Hossain, S. S.; Mutschke, G.; Yang, X.; Rox, H.; Weidinger, I. M.; Eckert, K. On the growth regimes of hydrogen bubbles at microelectrodes. Physical Chemistry Chemical Physics 2022, 24, 26738-26752.
(45) Park, S.; Liu, L.; Demirkır, Ç.; van der Heijden, O.; Lohse, D.; Krug, D.; Koper, M. T. Solutal Marangoni effect determines bubble dynamics during electrocatalytic hydrogen evolution. Nature Chemistry 2023, 1-9.
(46) Yang, X.; Karnbach, F.; Uhlemann, M.; Odenbach, S.; Eckert, K. Dynamics of single hydrogen bubbles at a platinum microelectrode. Langmuir 2015, 31, 8184-8193.
(47) Bashkatov, A.; Hossain, S. S.; Yang, X.; Mutschke, G.; Eckert, K. Oscillating hydrogen bubbles at Pt microelectrodes. Physical Review Letters 2019, 123, 214503.
(48) Kristof, P.; Pritzker, M. Effect of electrolyte composition on the dynamics of hydrogen gas bubble evolution at copper microelectrodes. Journal of Applied Electrochemistry 1997, 27, 255-265.
(49) Brandon, N.; Kelsall, G. Growth kinetics of bubbles electrogenerated at microelectrodes. Journal of Applied Electrochemistry 1985, 15, 475-484.
(50) Fernandez, D.; Maurer, P.; Martine, M.; Coey, J.; Möbius, M. E. Bubble formation at a gas-evolving microelectrode. Langmuir 2014, 30, 13065-13074.
(51) Massing, J.; Mutschke, G.; Baczyzmalski, D.; Hossain, S. S.; Yang, X.; Eckert, K.; Cierpka, C. Thermocapillary convection during hydrogen evolution at microelectrodes. Electrochimica Acta 2019, 297, 929-940.
(52) Hossain, S. S.; Mutschke, G.; Bashkatov, A.; Eckert, K. The thermocapillary effect on gas bubbles growing on electrodes of different sizes. Electrochimica Acta 2020, 353, 136461.
(53) Babich, A.; Bashkatov, A.; Yang, X.; Mutschke, G.; Eckert, K. In-situ measurements of temperature field and Marangoni convection at hydrogen bubbles using schlieren and PTV techniques. International Journal of Heat and Mass Transfer 2023, 215, 124466.
(54) Zhan, S.; Yuan, R.; Wang, X.; Zhang, W.; Yu, K.; Li, B.; Wang, Z.; Wang, J. Dynamics of growth and detachment of single hydrogen bubble on horizontal and vertical microelectrode surfaces considering liquid microlayer structure in water electrolysis. Physics of Fluids 2023, 35.
(55) Meulenbroek, A.; Vreman, A.; Deen, N. Competing Marangoni effects form a stagnant cap on the interface of a hydrogen bubble attached to a microelectrode. Electrochimica Acta 2021, 385, 138298.
(56) Perez Sirkin, Y. A.; Gadea, E. D.; Scherlis, D. A.; Molinero, V. Mechanisms of nucleation and stationary states of electrochemically generated nanobubbles. Journal of the American Chemical Society 2019, 141, 10801-10811.
(57) Chen, Q.; Wiedenroth, H. S.; German, S. R.; White, H. S. Electrochemical nucleation of stable
(58) German, S. R.; Edwards, M. A.; Ren, H.; White, H. S. Critical nuclei size, rate, and activation energy of
(59) Sepahi, F.; Verzicco, R.; Lohse, D.; Krug, D. Mass transport at gas-evolving electrodes. 2023.
(60) Young, N.; Goldstein, J. S.; Block, M. The motion of bubbles in a vertical temperature gradient. Journal of Fluid Mechanics 1959, 6, 350-356.
(61) Guelcher, S. A.; Solomentsev, Y. E.; Sides, P. J.; Anderson, J. L. Thermocapillary phenomena and bubble coalescence during electrolytic gas evolution. Journal of The Electrochemical Society 1998, 145, 1848.
(62) Lubetkin, S. Thermal Marangoni effects on gas bubbles are generally accompanied by solutal Marangoni effects. Langmuir 2003, 19, 10774-10778.
(63) Yang, X.; Baczyzmalski, D.; Cierpka, C.; Mutschke, G.; Eckert, K. Marangoni convection at electrogenerated hydrogen bubbles. Physical Chemistry Chemical Physics 2018, 20, 11542-11548.
(64) Soto, Á. M.; Maddalena, T.; Fraters, A.; Van Der Meer, D.; Lohse, D. Coalescence of diffusively growing gas bubbles. Journal of Fluid Mechanics 2018, 846, 143-165.
(65) Lv, P.; Peñas, P.; Eijkel, J.; Van Den Berg, A.; Zhang, X.; Lohse, D.; others Selfpropelled detachment upon coalescence of surface bubbles. Physical Review Letters 2021, 127, 235501.
(66) Sanjay, V.; Lohse, D.; Jalaal, M. Bursting bubble in a viscoplastic medium. Journal of Fluid Mechanics 2021, 922, A2.
(67) Thorncroft, G. E.; Klausner, J. F. Bubble forces and detachment models. Multiphase Science and Technology 2001, 13.
(68) Favre, L.; Colin, C.; Pujet, S.; Mimouni, S. An updated force balance approach to investigate bubble sliding in vertical flow boiling at low and high pressures. International Journal of Heat and Mass Transfer 2023, 211, 124227.
(69) Hossain, S. S.; Bashkatov, A.; Yang, X.; Mutschke, G.; Eckert, K. Force balance of hydrogen bubbles growing and oscillating on a microelectrode. Physical Review E 2022,
(70) Pande, N.; Mul, G.; Lohse, D.; Mei, B. Correlating the short-time current response of a hydrogen evolving nickel electrode to bubble growth. Journal of The Electrochemical Society 2019, 166, E280.
المعلومات الداعمة:
تعزيز الأداء في تطور الهيدروجين الكهروكيميائي من خلال ديناميات الفقاعات الناتجة عن التلاحم
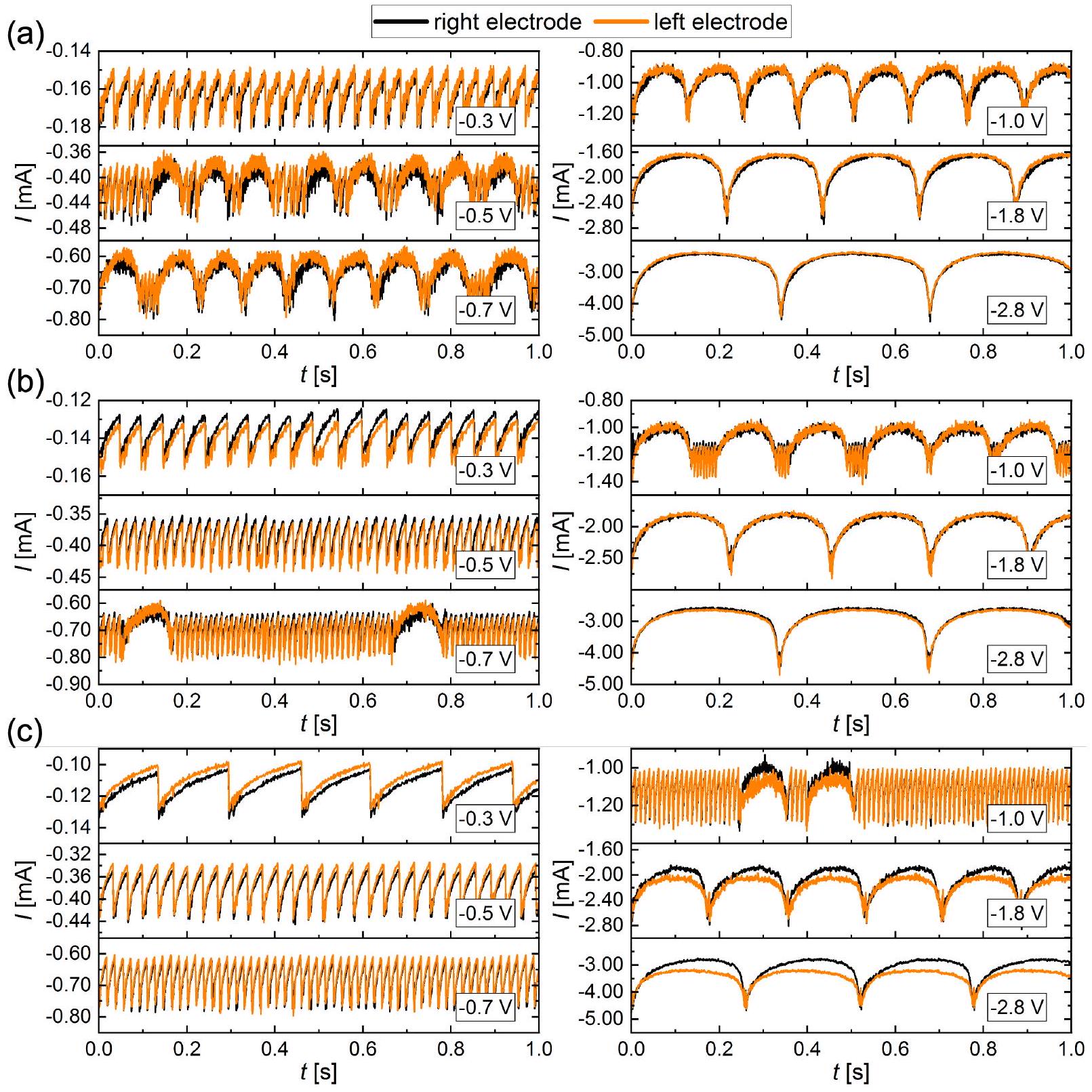
القطب الفردي: التوصيف

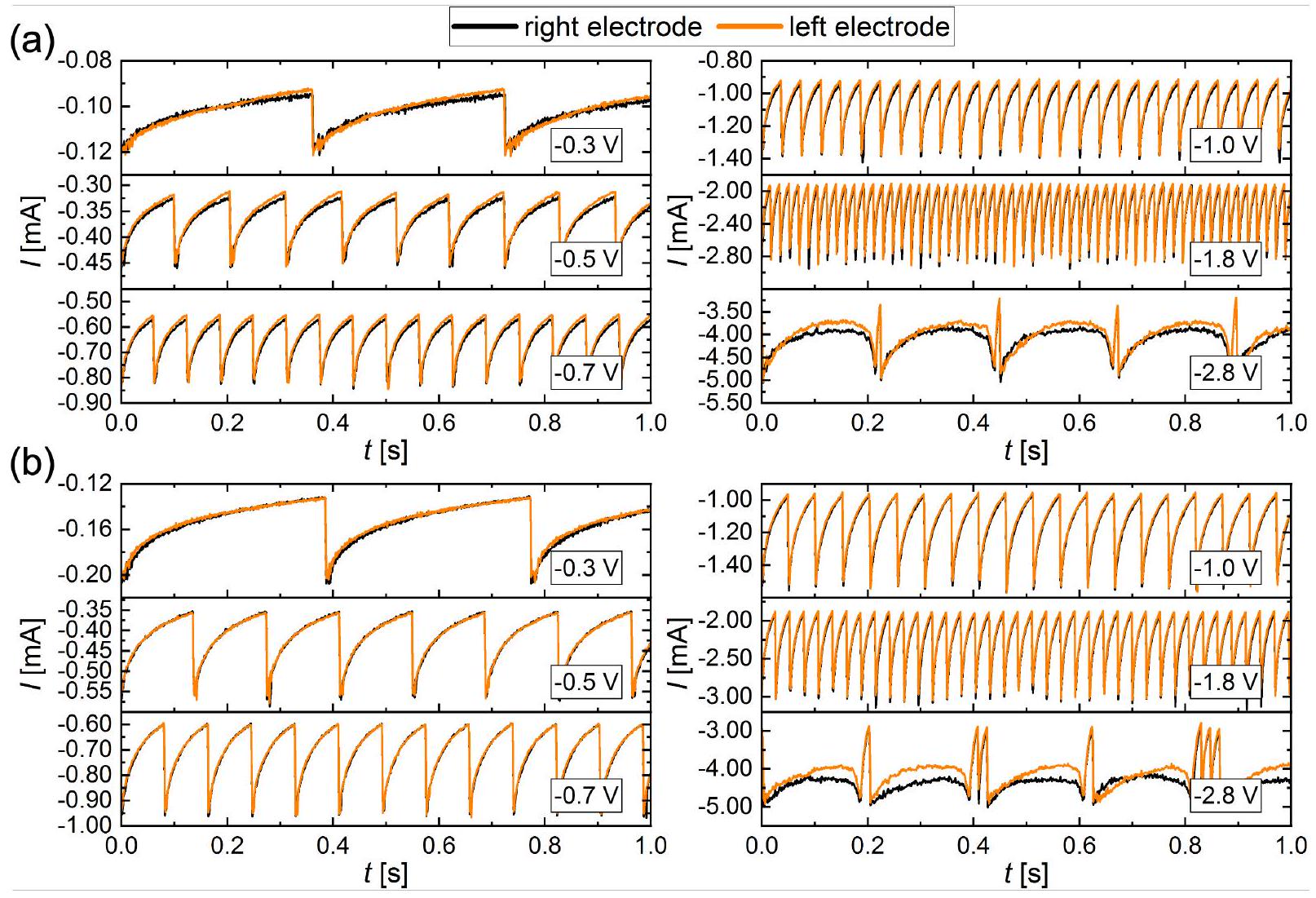
القطب الثنائي: التوصيف
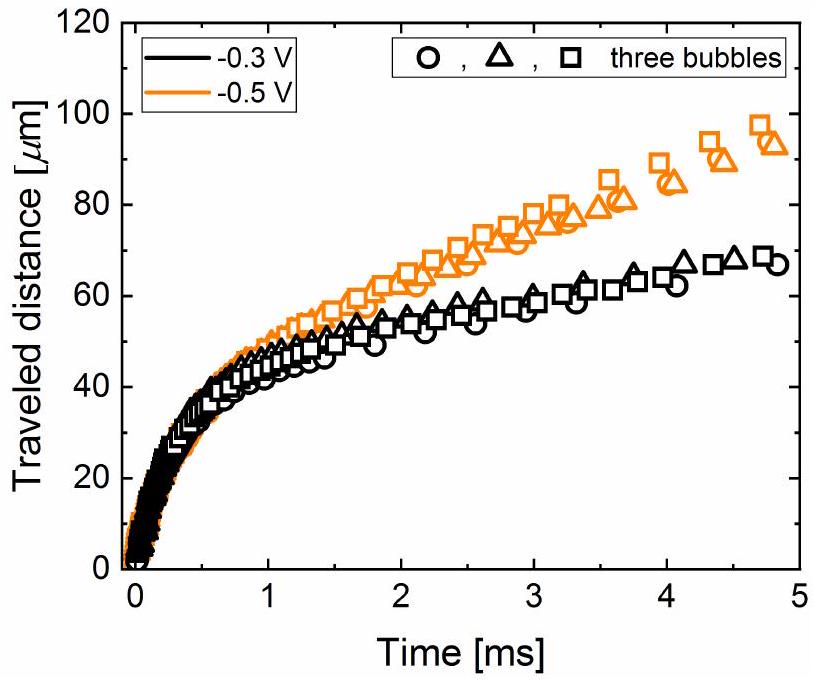
المسافات
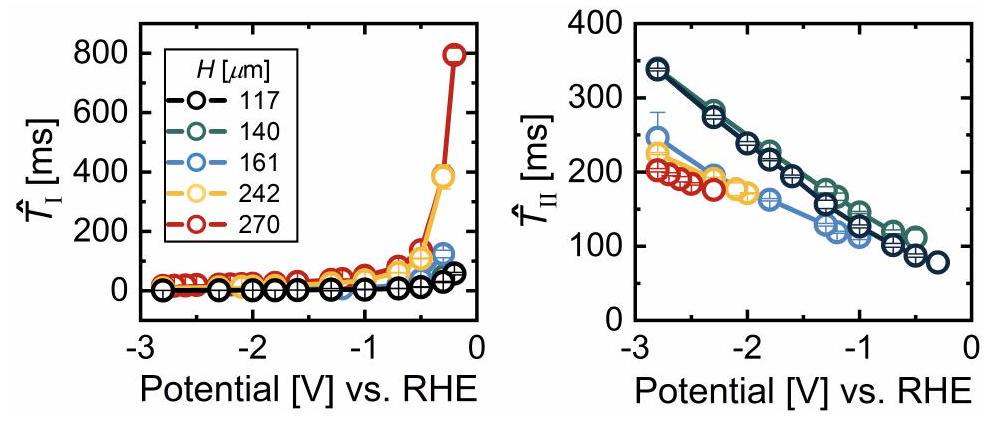

عد إلى القطب الكهربائي بشكل أكثر تكرارًا مع الابتعاد بسرعة قفز أعلى، كما تم التأكيد عليه بالفعل في المخطوطة (انظر الشكل 5).
العملية بواسطة توتر السطح واللزوجة وغالبًا ما يتم وصفها من حيث رقم أونيسورغ
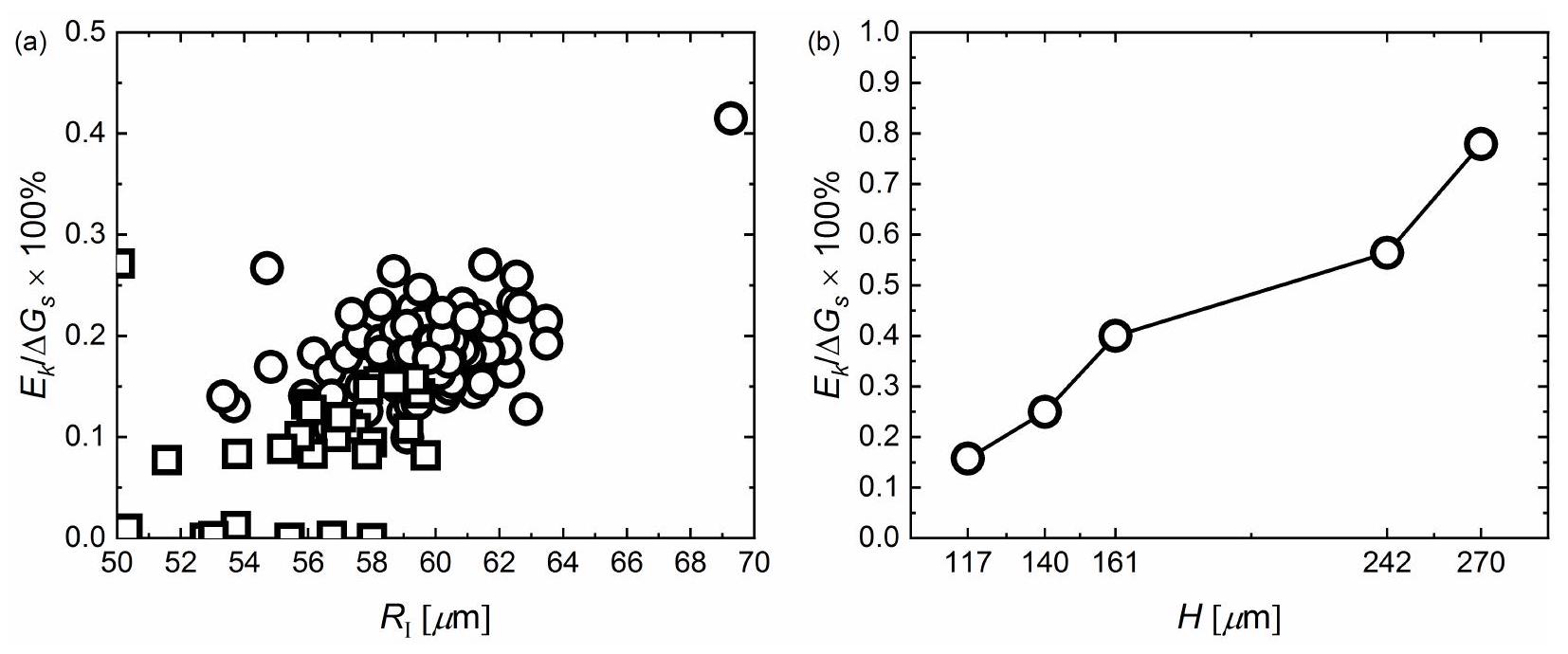
مخطط الطور: نموذج
من خلال استبدال
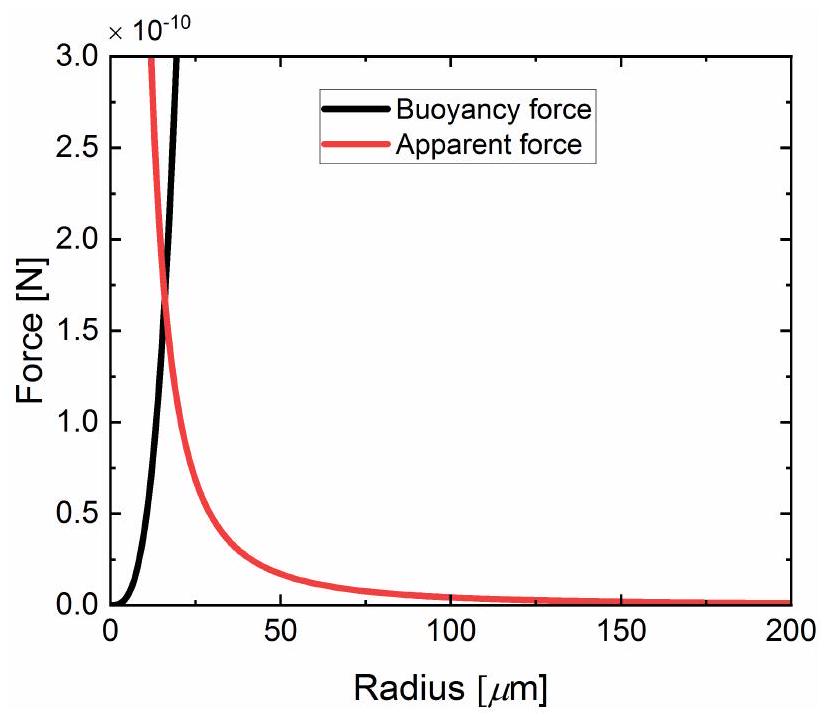
القوة الظاهرة: تفاعل الفقاعة-السجادة
أخيرًا، من خلال استبدال المعادلة 16 في المعادلة 15، تقرأ القوة الظاهرة
References
(2) Raza, M. Q.; Köckritz, M. v.; Sebilleau, J.; Colin, C.; Zupancic, M.; Bucci, M.; Troha, T.;
(3) Sanjay, V.; Lohse, D.; Jalaal, M. Bursting bubble in a viscoplastic medium. Journal of Fluid Mechanics 2021, 922, A2.
DOI: https://doi.org/10.1021/jacs.4c02018
PMID: https://pubmed.ncbi.nlm.nih.gov/38538570
Publication Date: 2024-03-27
Performance enhancement of electrocatalytic hydrogen evolution through coalescence-induced bubble dynamics
Abstract
The evolution of electrogenerated gas bubbles during water electrolysis can significantly hamper the overall process efficiency. Promoting the departure of electrochemically generated bubbles during (water) electrolysis is therefore beneficial. For a single bubble, a departure from the electrode surface occurs when buoyancy wins over the downward-acting forces (e.g. contact, Marangoni, and electric forces). In this work, the dynamics of a pair of
Introduction
sonication, centrifugal forces, mechanical convection, pressure modulation, external magnetic fields) and passive approaches.
to which coalescence-induced dynamics can be exploited to improve the performance of gas-evolving electrodes is still lacking. This also applies to parameter optimisation, which in view of complications such as a possible bubble return to the electrode surface,
Methods
glass cuvette (Hellma) with dimensions of

were processed by the software DaViS 10, which employs a Particle Tracking Velocimetry (PTV) algorithm to track each particle over 25 ms shortly before departure. Due to the limited number of particles close to or at the bubble-electrolyte interface, the resulting tracks of the particles were collected for 60 bubbles. Subsequently, the tracks were converted into a vector field using a binning function that interpolates local tracks on a specified fine grid.
Single electrode

Dual electrode
Modes of bubbles evolution

figure 3d along with the size evolution of the bubbles. The first bubble departure included in figure 3d proceeds analogously to the one shown in figure 3b, and the bubble continues to rise away from the electrode after the coalescence induced take-off. We will refer to this as ‘mode I’ from now on. However, as the corresponding shadowgraphs in figure 3e show, even though the bubble also jumps off after the second coalescence event, it is eventually brought back to the surface through repeated coalescence with newly formed bubbles at both electrodes (see period between

Phase diagram

between mode I and mode II is therefore governed by a competition between the departure or ‘jump’ velocity of a bubble after coalescence and the growth rate of bubbles at the electrode. A larger magnitude of electric current, increasing approximately linearly with
Performance vs. Inter-electrode distance,

does not exert a significant apparent force on the bubble (see Supporting Information for details).

in
Conclusions
Conflicts of interest
Acknowledgements
D.K., D.L. and M.T.M.K. received funding from the European Research Council (ERC) (BU-PACT grant agreement number 950111, ERC Advanced grant number 740479-DDD and ERC Advanced Grant ‘FRUMKIN’ number 101019998, respectively). We thank V. Sanjay for insightful discussions on the subject.
References
(2) Staffell, I.; Scamman, D.; Abad, A. V.; Balcombe, P.; Dodds, P. E.; Ekins, P.; Shah, N.; Ward, K. R. The role of hydrogen and fuel cells in the global energy system. Energy
(3) Dawood, F.; Anda, M.; Shafiullah, G. Hydrogen production for energy: An overview. International Journal of Hydrogen Energy 2020, 45, 3847-3869.
(4) Lee, J. K.; Lee, C.; Fahy, K. F.; Kim, P. J.; Krause, K.; LaManna, J. M.; Baltic, E.; Jacobson, D. L.; Hussey, D. S.; Bazylak, A. Accelerating bubble detachment in porous transport layers with patterned through-pores. ACS Applied Energy Materials 2020, 3, 9676-9684.
(5) Swiegers, G. F.; Terrett, R. N.; Tsekouras, G.; Tsuzuki, T.; Pace, R. J.; Stranger, R. The prospects of developing a highly energy-efficient water electrolyser by eliminating or mitigating bubble effects. Sustainable Energy & Fuels 2021, 5, 1280-1310.
(6) Yu, S.; Li, K.; Wang, W.; Xie, Z.; Ding, L.; Kang, Z.; Wrubel, J.; Ma, Z.; Bender, G.; Yu, H.; others Tuning Catalyst Activation and Utilization Via Controlled Electrode Patterning for Low-Loading and High-Efficiency Water Electrolyzers. Small 2022, 18, 2107745.
(7) Yuan, S.; Zhao, C.; Cai, X.; An, L.; Shen, S.; Yan, X.; Zhang, J. Bubble evolution and transport in PEM water electrolysis: Mechanism, impact, and management. Progress in Energy and Combustion Science 2023, 96, 101075.
(8) Zhao, X.; Ren, H.; Luo, L. Gas bubbles in electrochemical gas evolution reactions. Langmuir 2019, 35, 5392-5408.
(9) Angulo, A.; van der Linde, P.; Gardeniers, H.; Modestino, M.; Rivas, D. F. Influence of bubbles on the energy conversion efficiency of electrochemical reactors. Joule 2020, 4, 555-579.
(10) Angulo, A. E.; Frey, D.; Modestino, M. A. Understanding bubble-induced overpotential losses in multiphase flow electrochemical reactors. Energy & Fuels 2022, 36, 7908-7914.
(11) Shih, A. J.; Monteiro, M. C.; Dattila, F.; Pavesi, D.; Philips, M.; da Silva, A. H.; Vos, R. E.; Ojha, K.; Park, S.; van der Heijden, O.; others Water electrolysis. Nature Reviews Methods Primers 2022, 2, 84.
(12) He, Y.; Cui, Y.; Zhao, Z.; Chen, Y.; Shang, W.; Tan, P. Strategies for bubble removal in electrochemical systems. Energy Reviews 2023, 100015.
(13) Gross, S. J.; McDevitt, K. M.; Mumm, D. R.; Mohraz, A. Mitigating bubble traffic in
gas-evolving electrodes via spinodally derived architectures. ACS Applied Materials
(14) Tang, Z.; Wang, P.; Xu, B.; Meng, L.; Jiang, L.; Liu, H. Bioinspired Robust Water Repellency in High Humidity by Micro-meter-Scaled Conical Fibers: Toward a LongTime Underwater Aerobic Reaction. Journal of the American Chemical Society 2022, 144, 10950-10957.
(15) Krause, L.; Skibińska, K.; Rox, H.; Baumann, R.; Marzec, M. M.; Yang, X.; Mutschke, G.; Żabiński, P.; Lasagni, A. F.; Eckert, K. Hydrogen Bubble Size Distribution on Nanostructured Ni Surfaces: Electrochemically Active Surface Area Versus Wettability. ACS Applied Materials & Interfaces 2023, 15, 18290-18299.
(16) Nam, Y.; Aktinol, E.; Dhir, V. K.; Ju, Y. S. Single bubble dynamics on a superhydrophilic surface with artificial nucleation sites. International Journal of Heat and Mass Transfer 2011, 54, 1572-1577.
(17) Lu, Z.; Zhu, W.; Yu, X.; Zhang, H.; Li, Y.; Sun, X.; Wang, X.; Wang, H.; Wang, J.; Luo, J.; others Ultrahigh hydrogen evolution performance of under-water “superaerophobic”
(18) Li, Y.; Zhang, H.; Xu, T.; Lu, Z.; Wu, X.; Wan, P.; Sun, X.; Jiang, L. Under-water superaerophobic pine-shaped Pt nanoarray electrode for ultrahigh-performance hydrogen evolution. Advanced Functional Materials 2015, 25, 1737-1744.
(19) Hao, J.; Yang, W.; Huang, Z.; Zhang, C. Superhydrophilic and superaerophobic copper phosphide microsheets for efficient electrocatalytic hydrogen and oxygen evolution. Advanced Materials Interfaces 2016, 3, 1600236.
(20) Iwata, R.; Zhang, L.; Wilke, K. L.; Gong, S.; He, M.; Gallant, B. M.; Wang, E. N. Bubble growth and departure modes on wettable/non-wettable porous foams in alkaline water splitting. Joule 2021, 5, 887-900.
(21) Andaveh, R.; Darband, G. B.; Maleki, M.; Rouhaghdam, A. S. Superaerophobic/superhydrophilic surfaces as advanced electrocatalysts for the hydrogen evolution reaction: a comprehensive review. Journal of Materials Chemistry A 2022, 10, 51475173.
(22) Cheng, X.; Du, Z.-d.; Ding, Y.; Li, F.-y.; Hua, Z.-s.; Liu, H. Bubble Management for Electrolytic Water Splitting by Surface Engineering: A Review. Langmuir 2023,
(23) Winther-Jensen, O.; Chatjaroenporn, K.; Winther-Jensen, B.; MacFarlane, D. R. Towards hydrogen production using a breathable electrode structure to directly separate gases in the water splitting reaction. International Journal of Hydrogen Energy 2012, 37, 8185-8189.
(24) Tiwari, P.; Tsekouras, G.; Wagner, K.; Swiegers, G. F.; Wallace, G. G. A new class of bubble-free water electrolyzer that is intrinsically highly efficient. International Journal of Hydrogen Energy 2019, 44, 23568-23579.
(25) Tsekouras, G.; Terrett, R.; Yu, Z.; Cheng, Z.; Swiegers, G. F.; Tsuzuki, T.; Stranger, R.; Pace, R. J. Insights into the phenomenon of ‘bubble-free’ electrocatalytic oxygen evolution from water. Sustainable Energy & Fuels 2021, 5, 808-819.
(26) Hodges, A.; Hoang, A. L.; Tsekouras, G.; Wagner, K.; Lee, C.-Y.; Swiegers, G. F.; Wallace, G. G. A high-performance capillary-fed electrolysis cell promises more costcompetitive renewable hydrogen. Nature Communications 2022, 13, 1304.
(27) Kadyk, T.; Bruce, D.; Eikerling, M. How to Enhance Gas Removal from Porous Electrodes? Scientific Reports 2016, 6.
(28) Teschke, O.; Galembeck, F. A New Type of Separator for High Temperature Water Electrolyzers. Journal of The Electrochemical Society 1983, 130, 33-36.
(29) Teschke, O.; Galembeck, F. Effect of PTFE Coverage on the Performance of Gas Evolving Electrodes. Journal of The Electrochemical Society 1984, 131, 1095-1097.
(30) Brussieux, C.; Viers, P.; Roustan, H.; Rakib, M. Controlled electrochemical gas bubble release from electrodes entirely and partially covered with hydrophobic materials. Electrochimica Acta 2011, 56, 7194-7201.
(31) Lake, J. R.; Soto, Á. M.; Varanasi, K. K. Impact of Bubbles on Electrochemically Active Surface Area of Microtextured Gas-Evolving Electrodes. Langmuir 2022, 38, 3276-3283.
(32) Matsushima, H.; Nishida, T.; Konishi, Y.; Fukunaka, Y.; Ito, Y.; Kuribayashi, K. Water electrolysis under microgravity: Part 1. Experimental technique. Electrochimica Acta 2003, 48, 4119-4125.
(33) Zhou, J.; Zhang, Y.; Wei, J. A modified bubble dynamics model for predicting bubble departure diameter on micro-pin-finned surfaces under microgravity. Applied Thermal Engineering 2018, 132, 450-462.
(34) Brinkert, K.; Richter, M. H.; Akay, Ö.; Liedtke, J.; Giersig, M.; Fountaine, K. T.; Lewerenz, H.-J. Efficient solar hydrogen generation in microgravity environment. Nature Communications 2018, 9, 2527.
(35) Akay, Ö.; Bashkatov, A.; Coy, E.; Eckert, K.; Einarsrud, K. E.; Friedrich, A.; Kimmel, B.; Loos, S.; Mutschke, G.; Röntzsch, L.; others Electrolysis in reduced gravitational environments: current research perspectives and future applications. npj Microgravity 2022, 8, 56.
(36) Akay, Ö.; Poon, J.; Robertson, C.; Abdi, F. F.; Cuenya, B. R.; Giersig, M.; Brinkert, K. Releasing the bubbles: nanotopographical electrocatalyst design for efficient photoelectrochemical hydrogen production in microgravity environment. Advanced Science 2022, 9, 2105380.
(37) Raza, M. Q.; Köckritz, M. v.; Sebilleau, J.; Colin, C.; Zupancic, M.; Bucci, M.; Troha, T.; Golobic, I. Coalescence-induced jumping of bubbles in shear flow in microgravity. Physics of Fluids 2023, 35.
(38) Bashkatov, A.; Yang, X.; Mutschke, G.; Fritzsche, B.; Hossain, S. S.; Eckert, K. Dynamics of single hydrogen bubbles at Pt microelectrodes in microgravity. Physical Chemistry Chemical Physics 2021, 23, 11818-11830.
(39) Janssen, L. J.; Hoogland, J. The effect of electrolytically evolved gas bubbles on the thickness of the diffusion layer. Electrochimica Acta 1970, 15, 1013-1023.
(40) Sides, P. J.; Tobias, C. W. A close view of gas evolution from the back side of a transparent electrode. Journal of the Electrochemical Society 1985, 132, 583.
(41) Hashemi, S. M. H.; Karnakov, P.; Hadikhani, P.; Chinello, E.; Litvinov, S.; Moser, C.; Koumoutsakos, P.; Psaltis, D. A versatile and membrane-less electrochemical reactor for the electrolysis of water and brine. Energy & Environmental Science 2019, 12, 1592-1604.
(42) Ikeda, H.; Misumi, R.; Nishiki, Y.; Kuroda, Y.; Mitsushima, S. tert-Butyl-alcoholinduced breakage of the rigid bubble layer that causes overpotential in the oxygen evolution reaction during alkaline water electrolysis. Electrochimica Acta 2023, 452, 142283.
(43) Westerheide, D. E.; Westwater, J. Isothermal growth of hydrogen bubbles during electrolysis. AIChE Journal 1961, 7, 357-362.
(44) Bashkatov, A.; Hossain, S. S.; Mutschke, G.; Yang, X.; Rox, H.; Weidinger, I. M.; Eckert, K. On the growth regimes of hydrogen bubbles at microelectrodes. Physical Chemistry Chemical Physics 2022, 24, 26738-26752.
(45) Park, S.; Liu, L.; Demirkır, Ç.; van der Heijden, O.; Lohse, D.; Krug, D.; Koper, M. T. Solutal Marangoni effect determines bubble dynamics during electrocatalytic hydrogen evolution. Nature Chemistry 2023, 1-9.
(46) Yang, X.; Karnbach, F.; Uhlemann, M.; Odenbach, S.; Eckert, K. Dynamics of single hydrogen bubbles at a platinum microelectrode. Langmuir 2015, 31, 8184-8193.
(47) Bashkatov, A.; Hossain, S. S.; Yang, X.; Mutschke, G.; Eckert, K. Oscillating hydrogen bubbles at Pt microelectrodes. Physical Review Letters 2019, 123, 214503.
(48) Kristof, P.; Pritzker, M. Effect of electrolyte composition on the dynamics of hydrogen gas bubble evolution at copper microelectrodes. Journal of Applied Electrochemistry 1997, 27, 255-265.
(49) Brandon, N.; Kelsall, G. Growth kinetics of bubbles electrogenerated at microelectrodes. Journal of Applied Electrochemistry 1985, 15, 475-484.
(50) Fernandez, D.; Maurer, P.; Martine, M.; Coey, J.; Möbius, M. E. Bubble formation at a gas-evolving microelectrode. Langmuir 2014, 30, 13065-13074.
(51) Massing, J.; Mutschke, G.; Baczyzmalski, D.; Hossain, S. S.; Yang, X.; Eckert, K.; Cierpka, C. Thermocapillary convection during hydrogen evolution at microelectrodes. Electrochimica Acta 2019, 297, 929-940.
(52) Hossain, S. S.; Mutschke, G.; Bashkatov, A.; Eckert, K. The thermocapillary effect on gas bubbles growing on electrodes of different sizes. Electrochimica Acta 2020, 353, 136461.
(53) Babich, A.; Bashkatov, A.; Yang, X.; Mutschke, G.; Eckert, K. In-situ measurements of temperature field and Marangoni convection at hydrogen bubbles using schlieren and PTV techniques. International Journal of Heat and Mass Transfer 2023, 215, 124466.
(54) Zhan, S.; Yuan, R.; Wang, X.; Zhang, W.; Yu, K.; Li, B.; Wang, Z.; Wang, J. Dynamics of growth and detachment of single hydrogen bubble on horizontal and vertical microelectrode surfaces considering liquid microlayer structure in water electrolysis. Physics of Fluids 2023, 35.
(55) Meulenbroek, A.; Vreman, A.; Deen, N. Competing Marangoni effects form a stagnant cap on the interface of a hydrogen bubble attached to a microelectrode. Electrochimica Acta 2021, 385, 138298.
(56) Perez Sirkin, Y. A.; Gadea, E. D.; Scherlis, D. A.; Molinero, V. Mechanisms of nucleation and stationary states of electrochemically generated nanobubbles. Journal of the American Chemical Society 2019, 141, 10801-10811.
(57) Chen, Q.; Wiedenroth, H. S.; German, S. R.; White, H. S. Electrochemical nucleation of stable
(58) German, S. R.; Edwards, M. A.; Ren, H.; White, H. S. Critical nuclei size, rate, and activation energy of
(59) Sepahi, F.; Verzicco, R.; Lohse, D.; Krug, D. Mass transport at gas-evolving electrodes. 2023.
(60) Young, N.; Goldstein, J. S.; Block, M. The motion of bubbles in a vertical temperature gradient. Journal of Fluid Mechanics 1959, 6, 350-356.
(61) Guelcher, S. A.; Solomentsev, Y. E.; Sides, P. J.; Anderson, J. L. Thermocapillary phenomena and bubble coalescence during electrolytic gas evolution. Journal of The Electrochemical Society 1998, 145, 1848.
(62) Lubetkin, S. Thermal Marangoni effects on gas bubbles are generally accompanied by solutal Marangoni effects. Langmuir 2003, 19, 10774-10778.
(63) Yang, X.; Baczyzmalski, D.; Cierpka, C.; Mutschke, G.; Eckert, K. Marangoni convection at electrogenerated hydrogen bubbles. Physical Chemistry Chemical Physics 2018, 20, 11542-11548.
(64) Soto, Á. M.; Maddalena, T.; Fraters, A.; Van Der Meer, D.; Lohse, D. Coalescence of diffusively growing gas bubbles. Journal of Fluid Mechanics 2018, 846, 143-165.
(65) Lv, P.; Peñas, P.; Eijkel, J.; Van Den Berg, A.; Zhang, X.; Lohse, D.; others Selfpropelled detachment upon coalescence of surface bubbles. Physical Review Letters 2021, 127, 235501.
(66) Sanjay, V.; Lohse, D.; Jalaal, M. Bursting bubble in a viscoplastic medium. Journal of Fluid Mechanics 2021, 922, A2.
(67) Thorncroft, G. E.; Klausner, J. F. Bubble forces and detachment models. Multiphase Science and Technology 2001, 13.
(68) Favre, L.; Colin, C.; Pujet, S.; Mimouni, S. An updated force balance approach to investigate bubble sliding in vertical flow boiling at low and high pressures. International Journal of Heat and Mass Transfer 2023, 211, 124227.
(69) Hossain, S. S.; Bashkatov, A.; Yang, X.; Mutschke, G.; Eckert, K. Force balance of hydrogen bubbles growing and oscillating on a microelectrode. Physical Review E 2022,
(70) Pande, N.; Mul, G.; Lohse, D.; Mei, B. Correlating the short-time current response of a hydrogen evolving nickel electrode to bubble growth. Journal of The Electrochemical Society 2019, 166, E280.
Supporting Information:
Performance enhancement of electrocatalytic hydrogen evolution through coalescence-induced bubble dynamics
Single electrode: characterization


Dual electrode: characterization


distances



come back to the electrode more often moving away with even higher jumping velocity, as already emphasized in the manuscript (see figure 5).
process is controlled by surface tension and viscosity and is often characterized in terms of the Ohnesorge number

Phase diagram: model
By substituting
Apparent force: bubble-carpet interaction
Finally, by substituting eq. 16 into eq. 15 the apparent force reads

References
(2) Raza, M. Q.; Köckritz, M. v.; Sebilleau, J.; Colin, C.; Zupancic, M.; Bucci, M.; Troha, T.;
(3) Sanjay, V.; Lohse, D.; Jalaal, M. Bursting bubble in a viscoplastic medium. Journal of Fluid Mechanics 2021, 922, A2.
