تقييم فعالية الذاكرة طويلة وقصيرة المدى والشبكة العصبية الاصطناعية في التنبؤ بتركيزات الأوزون اليومية في مدينة لياوتشينغ Assessing the effectiveness of long short-term memory and artificial neural network in predicting daily ozone concentrations in Liaocheng City

المجلة: Scientific Reports، المجلد: 15، العدد: 1
DOI: https://doi.org/10.1038/s41598-025-91329-w
PMID: https://pubmed.ncbi.nlm.nih.gov/40000767
تاريخ النشر: 2025-02-25

تقارير علمية

افتح

تقييم فعالية الذاكرة طويلة وقصيرة المدى والشبكة العصبية الاصطناعية في التنبؤ بتركيزات الأوزون اليومية في مدينة لياوتشينغ

تشينغتشون ⊠ ، زينفانغ وزهاوشينغ وانغ

الملخص

تؤثر تلوث الأوزون على إنتاج الغذاء وصحة الإنسان وحياة الأفراد. بسبب التصنيع السريع والتحضر، شهدت لياوتشينغ زيادة في تركيز الأوزون على مدى عدة سنوات. لذلك، أصبح الأوزون مشكلة بيئية رئيسية في مدينة لياوتشينغ. تم إنشاء نماذج الذاكرة طويلة الأمد (LSTM) والشبكة العصبية الاصطناعية (ANN) للتنبؤ بتركيزات الأوزون في مدينة لياوتشينغ من 2014 إلى 2023. تظهر النتائج تحسنًا عامًا في دقة نموذج LSTM مقارنة بنموذج ANN. مقارنةً بـ ANN، شهد نموذج LSTM زيادة في معامل التحديد. ، قيمة تتراوح من 0.6779 إلى 0.6939، انخفاض في قيمة الجذر التربيعي لمتوسط الخطأ (RMSE) من إلى وانخفاض في قيمة الخطأ المطلق المتوسط (MAE) من إلى دقة التنبؤ لنموذج LSTM تفوق نموذج ANN من حيث R و RMSE و MAE. باختصار، يعتبر LSTM تقنية واعدة لتنبؤ تركيزات الأوزون. علاوة على ذلك، من خلال الاستفادة من البيانات التاريخية، يمكّن LSTM من إجراء تنبؤات دقيقة لتركيزات الأوزون المستقبلية على نطاق عالمي. سيفتح هذا النموذج آفاقًا جديدة للتحكم في تلوث الأوزون والتخفيف منه.

الكلمات الرئيسية الشبكة العصبية الاصطناعية، الذاكرة طويلة وقصيرة المدى، التعلم العميق، الأوزون
تؤثر تلوث الهواء على تغير المناخ وإنتاج الغذاء وحياة الإنسان تؤدي جودة الهواء السيئة سنويًا إلى حوالي 6.5 مليون وفاة مبكرة في جميع أنحاء العالم، مما يمثل حوالي من الوفيات العالمية الأوزون التعرض سنويًا يتسبب في حوالي 400 ألف وفاة مبكرة في جميع أنحاء العالم على الرغم من أن جودة الهواء في الصين تتحسن عامًا بعد عام، إلا أن الأوزون ( لا تزال تسبب حوالي 69 ألف حالة وفاة سنويًا لذلك، من المهم التنبؤ بدقة بالأوزون تركيزات لحياة الإنسان وإدارة جودة الهواء.
تتضمن أساليب التنبؤ بتلوث الهواء بشكل رئيسي المحاكاة العددية والأساليب المعتمدة على البيانات. تأخذ المحاكاة العددية في الاعتبار العمليات الفيزيائية والكيميائية، مثل انتشار ونقل الملوثات الهوائية. تتطلب هذه النماذج العددية معلمات معقدة. تشمل المحاكاة العددية المستخدمة على نطاق واسع نموذج أبحاث الطقس والتنبؤ (WRF) ونموذج WRF-CMAQ. بالإضافة إلى ذلك، تؤدي تعقيدات المحاكاة العددية إلى تكاليف حسابية مرتفعة وصعوبة في إيجاد الحل الأمثل. بالمقابل، تتميز الطرق المعتمدة على البيانات بالبساطة والسرعة والاقتصاد. تشمل الأساليب المعتمدة على البيانات تحليل الانحدار وتعلم الآلة. من بين هذه النماذج في تعلم الآلة، فإن الشبكة العصبية الاصطناعية (ANN) قد حسنت دقة التنبؤ مقارنة بالنماذج الخطية، وبالمقارنة مع المحاكاة العددية، فإن ANN لا تتطلب العمليات الكيميائية والفيزيائية الدقيقة. . علاوة على ذلك، تم استخدام الشبكات العصبية الاصطناعية على نطاق واسع في توقع تلوث الهواء تم نمذجة تركيزات الأوزون البيئي باستخدام الشبكات العصبية الاصطناعية مع المدخلات المثلى في ليمبايات بمدينة سورات (الهند) تظهر النتائج أن نمذجة الشبكات العصبية الاصطناعية تبدو طريقة واعدة لنمذجة تركيزات الأوزون. في السنوات الأخيرة، تم استخدام التعلم العميق على نطاق واسع لمشاكل توقع السلاسل الزمنية. الشبكات العصبية المتكررة (RNNs) مناسبة بشكل خاص لنمذجة
بيانات السلاسل الزمنية. بالمقارنة مع الشبكات العصبية الاصطناعية، يمكن للشبكات العصبية التكرارية أن تستقبل البيانات الأصلية كمدخلات وتتعلم العلاقات الزمنية المفيدة من بيانات السلاسل الزمنية التدريبية. ومع ذلك، فإن مشكلة التدرج في الشبكات العصبية التكرارية التقليدية تحد من قدرتها على التقاط الاعتمادات طويلة المدى، مما يؤدي إلى أداء ضعيف في توقع تلوث الهواء. . ومن ثم، فإن الذاكرة طويلة المدى قصيرة المدى (LSTM) هي بنية شبكة عصبية متكررة (RNN) وتخفف بشكل أكبر من مشكلة تلاشي التدرج في الشبكات العصبية التقليدية. لذا، أصبحت LSTM هي الطريقة الأكثر شعبية في التعلم العميق لتوقع تلوث الهواء. تم تقييم مقاييس الأداء لطرق مختلفة لمجموعة بيانات تلوث الهواء. يتمتع LSTM بأدنى قيمة لمتوسط الخطأ التربيعي (MSE) وهي 0.298، يليه DBN و RNN. من حيث متوسط الخطأ المطلق (MAE)، يمتلك LSTM أدنى قيمة وهي 0.192، يليه RNN و DBN. تُستخدم الشبكات العصبية طويلة الأمد (LSTMs) للتنبؤ بجودة الهواء في مدينة مدريد. عندما يتم استخدام LSTM المتصل بالكامل (FC-LSTM) للتنبؤ بالأوزون، فإنه يحقق أقل قيمة لجذر متوسط الخطأ التربيعي (RMSE). .
لذلك، كان الهدف من هذا البحث هو تقييم وتحديد النموذج الموثوق به للتنبؤ بتركيزات الأوزون في مدينة لياوتشينغ في الصين. تم اختيار بنية نموذج مناسبة للتنبؤ بتركيزات الأوزون من خلال المدخلات المختارة. تشير هذه الدراسة إلى أن LSTM هو حل محتمل للتنبؤ بتركيزات الأوزون.
البحث في توقع الأوزون ( لقد تقدم استخدام تقنيات الذكاء الاصطناعي (AI) في تقدير تركيزات جودة الهواء بشكل كبير في السنوات الأخيرة، مما يوفر نماذج قوية لتوقع جودة الهواء. تحقق الشبكة العصبية الاصطناعية (ANN) جذر متوسط مربع الخطأ (RMSE) قدره مع معامل التحديد 0.52. نموذج الشبكة العصبية الاصطناعية (ANN) للتنبؤ بتركيز الأوزون ليوم واحد قادم أكثر دقة بكثير من نموذج الانحدار الخطي المتعدد (MLR). نموذج الشبكة العصبية متعددة الطبقات (MLP) فعال في التنبؤ تركيزات في زغرب، مع أعلى 0.9 وأدنى RMSE من نموذج MLP المحسن يتفوق على الأساليب الأخرى، بما في ذلك نماذج الاستمرارية والانحدار الخطي، التي تعتمد على افتراضات أبسط وتفشل في التقاط تعقيدات الديناميات الجوية. تتفوق نماذج الشبكات العصبية الاصطناعية عمومًا على نماذج الانحدار المتعدد عند استخدام مدخلات إضافية مثل قيم التأخير أو المتوسطات المتحركة، مع معامل ارتباط (R) من تم استخدام مزيج من تحليل المكونات الرئيسية (PCA) والشبكات العصبية الاصطناعية (ANN) للتنبؤ بتركيزات الأوزون الكلي اليومية، وقد حقق أداءً جيدًا في مومباي وكولكاتا مع ارتباط عالٍ وأخطاء تنبؤ منخفضة. لقد أدت كل من نماذج SVM و ANN أداءً جيدًا في التنبؤ بتركيزات الأوزون، مع 0.9152 و 0.9122، و RMSE بقيمة 7.85 و 7.66، على التوالي يتم استخدام MLPANN لتوقع الحد الأقصى اليومي تركيزات الأوزون مع دمج البيانات غير الخطية. يتحسن RMSE من حوالي (نموذج فوتوكيميائي ثلاثي الأبعاد) إلى 17-18 مع نموذج MLP المحدث يتم استخدام الشبكة العصبية الاصطناعية للتنبؤ بتركيزات الأوزون في جينان، الصين، استنادًا إلى المعلمات الجوية والمتغيرات الزمنية. في مرحلة الاختبار، تحقق الشبكة العصبية الاصطناعية 0.8224 ، يتم حساب RMSE كـ ، ومتوسط الخطأ المطلق هو حقق نموذج MLR 0.491 ، بينما حقق نموذج الشبكة العصبية 0.767، مما يشير إلى أن نموذج الشبكة العصبية الاصطناعية كان أفضل في التنبؤ تركيزات لتوقع الحد الأقصى اليومي متوسط الأوزون (MDA8-O3) ليوم واحد مسبقًا، حقق نموذج CEEMD + CRJ + MLR متوسط خطأ مطلق (MAE) قدره ، و RMSE قدره يظهر نموذج الشبكة العصبية أداءً قويًا لـ التنبؤ، مع يتراوح من 0.49 إلى 0.68 خلال فترة التوقعات من اليوم 0 إلى اليوم 4، في مناطق ملوثة بشدة مثل دلهي، الهند يتم استخدام الشبكة العصبية التقدمية للتنبؤات ليوم واحد قادم متوسط تركيز الأوزون (8 hO3) في نوفي ساد، صربيا. بالنسبة لتوقعات 8 hO3، فإن RMSE ومعامل الارتباط (R) هما و0.910، على التوالي لمحطة دنيفنيك تم استخدام شبكة الأعصاب العامة للتراجع (GRANN) للتنبؤ بـ SOMO35 (مجموع المتوسطات) أكثر من 35 جزء في البليون) لـ 24 دولة أوروبية، مع يظهر الشبكة العصبية الاصطناعية (BP) معدل متوسط أقل معامل الارتباط 0.64، RMSE من ، مما يشير إلى دقة معتدلة ولكن عدم استقرار في التنبؤات، خاصة مع البيانات الكبيرة مجموعات البيانات في بكين. تفوق نموذج SVM-GABPNN على كل من BPANN و GABPANN من خلال تحسين دقة التنبؤ بتركيزات الأوزون بشكل كبير، مع متوسط R قدره 0.94، و RMSE قدره تؤدي الشبكات العصبية الاصطناعية (ANN) أداءً أفضل من النماذج الخطية ونماذج SVM في نمذجة الأوزون. قيم نماذج الانحدار الخطي و SVM هي ، على التوالي، لنيودلهي. وعلى العكس، فإن الشبكة العصبية الاصطناعية تعطي قيمة لـ . LR، الانحدار باستخدام آلات الدعم (SVR)، الانحدار باستخدام العمليات الغاوسية (GPR) والشبكات العصبية الاصطناعية (ANN) قادرون على تقديم أعلى ( و )، على التوالي يتم استخدام شبكة عصبية ذات أقل مربعات مخففة (DLS ANN) لتقدير تركيز الأوزون بناءً على المعلمات الجوية. يظهر نموذج DLSNN خطأ جذر متوسط مربع (RMSE) وخطأ متوسط مطلق (MAE) منخفضين جداً، ومرتفعين نسبياً. ، مؤكداً دقة التوقعات تم استخدام شبكة عصبية فوضوية (CANN) للتنبؤ بمستويات الأوزون في لانتشو. أظهرت CANN خطأ الجذر التربيعي المتوسط (RMSE) بين 2.90 و عبر المحطات و بين 0.9511 و 0.9728، متفوقًا على نماذج ANN و BP و MLR تم تطبيق تحويل المويجات (WT) لإزالة الضوضاء وتعزيز جودة بيانات الإدخال قبل إدخالها إلى نموذج الشبكة العصبية الاصطناعية (ANN). وقد أظهر WT-ANN دقة أكبر في توقع تركيزات الأوزون مقارنةً بالشبكة العصبية الاصطناعية وحدها، مع RMSE قدره 0.9313 جزء في المليون، وMAE من من في محطة DJ-3، حقق نموذج WFANN معامل ارتباط (R) قدره 0.97، مع MAPE قدره ، مقارنةً مع R لنموذج FANN البالغ 0.93 و MAPE لـ نموذج RFNN-GWO يتفوق على الآخرين (RMLP-ANN و RFNN) في توقع تركيزات O3 مع RMSE قدره معامل الارتباط (R) لـ (الاختبار). من خلال دمج نقاط القوة في الشبكات العصبية الاصطناعية وخوارزميات التحسين، تحقق RFNN-GWO دقة عالية واستقرارًا، مما يجعلها مناسبة لتوقع جودة الهواء في المناطق التي تحتوي على بيانات جوية وملوثات معقدة. تظهر الشبكة العصبية الاصطناعية مع تجميع k-means أداءً محسنًا في توقع تركيزات الأوزون مع تقليل بيانات التدريب في سيول، كوريا الجنوبية. بالمقارنة مع RFNN، يظهر RFNN-GOA دقة متفوقة في التنبؤ بمستويات الأوزون السطحي في مدينة أوسييك. نموذج FFBP مع 5 خلايا عصبية في الطبقة المخفية (M-5) لديه أفضل أداء مع 0.8344، و RMSE لـ . وبالمثل، يظهر نموذج LRNN مع 8 خلايا عصبية في الطبقة المخفية (M-8) أداءً جيدًا مع 0.8268 ، و RMSE لـ لقد أدت كل من نماذج FFBP و LRNN بشكل جيد، لكن نموذج FFBP تفوق قليلاً على نموذج LRNN من حيث المؤشرات الإحصائية. .
في السنوات الأخيرة، حاول الباحثون استخدام هياكل تعلم عميق متنوعة لتعزيز القدرة التنبؤية لتركيز الأوزون. يتم استخدام شبكة عصبية تلافيفية عميقة (CNN) للتنبؤ بمستويات الأوزون لمدة 24 ساعة في اليوم التالي استنادًا إلى بيانات الأرصاد الجوية وقياسات تلوث الهواء السابقة. يمكن أن نموذج CNN
توقع تركيزات الأوزون بدقة، مع أداء قوي (مؤشر الاتفاق (IOA) أكبر من 0.85 لـ 19 من 21 محطة) حقق نموذج CNN معامل ارتباط بيرسون (R) قدره 0.79، مما يشير إلى دقة توقعات جيدة إلى حد معقول. يتفوق نموذج الشبكة العصبية التكرارية (RNN) على نموذج WRF-CMAQ التقليدي في التنبؤ بمستويات الأوزون في هانغتشو، مع معامل الارتباط R (0.91) وجذر متوسط مربع الخطأ (RMSE) ( تلتقط الشبكة العصبية المتكررة (RNN) الأنماط الزمنية لتراكم الأوزون وتدهوره بشكل أفضل من طرق التعلم المتطرف (ELM) والشبكة العصبية متعددة الطبقات (MLP) وغابة عشوائية (RF). شبكة الأعصاب المتكررة (RNN) أكثر فعالية من نموذج الشبكة العصبية متعددة الطبقات (MLP) في التنبؤ. تركيزات.آيسيستخدم لتوقع الأوزون ( تركيزات 3 ساعات مقدماً مع معامل ارتباط أعلى (0.8967) وNMSE أقل (0.1174) في بيسكارا، إيطاليا .
لقد حققت شبكات LSTM (الذاكرة طويلة وقصيرة المدى) تقدمًا كبيرًا في التنبؤ بالأوزون المستويات، لا سيما بسبب قدرتها على التقاط الاعتمادات طويلة الأجل في بيانات السلاسل الزمنية. عند مقارنتها بخوارزميات أخرى مثل الشبكات العصبية الاصطناعية (ANN) وطرق الانحدار العشوائي (SGD)، تظهر LE-LSTM أداءً متفوقًا بدقة أعلى وخطأ أقل في توقعات تركيز الأوزون، لا سيما على مجموعات البيانات المتسلسلة والزمنية. نموذج الهجين CNN-LSTM يحسن بشكل كبير دقة التنبؤ مقارنة بالنماذج الأبسط مثل MLP، مع تقليل في RMSE وMAE وMAPE. تم اقتراح نموذج تعلم عميق هجين من تسلسل إلى تسلسل مع آلية انتباه (HSA-Net) لـ التنبؤ في بكين. نموذج HSA-Net يتفوق على النماذج الأساسية الأخرى (مثل Seq2Seq وLSTM وGRU) من حيث RMSE ( )، MAE ( )، و يتفوق نموذج CNN-Transformer في توقع تركيز الأوزون على النماذج الأخرى (ARIMA، CNN)، بقيمة RMSE تساوي يحقق نموذج TLSTM لتوقع تلوث الأوزون أفضل قيمة لجذر متوسط مربع الخطأ (15.5)، يليه نموذج TFF، ثم نموذج LSTM. . في التنبؤ، نموذج PSO-LSTM القيمة أعلى من نماذج RF و LSTM، مما يظهر تحسينات قدرها و على التوالي تم استخدام OzoneNet المستند إلى نموذج LSTM المدمج مع آلية الانتباه الذاتي في توقع تركيزات الأوزون. يتمتع OzoneNet بموثوقية وصلاحية أعلى، متفوقًا على النماذج المرجعية. يعتبر Bi-LSTM الأكثر فعالية في التنبؤ باتجاهات الأوزون على مستوى البلاد، حيث يحقق 0.66 ، و RMSE قدره 15.32 . بالمقابل، فإن نموذج المحول هو الأضعف أداءً، مع 0.57 ، و RMSE قدره .
باختصار، تُظهر نماذج الشبكات العصبية الاصطناعية (ANN) ونماذج الذاكرة طويلة الأمد (LSTM) أداءً قويًا في التنبؤ بتركيزات الأوزون، حيث تحافظ النماذج على مستويات مقبولة من دقة التنبؤ، كما يتضح من القيم المنخفضة لجذر متوسط مربع الخطأ (RMSE) ومتوسط الخطأ المطلق (MAE) والقيم العالية. تشير نجاحات نماذج الشبكات العصبية الاصطناعية (ANN) ونماذج الذاكرة طويلة الأمد (LSTM) إلى أن النماذج المعتمدة على البيانات أظهرت قدرة جيدة على التعميم وكفاءة في التعامل مع توقعات تركيز الأوزون. خاصة عند التعامل مع بيانات الأرصاد الجوية والملوثات المعقدة، يمكن لهذه النماذج تعلم الأنماط مباشرة من كمية كبيرة من البيانات التاريخية دون افتراضات فيزيائية مفرطة. لقد أظهرت هذه الدراسات إمكانيات هذه الطرق في توقع مستويات الأوزون، مما يعود بالفائدة على مراقبة البيئة والصحة العامة. تشير هذه الدراسات إلى أن نماذج ANN وLSTM هي أدوات موثوقة لتوقع تركيزات الأوزون في الهواء، حتى عند تطبيقها على بيانات جديدة وغير مرئية.
ومع ذلك، فإن معظم الأبحاث المتعمقة حول طرق الذكاء الاصطناعي في التنبؤ بتلوث الأوزون قد أغفلت استخدام المعلومات من البيانات السابقة. لذلك، تهدف هذه الدراسة إلى التحقيق في تأثير دمج البيانات المتأخرة على أداء طريقتين من طرق الذكاء الاصطناعي في التنبؤ بتلوث الأوزون.

منطقة الدراسة والبيانات

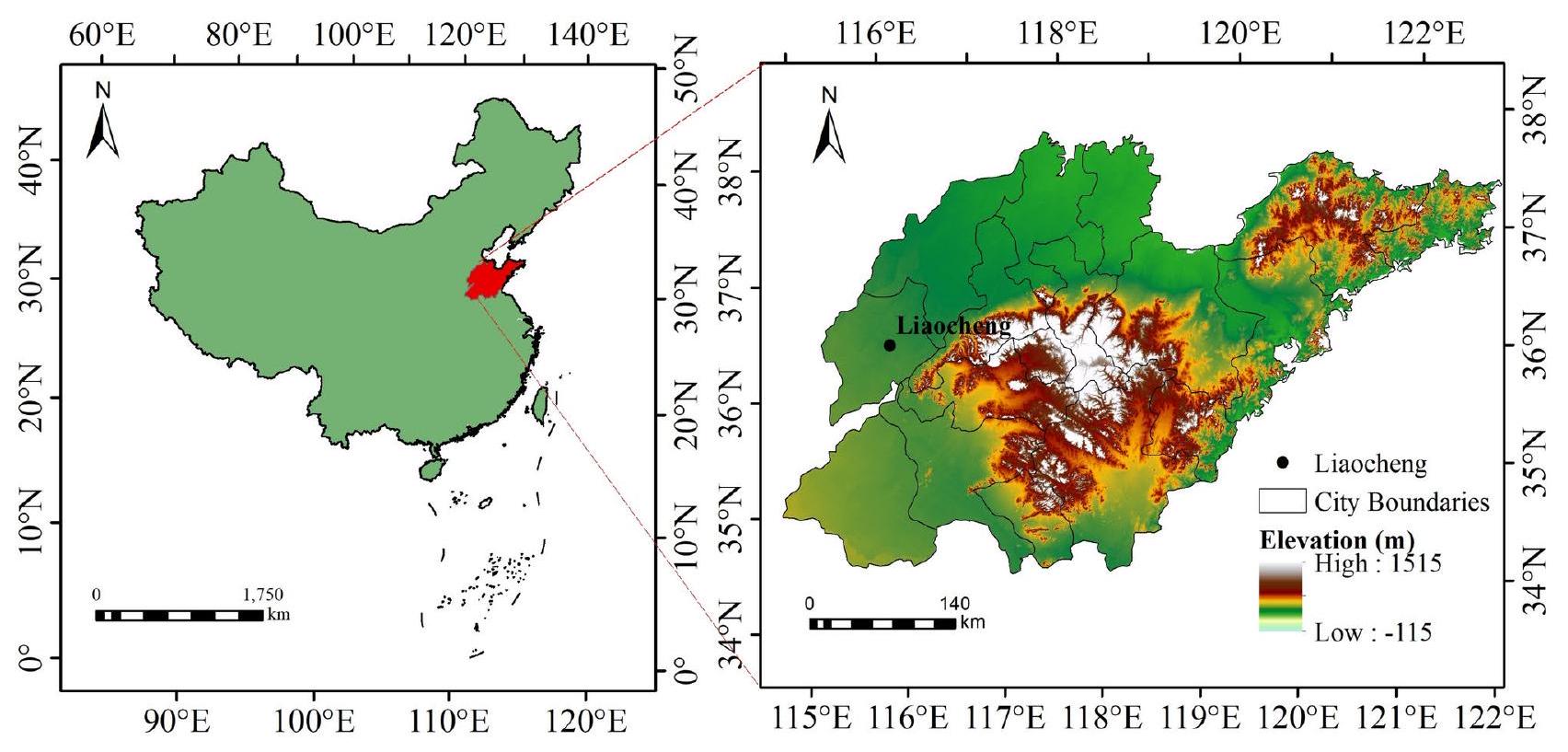
منطقة الدراسة

لياو تشينغ تقع في سهل شمال الصين، وقد تم تضمينها في استراتيجيات وطنية رئيسية مثل التنمية المنسقة لحماية البيئة والتنمية عالية الجودة لحوض نهر هوانغ. في عام 2023، حققت لياو تشينغ ناتجًا محليًا إجماليًا قدره 292.636 مليار يوان، مع نسبة 14.1:37.1:48.8 في الهيكل الصناعي. الإشعاع الشمسي السنوي الإجمالي في لياو تشينغ هو أعلى إشعاع شمسي يكون في الصيف، يليه الربيع، وأدنى مستوى يكون في الشتاء. متوسط ساعات سطوع الشمس السنوية في لياوتشينغ هو 2567 ساعة، مع أقصى حد يبلغ 274 ساعة في مايو وأدنى حد يبلغ 170 ساعة في يناير.

بيانات

من 1 يناير 2014 إلى 27 ديسمبر 2023، تم دراسة تركيزات الأوزون في لياوتشينغ في الصين.http://www.aqistudy.cn/) تم تقسيم بيانات الأوزون إلى ثلاثة مجموعات: فترة التدريب (من 1 يناير 2014 إلى 27 ديسمبر 2021)؛ فترة التحقق (من 28 ديسمبر 2021 إلى 27 ديسمبر 2022)؛ فترة التنبؤ (من 28 ديسمبر 2022 إلى 27 ديسمبر 2023).

المنهجية

الشبكة العصبية الاصطناعية (ANN)

تم بناء الشبكة العصبية الاصطناعية من طبقة أو عدة طبقات وسيطة، وطبقة عصبية للإخراج، وطبقة عصبية للإدخال. تتميز الشبكة العصبية الاصطناعية (ANN) بمجموعة من الخلايا العصبية المعالجة، ودالة تنشيط لكل خلية عصبية، والتعلم. تحتوي الشبكة العصبية الاصطناعية على طوبولوجيا الشبكة والمعلمات، مثل الطبقات المخفية، والعقد (الخلايا العصبية)، وقواعد التعلم، ودوال التنشيط. تم عرض هيكل الشبكة العصبية الاصطناعية في الشكل 2.
الانتشار العكسي هو طريقة مستخدمة على نطاق واسع لتدريب الشبكات العصبية الاصطناعية من خلال تقليل دالة الخطأ العالمية (E). تتضمن هذه العملية حساب الخطأ في توقعات الشبكة وضبط الأوزان وفقًا لذلك لتقليل هذا الخطأ. يتم تعريف E عمومًا على أنه مجموع الفروق المربعة بين المخرجات المرغوبة (Ai) والمخرجات المتوقعة (Bi) من الشبكة، كما هو موضح في المعادلة (1). .
يتم استخدام العامل عادةً لتبسيط حسابات المشتقات التي تحدث لاحقًا أثناء عملية الانتشار العكسي. لتقليل دالة الخطأ العالمية، يتم استخدام خوارزمية الانحدار التدرجي لتحديث أوزان
الشكل 1. موقع لياوتشينغ. تم إنشاء الخريطة باستخدام ArcGIS Pro 2.5 (ArcGIS Pro)، الرابط: https://www.esr iuk.com.
الشكل 2. هيكل الشبكة العصبية الاصطناعية لتوقع تركيزات الأوزون.
الشبكة. قاعدة تحديث الوزن تعتمد على التدرج السالب لدالة الخطأ بالنسبة لكل وزن، كما هو معبر عنه في المعادلة (2):
أين هو التغيير في الوزن بين الخلية العصبية j والخلية العصبية i ؛ و هو معدل التعلم، الذي يتحكم في حجم الخطوة لكل تحديث للوزن. يمثل تدرج دالة الخطأ بالنسبة للوزن △ Dji. يتم حساب هذا التدرج خلال عملية الانتشار العكسي.
هدف خوارزمية التدريب هو تحسين الأوزان (w) والانحيازات (b) لكل خلية عصبية لزيادة الدقة بين المخرجات المتوقعة والفعلية. تشمل خوارزمية الانتشار العكسي ست فئات: التكيف الذاتي
معدل التعلم، الزخم التكيفي، الانتشار العكسي المرن، كوازى-نيوتن، التدرج المترافق، والتقنين البايزي. نقارن 13 خوارزمية تدريب رئيسية لتحسين أداء الشبكات العصبية الاصطناعية، تحديدًا من حيث الدقة في الجدول 1. يتم تحديد أفضل خوارزمية تدريب من خلال نهج التجربة والخطأ. .
اختيار دالة النقل أمر حاسم لتوقع المخرجات، حيث يساعد في تلبية المتطلبات المحددة لعصبونات الشبكة. هناك أربعة أنواع من دوال النقل (دوال التنشيط) وهي: دالة النقل اللوغاريتمية السجومية (logsig، أو sigmoid)، دالة تنشيط الظل الزائد (tansig، أو tanh)، دالة النقل الخطية (purelin)، ووحدات خطية مصححة (relu، أو poslin)، على التوالي. تمثل المعادلات (3)-(6) دوال النقل:
حيث تمثل c المتغير المدخل المقابل.
معدل التعلم هو معلمة مهمة في خوارزمية الانتشار العكسي، تُستخدم لضبط الأوزان بعد كل تكرار. إنه يحدد السرعة التي يتم بها تحديث الأوزان. إذا تم تعيينه مرتفعًا جدًا، فقد تتجاوز النتائج القيمة المثلى. إذا تم تعيينه منخفضًا جدًا، فقد يكون الانحدار بطيئًا جدًا، مما يجعل عملية التحسين غير فعالة. في الشبكة العصبية الاصطناعية، يتم اختيار معدل التعلم ليكون من 0.001 إلى 0.1. بعد الاختبار، كان معدل التعلم 0.01، وحجم الدفعة الأمثل هو 16، وعدد العصور هو 200.

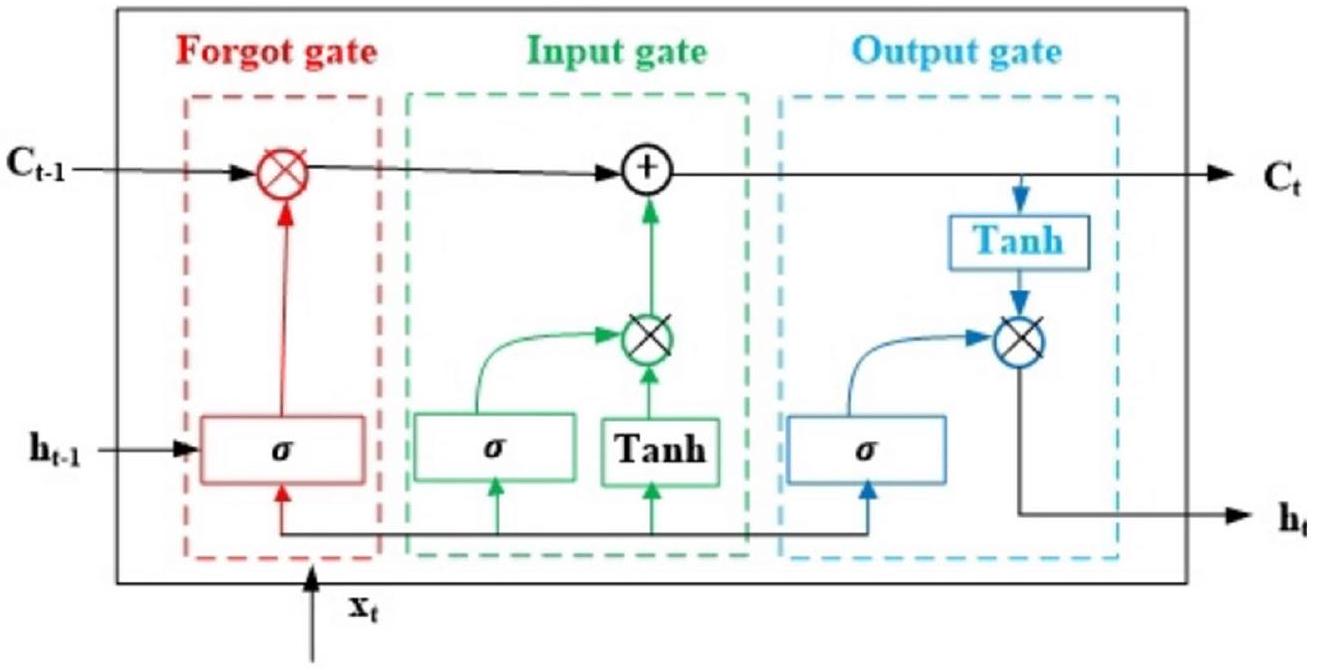
ذاكرة طويلة قصيرة المدى (LSTM)

LSTM هو نموذج RNN معدل يتمتع بقدرة قوية على معالجة البيانات الطويلة. تتكون وحدة LSTM من ثلاث وحدات بوابة ووحدة تخزين (ذاكرة) واحدة، حيث تلعب كل منها دورًا حيويًا في التحكم في تدفق المعلومات. هذه الوحدات البوابة هي بوابات الإدخال، والنسيان، والإخراج. )، والتي تُستخدم للتحكم في الإدخال، والنسيان، والإخراج للمعلومات. تُستخدم وحدة الذاكرة لتخزين وتحديث المعلومات. معًا، تسمح هذه البوابات لشبكة LSTM بتخزين المعلومات واستخدامها بشكل انتقائي، مما يجعل من الممكن التعلم من الاعتمادات القصيرة والطويلة الأمد. هيكل وحدة LSTM موضح في الشكل 3. هو حالة الذاكرة السابقة، تشير إلى معلومات الإخراج السابقة، تشير إلى معلومات الإدخال الجديدة، يمثل دالة السيغمويد المستخدمة في عمليات البوابة تُوصف عمليات هذه البوابات أدناه:
وظائف التدريب خوارزمية التدريب فئة
ترينبر الانتشار العكسي مع تنظيم بايزي (BR) التنظيم البايزي
تدريب خوارزمية ليفنبرغ-ماركوات (LM) للتراجع العكسي كوازى-نيوتن
تراينغديكس انحدار التدرج مع الزخم ومعدل التعلم التكيفي في الانتشار العكسي (GDX) معدل التعلم الذاتي التكيف
تدريب الانحدار التدرجي عبر الانتشار العكسي (GD) الزخم التكيفي
ترينغدم انحدار التدرج مع دالة الزخم (GDM) الزخم التكيفي
ترينغدا انحدار التدرج مع معدل تعلم تكيفي (GDA) معدل تعلم ذاتي التكيف
تدريب الانتشار العكسي المرن (RP) الانتشار العكسي المرن
ترين سي جي بي الانتشار العكسي بتدرج مترافق مع تحديثات بولاك-ريبيير (CGP) خوارزميات التدرج المترافق
تدريب الانتشار العكسي باستخدام تدرج مترافق مع فليتشر-ريفز (CGF) التدرج المترافق
ترين سي جي بي الانتشار العكسي بتدرج مترافق مع إعادة تشغيل باول-بييل (CGB) التدرج المترافق
تدريب الانتشار العكسي بتدرج مترافق مقاس (SCG) خوارزميات التدرج المترافق
تدريب بي إف جي الانتشار العكسي بطريقة BFGS كوانتي-نيوتن (BFGS) كوازى-نيوتن
ترينوس الانتشار العكسي باستخدام القاطع بخطوة واحدة (OSS) كوازى-نيوتن
الجدول 1. وصف لمختلف خوارزميات التدريب.
الشكل 3. مخطط هيكل الشبكة لـ LSTM.
حيث b هو معامل (الوزن) و W هو متجه الانحياز.
تُعتبر الشبكات العصبية طويلة المدى (LSTMs) شائعة بشكل خاص في تنبؤ السلاسل الزمنية بسبب قدرتها على التقاط الاعتمادات الزمنية طويلة المدى في البيانات. هذه ميزة كبيرة مقارنة بشبكات RNN التقليدية، التي غالبًا ما تواجه صعوبة في التعامل مع الاعتمادات طويلة المدى. كما أن LSTMs تتفوق في التقاط الأنماط غير الخطية في البيانات، مما يجعلها فعالة للغاية في التنبؤ من خلال استخدام كل من الذاكرة طويلة الأمد والذاكرة قصيرة المدى ، يمكن لشبكات الذاكرة طويلة الأمد (LSTMs) استرجاع المعلومات ذات الصلة على مقاييس زمنية مختلفة. وهذا يجعلها مناسبة بشكل خاص لمهام مثل التنبؤ، حيث أن فهم كل من الاتجاهات طويلة الأجل والتقلبات قصيرة الأجل أمر ضروري .
التحسين أمر حاسم في تدريب LSTM للعثور على المعلمات المثلى التي تقلل من دالة الخسارة. يتم استخدام مُحسِّن تقدير الزخم التكيفي (ADAM) على نطاق واسع بسبب مزيجه من الزخم ومعدلات التعلم التكيفية، مما يجعله فعالًا في التحسين العشوائي. يتطلب فقط تدرجات من الدرجة الأولى، ويستهلك ذاكرة قليلة، ويحسب معدلات تعلم تكيفية لكل معلمة باستخدام تقديرات اللحظات الأولى والثانية للتدرجات. يمكن أن يتقارب ADAM بشكل أسرع ويتفوق على الانحدار العشوائي (SGD). لذلك، يتم استخدام مُحسِّن ADAM في LSTM. اختيار معدل التعلم الصحيح أمر ضروري لتدريب نموذج التعلم العميق بشكل فعال. معدل التعلم هو 0.01، وحجم الدفعة هو 16، وعدد العصور هو 200.

التطبيع

تم تطبيع بيانات تركيز الأوزون باستخدام المعادلة (5) :
حيث، Y تشير إلى بيانات الأوزون المعيارية لـ يدل على القيمة القصوى لتسلسل الأوزون الخام، يشير إلى الحد الأدنى لقيمة سلسلة الأوزون الخام.
بعد تدريب النموذج، يتم عكس تطبيع تركيزات الأوزون المتوقعة باستخدام المعادلة (6):

معايير الأداء

من أجل تقييم أداء التنبؤ لنماذج تركيز الأوزون، معامل التحديد جذر متوسط مربع الخطأ (RMSE) ومتوسط الخطأ المطلق (MAE) تعرف على النحو التالي:
حيث يشير Pm إلى قيمة تركيزات الأوزون الملاحظة؛ و Km يشير إلى تركيزات الأوزون المتوقعة؛ و I هو طول البيانات. يمثل متوسط تركيزات الأوزون المرصودة، يمثل متوسط تركيزات الأوزون المتوقعة.

التحقق المتقاطع

التقييم المتقاطع (CV) هو نهج ناجح للحصول على المعلمات المثلى لنماذج الشبكات العصبية الاصطناعية (ANN) ونماذج الذاكرة طويلة الأمد (LSTM). عملية التحقق المتقاطع بعشرة أضعاف تتضمن تقسيم مجموعة البيانات إلى 10 مجموعات فرعية متساوية الحجم. يتم تخصيص مجموعة فرعية واحدة للاختبار، بينما تُستخدم المجموعات التسع المتبقية لتدريب النموذج. يتم تكرار هذه العملية عشر مرات، في كل مرة يتم فيها استخدام مجموعة فرعية مختلفة للاختبار والمجموعات المتبقية للتدريب. بنهاية العملية، تم استخدام كل طية مرة واحدة للاختبار وتسع مرات للتدريب. يتم تقييم أداء النموذج من خلال حساب مقياس الأداء لكل تكرار. تكون درجة الأداء النهائية هي متوسط الدرجات الفردية عبر جميع الطيات. تساعد هذه الطريقة في تقليل التباين في نتائج الأداء وتوفر تقديرًا أكثر موثوقية لكيفية أداء النموذج على البيانات غير المرئية. واحدة من المزايا الرئيسية للتحقق المتقاطع بعشرة أضعاف هي قدرتها على تقليل تحيز النموذج. نظرًا لأن النموذج يتم تدريبه واختباره على مجموعات بيانات مختلفة، فإن النتائج أقل عرضة للتأثر بتقسيم بيانات محدد. تساعد هذه الطريقة أيضًا في ضمان أن النموذج يمكنه التعميم بشكل جيد على بيانات جديدة، بدلاً من حفظ أو الإفراط في التكيف مع مجموعة فرعية معينة. بالإضافة إلى ذلك، يوفر التحقق المتقاطع بعشرة أضعاف تقييمًا شاملاً من خلال استخدام جميع البيانات المتاحة لكل من التدريب والاختبار، وهو ما يكون ذا قيمة خاصة عند العمل مع مجموعات بيانات صغيرة. نظرًا للأداء المتفوق لتقنية التحقق المتقاطع بعشر طيات، تم اختبار نتائج نماذج الشبكة العصبية الاصطناعية (ANN) ونماذج الذاكرة طويلة الأمد (LSTM) استنادًا إلى تقنية التحقق المتقاطع بعشر طيات.

النتائج

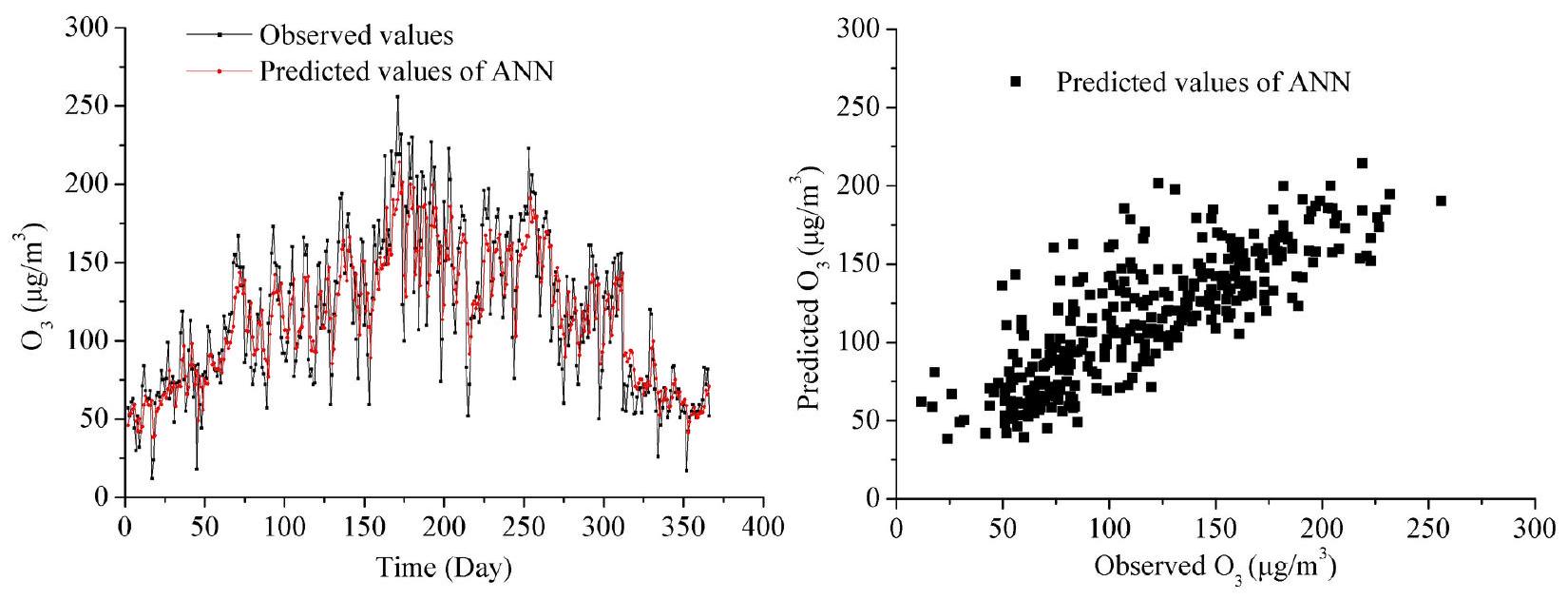
تحليل نتائج التنبؤ للشبكة العصبية الاصطناعية

تم اختبار متغيرات إدخال مختلفة لتحديد الهيكل الشبكي الأكثر دقة في التنبؤ بتركيزات الأوزون. يوضح الجدول 2 نتائج المحاكاة لتركيزات الأوزون خلال الفترات الثلاث. لقد حاولنا استخدام 1-21 يومًا كمدخلات وحصلنا على نتائج مختلفة. اتجاه نتائج المحاكاة مع قيم الإدخال لـ تتحسن الأيام تدريجياً، لكنها تتدهور مرة أخرى بعد 18 يومًا. من المهم أن استخدام أحدث 18 يومًا فقط يحاكي أفضل تركيزات الأوزون. تم اختيار 18 متغيرًا لإدخال النموذج. علاوة على ذلك، تحتوي الطبقة المخفية من نموذج الشبكة العصبية الاصطناعية على 6 خلايا عصبية. دوال التنشيط في الشبكة العصبية الاصطناعية هي logsig و purelin. تظهر مستويات دقة التنبؤ لهياكل الشبكات العصبية المختلفة في الجدول 2. جذر متوسط مربع الخطأ، ومتوسط الخطأ المطلق خلال فترة التنبؤ هي على التوالي. توضح الشكل 4 محاكاة مخرجات الشبكة العصبية الاصطناعية والقيم المستهدفة لتوقع تركيزات الأوزون. في فترة التنبؤ، يتم توقع تركيزات الأوزون في اليوم التالي باستخدام تركيزات الأوزون للأيام السابقة. القيم التدريبية والتحقق منها هي من 28 ديسمبر 2021 إلى 27 ديسمبر 2022. ثم بدأنا في التنبؤ من
أيام جذر متوسط مربع الخطأ (RMSE) ) ماي )
تدريب التحقق التنبؤ تدريب التحقق التنبؤ تدريب التحقق التنبؤ
1 0.7199 0.6704 0.6746 28.9068 ٢٨.٧٥١٦ ٢٨.٤٧٥٣ ٢٢.١١١٢ ٢٢.٧٢٥٠ 21.7433
2 0.7194 0.6699 0.6767 30.2199 30.1252 30.1126 23.0106 ٢٣.٦٧٢٥ ٢٤٫٠٩٠٥
٣ 0.7201 0.6708 0.6752 ٢٩.٠٣٩٤ ٢٨.٨٨٠٩ ٢٨.٧٦٢٠ 22.2106 ٢٢.٦٤٨١ ٢٢٫٦٠٨٦
٤ 0.7194 0.6688 0.6738 30.5321 30.5937 30.3191 ٢٣.٣١٠١ ٢٣.٥٠٥٧ ٢٢.١٧٧٠
٥ 0.7202 0.6681 0.6742 ٢٩.٢٣٧٢ ٢٩.٢٤٦١ ٢٩.٠٢٧٩ 22.3948 ٢٣.٠٤٧٥ 22.8921
٦ 0.7207 0.6636 0.6743 ٢٩.٥٨٧٤ ٢٩.٦٧٢٠ ٢٩.٠٦١٠ 23.2021 ٢٣.٧٦٥٦ 23.0427
٧ 0.7185 0.6740 0.6679 ٢٩.٢٩٧٩ ٢٩.٦٢٣٧ ٢٩.٢٥٦٨ 22.3965 ٢٣٫٢٤٥٧ ٢٣.١٨٢٥
٨ 0.7209 0.6753 0.6726 ٢٩.٠٥٢١ ٢٩.٠٧٨٩ ٢٨.٨٢٤٨ 22.2262 22.3580 21.7427
9 0.7217 0.6752 0.6759 ٢٨.٥٥٠٥ ٢٨.٥٤٠٩ ٢٨.٠٢٦٩ 21.8588 ٢٢.٩٥٧٧ 21.7169
10 0.7206 0.6750 0.6733 ٢٨.٥٢٧٣ ٢٨.٦٣٢٧ ٢٨.٢٨١١ 21.8717 22.3195 ٢١.٧١١٩
11 0.7213 0.6751 0.6705 ٢٨.٥٤٥٦ ٢٨.٥٦٧٤ ٢٨.٣٤٥٣ 21.8699 21.9867 21.7381
12 0.7340 0.6714 0.6698 ٢٩.٦٩٩٠ 30.1861 ٢٩.٥٠٦٨ ٢٢.٦٥٠٤ 22.8725 21.9138
١٣ 0.7338 0.6767 0.6759 ٢٨.٥٤٣١ ٢٨.٥٩٨٨ ٢٨.١١٦٢ 21.8645 21.9931 21.7150
14 0.7322 0.6792 0.6721 ٢٨.٩٥٠٤ ٢٨.٨٦٩٧ ٢٨.٤٧٣٧ 22.0829 ٢٢.٦٣١٦ 22.3236
15 0.7357 0.6800 0.6722 ٢٨.٥٧٠٢ ٢٨.٦٢٥٨ ٢٨.٣٧٨٣ ٢١.٧٨٦٧ 22.3737 ٢٢.٠٥٥٨
16 0.7344 0.6675 0.6647 ٢٨.٧٥٠٥ ٢٩.٣٣١٠ ٢٨.٦٦٤٩ 21.9436 ٢٢.٦٣٤٧ 21.8948
17 0.7362 0.6806 0.6714 ٢٨.٦٥٠٤ ٢٨.٢٣٧٨ ٢٨.٢٣٣٧ 21.8700 21.7673 21.7461
١٨ 0.7365 0.6816 0.6779 ٢٨.٥٠٩٥ ٢٨.٥٥١٤ ٢٧.٩٨٩٥ ٢١.٧٦٤٩ ٢٢.٢١٩٤ 21.6919
19 0.7298 0.6558 0.6609 ٢٩٫٠٩٠١ ٢٩.٨٦٣٠ 28.9438 22.3889 ٢٣.٦٨١٢ ٢٢.٩٩٧٤
20 0.7347 0.6804 0.6770 28.8931 ٢٩.٠٥٧٥ ٢٨.٤٣٦٥ ٢٢.٠١٧٦ ٢٢.٢٩٩٢ 21.7366
21 0.7356 0.6728 0.6722 31.7804 ٣٢.٠٩٥٦ 31.6421 ٢٤.٨٤١٧ ٢٦.٠٢٤٨ 25.9455
الجدول 2. مقارنة بين متغيرات الإدخال المختلفة (الأيام) لشبكة الأعصاب الاصطناعية.
الشكل 4. نتائج التنبؤ باستخدام نموذج الشبكة العصبية الاصطناعية.
وظائف التدريب جذر متوسط مربع الخطأ (RMSE) ) ماي )
تدريب التحقق التنبؤ تدريب التحقق التنبؤ تدريب التحقق التنبؤ
ترينبر 0.7365 0.6816 0.6779 ٢٨.٥٠٩٥ ٢٨.٥٥١٤ ٢٧.٩٨٩٥ ٢١.٧٦٤٩ ٢٢.٢١٩٤ 21.6919
تدريب 0.7175 0.6695 0.6616 ٢٨.٦١٥٨ ٢٨.٧٥١٧ 28.4215 ٢٢.٢٦٧٦ ٢٢.٩١٨٢ 22.2838
تراينغديكس 0.5898 0.5118 0.4879 ٤٥٫٠٨٨٥ 41.8351 41.8636 37.7704 ٣٤.٦٥٩٨ ٣٥.٠٦٩١
تدريب 0.6393 0.5572 0.5163 51.6911 ٤٧.٦٢٥٢ ٤٧.٤٩٥٣ ٤٣.٣٠٣٩ ٣٩.٠٦٨٤ ٣٩.٥٣٨١
ترينغدم 0.6970 0.6258 0.5978 30.5444 30.9063 ٣١.١٩٧٧ ٢٣.٣٨٠٧ ٢٤.١٣٢٣ ٢٤.٦٣٨٣
ترينغدا 0.6970 0.6258 0.5978 30.5444 30.9063 31.1977 ٢٣.٣٨٠٧ ٢٤.١٣٢٣ ٢٤.٦٣٨٣
تدريب دور 0.7277 0.6709 0.6762 28.9446 ٢٩.٠١٩٦ ٢٨.٠٦٧٢ ٢٢.٣٠٠٠ ٢٢.٨٢٧١ 22.1916
ترين سي جي بي 0.7243 0.6722 0.6616 28.8725 ٢٨.٦٧٥٨ ٢٨.٩٠٨٢ ٢٢.٤٥٣٤ ٢٢.٨٣٠٠ ٢٢.٢٢٩٩
تدريب 0.7255 0.6702 0.6775 ٢٨.٨٠٧٢ ٢٨.٦٦٨١ 28.9245 22.4128 ٢٢.٩٥٧٧ ٢٢.٢٥٨٢
ترين سي جي بي 0.7238 0.6734 0.6666 ٢٨.٩٠١٤ ٢٨.٧١٢١ ٢٨.٦٨٤٣ ٢٢.٤٩٩٤ 22.8450 ٢٢.٢٠٩٣
تدريب 0.7239 0.6678 0.6638 ٢٨.٩٩٥٦ ٢٨.٨٣٧٥ ٢٨.٨٠٦٦ ٢٢.٤٧٨٧ ٢٣.٠٣٦٤ ٢٢.١١٨٩
تدريب بي إف جي 0.7275 0.6698 0.6667 ٢٨.٩٩٨٨ ٢٨.٩٢٩١ 28.6813 ٢٢.٣٥٣٢ 22.9733 ٢٢٫٢٠٥٦
ترينوس 0.7219 0.6651 0.6653 ٢٩.٣٠٩٤ ٢٨.٩٤٩٩ 28.7389 ٢٢.٥٢٩٤ ٢٣.١١٢٨ ٢٢.٠٣٨١
الجدول 3. نتائج خوارزميات التدريب المختلفة في الشبكة العصبية الاصطناعية لـ محاكاة.
28 ديسمبر 2022 إلى 27 ديسمبر 2023. في السنة، تكون تركيزات الأوزون المتوقعة مشابهة للقيم الفعلية للأوزون.
تظهر الاختبارات الإحصائية للخوارزميات المختلفة في الشبكة العصبية الاصطناعية في الجدول 3. عند مقارنة الاختبارات، فإن trainbr يعطي أعلى ( 0.7365 )، أقل جذر متوسط مربع الخطأ ( 28.5095 )، وأقل متوسط خطأ مطلق ( 21.7649 ) في فترة التدريب. كما أن خوارزمية trainbr تنتهي بشكل جيد في مرحلة التحقق، مع ، RMSE (28.5514) و MAE (22.2194) على التوالي. في مرحلة التنبؤ، وMAE لـ trainbr هي على التوالي 0.6779 و 27.9895 و 21.6919، مما يفسر قوته التنبؤية.
تظهر الاختبارات الإحصائية لمجموعات مختلفة من دوال النقل (purelin (PU)، tansig (TA)، logsig (LO)، poslin (PO)) في الجدول 4. نتائج المجموعة (LO-PU) لديها أدنى قيم RMSE و MAE، وأعلى قيمة R، مما يثبت نجاح المجموعة. بالإضافة إلى ذلك، فإن هذه التكوينات تؤدي أيضًا بشكل جيد في مرحلة التحقق ولديها قدرة تنبؤية جيدة في فترة التنبؤ.

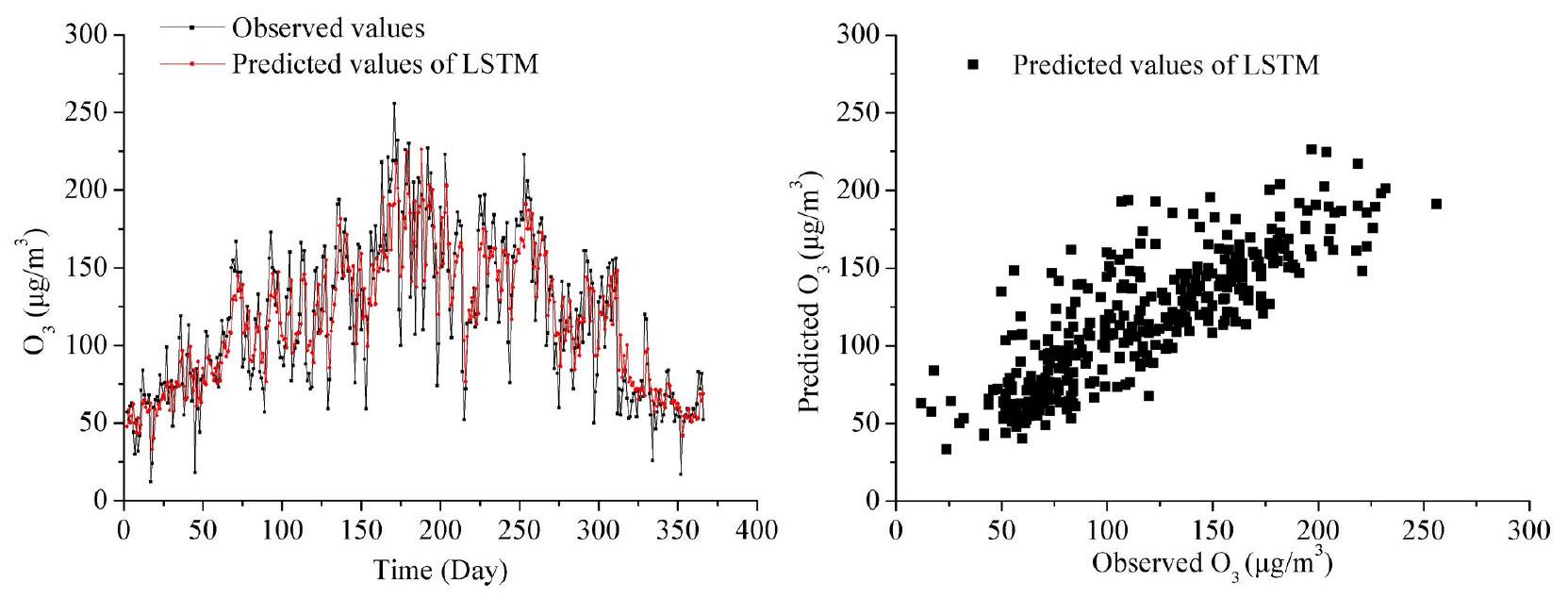
تحليل نتائج LSTM

تم إجراء تحليل LSTM للتنبؤ بتركيزات الأوزون في مدينة لياوتشينغ. من الضروري تحسين المعلمات الفائقة حيث تعتمد هذه القيم على تركيزات الأوزون. يمكن رؤية النتائج المتعلقة بالمتغيرات المدخلة والتحليل الإحصائي لنتائج المحاكاة في الجدول 5. وبالمثل، يمثل الجدول 5 MAE و RMSE لنموذج LSTM. عندما تتغير قيمة الإدخال من 1 إلى 18 يومًا، فإن تتحسن أيضًا نتائج المحاكاة، ثم، من 18 إلى 21 يومًا، تدهورت نتائج المحاكاة مرة أخرى. حدد التحليل تأخيرات لمدة 18 يومًا كعوامل مهمة في التنبؤ بتركيزات الأوزون اليومية. لذلك، فإن عدد المدخلات لخطوة زمن الأوزون هو 18. حجم الدفعة وعدد العصور المختارة لـ LSTM هما 16 و200 على التوالي. وظائف التنشيط لـ LSTM هي tanh وsigmoid، ومعدل التعلم هو 0.01. بالإضافة إلى ذلك، فإن المحسن هو Adam لهذه التجربة.
تظهر الشكل 5 الرسم البياني الذي يقارن بين تركيزات الأوزون المرصودة والمتوقعة لنموذج LSTM. يتضح أن هناك ارتباطًا قويًا بين قيم الأوزون الناتجة والقيم المستهدفة. يوضح الشكل بوضوح أن الإجمالي
دالة النقل جذر متوسط مربع الخطأ ماي
تدريب التحقق التنبؤ تدريب التحقق التنبؤ تدريب التحقق التنبؤ
تا-بو 0.7261 0.6651 0.6613 ٢٩.١٠٩٨ ٢٨.٧٥٩٧ ٢٨.٢٦٦٦ 21.8107 ٢٢.٤٣٣٦ 21.9249
تا-لو 0.7312 0.6666 0.6705 ٢٨.٧٤٥٤ ٢٨.٦٠٨٨ ٢٨.٢٨٠٣ 21.9803 22.4058 ٢٢.٣٢٨٤
وداعاً 0.7240 0.6563 0.6605 ٢٩.٢٣٣١ ٢٩.٤٠٣٣ ٢٨.٦٧٢٢ 21.8764 ٢٢.٥٢١٦ 22.2328
لو-بو 0.7365 0.6816 0.6779 ٢٨.٥٠٩٥ ٢٨.٥٥١٤ ٢٧.٩٨٩٥ 21.7649 ٢٢.٢١٩٤ 21.6919
لو-تا 0.7240 0.6626 0.6605 ٢٩.٢٣٧٥ ٢٩.٤٢٠٩ 28.6688 21.8794 ٢٣٫٢٤٦٠ 22.2513
لو-لو 0.7229 0.6612 0.6610 ٢٩.٣٠٧٠ ٢٩.٠٧٣٣ ٢٨.٤٤٤٦ ٢١.٩٥٠٠ 22.8055 22.7744
بو-تا 0.7143 0.6600 0.6703 ٢٩.٧٤٣٩ ٢٨.٦١٤٦ ٢٨.٢٨٣٨ ٢١.٩٨٣٢ 22.4110 ٢٢.٣٣٦٤
بيو-لو 0.7178 0.6615 0.6605 ٢٩.٥٩٨٠ ٢٨.٩٢٥٨ ٢٨.٦٧٧٧ ٢٢.١٧٥٤ ٢٢.٦٦٣٨ ٢٢.٧٤٥٨
بيو-بيو 0.7216 0.6606 0.6595 ٢٩.٣٣٤١ ٢٩.٣٣٩٣ ٢٨.٠٥٧٨ ٢٢.٥٧١٨ ٢٣.٠٩٣٦ 22.3539
تا-بو 0.7077 0.6619 0.6607 29.2008 ٢٨.٧١٨٦ ٢٨.٥٥٥٦ ٢٢.٨٩٥٤ ٢٢.٥٦٦٤ ٢٢.١٣٧٥
لو-بو 0.7195 0.6611 0.6615 ٢٩.٤٩٣٨ ٢٩.٠٩٤٢ 28.1946 ٢٢٫٠٣٨٧ 22.8510 22.7705
بو-بو 0.7209 0.6618 0.6619 ٢٩.٤١٤٠ ٢٩.٧٩٣٧ ٢٨.٩٨٦٨ 22.9791 ٢٢.٥١٤٦ 22.7470
PU-PO 0.7166 0.6609 0.6608 ٢٩.٧٦٨٩ ٢٩.٢٢٥٢ ٢٨.٥٢١١ 22.2734 22.9010 ٢٢.١٥٤٦
بو-لو 0.7169 0.6612 0.6604 ٢٩.٦٢٠٧ ٢٩.٠٨٢٣ 28.6772 ٢٢.٠٩٠١ 22.6724 ٢٢.٢٥٣٢
بو-بو 0.7170 0.6618 0.6610 ٢٩.٥٤٢١ ٢٩.٧٦١١ ٢٨.٤٠٦٦ ٢٢٫٠٦٤١ ٢٢.٥٢٥١ 22.7511
بو-تا 0.7174 0.6612 0.6619 ٢٩.٣٥٣٢ ٢٩.٠٨٩١ ٢٨.٠١٢٦ ٢٢.٠٠٨٠ 22.7055 ٢٢.٦٢٠٠
الجدول 4. نتائج دوال النقل المختلفة في الشبكة العصبية الاصطناعية لـ محاكاة.
أيام جذر متوسط مربع الخطأ (RMSE) ) ماي )
تدريب التحقق التنبؤ تدريب التحقق التنبؤ تدريب التحقق التنبؤ
1 0.7074 0.6530 0.6535 ٢٩٫٩٧٠١ ٢٩.٧٨١٤ ٢٨.٩٩٨٢ 22.8702 22.8105 ٢٢.١٦٧٣
2 0.7189 0.6545 0.6566 ٢٩.٣٧٦٨ ٢٩.٧٠١٧ 28.8565 22.3821 ٢٢.٧١٠٤ ٢٢.٠٤٧٣
٣ 0.7263 0.6705 0.6672 28.9846 ٢٨.٩٩٠٥ ٢٨.٣٩٠٨ ٢٢.٠٥٤٣ ٢٢.٢٠٤٤ ٢١.٩٨٩٤
٤ 0.7320 0.6726 0.6662 ٢٨.٦٨٣٣ ٢٨.٨٩٨٩ ٢٨.٤٢٧١ 21.7966 ٢٢.٠٩٧١ 21.7849
٥ 0.7379 0.6682 0.6761 ٢٨.٣٦٦٣ ٢٩.١٠٠٨ 27.9928 21.6099 ٢٢.٣٠٥١ ٢١.٤٣١٤
٦ 0.7384 0.6705 0.6767 ٢٨.٣٣٦٦ ٢٨.٩٩٧٨ 27.9644 ٢١.٥٣٧٧ 22.2521 21.1804
٧ 0.7423 0.6694 0.6842 ٢٨.١٢٦٠ ٢٩.٠٤٣٠ 27.6338 ٢١.٤٢٩١ ٢٢.٣١٣٣ ٢١.٠٣٥٣
٨ 0.7427 0.6784 0.6831 ٢٨.١٠٥٦ ٢٨.٦٤٠٨ ٢٧.٦٨٧١ 21.4157 21.9549 21.2736
9 0.7460 0.6815 0.6829 27.9226 ٢٨.٥٠٩٠ 27.7014 21.2723 21.9219 21.3349
10 0.7482 0.6811 0.6855 27.8022 ٢٨.٥٣٦٤ ٢٧.٥٨١٧ 21.1620 21.9089 21.1191
11 0.7491 0.6840 0.6826 ٢٧.٧٥٥٦ ٢٨.٣٩٤٥ 27.7119 ٢١.٠٦٤٣ 21.8384 21.2267
12 0.7484 0.6824 0.6833 ٢٧.٧٩٠٠ ٢٨.٤٧٠٨ 27.6793 ٢١.٠٩٥٦ 21.8943 ٢١.١٨٢٨
١٣ 0.7490 0.6878 0.6876 27.7566 ٢٨.٢٢٦٦ ٢٧.٤٩٤٩ ٢١.١٣٩٠ 21.7223 21.0147
14 0.7533 0.6906 0.6921 27.5190 ٢٨٫٠٩٠٤ 27.2943 ٢١.٠٠٤٩ 21.8952 20.8469
15 0.7547 0.6930 0.6879 27.4405 27.9839 27.4774 ٢٠.٩٣٣٣ 21.7072 21.1297
16 0.7563 0.6964 0.6807 ٢٧.٣٥٠٠ 27.8272 27.8038 20.9849 ٢١.٦٦٦٥ ٢١.٢٨٥٥
17 0.7561 0.6975 0.6829 27.3652 27.7974 27.7057 20.9517 ٢١.٦٤٧٨ ٢١.٢٤٣٩
١٨ 0.7577 0.6989 0.6939 27.2747 27.7139 27.2140 20.9027 21.6309 20.8825
19 0.7574 0.6975 0.6932 ٢٧.٣٦٥٨ 27.7230 ٢٧.٢٤٧٣ 20.9553 21.6801 20.8978
20 0.7572 0.6952 0.6899 ٢٧.٣٠٣٤ 27.8852 ٢٧.٣٨٩٣ 20.9360 21.6827 21.1164
21 0.7567 0.6919 0.6930 27.3311 ٢٨.٠٣٢٦ 27.2583 20.9318 ٢١.٦٢٦٦ 20.9265
الجدول 5. مقارنة بين متغيرات الإدخال المختلفة (الأيام) لنموذج LSTM.
أداء LSTM يتفوق على أداء ANN. اتجاه LSTM يتوافق بشكل أفضل مع الملاحظات مقارنةً بنموذج ANN.

تحليل نتائج LSTM و ANN لعملية التحقق المتقاطع بعشر طيات

استخدمنا طريقة التحقق العشرية لحساب جميع البيانات (2014-2023) وحصلنا على متوسط 10 نتائج حسابية. من الجدول 6، يمكن ملاحظة أن LSTM و ANN لديهما قدرة جيدة على التعميم من خلال التحقق المتقاطع.
الشكل 5. نتائج التنبؤ باستخدام نموذج LSTM.
نماذج R2 جذر متوسط مربع الخطأ ماي
تدريب التحقق تدريب التحقق تدريب التحقق
LSTM 0.738004 0.68879 27.87386 ٢٧.٤٦٥٦٩ 21.35167 21.38393
إيه إن إن 0.725225 0.673961 ٢٨.٧٢١٢١ 28.61427 ٢٢.٢٩٥٥٤ 22.37229
الجدول 6. مقارنة بين LSTM و ANN لعملية التحقق المتقاطع بعشر طيات.

نقاش

أولاً، تؤثر المتغيرات المدخلة بشكل كبير على كل من نماذج الشبكات العصبية الاصطناعية (ANN) ونماذج الذاكرة طويلة الأمد (LSTM) لـ تنبؤ. من خلال مقارنة أداء التنبؤ لكل من النموذجين مع متغيرات الإدخال المختلفة، قمنا بتحسين هياكل الشبكة لكلا النموذجين. ثانياً، فإن دوال التفعيل لها أيضاً تأثير معين على أداء الشبكة العصبية الاصطناعية. نموذج التنبؤ. من خلال تدريب دوال تنشيط مختلفة، يمكن لنموذج الشبكة العصبية الاصطناعية التعامل مع العلاقات غير الخطية بين المتغيرات المدخلة المعقدة. ومع ذلك، تفتقر الشبكة العصبية الاصطناعية إلى آلية الذاكرة، مما يجعل أدائها ضعيفًا في التقاط الاعتمادات طويلة الأجل. سلاسل زمنية، مما يجعل من الصعب التقاط التغيرات الديناميكية لـ هيكل LSTM يمكّنه من أخذ المعلومات الماضية على المدى الطويل والقصير في الاعتبار لذا، فإن LSTM هو الخيار الأفضل.
في هذا البحث، استخدمنا كل من نماذج LSTM و ANN للتنبؤ بتركيزات الأوزون في مدينة لياوتشينغ وقارنّا بين قدرتهما على التعميم ودقة الأداء. أظهر التحليل المقارن أن نموذج LSTM (مع تفوقت على الشبكة العصبية الاصطناعية (مع ) في التنبؤ بتركيزات الأوزون، كما هو موضح في الجدول 1 و 2. قيم الخطأ (MAE و RMSE) التي حققها نموذج LSTM المقترح أقل بكثير مقارنةً بشبكة ANN. قيم MAE و RMSE التي حققها نموذج LSTM المقترح في فترة التنبؤ هي و ، على التوالي. الـ قيمة نموذج LSTM المقترح هي 0.6939، وهي أكبر مقارنة بنموذج ANN. يتمتع LSTM بفارق مطلق أصغر بين قيمه المتوقعة والقيم الفعلية. تظهر تقنية LSTM قدرة تفوق في التعميم مقارنة بنموذج ANN.
تتوافق هذه النتيجة بشكل كبير مع الطبيعة المعقدة وغير الخطية لتركيزات الأوزون، مما يجعل نموذج LSTM هو النموذج المفضل للتنبؤ. فهرس . هذه النتائج تتماشى أيضًا مع نتائج دراسة أخرى قارنت أداء الشبكة العصبية متعددة الطبقات (MLP) و LSTM في تطوير نماذج فعالة لتوقع الأوزون. . مشابهة لنتائجنا، تظهر تحقيقاتهم أن الانحدار الخطي المتعدد (MLR) لديه أداء أقل مقارنة بشبكة الذاكرة الطويلة القصيرة (LSTM). تستخدم LSTM الاعتماديات في السلاسل الزمنية لتوليد قدرة أفضل على التعميم ودقة أعلى. تم استخدام كل من ANN و MLR للتنبؤ بتركيزات الأوزون في لانتشو. RMSE و كانت قيم ANN هي 7.8275 و 0.9238 ؛ بينما كانت RMSE و كانت قيم MLR هي 21.5847 و 0.5328. أظهرت ANN ملاءمة أفضل. كان RMSE لـ ANN أقل بكثير من ذلك الخاص بـ MLR، مما أكد دقتها وفعاليتها. أظهرت النتائج أن ANN كانت لديها أداء أفضل من MLR. تم استخدام الشبكات العصبية ذات الانتشار العكسي (BPANNs) للتنبؤ بـ تركيزات في حيدر أباد، الهند خلال 2014-2016. أظهرت كفاءة وأداء الشبكات العصبية الاصطناعية متعددة الطبقات (BPANNs) مستويات أعلى تم استخدام ANN و RNN (الشبكة العصبية التكرارية) و RFR (انحدار الغابة العشوائية) و LR (الانحدار الخطي) للتنبؤ بأوزون الهواء في مقاطعة سيتشوان، الصين. جذر متوسط مربع الخطأ (RMSE) ومتوسط الخطأ المطلق (MAE) لنموذج الانحدار الخطي (LR) هي 0.7271 و29.94 و24.4891. جذر متوسط مربع الخطأ (RMSE) ومتوسط الخطأ المطلق (MAE) لشبكة الأعصاب الاصطناعية متعددة الطبقات (BPANN) هي ، و جذر متوسط مربع الخطأ (RMSE) ومتوسط الخطأ المطلق (MAE) لشبكة الأعصاب المتكررة (RNN) هي ، و 20.0169. جذر متوسط مربع الخطأ (RMSE) ومتوسط الخطأ المطلق (MAE) لـ RFR هي 0.8215 و24.9195 و تتفوق نماذج ANN و RNN على نماذج RFR و LR عبر مجموعات متغيرة مختلفة. يمكن لكل من ANN و RNN التقاط العلاقات غير الخطية بين ميزات الإدخال و تركيزات. لذا، يمكن لنماذج الشبكات العصبية الاصطناعية والشبكات العصبية المتكررة نمذجة التفاعلات والأنماط المعقدة. مؤخرًا، تم تطبيق نماذج LSTM لتقدير تركيزات الأوزون السطحي اليومية في ثلاث تجمعات حضرية في الصين (حوض سيتشوان، سهل شمال الصين، ودلتا نهر اليانغتسي)، مع دقة RMSE. ما .
تم استخدام LSTM للحصول على القيم المتوقعة لـ في بكين. حقق LSTM أقل خطأ. كانت قيم MAE و RMSE، هم ، و تم تطبيق طريقة LSTM للتنبؤ بمستويات الأوزون الساعية في تركيا. بالنسبة للعصبونات المخفية وحجم العصر يأخذ RMSE قيمة تتراوح بين 10.86 و 13.38، بينما يأخذ MAE قيمًا في نطاق 7.45 و 7.672 و تتراوح القيمة من 0.92 إلى . علاوة على ذلك، تم اقتراح RF-CEEMDAN-Attention-LSTM للتنبؤ بالبيانات كل ثلاث ساعات تركيزات في تشنغدو. النموذج دمج غابة عشوائية (RF) وطريقة تحليل النمط التجريبي الكامل مع الضوضاء التكيفية (CEEMADN) ونموذج LSTM. أظهرت نتائج المحاكاة أن النموذج الهجين لم يكن له فقط تأثير أفضل في التوافق على قيم التركيز مقارنةً بالنماذج المماثلة الأخرى تم استخدام LSTM و MLR للتنبؤ بالأوزون في المحطتين في شنتشن، الصين. RMSE و MAE و لـ LSTM في محطة HQC هي 14.0588، 9.8924، و0.6068، على التوالي؛ بينما تلك القيم لـ MLR هي 16.8589، 12.0243، 0.4347، على التوالي. RMSE، MAE، و لـ LSTM في محطة HQC هي 14.0588 و 9.8924 و 0.6068، على التوالي؛ بينما تلك القيم لـ MLR هي ، على التوالي. علاوة على ذلك، RMSE و MAE و قيم LSTM في محطة NA هي 12.2361، 9.3810، و0.5226، على التوالي؛ بينما قيم MLR هي 12.9509، 10.0415، و0.4915، على التوالي. نتائج التنبؤ باستخدام LSTM أفضل من تلك الخاصة بـ MLR. يتمتع LSTM بأداء ممتاز في التعامل مع مشاكل التنبؤ بتركيز الأوزون، ولديه قوة تحمل جيدة وأداء عام جيد. بشكل عام، تعزز نتائج هذا البحث مزايا نماذج التعلم العميق، وخاصة طريقة LSTM في التنبؤ بدقة بتركيزات الأوزون، وتبرز الإمكانية لمعالجة تعقيد نمذجة تلوث الهواء.

الاستنتاجات

يمكن أن يؤدي التحسين المستمر لجودة الهواء إلى تلبية توقعات الناس لحياة أفضل. إن توقع تركيز الأوزون هو قضية مهمة للباحثين. إن توقع تركيزات الأوزون هو مسألة معقدة لأن العديد من المعايير تؤثر على تكوين الأوزون. لتحقيق الهدف، تم بناء نماذج LSTM و ANN في هذه الورقة البحثية لتوقع تركيزات الأوزون في مدينة لياوتشينغ. للتحقق من أداء نماذج LSTM و ANN المقترحة، تم إجراء تحليل مقارن بين كلا النموذجين والأعمال السابقة ذات الصلة باستخدام مؤشرات التقييم. خلال مرحلة التدريب، جذر متوسط مربع الخطأ (RMSE) ومتوسط الخطأ المطلق (MAE) لنموذج LSTM هي ، و على التوالي، بينما خلال مرحلة التحقق، هم ، و . في هذه الأثناء، خلال مرحلة التنبؤ، هم ، و يوفر نموذج LSTM نتائج أكثر دقة من نموذج ANN. تظهر النتائج أن نموذج LSTM لم يكن لديه فقط تأثير أفضل في التوافق على من نموذج ANN في مرحلة التدريب، ولكن النموذج كان لديه أيضًا أعلى قيمة لـ في مرحلة التنبؤ. يتفوق نموذج LSTM المقترح على تقنية ANN. بالمقارنة مع ANN، يظهر نموذج LSTM أداءً متفوقًا لقيم تركيز الأوزون العالية، مما له تأثير مهم على التحذير المبكر. يمكن للمسؤولين الحكوميين استخدام LSTM للتخطيط وتنفيذ استراتيجيات فعالة لتقليل تركيزات الأوزون وحماية صحة الناس.
في المستقبل، سيتم دراسة نماذج التنبؤ بتركيزات الأوزون اليومية لعدة أيام مقدماً. هناك بعض العوامل الأخرى التي تم أخذها في الاعتبار، مثل العوامل الجوية، والملوثات الهوائية، والتضاريس، والموقع، وما إلى ذلك. سنستخدم طرقاً جديدة للتنبؤ بالأوزون في مناطق أخرى، مثل LSTM ثنائي الاتجاه (BiLSTM)، والشبكة العصبية التلافيفية (CNN)، وCNN-LSTM، وCNN-BiLSTM، وTCN، والمحولات.

توفر البيانات

البيانات والمواد متاحة من المؤلف المراسل عند الطلب.
تاريخ الاستلام: 24 أبريل 2024؛ تاريخ القبول: 19 فبراير 2025
نُشر على الإنترنت: 25 فبراير 2025

References

  1. . et al. A quantitative assessment and process analysis of the contribution from meteorological conditions in an O 3 pollution episode in Guangzhou. China Atmos. Environ. 303, 119757. https://doi.org/10.1016/j.atmosenv.2023.119757 (2023).
  2. Wang, L., Zhao, B., Zhang, Y. & Hu, H. Correlation between surface PM2.5 and O3 in eastern China during 2015-2019: Spatiotemporal variations and meteorological impacts. Atmos. Environ. 294, 119520. https://doi.org/10.1016/j.atmosenv.2022.11 9520 (2023).
  3. Qi, Q., Wang, S., Zhao, H., Kota, S. H. & Zhang, H. Rice yield losses due to O3 pollution in China from 2013 to 2020 based on the WRF-CMAQ model. J. Clean. Prod. https://doi.org/10.1016/j.jclepro.2023.136801 (2023).
  4. Mo, S. et al. Sex disparity in cognitive aging related to later-life exposure to ambient air pollution. Sci. Total Environ. 886, 163980. https://doi.org/10.1016/j.scitotenv.2023.163980 (2023).
  5. Lyu, Y. et al. Tracking long-term population exposure risks to PM2.5 and ozone in urban agglomerations of China 2015-2021. Sci. Total Environ. 854, 158599. https://doi.org/10.1016/j.scitotenv.2022.158599 (2023).
  6. Guo, Q., He, Z. & Wang, Z. Long-term projection of future climate change over the twenty-first century in the Sahara region in Africa under four Shared Socio-Economic Pathways scenarios. Environ. Sci. Pollut. Res. 30, 22319-22329. https://doi.org/10.100 7/s11356-022-23813-z (2023).
  7. Guo, Q., He, Z. & Wang, Z. The characteristics of air quality changes in Hohhot City in China and their relationship with meteorological and socio-economic factors. Aerosol Air Qual. Res. 24, 230274. https://doi.org/10.4209/aaqr. 230274 (2024).
  8. Guo, Q., He, Z. & Wang, Z. Change in air quality during 2014-2021 in Jinan City in China and its influencing factors. Toxics 11, 210. https://doi.org/10.3390/toxics11030210 (2023).
  9. Shams, S. R. et al. Assessing the effectiveness of artificial neural networks (ANN) and multiple linear regressions (MLR) in forcasting AQI and PM10 and evaluating health impacts through AirQ+ (case study: Tehran). Environ. Pollut. 338, 122623. https://doi.org/10.1016/j.envpol.2023.122623 (2023).
  10. Xue, T. et al. Estimating the exposure-response function between long-term ozone exposure and under- 5 mortality in 55 lowincome and middle-income countries: a retrospective, multicentre, epidemiological study. Lancet Planet. Health 7, e736-e746. https://doi.org/10.1016/S2542-5196(23)00165-1 (2023).
  11. Chu, Y. et al. Three-hourly PM25 and O3 concentrations prediction based on time series decomposition and LSTM model with attention mechanism. Atmos. Pollut. Res. 14, 101879. https://doi.org/10.1016/j.apr.2023.101879 (2023).
  12. Huang, C. et al. Study on the assimilation of the sulphate reaction rates based on WRF-Chem/DART. Sci. China Earth Sci. 66, 2239-2253. https://doi.org/10.1007/s11430-023-1153-9 (2023).
  13. Wang, Y. et al. Ultra-high-resolution mapping of ambient fine particulate matter to estimate human exposure in Beijing. Commun. Earth Environ. 4, 451. https://doi.org/10.1038/s43247-023-01119-3 (2023).
  14. Mirzavand Borujeni, S., Arras, L., Srinivasan, V. & Samek, W. Explainable sequence-to-sequence GRU neural network for pollution forecasting. Sci. Rep. 13, 9940. https://doi.org/10.1038/s41598-023-35963-2 (2023).
  15. Guo, Q., He, Z. & Wang, Z. Simulating daily PM2.5 concentrations using wavelet analysis and artificial neural network with remote sensing and surface observation data. Chemosphere 340, 139886. https://doi.org/10.1016/j.chemosphere.2023.139886 (2023).
  16. Guo, Q., He, Z. & Wang, Z. Prediction of Hourly PM2.5 and PM10 Concentrations in Chongqing City in China Based on Artificial Neural Network. Aerosol Air Qual. Res. 23, 220448. https://doi.org/10.4209/aaqr. 220448 (2023).
  17. Guo, Q., He, Z. & Wang, Z. Predicting of daily PM2.5 concentration employing wavelet artificial neural networks based on meteorological elements in Shanghai China. Toxics 11, 51. https://doi.org/10.3390/toxics11010051 (2023).
  18. He, Z., Guo, Q., Wang, Z. & Li, X. Prediction of monthly PM2.5 concentration in Liaocheng in China employing artificial neural network. Atmosphere 13, 1221. https://doi.org/10.3390/atmos13081221 (2022).
  19. Guo, Q. et al. Air pollution forecasting using artificial and wavelet neural networks with meteorological conditions. Aerosol Air Qual. Res. 20, 1429-1439. https://doi.org/10.4209/aaqr.2020.03.0097 (2020).
  20. Kapadia, D. & Jariwala, N. Prediction of tropospheric ozone using artificial neural network (ANN) and feature selection techniques. Model. Earth Syst. Environ. 8, 2183-2192. https://doi.org/10.1007/s40808-021-01220-6 (2022).
  21. Guo, Q., He, Z. & Wang, Z. Prediction of monthly average and extreme atmospheric temperatures in Zhengzhou based on artificial neural network and deep learning models. Front. Forests Glob. Change 6, 1249300. https://doi.org/10.3389/ffgc.2023.1249300 (2023).
  22. He, Z. & Guo, Q. Comparative analysis of multiple deep learning models for forecasting monthly ambient PM2.5 concentrations: A case study in Dezhou City, China. Atmosphere 15, 1432. https://doi.org/10.3390/atmos15121432 (2024).
  23. Guo, Q. et al. A performance comparison study on climate prediction in Weifang city using different deep learning models. Water 16, 2870. https://doi.org/10.3390/w16192870 (2024).
  24. Guo, Q., He, Z. & Wang, Z. Monthly climate prediction using deep convolutional neural network and long short-term memory. Sci. Rep. 14, 17748. https://doi.org/10.1038/s41598-024-68906-6 (2024).
  25. Zhang, Y. et al. Prediction and cause investigation of ozone based on a double-stage attention mechanism recurrent neural network. Front. Environ. Sci. Eng. 17, 21. https://doi.org/10.1007/s11783-023-1621-4 (2022).
  26. Barthwal, A. & Goel, A. K. Advancing air quality prediction models in urban India: a deep learning approach integrating DCNN and LSTM architectures for AQI time-series classification. Model. Earth Syst. Environ. 10, 2935-2955. https://doi.org/10.1007/s4 0808-023-01934-9 (2024).
  27. Ding, W. & Sun, H. Prediction of PM2.5 concentration based on the weighted RF-LSTM model. Earth Sci. Inform. 16, 3023-3037. https://doi.org/10.1007/s12145-023-01111-7 (2023).
  28. Xu, S., Li, W., Zhu, Y. & Xu, A. A novel hybrid model for six main pollutant concentrations forecasting based on improved LSTM neural networks. Sci. Rep. 12, 14434. https://doi.org/10.1038/s41598-022-17754-3 (2022).
  29. Duan, J., Gong, Y., Luo, J. & Zhao, Z. Air-quality prediction based on the ARIMA-CNN-LSTM combination model optimized by dung beetle optimizer. Sci. Rep. 13, 12127. https://doi.org/10.1038/s41598-023-36620-4 (2023).
  30. Zhu, L., Husny, Z. J. B. M., Samsudin, N. A., Xu, H. & Han, C. Deep learning method for minimizing water pollution and air pollution in urban environment. Urban Clim. 49, 101486. https://doi.org/10.1016/j.uclim.2023.101486 (2023).
  31. Navares, R. & Aznarte, J. L. Predicting air quality with deep learning LSTM: Towards comprehensive models. Ecol. Inform. 55, 101019. https://doi.org/10.1016/j.ecoinf.2019.101019 (2020).
  32. Masood, A. & Ahmad, K. A review on emerging artificial intelligence (AI) techniques for air pollution forecasting: Fundamentals, application and performance. J. Clean. Prod. 322, 129072. https://doi.org/10.1016/j.jclepro.2021.129072 (2021).
  33. Cabaneros, S. M., Calautit, J. K. & Hughes, B. R. A review of artificial neural network models for ambient air pollution prediction. Environ. Model. Softw. 119, 285-304. https://doi.org/10.1016/j.envsoft.2019.06.014 (2019).
  34. Pan, Q., Harrou, F. & Sun, Y. A comparison of machine learning methods for ozone pollution prediction. J. Big Data 10, 63. https://doi.org/10.1186/s40537-023-00748-x (2023).
  35. Zhang, B., Zhang, Y. & Jiang, X. Feature selection for global tropospheric ozone prediction based on the BO-XGBoost-RFE algorithm. Sci. Rep. 12, 9244. https://doi.org/10.1038/s41598-022-13498-2 (2022).
  36. Zhang, W. et al. Parsimonious estimation of hourly surface ozone concentration across China during 2015-2020. Sci. Data 11, 492. https://doi.org/10.1038/s41597-024-03302-3 (2024).
  37. Chen, Y. et al. Seasonal predictability of the dominant surface ozone pattern over China linked to sea surface temperature. Clim. Atmos. Sci. 7, 17. https://doi.org/10.1038/s41612-023-00560-7 (2024).
  38. Liao, Q. et al. Deep learning for air quality forecasts: A review. Curr. Pollut. Rep. https://doi.org/10.1007/s40726-020-00159-z (2020).
  39. Malhotra, M., Walia, S., Lin, C.-C., Aulakh, I. K. & Agarwal, S. A systematic scrutiny of artificial intelligence-based air pollution prediction techniques, challenges, and viable solutions. J. Big Data 11, 142. https://doi.org/10.1186/s40537-024-01002-8 (2024).
  40. Kaur, M. et al. Computational deep air quality prediction techniques: a systematic review. Artif. Intell. Rev. 56, 2053-2098. https: //doi.org/10.1007/s10462-023-10570-9 (2023).
  41. Chaloulakou, A., Saisana, M. & Spyrellis, N. Comparative assessment of neural networks and regression models for forecasting summertime ozone in Athens. Sci. Total Environ. 313, 1-13. https://doi.org/10.1016/S0048-9697(03)00335-8 (2003).
  42. Hrust, L., Klaić, Z. B., Križan, J., Antonić, O. & Hercog, P. Neural network forecasting of air pollutants hourly concentrations using optimised temporal averages of meteorological variables and pollutant concentrations. Atmos. Environ. 43, 5588-5596. https://doi.org/10.1016/j.atmosenv.2009.07.048 (2009).
  43. Mahapatra, A. Prediction of daily ground-level ozone concentration maxima over New Delhi. Environ. Monit. Assess. 170, 159170. https://doi.org/10.1007/s10661-009-1223-z (2010).
  44. Chattopadhyay, G., Chattopadhyay, S. & Chakraborthy, P. Principal component analysis and neurocomputing-based models for total ozone concentration over different urban regions of India. Theor. Appl. Climatol. 109, 221-231. https://doi.org/10.1007/s00 704-011-0569-7 (2012).
  45. Luna, A. S., Paredes, M. L. L., de Oliveira, G. C. G. & Corrêa, S. M. Prediction of ozone concentration in tropospheric levels using artificial neural networks and support vector machine at Rio de Janeiro, Brazil. Atmos. Environ. 98, 98-104. https://doi.org/10.10 16/j.atmosenv.2014.08.060 (2014).
  46. Božnar, M. Z., Grašič, B., Mlakar, P., Gradišar, D. & Kocijan, J. Nonlinear data assimilation for the regional modeling of maximum ozone values. Environ. Sci. Pollut. Res. 24, 24666-24680. https://doi.org/10.1007/s11356-017-0059-2 (2017).
  47. Gao, M., Yin, L. & Ning, J. Artificial neural network model for ozone concentration estimation and Monte Carlo analysis. Atmos. Environ. https://doi.org/10.1016/j.atmosenv.2018.03.027 (2018).
  48. Sayahi, T. et al. Long-term calibration models to estimate ozone concentrations with a metal oxide sensor. Environ. Pollut. 267, 115363. https://doi.org/10.1016/j.envpol.2020.115363 (2020).
  49. Mo, Y. et al. A novel framework for daily forecasting of ozone mass concentrations based on cycle reservoir with regular jumps neural networks. Atmos. Environ. 220, 117072. https://doi.org/10.1016/j.atmosenv.2019.117072 (2020).
  50. Agarwal, S. et al. Air quality forecasting using artificial neural networks with real time dynamic error correction in highly polluted regions. Sci. Total Environ. 735, 139454. https://doi.org/10.1016/j.scitotenv.2020.139454 (2020).
  51. Malinović-Milićević, S. et al. Prediction of tropospheric ozone concentration using artificial neural networks at traffic and background urban locations in Novi Sad, Serbia. Environ. Monit. Assess. 193, 84. https://doi.org/10.1007/s10661-020-08821-1 (2021).
  52. Antanasijević, D., Pocajt, V., Perić-Grujić, A. & Ristić, M. Urban population exposure to tropospheric ozone: A multi-country forecasting of SOMO35 using artificial neural networks. Environ. Pollut. 244, 288-294. https://doi.org/10.1016/j.envpol.2018.10. 051 (2019).
  53. Feng, Y., Zhang, W., Sun, D. & Zhang, L. Ozone concentration forecast method based on genetic algorithm optimized back propagation neural networks and support vector machine data classification. Atmos. Environ. 45, 1979-1985. https://doi.org/10. 1016/j.atmosenv.2011.01.022 (2011).
  54. Meda, B. N. M., Mathew, A., Sarwesh, P., Shekar, P. R. & Sharma, K. V. Machine learning-based modeling of ground level ozone formation in Bangalore and New Delhi cities in India. Stochastic Environ. Res. Risk Assess. https://doi.org/10.1007/s00477-024-0 2845-6 (2024).
  55. Yafouz, A. et al. Comprehensive comparison of various machine learning algorithms for short-term ozone concentration prediction. Alex. Eng. J. 61, 4607-4622. https://doi.org/10.1016/j.aej.2021.10.021 (2022).
  56. Balram, D., Lian, K.-Y. & Sebastian, N. A novel soft sensor based warning system for hazardous ground-level ozone using advanced damped least squares neural network. Ecotoxicol. Environ. Saf. 205, 111168. https://doi.org/10.1016/j.ecoenv.2020.111168 (2020).
  57. Jia, B., Dong, R. & Du, J. Ozone concentrations prediction in Lanzhou, China, using chaotic artificial neural network. Chemometr. Intell. Lab. Syst. 204, 104098. https://doi.org/10.1016/j.chemolab.2020.104098 (2020).
  58. AlOmar, M. K., Hameed, M. M. & AlSaadi, M. A. Multi hours ahead prediction of surface ozone gas concentration: Robust artificial intelligence approach. Atmos. Pollut. Res. 11, 1572-1587. https://doi.org/10.1016/j.apr.2020.06.024 (2020).
  59. Dunea, D., Pohoata, A. & Iordache, S. Using wavelet-feedforward neural networks to improve air pollution forecasting in urban environments. Environ. Monit. Assess. 187, 477. https://doi.org/10.1007/s10661-015-4697-x (2015).
  60. Braik, M., Sheta, A. & Al-Hiary, H. Hybrid neural network models for forecasting ozone and particulate matter concentrations in the Republic of China. Air Qual. Atmos. Health 13, 839-851. https://doi.org/10.1007/s11869-020-00841-7 (2020).
  61. Park, J. Efficient ozone concentration trend prediction using ANN and K-means clustering. Earth Sci. Inform. 18, 163. https://do i.org/10.1007/s12145-024-01676-x (2025).
  62. Braik, M. et al. Predicting surface ozone levels in eastern Croatia: Leveraging recurrent fuzzy neural networks with grasshopper optimization algorithm. Water Air Soil Pollut. 235, 655. https://doi.org/10.1007/s11270-024-07378-w (2024).
  63. Gorai, A. K. & Mitra, G. A comparative study of the feed forward back propagation (FFBP) and layer recurrent (LR) neural network model for forecasting ground level ozone concentration. Air Qual. Atmos. Health 10, 213-223. https://doi.org/10.1007/s 11869-016-0417-0 (2017).
  64. Mu, L., Bi, S., Ding, X. & Xu, Y. Transformer-based ozone multivariate prediction considering interpretable and priori knowledge: A case study of Beijing, China. J. Environ. Manag. 366, 121883. https://doi.org/10.1016/j.jenvman.2024.121883 (2024).
  65. Zhou, J., Zhou, L., Cai, C. & Zhao, Y. Multi-step ozone concentration prediction model based on improved secondary decomposition and adaptive kernel density estimation. Process Saf. Environ. Prot. 190, 386-404. https://doi.org/10.1016/j.psep. 2 024.08.044 (2024).
  66. Wang, S. et al. A deep learning model integrating a wind direction-based dynamic graph network for ozone prediction. Sci. Total Environ. 946, 174229. https://doi.org/10.1016/j.scitotenv.2024.174229 (2024).
  67. Sayeed, A. et al. Using a deep convolutional neural network to predict 2017 ozone concentrations, 24 hours in advance. Neural Netw. 121, 396-408. https://doi.org/10.1016/j.neunet.2019.09.033 (2020).
  68. Eslami, E., Choi, Y., Lops, Y. & Sayeed, A. A real-time hourly ozone prediction system using deep convolutional neural network. Neural Comput. Appl. 32, 8783-8797. https://doi.org/10.1007/s00521-019-04282-x (2020).
  69. Feng, R. et al. Unveiling tropospheric ozone by the traditional atmospheric model and machine learning, and their comparison: A case study in hangzhou, China. Environ. Pollut. 252, 366-378. https://doi.org/10.1016/j.envpol.2019.05.101 (2019).
  70. Biancofiore, F. et al. Analysis of surface ozone using a recurrent neural network. Sci. Total Environ. 514, 379-387. https://doi.org /10.1016/j.scitotenv.2015.01.106 (2015).
  71. Hu, F., Zhu, Y., Liu, J. & Li, L. An efficient Long Short-Term Memory model based on Laplacian Eigenmap in artificial neural networks. Appl. Soft Comput. 91, 106218. https://doi.org/10.1016/j.asoc.2020.106218 (2020).
  72. Pak, U., Kim, C., Ryu, U., Sok, K. & Pak, S. A hybrid model based on convolutional neural networks and long short-term memory for ozone concentration prediction. Air Qual. Atmos. Health 11, 883-895. https://doi.org/10.1007/s11869-018-0585-1 (2018).
  73. Wang, H.-W. et al. Regional prediction of ground-level ozone using a hybrid sequence-to-sequence deep learning approach. . Clean. Prod. 253, 119841. https://doi.org/10.1016/j.jclepro.2019.119841 (2020).
  74. Chen, Y., Chen, X., Xu, A., Sun, Q. & Peng, X. A hybrid CNN-Transformer model for ozone concentration prediction. Air Qual. Atmos. Health 15, 1533-1546. https://doi.org/10.1007/s11869-022-01197-w (2022).
  75. Jiménez-Navarro, M. J., Martínez-Ballesteros, M., Martínez-Álvarez, F. & Asencio-Cortés, G. Explaining deep learning models for ozone pollution prediction via embedded feature selection. Appl. Soft Comput. 157, 111504. https://doi.org/10.1016/j.asoc. 20 24.111504 (2024).
  76. Chen, M. et al. Air Pollution prediction based on optimized deep learning neural networks: PSO-LSTM. Atmos. Pollut. Res. 16, 102413. https://doi.org/10.1016/j.apr.2025.102413 (2025).
  77. Tian, W., Ge, Z. & He, J. OzoneNet: A spatiotemporal information attention encoder model for ozone concentrations prediction with multi-source data. Air Qual. Atmos. Health 17, 2223-2234. https://doi.org/10.1007/s11869-024-01568-5 (2024).
  78. Lin, G., Zhao, H. & Chi, Y. A comprehensive evaluation of deep learning approaches for ground-level ozone prediction across different regions. Ecol. Inform. 86, 103024. https://doi.org/10.1016/j.ecoinf.2025.103024 (2025).
  79. Guo, Q. et al. Changes in Air Quality from the COVID to the Post-COVID Era in the Beijing-Tianjin-Tangshan Region in China. Aerosol Air Qual. Res. 21, 210270. https://doi.org/10.4209/aaqr. 210270 (2021).
  80. Goudarzi, G., Hopke, P. K. & Yazdani, M. Forecasting PM2.5 concentration using artificial neural network and its health effects in Ahvaz, Iran. Chemosphere 283, 131285. https://doi.org/10.1016/j.chemosphere.2021.131285 (2021).
  81. Nunnari, G. et al. Modelling SO2 concentration at a point with statistical approaches. Environ. Model. Softw. 19, 887-905. https:/ /doi.org/10.1016/j.envsoft.2003.10.003 (2004).
  82. Lim, C. E. et al. Predicting microbial fuel cell biofilm communities and power generation from wastewaters with artificial neural network. Int. J. Hydrogen Energy 52, 1052-1064. https://doi.org/10.1016/j.ijhydene.2023.08.290 (2024).
  83. Chinatamby, P. & Jewaratnam, J. A performance comparison study on PM2.5 prediction at industrial areas using different training algorithms of feedforward-backpropagation neural network (FBNN). Chemosphere 317, 137788. https://doi.org/10.1016/j.chem osphere.2023.137788 (2023).
  84. Khoshraftar, Z. Modeling of CO2 solubility and partial pressure in blended diisopropanolamine and 2-amino-2-methylpropanol solutions via response surface methodology and artificial neural network. Sci. Rep. 15, 1800. https://doi.org/10.1038/s41598-02 5-86144-2 (2025).
  85. Rene, E. R., Estefanía López, M., Veiga, M. C. & Kennes, C. Neural network models for biological waste-gas treatment systems. New Biotechnol. 29, 56-73. https://doi.org/10.1016/j.nbt.2011.07.001 (2011).
  86. Luo, J. & Gong, Y. Air pollutant prediction based on ARIMA-WOA-LSTM model. Atmos. Pollut. Res. 14, 101761. https://doi.org /10.1016/j.apr.2023.101761 (2023).
  87. Ma, J., Ding, Y., Cheng, J. C. P., Jiang, F. & Wan, Z. A temporal-spatial interpolation and extrapolation method based on geographic Long Short-Term Memory neural network for PM2.5. J. Clean. Prod. 237, 117729. https://doi.org/10.1016/j.jclepro.2019.117729 (2019).
  88. Mathivanan, S. K., Rajadurai, H., Cho, J. & Easwaramoorthy, S. V. A multi-modal geospatial-temporal LSTM based deep learning framework for predictive modeling of urban mobility patterns. Sci. Rep. 14, 31579. https://doi.org/10.1038/s41598-024-74237-3 (2024).
  89. Al Mehedi, M. A. et al. Predicting the performance of green stormwater infrastructure using multivariate long short-term memory (LSTM) neural network. J. Hydrol. 625, 130076. https://doi.org/10.1016/j.jhydrol.2023.130076 (2023).
  90. Toh, S. C., Lai, S. H., Mirzaei, M., Soo, E. Z. X. & Teo, F. Y. Sequential data processing for IMERG satellite rainfall comparison and improvement using LSTM and ADAM optimizer. Appl. Sci. 13, 7237. https://doi.org/10.3390/app13127237 (2023).
  91. Chang, Z., Zhang, Y. & Chen, W. Electricity price prediction based on hybrid model of adam optimized LSTM neural network and wavelet transform. Energy 187, 115804. https://doi.org/10.1016/j.energy.2019.07.134 (2019).
  92. Zhang, J. & Li, S. Air quality index forecast in Beijing based on CNN-LSTM multi-model. Chemosphere 308, 136180. https://doi. org/10.1016/j.chemosphere.2022.136180 (2022).
  93. Wang, Z. et al. Enhanced RBF neural network metamodelling approach assisted by sliced splitting-based K-fold cross-validation and its application for the stiffened cylindrical shells. Aerosp. Sci. Technol. 124, 107534. https://doi.org/10.1016/j.ast.2022.107534 (2022).
  94. Sejuti, Z. A. & Islam, M. S. A hybrid CNN-KNN approach for identification of COVID-19 with 5-fold cross validation. Sensors Int. 4, 100229. https://doi.org/10.1016/j.sintl.2023.100229 (2023).
  95. Hong, F., Ji, C., Rao, J., Chen, C. & Sun, W. Hourly ozone level prediction based on the characterization of its periodic behavior via deep learning. Process Saf. Environ. Prot. 174, 28-38. https://doi.org/10.1016/j.psep.2023.03.059 (2023).
  96. Zhang, B., Song, C., Li, Y. & Jiang, X. Spatiotemporal prediction of O3 concentration based on the KNN-Prophet-LSTM model. Heliyon 8, e11670. https://doi.org/10.1016/j.heliyon.2022.e11670 (2022).
  97. Ehteram, M., Najah Ahmed, A., Khozani, Z. S. & El-Shafie, A. Graph convolutional network – Long short term memory neural network- multi layer perceptron- Gaussian progress regression model: A new deep learning model for predicting ozone concertation. Atmos. Pollut. Res. 14, 101766. https://doi.org/10.1016/j.apr.2023.101766 (2023).
  98. Suraboyina, S., Allu, S. K., Anupoju, G. R. & Polumati, A. A comparative predictive analysis of back-propagation artificial neural networks and non-linear regression models in forecasting seasonal ozone concentrations. J. Earth Syst. Sci. 131, 189. https://doi. org/10.1007/s12040-022-01912-2 (2022).
  99. Zhou, Z., Qiu, C. & Zhang, Y. A comparative analysis of linear regression, neural networks and random forest regression for predicting air ozone employing soft sensor models. Sci. Rep. 13, 22420. https://doi.org/10.1038/s41598-023-49899-0 (2023).
  100. Zhang, X. et al. Estimation of lower-stratosphere-to-troposphere ozone profile using long short-term memory (LSTM). Remote Sens. https://doi.org/10.3390/rs13071374 (2021).
  101. Seng, D., Zhang, Q., Zhang, X., Chen, G. & Chen, X. Spatiotemporal prediction of air quality based on LSTM neural network. Alex. Eng. J. 60, 2021-2032. https://doi.org/10.1016/j.aej.2020.12.009 (2021).
  102. Ekinci, E., İlhan Omurca, S. & Özbay, B. Comparative assessment of modeling deep learning networks for modeling ground-level ozone concentrations of pandemic lock-down period. Ecol. Model. 457, 109676. https://doi.org/10.1016/j.ecolmodel.2021.109676 (2021).
  103. Cheng, Y., Zhu, Q., Peng, Y., Huang, X.-F. & He, L.-Y. Multiple strategies for a novel hybrid forecasting algorithm of ozone based on data-driven models. J. Clean. Prod. 326, 129451. https://doi.org/10.1016/j.jclepro.2021.129451 (2021).

شكر وتقدير

تم دعم هذا البحث من قبل مؤسسة شاندونغ الإقليمية للعلوم الطبيعية (رقم المنحة ZR2023MD075)، مختبر الدولة الرئيسي لعلوم التربة والجيولوجيا الرباعية (رقم المنحة SKLLQG2419)، LAC/CMA (رقم المنحة 2023B02)، برنامج العلوم الإنسانية والاجتماعية في التعليم العالي بمقاطعة شاندونغ (رقم المنحة J18RA196)، المؤسسة الوطنية للعلوم الطبيعية في الصين (رقم المنحة 41572150)، وبرنامج دعم أعضاء هيئة التدريس الشباب للابتكارات العلمية والتكنولوجية في مؤسسات التعليم العالي بمقاطعة شاندونغ (رقم المنحة 2021KJ085).

مساهمات المؤلفين

ساهم جميع المؤلفين في تصور وتصميم الدراسة. الكتابة والتحرير: ق.غ. وز.ح.; جمع البيانات الأولية: ق.غ. وز.ح. وز.و. قرأ جميع المؤلفين ووافقوا على النسخة النهائية من المخطوطة.

الإعلانات

المصالح المتنافسة

يعلن المؤلفون عدم وجود مصالح متنافسة.

معلومات إضافية

يجب توجيه المراسلات والطلبات للحصول على المواد إلى Q.G.
معلومات إعادة الطبع والتصاريح متاحة علىwww.nature.com/reprints.
ملاحظة الناشر: تظل شركة سبرينجر ناتشر محايدة فيما يتعلق بالمطالبات القضائية في الخرائط المنشورة والانتماءات المؤسسية.
الوصول المفتوح. هذه المقالة مرخصة بموجب رخصة المشاع الإبداعي النسب-غير التجاري-عدم الاشتقاق 4.0 الدولية، التي تسمح بأي استخدام غير تجاري، ومشاركة، وتوزيع، وإعادة إنتاج في أي وسيلة أو صيغة، طالما أنك تعطي الائتمان المناسب للمؤلفين الأصليين والمصدر، وتوفر رابطًا لرخصة المشاع الإبداعي، وتوضح إذا قمت بتعديل المادة المرخصة. ليس لديك إذن بموجب هذه الرخصة لمشاركة المواد المعدلة المشتقة من هذه المقالة أو أجزاء منها. الصور أو المواد الأخرى من طرف ثالث في هذه المقالة مشمولة في رخصة المشاع الإبداعي الخاصة بالمقالة، ما لم يُشار إلى خلاف ذلك في سطر الائتمان للمادة. إذا لم تكن المادة مشمولة في رخصة المشاع الإبداعي الخاصة بالمقالة وكان استخدامك المقصود غير مسموح به بموجب اللوائح القانونية أو يتجاوز الاستخدام المسموح به، ستحتاج إلى الحصول على إذن مباشرة من صاحب حقوق الطبع والنشر. لعرض نسخة من هذه الرخصة، قم بزيارة http://creativecommo ns.org/licenses/by-nc-nd/4.0/.
© المؤلفون 2025
  1. كلية الجغرافيا والبيئة، جامعة لياوتشينغ، لياوتشينغ 252000، الصين. معهد دراسات هوانغهي، جامعة لياوتشينغ، لياوتشينغ 252000، الصين. المختبر الوطني الرئيسي للتربة والجيولوجيا الرباعية، معهد بيئة الأرض، الأكاديمية الصينية للعلوم، شيآن 710061، الصين. المختبر الرئيسي للكيمياء الجوية، الإدارة الوطنية للأرصاد الجوية، بكين 100081، الصين. المختبر الرئيسي لمراقبة ونمذجة شبكة النظام البيئي، معهد علوم الجغرافيا والموارد الطبيعية، مركز بيانات علوم النظام البيئي الوطني، الأكاديمية الصينية للعلوم، بكين 100101، الصين. البريد الإلكتروني: guoqingchun@lcu.edu.cn

Journal: Scientific Reports, Volume: 15, Issue: 1
DOI: https://doi.org/10.1038/s41598-025-91329-w
PMID: https://pubmed.ncbi.nlm.nih.gov/40000767
Publication Date: 2025-02-25

scientific reports

OPEN

Assessing the effectiveness of long short-term memory and artificial neural network in predicting daily ozone concentrations in Liaocheng City

Qingchun ⊠ , Zhenfang & Zhaosheng Wang

Abstract

Ozone pollution affects food production, human health, and the lives of individuals. Due to rapid industrialization and urbanization, Liaocheng has experienced increasing of ozone concentration over several years. Therefore, ozone has become a major environmental problem in Liaocheng City. Long short-term memory (LSTM) and artificial neural network (ANN) models are established to predict ozone concentrations in Liaocheng City from 2014 to 2023. The results show a general improvement in the accuracy of the LSTM model compared to the ANN model. Compared to the ANN, the LSTM has an increase in determination coefficient , value from 0.6779 to 0.6939 , a decrease in root mean square error (RMSE) value from to and a decrease in mean absolute error (MAE) value from to . The prediction accuracy of the LSTM is superior to the ANN in terms of R, RMSE, and MAE. In summary, LSTM is a promising technique for predicting ozone concentrations. Moreover, by leveraging historical data and LSTM enables accurate predictions of future ozone concentrations on a global scale. This model will open up new avenues for controlling and mitigating ozone pollution.

Keywords Artificial neural network, Long short-term memory, Deep Learning, Ozone
Air pollution affects climate change, food production, and human life . Poor air quality annually leads to about 6.5 million premature deaths worldwide, accounting for about of global deaths . Ozone ( ) exposure annually causes about 400 thousand premature deaths worldwide . Although air quality in China is improving year by year, Ozone ( ) still cause about 69 thousand deaths per year . Therefore, it is important to accurate predict ozone concentrations for human life and air quality management.
Air pollution prediction approaches mainly includes numerical simulations and data-driven methods. The numerical simulations consider the physical and chemical processes, such as the diffusion and transportation of air pollutants. These numerical models require sophisticated parameterizations. The widely used numerical simulations contain the Weather Research and Forecasting (WRF) model and the WRF-CMAQ . Besides, the complexity of numerical simulations leads to high computational costs and difficulty in finding the optimal solution. In contrast, data-driven methods have the characteristics of simplicity, speed, and economy. Datadriven approaches includes regression analysis and machine learning . Among these machine learning models, artificial neural network (ANN) has improved prediction accuracy compared to linear models, and compared to numerical simulations, ANN does not require the precise chemical and physical processes . Furthermore, ANN has been widely used in air pollution prediction . Ambient ozone concentrations is modelled using ANN with optimal inputs at Limbayat of Surat city (India) . Results show that ANN modelling appears to be a promising method for modelling ozone concentrations. In recent years, Deep learning is broadly used for time series prediction problems . Recurrent neural networks (RNNs) are particularly suitable for modeling
time series data. Compared with ANN, RNNs can directly receive the original data as input and learn useful time correlations from training time series data . However, the gradient issue in traditional RNN limits its ability to capture long-term dependencies, resulting in poor air pollution forecast performance . Hence, long short-term memory (LSTM) is a RNN architecture and it further alleviates the vanishing gradient problem of vanilla . So, LSTM has become the most popular deep learning approach for air pollution prediction . The performance metrics of different methods are evaluated for the air pollution dataset. LSTM has the lowest MSE (mean square error) of 0.298 , followed by DBN and RNN. In terms of MAE (mean absolute error), LSTM has the lowest value of 0.192 , followed by RNN and DBN . LSTMs are used to predict air quality in in the city of Madrid. Fully connected LSTM (FC-LSTM) when predicting ozone, has the lowest RMSE (root mean squared error) of .
Therefore, this research was aimed to evaluate and identify the reliable model to predict ozone concentrations in Liaocheng City in China. Appropriate model architecture was selected to predict ozone concentrations by selected inputs. This study suggests that LSTM is a potential solution for predicting ozone concentrations.
The research on predicting ozone ( ) concentrations using artificial intelligence (AI) techniques has significantly advanced in recent years, offering robust models for air quality forecasting . ANN achieves a RMSE of with a coefficient of determination of 0.52 . the ANN model for prediction of 1 -day ahead ozone concentration is far more accurate than the multiple linear regression (MLR) model . The multi-layer perceptron (MLP) neural network model is effective for forecasting concentrations in Zagreb, with the highest of 0.9 and the lowest RMSE of . The optimized MLP model outperforms other approaches, including persistence models and linear regression, which rely on simpler assumptions and fail to capture the complexities of atmospheric dynamics . ANN models generally outperform multivariate regression (MR) models when using additional inputs like lag values or moving averages, with a correlation coefficient (R) of . Combination of principal component analysis (PCA) and ANN is used to forecast daily total ozone concentrations and performs well for Mumbai and Kolkata with high correlation and low prediction errors . Both SVM and ANN models performed well in predicting ozone concentrations, with of 0.9152 and 0.9122 , and RMSE of 7.85 and 7.66 , respectively . MLPANN is used for forecasting maximum daily ozone concentrations with nonlinear data assimilation. The RMSE improves from approximately (3D photochemical model) to 17-18 with the upgraded MLP model . ANN is used to predict ozone concentrations in Jinan, China, based on meteorological parameters and temporal covariates. In the testing phase, the ANN achieves an of 0.8224 , the RMSE is calculated as , and the MAE is . The MLR model achieved an of 0.491 , while the ANN model achieved an of 0.767 , indicating that the ANN model performed better in predicting concentrations . For forecasting maximum daily average ozone (MDA8-O3) 1 day in advance, the CEEMD + CRJ + MLR model achieved a MAE of , and a RMSE of . The ANN model demonstrates strong performance for forecasting, with a ranging from 0.49 to 0.68 over the forecast period from Day 0 to Day 4, in highly polluted regions like Delhi, India . Feedforward neural network is used for a day ahead predictions of average ozone concentration ( 8 hO 3 ) in Novi Sad, Serbia. For 8 hO 3 forecasting, RMSE and correlation coefficient (R) are and 0.910, respectively for the station Dnevnik . A General Regression ANN (GRANN) was used to predict SOMO35 (the sum of means over 35 ppb ) for 24 European countries, with . The Back Propagation (BP) ANN shows a lower average (correlation coefficient) of 0.64 , RMSE of , indicating moderate accuracy but instability in predictions, particularly with large datasets in Beijing. The SVM-GABPNN model outperformed both BPANN and GABPANN by significantly improving the prediction accuracy for ozone concentrations, with an average R of 0.94 , RMSE of . ANN performs better than linear and SVM models for modelling ozone. The values for linear and SVM models are , respectively, for Delhi. Conversely, the ANN yields value of . LR, Support Vector Regression (SVR), Gaussian Process Regression (GPR) and ANN are able to give the highest ( and ), respectively . A Damped Least Squares (DLS) ANN is used to estimate the concentration of ozone based on meteorological parameters. The DLSNN model demonstrates very low RMSE and MAE, relatively high , confirming the accuracy of the predictions . A Chaotic ANN (CANN) is used to predict ozone levels in Lanzhou. CANN showed RMSE between 2.90 and across stations and between 0.9511 and 0.9728 , outperforming ANN, BP, and MLR models . Wavelet Transform (WT) is applied to remove noise and enhance the quality of input data before feeding it to an ANN model. WT-ANN is shown to be more accurate for predicting ozone concentrations compared to the ANN alone with RMSE of 0.9313 ppm , MAE of of . At the DJ-3 station, the WFANN model achieved a correlation coefficient (R) of 0.97 , with a MAPE of , compared to the FANN model’s R of 0.93 and MAPE of . The RFNN-GWO model outperforms the others (RMLP-ANN and RFNN) in forecasting O3 concentrations with RMSE of , correlation coefficient (R) of (Testing). By combining the strengths of ANNs and optimization algorithms, RFNN-GWO achieves high accuracy and stability, making it suitable for predicting air quality in regions with complex meteorological and pollutant data .The ANN with k -means clustering shows improved performance in predicting ozone concentrations while reducing the training data in Seoul, South Korea . Compared to the RFNN, RFNN-GOA demonstrates superior accuracy in predicting surface ozone levels in Osijek city . FFBP model with 5 neurons in the hidden layer (M-5) has the best performance with of 0.8344 , and RMSE of . Similarly, the LRNN model with 8 neurons in the hidden layer (M-8) shows good performance with of 0.8268 , and RMSE of . Both FFBP and LRNN models performed well, but the FFBP model outperformed the LRNN model slightly in terms of statistical indices .
In recent years, researchers have attempted various deep learning architectures to enhance the predictive ability of ozone concentration . A deep convolutional neural network (CNN) is used to predict next-day 24-h ozone levels based on meteorological data and previous air pollution measurements. The CNN model could
accurately predict ozone concentrations, with a strong performance (index of agreement (IOA) greater than 0.85 for 19 of 21 stations) . The CNN model achieved a Pearson correlation coefficient (R) of 0.79 , indicating reasonably good prediction accuracy . RNN outperforms the traditional WRF-CMAQ model in predicting ozone levels in hangzhou, with R ( 0.91 ), and RMSE ( ). RNN captures the temporal patterns of ozone accumulation and decay better than extreme learning machine (ELM), MLP, and random forest (RF) methods . RNN is more effective than MLP model for forecasting concentrations.is used for forecasting ozone ( ) concentrations 3 h ahead with a higher correlation coefficient (0.8967) and a lower NMSE (0.1174) in Pescara, Italy .
LSTM (Long Short-Term Memory) networks have seen significant progress in predicting ozone ( ) levels, particularly due to their ability to capture long-term dependencies in time series data. When compared to other algorithms like ANN and Stochastic Gradient Descent (SGD), LE-LSTM exhibits superior performance with higher accuracy and lower error in ozone concentration predictions, particularly on sequential and time-series datasets . The CNN-LSTM hybrid model significantly improves prediction accuracy compared to simpler models like MLP, with a reduction in RMSE, MAE, and MAPE . A hybrid sequence-to-sequence deep learning model with attention mechanism (HSA-Net) is proposed for prediction in Beijing. The HSA-Net model outperforms other baseline models (such as Seq2Seq, LSTM, GRU) in terms of RMSE ( ), MAE ( ), and . CNN-Transformer for ozone concentration prediction outperforms other models (ARIMA, CNN), with an RMSE value of . The TLSTM for ozone pollution prediction achieves the best RMSE (15.5), followed by the TFF, and LSTM models . In prediction, the PSO-LSTM’s value is higher than the RF and LSTM models, showing improvements of and , respectively . OzoneNet based on LSTM model integrated the self-attention mechanism is used for ozone concentrations prediction. OzoneNet has higher reliability and validity, outperforming benchmark models . Bi-LSTM is the most effective for predicting nationwide ozone trends, achieving an of 0.66 , and an RMSE of 15.32 . In contrast, transformer is the poorest performing model, with an of 0.57 , and an RMSE of .
In summary, the ANN and LSTM models demonstrate strong performance in predicting ozone concentrations, the models maintain acceptable levels of prediction accuracy, as evidenced by the low RMSE and MAE values and the high . The success of ANN and LSTM models indicate that data-driven models have shown good generalization ability and efficiency in dealing with ozone concentration prediction. Especially when dealing with complex meteorological and pollutant data, these models can learn patterns directly from a large amount of historical data without excessive physical assumptions. These studies have demonstrated the potential of these methods to predict ozone levels, benefiting environmental monitoring and public health. These studies suggest that the ANN and LSTM models are reliable tools for forecasting ambient ozone concentrations, even when applied to new, unseen data.
However, most in-depth researches on artificial intelligence methods for predicting ozone pollution have overlooked the use of information from past data. Therefore, this study aims to investigate the impact of incorporating lagged data on the performance of two artificial intelligence methods in predicting ozone pollution.

Study area and data

Study area

Liaocheng is located in the North China Plain, and has been included in major national strategies such as the coordinated development of ecological protection and high-quality development of the Yellow River basin (Fig. 1). In 2023, Liaocheng achieved a gross domestic product of CNY 292.636 billion, with a proportion of 14.1:37.1:48.8 in the industrial structure. The annual total solar radiation in Liaocheng is . The solar radiation is highest in summer, followed by spring, and lowest in winter. The average annual sunshine hours in Liaocheng are 2567 h , with a maximum of 274 h in May and a minimum of 170 h in January.

Data

From January 1, 2014 to December 27, 2023, the ozone concentrations in Liaocheng in China are investigated (http://www.aqistudy.cn/) . These ozone data are divided into three subsets: training period (from January 1, 2014 to December 27, 2021); verification period (from December 28, 2021 to December 27, 2022); prediction period (from December 28, 2022 to December 27, 2023).

Methodology

Artificial neural network (ANN)

ANN is constructed by one or several intermediate layers, an output neural layer, and an input neural layer . ANN is characterised by a set of processing neurons, an activation function for each neuron, and learning. ANN has the network topology and parameters, such as hidden layers, nodes (neurons), learning rules, and activated functions. The structure of ANN has shown in Fig. 2.
Backpropagation is a widely used method for training artificial neural networks by minimizing the global error function (E). This process involves calculating the error in the network’s predictions and adjusting the weights accordingly to reduce this error. The E is generally defined as the sum of squared differences between the desired outputs ( Ai ) and the predicted outputs ( Bi ) from the network, as shown in Eq. (1) .
The factor is commonly used to simplify the derivative calculations that occur later during backpropagation. To minimize the global error function, the gradient descent algorithm is employed to update the weights of the
Fig. 1. Location of Liaocheng. The map is generated using ArcGIS Pro 2.5 (ArcGIS Pro), URL: https://www.esr iuk.com.
Fig. 2. ANN architecture for ozone concentrations predicting.
network. The weight update rule is based on the negative gradient of the error function with respect to each weight, as expressed in Eq. (2):
where is the change in the weight between neuron j and neuron i ; and is the learning rate, which controls the step size for each weight update. represents the gradient of the error function with respect to the weight △ Dji. This gradient is computed during the backpropagation process.
The training algorithm’s goal is to optimize the weights (w) and biases (b) of each neuron to maximize accuracy between predicted and actual outputs. The backpropagation algorithm includes six categories: self-adaptive
learning rate, adaptive momentum, resilient backpropagation, quasi-Newton, conjugate gradient, and Bayesian regularization. we compare 13 key training algorithms for improving ANN performance, specifically in terms of accuracy in Table 1. The best training algorithm is determined through a trial-and-error approach .
The choice of transfer function is crucial for output prediction, as it helps meet the specific requirements of the network neurons. Four types of transfer functions (activation functions) are logarithmic sigmoid transfer function (logsig,or sigmoid), hyperbolic tangent activation function (tansig,or tanh), linear transfer function (purelin), and rectified linear units (relu, or poslin), respectively . Equations (3)-(6) represent the transfer functions:
where c represents the corresponding input variable.
The learning rate is an important parameter in the back-propagation algorithm, used to adjust the weights after each iteration. It determines the speed at which the weights are updated. If it is set too high, the results may overshoot the optimal value. If it is set too low, the descent might be too slow, making the optimization process inefficient . In the ANN, the learning rate is chosen to be from 0.001 to 0.1 . After testing, the learning rate is 0.01 , optimal batch size is 16 , and the number of epochs is 200 .

Long short-term memory (LSTM)

LSTM is a revised RNN model with strong long data processing capability. The LSTM unit consists of three gate units and one storage (memory) unit, each playing a vital role in controlling the flow of information. These gate units are the input, forgetting and output gates ( ), which are employed to control the input, forgetting and output of information. The memory unit is employed to store and update the information. Together, these gates allow the LSTM to selectively store, forget, and output information, making it possible to learn from both short-term and long-term dependencies . The structure of the LSTM unit is shown in Fig. 3. is the previous memory state, denotes the previous output information, denotes the new input information, represents the sigmoid function used in the gating operations . The operations of these gates are described below:
Training functions Training algorithm Category
Trainbr Bayesian regularization backpropagation (BR) Bayesian Regularization
Trainlm Levenberg-Marquardt backpropagation (LM) Quasi-Newton
Traingdx Gradient descent with momentum and adaptive learning rate backpropagation (GDX) Self-Adaptive Learning Rate
Traingd Gradient descent backpropagation (GD) Adaptive Momentum
Traingdm Gradient descent with momentum backpropagation (GDM) Adaptive Momentum
Traingda Gradient descent with adaptive learning rate (GDA) self-adaptive learning rate
Trainrp Resilient backpropagation (RP) Resilient Backpropagation
Traincgp Conjugate gradient backpropagation with Polak-Ribiére updates (CGP) Conjugate Gradient Algorithms
Traincgf Conjugate gradient backpropagation with Fletcher-Reeves (CGF) Conjugate Gradient
Traincgb Conjugate gradient backpropagation with Powell-Beale restarts (CGB) Conjugate Gradient
Trainscg Scaled conjugate gradient backpropagation (SCG) Conjugate Gradient Algorithms
Trainbfg BFGS quasi-Newton backpropagation (BFGS) Quasi-Newton
Trainoss One-step secant backpropagation (OSS) Quasi-Newton
Table 1. Description of various training algorithms.
Fig. 3. The network structure diagram of LSTM.
where b is coefficient (Weight) and W is bias vector.
LSTMs are particularly popular in time series prediction because of their ability to capture long-range temporal dependencies in data. This is a significant advantage over traditional RNNs, which often struggle with long-term dependencies. LSTMs also excel at capturing nonlinear patterns in data, making them highly effective for forecasting . By using both long-term memory and short-term memory , LSTMs are able to recall relevant information at different time scales. This makes them particularly suitable for tasks like prediction, where understanding both long-term trends and short-term fluctuations is essential .
Optimization is crucial in LSTM training to find the optimal parameters that minimize the loss function. The Adaptive Moment Estimation (ADAM) optimizer is widely used due to its combination of momentum and adaptive learning rates, making it efficient for stochastic optimization. It only requires first-order gradients, consumes little memory, and computes adaptive learning rates for each parameter using estimates of the first and second moments of the gradients. ADAM can converge faster and outperform stochastic gradient descent (SGD) . Therefore, the ADAM optimizer is used in the LSTM. Selecting the correct learning rate is essential for training deep learning model effectively. The learning rate is 0.01 , batch size is 16 , and the number of epochs is 200 .

Normalization

Ozone Concentrations data were normalized using the Eq. (5) :
where, Y denotes the normalized ozone data of denotes the maximum value of the raw ozone sequence, denotes the minimum value of the raw ozone sequence.
After model training, the predicted ozone concentrations are reversely normalized using the Eq. (6):

Performance criteria

In order to appraise the predicting performance of the ozone concentration models, determination coefficient , root mean square error (RMSE), and mean absolute error (MAE) are defined as follows:
where Pm denotes the value of observed ozone concentrations; Km denotes the predicted ozone concentrations; and I is the length of data. denotes the average of the observed ozone concentrations, denotes the average of the forecasted ozone concentrations.

Cross-validation

Cross-validation (CV) is a successful approach to acquire the optimum parameters of ANN and LSTM models . The process of Ten-Fold Cross Validation involves splitting the dataset into 10 equally sized subsets. One subset is reserved for testing, while the remaining nine are used for training the model. This procedure is repeated ten times, each time using a different subset for testing and the remaining subsets for training. By the end of the process, each fold has been used once for testing and nine times for training. The model’s performance is evaluated by calculating a performance metric for each iteration. The final performance score is the average of the individual scores across all folds. This approach helps reduce the variance in performance results and provides a more reliable estimate of how the model will perform on unseen data. One of the main advantages of Ten-Fold Cross Validation is its ability to reduce model bias. Since the model is trained and tested on different data subsets, the results are less likely to be skewed by a specific data partition. This method also helps to ensure that the model can generalize well to new data, rather than memorizing or overfitting to a particular subset. Additionally, Ten-Fold Cross Validation provides a comprehensive evaluation by using all available data for both training and testing, which is particularly valuable when working with small datasets . Due to the superior performance of the tenfold-cross-validation, the results of ANN and LSTM models based on the tenfold-crossvalidation technique are tested.

Results

Prediction result analysis of ANN

Various input variables were tested to determine the most accurate network structure for predicting ozone concentrations. Table 2 shows simulation results of ozone concentrations during the three periods. We have tried using 1-21 days as input and obtained different results. The trend of simulation results with input values of days gradually improves, but deteriorates again after 18 days. It is important that using only the most recent 18 days simulates the best ozone concentrations. 18 variables were selected for the model input. Moreover, the hidden layer of the ANN model has 6 neurons. The activation functions of the ANN are logsig and purelin. The prediction accuracy levels of different neural network structures are shown in Table 2. The , RMSE, MAE during the predicting period are , respectively. Figure 4 illustrates the simulation of ANN output and target values of predicting ozone concentrations. In the forecast period, ozone concentrations in the next day are predicted employing previous days’ ozone concentrations. The training and verifying values are from December 28, 2021 to December 27, 2022. and then we began to predict from
Days RMSE ( ) MAE ( )
Training Verification Predicting Training Verification Predicting Training Verification Predicting
1 0.7199 0.6704 0.6746 28.9068 28.7516 28.4753 22.1112 22.7250 21.7433
2 0.7194 0.6699 0.6767 30.2199 30.1252 30.1126 23.0106 23.6725 24.0905
3 0.7201 0.6708 0.6752 29.0394 28.8809 28.7620 22.2106 22.6481 22.6086
4 0.7194 0.6688 0.6738 30.5321 30.5937 30.3191 23.3101 23.5057 22.1770
5 0.7202 0.6681 0.6742 29.2372 29.2461 29.0279 22.3948 23.0475 22.8921
6 0.7207 0.6636 0.6743 29.5874 29.6720 29.0610 23.2021 23.7656 23.0427
7 0.7185 0.6740 0.6679 29.2979 29.6237 29.2568 22.3965 23.2457 23.1825
8 0.7209 0.6753 0.6726 29.0521 29.0789 28.8248 22.2262 22.3580 21.7427
9 0.7217 0.6752 0.6759 28.5505 28.5409 28.0269 21.8588 22.9577 21.7169
10 0.7206 0.6750 0.6733 28.5273 28.6327 28.2811 21.8717 22.3195 21.7119
11 0.7213 0.6751 0.6705 28.5456 28.5674 28.3453 21.8699 21.9867 21.7381
12 0.7340 0.6714 0.6698 29.6990 30.1861 29.5068 22.6504 22.8725 21.9138
13 0.7338 0.6767 0.6759 28.5431 28.5988 28.1162 21.8645 21.9931 21.7150
14 0.7322 0.6792 0.6721 28.9504 28.8697 28.4737 22.0829 22.6316 22.3236
15 0.7357 0.6800 0.6722 28.5702 28.6258 28.3783 21.7867 22.3737 22.0558
16 0.7344 0.6675 0.6647 28.7505 29.3310 28.6649 21.9436 22.6347 21.8948
17 0.7362 0.6806 0.6714 28.6504 28.2378 28.2337 21.8700 21.7673 21.7461
18 0.7365 0.6816 0.6779 28.5095 28.5514 27.9895 21.7649 22.2194 21.6919
19 0.7298 0.6558 0.6609 29.0901 29.8630 28.9438 22.3889 23.6812 22.9974
20 0.7347 0.6804 0.6770 28.8931 29.0575 28.4365 22.0176 22.2992 21.7366
21 0.7356 0.6728 0.6722 31.7804 32.0956 31.6421 24.8417 26.0248 25.9455
Table 2. Comparison between various input variables (days) of ANN.
Fig. 4. The predicting results with the ANN model.
Training functions RMSE ( ) MAE ( )
Training Verification Predicting Training Verification Predicting Training Verification Predicting
Trainbr 0.7365 0.6816 0.6779 28.5095 28.5514 27.9895 21.7649 22.2194 21.6919
Trainlm 0.7175 0.6695 0.6616 28.6158 28.7517 28.4215 22.2676 22.9182 22.2838
Traingdx 0.5898 0.5118 0.4879 45.0885 41.8351 41.8636 37.7704 34.6598 35.0691
Traingd 0.6393 0.5572 0.5163 51.6911 47.6252 47.4953 43.3039 39.0684 39.5381
Traingdm 0.6970 0.6258 0.5978 30.5444 30.9063 31.1977 23.3807 24.1323 24.6383
Traingda 0.6970 0.6258 0.5978 30.5444 30.9063 31.1977 23.3807 24.1323 24.6383
Trainrp 0.7277 0.6709 0.6762 28.9446 29.0196 28.0672 22.3000 22.8271 22.1916
Traincgp 0.7243 0.6722 0.6616 28.8725 28.6758 28.9082 22.4534 22.8300 22.2299
Traincgf 0.7255 0.6702 0.6775 28.8072 28.6681 28.9245 22.4128 22.9577 22.2582
Traincgb 0.7238 0.6734 0.6666 28.9014 28.7121 28.6843 22.4994 22.8450 22.2093
Trainscg 0.7239 0.6678 0.6638 28.9956 28.8375 28.8066 22.4787 23.0364 22.1189
Trainbfg 0.7275 0.6698 0.6667 28.9988 28.9291 28.6813 22.3532 22.9733 22.2056
Trainoss 0.7219 0.6651 0.6653 29.3094 28.9499 28.7389 22.5294 23.1128 22.0381
Table 3. Results of various training algorithms in the ANN for simulating.
December 28, 2022 to December 27, 2023. In the year, the forecasting ozone concentrations are similar to the actual ozone values.
The statistical tests of the different algorithms in the ANN are displayed in Table 3. Comparing the tests, trainbr yields the highest ( 0.7365 ), the lowest RMSE ( 28.5095 ), and the lowest MAE ( 21.7649 ) in training period. The trainbr algorithm also finishs well in the validation phase, with , RMSE (28.5514) and MAE (22.2194), respectively. In the prediction stage, , and MAE of trainbr are respectively 0.6779 , 27.9895, and 21.6919, explaining its predictive power.
The statistical tests of different unions of transfer functions (purelin (PU), tansig (TA), logsig (LO), poslin (PO)) are displayed in Table 4. The results of union (LO-PU) have the lowest RMSE and MAE values, and the highest R value, proving a successful union. In addition, this configuration also completes well in validation phase and has good predictive ability in the prediction period.

Result analysis of LSTM

LSTM analysis was conducted to predict ozone concentrations in Liaocheng City. Optimization of hyperparameters is necessary as these values depend on the ozone concentrations. The outcomes for the input variables and statistical analysis of simulation results can be seen in Table 5. Similarly, Table 5 represent the , MAE and RMSE of the LSTM model. When the input value changes from 1 to 18 days, the simulation results also improve, and then, from 18 to 21 days, the simulation results deteriorate again. The analysis identified 18 day delays as significant factors in predicting the daily ozone concentrations. Therefore, the input number of the ozone time step is 18 . The batch size and epochs selected for LSTM are 16 and 200, respectively. The activation functions of LSTM are tanh and sigmoid, and learning rate is 0.01 . In addition, the optimizer is Adam for this experiment.
Figure 5 depicts the plot comparing the observed and predicted ozone concentrations for LSTM. It is seen that there is a high correlation between output and target ozone values. The figure shows clearly that the overall
Transfer function RMSE MAE
Training Verification Predicting Training Verification Predicting Training Verification Predicting
TA-PU 0.7261 0.6651 0.6613 29.1098 28.7597 28.2666 21.8107 22.4336 21.9249
TA-LO 0.7312 0.6666 0.6705 28.7454 28.6088 28.2803 21.9803 22.4058 22.3284
TA-TA 0.7240 0.6563 0.6605 29.2331 29.4033 28.6722 21.8764 22.5216 22.2328
LO-PU 0.7365 0.6816 0.6779 28.5095 28.5514 27.9895 21.7649 22.2194 21.6919
LO-TA 0.7240 0.6626 0.6605 29.2375 29.4209 28.6688 21.8794 23.2460 22.2513
LO-LO 0.7229 0.6612 0.6610 29.3070 29.0733 28.4446 21.9500 22.8055 22.7744
PU-TA 0.7143 0.6600 0.6703 29.7439 28.6146 28.2838 21.9832 22.4110 22.3364
PU-LO 0.7178 0.6615 0.6605 29.5980 28.9258 28.6777 22.1754 22.6638 22.7458
PU-PU 0.7216 0.6606 0.6595 29.3341 29.3393 28.0578 22.5718 23.0936 22.3539
TA-PO 0.7077 0.6619 0.6607 29.2008 28.7186 28.5556 22.8954 22.5664 22.1375
LO-PO 0.7195 0.6611 0.6615 29.4938 29.0942 28.1946 22.0387 22.8510 22.7705
PO-PO 0.7209 0.6618 0.6619 29.4140 29.7937 28.9868 22.9791 22.5146 22.7470
PU-PO 0.7166 0.6609 0.6608 29.7689 29.2252 28.5211 22.2734 22.9010 22.1546
PO-LO 0.7169 0.6612 0.6604 29.6207 29.0823 28.6772 22.0901 22.6724 22.2532
PO-PU 0.7170 0.6618 0.6610 29.5421 29.7611 28.4066 22.0641 22.5251 22.7511
PO-TA 0.7174 0.6612 0.6619 29.3532 29.0891 28.0126 22.0080 22.7055 22.6200
Table 4. Results of various transfer functions in the ANN for simulating.
Days RMSE ( ) MAE ( )
Training Verification Predicting Training Verification Predicting Training Verification Predicting
1 0.7074 0.6530 0.6535 29.9701 29.7814 28.9982 22.8702 22.8105 22.1673
2 0.7189 0.6545 0.6566 29.3768 29.7017 28.8565 22.3821 22.7104 22.0473
3 0.7263 0.6705 0.6672 28.9846 28.9905 28.3908 22.0543 22.2044 21.9894
4 0.7320 0.6726 0.6662 28.6833 28.8989 28.4271 21.7966 22.0971 21.7849
5 0.7379 0.6682 0.6761 28.3663 29.1008 27.9928 21.6099 22.3051 21.4314
6 0.7384 0.6705 0.6767 28.3366 28.9978 27.9644 21.5377 22.2521 21.1804
7 0.7423 0.6694 0.6842 28.1260 29.0430 27.6338 21.4291 22.3133 21.0353
8 0.7427 0.6784 0.6831 28.1056 28.6408 27.6871 21.4157 21.9549 21.2736
9 0.7460 0.6815 0.6829 27.9226 28.5090 27.7014 21.2723 21.9219 21.3349
10 0.7482 0.6811 0.6855 27.8022 28.5364 27.5817 21.1620 21.9089 21.1191
11 0.7491 0.6840 0.6826 27.7556 28.3945 27.7119 21.0643 21.8384 21.2267
12 0.7484 0.6824 0.6833 27.7900 28.4708 27.6793 21.0956 21.8943 21.1828
13 0.7490 0.6878 0.6876 27.7566 28.2266 27.4949 21.1390 21.7223 21.0147
14 0.7533 0.6906 0.6921 27.5190 28.0904 27.2943 21.0049 21.8952 20.8469
15 0.7547 0.6930 0.6879 27.4405 27.9839 27.4774 20.9333 21.7072 21.1297
16 0.7563 0.6964 0.6807 27.3500 27.8272 27.8038 20.9849 21.6665 21.2855
17 0.7561 0.6975 0.6829 27.3652 27.7974 27.7057 20.9517 21.6478 21.2439
18 0.7577 0.6989 0.6939 27.2747 27.7139 27.2140 20.9027 21.6309 20.8825
19 0.7574 0.6975 0.6932 27.3658 27.7230 27.2473 20.9553 21.6801 20.8978
20 0.7572 0.6952 0.6899 27.3034 27.8852 27.3893 20.9360 21.6827 21.1164
21 0.7567 0.6919 0.6930 27.3311 28.0326 27.2583 20.9318 21.6266 20.9265
Table 5. Comparison between various input variables (days) of LSTM.
performance of LSTM is superior to that of ANN. The trend of LSTM has better agreement with observations than the ANN model.

Result analysis of LSTM and ANN for tenfold-cross-validation

We used the tenfold validation method to calculate all data (2014-2023) and obtained the average of 10 calculation results. From Table 6, it can be seen that LSTM and ANN have good generalization ability through cross validation.
Fig. 5. The predicting results with the LSTM model.
Models R2 RMSE MAE
Training Verification Training Verification Training Verification
LSTM 0.738004 0.68879 27.87386 27.46569 21.35167 21.38393
ANN 0.725225 0.673961 28.72121 28.61427 22.29554 22.37229
Table 6. Comparison between LSTM and ANN for tenfold-cross-validation.

Discussion

Firstly, the input variables have a significant impact on both ANN and LSTM models for prediction. By comparing the prediction performance of both models with different input variables, we optimized the network structures of both models. Secondly, the activation functions also have a certain impact on the performance of the ANN prediction model. By training different activation functions, ANN model can handle nonlinear relationships between complex input variables. However, ANN lacks a memory mechanism, ANN performs poorly in capturing the long-term dependencies of time series, making it difficult to capture the dynamic changes of . The structure of LSTM enables it to consider past long and short-term information in prediction, therefore, LSTM is a better choice.
In this research, we employed both LSTM and ANN models to predict ozone concentrations in Liaocheng City and compared their generalization ability and performance accuracy. The comparative analysis demonstrated that the LSTM (with ) outperformed the ANN (with ) in predicting ozone concentrations, as indicated in Table 1 and 2. The error values (MAE and RMSE) achieved by the proposed LSTM model are very less when compared to the ANN. The MAE and RMSE values achieved by the proposed LSTM model in predicting period are and , respectively. The value of the proposed LSTM model is 0.6939 which is larger compared to the ANN model. LSTM has the smaller absolute difference between its predicted values and actual values. The LSTM technique exhibits superior generalization ability compared to the ANN model.
This finding is highly consistent with the complex and nonlinear nature of ozone concentrations, making the LSTM the preferred model for predicting index . These outcomes are also consistent with another study’s outcomes that compared the performance of multi-layer perceptron (MLP) and LSTM in developing effective ozone prediction models . Similar to our outcomes, their investigation shows that MLR has poorer performance compared to LSTM. LSTM utilizes the dependencies of time series to generate better generalization ability and higher accuracy . Both ANN and MLR were used to predict ozone concentrations in Lanzhou. RMSE and of ANN were 7.8275 and 0.9238 ; while RMSE and of MLR were 21.5847 and 0.5328 . ANN showed a better fit. The RMSE of ANN was much lower than that of MLR, which verified its accuracy and effectiveness. The results showed that ANN had better performance than MLR . Back-propagation ANNs (BPANNs) were used for the prediction of concentrations in Hyderabad, India during 2014-2016. The efficiency and performance of BPANNs showed higher . ANN, RNN (recurrent neural network), RFR (random forest regression) and LR (linear regression) were used to predict air ozone in Sichuan Province, China. , RMSE, and MAE of LR are 0.7271, 29.94, and 24.4891. , RMSE, and MAE of BPANN are , and , RMSE, and MAE of RNN are , and 20.0169. , RMSE, and MAE of RFR are 0.8215, 24.9195, and . ANN and RNN models outperform RFR and LR models across various variable sets. Both ANN and RNN can capture nonlinear relationships between input features and concentrations. So, ANN and RNN can model intricate complex interactions and patterns. Recently, LSTM models were applied to estimate daily surface ozone concentrations in three urban agglomerations in China (Sichuan Basin, North China Plain, and Yangtze River Delta), with the accuracy of RMSE , MAE .
LSTM was employed to obtain the predicted values of in Beijing. The LSTM achieved the smallest error. The values of MAE, and RMSE, are , and . LSTM method was applied to forecast hourly ozone levels in Turkey. For hidden neurons and epoch size , RMSE takes a value between 10.86 and 13.38, MAE takes values in the range of 7.45 and 7.672 and value varies from 0.92 to . Furthermore, RF-CEEMDAN-Attention-LSTM was proposed to predict three-hourly concentrations in Chengdu. The model integrated random forest (RF), complete ensemble empirical mode decomposition with adaptive noise (CEEMADN) method and LSTM model. The simulation results showed that the hybrid model not only had a better fitting effect on concentration values than other comparable models . LSTM and MLR were used to predict ozone at the two stations in Shenzhen, China. RMSE, MAE, and of the LSTM at HQC station are 14.0588, 9.8924, and 0.6068, respectively; while those values of the MLR are 16.8589, 12.0243, 0.4347, respectively. RMSE, MAE, and of the LSTM at HQC station are 14.0588, 9.8924, and 0.6068, respectively; while those values of the MLR are , respectively. Moreover, RMSE, MAE, and of the LSTM at NA station are 12.2361, 9.3810, and 0.5226, respectively; while those values of the MLR are 12.9509, 10.0415, and 0.4915, respectively . The prediction results of the LSTM are better than those of the MLR. The LSTM has excellent performance in dealing with ozone concentration forecasting problems, and it has good robustness and generalization performance. Overall, the findings of this research strengthen the advantages of deep learning models, particularly the LSTM method in accurately forecasting ozone concentrations, and highlight the potential for addressing the complexity of air pollution modeling.

Conclusions

Continuous improvement of air quality can meet people’s expectations for a better life. ozone concentration prediction is an important issue for researchers. Predicting ozone concentrations is a complex issue because Many parameters affect ozone formation. To achieve the objective, LSTM and ANN were built in this research paper to predict ozone concentrations in Liaocheng City. To check the performances of the proposed LSTM and ANN models, comparative analysis of both models with previous related works was completed using evaluation indicators. During the training phase, the , RMSE, and MAE of the LSTM model are , and , respectively, while during the verification phase, they are , and . Meanwhile, during the predicting phase, they are , and . The LSTM model provides more accurate results than the ANN. The results show that the LSTM model not only had a better fitting effect on than ANN model in the training phase, but the model also had the higher value for at the predicting phase. This proposed LSTM model outperforms the ANN technique. Compared with the ANN, the LSTM model exhibits superior performance for high ozone concentration values, which has an important effect on early warning. Government administrators can use the LSTM to plan and implement effective strategies to reduce ozone concentrations and protect people’s health.
In the future, multi-day ahead prediction models of daily ozone concentrations will be investigated. There are some other considered factors, such as meteorological factors, air pollutants, terrain, and location, etc. We will use new methods to predict ozone in other regions, such as bidirectional LSTM (BiLSTM), convolutional neural network (CNN),CNN-LSTM, CNN- BiLSTM, TCN and transformer.

Data availability

Data and materials are available from the corresponding author upon request.
Received: 24 April 2024; Accepted: 19 February 2025
Published online: 25 February 2025

References

  1. . et al. A quantitative assessment and process analysis of the contribution from meteorological conditions in an O 3 pollution episode in Guangzhou. China Atmos. Environ. 303, 119757. https://doi.org/10.1016/j.atmosenv.2023.119757 (2023).
  2. Wang, L., Zhao, B., Zhang, Y. & Hu, H. Correlation between surface PM2.5 and O3 in eastern China during 2015-2019: Spatiotemporal variations and meteorological impacts. Atmos. Environ. 294, 119520. https://doi.org/10.1016/j.atmosenv.2022.11 9520 (2023).
  3. Qi, Q., Wang, S., Zhao, H., Kota, S. H. & Zhang, H. Rice yield losses due to O3 pollution in China from 2013 to 2020 based on the WRF-CMAQ model. J. Clean. Prod. https://doi.org/10.1016/j.jclepro.2023.136801 (2023).
  4. Mo, S. et al. Sex disparity in cognitive aging related to later-life exposure to ambient air pollution. Sci. Total Environ. 886, 163980. https://doi.org/10.1016/j.scitotenv.2023.163980 (2023).
  5. Lyu, Y. et al. Tracking long-term population exposure risks to PM2.5 and ozone in urban agglomerations of China 2015-2021. Sci. Total Environ. 854, 158599. https://doi.org/10.1016/j.scitotenv.2022.158599 (2023).
  6. Guo, Q., He, Z. & Wang, Z. Long-term projection of future climate change over the twenty-first century in the Sahara region in Africa under four Shared Socio-Economic Pathways scenarios. Environ. Sci. Pollut. Res. 30, 22319-22329. https://doi.org/10.100 7/s11356-022-23813-z (2023).
  7. Guo, Q., He, Z. & Wang, Z. The characteristics of air quality changes in Hohhot City in China and their relationship with meteorological and socio-economic factors. Aerosol Air Qual. Res. 24, 230274. https://doi.org/10.4209/aaqr. 230274 (2024).
  8. Guo, Q., He, Z. & Wang, Z. Change in air quality during 2014-2021 in Jinan City in China and its influencing factors. Toxics 11, 210. https://doi.org/10.3390/toxics11030210 (2023).
  9. Shams, S. R. et al. Assessing the effectiveness of artificial neural networks (ANN) and multiple linear regressions (MLR) in forcasting AQI and PM10 and evaluating health impacts through AirQ+ (case study: Tehran). Environ. Pollut. 338, 122623. https://doi.org/10.1016/j.envpol.2023.122623 (2023).
  10. Xue, T. et al. Estimating the exposure-response function between long-term ozone exposure and under- 5 mortality in 55 lowincome and middle-income countries: a retrospective, multicentre, epidemiological study. Lancet Planet. Health 7, e736-e746. https://doi.org/10.1016/S2542-5196(23)00165-1 (2023).
  11. Chu, Y. et al. Three-hourly PM25 and O3 concentrations prediction based on time series decomposition and LSTM model with attention mechanism. Atmos. Pollut. Res. 14, 101879. https://doi.org/10.1016/j.apr.2023.101879 (2023).
  12. Huang, C. et al. Study on the assimilation of the sulphate reaction rates based on WRF-Chem/DART. Sci. China Earth Sci. 66, 2239-2253. https://doi.org/10.1007/s11430-023-1153-9 (2023).
  13. Wang, Y. et al. Ultra-high-resolution mapping of ambient fine particulate matter to estimate human exposure in Beijing. Commun. Earth Environ. 4, 451. https://doi.org/10.1038/s43247-023-01119-3 (2023).
  14. Mirzavand Borujeni, S., Arras, L., Srinivasan, V. & Samek, W. Explainable sequence-to-sequence GRU neural network for pollution forecasting. Sci. Rep. 13, 9940. https://doi.org/10.1038/s41598-023-35963-2 (2023).
  15. Guo, Q., He, Z. & Wang, Z. Simulating daily PM2.5 concentrations using wavelet analysis and artificial neural network with remote sensing and surface observation data. Chemosphere 340, 139886. https://doi.org/10.1016/j.chemosphere.2023.139886 (2023).
  16. Guo, Q., He, Z. & Wang, Z. Prediction of Hourly PM2.5 and PM10 Concentrations in Chongqing City in China Based on Artificial Neural Network. Aerosol Air Qual. Res. 23, 220448. https://doi.org/10.4209/aaqr. 220448 (2023).
  17. Guo, Q., He, Z. & Wang, Z. Predicting of daily PM2.5 concentration employing wavelet artificial neural networks based on meteorological elements in Shanghai China. Toxics 11, 51. https://doi.org/10.3390/toxics11010051 (2023).
  18. He, Z., Guo, Q., Wang, Z. & Li, X. Prediction of monthly PM2.5 concentration in Liaocheng in China employing artificial neural network. Atmosphere 13, 1221. https://doi.org/10.3390/atmos13081221 (2022).
  19. Guo, Q. et al. Air pollution forecasting using artificial and wavelet neural networks with meteorological conditions. Aerosol Air Qual. Res. 20, 1429-1439. https://doi.org/10.4209/aaqr.2020.03.0097 (2020).
  20. Kapadia, D. & Jariwala, N. Prediction of tropospheric ozone using artificial neural network (ANN) and feature selection techniques. Model. Earth Syst. Environ. 8, 2183-2192. https://doi.org/10.1007/s40808-021-01220-6 (2022).
  21. Guo, Q., He, Z. & Wang, Z. Prediction of monthly average and extreme atmospheric temperatures in Zhengzhou based on artificial neural network and deep learning models. Front. Forests Glob. Change 6, 1249300. https://doi.org/10.3389/ffgc.2023.1249300 (2023).
  22. He, Z. & Guo, Q. Comparative analysis of multiple deep learning models for forecasting monthly ambient PM2.5 concentrations: A case study in Dezhou City, China. Atmosphere 15, 1432. https://doi.org/10.3390/atmos15121432 (2024).
  23. Guo, Q. et al. A performance comparison study on climate prediction in Weifang city using different deep learning models. Water 16, 2870. https://doi.org/10.3390/w16192870 (2024).
  24. Guo, Q., He, Z. & Wang, Z. Monthly climate prediction using deep convolutional neural network and long short-term memory. Sci. Rep. 14, 17748. https://doi.org/10.1038/s41598-024-68906-6 (2024).
  25. Zhang, Y. et al. Prediction and cause investigation of ozone based on a double-stage attention mechanism recurrent neural network. Front. Environ. Sci. Eng. 17, 21. https://doi.org/10.1007/s11783-023-1621-4 (2022).
  26. Barthwal, A. & Goel, A. K. Advancing air quality prediction models in urban India: a deep learning approach integrating DCNN and LSTM architectures for AQI time-series classification. Model. Earth Syst. Environ. 10, 2935-2955. https://doi.org/10.1007/s4 0808-023-01934-9 (2024).
  27. Ding, W. & Sun, H. Prediction of PM2.5 concentration based on the weighted RF-LSTM model. Earth Sci. Inform. 16, 3023-3037. https://doi.org/10.1007/s12145-023-01111-7 (2023).
  28. Xu, S., Li, W., Zhu, Y. & Xu, A. A novel hybrid model for six main pollutant concentrations forecasting based on improved LSTM neural networks. Sci. Rep. 12, 14434. https://doi.org/10.1038/s41598-022-17754-3 (2022).
  29. Duan, J., Gong, Y., Luo, J. & Zhao, Z. Air-quality prediction based on the ARIMA-CNN-LSTM combination model optimized by dung beetle optimizer. Sci. Rep. 13, 12127. https://doi.org/10.1038/s41598-023-36620-4 (2023).
  30. Zhu, L., Husny, Z. J. B. M., Samsudin, N. A., Xu, H. & Han, C. Deep learning method for minimizing water pollution and air pollution in urban environment. Urban Clim. 49, 101486. https://doi.org/10.1016/j.uclim.2023.101486 (2023).
  31. Navares, R. & Aznarte, J. L. Predicting air quality with deep learning LSTM: Towards comprehensive models. Ecol. Inform. 55, 101019. https://doi.org/10.1016/j.ecoinf.2019.101019 (2020).
  32. Masood, A. & Ahmad, K. A review on emerging artificial intelligence (AI) techniques for air pollution forecasting: Fundamentals, application and performance. J. Clean. Prod. 322, 129072. https://doi.org/10.1016/j.jclepro.2021.129072 (2021).
  33. Cabaneros, S. M., Calautit, J. K. & Hughes, B. R. A review of artificial neural network models for ambient air pollution prediction. Environ. Model. Softw. 119, 285-304. https://doi.org/10.1016/j.envsoft.2019.06.014 (2019).
  34. Pan, Q., Harrou, F. & Sun, Y. A comparison of machine learning methods for ozone pollution prediction. J. Big Data 10, 63. https://doi.org/10.1186/s40537-023-00748-x (2023).
  35. Zhang, B., Zhang, Y. & Jiang, X. Feature selection for global tropospheric ozone prediction based on the BO-XGBoost-RFE algorithm. Sci. Rep. 12, 9244. https://doi.org/10.1038/s41598-022-13498-2 (2022).
  36. Zhang, W. et al. Parsimonious estimation of hourly surface ozone concentration across China during 2015-2020. Sci. Data 11, 492. https://doi.org/10.1038/s41597-024-03302-3 (2024).
  37. Chen, Y. et al. Seasonal predictability of the dominant surface ozone pattern over China linked to sea surface temperature. Clim. Atmos. Sci. 7, 17. https://doi.org/10.1038/s41612-023-00560-7 (2024).
  38. Liao, Q. et al. Deep learning for air quality forecasts: A review. Curr. Pollut. Rep. https://doi.org/10.1007/s40726-020-00159-z (2020).
  39. Malhotra, M., Walia, S., Lin, C.-C., Aulakh, I. K. & Agarwal, S. A systematic scrutiny of artificial intelligence-based air pollution prediction techniques, challenges, and viable solutions. J. Big Data 11, 142. https://doi.org/10.1186/s40537-024-01002-8 (2024).
  40. Kaur, M. et al. Computational deep air quality prediction techniques: a systematic review. Artif. Intell. Rev. 56, 2053-2098. https: //doi.org/10.1007/s10462-023-10570-9 (2023).
  41. Chaloulakou, A., Saisana, M. & Spyrellis, N. Comparative assessment of neural networks and regression models for forecasting summertime ozone in Athens. Sci. Total Environ. 313, 1-13. https://doi.org/10.1016/S0048-9697(03)00335-8 (2003).
  42. Hrust, L., Klaić, Z. B., Križan, J., Antonić, O. & Hercog, P. Neural network forecasting of air pollutants hourly concentrations using optimised temporal averages of meteorological variables and pollutant concentrations. Atmos. Environ. 43, 5588-5596. https://doi.org/10.1016/j.atmosenv.2009.07.048 (2009).
  43. Mahapatra, A. Prediction of daily ground-level ozone concentration maxima over New Delhi. Environ. Monit. Assess. 170, 159170. https://doi.org/10.1007/s10661-009-1223-z (2010).
  44. Chattopadhyay, G., Chattopadhyay, S. & Chakraborthy, P. Principal component analysis and neurocomputing-based models for total ozone concentration over different urban regions of India. Theor. Appl. Climatol. 109, 221-231. https://doi.org/10.1007/s00 704-011-0569-7 (2012).
  45. Luna, A. S., Paredes, M. L. L., de Oliveira, G. C. G. & Corrêa, S. M. Prediction of ozone concentration in tropospheric levels using artificial neural networks and support vector machine at Rio de Janeiro, Brazil. Atmos. Environ. 98, 98-104. https://doi.org/10.10 16/j.atmosenv.2014.08.060 (2014).
  46. Božnar, M. Z., Grašič, B., Mlakar, P., Gradišar, D. & Kocijan, J. Nonlinear data assimilation for the regional modeling of maximum ozone values. Environ. Sci. Pollut. Res. 24, 24666-24680. https://doi.org/10.1007/s11356-017-0059-2 (2017).
  47. Gao, M., Yin, L. & Ning, J. Artificial neural network model for ozone concentration estimation and Monte Carlo analysis. Atmos. Environ. https://doi.org/10.1016/j.atmosenv.2018.03.027 (2018).
  48. Sayahi, T. et al. Long-term calibration models to estimate ozone concentrations with a metal oxide sensor. Environ. Pollut. 267, 115363. https://doi.org/10.1016/j.envpol.2020.115363 (2020).
  49. Mo, Y. et al. A novel framework for daily forecasting of ozone mass concentrations based on cycle reservoir with regular jumps neural networks. Atmos. Environ. 220, 117072. https://doi.org/10.1016/j.atmosenv.2019.117072 (2020).
  50. Agarwal, S. et al. Air quality forecasting using artificial neural networks with real time dynamic error correction in highly polluted regions. Sci. Total Environ. 735, 139454. https://doi.org/10.1016/j.scitotenv.2020.139454 (2020).
  51. Malinović-Milićević, S. et al. Prediction of tropospheric ozone concentration using artificial neural networks at traffic and background urban locations in Novi Sad, Serbia. Environ. Monit. Assess. 193, 84. https://doi.org/10.1007/s10661-020-08821-1 (2021).
  52. Antanasijević, D., Pocajt, V., Perić-Grujić, A. & Ristić, M. Urban population exposure to tropospheric ozone: A multi-country forecasting of SOMO35 using artificial neural networks. Environ. Pollut. 244, 288-294. https://doi.org/10.1016/j.envpol.2018.10. 051 (2019).
  53. Feng, Y., Zhang, W., Sun, D. & Zhang, L. Ozone concentration forecast method based on genetic algorithm optimized back propagation neural networks and support vector machine data classification. Atmos. Environ. 45, 1979-1985. https://doi.org/10. 1016/j.atmosenv.2011.01.022 (2011).
  54. Meda, B. N. M., Mathew, A., Sarwesh, P., Shekar, P. R. & Sharma, K. V. Machine learning-based modeling of ground level ozone formation in Bangalore and New Delhi cities in India. Stochastic Environ. Res. Risk Assess. https://doi.org/10.1007/s00477-024-0 2845-6 (2024).
  55. Yafouz, A. et al. Comprehensive comparison of various machine learning algorithms for short-term ozone concentration prediction. Alex. Eng. J. 61, 4607-4622. https://doi.org/10.1016/j.aej.2021.10.021 (2022).
  56. Balram, D., Lian, K.-Y. & Sebastian, N. A novel soft sensor based warning system for hazardous ground-level ozone using advanced damped least squares neural network. Ecotoxicol. Environ. Saf. 205, 111168. https://doi.org/10.1016/j.ecoenv.2020.111168 (2020).
  57. Jia, B., Dong, R. & Du, J. Ozone concentrations prediction in Lanzhou, China, using chaotic artificial neural network. Chemometr. Intell. Lab. Syst. 204, 104098. https://doi.org/10.1016/j.chemolab.2020.104098 (2020).
  58. AlOmar, M. K., Hameed, M. M. & AlSaadi, M. A. Multi hours ahead prediction of surface ozone gas concentration: Robust artificial intelligence approach. Atmos. Pollut. Res. 11, 1572-1587. https://doi.org/10.1016/j.apr.2020.06.024 (2020).
  59. Dunea, D., Pohoata, A. & Iordache, S. Using wavelet-feedforward neural networks to improve air pollution forecasting in urban environments. Environ. Monit. Assess. 187, 477. https://doi.org/10.1007/s10661-015-4697-x (2015).
  60. Braik, M., Sheta, A. & Al-Hiary, H. Hybrid neural network models for forecasting ozone and particulate matter concentrations in the Republic of China. Air Qual. Atmos. Health 13, 839-851. https://doi.org/10.1007/s11869-020-00841-7 (2020).
  61. Park, J. Efficient ozone concentration trend prediction using ANN and K-means clustering. Earth Sci. Inform. 18, 163. https://do i.org/10.1007/s12145-024-01676-x (2025).
  62. Braik, M. et al. Predicting surface ozone levels in eastern Croatia: Leveraging recurrent fuzzy neural networks with grasshopper optimization algorithm. Water Air Soil Pollut. 235, 655. https://doi.org/10.1007/s11270-024-07378-w (2024).
  63. Gorai, A. K. & Mitra, G. A comparative study of the feed forward back propagation (FFBP) and layer recurrent (LR) neural network model for forecasting ground level ozone concentration. Air Qual. Atmos. Health 10, 213-223. https://doi.org/10.1007/s 11869-016-0417-0 (2017).
  64. Mu, L., Bi, S., Ding, X. & Xu, Y. Transformer-based ozone multivariate prediction considering interpretable and priori knowledge: A case study of Beijing, China. J. Environ. Manag. 366, 121883. https://doi.org/10.1016/j.jenvman.2024.121883 (2024).
  65. Zhou, J., Zhou, L., Cai, C. & Zhao, Y. Multi-step ozone concentration prediction model based on improved secondary decomposition and adaptive kernel density estimation. Process Saf. Environ. Prot. 190, 386-404. https://doi.org/10.1016/j.psep. 2 024.08.044 (2024).
  66. Wang, S. et al. A deep learning model integrating a wind direction-based dynamic graph network for ozone prediction. Sci. Total Environ. 946, 174229. https://doi.org/10.1016/j.scitotenv.2024.174229 (2024).
  67. Sayeed, A. et al. Using a deep convolutional neural network to predict 2017 ozone concentrations, 24 hours in advance. Neural Netw. 121, 396-408. https://doi.org/10.1016/j.neunet.2019.09.033 (2020).
  68. Eslami, E., Choi, Y., Lops, Y. & Sayeed, A. A real-time hourly ozone prediction system using deep convolutional neural network. Neural Comput. Appl. 32, 8783-8797. https://doi.org/10.1007/s00521-019-04282-x (2020).
  69. Feng, R. et al. Unveiling tropospheric ozone by the traditional atmospheric model and machine learning, and their comparison: A case study in hangzhou, China. Environ. Pollut. 252, 366-378. https://doi.org/10.1016/j.envpol.2019.05.101 (2019).
  70. Biancofiore, F. et al. Analysis of surface ozone using a recurrent neural network. Sci. Total Environ. 514, 379-387. https://doi.org /10.1016/j.scitotenv.2015.01.106 (2015).
  71. Hu, F., Zhu, Y., Liu, J. & Li, L. An efficient Long Short-Term Memory model based on Laplacian Eigenmap in artificial neural networks. Appl. Soft Comput. 91, 106218. https://doi.org/10.1016/j.asoc.2020.106218 (2020).
  72. Pak, U., Kim, C., Ryu, U., Sok, K. & Pak, S. A hybrid model based on convolutional neural networks and long short-term memory for ozone concentration prediction. Air Qual. Atmos. Health 11, 883-895. https://doi.org/10.1007/s11869-018-0585-1 (2018).
  73. Wang, H.-W. et al. Regional prediction of ground-level ozone using a hybrid sequence-to-sequence deep learning approach. . Clean. Prod. 253, 119841. https://doi.org/10.1016/j.jclepro.2019.119841 (2020).
  74. Chen, Y., Chen, X., Xu, A., Sun, Q. & Peng, X. A hybrid CNN-Transformer model for ozone concentration prediction. Air Qual. Atmos. Health 15, 1533-1546. https://doi.org/10.1007/s11869-022-01197-w (2022).
  75. Jiménez-Navarro, M. J., Martínez-Ballesteros, M., Martínez-Álvarez, F. & Asencio-Cortés, G. Explaining deep learning models for ozone pollution prediction via embedded feature selection. Appl. Soft Comput. 157, 111504. https://doi.org/10.1016/j.asoc. 20 24.111504 (2024).
  76. Chen, M. et al. Air Pollution prediction based on optimized deep learning neural networks: PSO-LSTM. Atmos. Pollut. Res. 16, 102413. https://doi.org/10.1016/j.apr.2025.102413 (2025).
  77. Tian, W., Ge, Z. & He, J. OzoneNet: A spatiotemporal information attention encoder model for ozone concentrations prediction with multi-source data. Air Qual. Atmos. Health 17, 2223-2234. https://doi.org/10.1007/s11869-024-01568-5 (2024).
  78. Lin, G., Zhao, H. & Chi, Y. A comprehensive evaluation of deep learning approaches for ground-level ozone prediction across different regions. Ecol. Inform. 86, 103024. https://doi.org/10.1016/j.ecoinf.2025.103024 (2025).
  79. Guo, Q. et al. Changes in Air Quality from the COVID to the Post-COVID Era in the Beijing-Tianjin-Tangshan Region in China. Aerosol Air Qual. Res. 21, 210270. https://doi.org/10.4209/aaqr. 210270 (2021).
  80. Goudarzi, G., Hopke, P. K. & Yazdani, M. Forecasting PM2.5 concentration using artificial neural network and its health effects in Ahvaz, Iran. Chemosphere 283, 131285. https://doi.org/10.1016/j.chemosphere.2021.131285 (2021).
  81. Nunnari, G. et al. Modelling SO2 concentration at a point with statistical approaches. Environ. Model. Softw. 19, 887-905. https:/ /doi.org/10.1016/j.envsoft.2003.10.003 (2004).
  82. Lim, C. E. et al. Predicting microbial fuel cell biofilm communities and power generation from wastewaters with artificial neural network. Int. J. Hydrogen Energy 52, 1052-1064. https://doi.org/10.1016/j.ijhydene.2023.08.290 (2024).
  83. Chinatamby, P. & Jewaratnam, J. A performance comparison study on PM2.5 prediction at industrial areas using different training algorithms of feedforward-backpropagation neural network (FBNN). Chemosphere 317, 137788. https://doi.org/10.1016/j.chem osphere.2023.137788 (2023).
  84. Khoshraftar, Z. Modeling of CO2 solubility and partial pressure in blended diisopropanolamine and 2-amino-2-methylpropanol solutions via response surface methodology and artificial neural network. Sci. Rep. 15, 1800. https://doi.org/10.1038/s41598-02 5-86144-2 (2025).
  85. Rene, E. R., Estefanía López, M., Veiga, M. C. & Kennes, C. Neural network models for biological waste-gas treatment systems. New Biotechnol. 29, 56-73. https://doi.org/10.1016/j.nbt.2011.07.001 (2011).
  86. Luo, J. & Gong, Y. Air pollutant prediction based on ARIMA-WOA-LSTM model. Atmos. Pollut. Res. 14, 101761. https://doi.org /10.1016/j.apr.2023.101761 (2023).
  87. Ma, J., Ding, Y., Cheng, J. C. P., Jiang, F. & Wan, Z. A temporal-spatial interpolation and extrapolation method based on geographic Long Short-Term Memory neural network for PM2.5. J. Clean. Prod. 237, 117729. https://doi.org/10.1016/j.jclepro.2019.117729 (2019).
  88. Mathivanan, S. K., Rajadurai, H., Cho, J. & Easwaramoorthy, S. V. A multi-modal geospatial-temporal LSTM based deep learning framework for predictive modeling of urban mobility patterns. Sci. Rep. 14, 31579. https://doi.org/10.1038/s41598-024-74237-3 (2024).
  89. Al Mehedi, M. A. et al. Predicting the performance of green stormwater infrastructure using multivariate long short-term memory (LSTM) neural network. J. Hydrol. 625, 130076. https://doi.org/10.1016/j.jhydrol.2023.130076 (2023).
  90. Toh, S. C., Lai, S. H., Mirzaei, M., Soo, E. Z. X. & Teo, F. Y. Sequential data processing for IMERG satellite rainfall comparison and improvement using LSTM and ADAM optimizer. Appl. Sci. 13, 7237. https://doi.org/10.3390/app13127237 (2023).
  91. Chang, Z., Zhang, Y. & Chen, W. Electricity price prediction based on hybrid model of adam optimized LSTM neural network and wavelet transform. Energy 187, 115804. https://doi.org/10.1016/j.energy.2019.07.134 (2019).
  92. Zhang, J. & Li, S. Air quality index forecast in Beijing based on CNN-LSTM multi-model. Chemosphere 308, 136180. https://doi. org/10.1016/j.chemosphere.2022.136180 (2022).
  93. Wang, Z. et al. Enhanced RBF neural network metamodelling approach assisted by sliced splitting-based K-fold cross-validation and its application for the stiffened cylindrical shells. Aerosp. Sci. Technol. 124, 107534. https://doi.org/10.1016/j.ast.2022.107534 (2022).
  94. Sejuti, Z. A. & Islam, M. S. A hybrid CNN-KNN approach for identification of COVID-19 with 5-fold cross validation. Sensors Int. 4, 100229. https://doi.org/10.1016/j.sintl.2023.100229 (2023).
  95. Hong, F., Ji, C., Rao, J., Chen, C. & Sun, W. Hourly ozone level prediction based on the characterization of its periodic behavior via deep learning. Process Saf. Environ. Prot. 174, 28-38. https://doi.org/10.1016/j.psep.2023.03.059 (2023).
  96. Zhang, B., Song, C., Li, Y. & Jiang, X. Spatiotemporal prediction of O3 concentration based on the KNN-Prophet-LSTM model. Heliyon 8, e11670. https://doi.org/10.1016/j.heliyon.2022.e11670 (2022).
  97. Ehteram, M., Najah Ahmed, A., Khozani, Z. S. & El-Shafie, A. Graph convolutional network – Long short term memory neural network- multi layer perceptron- Gaussian progress regression model: A new deep learning model for predicting ozone concertation. Atmos. Pollut. Res. 14, 101766. https://doi.org/10.1016/j.apr.2023.101766 (2023).
  98. Suraboyina, S., Allu, S. K., Anupoju, G. R. & Polumati, A. A comparative predictive analysis of back-propagation artificial neural networks and non-linear regression models in forecasting seasonal ozone concentrations. J. Earth Syst. Sci. 131, 189. https://doi. org/10.1007/s12040-022-01912-2 (2022).
  99. Zhou, Z., Qiu, C. & Zhang, Y. A comparative analysis of linear regression, neural networks and random forest regression for predicting air ozone employing soft sensor models. Sci. Rep. 13, 22420. https://doi.org/10.1038/s41598-023-49899-0 (2023).
  100. Zhang, X. et al. Estimation of lower-stratosphere-to-troposphere ozone profile using long short-term memory (LSTM). Remote Sens. https://doi.org/10.3390/rs13071374 (2021).
  101. Seng, D., Zhang, Q., Zhang, X., Chen, G. & Chen, X. Spatiotemporal prediction of air quality based on LSTM neural network. Alex. Eng. J. 60, 2021-2032. https://doi.org/10.1016/j.aej.2020.12.009 (2021).
  102. Ekinci, E., İlhan Omurca, S. & Özbay, B. Comparative assessment of modeling deep learning networks for modeling ground-level ozone concentrations of pandemic lock-down period. Ecol. Model. 457, 109676. https://doi.org/10.1016/j.ecolmodel.2021.109676 (2021).
  103. Cheng, Y., Zhu, Q., Peng, Y., Huang, X.-F. & He, L.-Y. Multiple strategies for a novel hybrid forecasting algorithm of ozone based on data-driven models. J. Clean. Prod. 326, 129451. https://doi.org/10.1016/j.jclepro.2021.129451 (2021).

Acknowledgements

This research was supported by Shandong Provincial Natural Science Foundation (Grant No. ZR2023MD075), State Key Laboratory of Loess and Quaternary Geology Foundation (Grant No. SKLLQG2419), LAC/CMA (Grant No. 2023B02), Shandong Province Higher Educational Humanities and Social Science Program (Grant No. J18RA196), the National Natural Science Foundation of China (Grant No. 41572150), and the Junior Faculty Support Program for Scientific and Technological Innovations in Shandong Provincial Higher Education Institutions (Grant No. 2021KJ085).

Author contributions

All authors contributed to the study conception and design. Writing and editing Q.G. and Z.H.; preliminary data collection: Q.G., Z.H. and Z.W. All authors read and approved the final manuscript.

Declarations

Competing interests

The authors declare no competing interests.

Additional information

Correspondence and requests for materials should be addressed to Q.G.
Reprints and permissions information is available at www.nature.com/reprints.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommo ns.org/licenses/by-nc-nd/4.0/.
© The Author(s) 2025
  1. School of Geography and Environment, Liaocheng University, Liaocheng 252000, China. Institute of Huanghe Studies, Liaocheng University, Liaocheng 252000, China. State Key Laboratory of Loess and Quaternary Geology, Institute of Earth Environment, Chinese Academy of Sciences, Xi’an 710061, China. Key Laboratory of Atmospheric Chemistry, China Meteorological Administration, Beijing 100081, China. Key Laboratory of Ecosystem Network Observation and Modeling, Institute of Geographic Sciences and Natural Resources Research, National Ecosystem Science Data Center, Chinese Academy of Sciences, Beijing 100101, China. email: guoqingchun@lcu.edu.cn