DOI: https://doi.org/10.1038/s41467-024-45670-9
PMID: https://pubmed.ncbi.nlm.nih.gov/38438350
تاريخ النشر: 2024-03-04
تنفيذ الأجهزة لشبكات عصبية اصطناعية تعتمد على الميمريستور
تم القبول: 1 فبراير 2024
نُشر على الإنترنت: 04 مارس 2024
(د) التحقق من التحديثات
الملخص
فرناندو أغيري
الملخص
تجرب الذكاء الاصطناعي (AI) حاليًا ازدهارًا مدفوعًا بتقنيات التعلم العميق (DL)، التي تعتمد على شبكات من وحدات حساب بسيطة متصلة تعمل بالتوازي. إن عرض النطاق الترددي المنخفض بين الذاكرة ووحدات المعالجة في آلات فون نيومان التقليدية لا يدعم متطلبات التطبيقات الناشئة التي تعتمد بشكل كبير على مجموعات كبيرة من البيانات. تساعد نماذج الحوسبة الأكثر حداثة، مثل التوازي العالي والحوسبة القريبة من الذاكرة، في تخفيف عنق الزجاجة في الاتصال بالبيانات إلى حد ما، ولكن هناك حاجة إلى مفاهيم تحولية. تعتبر الميمريستورز، وهي تقنية جديدة تتجاوز أشباه الموصلات المعدنية-أكسيد-المكمل (CMOS)، خيارًا واعدًا لأجهزة الذاكرة نظرًا لخصائصها الفريدة على مستوى الجهاز، مما يمكّن من التخزين والحوسبة مع بصمة صغيرة ومتوازية بشكل كبير وبطاقة منخفضة. نظريًا، يترجم هذا مباشرة إلى زيادة كبيرة في كفاءة الطاقة ومعدل الأداء الحاسوبي، ولكن لا تزال هناك تحديات عملية متنوعة. في هذا العمل، نستعرض أحدث الجهود لتحقيق الشبكات العصبية الاصطناعية (ANNs) القائمة على الميمريستور، موضحين بالتفصيل مبادئ العمل لكل كتلة والبدائل التصميمية المختلفة مع مزاياها وعيوبها، بالإضافة إلى الأدوات المطلوبة للتقدير الدقيق لمقاييس الأداء. في النهاية، نهدف إلى تقديم بروتوكول شامل للمواد والأساليب المعنية في الشبكات العصبية الميمريستورية لأولئك الذين يهدفون إلى البدء في العمل في هذا المجال والخبراء الذين يبحثون عن نهج شامل.
الأمن القومي، إلخ.
التحكم في الهواتف الذكية
استخدام وحدات معالجة الرسوميات (GPUs) لتنفيذ الشبكات العصبية الاصطناعية (انظر الشكل 1أ)، حيث يمكنها تنفيذ عمليات متعددة بشكل متوازي
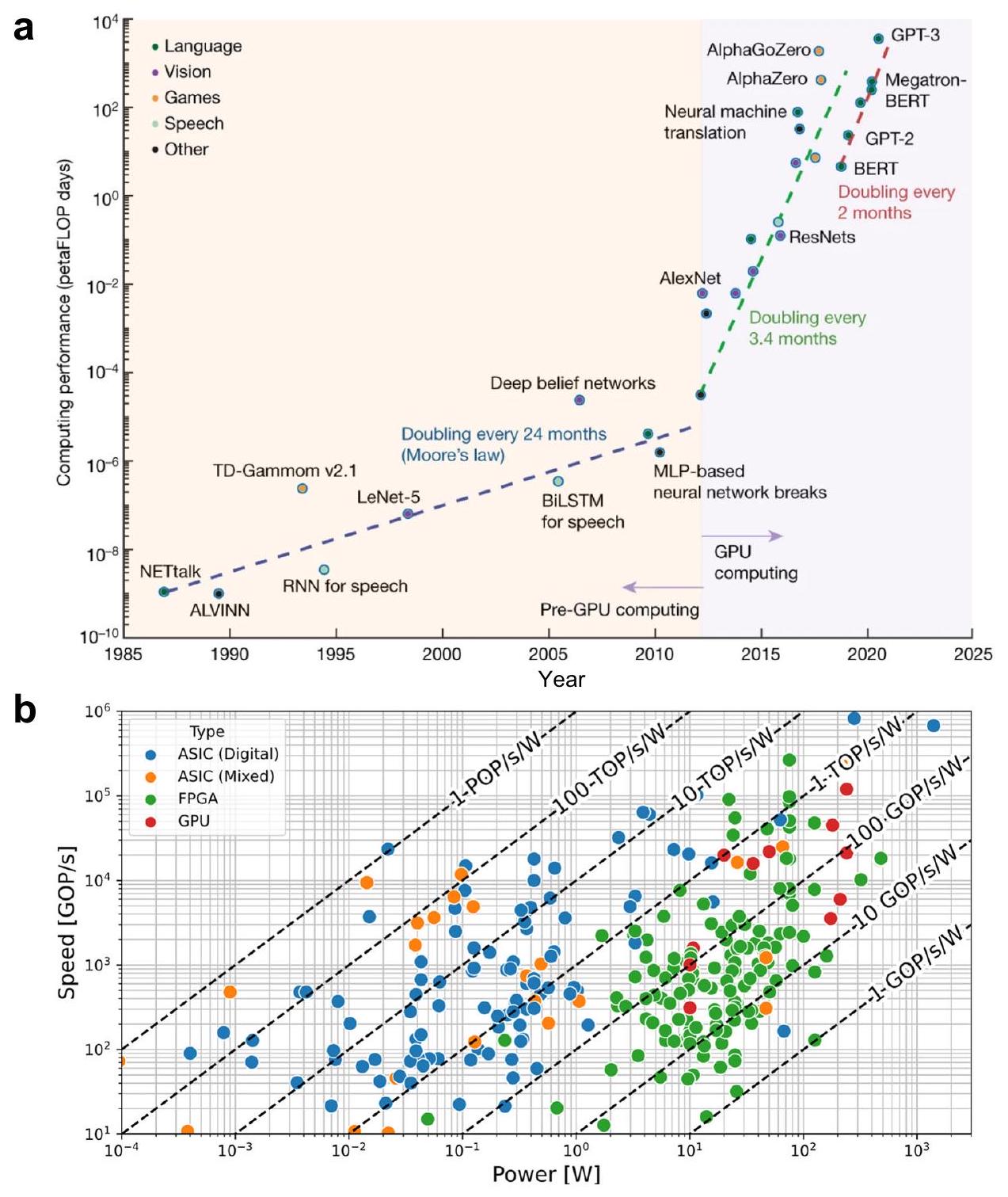
مجالات التطبيق
يمكن تصنيف الدوائر إلى فئتين. من ناحية، تعتبر معالجات تدفق البيانات معالجات مصممة خصيصًا لاستنتاج وتدريب الشبكات العصبية. نظرًا لأن حسابات تدريب واستنتاج الشبكات العصبية يمكن أن تُرتب بشكل حتمي تمامًا، فهي قابلة لمعالجة تدفق البيانات حيث يتم برمجة أو وضع وتوجيه الحسابات، والوصول إلى الذاكرة، وإجراءات الاتصالات بين وحدات المعالجة الحسابية بشكل صريح/ثابت على الأجهزة الحاسوبية. من ناحية أخرى، تدمج معجلات المعالجة في الذاكرة (PIM) عناصر المعالجة مع تكنولوجيا الذاكرة. من بين هذه المعجلات PIM توجد تلك المعتمدة على تكنولوجيا الحوسبة التناظرية التي تعزز دوائر الذاكرة الفلاش بقدرات الجمع والضرب التناظرية في المكان. يرجى الرجوع إلى المراجع الخاصة بـ Mythic.
دقة ANN عبر البرمجيات
هيكل ANNs المعتمدة على الميمريستور
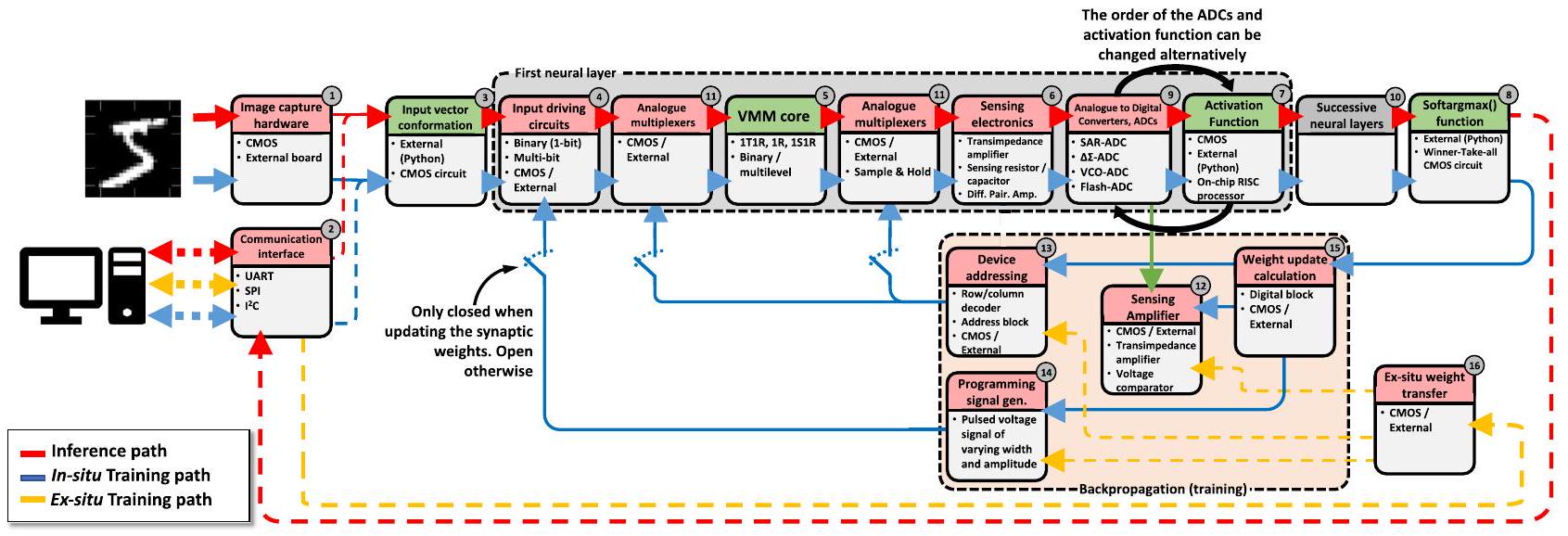
خلال التدريب خارج الموقع بواسطة الأسهم/الخطوط الصفراء. لكل صندوق، تشير الجزء العلوي (المُلوّن) إلى اسم الوظيفة التي يجب تحقيقها بواسطة الكتلة الدائرية، والجزء السفلي يشير إلى نوع الأجهزة المطلوبة. يشمل الصندوق المعنون بالطبقات العصبية المتعاقبة عدة كتل فرعية بهيكل مشابه للمجموعة المعنونة بالطبقة العصبية الأولى. 1S1R تعني 1 محدد 1 مقاوم بينما 1R تعني 1 مقاوم. UART وSPI و
ارتفاع عقدة التخزين مرتفع بما يكفي للاحتفاظ بالبيانات على المدى الطويل. أيضًا، تعمل VMM المعتمدة على الفلاش بطريقة مختلفة قليلاً عن VMM المعتمدة على SRAM. في VMM المعتمدة على الفلاش، يساهم كل عنصر ذاكرة بمقدار مختلف في التيار في كل عمود من مصفوفة التقاطع اعتمادًا على الجهد المطبق على المدخل أو صف التقاطع وعناصر المصفوفة مخزنة كشحن على البوابة العائمة
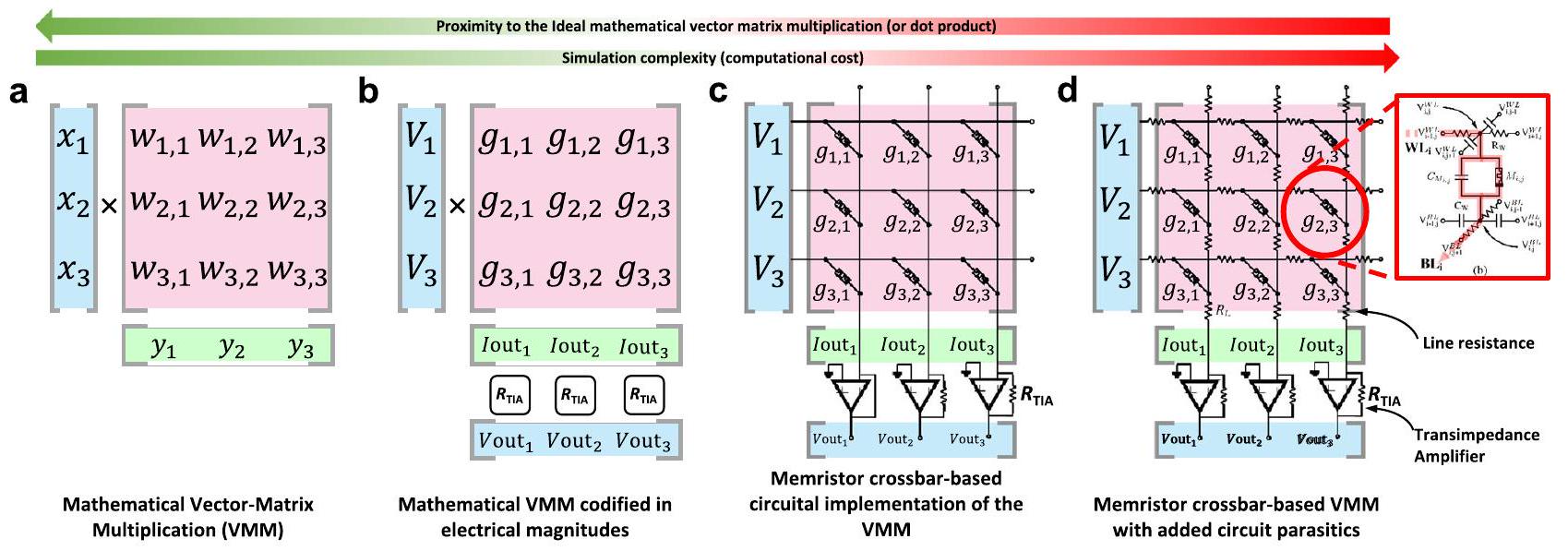
ميمريستور (1 R أو 1 M) أو مصفوفة تشابكية سلبية (الشكل 3c). عند استخدام مصفوفات تشابكية من الميمريستورات لأداء عمليات VMM، قد تكون هناك حاجة إلى دوائر إضافية عند الإدخال والإخراج لاستشعار و/أو تحويل الإشارات الكهربائية (انظر الصناديق الحمراء في الشكل 2). من أمثلة هذه الدوائر محولات من الرقمية إلى التناظرية (DAC)، ومن التناظرية إلى الرقمية (ADC) ومضخمات مقاومة التيار (TIA). لاحظ أن دراسات أخرى استخدمت تنفيذات تختلف قليلاً عن هذا المخطط، أي، دمج أو تجنب كتل معينة لتوفير المساحة و/أو تقليل استهلاك الطاقة (انظر الجدول 1).
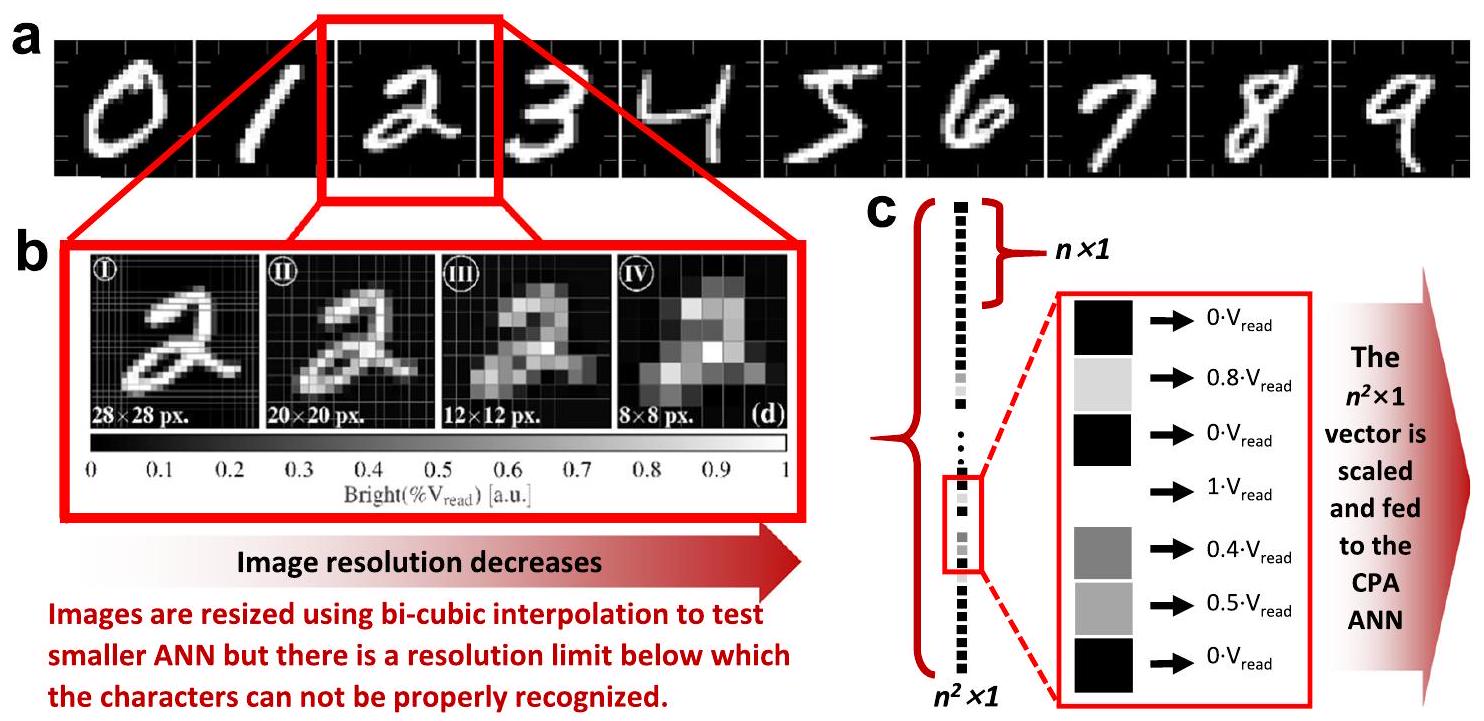
أجهزة التقاط الصور (الكتلة 1) وتشكيل متجه الإدخال (الكتلة 3)
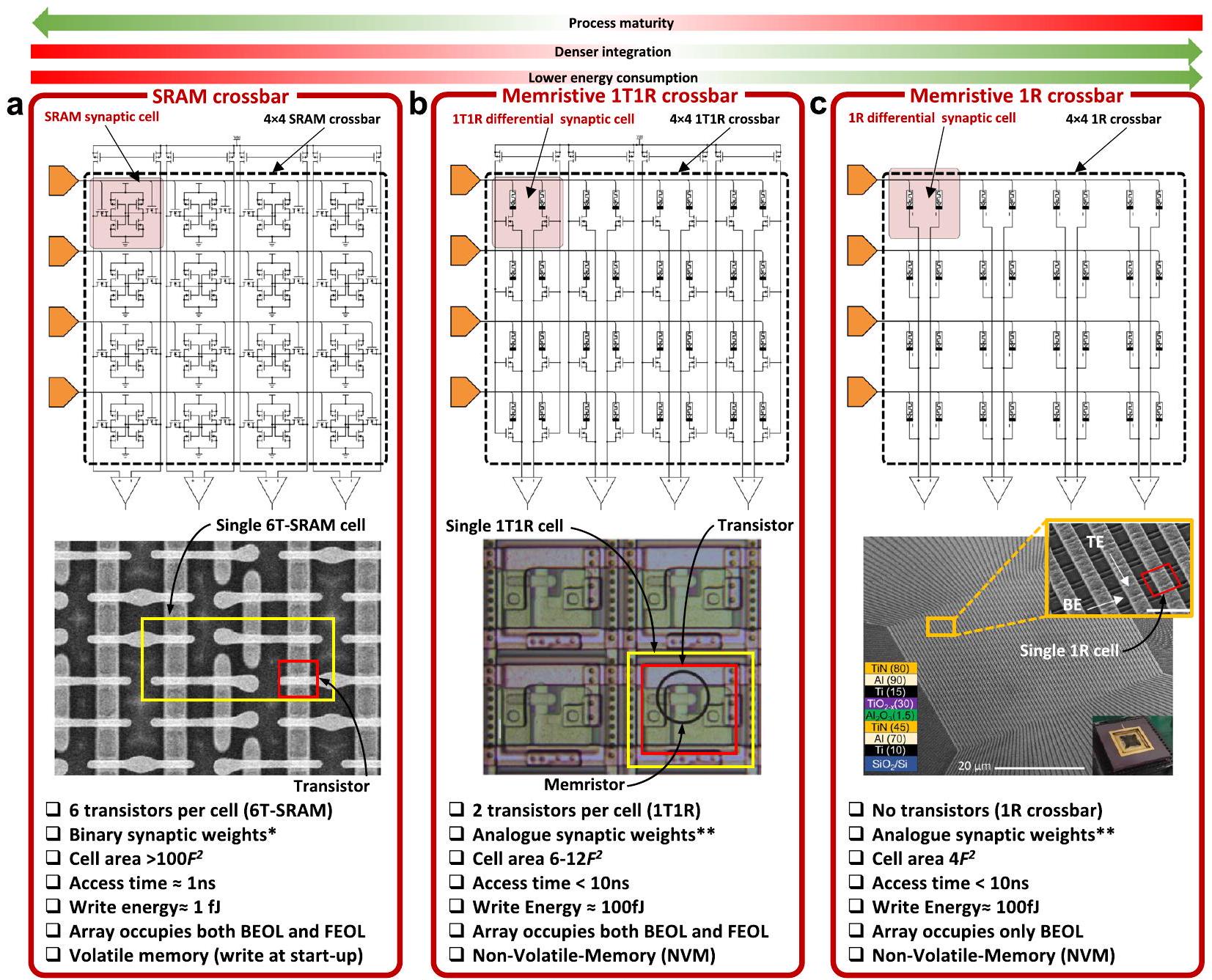
- يمكن أن يكون التخزين متعدد المستويات ممكنًا بواسطة خلايا SRAM أكثر تعقيدًا (مساحة خلية أكبر)
** الوزن التشابكي التناظري مرغوب فيه ولكن عادةً ما يتوفر عدد محدود فقط من المستويات المستقرة
مع الكثير من المجال للتحسين.ياماكا، م. SRAM منخفض الطاقة. في: كاواهارا، ت.، ميزونو، هـ. (محررون) الحوسبة الخضراء مع الذاكرة الناشئة. سبرينغر، نيويورك، نيويورك (2013)، معاد إنتاجه بإذن من SNCSC. تم تعديله بإذن بموجب ترخيص CC BY 4.0 من المرجع 54. تم تعديله بإذن بموجب ترخيص CC BY 4.0 من المرجع هو حجم الميزة للطباعة وتقدير الطاقة على مستوى الخلية. FEOL و BEOL تعني مقدمة خط الإنتاج ونهاية خط الإنتاج، على التوالي.
القسم. تعتبر كلتا الحالتين FPGA من أجل واجهة نظام اكتساب الصورة (أي مستشعر الصورة CMOS وخوارزمية تغيير الحجم) مع مصفوفة الميمريستور ودائرتها المحيطية. من ناحية أخرى، ركزت بعض الدراسات بشكل حصري على استخدام مصفوفة الميمريستور على واجهة اتصال على الشريحة للحصول على الصورة من جهاز كمبيوتر (على سبيل المثال، المرجع 54 يستخدم منفذ اتصال تسلسلي) تم تشكيله بالفعل في تنسيق الإدخال المطلوب.
نظرًا لأن هذه المجموعة البسيطة يمكن تصنيفها حتى مع الشبكات العصبية الصغيرة. لتقييم جهاز أو شريحة، من الضروري تقييم دقة نماذج الشبكات العصبية العميقة القياسية مثل
| عمل(ات) | جهاز | نوع الشبكة العصبية / مجموعة البيانات | حجم العارضة | عقدة CMOS | ADC | تركيب الخلية | دائرة الإدخال (DAC) | إلكترونيات الاستشعار | دالة التنشيط | محددات الصف/العمود | دالة تفعيل سوفت ماكس | الاستدلال/ التدريب | دائرة وزن البرنامج |
| 57 |
|
SLP، الترميز النادر، MLP/ الحروف اليونانية |
|
180 نانومتر | على الشريحة (13-بت) | 1ر | على الشريحة (6 بت) | تكامل الشحنة | رقمي على الشريحة (سيغمويد) | على الشريحة | خارج الشريحة (البرمجيات) | الاستدلال والتدريب | على الشريحة |
| ٥٥ | TiN/TaOx/ HfOx /TiN | سي إن إن / MNIST |
|
130 نانومتر | خارج الشريحة (8 بت) | تي تي 1 آر | على الشريحة (1-بت) | تكامل الشحنة | خارج الشريحة (البرمجيات: ReLU والتجمع الأقصى) | على الشريحة | خارج الشريحة (البرمجيات) | الاستدلال والتدريب | خارج الشريحة |
| ١٠٢ | Pt/Ta/Ta2O5/ Pt/Ti | MLP/MNIST |
|
|
غير متوفر | تي تي 1 آر | غير متوفر | غير متوفر | عتاد خارجي: ReLU | خارج الشريحة | خارج الشريحة (البرمجيات) | التعلم والتدريب | خارج الشريحة |
| 61 | لا توجد بيانات (تطوير ملكي) | بي إن إن، MNIST، CIFAR-10 |
|
90 نانومتر | على الشريحة (3 بت) | 1T1R | لم يتم التنفيذ | على الرقاقة (VSA) | على الشريحة (ثنائي) | على الشريحة | خارج الشريحة (البرمجيات)* | استنتاج فقط | خارج الشريحة |
| 113 | تا/تا أوكس/بلاتين | سي إن إن / MNIST |
|
180 نانومتر | على الشريحة | تي تي 1 آر | على الشريحة | على الشريحة (TIA) | خارج الشريحة (البرمجيات)* | على الشريحة | خارج الشريحة (البرمجيات)* | استنتاج فقط | خارج الشريحة |
| ١١٤، ١١٥ | تاوكس | سي إن إن/ MNIST |
|
180 نانومتر | على الشريحة (10 بت) | تي تي 1 آر | على الشريحة | على الرقاقة (TIA) | خارج الشريحة (البرمجيات)* | على الشريحة | خارج الشريحة (البرمجيات)* | استنتاج فقط | خارج الشريحة |
| ٢١٩ | W/TiN/TiON | بي إن إن/ MNIST |
|
65 نانومتر | على الشريحة (3 بت) | 1T1R | غير متوفر | على الرقاقة (CSA) | خارج الشريحة (FPGA: أقصى تجميع) | على الشريحة | خارج الشريحة (FPGA) | استنتاج فقط | خارج الشريحة |
| ١١٦ |
|
سي إن إن/ ‘ U ‘، ‘ M ‘،
|
|
لا توجد بيانات | خارج الشريحة | 1T1R | على الشريحة | خارج الشريحة (TIA) | على الشريحة (ReLU)، خارج الشريحة (البرمجيات: التجميع الأقصى) | خارج الشريحة | خارج الشريحة (وحدة التحكم الدقيقة) | الاستدلال والتدريب | خارج الشريحة |
| 272 | TiN/HfO2/Ti/TiN | بي إن إن / MNIST، CIFAR-10 | 1 كيلوبايت | 130 نانومتر | على الشريحة | 2T2R | لم يتم التنفيذ | أونشيب (PCSA) | على الشريحة (ثنائي) | على الشريحة | على الشريحة (ثنائي) | استنتاج فقط | خارج الشريحة |
| 99 |
|
MLP/MNIST | 2 ميغابايت | 180 نانومتر | على الشريحة (1-بت) | 1T1R | على الشريحة (1-بت) | على الشريحة | لا توجد بيانات | على الشريحة | لا توجد بيانات | استنتاج فقط | خارج الشريحة |
| 100 | ألCu/TiN/Ti/
|
MLP/ |
|
150 نانومتر | على الشريحة (1 أو 3 بت) | 1T1R | على الشريحة (1-بت) | على الشريحة | خارج الشريحة (البرمجيات)* | على الشريحة | خارج الشريحة (البرمجيات)* | استنتاج فقط | ذاكرة الوصول العشوائي الساكنة على الشريحة (SRAM) |
| ١٢٢ | PCM (لا توجد بيانات أخرى) | MLP/MNIST |
|
180 نانومتر | لا توجد بيانات | 3T1C + 2PCM | لا توجد بيانات | خارج الشريحة (البرمجيات) | خارج الشريحة (البرمجيات: ReLU) | خارج الشريحة | خارج الشريحة (البرمجيات) | استنتاج فقط | خارج الشريحة |
| 71,73 | PCM (لا توجد بيانات أخرى) | MLP/MNIST، ResNET-9/ CIFAR-10 |
|
14 نانومتر | على الشريحة | 4T4R | على الشريحة (8 بت) | على الرقاقة (مبني على CCO) | على الشريحة (ReLU) | على الشريحة | خارج الشريحة (البرمجيات) | استنتاج فقط | على الشريحة |
| 72 | PCM (لا توجد بيانات أخرى) | MLP/MNIST |
|
14 نانومتر | خارج الشريحة | 4T4R | على الشريحة (8 بت) | على الشريحة | خارج الشريحة (سيغمويد) | على الشريحة | خارج الشريحة (FPGA) | استنتاج فقط | على الشريحة |
| 273 | لا توجد بيانات | سي إن إن / CIFAR-10 |
|
55 نانومتر | على الشريحة | تي تي 1 آر | لا توجد بيانات | على الشريحة | خارج الشريحة (FPGA) | على الشريحة | خارج الشريحة (FPGA) | استنتاج فقط | خارج الشريحة |
| ٢٧٤ | TiN/HfO2/Ti/TiN | سي إن إن/ MNIST | 18 كيلوبايت | 130 نانومتر | خارج الشريحة* | تي تي 1 آر | خارج الشريحة* | خارج الشريحة* | خارج الشريحة (FPGA) | خارج الشريحة* | خارج الشريحة (FPGA) | استنتاج فقط | على الشريحة |
| 123 | TiN/HfO2/Ti/TiN | بي إن إن/ MNIST | 1 كيلوبايت | 130 نانومتر | غير متوفر | 2T2R | غير متوفر | على الشريحة | خارج الشريحة (البرمجيات)* | على الشريحة | خارج الشريحة (البرمجيات)* | استنتاج فقط | خارج الشريحة |
| ٢٧٥ |
|
MLP/MNIST | 158.8 كيلوبايت | 130 نانومتر | على الشريحة (8 بت) | 2T2R | على الشريحة (8 بت) | تكامل الشحنة | خارج الشريحة | على الشريحة | خارج الشريحة | استنتاج فقط | خارج الشريحة (FPGA) |
| 60 |
|
سي إن إن / MNIST، CIFAR-10 |
|
130 نانومتر | على الشريحة (8 بت) | 1T1R | على الشريحة | تكامل الشحنة | على الشريحة (تناظري: ReLU)، خارج الشريحة (FPGA: تجميع أقصى) | على الشريحة | خارج الشريحة (FPGA) | خارج الشريحة (البرمجيات) | على الشريحة |
مُتَسَلسِلَة لعرض
مع
دوائر القيادة المدخلة (الكتلة 4)
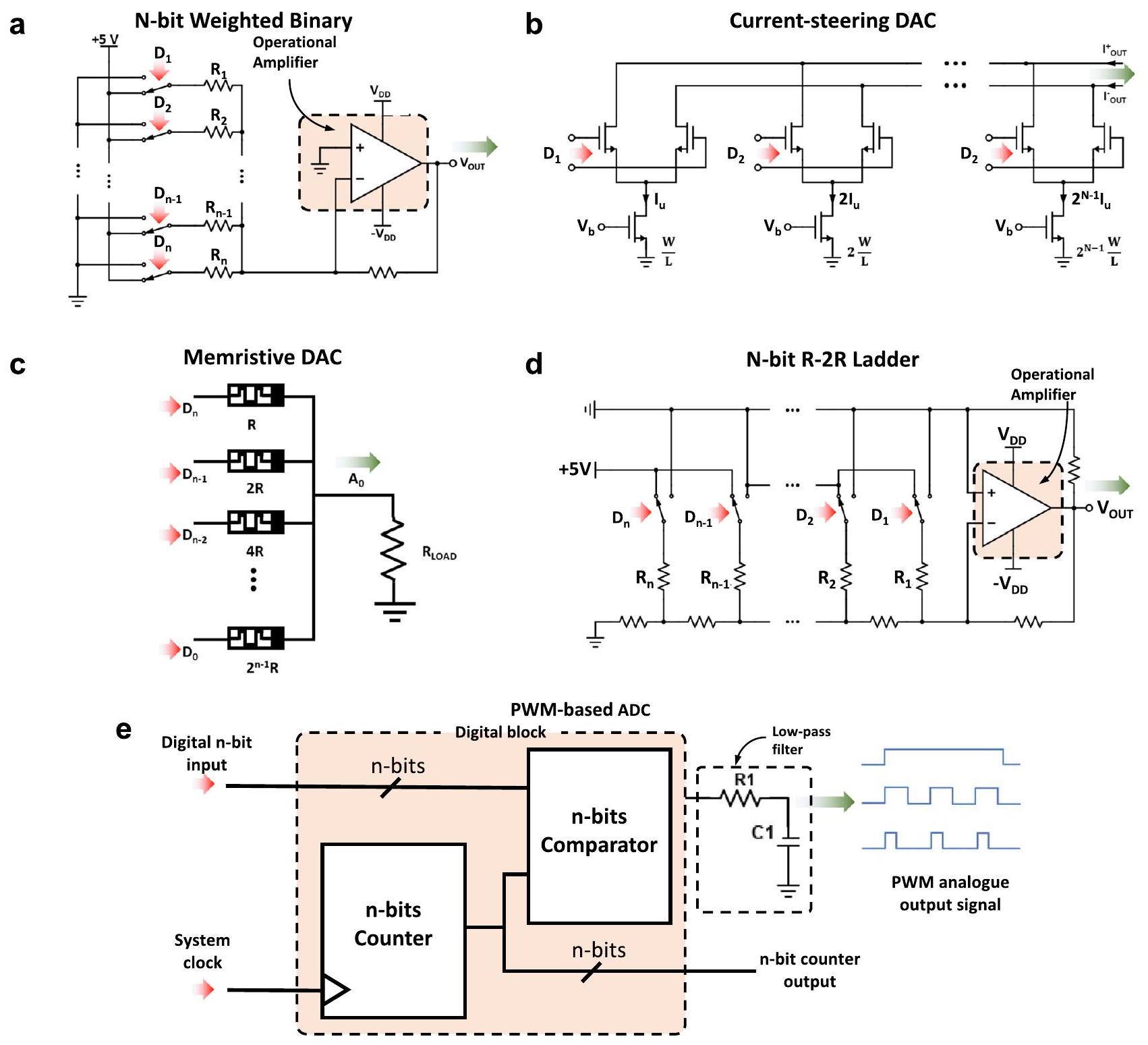
السعة
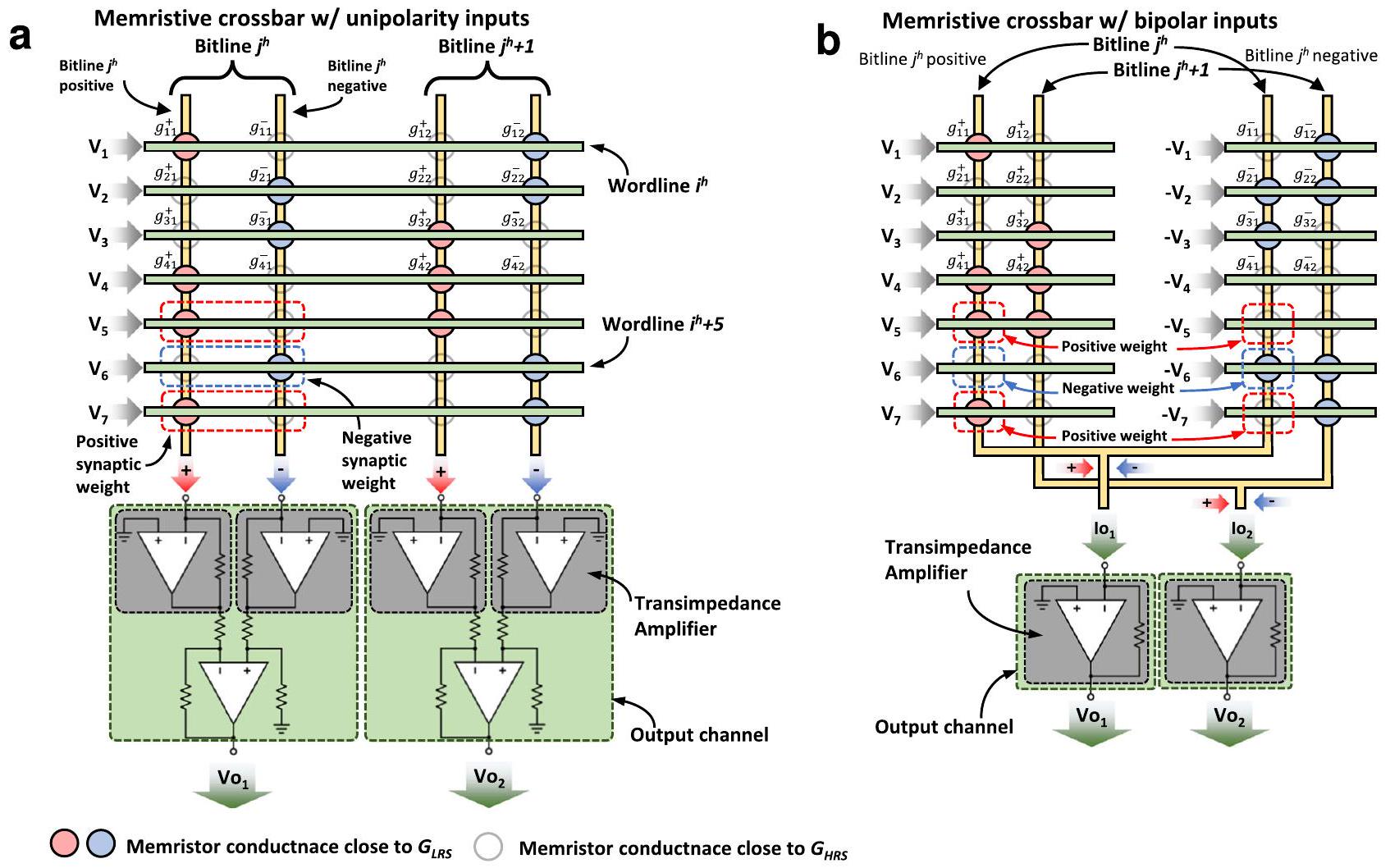
نواة VMM (الكتلة 5)
كل ميمريستور (
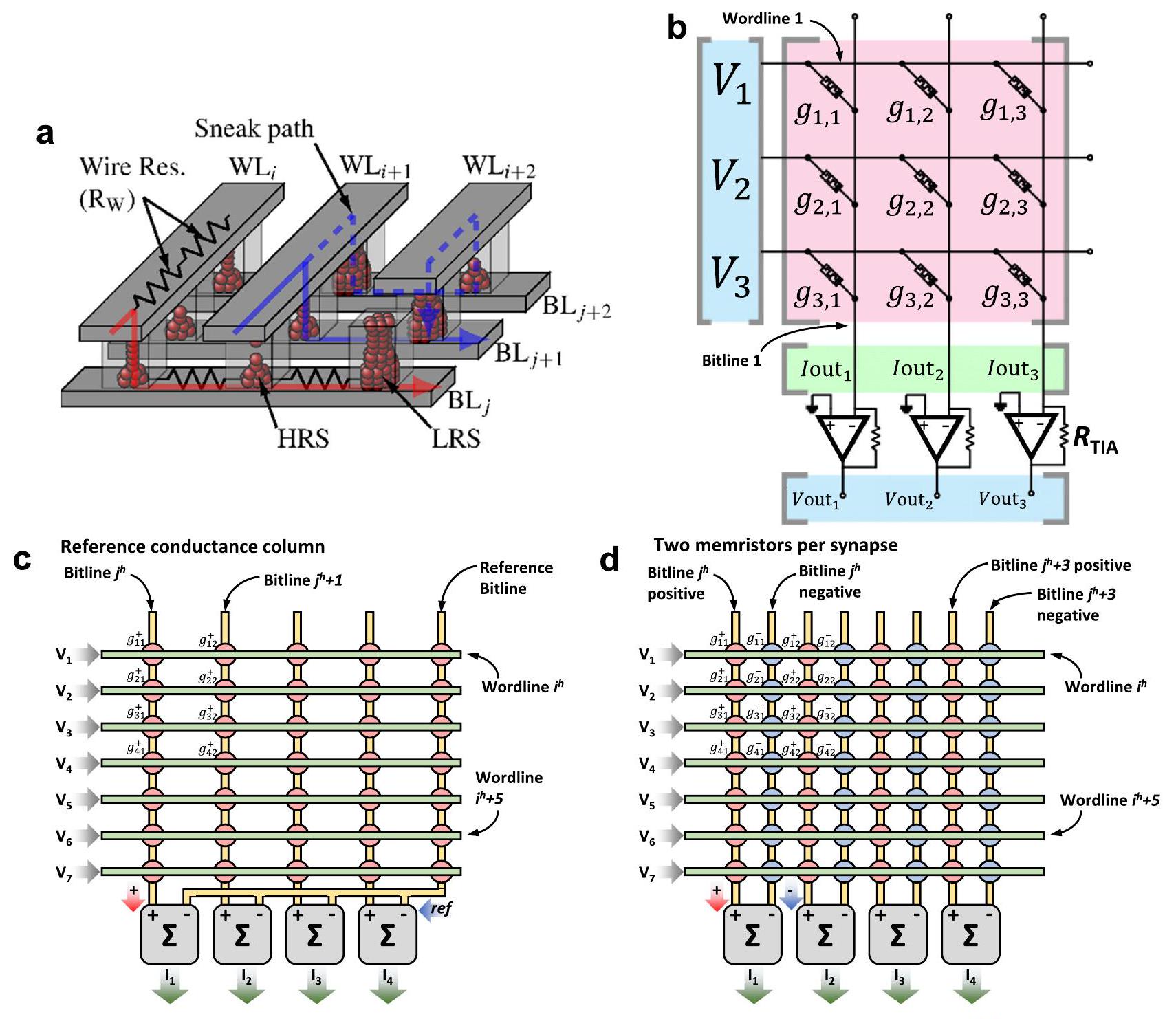
مستويات المقاومة في التقاطع، مما يجعلها أقل عرضة للضوضاء والتغيرات
بخط البت
إلكترونيات الاستشعار (الكتلة 6)
دالة التنشيط (الكتلة 7)
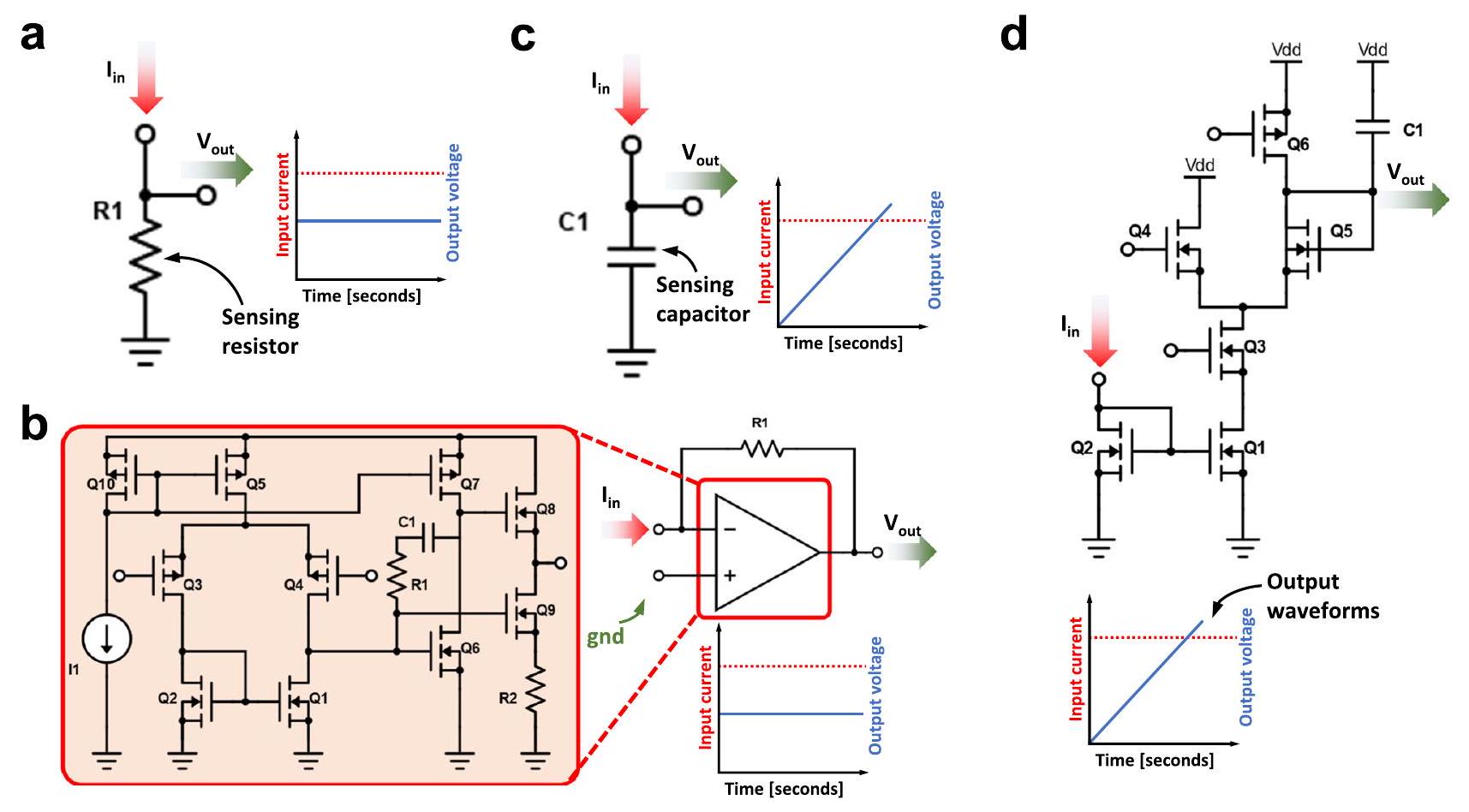
تحت نظام النانو أمبير، تعتبر تكامل الشحنة الخيار الأكثر ملاءمة لتحويل التيار إلى جهد. يمكن تحقيق ذلك باستخدام مكثف. وبالتالي، فإن القياس ليس فوريًا حيث يتطلب وقت تكامل ثابت وقابل للتحكم قبل القياس. لتقليل متطلبات المساحة لمكثف التكامل، يسمح استخدام مقسم التيار بتقليل التيار بشكل أكبر، ومعه، حجم المكثف المطلوب. التبادل في هذه الحالة هو مع الدقة (بشكل رئيسي بسبب عدم تطابق الترانزستورات) ونطاق جهد الخرج الديناميكي.
المخرجات، مضخمة. يجب أن يُلاحظ أنه على الرغم من عدم الضرورة في حالة الشبكات العصبية المنفذة في مجال البرمجيات، في حالة الشبكات العصبية المعتمدة على نوى الميمريستور-VMM، يجب أن تكون عناصر متجهات الإدخال لكل طبقة عصبية ضمن نطاق من الفولتية التناظرية. لهذا السبب، فإن دوال تفعيل ReLU، التي هي بطبيعتها دوال تفعيل غير محدودة.
لا يمكن تغيير تنفيذات دوال التنشيط المستندة إلى الدوائر المتكاملة في نفس الشريحة مثل تقنيات التقاطع بعد تصنيع الدائرة. يمكن تنفيذ مثل هذه الدوال في كل من المجالات الرقمية والتناظرية. يؤدي المعالجة في المجال الرقمي إلى زيادة الحمل الناتج عن محول التناظر إلى الرقمي (كما هو الحال في التنفيذات المستندة إلى البرمجيات) ولكنه يتأثر بشكل أقل بالضوضاء وعدم تطابق الترانزستورات. يتم عرض تنفيذ دالة ReLU المنشطة في المجال الرقمي المدمجة في دائرة الاستشعار في
التكوين.

دالة SoftArgMax (الكتلة 8)
الكتلة الحالية (غالبًا ما تُسمى دالة SoftArgMax أو دالة تنشيط SoftArgMax) التي تحتوي على عدد من المدخلات يساوي عدد خطوط البت، تقوم بتنفيذ معبر الميمريستور، وتطبق بشكل أساسي المعادلة 10:
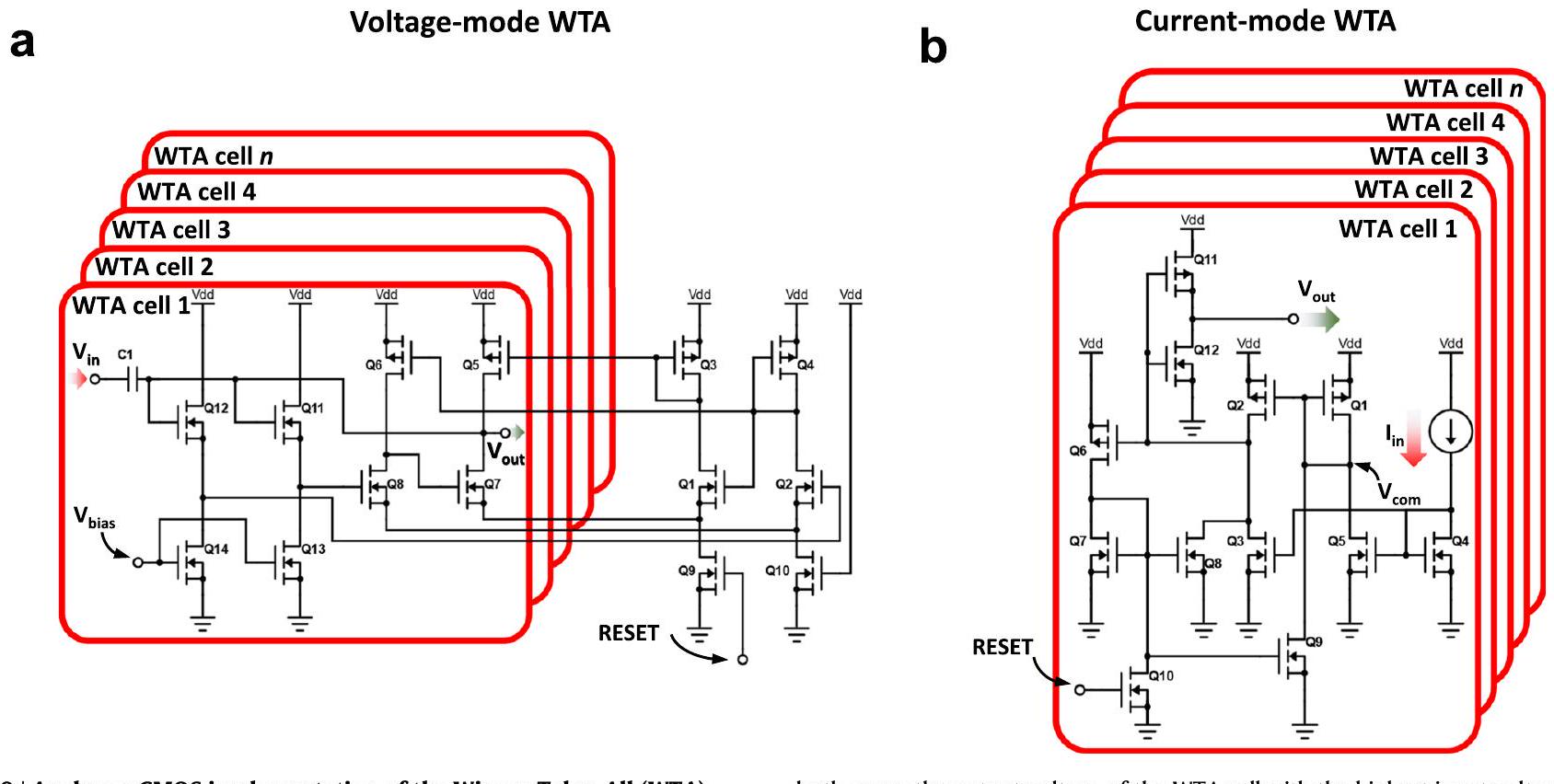
وظيفة. كتلة WTA CMOS مع مدخل جهد
المخرجات. يتم تحقيق هذا السلوك من خلال دمج وظيفتين،
القيمة في المتجه (مجموع احتمالات جميع العناصر يساوي 1). لاحظ أن
محولات التناظرية إلى الرقمية (الكتلة 9)
(يحدد المساحة المتاحة من السيليكون المخصصة للأوزان المشبكية، أي هياكل 1T1R، مما يؤثر بالتالي على التكلفة).
بلاط العارضة
تدريب الشبكة العصبية وتحديث وزن المشابك (الكتل 2، 11-15)
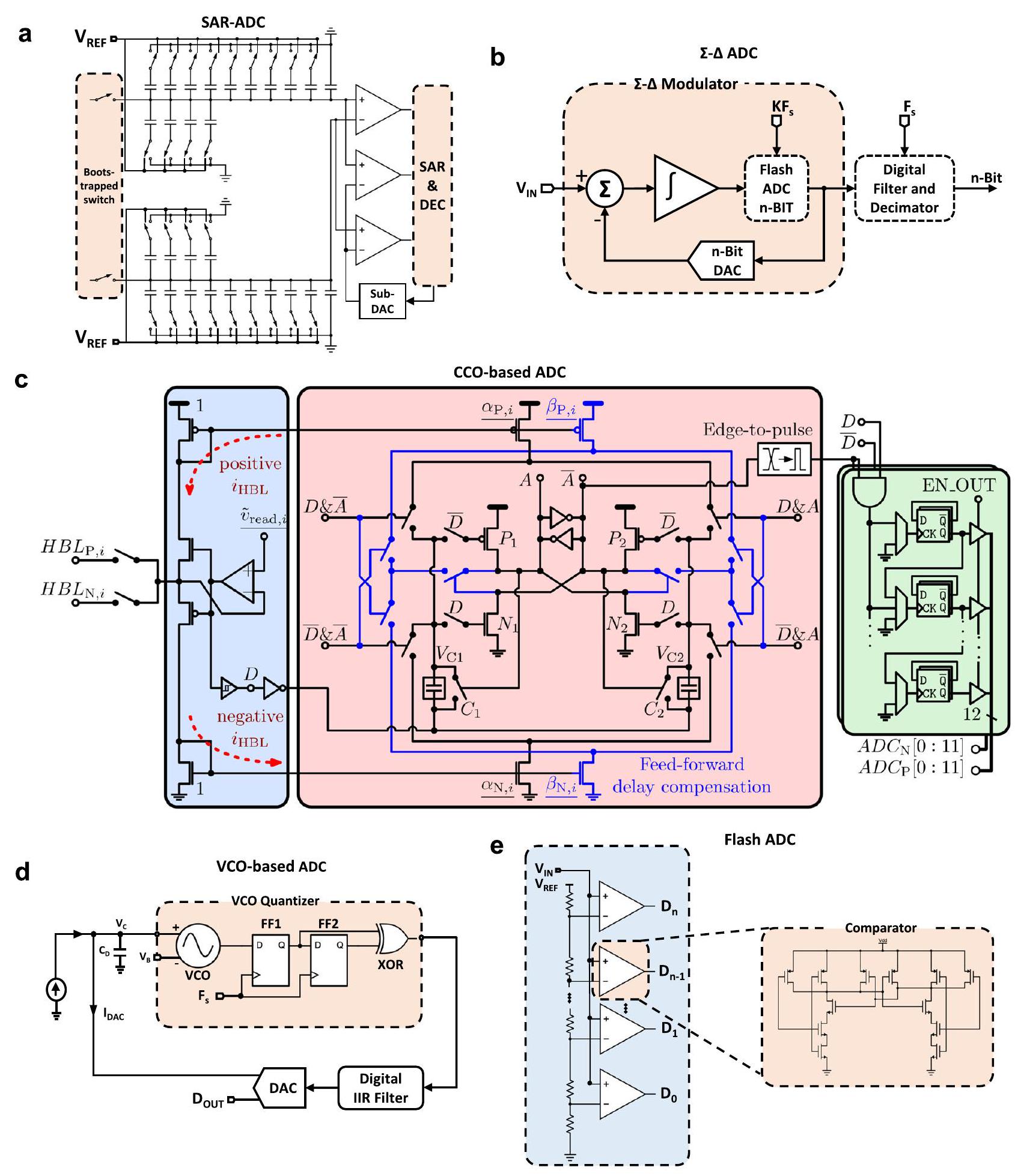
يجب ضبط أوزان المشابك إلى قيم تقلل من دالة الخسارة. لتحقيق هذا الهدف، يمكن استخدام عائلتين من الخوارزميات: الخوارزميات التي لا تعتمد على التدرج والخوارزميات المعتمدة على التدرج (كما هو موضح في الشكل 12أ). تشمل الطرق التي لا تعتمد على التدرج مثل تحسين سرب الجسيمات
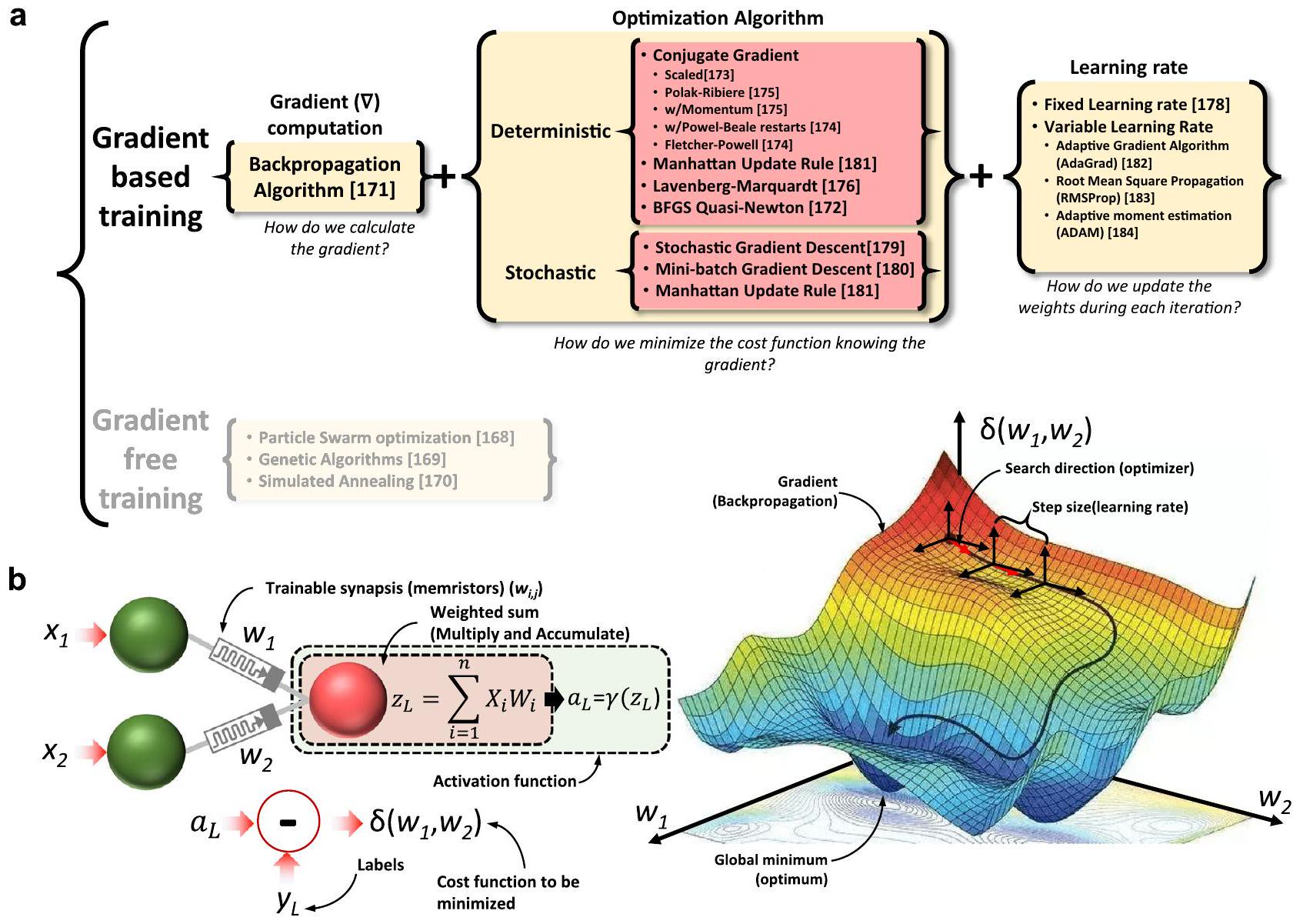
اقترح تنظيمًا للخوارزميات لـ (ط) حساب التدرج، (2) التحسين و (3) معدل التعلم.
دالة، التي تصف خطأ المخرجات (مقابل التسميات) لشبكة صغيرة تحتوي على مدخلين فقط ومخرج واحد (وبالتالي وزنين عصبيين، كما هو موضح في الشكل 12ب)، وهي
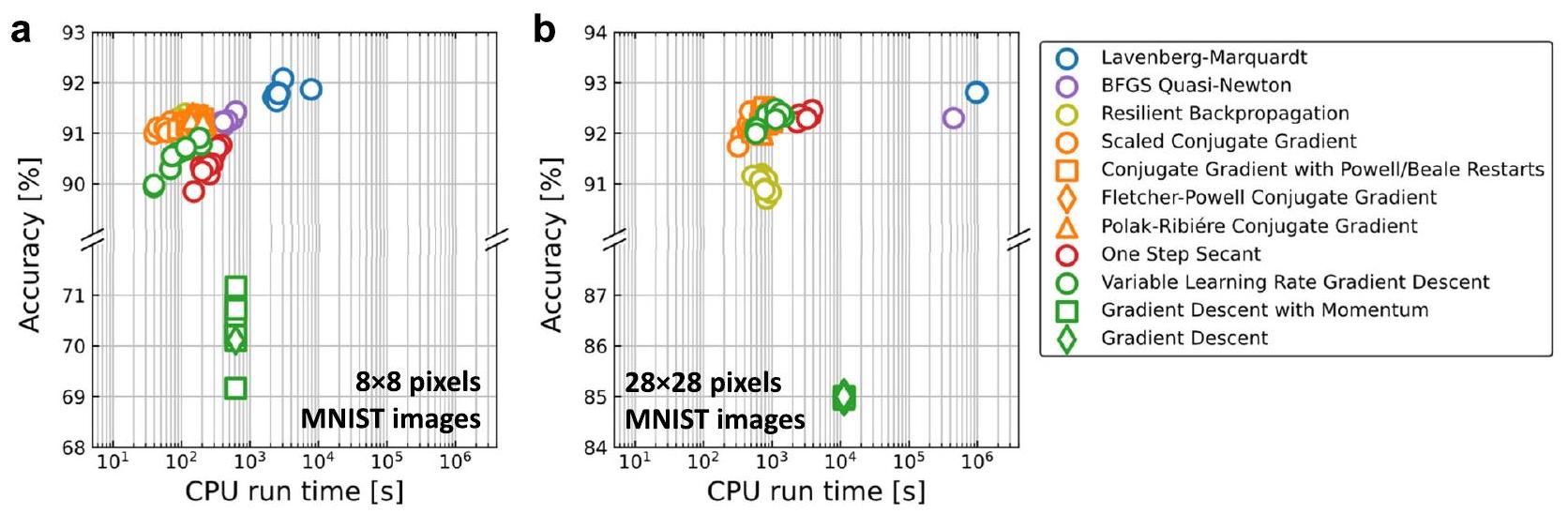
شرح الفقرة) ونسخها (الانحدار التدرجي مع الزخم
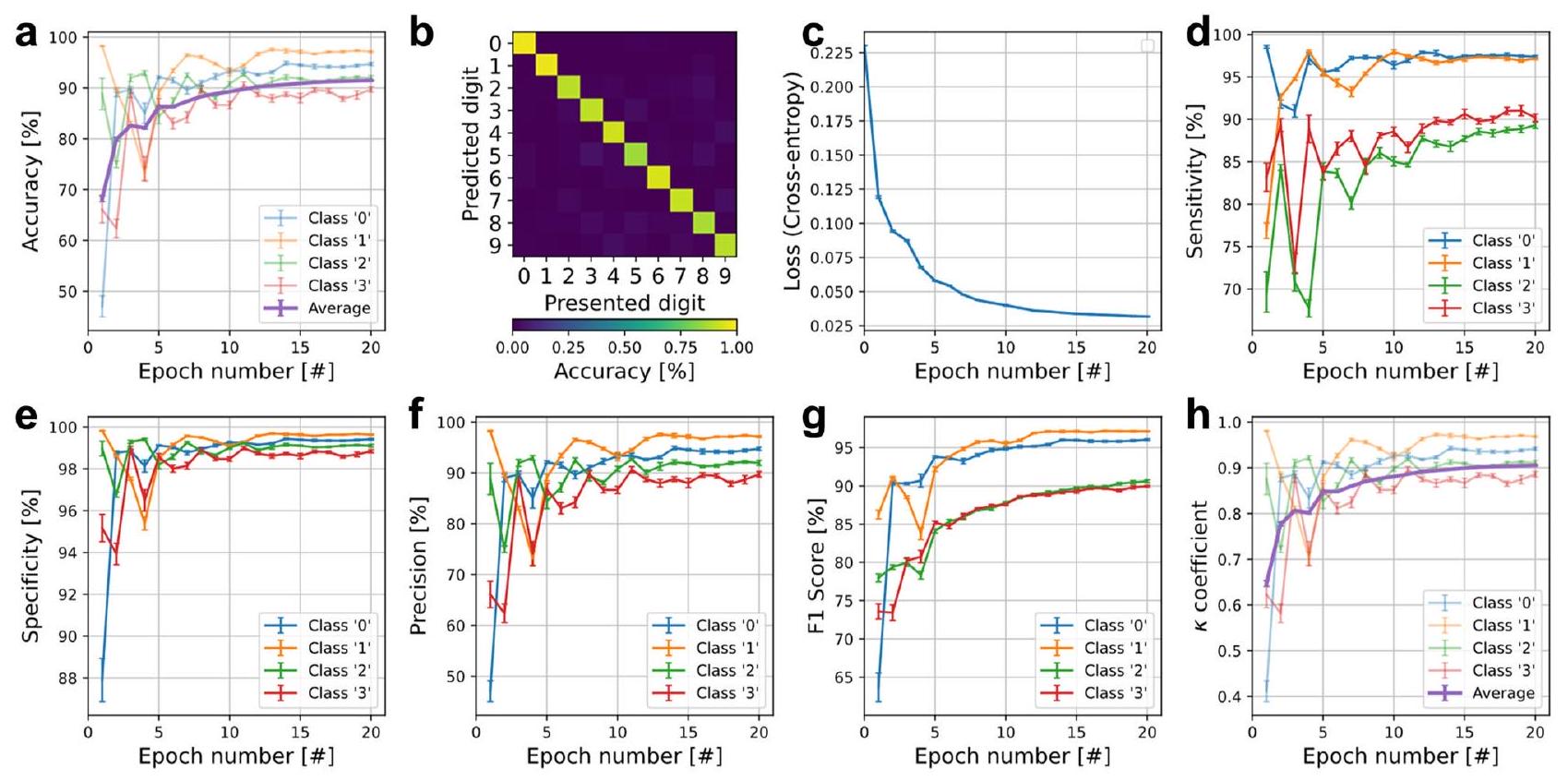
التحقق المتقاطع) حيث يتم تسجيل عدد صغير من صور التدريب والدقة اعتمادًا على خوارزمية التدريب. كمثال، توضح الخوارزمية التكميلية 2 الكود التفصيلي بلغة MATLAB المستخدم لهذا التحقق المتقاطع باستخدام 100 صورة. يتم تقسيم عدد صغير من صور التدريب إلى
| المقياس | التعبير | المعنى | القابلية للتطبيق | أمثلة | ||
| الدقة |
|
نسبة الأنماط المصنفة بشكل صحيح بالنسبة لعدد الأنماط الكلي | لتحديد أداء الشبكة العصبية الاصطناعية | لا ينطبق | ||
| الحساسية (تسمى أيضًا الاسترجاع) |
|
نسبة بين عدد ما تم التعرف عليه بشكل صحيح على أنه إيجابي إلى عدد ما كان إيجابيًا بالفعل | أماكن حيث تكون تصنيفات الإيجابيات ذات أولوية عالية | فحوصات الأمان في المطارات | ||
| الخصوصية |
|
نسبة بين عدد ما تم تصنيفه بشكل صحيح على أنه سلبي إلى عدد ما كان سلبيًا بالفعل | أماكن حيث تكون تصنيفات السلبيات ذات أولوية عالية | تشخيص حالة صحية قبل العلاج | ||
| الدقة |
|
عدد ما تم تصنيفه بشكل صحيح على أنه إيجابي من بين جميع الإيجابيات | لا ينطبق | كم عدد الذين قمنا بتصنيفهم كمرضى سكري هم في الواقع مرضى سكري؟ | ||
| درجة F1 |
|
إنها مقياس لأداء قدرة تصنيف النموذج | لا ينطبق | تعتبر درجة F1 مؤشرًا أفضل لأداء المصنف من مقياس الدقة العادي | ||
| معامل K |
|
تظهر النسبة بين دقة الشبكة ودقة العشوائية (في هذه الحالة، مع 10 فئات مخرجات، ستكون الدقة العشوائية 10%) | لا ينطبق | لا ينطبق | ||
| الانتروبيا المتقاطعة |
|
الفرق بين القيمة المتوقعة من قبل الشبكة العصبية الاصطناعية والقيمة الحقيقية | لا ينطبق | لا ينطبق |
في تدريب الوضع الحالي، كانت الممارسة المعتادة المبلغ عنها في الأدبيات لهذا النوع من التدريب هي استخدام ما يُعرف بقانون تحديث مانهاتن.
تصنيع/دمج شريحة الشبكة العصبية الاصطناعية
عندما تزداد إشارة الإدخال، تزداد أيضًا تعقيد دائرة المحول الرقمي إلى التناظري (ومعها، استهلاك الطاقة والمساحة). النهج الأكثر شيوعًا في هذا السياق هو استخدام محول رقمي إلى تناظري خارجي جاهز لتشغيل المدخلات التناظرية.
محاكاة الشبكات العصبية الميمريستية
محاكاة على مستوى الشبكة العصبية
| تجريبي/محاكاة | نوع | عملية (نانو متر) | قرار التفعيل | دقة الوزن | سرعة الساعة | عبء العمل المرجعي | تخزين الوزن |
|
|
حجم المصفوفة | نوع ADC | معدل الإنتاج (TOPS) | الكثافة (TOPS لكل
|
الكفاءة (TOPS لكل واط) | |
| NVIDIA T4
|
خبرة | فول سيMOS | 12 | عدد صحيح 8 بت | عدد صحيح 8 بت | 2.6 جيجاهرتز | ResNet-50 (حجم الدفعة = 128) | — | — | — | — | — | 22.2، 130 (ذروة) | 0.04، 0.24 (ذروة) | 0.32 |
| جوجل TPU v1
|
خبرة | فول سيMOS | ٢٨ | عدد صحيح 8 بت | عدد صحيح 8 بت | 700 ميغاهرتز | MLPs، LSTMs، CNNs | — | — | — | — | — | 21.4، 92 (ذروة) | 0.06، 0.28 (ذروة) | 2.3 (ذروة) |
| هابانّا غويّا إتش إل
|
خبرة | فول سي مو إس | 16 | عدد صحيح 16 بت | عدد صحيح 16 بت | 2.1 جيجاهرتز (وحدة المعالجة المركزية) | ResNet-50 (حجم الدفعة = 10) | — | — | — | — | — | 63.1 | — | 0.61 |
| دا ديا ناعو
|
نعم. | فول سي مو إس | ٢٨ | نقطة ثابتة 16 بت | نقطة ثابتة 16 بت | 606 ميغاهرتز | أداء قمة | — | — | — | — | — | ٥.٥٨ | 0.08 | 0.35 |
| UNPU
|
خبرة | فول سي مو إس | 65 | 16 بت | 1 بت | 200 ميغاهرتز | أداء قمة | — | — | — | — | — | 7.37 | 0.46 | 50.6 |
| إشارة مختلطة
|
خبرة | فول سي مو إس | ٢٨ | 1 بت | 1 بت | 10 ميغاهرتز | شبكة CNN ثنائية (CIFAR-10) | — | — | — | — | — | 0.478 | 0.1 | 532 |
| إسحاق
|
خبرة | RRAMCMOS | 32 | 16 بت | 16 بت | 1.2 جيجاهرتز | أداء قمة | ذاكرة الوصول العشوائي المقاومة
|
|
|
|
SAR (8 بت) | 41.3 | 0.48 | 0.63 |
| نيوتن
|
خبرة | RRAMCMOS | 32 | 16 بت | 16 بت | 1.2 جيجاهرتز | أداء قمة | ذاكرة الوصول العشوائي المقاومة
|
|
|
|
SAR (8 بت) | — | 0.68 | 0.92 |
| بوما
|
خبرة | RRAMCMOS | 32 | 16 بت | 16 بت | 1.0 جيجاهرتز | أداء قمة | ذاكرة الوصول العشوائي المقاومة
|
1 م | 100 ألف |
|
ريال سعودي | ٢٦.٢ | 0.29 | 0.42 |
| رئيسي
|
نعم. | RRAMCMOS | 65 | 6 بت | 8 بت | 3.0 جيجاهرتز (وحدة المعالجة المركزية) | — | ذاكرة الوصول العشوائي المقاومة | ٢٠ ك | 1 ك |
|
منحدر (6 بت) | — | — | — |
| آلة بولتزمان الميمريستive
|
نعم. | RRAMCMOS | ٢٢ | 32 بت | 32 بت | 3.2 جيجاهرتز (وحدة المعالجة المركزية) | — | ذاكرة الوصول العشوائي المقاومة | 1.1 غ | 315 ألف |
|
ريال سعودي | — | — | — |
| 3D-aCortex
|
خبرة | RRAMCMOS | ٥٥ | 4 بت | 4 بت | 1.0 جيجاهرتز | جي إن إم تي | فلاش NAND | — | 2.3 مليون |
|
زمني إلى رقمي (4 بت) | 10.7 | 0.58 | 70.4 |
| الذكاء الاصطناعي التناظري باستخدام شبكة كثيفة ثنائية الأبعاد
|
سيم | RRAMCMOS | 14 | 8 بت | تناظري | 1.0 جيجاهرتز | RNN/LSTM | PCM | لا توجد بيانات | لا توجد بيانات |
|
مذبذب متحكم فيه بالتيار | ٣٧٦.٧ | لا توجد بيانات | 65.6 |
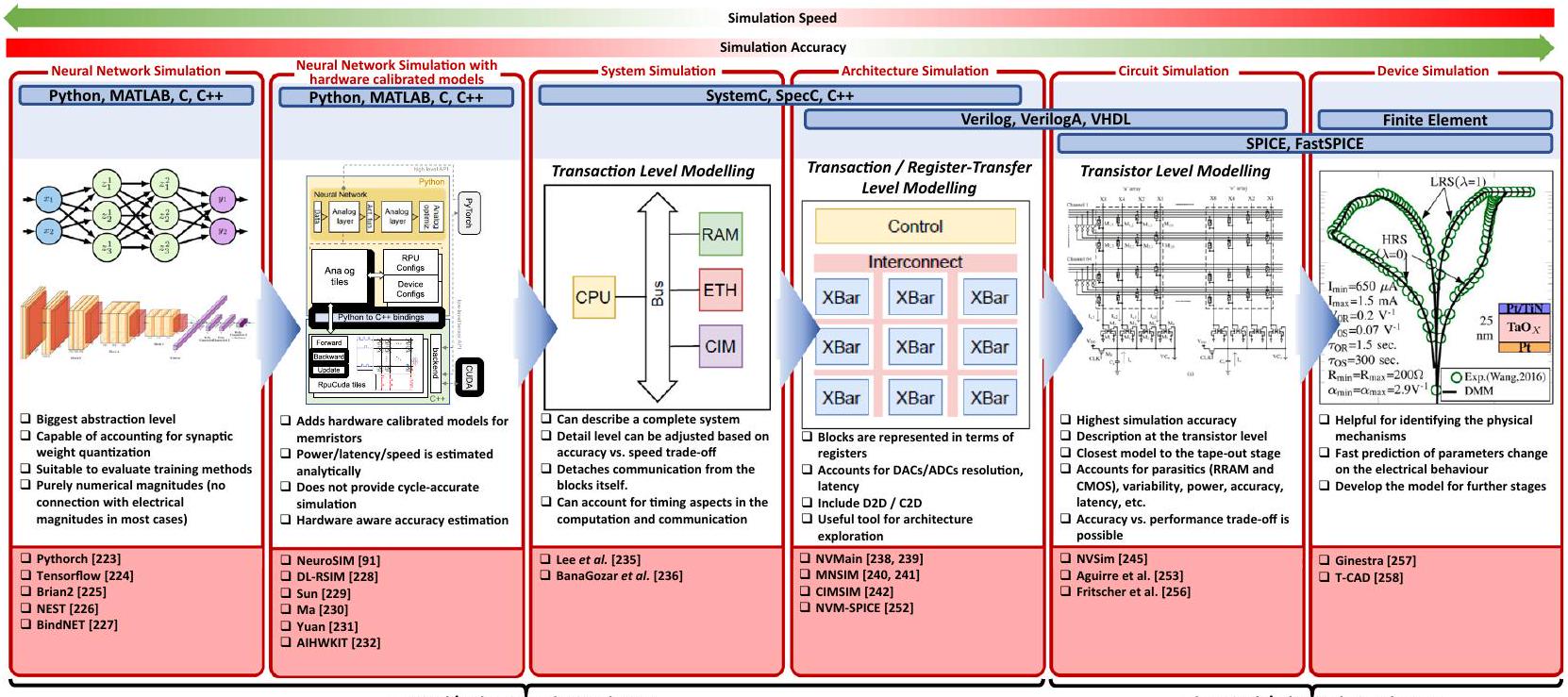
الرؤية ومعالجة اللغة الطبيعية. كلاهما مكتبات بايثون محسّنة للغاية لاستغلال وحدات معالجة الرسومات ووحدات المعالجة المركزية لمهام التعلم العميق. تتيح هذه المحاكيات تدريب وتطوير هياكل الشبكات العصبية المعقدة (مثل هياكل الشبكات العصبية التلافيفية مثل VGG و AlexNET أو الشبكات العصبية المتكررة – RNN). على الرغم من شعبيتها الكبيرة، فإن هذه المحاكيات لا توفر أي رابط على الإطلاق مع الأجهزة الميمريستيفية أو CMOS، حيث أن الكميات المعنية غير بعدية وتمثل الاتصالات المشبكية بقيم عددية غير مقيدة بشكل صارم.
اعتمدت من قبل صن وآخرون.
محاكاة على مستوى النظام
| إطار المحاكاة | سنة | منصة | تدريب | نوع المحاكاة | المصدر المفتوح | نوع الشبكة العصبية الاصطناعية | تطوير متوافق | طاقة | دقة | قوة | الكمون | التغير |
|
|
CMOS | وحدة معالجة الرسوميات |
| تينسورفلو
|
2015 | بايثون | نعم | شبكة عصبية | نعم | MLP، CNN | لا تطوير. | لا | نعم | لا | لا | نعم | لا | لا | لا | نعم |
| بايتورتش
|
2017 | بايثون | نعم | شبكة عصبية | نعم | MLP، CNN | لا تطوير. | لا | نعم | لا | لا | نعم | لا | لا | لا | نعم |
| عصبون
|
2006 | بايثون | نعم | شبكة عصبية | نعم | SNN | لا تطوير. | لا | نعم | لا | لا | نعم | لا | لا | لا | نعم |
| براين2
|
2019 | بايثون | نعم | شبكة عصبية | نعم | SNN | لا تطوير. | لا | نعم | لا | لا | نعم | لا | لا | لا | نعم |
| عش
|
2007 | بايثون | نعم | شبكة عصبية | نعم | SNN | لا تطوير. | لا | نعم | لا | لا | نعم | لا | لا | لا | نعم |
| بايندزنت
|
2018 | بايثون | نعم | شبكة عصبية | نعم | SNN | لا تطوير. | لا | نعم | لا | لا | نعم | لا | لا | لا | نعم |
| ميمتورش
|
٢٠٢٠ | بايثون، C++، كودا | لا | شبكة نيورلا | نعم | سي إن إن | ذاكرة الوصول العشوائي المقاومة | لا | نعم | لا | لا | نعم | لا | لا | لا | نعم |
| NVMain
|
2015 | C++ | لا | العمارة | نعم | ذاكرة | ذاكرة الوصول العشوائي المقاومة | نعم | لا | نعم | نعم | لا | لا | لا | لا | لا |
| بوما
|
2019 | C++ | لا | العمارة | لا | MLP، CNN | ذاكرة الوصول العشوائي المقاومة | نعم | نعم | نعم | نعم | لا | لا | لا | نعم | نعم |
| رابيد إن إن
|
2018 | C++ | لا | العمارة | لا | MLP، CNN | ذاكرة الوصول العشوائي المقاومة | نعم | نعم | نعم | نعم | نعم | لا | لا | نعم | لا |
| دي إل-آر إس آي إم
|
2018 | بايثون | لا | العمارة | لا | MLP، CNN | ذاكرة الوصول العشوائي المقاومة | لا | نعم | لا | لا | نعم | لا | لا | لا | نعم |
| طبقة الأنابيب
|
2017 | C++ | نعم | العمارة | لا | سي إن إن | ذاكرة الوصول العشوائي المقاومة | نعم | نعم | نعم | لا | لا | لا | لا | لا | |
| صغير ولكن دقيق
|
2019 | ماتلاب | لا | العمارة | نعم | سي إن إن، ريس نت | ذاكرة الوصول العشوائي المقاومة | نعم | نعم | نعم | لا | لا | لا | لا | لا | لا |
| يوان وآخرون
|
2019 | سي++، ماتلاب | نعم | العمارة | نعم | لا توجد بيانات | ذاكرة الوصول العشوائي المقاومة | لا | نعم | نعم | لا | لا | لا | لا | لا | نعم |
| سون وآخرون
|
2019 | بايثون | نعم | العمارة | لا | MLP | PCM، STT-RAM، ReRAM، SRAM، FeFET | نعم | نعم | نعم | لا | نعم | لا | لا | لا | لا |
| أ. تشين
|
2013 | ماتلاب | لا | دائرة | نعم | MLP | ذاكرة الوصول العشوائي المقاومة | لا | لا | نعم | لا | نعم | نعم | لا | لا | لا |
| CIM-SIM
|
2019 | SystemC (C++) | لا | العمارة | نعم | SLP | ذاكرة الوصول العشوائي المقاومة | لا | لا | لا | لا | لا | لا | لا | لا | لا |
| MNSIM
|
2018 | بايثون | لا | العمارة | نعم | سي إن إن | ذاكرة الوصول العشوائي المقاومة | نعم | لا | نعم | نعم | نعم | لا | لا | لا | نعم |
| NVSIM
|
2012 | C++ | لا | دائري | نعم | ذاكرة | PCM، STT-RAM، ReRAM، فلاش | نعم | لا | نعم | نعم | لا | لا | لا | لا | لا |
| كروس سيم
|
2017 | بايثون | لا توجد بيانات | دائري | نعم | لا توجد بيانات | PCM، ReRAM، فلاش | لا | نعم | لا | لا | نعم | نعم | لا | لا | نعم |
| نيرو سيم
|
٢٠٢٢ | بايثون، سي++ | نعم | دائري | نعم | MLP، CNN | PCM، STT-RAM، ReRAM، SRAM، FeFET | نعم | نعم | نعم | لا | نعم | لا | لا | لا | نعم |
| NVM-SPICE
|
2012 | غير محدد | لا | دائري | لا | SLP | ذاكرة الوصول العشوائي المقاومة | نعم | لا | نعم | نعم | نعم | لا | لا | نعم | لا |
| مجموعة تسريع الأجهزة التناظرية من IBM
|
٢٠٢١ | بايثون، C++، كودا | نعم | شبكة عصبية | نعم | MLP، CNN، LSTM | PCM | لا | نعم | لا | لا | نعم | لا | لا | لا | نعم |
| فريتشر وآخرون
|
2019 | مختلط (VHDL، Verilog، SPICE) | لا | دائري | لا | MLP | PCM، STT-RAM، ReRAM، SRAM، FeFET | نعم | نعم | نعم | نعم | نعم | نعم | نعم | نعم | نعم |
| أغيري وآخرون
|
٢٠٢٠ | مختلط (بايثون، ماتلاب، سبايس) | لا | دائري | لا | MLP | PCM، STT-RAM، ReRAM، SRAM، FeFET | نعم | نعم | نعم | نعم | نعم | نعم | نعم | نعم | نعم |
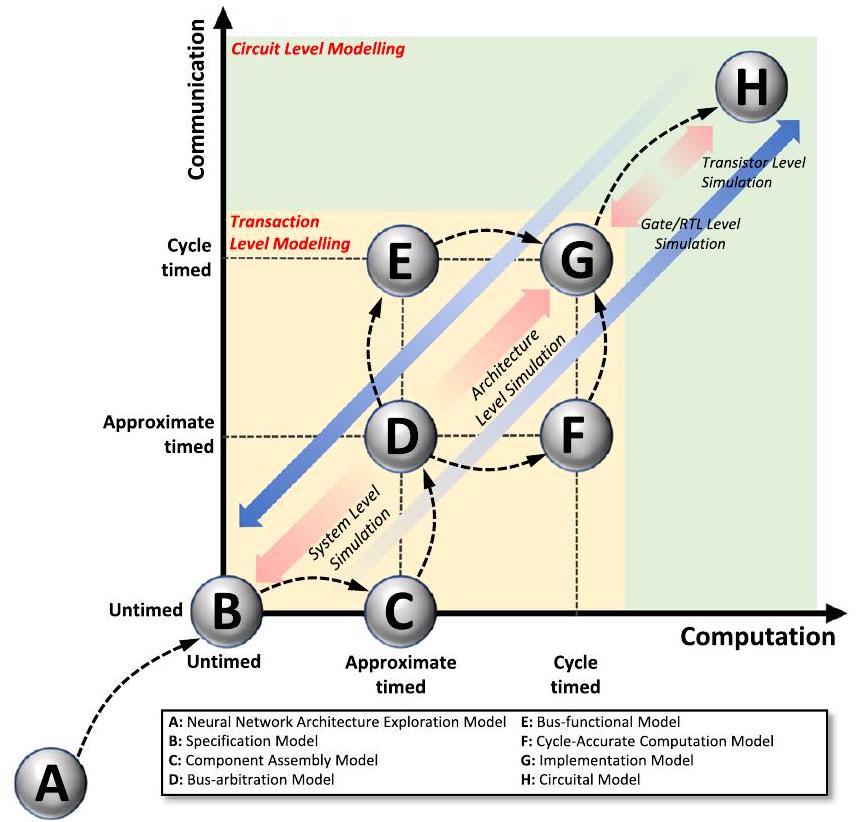
ممر الذاكرة، المحولات التناظرية/الرقمية، معدلات الإدخال الرقمية ومراحل العينة والاحتفاظ. علاوة على ذلك، يحتوي كل بلاط على وحدة تحكم مخصصة تنظم المكونات المسؤولة عن دفع الحساب.
محاكاة على مستوى العمارة
محاكاة مستوى الدائرة
ذاكرات غير متطايرة مثل STT-RAM وPCRAM وهياكل ReRAM. وهذا يسمح: i) بتقدير وقت الوصول، طاقة الوصول ومساحة السيليكون، ii) استكشاف مساحة التصميم، و iii) تحسين الشريحة لمقياس تصميم محدد واحد. ومع ذلك، وبالمثل لـ NVMain
تصميم مشترك للبرمجيات والأجهزة وبحث في بنية الشبكات العصبية المدركة للأجهزة
يمكن تخفيف العيوب غير المثالية المتعلقة بالميمريستور من خلال تحسين المعلمات المتعلقة بالبرمجيات لشبكة الأعصاب
مثال على تحليل ANN الميمريستيف
ترجمة الأوزان المشبكية من ANN القائم على البرمجيات إلى قيم توصيل
| نوع الشبكة العصبية | خوارزمية التعلم | قاعدة البيانات | الحجم | التدريب | الدقة | المنصة | المرجع. | |
| (محاكاة) | (تجريبية) | |||||||
| بيرسيبترون ذو طبقة واحدة (SLP) | الانتشار العكسي (تدرج مترافق مقاس) | MNIST (
|
طبقة واحدة (
|
خارج الموقع | ~91% | محاكاة SPICE نموذج QMM | 253 | |
| قاعدة تحديث مانهاتن | نمط مخصص | طبقة واحدة (
|
في الموقع | ND | تجريبي (
|
105 | ||
| وجه ييل | طبقة واحدة (
|
في الموقع |
|
تجريبي (
|
194 | |||
| بيرسيبترون متعدد الطبقات (MLP) | الانتشار العكسي (تدرج عشوائي متناقص) | MNIST (
|
طبقتان (
|
في الموقع |
|
|
تجريبي (
|
54 |
| الانتشار العكسي (تدرج مترافق مقاس) | MNIST (
|
k طبقات (
|
خارج الموقع |
|
محاكاة SPICE نموذج QMM | 253 | ||
| الانتشار العكسي | MNIST (14
|
طبقتان (
|
خارج الموقع | ~92% | ~82.3% | برمجيات/ تجريبي (
|
196 | |
| MNIST (22
|
طبقتان (
|
في الموقع | ~83% | ~81% | برمجيات/ تجريبي (PCM) | 267 | ||
| MNIST (28
|
طبقتان (
|
خارج الموقع | ~97% | برمجيات (بايثون) | 288 | |||
| الانتشار العكسي Sign | MNIST (
|
طبقة واحدة (
|
في الموقع | ~94.5% | برمجيات (MATLAB) | 289 | ||
| شبكة عصبية تلافيفية (CNN) | الانتشار العكسي | MNIST (
|
طبقة مزدوجة (الطبقة الأولى: تلافيفية، الطبقة الثانية: كاملة التوصيل) | في الموقع | حوالي 94% | برمجيات | ٢٦٨ | |
| شبكة الأعصاب النابضة (SNN) | المرونة المعتمدة على توقيت النبضات (غير خاضعة للإشراف) | MNIST (
|
طبقة مزدوجة (
|
في الموقع | ~93.5% | البرمجيات (C++ Xnet) | ٢٦٩ | |
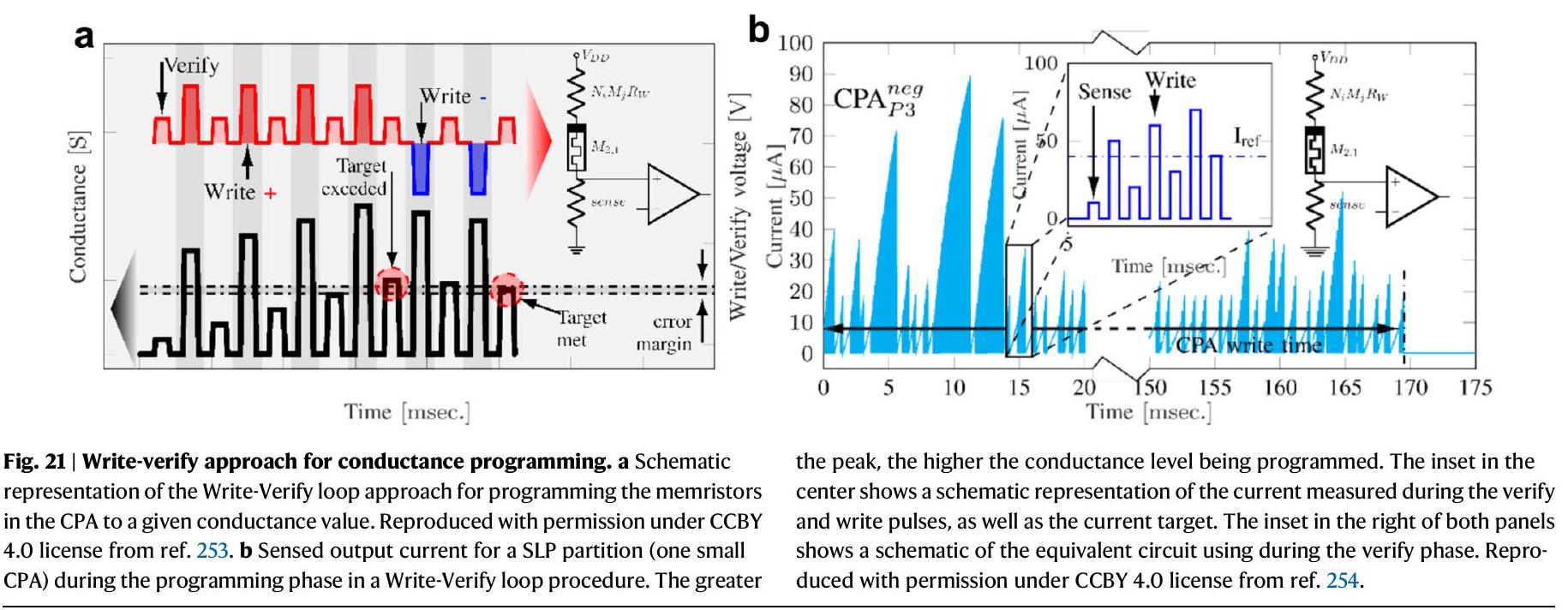
في معادلة الذاكرة التي تؤدي إلى التوصيل المستهدف. بالنسبة لحالة نموذج الميمود (QMM) شبه الثابت المعتبر في المراجع 250 و 253، يتم ذلك عن طريق ضبط المعامل التحكم.
تم تسليمها فعليًا إلى الميمريستورز). يتم الإشارة إلى عدد الأقسام بـ NP، ويعتمد الحجم الموصى به لكل قسم على نسبة التوصيلية بين الميمريستورز ومقاومة الأسلاك المعدنية. توضح الشكل التوضيحي 10 المبسط للعبور المقسم والاتصالات المطلوبة لتحقيق VMM الكامل. من خلال تفجير قابلية التكامل للعبور مع دوائر CMOS، يمكن وضع الاتصالات الرأسية المستخدمة لربط مخرجات أقسام العبور الرأسية تحت الهيكل المقسم (بالإضافة إلى الإلكترونيات الحسية التناظرية) مما يسمح للعبور المقسم بالحفاظ على استهلاك مساحة مشابه للحالة الأصلية غير المقسمة.
إنشاء تمثيل دائرة الشبكة العصبية الميمريستيفية
وسعات الخطوط المتداخلة (انظر الشكل المرفق الذي يظهر مخطط دائرة لخلية ميمريستيف في هيكل CPA مع الأخذ في الاعتبار مقاومة السلك الطفيلية والسعة المرتبطة). يتم التقاط جوانب مثل تباين الجهاز بواسطة نموذج الميمريستور المستخدم.

أ) الاتصال من جانب واحد (SSC) و (ب) الاتصال من جانبين (DSC). في حالة SSC، يتم تطبيق المحفزات المدخلة فقط على مدخلات جانب واحد من CPA، بينما الجانب الآخر هو

يستقبل كمدخلات حجم المصفوفة ونظام التقسيم، ويحدد تلقائيًا عدد الميمريستورات التي يجب وضعها وكيفية توصيلها بمقاومات الخطوط المجاورة لتحقيق الهيكل الكهربائي المتقاطع. يستخدم هذا الكود المصدر حلقات for متداخلة تتكرر عبر عدد الصفوف والأعمدة، مما ينشئ الهيكل المتقاطع. أيضًا، يتم إضافة السعة الطفيلية بين الخطوط المتوازية المجاورة في نفس المستوى (أي بين الصفوف والأعمدة المجاورة)، وبين تقاطعات الخطوط العلوية والسفلية، وبين الخطوط السفلية والأرض. من خلال ذلك، يمكننا حساب تأخير الانتشار عبر الهيكل المتقاطع، المعروف أيضًا بالكمون (أي عندما يكون الهدف هو قياس الوقت المنقضي منذ تطبيق نمط في مدخلات SLP حتى يستقر الناتج). نتيجة لذلك، يتم توصيل كل ميمريستور في الهيكل المتقاطع بـ 4 مقاومات و 5 مكثفات، كما هو موضح في الشكل 17d. كمثال، الكود الناتج لـ SPICE لتمييز SLP
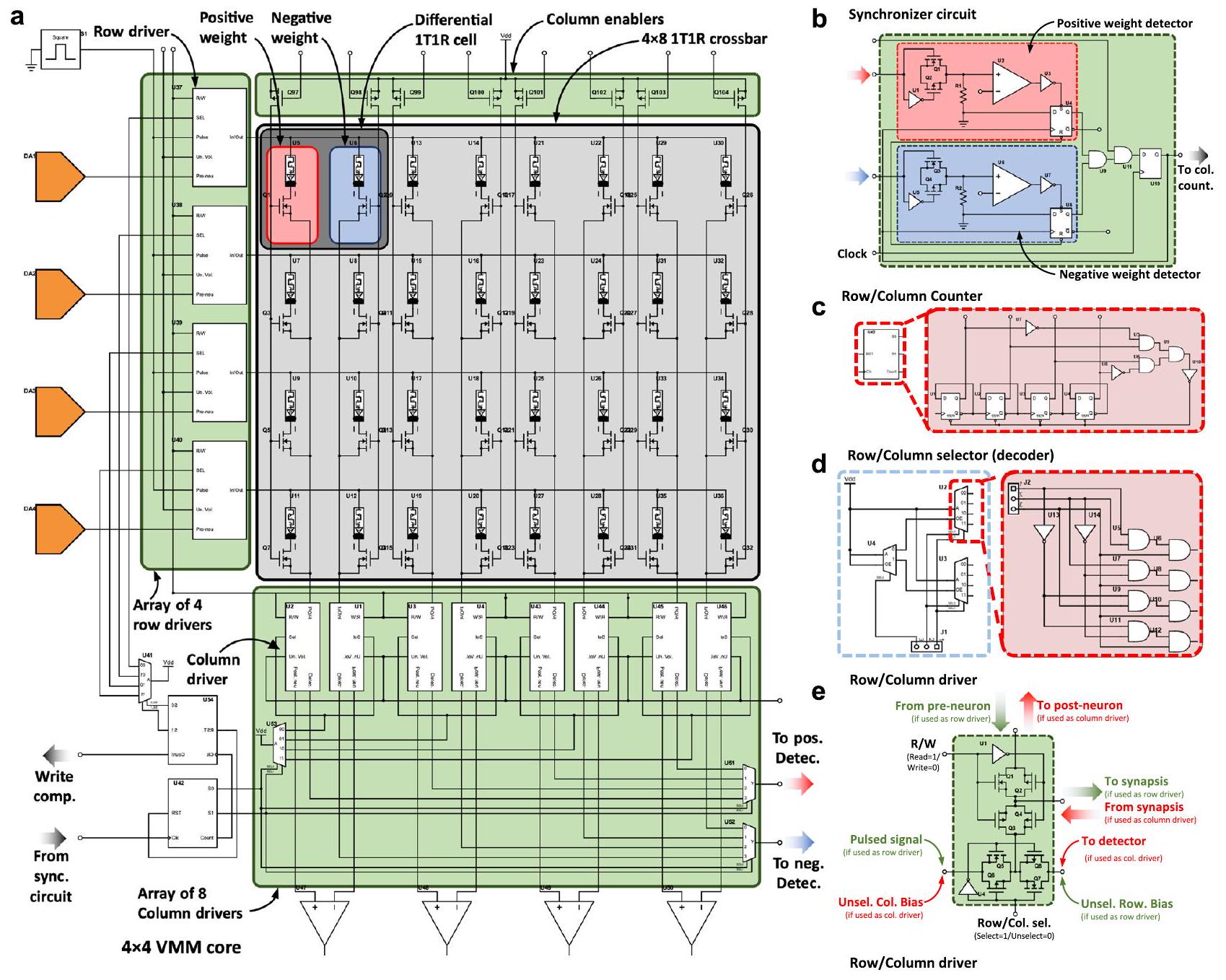
لتمكين الميمريستور المعنون بواسطة كتلة العنوان. سائق الصف والعمود، المستخدم لتطبيق الجهد على الصفوف أو مع إشارة البرمجة، ولربط الأعمدة بالعصبونات الناتجة (أثناء الاستدلال) أو مضخم الإشارة (أثناء التحقق من الكتابة).
تم حسابها عبر MATLAB. تتكون هذه الدائرة المحيطية من كتلة عنوان تقاطع، ومفككات عناوين الصفوف/الأعمدة، ومحددات الصفوف/الأعمدة، وكتلة تأكيد الكتابة (انظر الشكل التكميلي 9c على اليمين والشكل 19a). كتلة عنوان التقاطع (crossbar-AB) هي دائرة تنتج نبضة في كل مرة يتم فيها كتابة الميمريستور الموجود في موضع {i,j} بالكامل في جميع الأقسام (وبذلك تعمل كعداد، كما هو موضح في الشكل 19b)، مما يؤدي إلى
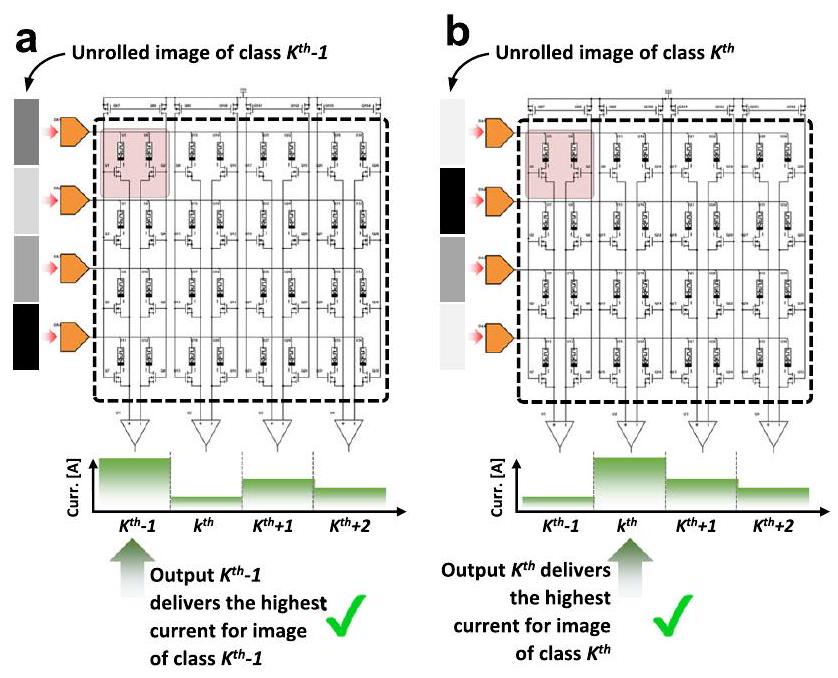

محاكاة SPICE واستخراج المقاييس
أو في الميمريستورز)، نسبة الإشارة إلى الضوضاء لإشارات التيار الناتجة، زمن الاستدلال، هوامش القراءة والكتابة (أي، الجزء من الجهد المطبق في مدخلات الشبكة المتقاطعة الذي يصل فعليًا إلى الميمريستورز أثناء عمليات القراءة أو الكتابة) والتردد التشغيلي الأقصى للدائرة العصبية الكاملة (الشبكة المتقاطعة بالإضافة إلى إلكترونيات CMOS).
التواصل بينهم. يعتمد اختيار تقنية المحاكاة الأكثر ملاءمة على متطلبات مرحلة التصميم المحددة: كلما اقتربت من مرحلة الطباعة، زادت دقة المحاكاة المطلوبة (يمكن تحقيقها من خلال محاكاة مستوى الدائرة)، بينما في مراحل التصميم المبكرة، يكفي نموذج مستوى النظام للحصول على تقدير سريع للأداء القابل للتحقيق في الشبكات العصبية الاصطناعية الكبيرة والمعقدة. في أي حال، فإن الجمع بشكل صحيح بين هذه الأدوات المختلفة للمحاكاة سيؤدي في النهاية إلى تحسين وتطوير الشبكات العصبية الميمريستيفية.
توفر البيانات
توفر الشيفرة
References
- European Commission, Harnessing the economic benefits of Artificial Intelligence. Digital Transformation Monitor, no. November, 8, 2017.
- Rattani, A. Reddy, N. and Derakhshani, R. “Multi-biometric Convolutional Neural Networks for Mobile User Authentication,” 2018 IEEE International Symposium on Technologies for Homeland Security, HST 2018, https://doi.org/10.1109/THS.2018. 85741732018.
- BBVA, Biometrics and machine learning: the accurate, secure way to access your bank Accessed: Jan. 21, 2024. [Online]. Available: https://www.bbva.com/en/biometrics-and-machine-learning-the-accurate-secure-way-to-access-your-bank/
- Amerini, I., Li, C.-T. & Caldelli, R. Social network identification through image classification with CNN. IEEE Access 7, 35264-35273 (2019).
- Ingle P. Y. and Kim, Y. G. “Real-time abnormal object detection for video surveillance in smart cities,” Sensors, 22,https://doi.org/10. 3390/s22103862 2022.
- Tan, X., Qin, T., F. Soong, and T.-Y. Liu, “A survey on neural speech synthesis,” https://doi.org/10.48550/arxiv.2106.15561 2021.
- “ChatGPT: Optimizing language models for dialogue.” Accessed: Feb. 13, 2023. [Online]. Available: https://openai.com/blog/ chatgpt/
- Hong, T., Choi, J. A., Lim, K. & Kim, P. Enhancing personalized ads using interest category classification of SNS users based on deep neural networks. Sens. 2021, Vol. 21, Page 199, 21, 199 (2020).
- McKee, S. A., Reflections on the memory wall in 2004 Computing Frontiers Conference, 162-167. https://doi.org/10.1145/977091. 9771152004.
- Mehonic, A. & Kenyon, A. J. Brain-inspired computing needs a master plan. Nature 604, 255-260 (2022).
- Zhang, C. et al. IMLBench: A machine learning benchmark suite for CPU-GPU integrated architectures. IEEE Trans. Parallel Distrib. Syst. 32, 1740-1752 (2021).
- Li, F., Ye, Y., Tian, Z. & Zhang, X. CPU versus GPU: which can perform matrix computation faster-performance comparison for basic linear algebra subprograms. Neural Comput. Appl. 31, 4353-4365 (2019).
- Farabet, C. Poulet, C., Han, J. Y. and LeCun, Y. CNP: An FPGAbased processor for Convolutional Networks, FPL 09: 19th International Conference on Field Programmable Logic and Applications, 32-37, https://doi.org/10.1109/FPL.2009.5272559 2009.
- Farabet, C. et al., NeuFlow: A runtime reconfigurable dataflow processor for vision, IEEE Computer Society Conference on
15. Zhang, C. et al., Optimizing FPGA-based accelerator design for deep convolutional neural networks, FPGA 2015-2015 ACM/ SIGDA International Symposium on Field-Programmable Gate Arrays, 161-170, https://doi.org/10.1145/2684746.2689060 2015.
16. Chakradhar, S., Sankaradas, M., Jakkula, V. and Cadambi, S. A dynamically configurable coprocessor for convolutional neural networks, Proc. Int. Symp. Comput. Archit., 247-257, https://doi. org/10.1145/1815961.1815993 2010.
17. Wei X. et al., Automated systolic array architecture synthesis for high throughput CNN Inference on FPGAs, Proc. Des. Autom. Conf., Part 128280, https://doi.org/10.1145/3061639. 30622072017.
18. Guo, K. et al., Neural Network Accelerator Comparison. Accessed: Jan. 10, 2023. [Online]. Available: https://nicsefc.ee.tsinghua.edu. cn/projects/neural-network-accelerator.html
19. Jouppi, N. P. et al., In-datacenter performance analysis of a tensor processing unit. Proc. Int. Symp. Comput. Archit., Part F128643, 1-12, https://doi.org/10.1145/3079856.3080246.2017,
20. AI Chip – Amazon Inferentia – AWS. Accessed: May 15, 2023. [Online]. Available: https://aws.amazon.com/machine-learning/ inferentia/
21. Talpes, E. et al. Compute solution for Tesla’s full self-driving computer. IEEE Micro 40, 25-35 (2020).
22. Reuther, A. et al, “AI and ML Accelerator Survey and Trends,” 2022 IEEE High Performance Extreme Computing Conference, HPEC 2022, https://doi.org/10.1109/HPEC55821.2022.9926331.2022,
23. Fick, L., Skrzyniarz, S., Parikh, M., Henry, M. B. and Fick, D. “Analog matrix processor for edge AI real-time video analytics,” Dig. Tech. Pap. IEEE Int. Solid State Circuits Conf, 2022-260-262, https://doi. org/10.1109/ISSCC42614.2022.9731773.2022,
24. “Gyrfalcon Unveils Fourth AI Accelerator Chip – EE Times.” Accessed: May 16, 2023. [Online]. Available: https://www. eetimes.com/gyrfalcon-unveils-fourth-ai-accelerator-chip/
25. Sebastian, A., Le Gallo, M., Khaddam-Aljameh, R. and Eleftheriou, E. “Memory devices and applications for in-memory computing,” Nat. Nanotechnol. 2020 15:7, 15, 529-544, https://doi.org/10. 1038/s41565-020-0655-z.
26. Zheng, N. and Mazumder, P. Learning in energy-efficient neuromorphic computing: algorithm and architecture co-design. WileyIEEE Press, Accessed: May 15, 2023. [Online]. Available: https:// ieeexplore.ieee.org/book/8889858 2020.
27. Orchard, G. et al., “Efficient Neuromorphic Signal Processing with Loihi 2,” IEEE Workshop on Signal Processing Systems, SiPS: Design and Implementation, 2021-October, 254-259, https://doi. org/10.1109/SIPS52927.2021.00053.2021,
28. “Microchips that mimic the human brain could make AI far more energy efficient | Science | AAAS.” Accessed: May 15, 2023. [Online]. Available: https://www.science.org/content/article/ microchips-mimic-human-brain-could-make-ai-far-more-energyefficient
29. Davies, M. et al., “Advancing neuromorphic computing with Loihi: A survey of results and outlook,” Proceedings of the IEEE, 109, 911-934,https://doi.org/10.1109/JPROC.2021.3067593.2021,
30. Barnell, M., Raymond, C., Wilson, M., Isereau, D. and Cicotta, C. “Target classification in synthetic aperture radar and optical imagery using loihi neuromorphic hardware,” in 2020 IEEE High Performance Extreme Computing Conference (HPEC), IEEE, 1-6. https://doi.org/10.1109/HPEC43674.2020.9286246.2020,
31. Viale, A., Marchisio, A., Martina, M., Masera, G., and Shafique, M. “CarSNN: An efficient spiking neural network for event-based autonomous cars on the Loihi Neuromorphic Research Processor,” 2021.
32. “Innatera Unveils Neuromorphic AI Chip to Accelerate Spiking Networks – EE Times.” Accessed: May 15, 2023. [Online]. Available: https://www.eetimes.com/innatera-unveils-neuromorphic-ai-chip-to-accelerate-spiking-networks/
33. Pei, J. et al. “Towards artificial general intelligence with hybrid Tianjic chip architecture,”. Nature 572, 106-111 (2019).
34. Merolla, P. A. et al. “A million spiking-neuron integrated circuit with a scalable communication network and interface,”. Science 345, 668-673 (2014).
35. Adam, G. C., Khiat, A., and Prodromakis, T. “Challenges hindering memristive neuromorphic hardware from going mainstream,” Nat. Commun., 9, Nature Publishing Group, 1-4, https://doi.org/10. 1038/s41467-018-07565-4.2018.
36. Sung, C., Hwang, H. & Yoo, I. K. “Perspective: A review on memristive hardware for neuromorphic computation,”. J. Appl. Phys. 124, 15 (2018).
37. Deng, L. et al. Energy consumption analysis for various memristive networks under different learning strategies,”. Phys. Lett. Sect. A: Gen. At. Solid State Phys. 380, 903-909 (2016).
38. Yu, S., Wu, Y., Jeyasingh, R., Kuzum, D. & Wong, H. S. P. “An electronic synapse device based on metal oxide resistive switching memory for neuromorphic computation,”. IEEE Trans. Electron Dev. 58, 2729-2737 (2011).
39. Shulaker, M. M. et al. “Three-dimensional integration of nanotechnologies for computing and data storage on a single chip,”. Nature 547, 74-78 (2017).
40. Li, C. et al. Three-dimensional crossbar arrays of self-rectifying Si/ SiO2/Si memristors. Nat. Commun. 2017 8:1 8, 1-9 (2017).
41. Yoon, J. H. et al. “Truly electroforming-free and low-energy memristors with preconditioned conductive tunneling paths,”. Adv. Funct. Mater. 27, 1702010 (2017).
42. Choi, B. J. et al. “High-speed and low-energy nitride memristors,”. Adv. Funct. Mater. 26, 5290-5296 (2016).
43. Strukov, D. B., Snider, G. S., Stewart, D. R. and Williams, R. S. “The missing memristor found,” Nature, 453,80-83, https://doi.org/10. 1038/nature06932.
44. “FUJITSU SEMICONDUCTOR MEMORY SOLUTION.” Accessed: Nov. 16, 2022. [Online]. Available: https://www.fujitsu.com/jp/ group/fsm/en/
45. “Everspin | The MRAM Company.” Accessed: Nov. 16, 2022. [Online]. Available: https://www.everspin.com/
46. “Yole Group.” Accessed: Nov. 16, 2022. [Online]. Available: https://www.yolegroup.com/?cn-reloaded=1
47. Stathopoulos, S. et al. “Multibit memory operation of metal-oxide Bi-layer memristors,”. Sci. Rep. 7, 1-7 (2017).
48. Wu, W. et al., “Demonstration of a multi-level
49. Yang, J. et al., “Thousands of conductance levels in memristors monolithically integrated on CMOS,” https://doi.org/10.21203/ RS.3.RS-1939455/V1.2022,
50. Goux, L. et al., “Ultralow sub-500nA operating current highperformance TiNไAl
51. Li, H. et al. “Memristive crossbar arrays for storage and computing applications,”. Adv. Intell. Syst. 3, 2100017 (2021).
52. Lin, P. et al. “Three-dimensional memristor circuits as complex neural networks,”. Nat. Electron. 3, 225-232 (2020).
53. Ishii, M. et al., “On-Chip Trainable 1.4M 6T2R PCM synaptic array with 1.6K Stochastic LIF neurons for spiking RBM,” Technical Digest – International Electron Devices Meeting, IEDM, 2019-
54. Li, C. et al. “Efficient and self-adaptive in-situ learning in multilayer memristor neural networks,”. Nat. Commun. 9, 1-8 (2018).
55. Yao, P. et al. “Fully hardware-implemented memristor convolutional neural network,”. Nature 577, 641-646 (2020).
56. Correll, J. M. et al., “An 8-bit 20.7 TOPS/W Multi-Level Cell ReRAMbased Compute Engine,” in 2022 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), IEEE, 264-265. https://doi.org/10.1109/VLSITechnologyandCir46769.2022. 9830490.2022,
57. Cai, F. et al., “A fully integrated reprogrammable memristorCMOS system for efficient multiply-accumulate operations,” Nat Electron, 2, no. July, 290-299, [Online]. Available: https://doi.org/ 10.1038/s41928-019-0270-x 2019.
58. Hung, J.-M., “An 8-Mb DC-Current-Free Binary-to-8b Precision ReRAM Nonvolatile Computing-in-Memory Macro using Time-Space-Readout with 1286.4-21.6TOPS/W for Edge-AI Devices,” in 2022 IEEE International Solid- State Circuits Conference (ISSCC), IEEE, 1-3. https://doi.org/10.1109/ISSCC42614.2022.9731715.2022,
59. Xue, C.-X., “15.4 A 22 nm 2 Mb ReRAM Compute-in-Memory Macro with 121-28TOPS/W for Multibit MAC Computing for Tiny AI Edge Devices,” in 2020 IEEE International Solid- State Circuits Conference – (ISSCC), IEEE, 2020, 244-246.
60. Wan, W. et al. “A compute-in-memory chip based on resistive random-access memory,”. Nature 608, 504-512 (2022).
61. Yin, S., Sun, X., Yu, S. & Seo, J. S. “High-throughput in-memory computing for binary deep neural networks with monolithically integrated RRAM and 90-nm CMOS,”. IEEE Trans. Electron. Dev. 67, 4185-4192 (2020).
62. Yan, X. et al. “Robust Ag/ZrO2/WS2/Pt Memristor for Neuromorphic Computing,”. ACS Appl Mater. Interfaces 11, 48029-48038 (2019).
63. Chen, Q. et al, “Improving the recognition accuracy of memristive neural networks via homogenized analog type conductance quantization,” Micromachines, 11, https://doi.org/10.3390/ MI11040427.2020,
64. Wang, Y. “High on/off ratio black phosphorus based memristor with ultra-thin phosphorus oxide layer,” Appl. Phys. Lett., 115, https://doi.org/10.1063/1.5115531.2019,
65. Xue, F. et al. “Giant ferroelectric resistance switching controlled by a modulatory terminal for low-power neuromorphic in-memory computing,”. Adv. Mater. 33, 1-12 (2021).
66. Pan, W.-Q. et al. “Strategies to improve the accuracy of memristorbased convolutional neural networks,”. Trans. Electron. Dev., 67, 895-901 (2020).
67. Seo, S. et al. “Artificial optic-neural synapse for colored and colormixed pattern recognition,”. Nat. Commun. 9, 1-8 (2018).
68. Chandrasekaran, S., Simanjuntak, F. M., Saminathan, R., Panda, D. and Tseng, T. Y., “Improving linearity by introducing Al in
69. Zhang, B. et al. ”
70. Feng, X. et al. “Self-selective multi-terminal memtransistor crossbar array for in-memory computing,”. ACS Nano 15, 1764-1774 (2021).
71. Khaddam-Aljameh, R.et al. “HERMES-Core-A1.59-TOPS/mm2PCM on
72. Narayanan, P. et al. “Fully on-chip MAC at 14 nm enabled by accurate row-wise programming of PCM-based weights and parallel vector-transport in duration-format,”. IEEE Trans. Electron Dev. 68, 6629-6636 (2021).
73. Le Gallo, M. et al., “A 64-core mixed-signal in-memory compute chip based on phase-change memory for deep neural network inference,” 2022, Accessed: May 09, 2023. [Online]. Available: https://arxiv.org/abs/2212.02872v1
74. Murmann, B. “Mixed-signal computing for deep neural network inference,”. IEEE Trans. Very Large Scale Integr. VLSI Syst. 29, 3-13 (2021).
75. Yin, S., Jiang, Z., Seo, J. S. & Seok, M. “XNOR-SRAM: In-memory computing SRAM macro for binary/ternary deep neural networks,”. IEEE J. Solid-State Circuits 55, 1733-1743 (2020).
76. Biswas, A. & Chandrakasan, A. P. “CONV-SRAM: An energyefficient SRAM with in-memory dot-product computation for lowpower convolutional neural networks,”. IEEE J. Solid-State Circuits 54, 217-230 (2019).
77. Valavi, H., Ramadge, P. J., Nestler, E. & Verma, N. “A 64-Tile 2.4-Mb In-memory-computing CNN accelerator employing chargedomain compute,”. IEEE J. Solid-State Circuits 54, 1789-1799 (2019).
78. Khwa, W. S. et al. “A 65 nm 4 Kb algorithm-dependent computing-in-memory SRAM unit-macro with 2.3 ns and 55.8TOPS/W fully parallel product-sum operation for binary DNN edge processors,”. Dig. Tech. Pap. IEEE Int. Solid State Circuits Conf. 61, 496-498 (2018).
79. Verma, N. et al. “In-memory computing: advances and prospects,”. IEEE Solid-State Circuits Mag. 11, 43-55 (2019).
80. Diorio, C., Hasler, P., Minch, A. & Mead, C. A. “A single-transistor silicon synapse,”. IEEE Trans. Electron. Dev. 43, 1972-1980 (1996).
81. Merrikh-Bayat, F. et al. “High-performance mixed-signal neurocomputing with nanoscale floating-gate memory cell arrays,”. IEEE Trans. Neural Netw. Learn Syst. 29, 4782-4790 (2018).
82. Wang, P. et al. “Three-dimensional NAND flash for vector-matrix multiplication,”. IEEE Trans. Very Large Scale Integr. VLSI Syst. 27, 988-991 (2019).
83. Bavandpour, M., Sahay, S., Mahmoodi, M. R. & Strukov, D. B. “3DaCortex: an ultra-compact energy-efficient neurocomputing platform based on commercial 3D-NAND flash memories,”. Neuromorph. Comput. Eng. 1, 014001 (2021).
84. Chu, M. et al. “Neuromorphic hardware system for visual pattern recognition with memristor array and CMOS neuron,”. IEEE Trans. Ind. Electron. 62, 2410-2419 (2015).
85. Yeo, I., Chu, M., Gi, S. G., Hwang, H. & Lee, B. G. “Stuck-at-fault tolerant schemes for memristor crossbar array-based neural networks,”. IEEE Trans. Electron Devices 66, 2937-2945 (2019).
86. LeCun, Y., Cortes, C., and Burges, C. J. C., “MNIST handwritten digit database of handwritten digits.” Accessed: Nov. 21, 2019. [Online]. Available: http://yann.lecun.com/exdb/mnist/
87. Krizhevsky, A., Nair, V., and Hinton, G. “The CIFAR-10 dataset.” Accessed: Apr. 04, 2023. [Online]. Available: https://www.cs. toronto.edu/~kriz/cifar.html
88. Deng, J. et al., “ImageNet: A large-scale hierarchical image database,” in 2009 IEEE Conference on Computer Vision and Pattern Recognition, IEEE, 2009, 248-255.
89. Simonyan, K. and Zisserman, A. “Very deep convolutional networks for large-scale image recognition,” 2014.
90. He, K., Zhang, X., Ren, S. and Sun, J. “Deep Residual Learning for Image Recognition,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, 770-778. https://doi.org/10. 1109/CVPR.2016.90.2016,
91. Chen, P. Y., Peng, X. & Yu, S. “NeuroSim: A circuit-level macro model for benchmarking neuro-inspired architectures in online learning,”. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 37, 3067-3080 (2018).
92. Wang, Q., Wang, X., Lee, S. H., Meng, F.-H. and Lu W. D., “A Deep Neural Network Accelerator Based on Tiled RRAM Architecture,” in
93. Kim, H., Mahmoodi, M. R., Nili, H. & Strukov, D. B. “4K-memristor analog-grade passive crossbar circuit,”. Nat. Commun. 12, 1-11 (2021).
94. Inc. The Mathworks, “MATLAB.” Natick, Massachusetts, 2019.
95. Amirsoleimani, A. et al. “In-memory vector-matrix multiplication in monolithic complementary metal-oxide-semiconductor-memristor integrated circuits: design choices, challenges, and perspectives,”. Adv. Intell. Syst. 2, 2000115, https://doi.org/10.1002/ AISY. 202000115 (2020).
96. Chakraborty, I. et al. “Resistive crossbars as approximate hardware building blocks for machine learning: opportunities and challenges,”. Proc. IEEE 108, 2276-2310 (2020).
97. Jain, S. et al. “Neural network accelerator design with resistive crossbars: Opportunities and challenges,”. IBM J. Res Dev. 63, 6 (2019).
98. Ankit, A. et al. “PANTHER: A Programmable Architecture for Neural Network Training Harnessing Energy-Efficient ReRAM,”. IEEE Trans. Comput. 69, 1128-1142 (2020).
99. Mochida, R. et al. “A 4M synapses integrated analog ReRAM based 66.5 TOPS/W neural-network processor with cell current controlled writing and flexible network architecture,” Digest of Technical Papers – Symposium on VLSI Technology, 175-176, Oct. 2018, 2018
100. Su, F. et al., “A 462 GOPs/J RRAM-based nonvolatile intelligent processor for energy harvesting loE system featuring nonvolatile logics and processing-in-memory,” Digest of Technical Papers Symposium on VLSI Technology, C260-C261, https://doi.org/10. 23919/VLSIT.2017.7998149.2017,
101. Han J. and Orshansky, M. “Approximate computing: An emerging paradigm for energy-efficient design,” in 2013 18th IEEE European Test Symposium (ETS), IEEE, 1-6. https://doi.org/10.1109/ETS. 2013.6569370.2013,
102. Kiani, F., Yin, J., Wang, Z., Joshua Yang, J. & Xia, Q. “A fully hardware-based memristive multilayer neural network,”. Sci. Adv. 7, 4801 (2021).
103. Gokmen, T. and Vlasov, Y. “Acceleration of deep neural network training with resistive cross-point devices: Design considerations,” Front. Neurosci., 10, no. JUL, https://doi.org/10.3389/fnins.2016. 00333.2016,
104. Fouda, M. E., Lee, S., Lee, J., Eltawil, A. & Kurdahi, F. “Mask technique for fast and efficient training of binary resistive crossbar arrays,”. IEEE Trans. Nanotechnol. 18, 704-716 (2019).
105. Prezioso, M. et al. “Training and operation of an integrated neuromorphic network based on metal-oxide memristors,”. Nature 521, 61-64 (2015).
106. Hu, M. et al. “Memristor crossbar-based neuromorphic computing system: A case study,”. IEEE Trans. Neural Netw. Learn Syst. 25, 1864-1878 (2014).
107. Hu, M. et al., “Dot-product engine for neuromorphic computing,” in DAC ’16: Proceedings of the 53rd Annual Design Automation Conference, New York, NY, USA: Association for Computing Machinery, 1-6. https://doi.org/10.1145/2897937.2898010.2016,
108. Liu, C., Hu, M., Strachan, J. P. and Li, H. H. “Rescuing memristorbased neuromorphic design with high defects,” in 2017 54th ACM/ EDAC/IEEE Design Automation Conference (DAC), Institute of Electrical and Electronics Engineers Inc., https://doi.org/10.1145/ 3061639.3062310.2017.
109. Romero-Zaliz, R., Pérez, E., Jiménez-Molinos, F., Wenger, C. & Roldán, J. B. “Study of quantized hardware deep neural networks based on resistive switching devices, conventional versus convolutional approaches,”. Electronics 10, 1-14 (2021).
110. Pérez, E. et al. “Advanced temperature dependent statistical analysis of forming voltage distributions for three different HfO 2 –
based RRAM technologies,”. Solid State Electron. 176, 107961 (2021).
111. Pérez-Bosch Quesada, E. et al. “Toward reliable compact modeling of multilevel 1T-1R RRAM devices for neuromorphic systems,”. Electronics 10, 645 (2021).
112. Xia, L. et al. “Stuck-at Fault Tolerance in RRAM Computing Systems,”. IEEE J. Emerg. Sel. Top. Circuits Syst., 8, 102-115 (2018).
113. Li, C. et al., “CMOS-integrated nanoscale memristive crossbars for CNN and optimization acceleration,” 2020 IEEE International Memory Workshop, IMW 2020 – Proceedings, https://doi.org/10. 1109/IMW48823.2020.9108112.2020,
114. Pedretti, G. et al. “Redundancy and analog slicing for precise inmemory machine learning – Part I: Programming techniques,”. IEEE Trans. Electron. Dev. 68, 4373-4378 (2021).
115. Pedretti, G. et al. “Redundancy and analog slicing for precise inmemory machine learning – Part II: Applications and benchmark,”. IEEE Trans. Electron. Dev. 68, 4379-4383 (2021).
116. Wang, Z. et al. “Fully memristive neural networks for pattern classification with unsupervised learning,”. Nat. Electron. 1, 137-145 (2018).
117. T. Rabuske and J. Fernandes, “Charge-Sharing SAR ADCs for lowvoltage low-power applications,” https://doi.org/10.1007/978-3-319-39624-8.2017,
118. Kumar, P. et al. “Hybrid architecture based on two-dimensional memristor crossbar array and CMOS integrated circuit for edge computing,”. npj 2D Mater. Appl. 6, 1-10 (2022).
119. Krestinskaya, O., Salama, K. N. & James, A. P. “Learning in memristive neural network architectures using analog backpropagation circuits,”. IEEE Trans. Circuits Syst. I: Regul. Pap. 66, 719-732 (2019).
120. Chua, L. O., Tetzlaff, R. and Slavova, A. Eds., Memristor Computing Systems. Springer International Publishing, https://doi.org/10. 1007/978-3-030-90582-8.2022.
121. Oh, S. et al. “Energy-efficient Mott activation neuron for fullhardware implementation of neural networks,”. Nat. Nanotechnol. 16, 680-687 (2021).
122. Ambrogio, S. et al. “Equivalent-accuracy accelerated neuralnetwork training using analogue memory,”. Nature 558, 60-67 (2018).
123. Bocquet, M. et al., “In-memory and error-immune differential RRAM implementation of binarized deep neural networks,” Technical Digest – International Electron Devices Meeting, IEDM, 20.6.120.6.4, Jan. 2019, https://doi.org/10.1109/IEDM.2018. 8614639.2018,
124. Cheng, M. et al., “TIME: A Training-in-memory architecture for Memristor-based deep neural networks,” Proc. Des. Autom. Conf., Part 12828, 0-5, https://doi.org/10.1145/3061639. 3062326.2017,
125. Chi, P. et al., “PRIME: A novel processing-in-memory architecture for neural network computation in ReRAM-based main memory,” Proceedings – 2016 43rd International Symposium on Computer Architecture, ISCA 2016, 27-39, https://doi.org/10.1109/ISCA. 2016.13.2016,
126. Krestinskaya, O., Choubey, B. & James, A. P. “Memristive GAN in Analog,”. Sci. Rep. 2020 10:1 10, 1-14 (2020).
127. Li, G. H. Y. et al., “All-optical ultrafast ReLU function for energyefficient nanophotonic deep learning,” Nanophotonics, https:// doi.org/10.1515/NANOPH-2022-0137/ASSET/GRAPHIC/J_ NANOPH-2022-0137_FIG_007.JPG.2022,
128. Ando, K. et al. “BRein memory: a single-chip binary/ternary reconfigurable in-memory deep neural network accelerator achieving 1.4 TOPS at 0.6 W,”. IEEE J. Solid-State Circuits 53, 983-994 (2018).
129. Price, M., Glass, J. & Chandrakasan, A. P. “A scalable speech recognizer with deep-neural-network acoustic models and voice-
activated power gating,”. Dig. Tech. Pap. IEEE Int Solid State Circuits Conf. 60, 244-245 (2017).
130. Yin, S. et al., “A 1.06-to-5.09 TOPS/W reconfigurable hybrid-neural-network processor for deep learning applications,” IEEE Symposium on VLSI Circuits, Digest of Technical Papers, C26-C27, https://doi.org/10.23919/VLSIC.2017.8008534.2017,
131. Chen, Y. H., Krishna, T., Emer, J. S. & Sze, V. “Eyeriss: An energyefficient reconfigurable accelerator for deep convolutional neural networks,”. IEEE J. Solid-State Circuits 52, 127-138 (2017).
132. Lazzaro, J., Ryckebusch, S. M., Mahowald, A. and Mead, C. A. “Winner-Take-All Networks of O(N) Complexity,” in Advances in Neural Information Processing Systems, D. Touretzky, Ed., MorganKaufmann, 1988.
133. Andreou, A. G. et al. “Current-mode subthreshold MOS circuits for analog VLSI neural systems,”. IEEE Trans. Neural Netw. 2, 205-213 (1991).
134. Pouliquen, P. O., Andreou, A. G., Strohbehn, K. and Jenkins, R. E. “Associative memory integrated system for character recognition,” Midwest Symposium on Circuits and Systems, 1, 762-765, https://doi.org/10.1109/MWSCAS.1993.342935.1993,
135. Starzyk, J. A. & Fang, X. “CMOS current mode winner-take-all circuit with both excitatory and inhibitory feedback,”. Electron. Lett. 29, 908-910 (1993).
136. DeWeerth, S. P. & Morris, T. G. “CMOS current mode winner-takeall circuit with distributed hysteresis,”. Electron. Lett. 31, 1051-1053 (1995).
137. Indiveri, G. “A current-mode hysteretic winner-take-all network, with excitatory and inhibitory coupling,”. Analog Integr. Circuits Signal Process 28, 279-291 (2001).
138. Tan, B. P. & Wilson, D. M. “Semiparallel rank order filtering in analog VLSI,”. IEEE Trans. Circuits Syst. II: Analog Digit. Signal Process. 48, 198-205 (2001).
139. Serrano, T. & Linares-Barranco, B. “Modular current-mode highprecision winner-take-all circuit,”. Proc. – IEEE Int. Symp. Circuits Syst. 5, 557-560 (1994).
140. Meador, J. L. and Hylander, P. D. “Pulse Coded Winner-Take-All Networks,” Silicon Implementation of Pulse Coded Neural Networks, 79-99, https://doi.org/10.1007/978-1-4615-2680-3_5.1994,
141. El-Masry, E. I., Yang, H. K. & Yakout, M. A. “Implementations of artificial neural networks using current-mode pulse width modulation technique,”. IEEE Trans. Neural Netw. 8, 532-548 (1997).
142. Choi, J. & Sheu, B. J. “A high-precision vlsi winner-take-all circuit for self-organizing neural networks,”. IEEE J. Solid-State Circuits 28, 576-584 (1993).
143. Yu, H. & Miyaoka, R. S. “A High-Speed and High-Precision Winner-Select-Output (WSO) ASIC,”. IEEE Trans. Nucl. Sci. 45, 772-776 (1998). PART 1.
144. Lau, K. T. and Lee, S. T. “A CMOS winner-takes-all circuit for selforganizing neural networks,” https://doi.org/10.1080/ 002072198134896, 84, 131-136, 2010
145. He, Y. & Sánchez-Sinencio, E. “Min-net winner-take-all CMOS implementation,”. Electron Lett. 29, 1237-1239 (1993).
146. Demosthenous, A., Smedley, S. & Taylor, J. “A CMOS analog winner-take-all network for large-scale applications,”. IEEE Trans. Circuits Syst. I: Fundam. Theory Appl. 45, 300-304 (1998).
147. Pouliquen, P. O., Andreou, A. G. & Strohbehn, K. “Winner-Takes-All associative memory: A hamming distance vector quantizer,”. Analog Integr. Circuits Signal Process. 1997 13:1 13, 211-222 (1997).
148. Fish, A., Milrud, V. & Yadid-Pecht, O. “High-speed and highprecision current winner-take-all circuit,”. IEEE Trans. Circuits Syst. II: Express Briefs 52, 131-135 (2005).
149. Ohnhäuser, F. “Analog-Digital Converters for Industrial Applications Including an Introduction to Digital-Analog Converters,” 2015.
150. Pavan, S., Schreier, R.. and Temes, G. C. “Understanding DeltaSigma Data Converters.”.
151. Walden, R. H. “Analog-to-digital converter survey and analysis,”. IEEE J. Sel. Areas Commun. 17, 539-550 (1999).
152. Harpe, P., Gao, H., Van Dommele, R., Cantatore, E. & Van Roermund, A. H. M. “A 0.20 mm 23 nW signal acquisition IC for miniature sensor nodes in 65 nm CMOS. IEEE J. Solid-State Circuits 51, 240-248 (2016).
153. Murmann, B. “ADC Performance Survey 1997-2022.” Accessed: Sep. 05, 2022. [Online]. Available: http://web.stanford.edu/ ~murmann/adcsurvey.html.
154. Ankit, A. et al., “PUMA: A Programmable Ultra-efficient Memristorbased Accelerator for Machine Learning Inference,” International Conference on Architectural Support for Programming Languages and Operating Systems – ASPLOS, 715-731, https://doi.org/10. 1145/3297858.3304049.2019,
155. Ni, L. et al., “An energy-efficient matrix multiplication accelerator by distributed in-memory computing on binary RRAM crossbar,” Proceedings of the Asia and South Pacific Design Automation Conference, ASP-DAC, 25-28-January-2016, 280-285, https://doi. org/10.1109/ASPDAC.2016.7428024.2016,
156. Wang, X., Wu, Y. and Lu, W. D. “RRAM-enabled AI Accelerator Architecture,” in 2021 IEEE International Electron Devices Meeting (IEDM), IEEE, 12.2.1-12.2.4. https://doi.org/10.1109/IEDM19574. 2021.9720543.2021,
157. Xiao, T. P. et al. On the Accuracy of Analog Neural Network Inference Accelerators. [Feature],” IEEE Circuits Syst. Mag. 22, 26-48 (2022).
158. Sun, X. et al, “XNOR-RRAM: A scalable and parallel resistive synaptic architecture for binary neural networks,” Proceedings of the 2018 Design, Automation and Test in Europe Conference and Exhibition, DATE 2018, 2018-January, 1423-1428, https://doi.org/ 10.23919/DATE.2018.8342235.2018,
159. Zhang, W. et al. “Neuro-inspired computing chips,”. Nat. Electron. 2020 3:7 3, 371-382 (2020).
160. Shafiee, A. et al., “ISAAC: A Convolutional Neural Network Accelerator with In-Situ Analog Arithmetic in Crossbars,” in Proceedings – 2016 43rd International Symposium on Computer Architecture, ISCA 2016, Institute of Electrical and Electronics Engineers Inc., 14-26. https://doi.org/10.1109/ISCA.2016.12.2016,
161. Fujiki, D., Mahlke, S. and Das, R. “In-memory data parallel processor,” in ACM SIGPLAN Notices, New York, NY, USA: ACM, 1-14. https://doi.org/10.1145/3173162.3173171.2018,
162. Nourazar, M., Rashtchi, V., Azarpeyvand, A. & Merrikh-Bayat, F. “Memristor-based approximate matrix multiplier,”. Analog. Integr. Circuits Signal Process 93, 363-373 (2017).
163. Saberi, M., Lotfi, R., Mafinezhad, K. & Serdijn, W. A. “Analysis of power consumption and linearity in capacitive digital-to-analog converters used in successive approximation ADCs,”. IEEE Trans. Circuits Syst. I: Regul. Pap. 58, 1736-1748 (2011).
164. Kull, L. et al. “A
165. Hagan, M., Demuth, H., Beale, M. and De Jesús, O. Neural Network Design, 2nd ed. Stillwater, OK, USA: Oklahoma State University, 2014.
166. Choi, S., Sheridan, P. & Lu, W. D. “Data clustering using memristor networks,”. Sci. Rep. 5, 1-10 (2015).
167. Khaddam-Aljameh, R. et al., “HERMES Core: A 14 nm CMOS and PCM-based In-Memory Compute Core using an array of
168. Kennedy, J. and Eberhart, R. “Particle swarm optimization,” Proceedings of ICNN’95 – International Conference on Neural Networks, 4, https://doi.org/10.1109/ICNN.1995.488968. 1942-1948,
169. Goldberg, D. E. & Holland, J. H. “Genetic Algorithms and machine learning. Mach. Learn. 3, 95-99 (1988).
170. Kirkpatrick, S., Gelatt, C. D. & Vecchi, M. P. “Optimization by simulated annealing,”. Science 220, 671-680 (1983).
171. Rumelhart, D. E., Hinton, G. E. & Williams, R. J. “Learning representations by back-propagating errors,”. Nature 323, 533-536 (1986).
172. Dennis, J. E. and Schnabel, R. B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations. Society for Industrial and Applied Mathematics, https://doi.org/10.1137/1. 9781611971200.1996.
173. Møller, M. F. “A scaled conjugate gradient algorithm for fast supervised learning,”. Neural Netw. 6, 525-533 (1993).
174. Powell, M. J. D. “Restart procedures for the conjugate gradient method,”. Math. Program. 12, 241-254 (1977).
175. Fletcher, R. “Function minimization by conjugate gradients,”. Comput. J. 7, 149-154 (1964).
176. Marquardt, D. W. “An algorithm for least-squares estimation of nonlinear parameters,”. J. Soc. Ind. Appl. Math. 11, 431-441 (1963).
177. Riedmiller, M. and Braun, H. “Direct adaptive method for faster backpropagation learning: The RPROP algorithm,” in 1993 IEEE International Conference on Neural Networks, Publ by IEEE, 586-591. https://doi.org/10.1109/icnn.1993.298623.1993,
178. Battiti, R. “First- and second-order methods for learning: between steepest descent and Newton’s Method,”. Neural Comput. 4, 141-166 (1992).
179. Bottou, L. “Stochastic gradient descent tricks,” Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 7700 LECTURE NO, 421-436, https://doi.org/10.1007/978-3-642-35289-8_25/ COVER.2012,
180. Li, M., Zhang, T., Chen, Y. and Smola, A. J. “Efficient mini-batch training for stochastic optimization,” Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 661-670, https://doi.org/10.1145/2623330. 2623612.2014,
181. Zamanidoost, E., Bayat, F. M., Strukov, D. and Kataeva, I. “Manhattan rule training for memristive crossbar circuit pattern classifiers,” WISP 2015 – IEEE International Symposium on Intelligent Signal Processing, Proceedings, https://doi.org/10.1109/WISP. 2015.7139171.2015,
182. Duchi, J., Hazan, E. & Singer, Y. “Adaptive subgradient methods for online learning and stochastic optimization,”. J. Mach. Learn. Res. 12, 2121-2159 (2011).
183. “Neural Networks for Machine Learning – Geoffrey Hinton – C. Cui’s Blog.” Accessed: Nov. 21, 2022. [Online]. Available: https:// cuicaihao.com/neural-networks-for-machine-learning-geoffreyhinton/
184. Kingma, D. P. and Ba, J. L. “Adam: A Method for Stochastic Optimization,” 3rd International Conference on Learning Representations, ICLR 2015 – Conference Track Proceedings, 2014, https://doi. org/10.48550/arxiv.1412.6980.
185. Zeiler, M. D. “ADADELTA: An adaptive learning rate method,” Dec. 2012, https://doi.org/10.48550/arxiv.1212.5701.
186. Xiong, X. et al. “Reconfigurable logic-in-memory and multilingual artificial synapses based on 2D heterostructures,”. Adv. Funct. Mater. 30, 2-7 (2020).
187. Zoppo, G., Marrone, F. & Corinto, F. “Equilibrium propagation for memristor-based recurrent neural networks,”. Front Neurosci. 14, 1-8 (2020).
188. Alibart, F., Zamanidoost, E. & Strukov, D. B. “Pattern classification by memristive crossbar circuits using ex situ and in situ training,”. Nat. Commun. 4, 1-7 (2013).
189. Joshi, V. et al., “Accurate deep neural network inference using computational phase-change memory,” Nat Commun, 11, https:// doi.org/10.1038/s41467-020-16108-9.2020,
190. Rasch, M. J. et al., “Hardware-aware training for large-scale and diverse deep learning inference workloads using in-memory computing-based accelerators,” 2023.
191. Huang, H.-M., Wang, Z., Wang, T., Xiao, Y. & Guo, X. “Artificial neural networks based on memristive devices: from device to system,”. Adv. Intell. Syst. 2, 2000149 (2020).
192. Nandakumar, S. R. et al., “Mixed-precision deep learning based on computational memory,” Front. Neurosci., 14, https://doi.org/10. 3389/fnins.2020.00406.2020,
193. Le Gallo, M. et al. “Mixed-precision in-memory computing,”. Nat. Electron. 1, 246-253 (2018).
194. Yao, P. et al., “Face classification using electronic synapses,” Nat. Commun., 8, May, 1-8, https://doi.org/10.1038/ ncomms15199.2017,
195. Papandreou, N. et al., “Programming algorithms for multilevel phase-change memory,” Proceedings – IEEE International Symposium on Circuits and Systems, 329-332, https://doi.org/10.1109/ ISCAS.2011.5937569.2011,
196. Milo, V. et al., “Multilevel HfO2-based RRAM devices for lowpower neuromorphic networks,” APL Mater, 7, https://doi.org/10. 1063/1.5108650.2019,
197. Yu, S. et al., “Scaling-up resistive synaptic arrays for neuroinspired architecture: Challenges and prospect,” in Technical Digest – International Electron Devices Meeting, IEDM, Institute of Electrical and Electronics Engineers Inc., 17.3.1-17.3.4. https://doi. org/10.1109/IEDM.2015.7409718.2015,
198. Woo, J. et al. “Improved synaptic behavior under identical pulses using AlOx/HfO2 bilayer RRAM array for neuromorphic systems,”. IEEE Electron. Device Lett. 37, 994-997 (2016).
199. Xiao, S. et al. “GST-memristor-based online learning neural networks,”. Neurocomputing 272, 677-682 (2018).
200. Tian, H. et al. “A novel artificial synapse with dual modes using bilayer graphene as the bottom electrode,”. Nanoscale 9, 9275-9283 (2017).
201. Shi, T., Yin, X. B., Yang, R. & Guo, X. “Pt/WO3/FTO memristive devices with recoverable pseudo-electroforming for time-delay switches in neuromorphic computing,”. Phys. Chem. Chem. Phys. 18, 9338-9343 (2016).
202. Menzel, S. et al. “Origin of the ultra-nonlinear switching kinetics in oxide-based resistive switches,”. Adv. Funct. Mater. 21, 4487-4492 (2011).
203. Buscarino, A., Fortuna, L., Frasca, M., Gambuzza, L. V. and Sciuto, G., “Memristive chaotic circuits based on cellular nonlinear networks,” https://doi.org/10.1142/SO218127412500708, 22,3, 2012
204. Li, Y. & Ang, K.-W. “Hardware implementation of neuromorphic computing using large-scale memristor crossbar arrays,”. Adv. Intell. Syst. 3, 2000137 (2021).
205. Zhu, J., Zhang, T., Yang, Y. & Huang, R. “A comprehensive review on emerging artificial neuromorphic devices,”. Appl Phys. Rev. 7, 011312 (2020).
206. Wang, Z. et al. “Engineering incremental resistive switching in TaOx based memristors for brain-inspired computing,”. Nanoscale 8, 14015-14022 (2016).
207. Park, S. M. et al. “Improvement of conductance modulation linearity in a
208. Slesazeck, S. & Mikolajick, T. “Nanoscale resistive switching memory devices: a review,”. Nanotechnology 30, 352003 (2019).
209. Waser, R., Dittmann, R., Staikov, C. & Szot, K. “Redox-based resistive switching memories nanoionic mechanisms, prospects, and challenges,”. Adv. Mater. 21, 2632-2663 (2009).
210. Ielmini, D. and Waser, R. Resistive Switching. Weinheim, Germany: Wiley-VCH Verlag GmbH & Co. KGaA, 2016.
211. Wouters, D. J., Waser, R. & Wuttig, M. “Phase-change and redoxbased resistive switching memories,”. Proc. IEEE 103, 1274-1288 (2015).
212. Pan, F., Gao, S., Chen, C., Song, C. & Zeng, F. “Recent progress in resistive random access memories: Materials, switching mechanisms, and performance,”. Mater. Sci. Eng. R: Rep. 83, 1-59 (2014).
213. Kim, S. et al. “Analog synaptic behavior of a silicon nitride memristor,”. ACS Appl Mater. Interfaces 9, 40420-40427 (2017).
214. Li, W., Sun, X., Huang, S., Jiang, H. & Yu, S. “A 40-nm MLC-RRAM compute-in-memory macro with sparsity control, On-Chip Writeverify, and temperature-independent ADC references,”. IEEE J. Solid-State Circuits 57, 2868-2877 (2022).
215. Buchel, J. et al., “Gradient descent-based programming of analog in-memory computing cores,” Technical Digest – International Electron Devices Meeting, IEDM, 3311-3314, 2022, https://doi.org/ 10.1109/IEDM45625.2022.10019486.2022,
216. Prezioso, M. et al. “Spike-timing-dependent plasticity learning of coincidence detection with passively integrated memristive circuits,”. Nat. Commun. 9, 1-8 (2018).
217. Park, S. et al., “Electronic system with memristive synapses for pattern recognition,” Sci. Rep., 5, https://doi.org/10.1038/ srep10123.2015,
218. Yu, S. et al., “Binary neural network with 16 Mb RRAM macro chip for classification and online training,” in Technical Digest – International Electron Devices Meeting, IEDM, Institute of Electrical and Electronics Engineers Inc., 16.2.1-16.2.4. https://doi.org/10.1109/ IEDM.2016.7838429.2017,
219. Chen, W. H. et al. “CMOS-integrated memristive non-volatile computing-in-memory for AI edge processors,”. Nat. Electron. 2, 420-428 (2019).
220. Chen, W. H. et al., “A 16 Mb dual-mode ReRAM macro with sub14ns computing-in-memory and memory functions enabled by self-write termination scheme,” Technical Digest – International Electron Devices Meeting, IEDM, 28.2.1-28.2.4, 2018,
221. Hu, M. et al., “Memristor-based analog computation and neural network classification with a dot product engine,” Adv. Mater., 30, https://doi.org/10.1002/adma.201705914.2018,
222. Li, C. et al. Analogue signal and image processing with large memristor crossbars. Nat. Electron 1, 52-59 (2018).
223. Paszke A. et al., “Automatic differentiation in PyTorch”.
224. Abadi, M. et al., “TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems,” 2015.
225. Stimberg, M., Brette, R. and Goodman, D. F. M. “Brian 2, an intuitive and efficient neural simulator,” Elife, 8, https://doi.org/10.7554/ ELIFE.47314.2019,
226. Spreizer, S. et al., “NEST 3.3,” Mar. 2022, https://doi.org/10.5281/ ZENODO. 6368024.
227. Hazan, H. et al. “BindsNET: A machine learning-oriented spiking neural networks library in python,”. Front Neuroinform 12, 89 (2018).
228. M. Y. Lin et al., “DL-RSIM: A simulation framework to enable reliable ReRAM-based accelerators for deep learning,” IEEE/ACM International Conference on Computer-Aided Design, Digest of Technical Papers, ICCAD, https://doi.org/10.1145/3240765. 3240800.2018,
229. Sun, X. & Yu, S. “Impact of non-ideal characteristics of resistive synaptic devices on implementing convolutional neural networks,”. IEEE J. Emerg. Sel. Top. Circuits Syst. 9, 570-579 (2019).
230. Ma, X. et al., “Tiny but Accurate: A Pruned, Quantized and Optimized Memristor Crossbar Framework for Ultra Efficient DNN Implementation,” Proceedings of the Asia and South Pacific Design Automation Conference, ASP-DAC, 2020-Janua, 301-306, https:// doi.org/10.1109/ASP-DAC47756.2020.9045658.2020,
231. Yuan, G. et al., “An Ultra-Efficient Memristor-Based DNN Framework with Structured Weight Pruning and Quantization Using ADMM,” Proceedings of the International Symposium on Low Power Electronics and Design, 2019, https://doi.org/10.1109/ ISLPED.2019.8824944.2019.
232. Rasch, M. J. et al., “A flexible and fast PyTorch toolkit for simulating training and inference on analog crossbar arrays,” 2021 IEEE 3rd International Conference on Artificial Intelligence Circuits and Systems, AICAS 2021, https://doi.org/10. 48550/arxiv.2104.02184.2021,
233. Grötker, T., “System design with SystemC,” 217, 2002.
234. Gajski, D. D. “SpecC: specification language and methodology,” 313, 2000.
235. Lee, M. K. F. et al. “A system-level simulator for RRAM-based neuromorphic computing chips,”. ACM Trans. Archit. Code Optim. (TACO) 15, 4 (2019).
236. BanaGozar, A. et al. “System simulation of memristor based computation in memory platforms,”. Lect. Notes Comput. Sci. (Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinforma.) 12471, 152-168 (2020).
237. Gai, L. and Gajski, D. “Transaction level modeling: an overview,” Hardware/Software Codesign – Proceedings of the International Workshop, 19-24, https://doi.org/10.1109/CODESS.2003. 1275250.2003,
238. Poremba, M. and Xie, Y. “NVMain: An architectural-level main memory simulator for emerging non-volatile memories,” Proceedings – 2012 IEEE Computer Society Annual Symposium on VLSI, ISVLSI 2012, 392-397, https://doi.org/10.1109/ISVLSI.2012.82.2012,
239. Poremba, M., Zhang, T. & Xie, Y. “NVMain 2.0: A user-friendly memory simulator to model (non-)volatile memory systems,”. IEEE Comput. Archit. Lett. 14, 140-143 (2015).
240. Xia, L. et al. “MNSIM: Simulation platform for memristor-based neuromorphic computing system,”. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 37, 1009-1022 (2018).
241. Zhu, Z. et al., “MNSIM 2.0: A behavior-level modeling tool for memristor-based neuromorphic computing systems,” in Proceedings of the ACM Great Lakes Symposium on VLSI, GLSVLSI, Association for Computing Machinery, 83-88. https://doi.org/10. 1145/3386263.3407647.2020,
242. Banagozar, A. et al., “CIM-SIM: Computation in Memory SIMulator,” in Proceedings of the 22nd International Workshop on Software and Compilers for Embedded Systems, SCOPES 2019, Association for Computing Machinery, Inc, 1-4. https://doi.org/10. 1145/3323439.3323989.2019,
243. Fei, X., Zhang, Y. & Zheng, W. “XB-SIM: A simulation framework for modeling and exploration of ReRAM-based CNN acceleration design,”. Tsinghua Sci. Technol. 26, 322-334 (2021).
244. Zahedi, M. et al. “MNEMOSENE: Tile architecture and simulator for memristor-based computation-in-memory,”. ACM J. Emerg. Technol. Comput. Syst. 18, 1-24 (2022).
245. Dong, X., Xu, C., Xie, Y. & Jouppi, N. P. “NVSim: A circuit-level performance, energy, and area model for emerging nonvolatile memory,”. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 31, 994-1007 (2012).
246. Song, L., Qian, X., Li, H. and Chen, Y. “PipeLayer: A Pipelined ReRAM-based accelerator for deep learning,” Proceedings –
247. Imani, M. et al., “RAPIDNN: In-Memory Deep Neural Network Acceleration Framework,” 2018.
248. Chen, A. “A comprehensive crossbar array model with solutions for line resistance and nonlinear device characteristics,”. IEEE Trans. Electron Devices 60, 1318-1326 (2013).
249. Aguirre, F. L. et al., “Line resistance impact in memristor-based multi layer perceptron for pattern recognition,” in 2021 IEEE 12th Latin American Symposium on Circuits and Systems, LASCAS 2021, Institute of Electrical and Electronics Engineers Inc., Feb. https://doi.org/10.1109/LASCAS51355.2021.9667132.2021.
250. Aguirre, F. L. et al. “Minimization of the line resistance impact on memdiode-based simulations of multilayer perceptron arrays applied to pattern recognition,”. J. Low. Power Electron. Appl. 11, 9 (2021).
251. Lee, Y. K. et al. “Matrix mapping on crossbar memory arrays with resistive interconnects and its use in in-memory compression of biosignals,”. Micromachines 10, 306 (2019).
252. Fei, W., Yu, H., Zhang, W. & Yeo, K. S. “Design exploration of hybrid CMOS and memristor circuit by new modified nodal analysis,”. IEEE Trans. Very Large Scale Integr. VLSI Syst. 20, 1012-1025 (2012).
253. Aguirre, F. L., Pazos, S. M., Palumbo, F., Suñé, J. & Miranda, E. “Application of the quasi-static memdiode model in cross-point arrays for large dataset pattern recognition,”. IEEE Access 8, 1-1 (2020).
254. Aguirre, F. L., Pazos, S. M., Palumbo, F., Suñé, J. & Miranda, E. “SPICE simulation of RRAM-based crosspoint arrays using the dynamic memdiode model,”. Front Phys. 9, 548 (2021).
255. Aguirre, F. L. et al. “Assessment and improvement of the pattern recognition performance of memdiode-based cross-point arrays with randomly distributed stuck-at-faults,”. Electron. 10, 2427 (2021).
256. Fritscher, M., Knodtel, J., Reichenbach, M. and Fey, D. “Simulating memristive systems in mixed-signal mode using commercial design tools,” 2019 26th IEEE International Conference on Electronics, Circuits and Systems, ICECS 2019, 225-228, https://doi. org/10.1109/ICECS46596.2019.8964856.2019,
257. Applied Materials, “Ginestra
258. “TCAD – Technology Computer Aided Design (TCAD) | Synopsys.” Accessed: Jan. 20, 2023. [Online]. Available: https://www. synopsys.com/silicon/tcad.html
259. Krestinskaya, O., Salama, K. N. & James, A. P. “Automating analogue AI chip design with genetic search,”. Adv. Intell. Syst. 2, 2000075 (2020).
260. Krestinskaya, O., Salama, K. and James, A. P. “Towards hardware optimal neural network selection with multi-objective genetic search,” Proceedings – IEEE International Symposium on Circuits and Systems, 2020, 2020, https://doi.org/10.1109/ISCAS45731. 2020.9180514/VIDEO.
261. Guan, Z. et al., “A hardware-aware neural architecture search pareto front exploration for in-memory computing,” in 2022 IEEE 16th International Conference on Solid-State & Integrated Circuit Technology (ICSICT), IEEE, 1-4. https://doi.org/10.1109/ ICSICT55466.2022.9963263.2022,
262. Li, G., Mandal, S. K., Ogras, U. Y. and Marculescu, R. “FLASH: Fast neural architecture search with hardware optimization,” ACM Trans. Embed. Compu. Syst., 20, https://doi.org/10.1145/ 3476994.2021,
263. Yuan, Z. et al. “NAS4RRAM: neural network architecture search for inference on RRAM-based accelerators,”. Sci. China Inf. Sci. 64, 160407 (2021).
264. Yan, Z., Juan, D.-C., Hu, X. S. and Shi, Y. “Uncertainty modeling of emerging device based computing-in-memory neural accelerators with application to neural architecture search,” in Proceedings of the 26th Asia and South Pacific Design Automation Conference, New York, NY, USA: ACM, 859-864. https://doi.org/ 10.1145/3394885.3431635.2021,
265. Sun H. et al., “Gibbon: Efficient co-exploration of NN model and processing-in-memory architecture,” in 2022 Design, Automation & Test in Europe Conference & Exhibition (DATE), IEEE, 867-872. https://doi.org/10.23919/DATE54114.2022. 9774605.2022,
266. Jiang, W. et al. Device-circuit-architecture co-exploration for computing-in-memory neural accelerators. IEEE Trans. Comput. 70, 595-605 (2021).
267. Burr, G. W. et al. Experimental demonstration and tolerancing of a large-scale neural network (165 000 Synapses) using phasechange memory as the synaptic weight element. IEEE Trans. Electron Devices 62, 3498-3507 (2015).
268. Dong, Z. et al. “Convolutional neural networks based on RRAM devices for image recognition and online learning tasks,”. IEEE Trans. Electron. Dev. 66, 793-801 (2019).
269. Querlioz, D., Bichler, O., Dollfus, P. & Gamrat, C. “Immunity to device variations in a spiking neural network with memristive nanodevices,”. IEEE Trans. Nanotechnol. 12, 288-295 (2013).
270. Guan, X., Yu, S. & Wong, H. S. P. “A SPICE compact model of metal oxide resistive switching memory with variations,”. IEEE Electron. Device Lett. 33, 1405-1407 (2012).
271. Liang, J., Yeh, S., Simon Wong, S. & Philip Wong, H. S. “Effect of wordline/bitline scaling on the performance, energy consumption, and reliability of cross-point memory array,”. ACM J. Emerg. Technol. Comput. Syst. 9, 1-14 (2013).
272. Hirtzlin, T. et al. “Digital biologically plausible implementation of binarized neural networks with differential hafnium oxide resistive memory arrays,”. Front Neurosci. 13, 1383 (2020).
273. Xue, C. X. et al., “A 1Mb Multibit ReRAM computing-in-memory macro with 14.6 ns Parallel MAC computing time for CNN based AI Edge processors,” Dig Tech Pap IEEE Int Solid State Circuits Conf, 2019-February, 388-390, https://doi.org/10.1109/ISSCC.2019. 8662395.2019,
274. Wu, T. F. et al., “A 43pJ/Cycle Non-Volatile Microcontroller with 4.7
275. Liu, Q. et al., “A Fully Integrated Analog ReRAM based 78.4TOPS/ W compute-in-memory chip with fully parallel MAC computing,” Dig. Tech. Pap. IEEE Int. Solid State Circuits Conf, 2020-February, 500-502, https://doi.org/10.1109/ISSCC19947.2020. 9062953.2020,
276. Xiao, T. P., Bennett, C. H., Feinberg, B., Agarwal, S. and Marinella, M. J. “Analog architectures for neural network acceleration based on non-volatile memory,” Applied Physics Reviews, 7, American Institute of Physics Inc., https://doi.org/10.1063/1. 5143815.2020.
277. “NVIDIA Data Center Deep Learning Product Performance | NVIDIA Developer.” Accessed: Nov. 28, 2022. [Online]. Available: https:// developer.nvidia.com/deep-learning-performance-traininginference
278. Habana L., “Goya
279. Chen Y. et al., “DaDianNao: A Machine-Learning Supercomputer,” Proceedings of the Annual International Symposium on Microarchitecture, MICRO, 2015-January, no. January, 609-622, https:// doi.org/10.1109/MICRO.2014.58.2015,
280. Lee, J. et al. “UNPU: An energy-efficient deep neural network accelerator with fully variable weight bit precision,”. IEEE J. SolidState Circuits 54, 173-185 (2019).
281. Bankman, D., Yang, L., Moons, B., Verhelst, M. & Murmann, B. “An always-on
282. Nag, A. et al. “Newton: Gravitating towards the physical limits of crossbar acceleration,”. IEEE Micro 38, 41-49 (2018).
283. Bojnordi M. N. and Ipek, E. “Memristive Boltzmann machine: A hardware accelerator for combinatorial optimization and deep learning,” Proceedings – International Symposium on HighPerformance Computer Architecture, 2016-April, 1-13, https://doi. org/10.1109/HPCA.2016.7446049.2016,
284. Jain, S. et al. “A heterogeneous and programmable compute-inmemory accelerator architecture for analog-AI using dense 2-D Mesh,”. IEEE Trans. Very Large Scale Integr. VLSI Syst. 31, 114-127 (2023).
285. Carnevale N. T. and Hines, M. L. “The NEURON book,” The NEURON Book, 1-457, https://doi.org/10.1017/ CBO9780511541612.2006,
286. Lammie, C., Xiang, W., Linares-Barranco, B. and Azghadi, M. R. “MemTorch: An Open-source Simulation Framework for Memristive Deep Learning Systems,” 1-14, 2020.
287. Xiao, T. P., Bennett, C. H., Feinberg, B., Marinella, M. J. and Agarwal, S. “CrossSim: accuracy simulation of analog in-memory computing,” https://github.com/sandialabs/cross-sim. Accessed: Sep. 06, 2022. [Online]. Available: https://github.com/ sandialabs/cross-sim
288. Mehonic, A., Joksas, D., Ng, W. H., Buckwell, M. & Kenyon, A. J. “Simulation of inference accuracy using realistic rram devices,”. Front. Neurosci. 13, 1-15 (2019).
289. Zhang, Q. et al. “Sign backpropagation: An on-chip learning algorithm for analog RRAM neuromorphic computing systems,”. Neural Netw. 108, 217-223 (2018).
290. Yamaoka, M. “Low-power SRAM,” in Green Computing with Emerging Memory: Low-Power Computation for Social Innovation, 9781461408123, Springer New York, 59-85. https://doi.org/10. 1007/978-1-4614-0812-3_4/TABLES/4.2013,
291. Starzyk, J. A. and Jan, Y. W. “Voltage based winner takes all circuit for analog neural networks,” Midwest Symposium on Circuits and Systems, 1, 501-504, https://doi.org/10.1109/mwscas.1996. 594211, 1996
الشكر والتقدير
مساهمات المؤلفين
المصالح المتنافسة
معلومات إضافية
المواد التكميلية المتاحة على
https://doi.org/10.1038/s41467-024-45670-9.
يجب توجيه المراسلات وطلبات المواد إلى ماريو لانزا.
http://www.nature.com/reprints
ملاحظة الناشر تظل Springer Nature محايدة فيما يتعلق بالمطالبات القضائية في الخرائط المنشورة والانتماءات المؤسسية.
© المؤلفون 2024
- البريد الإلكتروني: mario.lanza@kaust.edu.sa
DOI: https://doi.org/10.1038/s41467-024-45670-9
PMID: https://pubmed.ncbi.nlm.nih.gov/38438350
Publication Date: 2024-03-04
Hardware implementation of memristorbased artificial neural networks
Accepted: 1 February 2024
Published online: 04 March 2024
(D) Check for updates
Abstract
Fernando Aguirre
Abstract
Artificial Intelligence (AI) is currently experiencing a bloom driven by deep learning (DL) techniques, which rely on networks of connected simple computing units operating in parallel. The low communication bandwidth between memory and processing units in conventional von Neumann machines does not support the requirements of emerging applications that rely extensively on large sets of data. More recent computing paradigms, such as high parallelization and near-memory computing, help alleviate the data communication bottleneck to some extent, but paradigm- shifting concepts are required. Memristors, a novel beyond-complementary metal-oxide-semiconductor (CMOS) technology, are a promising choice for memory devices due to their unique intrinsic device-level properties, enabling both storing and computing with a small, massively-parallel footprint at low power. Theoretically, this directly translates to a major boost in energy efficiency and computational throughput, but various practical challenges remain. In this work we review the latest efforts for achieving hardware-based memristive artificial neural networks (ANNs), describing with detail the working principia of each block and the different design alternatives with their own advantages and disadvantages, as well as the tools required for accurate estimation of performance metrics. Ultimately, we aim to provide a comprehensive protocol of the materials and methods involved in memristive neural networks to those aiming to start working in this field and the experts looking for a holistic approach.
national security, etc.)
control in smartphones
using graphics processing units (GPUs) to implement the ANNs (see Fig. 1a), as these can perform multiple operations in parallel

application domains
circuits can be grouped in two categories. On one hand, dataflow processors are custom-designed processors for neural network inference and training. Since neural network training and inference computations can be entirely deterministically laid out, they are amenable to dataflow processing in which computations, memory accesses, and inter-ALU communications actions are explicitly/statically programmed or placed-and-routed onto the computational hardware. On the other hand, processor in memory (PIM) accelerators integrate processing elements with memory technology. Among such PIM accelerators are those based on an analogue computing technology that augments flash memory circuits with in-place analogue multiply-add capabilities. Please refer to the references for the Mythic
accuracy of an ANN via software
Structure of memristor-based ANNs

under ex-situ training is shown by the yellow arrows/lines. For each box, the upper (colored) part indicates the name of the function to realize by the circuital block, and the bottom part indicates the type of hardware required. The box titled successive neural layers would encompass multiple sub-blocks with a structure similar to the group titled First neural layer. 1S1R stands for 1Selector 1 Resistor while 1R stands for 1 Resistor. UART, SPI and
storage node is sufficiently high for long-term data retention. Also, flash-based VMM operates in a slightly different manner than SRAMbased VMM. In Flash-based VMM, each memory element contribute a different amount to the current in each column of the crossbar depending on the voltage applied to the input or crossbar row and matrix element are stored as charge on the floating gate
memristor ( 1 R or 1 M ) structures or passive crossbar (Fig. 3c). When using crossbar arrays of memristors to perform VMM operations, additional circuitry might be needed at the input and output to sense and/or convert electrical signals (see red boxes in Fig. 2). Examples of such circuits are digital-to-analogue (DAC), analogue-to-digital (ADC) converters and transimpedance amplifiers (TIA). Note that other studies employed implementations slightly different from this scheme, i.e., combining or avoiding certain blocks to save area and/or reduce power consumption (see Table 1).
Image capture hardware (block 1) and input vector conformation (block 3)

- Multi-level storage is possible by more complex SRAM cells (larger cell area)
** Analogue synaptic weight is desired but usually only a finite number of stable levels is available
with plenty of room for optimization.
section. Both cases consider an FPGA in order interface the image acquisition system (i.e. CMOS image sensor and the resizing algorithm) with the memristor crossbar and its peripheral circuitry. On the other hand, some studies exclusively focused on the memristor crossbar use an on-chip communication interface to acquire the image from a computer (e.g. ref. 54 uses a serial communication port) already shaped in the required input format.
point, since this simple dataset can be classified with even small neural networks. For benchmarking a device or a chip, it is essential to evaluate the accuracy of standard deep neural network models like
| Work(s) | Device | NN Type/ Dataset | Crossbar size | CMOS Node | ADC | Cell Structure | Input circuit (DAC) | Sensing Electronics | Activation function | Row/Col. Selectors | Softmax Activation Func. | Inference/ training | Weight Prog. circuitry |
| 57 |
|
SLP, Sparse coding, MLP/ Greek letters |
|
180 nm | On-chip (13-bit) | 1R | On-chip (6-bit) | Charge integration | On-chip digital (Sigmoid) | On-chip | Off-chip (Software) | Inference & training | On-chip |
| 55 | TiN/TaOx/ HfOx /TiN | CNN/MNIST |
|
130 nm | Off-chip (8-bit) | TT1R | On-chip (1-bit) | Charge integration | Off-chip (software: ReLU and max. Pooling) | On-chip | Off-chip (Software) | Inference & training | Off-chip |
| 102 | Pt/Ta/Ta2O5/ Pt/Ti | MLP/MNIST |
|
|
N/A | TT1R | N/A | N/A | Off-chip hardware: ReLU) | Off-chip | Off-chip (Software) | Learning & training | Off-chip |
| 61 | No data (propietary dev.) | BNN, MNIST, CIFAR-10 |
|
90 nm | On-chip (3-bit) | 1T1R | Not implemented | On-chip (VSA) | On-chip (Binary) | On-chip | Off-chip (software)* | Inference only | Off-chip |
| 113 | Ta/TaOx/Pt | CNN/MNIST |
|
180 nm | On-chip | TT1R | On-chip | On-chip (TIA) | Off-chip (software)* | On-chip | Off-chip (software)* | Inference only | Off-chip |
| 114,115 | TaOx | CNN/MNIST |
|
180 nm | On-chip (10-bit) | TT1R | On-chip | On-chip (TIA) | Off-chip (software)* | On-chip | Off-chip (software)* | Inference only | Off-chip |
| 219, | W/TiN/TiON | BNN/MNIST |
|
65 nm | On-chip (3-bit) | 1T1R | N/A | On-chip (CSA) | Off-chip (FPGA: max. Pooling) | On-chip | Off-chip (FPGA) | Inference only | Off-chip |
| 116 |
|
CNN/ ‘ U ‘, ‘ M , ‘
|
|
No data | Off-chip | 1T1R | On-chip | Off-chip (TIA) | On-chip (ReLU), Offchip (software: max. Pooling) | Off-chip | Off-chip (MCU) | Inference & training | Off-chip |
| 272 | TiN/HfO2/Ti/TiN | BNN/MNIST, CIFAR-10 | 1 Kb | 130 nm | On-chip | 2T2R | Not implemented | Onchip (PCSA) | On-chip (Binary) | On-chip | On-chip (Binary) | Inference only | Off-chip |
| 99 |
|
MLP/MNIST | 2 Mb | 180 nm | On-chip (1-bit) | 1T1R | On-chip (1-bit) | On-chip | No data | On-chip | No data | Inference only | Off-chip |
| 100 | AlCu/TiN/Ti/
|
MLP/ |
|
150 nm | On-chip (1 or 3-bit) | 1T1R | On-chip (1-bit) | On-chip | Off-chip (software)* | On-chip | Off-chip (software)* | Inference only | Onchip (SRAM) |
| 122 | PCM (no more data) | MLP/MNIST |
|
180 nm | No data | 3T1C + 2PCM | No data | Off-chip (software) | Off-chip (Software: ReLU) | Off-chip | Off-chip (Software) | Inference only | Off-chip |
| 71,73 | PCM (no more data) | MLP/MNIST, ResNET-9/ CIFAR-10 |
|
14 nm | On-chip | 4T4R | On-chip (8-bit) | On-chip (CCO-based) | On-chip (ReLU) | On-chip | Off-chip (Software) | Inference only | On-chip |
| 72, | PCM (no more data) | MLP/MNIST |
|
14 nm | Off-chip | 4T4R | On-chip (8-bit) | On-chip | Off-chip (Sigmoid) | On-chip | Off-chip (FPGA) | Inference only | On-chip |
| 273 | No data | CNN/ CIFAR-10 |
|
55 nm | On-chip | TT1R | No data | On-chip | Off-chip (FPGA) | On-chip | Off-chip (FPGA) | Inference only | Off-chip |
| 274 | TiN/HfO2/Ti/TiN | CNN/MNIST | 18 kB | 130 nm | Offchip* | TT1R | Off-chip* | Off-chip* | Off-chip (FPGA) | Off-chip* | Off-chip (FPGA) | Inference only | On-chip |
| 123 | TiN/HfO2/Ti/TiN | BNN/MNIST | 1 Kb | 130 nm | N/A | 2T2R | N/A | On-chip | Off-chip (software)* | On-chip | Off-chip (software)* | Inference only | Off-chip |
| 275 |
|
MLP/MNIST | 158.8 Kb | 130 nm | On-chip (8-bit) | 2T2R | On-chip (8-bit) | Charge integration | Off-chip | On-chip | Off-chip | Inference only | Offchip (FPGA) |
| 60 |
|
CNN/MNIST, CIFAR-10 |
|
130 nm | On-chip (8-bit) | 1T1R | On-chip | Charge integration | On-chip (analog: ReLU), Off-chip (FPGA: max. Pooling) | On-chip | Off-chip (FPGA) | Off-chip (Software) | On-chip |

concatenated to render a
with
Input driving circuits (Block 4)

capacitance,
VMM core (Block 5)
each memristor (

conductance levels of the crossbar, making it less susceptible to noise and variability
to bitline
Sensing electronics (Block 6)
Activation function (Block 7)

below the nano-ampere regime, charge integration is the most suitable option for current-voltage conversion. This can be achieved by using a capacitor. As such, the measurement is not instantaneous as a constant, controllable integration time is required before the measurement. d To minimize the area requirements of the integration capacitor, the use of a current divider allows to further reduce the current and, with it, the size of the required capacitor. The tradeoff in this case is with precision (mainly due to transistor mismatch) and output voltage dynamic range.
outputs, amplified. It must be noted, that although not necessary in the case of neural networks implemented in the software domain, in the case of neural networks based on memristor-VMM cores, the elements of the input vectors to each neural layer must be within a range of analogue voltages. For this reason, ReLU activation functions, which are by definition unbounded activation functions
based implementations of activation functions integrated into the same chip as a crossbar cannot be changed once the circuit is fabricated. Such activation functions can be implemented in both digital and analogue domains. Digital domain processing leads to the ADC overhead (same as for software-based implementations) but is less affected by the noise and transistor mismatches. Digital domain implementation of a ReLU activation integrated into the sensing circuit is shown in

configuration.

SoftArgMax function (Block 8)
current). This block (often named SoftArgMax function or SoftArgMax activation function) with as many inputs as bitlines has the memristor crossbar, basically implements Eq. 10:

function. a WTA CMOS block with voltage input
outputs. This behaviour is achieved by combining two functions, the
value in the vector (the summatory of the probabilities of all elements is equal to 1 ). Note that the
Analogue to digital converters (Block 9)
(limits the available silicon area to be destined to synaptic weights, that is the 1T1R structures, which thus affects cost).
crossbar tile
ANN training and synaptic weight update (Blocks 2, 11-15)

synaptic weights must be adjusted to values that minimize the loss function. To achieve this goal two families of algorithms could be employed: gradient-free and gradient-based algorithms (as shown in Fig. 12a). Gradient-free methods such as the Particle Swarm optimization

propose an organization of the algorithms for (i) gradient computation, (ii) optimization and (iii) learning rate.
function, which describes the error of the output (against the labels) for a small network with only two inputs and one output (and thereby 2 synaptic weights, as presented in Fig. 12b), that is

paragraph’s explanation) and its variants (Gradient Descent with Momentum
cross validation) in which a small number of training images and the accuracy depending on the training algorithm is recorded. As an example, Supplementary Algorithm 2 shows the detailed MATLAB code used for this k-fold cross validation using 100 images. The small number of training images is partitioned into
| Metric | Expression | Meaning | Applicability | Examples | ||
| Accuracy |
|
The ratio of correctly classified patterns respect to the total number of patterns | To quantify the performance of the ANN | N/A | ||
| Sensitivity (also called recall) |
|
Ratio between how much were correctly identified as positive to how much were actually positive | Places where classification of positives are high priority | Security checks in airports | ||
| Specificity |
|
Ratio between how much were correctly classified as negative to how much was actually negative | Places where classification of negatives are high priority | Diagnosing for a health condition before treatment | ||
| Precision |
|
How much were correctly classified as positive out of all positives | N/A | How many of those who we labeled as diabetic are actually diabetic? | ||
| F1-score |
|
It is a measure of performance of the model’s classification ability | N/A | F1 score is considered a better indicator of the classifier’s performance than the regular accuracy measure | ||
| K-coefficient |
|
It shows the ratio between the Network accuracy and the random accuracy (in this case, with 10 output classes, the random accuracy would be 10%) | N/A | N/A | ||
| Cross-Entropy |
|
Difference between the predicted value by the ANN and the true value | N/A | N/A |

in situ training, the usual practice reported in the literature for this kind of training has been the use of the so-called Manhattan Update Rule
Fabrication/integration of the ANN chip
the input signal increases, so does it the complexity of the DAC circuit (and with it, its power consumption and area). The most common approach in this contest is the use of an Off-the-shelf, external DAC to drive the analogue inputs
Simulation of memristive ANNs
Neural Network level simulation
| Exp./Sim | Type | Process (nm) | Activation resolution | Weight resolution | Clock speed | Benchmarked workload | Weight storage |
|
|
Array size | ADC type | Throughput (TOPS) | Density (TOPS per
|
Efficiency (TOPS per W) | |
| NVIDIA T4
|
Exp. | FullCMOS | 12 | 8-bit int | 8-bit int | 2.6 GHz | ResNet-50 (batch = 128) | — | — | — | — | — | 22.2, 130 (peak) | 0.04, 0.24 (peak) | 0.32 |
| Google TPU v1
|
Exp. | FullCMOS | 28 | 8-bit int | 8-bit int | 700 MHz | MLPs, LSTMs, CNNs | — | — | — | — | — | 21.4, 92 (peak) | 0.06, 0.28 (peak) | 2.3 (peak) |
| Habana Goya HL
|
Exp. | FullCMOS | 16 | 16-bit int | 16-bit int | 2.1 GHz (CPU) | ResNet-50 (batch = 10) | — | — | — | — | — | 63.1 | — | 0.61 |
| DaDianNao
|
Sim. | FullCMOS | 28 | 16-bit fixed-pt. | 16-bit fixed-pt. | 606 MHz | Peak performance | — | — | — | — | — | 5.58 | 0.08 | 0.35 |
| UNPU
|
Exp. | FullCMOS | 65 | 16 bits | 1 bit | 200 MHz | Peak performance | — | — | — | — | — | 7.37 | 0.46 | 50.6 |
| Reference mixed-signal
|
Exp. | FullCMOS | 28 | 1 bit | 1 bit | 10 MHz | Binary CNN (CIFAR-10) | — | — | — | — | — | 0.478 | 0.1 | 532 |
| ISAAC
|
Exp. | RRAMCMOS | 32 | 16 bits | 16 bits | 1.2 GHz | Peak performance | ReRAM (
|
|
|
|
SAR (8-bit) | 41.3 | 0.48 | 0.63 |
| Newton
|
Exp. | RRAMCMOS | 32 | 16 bits | 16 bits | 1.2 GHz | Peak performance | ReRAM (
|
|
|
|
SAR (8-bit) | — | 0.68 | 0.92 |
| PUMA
|
Exp. | RRAMCMOS | 32 | 16 bits | 16 bits | 1.0 GHz | Peak performance | ReRAM (
|
1 M | 100k |
|
SAR | 26.2 | 0.29 | 0.42 |
| PRIME
|
Sim. | RRAMCMOS | 65 | 6 bits | 8 bits | 3.0 GHz (CPU) | — | ReRAM | 20 k | 1 k |
|
Ramp (6-bit) | — | — | — |
| Memristive Boltzmann machine
|
Sim. | RRAMCMOS | 22 | 32 bits | 32 bits | 3.2 GHz (CPU) | — | ReRAM | 1.1 G | 315 k |
|
SAR | — | — | — |
| 3D-aCortex
|
Exp. | RRAMCMOS | 55 | 4 bits | 4 bits | 1.0 GHz | GNMT | NAND flash | — | 2.3 M |
|
Temporal to digital (4-bit) | 10.7 | 0.58 | 70.4 |
| Analog-AI Using Dense 2-D Mesh
|
Sim | RRAMCMOS | 14 | 8 bits | Analogue | 1.0 GHz | RNN/LSTM | PCM | No data | No data |
|
Current controlled oscillator based | 376.7 | No data | 65.6 |

vision and natural language processing. Both are Python libraries highly optimized to exploit GPUs and CPUs for deep learning tasks. These simulators allow training and developing complex neural network architectures (e.g., CNNs architectures such as the VGG and AlexNET or Recurrent Neural Networks – RNN). Although extremely popular, these simulators provide no link at all with memristive or CMOS devices, as in both cases the magnitudes involved are nondimensional and the synaptic connections are represented by loosely constrained numerical values.
adopted by Sun et al.
System-level simulation
| Simulation Framework | Year | Platform | Training | Simulation type | Open Source | Type of ANN | Compatible dev. | Energy | Accuracy | Power | Latency | Variability |
|
|
CMOS | GPU |
| Tensorflow
|
2015 | Python | Yes | Neural network | Yes | MLP, CNN | No dev. | No | Yes | No | No | Yes | No | No | No | Yes |
| Pytorch
|
2017 | Python | Yes | Neural network | Yes | MLP, CNN | No dev. | No | Yes | No | No | Yes | No | No | No | Yes |
| NEURON
|
2006 | Python | Yes | Neural network | Yes | SNN | No dev. | No | Yes | No | No | Yes | No | No | No | Yes |
| Brian2
|
2019 | Python | Yes | Neural network | Yes | SNN | No dev. | No | Yes | No | No | Yes | No | No | No | Yes |
| NEST
|
2007 | Python | Yes | Neural network | Yes | SNN | No dev. | No | Yes | No | No | Yes | No | No | No | Yes |
| BindsNET
|
2018 | Python | Yes | Neural network | Yes | SNN | No dev. | No | Yes | No | No | Yes | No | No | No | Yes |
| Memtorch
|
2020 | Python, C++, CUDA | No | Neurla network | Yes | CNN | RRAM | No | Yes | No | No | Yes | No | No | No | Yes |
| NVMain
|
2015 | C++ | No | Architecture | Yes | Memory | RRAM | Yes | No | Yes | Yes | No | No | No | No | No |
| PUMA
|
2019 | C++ | No | Architecture | No | MLP, CNN | RRAM | Yes | Yes | Yes | Yes | No | No | No | Yes | Yes |
| RAPIDNN
|
2018 | C++ | No | Architecture | No | MLP, CNN | RRAM | Yes | Yes | Yes | Yes | Yes | No | No | Yes | No |
| DL-RSIM
|
2018 | Python | No | Architecture | No | MLP, CNN | RRAM | No | Yes | No | No | Yes | No | No | No | Yes |
| PipeLayer
|
2017 | C++ | Yes | Architecture | No | CNN | RRAM | Yes | Yes | Yes | No | No | No | No | No | |
| Tiny but Accurate
|
2019 | MATLAB | No | Architecture | Yes | CNN, ResNET | RRAM | Yes | Yes | Yes | No | No | No | No | No | No |
| Yuan et al.
|
2019 | C++, MATLAB | Yes | Architecture | Yes | No data | RRAM | No | Yes | Yes | No | No | No | No | No | Yes |
| Sun et al.
|
2019 | Python | Yes | Architecture | No | MLP | PCM, STT-RAM, ReRAM, SRAM, FeFET | Yes | Yes | Yes | No | Yes | No | No | No | No |
| A. Chen
|
2013 | MATLAB | No | Circuit | Yes | MLP | RRAM | No | No | Yes | No | Yes | Yes | No | No | No |
| CIM-SIM
|
2019 | SystemC (C++) | No | Architecture | Yes | SLP | RRAM | No | No | No | No | No | No | No | No | No |
| MNSIM
|
2018 | Python | No | Architecture | Yes | CNN | RRAM | Yes | No | Yes | Yes | Yes | No | No | No | Yes |
| NVSIM
|
2012 | C++ | No | Circuital | Yes | Memory | PCM, STT-RAM, ReRAM, Flash | Yes | No | Yes | Yes | No | No | No | No | No |
| CrossSIM
|
2017 | Python | No data | Circuital | Yes | No data | PCM, ReRAM, Flash | No | Yes | No | No | Yes | Yes | No | No | Yes |
| NeuroSIM
|
2022 | Python, C++ | Yes | Circuital | Yes | MLP, CNN | PCM, STT-RAM, ReRAM, SRAM, FeFET | Yes | Yes | Yes | No | Yes | No | No | No | Yes |
| NVM-SPICE
|
2012 | Not specified | No | Circuital | No | SLP | RRAM | Yes | No | Yes | Yes | Yes | No | No | Yes | No |
| IBM Analog Hardware Acceleration Kit
|
2021 | Python, C++, CUDA | Yes | Neural network | Yes | MLP, CNN, LSTM | PCM | No | Yes | No | No | Yes | No | No | No | Yes |
| Fritscher et al.
|
2019 | Mixed (VHDL, Verilog, SPICE) | No | Circuital | No | MLP | PCM, STT-RAM, ReRAM, SRAM, FeFET | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Aguirre et al.
|
2020 | Mixed (Python, MATLAB, SPICE) | No | Circuital | No | MLP | PCM, STT-RAM, ReRAM, SRAM, FeFET | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |

memory crossbar, analogue/digital converters, digital input modulators and sample and hold stages. Furthermore, each tile has a dedicated controller orchestrating the components responsible for driving the computation.
Architecture-level simulation
Circuit level simulation
non-volatile memories like STT-RAM, PCRAM and ReRAM structures. This allows: i) estimation of access time, access energy and silicon area, ii) Design-Space exploration, and iii) optimization of the chip for one specific design metric. However, and similarly to NVMain
Software-hardware co-design and hardware-aware neural architecture search
memristor-related non-idealities can be mitigated by optimizing the software-related design parameters for the neural network
Example of memristive ANN analysis
Translation of the synaptic weights from the Software based ANN to conductance values
| Neural Network type | Learning algorithm | Database | Size | Training | Accuracy | Platform | Ref. | |
| (Sim.) | (Exp.) | |||||||
| Single-Layer Perceptron (SLP) | Backpropagation (Scaled Conjugate Gradient) | MNIST (
|
1 layer (
|
Ex-situ | ~91% | SPICE sim. QMM model | 253 | |
| Manhattan update rule | Custom pattern | 1 layer (
|
In-situ | ND | Exp.(
|
105 | ||
| Yale-Face | 1 layer (
|
In-situ |
|
Exp. (
|
194 | |||
| Multi-Layer Perceptron (MLP) | Backpropagation (Stochastic Gradient Descent) | MNIST (
|
2 layers (
|
In-situ |
|
|
Exp. (
|
54 |
| Backpropagation (Scaled Conjugate Gradient) | MNIST (
|
k layers (
|
Ex-situ |
|
SPICE sim. QMM model | 253 | ||
| Backpropagation | MNIST (14
|
2 layers (
|
Ex-situ | ~92% | ~82.3% | Software/ Exp. (
|
196 | |
| MNIST (22
|
2 layers (
|
In-situ | ~83% | ~81% | Software/ Exp. (PCM) | 267 | ||
| MNIST (28
|
2 layers (
|
Ex-situ | ~97% | Software (Python) | 288 | |||
| SignBackpropagation | MNIST (
|
2 layer (
|
In-situ | ~94.5% | Software (MATLAB) | 289 | ||
| Convolutional Neural Network (CNN) | Backpropagation | MNIST (
|
2 layer (1st Conv., 2nd FC) | In-situ | ~94% | Software | 268 | |
| Spiking Neural Network SNN) | Spike Timing Dependent Plasticity (Unsupervised) | MNIST (
|
2 layer (
|
In-situ | ~93.5% | Software (C+ + Xnet) | 269 | |
in the Memory Equation that leads to the target conductance. For the case of the Quasi-static Memdiode Model (QMM) considered in refs. 250,253 , this is done by adjusting the control parameter
actually delivered to the memristors). The number of partitions is denoted as NP, and the recommended size of each partition depends on the ratio of conductance between the memristors and the resistance of the metallic wires. Supplementary Fig 10 shows the simplified sketch of the partitioned crossbar and the interconnections required to realize the complete VMM. By exploding the integrability of the crossbar with CMOS circuitry, vertical interconnects used to connect the outputs of the vertical crossbar partitions may be placed under the partitioned structure (as well as the analogue sensing electronics) allowing the partitioned crossbar to maintain a similar area consumption than the original non-partitioned case
Creation of the memristive ANN circuit representation

and the interline capacitances (see the inset showing a circuit schematic of a memristive cell in a CPA structure considering the associated wire parasitic resistance and capacitance). Aspects such as device variability are captured by the memristor model employed.

a Single Side Connect (SSC) and (b) Dual Side Connect (DSC). On the SSC case, the input stimuli are applied only to the inputs of one side of the CPA, while the other is

receives as input arguments the array size and partitioning scheme, and it automatically determines the number of memristors to place and how to connect them to the adjacent line resistances to realize the crossbar electrical structure. Such a source code uses nested for loops that iterate over the number of rows and columns, creating the crossbar structure. Also, the parasitic capacitance between parallel adjacent lines in the same plane (i.e., between adjacent rows and columns), between the top-bottom line intersections, and between the bottom lines and ground are added. By this, we can account for the delay propagation through the crossbar, also known as latency (that is, when the goal is measuring the time elapsed since a pattern is applied in the SLP inputs until the output stabilizes). As a result, each memristor in the crossbar structure is connected to 4 resistors and 5 capacitors, as shown in Fig. 17d. As an example, the resulting SPICE code for a SLP to classify

to enable the memristor addressed by the address block. e Row and column driver, used to bias the rows with the voltage input or with the programming signal, and to connect the columns to the output neurons (during inference) or the sense amplifier (during write-verify).
calculated via MATLAB. This peripheral circuitry consists of a crossbar address block, Row/Column address decoders, Row/Column selectors, and a Write Acknowledge block (see Supplementary Fig. 9c right and Fig. 19a). The crossbar Address Block (crossbar-AB) is a circuit that produces a pulse every time the memristor located in the {i,j} position is completely written in all partitions (thereby working as a counter, as depicted in Fig. 19b), which thereby results in


SPICE Simulation and metrics extraction
or in the memristors), the Signal-to-Noise ratio of the output current signals, the inference latency, the read and write margins (that is, the portion of the voltage applied in the crossbar inputs that effectively reaches the memristors during the read or write operations) and the maximal operational frequency of the complete neuromorphic circuit (crossbar plus CMOS electronics).

communication between them. The selection of the most suitable simulation technique depends thereby in the requirements of the specific design stage: the closer it gets to the tape-out, higher accuracy in the simulation is required (achievable with circuit level simulations), instead, for the early design stages, system-level modelling is enough to get a quick estimation of the achievable performance in large, complex ANNs. In any case, properly combining this many different simulation tools will ultimately lead to the optimization and further development of the memristive ANNs.
Data availability
Code availability
References
- European Commission, Harnessing the economic benefits of Artificial Intelligence. Digital Transformation Monitor, no. November, 8, 2017.
- Rattani, A. Reddy, N. and Derakhshani, R. “Multi-biometric Convolutional Neural Networks for Mobile User Authentication,” 2018 IEEE International Symposium on Technologies for Homeland Security, HST 2018, https://doi.org/10.1109/THS.2018. 85741732018.
- BBVA, Biometrics and machine learning: the accurate, secure way to access your bank Accessed: Jan. 21, 2024. [Online]. Available: https://www.bbva.com/en/biometrics-and-machine-learning-the-accurate-secure-way-to-access-your-bank/
- Amerini, I., Li, C.-T. & Caldelli, R. Social network identification through image classification with CNN. IEEE Access 7, 35264-35273 (2019).
- Ingle P. Y. and Kim, Y. G. “Real-time abnormal object detection for video surveillance in smart cities,” Sensors, 22,https://doi.org/10. 3390/s22103862 2022.
- Tan, X., Qin, T., F. Soong, and T.-Y. Liu, “A survey on neural speech synthesis,” https://doi.org/10.48550/arxiv.2106.15561 2021.
- “ChatGPT: Optimizing language models for dialogue.” Accessed: Feb. 13, 2023. [Online]. Available: https://openai.com/blog/ chatgpt/
- Hong, T., Choi, J. A., Lim, K. & Kim, P. Enhancing personalized ads using interest category classification of SNS users based on deep neural networks. Sens. 2021, Vol. 21, Page 199, 21, 199 (2020).
- McKee, S. A., Reflections on the memory wall in 2004 Computing Frontiers Conference, 162-167. https://doi.org/10.1145/977091. 9771152004.
- Mehonic, A. & Kenyon, A. J. Brain-inspired computing needs a master plan. Nature 604, 255-260 (2022).
- Zhang, C. et al. IMLBench: A machine learning benchmark suite for CPU-GPU integrated architectures. IEEE Trans. Parallel Distrib. Syst. 32, 1740-1752 (2021).
- Li, F., Ye, Y., Tian, Z. & Zhang, X. CPU versus GPU: which can perform matrix computation faster-performance comparison for basic linear algebra subprograms. Neural Comput. Appl. 31, 4353-4365 (2019).
- Farabet, C. Poulet, C., Han, J. Y. and LeCun, Y. CNP: An FPGAbased processor for Convolutional Networks, FPL 09: 19th International Conference on Field Programmable Logic and Applications, 32-37, https://doi.org/10.1109/FPL.2009.5272559 2009.
- Farabet, C. et al., NeuFlow: A runtime reconfigurable dataflow processor for vision, IEEE Computer Society Conference on
15. Zhang, C. et al., Optimizing FPGA-based accelerator design for deep convolutional neural networks, FPGA 2015-2015 ACM/ SIGDA International Symposium on Field-Programmable Gate Arrays, 161-170, https://doi.org/10.1145/2684746.2689060 2015.
16. Chakradhar, S., Sankaradas, M., Jakkula, V. and Cadambi, S. A dynamically configurable coprocessor for convolutional neural networks, Proc. Int. Symp. Comput. Archit., 247-257, https://doi. org/10.1145/1815961.1815993 2010.
17. Wei X. et al., Automated systolic array architecture synthesis for high throughput CNN Inference on FPGAs, Proc. Des. Autom. Conf., Part 128280, https://doi.org/10.1145/3061639. 30622072017.
18. Guo, K. et al., Neural Network Accelerator Comparison. Accessed: Jan. 10, 2023. [Online]. Available: https://nicsefc.ee.tsinghua.edu. cn/projects/neural-network-accelerator.html
19. Jouppi, N. P. et al., In-datacenter performance analysis of a tensor processing unit. Proc. Int. Symp. Comput. Archit., Part F128643, 1-12, https://doi.org/10.1145/3079856.3080246.2017,
20. AI Chip – Amazon Inferentia – AWS. Accessed: May 15, 2023. [Online]. Available: https://aws.amazon.com/machine-learning/ inferentia/
21. Talpes, E. et al. Compute solution for Tesla’s full self-driving computer. IEEE Micro 40, 25-35 (2020).
22. Reuther, A. et al, “AI and ML Accelerator Survey and Trends,” 2022 IEEE High Performance Extreme Computing Conference, HPEC 2022, https://doi.org/10.1109/HPEC55821.2022.9926331.2022,
23. Fick, L., Skrzyniarz, S., Parikh, M., Henry, M. B. and Fick, D. “Analog matrix processor for edge AI real-time video analytics,” Dig. Tech. Pap. IEEE Int. Solid State Circuits Conf, 2022-260-262, https://doi. org/10.1109/ISSCC42614.2022.9731773.2022,
24. “Gyrfalcon Unveils Fourth AI Accelerator Chip – EE Times.” Accessed: May 16, 2023. [Online]. Available: https://www. eetimes.com/gyrfalcon-unveils-fourth-ai-accelerator-chip/
25. Sebastian, A., Le Gallo, M., Khaddam-Aljameh, R. and Eleftheriou, E. “Memory devices and applications for in-memory computing,” Nat. Nanotechnol. 2020 15:7, 15, 529-544, https://doi.org/10. 1038/s41565-020-0655-z.
26. Zheng, N. and Mazumder, P. Learning in energy-efficient neuromorphic computing: algorithm and architecture co-design. WileyIEEE Press, Accessed: May 15, 2023. [Online]. Available: https:// ieeexplore.ieee.org/book/8889858 2020.
27. Orchard, G. et al., “Efficient Neuromorphic Signal Processing with Loihi 2,” IEEE Workshop on Signal Processing Systems, SiPS: Design and Implementation, 2021-October, 254-259, https://doi. org/10.1109/SIPS52927.2021.00053.2021,
28. “Microchips that mimic the human brain could make AI far more energy efficient | Science | AAAS.” Accessed: May 15, 2023. [Online]. Available: https://www.science.org/content/article/ microchips-mimic-human-brain-could-make-ai-far-more-energyefficient
29. Davies, M. et al., “Advancing neuromorphic computing with Loihi: A survey of results and outlook,” Proceedings of the IEEE, 109, 911-934,https://doi.org/10.1109/JPROC.2021.3067593.2021,
30. Barnell, M., Raymond, C., Wilson, M., Isereau, D. and Cicotta, C. “Target classification in synthetic aperture radar and optical imagery using loihi neuromorphic hardware,” in 2020 IEEE High Performance Extreme Computing Conference (HPEC), IEEE, 1-6. https://doi.org/10.1109/HPEC43674.2020.9286246.2020,
31. Viale, A., Marchisio, A., Martina, M., Masera, G., and Shafique, M. “CarSNN: An efficient spiking neural network for event-based autonomous cars on the Loihi Neuromorphic Research Processor,” 2021.
32. “Innatera Unveils Neuromorphic AI Chip to Accelerate Spiking Networks – EE Times.” Accessed: May 15, 2023. [Online]. Available: https://www.eetimes.com/innatera-unveils-neuromorphic-ai-chip-to-accelerate-spiking-networks/
33. Pei, J. et al. “Towards artificial general intelligence with hybrid Tianjic chip architecture,”. Nature 572, 106-111 (2019).
34. Merolla, P. A. et al. “A million spiking-neuron integrated circuit with a scalable communication network and interface,”. Science 345, 668-673 (2014).
35. Adam, G. C., Khiat, A., and Prodromakis, T. “Challenges hindering memristive neuromorphic hardware from going mainstream,” Nat. Commun., 9, Nature Publishing Group, 1-4, https://doi.org/10. 1038/s41467-018-07565-4.2018.
36. Sung, C., Hwang, H. & Yoo, I. K. “Perspective: A review on memristive hardware for neuromorphic computation,”. J. Appl. Phys. 124, 15 (2018).
37. Deng, L. et al. Energy consumption analysis for various memristive networks under different learning strategies,”. Phys. Lett. Sect. A: Gen. At. Solid State Phys. 380, 903-909 (2016).
38. Yu, S., Wu, Y., Jeyasingh, R., Kuzum, D. & Wong, H. S. P. “An electronic synapse device based on metal oxide resistive switching memory for neuromorphic computation,”. IEEE Trans. Electron Dev. 58, 2729-2737 (2011).
39. Shulaker, M. M. et al. “Three-dimensional integration of nanotechnologies for computing and data storage on a single chip,”. Nature 547, 74-78 (2017).
40. Li, C. et al. Three-dimensional crossbar arrays of self-rectifying Si/ SiO2/Si memristors. Nat. Commun. 2017 8:1 8, 1-9 (2017).
41. Yoon, J. H. et al. “Truly electroforming-free and low-energy memristors with preconditioned conductive tunneling paths,”. Adv. Funct. Mater. 27, 1702010 (2017).
42. Choi, B. J. et al. “High-speed and low-energy nitride memristors,”. Adv. Funct. Mater. 26, 5290-5296 (2016).
43. Strukov, D. B., Snider, G. S., Stewart, D. R. and Williams, R. S. “The missing memristor found,” Nature, 453,80-83, https://doi.org/10. 1038/nature06932.
44. “FUJITSU SEMICONDUCTOR MEMORY SOLUTION.” Accessed: Nov. 16, 2022. [Online]. Available: https://www.fujitsu.com/jp/ group/fsm/en/
45. “Everspin | The MRAM Company.” Accessed: Nov. 16, 2022. [Online]. Available: https://www.everspin.com/
46. “Yole Group.” Accessed: Nov. 16, 2022. [Online]. Available: https://www.yolegroup.com/?cn-reloaded=1
47. Stathopoulos, S. et al. “Multibit memory operation of metal-oxide Bi-layer memristors,”. Sci. Rep. 7, 1-7 (2017).
48. Wu, W. et al., “Demonstration of a multi-level
49. Yang, J. et al., “Thousands of conductance levels in memristors monolithically integrated on CMOS,” https://doi.org/10.21203/ RS.3.RS-1939455/V1.2022,
50. Goux, L. et al., “Ultralow sub-500nA operating current highperformance TiNไAl
51. Li, H. et al. “Memristive crossbar arrays for storage and computing applications,”. Adv. Intell. Syst. 3, 2100017 (2021).
52. Lin, P. et al. “Three-dimensional memristor circuits as complex neural networks,”. Nat. Electron. 3, 225-232 (2020).
53. Ishii, M. et al., “On-Chip Trainable 1.4M 6T2R PCM synaptic array with 1.6K Stochastic LIF neurons for spiking RBM,” Technical Digest – International Electron Devices Meeting, IEDM, 2019-
54. Li, C. et al. “Efficient and self-adaptive in-situ learning in multilayer memristor neural networks,”. Nat. Commun. 9, 1-8 (2018).
55. Yao, P. et al. “Fully hardware-implemented memristor convolutional neural network,”. Nature 577, 641-646 (2020).
56. Correll, J. M. et al., “An 8-bit 20.7 TOPS/W Multi-Level Cell ReRAMbased Compute Engine,” in 2022 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), IEEE, 264-265. https://doi.org/10.1109/VLSITechnologyandCir46769.2022. 9830490.2022,
57. Cai, F. et al., “A fully integrated reprogrammable memristorCMOS system for efficient multiply-accumulate operations,” Nat Electron, 2, no. July, 290-299, [Online]. Available: https://doi.org/ 10.1038/s41928-019-0270-x 2019.
58. Hung, J.-M., “An 8-Mb DC-Current-Free Binary-to-8b Precision ReRAM Nonvolatile Computing-in-Memory Macro using Time-Space-Readout with 1286.4-21.6TOPS/W for Edge-AI Devices,” in 2022 IEEE International Solid- State Circuits Conference (ISSCC), IEEE, 1-3. https://doi.org/10.1109/ISSCC42614.2022.9731715.2022,
59. Xue, C.-X., “15.4 A 22 nm 2 Mb ReRAM Compute-in-Memory Macro with 121-28TOPS/W for Multibit MAC Computing for Tiny AI Edge Devices,” in 2020 IEEE International Solid- State Circuits Conference – (ISSCC), IEEE, 2020, 244-246.
60. Wan, W. et al. “A compute-in-memory chip based on resistive random-access memory,”. Nature 608, 504-512 (2022).
61. Yin, S., Sun, X., Yu, S. & Seo, J. S. “High-throughput in-memory computing for binary deep neural networks with monolithically integrated RRAM and 90-nm CMOS,”. IEEE Trans. Electron. Dev. 67, 4185-4192 (2020).
62. Yan, X. et al. “Robust Ag/ZrO2/WS2/Pt Memristor for Neuromorphic Computing,”. ACS Appl Mater. Interfaces 11, 48029-48038 (2019).
63. Chen, Q. et al, “Improving the recognition accuracy of memristive neural networks via homogenized analog type conductance quantization,” Micromachines, 11, https://doi.org/10.3390/ MI11040427.2020,
64. Wang, Y. “High on/off ratio black phosphorus based memristor with ultra-thin phosphorus oxide layer,” Appl. Phys. Lett., 115, https://doi.org/10.1063/1.5115531.2019,
65. Xue, F. et al. “Giant ferroelectric resistance switching controlled by a modulatory terminal for low-power neuromorphic in-memory computing,”. Adv. Mater. 33, 1-12 (2021).
66. Pan, W.-Q. et al. “Strategies to improve the accuracy of memristorbased convolutional neural networks,”. Trans. Electron. Dev., 67, 895-901 (2020).
67. Seo, S. et al. “Artificial optic-neural synapse for colored and colormixed pattern recognition,”. Nat. Commun. 9, 1-8 (2018).
68. Chandrasekaran, S., Simanjuntak, F. M., Saminathan, R., Panda, D. and Tseng, T. Y., “Improving linearity by introducing Al in
69. Zhang, B. et al. ”
70. Feng, X. et al. “Self-selective multi-terminal memtransistor crossbar array for in-memory computing,”. ACS Nano 15, 1764-1774 (2021).
71. Khaddam-Aljameh, R.et al. “HERMES-Core-A1.59-TOPS/mm2PCM on
72. Narayanan, P. et al. “Fully on-chip MAC at 14 nm enabled by accurate row-wise programming of PCM-based weights and parallel vector-transport in duration-format,”. IEEE Trans. Electron Dev. 68, 6629-6636 (2021).
73. Le Gallo, M. et al., “A 64-core mixed-signal in-memory compute chip based on phase-change memory for deep neural network inference,” 2022, Accessed: May 09, 2023. [Online]. Available: https://arxiv.org/abs/2212.02872v1
74. Murmann, B. “Mixed-signal computing for deep neural network inference,”. IEEE Trans. Very Large Scale Integr. VLSI Syst. 29, 3-13 (2021).
75. Yin, S., Jiang, Z., Seo, J. S. & Seok, M. “XNOR-SRAM: In-memory computing SRAM macro for binary/ternary deep neural networks,”. IEEE J. Solid-State Circuits 55, 1733-1743 (2020).
76. Biswas, A. & Chandrakasan, A. P. “CONV-SRAM: An energyefficient SRAM with in-memory dot-product computation for lowpower convolutional neural networks,”. IEEE J. Solid-State Circuits 54, 217-230 (2019).
77. Valavi, H., Ramadge, P. J., Nestler, E. & Verma, N. “A 64-Tile 2.4-Mb In-memory-computing CNN accelerator employing chargedomain compute,”. IEEE J. Solid-State Circuits 54, 1789-1799 (2019).
78. Khwa, W. S. et al. “A 65 nm 4 Kb algorithm-dependent computing-in-memory SRAM unit-macro with 2.3 ns and 55.8TOPS/W fully parallel product-sum operation for binary DNN edge processors,”. Dig. Tech. Pap. IEEE Int. Solid State Circuits Conf. 61, 496-498 (2018).
79. Verma, N. et al. “In-memory computing: advances and prospects,”. IEEE Solid-State Circuits Mag. 11, 43-55 (2019).
80. Diorio, C., Hasler, P., Minch, A. & Mead, C. A. “A single-transistor silicon synapse,”. IEEE Trans. Electron. Dev. 43, 1972-1980 (1996).
81. Merrikh-Bayat, F. et al. “High-performance mixed-signal neurocomputing with nanoscale floating-gate memory cell arrays,”. IEEE Trans. Neural Netw. Learn Syst. 29, 4782-4790 (2018).
82. Wang, P. et al. “Three-dimensional NAND flash for vector-matrix multiplication,”. IEEE Trans. Very Large Scale Integr. VLSI Syst. 27, 988-991 (2019).
83. Bavandpour, M., Sahay, S., Mahmoodi, M. R. & Strukov, D. B. “3DaCortex: an ultra-compact energy-efficient neurocomputing platform based on commercial 3D-NAND flash memories,”. Neuromorph. Comput. Eng. 1, 014001 (2021).
84. Chu, M. et al. “Neuromorphic hardware system for visual pattern recognition with memristor array and CMOS neuron,”. IEEE Trans. Ind. Electron. 62, 2410-2419 (2015).
85. Yeo, I., Chu, M., Gi, S. G., Hwang, H. & Lee, B. G. “Stuck-at-fault tolerant schemes for memristor crossbar array-based neural networks,”. IEEE Trans. Electron Devices 66, 2937-2945 (2019).
86. LeCun, Y., Cortes, C., and Burges, C. J. C., “MNIST handwritten digit database of handwritten digits.” Accessed: Nov. 21, 2019. [Online]. Available: http://yann.lecun.com/exdb/mnist/
87. Krizhevsky, A., Nair, V., and Hinton, G. “The CIFAR-10 dataset.” Accessed: Apr. 04, 2023. [Online]. Available: https://www.cs. toronto.edu/~kriz/cifar.html
88. Deng, J. et al., “ImageNet: A large-scale hierarchical image database,” in 2009 IEEE Conference on Computer Vision and Pattern Recognition, IEEE, 2009, 248-255.
89. Simonyan, K. and Zisserman, A. “Very deep convolutional networks for large-scale image recognition,” 2014.
90. He, K., Zhang, X., Ren, S. and Sun, J. “Deep Residual Learning for Image Recognition,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, 770-778. https://doi.org/10. 1109/CVPR.2016.90.2016,
91. Chen, P. Y., Peng, X. & Yu, S. “NeuroSim: A circuit-level macro model for benchmarking neuro-inspired architectures in online learning,”. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 37, 3067-3080 (2018).
92. Wang, Q., Wang, X., Lee, S. H., Meng, F.-H. and Lu W. D., “A Deep Neural Network Accelerator Based on Tiled RRAM Architecture,” in
93. Kim, H., Mahmoodi, M. R., Nili, H. & Strukov, D. B. “4K-memristor analog-grade passive crossbar circuit,”. Nat. Commun. 12, 1-11 (2021).
94. Inc. The Mathworks, “MATLAB.” Natick, Massachusetts, 2019.
95. Amirsoleimani, A. et al. “In-memory vector-matrix multiplication in monolithic complementary metal-oxide-semiconductor-memristor integrated circuits: design choices, challenges, and perspectives,”. Adv. Intell. Syst. 2, 2000115, https://doi.org/10.1002/ AISY. 202000115 (2020).
96. Chakraborty, I. et al. “Resistive crossbars as approximate hardware building blocks for machine learning: opportunities and challenges,”. Proc. IEEE 108, 2276-2310 (2020).
97. Jain, S. et al. “Neural network accelerator design with resistive crossbars: Opportunities and challenges,”. IBM J. Res Dev. 63, 6 (2019).
98. Ankit, A. et al. “PANTHER: A Programmable Architecture for Neural Network Training Harnessing Energy-Efficient ReRAM,”. IEEE Trans. Comput. 69, 1128-1142 (2020).
99. Mochida, R. et al. “A 4M synapses integrated analog ReRAM based 66.5 TOPS/W neural-network processor with cell current controlled writing and flexible network architecture,” Digest of Technical Papers – Symposium on VLSI Technology, 175-176, Oct. 2018, 2018
100. Su, F. et al., “A 462 GOPs/J RRAM-based nonvolatile intelligent processor for energy harvesting loE system featuring nonvolatile logics and processing-in-memory,” Digest of Technical Papers Symposium on VLSI Technology, C260-C261, https://doi.org/10. 23919/VLSIT.2017.7998149.2017,
101. Han J. and Orshansky, M. “Approximate computing: An emerging paradigm for energy-efficient design,” in 2013 18th IEEE European Test Symposium (ETS), IEEE, 1-6. https://doi.org/10.1109/ETS. 2013.6569370.2013,
102. Kiani, F., Yin, J., Wang, Z., Joshua Yang, J. & Xia, Q. “A fully hardware-based memristive multilayer neural network,”. Sci. Adv. 7, 4801 (2021).
103. Gokmen, T. and Vlasov, Y. “Acceleration of deep neural network training with resistive cross-point devices: Design considerations,” Front. Neurosci., 10, no. JUL, https://doi.org/10.3389/fnins.2016. 00333.2016,
104. Fouda, M. E., Lee, S., Lee, J., Eltawil, A. & Kurdahi, F. “Mask technique for fast and efficient training of binary resistive crossbar arrays,”. IEEE Trans. Nanotechnol. 18, 704-716 (2019).
105. Prezioso, M. et al. “Training and operation of an integrated neuromorphic network based on metal-oxide memristors,”. Nature 521, 61-64 (2015).
106. Hu, M. et al. “Memristor crossbar-based neuromorphic computing system: A case study,”. IEEE Trans. Neural Netw. Learn Syst. 25, 1864-1878 (2014).
107. Hu, M. et al., “Dot-product engine for neuromorphic computing,” in DAC ’16: Proceedings of the 53rd Annual Design Automation Conference, New York, NY, USA: Association for Computing Machinery, 1-6. https://doi.org/10.1145/2897937.2898010.2016,
108. Liu, C., Hu, M., Strachan, J. P. and Li, H. H. “Rescuing memristorbased neuromorphic design with high defects,” in 2017 54th ACM/ EDAC/IEEE Design Automation Conference (DAC), Institute of Electrical and Electronics Engineers Inc., https://doi.org/10.1145/ 3061639.3062310.2017.
109. Romero-Zaliz, R., Pérez, E., Jiménez-Molinos, F., Wenger, C. & Roldán, J. B. “Study of quantized hardware deep neural networks based on resistive switching devices, conventional versus convolutional approaches,”. Electronics 10, 1-14 (2021).
110. Pérez, E. et al. “Advanced temperature dependent statistical analysis of forming voltage distributions for three different HfO 2 –
based RRAM technologies,”. Solid State Electron. 176, 107961 (2021).
111. Pérez-Bosch Quesada, E. et al. “Toward reliable compact modeling of multilevel 1T-1R RRAM devices for neuromorphic systems,”. Electronics 10, 645 (2021).
112. Xia, L. et al. “Stuck-at Fault Tolerance in RRAM Computing Systems,”. IEEE J. Emerg. Sel. Top. Circuits Syst., 8, 102-115 (2018).
113. Li, C. et al., “CMOS-integrated nanoscale memristive crossbars for CNN and optimization acceleration,” 2020 IEEE International Memory Workshop, IMW 2020 – Proceedings, https://doi.org/10. 1109/IMW48823.2020.9108112.2020,
114. Pedretti, G. et al. “Redundancy and analog slicing for precise inmemory machine learning – Part I: Programming techniques,”. IEEE Trans. Electron. Dev. 68, 4373-4378 (2021).
115. Pedretti, G. et al. “Redundancy and analog slicing for precise inmemory machine learning – Part II: Applications and benchmark,”. IEEE Trans. Electron. Dev. 68, 4379-4383 (2021).
116. Wang, Z. et al. “Fully memristive neural networks for pattern classification with unsupervised learning,”. Nat. Electron. 1, 137-145 (2018).
117. T. Rabuske and J. Fernandes, “Charge-Sharing SAR ADCs for lowvoltage low-power applications,” https://doi.org/10.1007/978-3-319-39624-8.2017,
118. Kumar, P. et al. “Hybrid architecture based on two-dimensional memristor crossbar array and CMOS integrated circuit for edge computing,”. npj 2D Mater. Appl. 6, 1-10 (2022).
119. Krestinskaya, O., Salama, K. N. & James, A. P. “Learning in memristive neural network architectures using analog backpropagation circuits,”. IEEE Trans. Circuits Syst. I: Regul. Pap. 66, 719-732 (2019).
120. Chua, L. O., Tetzlaff, R. and Slavova, A. Eds., Memristor Computing Systems. Springer International Publishing, https://doi.org/10. 1007/978-3-030-90582-8.2022.
121. Oh, S. et al. “Energy-efficient Mott activation neuron for fullhardware implementation of neural networks,”. Nat. Nanotechnol. 16, 680-687 (2021).
122. Ambrogio, S. et al. “Equivalent-accuracy accelerated neuralnetwork training using analogue memory,”. Nature 558, 60-67 (2018).
123. Bocquet, M. et al., “In-memory and error-immune differential RRAM implementation of binarized deep neural networks,” Technical Digest – International Electron Devices Meeting, IEDM, 20.6.120.6.4, Jan. 2019, https://doi.org/10.1109/IEDM.2018. 8614639.2018,
124. Cheng, M. et al., “TIME: A Training-in-memory architecture for Memristor-based deep neural networks,” Proc. Des. Autom. Conf., Part 12828, 0-5, https://doi.org/10.1145/3061639. 3062326.2017,
125. Chi, P. et al., “PRIME: A novel processing-in-memory architecture for neural network computation in ReRAM-based main memory,” Proceedings – 2016 43rd International Symposium on Computer Architecture, ISCA 2016, 27-39, https://doi.org/10.1109/ISCA. 2016.13.2016,
126. Krestinskaya, O., Choubey, B. & James, A. P. “Memristive GAN in Analog,”. Sci. Rep. 2020 10:1 10, 1-14 (2020).
127. Li, G. H. Y. et al., “All-optical ultrafast ReLU function for energyefficient nanophotonic deep learning,” Nanophotonics, https:// doi.org/10.1515/NANOPH-2022-0137/ASSET/GRAPHIC/J_ NANOPH-2022-0137_FIG_007.JPG.2022,
128. Ando, K. et al. “BRein memory: a single-chip binary/ternary reconfigurable in-memory deep neural network accelerator achieving 1.4 TOPS at 0.6 W,”. IEEE J. Solid-State Circuits 53, 983-994 (2018).
129. Price, M., Glass, J. & Chandrakasan, A. P. “A scalable speech recognizer with deep-neural-network acoustic models and voice-
activated power gating,”. Dig. Tech. Pap. IEEE Int Solid State Circuits Conf. 60, 244-245 (2017).
130. Yin, S. et al., “A 1.06-to-5.09 TOPS/W reconfigurable hybrid-neural-network processor for deep learning applications,” IEEE Symposium on VLSI Circuits, Digest of Technical Papers, C26-C27, https://doi.org/10.23919/VLSIC.2017.8008534.2017,
131. Chen, Y. H., Krishna, T., Emer, J. S. & Sze, V. “Eyeriss: An energyefficient reconfigurable accelerator for deep convolutional neural networks,”. IEEE J. Solid-State Circuits 52, 127-138 (2017).
132. Lazzaro, J., Ryckebusch, S. M., Mahowald, A. and Mead, C. A. “Winner-Take-All Networks of O(N) Complexity,” in Advances in Neural Information Processing Systems, D. Touretzky, Ed., MorganKaufmann, 1988.
133. Andreou, A. G. et al. “Current-mode subthreshold MOS circuits for analog VLSI neural systems,”. IEEE Trans. Neural Netw. 2, 205-213 (1991).
134. Pouliquen, P. O., Andreou, A. G., Strohbehn, K. and Jenkins, R. E. “Associative memory integrated system for character recognition,” Midwest Symposium on Circuits and Systems, 1, 762-765, https://doi.org/10.1109/MWSCAS.1993.342935.1993,
135. Starzyk, J. A. & Fang, X. “CMOS current mode winner-take-all circuit with both excitatory and inhibitory feedback,”. Electron. Lett. 29, 908-910 (1993).
136. DeWeerth, S. P. & Morris, T. G. “CMOS current mode winner-takeall circuit with distributed hysteresis,”. Electron. Lett. 31, 1051-1053 (1995).
137. Indiveri, G. “A current-mode hysteretic winner-take-all network, with excitatory and inhibitory coupling,”. Analog Integr. Circuits Signal Process 28, 279-291 (2001).
138. Tan, B. P. & Wilson, D. M. “Semiparallel rank order filtering in analog VLSI,”. IEEE Trans. Circuits Syst. II: Analog Digit. Signal Process. 48, 198-205 (2001).
139. Serrano, T. & Linares-Barranco, B. “Modular current-mode highprecision winner-take-all circuit,”. Proc. – IEEE Int. Symp. Circuits Syst. 5, 557-560 (1994).
140. Meador, J. L. and Hylander, P. D. “Pulse Coded Winner-Take-All Networks,” Silicon Implementation of Pulse Coded Neural Networks, 79-99, https://doi.org/10.1007/978-1-4615-2680-3_5.1994,
141. El-Masry, E. I., Yang, H. K. & Yakout, M. A. “Implementations of artificial neural networks using current-mode pulse width modulation technique,”. IEEE Trans. Neural Netw. 8, 532-548 (1997).
142. Choi, J. & Sheu, B. J. “A high-precision vlsi winner-take-all circuit for self-organizing neural networks,”. IEEE J. Solid-State Circuits 28, 576-584 (1993).
143. Yu, H. & Miyaoka, R. S. “A High-Speed and High-Precision Winner-Select-Output (WSO) ASIC,”. IEEE Trans. Nucl. Sci. 45, 772-776 (1998). PART 1.
144. Lau, K. T. and Lee, S. T. “A CMOS winner-takes-all circuit for selforganizing neural networks,” https://doi.org/10.1080/ 002072198134896, 84, 131-136, 2010
145. He, Y. & Sánchez-Sinencio, E. “Min-net winner-take-all CMOS implementation,”. Electron Lett. 29, 1237-1239 (1993).
146. Demosthenous, A., Smedley, S. & Taylor, J. “A CMOS analog winner-take-all network for large-scale applications,”. IEEE Trans. Circuits Syst. I: Fundam. Theory Appl. 45, 300-304 (1998).
147. Pouliquen, P. O., Andreou, A. G. & Strohbehn, K. “Winner-Takes-All associative memory: A hamming distance vector quantizer,”. Analog Integr. Circuits Signal Process. 1997 13:1 13, 211-222 (1997).
148. Fish, A., Milrud, V. & Yadid-Pecht, O. “High-speed and highprecision current winner-take-all circuit,”. IEEE Trans. Circuits Syst. II: Express Briefs 52, 131-135 (2005).
149. Ohnhäuser, F. “Analog-Digital Converters for Industrial Applications Including an Introduction to Digital-Analog Converters,” 2015.
150. Pavan, S., Schreier, R.. and Temes, G. C. “Understanding DeltaSigma Data Converters.”.
151. Walden, R. H. “Analog-to-digital converter survey and analysis,”. IEEE J. Sel. Areas Commun. 17, 539-550 (1999).
152. Harpe, P., Gao, H., Van Dommele, R., Cantatore, E. & Van Roermund, A. H. M. “A 0.20 mm 23 nW signal acquisition IC for miniature sensor nodes in 65 nm CMOS. IEEE J. Solid-State Circuits 51, 240-248 (2016).
153. Murmann, B. “ADC Performance Survey 1997-2022.” Accessed: Sep. 05, 2022. [Online]. Available: http://web.stanford.edu/ ~murmann/adcsurvey.html.
154. Ankit, A. et al., “PUMA: A Programmable Ultra-efficient Memristorbased Accelerator for Machine Learning Inference,” International Conference on Architectural Support for Programming Languages and Operating Systems – ASPLOS, 715-731, https://doi.org/10. 1145/3297858.3304049.2019,
155. Ni, L. et al., “An energy-efficient matrix multiplication accelerator by distributed in-memory computing on binary RRAM crossbar,” Proceedings of the Asia and South Pacific Design Automation Conference, ASP-DAC, 25-28-January-2016, 280-285, https://doi. org/10.1109/ASPDAC.2016.7428024.2016,
156. Wang, X., Wu, Y. and Lu, W. D. “RRAM-enabled AI Accelerator Architecture,” in 2021 IEEE International Electron Devices Meeting (IEDM), IEEE, 12.2.1-12.2.4. https://doi.org/10.1109/IEDM19574. 2021.9720543.2021,
157. Xiao, T. P. et al. On the Accuracy of Analog Neural Network Inference Accelerators. [Feature],” IEEE Circuits Syst. Mag. 22, 26-48 (2022).
158. Sun, X. et al, “XNOR-RRAM: A scalable and parallel resistive synaptic architecture for binary neural networks,” Proceedings of the 2018 Design, Automation and Test in Europe Conference and Exhibition, DATE 2018, 2018-January, 1423-1428, https://doi.org/ 10.23919/DATE.2018.8342235.2018,
159. Zhang, W. et al. “Neuro-inspired computing chips,”. Nat. Electron. 2020 3:7 3, 371-382 (2020).
160. Shafiee, A. et al., “ISAAC: A Convolutional Neural Network Accelerator with In-Situ Analog Arithmetic in Crossbars,” in Proceedings – 2016 43rd International Symposium on Computer Architecture, ISCA 2016, Institute of Electrical and Electronics Engineers Inc., 14-26. https://doi.org/10.1109/ISCA.2016.12.2016,
161. Fujiki, D., Mahlke, S. and Das, R. “In-memory data parallel processor,” in ACM SIGPLAN Notices, New York, NY, USA: ACM, 1-14. https://doi.org/10.1145/3173162.3173171.2018,
162. Nourazar, M., Rashtchi, V., Azarpeyvand, A. & Merrikh-Bayat, F. “Memristor-based approximate matrix multiplier,”. Analog. Integr. Circuits Signal Process 93, 363-373 (2017).
163. Saberi, M., Lotfi, R., Mafinezhad, K. & Serdijn, W. A. “Analysis of power consumption and linearity in capacitive digital-to-analog converters used in successive approximation ADCs,”. IEEE Trans. Circuits Syst. I: Regul. Pap. 58, 1736-1748 (2011).
164. Kull, L. et al. “A
165. Hagan, M., Demuth, H., Beale, M. and De Jesús, O. Neural Network Design, 2nd ed. Stillwater, OK, USA: Oklahoma State University, 2014.
166. Choi, S., Sheridan, P. & Lu, W. D. “Data clustering using memristor networks,”. Sci. Rep. 5, 1-10 (2015).
167. Khaddam-Aljameh, R. et al., “HERMES Core: A 14 nm CMOS and PCM-based In-Memory Compute Core using an array of
168. Kennedy, J. and Eberhart, R. “Particle swarm optimization,” Proceedings of ICNN’95 – International Conference on Neural Networks, 4, https://doi.org/10.1109/ICNN.1995.488968. 1942-1948,
169. Goldberg, D. E. & Holland, J. H. “Genetic Algorithms and machine learning. Mach. Learn. 3, 95-99 (1988).
170. Kirkpatrick, S., Gelatt, C. D. & Vecchi, M. P. “Optimization by simulated annealing,”. Science 220, 671-680 (1983).
171. Rumelhart, D. E., Hinton, G. E. & Williams, R. J. “Learning representations by back-propagating errors,”. Nature 323, 533-536 (1986).
172. Dennis, J. E. and Schnabel, R. B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations. Society for Industrial and Applied Mathematics, https://doi.org/10.1137/1. 9781611971200.1996.
173. Møller, M. F. “A scaled conjugate gradient algorithm for fast supervised learning,”. Neural Netw. 6, 525-533 (1993).
174. Powell, M. J. D. “Restart procedures for the conjugate gradient method,”. Math. Program. 12, 241-254 (1977).
175. Fletcher, R. “Function minimization by conjugate gradients,”. Comput. J. 7, 149-154 (1964).
176. Marquardt, D. W. “An algorithm for least-squares estimation of nonlinear parameters,”. J. Soc. Ind. Appl. Math. 11, 431-441 (1963).
177. Riedmiller, M. and Braun, H. “Direct adaptive method for faster backpropagation learning: The RPROP algorithm,” in 1993 IEEE International Conference on Neural Networks, Publ by IEEE, 586-591. https://doi.org/10.1109/icnn.1993.298623.1993,
178. Battiti, R. “First- and second-order methods for learning: between steepest descent and Newton’s Method,”. Neural Comput. 4, 141-166 (1992).
179. Bottou, L. “Stochastic gradient descent tricks,” Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 7700 LECTURE NO, 421-436, https://doi.org/10.1007/978-3-642-35289-8_25/ COVER.2012,
180. Li, M., Zhang, T., Chen, Y. and Smola, A. J. “Efficient mini-batch training for stochastic optimization,” Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 661-670, https://doi.org/10.1145/2623330. 2623612.2014,
181. Zamanidoost, E., Bayat, F. M., Strukov, D. and Kataeva, I. “Manhattan rule training for memristive crossbar circuit pattern classifiers,” WISP 2015 – IEEE International Symposium on Intelligent Signal Processing, Proceedings, https://doi.org/10.1109/WISP. 2015.7139171.2015,
182. Duchi, J., Hazan, E. & Singer, Y. “Adaptive subgradient methods for online learning and stochastic optimization,”. J. Mach. Learn. Res. 12, 2121-2159 (2011).
183. “Neural Networks for Machine Learning – Geoffrey Hinton – C. Cui’s Blog.” Accessed: Nov. 21, 2022. [Online]. Available: https:// cuicaihao.com/neural-networks-for-machine-learning-geoffreyhinton/
184. Kingma, D. P. and Ba, J. L. “Adam: A Method for Stochastic Optimization,” 3rd International Conference on Learning Representations, ICLR 2015 – Conference Track Proceedings, 2014, https://doi. org/10.48550/arxiv.1412.6980.
185. Zeiler, M. D. “ADADELTA: An adaptive learning rate method,” Dec. 2012, https://doi.org/10.48550/arxiv.1212.5701.
186. Xiong, X. et al. “Reconfigurable logic-in-memory and multilingual artificial synapses based on 2D heterostructures,”. Adv. Funct. Mater. 30, 2-7 (2020).
187. Zoppo, G., Marrone, F. & Corinto, F. “Equilibrium propagation for memristor-based recurrent neural networks,”. Front Neurosci. 14, 1-8 (2020).
188. Alibart, F., Zamanidoost, E. & Strukov, D. B. “Pattern classification by memristive crossbar circuits using ex situ and in situ training,”. Nat. Commun. 4, 1-7 (2013).
189. Joshi, V. et al., “Accurate deep neural network inference using computational phase-change memory,” Nat Commun, 11, https:// doi.org/10.1038/s41467-020-16108-9.2020,
190. Rasch, M. J. et al., “Hardware-aware training for large-scale and diverse deep learning inference workloads using in-memory computing-based accelerators,” 2023.
191. Huang, H.-M., Wang, Z., Wang, T., Xiao, Y. & Guo, X. “Artificial neural networks based on memristive devices: from device to system,”. Adv. Intell. Syst. 2, 2000149 (2020).
192. Nandakumar, S. R. et al., “Mixed-precision deep learning based on computational memory,” Front. Neurosci., 14, https://doi.org/10. 3389/fnins.2020.00406.2020,
193. Le Gallo, M. et al. “Mixed-precision in-memory computing,”. Nat. Electron. 1, 246-253 (2018).
194. Yao, P. et al., “Face classification using electronic synapses,” Nat. Commun., 8, May, 1-8, https://doi.org/10.1038/ ncomms15199.2017,
195. Papandreou, N. et al., “Programming algorithms for multilevel phase-change memory,” Proceedings – IEEE International Symposium on Circuits and Systems, 329-332, https://doi.org/10.1109/ ISCAS.2011.5937569.2011,
196. Milo, V. et al., “Multilevel HfO2-based RRAM devices for lowpower neuromorphic networks,” APL Mater, 7, https://doi.org/10. 1063/1.5108650.2019,
197. Yu, S. et al., “Scaling-up resistive synaptic arrays for neuroinspired architecture: Challenges and prospect,” in Technical Digest – International Electron Devices Meeting, IEDM, Institute of Electrical and Electronics Engineers Inc., 17.3.1-17.3.4. https://doi. org/10.1109/IEDM.2015.7409718.2015,
198. Woo, J. et al. “Improved synaptic behavior under identical pulses using AlOx/HfO2 bilayer RRAM array for neuromorphic systems,”. IEEE Electron. Device Lett. 37, 994-997 (2016).
199. Xiao, S. et al. “GST-memristor-based online learning neural networks,”. Neurocomputing 272, 677-682 (2018).
200. Tian, H. et al. “A novel artificial synapse with dual modes using bilayer graphene as the bottom electrode,”. Nanoscale 9, 9275-9283 (2017).
201. Shi, T., Yin, X. B., Yang, R. & Guo, X. “Pt/WO3/FTO memristive devices with recoverable pseudo-electroforming for time-delay switches in neuromorphic computing,”. Phys. Chem. Chem. Phys. 18, 9338-9343 (2016).
202. Menzel, S. et al. “Origin of the ultra-nonlinear switching kinetics in oxide-based resistive switches,”. Adv. Funct. Mater. 21, 4487-4492 (2011).
203. Buscarino, A., Fortuna, L., Frasca, M., Gambuzza, L. V. and Sciuto, G., “Memristive chaotic circuits based on cellular nonlinear networks,” https://doi.org/10.1142/SO218127412500708, 22,3, 2012
204. Li, Y. & Ang, K.-W. “Hardware implementation of neuromorphic computing using large-scale memristor crossbar arrays,”. Adv. Intell. Syst. 3, 2000137 (2021).
205. Zhu, J., Zhang, T., Yang, Y. & Huang, R. “A comprehensive review on emerging artificial neuromorphic devices,”. Appl Phys. Rev. 7, 011312 (2020).
206. Wang, Z. et al. “Engineering incremental resistive switching in TaOx based memristors for brain-inspired computing,”. Nanoscale 8, 14015-14022 (2016).
207. Park, S. M. et al. “Improvement of conductance modulation linearity in a
208. Slesazeck, S. & Mikolajick, T. “Nanoscale resistive switching memory devices: a review,”. Nanotechnology 30, 352003 (2019).
209. Waser, R., Dittmann, R., Staikov, C. & Szot, K. “Redox-based resistive switching memories nanoionic mechanisms, prospects, and challenges,”. Adv. Mater. 21, 2632-2663 (2009).
210. Ielmini, D. and Waser, R. Resistive Switching. Weinheim, Germany: Wiley-VCH Verlag GmbH & Co. KGaA, 2016.
211. Wouters, D. J., Waser, R. & Wuttig, M. “Phase-change and redoxbased resistive switching memories,”. Proc. IEEE 103, 1274-1288 (2015).
212. Pan, F., Gao, S., Chen, C., Song, C. & Zeng, F. “Recent progress in resistive random access memories: Materials, switching mechanisms, and performance,”. Mater. Sci. Eng. R: Rep. 83, 1-59 (2014).
213. Kim, S. et al. “Analog synaptic behavior of a silicon nitride memristor,”. ACS Appl Mater. Interfaces 9, 40420-40427 (2017).
214. Li, W., Sun, X., Huang, S., Jiang, H. & Yu, S. “A 40-nm MLC-RRAM compute-in-memory macro with sparsity control, On-Chip Writeverify, and temperature-independent ADC references,”. IEEE J. Solid-State Circuits 57, 2868-2877 (2022).
215. Buchel, J. et al., “Gradient descent-based programming of analog in-memory computing cores,” Technical Digest – International Electron Devices Meeting, IEDM, 3311-3314, 2022, https://doi.org/ 10.1109/IEDM45625.2022.10019486.2022,
216. Prezioso, M. et al. “Spike-timing-dependent plasticity learning of coincidence detection with passively integrated memristive circuits,”. Nat. Commun. 9, 1-8 (2018).
217. Park, S. et al., “Electronic system with memristive synapses for pattern recognition,” Sci. Rep., 5, https://doi.org/10.1038/ srep10123.2015,
218. Yu, S. et al., “Binary neural network with 16 Mb RRAM macro chip for classification and online training,” in Technical Digest – International Electron Devices Meeting, IEDM, Institute of Electrical and Electronics Engineers Inc., 16.2.1-16.2.4. https://doi.org/10.1109/ IEDM.2016.7838429.2017,
219. Chen, W. H. et al. “CMOS-integrated memristive non-volatile computing-in-memory for AI edge processors,”. Nat. Electron. 2, 420-428 (2019).
220. Chen, W. H. et al., “A 16 Mb dual-mode ReRAM macro with sub14ns computing-in-memory and memory functions enabled by self-write termination scheme,” Technical Digest – International Electron Devices Meeting, IEDM, 28.2.1-28.2.4, 2018,
221. Hu, M. et al., “Memristor-based analog computation and neural network classification with a dot product engine,” Adv. Mater., 30, https://doi.org/10.1002/adma.201705914.2018,
222. Li, C. et al. Analogue signal and image processing with large memristor crossbars. Nat. Electron 1, 52-59 (2018).
223. Paszke A. et al., “Automatic differentiation in PyTorch”.
224. Abadi, M. et al., “TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems,” 2015.
225. Stimberg, M., Brette, R. and Goodman, D. F. M. “Brian 2, an intuitive and efficient neural simulator,” Elife, 8, https://doi.org/10.7554/ ELIFE.47314.2019,
226. Spreizer, S. et al., “NEST 3.3,” Mar. 2022, https://doi.org/10.5281/ ZENODO. 6368024.
227. Hazan, H. et al. “BindsNET: A machine learning-oriented spiking neural networks library in python,”. Front Neuroinform 12, 89 (2018).
228. M. Y. Lin et al., “DL-RSIM: A simulation framework to enable reliable ReRAM-based accelerators for deep learning,” IEEE/ACM International Conference on Computer-Aided Design, Digest of Technical Papers, ICCAD, https://doi.org/10.1145/3240765. 3240800.2018,
229. Sun, X. & Yu, S. “Impact of non-ideal characteristics of resistive synaptic devices on implementing convolutional neural networks,”. IEEE J. Emerg. Sel. Top. Circuits Syst. 9, 570-579 (2019).
230. Ma, X. et al., “Tiny but Accurate: A Pruned, Quantized and Optimized Memristor Crossbar Framework for Ultra Efficient DNN Implementation,” Proceedings of the Asia and South Pacific Design Automation Conference, ASP-DAC, 2020-Janua, 301-306, https:// doi.org/10.1109/ASP-DAC47756.2020.9045658.2020,
231. Yuan, G. et al., “An Ultra-Efficient Memristor-Based DNN Framework with Structured Weight Pruning and Quantization Using ADMM,” Proceedings of the International Symposium on Low Power Electronics and Design, 2019, https://doi.org/10.1109/ ISLPED.2019.8824944.2019.
232. Rasch, M. J. et al., “A flexible and fast PyTorch toolkit for simulating training and inference on analog crossbar arrays,” 2021 IEEE 3rd International Conference on Artificial Intelligence Circuits and Systems, AICAS 2021, https://doi.org/10. 48550/arxiv.2104.02184.2021,
233. Grötker, T., “System design with SystemC,” 217, 2002.
234. Gajski, D. D. “SpecC: specification language and methodology,” 313, 2000.
235. Lee, M. K. F. et al. “A system-level simulator for RRAM-based neuromorphic computing chips,”. ACM Trans. Archit. Code Optim. (TACO) 15, 4 (2019).
236. BanaGozar, A. et al. “System simulation of memristor based computation in memory platforms,”. Lect. Notes Comput. Sci. (Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinforma.) 12471, 152-168 (2020).
237. Gai, L. and Gajski, D. “Transaction level modeling: an overview,” Hardware/Software Codesign – Proceedings of the International Workshop, 19-24, https://doi.org/10.1109/CODESS.2003. 1275250.2003,
238. Poremba, M. and Xie, Y. “NVMain: An architectural-level main memory simulator for emerging non-volatile memories,” Proceedings – 2012 IEEE Computer Society Annual Symposium on VLSI, ISVLSI 2012, 392-397, https://doi.org/10.1109/ISVLSI.2012.82.2012,
239. Poremba, M., Zhang, T. & Xie, Y. “NVMain 2.0: A user-friendly memory simulator to model (non-)volatile memory systems,”. IEEE Comput. Archit. Lett. 14, 140-143 (2015).
240. Xia, L. et al. “MNSIM: Simulation platform for memristor-based neuromorphic computing system,”. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 37, 1009-1022 (2018).
241. Zhu, Z. et al., “MNSIM 2.0: A behavior-level modeling tool for memristor-based neuromorphic computing systems,” in Proceedings of the ACM Great Lakes Symposium on VLSI, GLSVLSI, Association for Computing Machinery, 83-88. https://doi.org/10. 1145/3386263.3407647.2020,
242. Banagozar, A. et al., “CIM-SIM: Computation in Memory SIMulator,” in Proceedings of the 22nd International Workshop on Software and Compilers for Embedded Systems, SCOPES 2019, Association for Computing Machinery, Inc, 1-4. https://doi.org/10. 1145/3323439.3323989.2019,
243. Fei, X., Zhang, Y. & Zheng, W. “XB-SIM: A simulation framework for modeling and exploration of ReRAM-based CNN acceleration design,”. Tsinghua Sci. Technol. 26, 322-334 (2021).
244. Zahedi, M. et al. “MNEMOSENE: Tile architecture and simulator for memristor-based computation-in-memory,”. ACM J. Emerg. Technol. Comput. Syst. 18, 1-24 (2022).
245. Dong, X., Xu, C., Xie, Y. & Jouppi, N. P. “NVSim: A circuit-level performance, energy, and area model for emerging nonvolatile memory,”. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 31, 994-1007 (2012).
246. Song, L., Qian, X., Li, H. and Chen, Y. “PipeLayer: A Pipelined ReRAM-based accelerator for deep learning,” Proceedings –
247. Imani, M. et al., “RAPIDNN: In-Memory Deep Neural Network Acceleration Framework,” 2018.
248. Chen, A. “A comprehensive crossbar array model with solutions for line resistance and nonlinear device characteristics,”. IEEE Trans. Electron Devices 60, 1318-1326 (2013).
249. Aguirre, F. L. et al., “Line resistance impact in memristor-based multi layer perceptron for pattern recognition,” in 2021 IEEE 12th Latin American Symposium on Circuits and Systems, LASCAS 2021, Institute of Electrical and Electronics Engineers Inc., Feb. https://doi.org/10.1109/LASCAS51355.2021.9667132.2021.
250. Aguirre, F. L. et al. “Minimization of the line resistance impact on memdiode-based simulations of multilayer perceptron arrays applied to pattern recognition,”. J. Low. Power Electron. Appl. 11, 9 (2021).
251. Lee, Y. K. et al. “Matrix mapping on crossbar memory arrays with resistive interconnects and its use in in-memory compression of biosignals,”. Micromachines 10, 306 (2019).
252. Fei, W., Yu, H., Zhang, W. & Yeo, K. S. “Design exploration of hybrid CMOS and memristor circuit by new modified nodal analysis,”. IEEE Trans. Very Large Scale Integr. VLSI Syst. 20, 1012-1025 (2012).
253. Aguirre, F. L., Pazos, S. M., Palumbo, F., Suñé, J. & Miranda, E. “Application of the quasi-static memdiode model in cross-point arrays for large dataset pattern recognition,”. IEEE Access 8, 1-1 (2020).
254. Aguirre, F. L., Pazos, S. M., Palumbo, F., Suñé, J. & Miranda, E. “SPICE simulation of RRAM-based crosspoint arrays using the dynamic memdiode model,”. Front Phys. 9, 548 (2021).
255. Aguirre, F. L. et al. “Assessment and improvement of the pattern recognition performance of memdiode-based cross-point arrays with randomly distributed stuck-at-faults,”. Electron. 10, 2427 (2021).
256. Fritscher, M., Knodtel, J., Reichenbach, M. and Fey, D. “Simulating memristive systems in mixed-signal mode using commercial design tools,” 2019 26th IEEE International Conference on Electronics, Circuits and Systems, ICECS 2019, 225-228, https://doi. org/10.1109/ICECS46596.2019.8964856.2019,
257. Applied Materials, “Ginestra
258. “TCAD – Technology Computer Aided Design (TCAD) | Synopsys.” Accessed: Jan. 20, 2023. [Online]. Available: https://www. synopsys.com/silicon/tcad.html
259. Krestinskaya, O., Salama, K. N. & James, A. P. “Automating analogue AI chip design with genetic search,”. Adv. Intell. Syst. 2, 2000075 (2020).
260. Krestinskaya, O., Salama, K. and James, A. P. “Towards hardware optimal neural network selection with multi-objective genetic search,” Proceedings – IEEE International Symposium on Circuits and Systems, 2020, 2020, https://doi.org/10.1109/ISCAS45731. 2020.9180514/VIDEO.
261. Guan, Z. et al., “A hardware-aware neural architecture search pareto front exploration for in-memory computing,” in 2022 IEEE 16th International Conference on Solid-State & Integrated Circuit Technology (ICSICT), IEEE, 1-4. https://doi.org/10.1109/ ICSICT55466.2022.9963263.2022,
262. Li, G., Mandal, S. K., Ogras, U. Y. and Marculescu, R. “FLASH: Fast neural architecture search with hardware optimization,” ACM Trans. Embed. Compu. Syst., 20, https://doi.org/10.1145/ 3476994.2021,
263. Yuan, Z. et al. “NAS4RRAM: neural network architecture search for inference on RRAM-based accelerators,”. Sci. China Inf. Sci. 64, 160407 (2021).
264. Yan, Z., Juan, D.-C., Hu, X. S. and Shi, Y. “Uncertainty modeling of emerging device based computing-in-memory neural accelerators with application to neural architecture search,” in Proceedings of the 26th Asia and South Pacific Design Automation Conference, New York, NY, USA: ACM, 859-864. https://doi.org/ 10.1145/3394885.3431635.2021,
265. Sun H. et al., “Gibbon: Efficient co-exploration of NN model and processing-in-memory architecture,” in 2022 Design, Automation & Test in Europe Conference & Exhibition (DATE), IEEE, 867-872. https://doi.org/10.23919/DATE54114.2022. 9774605.2022,
266. Jiang, W. et al. Device-circuit-architecture co-exploration for computing-in-memory neural accelerators. IEEE Trans. Comput. 70, 595-605 (2021).
267. Burr, G. W. et al. Experimental demonstration and tolerancing of a large-scale neural network (165 000 Synapses) using phasechange memory as the synaptic weight element. IEEE Trans. Electron Devices 62, 3498-3507 (2015).
268. Dong, Z. et al. “Convolutional neural networks based on RRAM devices for image recognition and online learning tasks,”. IEEE Trans. Electron. Dev. 66, 793-801 (2019).
269. Querlioz, D., Bichler, O., Dollfus, P. & Gamrat, C. “Immunity to device variations in a spiking neural network with memristive nanodevices,”. IEEE Trans. Nanotechnol. 12, 288-295 (2013).
270. Guan, X., Yu, S. & Wong, H. S. P. “A SPICE compact model of metal oxide resistive switching memory with variations,”. IEEE Electron. Device Lett. 33, 1405-1407 (2012).
271. Liang, J., Yeh, S., Simon Wong, S. & Philip Wong, H. S. “Effect of wordline/bitline scaling on the performance, energy consumption, and reliability of cross-point memory array,”. ACM J. Emerg. Technol. Comput. Syst. 9, 1-14 (2013).
272. Hirtzlin, T. et al. “Digital biologically plausible implementation of binarized neural networks with differential hafnium oxide resistive memory arrays,”. Front Neurosci. 13, 1383 (2020).
273. Xue, C. X. et al., “A 1Mb Multibit ReRAM computing-in-memory macro with 14.6 ns Parallel MAC computing time for CNN based AI Edge processors,” Dig Tech Pap IEEE Int Solid State Circuits Conf, 2019-February, 388-390, https://doi.org/10.1109/ISSCC.2019. 8662395.2019,
274. Wu, T. F. et al., “A 43pJ/Cycle Non-Volatile Microcontroller with 4.7
275. Liu, Q. et al., “A Fully Integrated Analog ReRAM based 78.4TOPS/ W compute-in-memory chip with fully parallel MAC computing,” Dig. Tech. Pap. IEEE Int. Solid State Circuits Conf, 2020-February, 500-502, https://doi.org/10.1109/ISSCC19947.2020. 9062953.2020,
276. Xiao, T. P., Bennett, C. H., Feinberg, B., Agarwal, S. and Marinella, M. J. “Analog architectures for neural network acceleration based on non-volatile memory,” Applied Physics Reviews, 7, American Institute of Physics Inc., https://doi.org/10.1063/1. 5143815.2020.
277. “NVIDIA Data Center Deep Learning Product Performance | NVIDIA Developer.” Accessed: Nov. 28, 2022. [Online]. Available: https:// developer.nvidia.com/deep-learning-performance-traininginference
278. Habana L., “Goya
279. Chen Y. et al., “DaDianNao: A Machine-Learning Supercomputer,” Proceedings of the Annual International Symposium on Microarchitecture, MICRO, 2015-January, no. January, 609-622, https:// doi.org/10.1109/MICRO.2014.58.2015,
280. Lee, J. et al. “UNPU: An energy-efficient deep neural network accelerator with fully variable weight bit precision,”. IEEE J. SolidState Circuits 54, 173-185 (2019).
281. Bankman, D., Yang, L., Moons, B., Verhelst, M. & Murmann, B. “An always-on
282. Nag, A. et al. “Newton: Gravitating towards the physical limits of crossbar acceleration,”. IEEE Micro 38, 41-49 (2018).
283. Bojnordi M. N. and Ipek, E. “Memristive Boltzmann machine: A hardware accelerator for combinatorial optimization and deep learning,” Proceedings – International Symposium on HighPerformance Computer Architecture, 2016-April, 1-13, https://doi. org/10.1109/HPCA.2016.7446049.2016,
284. Jain, S. et al. “A heterogeneous and programmable compute-inmemory accelerator architecture for analog-AI using dense 2-D Mesh,”. IEEE Trans. Very Large Scale Integr. VLSI Syst. 31, 114-127 (2023).
285. Carnevale N. T. and Hines, M. L. “The NEURON book,” The NEURON Book, 1-457, https://doi.org/10.1017/ CBO9780511541612.2006,
286. Lammie, C., Xiang, W., Linares-Barranco, B. and Azghadi, M. R. “MemTorch: An Open-source Simulation Framework for Memristive Deep Learning Systems,” 1-14, 2020.
287. Xiao, T. P., Bennett, C. H., Feinberg, B., Marinella, M. J. and Agarwal, S. “CrossSim: accuracy simulation of analog in-memory computing,” https://github.com/sandialabs/cross-sim. Accessed: Sep. 06, 2022. [Online]. Available: https://github.com/ sandialabs/cross-sim
288. Mehonic, A., Joksas, D., Ng, W. H., Buckwell, M. & Kenyon, A. J. “Simulation of inference accuracy using realistic rram devices,”. Front. Neurosci. 13, 1-15 (2019).
289. Zhang, Q. et al. “Sign backpropagation: An on-chip learning algorithm for analog RRAM neuromorphic computing systems,”. Neural Netw. 108, 217-223 (2018).
290. Yamaoka, M. “Low-power SRAM,” in Green Computing with Emerging Memory: Low-Power Computation for Social Innovation, 9781461408123, Springer New York, 59-85. https://doi.org/10. 1007/978-1-4614-0812-3_4/TABLES/4.2013,
291. Starzyk, J. A. and Jan, Y. W. “Voltage based winner takes all circuit for analog neural networks,” Midwest Symposium on Circuits and Systems, 1, 501-504, https://doi.org/10.1109/mwscas.1996. 594211, 1996
Acknowledgements
Author contributions
Competing interests
Additional information
supplementary material available at
https://doi.org/10.1038/s41467-024-45670-9.
Correspondence and requests for materials should be addressed to Mario Lanza.
http://www.nature.com/reprints
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
© The Author(s) 2024
- e-mail: mario.lanza@kaust.edu.sa
