دور التغيرات المفاجئة في التنبؤ بالتقلبات في أسواق المحاصيل الحيوية تحت الانقطاعات الهيكلية
معلومات المقال
الكلمات المفتاحية:
تنبؤ التقلبات
التحولات المفاجئة في التباين
نماذج MSGARCH
SV
الانقطاعات الهيكلية
الملخص
لقد حظي التنبؤ بتقلبات السلع الحيوية باهتمام كبير بسبب أهميته في إنتاج الوقود الحيوي واستهلاك الأسر. لقد أثارت عدة أحداث متطرفة، بما في ذلك جائحة COVID-19، اهتمامًا بدراسة دور الانقطاعات الهيكلية في نمذجة التقلبات والتنبؤ بها في هذه الأسواق. تدرس هذه الدراسة بشكل موسع أداء التنبؤ للنماذج الاقتصادية على مدى آفاق متعددة باستخدام نهج نافذة متحركة، مع وبدون احتساب التغيرات الهيكلية. نستغل خوارزمية ICSS لتحديد نوافذ التقدير داخل العينة لاستيعاب الانقطاعات الهيكلية. نحن نمدد الإجراء إلى ما بعد نماذج GARCH. أيضًا، تحدد معلومات الانقطاع المكتشفة دمى النظام. تقيّم الدراسة بشكل مبتكر أداء التنبؤ لنماذج معينة من فئة GARCH من خلال دمج المتغيرات الثنائية للتحولات المفاجئة في التباين غير المشروط. تكشف نتائجنا أن الأخذ في الاعتبار الانقطاعات الهيكلية المكتشفة داخليًا من خلال المتغيرات الدمية يؤدي إلى مكاسب كبيرة في دقة التنبؤ.
1. المقدمة
أنشأته وكالة حماية البيئة الأمريكية (EPA) التي تحدد أهدافًا سنوية لاستخدام الوقود الحيوي، بما في ذلك الديزل الحيوي، في قطاع النقل الأمريكي.
[69] يشير إلى أنه، مقارنة بمستويات الأسعار، تحمل صدمات الأسعار عمومًا معلومات أساسية للمنتج أو المستهلك – حيث أن التقلبات السعرية المفرطة
2. البيانات والإحصاءات الوصفية
3. النماذج التجريبية
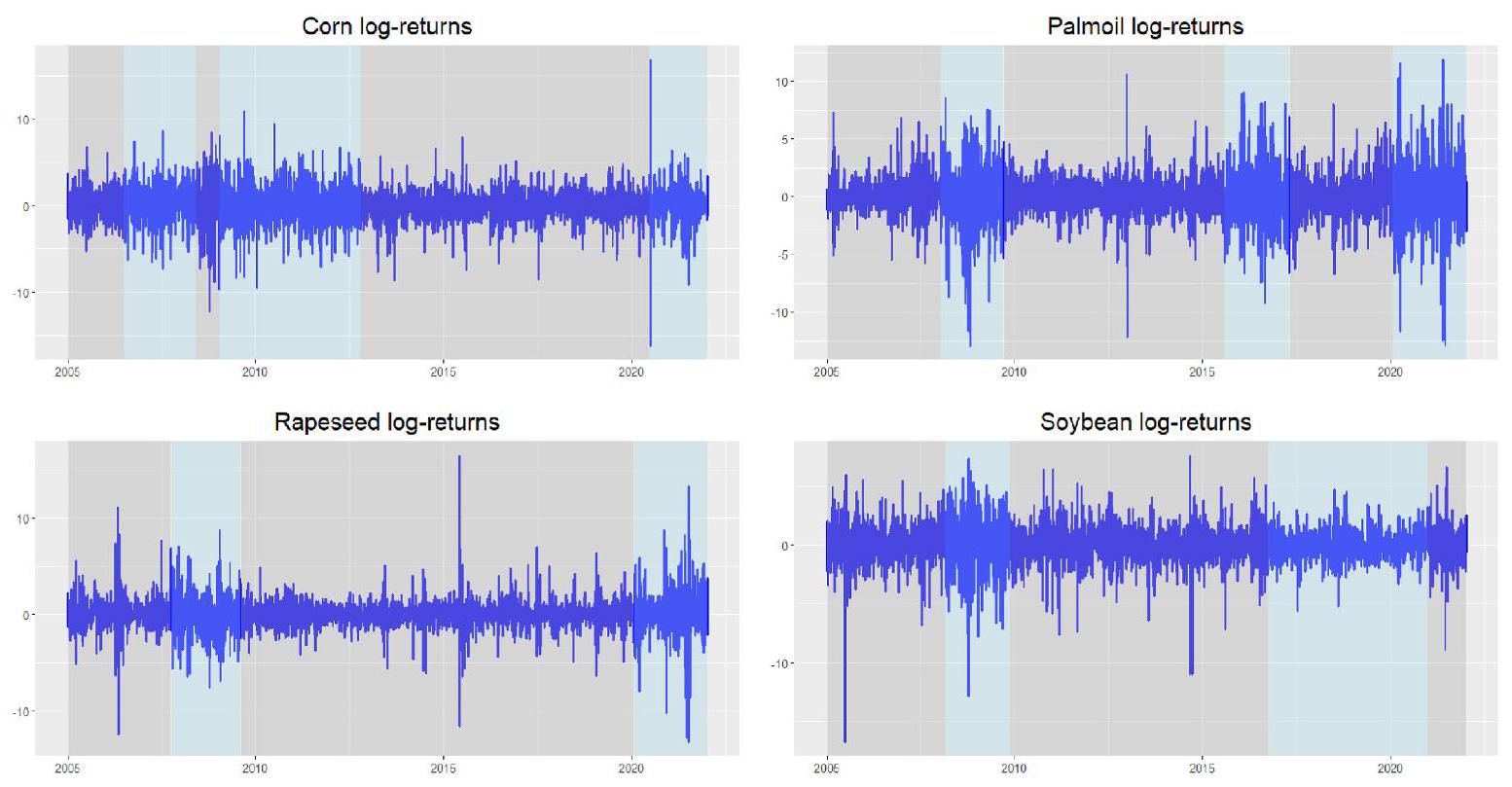
إحصائيات ملخصة لعوائد السجل اليومية.
| ذرة | زيت النخيل | زيت اللفت | فول الصويا | |
| حد أدنى | -16.191 | -12.921 | -13.239 | -16.741 |
| الحد الأقصى | ١٦.٧٩٩ | 11.829 | ١٦.٤٠٦ | 7.573 |
| معنى | 0.0259 | 0.0258 | 0.0272 | 0.021 |
| الانحراف المعياري | 1.9277 | 1.9649 | 1.5248 | 1.561 |
| الانحراف | -0.1608 | -0.0516 | 0.0681 | -0.769 |
| زيادة | 5.2627 | 5.3704 | 13.064 | ٧.٥٣٦ |
| جي-بي | 5150.23 | 5344.01 | ٣١,٦١٤.٢٣ | 10,958.59 |
| [0.000] | [0.000] | [0.000] | [0.000] | |
| ق(10) | ١٦.٨٨٨ | 153.13 | ١٧٧.٩٢ | 16.02 [0.099] |
| [0.076] | [0.000] | [0.000] | ||
|
|
٤٨١.٩٧ | ٨٥٠.١٤ | 748.26 | ٣٩١.٩٢ |
| [0.000] | [0.000] | [0.000] | [0.000] | |
| أرك(5) | 8791.4 | ٩٤٨٠.٨ | 12,044 | 15,568 |
| [0.000] | [0.000] | [0.000] | [0.000] | |
| أرك(10) | ٤٨١.٩٧ | ٨٥٠.١٤ | 748.26 | ٣٩١.٩٢ |
| [0.000] | [0.000] | [0.000] | [0.000] | |
| مؤشر الذيل | 3.357 [2.91، | 3.007 [2.61، | 3.453 [2.99، | 2.750 [2.38، |
| 3.80] | 3.40] | 3.91] | 3.11] | |
| عدد الملاحظات | 4440 | ٤٤٣٩ | 4440 | 4440 |
نماذج.
3.1. نماذج فئة GARCH
أين
نستخدم أيضًا نموذج Beta-t-skew-EGARCH في المرجع [32]؛ الذي نوجه القراء المهتمين لمزيد من التفاصيل.
3.2. نماذج التقلب العشوائي
نفترض أن العمليات
3.3. نماذج ذات انقطاعات محددة داخليًا
3.4. نماذج GARCH ذات التحويل ماركوف
أين
3.5. نماذج بأحجام نوافذ مختلفة
4. النتائج والمناقشة
4.1. مقاييس الخسارة وتحليل خارج العينة
QLIKE
في مقاييس الخسارة، نشير إلى وكيل للتقلبات اللاحقة (أي العوائد المربعة) بـ
4.2. توزيع الأدوار في التنبؤ
4.3. دقة التنبؤ على المدى القصير والطويل
مجموعة ثقة النموذج للذرة (
| آفاق التنبؤ | |||||||
| 1 | ٥ | 20 | 40 | ||||
| نماذج | قيمة p | نماذج | قيمة p | نماذج | قيمة p | نماذج | قيمة p |
| ماي | |||||||
| ICSS-آخر-BR-Skt-EGARCH | 1.000 | ICSS-آخر-BR-Skt-EGARCH | 1.000 | ICSS-آخر-BR-Skt-EGARCH | 1.000 | ICSS-آخر-BR-Skt-EGARCH | 1.000 |
| HMAE | |||||||
| MS-GARCH-N | 1.000 |
|
1.000 | 1.00-هم | 1.000 |
|
1.000 |
| 1.00-جارش-إس إس تي دي | 0.707 | MS-EGARCH-N | 0.170 | MS-EGARCH-N | 0.498 | MS-EGARCH-N | 0.428 |
| ICSS-GARCH-SSTD | 0.384 | ICSS-GARCH-N | 0.281 | ICSS-EGARCH-N | 0.425 | ||
| 0.25-EGARCH-SSTD | 0.415 | ||||||
| ICSS-آخر-BR-HM | 0.200 | ||||||
| 1.00-SV-ليف | 0.106 | ||||||
| 0.5-Skt-EGARCH. | 0.106 | ||||||
| HMSE | |||||||
| MS-GARCH-N | 1.000 |
|
1.000 | 1.00-هـ م | 1.000 |
|
1.000 |
| 0.25-جارش-STD | 0.106 | MS-EGARCH-N | 0.204 | MS-EGARCH-N | 0.375 | MS-EGARCH-N | 0.878 |
| 1.00-سف | 0.106 | ICSS-آخر-BR-HM | 0.171 | ICSS-EGARCH-N | 0.329 | 0.25-Skt-EGARCH | 0.878 |
| 1.00-جارش-ن | 0.106 | ICSS-آخر-BR-SVT | 0.171 | ICSS-آخر-BR-HM | 0.154 |
|
0.591 |
| ICSS-GARCH-N | 0.106 | 0.25-SVT | 0.169 | 0.5-SVt | 0.154 | ICSS-EGARCH-N | 0.516 |
| 0.5-جارش-ن | 0.106 | 0.5-SVt | 0.162 |
|
0.154 | 1.00-SV-ليف | 0.516 |
| 0.25-SVT | 0.106 |
|
0.125 |
|
0.154 | ICSS-آخر-BR-HM | 0.516 |
| ICSS-آخر-BR-HM | 0.106 |
|
0.125 | 1.00-SV-ليف | 0.154 | 0.5-SV-ليف | 0.466 |
|
|
0.125 |
|
0.154 | 0.25-SVT | 0.384 | ||
| ICSS-آخر-BR-SV | 0.100 | ||||||
| كيو لايك | |||||||
| MS-GARCH-N | 1.000 | MS-EGARCH-N | 1.000 | MS-EGARCH-N | 1.000 | 0.25-EGARCH-SSTD | 1.000 |
| 0.5-جارش-ن | 0.920 |
|
0.936 |
|
0.857 | 0.5-Skt-EGARCH | 0.832 |
| 0.25-جارتش-STD | 0.920 | ICSS-آخر-BR-HM | 0.936 | 0.25-EGARCH-SSTD | 0.857 |
|
0.832 |
| 1.00-جارش-ن | 0.812 | 0.25-Skt-EGARCH | 0.936 | 0.5-Skt-EGARCH | 0.604 | ICSS-EGARCH-N | 0.832 |
| ICSS-GARCH-N | 0.777 | 0.5-Skt-EGARCH | 0.877 | 0.5-SVT | 0.492 | MS-EGARCH-N | 0.832 |
| 1.00-سف | 0.777 | 0.5-SVT | 0.739 | 0.25-SV-ليف | 0.431 | 1.00-SV-ليف | 0.801 |
| 0.5-SVT | 0.777 | ICSS-EGARCH-GHYP | 0.739 | ICSS-آخر-BR-HM | 0.431 | 0.5-SVT | 0.633 |
| 0.25-SVT | 0.752 | 0.25-SVT | 0.677 | ICSS-GJR-GARCH-N | 0.357 | 0.25-SVT | 0.509 |
| ICSS-آخر-BR-HM | 0.325 | 1.00-SV-ليف | 0.591 | 1.00-سف | 0.357 | ICSS-آخر-BR-HM | 0.496 |
| ICSS-آخر-BR-SV-مستوى | 0.142 | ||||||
تأخذ في الاعتبار الانكسارات الهيكلية الذاتية (باستخدام دمى الانكسار المعتمدة على ICSS والعينة الفرعية الأخيرة) وتؤدي بشكل جيد؛ يليها في الأداء نماذج GARCH ذات التحول ماركوف. ثم نركز على أداء نماذج النظام الواحد المقدرة باستخدام نوافذ كاملة ونصف وربع الحجم على المدى القصير والطويل. نجد أن نماذج GARCH ذات النظام الواحد مع نافذة كاملة تؤدي بشكل أفضل على المدى القصير مقارنةً بالمدى الطويل، بينما تظهر نماذج النظام الواحد ذات أحجام النوافذ نصف وربع أداءً مشابهًا على الآفاق القصيرة والطويلة.
4.4. اختبار اتجاه التغيير
مجموعة ثقة النموذج لزيت النخيل (
| آفاق التنبؤ | |||||||
| 1 | ٥ | 20 | 40 | ||||
| نماذج | قيمة p | نماذج | قيمة p | نماذج | قيمة p | نماذج | قيمة p |
| ماي | |||||||
| ICSS-آخر-BR-Skt-EGARCH | 1.000 | ICSS-آخر-BR-Skt-EGARCH | 1.000 | ICSS-آخر-BR-Skt-EGARCH | 1.000 | 0.5-Skt-EGARCH | 1.000 |
| 0.5-Skt-EGARCH | 0.611 | 0.5-Skt-EGARCH | 0.247 | 0.5-Skt-EGARCH | 0.533 | ICSS-آخر-BR-Skt-EGARCH | 0.862 |
|
|
0.114 | 0.5-SV-ليف | 0.513 | 0.25-Skt-EGARCH | 0.543 | ||
| 0.25-Skt-EGARCH | 0.215 | 0.5-SVT | 0.297 | ||||
| HMAE | |||||||
| 0.5-Skt-EGARCH | 1.000 | ICSS-آخر-BR-HM | 1.000 | 0.5-GJR-GARCH-STD | 1.000 | 0.5-GJR-GARCH-STD | 1.000 |
| ICSS-GARCH-STD | 0.668 | 0.5-جارش-ستاندرد | 0.243 | ||||
| 0.25-Skt-EGARCH | 0.668 | 0.5-SVT | 0.108 | ||||
| HMSE | |||||||
| 0.5-جارش-STD | 1.000 | 0.5-GJR-GARCH-STD | 1.000 | 0.5-GJR-GARCH-STD | 1.000 | 0.5-GJR-GARCH-STD | 1.000 |
| MS-GJR-GARCH-STD | 0.367 | ||||||
| ICSS-GJR-GARCH-STD | 0.367 | ||||||
| 0.25-GJR-GARCH-N | 0.367 | ||||||
| 1.00-GJR-GARCH-STD | 0.367 | ||||||
| كيو لايك | |||||||
| 0.5-جارش-STD | 1.000 | 0.5-جارش-STD | 1.000 | 0.5-GJR-GARCH-STD | 1.000 | 0.5-GJR-GARCH-SSTD | 1.000 |
| MS-GJR-GARCH-STD | 0.456 | ICSS-GARCH-STD | 0.644 | 1.00-SVT | 0.503 | 1.00-Skt-EGARCH | 0.594 |
| ICSS-GARCH-STD | 0.456 | MS-GJR-GARCH-SSTD | 0.644 | ICSS-GJR-GARCH-STD | 0.503 | 0.25-Skt-EGARCH | 0.594 |
| 1.00-جارتش-STD | 0.456 | 0.25-Skt-EGARCH | 0.644 | MS-GARCH-SSTD | 0.503 | ICSS-GJR-GARCH-SSTD | 0.430 |
| 1.00-جارش | 0.644 | 0.25-Skt-EGARCH | 0.503 | MS-GJR-GARCH-SSTD | 0.278 | ||
| 1.00-SVT | 0.201 | 1.00-EGARCH-N | 0.106 | ||||
مجموعة ثقة النموذج لزيت اللفت (
| آفاق التنبؤ | |||||||
| 1 | ٥ | 20 | 40 | ||||
| نماذج | قيمة p | نماذج | قيمة p | نماذج | قيمة p | نماذج | قيمة p |
| ماي | |||||||
| 0.5-Skt-EGARCH | 1.000 | 0.5-Skt-EGARCH | 1.000 | 0.5-Skt-EGARCH | 1.000 | 0.5-Skt-EGARCH | 1.000 |
| ICSS-آخر-BR-ES | 0.199 | ICSS-آخر-BR-ES | 0.618 | ICSS-آخر-BR-ES | 0.285 | ||
| 0.5-SV-ليف | 0.53 | 0.5-SV-ليف | 0.185 | ||||
| 0.25-Skt-EGARCH | 0.337 | 0.25-Skt-EGARCH | 0.185 | ||||
| 0.25-SV-ليف | 0.191 | 0.25-SV | 0.134 | ||||
| HMAE | |||||||
| 0.25-EGARCH-STD | 1.000 | 0.25-جارتش-STD | 1.000 | 0.5-جارش-إس إس تي دي | 1.000 | 0.25-GJR-GARCH-SSTD | 1.000 |
| ICSS-GARCH-SSTD | 0.67 | ICSS-EGARCH-SSTD | 0.702 | ||||
| MS-GJR-GARCH-STD | 0.67 | MS-GJR-GARCH-STD | 0.300 | ||||
| 1.00-جارش-ن | 0.67 | ||||||
| HMSE | |||||||
| MS-EGARCH-SSTD | 1.000 | 0.25-جارش-إس إس تي دي | 1.000 | 0.5-جارش-STD | 1.000 | 0.25-GJR-GARCH-SSTD | 1.000 |
| ICSS-GJR-GARCH-N | 0.863 | ICSS-EGARCH-SSTD | 0.776 | ||||
| 1.00-جارش-ن | 0.863 | MS-GJR-GARCH-STD | 0.145 | ||||
| 0.25-Skt-EGARCH | 0.863 | ||||||
| 0.5-Skt-EGARCH | 0.742 | ||||||
| كيو لايك | |||||||
| 0.5-Skt-EGARCH | 1.000 | MS-GJR-GARCH-STD | 1.000 | MS-GJR-GARCH-STD | 1.000 | MS-GJR-GARCH-STD | 1.000 |
| MS-EGARCH-SSTD | 0.999 | ICSS-GJR-GARCH-N | 0.129 | ICSS-GJR-GARCH-SSTD | 0.692 | ||
| 1.00-Skt-EGARCH | 0.999 | 0.25-Skt-EGARCH | 0.129 | ||||
| ICSS-GARCH-N | 0.966 | 1.00-GJR-GARCH-N | 0.129 | ||||
| 0.25-Skt-EGARCH | 0.943 | 0.5-Skt-EGARCH | 0.107 | ||||
مجموعة ثقة النموذج لفول الصويا (
| آفاق التنبؤ | |||||||
| 1 | ٥ | 20 | 40 | ||||
| نماذج | قيمة p | نماذج | قيمة p | نماذج | قيمة p | نماذج | قيمة p |
| ماي | |||||||
| ICSS-آخر-BR-HM | 1.000 | ICSS-آخر-BR-Skt-EGARCH | 1.000 | 0.5-Skt-EGARCH | 1.000 | ICSS-آخر-BR-Skt-EGARCH | 1.000 |
| 0.5-Skt-EGARCH | 0.135 | ||||||
| HMAE | |||||||
| 1.00-هـ م | 1.000 |
|
1.000 |
|
1.000 | ICSS-EGARCH-STD | 1.000 |
| ICSS-EGARCH-STD | 0.371 | ICSS-EGARCH-STD | 0.105 |
|
0.889 | ||
| HMSE | |||||||
| 1.00-هـ م | 1.000 | ICSS-EGARCH-STD | 1.000 | ICSS-GARCH-STD | 1.000 | ICSS-EGARCH-STD | 1.000 |
| MS-EGARCH-N | 0.578 |
|
0.433 | 1.00-هم | 0.395 | ||
| ICSS-EGARCH-GHYP | 0.147 | MS-EGARCH-N | 0.113 | ||||
| كيو لايك | |||||||
| ICSS-EGARCH-GHYP | 1.000 | 1.00-SVT | 1.000 | 1.00-SVT | 1.000 | MS-GJR-GARCH-SSTD | 1.000 |
| 1.00-SVT | 0.637 | 1.00-EGARCH-GHYP | 0.254 | MS-GJR-GARCH-SSTD | 0.711 | 1.00-SVT | 0.637 |
| 1.00-EGARCH-GHYP | 0.55 | 0.5-SVT | 0.254 | 1.00-EGARCH-GHYP | 0.615 | 0.5-SVT | 0.507 |
| 0.5-SVT | 0.55 | ICSS-EGARCH-GHYP | 0.254 | 0.5-SVT | 0.615 | 1.00-EGARCH-GHYP | 0.101 |
| 0.25-جارش-إس إس تي دي | 0.55 | 0.25-SVT | 0.254 | 0.5-EGARCH-GHYP | 0.607 | 0.5-إي غارش-جي هايبر | 0.101 |
| 0.5-جارش-ن | 0.537 | 0.5-إي غارش-ن | 0.254 | 0.25-جارتش-STD | 0.595 | 0.25-SVT | 0.101 |
| 0.25-SVT | 0.424 | 0.25-جارتش-STD | 0.254 | ICSS-GARCH-GHYP | 0.397 | ||
| MS-GJR-GARCH-SSTD | 0.114 | MS-GJR-GARCH-SSTD | 0.118 | 0.25-SVT | 0.335 | ||
| ICSS-آخر-BR-SVT | 0.177 | ||||||
| ICSS-آخر-BR-GARCH-STD | 0.121 | ||||||
الانقطاعات) عبر جميع آفاق التنبؤ المعنية.
وفقًا لنتائج MCS، فإن النماذج التي تتجاهل عدم الاستقرار (مثل النماذج ذات النظام الواحد) تظهر دقة تنبؤ أقل فيما يتعلق بحركات التقلب. علاوة على ذلك، فإن النماذج ضمن فئة GARCH التي تدمج متغيرات كسر قائمة على ICSS ونماذج MS-GARCH لا تقدم تنبؤات جيدة لاتجاه التقلب. كما نلاحظ أنه عند دمجها مع الكسور، فإن نماذج ES لبعض خطوات التنبؤ تتنبأ بدقة بتقلبات الذرة الصاعدة والهابطة.
5. الخاتمة
عبر جميع آفاق التنبؤ لجميع السلع الحيوية المعتمدة. على وجه الخصوص، تتفوق نماذج آخر فترة على جميع النماذج الأخرى في هذا الاختبار. وفقًا لنتائج MCS، تظهر النماذج التي تتجاهل عدم الاستقرار (مثل نماذج النظام الواحد) دقة تنبؤ أقل لحركات التقلب.
بيان مساهمة مؤلفي CRediT
تنسيق، تحقيق، برمجيات، تحقق.
إعلان عن الذكاء الاصطناعي التوليدي والتقنيات المدعومة بالذكاء الاصطناعي في عملية الكتابة
إعلان عن تضارب المصالح
المصالح أو العلاقات الشخصية التي قد تبدو أنها تؤثر على العمل المبلغ عنه في هذه الورقة.
توفر البيانات
شكر وتقدير
الملحق
النماذج الاقتصاد قياسية
1 Single regime with whole window size GARCH-class models
1.0-GARCH-ST, 1.0-GARCH-N, 1.0-GARCH-SST, 1.0-GJR-GARCH-N, 1.0-GARCH-GHYP, 1.0-GJR-GARCH-ST, 1.0-GJR-
GARCH-GHYP, 1.0-GJR-GARCH-SST, 1.0-EGARCH-ST, 1.0-EGARCH-N, 1.0-EGARCH-SST, 1.0-EGARCH-GHYP, 1.0-two-
comp-Beta-t-EGARCH, 1.0-one-comp-Beta-t-EGARCH
2 Single regime with half window size GARCH-class models
0.5-GARCH-ST, 0.5-GARCH-N, 0.5-GARCH-SST, 0.5-GARCH-GHYP, 0.5-GJR-GARCH-ST, 0.5-GJR-GARCH-N, 0.5-GJR-
GARCH-SST, 0.5-GJR-GARCH-GHYP, 0.5-EGARCH-ST, 0.5-EGARCH-N, 0.5-EGARCH-SST, 0.5-EGARCH-GHYP, 0.5-two-
comp-Beta-t-EGARCH, 0.5-one-comp-Beta-t-EGARCH
3 Single regime with quarter window size GARCH-class models
0.25-GARCH-ST, 0.25-GARCH-N, 0.25-GARCH-SST, 0.25-GARCH-GHYP, 0.25-GJR-GARCH-ST, 0.25-GJR-GARCH-N,
0.25-GJR-GARCH-SST, 0.25-GJR-GARCH-GHYP, 0.25-EGARCH-ST, 0.25-EGARCH-N, 0.25-EGARCH-SST, 0.25-EGARCH-
GHYP, 0.25-two-comp-Beta-t-EGARCH, 0.25-one-comp-Beta-t-EGARCH
4 Single regime with full window size SV models
1.0-SVT, 1.0-SV, 1.0-SV-lev
5 text { Single regime with half window size SV models }
0.5-SVT, 0.5-SV, 0.5-SV-lev
6 Single regime with quarter window size SV models
0.25-SVT, 0.25-SV, 0.25-SV-lev
7 text { ICSS regime dummy GARCH-class models }
ICSS-GARCH-ST, ICSS-GARCH-N, ICSS-GARCH-SST, ICSS-GARCH-GHYP, ICSS-GJR-GARCH-ST, ICSS-GJR-GARCH-N,
ICSS-GJR-GARCH-SST, ICSS-GJR-GARCH-GHYP, ICSS-EGARCH-ST, ICSS-EGARCH-N, ICSS-EGARCH-SST, ICSS-EGARCH-
GHYP
8 ICSS last break period GARCH-class models
ICSS-Last-BR-GARCH-ST, ICSS-Last-BR-GARCH-N, ICSS-Last-BR-GARCH-SST, ICSS-Last-BR-GARCH-GHYP, ICSS-Last-BR-
GJR-GARCH-ST, ICSS-Last-BR-GJR-GARCH-N, ICSS-Last-BR-GJR-GARCH-SST, ICSS-Last-BR-GJR-GARCH-GHYP, ICSS-
Last-BR-EGARCH-ST, ICSS-Last-BR-EGARCH-N, ICSS-Last-BR-EGARCH-SST, ICSS-Last-BR-EGARCH-GHYP, ICSS-Last-BR-
two-comp-Beta-t-EGARCH, ICSS-Last-BR-one-comp-Beta-t-EGARCH
9 ICSS last break period SV models
ICSS-Last-BR-SVT, ICSS-Last-BR-SV, ICSS-Last-BR-SV-lev
10 Markov-switching GARCH models
MS-GARCH-ST, MS-GARCH-N, MS-GARCH-SST, MS-GJR-GARCH-ST, MS-GJR-GARCH-N, GJR-MS-GARCH-SST, MS-
EGARCH-ST, MS-EGARCH-N, MS-EGARCH-SST
11 Full, half, and quarter window size single regime HM, ES models
1.0-ES, 1.0-HM, 0.5-ES, 0.5-HM, 0.25-ES, 0.25.0-HM
12 ICSS last break period HM and ES models
ICSS-Last-BR-ES, ICSS-Last-BR-HM
References
[2] Amendola A, Braione M, Candila V, Storti G. A Model Confidence Set approach to the combination of multivariate volatility forecasts. Int
[3] Anjum H, Malik F. Forecasting risk in the US Dollar exchange rate under volatility shifts. N Am J Econ Finance 2020;54:101257. https://doi.org/10.1016/j. najef.2020.101257.
[4] Apergis N, Payne JE, Menyah K, Wolde-Rufael Y. On the causal dynamics between emissions, nuclear energy, renewable energy, and economic growth. Ecol Econ 2010;69:2255-60. https://doi.org/10.1016/j.ecolecon.2010.06.014.
[5] Ardia D, Bluteau K, Boudt K, Catania L. Forecasting risk with Markov-switching GARCH models: a large-scale performance study. Int J Forecast 2018;34:733-47.
[6] Ardia D, Bluteau K, Boudt K, Catania L, Trottier D-A. Markov-switching GARCH models in R : the MSGARCH package. J Stat Software 2019;91. https://doi.org/ 10.18637/jss.v091.i04.
[7] Berger J, Dalheimer B, Brümmer B. Effects of variable EU import levies on corn price volatility. Food Pol 2021;102:102063. https://doi.org/10.1016/j. foodpol.2021.102063.
[8] Bergsli Lø, Lind AF, Molnár P, Polasik M. Forecasting volatility of bitcoin. Res Int Bus Finance 2022;59:101540. https://doi.org/10.1016/j.ribaf.2021.101540.
[9] Bergtold JS, Shanoyan A, Fewell JE, Williams JR. Annual bioenergy crops for biofuels production: farmers’ contractual preferences for producing sweet sorghum. Energy 2017;119:724-31. https://doi.org/10.1016/j. energy.2016.11.032.
[10] Bollerslev T. Generalized autoregressive conditional heteroskedasticity. J Economtrics 1986;31:307-27.
[11] Bollerslev T. The story of GARCH: a personal odyssey. J Econom 2023;234:96-100.
[12] Bouri E, Dutta A, Saeed T. Forecasting ethanol price volatility under structural breaks. Biofuels, Bioprod. Bioref. 2021;15:250-6. https://doi.org/10.1002/ bbb. 2158.
[13] Carpio LGT. The effects of oil price volatility on ethanol, gasoline, and sugar price forecasts. Energy 2019;181:1012-22. https://doi.org/10.1016/j. energy.2019.05.067.
[14] Chang T-H, Su H-M. The substitutive effect of biofuels on fossil fuels in the lower and higher crude oil price periods. Energy 2010;35:2807-13.
[15] Charfeddine L. True or spurious long memory in volatility: further evidence on the energy futures markets. Energy Pol 2014;71:76-93. https://doi.org/10.1016/j. enpol.2014.04.027.
[16] Charles A, Darné O. Forecasting crude-oil market volatility: further evidence with jumps. Energy Econ 2017;67:508-19. https://doi.org/10.1016/j. eneco.2017.09.002.
[17] Cheng IH, Xiong W. Financialization of commodity markets. Annu Rev Financ Econ 2014;6:419-41.
[18] Chuang I-Y, Lu J-R, Lee P-H. Forecasting volatility in the financial markets: a comparison of alternative distributional assumptions. Appl Financ Econ 2007;17: 1051-60. https://doi.org/10.1080/09603100600771000.
[19] Degiannakis S, Filis G. Forecasting oil price realized volatility using information channels from other asset classes. J Int Money Finance 2017;76:28-49. https://doi. org/10.1016/j.jimonfin.2017.05.006.
[20] Degiannakis S, Filis G, Klein T, Walther T. Forecasting realized volatility of agricultural commodities. Int J Forecast 2022;38:74-96. https://doi.org/10.1016/ j.ijforecast.2019.08.011.
[21] Dutta A, Junttila J, Uddin GS. Forecasting the volatility of biofuel feedstock prices: the US Evidence. Biofuels Bioprod Bioref 2019;13:912-9.
[22] EBB. About biodiesel. European Biodiesel Board. https://ebb-eu.org/(accessed 21 February 2023)..
[23] EIA. Monthly biodiesel production report. U.S. Energy Information Administration; 2020. https://www.eia.gov/biofuels/biodiesel/production/. [Accessed 21 February 2023].
[24] Engle RF. Autoregressive conditional heteroscedasticity with estimates of the variance of U.K. inflation. Econometrica 1982;50:987-1008.
[25] Ewing BT, Malik F. Estimating volatility persistence in oil prices under structural breaks. Financ Rev 2010;45:1011-23. https://doi.org/10.1111/j.15406288.2010.00283.x.
[26] Galanos A. Rugarch: univariate GARCH models. 2022. https://cran.r-project.org/ web/packages/rugarch/rugarch.pdf.
[27] Glosten LR, Jagannathan R, Runkle D. On the relation between the expected value and the volatility of the nominal excess return on stocks. J Finance 1993;XLVIII.
[28] Haas M, Mittnik S, Paolella M. A new approach to Markov-switching GARCH models. J Financ Econom 2004;2:493-530.
[29] Hajkowicz S, Negra C, Barnett P, Clark M, Harch B, Keating B. Food price volatility and hunger alleviation – can Cannes work? Agric Food Secur 2012;1. https://doi. org/10.1186/2048-7010-1-8.
[30] Hansen PR, Lunde A, Nason JM. The model confidence set. Econometrica 2011;79: 453-97.
[31] Harvey A, Ruiz E, Shephard N. Multivariate stochastic variance models. Rev Econ Stud 1994;61:247-64.
[32] Harvey A, Sucarrat G. EGARCH models with fat tails, skewness and leverage. Comput Stat Data Anal 2014;76:320-38. https://doi.org/10.1016/j. csda.2013.09.022.
[33] Hasanov AS, Avazkhodjaev SS. Stochastic volatility models with endogenous breaks in volatility forecasting. In: Terzioglu MK, editor. Advances in econometrics, operational research, data science and actuarial studies. Cham: Springer International Publishing; 2022. p. 81-97.
[34] Hasanov AS, Poon WC, Al-Freedi A, Heng ZY. Forecasting volatility in the biofuel feedstock markets in the presence of structural breaks: a comparison of alternative distribution functions. Energy Econ 2018;70:307-33. https://doi.org/10.1016/j. eneco.2018.01.011.
[35] Hasanov AS, Shaiban MS, Al-Freedi A. Forecasting volatility in the petroleum futures markets: a re-examination and extension. Energy Econ 2020;86:104626. https://doi.org/10.1016/j.eneco.2019.104626.
[36] Hasanov AS, Shitan M. Modeling inflation volatility: evidence from two post-Soviet economies. Int J Stat Sci 2012;12:9-27.
[37] Hill BM. A simple general approach to inference about the tail of a distribution. Ann Stat 1975;3:1163-74. https://doi.org/10.1214/aos/1176343247.
[38] Hosszejni D, Kastner G. Efficient bayesian inference for stochastic volatility (SV). The “stochvol” R package version 3.2.0 2022. https://cran.r-project.org/web/p ackages/stochvol/stochvol.pdf.
[39] Hyndman R, Athanasopoulos G, Bergmeir C, Caceres G, Chhay L, Kuroptev K, O’Hara-Wild M, Petropoulos F, Razbash S, Wang E, Yasmeen F. Forecast:
forecasting functions for time series and linear models. 2022. https://cran.r-project .org/web/packages/forecast/forecast.pdf.
[40] Inclán C, Tiao GC. Use of cumulative sums of squares for retrospective detection of changes of variance. J Am Stat Assoc 1994;89:913-23.
[41] Kang SH, Cheong C, Yoon S-M. Structural changes and volatility transmission in crude oil markets. Phys Stat Mech Appl 2011;390:4317-24. https://doi.org/ 10.1016/j.physa.2011.06.056.
[42] Kang SH, Kang S-M, Yoon S-M. Forecasting volatility of crude oil markets. Energy Econ 2009;31:119-25. https://doi.org/10.1016/j.eneco.2008.09.006.
[43] Klein T, Walther T. Oil price volatility forecast with mixture memory GARCH. Energy Econ 2016;58:46-58. https://doi.org/10.1016/j.eneco.2016.06.004.
[44] Kumar D, Maheswaran S. Modelling asymmetry and persistence under the impact of sudden changes in the volatility of the Indian stock market. IIMB Manage Rev 2012;24:123-36.
[45] Lamoureux CG, Lastrapes WD. Persistence in variance, structural change, and the GARCH model. J Bus Econ Stat 1990;8:225. https://doi.org/10.2307/1391985.
[46] Law SH. Has stock market volatility in the Kuala Lumpur Stock Exchange returned to pre-Asian financial crisis levels? ASEAN Econ Bull 2006;23:212-29.
[47] Li X, Guo Q, Liang C, Umar M. Forecasting gold volatility with geopolitical risk indices. Res Int Bus Finance 2023;64:101857. https://doi.org/10.1016/j. ribaf.2022.101857.
[48] Li Y, Liang C, Ma F, Wang J. The role of the IDEMV in predicting European stock market volatility during the COVID-19 pandemic. Finance Res Lett 2020;36: 101749. https://doi.org/10.1016/j.frl.2020.101749.
[49] Liu J, Wei Y, Ma F, Wahab M. Forecasting the realized range-based volatility using dynamic model averaging approach. Econ Modell 2017;61:12-26. https://doi.org/ 10.1016/j.econmod.2016.11.020.
[50] Liu Y, Niu Z, Suleman MT, Yin L, Zhang H. Forecasting the volatility of crude oil futures: the role of oil investor attention and its regime switching characteristics under a high-frequency framework. Energy 2022;238:121779. https://doi.org/ 10.1016/j.energy.2021.121779.
[51] Lyócsa S, Molnár P. Exploiting dependence: day-ahead volatility forecasting for crude oil and natural gas exchange-traded funds. Energy 2018;155:462-73. https://doi.org/10.1016/j.energy.2018.04.194.
[52] Lyócsa S, Molnár P, Todorova N. Volatility forecasting of non-ferrous metal futures: covariances, covariates or combinations? J Int Financ Mark Inst Money 2017;51: 228-47. https://doi.org/10.1016/j.intfin.2017.08.005.
[53] Lyócsa S, Molnár P, Výrost T. Stock market volatility forecasting: do we need highfrequency data? Int J Forecast 2021;37:1092-110.
[54] Mei D, Xie Y. U.S. grain commodity futures price volatility: does trade policy uncertainty matter? Finance Res Lett 2022;48:103028. https://doi.org/10.1016/j. frl.2022.103028.
[55] Nelson DB. Conditional heteroskedasticity in asset returns: a new approach. Econometrica 1991;59:347-70.
[56] Nomikos NK, Pouliasis PK. Forecasting petroleum futures markets volatility: the role of regimes and market conditions. Energy Econ 2011;33:321-37. https://doi. org/10.1016/j.eneco.2010.11.013.
[57] Park B-J. The COVID-19 pandemic, volatility, and trading behavior in the bitcoin futures market. Res Int Bus Finance 2022;59:101519. https://doi.org/10.1016/j. ribaf.2021.101519.
[58] Peng L, Liang C. Sustainable development during the post-COVID-19 period: role of crude oil. Resour Pol 2023;85:103843. https://doi.org/10.1016/j. resourpol.2023.103843.
[59] Pesaran MH, Timmermann A. Selection of estimation window in the presence of structural breaks. J Econom 2007;137:134-61.
[60] Qian L, Wang J, Ma F, Li Z. Bitcoin volatility predictability-The role of jumps and regimes. Finance Res Lett 2022;47:102687. https://doi.org/10.1016/j. frl.2022.102687.
[61] Rapach DE, Strauss JK. Structural breaks and GARCH models of exchange rate volatility. J Appl Econ 2008;23:65-90. https://doi.org/10.1002/jae.976.
[62] Sadorsky P. Modeling and forecasting petroleum futures volatility. Energy Econ 2006;28:467-88. https://doi.org/10.1016/j.eneco.2006.04.005.
[63] Salisu AA, Gupta R, Bouri E, Ji Q. The role of global economic conditions in forecasting gold market volatility: evidence from a GARCH-MIDAS approach. Res Int Bus Finance 2020;54:101308. https://doi.org/10.1016/j.ribaf.2020.101308.
[64] Sansó A, Arragó V, Carrion JL. Testing for change in the unconditional variance of financial time series. Rev Econ Financ 2004;4:32-53.
[65] Segnon M, Bekiros S. Forecasting volatility in bitcoin market. Ann Finance 2020; 16:435-62. https://doi.org/10.1007/s10436-020-00368-y.
[66] Segnon M, Gupta R, Wilfling B. Forecasting stock market volatility with regimeswitching GARCH-MIDAS: the role of geopolitical risks. Int J Forecast 2023. https://doi.org/10.1016/j.ijforecast.2022.11.007.
[67] Serra T. Volatility spillovers between food and energy markets: a semiparametric approach. Energy Econ 2011;33:1155-64. https://doi.org/10.1016/j. eneco.2011.04.003.
[68] Sucarrat G. Betategarch: simulation, estimation and forecasting of beta-skew-tEGARCH models. 2022. https://cran.r-project.org/web/packages/betategarch/be tategarch.pdf.
[69] Swinnen J, Squicciarini P. Mixed messages on prices and food security. Science 2012;335:405-6.
[70] Umar M, Su C-W, Rizvi SKA, Shao X-F. Bitcoin: a safe haven asset and a winner amid political and economic uncertainties in the US? Technol Forecast Soc Change 2021;167:120680.
[71] USDA. Oilseeds: world markets and trade. United States Department of Agriculture; 2023. https://apps.fas.usda.gov/psdonline/circulars/oilseeds.pdf. [Accessed 21 February 2023].
[72] Wang L, Wu J, Cao Y, Hong Y. Forecasting renewable energy stock volatility using short and long-term Markov switching GARCH-MIDAS models: either, neither or both? Energy Econ 2022;111:106056. https://doi.org/10.1016/j. eneco.2022.106056.
[73] Wong ZY, Chin WC, Tan SH. Daily value-at-risk modeling and forecast evaluation: the realized volatility approach. J Finance Data Sci 2016;2:171-87. https://doi. org/10.1016/j.jfds.2016.12.001.
[74] Yahya M, Kanjilal K, Dutta A, Uddin GS, Ghosh S. Can clean energy stock price rule oil price? New evidences from a regime-switching model at first and second moments. Energy Econ 2021;95:105116. https://doi.org/10.1016/j. eneco.2021.105116.
- Corresponding author. Monash University Malaysia campus, Jalan Lagoon Selatan, 46150 Bandar Sunway, Selangor, Malaysia.
E-mail addresses: akram.hasanov@monash.edu (A.S. Hasanov), a.burkhanov@tsue.uz (A.U. Burkhanov), b.usmonov@tsue.uz (B. Usmonov), n.xajimuratov@tsue. uz (N.S. Khajimuratov), eshmamatovamadina@tsue.uz (M.M. Khurramova).
DOI: https://doi.org/10.1016/j.energy.2024.130535
Publication Date: 2024-02-08
The role of sudden variance shifts in predicting volatility in bioenergy crop markets under structural breaks
A R T I C L E I N F O
Keywords:
Volatility forecasting
Sudden variance shifts
MSGARCH models
SV
Structural breaks
Abstract
Forecasting bioenergy feedstock commodity volatility has received significant attention due to its importance in biofuel production and household consumption. Several extreme events, including the COVID-19 pandemic, have sparked interest in studying the role of structural breaks on volatility modeling and prediction in these markets. This study extensively examines the prediction performance of econometric models at multiple horizons using a rolling-window approach, with and without accommodating structural changes. We exploit the ICSS algorithm to determine the in-sample estimation windows to accommodate structural breaks. We extend the procedure beyond GARCH-class models. Also, the detected break information defines the regime dummies. The study innovatively evaluates the prediction performance of specific GARCH-class models by incorporating binary variables for sudden shifts in unconditional variance. Our findings reveal that accounting for the endogenously detected structural breaks through the dummy variables leads to considerable forecast accuracy gains.
1. Introduction
established by the US Environmental Protection Agency (EPA) that sets annual targets for the use of biofuels, including biodiesel, in the US transportation sector.
[69] note that, compared to price levels, price shocks generally carry information that is essential for the producer or the consumer- excessive
2. Data and descriptive statistics
3. Empirical models

Summary statistics for the daily log returns.
| Corn | Palm oil | Rapeseed oil | Soybean | |
| Minimum | -16.191 | -12.921 | -13.239 | -16.741 |
| Maximum | 16.799 | 11.829 | 16.406 | 7.573 |
| Mean | 0.0259 | 0.0258 | 0.0272 | 0.021 |
| Std. dev. | 1.9277 | 1.9649 | 1.5248 | 1.561 |
| Skewness | -0.1608 | -0.0516 | 0.0681 | -0.769 |
| Excess | 5.2627 | 5.3704 | 13.064 | 7.536 |
| J-B | 5150.23 | 5344.01 | 31,614.23 | 10,958.59 |
| [0.000] | [0.000] | [0.000] | [0.000] | |
| Q(10) | 16.888 | 153.13 | 177.92 | 16.02 [0.099] |
| [0.076] | [0.000] | [0.000] | ||
|
|
481.97 | 850.14 | 748.26 | 391.92 |
| [0.000] | [0.000] | [0.000] | [0.000] | |
| ARCH(5) | 8791.4 | 9480.8 | 12,044 | 15,568 |
| [0.000] | [0.000] | [0.000] | [0.000] | |
| ARCH(10) | 481.97 | 850.14 | 748.26 | 391.92 |
| [0.000] | [0.000] | [0.000] | [0.000] | |
| Tail index | 3.357 [2.91, | 3.007 [2.61, | 3.453 [2.99, | 2.750 [2.38, |
| 3.80] | 3.40] | 3.91] | 3.11] | |
| No. of Obs | 4440 | 4439 | 4440 | 4440 |
models.
3.1. The GARCH-class models
where
We also employ the Beta-t-skew-EGARCH model in Ref. [32]; to which we refer interested readers for further details.
3.2. The stochastic volatility models
We assume that the processes
3.3. Models with endogenously determined breaks
3.4. Markov-switching GARCH models
where
3.5. Models with different window sizes
4. Results and discussion
4.1. Loss metrics and out-of-sample analysis
QLIKE
In the loss measures, we denote a proxy for ex post volatility (i.e., squared returns) by
4.2. The role distributions in forecasting
4.3. Forecast accuracy in the short and long term
Model confidence set for corn (
| Forecast horizons | |||||||
| 1 | 5 | 20 | 40 | ||||
| Models | p-value | Models | p-value | Models | p-value | Models | p-value |
| MAE | |||||||
| ICSS-Last-BR-Skt-EGARCH | 1.000 | ICSS-Last-BR-Skt-EGARCH | 1.000 | ICSS-Last-BR-Skt-EGARCH | 1.000 | ICSS-Last-BR-Skt-EGARCH | 1.000 |
| HMAE | |||||||
| MS-GARCH-N | 1.000 |
|
1.000 | 1.00-HM | 1.000 |
|
1.000 |
| 1.00-GARCH-SSTD | 0.707 | MS-EGARCH-N | 0.170 | MS-EGARCH-N | 0.498 | MS-EGARCH-N | 0.428 |
| ICSS-GARCH-SSTD | 0.384 | ICSS-GARCH-N | 0.281 | ICSS-EGARCH-N | 0.425 | ||
| 0.25-EGARCH-SSTD | 0.415 | ||||||
| ICSS-Last-BR-HM | 0.200 | ||||||
| 1.00-SV-lev | 0.106 | ||||||
| 0.5-Skt-EGARCH. | 0.106 | ||||||
| HMSE | |||||||
| MS-GARCH-N | 1.000 |
|
1.000 | 1.00-HM | 1.000 |
|
1.000 |
| 0.25-GARCH-STD | 0.106 | MS-EGARCH-N | 0.204 | MS-EGARCH-N | 0.375 | MS-EGARCH-N | 0.878 |
| 1.00-SV | 0.106 | ICSS-Last-BR-HM | 0.171 | ICSS-EGARCH-N | 0.329 | 0.25-Skt-EGARCH | 0.878 |
| 1.00-GARCH-N | 0.106 | ICSS-Last-BR-SVT | 0.171 | ICSS-Last-BR-HM | 0.154 |
|
0.591 |
| ICSS-GARCH-N | 0.106 | 0.25-SVt | 0.169 | 0.5-SVt | 0.154 | ICSS-EGARCH-N | 0.516 |
| 0.5-GARCH-N | 0.106 | 0.5-SVt | 0.162 |
|
0.154 | 1.00-SV-lev | 0.516 |
| 0.25-SVT | 0.106 |
|
0.125 |
|
0.154 | ICSS-Last-BR-HM | 0.516 |
| ICSS-Last-BR-HM | 0.106 |
|
0.125 | 1.00-SV-lev | 0.154 | 0.5-SV-lev | 0.466 |
|
|
0.125 |
|
0.154 | 0.25-SVT | 0.384 | ||
| ICSS-Last-BR-SV | 0.100 | ||||||
| QLIKE | |||||||
| MS-GARCH-N | 1.000 | MS-EGARCH-N | 1.000 | MS-EGARCH-N | 1.000 | 0.25-EGARCH-SSTD | 1.000 |
| 0.5-GARCH-N | 0.920 |
|
0.936 |
|
0.857 | 0.5-Skt-EGARCH | 0.832 |
| 0.25-GARCH-STD | 0.920 | ICSS-Last-BR-HM | 0.936 | 0.25-EGARCH-SSTD | 0.857 |
|
0.832 |
| 1.00-GARCH-N | 0.812 | 0.25-Skt-EGARCH | 0.936 | 0.5-Skt-EGARCH | 0.604 | ICSS-EGARCH-N | 0.832 |
| ICSS-GARCH-N | 0.777 | 0.5-Skt-EGARCH | 0.877 | 0.5-SVT | 0.492 | MS-EGARCH-N | 0.832 |
| 1.00-SV | 0.777 | 0.5-SVT | 0.739 | 0.25-SV-lev | 0.431 | 1.00-SV-lev | 0.801 |
| 0.5-SVT | 0.777 | ICSS-EGARCH-GHYP | 0.739 | ICSS-Last-BR-HM | 0.431 | 0.5-SVT | 0.633 |
| 0.25-SVT | 0.752 | 0.25-SVT | 0.677 | ICSS-GJR-GARCH-N | 0.357 | 0.25-SVT | 0.509 |
| ICSS-Last-BR-HM | 0.325 | 1.00-SV-lev | 0.591 | 1.00-SV | 0.357 | ICSS-Last-BR-HM | 0.496 |
| ICSS-Last-BR-SV-lev | 0.142 | ||||||
account for endogenous structural breaks (using ICSS-based break dummies and the last-break sub-sample) perform well; these are followed in performance by Markov-switching GARCH models. We then narrow our focus to the performance of single-regime models estimated using whole, half-, and quarter-size windows over the short and long term. We find that single-regime full-window GARCH models perform better in the short than in the long term, while single-regime models with half- and quarter-window sizes exhibit similar performance for short- and long-term horizons.
4.4. Direction-of-change test
Model confidence set for palm oil (
| Forecast horizons | |||||||
| 1 | 5 | 20 | 40 | ||||
| Models | p-value | Models | p-value | Models | p-value | Models | p-value |
| MAE | |||||||
| ICSS-Last-BR-Skt-EGARCH | 1.000 | ICSS-Last-BR-Skt-EGARCH | 1.000 | ICSS-Last-BR-Skt-EGARCH | 1.000 | 0.5-Skt-EGARCH | 1.000 |
| 0.5-Skt-EGARCH | 0.611 | 0.5-Skt-EGARCH | 0.247 | 0.5-Skt-EGARCH | 0.533 | ICSS-Last-BR-Skt-EGARCH | 0.862 |
|
|
0.114 | 0.5-SV-lev | 0.513 | 0.25-Skt-EGARCH | 0.543 | ||
| 0.25-Skt-EGARCH | 0.215 | 0.5-SVT | 0.297 | ||||
| HMAE | |||||||
| 0.5-Skt-EGARCH | 1.000 | ICSS-Last-BR-HM | 1.000 | 0.5-GJR-GARCH-STD | 1.000 | 0.5-GJR-GARCH-STD | 1.000 |
| ICSS-GARCH-STD | 0.668 | 0.5-GARCH-STD | 0.243 | ||||
| 0.25-Skt-EGARCH | 0.668 | 0.5-SVT | 0.108 | ||||
| HMSE | |||||||
| 0.5-GARCH-STD | 1.000 | 0.5-GJR-GARCH-STD | 1.000 | 0.5-GJR-GARCH-STD | 1.000 | 0.5-GJR-GARCH-STD | 1.000 |
| MS-GJR-GARCH-STD | 0.367 | ||||||
| ICSS-GJR-GARCH-STD | 0.367 | ||||||
| 0.25-GJR-GARCH-N | 0.367 | ||||||
| 1.00-GJR-GARCH-STD | 0.367 | ||||||
| QLIKE | |||||||
| 0.5-GARCH-STD | 1.000 | 0.5-GARCH-STD | 1.000 | 0.5-GJR-GARCH-STD | 1.000 | 0.5-GJR-GARCH-SSTD | 1.000 |
| MS-GJR-GARCH-STD | 0.456 | ICSS-GARCH-STD | 0.644 | 1.00-SVT | 0.503 | 1.00-Skt-EGARCH | 0.594 |
| ICSS-GARCH-STD | 0.456 | MS-GJR-GARCH-SSTD | 0.644 | ICSS-GJR-GARCH-STD | 0.503 | 0.25-Skt-EGARCH | 0.594 |
| 1.00-GARCH-STD | 0.456 | 0.25-Skt-EGARCH | 0.644 | MS-GARCH-SSTD | 0.503 | ICSS-GJR-GARCH-SSTD | 0.430 |
| 1.00-GARCH | 0.644 | 0.25-Skt-EGARCH | 0.503 | MS-GJR-GARCH-SSTD | 0.278 | ||
| 1.00-SVT | 0.201 | 1.00-EGARCH-N | 0.106 | ||||
Model confidence set for rapeseed (
| Forecast horizons | |||||||
| 1 | 5 | 20 | 40 | ||||
| Models | p-value | Models | p-value | Models | p-value | Models | p-value |
| MAE | |||||||
| 0.5-Skt-EGARCH | 1.000 | 0.5-Skt-EGARCH | 1.000 | 0.5-Skt-EGARCH | 1.000 | 0.5-Skt-EGARCH | 1.000 |
| ICSS-Last-BR-ES | 0.199 | ICSS-Last-BR-ES | 0.618 | ICSS-Last-BR-ES | 0.285 | ||
| 0.5-SV-lev | 0.53 | 0.5-SV-lev | 0.185 | ||||
| 0.25-Skt-EGARCH | 0.337 | 0.25-Skt-EGARCH | 0.185 | ||||
| 0.25-SV-lev | 0.191 | 0.25-SV | 0.134 | ||||
| HMAE | |||||||
| 0.25-EGARCH-STD | 1.000 | 0.25-GARCH-STD | 1.000 | 0.5-GARCH-SSTD | 1.000 | 0.25-GJR-GARCH-SSTD | 1.000 |
| ICSS-GARCH-SSTD | 0.67 | ICSS-EGARCH-SSTD | 0.702 | ||||
| MS-GJR-GARCH-STD | 0.67 | MS-GJR-GARCH-STD | 0.300 | ||||
| 1.00-GARCH-N | 0.67 | ||||||
| HMSE | |||||||
| MS-EGARCH-SSTD | 1.000 | 0.25-GARCH-SSTD | 1.000 | 0.5-GARCH-STD | 1.000 | 0.25-GJR-GARCH-SSTD | 1.000 |
| ICSS-GJR-GARCH-N | 0.863 | ICSS-EGARCH-SSTD | 0.776 | ||||
| 1.00-GARCH-N | 0.863 | MS-GJR-GARCH-STD | 0.145 | ||||
| 0.25-Skt-EGARCH | 0.863 | ||||||
| 0.5-Skt-EGARCH | 0.742 | ||||||
| QLIKE | |||||||
| 0.5-Skt-EGARCH | 1.000 | MS-GJR-GARCH-STD | 1.000 | MS-GJR-GARCH-STD | 1.000 | MS-GJR-GARCH-STD | 1.000 |
| MS-EGARCH-SSTD | 0.999 | ICSS-GJR-GARCH-N | 0.129 | ICSS-GJR-GARCH-SSTD | 0.692 | ||
| 1.00-Skt-EGARCH | 0.999 | 0.25-Skt-EGARCH | 0.129 | ||||
| ICSS-GARCH-N | 0.966 | 1.00-GJR-GARCH-N | 0.129 | ||||
| 0.25-Skt-EGARCH | 0.943 | 0.5-Skt-EGARCH | 0.107 | ||||
Model confidence set for soybean (
| Forecast horizons | |||||||
| 1 | 5 | 20 | 40 | ||||
| Models | p-value | Models | p-value | Models | p-value | Models | p-value |
| MAE | |||||||
| ICSS-Last-BR-HM | 1.000 | ICSS-Last-BR-Skt-EGARCH | 1.000 | 0.5-Skt-EGARCH | 1.000 | ICSS-Last-BR-Skt-EGARCH | 1.000 |
| 0.5-Skt-EGARCH | 0.135 | ||||||
| HMAE | |||||||
| 1.00-HM | 1.000 |
|
1.000 |
|
1.000 | ICSS-EGARCH-STD | 1.000 |
| ICSS-EGARCH-STD | 0.371 | ICSS-EGARCH-STD | 0.105 |
|
0.889 | ||
| HMSE | |||||||
| 1.00-HM | 1.000 | ICSS-EGARCH-STD | 1.000 | ICSS-GARCH-STD | 1.000 | ICSS-EGARCH-STD | 1.000 |
| MS-EGARCH-N | 0.578 |
|
0.433 | 1.00-HM | 0.395 | ||
| ICSS-EGARCH-GHYP | 0.147 | MS-EGARCH-N | 0.113 | ||||
| QLIKE | |||||||
| ICSS-EGARCH-GHYP | 1.000 | 1.00-SVT | 1.000 | 1.00-SVT | 1.000 | MS-GJR-GARCH-SSTD | 1.000 |
| 1.00-SVT | 0.637 | 1.00-EGARCH-GHYP | 0.254 | MS-GJR-GARCH-SSTD | 0.711 | 1.00-SVT | 0.637 |
| 1.00-EGARCH-GHYP | 0.55 | 0.5-SVT | 0.254 | 1.00-EGARCH-GHYP | 0.615 | 0.5-SVT | 0.507 |
| 0.5-SVT | 0.55 | ICSS-EGARCH-GHYP | 0.254 | 0.5-SVT | 0.615 | 1.00-EGARCH-GHYP | 0.101 |
| 0.25-GARCH-SSTD | 0.55 | 0.25-SVT | 0.254 | 0.5-EGARCH-GHYP | 0.607 | 0.5-EGARCH-GHYP | 0.101 |
| 0.5-GARCH-N | 0.537 | 0.5-EGARCH-N | 0.254 | 0.25-GARCH-STD | 0.595 | 0.25-SVT | 0.101 |
| 0.25-SVT | 0.424 | 0.25-GARCH-STD | 0.254 | ICSS-GARCH-GHYP | 0.397 | ||
| MS-GJR-GARCH-SSTD | 0.114 | MS-GJR-GARCH-SSTD | 0.118 | 0.25-SVT | 0.335 | ||
| ICSS-Last-BR-SVT | 0.177 | ||||||
| ICSS-Last-BR-GARCH-STD | 0.121 | ||||||
breaks) across all forecast horizons under consideration.
In line with the MCS results, models neglecting instabilities (such as single-regime models) demonstrate inferior forecasting accuracy with respect to volatility movements. Further, models within the GARCH class that integrate ICSS-based break dummy variables and MS-GARCH models do not provide good forecasts of volatility direction. We also observe that, when integrated with breaks, the ES models for some forecast steps precisely forecast corn’s upward and downward volatility (with DoC
5. Conclusion
across all forecast horizons for all bioenergy commodities considered. In particular, the last-break models outperform all others under this test. In line with the MCS results, models neglecting instabilities (such as singleregime models) demonstrate inferior forecasting accuracy for volatility movements.
CRediT authorship contribution statement
curation, Investigation, Software, Validation.
Declaration of generative AI and AI-assisted technologies in the writing process
Declaration of competing interest
interests or personal relationships that could have appeared to influence the work reported in this paper.
Data availability
Acknowledgments
Appendix
The econometric models
1 Single regime with whole window size GARCH-class models
1.0-GARCH-ST, 1.0-GARCH-N, 1.0-GARCH-SST, 1.0-GJR-GARCH-N, 1.0-GARCH-GHYP, 1.0-GJR-GARCH-ST, 1.0-GJR-
GARCH-GHYP, 1.0-GJR-GARCH-SST, 1.0-EGARCH-ST, 1.0-EGARCH-N, 1.0-EGARCH-SST, 1.0-EGARCH-GHYP, 1.0-two-
comp-Beta-t-EGARCH, 1.0-one-comp-Beta-t-EGARCH
2 Single regime with half window size GARCH-class models
0.5-GARCH-ST, 0.5-GARCH-N, 0.5-GARCH-SST, 0.5-GARCH-GHYP, 0.5-GJR-GARCH-ST, 0.5-GJR-GARCH-N, 0.5-GJR-
GARCH-SST, 0.5-GJR-GARCH-GHYP, 0.5-EGARCH-ST, 0.5-EGARCH-N, 0.5-EGARCH-SST, 0.5-EGARCH-GHYP, 0.5-two-
comp-Beta-t-EGARCH, 0.5-one-comp-Beta-t-EGARCH
3 Single regime with quarter window size GARCH-class models
0.25-GARCH-ST, 0.25-GARCH-N, 0.25-GARCH-SST, 0.25-GARCH-GHYP, 0.25-GJR-GARCH-ST, 0.25-GJR-GARCH-N,
0.25-GJR-GARCH-SST, 0.25-GJR-GARCH-GHYP, 0.25-EGARCH-ST, 0.25-EGARCH-N, 0.25-EGARCH-SST, 0.25-EGARCH-
GHYP, 0.25-two-comp-Beta-t-EGARCH, 0.25-one-comp-Beta-t-EGARCH
4 Single regime with full window size SV models
1.0-SVT, 1.0-SV, 1.0-SV-lev
5 text { Single regime with half window size SV models }
0.5-SVT, 0.5-SV, 0.5-SV-lev
6 Single regime with quarter window size SV models
0.25-SVT, 0.25-SV, 0.25-SV-lev
7 text { ICSS regime dummy GARCH-class models }
ICSS-GARCH-ST, ICSS-GARCH-N, ICSS-GARCH-SST, ICSS-GARCH-GHYP, ICSS-GJR-GARCH-ST, ICSS-GJR-GARCH-N,
ICSS-GJR-GARCH-SST, ICSS-GJR-GARCH-GHYP, ICSS-EGARCH-ST, ICSS-EGARCH-N, ICSS-EGARCH-SST, ICSS-EGARCH-
GHYP
8 ICSS last break period GARCH-class models
ICSS-Last-BR-GARCH-ST, ICSS-Last-BR-GARCH-N, ICSS-Last-BR-GARCH-SST, ICSS-Last-BR-GARCH-GHYP, ICSS-Last-BR-
GJR-GARCH-ST, ICSS-Last-BR-GJR-GARCH-N, ICSS-Last-BR-GJR-GARCH-SST, ICSS-Last-BR-GJR-GARCH-GHYP, ICSS-
Last-BR-EGARCH-ST, ICSS-Last-BR-EGARCH-N, ICSS-Last-BR-EGARCH-SST, ICSS-Last-BR-EGARCH-GHYP, ICSS-Last-BR-
two-comp-Beta-t-EGARCH, ICSS-Last-BR-one-comp-Beta-t-EGARCH
9 ICSS last break period SV models
ICSS-Last-BR-SVT, ICSS-Last-BR-SV, ICSS-Last-BR-SV-lev
10 Markov-switching GARCH models
MS-GARCH-ST, MS-GARCH-N, MS-GARCH-SST, MS-GJR-GARCH-ST, MS-GJR-GARCH-N, GJR-MS-GARCH-SST, MS-
EGARCH-ST, MS-EGARCH-N, MS-EGARCH-SST
11 Full, half, and quarter window size single regime HM, ES models
1.0-ES, 1.0-HM, 0.5-ES, 0.5-HM, 0.25-ES, 0.25.0-HM
12 ICSS last break period HM and ES models
ICSS-Last-BR-ES, ICSS-Last-BR-HM
References
[2] Amendola A, Braione M, Candila V, Storti G. A Model Confidence Set approach to the combination of multivariate volatility forecasts. Int
[3] Anjum H, Malik F. Forecasting risk in the US Dollar exchange rate under volatility shifts. N Am J Econ Finance 2020;54:101257. https://doi.org/10.1016/j. najef.2020.101257.
[4] Apergis N, Payne JE, Menyah K, Wolde-Rufael Y. On the causal dynamics between emissions, nuclear energy, renewable energy, and economic growth. Ecol Econ 2010;69:2255-60. https://doi.org/10.1016/j.ecolecon.2010.06.014.
[5] Ardia D, Bluteau K, Boudt K, Catania L. Forecasting risk with Markov-switching GARCH models: a large-scale performance study. Int J Forecast 2018;34:733-47.
[6] Ardia D, Bluteau K, Boudt K, Catania L, Trottier D-A. Markov-switching GARCH models in R : the MSGARCH package. J Stat Software 2019;91. https://doi.org/ 10.18637/jss.v091.i04.
[7] Berger J, Dalheimer B, Brümmer B. Effects of variable EU import levies on corn price volatility. Food Pol 2021;102:102063. https://doi.org/10.1016/j. foodpol.2021.102063.
[8] Bergsli Lø, Lind AF, Molnár P, Polasik M. Forecasting volatility of bitcoin. Res Int Bus Finance 2022;59:101540. https://doi.org/10.1016/j.ribaf.2021.101540.
[9] Bergtold JS, Shanoyan A, Fewell JE, Williams JR. Annual bioenergy crops for biofuels production: farmers’ contractual preferences for producing sweet sorghum. Energy 2017;119:724-31. https://doi.org/10.1016/j. energy.2016.11.032.
[10] Bollerslev T. Generalized autoregressive conditional heteroskedasticity. J Economtrics 1986;31:307-27.
[11] Bollerslev T. The story of GARCH: a personal odyssey. J Econom 2023;234:96-100.
[12] Bouri E, Dutta A, Saeed T. Forecasting ethanol price volatility under structural breaks. Biofuels, Bioprod. Bioref. 2021;15:250-6. https://doi.org/10.1002/ bbb. 2158.
[13] Carpio LGT. The effects of oil price volatility on ethanol, gasoline, and sugar price forecasts. Energy 2019;181:1012-22. https://doi.org/10.1016/j. energy.2019.05.067.
[14] Chang T-H, Su H-M. The substitutive effect of biofuels on fossil fuels in the lower and higher crude oil price periods. Energy 2010;35:2807-13.
[15] Charfeddine L. True or spurious long memory in volatility: further evidence on the energy futures markets. Energy Pol 2014;71:76-93. https://doi.org/10.1016/j. enpol.2014.04.027.
[16] Charles A, Darné O. Forecasting crude-oil market volatility: further evidence with jumps. Energy Econ 2017;67:508-19. https://doi.org/10.1016/j. eneco.2017.09.002.
[17] Cheng IH, Xiong W. Financialization of commodity markets. Annu Rev Financ Econ 2014;6:419-41.
[18] Chuang I-Y, Lu J-R, Lee P-H. Forecasting volatility in the financial markets: a comparison of alternative distributional assumptions. Appl Financ Econ 2007;17: 1051-60. https://doi.org/10.1080/09603100600771000.
[19] Degiannakis S, Filis G. Forecasting oil price realized volatility using information channels from other asset classes. J Int Money Finance 2017;76:28-49. https://doi. org/10.1016/j.jimonfin.2017.05.006.
[20] Degiannakis S, Filis G, Klein T, Walther T. Forecasting realized volatility of agricultural commodities. Int J Forecast 2022;38:74-96. https://doi.org/10.1016/ j.ijforecast.2019.08.011.
[21] Dutta A, Junttila J, Uddin GS. Forecasting the volatility of biofuel feedstock prices: the US Evidence. Biofuels Bioprod Bioref 2019;13:912-9.
[22] EBB. About biodiesel. European Biodiesel Board. https://ebb-eu.org/(accessed 21 February 2023)..
[23] EIA. Monthly biodiesel production report. U.S. Energy Information Administration; 2020. https://www.eia.gov/biofuels/biodiesel/production/. [Accessed 21 February 2023].
[24] Engle RF. Autoregressive conditional heteroscedasticity with estimates of the variance of U.K. inflation. Econometrica 1982;50:987-1008.
[25] Ewing BT, Malik F. Estimating volatility persistence in oil prices under structural breaks. Financ Rev 2010;45:1011-23. https://doi.org/10.1111/j.15406288.2010.00283.x.
[26] Galanos A. Rugarch: univariate GARCH models. 2022. https://cran.r-project.org/ web/packages/rugarch/rugarch.pdf.
[27] Glosten LR, Jagannathan R, Runkle D. On the relation between the expected value and the volatility of the nominal excess return on stocks. J Finance 1993;XLVIII.
[28] Haas M, Mittnik S, Paolella M. A new approach to Markov-switching GARCH models. J Financ Econom 2004;2:493-530.
[29] Hajkowicz S, Negra C, Barnett P, Clark M, Harch B, Keating B. Food price volatility and hunger alleviation – can Cannes work? Agric Food Secur 2012;1. https://doi. org/10.1186/2048-7010-1-8.
[30] Hansen PR, Lunde A, Nason JM. The model confidence set. Econometrica 2011;79: 453-97.
[31] Harvey A, Ruiz E, Shephard N. Multivariate stochastic variance models. Rev Econ Stud 1994;61:247-64.
[32] Harvey A, Sucarrat G. EGARCH models with fat tails, skewness and leverage. Comput Stat Data Anal 2014;76:320-38. https://doi.org/10.1016/j. csda.2013.09.022.
[33] Hasanov AS, Avazkhodjaev SS. Stochastic volatility models with endogenous breaks in volatility forecasting. In: Terzioglu MK, editor. Advances in econometrics, operational research, data science and actuarial studies. Cham: Springer International Publishing; 2022. p. 81-97.
[34] Hasanov AS, Poon WC, Al-Freedi A, Heng ZY. Forecasting volatility in the biofuel feedstock markets in the presence of structural breaks: a comparison of alternative distribution functions. Energy Econ 2018;70:307-33. https://doi.org/10.1016/j. eneco.2018.01.011.
[35] Hasanov AS, Shaiban MS, Al-Freedi A. Forecasting volatility in the petroleum futures markets: a re-examination and extension. Energy Econ 2020;86:104626. https://doi.org/10.1016/j.eneco.2019.104626.
[36] Hasanov AS, Shitan M. Modeling inflation volatility: evidence from two post-Soviet economies. Int J Stat Sci 2012;12:9-27.
[37] Hill BM. A simple general approach to inference about the tail of a distribution. Ann Stat 1975;3:1163-74. https://doi.org/10.1214/aos/1176343247.
[38] Hosszejni D, Kastner G. Efficient bayesian inference for stochastic volatility (SV). The “stochvol” R package version 3.2.0 2022. https://cran.r-project.org/web/p ackages/stochvol/stochvol.pdf.
[39] Hyndman R, Athanasopoulos G, Bergmeir C, Caceres G, Chhay L, Kuroptev K, O’Hara-Wild M, Petropoulos F, Razbash S, Wang E, Yasmeen F. Forecast:
forecasting functions for time series and linear models. 2022. https://cran.r-project .org/web/packages/forecast/forecast.pdf.
[40] Inclán C, Tiao GC. Use of cumulative sums of squares for retrospective detection of changes of variance. J Am Stat Assoc 1994;89:913-23.
[41] Kang SH, Cheong C, Yoon S-M. Structural changes and volatility transmission in crude oil markets. Phys Stat Mech Appl 2011;390:4317-24. https://doi.org/ 10.1016/j.physa.2011.06.056.
[42] Kang SH, Kang S-M, Yoon S-M. Forecasting volatility of crude oil markets. Energy Econ 2009;31:119-25. https://doi.org/10.1016/j.eneco.2008.09.006.
[43] Klein T, Walther T. Oil price volatility forecast with mixture memory GARCH. Energy Econ 2016;58:46-58. https://doi.org/10.1016/j.eneco.2016.06.004.
[44] Kumar D, Maheswaran S. Modelling asymmetry and persistence under the impact of sudden changes in the volatility of the Indian stock market. IIMB Manage Rev 2012;24:123-36.
[45] Lamoureux CG, Lastrapes WD. Persistence in variance, structural change, and the GARCH model. J Bus Econ Stat 1990;8:225. https://doi.org/10.2307/1391985.
[46] Law SH. Has stock market volatility in the Kuala Lumpur Stock Exchange returned to pre-Asian financial crisis levels? ASEAN Econ Bull 2006;23:212-29.
[47] Li X, Guo Q, Liang C, Umar M. Forecasting gold volatility with geopolitical risk indices. Res Int Bus Finance 2023;64:101857. https://doi.org/10.1016/j. ribaf.2022.101857.
[48] Li Y, Liang C, Ma F, Wang J. The role of the IDEMV in predicting European stock market volatility during the COVID-19 pandemic. Finance Res Lett 2020;36: 101749. https://doi.org/10.1016/j.frl.2020.101749.
[49] Liu J, Wei Y, Ma F, Wahab M. Forecasting the realized range-based volatility using dynamic model averaging approach. Econ Modell 2017;61:12-26. https://doi.org/ 10.1016/j.econmod.2016.11.020.
[50] Liu Y, Niu Z, Suleman MT, Yin L, Zhang H. Forecasting the volatility of crude oil futures: the role of oil investor attention and its regime switching characteristics under a high-frequency framework. Energy 2022;238:121779. https://doi.org/ 10.1016/j.energy.2021.121779.
[51] Lyócsa S, Molnár P. Exploiting dependence: day-ahead volatility forecasting for crude oil and natural gas exchange-traded funds. Energy 2018;155:462-73. https://doi.org/10.1016/j.energy.2018.04.194.
[52] Lyócsa S, Molnár P, Todorova N. Volatility forecasting of non-ferrous metal futures: covariances, covariates or combinations? J Int Financ Mark Inst Money 2017;51: 228-47. https://doi.org/10.1016/j.intfin.2017.08.005.
[53] Lyócsa S, Molnár P, Výrost T. Stock market volatility forecasting: do we need highfrequency data? Int J Forecast 2021;37:1092-110.
[54] Mei D, Xie Y. U.S. grain commodity futures price volatility: does trade policy uncertainty matter? Finance Res Lett 2022;48:103028. https://doi.org/10.1016/j. frl.2022.103028.
[55] Nelson DB. Conditional heteroskedasticity in asset returns: a new approach. Econometrica 1991;59:347-70.
[56] Nomikos NK, Pouliasis PK. Forecasting petroleum futures markets volatility: the role of regimes and market conditions. Energy Econ 2011;33:321-37. https://doi. org/10.1016/j.eneco.2010.11.013.
[57] Park B-J. The COVID-19 pandemic, volatility, and trading behavior in the bitcoin futures market. Res Int Bus Finance 2022;59:101519. https://doi.org/10.1016/j. ribaf.2021.101519.
[58] Peng L, Liang C. Sustainable development during the post-COVID-19 period: role of crude oil. Resour Pol 2023;85:103843. https://doi.org/10.1016/j. resourpol.2023.103843.
[59] Pesaran MH, Timmermann A. Selection of estimation window in the presence of structural breaks. J Econom 2007;137:134-61.
[60] Qian L, Wang J, Ma F, Li Z. Bitcoin volatility predictability-The role of jumps and regimes. Finance Res Lett 2022;47:102687. https://doi.org/10.1016/j. frl.2022.102687.
[61] Rapach DE, Strauss JK. Structural breaks and GARCH models of exchange rate volatility. J Appl Econ 2008;23:65-90. https://doi.org/10.1002/jae.976.
[62] Sadorsky P. Modeling and forecasting petroleum futures volatility. Energy Econ 2006;28:467-88. https://doi.org/10.1016/j.eneco.2006.04.005.
[63] Salisu AA, Gupta R, Bouri E, Ji Q. The role of global economic conditions in forecasting gold market volatility: evidence from a GARCH-MIDAS approach. Res Int Bus Finance 2020;54:101308. https://doi.org/10.1016/j.ribaf.2020.101308.
[64] Sansó A, Arragó V, Carrion JL. Testing for change in the unconditional variance of financial time series. Rev Econ Financ 2004;4:32-53.
[65] Segnon M, Bekiros S. Forecasting volatility in bitcoin market. Ann Finance 2020; 16:435-62. https://doi.org/10.1007/s10436-020-00368-y.
[66] Segnon M, Gupta R, Wilfling B. Forecasting stock market volatility with regimeswitching GARCH-MIDAS: the role of geopolitical risks. Int J Forecast 2023. https://doi.org/10.1016/j.ijforecast.2022.11.007.
[67] Serra T. Volatility spillovers between food and energy markets: a semiparametric approach. Energy Econ 2011;33:1155-64. https://doi.org/10.1016/j. eneco.2011.04.003.
[68] Sucarrat G. Betategarch: simulation, estimation and forecasting of beta-skew-tEGARCH models. 2022. https://cran.r-project.org/web/packages/betategarch/be tategarch.pdf.
[69] Swinnen J, Squicciarini P. Mixed messages on prices and food security. Science 2012;335:405-6.
[70] Umar M, Su C-W, Rizvi SKA, Shao X-F. Bitcoin: a safe haven asset and a winner amid political and economic uncertainties in the US? Technol Forecast Soc Change 2021;167:120680.
[71] USDA. Oilseeds: world markets and trade. United States Department of Agriculture; 2023. https://apps.fas.usda.gov/psdonline/circulars/oilseeds.pdf. [Accessed 21 February 2023].
[72] Wang L, Wu J, Cao Y, Hong Y. Forecasting renewable energy stock volatility using short and long-term Markov switching GARCH-MIDAS models: either, neither or both? Energy Econ 2022;111:106056. https://doi.org/10.1016/j. eneco.2022.106056.
[73] Wong ZY, Chin WC, Tan SH. Daily value-at-risk modeling and forecast evaluation: the realized volatility approach. J Finance Data Sci 2016;2:171-87. https://doi. org/10.1016/j.jfds.2016.12.001.
[74] Yahya M, Kanjilal K, Dutta A, Uddin GS, Ghosh S. Can clean energy stock price rule oil price? New evidences from a regime-switching model at first and second moments. Energy Econ 2021;95:105116. https://doi.org/10.1016/j. eneco.2021.105116.
- Corresponding author. Monash University Malaysia campus, Jalan Lagoon Selatan, 46150 Bandar Sunway, Selangor, Malaysia.
E-mail addresses: akram.hasanov@monash.edu (A.S. Hasanov), a.burkhanov@tsue.uz (A.U. Burkhanov), b.usmonov@tsue.uz (B. Usmonov), n.xajimuratov@tsue. uz (N.S. Khajimuratov), eshmamatovamadina@tsue.uz (M.M. Khurramova).
