فضاء التصميم للجهود بين الذرات المركزية حول الذرات المتساوية E(3) The design space of E(3)-equivariant atom-centred interatomic potentials

المجلة: Nature Machine Intelligence، المجلد: 7، العدد: 1
DOI: https://doi.org/10.1038/s42256-024-00956-x
PMID: https://pubmed.ncbi.nlm.nih.gov/39877429
تاريخ النشر: 2025-01-15

فضاء التصميم للجهود بين الذرات المركزية حول الذرات المتساوية E(3)

تاريخ الاستلام: 8 ديسمبر 2022
تم القبول: 13 نوفمبر 2024
نُشر على الإنترنت: 15 يناير 2025
تحقق من التحديثات

إلياس باتاتيا سيمون باتزنر داود بيتر كوفاتش¹، ألبرت موساليان³، غريغور ن. س. سيم رالف دراوتز كريستوف أورتر بوريس كوزينسكي وغابور تشاني ⟶

الملخص

محاكاة الديناميكا الجزيئية هي أداة مهمة في علوم المواد الحاسوبية والكيمياء، وفي العقد الماضي تم إحداث ثورة فيها بواسطة التعلم الآلي. لقد أنتج هذا التقدم السريع في إمكانيات التفاعل بين الذرات عددًا من الهياكل الجديدة في السنوات القليلة الماضية. ومن بين هذه الهياكل، يُعتبر توسيع الكتل الذرية بارزًا، حيث وحد العديد من الأفكار السابقة حول الوصف القائم على كثافة الذرات، وPotentials Interatomic Equivariant Neural (NequIP)، وهو شبكة عصبية تمرير الرسائل مع ميزات متساوية أظهرت دقة متقدمة في ذلك الوقت. هنا نقوم ببناء إطار رياضي يوحد هذه النماذج: يتم توسيع توسيع الكتل الذرية وإعادة صياغته كطبقة واحدة من هيكل متعدد الطبقات، بينما يُفهم النسخة الخطية من NequIP كنوع معين من التبسيط لنموذج متعدد الحدود أكبر بكثير. يوفر إطارنا أيضًا أداة عملية لاستكشاف خيارات مختلفة بشكل منهجي في هذه المساحة التصميمية الموحدة. دراسة إلغاء NequIP، من خلال مجموعة من التجارب التي تبحث في دقة النطاقين الداخلي والخارجي والتقدير السلس بعيدًا جدًا عن بيانات التدريب، تسلط بعض الضوء على الخيارات التصميمية الحرجة لتحقيق دقة عالية. نسخة مبسطة جدًا من NequIP، التي نسميها BOTnet (شبكة موتر مرتبة حسب الجسم)، لها هيكل قابل للتفسير وتحافظ على دقتها في مجموعات البيانات المرجعية.

لقد حدثت ثورة في النمذجة الذرية على مدار العقد الماضي، مما أدى إلى الاعتماد الواسع على إمكانيات التعلم الآلي بين الذرات، لا سيما في علوم المواد. تم اقتراح مجموعة واسعة من الهياكل النموذجية المختلفة في الأدبيات. عادةً ما يتم بناء هذه النماذج لتبدأ بوصف (مجموعة من الأرقام) لتمثيل بيئة الذرة. كانت المفتاح لنجاح هذه النماذج هو جعل هذا الوصف غير متغير تحت مجموعة التناظر من التناظرات الإقليدية (الترجمة، الدوران والانعكاس) في الفضاء ثلاثي الأبعاد (E(3))، فضلاً عن
تباديل الذرات من نفس العنصر في البيئة مثالان على مثل هذه الأوصاف هما دوال التناظر المركزية حول الذرة (ACSF) وتداخل المواقع الذرية السلس (SOAP) تم بناء العديد من الإمكانيات بين الذرات باستخدام هذه الأوصاف، وتم استخدامها لاحقًا لنمذجة المواد (انظر المراجعات الحديثة المقابلة). مؤخراً، تم الاعتراف بأن كلا الطريقتين يمكن فهمهما كحالات خاصة من توسيع الكتل الذرية (ACE). . كانت الفكرة الرئيسية لـ ACE هي تقديم مجموعة كاملة من دوال الأساس (باستخدام التوافقيات الكروية وقطر متعامد
الأساس) للبيئة الذرية التي تم بناؤها باستخدام تسلسل توسيع ترتيب الجسم. العديد من الوصفيات المقترحة سابقًا تتناسب مع إطار عمل ACE، مع الاختلافات الرئيسية كونها الحد الأقصى لترتيب توسيع الجسم (ثلاثي الجسم لـ ACSF وSOAP، رباعي الجسم للبيسبيكتروم وما إلى ذلك) والاختيارات المحددة لدوال القاعدة الشعاعية تُستخدم طريقة بديلة لتعريف الميزات المماثلة لـ ACE بواسطة إمكانيات موتر العزم. ، والتي تبني مجموعة شاملة للبيئة الذرية باستخدام موترات كارتيسية يمكن التعبير عنها كتحويل خطي لأساس ACE. يمتد ACE بشكل طبيعي إلى الميزات المتكافئة ولتضمين متغيرات تتجاوز الهندسة، مثل الشحنات أو العزوم المغناطيسية. بالنسبة لوصف معين، يتم ضبط الطاقة الذرية باستخدام خريطة خطية بسيطة. عملية غاوسية أو شبكة عصبية ذات اتجاه أمامي تم بناء نماذج أخرى تعتمد على الوصف للجزئيات أو الهياكل بالكامل مباشرة، بدلاً من تفكيكها إلى مساهمات ذرية. .
بالتوازي مع تطوير نماذج تستخدم أوصاف البيئات المركزية للذرات، استكشفت مجموعات أخرى استخدام الشبكات العصبية ذات تمرير الرسائل (MPNNs) لتناسب الإمكانيات بين الذرات. تمثل هذه النماذج الهيكل الذري كرسوم بيانية حيث يربط حافة بين عقدتين (ذرتين) إذا كانت المسافة بينهما أقل من حد ثابت. ثم تطبق النماذج سلسلة من عمليات الالتفاف أو تمرير الرسائل على هذه الرسوم البيانية لتعلم تمثيل لبيئة كل ذرة. يتم تحويل هذا التمثيل المتعلم إلى طاقة الموقع عبر دالة قراءة (انظر الطرق لوصف أكثر تفصيلاً للإمكانات ذات تمرير الرسائل). كانت النماذج المبكرة في هذه الفئة، مثل SchNet شبكات الأعصاب لنقل الرسائل (MPNN) فيز نت ودايم نت استخدمت ميزات داخلية غير متغيرة تحت دوران هيكل الإدخال.
ابتكار رئيسي في شبكة الغطاس شبكات حقول التنسور وشبكات الأعصاب التلافيفية ثلاثية الأبعاد القابلة للتوجيه (CNNs) كان الهدف هو إنشاء ميزات داخلية متساوية تتغير (تحت عمليات التماثل للإدخال) مثل التمثيلات غير القابلة للاختزال لمجموعة التماثل وبناء الثوابت فقط في الخطوة الأخيرة. على سبيل المثال، يمكن أن تدور الميزات داخل الشبكة مع الهيكل تمامًا كما يفعل المتجه الإقليدي. لإنشاء هذه الميزات المتساوية داخل الشبكة، قدمت هذه الشبكات نوعًا من العمليات غير الخطية – منتج موتر متساوي يربط الميزات عبر معاملات كليبسش-غوردان – مما يؤدي إلى ميزات ناتجة ذات تماثل مرغوب. تم تقديم فكرة ربط العمليات المتساوية مع تمرير الرسائل على رسم الذرات مع إمكانيات بين الذرات المتساوية العصبية (NequIP). وحسنت على دقة الحالة المتقدمة في ذلك الوقت بمعدل يقارب الضعف عبر عدة مجموعات بيانات. تم نشر عدة نماذج تمرير رسائل متكافئة لاحقًا (على سبيل المثال، EGNN باين نيوتن نت جم نت تورش إم دي – نت و SEGNN تم تقديم إمكانات عميقة بديلة متساوية التباين للتفاعل بين الذرات مؤخرًا والتي لا تستخدم تمرير الرسائل المركزية حول الذرات. وأظهرت بشكل صريح قابلية توسيع النماذج المتكافئة لتشمل ملايين الذرات.
في هذه المقالة، نصف إطار عمل يسمى Multi-ACE بهدف توحيد البناء الرياضي لشبكات الأعصاب متعددة الجوانب (MPNNs) وACE. يمكن فهم البناء على أنه MPNN يستخدم ACE كالتفاف في كل طبقة من الشبكة. نقدم مساحة تصميم شاملة لإنشاء إمكانيات بين الذرات في التعلم الآلي التي تتضمن معظم النماذج المنشورة سابقًا. وقد حددت الأعمال السابقة ارتباطًا بين ترتيب الجسم وMPNNs. . بالتزامن مع إصدار النسخة الأولية من عملنا المصدر 33 بحث في العلاقة الرسمية بين الشبكات المعتمدة على تمرير الرسائل ووصف الكثافة الذرية. قام المؤلفون بربط هذه المفاهيم من خلال تفسير الشبكات المعتمدة على تمرير الرسائل كتمثيلات كثافة ذرية متعددة المراكز. يوسع عملنا هذه الأفكار من خلال تعريف مساحة تصميم شاملة للجهود بين الذرات المتمركزة حول الذرات، وتقديم تحليل مفصل لكل من مكونات الإطار. كما نوضح كيف تتوافق النماذج المنشورة سابقًا مع نقاط مختلفة في مساحة التصميم ونحلل جميع مكونات النماذج بشكل شامل.
الشكل 1 | بناء ميزات ACE ذات ترتيب الجسم العالي. أولاً، يتم بناء رسم بياني للجوار مع وضع علامة على كل عقدة بحالتها. ثم يتم حساب قاعدة الجسيم الواحد لكل حافة. بعد ذلك، يتم إجراء عملية تجميع لإنشاء ميزات غير حساسة للتبديل. وظائف البيئات شبه المحلية. لبناء ميزات من رتبة أعلى، يتم تشكيل قاعدة المنتج من خلال أخذ ناتج الضرب لجميع المؤشرات المرتبطة بـ الوظائف. أخيرًا، لإنشاء رسائل متكافئة، تتكون الأساس من تحديد التماثل المطلوب أولاً ثم تقييم التكامل المتناظر المقابل. الثابت الأساس موضح هنا.
أظهرت ورقتان بحثيتان حديثتان فائدة مساحة تصميم Multi-ACE. ML-ACE استخدموا مجموعة متكاملة، ثابتة من طبقات Multi-ACE تتوافق مع نقطة في فضاء التصميم. قاموا بربط بين MPNNs و ACE من خلال توسيع سلسلة القوى لهاملتونيان الهيكل الإلكتروني. الورقة الثانية الحديثة، التي تعتمد على المسودة السابقة من هذا العمل، تم تقديم MACE الذي يستخدم مجموعة من طبقات Multi-ACE المعتمدة على تحليل التنسور والمتساوية، وأظهر أن طبقتين فقط من هذا النوع يمكن أن تحقق دقة متقدمة بتكلفة حسابية منخفضة.
باستخدام إطار العمل Multi-ACE، من الممكن استكشاف خيارات النمذجة المختلفة بشكل منهجي. نحن نوضح ذلك من خلال أمثلة باستخدام كود يسمى BOTNet. (شبكة التنسور المرتبة للجسم؛ موصوفة بالتفصيل في المعلومات التكميلية) ونقدم دراسة مفصلة حول الابتكارات و’الحيل’ في نموذج NequIP التي تعتبر أساسية لتحقيق دقتها العالية.

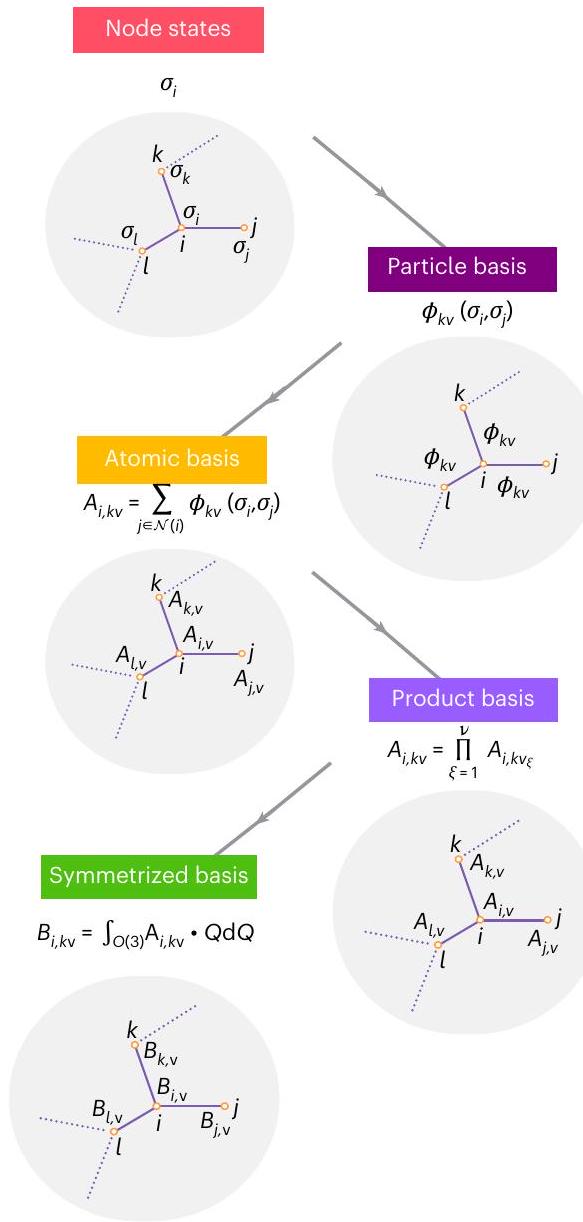
متعدد-ACE

في هذا القسم، نوضح كيف يمكن دمج عدة طبقات ACE متساوية التماثل لبناء نموذج تمرير الرسائل. (انظر الطرق لمقدمة عامة عن إمكانيات التفاعل بين الذرات عبر تمرير الرسائل والإصدار القياسي ACE وإصداره المتكافئ). الإطار الناتج
الشكل 2 | هيكل الكتل لمصفوفات الوزن لعملية خطية متساوية. حيث أن التركيبات الخطية فقط من ميزات نفس التمثيلات يسمح بالتفاعل، تكون مصفوفة الوزن قطرية كتلية.
يشمل معظم إمكانيات التفاعلات بين الذرات المعتمدة على الشبكات العصبية ذات التمرير الرسائلي المتساوي. إذا تم استخدام طبقة واحدة فقط من تمرير الرسائل، يمكن تقليل الإطار إلى ACE خطي أو النماذج الأخرى المعتمدة على الوصف المركزي للذرات.
استخدام لحالة العقد و لرسالة مجمعة في التكرار الذرة المركزية يمكننا تعريف نموذج Multi-ACE على النحو التالي. أولاً، نحدد الرسالة مع ناتج طبقة ACE المتكافئة ونحدد كيفية استخدامها لتشكيل حالة العقدة التالية. تُحدث حالات الذرات من خلال تعيين مخرجات الطبقة السابقة إلى الميزة :
أين هو متجه الموقع الكارتيزي لـ هي سمات عقد غير قابلة للتغيير (مثل الترميز الأحادي للأرقام الذرية)، هي مجموعة من الرسائل كما هو محدد في المعادلة (21) و هي دالة التحديث لكل طبقة. في معظم الشبكات العصبية المعتمدة على الرسوم البيانية، قناة الرسالة تتوافق مع بُعد التضمين المتعلم للعناصر الكيميائية نحتاج إلى توسيع قاعدة الجسيم الواحد، ، من ACE المتناظر (من المعادلة (13)؛ الطرق) لدمج الاعتماد على مخرجات الطبقة السابقة، والتي يمكن تحقيقها من خلال جعلها حجة لـ الوظائف:
أين هي دوال شعاعية، هي التوافقيات الكروية، هي دوال تضمين العقد العامة و هو ترتيب الارتباط المحلي لكل طبقة هي مؤشرات، هو عدد طبقات تمرير الرسائل، هي ذرات مجاورة، هي الخصائص الكيميائية و هو الترتيب الداخلي لتوسع التوافقيات الكروية داخل الطبقة في قاعدة الجسيم الواحد. لقد أضفنا أيضًا المؤشر إلى قاعدة الجسيم الواحد لتمكين مجموعة مختلفة من دوال قاعدة الجسيم الواحد لتكون مدرجة للرسائل مع تناظر مختلف يتوافق مع يمكن توسيع قاعدة الجسيم الواحد بشكل أكبر لتشمل النماذج المعتمدة على الانتباه من خلال إضافة حجج إضافية إلى تعمل كـ ، حيث يمثل جيران الذرة .
نحن الآن نربط معادلات إطار عمل MPNN بتلك الخاصة بإطار عمل Multi-ACE. أولاً، نحدد دالة الرسالة مع قاعدة الجسيم الواحد في المعادلة (2):
بعد ذلك نحدد عملية التجميع غير القابلة للتبديل. من المعادلة (23). للحصول على رسالة متعددة الجسيمات متناظرة ترتيب الارتباط يجب أن تقوم عملية التجميع بربط قاعدة الجسيمات الفردية التي تتكون من جسيمين بمجموعة من الميزات المتناظرة ذات الأبعاد المتعددة التي يمكن دمجها بطريقة قابلة للتعلم لتشكيل الرسالة على كل عقدة. هذا ما يحققه الشكل المعادل لـ ACE في المرجع 7. بهذه الطريقة، نحصل على المعادلة المركزية لـ Multi-ACE:
أين هي أوزان قابلة للتعلم و يساوي ترتيب الجسم ناقص 1. تشير إلى معاملات كليبسش-غوردان العامة المحددة في المعادلة (20) و يعدد جميع التركيبات لتماثل معين. يتم توضيح المخطط العام لتمرير الرسائل من الدرجة الأعلى في الشكل 1.
وظيفة التحديث من المعادلة (24) تتوافق مع تركيبة خطية قابلة للتعلم من القنوات غير المتصلة للرسالة المتماثلة ويمكن كتابتها كالتالي:
أين هو مصفوفة أوزان قطرية كتلية (الشكل 2) من البعد هو عدد غير مرتبط القنوات في الرسالة و هو الحد الأقصى لترتيب التناظر في الرسالة التي تُنقل من طبقة إلى أخرى. يمكن أن تعتمد أيضًا على الخصائص (مثل العنصر الكيميائي) للذرة المركزية من خلال ما يسمى بالاتصال الذاتي (انظر أدناه للتفاصيل). يمكن أن تكون دوال التحديث التي تعمل على الميزات المتكافئة غير خطية أيضًا، ولكن لكي يحدث ذلك، يجب أن تكون للدوال شكل معين (انظر المرجع 22 والمعلومات التكميلية). بعد الـ الطبقة، دالة قراءة قابلة للتعلم (خطية أو غير خطية) (يمكن أن تعتمد على الرسالة النهائية أو جميع الرسائل السابقة) تعطي طاقة الموقع للذرة. .
نوضح الخيارات لوظيفة الرسالة، والتجميع المتماثل، ووظيفة التحديث لثلاثة نماذج مختلفة في الجدول الإضافي 1.

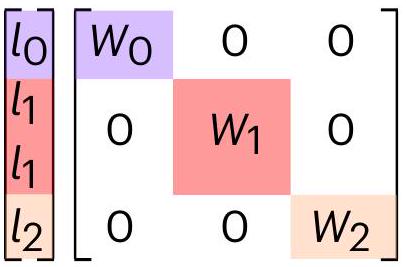
ترابط القنوات

أحد الخيارات التصميمية المهمة في نماذج ACE هو كيفية تفاعل القنوات عند تشكيل قاعدة المنتج. يؤثر هذا الخيار بشكل كبير على مقياس عدد الميزات، وبالتالي فهو جزء أساسي من مساحة التصميم. يتم توضيح ذلك بشكل أفضل من خلال النظر في درجة الحرية فيما يتعلق بمعالجة العناصر الكيميائية المختلفة. في حالة ACE الخطي العام، ووصفيات مشابهة مثل SOAP، تكون قناة العنصر في قاعدة الجسيم الواحد فهرسًا متقطعًا. عند تشكيل دوال القاعدة ذات الأبعاد العليا التي ستنتج الميزات، يتم ربط هذه القنوات، مما يشكل جميع التركيبات الممكنة. على سبيل المثال، إذا كان هناك أربعة عناصر كيميائية مختلفة، فإن عدد دوال القاعدة ذات الثلاثة أجسام سيكون متناسبًا مع النهج البديل، الذي تستخدمه معظم الشبكات العصبية المعتمدة على الرسائل، هو رسم العناصر الكيميائية إلى مجموعة من المتجهات ذات الطول الثابت عبر تحويل قابل للتعلم. عندما تتشكل الميزات ذات الرتبة الأعلى خلال مرحلة تمرير الرسائل، فإن هذه القنوات غير مرتبطة؛ وبالتالي فإن عدد الميزات لا يعتمد على عدد العناصر الكيميائية. بدلاً من ذلك، يتم خلط القنوات خلال مرحلة التحديث. يمكن أيضًا فهم هذه القنوات غير المرتبطة من حيث تحليل الموتر للصيغة المرتبطة بالكامل كما هو موضح في المرجع 37.
يمكن اتخاذ خيارات مماثلة لوظائف القاعدة الشعاعية. تستخدم ACE الخطية وظائف قاعدة شعاعية متعامدة وتشكل جميع التركيبات الممكنة (حتى التقطيع بواسطة الدرجة العليا للحدود) للميزات ذات الرتبة الأعلى. على سبيل المثال، بالنسبة لوظائف الأجسام الثلاثة، فإن الجزء الشعاعي له الشكل لكل التركيبات المسموح بها . بالمقابل، يتعلم NequIP مجموعة منفصلة (غير خطية) من الميزات الشعاعية لكل قاعدة جزيئية واحدة، كما هو موضح في المعادلة (6). لذلك، هناك دالة أساس شعاعية واحدة قابلة للتعلم لكل قناة التوافقيات الكروية تماثل ميزات الجوار وتناظر المخرجات القنوات غير المتصلة تُخلط فقط خلال مرحلة التحديث.
الجدول 1 | الخيارات المختلفة في الشكل متعدد ACE تؤدي إلى نماذج مختلفة في الأدبيات
تحديث ترتيب الارتباط الكلي التزاوج (ف)
صابون 0 ٢ 1
ACE الخطي 0 1
تتبع 0 1 لم
شنت 0 0 1 (المقادير)
دايم نت 0 0 ٢ 2T (المقادير)
الغطاس 1 (المتجهات الكروية)
نيكولب 1 (المتجهات الكروية)
جيم نت ٣ (المتجهات الكروية)
مايس (المتجهات الكروية)
نيوتن نت 1 1 1 المتجهات الكارتيزية –
EGNN 1 1 1 المتجهات الكارتيزية –
باين 1 1 1 المتجهات الكارتيزية –
تورش إم دي-نت 1 1 1 المتجهات الكارتيزية –
الداخلي يحدد المعلومات الزاوية المحتواة في وظيفة الرسائل مؤشر بأعلى الأوزان للتمثيلات غير القابلة للاختزال لـ التحديث يحدد المعلومات الزاوية في دالة التحديث. يتوافق ترتيب الارتباط الكلي مع ترتيب الارتباط للنموذج بالكامل كدالة للذرات الفردية. تتوافق النماذج التسعة العليا مع إمكانيات بين الذرات المتناظرة كروياً، بينما تتوافق النماذج الأربعة السفلى مع إمكانيات بين الذرات المتناظرة كارتيسياً. -، غير قابل للتطبيق.
التحليل ضمن مساحة التصميم يؤدي إلى سؤال حول الكمية المثلى من الترابط ضمن قاعدة المنتج في الطيف بين الترابط الكامل لنموذج ACE الخطي وغياب الترابط في NequIP.

تفسير النماذج كـ Multi-ACE

يتضمن إطار العمل Multi-ACE العديد من الشبكات المعتمدة على تمرير الرسائل المتكافئة التي تم نشرها سابقًا. تعتبر المواصفة الأساسية لنموذج Multi-ACE و . تشمل الخيارات الأخرى أنواع الميزات (أساس كارتيسي أو كروي) ونوع الاعتماد على الأساس الشعاعي على في المعادلة (2). لاحظ أن غير الخطيات النقطية الموجودة في بعض تلك النماذج تؤثر على كل من الارتباط المحلي والارتباط الكلي، كما هو موضح أدناه. من أجل البساطة، اخترنا عدم أخذها في الاعتبار في المناقشة التالية. يتم تلخيص مقارنة خيارات التصميم في النماذج المختلفة في الجدول 1.
يمكن الحصول على الالتفاف لشبكة SchNet من خلال اعتبار و تتضمن شبكة ديم نت لنقل الرسائل الثابتة رسائل ذات ترتيب ارتباط أعلى (بدقة، رسائل ثلاثية الجسم من خلال دمج المعلومات الزاوية)، مما يعني أن و “نكيب” يتوافق مع و حيث يمكن تبسيط التماثل في المعادلة (4) باستخدام معاملات كليبسش-غوردان العادية، :
نموذج MACE يتبع رسالة Multi-ACE في المعادلة (4) ويجمع بين ترتيب الارتباط المحلي العالي والرسائل المتكافئة في قاعدة كروية.
النماذج في الجزء السفلي من الجدول لا تستخدم توسيع التوافقيات الكروية ولكنها تعمل مع موترات كارتيسية. ومع ذلك، فإنها تتناسب مع هذا الإطار من خلال اعتبار تكافؤ المتجهات و الموترات الكروية. الإزاحات الإحداثية الموجودة في EGNN ونيوتن نت على سبيل المثال، يمكن إعادة كتابته كـ التوسع الكروي للبيئة من خلال تغيير الأساس.
الشكل 3 | المجال الاستقبالي لشبكات الرسائل المتعددة. مقارنة بين المجموعات التي تشكلت من خلال دورتين من تمرير الرسائل مع حد القطع في كل تكرار على اليسار لشبكة الرسوم البيانية المعتمدة على الرسوم البيانية (MPNN) والعناقيد التي شكلتها ACE مع حد القطع على اليمين. من حيث المبدأ، كلا الطريقتين تدمجان معلومات من مسافة تصل إلى ولكن في حالة MPNN، فإن الذرات التي يمكن الوصول إليها فقط من خلال سلسلة من الوسائط الأقرب هي التي تساهم.
استنادًا إلى النماذج المعروضة في الجدول 1، يتيح لنا إطار العمل Multi-ACE تحديد مسارين رئيسيين تم اتباعهما حتى الآن في بناء إمكانيات التفاعل بين الذرات. النماذج إما تحتوي على عدد قليل من الطبقات وترتيب ارتباط محلي عالٍ، مثل ACE الخطي (ونماذج أخرى تعتمد على الوصف)، أو تحتوي على العديد من الطبقات وترتيب ارتباط محلي منخفض، مشابه لـ NequIP.

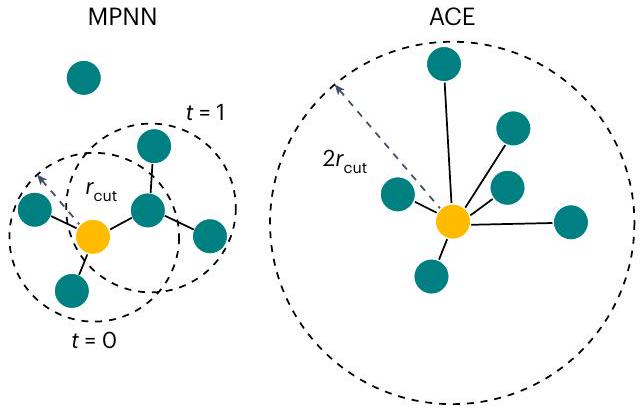
تمرير الرسائل كطريقة مستوحاة كيميائيًا للتقليل من الكثافة

أحد الجوانب المركزية لنماذج تمرير الرسائل هو معالجة المعلومات شبه المحلية: بينما في أساليب مثل ACE يؤثر الطاقة الذرية فقط على الذرات المجاورة ضمن كرة القطع المحلية، فإن الشكل الرسمي لتمرير الرسائل ينشر المعلومات بشكل تكراري، مما يسمح بتواصل المعلومات شبه المحلية. تقوم الشبكات العصبية المتغيرة مثل NequIP بتحديث حالات الذرات بناءً على حاصل الضرب التنسوري بين ميزات الحواف وحالات الذرات المجاورة، مما يؤدي إلى انتشار المعلومات ‘على شكل سلسلة’.
على وجه التحديد، اعتبر بنية تمرير الرسائل المبسطة للغاية مع قناة واحدة فقط وتحديث هذه هي الهوية فقط:
الجدول 2 | خطأ الجذر التربيعي المتوسط على مجموعة بيانات 3BPA مع شبكات NequIP بحجم تضمين كيميائي مختلف
16 32 64 128
عدد المعلمات ٤٣٧,٣٣٦ 1,130,648 3,415,832 11,580,440
300 ألف 3.7 3.1 3.0 (0.2) 2.9
Å 12.9 11.9 11.6 (0.2) 10.6
600 ألف 12.9 12.7 11.9 (1.1) 10.7
Å ٣٢.١ 30.3 ٢٩.٤ (٠.٨) ٢٦.٩
1,200,000 ٤٨.٦ ٤٩.٥ ٤٩.٨ (٤.٠) ٤٦.٠
Å ١٠٤.٢ 101.6 97.1 (5.6) 86.6
طاقة ) و القوة ( تظهر الأخطاء لشبكات NequIP ذات حجم متجه الميزات المتزايد، المدربة والمختبرة على تكوينات الجزيء المرن الشبيه بالعقاقير 3-(بنزيل أوكسي) بيريدين-2-أمين (3BPA) عند درجات الحرارة المشار إليها. تم تدريب جميع النماذج عند 300 كلفن. تم توليد جميع النتائج باستخدام قاعدة كود nequip. الأرقام بالخط العريض تت correspond إلى أدنى خطأ في كل صف. تم تدريب ثلاثة نماذج (باستخدام بذور عشوائية مختلفة لتهيئة الأوزان) مع 64 قناة، والانحراف المعياري للأخطاء موضح بين قوسين في العمود المقابل.
يمكننا كتابة المثال البسيط لتحديث ذو طبقتين بشكل صريح:
حيث افترضنا أن هو تمثيل عددي قابل للتعلم للعناصر الكيميائية، بحيث لا يمتلك .
هذا يحدد نمط تدفق المعلومات الذي تكون فيه حالة يتم تمريرها أولاً إلى الذرة ، مما أدى إلى يتم التقاط الارتباط. ثم يتم تمريره إلى الذرة ، الذي يشفر التفاعل الثلاثي بين الذرات ( على الذرة . هذه الخطة تحفز آلية انتشار متسلسلة ( )، وهو مختلف عن النماذج المحلية مثل ACE، حيث تكون العلاقة الثلاثية على الذرة ينبع من تفاعل بين ( ) و ( ).
يمكن للمرء بعد ذلك، تحت فرضية الخطية، أن ينظر إلى الشبكات العصبية المعادلة المتناظرة كإسقاط لنموذج ACE ذو طبقة واحدة مكافئ والذي يمتلك بدلاً من ذلك نصف قطر قطع أكبر. ، حيث هو الحد الأقصى للمسافة بين الذرات التي يمكن أن ترى بعضها البعض في -طبقة MPNN. بينما في ACE ذات الطبقة الواحدة، جميع المجموعات مع الذرة المركزية سيتم اعتبار ذلك، حيث يقوم الشكل الرياضي MPNN بتقليل هذا ليشمل فقط المسارات على الرسم البياني (الذي يتم تحفيزه بواسطة الحدود المحلية) بطول ينتهي على ذرة .
في الممارسة العملية، للإعدادات النموذجية لـ و نموذج محلي مثل ACE مع حد أقصى لـ سيكون غير عملي بسبب العدد الكبير من الذرات في الجوار. علاوة على ذلك، فإن الكتل التي تم إنشاؤها بواسطة تمثيلات مركز الذرة لقطع مكافئ لـ MPNNs أقل واقعية، كما هو موضح في الشكل 3. معظم التفاعلات الفيزيائية في الكيمياء قصيرة المدى وتنتشر المعلومات شبه المحلية في آلية تشبه السلسلة، مما يجعل تخفيض تمرير الرسائل يتوافق مع طوبولوجيا الروابط الكيميائية. يمكن العثور على مناقشة أكثر عمقًا حول العلاقة بين تمرير الرسائل والمعلومات شبه المحلية في المراجع 33،34.

الخيارات في فضاء تصميم الإمكانات بين الذرات المتكافئة

لجعل نظرية Multi-ACE الموضحة أعلاه ذات فائدة عملية، قمنا بتحليل مساحة تصميم إمكانيات التفاعل بين الذرات المتوافقة مع E (3). ركزنا على نموذجين من نماذج تمرير الرسائل المتوافقة: NequIP. وإصدارها الخطي المرتب، BOTNet (انظر المعلومات التكميلية للمعمارية الدقيقة لـ BOTNet). نوضح كيف تؤثر الخيارات المحددة في مساحة التصميم على أداء النماذج من حيث دقة المجال الداخلي والتوسع السلس، ونقارنها مع ACE الخطي، الذي يقع في نقطة مختلفة تمامًا من الإطار.

أساس الجسيم الواحد

تعتبر قاعدة الجسيم الواحد في صميم أي جهد بين الذرات يعتمد على تمرير الرسائل (الطرق). في الحالة الأكثر عمومية، يتم الإشارة إلى قاعدة الجسيم الواحد بـ كما تم تقديمه في المعادلة (2). أدناه، نقوم بتحليل بعض الخيارات التي يمكن اتخاذها بشأن معالجة العناصر الكيميائية عبر الوظائف وعلاج .
معالجة العناصر الكيميائية. إن الإدماج المستمر المستخدم في الشبكات العصبية متعددة الطبقات (MPNNs) يشبه وجود العديد من وحدات التحكم الخطية المنفصلة التي تكون حساسة جميعها للعناصر الكيميائية بطريقة قابلة للتعلم مختلفة. بعد كل خطوة من خطوات تمرير الرسائل، يتم خلط قنوات العناصر الكيميائية من خلال تحويل قابل للتعلم. من المثير للاهتمام أن الهوية الكيميائية للذرة المجاورة (المرسل) تدخل مباشرة فقط في التكرار. متى هو الترميز الأحادي للعناصر الكيميائية؛ بعد ذلك، يعتمد فقط بشكل غير مباشر على عنصر المرسل من خلال مخرجات الطبقة السابقة.
في هذا القسم نقوم بتحليل تأثير الزيادة ، الذي يتوافق مع بُعد تضمين العنصر الكيميائي. الجدول 2 يقارن نماذج NequIP مع زيادة يؤثر عدد القنوات غير المتصلة (الكيميائية) بشكل كبير على عدد المعلمات. ومع ذلك، فإن التدرج تقريبًا خطي مع عدد القنوات، بدلاً من أن يكون قانون قوة (يساوي ترتيب الارتباط) مع عدد العناصر المختلفة، وهو ما سيكون عليه الحال إذا تم استخدام فهرس عنصر كيميائي منفصل والأساس الخطي الكامل لـ ACE. يتم وصف العلاقة الرسمية بين المعالجات المتصلة بالكامل وغير المتصلة للعناصر الكيميائية في المرجع 37. ومن المثير للاهتمام أيضًا أن النماذج المفرطة المعلمات، كما هو معتاد في التعلم العميق، غالبًا ما تحقق نتائج أفضل. ليس فقط في النطاق (عند درجات حرارة منخفضة) ولكن أيضًا عند الاستقراء خارج النطاق (عند درجات حرارة مرتفعة).
ميزة إضافية لنهج تضمين العناصر هي أنه يسمح ببعض التعلم الكيميائي. يمكن أن تتعلم التضمينات تمثيلاً كامناً للعناصر الكيميائية وتقدم توقعات ذات مغزى لتركيبات من العناصر التي لا تظهر في نفس الوقت في مجموعة التدريب. يتم تقديم عرض لهذا التعلم الكيميائي أيضًا في المعلومات التكميلية لمقارنة NequIP و BOTNet مع ACE الخطي غير المدمج بالعناصر. تُظهر التجربة كيف يؤدي تضمين العناصر إلى منحنيات ديمر منطقية من الناحية الفيزيائية، حتى للتفاعلات التي لا توجد في مجموعة التدريب.
الأساس الشعاعي. هناك حرية كبيرة في اختيار شكل وظيفي لـ . في سياق تمثيلات البيئة المعتمدة على كثافة الذرات مثل والطيف الثنائي (SNAP) لقد كانت أهمية الأساس الشعاعي معروفة منذ زمن طويل، وتم تطوير العديد من الاستراتيجيات لتحسينه. كان اعتماد أفضل أساس شعاعي مصدرًا مستمرًا للتحسين للنماذج في الماضي. على سبيل المثال، في حالة SOAP، أدى تحسين الأساس الشعاعي إلى نماذج كانت أكثر كفاءة، وأكثر سلاسة، وأسرع. .
الخيار الأكثر بساطة لقاعدة شعاعية، المستخدمة (على سبيل المثال) من قبل ACE الخطي، هو مجموعة من دوال الأساس متعددة الحدود المتعامدة الثابتة التي تكون متطابقة لكل عنصر كيميائي ولا تعتمد على تعتمد الأنواع الذرية فقط من خلال تحويل المسافة. . يقوم تحويل المسافة هذا بتعديل المسافات بين الذرات لتكون في نطاق الأساس الشعاعي العمودي. يمكن أن تكون صيغته
الجدول 3 | أخطاء الطاقة والقوة الجذرية المتوسطة التربيعية في مجموعة بيانات 3BPA لاختيارات مختلفة من النماذج غير الخطية والخطية
نموذج نيكويب تان نيكويب سيلو نيكويب الخطي شبكة بوت خطية شبكة الروبوتات
رمز شبكة الروبوتات نيكويب شبكة الروبوتات شبكة الروبوتات شبكة الروبوتات
300 ألف ٤.٨ 3.0 (0.2) 3.7 ٣.٣ 3.1 (0.13)
Å 18.5 11.6 (0.2) 13.9 12.0 11.0 (0.14)
600 ك ٢٠.١ 11.9 (1.1) 15.4 11.8 11.5 (0.6)
Å 42.5 ٢٩.٤ (٠.٨) ٣٤.١ 30.0 ٢٦.٧ (٠.٢٩)
1,200 ألف 75.7 ٤٩.٨ (٤.٠) 61.92 53.7 ٣٩.١ (١.١)
Å 156.1 ٩٧.١ (٥.٦) ١٠٩.٥ 97.8 81.1 (1.5)
النماذج في أول عمودين من البيانات تستخدم والنماذج في الأعمدة المتبقية تستخدم (معلومات إضافية). تشير النماذج الخطية إلى النماذج التي لا تحتوي على أي تفعيل غير خطي. الأرقام بالخط العريض تت correspond إلى أدنى خطأ في كل صف.
تعتمد على العناصر الكيميائية للذرتين، مع الأخذ في الاعتبار الفروق في أنصاف الأقطار الذرية.
مؤخراً، أظهرت العديد من الأعمال أنه يمكن أن يكون من المفيد تحسين الأساس الشعاعي بطريقة مدفوعة بالبيانات. يمكن القيام بذلك مسبقاً. أو يمكن تحسينه أثناء تدريب النموذج .
تستخدم NequIP أيضًا قاعدة شعاعية قابلة للتعلم تعتمد على الزوج المرتب ( )، حيث يتوافق مع تمثيل التوافقيات الكروية إلى تمثيل الرسالة المتساوية وهناك قاعدة شعاعية مختلفة لكل منها :
حيث أن MLP هو شبكة عصبية متعددة الطبقات. عادةً، يكون عدد الطبقات المستخدمة في هذه الشبكة ثلاث طبقات. هي مجموعة من متعددات حدود بيسل هي دالة قطع بحيث لكن عدم فرض التعامد بين دوال الأساس المختلفة. هذا النوع من الأساس الشعاعي يسمح بمرونة محسّنة في الدقة المكانية عند دمج ميزات ذات تناظرات مختلفة. نشير إلى هذا الأساس الشعاعي باسم الأساس الشعاعي غير المعتمد على العناصر، حيث إنه مستقل عن العناصر الكيميائية.
تستخدم BOTNet قاعدة شعاعية قابلة للتعلم مشابهة، لكنها تعتمد أيضًا على عنصر الذرة الكيميائي للمرسل. يتم تحقيق ذلك من خلال تشكيل دوال قاعدة شعاعية مع مؤشر متعدد يعمل على أغطية السرير . هذا يعني أن BOTNet سيكون لديه قاعدة شعاعية منفصلة في كل قناة تضمين كيميائي لكل عنصر كيميائي جار وأن ستختار الدالة المناسبة بناءً على اعتمادها على (انظر المعادلة (2)). يمكن كتابة هذه القاعدة الشعاعية على النحو التالي:
أين هو مصفوفة من الأوزان بأبعاد [ ، هو عدد دوال بيسل الأساسية و هو عدد تركيبات المنتجات ذات التناظر المعطى بين الميزة المتكافئة والتناغمات الكروية. نشير إلى هذا النوع من الأساس الشعاعي باسم الأساس الشعاعي المعتمد على العنصر لأنه يعتمد بشكل صريح على العنصر الكيميائي للذرة. عبر مصفوفة الوزن.
لقد لاحظنا أن الأساس الشعاعي المعتمد على العنصر يعطي دقة تدريب وتحقق أفضل. ومع ذلك، بالنسبة للتقدير المتطرف (مثل كسر الروابط)، وجدنا أن الأساس الشعاعي غير المعتمد هو الخيار الأفضل، خاصة مع التطبيع الصحيح (كما تم مناقشته في المعلومات التكميلية).

تنشيطات غير خطية

ترتيب الجسم، كما هو معرف في الطرق، هو خاصية مركزية في مجالات القوة الكلاسيكية وقد أثبت أنه تقريبة ناجحة جدًا للأنظمة الميكانيكية الكمومية. . النسخة الخطية من ACE مرتبة حسب الجسم من حيث البناء، لكن معظم أساليب التعلم الآلي الأخرى لا تمتلك هذه البنية. كان يُعتقد أن استخدام النماذج المرتبة حسب الجسم
لتكون مفيدة لأنها تعزز تعلم التمثيلات ذات الأبعاد المنخفضة للبيانات، وهو انحياز استقرائي ممتاز لتحسين الاستقراء. في ما يلي، نقوم بتحليل تفعيلات غير الخطية المختلفة وتأثيراتها على ترتيب الجسم.
معادلة تمرير الرسائل ACE في المعادلة (4) هي عملية غير خطية وترتبط أساسًا بمنتج التنسور لـ المجموعة. تأثير هذه غير الخطية الناتجة عن حاصل الضرب التنسوري هو زيادة ترتيب الجسم لكل طبقة بواسطة تم نشر معظم هياكل MPNN سابقًا بالإضافة إلى حاصل الضرب التنسوري، من الممكن تضمين أنواع أخرى من عدم الخطية في من المعادلة (1) عن طريق أخذ أين هو دالة غير خطية عامة و هو مصفوفة الأوزان القابلة للتعلم التي تخلط بشكل خطي من المهم أن نلاحظ أن لا تحافظ على التماثل عندما تُطبق على الميزات التماثلية. استراتيجية شائعة هي استخدام غير خطيات تماثلية محكومة، والتي تم تلخيصها في المعلومات التكميلية. في ما يلي، عندما نقارن غير الخطيات، تختلف النماذج فقط في اختيار غير الخطيات المطبقة على الأجزاء الثابتة من النماذج؛ حيث يتم الاحتفاظ دائمًا بنفس غير الخطيات التماثلية.
إذا كان النموذج مرتّبًا بشكل صريح وفقًا للجسم ومتساويًا، فإنه يمكن استخدام مجموعة أصغر من غير الخطيات التي تحافظ على التساوي. الملاحظة المركزية هي أن غير الخطية تحافظ على ترتيب الجسم إذا كانت تقبل توسع تايلور محدود. يتم تقديم مثال تفصيلي يوضح كيف أن وحدة سيغمويد الخطية (SiLU) تدمر الهيكل المرتب للجسم في المعلومات التكميلية. هناك نوعان من غير الخطيات التي تحافظ على الهيكل المرتب للجسم؛ الأول يعرف باسم خدعة النواة ويتكون من استخدام غير الخطيات ذات توسع تايلور محدود (مثل المعيار المربع) لرفع ترتيب الجسم للتمثيل. .
النهج المتبع في تصميم BOTNet كان إنشاء نموذج مرتّب للجسم خلال أول خمس طبقات من تمرير الرسائل من خلال إزالة جميع التفعيلات غير الخطية من التحديث ولكن جعل القراءة الأخيرة غير خطية بترتيب جسم لانهائي. بهذه الطريقة، تكون وظيفة القراءة الأخيرة مسؤولة عن تمثيل المتبقي من توسيع ترتيب الجسم الذي لم يتم التقاطه بواسطة الطبقات الخمس الأولى. يفرض هذا التحلل الطاقي تعلم الهياكل ذات الأبعاد المنخفضة لأن الجزء المنخفض من ترتيب الجسم من الطاقة يظهر بشكل صريح. التوسع الطاقي المقابل لـ BOTNet هو:
أين هو مصطلح غير خطي عام يأخذ في الاعتبار جميع المساهمات المفقودة التي لم يتم التقاطها بواسطة الطبقات المرتبة السابقة.
تتم مقارنة النماذج التي تستخدم غير خطيات مختلفة في الجدول 3. من الواضح أنه في حالة NequIP، فإن اختيار غير الخطية أمر حاسم؛ حيث أن استخدام tanh بدلاً من SiLU يجعل النتائج أسوأ بشكل ملحوظ. هذا
من المحتمل أن يكون ذلك لأن دالة التانجنت المائل (tanh) لديها تدرج يساوي 0 للإدخالات الكبيرة الموجبة والسالبة، مما يجعل عملية التحسين صعبة بسبب تلاشي التدرجات. . هذا يجعل النماذج التي تستخدم غير الخطية tanh أسوأ حتى من عدم استخدام أي غير خطيات على الإطلاق (بخلاف حاصل الضرب التنسوري). في حالة BOTNet، يمكننا أن نرى أن إضافة طبقة غير خطية إلى نموذج مرتب بدقة حسب الجسم لأخذ في الاعتبار الحدود العليا في التوسع المرتب حسب الجسم المقطوع يحسن النتائج بشكل كبير. تشير صف التوحيد إلى نوع توحيد البيانات المستخدم في التجارب (للحصول على مزيد من المعلومات حول التوحيد، انظر المعلومات التكميلية).

نقاش

في هذه المقالة قدمنا Multi-ACE، وهو إطار عمل يتضمن العديد من الدراسات المنشورة سابقًا يمكن فهم إمكانيات التعلم الآلي بين الذرات المتساوية (أو الثابتة). باستخدام هذا الإطار، حددنا مساحة تصميم كبيرة ودرسنا بشكل منهجي كيف تؤثر الخيارات المختلفة التي تم اتخاذها في النماذج المختلفة على الدقة، والسلاسة، والتقدير الخارجي لإمكانات التفاعل بين الذرات الملائمة. في المعلومات التكميلية، نعرض أداء نماذج الشبكات العصبية الرسومية المتساوية في سياق أوسع، مقارنين إياها بالأساليب السابقة.
استخدمنا NequIP كمثال لاستكشاف كل من خيارات التصميم وأنشأنا نموذج BOTNet، الذي يحتفظ بأهم العناصر الأساسية لـ NequIP (منتج التنسور المتساوي والهيكل المتبقي القابل للتعلم) ولكنه يتخذ خيارات مختلفة بالنسبة للأساس الشعاعي، واستخدام التنشيطات غير الخطية والقراءات، مما يجعله نموذج MPNN مرتّب جسديًا بشكل صريح. كما تبرز دراستنا الأهمية الحاسمة للتطبيع الداخلي وتأثير تطبيع البيانات على كل من الدقة والتوقع. تتعلق منطقة مثيرة للاهتمام بشكل خاص من فضاء التصميم باستخدام ميزات محلية متعددة الجسيمات في نموذج تمرير الرسائل، والتي كانت موضوعًا للتحقيق في بعض الدراسات. .

طرق

ACE المتساوي مع تضمين مستمر وقنوات غير مرتبطة

ACE تم اقتراحه في الأصل كإطار لاستنتاج قاعدة متعددة الحدود المتماثلة المرتبة بكفاءة لتمثيل دوال الجوار الذري. وقد أظهر أنه تم اقتراح العديد من تمثيلات الحقول الذرية المتماثلة سابقًا. مثل ACSF صابون دوال الأساس المحتملة لموتر اللحظة والبيسبكترا الفائقة الكروية مستخدم من قبل SNAP يمكن التعبير عنها من حيث أساس ACE .
فيما يلي نقدم نسخة من صيغة ACE لاشتقاق وظائف الأساس الثابتة والمتناظرة التي تتضمن تضمينًا مستمرًا للعناصر الكيميائية وستكون بمثابة لبنة أساسية مهمة في إطار عمل Multi-ACE.
أساس الجسيم الواحد. الخطوة الأولى في بناء إطار عمل ACE هي تعريف أساس الجسيم الواحد، الذي يُستخدم لوصف الترتيب المكاني للذرات. حول الذرة :
حيث المؤشرات و تشير إلى العناصر الكيميائية للذرات و تتكون دوال الأساس لجسيم واحد كمنتج لمجموعة من دوال الأساس الشعاعية المتعامدة. والأشكال الكروية الحجة الموضعية يمكن الحصول على في المعادلة (12) من مما يعني أن قيمة دالة الأساس لجسيم واحد تعتمد على حالات ذرتين.
الصياغة في المعادلة (12) تستخدم تسميات العناصر الكيميائية المنفصلة. العيب في هذا النهج هو أن عدد الدوال الأساسية المختلفة يزداد بسرعة مع زيادة عدد العناصر الكيميائية في النظام. بالنظر إلى عناصر كيميائية مختلفة وأقصى ترتيب للجسم عدد دوال الأساس يتناسب مع .
على النقيض من ذلك، تستفيد الشبكات العصبية القائمة على الرسوم البيانية (MPNNs) عادةً من خريطة قابلة للتعلم من تسميات العناصر الكيميائية المنفصلة إلى تمثيل ثابت الطول مستمر. استخدام مثل هذا التضمين مع ACE يلغي زيادة عدد الدوال الأساسية مع عدد العناصر الكيميائية. يمكن تعميم قاعدة الجسيم الواحد للسماح بهذا التضمين المستمر من خلال مجموعة من الدوال التي نشرح مؤشريها أدناه:
أين هي دالة عامة للخصائص الكيميائية و ومزود بمؤشرين، و ، وكذلك قاعدة الشعاع. من بين هذه، مع و سيتم ربطها معًا عندما نشكل دوال الأساس متعددة الجسيمات (انظر المعادلة (15)). يتم جمع هذه المؤشرات المترابطة في مؤشر متعدد واحد. ) لسهولة التدوين. نشير إلى كفهرس غير مرتبط.
ما وراء تسميات العناصر الكيميائية، يمكن أن يفسر اعتماد دوال الأساس لجسيم واحد على سمات أخرى للذرات، مثل الشحنة، والعزم المغناطيسي أو الميزات القابلة للتعلم. علاوة على ذلك، فإن ناتج يمكن أن تكون ثابتة أو متساوية بالنسبة للدورات. في حالة المخرجات المتساوية، (في الحالة غير المتصلة) أو (في الحالة المترابطة) ستكون مؤشرات متعددة تحتوي على مؤشرات إضافية (على سبيل المثال، و ) التي تصف خصائص التحول لهذه المخرجات.
لاستعادة المعادلة (12) مع تسميات العناصر المنفصلة، نحدد إلى وافترض أن (أي أنه لا توجد مؤشرات غير مرتبطة). علاوة على ذلك، نحدد لتكون متعددة الفهارس ( ) مع كونه محدد فهرس . في هذه الحالة، الفهرس من في المعادلة (12) هي أيضًا جزء من .
في لغة الشبكات العصبية الجرافية متعددة الجزيئات، يمكن اعتبار قيم دوال الأساس لجزيء واحد كميزات حواف لنموذج الشبكة العصبية الجرافية. ستكون هذه الشبكة موجهة، حيث إن دوال الأساس لجزيء واحد ليست متناظرة بالنسبة لتبديل الذرة المركزية. والذرة المجاورة .
وظائف الأساس من الرتبة العليا. كانت إحدى الابتكارات الرئيسية في ACE هي بناء قاعدة كاملة للعديد من الأجسام، والتي يمكن حسابها بتكلفة ثابتة لكل وظيفة أساس. يمكن حساب ميزات النظام عالي الجسم دون الحاجة إلى جمع جميع الثلاثيات والرباعيات وما إلى ذلك بشكل صريح، وهو ما يتحقق من خلال ما أصبح يُعرف بخدعة الكثافة. تم تقديمه في الأصل للتقييم السريع لوصفيات عالية الترتيب. . هذا يسمح بتوسيع أي دالة متساوية E (3) من جيرة ذرية باستخدام توسيع منظم حسب الجسم بتكلفة حسابية منخفضة .
الخطوة التالية في بناء ACE تشبه تمرير الرسائل التقليدي: نقوم بجمع قيم دوال الأساس لجسيم واحد التي تم تقييمها على الجيران لتشكيل الذرة أو الأساس. يتوافق هذا مع إسقاط قاعدة الجسيم الواحد على الكثافة الذرية. لذلك، في أدبيات تمثيل البيئة الذرية، يُشار إلى هذه الخطوة غالبًا باسم إسقاط الكثافة. :
ال الأساس غير متغير بالنسبة لتباديل الذرات المجاورة، وعناصره هي دوال ثنائية الجسم بمعنى التعريف في المعادلة (27). هذا يعني أن هذا الأساس يمكن أن يمثل دوال تعتمد على مواقع جميع الجيران ولكن يمكن تفكيكه إلى مجموع من الحدود الثنائية الجسم.
ثم، لإنشاء دوال أساسية بترتيب أعلى، نقوم بتكوين نواتج من الـ دوال الأساس للحصول على قاعدة المنتج، :
أين يشير إلى ترتيب الارتباط ومؤشر المصفوفة يجمع المؤشرات المتعددة للفرد -دوال الأساس، تمثل
الأساس الناتج هو أساس كامل من الدوال الثابتة تحت التبديل لبيئة الذرات.
أخذ حاصل ضرب تؤدي دوال الأساس إلى دوال الأساس من ترتيب الارتباط ، التي لها ترتيب جسدي بسبب الذرة المركزية. في لغة التمثيلات المعتمدة على الكثافة، تتوافق هذه المنتجات التنسورية مع الارتباطات لكثافة الذرات في الجوار الذري .
على سبيل المثال، تكون دوال الأساس ذات الأربعة أجسام على الشكل:
أين . هذا يوضح الفرق بين غير المتصل القنوات (البعد) والمقترنة القنوات: لم نقم بتشكيل منتجات فيما يتعلق بالمؤشرات التي تم جمعها في لاحظ أنه في ACE الخطي، كما هو موصوف في المراجع. يتم أخذ حاصل الضرب التنسوري بالنسبة لجميع المؤشرات (الشعاعية، الزاوية وعناصر الكيمياء) في v، ولا تُستخدم مؤشرات غير مرتبطة.
تماثل دوال الأساس. الأساس الناتج في القسم السابق يمتد خطيًا على فضاء الدوال الثابتة تحت التباديل والترجمات ولكنه لا يأخذ في الاعتبار الثبات الدوراني أو التماثل في الخصائص المتوقعة أو الميزات الوسيطة. لإنشاء دوال أساس ثابتة دورانيًا أو متساوية، يجب تماثل الأساس الناتج بالنسبة إلى تأخذ عملية التماثل شكلها الأكثر عمومية كمتوسط على جميع التدويرات الممكنة للجوار. في حالة دوال الأساس غير القابلة للدوران، يتم التعبير عن هذا المتوسط كتكامل لمنتج الأساس على البيئات المحلية المدورة:
حيث نحدد بشكل صريح اعتماد قاعدة المنتج على الحالات الذرية، و يدل على فعل الدوران على زوج من الحالات الذرية. التكامل أعلاه هو مجرد شكلي. لإنشاء مجموعة ممتدة من المتناظر بدلاً من الوظائف المذكورة أعلاه، يمكن استخدام انقباضات التنسور حيث يتم التعبير عن الاعتماد الزاوي لقاعدة المنتج باستخدام نواتج من التوافقيات الكروية (انظر المعادلة (20) أدناه).
يمكن تعميم بناء المعادلة (17) بسهولة إذا كانت الميزات المتكافئة مطلوبة. . إذا كانت حركة دوران على ميزة يمثل بواسطة مصفوفة ثم يمكننا كتابة قيد التماثل على النحو التالي:
للتوسع الخطي يجب أن تلبي دوال الأساس نفس التماثلات. يتم تحقيق ذلك من خلال تعريف الأساس المتماثل كالتالي:
أين هو أساس فضاء الميزات . يمكن تطبيق هذا النهج لتحديد معلمات التنسورات من أي رتبة، سواء في الإحداثيات الكارتيزية أو الكروية. على سبيل المثال، إذا كان يمثل متجه ثلاثي الأبعاد إقليدي، يمكن أن تكون فقط الثلاثة متجهات الوحدة الكارتيزية، و .
من هنا نركز على الميزات الكروية التوافقية ووسمها وبناءً عليه، مع الدوال الأساسية المقابلة المشار إليها المصفوفات تصبح ويجنر- المصفوفات؛ أي، .
يمكن تقليل التكامل على الدورانات إلى تكرارات لمنتجات مصفوفات ويجنر-دي وإجراءه بشكل صريح كإجراء انكماش للموتر. من الممكن بعد ذلك إنشاء مجموعة شاملة من – الميزات المتكافئة للتكاملات من أنواع المعادلات (17) و (19) باستخدام العمليات الخطية. يمكن تحقيق ذلك من خلال إدخال معاملات الاقتران العامة:
حيث مؤشر المخرجات يعدد التركيبات المختلفة الممكنة لـ التي لديها للحصول على مناقشة مفصلة للحالة الثابتة، انظر المرجع 8.
باستخدام الإحداثيات الكروية للميزات، يتوافق مع معاملات كليبسش-غوردان العامة و يتوافق مع التسمية المعتادة لـ التمثيلات غير القابلة للاختزال. يمكن إدخال درجة إضافية من الحرية من خلال وجود أساس المنتج لكل (على سبيل المثال، من خلال اختيار دوال أساس جزيئية فردية مختلفة اعتمادًا على ). هذا خيار تم اتخاذه لـ NequIP. يتم تلخيص إنشاء دوال أساس عالية الترتيب المتماثلة في الشكل 1.
الوظائف تشكل مجموعة شاملة، مما يعني أن جميع تعمل وظائف الجسم بالتناظر يمكن تمثيل البيئة الذرية كمزيج خطي من وظائف قيم الـ يمكن دمج الوظائف في مخرج على كل ذرة وكل قناة عبر تحويل خطي قابل للتعلم:
أخيرًا، لتوليد الناتج المستهدف للذرة يمكن خلطها عبر دالة قابلة للتعلم (خطية أو غير خطية) .

إمكانات MPNN

في هذا القسم، نقوم بتلخيص إطار عمل MPNN لتناسب الإمكانيات بين الذرات واستخدام هذا الإطار لتوضيح الروابط بين ACE الخطية و MPNNs. تساعد المقارنة بين مجموعة واسعة من النماذج ضمن هذا الإطار في تحديد وشرح أوجه التشابه والاختلاف الرئيسية بينها.
شبكات الأعصاب الرسومية متعددة المعلمات (MPNNs) هي فئة من الشبكات العصبية الرسومية التي يمكن أن تضع معلمة لتعيين من فضاء الرسوم البيانية المعلّمة إلى فضاء متجهات الميزات. يمكن استخدامها لوضع معلمة للطاقات بين الذرات من خلال جعل الذرات تتوافق مع عقد الرسوم البيانية، وتربط حافة بين عقدتين إذا كانت المسافة بينهما أقل من . يقوم النموذج بربط مجموعة من الذرات بأنواع العناصر الموضوعة في الفضاء الإقليدي ثلاثي الأبعاد بالطاقة الكامنة الكلية. عادةً، هو أكبر بعدة مرات من طول الرابطة التساهمية. وبالتالي، فإن الرسم البياني المقابل يختلف تمامًا عن الرسم البياني للرابطة الذي يتم رسمه عادةً لجزيء؛ بل إنه يمثل العلاقات المكانية بين الذرات على مقياس طول أكبر. نحن نحدد مجموعة الجيران لذرة (أي، الذرات ضمن مسافة القطع) .

الدول شبه المحلية

نحن نحدد حالة الذرة كـ tuple :
أين تشير إلى متجه موقع الذرة الكارتيزي. مجموعة من خصائصه الثابتة مثل العنصر الكيميائي (يمثل عادةً بواسطة ترميز واحد حار)، و ميزاته القابلة للتعلم. هذه الميزات، على عكس السمات، يتم تحديثها بعد كل تكرار لتمرير الرسائل على أساس حالات الذرات المتصلة بالذرة . نشير إلى الحالات على أنها شبه محلية، حيث ستعتمد الخصائص في النهاية على حالات الذرات البعيدة (حوالي 10 إلى Åاعتمادًا على حدود الحي المحلي وعدد التكرارات). يتم استخدام آلية قطع سلسة بحيث تكون التحديثات مستمرة عندما تخرج الذرات أو تدخل حي بعضها المحلي.

صيغة تمرير الرسائل

نقوم بإعادة صياغة معادلات MPNN الأصلية للحالات الذرية. بشكل عام، يتكون جهد MPNN من مرحلة تمرير الرسائل ومرحلة القراءة. في مرحلة تمرير الرسائل، تُحدث بناءً على مشتق من حالات الذرات المجاورة ضمن المجموعة :
أين يشير إلى عملية تجميع غير حساسة للتبديل على جيران الذرة ، و يمكن أن يتوافق مع، على سبيل المثال، متوسط عدد الجيران عبر مجموعة التدريب (انظر المعلومات التكميلية لتحليل مفصل لدور هذا التطبيع). يشير إلى دالة قابلة للتعلم تعمل على حالات الذرات و أكثر عمليات التجميع غير القابلة للتبديل استخدامًا هي الجمع على الجيران. هذه العملية تخلق والتي هي ذات طبيعة ثنائية الجسم – أي، تركيبات خطية من الدوال التي تعتمد في الوقت نفسه على ميزات ذرتين فقط. ثم يمكن دمجه مع ميزات الذرة بواسطة دالة تحديث قابلة للتعلم، :
في من الممكن تشكيل رسائل من ترتيب أعلى للجسم عن طريق (على سبيل المثال) تطبيق دالة مربعة على الرسالة للحصول على تركيبة خطية من دوال ثلاثية الأبعاد تعتمد في الوقت نفسه على الذرة المركزية وجارين لها. و اعتمد على مؤشر التكرار .
في مرحلة القراءة، وظيفة قابلة للتعلم قم بربط الحالات الذرية بالطاقة في المواقع الذرية:
في هذه المرحلة، تستخدم بعض النماذج الحالات الذرية من كل تكرار، بينما تستخدم أخرى فقط دالة قراءة واحدة تأخذ الحالة بعد التكرار النهائي وتربطها بطاقة الموقع.

رسائل متكافئة

الخصائص الفيزيائية، مثل الطاقة أو لحظة ثنائي القطب، تتحول بطرق محددة تحت تأثير عمليات التناظر معينة، مثل الترجمات والدورات لإحداثيات الذرات. بالنسبة للنمذجة الذرية، فإن مجموعة التماثل هي ذات اهتمام خاص. على سبيل المثال، إذا تم تدوير جزيء في الفضاء، يجب أن يدور العزم الثنائي المتوقع وفقًا لذلك، في حين يجب أن تظل الطاقة دون تغيير. هنا قمنا بتقييد أنفسنا بالتماثلات الدورانية والانعكاسية، مجموعة، حيث يمكن ضمان عدم تغير الترجمة من خلال العمل مع متجهات إزاحة الذرات. .
طريقة بسيطة ومريحة لضمان أن مخرجات النماذج تتحول بشكل صحيح هي فرض قيود على التمثيلات الداخلية للنموذج لاحترام هذه التناظرات. نصنف ميزات الشبكة العصبية المتناظرة بناءً على كيفية تحولها تحت عمليات التناظر للمدخلات. بشكل رسمي يمكننا أن نفكر في كنتيجة لمواقع المدخلات (هنا الاعتماد على السمات يتم كتمه من أجل الإيجاز). ثم نقول أن هو متساوي الدوران (مع إذا تحولت وفقًا للتمثيل غير القابل للاختزال من مجموعة التماثل:
أين يدل على فعل مصفوفة دوران عشوائية على مجموعة المواقع الذرية ( ) و هو مصفوفة ويجنر-دي المقابلة، التمثيلات غير القابلة للاختزال لـ مجموعة . ومن ثم، رسالة مؤرشفة بواسطة يتحول مثل التوافقيات الكروية تحت الدوران.
خيار عملي مهم لتنفيذ الشبكات العصبية المتكافئة هو الأساس الذي يتم فيه التعبير عن الميزات والرسائل. في بقية هذه المقالة، سنفترض أنها مشفرة في
الإحداثيات الكروية. هذا يتماشى مع العديد من النماذج المتكافئة مثل SOAP-GAP سناب ACE وتنفيذاتها التكرارية مثل المرجع 50، NICE نيكويب محول متساوي التباين و SEGNNs “. بالمقابل، بعض الشبكات العصبية المتناظرة (مثل نيوتن نت) EGNN أو باين ) التعبير عن الميزات في الإحداثيات الكارتيزية. نظرًا لأن النماذج في هذه الفئة الأخيرة تستخدم المتجهات الإقليدية، التي تتوافق مع تتناسب المتجهات الكروية مع نفس الإطار من خلال تغيير الأساس. تتحول المتجهات الكروية وفقًا لـ التي تت correspond إلى مصفوفات الدوران. بعض النماذج، مثل SchNet ودايم نت استخدم فقط الرسائل الثابتة (أي، التوافقية).

رسائل مرتبة حسب الجسم

توسيع ترتيب الجسم لدالة متعددة المتغيرات العامة هو
إذا كانت شدة الحدود العليا صغيرة بما يكفي بحيث يمكن قطعها، فإن هذا التوسع يمكن أن يكون أداة قوية لتقريب الدوال ذات الأبعاد العالية. كما يظهر مفهوم ترتيب الجسم في ميكانيكا الكم. وهناك أدلة تجريبية وفيرة تشير إلى أن توسيع الطاقة الكامنة المرتبطة بالجسم يتقارب بسرعة للعديد من الأنظمة. .
من خلال التحكم بشكل صريح في ترتيب الجسم، يمكن للمرء أن يتعلم بكفاءة تمثيلات ذات أبعاد منخفضة تت correspond إلى مصطلحات ذات ترتيب منخفض. يُقترح أن يؤدي ذلك إلى إمكانيات بين الذرات مع قدرة محسّنة على التعميم. . لرسالة يمكن تعريف ترتيب الجسم على أنه أكبر عدد صحيح بحيث:
يمسك، حيث العناصر في الزوج ( ) جميعها متميزة، ولجميع الجانب الأيسر من المعادلة (28) يساوي صفرًا بشكل متطابق .
نطلق على النموذج اسم مرتّب الجسم إذا كان يمكن كتابته بشكل صريح في صيغة المعادلة (27) مع جميع الحدود حتى الحاضر. هذا يتناقض مع النماذج غير المرتبة جسديًا، حيث إما أن يكون التوسع لانهائي أو أن مجموعة فرعية فقط من الحدود موجودة. لتحقيق ترتيب الجسم في نموذج MPNN، يحتاج المرء إلى وظائف تحديث وقراءة خطية. وذلك لأن وظائف التنشيط غير الخطية، مثل دالة الظل الزائدي (tanh)، والدالة الأسية، وتطبيع المتجهات، لها توسعات لانهائية في سلسلة تايلور، مما يجعل ترتيب الجسم لانهائيًا دون أن تكون جميع الحدود في المعادلة (27) موجودة بشكل صريح.

توفر البيانات

تُوصف مجموعات البيانات المستخدمة في التجارب الحاسوبية في المعلومات التكميلية وهي متاحة عبر زينودو علىhttps://doi.org/10.5281/zenodo. 14013500 (مرجع 61).

توفر الشيفرة

تم استخدام كودين مختلفين لإجراء التجارب. جميع التجارب الم labeled ‘nequip’ في الجدول 3 تم إجراؤها باستخدام NequIP (github.com/mir-group/nequip) الإصدار 0.5.4، المتاح عبر Zenodo. بالإضافة إلى الإصدار 0.4.4 من مكتبة e3nn وإصدار PyTorch 1.10.0 (المرجع 64). جميع التجارب المعنونة ‘botnet’ في الجدول 3 تم إجراؤها باستخدام BOTNet المتوفر عبر GitHub فيغيت هاب.كوم/gncs/botnet وتم استخدامه بالتزامن مع الإصدار 0.3.2 من مكتبة e3nn وإصدار 1.8.0 من PyTorch . إذا لم يتم تحديد الرمز بشكل صريح (في قسم المعايير في المعلومات التكميلية)، فقد استخدمنا الرمز الذي يحمل الاسم نفسه لكل نموذج.

References

  1. Musil, F. et al. Physics-inspired structural representations for molecules and materials. Chem. Rev. 121, 9759-9815 (2021).
  2. Behler, J. & Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 98, 146401 (2007).
  3. Bartók, A. P., Kondor, R. & Csányi, G. On representing chemical environments. Phys. Rev. B 87, 184115 (2013).
  4. Behler, J. Four generations of high-dimensional neural network potentials. Chem. Rev. 121, 10037-10072 (2021).
  5. Deringer, V. L. et al. Gaussian process regression for materials and molecules. Chem. Rev. 121, 10073-10141 (2021).
  6. Cheng, B. et al. Mapping materials and molecules. Acc. Chem. Res. 53, 1981-1991 (2020).
  7. Drautz, R. Atomic cluster expansion for accurate and transferable interatomic potentials. Phys. Rev. B 99, 014104 (2019).
  8. Dusson, G. et al. Atomic cluster expansion: completeness, efficiency and stability. J. Comput. Phys. 454, 110946 (2022).
  9. Bartók, A. P., Payne, M. C., Kondor, R. & Csányi, G. Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 104, 136403 (2010).
  10. Shapeev, A. V. Moment tensor potentials: a class of systematically improvable interatomic potentials. Multisc. Model. Sim. 14, 1153-1173 (2016).
  11. Drautz, R. Atomic cluster expansion of scalar, vectorial, and tensorial properties including magnetism and charge transfer. Phys. Rev. B 102, 024104 (2020).
  12. Kovács, D. P. et al. Linear atomic cluster expansion force fields for organic molecules: beyond RMSE. J. Chem. Theor. Comput. 17, 7696-7711 (2021).
  13. Keith, J. A. et al. Combining machine learning and computational chemistry for predictive insights into chemical systems. Chem. Rev. 121, 9816-9872 (2021).
  14. Faber, F. A., Christensen, A. S., Huang, B. & von Lilienfeld, O. A. Alchemical and structural distribution based representation for universal quantum machine learning. J. Chem. Phys. 148, 241717 (2018).
  15. Zhu, L. et al. A fingerprint based metric for measuring similarities of crystalline structures. J. Chem. Phys. 144, 034203 (2016).
  16. Schütt, K. et al. SchNet: a continuous-filter convolutional neural network for modeling quantum interactions. In Advances in Neural Information Processing Systems Vol. 30 (eds Guyon, I. et al.) (Curran Associates, Inc., 2017); https://proceedings.neurips.cc/paper/2017/ file/303ed4c69846ab36c2904d3ba8573050-Paper.pdf
  17. Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O. & Dahl, G. E. Neural message passing for quantum chemistry. In Proc. 34th International Conference on Machine Learning Vol. 70 (eds Precup, D. & Teh, Y. W.) 1263-1272 (PMLR, 2017); https://proceedings.mlr. press/v70/gilmer17a.html
  18. Unke, O. T. & Meuwly, M. PhysNet: a neural network for predicting energies, forces, dipole moments, and partial charges. J. Chem. Theor. Comput. 15, 3678-3693 (2019).
  19. Gasteiger, J., Groß, J. & Günnemann, S. Directional message passing for molecular graphs. In Proc. International Conference on Leaning Representations (2020); https://iclr.cc/virtual_2020/ poster_B1eWbxStPH.html
  20. Anderson, B., Hy, T. S. & Kondor, R. Cormorant: covariant molecular neural networks. In Proc. 33rd Conference on Neural Information Processing Systems (eds Larochelle, H. et al.) (Curran Associates, 2019); https://proceedings.neurips.cc/paper/2019/file/ 03573b32b2746e6e8ca98b9123f2249b-Paper.pdf
  21. Thomas, N. et al. Tensor field networks: rotation- and translationequivariant neural networks for 3d point clouds. Preprint at http://arxiv.org/abs/1802.08219 (2018).
  22. Weiler, M., Geiger, M., Welling, M., Boomsma, W. & Cohen, T. 3D steerable CNNs: learning rotationally equivariant features in volumetric data. In Proc. 31st Conference on Neural Information Processing Systems (eds Bengio, S. et al.) (Curran Associates, 2018).
  23. Batzner, S. et al. E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials. Nat. Commun. 13, 2453 (2022).
  24. Satorras, V. G., Hoogeboom, E. & Welling, M. E(n) equivariant graph neural networks. In Proc. 38th International Conference on Machine Learning Vol. 139 (eds Meila, M. & Zhang, T.) 9323-9332 (PMLR, 2021).
  25. Schütt, K. T., Unke, O. T. & Gastegger, M. Equivariant message passing for the prediction of tensorial properties and molecular spectra. In Proc. 38th International Conference on Machine Learning Vol. 139 (eds Meila, M. & Zhang, T.) 9377-9388 (PMLR, 2021).
  26. Haghighatlari, M. et al. NewtonNet: a Newtonian message passing network for deep learning of interatomic potentials and forces. Digit. Discov. 1, 333-343 (2022).
  27. Klicpera, J., Becker, F. & Günnemann, S. Gemnet: universal directional graph neural networks for molecules. In Advances in Neural Information Processing Systems 34 (NeurIPS 2021) (eds Ranzato, M. et al.) 6790-6802 (Curran Associates, 2021).
  28. Thölke, P. & Fabritiis, G. D. Equivariant transformers for neural network based molecular potentials. In International Conference on Learning Representations (2022); https://openreview.net/ forum?id=zNHzqZ9wrRB
  29. Brandstetter, J., Hesselink, R., van der Pol, E., Bekkers, E. J. & Welling, M. Geometric and physical quantities improve equivariant message passing. In International Conference on Learning Representations (2021).
  30. Musaelian, A. et al. Learning local equivariant representations for large-scale atomistic dynamics. Nat. Commun. 14, 579 (2023).
  31. Kondor, R. N-body networks: a covariant hierarchical neural network architecture for learning atomic potentials. Preprint at https://arxiv.org/abs/1803.01588 (2018).
  32. Batatia, I. et al. The design space of E(3)-equivariant atom-centered interatomic potentials. Preprint at https://arXiv.org/abs/2205.06643 (2022).
  33. Nigam, J., Pozdnyakov, S., Fraux, G. & Ceriotti, M. Unified theory of atom-centered representations and message-passing machine-learning schemes. J. Chem. Phys. 156, 204115 (2022).
  34. Bochkarev, A., Lysogorskiy, Y., Ortner, C., Csányi, G. & Drautz, R. Multilayer atomic cluster expansion for semilocal interactions. Phys. Rev. Res. 4, LO42O19 (2022).
  35. Batatia, I., Kovacs, D. P., Simm, G. N. C., Ortner, C. & Csanyi, G. MACE: Higher order equivariant message passing neural networks for fast and accurate force fields. In Advances in Neural Information Processing Systems (NeurIPS2O22) (eds Koyejo,S. et al.) Curran Associates, 2022); https://proceedings.neurips.cc/ paper_files/paper/2022/hash/4a36c3c51af11ed9f34615b81ed b5bbc-Abstract-Conference.html
  36. Batatia, I. et al. Code for the paper titled “The Design Space of E(3)-Equivariant Atom-Centered Interatomic Potentials”. Github https://github.com/gncs/botnet/tree/v1.0.1 (2024).
  37. Darby, J. P. et al. Tensor-reduced atomic density representations. Phys. Rev. Lett. 131, 028001 (2023).
  38. Allen-Zhu, Z., Li, Y. & Liang, Y. Learning and generalization in overparameterized neural networks, going beyond two layers. In Neural Information Processing Systems (2018).
  39. Lopanitsyna, N., Fraux, G., Springer, M. A., De, S. & Ceriotti, M. Modeling high-entropy transition metal alloys with alchemical compression. Phys. Rev. Mater. 7, 045802 (2023).
  40. Thompson, A., Swiler, L., Trott, C., Foiles, S. & Tucker, G. Spectral neighbor analysis method for automated generation of quantumaccurate interatomic potentials. J. Comput. Phys. 285, 316-330 (2015).
  41. Caro, M. A. Optimizing many-body atomic descriptors for enhanced computational performance of machine learning based interatomic potentials. Phys. Rev. B 100, 024112 (2019).
  42. Musil, F. et al. Efficient implementation of atom-density representations. J. Chem. Phys. 154, 114109 (2021).
  43. Himanen, L. et al. DScribe: library of descriptors for machine learning in materials science. Comp. Phys. Commun. 247, 106949 (2020).
  44. Goscinski, A., Musil, F., Pozdnyakov, S., Nigam, J. & Ceriotti, M. Optimal radial basis for density-based atomic representations. J. Chem. Phys. 155, 104106 (2021).
  45. Bigi, F., Huguenin-Dumittan, K. K., Ceriotti, M. & Manolopoulos, D. E. A smooth basis for atomistic machine learning. J. Chem. Phys. 157, 243101 (2022).
  46. Witt, W. C. et al. ACEpotentials.jl: a Julia implementation of the atomic cluster expansion. J. Chem. Phys. 159, 164101 (2023); https://pubs.aip.org/aip/jcp/article/159/16/164101/2918010/ ACEpotentials-jl-A-Julia-implementation-of-the
  47. Goscinski, A., Musil, F., Pozdnyakov, S., Nigam, J. & Ceriotti, M. Optimal radial basis for density-based atomic representations. J. Chem. Phys. 155, 104106 (2021).
  48. Bochkarev, A. et al. Efficient parametrization of the atomic cluster expansion. Phys. Rev. Mater. 6, 013804 (2022).
  49. Elfwing, S., Uchibe, E. & Doya, K. Sigmoid-weighted linear units for neural network function approximation in reinforcement learning. Neural Networks 107, 3-11 (2018); https://doi.org/10.1016/ j.neunet.2017.12.012
  50. Lysogorskiy, Y. et al. Performant implementation of the atomic cluster expansion (PACE) and application to copper and silicon. npj Comput. Mater. 7, 97 (2021).
  51. Kaliuzhnyi, I. & Ortner, C. Optimal evaluation of symmetry-adapted -correlations via recursive contraction of sparse symmetric tensors. J. Numerical Mathematics (2024); https://doi.org/10.1515/ jnma-2024-0025
  52. Zhang, L. et al. Equivariant analytical mapping of first principles Hamiltonians to accurate and transferable materials models. npj Comput. Mater. 8, 158 (2022); https://www.nature.com/articles/ s41524-022-00843-2
  53. Nigam, J., Pozdnyakov, S. & Ceriotti, M. Recursive evaluation and iterative contraction of -body equivariant features. J. Chem. Phys. 153, 121101 (2020).
  54. Battaglia, P. W. et al. Relational inductive biases, deep learning, and graph networks. Preprint at https://arxiv.org/abs/1806.01261 (2018).
  55. Bronstein, M. M., Bruna, J., Cohen, T. & Velićković, P. Geometric deep learning: grids, groups, graphs, geodesics, and gauges. Preprint at https://arxiv.org/abs/2104.13478 (2021).
  56. Weyl, H. The Classical Groups: Their Invariants and Representations (Princeton Univ. Press, 1939).
  57. Thomas, J., Chen, H. & Ortner, C. Body-ordered approximations of atomic properties. Arch. Rational Mech. Anal. 246, 1-60 (2022); https://doi.org/10.1007/s00205-022-01809-w
  58. Drautz, R. & Pettifor, D. G. Valence-dependent analytic bond-order potential for transition metals. Phys. Rev. B 74, 174117 (2006).
  59. van der Oord, C., Dusson, G., Csányi, G. & Ortner, C. Regularised atomic body-ordered permutation-invariant polynomials for the construction of interatomic potentials. Mach. Learn. Sci. Technol. 1, 015004 (2020).
  60. Drautz, R., Fähnle, M. & Sanchez, J. M. General relations between many-body potentials and cluster expansions in multicomponent systems. J. Phys. Condens. Matter 16, 3843 (2004).
  61. Kovács, D. P. et al. BOTNet datasets: v0.1.O. Zenodo https://doi.org/ 10.5281/zenodo. 14013500 (2024).
  62. Musaelian, M. et al. NEquIP: v0.5.4. Zenodo https://doi.org/10.5281/ zenodo. 14013469 (2024).
  63. Geiger, M. et al. E3NN v0.5.4. Zenodo https://doi.org/10.5281/ zenodo. 5292912 (2020).
  64. Paszke, A. et al. Pytorch: an imperative style, high-performance deep learning library. In Advances in Neural Information Processing Systems Vol. 32 (eds Wallach, H. et al.) 8026-8037 (Curran Associates, Inc., 2019).
  65. Sim, G. & Batatia, I. Body-ordered Tensor Network (BOTNet). Zenodo https://doi.org/10.5281/zenodo. 14052468 (2024).

شكر وتقدير

تم تنفيذ هذا العمل باستخدام الموارد المقدمة من خدمة كامبريدج للاكتشاف المدفوع بالبيانات (CSD3)، التي تديرها خدمة الحوسبة البحثية بجامعة كامبريدج (www.csd3).كام.أك.uk) المقدمة من Dell EMC و Intel باستخدام تمويل من المستوى الثاني من مجلس أبحاث الهندسة والعلوم الفيزيائية (رقم المنحة الرأسمالية EP/TO22159/1) وتمويل DiRAC من مجلس مرافق العلوم والتكنولوجيا (www.dirac.ac.uk). يعترف D.P.K. بالدعم من أسترازينيكا ومجلس أبحاث الهندسة والعلوم الفيزيائية. C.O. مدعوم من منحة مشروع أبحاث ليفرهولم رقم RPG-2017-191 ومن مجلس أبحاث العلوم الطبيعية والهندسة في كندا (NSERC) تحت رقم مرجعي للتمويل IDGRO19381. تم دعم العمل في جامعة هارفارد من قبل أبحاث بوش، وزارة الطاقة الأمريكية، مكتب العلوم الأساسية للطاقة، تحت رقم الجائزة DE-SCOO22199، والهندسة المعمارية المدمجة للميكروية للتحفيز المستدام (IMASC)، وهو مركز أبحاث حدود الطاقة، تحت رقم الجائزة DE-SCOO12573 ومن قبل NSF من خلال منحة مركز أبحاث المواد في جامعة هارفارد رقم DMR-2011754. A.M. مدعوم من وزارة الطاقة الأمريكية، مكتب العلوم، مكتب أبحاث الحوسبة العلمية المتقدمة، زمالة دراسات العلوم الحاسوبية تحت رقم الجائزة DE-SC0021110. نحن نعترف بالموارد الحاسوبية المقدمة من مجموعة حوسبة أبحاث العلوم في قسم العلوم بجامعة هارفارد.

مساهمات المؤلفين

قام I.B. و S.B. و G.C. و B.K. بتصميم البحث وتخطيط التعاون. قام I.B. و G.N.C.S. بتنفيذ برنامج BOTNet. تم إجراء التجارب العددية بواسطة I.B. (رمز BOTNet) و S.B. و A.M. (رمز NequIP) و D.P.K. (ACE الخطي). قام I.B. و D.P.K. بإنتاج مجموعات البيانات. اقترح S.B. و A.M. و B.K. الروابط النظرية بين ACE و NequIP. اقترح G.C. و R.D. و C.O. مبادئ Multi-ACE وقام I.B. و D.P.K. و C.O. بتطوير المعادلات. قام I.B. و D.P.K. و C.O. و G.C.N.S. بصياغة نص المخطوطة والرسوم التوضيحية. قام جميع المؤلفين بتحرير المخطوطة.

المصالح المتنافسة

يمتلك G.C. و C.O. حصصًا في شركة Symmetric Group LLP، التي ترخص مجالات القوة تجاريًا. يمتلك G.C. حصة في شركة Ångström AI, Inc. بينما يمتلك R.D. مصلحة في شركة ACEworks GmbH. جميع المؤلفين الآخرين يعلنون عدم وجود مصالح متنافسة.

معلومات إضافية

البيانات الموسعة متاحة لهذا البحث فيhttps://doi.org/10.1038/s42256-024-00956-x.
معلومات إضافية النسخة الإلكترونية تحتوي على مواد إضافية متاحة فيhttps://doi.org/10.1038/s42256-024-00956-x.
يجب توجيه المراسلات والطلبات للحصول على المواد إلى إلياس باتاتيا أو غابور تشاني.
تُعرب مجلة Nature Machine Intelligence عن شكرها لمهند بوجوجيسكي، غيوم فورو، وريان-رايس غريفيثس على مساهمتهم في مراجعة الأقران لهذا العمل.
معلومات إعادة الطباعة والتصاريح متاحة علىwww.nature.com/reprints.
ملاحظة الناشر: تظل شركة سبرينجر ناتشر محايدة فيما يتعلق بالمطالبات القضائية في الخرائط المنشورة والانتماءات المؤسسية.
الوصول المفتوح هذه المقالة مرخصة بموجب رخصة المشاع الإبداعي النسب 4.0 الدولية، التي تسمح بالاستخدام والمشاركة والتكيف والتوزيع وإعادة الإنتاج بأي وسيلة أو صيغة، طالما أنك تعطي الائتمان المناسب للمؤلفين الأصليين والمصدر، وتوفر رابطًا لرخصة المشاع الإبداعي.
وحدد ما إذا تم إجراء تغييرات. الصور أو المواد الأخرى من طرف ثالث في هذه المقالة مشمولة في ترخيص المشاع الإبداعي للمقالة، ما لم يُشار إلى خلاف ذلك في سطر الائتمان للمادة. إذا لم تكن المادة مشمولة في ترخيص المشاع الإبداعي للمقالة وكان استخدامك المقصود غير مسموح به بموجب اللوائح القانونية أو يتجاوز الاستخدام المسموح به، فسيتعين عليك الحصول على إذن مباشرة من صاحب حقوق الطبع والنشر. لعرض نسخة من هذا الترخيص، قم بزيارةhttp://creativecommons.org/licenses/بواسطة/4.0/.
(ج) المؤلف(ون) 2025
البيانات الموسعة الجدول 1 | إمكانيات التعلم الآلي المختلفة في إطار الشبكات العصبية متعددة الطبقات
شنت نيكويب ACE الخطي
وظيفة الرسالة
تجميع متماثل
وظيفة التحديث –
نحدد SchNet وNequIP وACE كأمثلة على الشبكات العصبية الرسومية (MPNNs) ونظهر مكوناتها الصريحة في فضاء التصميم: الرسالة، التجميع المتماثل، ودوال التحديث. لاحظ أنه في NequIP، فإن اختيار غير الخطية ليس ثابتًا، وقد اخترنا تفعيلًا مقننًا باستخدام tanh ليظهر هنا. في كل حالة، يتم عرض المعلمات القابلة للتعلم (الأوزان) كـ والتحيزات كـ .
  1. ¹مختبر الهندسة، جامعة كامبريدج، كامبريدج، المملكة المتحدة. ²قسم الكيمياء، ENS باريس-ساكلاي، جامعة باريس-ساكلاي، غيف-سور-إيفيت، فرنسا. مدرسة جون أ. بولسون للهندسة والعلوم التطبيقية، جامعة هارفارد، كامبريدج، ماساتشوستس، الولايات المتحدة الأمريكية. ICAMS، جامعة روهر-بوخوم، بوخوم، ألمانيا. قسم الرياضيات، جامعة كولومبيا البريطانية، فانكوفر، كولومبيا البريطانية، كندا. مركز أبحاث وتكنولوجيا روبرت بوش ذ.م.م، ووتيرتاون، ماساتشوستس، الولايات المتحدة الأمريكية. العنوان الحالي: أبحاث مايكروسوفت AI للعلوم، كامبريدج، المملكة المتحدة. ساهم هؤلاء المؤلفون بالتساوي: إلياس باتاتيا، سيمون باتزنر. البريد الإلكتروني: ib467@cam.ac.uk; gc121@cam.ac.uk

Journal: Nature Machine Intelligence, Volume: 7, Issue: 1
DOI: https://doi.org/10.1038/s42256-024-00956-x
PMID: https://pubmed.ncbi.nlm.nih.gov/39877429
Publication Date: 2025-01-15

The design space of E(3)-equivariant atom-centred interatomic potentials

Received: 8 December 2022
Accepted: 13 November 2024
Published online: 15 January 2025
Check for updates

Ilyes Batatia , Simon Batzner , Dávid Péter Kovács¹, Albert Musaelian³, Gregor N. C. Simm , Ralf Drautz , Christoph Ortner , Boris Kozinsky & Gábor Csányi ⟶

Abstract

Molecular dynamics simulation is an important tool in computational materials science and chemistry, and in the past decade it has been revolutionized by machine learning. This rapid progress in machine learning interatomic potentials has produced a number of new architectures in just the past few years. Particularly notable among these are the atomic cluster expansion, which unified many of the earlier ideas around atom-density-based descriptors, and Neural Equivariant Interatomic Potentials (NequIP), a message-passing neural network with equivariant features that exhibited state-of-the-art accuracy at the time. Here we construct a mathematical framework that unifies these models: atomic cluster expansion is extended and recast as one layer of a multi-layer architecture, while the linearized version of NequIP is understood as a particular sparsification of a much larger polynomial model. Our framework also provides a practical tool for systematically probing different choices in this unified design space. An ablation study of NequIP, via a set of experiments looking at in- and out-of-domain accuracy and smooth extrapolation very far from the training data, sheds some light on which design choices are critical to achieving high accuracy. A much-simplified version of NequIP, which we call BOTnet (for body-ordered tensor network), has an interpretable architecture and maintains its accuracy on benchmark datasets.

There has been a revolution in atomistic modelling over the past decade, leading to the widespread adoption of machine learning interatomic potentials, particularly in materials science. A broad range of different model architectures have been proposed in the literature. These models are typically constructed to start with a descriptor (an array of numbers) to represent the environment of an atom. The key to the success of these models was making this descriptor invariant under the symmetry group of Euclidean symmetries (translation, rotation and reflection) of three-dimensional space (E(3)), as well as under the
permutations of atoms of the same element in the environment . Two examples of such descriptors are the atom-centred symmetry functions (ACSF) and the smooth overlap of atomic positions (SOAP) . Many interatomic potentials have been built using these descriptors and subsequently used to model materials (see corresponding recent reviews ). More recently, it has been recognized that both of these methods can be understood as special cases of the Atomic Cluster Expansion (ACE) . The key idea of ACE was to introduce a complete set of basis functions (using spherical harmonics and an orthogonal radial
basis) for the atomic environment that is built using the body-order expansion hierarchy. Many previously proposed descriptors fit into the ACE framework, with the key differences being the maximum order of the body-order expansion (three-body for ACSF and SOAP, four-body for the bispectrum and so on) and specific choices of the radial basis functions . An alternative way of defining features analogous to ACE is used by moment tensor potentials , which construct a spanning set for the atomic environment using Cartesian tensors that can be expressed as a linear transformation of the ACE basis. ACE naturally extends to equivariant features and to include variables beyond geometry, such as charges or magnetic moments . For a given descriptor, the atomic energy is fitted using a simple linear map , a Gaussian process or a feed-forward neural network . Other descriptor-based models have been built for entire molecules or structures directly, rather than decomposed into atomic contributions .
In parallel to the development of models using descriptors of atom-centred environments, other groups explored the use of message-passing neural networks (MPNNs) to fit interatomic potentials. These models represent the atomic structure as a graph in which an edge connects two nodes (atoms) if their distance is smaller than a fixed cutoff. The models then apply a series of convolution or message-passing operations on this graph to learn a representation of the environment of each atom. This learned representation is mapped to the site energy via a readout function (see the Methods for a more detailed description of message-passing potentials). Early models in this class, such as SchNet , Message Passing Neural Networks (MPNN) , PhysNet and DimeNet , used internal features that are invariant under rotations of the input structure.
A key innovation of the Cormorant network , tensor-field networks and steerable 3D convolutional neural networks (CNNs) was to create equivariant internal features that transform (under the symmetry operations of the input) like the irreducible representations of the symmetry group and construct invariants only at the very last step. For example, features inside the network can rotate with the structure just like a Euclidean vector would. To create these equivariant features inside the network, these networks introduced a type of nonlinear operation-an equivariant tensor product that couples features via the Clebsch-Gordan coefficients-resulting in output features of a desired symmetry. The idea of coupling equivariant operations with message passing on the graph of atoms was introduced with Neural Equivariant Interatomic Potentials (NequIP) and improved on the state-of-the-art accuracy at the time by a factor of about two across multiple datasets. Several equivariant message-passing models were subsequently published (for example, EGNN , PaiNN , NewtonNet , GemNet , TorchMD-Net and SEGNN ). An alternative equivariant deep learning interatomic potential was also introduced recently that does not make use of atom-centred message passing and explicitly demonstrated the scalability of equivariant models to millions of atoms.
In this Article we describe a framework called Multi-ACE with the aim of unifying the mathematical construction of MPNNs and ACE. The construction can be understood as a MPNN using ACE as the convolution in each layer of the network. We set out a comprehensive design space for creating machine learning interatomic potentials that incorporates most previously published models. Previous work has identified a connection between body order and MPNNs . Simultaneously with release of the preprint version of our work , ref. 33 investigated the formal connection between message-passing networks and atomic-density-based descriptors. The authors made the connection by interpreting message-passing networks as multicentred atomic-density representations. Our work extends these ideas by defining a comprehensive design space for atom-centred interatomic potentials and by giving a detailed analysis of each of the components of the framework. We also demonstrate how previously published models correspond to different points in the design space and comprehensively analyse all components of the models.
Fig. 1 | Construction of high-body-order ACE features. First a neighbourhood graph is constructed with each node labelled with its state. The one-particle basis is then computed for each edge. After that, a pooling operation is performed to create permutation-invariant functions of semi-local environments. To construct higher-body-order features, the product basis is formed by taking the tensor products of all coupled indices of the functions. Finally, to create equivariant messages, the basis is formed by first specifying the required equivariance and then evaluating the corresponding symmetrization integral. The invariant basis is shown here.
Two recent papers have demonstrated the usefulness of the Multi-ACE design space. ML-ACE used a fully coupled, invariant stack of Multi-ACE layers corresponding to a point in the design space. They made a connection between MPNNs and ACE via the power-series expansion of the electronic structure Hamiltonian. The second recent paper, building on the preprint of this work, introduced MACE , which uses a tensor-decomposed, equivariant stack of Multi-ACE layers, and showed that just two such layers could reach state-of-the-art accuracy at a reduced computational cost.
Using the Multi-ACE framework, it is possible to systematically probe different modelling choices. We demonstrate this through examples using a code called BOTNet (Body Ordered Tensor Network; described in detail in the Supplementary Information) and present a detailed study on which innovations and ‘tricks’ of the NequIP model are essential to achieving its high accuracy.

Multi-ACE

In this section, we show how multiple equivariant ACE layers can be combined to build a message-passing model (see the Methods for a general introduction to message-passing interatomic potentials and the standard ACE and its equivariant version). The resulting framework
Fig. 2 | Block structure of weight matrices for an equivariant linear operation. As only linear combinations of features of the same representations ( ) are allowed to interact, the weight matrix is block diagonal.
encompasses most equivariant MPNN-based interatomic potentials. If a single message-passing layer is used, the framework can be reduced to linear ACE or the other atom-centred descriptor-based models.
Using for a node state and for an aggregated message at iteration of central atom , we can define the Multi-ACE model as follows. First we identify the message with the output of an equivariant ACE layer and specify how it is used to form the next node state . The states of the atoms are updated by assigning the output of the previous layer to the feature :
where is the Cartesian position vector of are immutable node attributes (e.g. one-hot encoding of atomic numbers), is a set of messages as defined in equation (21) and is the update function for each layer. In most MPNNs, the channel of the message corresponds to the dimension of the learned embedding of the chemical elements . We need to extend the one-particle basis, , of equivariant ACE (from equation (13); Methods) to incorporate the dependence on the output of the previous layer, which can be achieved by making it an argument of the functions:
where are radial functions, are spherical harmonics, are generic node embedding functions and is the local correlation order of each layer are indices, is the number of message-passing layers, are neighbouring atoms, are chemical attributes and is the internal order of the spherical harmonic expansion within the layer in the one-particle basis. We have also added the index to the one-particle basis to enable a different set of one-particle basis functions to be included for messages with different symmetry corresponding to . The one-particle basis can be further extended to encompass attention-based models by adding additional arguments to the function as , where represents the neighbours of atom .
We now relate the equations of the MPNN framework to those of the Multi-ACE framework. First we identify the message function with the one-particle basis of equation (2):
Next we define the permutation-invariant pooling operation of equation (23). To obtain a symmetric many-body message of correlation order , the pooling operation must map the one-particle basis that is two-body to a set of many-body symmetric features that can be combined in a learnable way to form the message on each node. This is what the equivariant ACE formalism of ref. 7 achieves. In this way, we obtain the central equation of Multi-ACE:
where are learnable weights and equals the body order minus 1 . denotes the generalized Clebsch-Gordan coefficients defined in equation (20) and enumerates all the combinations for a given symmetry. The general scheme of higher-order message passing is illustrated in Fig. 1.
The update function from equation (24) corresponds to a learnable linear combination of the uncoupled channels of the symmetrized message and can be written as:
where is a block diagonal weight array (Fig. 2) of dimension is the number of uncoupled channels in the message and is the maximum order of symmetry in the message that is passed from one layer to the next. can also depend on the attributes (such as the chemical element) of the central atom via a so-called self-connection (see below for details). The update functions acting on equivariant features can also be nonlinear, but for that to occur, the functions must have a particular form (see ref. 22 and the Supplementary Information). After the th layer, a learnable (linear or nonlinear) readout function (that can depend on the final message or all previous ones) gives the site energy of atom .
We illustrate the choices for the message function, symmetric pooling and update function for three different models in Extended Data Table 1.

Coupling of channels

One important design choice in ACE models is how channels interact when forming the product basis. This choice affects the scaling of the number of features substantially and is therefore an essential part of the design space. This is best illustrated by considering the degree of freedom regarding the handling of different chemical elements. In the case of general linear ACE, and other similar descriptors such as SOAP, the element channel of the one-particle basis is a discrete index. When forming the higher-order many-body basis functions that will produce the features, these channels are coupled, forming all possible combinations. For example, if there are four different chemical elements, the number of three-body basis functions will be proportional to . The alternative approach, employed by most MPNNs, is to map the chemical elements to a set of fixed-length vectors via a learnable transformation. When the higher-order features are formed during the message-passing phase, these channels are not coupled; hence the number of features does not depend on the number of chemical elements. Instead, the channels are mixed during the update phase. These uncoupled channels can also be understood in terms of a tensor decomposition of the fully coupled form as demonstrated in ref. 37.
Similar choices can be made for the radial basis functions. Linear ACE uses orthonormal radial basis functions and forms all possible combinations (up to truncation by the maximum polynomial degree) for the higher-order features. For example, for the three-body functions, the radial part has the form for all allowed combinations of . By contrast, NequIP learns a separate (nonlinear) combination of radial features for each one-particle basis, as shown in equation (6). There is therefore a single learnable radial basis function for each channel , spherical harmonic , neighbour feature symmetry and output symmetry . The uncoupled channels are mixed only during the update phase.
Table 1 | Different choices in the Multi-ACE formalism lead to different models in the literature
Update Total correlation order Coupling (v)
SOAP 0 2 1
Linear ACE 0 1
TrACE 0 1 lm
SchNet 0 0 1 (scalars)
DimeNet 0 0 2 2T (scalars)
Cormorant 1 (spherical vectors)
NequlP 1 (spherical vectors)
GemNet 3 (spherical vectors)
MACE (spherical vectors)
NewtonNet 1 1 1 Cartesian vectors –
EGNN 1 1 1 Cartesian vectors –
PaINN 1 1 1 Cartesian vectors –
TorchMD-Net 1 1 1 Cartesian vectors –
The internal specifies the angular information contained on the messaging function indexed by the highest weights of the irreducible representations of . The update specifies the angular information in the update function. The total correlation order corresponds to the correlation order of the entire model as a function of individual atoms. The top nine models correspond to spherical equivariant interatomic potentials, whereas the bottom four models correspond to Cartesian equivariant interatomic potentials. -, not applicable.
The analysis within the design space leads to the question of the optimal amount of coupling within the product basis in the spectrum between the full coupling of linear ACE and lack of coupling in NequIP.

Interpreting models as Multi-ACE

The Multi-ACE framework includes many of the previously published equivariant message-passing networks. The most basic specification of a Multi-ACE model considers and . Other choices include the types of feature (Cartesian or spherical basis) and the type of dependence of the radial basis on in equation (2). Note that the pointwise nonlinearities present in some of those models affect both the local correlation and the total correlation, as discussed below. For simplicity, we chose not to consider them in the following discussion. A comparison of the design choices in different models is summarized in Table 1.
The convolution of the SchNet network can be obtained by considering and . The DimeNet invariant message-passing network includes higher-correlation-order messages (more precisely, three-body messages by incorporating angular information), meaning that and . NequIP corresponds to and , where the symmetrization of equation (4) can be simplified using ordinary Clebsch-Gordan coefficients, :
The MACE model follows the Multi-ACE message of equation (4) and combines high local correlation order with equivariant messages in a spherical basis.
The models in the lower part of the table do not use a spherical harmonics expansion but work with Cartesian tensors. Nonetheless, they fit into this framework by considering the equivalence of vectors and spherical tensors. The coordinate displacements present in EGNN and NewtonNet , for example, can thus be rewritten as an spherical expansion of the environment via a change of basis.
Fig. 3 | Receptive field of MPNNs. Comparison of the clusters formed by two iterations of message passing with cutoff at each iteration on the left for an MPNN and the clusters formed by ACE with cutoff on the right. In principle, both methods incorporate information from a distance of up to , but in the case of the MPNN, only atoms that can be reached through a chain of closer intermediates contribute.
Based on the models presented in Table 1, the Multi-ACE framework lets us identify two main routes that have been taken thus far in building interatomic potentials. The models have either few layers and high local correlation order, like linear ACE (and other descriptor-based models), or many layers and low local correlation order, similar to NequIP.

Message passing as a chemically inspired sparsification

One central aspect of message-passing models is the treatment of semi-local information: while in approaches such as ACE the atomic energy is only influenced by neighbouring atoms within the local cutoff sphere, the message-passing formalism iteratively propagates information, allowing semi-local information to be communicated. Equivariant MPNNs like NequIP update atom states on the basis of a tensor product between edge features and neighbouring atoms’ states, which leads to ‘chain-like’ information propagation.
Specifically, consider a much-simplified message-passing architecture with a single channel and an update that is just the identity:
Table 2 | Root-mean-square error on the 3BPA dataset with NequIP networks of different chemical embedding size
16 32 64 128
Number of parameters 437,336 1,130,648 3,415,832 11,580,440
300K 3.7 3.1 3.0 (0.2) 2.9
Å 12.9 11.9 11.6 (0.2) 10.6
600K 12.9 12.7 11.9 (1.1) 10.7
Å 32.1 30.3 29.4 (0.8) 26.9
1,200K 48.6 49.5 49.8 (4.0) 46.0
Å 104.2 101.6 97.1 (5.6) 86.6
Energy ( ) and force ( ) errors are shown for NequIP networks of increasing feature vector size, trained and tested on configurations of the flexible drug-like molecule 3-(benzyloxy) pyridin-2-amine (3BPA) at the temperatures indicated. All models were trained at 300 K . All results were generated with the nequip code base. Bold numbers correspond to lowest error in each row. Three models were trained (using different random seeds to initialise the weights) with 64 channels, and the standard deviation of the errors are shown in parentheses in the corresponding column.
We can write out the simple example of a two-layer update explicitly:
where we have assumed that is a scalar, learnable embedding of the chemical elements, such that it does not possess .
This defines a pattern of information flow in which the state of is first passed on to atom , resulting in the correlation being captured. This is then passed on to atom , which encodes the three-body interaction between atoms ( ) on atom . This scheme induces a chain-wise propagation mechanism ( ), which is different from local models like ACE, in which the three-body correlation on atom stems from an interaction between ( ) and ( ).
One can then, under the assumption of linearity, view equivariant MPNNs as a sparsification of an equivalent one-layer ACE model that instead has a larger cutoff radius , where is the maximal distance of atoms that can see each other in a -layer MPNN. While in a one-layer ACE, all clusters with central atom would be considered, the MPNN formalism sparsifies this to only include walks along the graph (the topology of which is induced by local cutoffs) of length that end on atom .
In practice, for typical settings of and , a local model like ACE with a cut off of would be impractical due to the large number of atoms in the neighbourhood. Moreover, the clusters created by atom-centred representations for an equivalent cutoff to MPNNs are less physical, as illustrated in Fig. 3. Most physical interactions in chemistry are short-range and semi-local information propagates in a chain-like mechanism, thus making the message-passing sparsification correspond to the chemical bond topology. A more in-depth discussion on the relationship between message passing and semi-local information can be found in refs. 33,34.

Choices in the equivariant interatomic potential design space

To render the Multi-ACE theory set out above of practical use, we analysed the design space of E (3)-equivariant interatomic potentials. We focused on two equivariant message-passing models: NequIP and its linearized body-order version, BOTNet (see the Supplementary Information for the precise architecture of BOTNet). We show how specific choices in the design space affect the performance of the models in terms of in-domain accuracy and smooth extrapolation and compare them with linear ACE, which is at a very different point of the framework.

One-particle basis

The one-particle basis is at the core of any message-passing interatomic potential (Methods). In the most general case, the one-particle basis is denoted as introduced in equation (2). Below, we analyse some of the choices that can be made regarding the treatment of the chemical elements via the functions and the treatment of .
Treatment of the chemical elements. The continuous embedding used in MPNNs is analogous to having many separate linear ACEs that are all sensitive to the chemical elements in a different learnable way. After each message-passing step, the chemical element channels are mixed via a learnable transformation. It is interesting to note that the chemical identity of the neighbouring atom (the sender) only enters directly at iteration when is the one-hot encoding of the chemical elements; after this it is only indirectly dependent on the sender element via the output of the previous layer.
In this section we analyse the effect of increasing , which corresponds to the dimension of the chemical element embedding. Table 2 compares NequIP models with increasing . The number of uncoupled (chemical) channels substantially affects the number of parameters. However, the scaling is nearly linear with the number of channels, rather than a power law (equal to the correlation order) with the number of different elements, which would be the case if a discrete chemical element index and the complete linear ACE basis were used. The formal relationship between the fully coupled and uncoupled treatments of the chemical elements is described in ref. 37 . It is also interesting to note that, as is typical in deep learning, over-parameterized models often achieve better results not only in-domain(at low temperature) but also when extrapolating out-of-domain (at high temperature).
A further advantage of the element embedding approach is that it allows some alchemical learning. The embeddings can learn a latent representation of the chemical elements and provide meaningful predictions for combinations of elements that do not appear simultaneously in the training set . A demonstration of this alchemical learning is also presented in the Supplementary Information to compare NequIP and BOTNet to the non-element-embedded linear ACE. The experiment shows how the element embedding leads to physically sensible dimer curves, even for interactions that are not present in the training set.
Radial basis. There is considerable freedom in choosing a functional form for . In the context of atom-density-based environment representations such as and the bispectrum (SNAP) , the importance of the radial basis has been long known, and many strategies have been developed to improve it. Adopting the best radial basis has been a continuous source of improvement for models in the past. For example, in the case of SOAP, improving the radial basis led to models that were more efficient, smoother and faster .
The most straightforward choice for a radial basis, used (for example) by linear ACE, is a set of fixed orthogonal polynomial basis functions that are the same for each chemical element and do not depend on . The dependence on the atom types only enters via the distance transform . This distance transform scales the interatomic distances to be in the domain of the orthogonal radial basis. Its form can be
Table 3 | Root-mean-square energy and force errors on the 3BPA dataset for different choices of nonlinear and linear models
Model NequIP tanh NequIP Silu NequIP linear BOTNet linear BOTNet
Code botnet nequip botnet botnet botnet
300K 4.8 3.0 (0.2) 3.7 3.3 3.1 (0.13)
Å 18.5 11.6 (0.2) 13.9 12.0 11.0 (0.14)
600 K 20.1 11.9 (1.1) 15.4 11.8 11.5 (0.6)
Å 42.5 29.4 (0.8) 34.1 30.0 26.7 (0.29)
1,200K 75.7 49.8 (4.0) 61.92 53.7 39.1 (1.1)
Å 156.1 97.1 (5.6) 109.5 97.8 81.1 (1.5)
Models in the first two columns of data use and the models in the remaining columns use (Supplementary Information). Linear models refer to models without any nonlinear activation. Bold numbers correspond to lowest error in each row.
dependent on the chemical elements of the two atoms, accounting for the differences in atomic radii.
Recently, much work has shown that it can be advantageous to optimize the radial basis in a data-driven way. This can be done a priori or can be optimized during the training of the model .
NequIP also uses a learnable radial basis that is dependent on the tuple ( ), where corresponds to the representation of the spherical harmonics to the representation of the equivariant message and there is a different radial basis for each :
where MLP is a multi-layer perceptron. Typically, the number of layers used in this MLP is three. are a set of Bessel basis polynomials and is a cutoff function such that but orthogonality of the different basis functions is not enforced. This type of radial basis allows improved flexibility in spatial resolution when combining features of different symmetries. We refer to this radial basis as the element-agnostic radial basis, as it is independent of the chemical elements.
BOTNet uses a similar learnable radial basis, but it is also dependent on the sender atom chemical element. This is achieved by forming radial basis functions with the multi-index running over . bedding . This means that BOTNet will have a separate radial basis in each chemical embedding channel for each neighbour chemical element and that the function will pick up the appropriate one via its dependence on (see equation (2)). This radial basis can be written as:
where is an array of weights of dimensions [ , is the number of Bessel basis functions and is the number of combination of products of a given symmetry between the equivariant feature and the spherical harmonics. We refer to this type of radial basis as the element-dependent radial basis because it explicitly depends on the chemical element of atom via the weight array.
We have observed that the element-dependent radial basis gives better training and validation accuracy. However, for extreme extrapolation (such as with bond breaking), we have found that the agnostic radial basis is a better choice, particularly with the correct normalization (as discussed in the Supplementary Information).

Nonlinear activations

The body ordering, as defined in the Methods, is a central property of classical force fields and has proved to be a very successful approximation of quantum mechanical systems . The linear version of ACE is body ordered by construction, but most other machine learning approaches do not have this structure. The use of body-ordered models was thought
to be beneficial because it enforces the learning of low-dimensional representations of the data, which is an excellent inductive bias for better extrapolation. In the following, we analyse different nonlinear activations and their effects on body ordering.
The ACE message-passing equation in equation (4) is a nonlinear operation and is fundamentally related to the tensor product of the group. The effect of this tensor-product nonlinearity is to increase the body order of each layer by . Most previously published MPNN architectures have . Beyond the tensor product, it is possible to include other types of nonlinearity in of equation (1) by taking where is a generic nonlinear function and is an learnable weight matrix that linearly mixes . It is important to note that does not preserve equivariance when applied to equivariant features. A common strategy is to use gated equivariant nonlinearities, which are summarized in the Supplementary Information. In the following, when we compare nonlinearities the models differ only in the choice of nonlinearities applied to the invariant parts of the models; the equivariant nonlinearities are always kept the same.
If the model is explicitly body-ordered and equivariant, only a smaller subset of nonlinearities that preserve the equivariance can then be used. The central remark is that a nonlinearity preserves body ordering if it admits a finite Taylor expansion. A detailed example showing how the Sigmoid Linear Unit (SiLU) nonlinearity destroys the body-ordered structure is presented in the Supplementary Information. Two types of nonlinearity preserve the body-ordered structure; the first is known as the kernel trick and consists of using nonlinearities with a finite Taylor expansion (such as the squared norm) to raise the body order of the representation .
The approach taken in designing BOTNet was to create a bodyordered model during the first five message-passing layers by removing all nonlinear activations from the update but making the last readout nonlinear with an infinite body order. In this way, the last readout function is responsible for representing the residual of the body-order expansion not captured by the first five layers. This energy decomposition enforces the learning of low-dimensional structures because the low-body-order part of the energy appears explicitly. The corresponding energy expansion of BOTNet is:
where is a general nonlinear term that accounts for all of the missing contributions not captured by the previous body-ordered layers.
Models that use different nonlinearities are compared in Table 3. It is clear that in the case of NequIP, the choice of nonlinearity is crucial; using tanh instead of SiLU makes the results significantly worse. This
is probably because the tanh function has 0 gradient for large positive and negative inputs, which makes the optimization difficult due to vanishing gradients . This makes models with tanh nonlinearity even worse than not using any nonlinearities at all (other than the tensor product). In the case of BOTNet, we can see that adding a nonlinear layer to a strictly body-ordered model to account for the higher-order terms in the truncated body-ordered expansion significantly improves the results. The normalization row indicates the type of data normalization used for the experiments (for further information on normalization, see the Supplementary Information).

Discussion

In this Article we have introduced Multi-ACE, a framework in which many previously published -equivariant (or invariant) machine learning interatomic potentials can be understood. Using this framework, we have identified a large design space and have systematically studied how different choices made in the different models affect the accuracy, smoothness and extrapolation of the fitted interatomic potentials. In the Supplementary Information we show the performance of the equivariant graph neural network models in a broader context, comparing them with earlier approaches.
We used NequIP as an example to probe each of the design choices and created the BOTNet model, which retains the most crucial elements of NequIP (the equivariant tensor product and the learnable residual architecture) but makes different choices for the radial basis, the use of nonlinear activations and readouts, making it an explicitly body-ordered MPNN model. Our study also highlights the crucial importance of internal normalization and the effect of data normalization on both accuracy and extrapolation. One particularly interesting region of the design space relates to the use of locally many-body features in a message-passing model, which has been the subject of investigation in some studies .

Methods

Equivariant ACE with continuous embedding and uncoupled channels

ACE was originally proposed as a framework for deriving an efficient body-ordered symmetric polynomial basis to represent functions of atomic neighbourhoods. It has been shown that many of the previously proposed symmetrized atomic field representations , such as ACSF , SOAP , moment tensor potential basis functions and the hyperspherical bispectrum used by SNAP , can be expressed in terms of the ACE basis .
In the following we present a version of the ACE formalism for deriving -invariant and equivariant basis functions that incorporates a continuous embedding of chemical elements and will serve as an important building block of the Multi-ACE framework.
One-particle basis. The first step in constructing the ACE framework is to define the one-particle basis, which is used to describe the spatial arrangement of atoms around the atom :
where the indices and refer to the chemical elements of atoms and . The one-particle basis functions are formed as the product of a set of orthogonal radial basis functions and spherical harmonics . The positional argument in equation (12) can be obtained from , meaning that the value of the one-particle basis function depends on the states of two atoms.
The formulation in equation (12) uses discrete chemical element labels. The drawback of this approach is that the number of different basis functions rapidly increases with the number of chemical elements in the system. Given different chemical elements and maximum body order , the number of basis functions is proportional to .
By contrast, MPNNs typically leverage a learnable mapping from the discrete chemical element labels to a continuous fixed-length representation. Using such an embedding with ACE eliminates the scaling of the number of basis functions with the number of chemical elements. The one-particle basis can be generalized to allow this continuous embedding via a set of functions whose two indices we explain below:
where is a generic function of the chemical attributes and and is endowed with two indices, and , and the radial basis likewise. Of these, , together with and , will be coupled together when we form many-body basis functions (see equation (15)). These coupled indices are collected into a single multi-index ( ) for ease of notation. We refer to as the uncoupled index.
Beyond the chemical element labels, can account for the dependence of the one-particle basis functions on other attributes of the atoms, such as the charge, magnetic moment or learnable features. Furthermore, the output of can be invariant or equivariant to rotations. In the case of equivariant outputs, (in the uncoupled case) or (in the coupled case) will themselves be multi-indices that contain additional indices (for example, and ) that describe the transformation properties of these outputs.
To recover equation (12) with the discrete element labels, we set to and assume that (that is, there are no uncoupled indices). Furthermore, we set to be a multi-index ( ) with being an index selector . In this case, the index of in equation (12) is also part of .
In the language of MPNNs, the values of the one-particle basis functions would be thought of as edge features of a graph neural network model. This graph would be directed, as the one-particle basis functions are not symmetric with respect to the swapping of the central atom and the neighbouring atom .
Higher-order basis functions. A key innovation of ACE was the construction of a complete many-body basis, which can be computed at a constant cost per basis function . The high-body-order features can be computed without having to explicitly sum over all triplets, quadruplets and so on, which is achieved by what came to be called the density trick , introduced originally for the fast evaluation of high-body-order descriptors . This allows any E (3)-equivariant function of an atomic neighbourhood to be expanded using a systematic body-ordered expansion at a low computational cost .
The next step of the ACE construction is analogous to traditional message passing: we sum the values of the one-particle basis functions evaluated on the neighbours to form the atomic or basis. This corresponds to a projection of the one-particle basis on the atomic density. Therefore, in the atomic environment representation literature, this step is often referred to as the density projection :
The basis is invariant with respect to the permutations of the neighbouring atoms, and its elements are two-body functions in the sense of the definition in equation (27). This means that this basis can represent functions that depend on all neighbours’ positions but can be decomposed into a sum of two-body terms.
Then, to create basis functions with higher body order, we form products of the basis functions to obtain the product basis, :
where denotes the correlation order and the array index collects the multi-indices of the individual -basis functions, representing a
tuple. The product basis is a complete basis of permutation-invariant functions of the atomic environment.
Taking the product of basis functions results in basis functions of correlation order , which thus have body order due to the central atom. In the language of density-based representations, these tensor products correspond to correlations of the density of atoms in the atomic neighbourhood .
For example, the , four-body basis functions have the form:
where . This illustrates the difference between the uncoupled channels (dimension) and the coupled channels: we did not form products with respect to the indices collected in . Note that in linear ACE, as described in refs. , the tensor product is taken with respect to all of the indices (radial, angular and chemical elements) in v, and no uncoupled indices are used.
Symmetrization of basis functions. The product basis constructed in the previous section linearly spans the space of permutationally and translationally invariant functions but does not account for rotational invariance or equivariance of the predicted properties or intermediate features. To create rotationally invariant or equivariant basis functions, the product basis must be symmetrized with respect to . The symmetrization takes its most general form as an averaging over all possible rotations of the neighbourhood. In the case of rotationally invariant basis functions, this averaging is expressed as an integral of the product basis over rotated local environments:
where we explicitly define the dependence of the product basis on the atomic states, and denotes the action of the rotation on a pair of atomic states. The above integral is purely formal. To explicitly create a spanning set of the symmetric functions above, one can instead use tensor contractions as the angular dependence of the product basis is expressed using products of spherical harmonics (see equation (20) below).
The construction of equation (17) is readily generalized if equivariant features are required . If the action of a rotation on a feature is represented by a matrix , then we can write the equivariance constraint as:
To linearly expand , the basis functions must satisfy the same symmetries. This is achieved by defining the symmetrized basis as:
where is a basis of the feature space . This approach can be applied to parameterize tensors of any order, both in Cartesian and spherical coordinates. For instance, if represents a Euclidean three vector, can just be the three Cartesian unit vectors, and .
From here we focus on features with spherical equivariance and label them accordingly, with the corresponding basis functions denoted . The matrices become the Wigner- matrices; that is, .
The integration over the rotations can be reduced to recursions of products of Wigner-D matrices and carried out explicitly as a tensor contraction . It is then possible to create a spanning set of -equivariant features of the integrals of the types of equations (17) and (19) using linear operations. This can be done by introducing the generalized coupling coefficients:
where the output index enumerates the different possible combinations of that have . For a detailed discussion of the invariant case, see ref. 8.
Using spherical coordinates for the features, corresponds to the generalized Clebsch-Gordan coefficients and corresponds to the usual labelling of the irreducible representations. An additional degree of freedom can be introduced by having a different product basis for each (for example, by choosing different one-particle basis functions depending on ). This is a choice made for NequIP. The creation of symmetric high-body-order basis functions is summarized in Fig. 1.
The functions form a spanning set, meaning that all ( )-body functions with symmetry of the atomic environment can be represented as a linear combination of functions .The values of the functions can be combined into an output on each atom and each channel via a learnable linear transformation:
Finally, to generate the target output for atom can be mixed via a learnable (linear or nonlinear) function .

MPNN potentials

In this section we summarize the MPNN framework for fitting interatomic potentials and use this framework to elucidate the connections between linear ACE and MPNNs. The comparison of a wide range of models within this framework helps to identify and explain their key similarities and differences.
MPNNs are a class of graph neural networks that can parameterize a mapping from the space of labelled graphs to a vector space of features. They can be used to parameterize interatomic potentials by making atoms correspond to the nodes of the graph, and an edge connects two nodes if their distance is less than . The model maps a set of atoms with element types positioned in the three-dimensional Euclidean space to the total potential energy. Typically, is several times larger than the length of a covalent bond. Thus, the corresponding graph is quite different from the typically drawn bonding graph of a molecule; instead, it represents the spatial relationships between atoms on a larger length scale. We denote the set of neighbours of an atom (that is, atoms within the cutoff distance) .

Semi-local states

We denote the state of an atom as the tuple :
where denotes the atom’s Cartesian position vector, a set of its fixed attributes such as the chemical element (typically represented by a one-hot encoding), and its learnable features. These features, unlike the attributes, are updated after each message-passing iteration on the basis of the states of the atoms connected to atom . We refer to the states as semi-local, as the features will ultimately depend on the states of atoms far away (around 10 to Å, depending on the local neighbourhood cutoff and the number of iterations). A smooth cutoff mechanism is employed such that the updates are continuous when atoms leave or enter each other’s local neighbourhood.

Message-passing formalism

We reformulate the original MPNN equations for atomic states. In general, an MPNN potential consists of a message-passing phase and a readout phase. In the message-passing phase, are updated based on derived from the states of the neighbouring atoms within the set :
where refers to a permutation-invariant pooling operation over the neighbours of atom , and can correspond to, for example, the average number of neighbours across the training set (see the Supplementary Information for a detailed analysis of the role of this normalization). denotes a learnable function acting on the states of atoms and . The most widely used permutation-invariant pooling operation is the sum over the neighbours. This operation creates , which are two-body in nature-that is, linear combinations of functions that simultaneously depend on the features of only two atoms. Then can be combined with the features of atom by a learnable update function, :
In , it is possible to form higher-body-order messages by (for example) applying a square function to the message to obtain a linear combination of three-body functions that simultaneously depend on the central atom and two of its neighbours. Both and , depend on the iteration index .
In the readout phase, learnable function map the atomic states onto atomic site energies:
At this point, some models use the atomic states from every iteration, while others use only a single readout function that takes the state after the final iteration and maps it to the site energy.

Equivariant messages

Physical properties, such as the energy or the dipole moment, transform in specific ways under the action of certain symmetry operations, such as translations and rotations of the atomic coordinates. For atomistic modelling, the symmetry group is of special interest. For example, if a molecule is rotated in space, the predicted dipole moment should rotate accordingly, whereas the energy should remain unchanged. Here we restricted ourselves to rotational and reflectional symmetries, the group, as translation invariance can be ensured by working with interatomic displacement vectors .
A straightforward and convenient way to ensure that the outputs of models transform correctly is to impose constraints on the internal representations of the model to respect these symmetries. We categorize the features of an equivariant neural network based on how they transform under the symmetry operations of the inputs. Formally we can think of as a function of the input positions (here the dependence on attributes is suppressed for the sake of brevity). Then we say that is rotationally equivariant (with ) if it transforms according to the irreducible representation of the symmetry group:
where denotes the action of an arbitrary rotation matrix on the set of atomic positions ( ) and is the corresponding Wigner-D matrix, the irreducible representations of the group . Hence, a message indexed by transforms like the spherical harmonic under rotation.
An important practical choice for implementing equivariant neural networks is the basis in which features and messages are expressed. For the rest of this Article, we will assume that they are encoded in
spherical coordinates. This is in line with many equivariant models such as SOAP-GAP , SNAP , ACE and its recursive implementations such as ref. 50, NICE , NequIP , equivariant transformer and SEGNNs . By contrast, some equivariant MPNNs (such as NewtonNet , EGNN or PaINN ) express the features in Cartesian coordinates. Given that models in this latter class use Euclidean vectors, which correspond to spherical vectors, they fit into the same framework through a change of basis. Spherical vectors transform according to , which correspond to rotation matrices. Some models, such as SchNet and DimeNet , employ only invariant messages (that is, equivariance).

Body-ordered messages

The body-order expansion of a general multivariate function is
If the magnitude of higher-order terms is sufficiently small that they can be truncated, this expansion can be a powerful tool for approximating high-dimensional functions. The concept of body ordering also appears in quantum mechanics , and there is ample empirical evidence that a body-ordered expansion of the potential energy converges rapidly for many systems .
By explicitly controlling the body order, one can efficiently learn low-dimensional representations corresponding to low-body-order terms. This is suggested to lead to interatomic potentials with enhanced generalization ability . For a message , the body order can be defined as the largest integer such that:
holds, where the elements in the tuple ( ) are all distinct, and for all the left-hand side of equation (28) is identically zero .
We call a model body-ordered if it can be written explicitly in the form of equation (27) with all terms up to present. This is in contrast to non-body-ordered models, in which either the expansion is infinite or only a subset of terms is present. To achieve body ordering in an MPNN model one needs linear update and readout functions. This is because nonlinear activation functions, such as the hyperbolic tangent function (tanh), the exponential function and vector normalizations, have infinite Taylor-series expansions, which make the body order infinite without all the terms in equation (27) being explicitly present.

Data availability

The datasets used in the computational experiments are described in the Supplementary Information and are available via Zenodo at https://doi.org/10.5281/zenodo. 14013500 (ref. 61).

Code availability

Two different codes were used to conduct the experiments. All experiments labelled ‘nequip’ in Table3 were conducted with NequIP (github. com/mir-group/nequip) version 0.5.4, which is available via Zenodo , in conjunction with version 0.4.4 of the e3nn library and PyTorch version 1.10.0 (ref. 64). All experiments labelled ‘botnet’ in Table 3 were conducted with BOTNet , which is available via GitHub at github.com/ gncs/botnet and was used in conjunction with version 0.3.2 of the e3nn library and version 1.8.0 of PyTorch . If the code is not explicitly specified (in the benchmark section of the Supplementary Information), we used the eponymous code for each model.

References

  1. Musil, F. et al. Physics-inspired structural representations for molecules and materials. Chem. Rev. 121, 9759-9815 (2021).
  2. Behler, J. & Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 98, 146401 (2007).
  3. Bartók, A. P., Kondor, R. & Csányi, G. On representing chemical environments. Phys. Rev. B 87, 184115 (2013).
  4. Behler, J. Four generations of high-dimensional neural network potentials. Chem. Rev. 121, 10037-10072 (2021).
  5. Deringer, V. L. et al. Gaussian process regression for materials and molecules. Chem. Rev. 121, 10073-10141 (2021).
  6. Cheng, B. et al. Mapping materials and molecules. Acc. Chem. Res. 53, 1981-1991 (2020).
  7. Drautz, R. Atomic cluster expansion for accurate and transferable interatomic potentials. Phys. Rev. B 99, 014104 (2019).
  8. Dusson, G. et al. Atomic cluster expansion: completeness, efficiency and stability. J. Comput. Phys. 454, 110946 (2022).
  9. Bartók, A. P., Payne, M. C., Kondor, R. & Csányi, G. Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 104, 136403 (2010).
  10. Shapeev, A. V. Moment tensor potentials: a class of systematically improvable interatomic potentials. Multisc. Model. Sim. 14, 1153-1173 (2016).
  11. Drautz, R. Atomic cluster expansion of scalar, vectorial, and tensorial properties including magnetism and charge transfer. Phys. Rev. B 102, 024104 (2020).
  12. Kovács, D. P. et al. Linear atomic cluster expansion force fields for organic molecules: beyond RMSE. J. Chem. Theor. Comput. 17, 7696-7711 (2021).
  13. Keith, J. A. et al. Combining machine learning and computational chemistry for predictive insights into chemical systems. Chem. Rev. 121, 9816-9872 (2021).
  14. Faber, F. A., Christensen, A. S., Huang, B. & von Lilienfeld, O. A. Alchemical and structural distribution based representation for universal quantum machine learning. J. Chem. Phys. 148, 241717 (2018).
  15. Zhu, L. et al. A fingerprint based metric for measuring similarities of crystalline structures. J. Chem. Phys. 144, 034203 (2016).
  16. Schütt, K. et al. SchNet: a continuous-filter convolutional neural network for modeling quantum interactions. In Advances in Neural Information Processing Systems Vol. 30 (eds Guyon, I. et al.) (Curran Associates, Inc., 2017); https://proceedings.neurips.cc/paper/2017/ file/303ed4c69846ab36c2904d3ba8573050-Paper.pdf
  17. Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O. & Dahl, G. E. Neural message passing for quantum chemistry. In Proc. 34th International Conference on Machine Learning Vol. 70 (eds Precup, D. & Teh, Y. W.) 1263-1272 (PMLR, 2017); https://proceedings.mlr. press/v70/gilmer17a.html
  18. Unke, O. T. & Meuwly, M. PhysNet: a neural network for predicting energies, forces, dipole moments, and partial charges. J. Chem. Theor. Comput. 15, 3678-3693 (2019).
  19. Gasteiger, J., Groß, J. & Günnemann, S. Directional message passing for molecular graphs. In Proc. International Conference on Leaning Representations (2020); https://iclr.cc/virtual_2020/ poster_B1eWbxStPH.html
  20. Anderson, B., Hy, T. S. & Kondor, R. Cormorant: covariant molecular neural networks. In Proc. 33rd Conference on Neural Information Processing Systems (eds Larochelle, H. et al.) (Curran Associates, 2019); https://proceedings.neurips.cc/paper/2019/file/ 03573b32b2746e6e8ca98b9123f2249b-Paper.pdf
  21. Thomas, N. et al. Tensor field networks: rotation- and translationequivariant neural networks for 3d point clouds. Preprint at http://arxiv.org/abs/1802.08219 (2018).
  22. Weiler, M., Geiger, M., Welling, M., Boomsma, W. & Cohen, T. 3D steerable CNNs: learning rotationally equivariant features in volumetric data. In Proc. 31st Conference on Neural Information Processing Systems (eds Bengio, S. et al.) (Curran Associates, 2018).
  23. Batzner, S. et al. E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials. Nat. Commun. 13, 2453 (2022).
  24. Satorras, V. G., Hoogeboom, E. & Welling, M. E(n) equivariant graph neural networks. In Proc. 38th International Conference on Machine Learning Vol. 139 (eds Meila, M. & Zhang, T.) 9323-9332 (PMLR, 2021).
  25. Schütt, K. T., Unke, O. T. & Gastegger, M. Equivariant message passing for the prediction of tensorial properties and molecular spectra. In Proc. 38th International Conference on Machine Learning Vol. 139 (eds Meila, M. & Zhang, T.) 9377-9388 (PMLR, 2021).
  26. Haghighatlari, M. et al. NewtonNet: a Newtonian message passing network for deep learning of interatomic potentials and forces. Digit. Discov. 1, 333-343 (2022).
  27. Klicpera, J., Becker, F. & Günnemann, S. Gemnet: universal directional graph neural networks for molecules. In Advances in Neural Information Processing Systems 34 (NeurIPS 2021) (eds Ranzato, M. et al.) 6790-6802 (Curran Associates, 2021).
  28. Thölke, P. & Fabritiis, G. D. Equivariant transformers for neural network based molecular potentials. In International Conference on Learning Representations (2022); https://openreview.net/ forum?id=zNHzqZ9wrRB
  29. Brandstetter, J., Hesselink, R., van der Pol, E., Bekkers, E. J. & Welling, M. Geometric and physical quantities improve equivariant message passing. In International Conference on Learning Representations (2021).
  30. Musaelian, A. et al. Learning local equivariant representations for large-scale atomistic dynamics. Nat. Commun. 14, 579 (2023).
  31. Kondor, R. N-body networks: a covariant hierarchical neural network architecture for learning atomic potentials. Preprint at https://arxiv.org/abs/1803.01588 (2018).
  32. Batatia, I. et al. The design space of E(3)-equivariant atom-centered interatomic potentials. Preprint at https://arXiv.org/abs/2205.06643 (2022).
  33. Nigam, J., Pozdnyakov, S., Fraux, G. & Ceriotti, M. Unified theory of atom-centered representations and message-passing machine-learning schemes. J. Chem. Phys. 156, 204115 (2022).
  34. Bochkarev, A., Lysogorskiy, Y., Ortner, C., Csányi, G. & Drautz, R. Multilayer atomic cluster expansion for semilocal interactions. Phys. Rev. Res. 4, LO42O19 (2022).
  35. Batatia, I., Kovacs, D. P., Simm, G. N. C., Ortner, C. & Csanyi, G. MACE: Higher order equivariant message passing neural networks for fast and accurate force fields. In Advances in Neural Information Processing Systems (NeurIPS2O22) (eds Koyejo,S. et al.) Curran Associates, 2022); https://proceedings.neurips.cc/ paper_files/paper/2022/hash/4a36c3c51af11ed9f34615b81ed b5bbc-Abstract-Conference.html
  36. Batatia, I. et al. Code for the paper titled “The Design Space of E(3)-Equivariant Atom-Centered Interatomic Potentials”. Github https://github.com/gncs/botnet/tree/v1.0.1 (2024).
  37. Darby, J. P. et al. Tensor-reduced atomic density representations. Phys. Rev. Lett. 131, 028001 (2023).
  38. Allen-Zhu, Z., Li, Y. & Liang, Y. Learning and generalization in overparameterized neural networks, going beyond two layers. In Neural Information Processing Systems (2018).
  39. Lopanitsyna, N., Fraux, G., Springer, M. A., De, S. & Ceriotti, M. Modeling high-entropy transition metal alloys with alchemical compression. Phys. Rev. Mater. 7, 045802 (2023).
  40. Thompson, A., Swiler, L., Trott, C., Foiles, S. & Tucker, G. Spectral neighbor analysis method for automated generation of quantumaccurate interatomic potentials. J. Comput. Phys. 285, 316-330 (2015).
  41. Caro, M. A. Optimizing many-body atomic descriptors for enhanced computational performance of machine learning based interatomic potentials. Phys. Rev. B 100, 024112 (2019).
  42. Musil, F. et al. Efficient implementation of atom-density representations. J. Chem. Phys. 154, 114109 (2021).
  43. Himanen, L. et al. DScribe: library of descriptors for machine learning in materials science. Comp. Phys. Commun. 247, 106949 (2020).
  44. Goscinski, A., Musil, F., Pozdnyakov, S., Nigam, J. & Ceriotti, M. Optimal radial basis for density-based atomic representations. J. Chem. Phys. 155, 104106 (2021).
  45. Bigi, F., Huguenin-Dumittan, K. K., Ceriotti, M. & Manolopoulos, D. E. A smooth basis for atomistic machine learning. J. Chem. Phys. 157, 243101 (2022).
  46. Witt, W. C. et al. ACEpotentials.jl: a Julia implementation of the atomic cluster expansion. J. Chem. Phys. 159, 164101 (2023); https://pubs.aip.org/aip/jcp/article/159/16/164101/2918010/ ACEpotentials-jl-A-Julia-implementation-of-the
  47. Goscinski, A., Musil, F., Pozdnyakov, S., Nigam, J. & Ceriotti, M. Optimal radial basis for density-based atomic representations. J. Chem. Phys. 155, 104106 (2021).
  48. Bochkarev, A. et al. Efficient parametrization of the atomic cluster expansion. Phys. Rev. Mater. 6, 013804 (2022).
  49. Elfwing, S., Uchibe, E. & Doya, K. Sigmoid-weighted linear units for neural network function approximation in reinforcement learning. Neural Networks 107, 3-11 (2018); https://doi.org/10.1016/ j.neunet.2017.12.012
  50. Lysogorskiy, Y. et al. Performant implementation of the atomic cluster expansion (PACE) and application to copper and silicon. npj Comput. Mater. 7, 97 (2021).
  51. Kaliuzhnyi, I. & Ortner, C. Optimal evaluation of symmetry-adapted -correlations via recursive contraction of sparse symmetric tensors. J. Numerical Mathematics (2024); https://doi.org/10.1515/ jnma-2024-0025
  52. Zhang, L. et al. Equivariant analytical mapping of first principles Hamiltonians to accurate and transferable materials models. npj Comput. Mater. 8, 158 (2022); https://www.nature.com/articles/ s41524-022-00843-2
  53. Nigam, J., Pozdnyakov, S. & Ceriotti, M. Recursive evaluation and iterative contraction of -body equivariant features. J. Chem. Phys. 153, 121101 (2020).
  54. Battaglia, P. W. et al. Relational inductive biases, deep learning, and graph networks. Preprint at https://arxiv.org/abs/1806.01261 (2018).
  55. Bronstein, M. M., Bruna, J., Cohen, T. & Velićković, P. Geometric deep learning: grids, groups, graphs, geodesics, and gauges. Preprint at https://arxiv.org/abs/2104.13478 (2021).
  56. Weyl, H. The Classical Groups: Their Invariants and Representations (Princeton Univ. Press, 1939).
  57. Thomas, J., Chen, H. & Ortner, C. Body-ordered approximations of atomic properties. Arch. Rational Mech. Anal. 246, 1-60 (2022); https://doi.org/10.1007/s00205-022-01809-w
  58. Drautz, R. & Pettifor, D. G. Valence-dependent analytic bond-order potential for transition metals. Phys. Rev. B 74, 174117 (2006).
  59. van der Oord, C., Dusson, G., Csányi, G. & Ortner, C. Regularised atomic body-ordered permutation-invariant polynomials for the construction of interatomic potentials. Mach. Learn. Sci. Technol. 1, 015004 (2020).
  60. Drautz, R., Fähnle, M. & Sanchez, J. M. General relations between many-body potentials and cluster expansions in multicomponent systems. J. Phys. Condens. Matter 16, 3843 (2004).
  61. Kovács, D. P. et al. BOTNet datasets: v0.1.O. Zenodo https://doi.org/ 10.5281/zenodo. 14013500 (2024).
  62. Musaelian, M. et al. NEquIP: v0.5.4. Zenodo https://doi.org/10.5281/ zenodo. 14013469 (2024).
  63. Geiger, M. et al. E3NN v0.5.4. Zenodo https://doi.org/10.5281/ zenodo. 5292912 (2020).
  64. Paszke, A. et al. Pytorch: an imperative style, high-performance deep learning library. In Advances in Neural Information Processing Systems Vol. 32 (eds Wallach, H. et al.) 8026-8037 (Curran Associates, Inc., 2019).
  65. Sim, G. & Batatia, I. Body-ordered Tensor Network (BOTNet). Zenodo https://doi.org/10.5281/zenodo. 14052468 (2024).

Acknowledgements

This work was performed using resources provided by the Cambridge Service for Data Driven Discovery (CSD3), which is operated by the University of Cambridge Research Computing Service (www.csd3. cam.ac.uk) provided by Dell EMC and Intel using Tier-2 funding from the Engineering and Physical Sciences Research Council (capital grant number EP/TO22159/1) and DiRAC funding from the Science and Technology Facilities Council (www.dirac.ac.uk). D.P.K. acknowledges support from AstraZeneca and the Engineering and Physical Sciences Research Council. C.O. is supported by Leverhulme Research Project grant number RPG-2017-191 and by the Natural Sciences and Engineering Research Council of Canada (NSERC) under funding reference number IDGRO19381. Work at Harvard University was supported by Bosch Research, the US Department of Energy, Office of Basic Energy Sciences, under award number DE-SCOO22199, the Integrated Mesoscale Architectures for Sustainable Catalysis (IMASC), an Energy Frontier Research Center, under award number DE-SCOO12573 and by the NSF through Harvard University Materials Research Science and Engineering Center grant number DMR-2011754. A.M. is supported by US Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Computational Science Graduate Fellowship under award number DE-SC0021110. We acknowledge computing resources provided by the Harvard University FAS Division of Science Research Computing Group.

Author contributions

I.B., S.B., G.C. and B.K. conceived the research and planned the collaboration. I.B. and G.N.C.S. implemented the BOTNet software. Numerical experiments were performed by I.B. (BOTNet code), S.B. and A.M. (NequIP code) and D.P.K. (linear ACE). I.B. and D.P.K. produced the datasets. S.B., A.M. and B.K. proposed the theoretical connections between ACE and NequIP. G.C., R.D. and C.O. suggested the principles of Multi-ACE and I.B., D.P.K. and C.O. developed the equations. I.B., D.P.K., C.O. and G.C.N.S. drafted the manuscript text and figures. All authors edited the manuscript.

Competing interests

G.C. and C.O. have equity stakes in Symmetric Group LLP, which licenses force fields commercially. G.C. has an equity stake in Ångström AI, Inc. R.D. has an equity interest in ACEworks GmbH. All other authors declare no competing interests.

Additional information

Extended data is available for this paper at https://doi.org/10.1038/s42256-024-00956-x.
Supplementary information The online version contains supplementary material available at https://doi.org/10.1038/s42256-024-00956-x.
Correspondence and requests for materials should be addressed to Ilyes Batatia or Gábor Csányi.
Peer review information Nature Machine Intelligence thanks Mihail Bogojeski, Guillaume Fraux and Ryan-Rhys Griffiths for their contribution to the peer review of this work.
Reprints and permissions information is available at www.nature.com/reprints.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence,
and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/ by/4.0/.
(c) The Author(s) 2025
Extended Data Table 1 | Different machine learning potentials in the framework of MPNNs
SchNet NequIP Linear ACE
Message function
Symmetric pooling
Update function –
We identify SchNet, NequIP, and ACE as examples of MPNNs and exhibit their explicit components in the design space: the message, symmetric pooling, and update functions. Note that in NequIP, the choice of nonlinearity is not fixed, and we have chosen a normed activation with tanh to be shown here. In each case, learnable parameters (weights) are shown as and biases as .
  1. ¹Engineering Laboratory, University of Cambridge, Cambridge, UK. ²Department of Chemistry, ENS Paris-Saclay, Université Paris-Saclay, Gif-sur-Yvette, France. John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, USA. ICAMS, Ruhr-Universität Bochum, Bochum, Germany. Department of Mathematics, University of British Columbia, Vancouver, British Columbia, Canada. Robert Bosch LLC Research and Technology Center, Watertown, MA, USA. Present address: Microsoft Research AI for Science, Cambridge, UK. These authors contributed equally: Ilyes Batatia, Simon Batzner. e-mail: ib467@cam.ac.uk; gc121@cam.ac.uk