نموذج فرق محدود مضغوط لحل نموذج تسعير خيارات بلاك-شولز الكسرية A compact finite difference scheme for solving fractional Black-Scholes option pricing model

المجلة: Journal of Inequalities and Applications، المجلد: 2025، العدد: 1
DOI: https://doi.org/10.1186/s13660-025-03261-2
تاريخ النشر: 2025-03-18

نموذج فرق محدود مضغوط لحل نموذج تسعير خيارات بلاك-شولز الكسرية

يويلونغ فنغ , شيندونغ تشانغ , يان تشين و ليلي وي

*المراسلة:
liaoyuan1126@163.com
كلية إحصاءات البيانات الكبيرة، جامعة قويتشو للمالية والاقتصاد، قويتشو، 550025، جمهورية الصين الشعبية
القائمة الكاملة لمعلومات المؤلفين متاحة في نهاية المقالة

الملخص

في هذا العمل، نقدم طريقة فرق نهائية مضغوطة (CFD) فعالة لحل نموذج تسعير خيارات بلاك-شولز الكسرية (TFBS). يتم وصف المشتق الكسرية الزمنية باستخدام المشتق الكسرية كابوتو-فابريزيو (C-F)، وتستخدم طريقة فرق نهائية مضغوطة لتفكيك المشتق المكاني. المساهمة الرئيسية في هذا العمل هي تطوير مخطط تفاضلي عالي الرتبة لنموذج TFBS. في المخطط العددي، قمنا بتطوير معدل تقارب قدره , حيث يدل على الخطوة الزمنية و يمثل الخطوة المكانية. للتحقق من فعالية الطريقة المقترحة، قمنا بإجراء تحليل الاستقرار وتقدير الخطأ باستخدام طريقة فورييه. علاوة على ذلك، تم إجراء سلسلة من التجارب العددية، وأظهرت النتائج العددية النظام النظري للدقة ووضحت فعالية الطريقة المقترحة.

تصنيف موضوع الرياضيات: 65M06؛ 65M12؛ 47F05؛ 35S10
الكلمات الرئيسية: نموذج بلاك-شولز؛ المشتق الكسرية كابوتو-فابريزيو؛ طريقة فرق نهائية مضغوطة؛ الاستقرار؛ تقدير الخطأ

1 المقدمة

تعتبر المعادلات التفاضلية الكسرية، نظرًا لقدرتها على نمذجة ظواهر معينة بدقة أكبر، قد وجدت تطبيقات واسعة في مجالات متنوعة، بما في ذلك الكهرباء [1،2]، نظرية التحكم [3،4]، البصريات [5،6]، اللدونة اللزجة [7،8]، ميكانيكا السوائل [9] والهندسة الطبية الحيوية [10،11]. علاوة على ذلك، تم استخدامها أيضًا لمحاكاة المشكلات المالية [12-15].
نموذج بلاك-شولز (BS)، الذي قدمه بلاك وشولز وميرتون [16، 17]، يقدم صيغة تسعير للخيارات الأوروبية واستراتيجية محفظة تحوط. يعمل هذا النموذج تحت افتراضات صارمة: أسواق خالية من الاحتكاك، حركات أسعار مستمرة وسلسة، وممارسة الخيارات فقط عند الاستحقاق. قام جوماري [18، 19] بصياغة نسخ كسرية زمنية ومكانية من معادلات BS ثم استخرج محفظة مورتون كسرية مثلى. في مجال الأسواق المالية أو تسعير الخيارات، تحمل معادلة BS الكسرية إمكانيات هائلة للتطبيق. يمكن أن توفر للمستثمرين معلومات أكثر دقة،
© المؤلفون 2025. الوصول المفتوح. هذه المقالة مرخصة بموجب رخصة المشاع الإبداعي للاستخدام غير التجاري، والتي تسمح بأي استخدام غير تجاري، ومشاركة، وتوزيع وإعادة إنتاج في أي وسيلة أو صيغة، طالما أنك تعطي الائتمان المناسب للمؤلفين الأصليين والمصدر، وتوفر رابطًا لرخصة المشاع الإبداعي، وتوضح إذا قمت بتعديل المادة المرخصة. ليس لديك إذن بموجب هذه الرخصة لمشاركة المواد المعدلة المشتقة من هذه المقالة أو أجزاء منها. الصور أو المواد الأخرى من طرف ثالث في هذه المقالة مشمولة في رخصة المشاع الإبداعي للمقالة، ما لم يُشار إلى خلاف ذلك في سطر ائتمان للمادة. إذا لم تكن المادة مشمولة في رخصة المشاع الإبداعي للمقالة واستخدامك المقصود غير مسموح به بموجب اللوائح القانونية أو يتجاوز الاستخدام المسموح به، ستحتاج إلى الحصول على إذن مباشرة من صاحب حقوق الطبع والنشر. لعرض نسخة من هذه الرخصة، قم بزيارة http://creativecommons.org/licenses/by-nc-nd/ 4.0/.
تتيح منهجيات تسعير الخيارات المنسقة، مما يمكنهم من اتخاذ قرارات استثمارية أكثر اطلاعًا. بالإضافة إلى ذلك، يمكن استغلال هذا النموذج في إدارة المخاطر وتحسين المحفظة، مما يساعد المستثمرين في تحقيق أقصى عوائد استثمارية مع الحفاظ على مستوى مقبول من المخاطر. مع استمرار تطور الأسواق المالية وتعقيدها بشكل متزايد، فإن آفاق تطبيق معادلة BS الكسرية تتجه نحو التوسع أكثر. في هذه الورقة، نعتبر نموذج TFBS التالي من الشكل [20، 21]
مع شروط الحدود
وشروط نهائية
حيث هو مشغل من رتبة كسرية، يدل على سعر خيار أوروبي لسعر السهم في الوقت هو التقلب، هو سعر الفائدة الخالي من المخاطر، و هو تاريخ استحقاق العقد. و هما الخصومات المدفوعة عند ضرب الحاجز المقابل، و هي دالة الدفع. في [21]، هو مشتق كسرية ريمان-ليوفيلي المعدل. في هذه الورقة، يُستخدم كمشتق كابوتو-فابريزيو (C-F) الكسرية، والذي يُعرف بأنه
في عام 2015، اقترح كابوتو وفابريزيو مفهومًا جديدًا للمشتق الكسرية [22]، المعروف بمشتق C-F الكسرية. تم صياغة هذا التعريف بطريقة بسيطة وواضحة، مما يجعل تطبيقه في النمذجة المالية أكثر سهولة. خاصة عند معالجة المشتقات الكسرية الزمنية، فإن التعامل الرياضي مع المشتق C-F الكسرية يكون بديهيًا نسبيًا، مما يساعد في عمليات الاشتقاق والحساب. في مجال تحليل الأسواق المالية، غالبًا ما تتأثر تقلبات الأسعار بالبيانات التاريخية، مما يؤدي إلى تأثير الذاكرة. غالبًا ما تفشل النماذج التقليدية التي تعتمد على المشتقات ذات الرتبة الصحيحة في التقاط ديناميات السوق بالكامل بسبب هذا التأثير. ومع ذلك، فإن المشتق الكسرية كابوتو-فابريزيو، الذي يستخدم دالة نواة غير مفردة، يقدم عدة مزايا، مثل التعامل الأسهل مع الشروط الأولية وزيادة الاستقرار العددي مقارنةً بالمشتقات الكسرية الأخرى. وهذا يجعله فعالًا بشكل خاص في التقاط تأثيرات الذاكرة. هذه القدرة حاسمة لمحاكاة الظواهر المالية المعقدة. للحصول على مزيد من الرؤى حول تقدم المشتق C-F الكسرية، يمكن الرجوع إلى المراجع [23-30]. مع تعميق البحث في المعادلات التفاضلية الكسرية الزمنية، غالبًا ما يكون من الصعب الحصول على حلول دقيقة لمثل هذه المعادلات. لذلك، يصبح دراسة الحلول العددية لمثل هذه المعادلات أمرًا مهمًا بشكل خاص. في السنوات الأخيرة، يمكن العثور على طرق عددية للمعادلات الكسرية في [31-37]، من بين آخرين. في الوقت نفسه، اقترح مؤلفون مختلفون العديد من الطرق
لحل معادلة TFBS. على سبيل المثال، استخدم حق وحسين [38] طريقة سلسلة القوة المتبقية وطريقة خالية من الشبكة تعتمد على التجميع لحل فئة من نماذج TFBS ذات معاملات ثابتة ومتغيرة. قدم غولباباي وآخرون [39] حلاً عدديًا لنموذج TFBS باستخدام طريقة الدوال الأساسية الشعاعية، والتي تتميز بأنها مخطط خالي من الشبكة. اقترح فادوجبا [40] تطبيق طريقة تحليل الهوموتوب في تقييم خيار شراء أوروبي مع معادلة TFBS. استخدم غولباباي ونيكان [41] طريقة المربعات الأقل المتحركة للحصول على حل تقريبي لنموذج TFBS. استخدم آن وآخرون [42] طريقة طيفية زمنية لتطوير مخطط عددي لحل نموذج TFBS مع دالة دفع سلسة. قدم طاغيبور وأمينكه [43] طريقة تجميع طيفية فعالة تعتمد على دوال بيل الكسرية لحل معادلة TFBS. طور كازمي [44] مخططًا عدديًا لحل معادلة TFBS التي تحكم الخيارات الأوروبية بمعدل تقارب قدره . بالإضافة إلى ذلك، تم تقديم استقراء ريتشاردسون للحصول على نسخة معدلة من الطريقة، والتي تظهر تقاربًا أسرع لمعادلة TFBS مع بيانات أولية غير سلسة. اقترح أقدام وآخرون [45] طريقة فعالة لتقدير نموذج BS الكسري، باستخدام تركيب متعددات جينغنباور المتعامدة وتقريب المشتق الكسري بناءً على المشتق الكسري كابوتو. إن التعامد لمتعددات جينغنباور والمصفوفات التشغيلية يقلل بشكل كبير من وقت الحساب ويعزز السرعة. تتعلق المقالات المذكورة أعلاه حول المعادلات التفاضلية الكسريّة بشكل أساسي بمشتقات كابوتو الكسريّة ومشتقات ريمان-ليوفيلي. ومن الجدير بالذكر أن عددًا محدودًا فقط من الطرق العددية قد تم اقتراحها في الأدبيات لحل المعادلة (1.1) بمشتق C-F الكسري. نلاحظ أنه لا توجد حاليًا أي خطة عددية عالية الترتيب متاحة لمعادلة BS التفاضلية الكسريّة بمشتق C-F الكسري. على الرغم من أنه تم تقديم بعض التقنيات العددية لمعالجة هذه المشكلة، إلا أن هذه الطرق عادة ما تكون من ترتيب مكاني منخفض.
الهدف الرئيسي من هذه الورقة هو حل نموذج تسعير الخيارات باستخدام نموذج بلاك-شولز الكسري باستخدام مخطط الفرق المضغوط وتقديم تحليل الاستقرار والتقارب. المخطط المضغوط هو طريقة عالية الرتبة تقسم مجال الحل المستمر إلى نقاط شبكة متقطعة وتستبدل المشتقات بالفروق، مما يحول المعادلات التفاضلية إلى معادلات جبرية للحصول على حلول عددية. بالإضافة إلى ذلك، عند حل هذه الأنظمة من المعادلات، تكون مصفوفة المعاملات للنظام الخطي مصفوفة قطرية، مما يمكن حلها بسهولة. لذلك، في هذه الورقة، قمنا بتطوير طريقة عددية تعتمد على طريقة الفرق المحدودة المضغوطة للحصول على الحل العددي للمعادلة (1.1). للتحقق من فعالية الطريقة المقترحة، قمنا بإجراء تحليل الاستقرار وتقدير الخطأ باستخدام طريقة فورييه. علاوة على ذلك، تم إجراء سلسلة من التجارب العددية، وتظهر النتائج العددية أداءً حسابيًا جيدًا، مما يدعم تحليلنا النظري.
الهيكل التنظيمي لهذه المقالة هو كما يلي. في القسم 2، نقدم بعض الرموز والليمات لبناء المخطط المنفصل للمعادلة (1.1). يتم تقديم تحليل الاستقرار والتقارب للمخطط المنفصل الذي تم بناؤه في القسم 3، وتُعطى بعض التجارب العددية في القسم 4. أخيرًا، يقدم القسم 5 خلاصة موجزة.

2 بناء نظام عددي من الرتبة الرابعة

مجموعة و ويدل على لحل المعادلة (1.1)، نقوم بتحويل مجالها غير المحدود إلى مجال محدود من خلال القطع. وبالتالي، يمكن تغيير المعادلة (1.1) إلى:
أين و هي جميعها دوال معطاة وناعمة بما فيه الكفاية.
في هذا القسم، نعتبر بشكل أساسي بناء المخطط المنفصل للمعادلة (2.1). بالنسبة للأعداد الصحيحة الموجبة المعطاة و دع و حدد فضاء دالة الشبكة . دع و . لأي دالة نحن نحدد الرموز التالية:
نستخدم و للدلالة على مشغلين مضغوطين بالشكلين التاليين:
للمشغل المضغوط يمكن العثور على اللمحة التالية في [46].
اللمّا 2.1 ([46]) دع كن مشغلاً مضغوطًا. افترض . ثم، ما يلي ينطبق:
باستخدام المعادلة (2.2)، لدينا . وبالتالي، فإن اللمحة 2.1 تشير إلى أن . مشابه للمشغل المضغوط يمكننا الحصول على اللممة التالية للمشغل المضغوط .
اللمّا 2.2 دع كن مشغلاً مضغوطًا كما في المعادلة (2.3). افترض . ثم، ما يلي ينطبق:
أين . علاوة على ذلك، فإنه يعتقد أن
باستخدام المعادلة (2.3)، لدينا . وبالتالي، فإن اللمحة 2.2 تشير إلى أن .
نقدم الآن بعض القضايا التي ستستخدم في التحليل التالي. يتم تقريب المشتق الكسرية من نوع C-F بالصيغة التالية، كما هو مذكور في [47].
اللمّا 2.3 ([47]) دع مع . ثم، فإن المعادلة التالية صحيحة:
دع مع . ثم، باستخدام اللمحة 2.3، يمكننا أن نحصل على “. وبالتالي، في العقدة المعطاة ( )، تلميح 2.3 يعني أن المعادلة (2.1) يمكن إعادة كتابتها على النحو التالي:
باستخدام اللمتين 2.1 و 2.2، يمكننا أن نثبت أن و لذلك، يمكن إعادة كتابة المعادلة (2.4) على النحو التالي:
أين مع هو ثابت إيجابي. من السهل الحصول على اللمحة التالية من خلال الحسابات المباشرة.
اللمّا 2.4 دع مع . ثم، يُفترض أن
يدل على كنموذج عددي لـ وتجاهل المصطلح الصغير في المعادلة (2.5)، يمكننا الحصول على المخطط العددي من الرتبة الرابعة للمعادلة (2.1):
ضرب كلا الجانبين من المعادلة (2.6) في وبت simplifying، نحصل على
أين و يمكن تفكيك الشروط الابتدائية والحدودية للمعادلة (2.1) على النحو التالي:
في المعادلة (2.7)، بالنسبة للنقاط خارج المنطقة التي هي نستخدم الصيغ التقريبية التالية لحساب القيم:
و
لزيادة الوضوح وتحسين قابلية القراءة، قدمنا خوارزمية مفصلة خطوة بخطوة لتنفيذ نظامنا العددي المقترح. الخوارزمية العددية هي كما يلي:
الخطوة 1. تحديد نطاق تقسيم المجال وأحجام الخطوات و حدد التقلب معدل خالي من المخاطر ، ومعلمات عددية أخرى، وظروف حدودية.
الخطوة 2. احسب القيمة الدقيقة .
الخطوة 3. الحصول على مصفوفات المعاملات على الجانب الأيسر و على الجانب الأيمن من المعادلة (2.7) في جميع العقد المنفصلة.
الخطوة 4. استخدم تنسيقات تقريبية للتعامل مع العقد خارج الحدود، وقدم مصفوفات و .
الخطوة 5. احسب القيمة العددية لـ بواسطة .
الخطوة 6. احسب الخطأ المقابل .
الخطوة 7. إنهاء العملية بكتابة البيانات.

3 تحليل الاستقرار وتقدير الخطأ

في هذا القسم، سننظر في تحليل الاستقرار وتقدير الخطأ للمعادلة (2.7). لراحتنا، نسمح لتمثيل قيم مختلفة في مواقع مختلفة. دع كن
الحل التقريبي للمعادلة (2.7)، وتعريف مع و ، و مع ، على التوالي. باستخدام المعادلة (2.7)، نحصل على معادلة خطأ التقريب التالية:
بعد ذلك، نعتبر تحليل الاستقرار والتقارب للمعادلة (3.1) باستخدام طريقة فورييه. لتطبيق طريقة فورييه، نحتاج إلى توسيع نطاق الدالة. وبالتالي، نحدد دالة الشبكة التالية:
ثم سلسلة فورييه لـ هو
أين و .
باستخدام معادلة بارسفال لدينا
إيجار واستبداله في المعادلة (3.1) بواسطة الهوية و لدينا
يتبع أن
أين و في ضوء و لدينا
من المعادلة أعلاه، يمكننا أن نستنتج أن
النظرية 3.1 دع كن الحل للمعادلة (3.5)، إذن فإنه ينطبق أن
دليل لـ من المعادلة (3.5)، نحصل على
الآن، نفترض أن
لـ باستخدام المعادلة (3.5)، لدينا
هذا يكمل إثبات النظرية.
النظرية التالية تتعلق باستقرار المخطط المتقطع المعادلة (2.7).
النظرية 3.2 المخطط العددي المعادلة (2.7) مستقر بلا شروط.
إثبات باستخدام المعادلة (3.3) ونتيجة النظرية 3.1، نحصل على
مما يعني أن الخوارزمية العددية من الرتبة الرابعة المعادلة (2.7) مستقرة بلا شروط.
بعد ذلك، يتم تقديم تحليل التقارب للمخطط المنفصل المعادلة (2.7). بالمثل، دع
ويدل على
طرح المعادلة (2.6) من المعادلة (2.5) وملاحظة لدينا
أين مماثل للمعادلة (3.2)، يمكننا تعريف دوال الشبكة و تطبيق نفس أفكار تحليل الاستقرار، و يمكن توسيعه إلى سلسلة فورييه التالية:
أين و افترض أن و يمكن اختياره كـ و ، على التوالي. استبدال تعبيرات و إلى المعادلة (3.7) يعطي
يتبع ذلك أن
أين ، و مقدمة كما في المعادلة (3.5).
النظرية 3.3 دع كن حلاً للمعادلة (3.9). ثم، هناك ثابت موجب بحيث
الدليل وفقًا للمعادلة (3.9)، نحصل على
منذ ، من خلال تقارب السلاسل يوجد ثابت موجب بحيث
من المعادلة (3.10)، لـ لدى المرء
الآن، نفترض أن
وتدل على .
لـ ، وفقًا للمعادلة (3.10) واللما 2.4، لدينا
هذا يكمل إثبات النظرية.
النظرية 3.4 إن الخوارزمية العددية المعادلة (2.7) متقاربة، وتتحقق تقديرات الخطأ التالية
إثبات باستخدام معادلة بارسفال وتعريف -نورم، لدينا
باستخدام نتيجة النظرية 3.3، نحصل على
مما يعني أن الخوارزمية العددية المعادلة (2.7) متقاربة وأن رتبة التقارب هي .

4 النتائج العددية

في هذا القسم، نقدم عدة أمثلة عددية للتحقق من التحليل النظري من خلال مقارنة الحلول الدقيقة والحلول العددية. تم إجراء التجارب العددية في MATLAB R2020b على جهاز كمبيوتر مزود بمعالج AMD Ryzen 7 7840H وذاكرة RAM سعتها 32 جيجابايت. يتم تعريف الأخطاء على النحو التالي:
لـ -خطأ و -خطأ، سيتم استخدام معدلات التقارب التالية في الاختبارات العددية. معدل تقارب الوقت هو
أين و تشير إلى الأخطاء المرتبطة بأحجام الشبكة و ، على التوالي. معدل تقارب الفضاء هو
أين و تشير إلى الأخطاء المرتبطة بأحجام الشبكة و ، على التوالي.
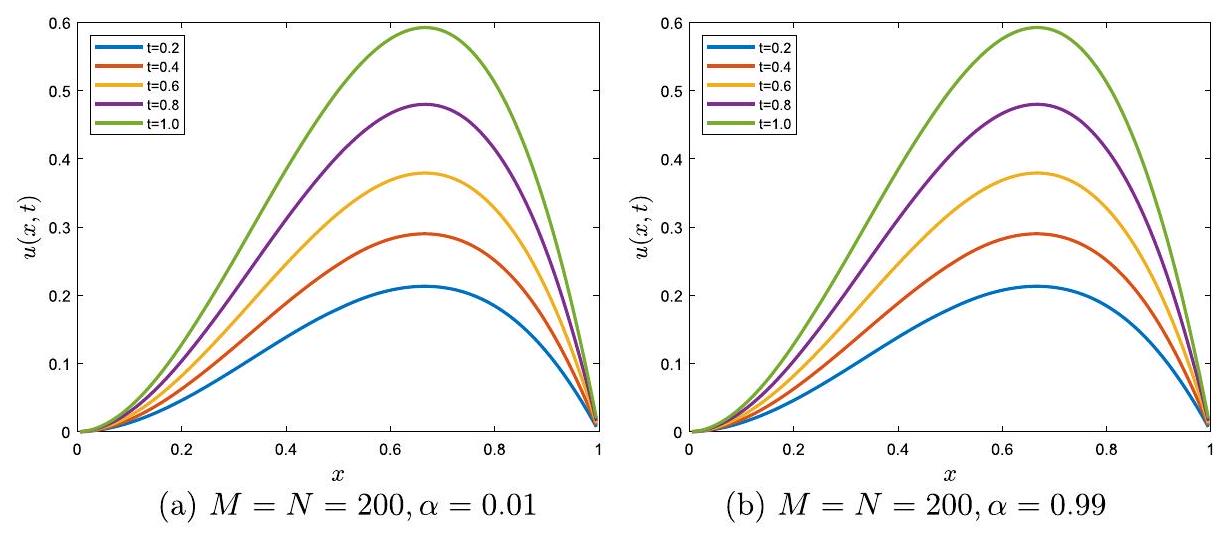
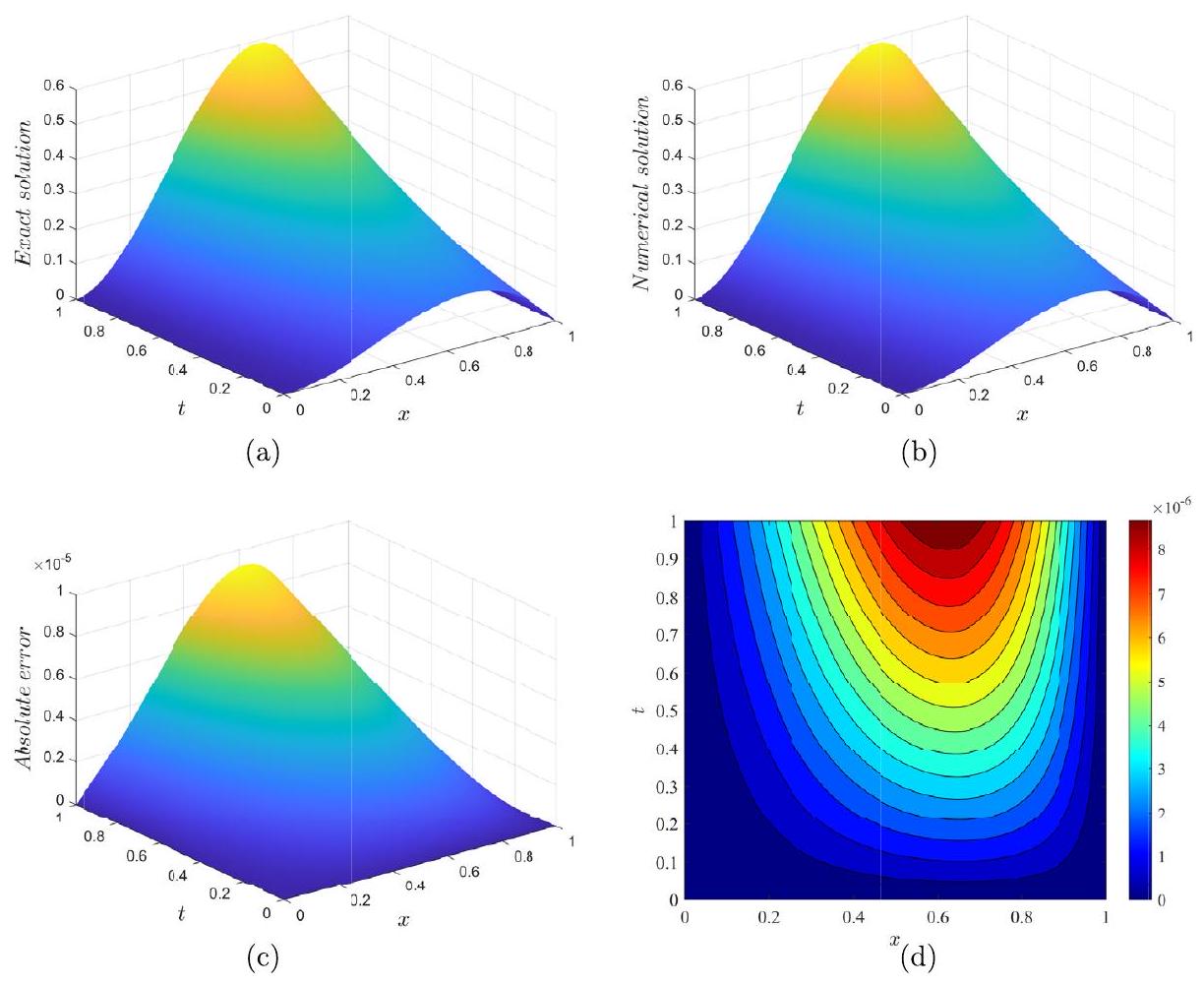
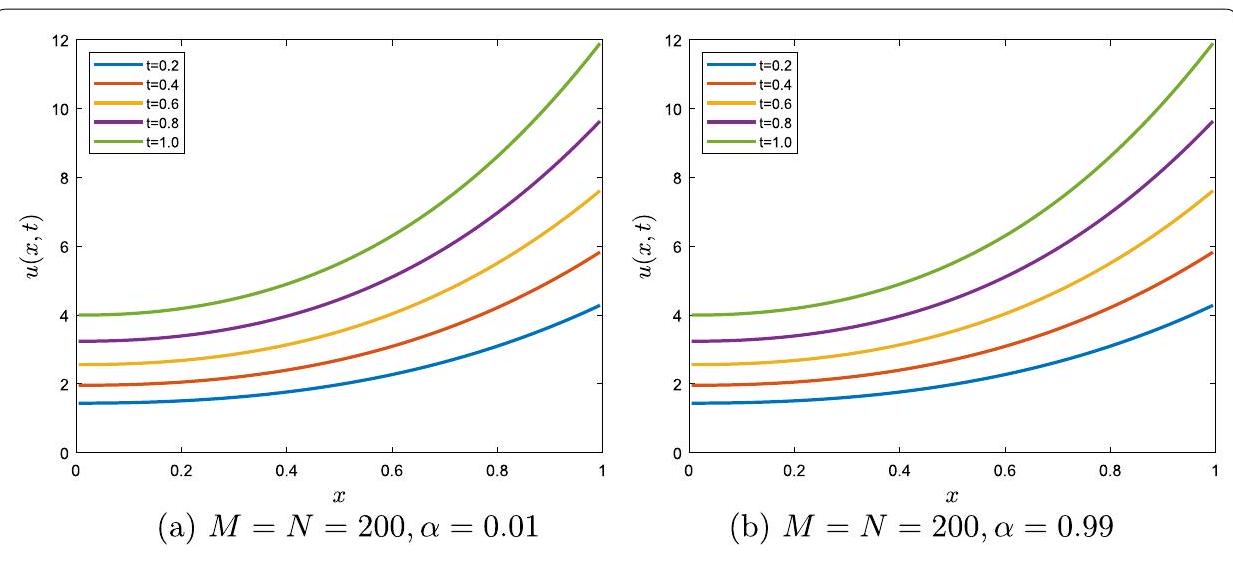
مثال 1 نعتبر المعادلة (2.1) مع و .
حيث مصطلح المصدر قيم المعلمات ذات الصلة ، و المرتبطة بالمثال تعتبر كـ , و .
في هذا المثال، معدلات التقارب الزمني مع اختلاف (هنا مبين في الجدول 1. من الجدول 1، يمكننا أن نجد أن دقة الوقت قريبة من المعدل الأمثل. . وبالمثل، فإن معدلات التقارب المكاني مع اختلاف (هنا مبين في الجدول 2، الذي يظهر أن دقة الفضاء قريبة من المعدل الأمثل .
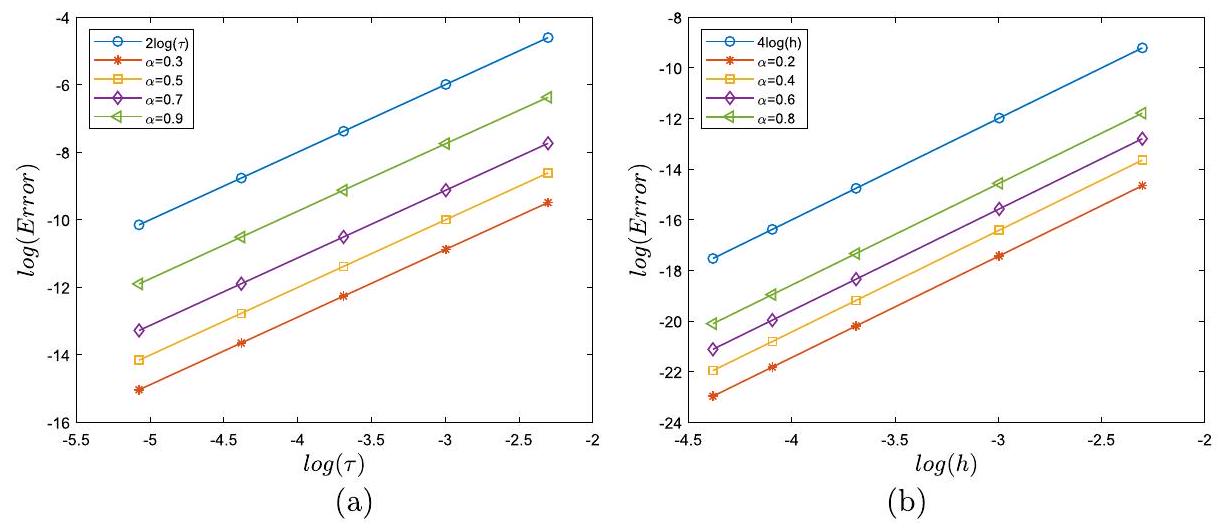
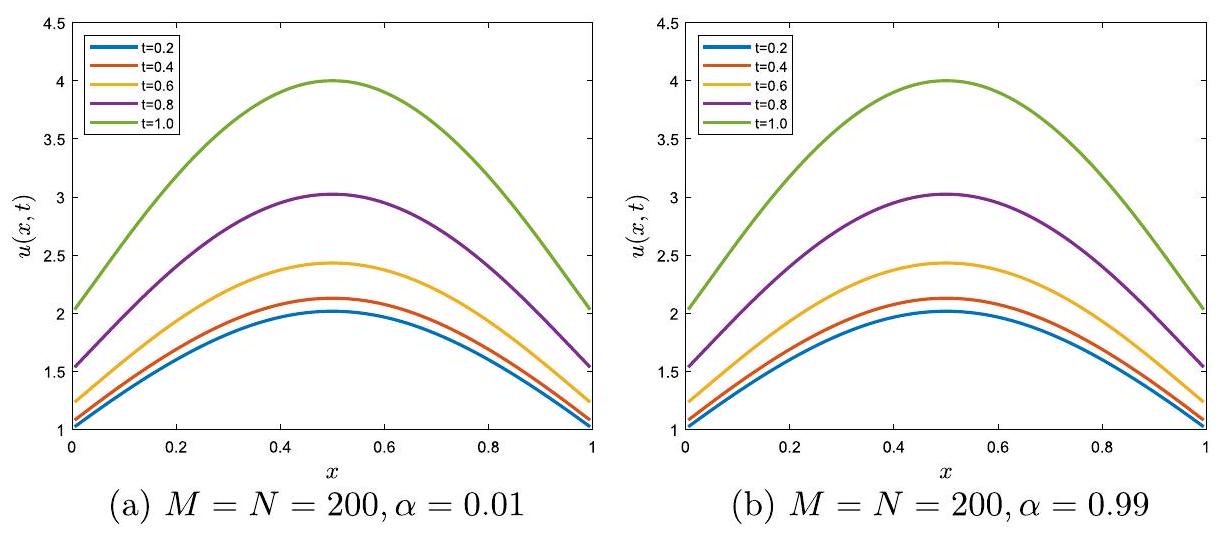
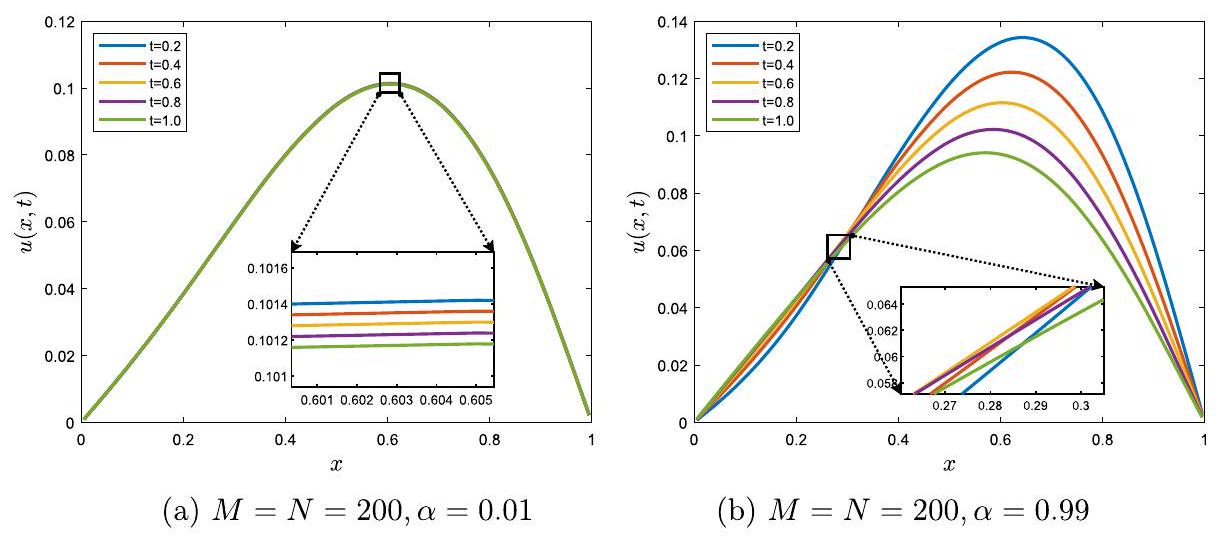
في الشكل 1(أ)، نرسم (خطأ) كدالة لـ لقيم مختلفة من (هنا ). بالمثل، في الشكل 1(b)، نقوم برسم خطأ كنتيجة لـ لـ ،
الجدول 1 المثال 1: الأخطاء، معدلات التقارب الزمني، وأوقات وحدة المعالجة المركزية
M ن -خطأ معدل زمن وحدة المعالجة المركزية
0.2 100 10 – 0.0113
100 15 2.00 0.0123
100 20 2.00 0.0132
100 ٢٥ 2.00 0.0138
100 30 2.00 0.0158
0.5 100 10 – 0.0112
100 15 2.00 0.0121
100 20 2.00 0.0130
100 25 2.00 0.0153
100 30 2.00 0.0157
0.8 100 10 – 0.0116
100 15 2.00 0.0126
100 20 2.00 0.0134
100 ٢٥ 2.00 0.0148
100 30 2.00 0.0172
الجدول 2 المثال 1: الأخطاء، معدلات التقارب المكاني، وأوقات وحدة المعالجة المركزية
M -خطأ معدل زمن وحدة المعالجة المركزية
0.3 10 100 – 0.0184
15 225 ٤.٠٠ 0.0450
20 ٤٠٠ ٤.٠٠ 0.1191
25 625 ٤.٠٠ 0.2795
30 ٩٠٠ ٤.٠٠ 0.5791
0.6 10 100 – 0.0166
15 225 ٤.٠٠ 0.0431
20 ٤٠٠ ٤.٠٠ 0.1230
٢٥ 625 ٤.٠٠ 0.2811
30 ٩٠٠ ٤.٠٠ 0.5797
0.9 10 100 – 0.0166
15 225 ٤.٠٠ 0.0451
20 ٤٠٠ ٤.٠٠ 0.1243
25 625 ٤.٠٠ 0.2828
30 ٩٠٠ ٤.٠٠ 0.5787
شكل كنتيجة لـ و على التوالي، بالنسبة لـ : (أ) ; (ب)
الشكل 2 رسم بياني للحل العددي للمثال 1 مع المعطيات على مستويات زمنية مختلفة
الشكل 3 المثال 1 مع في و : (أ) الحل الدقيق؛ (ب) الحل العددي؛ (ج) الخطأ المطلق؛ (د) رسم بياني لمستوى الخطأ
0.4، 0.6، 0.8. الشكل 2 يقدم الحل العددي للمعادلة (2.7) للمعطيات المعطاة على مستويات زمنية مختلفة. توضح الأشكال 3 و 4 الحل الدقيق، الحل العددي، الخطأ المطلق، ورسم الكنتور للخطأ مع في و 0.95، على التوالي. من الأشكال 3 و 4، نلاحظ أن الحل العددي للمعادلة (2.7) يتطابق بشكل وثيق مع الحل الدقيق.
المثال 2 في المثال الثاني، نعتبر المعادلة (2.1) مع ، و الحل الدقيق هو
الشكل 4 المثال 1 مع في و : (أ) الحل الدقيق؛ (ب) الحل العددي؛ (ج) الخطأ المطلق؛ (د) رسم بياني لمستوى الخطأ
  1. ، ومصطلح المصدر هو قيم المعلمات ذات الصلة ، و المرتبطة بالمثال تعتبر كـ و .
في المثال الثاني، تظهر النتائج العددية في الجدولين 3 و 4. يعرض الجدول 3 الأخطاء ومعدلات التقارب الزمني لـ مع في مختلف يمكننا أن نجد أن دقة الوقت قريبة من المعدل الأمثل . هذا يتماشى مع تحليلنا النظري. الجدول 4 يعرض الأخطاء ومعدلات التقارب المكاني لـ مع تشير البيانات في الجدول 4 إلى أن دقة الفضاء قريبة من المعدل الأمثل. الجدول 5 يقارن -أخطاء طريقتنا مقارنةً بالطرق الأخرى في و وفقًا للبيانات في الجدول 5، يمكننا استخلاص الاستنتاجات التالية: حتى عند استخدام عدد قليل جداً من العقد المنفصلة، فإن نتائجنا أفضل من النتائج في [48]؛ ii) بالمقارنة مع النتائج في [49]، على الرغم من استخدام عدد أقل من العقد في [49]، فإن دقة حساباتنا أعلى بكثير؛ iii) عند استخدام نفس عدد العقد المنفصلة، فإن نتائجنا أفضل من النتائج في [50]. الشكل 5 يوضح الحل العددي للمثال الثاني المعطى. على مستويات زمنية مختلفة. هذه النتائج العددية تتوافق مع الحل الدقيق.
المثال 3 في المثال الثالث، نعتبر المعادلة (2.1) مع . في أي، ، و مصطلح المصدر
الجدول 3 المثال 2: الأخطاء، معدلات التقارب الزمني، وأوقات وحدة المعالجة المركزية
M ن -خطأ معدل زمن وحدة المعالجة المركزية
0.2 ٢٠٠ ٥ – 0.0258
٢٠٠ 10 2.00 0.0342
٢٠٠ 15 2.00 0.0413
٢٠٠ 20 2.00 0.0462
٢٠٠ ٢٥ 2.00 0.0512
0.5 ٢٠٠ ٥ – 0.0256
٢٠٠ 10 2.00 0.0352
٢٠٠ 15 2.00 0.0400
٢٠٠ 20 2.00 0.0465
٢٠٠ ٢٥ 2.00 0.0520
0.8 ٢٠٠ ٥ – 0.0248
٢٠٠ 10 1.99 0.0354
٢٠٠ 15 2.00 0.0408
٢٠٠ 20 2.00 0.0450
٢٠٠ 25 2.00 0.0519
الجدول 4 المثال 2: الأخطاء، معدلات التقارب المكاني، وأوقات وحدة المعالجة المركزية
M ن -خطأ معدل زمن وحدة المعالجة المركزية
0.3 10 100 – 0.0389
15 225 ٤.٠٠ 0.1040
20 ٤٠٠ ٤.٠٠ 0.2452
25 625 ٤.٠٠ 0.5672
30 ٩٠٠ ٤.٠٠ 1.0806
0.6 10 100 – 0.0405
15 225 ٤.٠٠ 0.0842
20 ٤٠٠ ٤.٠٠ 0.2597
25 625 ٤.٠٠ 0.5239
30 ٩٠٠ ٤.٠٠ 1.0479
0.9 10 100 – 0.0375
15 225 ٤.٠٠ 0.0853
20 ٤٠٠ ٤.٠٠ 0.2361
25 625 ٤.٠٠ 0.5405
30 ٩٠٠ ٤.٠٠ 1.0709
الجدول 5 المثال 2: مقارنة طريقتنا مع طرق أخرى في
ن طريقة [48] طريقة [49] طريقة [50] طريقتنا
10
20
40
٨٠
١٦٠
قيم المعلمات ذات الصلة ، و المرتبطة بالمثال تعتبر كـ و .
في المثال الثالث، تظهر النتائج العددية في الجدولين 6 و 7. في الجدول 6، تظهر الأخطاء ومعدلات التقارب الزمني في . تكشف هذه البيانات أن الترتيب الحسابي للمخططات المقترحة لدينا في مكون الزمن هو تقريبًا 2. في الجدول 7، يتم عرض الأخطاء ومعدلات التقارب المكاني في . تشير هذه البيانات إلى أن الترتيب الحسابي للمخططات المقترحة لدينا في تركيب الفضاء-
الشكل 5 رسم بياني للحل العددي للمثال 2 المعطى على مستويات زمنية مختلفة
الجدول 6 المثال 3: الأخطاء، معدلات التقارب الزمني، وأوقات وحدة المعالجة المركزية
M ن -خطأ معدل زمن وحدة المعالجة المركزية
0.2 ٢٠٠ ٥ – 0.0287
٢٠٠ 10 2.00 0.0411
٢٠٠ 15 2.00 0.0454
٢٠٠ 20 2.00 0.0514
٢٠٠ ٢٥ 2.00 0.0552
0.5 ٢٠٠ ٥ – 0.0292
٢٠٠ 10 1.99 0.0396
٢٠٠ 15 2.00 0.0439
٢٠٠ 20 2.00 0.0483
٢٠٠ ٢٥ 2.00 0.0542
0.8 ٢٠٠ ٥ – 0.0269
٢٠٠ 10 1.97 0.0369
٢٠٠ 15 1.99 0.0384
٢٠٠ 20 1.99 0.0432
٢٠٠ ٢٥ 2.00 0.0518
الجدول 7 المثال 3: الأخطاء، معدلات التقارب المكاني، وأوقات المعالجة المركزية
M ن -خطأ معدل زمن وحدة المعالجة المركزية
0.3 40 ١٦٠٠ – ٣.١٣٩٦
٤٥ ٢٠٢٥ ٤.٠٣ ٥.٢٢٤٦
50 ٢٥٠٠ ٤.٠٢ 10.0944
٥٥ 3025 ٤.٠٢ 15.3994
60 ٣٦٠٠ ٤.٠١ ٢٢٫٩٩٠٥
0.6 40 ١٦٠٠ – 3.1529
٤٥ ٢٠٢٥ ٤.٠٢ 5.1031
50 ٢٥٠٠ ٤.٠٢ 10.1676
٥٥ 3025 ٤.٠١ 15.1544
60 ٣٦٠٠ ٤.٠١ ٢٢.٦٢٩٦
0.9 40 ١٦٠٠ – 3.1531
٤٥ ٢٠٢٥ ٤.٠٠ 5.1108
50 ٢٥٠٠ ٤.٠٠ 10.5489
٥٥ 3025 ٤.٠٠ 14.9813
60 ٣٦٠٠ ٤.٠٠ ٢٢.٧١١٣
الشكل 6 رسم بياني للحل العددي للمثال 3 المعطى على مستويات زمنية مختلفة
الجدول 8 المثال 4: الأخطاء، معدلات التقارب الزمني، وأوقات وحدة المعالجة المركزية
M ن -خطأ معدل زمن وحدة المعالجة المركزية
0.3 ٢٥ ٤٨٠ – 0.3451
٢٥ ٤٩٠ 2.05 0.3502
٢٥ ٥٠٠ 2.10 0.3624
٢٥ 510 2.15 0.3896
25 520 2.19 0.4063
0.6 ٢٥ ٤٨٠ – 0.3251
٢٥ ٤٩٠ 2.00 0.3428
25 ٥٠٠ 2.02 0.3690
٢٥ 510 2.06 0.3730
٢٥ 520 2.10 0.3899
0.9 25 ٤٨٠ – 0.3269
٢٥ ٤٩٠ 1.94 0.3455
٢٥ ٥٠٠ 1.98 0.3605
٢٥ 510 2.02 0.3886
٢٥ 520 2.07 0.4008
الناتج حوالي 4، وهو متسق مع النتائج النظرية. الشكل 6 يوضح الحل العددي للمثال الثالث مع لـ المعطى على مستويات زمنية مختلفة. النتائج العددية المذكورة أعلاه تُظهر مرة أخرى أنه في الحالة التي تكون فيها الحلول الدقيقة معروفة، فإن الطريقة المقترحة في هذه الورقة تتمتع باستقرار عددي جيد وسرعة تقارب عالية، وهو ما يتماشى مع تحليلنا النظري. من أجل التحقق من فعالية الطريقة المقترحة في هذه الورقة، ستتناول المثال العددي التالي (انظر المثال 4) الحالة التي تكون فيها الحلول الدقيقة غير معروفة.
مثال 4 في هذا المثال، المصطلح الأول هو ، وعبارة القوة هي . نحن نعتبر ، و .
يتم استخدام هذا المثال لاختبار الحالة التي تكون فيها الحلول الدقيقة غير معروفة. بالنسبة للاتجاه الزمني، نعتبر الحلول على الشبكات الدقيقة. و ) كحلول دقيقة والحلول على الشبكات الخشنة كحلول عددية في الجدول 8. تظهر البيانات في الجدول 8 أن دقة من الدرجة الثانية قد تم التحقق منها. من أجل التحقق من الدقة ومعدل التقارب في الاتجاه المكاني، نتعامل مع الحلول على الشبكات الدقيقة ( و ) كحلول دقيقة، بينما الحلول على الخشنة
الجدول 9 المثال 4: الأخطاء، معدلات التقارب المكاني، وأوقات وحدة المعالجة المركزية
M ن -خطأ معدل زمن وحدة المعالجة المركزية
0.2 ٥ ٦٠٠ – 0.3559
10 ٦٠٠ 3.66 0.3813
15 ٦٠٠ ٤.٤٣ 0.4279
20 ٦٠٠ ٤.٥٥ 0.4674
30 ٦٠٠ ٤.٥٦ 0.5084
0.5 ٥ ٦٠٠ – 0.3635
10 ٦٠٠ 3.92 0.3873
15 ٦٠٠ ٤.٦٥ 0.4169
20 ٦٠٠ ٤.٦٣ 0.4559
30 ٦٠٠ ٤.٤٩ 0.4947
0.8 ٥ ٦٠٠ – 0.3603
10 ٦٠٠ 3.69 0.3824
15 ٦٠٠ 3.66 0.4160
20 ٦٠٠ ٤.٢١ 0.4518
30 ٦٠٠ ٤.٥٦ 0.5056
الشكل 7 رسم بياني للحل العددي للمثال 4 المعطى على مستويات زمنية مختلفة
الشبكات ( تعتبر ( ) حلولاً عددية. يوضح الجدول 9 أن الدقة من الرتبة الرابعة في الاتجاه المكاني تم التحقق منها. يوضح الشكل 7 الحل العددي للمثال الرابع المعطى على مستويات زمنية مختلفة. توضح الشكل 7 بوضوح أن المشتق من الرتبة الكسرية له تأثير محلي على شكل الحلول العددية.

5 الاستنتاج

في هذه الورقة، نقترح مخطط فرق محدود مضغوط لحل نموذج تسعير خيارات بلاك-شولز الكسرية الزمنية. ترتيب التقارب للمخطط العددي المقترح هو ، حيث و هما حجم الخطوات الزمنية والمكانية، على التوالي. على حد علمنا، لا يوجد مخطط عددي من هذا النوع العالي للترتيب لنموذج تسعير خيارات بلاك-شولز الكسرية مع المشتق الكسرى كابوتو-فابريزيو. تم تحليل الاستقرار وتقدير الخطأ للمخطط المقترح باستخدام طريقة فورييه. تم تقديم أربعة أمثلة عددية للتحقق من دقة المخطط الجديد، وتؤكد النتائج التحليل النظري. باختصار، فإن المخطط العددي المقترح فعال للغاية لحل نموذج تسعير خيارات بلاك-شولز الكسرية الزمنية مع المشتق الكسرى كابوتو-فابريزيو. يمكن توسيع الطريقة المقترحة لحل
معادلات تفاضلية جزئية كسرية زمنية أخرى من نوع مشابه مع المشتق الكسرى كابوتو-فابريزيو.

الشكر والتقدير

نود أن نشكر المراجعين والمحرر على القراءة الدقيقة للورقة وعلى تعليقاتهم واقتراحاتهم الممتازة التي أدت إلى مراجعة وتعزيز أجزاء من هذه الورقة.

مساهمات المؤلفين

كتب Y.L. Feng و X.D. Zhang النص الرئيسي للمخطوطة، وأعد Y. Chen و L.L. Wei الأشكال والجداول. راجع جميع المؤلفين المخطوطة.

التمويل

تم دعم هذا العمل من قبل جامعة قويتشو للمالية والاقتصاد من خلال مشروع الابتكار والاستكشاف الأكاديمي الناشئ (رقم 2024XSXMB13)، وصندوق معهد علوم التعقيد، جامعة تكنولوجيا هنان (رقم CSKFJJ-2025-33) ومؤسسة العلوم الطبيعية لمنطقة شينجيانغ الويغورية ذاتية الحكم (رقم 2022D01E13).

توفر البيانات

لم يتم إنشاء أو تحليل أي مجموعات بيانات خلال الدراسة الحالية.

الإعلانات

غير قابل للتطبيق.

المصالح المتنافسة

يعلن المؤلفون عدم وجود مصالح متنافسة.

تفاصيل المؤلف

مدرسة العلوم الرياضية، جامعة شينجيانغ العادية، أورومتشي، شينجيانغ 830017، جمهورية الصين الشعبية. كلية إحصائيات البيانات الكبيرة، جامعة قويتشو للمالية والاقتصاد، قويتشو، 550025، جمهورية الصين الشعبية. كلية الدراسات العامة، جامعة شينجيانغ للتكنولوجيا، هوتان، 848000، جمهورية الصين الشعبية. مدرسة الرياضيات والإحصاء، جامعة تكنولوجيا هنان، تشنغتشو، 450001، جمهورية الصين الشعبية.
تاريخ الاستلام: 1 نوفمبر 2024 تاريخ القبول: 28 يناير 2025 تاريخ النشر على الإنترنت: 18 مارس 2025

References

  1. Faridi, W.A., Bakar, M.A., Akgül, A., El-Rahman, M.A., El Din, S.M.: Exact fractional soliton solutions of thin-film ferroelectric material equation by analytical approaches. Alex. Eng. J. 78, 483-497 (2023)
  2. Hosseini, V.R., Mehrizi, A.A., Karimi-Maleh, H., Naddafi, M.: A numerical solution of fractional reaction-convection-diffusion for modeling PEM fuel cells based on a meshless approach. Eng. Anal. Bound. Elem. 155, 707-716 (2023)
  3. Kavitha, K., Vijayakumar, V., Udhayakumar, R., Ravichandran, C.: Results on controllability of Hilfer fractional differential equations with infinite delay via measures of noncompactness. Asian J. Control 24, 1406-1415 (2022)
  4. Selvam, A.P., Vellappandi, M., Govindaraj, V.: Controllability of fractional dynamical systems with -Caputo fractional derivative. Phys. Scr. 98, 025206 (2023)
  5. Alchikh, R., Khuri, S.A.: Numerical solution of a fractional differential equation arising in optics. Optik 208, 163911 (2020)
  6. Murad, M.A.S.: New optical soliton solutions for time-fractional Kudryashov’s equation in optical fiber. Optik 283, 170897 (2023)
  7. Shen, L.J.: Fractional derivative models for viscoelastic materials at finite deformations. Int. J. Solids Struct. 190, 226-237 (2020)
  8. Bhangale, N., Kachhia, K.B., Gómez-Aguilar, J.F.: Fractional viscoelastic models with Caputo generalized fractional derivative. Math. Methods Appl. Sci. 46, 7835-7846 (2023)
  9. Arqub, O.A.: Numerical simulation of time-fractional partial differential equations arising in fluid flows via reproducing Kernel method. Int. J. Numer. Methods Heat Fluid Flow 30, 4711-4733 (2020)
  10. Kumar, D., Seadawy, A.R., Joardar, A.K.: Modified Kudryashov method via new exact solutions for some conformable fractional differential equations arising in mathematical biology. Chin. J. Phys. 56, 75-85 (2018)
  11. Khan, H., Ahmed, S., Alzabut, J., Azar, A.T.: A generalized coupled system of fractional differential equations with application to finite time sliding mode control for leukemia therapy. Chaos Solitons Fractals 174, 113901 (2023)
  12. Fall, A.N., Ndiaye, S.N., Sene, N.: Black-Scholes option pricing equations described by the Caputo generalized fractional derivative. Chaos Solitons Fractals 125, 108-118 (2019)
  13. Roul, P.: A high accuracy numerical method and its convergence for time-fractional Black-Scholes equation governing European options. Appl. Numer. Math. 151, 472-493 (2020)
  14. Nuugulu, S.M., Gideon, F., Patidar, K.C.: A robust numerical scheme for a time-fractional Black-Scholes partial differential equation describing stock exchange dynamics. Chaos Solitons Fractals 145, 110753 (2021)
  15. Zhang, H.M., Zhang, M.C., Liu, F.W., Shen, M.: Review of the fractional Black-Scholes equations and their solution techniques. Fractal Fract. 8, 101 (2024)
  16. Black, F., Scholes, M.: The pricing of options and corporate liabilities. J. Polit. Econ. 81, 637-654 (1973)
  17. Merton, R.C.: Theory of rational option pricing. Bell J. Econ. Manag. Sci. 4, 141-183 (1973)
  18. Jumarie, G.: Stock exchange fractional dynamics defined as fractional exponential growth driven by (usual) Gaussian white noise. Application to fractional Black-Scholes equations. Insur. Math. Econ. 42, 271-287 (2008)
  19. Jumarie, G.: Derivation and solutions of some fractional Black Scholes equations in coarse-grained space and time. Application to Merton’s optimal portfolio. Comput. Math. Appl. 59, 1142-1164 (2010)
  20. Chen, W.T., Xu, X., Zhu, S.P.: Analytically pricing double barrier options based on a time-fractional Black-Scholes equation. Comput. Math. Appl. 69, 1407-1419 (2015)
  21. Roul, P., Goura, V.M.K.P.: A compact finite difference scheme for fractional Black-Scholes option pricing model. Appl. Numer. Math. 166, 40-60 (2021)
  22. Caputo, M., Fabrizio, M.: A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 1, 73-85 (2015)
  23. Atangana, A., Alqahtani, R.T.: Numerical approximation of the space-time Caputo-Fabrizio fractional derivative and application to groundwater pollution equation. Adv. Differ. Equ. 2016, 156 (2016)
  24. Djida, J.D., Atangana, A.: More generalized groundwater model with space-time Caputo-Fabrizio fractional differentiation. Numer. Methods Partial Differ. Equ. 33, 1616-1627 (2017)
  25. Firoozjaee, M.A., Jafari, H., Lia, A., Baleanu, D.: Numerical approach of Fokker-Planck equation with Caputo-Fabrizio fractional derivative using Ritz approximation. J. Comput. Appl. Math. 339, 367-373 (2018)
  26. Rubbab, Q., Nazeer, M., Ahmad, F., Chu, Y.M., Khan, M.I., Kadry, S.: Numerical simulation of advection-diffusion equation with Caputo-Fabrizio time fractional derivative in cylindrical domains: applications of pseudo-spectral collocation method. Alex. Eng. J. 60, 1731-1738 (2021)
  27. Nieto, J.J.: Solution of a fractional logistic ordinary differential equation. Appl. Math. Lett. 123, 107568 (2022)
  28. Kebede, S.G., Lakoud, A.G.: Analysis of mathematical model involving nonlinear systems of Caputo-Fabrizio fractional differential equation. Bound. Value Probl. 2023, 44 (2023)
  29. Souigat, A., Korichi, Z., Meftah, M.T.: Solution of the fractional diffusion equation by using Caputo-Fabrizio derivative: application to intrinsic arsenic diffusion in germanium. Rev. Mex. Fis. 70, 010501 (2024)
  30. Hussein, M.A.: Using the Elzaki decomposition method to solve nonlinear fractional differential equations with the Caputo-Fabrizio fractional operator. Baghdad Sci. J. 21, 1044-1054 (2024)
  31. Amin, M., Abbas, M., Iqbal, M.K., Baleanu, D.: Non-polynomial quintic spline for numerical solution of fourth-order time fractional partial differential equations. Adv. Differ. Equ. 2019, 183 (2019)
  32. Amin, M., Abbas, M., Iqbal, M.K., Ismail, A.I.M., Baleanu, D.: A fourth order non-polynomial quintic spline collocation technique for solving time fractional superdiffusion equations. Adv. Differ. Equ. 2019, 514 (2019)
  33. Amin, M., Abbas, M., Iqbal, M.K., Baleanu, D.: Numerical treatment of time-fractional Klein-Gordon equation using redefined extended cubic B-spline functions. Front. Phys. 8, 288 (2020)
  34. Amin, M., Abbas, M., Baleanu, D., Iqbal, M.K., Riaz, M.B.: Redefined extended cubic B-spline functions for numerical solution of time-fractional telegraph equation. Comput. Model. Eng. Sci. 127, 361-384 (2021)
  35. Mesgarani, H., Aghdam, Y.E., Khoshkhahtinat, M., Farnam, B.: Analysis of the numerical scheme of the one-dimensional fractional Rayleigh-Stokes model arising in a heated generalized problem. AIP Adv. 13, 085024 (2023)
  36. Aghdam, Y.E., Mesgarani, H., Asadi, Z., Nguyen, V.T.: Investigation and analysis of the numerical approach to solve the multi-term time-fractional advection-diffusion model. AIMS Math. 8, 29474-29489 (2023)
  37. Aghdam, Y.E., Mesgarani, H., Asadi, Z.: Estimate of the fractional advection-diffusion equation with a time-fractional term based on the shifted Legendre polynomials. J. Math. Model. 11, 731-744 (2023)
  38. Haq, S., Hussain, M.: Selection of shape parameter in radial basis functions for solution of time-fractional Black-Scholes models. Appl. Math. Comput. 335, 248-263 (2018)
  39. Golbabai, A., Nikan, O., Nikazad, T.: Numerical analysis of time fractional Black-Scholes European option pricing model arising in financial market. Comput. Appl. Math. 38, 1-24 (2019)
  40. Fadugba, S.E.: Homotopy analysis method and its applications in the valuation of European call options with time-fractional Black-Scholes equation. Chaos Solitons Fractals 141, 110351 (2020)
  41. Golbabai, A., Nikan, O.: A computational method based on the moving least-squares approach for pricing double barrier options in a time-fractional Black-Scholes model. Comput. Econ. 55, 119-141 (2020)
  42. An, X.Y., Liu, F.W., Zheng, M.L., Anh, V.V., Turner, I.W.: A space-time spectral method for time-fractional Black-Scholes equation. Appl. Numer. Math. 165, 152-166 (2021)
  43. Taghipour, M., Aminikhah, H.: A spectral collocation method based on fractional Pell functions for solving time-fractional Black-Scholes option pricing model. Chaos Solitons Fractals 163, 112571 (2022)
  44. Kazmi, K.: A second order numerical method for the time-fractional Black-Scholes European option pricing model. J. Comput. Appl. Math. 418, 114647 (2023)
  45. Aghdam, Y.E., Mesgarani, H., Amin, A., Gómez-Aguilar, J.F.: An efficient numerical scheme to approach the time fractional Black-Scholes model using orthogonal Gegenbauer polynomials. Comput. Econ. 64, 211-224 (2024)
  46. Sun, Z.Z.: Compact difference scheme for heat equation with Neumann boundary conditions. Numer. Methods Partial Differ. Equ. 25, 1320-1341 (2009)
  47. Shi, J.K., Chen, M.H.: A second-order accurate scheme for two-dimensional space fractional diffusion equations with time Caputo-Fabrizio fractional derivative. Appl. Numer. Math. 151, 246-262 (2020)
  48. Akram, T., Abbas, M., Abualnaja, K.M., Iqbal, A., Majeed, A.: An efficient numerical technique based on the extended cubic B-spline functions for solving time fractional Black-Scholes model. Eng. Comput. 38, 1705-1716 (2022)
  49. Mesgarani, H., Ahanj, S., Aghdam, Y.E.: Numerical investigation of the time-fractional Black-Scholes equation with barrier choice of regulating European option. J. Math. Model. 10, 1-10 (2022)
  50. Abdi, N., Aminikhah, H., Sheikhani, A.H.R.: High-order compact finite difference schemes for the time-fractional Black-Scholes model governing European options. Chaos Solitons Fractals 162, 112423 (2022)

ملاحظة الناشر

تظل Springer Nature محايدة فيما يتعلق بالمطالبات القضائية في الخرائط المنشورة والانتماءات المؤسسية.

Journal: Journal of Inequalities and Applications, Volume: 2025, Issue: 1
DOI: https://doi.org/10.1186/s13660-025-03261-2
Publication Date: 2025-03-18

A compact finite difference scheme for solving fractional Black-Scholes option pricing model

Yuelong Feng , Xindong Zhang , Yan Chen and Leilei Wei

*Correspondence:
liaoyuan1126@163.com
College of Big Data Statistics, Guizhou University of Finance and Economics, Guiyang, 550025, P.R. China
Full list of author information is available at the end of the article

Abstract

In this work, we introduce an efficient compact finite difference (CFD) method for solving the time-fractional Black-Scholes (TFBS) option pricing model. The time-fractional derivative is described using Caputo-Fabrizio (C-F) fractional derivative, and a compact finite difference method is employed to discretize the spatial derivative. The main contribution of this work is to develop a high-order discrete scheme for the TFBS model. In the numerical scheme, we have developed a convergence rate of , where denotes the temporal step and represents the spatial step. To verify the effectiveness of the proposed method, we have conducted stability analysis and error estimation using the Fourier method. Furthermore, a series of numerical experiments were conducted, and the numerical results demonstrated the theoretical order of accuracy and illustrated the effectiveness of the proposed method.

Mathematics Subject Classification: 65M06; 65M12; 47F05; 35S10
Keywords: Black-Scholes model; Caputo-Fabrizio fractional derivative; Compact finite difference method; Stability; Error estimate

1 Introduction

Fractional differential equations, owing to their capacity to model certain phenomena with greater precision, have found widespread applications across diverse fields, including electricity [1,2], control theory [3,4], optics [5,6], viscoplasticity [7,8], fluid mechanics [9] and biomedical engineering [10,11]. Furthermore, they have also been used to simulate financial problems [12-15].
The Black-Scholes (BS) model, introduced by Black, Scholes and Merton [16, 17], offers both a pricing formula for European options and a hedging portfolio strategy. This model operates under strict assumptions: frictionless markets, continuous and smooth price movements, and option exercise only at maturity. Jumarie [18, 19] formulated both time- and space-fractional versions of BS equations and then derived an optimal fractional Merton portfolio. In the realm of financial markets or option pricing, the fractional BS equation holds immense potential for application. It can provide investors with more ac-
© The Author(s) 2025. Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/ 4.0/.
curate option pricing methodologies, enabling them to make more informed investment decisions. Additionally, this model can be harnessed in risk management and portfolio optimization, aiding investors in achieving maximum investment returns while maintaining an acceptable level of risk. As financial markets continue to evolve and become increasingly complex, the application prospects of the fractional BS equation are poised to broaden even further. In this paper, we consider the following TFBS model of the form [20, 21],
with boundary conditions
and terminal condition
where is a fractional order operator, denotes the price of a European option for stock price at time is the volatility, is the risk-free interest rate, and is the maturity date of the contract. and are the rebates paid when the corresponding barrier is hit, and is the payoff function. In [21], is a modified right Riemann-Liouville fractional derivative. In this paper, is used as Caputo-Fabrizio (C-F) fractional derivative, which is defined as
In 2015, Caputo and Fabrizio proposed a novel concept of fractional derivative [22], known as the C-F fractional derivative. This definition is formulated in a straightforward and clear manner, making its application in financial modeling more straightforward. Especially when addressing time-fractional derivatives, the mathematical handling of the C-F fractional derivative is relatively intuitive, which aids in derivation and computation processes. In the realm of financial market analysis, price fluctuations are frequently influenced by historical data, resulting in a memory effect. Traditional models that rely on integer-order derivatives often fail to fully capture market dynamics due to this memory effect. However, the Caputo-Fabrizio fractional derivative, which employs a nonsingular kernel function, offers several advantages, such as simpler handling of initial conditions and enhanced numerical stability compared to other fractional derivatives. This makes it particularly effective at capturing memory effects. This capability is crucial for simulating complex financial phenomena. For further insights into the advancements of the C-F fractional derivative, one can refer to references [23-30]. With the deepening of research on time fractional differential equations, it is often difficult to obtain exact solutions for such equations. Therefore, studying the numerical solutions of such equations becomes particularly important. In recent years, numerical methods for fractional equations can be found in [31-37], among others. Meanwhile, different authors proposed many methods
for solving the TFBS equation. For instance, Haq and Hussain [38] applied the Residual Power Series method and a collocation-based mesh-free method to solve a class of TFBS models with constant and variable coefficients. Golbabai et al. [39] presented a numerical solution for the TFBS model using the radial basis functions method, which is characterized as a mesh-free scheme. Fadugba [40] proposed the application of the homotopy analysis method in the valuation of a European call option with a TFBS equation. Golbabai and Nikan [41] used the moving least-squares method to obtain an approximation solution of the TFBS model. An et al. [42] employed a space-time spectral method to develop a numerical scheme for solving the TFBS model with a smooth payoff function. Taghipour and Aminikhah [43] presented an efficient spectral collocation method based on fractional Pell functions for solving the TFBS equation. Kazmi [44] developed a numerical scheme to solve the TFBS equation governing European options with a convergence order of . Additionally, Richardson extrapolation was also introduced to obtain a modified version of the method, which exhibits faster convergence for the TFBS equation with non-smooth initial data. Aghdam et al. [45] proposed an efficient method for estimating the fractional BS model, utilizing the composition of orthogonal Gegenbauer polynomials and the approximation of the fractional derivative based on the Caputo fractional derivative. The orthogonality of Gegenbauer polynomials and operational matrices significantly reduces computation time and enhances speed. The above-mentioned articles on fractional differential equations primarily involve the Caputo fractional and RiemannLiouville fractional derivatives. Notably, only a limited number of numerical methods have been proposed in the literature for solving Eq. (1.1) with C-F fractional derivative. We observe that no such high-order numerical scheme is currently available for the fractional BS differential equation with a C-F fractional derivative. Although some numerical techniques have been introduced to address this issue, these methods are typically of low spatial order.
The main purpose of this paper is to solve the fractional Black-Scholes option pricing model using the compact difference scheme and provide stability and convergence analysis. The compact scheme is a high-order method that divides the continuous solution domain into discrete grid points and replaces differentials with differences, thereby transforming differential equations into algebraic equations to obtain numerical solutions. Additionally, when solving these equation systems, the coefficient matrix of the linear system is a diagonal matrix, which can be solved easily. Therefore, in this paper, we have developed a numerical method based on the compact finite difference method to obtain the numerical solution of Eq. (1.1). To verify the effectiveness of the proposed method, we have conducted stability analysis and error estimation using the Fourier method. Furthermore, a series of numerical experiments have been conducted, and the numerical results demonstrate good computational performance, thereby corroborating our theoretical analysis.
The organizational structure of this article is as follows. In Sect. 2, we offer some notations and lemmas to construct the discrete scheme of Eq. (1.1). The stability and convergence analysis of the constructed discrete scheme is presented in Sect. 3, and some numerical experiments are given in Sect. 4. Finally, Sect. 5 gives a brief conclusion.

2 Construction of fourth-order numerical scheme

Set and and denote . To solve Eq. (1.1), we transform its unbounded domain into a finite one via truncation. Thus, Eq. (1.1) can be changed into:
where and are all given and sufficiently smooth functions.
In this section, we mainly consider the construction of discrete scheme for Eq. (2.1). For given positive integers and , let and . Define a grid function space . Let and . For any function , we define the following notations:
We use and to denote two compact operators with the following forms:
For compact operator , the following lemma can be found in [46].
Lemma 2.1 ([46]) Let be a compact operator. Suppose . Then, the following holds:
Using Eq. (2.2), we have . Thus, Lemma 2.1 implies that . Similar to the compact operator , we can obtain the following lemma for compact operator .
Lemma 2.2 Let be a compact operator as in Eq. (2.3). Suppose . Then, the following holds:
where . Furthermore, it holds that
Using Eq. (2.3), we have . Thus, Lemma 2.2 implies that .
We now introduce some lemmas that will be used in the following analysis. The time C-F fractional derivative is approximated by the following formula, as given in [47].
Lemma 2.3 ([47]) Let with . Then, the following equality holds:
Let with . Then, using Lemma 2.3, we can get that . Thus, at the given node ( ), Lemma 2.3 implies that Eq. (2.1) can be rewritten as follows:
Using Lemmas 2.1 and 2.2, we can show that and . Therefore, Eq. (2.4) can be rewritten as follows:
where with is a positive constant. It is easy to get the following lemma by direct computations.
Lemma 2.4 Let with . Then, it holds that
Denoting as the numerical approximation of and omitting the small term in Eq. (2.5), we can get the following fourth-order numerical scheme for Eq. (2.1):
Multiplying both sides of Eq. (2.6) by and simplifying, we obtain
where and . The initial and boundary conditions of Eq. (2.1) can be discretized as follows:
In Eq. (2.7), for the points outside the region that are , we use the following approximate formats to calculate the values:
and
To enhance clarity and improve readability, we have provided a detailed, step-by-step algorithm for implementing our proposed numerical scheme. The numerical algorithm is as follows:
Step 1. Determine the partitioning domain range and step sizes and , define the volatility , risk-free rate , other numerical parameters, and boundary conditions.
Step 2. Calculate the exact value .
Step 3. Obtain the coefficient matrices on the left-hand side and on the right-hand side of Eq. (2.7) at all discrete nodes.
Step 4. Use approximate formats to handle nodes beyond the boundary, and supplement matrices and .
Step 5. Calculate the numerical value of by .
Step 6. Calculate the corresponding error .
Step 7. Finish the process by writing the data.

3 Stability analysis and error estimation

In this section, we will consider the stability analysis and error estimation of Eq. (2.7). For convenience, we allow to represent different values at different positions. Let be the
approximate solution of Eq. (2.7), and define with and , and with , respectively. Using Eq. (2.7), we obtain the following round-off error equation:
Next, we consider the stability and convergence analysis of Eq. (3.1) using the Fourier method. To apply the Fourier method, we need to extend the function’s domain. Thus, we define the following grid function:
then the Fourier series for is
where and .
Using the Parseval equality , we have
Letting and substituting it into Eq. (3.1), by the identify and , we have
It follows that
where and . In view of and , we have
From the above equation, we can obtain that
Theorem 3.1 Let be the solution to Eq. (3.5), then it holds that
Proof For , from Eq. (3.5), we get
Now, we assume that
For , using Eq. (3.5), we have
This completes the proof of the theorem.
The following theorem is about stability of discrete scheme Eq. (2.7).
Theorem 3.2 The numerical scheme Eq. (2.7) is unconditionally stable.
Proof Using Eq. (3.3) and the result of Theorem 3.1, we get
which implies that the fourth-order numerical scheme Eq. (2.7) is unconditionally stable.
Next, the convergence analysis of discrete scheme Eq. (2.7) is given. Similarly, let
and denote
Subtracting Eq. (2.6) from Eq. (2.5) and noticing , we have
where . Similar to Eq. (3.2), we can define grid functions and . Applying the same ideas of stability analysis, and can be expanded into the following Fourier series:
where and . Assume that and can be chosen as and , respectively. Substituting the expressions of and into Eq. (3.7) gives
It follows that
where , and are given as in Eq. (3.5).
Theorem 3.3 Let be the solution to Eq. (3.9). Then, there is a positive constant , such that
Proof According to Eq. (3.9), we obtain
Since , by the convergence of series , there exists a positive constant such that
From Eq. (3.10), for , one has
Now, we assume that
and denote .
For , by Eq. (3.10) and Lemma 2.4, we have
This completes the proof of the theorem.
Theorem 3.4 The numerical scheme Eq. (2.7) is convergent, and the following error estimate holds
Proof Using Parseval’s equality and the definition of -norm, we have
Using the result of Theorem 3.3, we get
which implies that the numerical scheme Eq. (2.7) is convergent and the order of convergence is .

4 Numerical results

In this section, we present several numerical examples to validate the theoretical analysis by comparing exact and numerical solutions. Numerical experiments are preformed in MATLAB R2020b on a PC with an AMD Ryzen 7 7840H and 32 GB of RAM. The errors are defined as follows:
For -Error and -Error, the following convergence rates will be used in numerical tests. The time convergence rate is
where and denote the errors corresponding to mesh sizes and , respectively. The space convergence rate is
where and denote the errors corresponding to mesh sizes and , respectively.
Example 1 We consider Eq. (2.1) with and .
where the source term . The values of relevant parameters , and associated with the example are considered as , and .
In this example, the temporal convergence rates with different (here ) are shown in Table 1. From Table 1, we can find that the time accuracy is close to the optimal rate . Similarly, the spatial convergence rates with different (here ) are shown in Table 2, which shows that the space accuracy is close to the optimal rate .
In Fig. 1(a), we plot (Error) as a function of for different values of (here ). Similarly, in Fig.1(b), we plot Error as a function of for ,
Table 1 Example 1: Errors, temporal convergence rates, and CPU times
M N -error Rate CPU time(s)
0.2 100 10 – 0.0113
100 15 2.00 0.0123
100 20 2.00 0.0132
100 25 2.00 0.0138
100 30 2.00 0.0158
0.5 100 10 – 0.0112
100 15 2.00 0.0121
100 20 2.00 0.0130
100 25 2.00 0.0153
100 30 2.00 0.0157
0.8 100 10 – 0.0116
100 15 2.00 0.0126
100 20 2.00 0.0134
100 25 2.00 0.0148
100 30 2.00 0.0172
Table 2 Example 1: Errors, spatial convergence rates, and CPU times
M -error Rate CPU time(s)
0.3 10 100 – 0.0184
15 225 4.00 0.0450
20 400 4.00 0.1191
25 625 4.00 0.2795
30 900 4.00 0.5791
0.6 10 100 – 0.0166
15 225 4.00 0.0431
20 400 4.00 0.1230
25 625 4.00 0.2811
30 900 4.00 0.5797
0.9 10 100 – 0.0166
15 225 4.00 0.0451
20 400 4.00 0.1243
25 625 4.00 0.2828
30 900 4.00 0.5787
Figure as a function of and , respectively, for given : (a) ; (b)
Figure 2 Graph of numerical solution for Example 1 with given at different time levels
Figure 3 Example 1 with at and : (a) exact solution; (b) numerical solution; (c) absolute error; (d) contour plot of error
0.4, 0.6, 0.8. Figure 2 presents the numerical solution to Eq. (2.7) for given at different time levels. Figures 3 and 4 illustrate the exact solution, numerical solution, absolute error, and contour plot of the error with at and 0.95 , respectively. From Figs. 3 and 4, we observe that the numerical solution to Eq. (2.7) closely matches the exact solution.
Example 2 In the second example, we consider Eq. (2.1) with , and . The exact solution is
Figure 4 Example 1 with at and : (a) exact solution; (b) numerical solution; (c) absolute error; (d) contour plot of error
  1. , and the source term is . The values of relevant parameters , and associated with the example are considered as and .
In the second example, the numerical results are shown in Tables 3 and 4. Table 3 displays the errors and temporal convergence rates for with at different . We can find that the time accuracy is close to the optimal rate . That is in accordance with our theoretical analysis. Table 4 displays the errors and spatial convergence rates for with . The data in Table 4 indicates that the space accuracy is close to the optimal rate . Table 5 compares -Errors of our method with the other methods at and . According to the data in Table 5, we can draw the following conclusions: ) Even using very few discrete nodes, our results are better than the results in [48]; ii) Compared with the results in [49], although fewer nodes are used in [49], our calculation accuracy is much higher; iii) When using the same number of discrete nodes, our results are better than the results in [50]. Figure 5 shows the numerical solution of the second example for given at different time levels. These numerical results are consistent with the exact solution.
Example 3 In the third example, we consider Eq. (2.1) with . In which, , and . The source term
Table 3 Example 2: Errors, temporal convergence rates, and CPU times
M N -error Rate CPU time(s)
0.2 200 5 – 0.0258
200 10 2.00 0.0342
200 15 2.00 0.0413
200 20 2.00 0.0462
200 25 2.00 0.0512
0.5 200 5 – 0.0256
200 10 2.00 0.0352
200 15 2.00 0.0400
200 20 2.00 0.0465
200 25 2.00 0.0520
0.8 200 5 – 0.0248
200 10 1.99 0.0354
200 15 2.00 0.0408
200 20 2.00 0.0450
200 25 2.00 0.0519
Table 4 Example 2: Errors, spatial convergence rates, and CPU times
M N -error Rate CPU time(s)
0.3 10 100 – 0.0389
15 225 4.00 0.1040
20 400 4.00 0.2452
25 625 4.00 0.5672
30 900 4.00 1.0806
0.6 10 100 – 0.0405
15 225 4.00 0.0842
20 400 4.00 0.2597
25 625 4.00 0.5239
30 900 4.00 1.0479
0.9 10 100 – 0.0375
15 225 4.00 0.0853
20 400 4.00 0.2361
25 625 4.00 0.5405
30 900 4.00 1.0709
Table 5 Example 2: Comparison of our method with other methods at
N Method of [48] Method of [49] Method of [50] Our method
10
20
40
80
160
. The values of relevant parameters , and associated with the example are considered as and .
In the third example, the numerical results are shown in Tables 6 and 7. In Table 6, the errors and temporal convergence rates are shown at . These data reveal that the computational order of our proposed schemes in the time component is approximately 2. In Table 7, the errors and spatial convergence rates are shown at . These data indicate that the computational order of our proposed schemes in the space compo-
Figure 5 Graph of numerical solution for Example 2 for given at different time levels
Table 6 Example 3: Errors, temporal convergence rates, and CPU times
M N -error Rate CPU time(s)
0.2 200 5 – 0.0287
200 10 2.00 0.0411
200 15 2.00 0.0454
200 20 2.00 0.0514
200 25 2.00 0.0552
0.5 200 5 – 0.0292
200 10 1.99 0.0396
200 15 2.00 0.0439
200 20 2.00 0.0483
200 25 2.00 0.0542
0.8 200 5 – 0.0269
200 10 1.97 0.0369
200 15 1.99 0.0384
200 20 1.99 0.0432
200 25 2.00 0.0518
Table 7 Example 3: Errors, spatial convergence rates, and CPU times
M N -error Rate CPU time(s)
0.3 40 1600 – 3.1396
45 2025 4.03 5.2246
50 2500 4.02 10.0944
55 3025 4.02 15.3994
60 3600 4.01 22.9905
0.6 40 1600 – 3.1529
45 2025 4.02 5.1031
50 2500 4.02 10.1676
55 3025 4.01 15.1544
60 3600 4.01 22.6296
0.9 40 1600 – 3.1531
45 2025 4.00 5.1108
50 2500 4.00 10.5489
55 3025 4.00 14.9813
60 3600 4.00 22.7113
Figure 6 Graph of numerical solution for Example 3 for given at different time levels
Table 8 Example 4: Errors, temporal convergence rates, and CPU times
M N -error Rate CPU time(s)
0.3 25 480 – 0.3451
25 490 2.05 0.3502
25 500 2.10 0.3624
25 510 2.15 0.3896
25 520 2.19 0.4063
0.6 25 480 – 0.3251
25 490 2.00 0.3428
25 500 2.02 0.3690
25 510 2.06 0.3730
25 520 2.10 0.3899
0.9 25 480 – 0.3269
25 490 1.94 0.3455
25 500 1.98 0.3605
25 510 2.02 0.3886
25 520 2.07 0.4008
nent is approximately 4 , which is consistent with theoretical results. Figure 6 shows the numerical solution of the third example with for given at different time levels. The above numerical results once again demonstrate that, in the case where the exact solution is known, the method proposed in this paper has good numerical stability and high convergence speed, which is consistent with our theoretical analysis. In order to verify the effectiveness of the method proposed in this paper, the following numerical example (See Example 4) will consider the case where the exact solution is unknown.
Example 4 In this example, the initial term is , and the force term is . We consider , and .
This example is used to test the case that the exact solution is unknown. For the temporal direction, we consider the solutions on the fine grids ( and ) as exact solutions and the solutions on coarse grids as numerical solutions in Table 8 . The data in Table 8 shows that the second-order accuracy is verified. In order to verify the accuracy and convergence rate in the spatial direction, we treat the solutions on the fine grids ( and ) as the exact solutions, while the solutions on coarse
Table 9 Example 4: Errors, spatial convergence rates, and CPU times
M N -error Rate CPU time(s)
0.2 5 600 – 0.3559
10 600 3.66 0.3813
15 600 4.43 0.4279
20 600 4.55 0.4674
30 600 4.56 0.5084
0.5 5 600 – 0.3635
10 600 3.92 0.3873
15 600 4.65 0.4169
20 600 4.63 0.4559
30 600 4.49 0.4947
0.8 5 600 – 0.3603
10 600 3.69 0.3824
15 600 3.66 0.4160
20 600 4.21 0.4518
30 600 4.56 0.5056
Figure 7 Graph of numerical solution for Example 4 for given at different time levels
grids ( ) are considered numerical solutions. Table 9 shows that the fourth-order accuracy in spatial direction is verified. Figure 7 shows the numerical solution of the fourth example for given at different time levels. Figure 7 clearly shows that the fractional order derivative has a local impact on the contour of the numerical solutions.

5 Conclusion

In this paper, we propose a compact finite difference scheme for solving the time-fractional Black-Scholes option pricing model. The convergence order of the proposed numerical scheme is , where and are the temporal and spatial step sizes, respectively. To the best of our knowledge, no such a high-order numerical scheme exists for the fractional Black-Scholes option pricing model with Caputo-Fabrizio fractional derivative. The stability and error estimation of the proposed scheme are analyzed using the Fourier method. Four numerical examples are provided to verify the accuracy of the new scheme, and the results confirm the theoretical analysis. In summary, the proposed numerical scheme is highly effective for solving the time-fractional Black-Scholes option pricing model with Caputo-Fabrizio fractional derivative. The proposed method can be extended to solve
other time-fractional partial differential equations of a similar type with Caputo-Fabrizio fractional derivative.

Acknowledgements

We would like to thank the reviewers and editor for the careful reading of the paper and for their excellent comments and suggestions which have led to revising and enhancing portions of this paper.

Author contributions

Y.L. Feng and X.D. Zhang wrote the main manuscript text, and Y. Chen and L.L. Wei prepared figures and tables . All authors reviewed the manuscript.

Funding

This work was supported by Guizhou University of Finance and Economics Innovation Exploration and Academic Emerging Project (No. 2024XSXMB13), Fund of Institute of Complexity Science, Henan University of Technology (No. CSKFJJ-2025-33) and Natural Science Foundation of Xinjiang Uygur Autonomous Region (No. 2022D01E13).

Data Availability

No datasets were generated or analysed during the current study.

Declarations

Not applicable.

Competing interests

The authors declare no competing interests.

Author details

School of Mathematical Sciences, Xinjiang Normal University, Urumqi, Xinjiang 830017, P.R. China. College of Big Data Statistics, Guizhou University of Finance and Economics, Guiyang, 550025, P.R. China. College of General Studies, Xinjiang University of Technology, Hotan, 848000, P.R. China. School of Mathematics and Statistics, Henan University of Technology, Zhengzhou, 450001, P.R. China.
Received: 1 November 2024 Accepted: 28 January 2025 Published online: 18 March 2025

References

  1. Faridi, W.A., Bakar, M.A., Akgül, A., El-Rahman, M.A., El Din, S.M.: Exact fractional soliton solutions of thin-film ferroelectric material equation by analytical approaches. Alex. Eng. J. 78, 483-497 (2023)
  2. Hosseini, V.R., Mehrizi, A.A., Karimi-Maleh, H., Naddafi, M.: A numerical solution of fractional reaction-convection-diffusion for modeling PEM fuel cells based on a meshless approach. Eng. Anal. Bound. Elem. 155, 707-716 (2023)
  3. Kavitha, K., Vijayakumar, V., Udhayakumar, R., Ravichandran, C.: Results on controllability of Hilfer fractional differential equations with infinite delay via measures of noncompactness. Asian J. Control 24, 1406-1415 (2022)
  4. Selvam, A.P., Vellappandi, M., Govindaraj, V.: Controllability of fractional dynamical systems with -Caputo fractional derivative. Phys. Scr. 98, 025206 (2023)
  5. Alchikh, R., Khuri, S.A.: Numerical solution of a fractional differential equation arising in optics. Optik 208, 163911 (2020)
  6. Murad, M.A.S.: New optical soliton solutions for time-fractional Kudryashov’s equation in optical fiber. Optik 283, 170897 (2023)
  7. Shen, L.J.: Fractional derivative models for viscoelastic materials at finite deformations. Int. J. Solids Struct. 190, 226-237 (2020)
  8. Bhangale, N., Kachhia, K.B., Gómez-Aguilar, J.F.: Fractional viscoelastic models with Caputo generalized fractional derivative. Math. Methods Appl. Sci. 46, 7835-7846 (2023)
  9. Arqub, O.A.: Numerical simulation of time-fractional partial differential equations arising in fluid flows via reproducing Kernel method. Int. J. Numer. Methods Heat Fluid Flow 30, 4711-4733 (2020)
  10. Kumar, D., Seadawy, A.R., Joardar, A.K.: Modified Kudryashov method via new exact solutions for some conformable fractional differential equations arising in mathematical biology. Chin. J. Phys. 56, 75-85 (2018)
  11. Khan, H., Ahmed, S., Alzabut, J., Azar, A.T.: A generalized coupled system of fractional differential equations with application to finite time sliding mode control for leukemia therapy. Chaos Solitons Fractals 174, 113901 (2023)
  12. Fall, A.N., Ndiaye, S.N., Sene, N.: Black-Scholes option pricing equations described by the Caputo generalized fractional derivative. Chaos Solitons Fractals 125, 108-118 (2019)
  13. Roul, P.: A high accuracy numerical method and its convergence for time-fractional Black-Scholes equation governing European options. Appl. Numer. Math. 151, 472-493 (2020)
  14. Nuugulu, S.M., Gideon, F., Patidar, K.C.: A robust numerical scheme for a time-fractional Black-Scholes partial differential equation describing stock exchange dynamics. Chaos Solitons Fractals 145, 110753 (2021)
  15. Zhang, H.M., Zhang, M.C., Liu, F.W., Shen, M.: Review of the fractional Black-Scholes equations and their solution techniques. Fractal Fract. 8, 101 (2024)
  16. Black, F., Scholes, M.: The pricing of options and corporate liabilities. J. Polit. Econ. 81, 637-654 (1973)
  17. Merton, R.C.: Theory of rational option pricing. Bell J. Econ. Manag. Sci. 4, 141-183 (1973)
  18. Jumarie, G.: Stock exchange fractional dynamics defined as fractional exponential growth driven by (usual) Gaussian white noise. Application to fractional Black-Scholes equations. Insur. Math. Econ. 42, 271-287 (2008)
  19. Jumarie, G.: Derivation and solutions of some fractional Black Scholes equations in coarse-grained space and time. Application to Merton’s optimal portfolio. Comput. Math. Appl. 59, 1142-1164 (2010)
  20. Chen, W.T., Xu, X., Zhu, S.P.: Analytically pricing double barrier options based on a time-fractional Black-Scholes equation. Comput. Math. Appl. 69, 1407-1419 (2015)
  21. Roul, P., Goura, V.M.K.P.: A compact finite difference scheme for fractional Black-Scholes option pricing model. Appl. Numer. Math. 166, 40-60 (2021)
  22. Caputo, M., Fabrizio, M.: A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 1, 73-85 (2015)
  23. Atangana, A., Alqahtani, R.T.: Numerical approximation of the space-time Caputo-Fabrizio fractional derivative and application to groundwater pollution equation. Adv. Differ. Equ. 2016, 156 (2016)
  24. Djida, J.D., Atangana, A.: More generalized groundwater model with space-time Caputo-Fabrizio fractional differentiation. Numer. Methods Partial Differ. Equ. 33, 1616-1627 (2017)
  25. Firoozjaee, M.A., Jafari, H., Lia, A., Baleanu, D.: Numerical approach of Fokker-Planck equation with Caputo-Fabrizio fractional derivative using Ritz approximation. J. Comput. Appl. Math. 339, 367-373 (2018)
  26. Rubbab, Q., Nazeer, M., Ahmad, F., Chu, Y.M., Khan, M.I., Kadry, S.: Numerical simulation of advection-diffusion equation with Caputo-Fabrizio time fractional derivative in cylindrical domains: applications of pseudo-spectral collocation method. Alex. Eng. J. 60, 1731-1738 (2021)
  27. Nieto, J.J.: Solution of a fractional logistic ordinary differential equation. Appl. Math. Lett. 123, 107568 (2022)
  28. Kebede, S.G., Lakoud, A.G.: Analysis of mathematical model involving nonlinear systems of Caputo-Fabrizio fractional differential equation. Bound. Value Probl. 2023, 44 (2023)
  29. Souigat, A., Korichi, Z., Meftah, M.T.: Solution of the fractional diffusion equation by using Caputo-Fabrizio derivative: application to intrinsic arsenic diffusion in germanium. Rev. Mex. Fis. 70, 010501 (2024)
  30. Hussein, M.A.: Using the Elzaki decomposition method to solve nonlinear fractional differential equations with the Caputo-Fabrizio fractional operator. Baghdad Sci. J. 21, 1044-1054 (2024)
  31. Amin, M., Abbas, M., Iqbal, M.K., Baleanu, D.: Non-polynomial quintic spline for numerical solution of fourth-order time fractional partial differential equations. Adv. Differ. Equ. 2019, 183 (2019)
  32. Amin, M., Abbas, M., Iqbal, M.K., Ismail, A.I.M., Baleanu, D.: A fourth order non-polynomial quintic spline collocation technique for solving time fractional superdiffusion equations. Adv. Differ. Equ. 2019, 514 (2019)
  33. Amin, M., Abbas, M., Iqbal, M.K., Baleanu, D.: Numerical treatment of time-fractional Klein-Gordon equation using redefined extended cubic B-spline functions. Front. Phys. 8, 288 (2020)
  34. Amin, M., Abbas, M., Baleanu, D., Iqbal, M.K., Riaz, M.B.: Redefined extended cubic B-spline functions for numerical solution of time-fractional telegraph equation. Comput. Model. Eng. Sci. 127, 361-384 (2021)
  35. Mesgarani, H., Aghdam, Y.E., Khoshkhahtinat, M., Farnam, B.: Analysis of the numerical scheme of the one-dimensional fractional Rayleigh-Stokes model arising in a heated generalized problem. AIP Adv. 13, 085024 (2023)
  36. Aghdam, Y.E., Mesgarani, H., Asadi, Z., Nguyen, V.T.: Investigation and analysis of the numerical approach to solve the multi-term time-fractional advection-diffusion model. AIMS Math. 8, 29474-29489 (2023)
  37. Aghdam, Y.E., Mesgarani, H., Asadi, Z.: Estimate of the fractional advection-diffusion equation with a time-fractional term based on the shifted Legendre polynomials. J. Math. Model. 11, 731-744 (2023)
  38. Haq, S., Hussain, M.: Selection of shape parameter in radial basis functions for solution of time-fractional Black-Scholes models. Appl. Math. Comput. 335, 248-263 (2018)
  39. Golbabai, A., Nikan, O., Nikazad, T.: Numerical analysis of time fractional Black-Scholes European option pricing model arising in financial market. Comput. Appl. Math. 38, 1-24 (2019)
  40. Fadugba, S.E.: Homotopy analysis method and its applications in the valuation of European call options with time-fractional Black-Scholes equation. Chaos Solitons Fractals 141, 110351 (2020)
  41. Golbabai, A., Nikan, O.: A computational method based on the moving least-squares approach for pricing double barrier options in a time-fractional Black-Scholes model. Comput. Econ. 55, 119-141 (2020)
  42. An, X.Y., Liu, F.W., Zheng, M.L., Anh, V.V., Turner, I.W.: A space-time spectral method for time-fractional Black-Scholes equation. Appl. Numer. Math. 165, 152-166 (2021)
  43. Taghipour, M., Aminikhah, H.: A spectral collocation method based on fractional Pell functions for solving time-fractional Black-Scholes option pricing model. Chaos Solitons Fractals 163, 112571 (2022)
  44. Kazmi, K.: A second order numerical method for the time-fractional Black-Scholes European option pricing model. J. Comput. Appl. Math. 418, 114647 (2023)
  45. Aghdam, Y.E., Mesgarani, H., Amin, A., Gómez-Aguilar, J.F.: An efficient numerical scheme to approach the time fractional Black-Scholes model using orthogonal Gegenbauer polynomials. Comput. Econ. 64, 211-224 (2024)
  46. Sun, Z.Z.: Compact difference scheme for heat equation with Neumann boundary conditions. Numer. Methods Partial Differ. Equ. 25, 1320-1341 (2009)
  47. Shi, J.K., Chen, M.H.: A second-order accurate scheme for two-dimensional space fractional diffusion equations with time Caputo-Fabrizio fractional derivative. Appl. Numer. Math. 151, 246-262 (2020)
  48. Akram, T., Abbas, M., Abualnaja, K.M., Iqbal, A., Majeed, A.: An efficient numerical technique based on the extended cubic B-spline functions for solving time fractional Black-Scholes model. Eng. Comput. 38, 1705-1716 (2022)
  49. Mesgarani, H., Ahanj, S., Aghdam, Y.E.: Numerical investigation of the time-fractional Black-Scholes equation with barrier choice of regulating European option. J. Math. Model. 10, 1-10 (2022)
  50. Abdi, N., Aminikhah, H., Sheikhani, A.H.R.: High-order compact finite difference schemes for the time-fractional Black-Scholes model governing European options. Chaos Solitons Fractals 162, 112423 (2022)

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.