أساس عصبي فسيولوجي لتخطيط الدماغ الكهربائي غير الدوري والاتجاه الطيفي الخلفي A neurophysiological basis for aperiodic EEG and the background spectral trend

المجلة: Nature Communications، المجلد: 15، العدد: 1
DOI: https://doi.org/10.1038/s41467-024-45922-8
PMID: https://pubmed.ncbi.nlm.nih.gov/38374047
تاريخ النشر: 2024-02-19

أساس عصبي فسيولوجي لتخطيط الدماغ الكهربائي غير الدوري والاتجاه الطيفي الخلفي

تاريخ الاستلام: 6 سبتمبر 2023
تم القبول: 6 فبراير 2024
نُشر على الإنترنت: 19 فبراير 2024
(د) التحقق من التحديثات

نيكلاس براك © فلافي دوك ألكسندر روكوس © فرانسيس أرسينو شيفا شاهيري © أنمار خضر (1) وجيل بلورد (1)

تظهر تخطيط الدماغ الكهربائي (EEGs) مزيجًا من التذبذبات الإيقاعية والعريضة النطاق، حيث تظهر الأخيرة كـ الاتجاه الطيفي. بينما من المعروف أن تذبذبات الشبكة تولد تخطيط دماغي كهربائي إيقاعي، لا يزال الأساس العصبي لتخطيط الدماغ الكهربائي العريض النطاق غير مفسر. هنا، نستخدم النمذجة الفيزيائية الحيوية لإظهار أن النشاط العصبي غير الدوري يمكن أن يولد إمكانيات قابلة للاكتشاف على فروة الرأس ويشكل ميزات تخطيط الدماغ الكهربائي العريض النطاق، ولكن هذه الإشارات غير الدورية لا تؤثر بشكل كبير على قياس إيقاع الدماغ. أظهر تحليل النموذج الإضافي أن إشارات تخطيط الدماغ الكهربائي الإيقاعي تتعرض للتشويه بشكل عميق بسبب التغيرات في خصائص المشابك. لفحص هذا السيناريو، قمنا بتسجيل تخطيط الدماغ الكهربائي لموضوعات بشرية تم إعطاؤها بروبوفول، وهو مخدر عام وناهض لمستقبلات GABA. تسبب إعطاء الدواء في تغييرات في تخطيط الدماغ الكهربائي العريض النطاق التي تطابقت كميًا مع التأثيرات المعروفة للبروبوفول على مستقبلات GABA. استخدمنا نموذجنا لتصحيح هذه التغييرات العريضة المربكة، مما كشف أن قوة دلتا، بشكل فريد، زادت خلال ثوانٍ من فقدان الأفراد للوعي. بشكل عام، يوضح هذا العمل كيف تتشكل إشارات تخطيط الدماغ الكهربائي بواسطة عوامل فيزيولوجية عصبية بخلاف إيقاعات الدماغ ويبين كيف يمكن أن تقوض هذه الإشارات التفسير التقليدي لتخطيط الدماغ الكهربائي.
تظهر تخطيط الدماغ الكهربائي (EEGs) مزيجًا من التذبذبات الدورية وغير الدورية. لقد أثبتت أبحاث تقارب القرن من الزمن أن إشارات EEG الدورية تتولد عن تذبذبات عصبية متزامنة. . على النقيض من ذلك، تظل إشارات EEG غير الدورية غير مفهومة بشكل نسبي. بينما تنتج إشارات EEG الدورية قممًا في طيف القدرة، يظهر المكون غير الدوري كالاتجاه الطيفي الخلفي الذي يتلاشى بشكل واضح سلوك اختلافات في الأس exponent الطيفي، لقد تم ربطها بالشيخوخة، والأداء المعرفي، والاضطرابات العصبية، والتخدير، والنوم بالإضافة إلى كونه علامة حيوية مفيدة، تم اقتراح أن اتجاه الطيف الكهربائي للدماغ قد يتغير بشكل مستقل عن التذبذبات العصبية وأن إزالة الاتجاه الطيفي ضرورية لتحديد الفروق بدقة في إيقاعات الدماغ. لذا فإن فك شفرة الأساس العصبي الفسيولوجي لـ EEG غير الدوري ضروري لتفسير مؤشرات EEG بشكل صحيح ولتحسين الخوارزميات التي تقيس إيقاعات الدماغ.
توجد فرضيتان رئيسيتان حول كيفية توليد الاتجاه الطيفي لتخطيط الدماغ الكهربائي (EEG) بواسطة الدماغ. تتنبأ فرضية مقياس الزمن المشبكي بأن الاتجاه الطيفي لتخطيط الدماغ الكهربائي هو نتيجة طبيعية للتيارات المشبكية المتناقصة بشكل أسي، وبالتالي فإن النشاط الشبكي غير المتزامن سينتج طيفًا بـ أو “الاتجاه اللورنتزي” الفرضية الثانية تستند إلى نظرية الحرج الذاتي التنظيم التي تفترض أن انتشار إمكانيات العمل عبر الشبكات العصبية ينتج ما يسمى بـ “الانهيارات” من النشاط مع مقادير تتبع توزيع لقد تم الافتراض أن مثل هذه الديناميات الانهيارية بدورها تولد اتجاه في تختلف هذه النظريات في جانبين مهمين. أولاً، تفترض فرضية الانهيار الثلجي أن الاتجاه في طيف EEG يحمل معلومات عن ديناميات الدماغ، بينما فرضية الأوقات المشبكية غير متحيزة. ثانياً، تقترح النظريتان أشكالاً مختلفة للاتجاه الطيفي وبالتالي تقترحان طرقاً مميزة لإزالة الاتجاه من طيف EEG. .
على الرغم من هذه الفرضيات، فإن مفهوم تخطيط الدماغ غير الدوري نفسه لا يزال مثيرًا للجدل. يجادل البعض بأن الاتجاه الظاهر في طيف تخطيط الدماغ هو ظاهرة ثانوية ناتجة عن إيقاعات الدماغ الأبطأ التي تستقطب مجموعات أكبر من الخلايا العصبية. وفقًا لهذا الرأي، فإن طيف تخطيط الدماغ الكهربائي لا يتطلب إزالة الاتجاه، ومؤشر الطيف هو مقياس مختلط لمختلف التغيرات في إيقاعات الدماغ.
لذا تبقى ثلاثة أسئلة مفتوحة: (1) هل يمكن أن تعكس إشارات تخطيط الدماغ الكهربائي النشاط العصبي غير المنتظم؟ (2) إذا كان الأمر كذلك، كيف تشكل هذه الإشارات طيف تخطيط الدماغ الكهربائي؟ (3) هل تحتاج أطياف تخطيط الدماغ الكهربائي إلى إزالة الاتجاه، وإذا كان الأمر كذلك، ما هي الطريقة الأكثر دلالة من الناحية الفسيولوجية لإزالة الاتجاه؟ للتحقيق في هذه الأسئلة، قمنا بدمج النمذجة العددية للأمكانيات السطحية مع الحسابات الفيزيائية الحيوية للثنائيات العصبية الفردية. باستخدام هذا النهج، قمنا بمحاكاة إشارات EEG البيوفيزيائية الواقعية التي تم إنشاؤها بواسطة شبكات تظهر مجموعة من الديناميكيات. كشفت هذه المحاكاة عن عدة آليات، بالإضافة إلى إيقاعات الدماغ، التي تؤثر على إشارات EEG وتشكل معًا الاتجاه الطيفي. لاختبار توقعات النموذج، قمنا بتسجيل EEG للأشخاص الذين يتلقون حقنة من دواء البروبوفل، وهو مخدر عام يستهدف مستقبلات GABA ويبطئ زمن تلاشي التيارات المشبكية المثبطة. حددت هذه التجارب تغييرات محددة في تخطيط الدماغ الكهربائي (EEG) خلال إعطاء البروبوفل، والتي كان من المتوقع أن تؤثر على تقديرات إيقاعات الدماغ. باستخدام رؤى نمذجة لدينا، قمنا بتصحيح هذه المصادر من التلوث وأعدنا تقييم التوقيعات المعروفة لتخطيط الدماغ الكهربائي لفقدان الوعي. بشكل عام، تطور هذه الدراسة نظرية قائمة على الأسس البيوفيزيائية تصف الأساس العصبي للإمكانات القشرية غير الدورية وتقدم استنتاجات عملية لتحليل الطيف لبيانات تخطيط الدماغ الكهربائي.

النتائج

لا يمكن لتخطيط الدماغ الكهربائي أن يعكس النشاط العصبي غير المتزامن

لفهم علم الأعصاب الفيزيولوجي الذي يكمن وراء اتجاه طيف EEG، بدأنا بالتحقيق في خصائص توليد EEG على مستوى الخلية العصبية الفردية. هذه الخصائص مفيدة لأنها تشكل EEG الجماعي بغض النظر عن التماسك أو التزامن العصبي.
(انظر التعريفات والإطار النظري في الطرق). لفحص هذه الخصائص، قمنا بإجراء محاكاة لنماذج الخلايا العصبية المفصلة من الناحية البيوفيزيائية والشكلية (الشكل 1أ). في البداية، لم نفترض أي ديناميات للخلايا العصبية السابقة المشبكية، وبالتالي قمنا بنمذجة المدخلات المشبكية باستخدام سلاسل نبضات بواسون المستقلة (الشكل 1أ)، وهو افتراض سنقوم بتخفيفه لاحقًا. من هذه التيارات، تم حساب ثنائي القطب لخلايا عصبية مفردة. (الشكل 1ب). تم وضع الخلية العصبية في موقع عشوائي في القشرة وتم حساب إشارة EEG للخلية العصبية الواحدة باستخدام نموذج رأس نيويورك (الشكل 1ج). تم تكرار هذه العملية بالكامل عدة مرات مع أشكال مختلفة تمثل الخلايا العصبية (الجدول S1) ومع وضع الخلايا العصبية في مواقع مختلفة في القشرة. الطيف المتوسط، الذي سنشير إليه بالطيف الوحدوي، هو الطيف المتوقع لتخطيط الدماغ الكهربائي الناتج عن خلية عصبية قشرية متوسطة واحدة (الشكل 1د).
عرض الطيف الوحدوي ميزتين هامتين. أولاً، حتى مع المدخلات المشبكية العشوائية، أظهر الطيف الوحدوي اتجاهًا. يمكن وصف هذا الاتجاه بأنه مجموع دالتين لورنتزيتين.
كما تنبأت النماذج الخطية البسيطة لتوليد EEG (الشكل 1د). الأبطأ ( ) وأسرع ( كانت الأطر الزمنية محكومة بحركيات إلغاء تنشيط مستقبلات GABA (GABARs) ومُستقبلات AMPA (AMPARs)، على التوالي (الشكل 1e، f). تؤكد هذه المحاكاة التوقعات السابقة بأن المساهمة النسبية للتيارات المثيرة والمثبطة في إشارة EEG تؤثر بشكل أساسي على الاتجاه الطيفي. .
ثانيًا، يعكس الطيف الموحد السعة التي يساهم بها متوسط الخلايا العصبية في إشارة EEG. للتحقيق في هذه الفكرة بمزيد من التفصيل، قمنا بدراسة تأثير تغيير جميع معلمات النموذج ضمن نطاقات فسيولوجية معقولة (الشكل 1g). أظهر قياس القدرة المتوسطة لإشارات EEG الناتجة من خلية عصبية واحدة
الشكل 1 | لا يمكن لتخطيط الدماغ الكهربائي أن يعكس النشاط العصبي غير المتزامن. أ مثال على شكل طبقة الخلايا العصبية الهرمية. تم محاكاة المدخلات عند مشابك AMPAR (بالأحمر) و GABAR (بالأزرق) باستخدام سلاسل نبضات بواسون، كما هو موضح في الرسم البياني. تم عرض 1000 مشبك فقط من أجل الوضوح. تم تعديل شكل الخلية العصبية من Budd، J. M. L. وآخرون. تتاجر أشجار المحاور القشرية في الحفاظ على المواد وتأخير التوصيل. PLoS Comput. Biol. 6، e1000711 (2010). ب. تم حساب مكونات x و y و z من متجه ثنائي القطب لخلية عصبية واحدة، محسوبة من (أ). ج. اليسار: تم محاكاة إشارات EEG لخلية عصبية واحدة في موقع القطب المحدد، مع وجود الخلية العصبية في مواقع مصدر مختلفة، مثل الموقع A و B. اليمين: طيف EEG المتوسط الموقع (بالأسود) المحسوب عن طريق المتوسط على مواقع المصدر الموضحة بالنقاط السوداء على نموذج الدماغ. Loc.=الموقع؛ Avg.=المتوسط. د. تم توليد الطيف المتوسط الموقع من 1000 محاكاة لـ 11 شكلًا تمثيليًا للخلية العصبية (الجدول S1). تم ملاءمة الطيف بواسطة المعادلة 1 ومكونان لورنتزيان موضحان بخطوط حمراء متقطعة. تم حساب الطيف الأحادي أثناء تغيير
ديناميات إلغاء تنشيط GABARs ( ) وتم تقدير المعامل خط أحمر له ميل 1. ف. نفس الشيء كما في e، ولكن يظهر كدالة لديناميات إلغاء تنشيط AMPARs . ج. توزيعات العينة لمعاملات النموذج. ، و تمثل معدل الإدخال المتوسط، وثابت زمن إلغاء التنشيط، وأقصى توصيل لمشابك AMPAR. ، و تمثل نفس المعاملات لمشابك GABAR. و تمثل الجهد العكسي وتوصيل تيار تسرب الغشاء الساكن. توزيع قوة EEG لخلية عصبية واحدة (متوسط الموقع كما في ج) بناءً على 20000 محاكاة مع معاملات مأخوذة من التوزيعات الموضحة في (ج) وأشكال مأخوذة كما هو موضح في الجدول S1. أنا. الأسود: الطيف الوسيط لـ EEG عبر 14 موضوعًا، مع نطاقات خطأ تشير إلى الحد الأدنى والحد الأقصى لكثافة الطيف. الرمادي: الطيف المتوقع لـ EEG من 16 مليار خلية عصبية غير مترابطة تتلقى إدخال مشبكي بواسوني (رمادي)، مع قيم معاملات مأخوذة من التوزيعات في (ج). تعكس نطاقات الخطأ نطاق الكوانتيل من 5-95%.
الشكل 2 | تتطلب إشارات EEG القابلة للاكتشاف فقط ثنائيات قطبية ضعيفة ومتزامنة محليًا. أ. مخطط يعرض نواة الربط المستخدمة لربط ثنائيات قطبية لخلية عصبية واحدة. النواة هي دالة غاوسية بحد أقصى من و تباين الطيف الوسيط لـ EEG عبر 14 موضوعًا بشريًا (رمادي؛ نفس نطاقات الخطأ كما في الشكل 1i)، والطيف الأحادي المحاكى (أسود؛ نفس الشكل 1d) مقاس بمقادير تعسفية لتحديد حد أدنى وحد أقصى لسعة اتجاه الطيف. ج. خريطة حرارية للقوة الإجمالية لـ EEG المحاكية الناتجة عن 16 مليار خلية عصبية مع ثنائيات قطبية مرتبطة بالنواة في (أ)، ومعاملات مختلفة من و . الخطوط السوداء هي منحنيات المستوى التي تمثل الحدود الدنيا والعليا لسعة الاتجاه الطيفي التي تم الحصول عليها في (ب).
مجموعة من السعات الممكنة لمساهمة الخلايا العصبية الفردية في إشارة EEG (الشكل 1h). تظهر هذه المحاكاة أنه لا يمكن لأي معاملات فسيولوجية معقولة أن تسمح لـ 16 مليار خلية عصبية غير مترابطة بتوليد إشارات EEG قابلة للاكتشاف (الشكل 1i). والأهم من ذلك، أن هذه الحسابات تحدد مدى بعد قشرة غير متزامنة تمامًا عن توليد إشارات EEG قابلة للاكتشاف. تأخذ هذه الحسابات في الاعتبار قوة EEG التي تساهم بها سعات التيار المشبكي، هندسة الخلايا العصبية، معدل إطلاق النار المتوسط للخلايا العصبية، عدد الخلايا العصبية، توصيل الأنسجة المختلفة، وهندسة القشرة. لذلك، تشير هذه النتيجة إلى أن الديناميات العصبية مسؤولة عن الفرق التقريبي بأربعة أوامر من حيث الحجم بين الطيف غير المتزامن المحاكى وسجلات EEG الحقيقية.

تتطلب EEG القابلة للاكتشاف فقط ثنائيات قطبية ضعيفة ومتزامنة محليًا

إذا كانت سعة إشارات EEG تمنع النشاط غير المتزامن من تشكيل أطياف EEG، فما أنواع النشاط غير الإيقاعي التي يمكن أن تؤثر على إشارات EEG؟ للبدء في معالجة هذا السؤال، قمنا أولاً بتحديد بشكل عام مقدار ارتباط الثنائيات القطبية المطلوب لتوليد إشارات EEG قابلة للاكتشاف. للقيام بذلك، فرضنا تنظيمًا مكانيًا مبسطًا على نموذج قشري حيث تنتج الخلايا العصبية المجاورة ثنائيات قطبية مرتبطة. على وجه التحديد، كانت ثنائيات قطبية للخلايا العصبية المفصولة بمقدار ملم مرتبطة بمعامل ، حيث هو أقصى ارتباط ثنائي القطب و هو المقياس المكاني الذي تتناقص عنده الارتباطات (الشكل 2أ). بناءً على هذا المخطط الارتباطي، وهندسة القشرة، وكثافات الخلايا العصبية المتوسطة، وسعات EEG لخلية عصبية واحدة من القسم السابق، قدرنا قوة إشارة EEG الجماعية التي سيتم إنتاجها بقيم مختلفة من و (انظر الطرق). لالتقاط الاتجاه الطيفي لـ EEG، قدرنا أن إشارات EEG العريضة تحتاج إلى أن يكون لها قوة إجمالية تتراوح بين 50 و (الشكل 2ب). وبالتالي، لكي تولد النشاط العصبي إشارات EEG قابلة للاكتشاف، يجب أن يكون هذا النشاط قادرًا على دفع ثنائيات قطبية لخلية عصبية واحدة مرتبطة حتى قيمة ( ) من (الشكل 1ج)، مع افتراض نطاق ليبرالي لـ من (الشكل 1ج؛ انظر الطرق). بينما تثبت وجود إيقاعات EEG أن التذبذبات العصبية يمكن أن تولد الثنائيات القطبية المطلوبة
التزامن، لا يزال يتعين تحديد ما إذا كان وكيف يمكن تحقيق مثل هذا الدرجة من تماسك الثنائيات القطبية بواسطة النشاط العصبي غير الإيقاعي.

توبولوجيا المشبك كافية لارتباطات الثنائيات القطبية

للتحقيق في قدرة النشاط العصبي على توليد ثنائيات قطبية متماسكة، قمنا بمحاكاة أزواج من الخلايا العصبية وحققنا في مستوى الارتباط القابل للتحقيق بين ثنائيات قطبية لخلية عصبية واحدة. في محاكاة لدينا، لاحظنا أنه إذا تم تنشيط مشبك واحد، يمكن التنبؤ بدقة بتوجه الثنائي القطب الناتج من توجه المشبك بالنسبة للجسم الخلوي (الشكل 3أ، ب). كانت هذه النتيجة صحيحة عبر جميع أشكال الخلايا العصبية التي تم التحقيق فيها (الشكل S1). من هذه الملاحظة، وضعنا نموذجًا بسيطًا لتماسك الثنائي القطب. لتوليد الإدخال المشبكي، قمنا بإسقاط مشابك خليتين عصبيتين على كرة وارتبطنا مدخلات المشابك ذات المسافات الزاوية القريبة (الشكل 3ج). من خلال تغيير أقصى ارتباط بين المشابك، يمكن ضبط ارتباط الثنائي القطب بين خلايا عصبية بأشكال مختلفة بشكل مستمر بين 0 و (الشكل 3د، هـ). أدى خلط موقع المشابك إلى إلغاء أي ارتباط ثنائي القطب (الشكل 3د). تظهر هذه النتائج أنه لتوليد إشارات EEG قابلة للاكتشاف، من الضروري والكافي أن يظهر الإدخال المشبكي ارتباطًا زمنيًا ومكانيًا. هذه الشروط لا تمنع بحد ذاتها أي نوع محدد من الديناميات العصبية. في الواقع، اعتمد هذا النموذج البسيط على نبضات مأخوذة بشكل مستقل في كل نقطة زمنية وبالتالي أنتج إشارات EEG بدون ارتباط زمني ذاتي وطيف بنفس شكل الطيف الأحادي غير المتزامن (الشكل 3و). لذلك، تعتمد إمكانية إشارات EEG غير الدورية فقط على قدرة شبكة من الخلايا العصبية على توليد نشاط غير إيقاعي بمستويات الارتباط الزمني والمكاني المطلوبة.

يمكن للشبكات تحت الحرجة توليد إشارات EEG غير دورية

بعد ذلك، تحققنا من نماذج الشبكات التي يمكن أن تولد إشارات EEG قابلة للاكتشاف وغير دورية. لتحديد ما إذا كان يمكن للنشاط الشبكي إنتاج ثنائيات قطبية متماسكة، استخدمنا النتائج من القسم السابق (الشكل 3). بعد محاكاة مجموعة من الخلايا العصبية السابقة، استخدمنا خوارزمية UMAP لإدماج المجموعة على كرة بطريقة تقلل المسافة بين الخلايا العصبية السابقة ذات النشاط النبضي المرتبط (الشكل 4أ). ثم تم إسقاط هذه الخلايا العصبية السابقة على الشجيرات الخاصة بالزوج ما بعد المشبكي (الشكل 4أ). من خلال البناء، يجب أن تكون المشابك ذات الارتباطات الأعلى ذات مسافات زاوية أصغر، وبالتالي تحسين تماسك الثنائي القطب. بشكل فعال، تختبر هذه العملية ما إذا كان من الممكن هندسيًا لشبكة توليد إدخال مشبكي متماسك بما فيه الكفاية لتوليد EEG.
لفهم آليات توليد تخطيط الدماغ غير الدوري، حاولنا بناء أبسط شبكة يمكن أن تولد تماسك ثنائي القطب. تظهر نتائجنا السابقة أن الشبكات المتصلة عشوائيًا لا يمكنها توليد أقطاب متماسكة، لأنها لا تستطيع إنتاج نشاط مكاني مترابط. لذلك، استمررنا في استخدام أبسط شبكة عصبية تظهر طوبولوجيا مكانية، وهي شبكة مكانية. لبناء الشبكة، تم تضمين كل خلية عصبية في مستوى وتم ربطها بشكل تفضيلي بالخلايا العصبية القريبة (الشكل 4ب). من أجل البساطة، قمنا بنمذجة الخلايا العصبية الفردية كعقد ثنائية، أي أن كل خلية عصبية كانت إما تنفجر أو هادئة. انتشرت النبضات على طول اتصالات الشبكة، مما تسبب في إطلاق الخلايا العصبية التالية مع بعض الاحتمالية (الشكل 4ب). يقع هذا النموذج البسيط ضمن فئة الشبكة المتفرعة، لأن الديناميات تحكمها معلمة واحدة تُسمى عدد التفرع، والذي يُشار إليه بـ ، الذي يعكس متوسط عدد النبضات التي تم استثارتها بنجاح عبر الشبكة عندما يطلق خلية عصبية واحدة.
كشفت محاكياتنا أن أقصى ارتباط ثنائي القطب يمكن تحقيقه زاد مع عدد تفرعات الشبكة (الشكل 4c، d). شبكة غير متزامنة بالكامل ( ) كان غير قادر بشكل غير مفاجئ على توليد علاقات بين ثنائيات الخلايا العصبية الفردية (الشكل 4d). من ناحية أخرى، كانت الشبكة تحت الحرجة قليلاً ( كان قادرًا على
الشكل 3 | نموذج بسيط لارتباط ثنائي القطب يلتقط سعة EEG واسعة النطاق ولكن ليس القدرة الترددية المنخفضة. أ تم تنشيط مشبك واحد في الموقع المحدد بالسهم الأزرق، مما أدى إلى توليد استجابة في ثنائي القطب لخلية عصبية واحدة، . يتم توجيه متجه ثنائي القطب في ذروة الاستجابة نحو موقع المشبك، المحدد في الإحداثيات الكروية مع جسم الخلية كنقطة الأصل. تم تعديل شكل الخلايا العصبية من Budd، J. M. L. وآخرون. تتاجر أشجار المحاور القشرية الجديدة بالحفاظ على المواد وتأخير التوصيل. PLoS Comput. Biol. 6، e1000711 (2010). ب تم تكرار المحاكاة في (أ) 600 مرة مع أشكال خلايا عصبية ومواقع مشابك مختلفة. يُظهر رسم متجه الثنائي القطب في ذروة الاستجابة مقابل موقع المشبك المحفز علاقة قوية وخطية. بعض النقاط لم تُرسم من أجل الوضوح. حجم النقطة يتناسب مع سعة الثنائي القطب في الذروة. rel.=نسبي. ج مخطط يوضح النموذج الأدنى لتوافق الثنائي القطب. تم إسقاط المشابك على كل خلية عصبية ما بعد المشبك في الزوج على كرة. ثم تم تعريف مصفوفة التوافق بين جميع المشابك.
بحيث تكون المشابك العصبية مفصولة بزاوية على الكرة كانت مرتبطة بـ . تم تعديل شكل الخلية العصبية اليسرى من Budd، J. M. L. وآخرون. توازن بين الحفاظ على المواد وتأخير التوصيل في أشجار المحاور القشرية الجديدة. PLoS Comput. Biol. 6، e1000711 (2010). تم تعديل توضيح الخلية العصبية اليمنى، بإذن من SNCSC، من Mainen، Z. F. و Sejnowski، T. J. تأثير الهيكل الشجيري على نمط الإطلاق في نماذج الخلايا العصبية القشرية الجديدة. Nature 382، 363-366 (1996)، Springer Nature. د مثال على إشارات EEG لخلية عصبية واحدة من الخلايا العصبية المذكورة في (ج). هـ الارتباط بين ثنائي القطب لخلية عصبية واحدة كدالة لـ تمثل الخطوط العمودية فترات الثقة للمتوسط عندما يتم خلط مواقع المشابك، لم تعد الأقطاب مرتبطة (رمادي). طيف الوحدة للخلايا العصبية التي تتلقى المدخلات المحسوبة باستخدام النموذج الأدنى (أسود)، مقاس لمقارنة شكل الطيف مع الطيف المتوسط لتخطيط الدماغ الكهربائي لـ 14 موضوعًا (خط رمادي؛ نفس الشكل 1i).
توليد ثنائيات كانت مرتبطة بـ لزوجة متوسطة من الخلايا العصبية ما بعد المشبك (المتوسط SE، ؛ الأشكال المأخوذة كما هو موضح في الجدول S1؛ المعلمات الفيزيائية الحيوية المأخوذة كما في الشكل 1g). هذا العدد من التفرعات مهم لأن الأعمال السابقة وجدت أن الشبكات التي تحتوي على عدد تفرعات من تمت إعادة إنتاج الديناميات الحية لنبضات القشرة بشكل وثيق عبر العديد من الأنواع المختلفة ، مما يجعل هذه قيمة معلمة قابلة للتطبيق من الناحية الفسيولوجية. أدى وضع عدم كفاءة المشابك إلى انخفاض نسبي في ارتباط ثنائي القطب، مما كشف أن الديناميات دون الحرجة لا تزال قادرة على دفع ثنائيات القطب المتماسكة مع وضع مشابك غير مثالي (الشكل 4e). استنادًا إلى سعة الطيف الأحادي المحسوب (الشكل 4f)، قدرنا أن نشاط الشبكة دون الحرجة يمكن أن ينتج سعات EEG واقعية مع كفاءة مشابك منخفضة تصل إلى (الشكل 4 ج؛ انظر الطرق). كمرجع، مؤشر الأمثلية لـ يعني أن المشابك المرتبطة بقوة ستقع في المتوسط على نفس نصف الكرة من خلاياها العصبية المعنية، وهو هندسة تذكر بتقسيم القمة والقاعدة في خلايا الهرم العصبية القشرية.
من الجدير بالذكر أن الارتباطات القوية للثنائيات تزامنت مع الارتباطات الزمنية الأطول في نشاط الشبكة (الشكل 4f)، وهو ظاهرة ناتجة مباشرة عن سببية انتشار النبضات (الشكل 4b). وهذا يعني أن إشارات EEG الناتجة عن انتشار النبضات القشرية يجب أن تكون لها طاقة أعلى عند الترددات المنخفضة إذا كانت الإشارات لتكون ذات سعات قابلة للاكتشاف. توضح هذه النتيجة قيدًا أساسيًا قد يفسر جزئيًا توسيع طيف EEG عند مستويات أدنى
تظهر هذه النتائج بشكل أوسع آلية بيولوجية فيزيائية قابلة للتطبيق تسمح للنشاط العصبي غير المنتظم بتوليد إشارات EEG، وبالتالي التأثير على الميزات العريضة لطيف EEG.
يمكن أن تؤدي التغيرات في تخطيط الدماغ الكهربائي ذو النطاق الضيق إلى نشاط غير منتظم. تُظهر الحسابات أعلاه أن النشاط العصبي غير المنتظم يمكن أن يولد نظريًا إشارات تخطيط دماغ كهربائي عريضة النطاق، مما يعني أن قوة تخطيط الدماغ الكهربائي ذو النطاق الضيق لا تحتاج بالضرورة إلى أن تعكس إيقاعات الدماغ. لذلك، تساءلنا عما إذا كانت إشارات تخطيط الدماغ الكهربائي التي تنتج عن النشاط غير المنتظم يمكن أن تخلط بين التفسير التقليدي لتخطيط الدماغ الكهربائي، وهو أن التغيرات في قوة النطاق تعكس اختلافات في التذبذبات العصبية. لمعالجة هذا السؤال، اعتبرنا سيناريو حيث يتم توليد إشارة تخطيط الدماغ الكهربائي بواسطة مجموعتين فرعيتين من الخلايا العصبية: مجموعة تظهر تذبذبات متزامنة، ومجموعة ثانية تظهر ديناميات دون الحرجة. إذا كانت هذه المجموعات السكانية مستقلة تمامًا عن بعضها البعض، فإن مساهمات EEG الخاصة بها ستضاف معًا خطيًا حسب التعريف. للتحقيق بشكل أعمق، قمنا بمحاكاة السيناريو الذي يتم فيه خلط إشارات ما بعد المشبك من المجموعتين (الشكل 5a). يمكن أن يكون أحد تفسيرات هذا الإعداد هو أن خلية عصبية قشرية تتلقى مدخلات تذبذبية من، على سبيل المثال، المهاد، بينما تتلقى أيضًا مدخلات دون حرجة من الدوائر القشرية المحلية. بالمقارنة مع الخلايا العصبية التي تتلقى مدخلات تذبذبية بالكامل أو مدخلات دون حرجة بالكامل، أنتجت الخلية العصبية التي تتلقى مدخلات مختلطة طيف EEG موحدًا الذي
الشكل 4 | يمكن أن تفسر ديناميات الشبكة تحت الحرجة سعة وقوة التردد المنخفض لتخطيط الدماغ الكهربائي العريض النطاق. توضيح للخوارزمية المستخدمة لتحسين تماسك القطب. Nrn. = خلية عصبية. تم تعديل شكل الخلية العصبية اليسرى من Budd، J. M. L. وآخرون. تتاجر أشجار المحاور القشرية الجديدة بالحفاظ على المواد وتأخير التوصيل. PLoS Comput. Biol. 6، e1000711 (2010). تم تعديل توضيح الخلية العصبية اليمنى، بإذن من SNCSC، من Mainen، Z. F. و Sejnowski، T. J. تأثير الهيكل الشجيري على نمط الإطلاق في خلايا عصبية قشرية نموذجية. Nature 382، 363-366 (1996)، Springer Nature. ب توضيح للقواعد المستخدمة لإنتاج التزامن الزماني المكاني في شبكة قبل المشبك. القاعدة رقم 1: يتم فرض طوبولوجيا الشبكة من خلال جعل احتمال الاتصالات الثنائية، تنخفض بشكل أسي مع المسافة، القاعدة رقم 2: احتمال إطلاق العصبون، يعتمد على معدل إطلاق أساسي لـ بالإضافة إلى متوسط نشاط جيرانه مقاسًا بـ هو معدل إطلاق نار متوسط محدد مسبقًا؛ هو عدد التفرعات في الشبكة. corr.=الارتباط. c أمثلة على إشارات EEG لخلية عصبية واحدة من خليتين عصبيتين تتلقيان مدخلات من نموذج الشبكة مع عدد تفرعات
عندما تم تحسين مواقع المشابك كما هو موضح في (أ). أسفل: رسم بياني نقطي للإدخال المشبكي لخلية عصبية واحدة. د الارتباط بين ثنائي القطب لخلية عصبية واحدة كدالة لعدد التفرعات، ، من الشبكة السابقة المشبكية. تزداد ارتباطات ثنائي القطب مع (نقاط ملونة)، ولكن ليس عندما يتم خلط مواقع المشابك (رمادي). الوسيط (نقاط) ونطاق الكمية من 5-95% (خطوط عمودية) عبر تمت محاكاة أزواج مع أشكال تم اختيارها عشوائيًا (الجدول S1) وقيم معلمات بيولوجية فيزيائية تم اختيارها عشوائيًا (كما في الشكل 1g). يمكن ضبط ارتباط ثنائي القطب عن طريق وضع المشابك بشكل غير مثالي (انظر الطرق). يتم عرض الاستيفاء التكعيبي بين مؤشرات الأمثلية المحاكاة مع الخط الصلب. الوسيط (النقاط) و نطاق الكوانتيل (الخطوط العمودية) عبر محاكاة. طيف موحد تم حسابه لأعداد تفرع مختلفة. تعكس نطاقات الخطأ فترة الثقة للمتوسط. الطيف الموحد من (f) مقاس بناءً على مؤشر الأمثلية المشبكية 0.25 (الألوان كما في ). قيمة تم تحديده من وتم تحديد عامل القياس النهائي كما هو موضح في الشكل 2. الرمادي: الطيف الكهربائي للدماغ الوسيط لـ 14 موضوعًا (نفسه كما في الشكل 1i).
أظهرت ظاهرة مختلطة (الشكل 5ب). أدى زيادة قوة المدخلات المتذبذبة و/أو غير الدورية إلى تغيير سعة الذروة الطيفية و/أو الاتجاه الطيفي (الشكل 5ج-هـ). ومع ذلك، لم تؤدي التغييرات في الاتجاه الطيفي إلى تغيير مضاعف في سعة ذروة التذبذب. ونتيجة لذلك، فإن قياس سعة ذروات التذبذب بالنسبة للاتجاه الطيفي أنتج تفسيرات غير صحيحة (الشكل 5و-ز): حيث أن قسمة سعة الذروة على الاتجاه الخلفي اقترحت بشكل خاطئ أن الإيقاع العصبي انخفض عندما أصبحت النشاطات غير الدورية أقوى (الشكل 5د، ز)، وقد قدرت بشكل كبير زيادة الإيقاع العصبي عندما زادت النشاطات غير الدورية في الوقت نفسه (الشكل 5هـ، ح). لذلك، استنتجنا أنه إذا كانت الذروة الطيفية واضحة، فإن النشاط العصبي غير الإيقاعي له تأثير مضلل ضئيل وأن إزالة الاتجاه غير ضرورية. ومع ذلك، من المهم أنه إذا لم تكن هناك ذروة طيفية واضحة، فلا يوجد ضمان بأن التغييرات في القوة ناتجة عن اختلافات في التذبذبات العصبية.

ميل الطيف هو مقياس غير متسق لتوازن EI

ركزت النتائج المذكورة أعلاه على دور الديناميات العصبية في تشكيل طيف EEG. ومع ذلك، تُظهر الشكل 1d-f أن حركيات الاستجابات ما بعد المشبكية تؤثر أيضًا على الخصائص العريضة لطيف EEG. للتحقيق بشكل أعمق في هذه الآلية التي تشكل طيف EEG، قمنا بإجراء تحليل حساسية كامل لحد الميل الطيفي بالنسبة للمعلمات البيوفيزيائية في نماذج الخلايا العصبية الفردية. تم محاكاة طيف EEG الوحدوي مع العديد من قيم المعلمات المختلفة (الشكل 6a) وتم حساب الحد العام لميل الطيف. بين 1 و 40 هرتز (الشكل 6ب). كشفت هذه المحاكاة أن الميل الطيفي تأثر باستمرار بأربعة معايير: ، ، و (الشكل 6ج). يمكن تفسير هذه النتائج من خلال المعادلة 1. المعامل يحدد مباشرة المقياس الزمني البطيء، ، من الطيف الموحد (الشكل 1d)، في حين أن التوصيلات المشبكية، و ،
تحكم مباشرة في مساهمات التيارات المشبكية المثبطة والمثيرة، على التوالي. جهد الانعكاس، تغير تيار التسرب الميل الطيفي لأنه عندما أكثر استقطابًا، تتعرض المستقبلات لقوة دافعة أعلى، مما يعزز مساهمات التيارات المثبطة.
من المدهش أن تحليل ميل الطيف كشف عن تفاعل قوي بين وكلاهما و (الشكل 6ج). عندما كانت موصلية التسرب منخفضة ( )، وُجد أن الميل الطيفي مرتبط سلبًا بـ نسبة (الشكل 6د، هـ؛ الشكل S2ب)، والتي تتعارض مع توقعات النماذج الخطية لتوليد EEG . السبب هو أنه عندما كانت موصلية التسرب منخفضة، كانت النسب الأعلى من E:I تدفع الجهد الغشائي المتوسط بالقرب من إمكانيات الانعكاس لمستقبلات GABA (الشكل S2a). هذا تسبب في أن الخلايا العصبية ذات ال لتجربة قوى الدفع GABAR المتلاشية وقوى الدفع AMPAR المعززة عند قيم E:I العالية، مما يجعل الميل الطيفي بشكل غير متوقع مضادًا مرتبطًا مع نسبة E:I (الشكل 6e). ومع ذلك، عندما كانت موصلية التسرب عالية ( )، كانت جهد الغشاء يتقلب بشكل أقل وظل ضمن نطاق خطي نسبيًا (الشكل S2a). وبالتالي، كان الميل الطيفي مرتبطًا إيجابيًا بنسبة E:I (الشكل 6e) كما تنبأت به النماذج الخطية لتوليد EEG. تم ملاحظة تأثير مشابه وإن كان أضعف في العلاقة بين الميل الطيفي و النسبة (الشكل S2c). بشكل عام، نستنتج أن الاتجاه الطيفي العام يتأثر بشكل كبير بالمعايير الحيوية الفيزيائية التي تغير الاستجابات ما بعد المشبكية، لكن التغيرات في قيمة الميل لا تخبر وحدها عن المعايير التي تتغير.

تغيرات في الاستجابات المشبكية تعقد قياس إيقاعات الدماغ

تغيرات في الاستجابات ما بعد المشبكية تغير طيف EEG بطريقة مختلفة جوهريًا عن النشاط العصبي غير الإيقاعي. ما بعد المشبكية
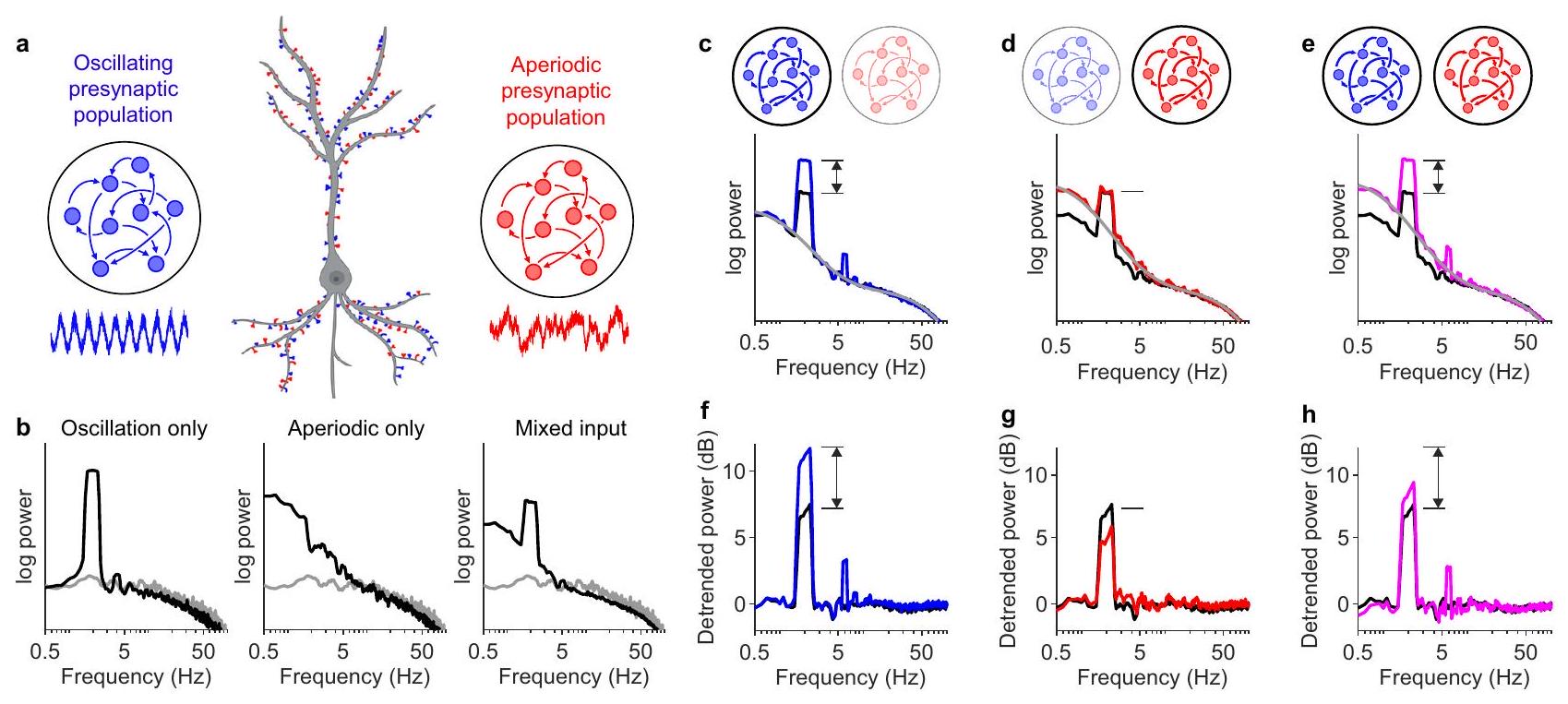
الشكل 5 | قياس قوة الذروة التذبذبية بالنسبة للاتجاه الطيفي قد ينتج عنه نتائج مضللة. أ توضيح لنموذج الإدخال المختلط. نصف مشابك العصبون تلقت إدخالاً تذبذبيًا إيقاعيًا (أزرق) والنصف الآخر تلقى إدخالًا من شبكة تحت حرجة (أحمر). تم ضبط قوى الديناميات التذبذبية وتحت الحرجة عن طريق ضبط معلمين، و على التوالي، والتي حددت الدرجة التي تختلف بها المدخلات المشبكية عن عمليات بواسون المتجانسة. انظر الطرق للحصول على التفاصيل. تم إنشاء رسم توضيحي للخلية العصبية باستخدام BioRender.com. ب الطيف الوحدوي للخلايا العصبية التي تتلقى مدخلات بواسون (رمادي)، مقارنةً بالطيف الوحدوي للخلايا العصبية التي تتلقى مدخلات بالكامل من المجموعة المتذبذبة (يسار؛ أسود)، بالكامل من المجموعة تحت الحرجة (وسط؛ أسود)، أو مدخلات مختلطة كما في (أ) (يمين؛ أسود): . تم تعزيز المدخل التذبذبي من خلال زيادة من 0.1 (أسود) إلى 0.5 (أزرق)، مع ثابت عند 0.1.
الشكل 6 | حساسية الميل الطيفي للمعلمات البيوفيزيائية الحاكمة
استجابات ما بعد المشبك. أ توزيع العينات لبارامترات النموذج، نفس تلك المستخدمة في الشكل 1g. ب مثال لطيف من طيف EEG لخلية عصبية واحدة، تم ملاءمته بالمعادلة بين 1 و 40 هرتز. ج حساسية الميل الطيفي، ، لنمذجة المعلمات، مع تفاعلات من الدرجة الأولى والثانية، تم حسابها من 20,000
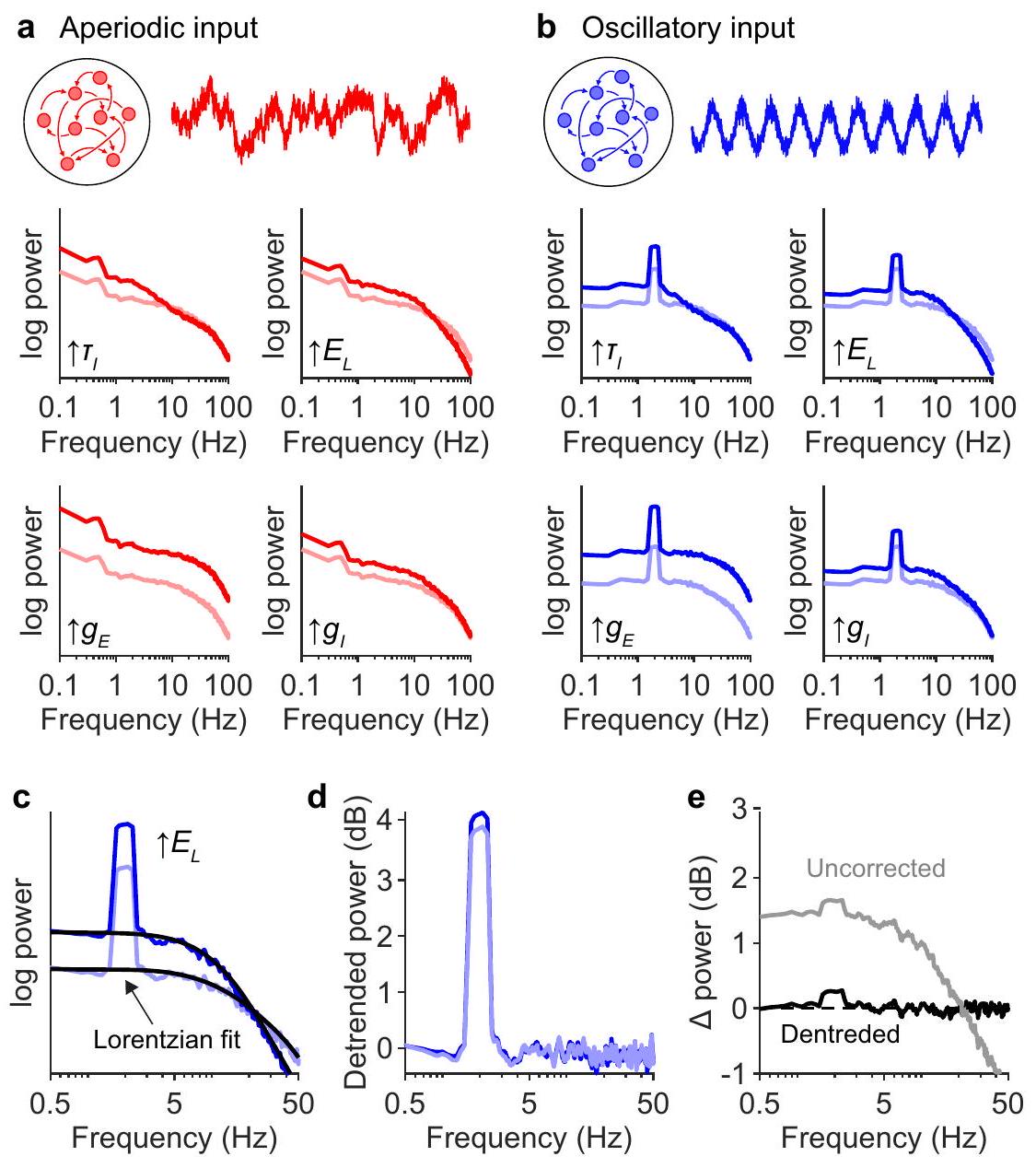
طيف محاكى. تم حساب متوسط الطيف المحاكى بناءً على النسبة بين و نسب E:I المنخفضة تتوافق مع مزيد من التثبيط. تم رسم الميل الطيفي مقابل نسبة لكل محاكاة. اليسار: محاكاة حيث كانت موصلية التسرب منخفضة ( المحاكاة). اليمين: محاكاة حيث كانت موصلية التسرب عالية ( محاكاة).
الشكل 7 | التغيرات في الآليات ما بعد المشبكية تعقد قياس إيقاعات الدماغ. أ الطيف الوحدوي للخلايا العصبية التي تتلقى مدخلات دون العتبة تمامًا ( ; انظر الشكل 5أ)، قبل وبعد أربعة تغييرات في المعلمات: الرسم الفرعي الذي يتوافق مع ( ) يظهر الطيف الوحدوي عندما تم زيادته من 10 مللي ثانية (وردي) إلى 30 مللي ثانية (أحمر)؛ ( ) يظهر طيفًا وحيدًا عندما تم زيادته من -60 مللي فولت (وردي) إلى -45 مللي فولت (أحمر)؛ يظهر طيفًا موحدًا عندما تم زيادته من 0.7 نانوثانية (وردي) إلى 1.4 نانوثانية (أحمر)؛ و( ) يظهر طيفًا وحيدًا عندما تم زيادته من 0.7 نانوثانية (وردي) إلى 1.4 نانوثانية (أحمر). لاحظ التغيرات في الطيف الأحادي على الرغم من عدم وجود تغييرات في ديناميات المدخلات المشبكية. ب نفس الشيء كما في (أ)، ولكن بالنسبة للخلايا العصبية التي تتلقى مدخلات متذبذبة بالكامل. ; انظر الشكل 5أ). في
الشكل S3، نعرض أمثلة على أنواع مختلفة من المدخلات الإيقاعية. ج مثال على الاتجاه الطيفي الملائم. هنا، يتم عرض الطيف الأحادي للمدخلات الجيبية قبل وبعد الزيادة. تمت ملاءمة الأطياف باستخدام خوارزمية مشابهة لـ FOOOF ، باستثناء أن الاتجاه هنا تم نمذجته باستخدام المعادلة 1 (الخطوط السوداء). انظر أمثلة أخرى في الشكل S4. د الطيف من (ج)، تم إزالة الاتجاه عنه عن طريق قسمة الطيف على التناسبات اللورنتزية الخاصة به. انظر أمثلة أخرى في الشكل S4. هـ التغير في كثافة الطيف EEG الناتج عن الزيادة باللون الرمادي هو التغير الخام في الطيف الوحدوي، بينما باللون الأسود هو الفرق بين الأطياف التي تم إزالة الاتجاه منها. لقد صحح إزالة الاتجاه من الأطياف باستخدام المعادلة 1 تأثيرات الزيادة ويشير بشكل صحيح إلى أنه لا توجد تغييرات في الديناميات العصبية.
تتفاعل الديناميات بشكل فعال كالتفاف مع المدخلات المشبكية، وبالتالي يجب أن تتفاعل مع القمم التذبذبية بطريقة مضاعفة. علاوة على ذلك، يجب أن تؤثر الآليات ما بعد المشبكية على الطاقة الناتجة عن جميع أنواع الديناميات العصبية بشكل متساوٍ. لاختبار ذلك، قمنا بتغيير منهجي للمعلمات الفيزيائية الحيوية التي تحكم التيارات ما بعد المشبكية وحللنا الطيف الوحدوي الناتج عن أنواع مختلفة من المدخلات المشبكية، بما في ذلك الضوضاء البيضاء (الشكل S3)، والديناميات دون الحرجة (الشكل 7a)، بالإضافة إلى ثلاثة أنواع من الديناميات التي تظهر قمم طيفية: نموذج إيسينغ المتكرر المقترح حديثًا الذي يظهر التعايش بين التذبذبات والانهيارات. (الشكل S3)، نظام من الدرجة الثانية غير مخمد مدفوع بالضوضاء البيضاء (الشكل S3)، وأخيرًا إيقاع جيبي بسيط (الشكل 7b). قمنا بدراسة تأثيرات المعلمات العصبية الفسيولوجية التي تؤثر على الميل الطيفي، كما حددها تحليل الحساسية لدينا (الشكل 6c): حركيات GABAR جهد عكس تيار التسرب والموصلات الكهربائية المثيرة ( ) و مثبط ( تغيير هذه المعلمات غير الطيف الوحدوي بطرق مميزة، ولكن الأهم من ذلك أنه كان له تأثيرات متطابقة عبر الأنواع المختلفة من ديناميات المدخلات (الشكل 7 أ، ب؛ الشكل S3).
التغيرات الطيفية الناتجة عن تغيير المعايير البيوفيزيائية لا تعكس اختلافات في الديناميات العصبية وبالتالي تمثل عوامل مشوشة لتحليل EEG. لتصحيح تأثيرات هذه التغيرات في المعايير، نقوم بتناسب الجزء من الاتجاه الطيفي الناتج عن أوقات التوصيل المشبكي باستخدام خوارزمية مشابهة لـ FOOOF. باستثناء أن الاتجاه الخلفي تم نمذجته باستخدام المعادلة 1 (الشكل 7c؛ الشكل S4). كما هو متوقع، فإن إزالة الاتجاه من الطيف بهذه الطريقة صححت التأثيرات المربكة لتغيرات المعلمات (الشكل 7d، e؛ الشكل S4).
في الختام، تشير نتائج نمذجة لدينا إلى وجود آليتين متميزتين للتفاعل بين القمة والاتجاه في طيف EEG. في حالة واحدة، هناك تغييرات في المساهمة النسبية للنشاط العصبي الإيقاعي وغير الإيقاعي في إشارة EEG. في هذه الحالة، تتغير القمم والاتجاه الطيفي بشكل مستقل نسبيًا عن بعضها البعض، وبالتالي فإن إزالة الاتجاه غير ضرورية لت quantifying سعة القمم الطيفية (انظر المناقشة). في الحالة الأخرى، تؤدي التغييرات في المعلمات الفيزيائية الحيوية إلى تغيير آلية توليد EEG نفسها. في هذه الحالة، تكون الفروقات في EEG غير مرتبطة بالديناميات العصبية؛ يمكن أن تؤدي هذه التغييرات إلى تشويش إشارات EEG من جميع المصادر العصبية، وبالتالي يمكن أن تتعرض حتى سعات القمم الطيفية للتلف المحتمل.
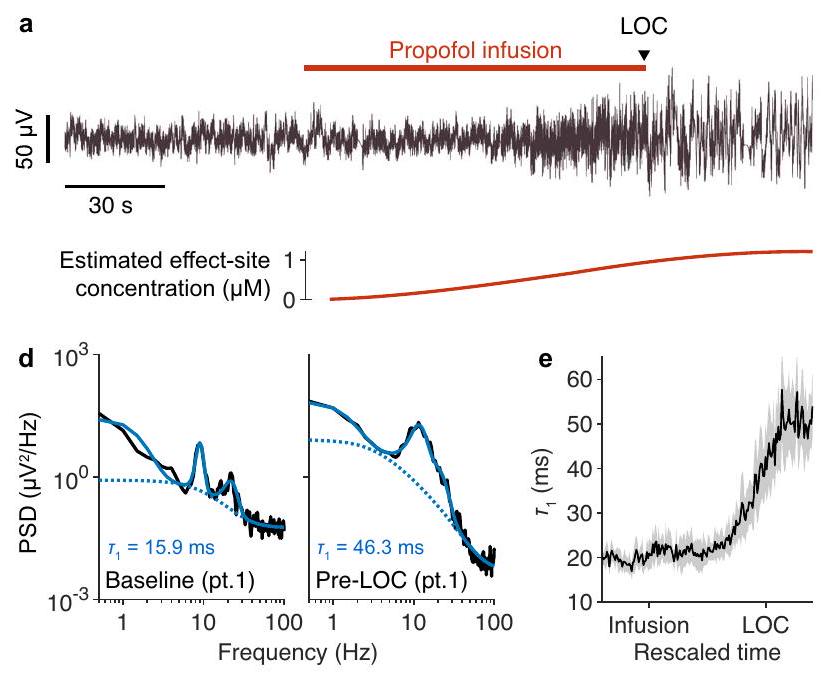
الشكل 8 | النموذج يتنبأ وي quantifies تأثيرات إدارة البروبوفل على طيف EEG. أ إشارة EEG تمثيلية، موقع تسجيل Cz، لموضوع يتلقى تسريبًا من البروبوفل حتى فقدان الوعي (LOC). يتم رسم التركيز المقدر لموقع التأثير للبروبوفل أدناه. ب متوسط طيف الترددات المتزامن مع LOC لـ 14 موضوعًا. ج متوسط طيف الطاقة في الحالة الأساسية (أسود)، متوسط بين 0 و 10 ثوانٍ قبل تسريب البروبوفل، وبعد تسريب البروبوفل (أحمر)، متوسط بين 0 و 10 ثوانٍ قبل LOC. الظل يعكس فترات الثقة للمتوسط الموضوعات). د الطيف الكهربائي للدماغ التمثيلي عند خط الأساس، قبل ضخ البروبوofول (يسار، أسود) و0-10 ثوانٍ قبل فقدان الوعي (يمين، أسود). تم تعديل الطيف باستخدام المعادلة 6 (انظر الطرق)، باستخدام خوارزمية تعديل مشابهة لـ FOOOF. الذي يفسر عدة قمم غاوسية في الطيف (باللون الأزرق الصلب). يتم عرض الاتجاه الملائم مع
خط متقطع. المعلمة ، مقدر من التوافقات مع الأطياف المحسوبة في نوافذ زمنية مدتها 2 ثانية، مرسومة بالنسبة للوقت المعاد قياسه. تعكس التظليل فترات الثقة للمتوسط المواضيع). يسار: التغير المطوي في القيمة المقدرة لـ تم رسمها مقابل التركيز المقدر لموقع تأثير البروبوofول. الخط الأسود يحدد المتوسط لكل تركيز من البروبوofول. اليمين: تم تراكب مخطط الاستجابة للجرعة المقدر من اللوحة اليسرى (الألوان الداكنة تعكس كثافة أعلى من النقاط) مع بيانات في المختبر مأخوذة من أربع دراسات: الدراسة رقم 1 الدراسة رقم 2 الدراسة رقم 3 ، والدراسة رقم 4 تم تقديم قيم البيانات المأخوذة من هذه الدراسات في الجدول S2. الخط الأسود المتقطع هو دالة هيل الملائمة للبيانات من الدراسات الأربع: ومعامل هيل .
النموذج يتنبأ ويquantifies تأثيرات البروبوفل على طيف EEG. تشير النتائج أعلاه إلى أن إزالة الاتجاه الطيفي قد تكون مهمة في التجارب الدوائية حيث تستهدف العديد من الأدوية قنوات الأيونات وتغير الاستجابات بعد المشبكية. لاختبار هذا التنبؤ النموذجي، قمنا بالتحقيق في توقيعات EEG للمخدر العام البروبوفل، معدل مستقبلات يطيل زمن تلاشي التثبيط المشبكي قمنا بتسجيل تخطيط الدماغ الكهربائي لـ 14 شخصًا خلال تسريب ثابت لمادة البروبوفل استمر حتى فقدان الوعي (LOC) (الشكل 8a). تم تحديد لحظة فقدان الوعي من خلال سقوط جسم ممسك به، والذي ثبت أنه يوفر مقياسًا دقيقًا وثنائيًا لفقدان الوعي مع توقيت دقيق. تم حساب الطيف الترددي المحاذي لموقع LOC من قناة Cz، والذي أظهر زيادة في قوة الترددات المنخفضة وانخفاضًا في قوة الترددات العالية بدءًا من قبل فقدان الوعي (الشكل 8ب). مقارنةً بالطيف الترددي المتوسط عند خط الأساس ( قبل تسريب البروبوofول) إلى ما بعد تسريب البروبوofول ( قبل LOC) أظهر زيادة في الطاقة ذات التردد المنخفض وانخفاضًا في الطاقة ذات التردد العالي، مما أعطى مظهرًا لدوران طيف الطاقة (الشكل 8c).
تشير نتائج نمذجة لدينا إلى أن البروبوفول يزيد من قوة الترددات المنخفضة من خلال زيادة المقياس الزمني البطيء، ، من الاتجاه الطيفي (الأشكال 1د، هـ؛ 7). لاختبار ذلك، قمنا بتقدير من بيانات تخطيط الدماغ الكهربائي عن طريق ملاءمة معادلة معدلة 1 لطيف تخطيط الدماغ الكهربائي (المعادلة 6؛ انظر الطرق). كانت هذه الوظيفة المعدلة تناسب الاتجاه الطيفي بشكل جيد باستثناء الترددات الأقل من (الشكل 8d؛ الشكل S5a-c)، حيث تشير نتائج نمذجة لدينا إلى أن الاتجاه الطيفي ملون بشكل أساسي بواسطة الديناميات العصبية، مثل تذبذبات دلتا و/أو نشاط الشبكة تحت الحرجة، ولكن ليس الحركيات المشبكية (الأشكال 4 و 5). تدعم هذه التفسير، التردد المنخفض ( جزء من الاتجاه كان يتزايد وينقص من ثانية إلى أخرى، أحيانًا يختفي تمامًا، في حين أن المقياس الزمني المشبكي الملائم ظل ثابتًا بين نوافذ الزمن (الشكل S5c). المقياس الزمني المستخرج، كان متسقًا بشكل ملحوظ قبل حقن البروبوofول، مع قيمة متوسطة قدرها (يعني SE، ) (الشكل 8e). بعد حقن البروبوofول، بدأت في الزيادة، وبلغت قيمة ( مزدوجة الذيل المقترنة -اختبار)
0-10 ثانية قبل فقدان الوعي (الشكل 8e). لوحظت تغييرات مماثلة في مواقع أقطاب كهربائية أخرى (الشكل S6). من خلال رسم القيمة المقدرة لـ في كل نقطة زمنية مقابل التركيز المقدر لموقع التأثير من البروبوفل، الذي تم قياسه باستخدام نموذج مارش قمنا بإنشاء منحنى استجابة الجرعة لتغير الطي في ضد التركيز المقدر للبروبوفول (الشكل 8f). منحنى الاستجابة للجرعة المستنتج لـ تمت مطابقة القياسات الكمية في المختبر لديناميات التيار المثبط بعد المشبكي في وجود البروبوofول المطبق في الحمام (الشكل 8f). وبالتالي، التغييرات في كانت متسقة مع التوقعات بناءً على علم الأدوية المعروف للبروبوفول. تدعم هذه الملاحظات توقع النموذج بأن حركيات مستقبلات GABA تؤثر بشكل كبير على طيف EEG وأن التغيرات الواسعة النطاق في EEG لا تعكس بالضرورة اختلافات في ديناميات الدماغ.

تصحيح أوقات المشابك يكشف عن توقيع فريد لـ LOC

تنبأت نتائج نمذجة لدينا بأن تأثير البروبوفول على أوقات التوصيل المشبكي سيؤدي إلى أخطاء في التقديرات التقليدية لإيقاعات الدماغ. وقد اقترحت الدراسات السابقة أن فقدان الوعي الناتج عن البروبوفول مرتبط بتغيرات في دلتا ( )، ألفا ( )، وبيتا ( نطاقات التردد . للتحقيق في عواقب إزالة الاتجاه الطيفي على توقيعات EEG لحالة فقدان الوعي، قمنا بمقارنة الطاقة الترددية الخام مع الطاقة الترددية التي تم إزالة اتجاهها في نطاقات التردد دلتا وألفا وبيتا. لمقارنة ديناميات EEG عبر الأفراد، تم محاذاة البيانات في نفس الوقت مع لحظة حقن البروبوبول وفقدان الوعي؛ تم ذلك عن طريق إعادة قياس الوقت في كل تجربة بناءً على زمن فقدان الوعي (الوسيط: 135 ثانية؛ النطاق: ). تم الحصول على نتائج مماثلة عندما لم يتم إعادة قياس الوقت (الشكل S5d). يتماشى ذلك مع الدراسات السابقة , زادت الطاقة الأساسية المعدلة في نطاق دلتا وألفا وبيتا بعد تسريب البروبوفل (الشكل 9أ-ج). بينما زادت طاقة ألفا بسرعة واستقرت قبل فقدان الوعي، ارتفعت طاقة دلتا ببطء واستمرت في الزيادة حتى بعد فقدان الوعي (الشكل 9د). من الجدير بالذكر أن طاقة بيتا زادت بالتزامن مع طاقة ألفا، لكنها بدأت في الانخفاض قبل فقدان الوعي، في النهاية
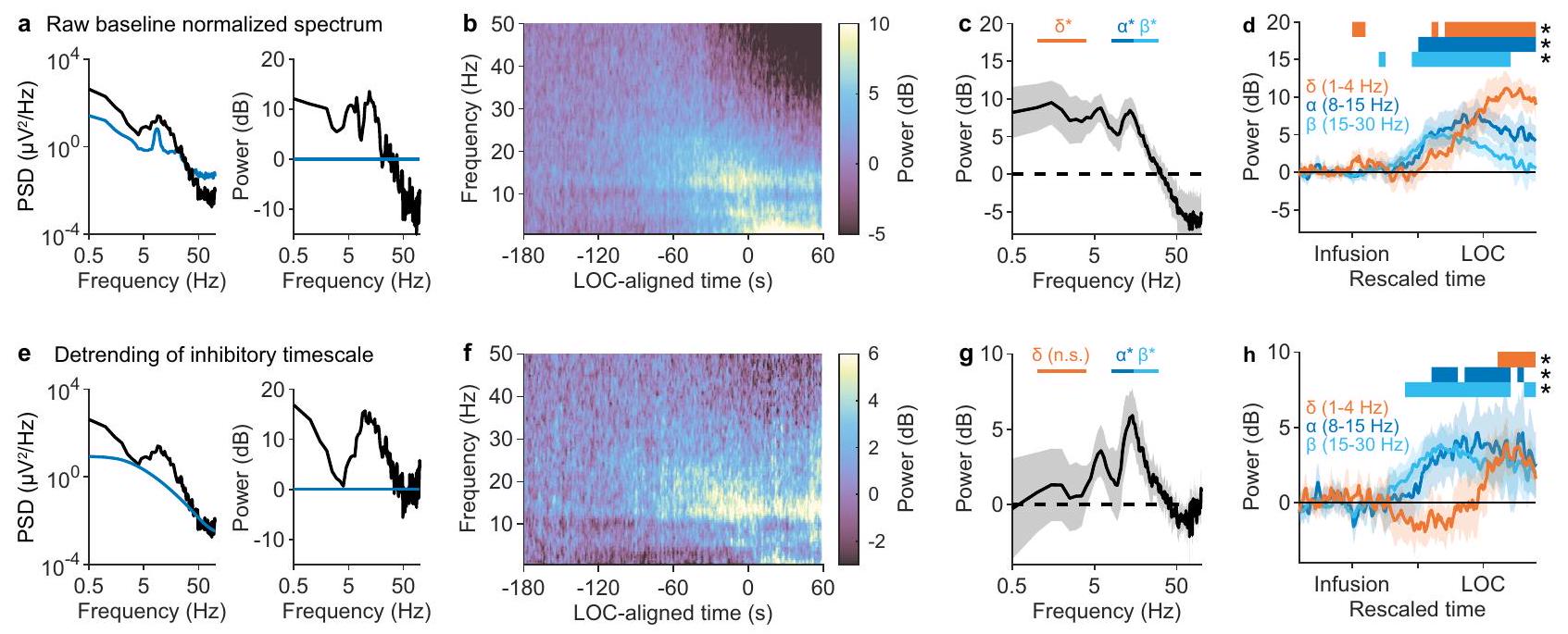
الشكل 9 | تصحيح مقاييس الزمن المشبكي يكشف عن توقيع فريد لفقدان الوعي. أ اليسار: طيف طاقة EEG التمثيلي بعد فقدان الوعي (أسود) لموضوع واحد، متراكب على طيف الطاقة عند الخط الأساسي (أزرق). اليمين: طيف الطاقة بعد فقدان الوعي (أسود) معدل إلى الخط الأساسي. ب متوسط طيف الطاقة المعدل عند الخط الأساسي ( الموضوعات). ج متوسط الطاقة المعدلة عند الخط الأساسي قبل فقدان الوعي (التظليل: فترة الثقة للمتوسط). كانت الطاقة مرتفعة بشكل ملحوظ ضمن نطاقات دلتا ( , اختبار الإشارة ذو الذيل الأيمن؛ الموضوعات)، ألفا ( ), وبيتا ( ) ترددات النطاق. تغيرات في طاقة ألفا وبيتا ودلتا، متوافقة مع كل من لحظة تسريب البروبوفل وفقدان الوعي، متوسط عبر الموضوعات (التظليل: فترة الثقة 95% للمتوسط). تشير القضبان فوق الرسم إلى 0.05 -أقسام طويلة من الزمن المعاد قياسه حيث يوجد زيادة إحصائية
ملحوظة ( , اختبار الإشارة ذو الذيل الأيمن) في طاقة النطاق الترددي المقابل. الشكل S5د يظهر النتائج بدون زمن معاد قياسه. هـ اليسار: طيف EEG بعد فقدان الوعي، نفس الشيء كما في أ، متراكب مع مقياس الزمن المثبط الملائم (المعادلة 6). القمم الغاوسية الملائمة غير معروضة. اليمين: الطاقة المعدلة، تعرف بأنها الطاقة بالنسبة لمقياس الزمن المثبط الملائم، بالديسيبل. متوسط طيف الطاقة المعدلة، معدل إلى الخط الأساسي ( الموضوعات). ز الطاقة المعدلة 0-10 ثوانٍ قبل فقدان الوعي، معدل إلى الخط الأساسي (التظليل: فترة الثقة 95% للمتوسط). كانت الطاقة مرتفعة بشكل ملحوظ ضمن نطاقات ألفا ( ) وبيتا، ( )، ولكن ليس دلتا ( ) ترددات النطاق. كانت اختبارات الأهمية كما في ( ). نفس الشيء كما في (د)، ولكن لطاقة معدلة، معدل إلى الخط الأساسي.
مما أدى إلى طاقة بيتا ليست مختلفة إحصائيًا عن الخط الأساسي بعد فقدان الوعي (الشكل 9د).
لتصحيح التأثيرات المربكة للبروبوفل، قسمنا طاقة EEG عند كل نقطة زمنية بواسطة مقاييس الزمن المشبكي المقدرة الملائمة من القسم السابق (الشكل 9هـ). ثم قمنا بتعديل الطاقة المعدلة بواسطة الطاقة المعدلة عند الخط الأساسي (الشكل 9و)، بحيث تعكس التغيرات في طاقة النطاق التغيرات الطيفية غير المفسرة بزيادة في . أزال هذا الإجراء تمامًا الدوران الظاهر في أطياف EEG بعد تسريب البروبوفل (الشكل 9ز). نتيجة لهذا التعديل، زادت الطاقة في نطاقات ألفا وبيتا ودلتا بوضوح في أوقات متميزة (الشكل 9ح). ظهرت طاقة ألفا وبيتا بعد تسريب البروبوفل واستقرت قبل فقدان الوعي بفترة طويلة. بالمقابل، لم تزد طاقة دلتا المعدلة حتى لحظة فقدان الوعي، حيث زادت بشكل حاد (الشكل 9ح؛ الشكل S5د). باختصار، بينما فشل إشارة EEG الخام في إظهار إشارة مرتبطة بالوقت بشكل قوي في لحظة فقدان الوعي، كشف إزالة التأثيرات المتوقعة للبروبوفل عن زيادة حادة في طاقة دلتا خلال ثوانٍ من فقدان الوعي. تشير هذه التحليلات، جنبًا إلى جنب مع نتائج نمذجة لدينا، إلى أن التغيرات الدوائية في الحركيات المشبكية قد تخفي الديناميات الحقيقية للاهتزازات العصبية عندما لا يتم إجراء تعديل طيفي. بالإضافة إلى ذلك، تشير هذه النتائج إلى أدوار متميزة لطاقة ألفا ودلتا في وظيفة البروبوفل كمسكن عام.

نقاش

في هذه الدراسة، استكشفنا الأساس العصبي لاتجاه طيف EEG وفحصنا تداعياته على تفسير وتحليل EEG. خرجت عدة استنتاجات مهمة من هذه التحقيقات. أولاً، قدم هذا العمل دليلًا حيويًا على أن النشاط العصبي غير الإيقاعي قادر على توليد إشارات EEG قابلة للاكتشاف. ثانيًا، عززت نمذجاتنا توقعات النماذج الحسابية الأبسط وأشارت إلى أن اتجاه طيف EEG يتشكل من تفاعلات العديد من العوامل، بما في ذلك الحركيات المشبكية، نسبة الإثارة إلى التثبيط، وديناميات الشبكة غير الدورية. ثالثًا، كشفت تحليلاتنا أن
أ amplitudes الذروة الطيفية تتأثر بشكل ضئيل بتقلبات النشاط العصبي غير الإيقاعي. من ناحية أخرى، وجدنا أن التغيرات النظامية في خصائص تيار المشبك تتطلب تعديلًا لتفسير التغيرات الطيفية بدقة كاختلافات في النشاط العصبي. اقترحت نتائجنا أن هذا السيناريو الأخير مهم بشكل خاص لتسجيلات EEG المستخدمة بالتزامن مع التدخلات الدوائية.
يفترض التحليل الطيفي التقليدي أن طاقة EEG ضمن نطاقات التردد الكانونية تعكس إيقاعات دماغية متنوعة. تتحدى نتائج نمذجاتنا بشكل جدي هذا الافتراض. على وجه التحديد، إذا لم يكن هناك ذروة طيفية واضحة ضمن نطاق تردد معين، فإن عملنا يبرر فرضية بديلة معقولة فسيولوجيًا وواقعية حيويًا، وهي أن طاقة النطاق تعكس النشاط العصبي العريض النطاق. وبالتالي، تتحقق نتائجنا من الافتراض الرئيسي لطرق تعديل الطيف، مثل خوارزمية FOOOF ، وهو أن اكتشاف الذروة هو شرط ضروري لتQuantifying الطاقة الاهتزازية. بينما يمكن أن تعكس الطاقة الموجودة خارج الذروات الطيفية الإيقاعات العصبية، لا يوجد ضمان نظري لهذه التفسير بناءً على التحليل الطيفي وحده.
من المهم أن نتائجنا لا تدعم بالضرورة نهجًا قائمًا على البيانات فقط لتعديل أطياف EEG. بينما تؤثر التغيرات في النشاط غير الإيقاعي على الذروات الطيفية بطريقة إضافية (الشكل 5)، فإن التغيرات في التيارات المشبكية تقوم بتعديل الذروات الطيفية بشكل مضاعف (الشكل 7)؛ وبالتالي تتطلب هذان الآليتان طريقتين متميزتين للتعديل، أي، تعديل طرح مقابل تعديل قسمة، على التوالي. بدون معرفة مسبقة، من غير الواضح أي طريقة مطلوبة. علاوة على ذلك، نظرًا لارتفاع الذروات فوق الاتجاه الخلفي النموذجي في أطياف EEG، فإن التغيرات الإضافية الصغيرة في الاتجاه ستغير الذروة بشكل ضئيل مقارنة بالأخطاء الناتجة عن تعديل غير صحيح (الشكل 5). بشكل عام، نستنتج أنه يجب عدم إجراء تعديل طيفي ما لم يكن هناك مبرر واضح فسيولوجيًا وحيويًا.
في التحليل المقدم هنا، كانت هناك معرفة مسبقة بعمل البروبوفل الموثق جيدًا على حركيات GABAR , مما يشير بوضوح
إلى ضرورة تعديل القسمة. لتقليل فرص الإفراط في التكيف، قمنا بتقييد قيم المعلمات إلى نطاقات معقولة فسيولوجيًا، وتحققنا من أن التغيرات الطيفية الملائمة و القيم تطابقت كميًا مع التوقعات. ومع ذلك، كان من المحتمل أن يكون تحليلنا للأطياف إلى مكونات فسيولوجية متميزة غير كامل، خاصة بالنظر إلى أن التغيرات في حركيات GABAR قد أثرت أيضًا على ديناميات الشبكة غير الدورية (انظر أدناه). على الرغم من أنه من المتوقع أن تؤثر المشابك المثبطة ومقاييس الزمن الشبكي على الأطياف في نطاقات تردد مختلفة (الأشكال 1، 4، 5، 7)، فإن هذه النطاقات تتداخل، مما يجعل من الصعب فصل هذين الآليتين بشكل قاطع. قد تكون مثل هذه التحذيرات قابلة للتعامل معها مع تحسينات مستقبلية على خوارزميات تعديل EEG، على سبيل المثال، من خلال تضمين معلومات الطور أو استخدام نماذج توليدية لتحسين استنتاج المعلمات .
أشارت النمذجات السابقة إلى أن الأس exponent الطيفي لـ EEG يعكس نسبة E:I، والتي تعتمد على الافتراض بأن طاقة التردد المنخفض تهيمن عليها التيارات المثبطة . تؤكد نتائجنا بشكل عام هذا الافتراض، مما يشير إلى أن نسبة E:I هي محرك مهم لاتجاه الطيف. ومع ذلك، تظهر نتائجنا أيضًا أن الأس exponent الطيفي ليس مقياسًا موثوقًا لنسبة E:I بسبب عدم الخطية في ديناميات جهد الغشاء المتعلقة بجهود الانعكاس لـ AMPARs وGABARs (الشكل 6)، وهو جانب لم يؤخذ في الاعتبار في الأعمال السابقة . بالإضافة إلى ذلك، وجدنا أن معلمات حيوية أخرى، مثل مقاييس الزمن المشبكي والتيارات المتسربة تساهم في تشكيل اتجاه طيف EEG. تتماشى هذه النتائج مع الدراسات السابقة التي ربطت مقاييس الزمن العصبية بمستويات التعبير عن قنوات الأيونات المختلفة ووحدات المستقبلات. . يبدو من المحتمل أن التغيرات في الاتجاه الطيفي يمكن أن تعكس عددًا كبيرًا من الآليات الفسيولوجية التي تتقارب للتحكم في حركيات المشابك ونسبة E:I الفعالة. هناك آليات فيزيائية حيوية أخرى لم يتم استكشافها هنا، مثل التيارات الغشائية النشطة. وارتفاعات الكالسيوم الشجرية يمكن أن تساهم أيضًا في تشكيل طيف EEG من خلال تغيير حركيات الاستجابة ما بعد المشبكية والسعات. بشكل عام، نستنتج أن الأس exponent الطيفي يعكس عوامل فسيولوجية أخرى غير التذبذبات العصبية، وبالتالي فهو علامة حيوية مكملة لتQuantification إيقاع الدماغ.
بينما اقترحت عدة دراسات أن الحرج الانهياري قد يكون مسؤولاً عن النطاق الترددي توسيع في طيف تخطيط الدماغ الكهربائي تدعم نتائجنا نماذج أخرى من الشبكات العصبية المتكررة وتشير إلى أن حرج الانهيار الثلجي من المحتمل أن يساهم فقط في مكونات التردد الأبطأ من تخطيط الدماغ الكهربائي (الشكل 4، في الحد كما ). بشكل عام، يقترح نموذجنا آلية أساسية للتفسير الملاحظ اتجاه يمكن مقارنته بالذي تم اقتراحه حول كيفية إنتاج الشبكات التذبذبية البحتة لمثل هذا الاتجاه. في حالة التذبذب، تم اقتراح أن الشبكات الكبيرة تتذبذب بشكل أبطأ من الشبكات الصغيرة، مما يؤدي إلى اتجاه تشير نتائجنا إلى أن النبضات المتكررة التي تظهر أوقات ارتباط أطول يمكن أن تنتج ثنائيات أكثر تماسكًا، مما يساهم بشكل أكبر في إشارة EEG. وهذا بدوره قد يتسبب في هيمنة طيف EEG على إشارات غير دورية ذات ترددات منخفضة. على الرغم من أنه لا يزال تحديًا تقنيًا، يمكن اختبار نموذجنا من خلال توسيع العمل الأخير الذي يصف التجمع الوظيفي للمشابك داخل فروع الشجيرات الفردية. ومن خلال قياس العلاقات الهندسية بين المشابك العصبية المرتبطة عبر الخلايا العصبية المجاورة.
تعتبر إيقاعات دلتا سمة شائعة للتخدير العام، حيث يمكن تحفيزها بسهولة في البشر بواسطة البروبوفل، والسيفوفلوران، والثيوبنتال، والزينون. مما قد يشير إلى توقيع عالمي للوعي غير الواعي يربط بين التخدير العام والنوم حسب علمنا، لم يتم الإبلاغ عن مثل هذا التغيير المفاجئ في قوة دلتا كما هو موضح هنا في دراسات تخطيط الدماغ الكهربائي، حتى عندما تم تحديد لحظة فقدان الوعي بدقة زمنية عالية. على الرغم من أن إزالة الاتجاه من القوة تعتمد عمليًا على نماذج مبسطة لطيف EEG، فإن تحليلنا يظهر بوضوح أن التغيرات البطيئة في قوة دلتا قبل فقدان الوعي يمكن تفسيرها من خلال تأثير البروبوفول على حركيات مستقبلات GABA، وبالتالي يوضح أن قوة دلتا التي تنشأ من
تظهر التغيرات في الديناميات العصبية بعد الزيادة التي يسببها البروبوفول في قوة ألفا وبيتا (الشكل 9). وفقًا لمحاكياتنا، من الممكن أن الزيادة الملحوظة في قوة التردد المنخفض تعود إلى اقتراب الدماغ من حالة حرجة الانهيار (الأشكال 4 و5). تتعارض مع هذا التفسير نماذج الشبكات المثيرة/المثبطة، التي تقترح أن زيادة المثبطات تعزز الحالة غير المتزامنة. . علاوة على ذلك، أشارت التحليلات المفصلة لإشارات EEG إلى أن حالات الوعي المتغيرة مرتبطة بالابتعاد عن الديناميات الحرجة، وليس الاقتراب منها. استنادًا إلى هذه الدراسات، يجب أن نتوقع تغييرات في أهمية الشبكة تؤدي إلى انخفاض في قوة دلتا. يبدو من المحتمل، لذلك، أن الزيادة في قوة دلتا في لحظة فقدان الوعي مرتبطة بتغيرات في إيقاعات دلتا. إذا كان الأمر كذلك، فإن ملاحظاتنا تدعم الرأي القائل بأن إيقاعات دلتا أساسية لفقدان الوعي. يمكن استخدام بروتوكول تركيز موقع التأثير المستهدف للتحقيق في جرعات أقل من البروبوفول بمزيد من التفصيل، والتي تشير ملاحظاتنا إلى أنها قد تحفز إيقاعات ألفا ولكن ليس إيقاعات دلتا. إذا كان الأمر كذلك، يمكن استخدام هذه التجارب لتفكيك الارتباطات السلوكية لهذين الإيقاعين بمزيد من التفصيل.
باختصار، نستنتج أن النشاط العصبي غير الدوري يمكن أن يساهم في إشارات تخطيط الدماغ (EEG)، وأن الاتجاه الطيفي يتشكل أيضًا من خلال العديد من الآليات الفسيولوجية، مثل توازن الإثارة/التثبيط وأوقات المشابك. نستنتج أن الأس exponent الطيفي ليس مجرد مقياس مختلط لإيقاعات الدماغ وبالتالي يوفر علامة حيوية مكملة لحالة الدماغ. ومع ذلك، نستنتج أيضًا أن الأس exponent الطيفي ليس له تفسير فسيولوجي وحيد. أخيرًا، نستنتج أن طيف تخطيط الدماغ يحتاج إلى إزالة الاتجاه عند قياس إيقاعات الدماغ، ولكن فقط إذا تم تغيير خصائص التيار بعد المشبكي بشكل منهجي. خلاف ذلك، من المحتمل أن يؤدي إزالة الاتجاه إلى إدخال أخطاء كبيرة في قياس إيقاعات الدماغ، وبالتالي يجب تجنبها.

طرق

تعريفات وإطار نظري

يمكن وصف إشارة تخطيط الدماغ الكهربائي (EEG) على أنها التركيب الخطي للحقول الكهربائية الناتجة عن جميع الخلايا العصبية في الدماغ. نشير إلى المساهمة الفردية لخلية عصبية واحدة في إشارة EEG الجماعية باسم EEG خلية عصبية واحدة. بعبارة أخرى، فإن إشارة EEG الجماعية هي الجمع الخطي لـ تخطيط الدماغ الكهربائي لخلية واحدة. هذا يعني أن كثافة الطيف الترددي لإشارة تخطيط الدماغ الكهربائي يمكن التعبير عنها كـ
هنا، هو طيف القوة لتخطيط الدماغ الكهربائي لخلية عصبية واحدة تم إنشاؤه بواسطة خلية عصبية معينة ، و هو التماسك بين تخطيط الدماغ الكهربائي لخلية عصبية واحدة وعصبون يُعتقد أن القمم الطيفية تظهر بسبب التماسك عند تردد معين. . لأن دالة التماسك، يتفاعل بشكل مضاعف مع طيف EEG لخلية عصبية واحدة، ستتحكم الميزات الطيفية لـ EEG الجماعي جزئيًا في الميزات الطيفية التي تفرضها الخلايا العصبية على مستوى الخلية الفردية. علاوة على ذلك، سيكون هذا التأثير مستقلًا عن طبيعة ديناميات الدماغ، باستثناء ما إذا كانت هذه الديناميات تغير طيف EEG للخلية العصبية الفردية. بشكل عام، تتعلق هذه الورقة البحثية بالتحقيق في كيفية تأثير إشارات EEG للخلية العصبية الفردية ذات النطاق العريض على الميزات الطيفية لـ EEG الجماعي.

محاكاة الخلايا العصبية ما بعد المشبك

كانت أشكال الخلايا العصبية بالإضافة إلى وفرتها النسبية هي نفسها التي استخدمها هاجن وآخرون. (الجدول S1). تم استخدام نفس المعلمات الفيزيائية الحيوية لجميع أنواع الخلايا العصبية. بالنسبة للمحاكاة، تم تقسيم الأشكال بحيث كان كل قسم أقل من تم نمذجة كل خلية عصبية بعد المشبك بمقاومة محورية وسعة غشاء . كانت جميع المقصورات سلبية. كانت أقصى موصلية للتسرب كان
تم التحقيق فيه في نطاق من 0.01 إلى وإمكانات عكس التسرب ( تم التحقيق في نطاق من -75 إلى -45 مللي فولت (الشكل 1g). كان عدد المشابك لكل خلية مساوياً للطول الكلي للتغصنات مضروباً في كثافة قدرها مشبك واحد لكل للتشابكات المثيرة و0.15 تشابك لكل للتشابكات المثبطة تم توزيع المشابك العصبية بين جميع الأقسام بشكل متناسب مع مساحة سطح الأقسام. تم نمذجة التيارات ما بعد المشبكية كفرق من الأسية. كانت للمشابك المثيرة جهد عكسي قدره 0 مللي فولت، وزمن صعود قدره 0.3 مللي ثانية، وثابت زمن الانحلال ( بين 1 و 3.5 مللي ثانية، وذروة التوصيل بين 0.2 و 2 نانوثانية (الشكل 1g). كانت المشابك المثبطة لها جهد عكسي قدره -80 مللي فولت، وزمن ارتفاع قدره 2 مللي ثانية، وثابت زمن الانحلال ( بين 5 و 20 مللي ثانية، وذروة التوصيل بين 0.2 و 2 نانوثانية (الشكل 1g). لتوضيح طيف أمثلة محددة، مثل تلك المعروضة في الأشكال 1d و 2f و 4f و g و 5 و 7، تم استخدام مجموعة المعلمات التالية: ، ، و تمت جميع محاكاة الخلايا العصبية باستخدام بايثون 3.8.10 مع حزمة LFPy 2.2.4 تشغيل بيئة محاكاة NEURON في الخلفية .

تقدير سعة EEG الجماعية

نظرًا لأن ثنائيات القطب تتجمع بشكل خطي، يمكن تحليل إشارة EEG الناتجة عن N من الخلايا العصبية على أنها تراكب لإشارات EEG لخلايا عصبية فردية N. وبالتالي، سيكون لدى EEG الجماعي متوسط طاقة قدره ، حيث يتم إنتاج إشارات EEG من خلية عصبية واحدة بواسطة الخلايا العصبية و لديه قوى متوسطة و على التوالي، وارتباط ثنائي يجب أن تنشأ الارتباطات ثنائية القطب إذا تم استيفاء شرطين: (1) المدخلات المشبكية مرتبطة، والتي افترضنا أنها تقل مع المسافة؛ و(2) اتجاهات ثنائية القطب متراصة، والتي افترضنا أنها تعتمد على كل من الشرط 1 وزاوية المحاور القمية-القاعدية للخلايا العصبية. لذلك قمنا بنمذجة الارتباط ثنائي القطب لخلتين عصبيتين كـ ، حيث هو المسافة بين الخلايا العصبية الاثنين، هو مقياس مكاني معين للارتباط، و هو الزاوية بين المحاور القمية القاعدية للخلايا العصبية المعنية. قمنا بتقدير هذه المعلمات باستخدام نموذج الدماغ التشريحي ICBM152 v6. ، بافتراض كثافة متجانسة من عصبونات لكل منطقة السطح القشري .
قالب الدماغ هو شبكة مثلثية بأوجه ذات مساحات والمتجهات العمودية نقطة عشوائية على الشبكة، استخدمنا نقاط الرأس للشبكة لحساب “العدد الموقّع” للخلايا العصبية ضمن نصف قطر معين بشكل تحليلي ، المقدمة من
أين هو كسر وجه شبكة مثلثية الذي يتقاطع مع كرة نصف قطرها متمركز عند النقطة لقد كررنا هذا أوقات مع نقاط انطلاق مختلفة، لتقدير متوسط . هذا سمح لنا بتقدير متوسط الارتباط الثنائي عبر القشرة بأكملها باستخدام الصيغة التالية
يتبع ذلك أن القدرة المتوقعة للإشارة من إشارة EEG الجماعية هي ، حيث هو القدرة المتوقعة لخلية عصبية واحدة في تخطيط الدماغ الكهربائي (الشكل 1).
الكمية التجريبية لـ سيتطلب قياس ومقارنة ثنائيات القطب المعزولة للخلايا العصبية الفردية، وهي عملية غير ممكنة. ومع ذلك، تم التحقيق في الارتباطات في إمكانيات الغشاء تحت العتبة في القطط، سواء في وجود أو غياب التذبذبات. . كشفت هذه التجارب أنه في غياب التذبذبات، كانت التقلبات دون العتبة مرتبطة بين خلايا القشرة الجديدة حتى مفصولين، لكن كانوا
غير مترابط بين الخلايا العصبية بعيد لأن ثنائيات القطب تتولد بشكل أساسي من التيارات تحت العتبة تشير هذه البيانات إلى حد أدنى وحد أقصى محتمل لـ .

نموذج الشبكة دون الحرجة

تم ربط الخلايا العصبية السابقة المشبكية بـ الخلايا العصبية الأخرى في الشبكة السابقة المشبكية. تم تحديد احتمال ارتباط خليتين عصبيتين بناءً على المسافة بينهما، باستخدام نواة اقتران تتناقص بشكل أسي. أجبرت هذه القاعدة على أن تكون اتصالات الشبكة محلية بطبيعتها. كل خلية عصبية اتبعت عملية نقطة بواسون بمعدل ، حيث تم أخذ عينة من التوزيع الموضح في الشكل 1 ج. عندما أطلق عصبون إشارة، كان لكل من جيرانه من العصبونات احتمال إطلاق جهد الفعل خلال الأربعة التالية . المعامل وبذلك تم ضبط كمية انتشار النبضات في الشبكة، مما غير سلوك الشبكة من غير متزامن تمامًا عندما ، إلى قرب حرج الانهيار الثلجي كـ تم الاقتراب 1. تم استخدام الصياغة أعلاه لمحاكاة الخلايا العصبية المثيرة قبل المشبك. كما أضفنا خلايا عصبية مثبطة تشكل 15% من الشبكة بأكملها. تم أخذ سلاسل الطلقات للخلايا العصبية المثبطة من سلاسل الطلقات للخلايا العصبية المثيرة القريبة وتم تكملتها بعمليات بواسون المستقلة. كانت الإجراء بحيث يتم تحفيز إطلاق الخلايا العصبية المثبطة من خلال الاتصالات المتكررة بنفس النسبة مثل الخلايا العصبية المثيرة وتبعت معدل إطلاق محدد مسبقًا. في هذا الإعداد، تم نمذجة تأثير الخلايا العصبية المثبطة على الشبكة بشكل ضمني في عدد التفرعات. لكن لم يتم تمثيلها بشكل صريح في اتصالات الشبكة. سمحت هذه التبسيط بأن يكون عدد تفرعات الشبكة محكوماً بالكامل بمعامل واحد. .

تضمين المشابك العصبية على الشجيرات ما بعد المشبكية

تم نمذجة التزامن ثنائي القطب سابقًا إما عن طريق فصل المدخلات المثبطة والمثيرة إلى أقسام جسدية وقمية، على التوالي. أو من خلال إدخال عكسي في الحُجَيْرَات القاعدية والقمية ; يمكن اعتبار كلا النموذجين كخرائط مثالية لاثنين من السكان المتضادين من المشابك. مستلهمين من هذه النماذج، قمنا بتطوير إجراء لتوليد تزامن ثنائي القطب بناءً على أي طوبولوجيا قبل المشبك. أولاً، تم تحديد الارتباط الثنائي بين كل زوج من الخلايا العصبية قبل المشبكية بواسطة معامل تداخل وقت الطلقات (STTC) ، مقياس لارتباط سلسلة النبضات يأخذ في الاعتبار احتمال تداخل النبضات بالصدفة. تم حساب الارتباطات الزوجية بين جميع الخلايا العصبية السابقة المشبكية استنادًا إلى محاكاة طويلة لمدة 40 ثانية للشبكات السابقة المشبكية. خوارزمية تقريب وتخفيض الأبعاد الموحد (UMAP)، وهي تقنية لتقليل الأبعاد ثم تم استخدامه لإسقاط الشبكة السابقة المشبكية بشكل مثالي على كرة بحيث يتم تقليل الزاوية بين الخلايا العصبية السابقة المشبكية ذات STTCs العالية. بعد هذه الخطوة، تم إسقاط الشجيرات الخاصة بالخلايا العصبية اللاحقة المشبكية بشكل عمودي على الكرة. أخيرًا، تم تنفيذ الإجراء التالي حتى تتشكل جميع الاتصالات بين الخلايا العصبية السابقة واللاحقة المشبكية: (1) تم اختيار قطعة شجيرة عصبية لاحقة بشكل عشوائي (مع الاستبدال) مع احتمال يتناسب مع مساحتها السطحية؛ (2) تم اختيار الخلية العصبية السابقة الأقرب على الإسقاط الكروي وتشكيل اتصال.
لنمذجة وضع المشابك غير المثالي، قمنا بتشويش التضمين الكروي عشوائيًا قبل رسم المشابك. تم تشويش كل نقطة في التضمين بمسافة على اتجاه مختار عشوائيًا، حيث زي موحد . هنا، هو ما نشير إليه بمؤشر الأمثلية (الشكل 4e). من خلال البناء، عندما ، فإن النقاط على الكرة لا تتأثر على الإطلاق، بينما عندما جميع النقاط على الكرة تتعرض لاضطراب بمسافة مأخوذة من الدالة . وبالتالي، ل توزيع النقاط على الكرة عشوائي بشكل موحد.
يمكن اعتبار هذه العملية نموذجًا لارتباط ثنائي القطب يتجاوز المدخلات الثنائية. بدلاً من ذلك، يمكن اعتبار هذه العملية من حيث الملاحظات من الآونة الأخيرة.
الدراسات التي أفادت بأن المدخلات المشبكية المرتبطة وظيفيًا تتجمع ضمن فروع دندريتية فردية، وأن المدخلات من مجموعات مسبقة التشابك مشابهة تستهدف أقسام دندريتية مشابهة في المجموعة ما بعد المشبكية. تشير هذه الملاحظات التجريبية إلى وجود خريطة أكثر استمرارية للإدخال المشبكي على طول الشجيرات مقارنةً بنموذج تقسيم قمي-قاعدي صارم، وهو ما يتم تحقيقه بالضبط عند تطبيق خوارزمية الخريطة المذكورة على طوبولوجيا شبكة قبل المشبك المستمرة، مثل الشبكة السطحية تحت الحرجة المستخدمة في الشكل 5.

مدخلات مشبكية مختلطة

لتمثيل المدخلات الاهتزازية، استخدمنا صيغة منشورة لتوليد الإيقاع، حيث تم تطبيق مدخلات جيبية متعاكسة على الشجيرات القمية والقاعدية. . على وجه التحديد، تلقت كل مشبك عصبي على الخلية العصبية عملية نقطة بواسون غير متجانسة كمدخل، مع دالة معدل ، حيث يعتمد على ما إذا كانت المشبك مثيرًا أو مثبط يعدل قوة الإيقاع، و للتشابكات الشجرية القمية و للتشابكات الشجرية القاعدية. من أجل البساطة، لنموذج إيقاعات أخرى، قمنا بتعميم هذا الشكل من خلال تعريف دالة المعدل لكل تشابك على أنها ، حيث إذا كانت المشبك مشبكًا قميًا و إذا كانت المشبك مشبكًا قاعديًا، لأي سلسلة زمنية بمتوسط صفر وتباين وحدة. كانت هذه المنهجية أبسط من نمذجة الشبكات لكل نوع من الديناميات ودمج المشابك كما هو موضح في القسم أعلاه، ولكن الأهم من ذلك أن هذه المنهجية سمحت لنا بإجراء مقارنات مباشرة بين إشارات EEG المودلة التي تم إنشاؤها بواسطة دوال معدل مختلفة.

تصميم التجربة والإجراء

بعد موافقة مجلس أخلاقيات MNH، قمنا بتجنيد 16 مريضًا من فئة الجمعية الأمريكية لطب التخدير (ASA) من الفئة I أو II (تتراوح أعمارهم بين 18-65 عامًا) الذين قدموا لإجراء جراحة القرص القطني كمواضيع للدراسة. قدم جميع المشاركين موافقة خطية مستنيرة للمشاركة في الدراسة. تم تطبيق معايير الرعاية الخاصة بجمعية أطباء التخدير الكندية فيما يتعلق بالمراقبة والمعدات ومقدمي الرعاية بشكل صارم. تم استخدام أقطاب كهربائية على شكل كوب ذهبي (Fz، Cz، Pz، C3، C4، CP3، CP4، M2 كمرجع؛ FC1 كأرضية؛ مقاومة ) تم لصقها بفروة الرأس للحصول على تسجيل EEG مستمر، والذي تم تضخيمه بـ تم تمرير النطاق ورقمنته بسرعة 1024 هرتز. لكل مشارك، حصلنا على تسجيل لمدة دقيقتين خلال فترة الأكسجة المسبقة مع إغلاق العينين. ثم طُلب من المشارك أن يمسك بجسم (أسطوانة وزنها 0.5 كجم؛ بقطر 2.5 سم وطول 15 سم) في وضع عمودي بيده المهيمنة وأن يبقي عينيه مغلقتين. استمرت الأكسجة المسبقة لمدة دقيقتين إضافيتين. ليدوكائين تم إعطاؤه لتخفيف الانزعاج الناتج عن حقن البروبوofول. تم إعطاء جميع الأدوية عن طريق الوريد عبر قسطرة موضوعة في الذراع غير السائدة. تم إعطاء البروبوofول بمعدل واستمر ذلك حتى سقط الأسطوانة من يد المشارك. بعد فقدان الوعي، تم تطبيق رفع الفك برفق إذا لزم الأمر لتخفيف انسداد مجرى الهواء. تم تقييم قدرة المشاركين على الاستجابة للأوامر الصوتية العالية بعد 60 ثانية من سقوط الجسم: جميعهم فشلوا في الاستجابة وظلوا غير متحركين. ثم تم إنهاء الدراسة.

تحليل البيانات

تم استبعاد مشاركين اثنين بسبب عدم الامتثال للتعليمات خلال مرحلة الإدخال. كان أحدهما يتحدث باستمرار، والآخر كان يتحرك بذراعه المهيمنة. وبالتالي، كانت مجموعة البيانات النهائية مبنية على 14 شخصًا (10 ذكور؛ 12 يميني اليد). تم إزالة الشوائب في البيانات بعد الفحوصات البصرية لسلاسل الزمن. تم حساب طيف الترددات باستخدام طريقة متعددة الأشرطة، مع استخدام ثلاثة أشرطة على نوافذ مدتها 2 ثانية، مع تداخل قدره 1.9 ثانية. تم حساب متوسطات المجموعة إما كمتوسط كثافة الطاقة الطيفية عبر المشاركين مع الوقت المتماشي مع LOC، أو مع إعادة قياس الوقت بحيث يتم محاذاة كل من بداية التسريب وLOC عبر الأفراد. لإعادة قياس الوقت، تم تعديل الوقت المتماشي مع LOC لكل مشارك بناءً على فترة الانتظار من التسريب إلى LOC.
وبالتالي، فإن قيمة الوقت المعاد قياسها -1 تعادل لحظة بدء تسريب البروبوفل، وقيمة الوقت المعاد قياسها 0 تعادل لحظة فقدان الوعي.

تركيز البروبوofول المقدر

لتقدير تركيز الموقع الفعال للبروبوفول لكل موضوع، استخدمنا نموذج مارش، وهو نموذج حركية دوائية متعددة الحجرات. استخدمنا بلازما لتحديد ثابت معدل التوازن في موقع التأثير قيم أسرع وأبطأ لـ سوف تنقل منحنى الجرعة-الاستجابة المقدر في الشكل 8f إلى اليمين واليسار، على التوالي، ولكن من غير المتوقع أن تغير نتائجنا بشكل نوعي.

إزالة الاتجاه من طيف EEG

لإزالة الاتجاه من طيف EEG، استخدمنا نسخة معدلة من خوارزمية FOOOF حيث يتم ضبط اتجاه خلفي بالإضافة إلى عدة دوال غاوسية لحساب القمم التذبذبية. تم إزالة القمم عند 60 هرتز بسبب الضوضاء من الطيف باستخدام دالة fillgaps في MATLAB قبل ضبط الاتجاه الطيفي. يوفر خوارزم FOOOF خيارين للاتجاه الخلفي، أو . هنا، أردنا دالة خلفية يمكن تفسيرها من الناحية البيوفيزيائية، ولذلك بدأنا بمجموع دالتين لورنتزيتين (المعادلة 1). هذه الدالة هي حل تحليلي دقيق لنموذج الحوسبة لجاو وآخرين. ولها عدة فوائد. أولاً، توفر ملاءمات دقيقة لمحاكياتنا، مما أتاح لنا التحقيق في العواقب النظرية لإزالة الاتجاهات من طيف EEG. ثانياً، فإن المعلمات قابلة للتفسير من الناحية الفسيولوجية. و تعكس حركيات مستقبلات GABA وAMPAR (الشكل 1)، بينما و تعكس سعات المساهمات المثبطة والمثيرة للإشارات الكهربائية الدماغية. ثالثًا، يُعتقد أن الأس exponent الطيفي، يعكس المساهمة النسبية للتحفيز في التثبيط ، أي أنه يعتمد على نسبة إلى (الشكل 1). ومع ذلك، وجدنا هنا أن هذا ليس هو الحال دائمًا (الشكل 6). لذلك، فإن المعادلة 1 تضع افتراضات أقل حول معلماتها مقارنةً بالخيارين المقدمين من حزمة FOOOF.
لتحليل البيانات التجريبية، قمنا بتعديل المعادلة 1 لتوفير ملاءمات أفضل للبيانات وتقليل فرص الإفراط في التكيف. على عكس محاكياتنا، وجدنا أن الطاقة عالية التردد استقرت في بياناتنا حول النقطة التي كنا نتوقع أن يؤثر فيها مقياس الزمن المشبكي المثير (الشكل 1d، f). لذلك، استبدلنا الحد الثاني في المعادلة بحد ثابت،
هذا الحد الثابت، يُسجل الأوقات السريعة المثيرة بالإضافة إلى أي مساهمات عالية التردد من إمكانيات العمل نشاط العضلات وضوضاء المضخم ، التي لم تكن موجودة في محاكياتنا. من المهم أن هذه المعادلة تحتوي على معلمات يمكن تفسيرها فسيولوجيًا، مع تعكس مقاييس الزمن المشبكي المثبطة (الشكل 1d، e)، يمكننا تقييد نطاق لتجنب الإفراط في التكيف. على وجه التحديد، قمنا بتقييد أن تكون أكبر من 10 مللي ثانية وأقل من 75 مللي ثانية عند ملاءمة بيانات البروبوofول، حيث توقعنا أن يزيد البروبوofول من النطاق الفسيولوجي لديناميكية مستقبلات GABA (الجدول S2).
كانت هذه المعادلة المعدلة تناسب طيف EEG في ظروف القاعدة بشكل جيد، ولكن بعد حقن البروبوبول، لم تتدهور المعادلة بسرعة كافية لالتقاط طيف EEG (الشكل S7). وكان ذلك على ما يبدو لأن المعادلات الأصلية قد بسّطت بشكل مفرط حركيات المشابك المثبطة. ومن الجدير بالذكر أن المعادلة 1 هي حل تحليلي للاستجابات المشبكية المتدهورة بشكل أسي، في حين أن الاستجابات المشبكية الحقيقية تتميز بوقت ارتفاع ووقت تدهور: وبالتالي، فإن دالة الاستجابة المشبكية الأكثر دقة لطيف الطاقة تُعطى بواسطة
حيث يكون الحد الأول هو الحل التحليلي لطيف الطاقة لفارق الأسية. هو زمن ارتفاع التيارات المشبكية المثبطة، والذي قمنا بتثبيته عند للحفاظ على عدد معلمات التناسب منخفضًا من الجدير بالذكر أنه إذا قمنا بإصلاح كلاهما و قيم قابلة للتصديق من الناحية الفسيولوجية يمكن التقاط جميع بياناتنا الأساسية ببساطة عن طريق تغيير و (الشكل S5a). علاوة على ذلك، قدم ملاءمة المعادلة 6 تقديرات متسقة وقابلة للتطبيق من الناحية الفسيولوجية لـ كلاهما عند خط الأساس وبعد تسريب البروبوofول (الشكل 8e، f). وبالتالي، فإن المعادلة 6 مدفوعة بالبيوفيزياء، وقابلة للتفسير الفسيولوجي، ولها فقط ثلاثة معلمات للتناسب، وقد التقطت بياناتنا بشكل جيد سواء عند خط الأساس أو بعد تسريب البروبوofول (الشكل 8d؛ الشكل S5a-c).

ملخص التقرير

معلومات إضافية حول تصميم البحث متاحة في ملخص تقارير مجموعة ناتشر المرتبط بهذه المقالة.

توفر البيانات

تم رفع مخططات EEG المحسوبة لجميع المشاركين إلى Figshare (https://doi.org/10.6084/m9.figshare.24777990مع جميع نتائج المحاكاة المطلوبة لإعادة إنتاج أشكالنا. يتم توفير بيانات المصدر مع هذه الورقة.

توفر الشيفرة

الكود المستخدم لتشغيل المحاكيات، تحليل البيانات، وإنشاء أشكال المخطوطات تم إيداعه في زينودو (https://doi.org/10.5281/zenodo.10359818) ومتاحة أيضًا على GitHub (github.com/niklasbrake/EEG_modelling).

References

  1. Berger, H. Über das elektrenkephalogramm des menschen. Arch. Psychiatr. Nervenkr. 87, 527-570 (1929).
  2. Steriade, M. Cellular substrates of brain rhythms. Electroencephalogr. Basic Princ. Clin. Appl. Relat. fields 5, 31-83 (2005).
  3. Nunez, P. L. & Srinivasan, R. Electric Fields of the Brain (Oxford Univ. Press, Oxford, 2006). https://doi.org/10.1093/acprof:oso/ 9780195050387.001.0001.
  4. Buzsáki, G., Anastassiou, C. A. & Koch, C. The origin of extracellular fields and currents – EEG, ECoG, LFP and spikes. Nat. Rev. Neurosci. 13, 407-420 (2012).
  5. Pritchard, W. S. The brain in fractal time: f-like power spectrum scaling of the human electroencephalogram. Int. J. Neurosci. 66, 119-129 (1992).
  6. Manning, J. R., Jacobs, J., Fried, I. & Kahana, M. J. Broadband shifts in local field potential power spectra are correlated with singleneuron spiking in humans. J. Neurosci. 29, 13613-13620 (2009).
  7. Miller, K. J., Sorensen, L. B., Ojemann, J. G. & Den Nijs, M. Power-law scaling in the brain surface electric potential. PLoS Comput. Biol. 5, e1000609 (2009).
  8. He, B. J. Scale-free brain activity: past, present, and future. Trends Cogn. Sci. 18, 480-487 (2014).
  9. Voytek, B. et al. Age-related changes in neural electrophysiological noise. J. Neurosci. 35, 13257-13265 (2015).
  10. Roche, K. J. et al. Electroencephalographic spectral power as a marker of cortical function and disease severity in girls with rett syndrome. J. Neurodev. Disord. 11, 15 (2019).
  11. Colombo, M. A. et al. The spectral exponent of the resting EEG indexes the presence of consciousness during unresponsiveness induced by propofol, xenon, and ketamine. Neuroimage 189, 631-644 (2019).
  12. Ouyang, G., Hildebrandt, A., Schmitz, F. & Herrmann, C. S. Decomposing alpha and brain activities reveals their differential associations with cognitive processing speed. Neuroimage 205, 116304 (2020).
  13. Lendner, J. D. et al. An electrophysiological marker of arousal level in humans. Elife 9, 1-29 (2020).
  14. Donoghue, T. et al. Parameterizing neural power spectra into periodic and aperiodic components. Nat. Neurosci. 23, 1655-1665 (2020).
  15. Bédard, C., Kröger, H. & Destexhe, A. Does the frequency scaling of brain signals reflect self-organized critical states? Phys. Rev. Lett. 97, 118102 (2006).
  16. Gao, R., Peterson, E. J. & Voytek, B. Inferring synaptic excitation/ inhibition balance from field potentials. Neuroimage 158, 70-78 (2017).
  17. Bak, P., Tang, C. & Wiesenfeld, K. Self-organized criticality: an explanation of the noise. Phys. Rev. Lett. 59, 381-384 (1987).
  18. Beggs, J. M. & Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167-11177 (2003).
  19. Priesemann, V. Spike avalanches in vivo suggest a driven, slightly subcritical brain state. Front. Syst. Neurosci. 8, 108 (2014).
  20. Chaudhuri, R., He, B. J. & Wang, X. J. Random recurrent networks near criticality capture the broadband power distribution of human ECoG dynamics. Cereb. Cortex 28, 3610-3622 (2018).
  21. Lombardi, F., Herrmann, H. J. & de Arcangelis, L. Balance of excitation and inhibition determines power spectrum in neuronal networks. Chaos Interdiscip. J. Nonlinear Sci. 27, 047402 (2017).
  22. Buzsáki, G. & Draguhn, A. Neuronal olscillations in cortical networks. Science 304, 1926-1929 (2004).
  23. Buzsáki, G. & Vöröslakos, M. Brain rhythms have come of age. Neuron 111, 922-926 (2023).
  24. Huang, Y., Parra, L. C. & Haufe, S. The New York head-a precise standardized volume conductor model for EEG source localization and tES targeting. Neuroimage 140, 150-162 (2016).
  25. Hagen, E. et al. Hybrid scheme for modeling local field potentials from point-neuron networks. Cereb. Cortex 26, 4461-4496 (2016).
  26. Næss, S. et al. Biophysically detailed forward modeling of the neural origin of eeg and meg signals. Neuroimage 225, 117467 (2021).
  27. Orser, B. A., Wang, L. Y., Pennefather, P. S. & MacDonald, J. F. Propofol modulates activation and desensitization of receptors in cultured murine hippocampal neurons. J. Neurosci. 14, 7747-7760 (1994).
  28. Kitamura, A., Marszalec, W., Yeh, J. Z. & Narahashi, T. Effects of halothane and propofol on excitatory and inhibitory synaptic transmission in rat cortical neurons. J. Pharmacol. Exp. Ther. 304, 162-171 (2003).
  29. Whittington, M. A., Jefferys, J. G. R. & Traub, R. D. Effects of intravenous anaesthetic agents on fast inhibitory oscillations in the rat hippocampus in vitro. Br. J. Pharmacol. 118, 1977-1986 (1996).
  30. Franks, N. P. General anaesthesia: from molecular targets to neuronal pathways of sleep and arousal. Nat. Rev. Neurosci. 9, 370-386 (2008).
  31. McInnes, L., Healy, J. & Melville, J. UMAP: uniform manifold approximation and projection for dimension reduction. Preprint at https://arxiv.org/abs/1802.03426 (2020).
  32. Wilting, J. & Priesemann, V. Between perfectly critical and fully irregular: a reverberating model captures and predicts cortical spike propagation. Cereb. Cortex 29, 2759-2770 (2019).
  33. Suryadi, Cheng, R.-K., Birkett, E., Jesuthasan, S. & Chew, L. Y. Dynamics and potential significance of spontaneous activity in the habenula. eneuro 9, ENEURO.0287-21.2022 (2022).
  34. Lombardi, F., Pepić, S., Shriki, O., Tkačik, G. & De Martino, D. Statistical modeling of adaptive neural networks explains co-existence of avalanches and oscillations in resting human brain. Nat. Comput. Sci. 3, 254-263 (2023).
  35. Guay, C. S. & Plourde, G. Handgrip dynamometry for continuous assessment of volitional control during induction of anesthesia: a prospective observational study. Can. J. Anesth. Can. d’Anesth.ésie 66, 48-56 (2019).
  36. Cummings, G. C. et al. Dose requirements of (Propofol, ‘Diprivan’) in a new formulation for induction of anaesthesia. Anaesthesia 39, 1168-1171 (1984).
  37. Marsh, B., White, M., Morton, N. & Kenny, G. N. C. Pharmacokinetic model driven infusion of propofol in children. Br. J. Anaesth. 67, 41-48 (1991).
  38. Purdon, P. L. et al. Electroencephalogram signatures of loss and recovery of consciousness from propofol. Proc. Natl Acad. Sci. USA 110, E1142-E1151 (2013).
  39. Li, J. & Shew, W. L. Tuning network dynamics from criticality to an asynchronous state. PLOS Comput. Biol. 16, e1008268 (2020).
  40. Zeraati, R., Engel, T. A. & Levina, A. A flexible bayesian framework for unbiased estimation of timescales. Nat. Comput. Sci. 2, 193-204 (2022).
  41. Gao, R., van den Brink, R. L., Pfeffer, T. & Voytek, B. Neuronal timescales are functionally dynamic and shaped by cortical microarchitecture. Elife 9, e61277 (2020).
  42. Reimann, M. W. et al. A biophysically detailed model of neocortical local field potentials predicts the critical role of active membrane currents. Neuron 79, 375-390 (2013).
  43. Suzuki, M. & Larkum, M. E. Dendritic calcium spikes are clearly detectable at the cortical surface. Nat. Commun. 8, 276 (2017).
  44. Petermann, T. et al. Spontaneous cortical activity in awake monkeys composed of neuronal avalanches. Proc. Natl Acad. Sci. USA 106, 15921-15926 (2009).
  45. Iacaruso, M. F., Gasler, I. T. & Hofer, S. B. Synaptic organization of visual space in primary visual cortex. Nature 547, 449-452 (2017).
  46. Scholl, B., Wilson, D. E. & Fitzpatrick, D. Local order within global disorder: synaptic architecture of visual space. Neuron 96, 1127-1138.e4 (2017).
  47. Kerlin, A. et al. Functional clustering of dendritic activity during decision-making. Elife 8, e46966 (2019).
  48. Ju, N. et al. Spatiotemporal functional organization of excitatory synaptic inputs onto macaque v1 neurons. Nat. Commun. 11, 697 (2020).
  49. Lafourcade, M. et al. Differential dendritic integration of long-range inputs in association cortex via subcellular changes in synaptic ampa-to-nmda receptor ratio. Neuron 110, 1532-1546.e4 (2022).
  50. Gugino, L. D. et al. Quantitative eeg changes associated with loss and return of consciousness in healthy adult volunteers anaesthetized with propofol or sevoflurane. Br. J. Anaesth. 87, 421-428 (2001).
  51. Murphy, M. et al. Propofol anesthesia and sleep: a high-density EEG study. Sleep 34, 283-291 (2011).
  52. Lewis, L. D. et al. Rapid fragmentation of neuronal networks at the onset of propofol-induced unconsciousness. Proc. Natl Acad. Sci. USA 109, E3377-E3386 (2012).
  53. Huupponen, E. et al. Electroencephalogram spindle activity during dexmedetomidine sedation and physiological sleep. Acta Anaesthesiol. Scand. 52, 289-294 (2008).
  54. Ma, J. & Leung, L. S. Limbic system participates in mediating the effects of general anesthetics. Neuropsychopharmacology 31, 1177-1192 (2006).
  55. Johnson, B. W., Sleigh, J. W., Kirk, I. J. & Williams, M. L. High-density EEG mapping during general anaesthesia with xenon and propofol: a pilot study. Anaesth. Intensive Care 31, 155-163 (2003).
  56. Amzica, F. & Steriade, M. Electrophysiological correlates of sleep delta waves. Electroencephalogr. Clin. Neurophysiol. 107, 69-83 (1998).
  57. Steriade, M. Corticothalamic resonance, states of vigilance and mentation. Neuroscience 101, 243-276 (2000).
  58. Le Masson, G., Renaud-Le Masson, S., Debay, D. & Bal, T. Feedback inhibition controls spike transfer in hybrid thalamic circuits. Nature 417, 854-858 (2002).
  59. Tagliazucchi, E. et al. Increased global functional connectivity correlates with LSD-induced ego dissolution. Curr. Biol. 26, 1043-1050 (2016).
  60. Toker, D. et al. Consciousness is supported by near-critical slow cortical electrodynamics. Proc. Natl Acad. Sci. USA 119, 1-12 (2022).
  61. Malmivuo, J. & Plonsey, R. Bioelectromagnetism (Oxford Univ. Press, Oxford, 1995).
  62. Palmer, L., Murayama, M. & Larkum, M. Inhibitory regulation of dendritic activity in vivo. Front. Neural Circuits 6, 26 (2012).
  63. lascone, D. M. et al. Whole-neuron synaptic mapping reveals spatially precise excitatory/inhibitory balance limiting dendritic and somatic spiking. Neuron 106, 566-578.e8 (2020).
  64. Karimi, A., Odenthal, J., Drawitsch, F., Boergens, K. M. & Helmstaedter, M. Cell-type specific innervation of cortical pyramidal cells at their apical dendrites. Elife 9, 1-23 (2020).
  65. Hagen, E., Næss, S., Ness, T. V. & Einevoll, G. T. Multimodal modeling of neural network activity: computing lfp, ecog, eeg, and meg signals with lfpy 2.0. Front. Neuroinform. 12, 92 (2018).
  66. Carnevale, N. T. & Hines, M. L. The NEURON Book (Cambridge University Press, 2006). https://doi.org/10.1017/ CBO9780511541612.
  67. Fonov, V., Evans, A., McKinstry, R., Almli, C. & Collins, D. Unbiased nonlinear average age-appropriate brain templates from birth to adulthood. Neuroimage 47, S102 (2009).
  68. Fonov, V. et al. Unbiased average age-appropriate atlases for pediatric studies. Neuroimage 54, 313-327 (2011).
  69. Carlo, C. N. & Stevens, C. F. Structural uniformity of neocortex, revisited. Proc. Natl Acad. Sci. USA 110, 1488-1493 (2013).
  70. Volgushev, M., Chauvette, S. & Timofeev, I. Long-range correlation of the membrane potential in neocortical neurons during slow oscillation. in Progress in Brain Research 181-199 (2011). https://doi. org/10.1016/B978-0-444-53839-0.00012-0.
  71. Einevoll, G. T., Kayser, C., Logothetis, N. K. & Panzeri, S. Modelling and analysis of local field potentials for studying the function of cortical circuits. Nat. Rev. Neurosci. 14, 770-785 (2013).
  72. Jones, S. R. et al. Quantitative analysis and biophysically realistic neural modeling of the MEG mu rhythm: rhythmogenesis and modulation of sensory-evoked responses. J. Neurophysiol. 102, 3554-3572 (2009).
  73. Studenova, A. A., Villringer, A. & Nikulin, V. V. Non-zero mean alpha oscillations revealed with computational model and empirical data. PLoS Comput. Biol. 18, e1010272 (2022).
  74. Cutts, C. S. & Eglen, S. J. Detecting pairwise correlations in spike trains: an objective comparison of methods and application to the study of retinal waves. J. Neurosci. 34, 14288-14303 (2014).
  75. Struys, M. M. R. F. et al. Comparison of plasma compartment versus two methods for effect compartment-controlled target-controlled infusion for propofol. Anesthesiology 92, 399-399 (2000).
  76. Muthukumaraswamy, S. D. High-frequency brain activity and muscle artifacts in MEG/EEG: a review and recommendations. Front. Hum. Neurosci. 7, 138 (2013).
  77. Sceniak, M. P. & Maclver, M. B. Slow mediated synaptic transmission in rat visual cortex. BMC Neurosci. 9, 8 (2008).
  78. Brake, N. et al. EEG data during propofol anesthesia and a biophysical model of the EEG spectral trend. figshare. https://doi.org/10. 6084/m9.figshare. 24777990 (2023).
  79. Brake, N. niklasbrake/EEG_modelling: Manuscript revisions (v1.0.0). Zenodo. https://zenodo.org/doi/10.5281/zenodo. 10359817 (2023).

شكر وتقدير

تم دعم هذا العمل من قبل مجلس أبحاث العلوم الطبيعية والهندسة في كندا (NSERC) منحة الاكتشاف (RGPIN-2019O4520) إلى A.K. تم دعم N.B. من قبل منحة الدراسات العليا NSERC-CREATE في الديناميات المعقدة وصندوق أبحاث كيبيك.
  • منحة تدريب الدكتوراه في الطبيعة والتكنولوجيا (FRQNT). لم يكن للممولين أي دور في تصميم الدراسة، جمع البيانات وتحليلها، اتخاذ قرار النشر، أو إعداد المخطوطة.

مساهمات المؤلفين

تصور: ن.ب.، ج.ب. و أ.ك. تنسيق البيانات: ن.ب. و ج.ب. التحليل الرسمي: ن.ب. الحصول على التمويل: أ.ك. و ج.ب. التحقيق: ن.ب.، ف.د.، أ.ر.، ف.أ.، س.س. و ج.ب. المنهجية: ن.ب. إدارة المشروع: أ.ك. و ج.ب. البرمجيات: ن.ب. الإشراف: أ.ك. و ج.ب. التصور: ن.ب. كتابة المسودة الأصلية: ن.ب. الكتابة – المراجعة والتحرير: ن.ب.، أ.ك. و ج.ب.

المصالح المتنافسة

يعلن المؤلفون عدم وجود مصالح متنافسة.

معلومات إضافية

معلومات إضافية النسخة الإلكترونية تحتوي على
المواد التكميلية متاحة على
https://doi.org/10.1038/s41467-024-45922-8.
يجب توجيه المراسلات والطلبات للحصول على المواد إلى أنمار خضر أو جيل بلورد.
معلومات مراجعة الأقران تشكر مجلة Nature Communications ريتشارد قاو وبالاز هانغيا على مساهمتهما في مراجعة هذا العمل. يتوفر ملف مراجعة الأقران.
معلومات إعادة الطباعة والتصاريح متاحة على
http://www.nature.com/reprints
ملاحظة الناشر: تظل شركة سبرينجر ناتشر محايدة فيما يتعلق بالمطالبات القضائية في الخرائط المنشورة والانتماءات المؤسسية.
الوصول المفتوح. هذه المقالة مرخصة بموجب رخصة المشاع الإبداعي النسب 4.0 الدولية، التي تسمح بالاستخدام والمشاركة والتكيف والتوزيع وإعادة الإنتاج بأي وسيلة أو صيغة، طالما أنك تعطي الائتمان المناسب للمؤلفين الأصليين والمصدر، وتوفر رابطًا لرخصة المشاع الإبداعي، وتوضح ما إذا تم إجراء تغييرات. الصور أو المواد الأخرى من طرف ثالث في هذه المقالة مشمولة في رخصة المشاع الإبداعي الخاصة بالمقالة، ما لم يُشار إلى خلاف ذلك في سطر الائتمان للمواد. إذا لم تكن المادة مشمولة في رخصة المشاع الإبداعي الخاصة بالمقالة وكان استخدامك المقصود غير مسموح به بموجب اللوائح القانونية أو يتجاوز الاستخدام المسموح به، ستحتاج إلى الحصول على إذن مباشرة من صاحب حقوق الطبع والنشر. لعرض نسخة من هذه الرخصة، قم بزيارة http://creativecommons.org/licenses/by/4.0/.
© المؤلفون 2024
  1. ¹برنامج الدكتوراه في علوم الحياة الكمية، جامعة مكغيل، مونتريال، كندا. قسم الفسيولوجيا، جامعة مكغيل، مونتريال، كندا.
    قسم التخدير، جامعة مكغيل، مونتريال، كندا. كلية التمريض، جامعة مكغيل، مونتريال، كندا.
    البريد الإلكتروني: anmar.khadra@mcgill.ca; gilles.plourde@mcgill.ca

Journal: Nature Communications, Volume: 15, Issue: 1
DOI: https://doi.org/10.1038/s41467-024-45922-8
PMID: https://pubmed.ncbi.nlm.nih.gov/38374047
Publication Date: 2024-02-19

A neurophysiological basis for aperiodic EEG and the background spectral trend

Received: 6 September 2023
Accepted: 6 February 2024
Published online: 19 February 2024
(D) Check for updates

Niklas Brake © , Flavie Duc , Alexander Rokos © , Francis Arseneau , Shiva Shahiri © , Anmar Khadra (1) & Gilles Plourde (1)

Electroencephalograms (EEGs) display a mixture of rhythmic and broadband fluctuations, the latter manifesting as an apparent spectral trend. While network oscillations are known to generate rhythmic EEG, the neural basis of broadband EEG remains unexplained. Here, we use biophysical modelling to show that aperiodic neural activity can generate detectable scalp potentials and shape broadband EEG features, but that these aperiodic signals do not significantly perturb brain rhythm quantification. Further model analysis demonstrated that rhythmic EEG signals are profoundly corrupted by shifts in synapse properties. To examine this scenario, we recorded EEGs of human subjects being administered propofol, a general anesthetic and GABA receptor agonist. Drug administration caused broadband EEG changes that quantitatively matched propofol’s known effects on GABA receptors. We used our model to correct for these confounding broadband changes, which revealed that delta power, uniquely, increased within seconds of individuals losing consciousness. Altogether, this work details how EEG signals are shaped by neurophysiological factors other than brain rhythms and elucidates how these signals can undermine traditional EEG interpretation.
Electroencephalograms (EEGs) display a mixture of periodic and aperiodic fluctuations. Almost a century of research has established that periodic EEG signals are generated by synchronous neural oscillations . In contrast, aperiodic EEG signals remain relatively poorly understood. Whereas periodic EEG signals produce peaks in power spectra, the aperiodic component manifests as the background spectral trend that decays with apparent behaviour . Differences in the spectral exponent, , have been correlated with aging, cognitive performance, neurological disorders, anesthesia, and sleep . In addition to being a useful biomarker, it has been proposed that the EEG spectral trend may change independently of neural oscillations and that spectral detrending is necessary to accurately quantify differences in brain rhythms . Deciphering the neurophysiological basis of aperiodic EEG is thus necessary for correctly interpreting EEG biomarkers and for improving algorithms that quantify brain rhythms.
There exist two main hypotheses for how the EEG spectral trend is generated by the brain. The synaptic timescale hypothesis predicts that the EEG spectral trend is a natural consequence of exponentially decaying synaptic currents, and that consequently asynchronous network activity will produce a spectrum with a or “Lorentzian” trend . The second hypothesis is based on the theory of self-organized criticality which posits that the propagation of action potentials throughout neural networks produces so-called “avalanches” of activity with magnitudes following a distribution . It has been hypothesized that such avalanche dynamics in turn generate a trend in . These theories are different in two important respects. Firstly, the avalanche hypothesis implies that the trend in EEG spectra is informative about the dynamics of the brain, while the synaptic timescales hypothesis is agnostic. Secondly, the two theories suggest different shapes for the spectral trend and therefore propose distinct methods for detrending EEG spectra .
Despite these hypotheses, the concept of aperiodic EEG itself remains controversial. Some argue that the apparent trend in EEG spectra is an epiphenomenon caused by slower brain rhythms recruiting larger populations of neurons . According to this viewpoint, the EEG spectrum does not require detrending and the spectral exponent is a conflated measure of various changes in brain rhythms.
Three questions therefore remain open: (1) can EEG signals reflect arrhythmic neural activity? (2) if so, how do these signals shape EEG spectra? (3) do EEG spectra need to be detrended, and if so, what is the most physiologically meaningful method of detrending? To investigate these questions, we combined numerical forward modelling of scalp potentials with biophysical calculations of single-neuron dipoles . With this approach, we simulated biophysically realistic EEG signals generated by networks exhibiting a range of dynamics. These simulations revealed several mechanisms, besides brain rhythms, that affect EEG signals and together shape the spectral trend. To test model predictions, we recorded EEG of humans receiving an infusion of the drug propofol, a general anesthetic that targets GABA receptors and slows the decay time of inhibitory synaptic currents . These experiments identified specific EEG changes during propofol administration that were expected to contaminate brain rhythm estimates. Using our modelling insights, we corrected for these sources of contamination and reevaluated known EEG signatures of losing consciousness. Overall, this study develops a biophysically grounded theory describing the neural basis of aperiodic scalp potentials and provides practical conclusions for the spectral analysis of EEG data.

Results

EEG cannot reflect asynchronous neural activity

To understand the neurophysiology that underlies the EEG spectral trend, we began by investigating the properties of EEG generation at the single-neuron level. These properties are informative because they shape the ensemble EEG regardless of coherence or neural synchrony
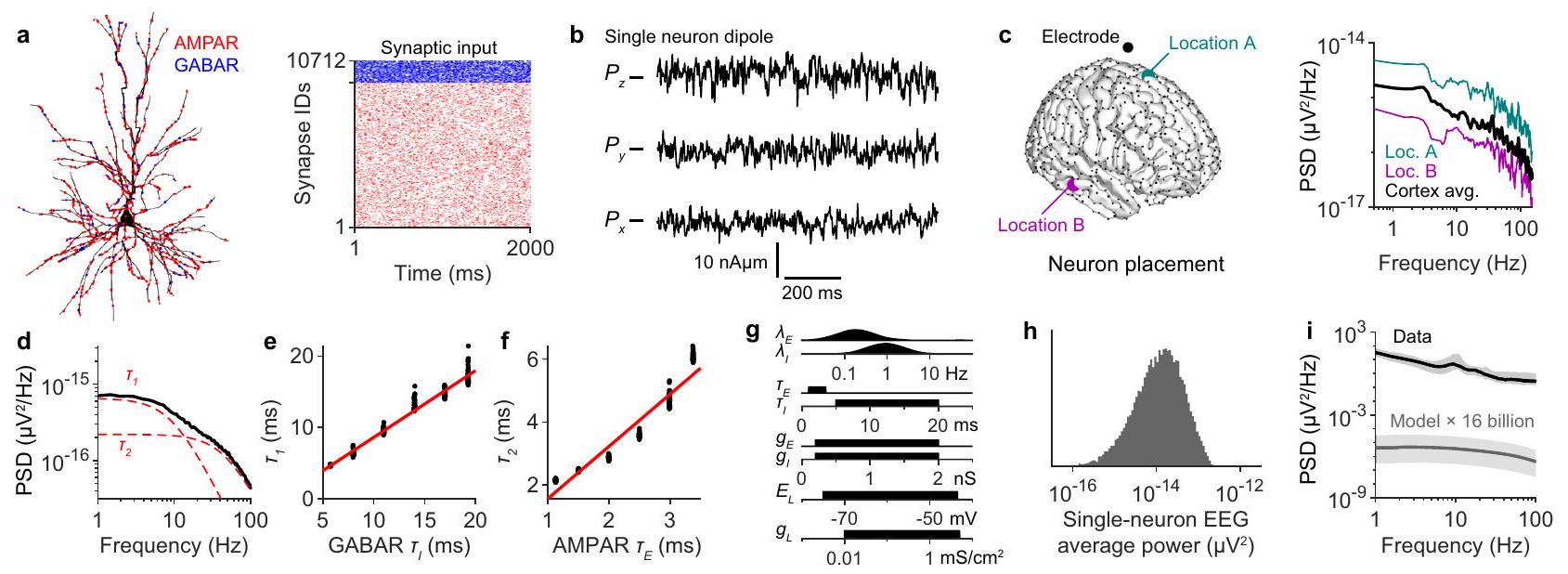
(See Definitions and theoretical framework in Methods). To examine these properties, we performed simulations of biophysically and morphologically detailed neuron models (Fig. 1a). To start, we did not assume any dynamics of presynaptic neurons and therefore modelled synaptic input with independent Poisson spike trains (Fig. 1a), an assumption that we relax later. From these currents, a single-neuron dipole was computed (Fig. 1b). The neuron was placed at a random location in the cortex and the single-neuron EEG signal was calculated using the New York head model (Fig. 1c). This entire procedure was repeated many times with various representative neuron morphologies (Table S1) and with the neurons placed at various locations in the cortex. The average spectrum, which we will refer to as a unitary spectrum, is the expected EEG spectrum generated by a single average cortical neuron (Fig. 1d).
The unitary spectrum exhibited two important features. First, even with random synaptic input, the unitary spectrum displayed a trend. This trend could be described as the sum of two Lorentzian functions
as predicted by simple linear models of EEG generation (Fig. 1d). The slower ( ) and faster ( ) timescales were governed by the deactivation kinetics of GABA receptors (GABARs) and AMPA receptors (AMPARs), respectively (Fig. 1e, f). These simulations validate previous predictions that the relative contribution of excitatory and inhibitory currents to the EEG signal fundamentally affects the spectral trend .
Second, the unitary spectrum reflects the amplitude with which an average neuron contributes to the EEG signal. To investigate this idea in more detail, we examined the effect of varying all the model parameters within physiologically reasonable ranges (Fig. 1g). Measuring the average power of the resulting single-neuron EEGs revealed
Fig. 1 | EEG cannot reflect asynchronous neural activity. a Example morphology of a layer pyramidal neuron. Inputs at AMPAR (red) and GABAR (blue) synapses were simulated with Poissonian spike trains, shown in raster plot. Only 1000 synapses shown for clarity. Neuron morphology adapted from Budd, J. M. L. et al. Neocortical axon arbors trade-off material and conduction delay conservation. PLoS Comput. Biol. 6, e1000711 (2010). b The x, y, and z components of the single-neuron dipole vector, calculated from (a). c Left: single-neuron EEG signals were simulated at the marked electrode location, with the neuron located at various source locations, e.g., location A and B. Right: the location-averaged EEG spectrum (black) computed by averaging over the source locations shown in black dots on the brain template. Loc.=location; Avg.=average. d Location-averaged spectrum generated from 1000 simulations of 11 representative neuron morphologies (Table S1). The spectrum was fit by Eq. 1 and the two Lorentzian components are shown in dashed red lines. The unitary spectrum was calculated while varying the
deactivation kinetics of GABARs ( ) and the parameter was estimated. Red line has a slope of 1 . f Same as e, but showing as a function of the deactivation kinetics of AMPARs . g Sampling distributions for model parameters. , and represent the average input rate, the deactivation time constant, and maximal conductance for AMPAR synapses. , and represent the same parameters for GABAR synapses. and represent the reversal potential and conductance of the passive membrane leak current. Distribution of single-neuron EEG power (loca-tion-averaged as in c) based on 20,000 simulations with parameters sampled from the distributions shown in (g) and morphologies sampled as described in Table S1. i Black: Median EEG spectrum across 14 subjects, with error bands indicating minimum and maximum spectral density. Grey: the predicted EEG spectrum of 16 billion uncorrelated neurons receiving Poissonian synaptic input (grey), with parameter values sampled from the distributions in (g). Error bands reflect 5-95% quantile range.
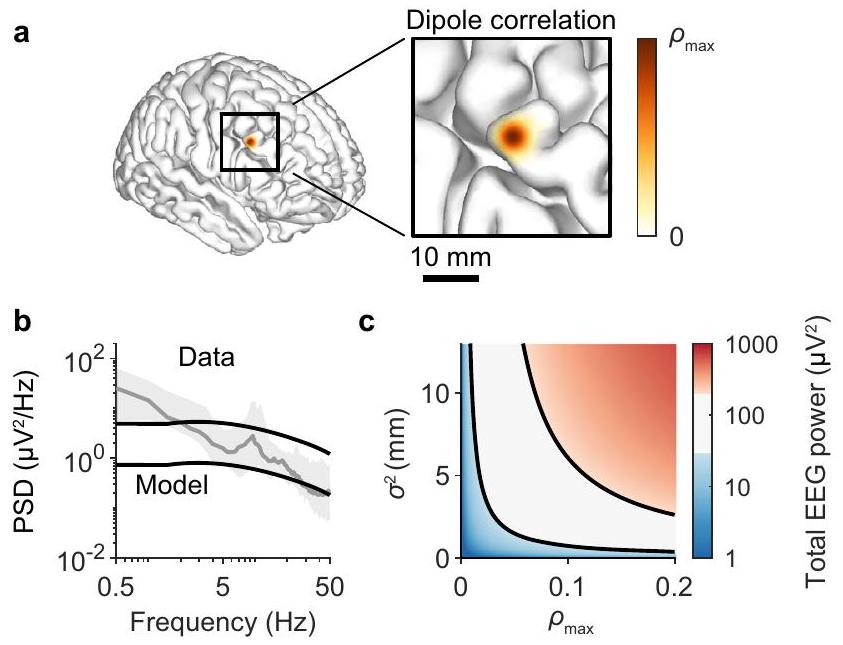
Fig. 2 | Detectable EEG signals require only weak, locally synchronized dipoles. a Schematic displaying the coupling kernel used to correlate single-neuron dipoles. The kernel is a Gaussian function with peak of and variance Median EEG spectrum across 14 human subjects (grey; same error bands as Fig. 1i), and simulated unitary spectrum (black; same as Fig. 1d) scaled by arbitrary amounts to determine a lower and upper bound of the spectral trend amplitude. c Heatmap of the total simulated EEG power produced by 16 billion neurons with dipoles coupled with the kernel in (a), and parameterized with various values of and . The black lines are level curves representing the lower and upper bounds for the spectral trend magnitude obtained in (b).
a range of possible amplitudes for the contribution of individual neurons to the EEG signal (Fig. 1h). These simulations show that no physiologically plausible parameters could allow 16 billion uncorrelated neurons to generate detectable EEG signals (Fig. 1i). More importantly, these calculations quantify how far off a completely asynchronous cortex is from generating detectable EEG signals. These calculations account for the EEG strength contributed by synaptic current amplitudes, neuron geometry, average firing rate of neurons, the number of neurons, the conductivity of various tissues, and the geometry of the cortex. Therefore, this result indicates that neural dynamics are responsible for the approximate four orders of magnitude difference between the simulated asynchronous spectrum and real EEG recordings.

Detectable EEG requires only weak, locally synchronized dipoles

If the amplitude of EEG signals precludes asynchronous activity from shaping EEG spectra, what types of arrhythmic activity could influence EEG signals? To begin addressing this question, we first quantified in general how much dipole correlation is required to generate detectable EEG signals. To do so, we imposed a simplified spatial organization on a cortical template whereby neighbouring neurons produced correlated dipoles. Specifically, the dipoles of neurons separated by mm were correlated with a coefficient of , where is the maximal dipole correlation and is the spatial scale over which correlations decline (Fig. 2a). Based on this correlation scheme, the geometry of the cortex, average densities of neurons, and the single-neuron EEG amplitudes from the previous section, we estimated the power of the ensemble EEG signal that would be produced with different values of and (see Methods). To capture the EEG spectral trend, we estimated that broadband EEG signals need to have a total power of between 50 and (Fig. 2b). Thus for neural activity to generate detectable EEG signals, this activity needs to be capable of driving single-neuron dipoles that are correlated up to a value ( ) of (Fig. 1c), assuming a liberal range for of (Fig. 1c; see Methods). While the existence of EEG rhythms prove that neural oscillations can generate the requisite dipole
synchrony, it remains to be determined if and how such a degree of dipole coherence may be achieved by arrhythmic neural activity.

Synapse topology is sufficient for dipole correlations

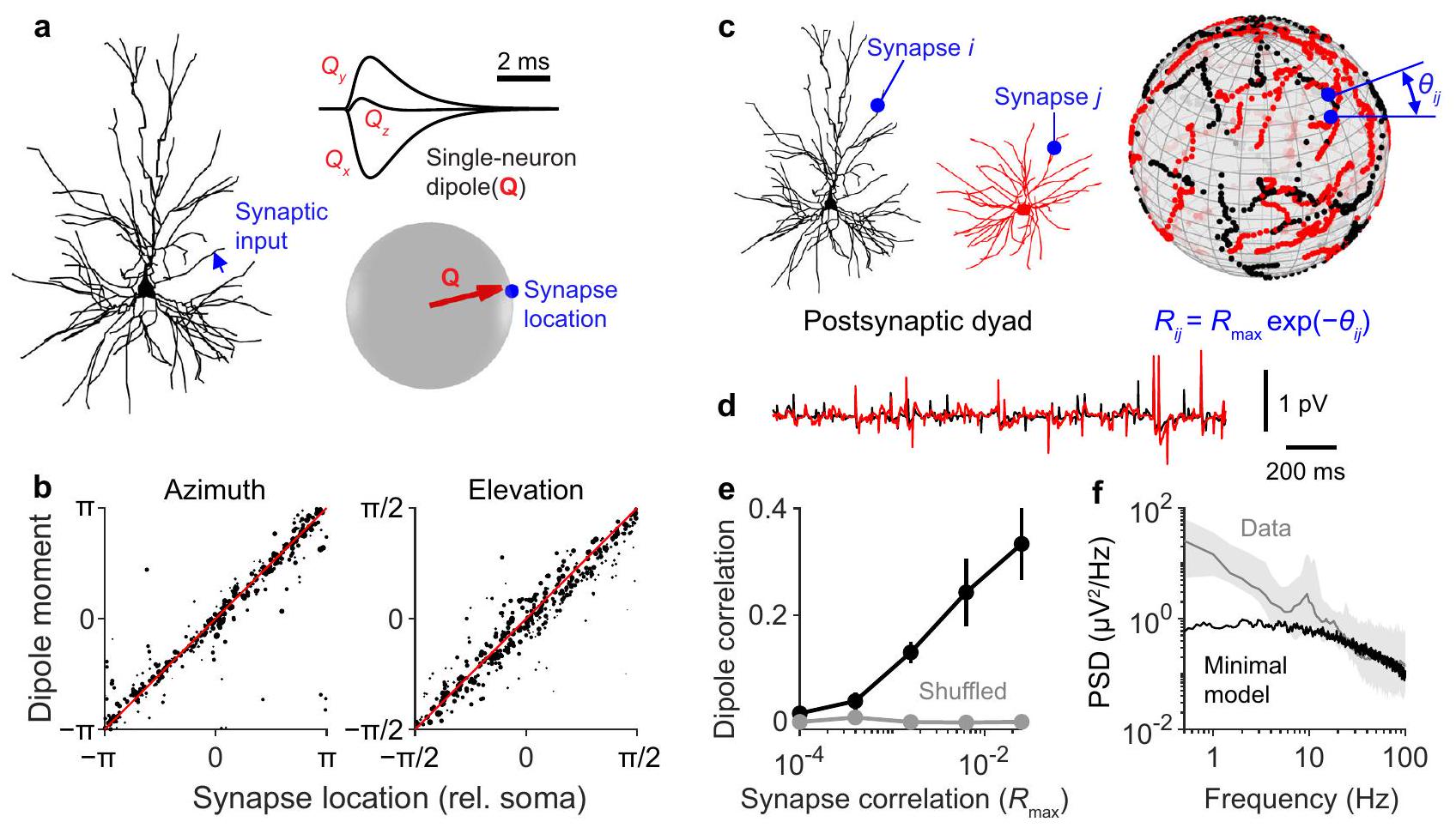
To investigate the ability of neural activity to generate coherent dipoles, we simulated dyads of neurons and investigated the level of correlation achievable between the two single-neuron dipoles. In our simulations, we noticed that if a single synapse was activated, the orientation of the resulting dipole could be accurately predicted by the orientation of the synapse relative to the soma (Fig. 3a, b). This result held across all neuron morphologies investigated (Fig. S1). From this observation, we devised a minimal model of dipole coherence. To generate synaptic input, we projected the synapses of two neurons onto a sphere and correlated the inputs of synapses with close angular distances (Fig. 3c). By changing the maximal correlation between synapses, dipole correlation between neurons of various morphologies could be tuned continuously between 0 and (Fig. 3d, e). Shuffling the location of the synapses abolished any dipole correlation (Fig. 3d). These results demonstrate that to generate detectable EEG signals, it is necessary and sufficient for synaptic input to exhibit temporal and spatial correlation. These conditions do not by themselves preclude any specific type of neural dynamics. Indeed this minimal model relied on independently sampled spikes at every time point and thus generated EEG signals with no temporal autocorrelation and a spectrum with the same shape as the asynchronous unitary spectrum (Fig. 3f). Therefore, the plausibility of aperiodic EEG signals depends solely on the ability for a network of neurons to generate arrhythmic activity with the requisite levels of spatiotemporal correlation.

Subcritical networks can generate aperiodic EEG signals

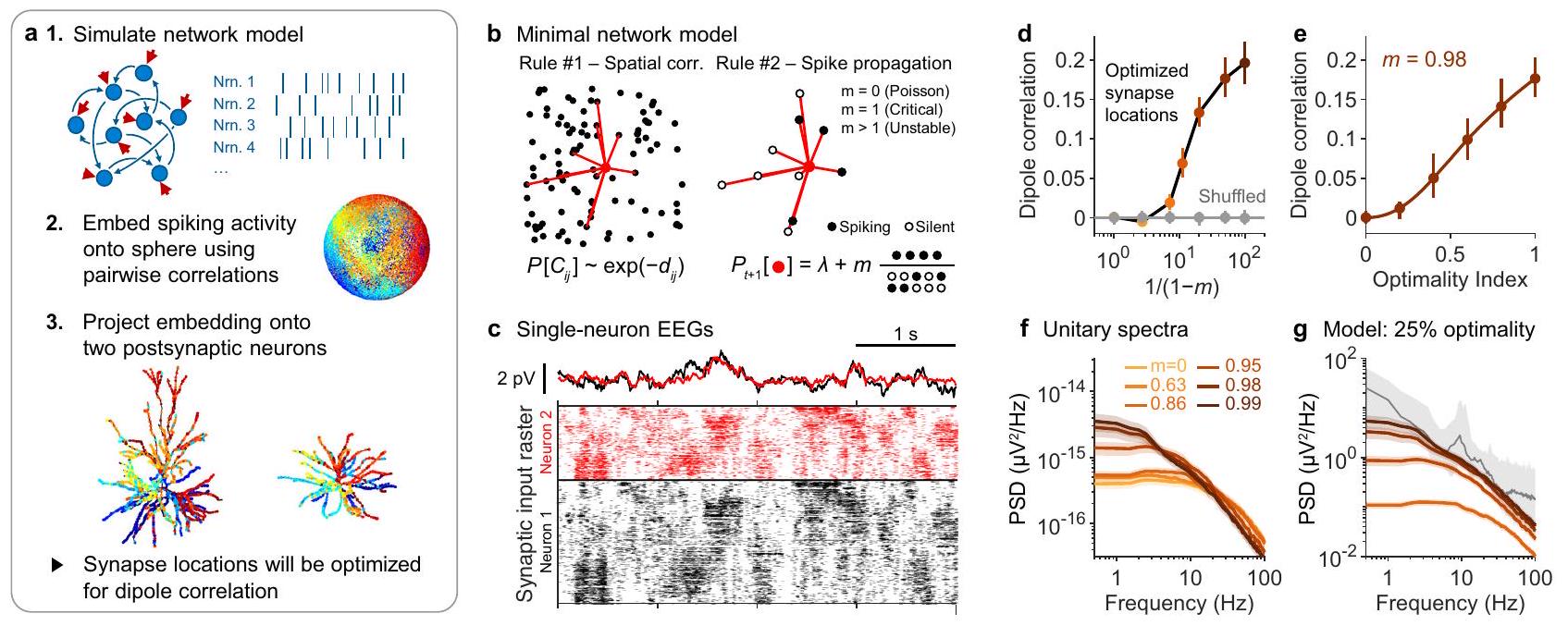
We next investigated network models that could generate detectable, aperiodic EEG signals. To determine whether network activity could produce coherent dipoles, we utilized the results from the previous section (Fig. 3). After simulating a presynaptic neuron population, we used the UMAP algorithm to embed the population onto a sphere in such a way that minimized the distance between presynaptic neurons with correlated spiking activity (Fig. 4a). These presynaptic neurons were then projected onto the dendrites of the postsynaptic dyad (Fig. 4a). By construction, synapses with higher correlations should have smaller angular distances, thus optimizing for dipole coherence. Effectively, this procedure tests whether it is geometrically possible for a network to generate sufficiently coherent synaptic input for EEG generation.
To understand the mechanisms of aperiodic EEG generation, we attempted to construct the simplest network that could generate dipole coherence. Our previous results demonstrate that randomly connected networks cannot generate coherent dipoles, because they cannot produce spatially correlated activity. We therefore continued on to use the simplest neural network that exhibits spatial topology, namely, a spatial network. To construct the network, each neuron was embedded in a plane and connected preferentially to nearby neurons (Fig. 4b). For simplicity, we modelled individual neurons as binary nodes, i.e., each neuron was either spiking or quiescent. Spikes propagated along network connections, causing subsequent neurons to fire with some probability (Fig. 4b). This simple model falls within the category of a branching network, because the dynamics are governed by a single parameter called the branching number, denoted by , which reflects the average number of spikes successfully elicited across the network when a single neuron fires.
Our simulations revealed that the maximal achievable dipole correlation increased with the network’s branching number (Fig. 4c,d). A purely asynchronous network ( ) was unsurprisingly incapable of generating correlations among single-neuron dipoles (Fig. 4d). On the other hand, a slightly subcritical network ( ) was capable of
Fig. 3 | A minimal model of dipole correlation captures broadband EEG amplitude but not low frequency power. a A single synapse was activated at the location specified by the blue arrow, generating a response in the single-neuron dipole, . The dipole vector at the peak of the response is oriented towards the synapse location, defined in spherical coordinates with the soma as the origin. Neuron morphology adapted from Budd, J. M. L. et al. Neocortical axon arbors trade-off material and conduction delay conservation. PLoS Comput. Biol. 6, e1000711 (2010). b The simulation in a was repeated 600 times with different neuron morphologies and synapse locations. Plotting the dipole orientation at the peak of the response against the location of the stimulated synapse shows a strong, linear relationship. Some points not plotted for clarity. Dot size is proportional to peak dipole amplitude. rel.=relative. c Schematic showing the minimal model for dipole correlation. Synapses on each postsynaptic neuron in the dyad were projected onto a sphere. A correlation matrix among all synapses was then defined
such that synapses separated by an angle on the sphere were correlated by . The left neuron’s morphology is adapted from Budd, J. M. L. et al. Neocortical axon arbors trade-off material and conduction delay conservation. PLoS Comput. Biol. 6, e1000711 (2010). The illustration of the right neuron is adapted, with permission from SNCSC, from Mainen, Z. F. & Sejnowski, T. J. Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 382, 363-366 (1996), Springer Nature. d Example of single-neuron EEG signals of the two neurons shown in (c). e Correlation between two single-neuron dipoles as a function of . Vertical lines represent confidence intervals of the mean ( different morphology pairs). When synapse locations are shuffled, dipoles are no longer correlated (grey). The unitary spectrum of neurons receiving input calculated with the minimal model (black), scaled to compare the shape of the spectrum with median EEG spectrum of 14 subjects (grey line; same as Fig. 1i).
generating dipoles that were correlated by for an average pair of postsynaptic neurons (mean SE, ; morphologies sampled as described in Table S1; biophysical parameters sampled as in Fig. 1g). This branching number is significant because previous work has found that networks with a branching number of closely reproduced the in vivo dynamics of cortical spiking across many different species , making this a physiologically plausible parameter value. Placing synapses suboptimality led to proportionally lower dipole correlation, revealing that subcritical dynamics can still drive coherent dipoles with suboptimal synapse placement (Fig. 4e). Based on the amplitude of the computed unitary spectrum (Fig. 4f), we estimated that subcritical network activity can produce realistic EEG amplitudes with synapse optimality as low as (Fig. 4 g ; see Methods). As a reference, an optimality index of means that strongly correlated synapses will on average lie on the same hemisphere of their respective neurons, a geometry reminiscent of the apical-basal compartmentalization of cortical pyramidal neurons.
Notably, stronger dipole correlations coincided with longer temporal autocorrelations in network activity (Fig. 4f), a phenomenon directly resulting from the causality of spike propagation (Fig. 4b). This means that EEG signals produced by propagating cortical spikes must have higher power at low frequencies if the signals are to be of detectable amplitudes. This result illustrates a fundamental constraint that may in part explain the scaling of EEG spectra at lower
frequencies (Fig. 4g). More broadly, these results demonstrate a biophysically feasible mechanisms that allows arrhythmic neural activity to generate EEG signals, and to consequently influence the broadband features of EEG spectra.
Narrowband EEG changes could result from arrhythmic activity The above calculations show that arrhythmic neural activity can in theory generate broadband EEG signals, meaning that narrowband EEG power need not reflect brain rhythms. We therefore asked whether EEG signals that are produced by arrhythmic activity can confound traditional EEG interpretation, namely, that changes in bandpower reflect differences in neural oscillations. To address this question, we considered a scenario where the EEG signal is generated by two subpopulations of neurons: a population exhibiting synchronous oscillations, and a second population exhibiting subcritical dynamics ( ). If these population are completely independent of one another, their EEG contributions will by definition add together linearly. To investigate further, we simulated the scenario in which the two populations’ postsynaptic signals are intermixed (Fig. 5a). One interpretation of this setup could be a cortical neuron that is receiving oscillatory input from, say, the thalamus, while also receiving subcritical input from the local cortical circuitry. Compared to neurons receiving entirely oscillatory input or entirely subcritical input, the neuron receiving mixed input produced a unitary EEG spectrum that
Fig. 4 | Subcritical network dynamics can explain the amplitude and low frequency power of broadband EEG. a llustration of the algorithm for optimizing dipole coherence. Nrn. = neuron. The left neuron morphology is adapted from Budd, J. M. L. et al. Neocortical axon arbors trade-off material and conduction delay conservation. PLoS Comput. Biol. 6, e1000711 (2010). The illustration of the right neuron is adapted, with permission from SNCSC, from Mainen, Z. F. & Sejnowski, T. J. Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 382, 363-366 (1996), Springer Nature. b Illustration of the rules used to produce spatiotemporal synchrony in a presynaptic network. Rule #1: network topology is enforced by making the probability of pairwise connections, , decrease exponentially with distance, . Rule #2: the probability of a neuron firing, , depends on a baseline firing rate of plus the average activity of its neighbours scaled by is a predefined average firing rate; is the branching number of the network. corr.=correlation. c Examples of single-neuron EEG signals of two neurons receiving input from the network model with a branching number
, when synapse locations have been optimized as described in (a). Bottom: a raster plot of synaptic input for the two neurons. d Correlation between two single-neuron dipoles as a function of the branching number, , of the presynaptic network. Dipole correlation increases with (coloured dots), but not when synapse locations are shuffled (grey). Median (dots) and 5-95% quantile range (vertical lines) across simulated dyads with randomly sampled morphologies (Table S1) and randomly sampled biophysical parameter values (as in Fig. 1g). e Dipole correlation can be tuned by placing synapses suboptimally (see Methods). Cubic interpolation between simulated optimality indices is shown with the solid line. Median (dots) and quantile range (vertical lines) across simulations. Unitary spectra calculated for different branching numbers. Error bands reflect confidence interval of the mean. The unitary spectra from (f) scaled based on a synapse optimality index of 0.25 (colours same as in ). The value of was determined from and the final scaling factor was determined as in Fig. 2. Grey: median EEG spectrum of 14 subjects (same as Fig. 1i).
exhibited a mixed phenotype (Fig. 5b). Increasing the strength of the oscillatory and/or aperiodic input altered the amplitude of the spectral peak and/or spectral trend (Fig. 5c-e). However, changes to the spectral trend did not multiplicatively scale the oscillatory peak amplitude. As a result, quantifying the amplitude of oscillatory peaks relative to the spectral trend produced incorrect interpretations (Fig. 5f-h): dividing the peak amplitude by the background trend erroneously suggested that the neural rhythm decreased when aperiodic activity became stronger (Fig. 5d, g), and severely underestimated the neural rhythm increase when aperiodic activity increased concomitantly (Fig. 5e, h). We therefore concluded that if a spectral peak is clearly discernible, then arrhythmic neural activity has a minimal confounding influence and detrending is unnecessary. Importantly, however, if no spectral peak is obvious, then there is no guarantee that changes in power result from differences in neural oscillations.

Spectral slope is an inconsistent measure of EI balance

The above results focused on the role of neural dynamics in shaping the EEG spectrum. However, Fig. 1d-f shows that the kinetics of postsynaptic responses also impact the broadband properties of EEG spectra. To further investigate this mechanism shaping EEG spectra, we performed a full sensitivity analysis of the spectral slope with respect to the biophysical parameters in the single-neuron models. The unitary EEG spectrum was simulated with many different parameter values (Fig. 6a) and the overall slope of the spectrum was calculated between 1 and 40 Hz (Fig. 6b). These simulations revealed that the spectral slope was consistently affected by four parameters: , , and (Fig. 6c). These results can be explained through Eq. 1. The parameter directly determines the slow timescale, , of the unitary spectrum (Fig. 1d), whereas synaptic conductances, and ,
directly govern the contributions of inhibitory and excitatory synaptic currents, respectively. The reversal potential, , of the leak current alters the spectral slope because when is more depolarized, receptors experience a higher driving force, thus amplifying the contributions of inhibitory currents.
Surprisingly, the analysis of the spectral slope revealed a strong interaction between and both and (Fig. 6c). When the leak conductance was low ( ), the spectral slope was found to be negatively correlated with the ratio (Fig. 6d, e; Fig. S2b), which contradicts the predictions of linear models of EEG generation . The reason is that when the leak conductance was low, higher E:I ratios drove the average membrane potential close to the reversal potentials of GABA receptors (Fig. S2a). This caused neurons with low to experience vanishing GABAR driving forces and amplified AMPAR driving forces at high E:I values, consequently and counterintuitively making the spectral slope anticorrelated with the E:I ratio (Fig. 6e). However, when the leak conductance was high ( ), the membrane potential fluctuated less and stayed within a relatively linear regime (Fig. S2a). Consequently the spectral slope was positively correlated with E:I ratio (Fig. 6e) as predicted by linear models of EEG generation . A similar albeit weaker effect was observed in the relationship between the spectral slope and the ratio (Fig. S2c). Generally, we conclude that the overall spectral trend is significantly affected by biophysical parameters that alter postsynaptic responses, but changes in the slope value do not alone inform what parameters are changing.

Changes to synaptic responses confound brain rhythm quantification

Differences in postsynaptic responses alter EEG spectra in a fundamentally different way to arrhythmic neural activity. Postsynaptic
Fig. 5 | Measuring oscillatory peak power relative to spectral trend may produce misleading results. a Illustration of mixed input model. Half of the neuron’s synapses received oscillatory rhythmic input (blue) and the other half received input from a subcritical network (red). The strengths of oscillatory and subcritical dynamics were adjusted by tuning two parameters, and , respectively, which determined the degree to which synaptic inputs differed from homogenous Poisson processes. See Methods for details. Neuron illustration created with BioRender.com. b Unitary spectrum for neurons receiving Poisson input (grey), compared with the unitary spectra for neurons receiving input entirely from the oscillatory population (left; black), entirely from the subcritical population (middle; black), or mixed input as in (a) (right; black): . c Oscillatory input was strengthened by increasing from 0.1 (black) to 0.5 (blue), with fixed at 0.1 .
Fig. 6 | Sensitivity of spectral slope to biophysical parameters governing
postsynaptic responses. a Sampling distributions for model parameters, the same as the ones used in Fig. 1g. b Example single-neuron EEG spectrum, fitted with the equation between 1 and 40 Hz . c Sensitivity of the spectral slope, , to model parameters, with first and second order interactions, calculated from 20,000
simulated spectra. d Simulated spectra were averaged depending on the ratio between and . Lower E:I ratios correspond to more inhibition. The spectral slope is plotted against the ratio for each simulation. Left: simulation where the leak conductance was low ( simulations). Right: simulation where the leak conductance was high ( simulations).
Fig. 7 | Changes in postsynaptic mechanisms confound brain rhythm quantification. a Unitary spectra for neurons receiving entirely subcritical input ( ; see Fig. 5a), before and after four parameter changes: subplot corresponding to ( ) shows the unitary spectrum when was increased from 10 ms (pink) to 30 ms (red); ( ) shows unitary spectrum when was increased from -60 mV (pink) to -45 mV (red); shows unitary spectrum when was increased from 0.7 nS (pink) to 1.4 nS (red); and ( ) shows unitary spectrum when was increased from 0.7 nS (pink) to 1.4 nS (red). Note the changes in the unitary spectra despite there being no changes in synaptic input dynamics. b Same as in (a), but for neurons receiving entirely oscillatory input ( ; see Fig. 5a). In
Fig. S3, we show examples of different types of rhythmic input. c Example of fitted spectral trend. Here, the unitary spectrum of sinusoidal input is shown before and after increasing . The spectra were fit using a FOOOF-like algorithm , except that here the trend was modelled using Eq. 1 (black lines). See other examples in Fig. S4. d Spectra from (c), detrended by dividing the spectra by their respective Lorentzian fits. See other examples in Fig. S4. e Change in EEG spectral density caused by increasing . In grey is the raw change in the unitary spectra, while in black is the difference between the detrended spectra. Detrending the spectra with Eq. 1 has corrected for the effects of increasing and correctly indicates that there are no changes in neural dynamics.
kinetics effectively interact as a convolution with synaptic input and should therefore interact with oscillatory peaks in a multiplicative manner. Moreover, postsynaptic mechanisms should affect power generated by all types of neural dynamics equally. To test this, we systematically altered the biophysical parameters that govern postsynaptic currents and analyzed the unitary spectra generated by various types of synaptic inputs, including white noise (Fig. S3), subcritical dynamics (Fig. 7a), as well as three types of dynamics that exhibit spectral peaks: a recently proposed recurrent Ising model that exhibits co-existence of oscillations and avalanches (Fig. S3), an underdamped second-order system driven by white noise (Fig. S3), and finally a simple sinusoidal rhythm (Fig. 7b). We investigated the effects of neurophysiological parameters that affect the spectral slope, as identified by our sensitivity analysis (Fig. 6c): GABAR kinetics , the leak current reversal potential , and the conductances of excitatory ( ) and inhibitory ( ) synapses. Changing these parameters altered the unitary spectra in distinct manners, but importantly had identical effects across the different types of the input dynamics (Fig. 7a, b; Fig. S3).
The spectral changes caused by altering biophysical parameters do not reflect differences in neural dynamics and therefore represent confounds for EEG analysis. To correct for the effects of these parameter changes, we fit the part of the spectral trend produced by synaptic timescales using a FOOOF-like algorithm , except that the background trend was modelled using Eq. 1 (Fig. 7c; Fig. S4). As anticipated, detrending the spectra in this way corrected for the confounding effects of the parameter changes (Fig. 7d, e; Fig. S4).
In conclusion, our modelling results indicate that there are two distinct mechanisms of peak-trend interaction in EEG spectra. In one case, there are changes in the relative contribution of rhythmic and arrhythmic neural activity to the EEG signal. In this case, the peaks and spectral trend change relatively independently from one another, and thus detrending is unnecessary for quantifying spectral peak amplitudes (see Discussion). In the other case, changes in biophysical parameters alter the mechanism of EEG generation itself. In this case, EEG differences are unrelated to neural dynamics; these changes can confound EEG signals from all neural sources, and thus even spectral peak amplitudes can be potentially corrupted.
Fig. 8 | Model predicts and quantifies effects of propofol administration on EEG spectra. a Representative EEG signal, Cz recording site, of a subject receiving an infusion of propofol until loss of consciousness (LOC). The estimated effect-site concentration of propofol is plotted below. b Mean LOC-aligned spectrogram of 14 subjects. c Average power spectrum at baseline (black), averaged between 0 and 10 s prior to propofol infusion, and after propofol infusion (red), averaged between 0 and 10 s prior to LOC. Shading reflects confidence intervals of the mean ( subjects). d Representative EEG spectrum at baseline, prior to propofol infusion (left, black) and 0-10 s prior to LOC (right, black). Spectra have been fitted with Eq. 6 (see Methods), using a FOOOF-like fitting algorithm that accounts for several Gaussian peaks in the spectra (solid blue). Fitted trend is shown with
dashed line. The parameter , estimated from fits to spectra computed in 2-s windows, plotted with respect to rescaled time. Shading reflects confidence intervals of the mean ( subjects). Left: fold change in the estimated value of plotted against the estimated effect-site concentration of propofol. Black line marks the mean for each concentration of propofol. Right: The estimated doseresponse plot from the left panel (darker colours reflect higher density of points) is superimposed with in vitro data taken from four studies: Study #1 , Study #2 , Study #3 , and Study #4 . The data values taken from these studies are presented in Table S2. The dash black line is a fitted Hill function to the data from the four studies: and Hill coefficient .
Model predicts and quantifies effects of propofol on EEG spectra The above results suggest that spectral detrending may be important in pharmacological experiments since many drugs target ion channels and alter postsynaptic responses. To test this model prediction, we investigated the EEG signatures of the general anesthetic propofol, a receptor modulator that lengthens the decay time of synaptic inhibition . We recorded the EEG of 14 subjects during a fixed-rate infusion of propofol lasting until loss of consciousness (LOC) (Fig. 8a). The moment of LOC was identified by the dropping of a held object, which has been shown to provide an accurate, binary measure of LOC with precise timing . The median LOC-aligned spectrogram was calculated from the Cz channel, which revealed an increase in low frequency power and a decrease in high frequency power starting before LOC (Fig. 8b). Comparing the average power spectrum at baseline ( prior to propofol infusion) to that following propofol infusion ( prior to LOC) revealed an increase in low frequency power and a decrease in high frequency power, thus giving the appearance of a rotation of the power spectrum (Fig. 8c).
Our modelling results suggest that propofol inflates low frequency power by increasing the slow timescale, , of the spectral trend (Figs. 1d, e; 7). To test this, we estimated from the EEG data by fitting a modified Eq. 1 to the EEG spectra (Eq. 6; see Methods). This modified function fit the spectral trend well except at frequencies less than (Fig. 8d; Fig. S5a-c), where our modelling results suggest the spectral trend is coloured primarily by neural dynamics, such as delta oscillations and/or subcritical network activity, but not synaptic kinetics (Figs. 4 and 5). Corroborating this interpretation, the low frequency ( ) part of the trend waxed and waned from second to second, occasionally disappearing entirely, whereas the fitted synaptic timescale remained stable between time windows (Fig. S5c). The extracted timescale, , was remarkably consistent prior to the infusion of propofol, with an average value of (mean SE, ) (Fig. 8e). Following the infusion of propofol, began increasing, reaching a value of ( ; paired two-tailed -test)
0-10 s prior to LOC (Fig. 8e). Similar changes were observed at other electrode sites (Fig. S6). By plotting the estimated value of at each time point against the estimated effect-site concentration of propofol, quantified using the Marsh model , we constructed a dose-response curve of fold change in against estimated propofol concentration (Fig. 8f). The inferred dose-response curve for quantitatively matched in vitro measurements of inhibitory postsynaptic current kinetics in the presence of bath applied propofol (Fig. 8f). Thus, the changes in were consistent with expectations based on propofol’s known pharmacology. These observations support the model’s prediction that GABAR kinetics significantly shape EEG spectra and that broadband EEG changes do not necessarily reflect differences in brain dynamics.

Correcting for synaptic timescales reveals a unique signature of LOC

Our modelling results predicted that propofol’s effect on synaptic timescales will produce errors in conventional quantifications of brain rhythms. Past studies have suggested that LOC from propofol is associated with changes in the delta ( ), alpha ( ), and beta ( ) frequency ranges . To investigate the consequences of spectral detrending on EEG signatures of LOC, we compared raw bandpower to detrended bandpower in the delta, alpha, and beta frequency ranges. To compare EEG dynamics across individuals, data were aligned simultaneously to the moment of propofol infusion and LOC; this was done by rescaling time in each experiment by the latency to LOC (median: 135 s ; range: ). Similar results were obtained when time was not rescaled (Fig. S5d). Consistent with previous studies , raw baseline-normalized power increased in the delta, alpha, and beta band following propofol infusion (Fig. 9a-c). Whereas alpha power increased quickly and plateaued prior to LOC, delta power rose slowly and continued increasing until after LOC (Fig. 9d). Notably, beta power increased concomitantly with alpha power, but then began decreasing prior to LOC, eventually
Fig. 9 | Correcting for synaptic timescales reveals a unique signature of losing consciousness. a Left: representative EEG power spectrum following LOC (black) of a single subject, superimposed on the power spectrum at baseline (blue). Right: power spectrum following LOC (black) normalized to baseline. b Mean baseline normalized spectrogram ( subjects). c Average baseline-normalized power prior to LOC (shading: confidence interval of mean). Power was significantly elevated within the delta ( , right-tailed sign test; subjects), alpha ( ), and beta ( ) frequency bands. Changes in alpha, beta, and delta power, aligned to both moment of propofol infusion and LOC, averaged across subjects (shading: 95% confidence interval of mean). Bars above graph indicate 0.05 -long segments of rescaled time where there is a statistically
significant increase ( , right-tailed sign test) in the corresponding frequency band power. Fig. S5d shows results without rescaled time. e Left: EEG spectrum following LOC, same as a, superimposed with fitted inhibitory timescale (Eq. 6). Fitted Gaussian peaks not shown. Right: detrended power, defined as power relative to fitted inhibitory timescale, in decibels. Mean detrended spectrogram, normalized to baseline ( subjects). g Detrended power 0-10 s prior to LOC, normalized to baseline (shading: 95% confidence interval of mean). Power was significantly elevated within the alpha ( ) and beta, ( ), but not delta ( ) frequency bands. Significance testing same as ( ). Same as in (d), but for detrended power, normalized to baseline.
producing a beta power not statistically different from baseline postLOC (Fig. 9d).
To correct for the confounding effects of propofol, we divided EEG power at each timepoint by the estimated synaptic timescales fitted from the previous section (Fig. 9e). We then normalized detrended power by the detrended power at baseline (Fig. 9f), such that changes in bandpower reflected the spectral changes unexplained by the increase in . This procedure entirely removed the apparent rotation in the EEG spectra following propofol infusion (Fig. 9g). As a result of this detrending, power in the alpha, beta, and delta bands clearly increased at distinct times (Fig. 9h). Alpha and beta power appeared following propofol infusion and plateaued well before LOC. In contrast, detrended delta power did not increase until the moment of LOC, at which point it increased sharply (Fig. 9h; Fig. S5d). In summary, whereas the raw EEG signal failed to exhibit a strongly timelocked signal at the moment of LOC, removing the anticipated confounds of propofol revealed a sharp increase in delta power within seconds of LOC. This analysis combined with our modelling results suggest that pharmacological changes to synaptic kinetics may mask the true dynamics of neural oscillations when spectral detrending is not performed. In addition, these results point to distinct roles for alpha and delta power in the function of propofol as a general anesthetic.

Discussion

In this study, we explored the neural basis of the EEG spectral trend and examined its implications for EEG interpretation and analysis. Several important conclusions came out of this investigation. First, this work provided biophysical evidence that arrhythmic neural activity is capable of generating detectable EEG signals. Second, our modelling consolidated the predictions of simpler computational models and indicated that the EEG spectral trend is shaped by the interactions of many factors, including synaptic kinetics, excitatory-inhibitory ratio, and aperiodic network dynamics. Third, our analysis revealed that
spectral peak amplitudes are minimally affected by fluctuations in arrhythmic neural activity. On the other hand, we found that systemic changes in synaptic current properties do necessitate detrending to accurately interpret spectral changes as variations in neural activity. Our results suggested that this latter scenario is particularly important for EEG recordings used in tandem with pharmacological interventions.
Traditional spectral analysis assumes that EEG power within canonical frequency bands reflect various brain rhythms. Our modelling results seriously challenge this assumption. Specifically, if a spectral peak is not evident within a given frequency band, our work justifies a physiologically plausible and biophysically realistic alternative hypothesis, namely, that the bandpower reflects broadband neural activity. Our results thus validate the principle assumption of spectral detrending methods, such as the FOOOF algorithm , which is that peak detection is a necessary prerequisite to quantifying oscillatory power. While power lying outside spectral peaks could potentially reflect neural rhythms, there is no theoretical guarantee for this interpretation based on spectral analysis alone.
Importantly, our results do not necessarily support a purely datadriven approach to detrending EEG spectra. While changes in arrhythmic activity affect spectral peaks in an additive manner (Fig. 5), changes in synaptic currents multiplicatively scale spectral peaks (Fig. 7); these two mechanisms thus require two distinct methods of detrending, i.e., subtractive versus divisive detrending, respectively. Without prior knowledge, it is unclear which method is required. Moreover, given the amplitude of peaks above the background trend typical in EEG spectra, small additive changes in the trend would alter the peak amplitudes minimally compared to the errors introduced by incorrectly detrending (Fig. 5). Overall, we conclude that spectral detrending should not be performed unless there is clear physiological and biophysical justification and validation.
In the analysis presented here, there was prior knowledge of the well-documented action of propofol on GABAR kinetics , clearly
indicating the necessity for divisive detrending. To mitigate the chances of overfitting, we constrained parameter values to physiologically reasonable ranges, and validated that the fitted spectral changes and values quantitatively matched expectations. Even so, our decomposition of spectra into physiologically distinct components was likely imperfect, especially considering that changes to GABAR kinetics also probably affected aperiodic network dynamics (see below). Although inhibitory synapses and network timescales are expected to affect spectra in different frequency ranges (Figs. 1, 4, 5, 7), these ranges overlap, making it challenging to definitively disambiguate these two mechanisms. Such caveats may be addressable with future refinements to EEG detrending algorithms, e.g., by including phase information or using generative models to improve parameter inference .
Past modelling has suggested that the EEG spectral exponent reflects the E:I ratio, which relies on the assumption that low frequency power is dominated by inhibitory currents . Our results broadly validate this assumption, suggesting that the E:I ratio is an important driver of the spectral trend. However, our results also demonstrate that the spectral exponent is not a reliable measure of E:I ratio because of nonlinearities in membrane potential dynamics related to the reversal potentials of AMPARs and GABARs (Fig. 6), an aspect not considered in previous work . In addition, we found that other biophysical parameters, such as synaptic timescales and leak currents contribute to shaping the EEG spectral trend. These findings are consistent with past studies that have associated neuronal timescales with the expression levels of various ion channels and receptor subunits . It seems likely that changes in the spectral trend can reflect a large number of physiological mechanisms that converge to govern synaptic kinetics and the effective E:I ratio. Other biophysical mechanisms not explored here, such as active membrane currents and dendritic calcium spikes , could also potentially contribute to shaping EEG spectra by changing postsynaptic response kinetics and amplitudes. Broadly, we conclude that the spectral exponent reflects physiological factors other than neural oscillations and is therefore a complementary biomarker to brain rhythm quantification.
While several studies have suggested that avalanche criticality may be responsible for broadband scaling in EEG spectra , our results corroborate other models of recurrent neural networks and indicate that avalanche criticality would likely contribute to only slower frequency components of EEG (Fig. 4, in the limit as ). In a general sense, our model suggests an underlying mechanism for the observed trend comparable to that proposed for how purely oscillatory networks might produce such a trend. In the oscillatory case, it has been suggested that large networks oscillate slower than smaller networks, thus leading to a trend . Our results suggest that propagating spikes that exhibit longer correlation timescales can produce more coherent dipoles, thus contributing more to the EEG signal. This in turn would cause EEG spectra to be dominated by lower frequency aperiodic signals. While still technically challenging, our model could be tested by extending recent work characterizing the functional clustering of synapses within individual dendritic branches , and by measuring the geometric relations between correlated synapses across neighbouring neurons.
Delta rhythms are a ubiquitous feature of general anesthesia, being readily induced in humans by propofol, sevoflurane, thiopental, and xenon , potentially indicating a universal signature of unconsciousness bridging both general anesthesia and sleep . To the best of our knowledge, such an abrupt change in delta power as reported here has not been previously reported in EEG studies, even when the moment of LOC was resolved with high temporal precision . Although practically detrending power relies on simplified models of EEG spectra, our analysis clearly shows that the slow changes in delta power prior to LOC can be explained by propofol’s action on GABAR kinetics, and thus demonstrates that delta power originating from
changes in neural dynamics appears after the propofol-induced increase in alpha and beta power (Fig. 9). According to our simulations, it is possible that the observed increase in low frequency power is due to the brain moving closer to avalanche criticality (Figs. 4 and 5). Opposing this interpretation are models of excitatory/inhibitory networks, which suggest that increasing inhibition promotes the asynchronous state . Furthermore, detailed analyses of EEG signals have suggested that altered states of consciousness are related to a departure away from, and not towards, critical dynamics . Based on these studies, we should rather expect changes in network criticality that decrease delta power. It seems likely, therefore, that the increase in delta power at the moment of LOC is related to changes in delta rhythms. If so, our observations lend evidence to the view that delta rhythms are fundamental to losing consciousness. A target effect-site concentration protocol could be used to investigate lower doses of propofol in more detail, which our observations suggest may induce alpha rhythms but not delta rhythms. If so, these experiments could be used to dissect the behavioural correlates of these two rhythms in more detail.
In summary, we conclude that aperiodic neural activity can contribute to EEG signals, and that the spectral trend is further shaped by many physiological mechanisms, such as excitatory/inhibitory balance and synaptic timescales. We conclude that the spectral exponent is not merely a conflated measure of brain rhythms and thus provides a complementary biomarker of brain state. However, we also conclude that the spectral exponent does not have a singular physiological interpretation. Finally, we conclude that EEG spectra do need to be detrended when quantifying brain rhythms, but only if postsynaptic current properties are systematically altered. Otherwise, detrending likely introduces significant errors to brain rhythm quantification and should therefore be avoided.

Methods

Definitions and theoretical framework

The EEG signal can be described as the linear superposition of electric fields generated by all neurons in the brain . We refer to the individual contribution of a single neuron to the ensemble EEG signal as a single-neuron EEG. Otherwise stated, the ensemble EEG signal is the linear summation of single-neuron EEGs. This means that the power spectral density of an EEG signal can be expressed as
Here, is the power spectrum of the single-neuron EEG generated by a given neuron , and is the coherence between the single-neuron EEG of neuron and neuron . Spectral peaks are thought to appear due to coherence at a given frequency . Because the coherence function, , interacts multiplicatively with single neuron EEG spectra, the spectral features of the ensemble EEG will be governed in part by the spectral features imparted by neurons at the single cell level. Moreover, this influence will be independent of the nature of brain dynamics, except insofar as these dynamics alter the single-neuron EEG spectrum. Broadly, this paper concerns itself with investigating how broadband single-neuron EEG signals influence the spectral features of the ensemble EEG.

Postsynaptic neuron simulations

Neuron morphologies as well as their relative abundance were the same as those used by Hagen et al. (Table S1). The same biophysical parameters were used for all neuron subtypes. For simulations, morphologies were segmented such that each compartment was less than . Each postsynaptic neuron was modelled with an axial resistance and a membrane capacitance of . All compartments were passive. The maximal leak conductance was
investigated in a range from 0.01 to and the leak reversal potential ( ) was investigated in a range from -75 to -45 mV (Fig. 1g). The number of synapses for each cell was equal to the total dendritic length times a density of 1 synapse per for excitatory synapses and 0.15 synapses per for inhibitory synapses . Synapses were distributed among all compartments proportionally to the compartments’ surface area. Post-synaptic currents were modelled as the difference of exponentials. Excitatory synapses had a reversal potential of 0 mV , a rise time of 0.3 ms , a decay time constant ( ) between 1 and 3.5 ms , and a peak conductance ( ) between 0.2 and 2 nS (Fig. 1g). Inhibitory synapses had a reversal potential of -80 mV , a rise time of 2 ms , a decay time constant ( ) between 5 and 20 ms , and a peak conductance between 0.2 and 2 nS (Fig. 1g). For illustrating specific example spectra, e.g., those shown in Figs. 1d, 2f, 4f, g, 5 and 7, the following parameter set was used: , , and . All simulations of neurons were performed in Python 3.8.10 using the package LFPy 2.2.4 , running the NEURON simulation environment under the hood .

Ensemble EEG amplitude estimation

Because dipoles sum linearly, the EEG signal generated by N neurons can be decomposed as a superposition of N single-neuron EEG signals. It follows that the ensemble EEG will have an average power of , where the single-neuron EEG signals produced by neurons and have average powers of and , respectively, and a pairwise correlation of . Dipole correlations should arise if two conditions are satisfied: (1) synaptic inputs are correlated, which we assumed to decrease with distance; and (2) dipole orientations are aligned, which we assumed depends on both condition 1 and on the angle between the apical-basal axes of the neurons. We therefore modelled the dipole correlation of two neurons as , where is the distance between the two neurons, is some characteristic spatial scale of correlation, and is the angle between the apical-basal axes of the respective neurons. We estimated these parameters using the ICBM152 v6 anatomical brain template , assuming a uniform density of neurons per of cortical surface area .
The brain template is a triangular mesh with faces of areas and normal vectors . Given a random point, , on the mesh, we used the vertex points of the mesh to analytically calculate the “signed number” of neurons within a given radius , given by
where is the fraction of triangular mesh face that intersects a ball of radius centred at point . We repeated this times with different starting points, , to estimate an average . This allowed us to estimate the average pairwise correlation across the entire cortex with the following formula
It follows that the expected signal power of the ensemble EEG signal is , where is the expected power of a single-neuron EEG (Fig. 1).
Experimental quantification of would require measuring and comparing the isolated dipoles of individual neurons, a procedure that is not possible. However, correlations in subthreshold membrane potentials have been investigated in cats, both in the presence and absence of oscillations . These experiments revealed that in the absence of oscillations, subthreshold fluctuations were correlated between neocortical neurons up to apart, but were
uncorrelated between neurons apart . Because dipoles are predominantly generated by subthreshold currents , these data suggest a possible lower and upper bound for .

Subcritical network model

Presynaptic neurons were connected to other neurons in the presynaptic network. The probability of two neurons being connected was determined by their distance, using an exponentially decaying coupling kernel. This rule forced network connectivity to be local in nature. Each neuron followed a Poisson point process with a rate , where was sampled from the distribution shown in Fig. 1 g . When a neuron spiked, each of its neighbouring neurons had a probability of of firing an action potential within the following 4 . The parameter thus tuned the amount of spike propagation in the network, changing the network behaviour from completely asynchronous when , to near avalanche criticality as approached 1 . The above formalism was used to simulate excitatory presynaptic neurons. We also added inhibitory neurons totalling 15% of the entire network. Spike trains for inhibitory neurons were sampled from the spike trains of nearby excitatory neurons and supplemented with independent Poisson processes. The procedure was such that inhibitory neuron firing was driven by recurrent connections to the same proportion as excitatory neurons and followed a predetermined firing rate ( ). In this setup, the influence of inhibitory neurons on the network was modelled implicitly in the branching number , but were not explicitly represented in the network connections. This simplification allowed the effective branching number of the network to be entirely governed by a single parameter .

Embedding synapses onto postsynaptic dendrites

Dipole synchrony has been previously modelled either by separating inhibitory and excitatory input into somatic and apical compartments, respectively , or by having counterphase input into the basal and apical compartments ; both of these models can be thought of as optimal mappings of two anticorrelated populations of synapses. Inspired by these models, we developed a procedure to generate dipole synchrony given any presynaptic topology. First, the pairwise correlation between each pair of presynaptic neurons was determined by the spike time tiling coefficient (STTC) , a measure of spike train correlation which accounts for the likelihood of spikes overlapping by chance. The pairwise correlations among all presynaptic neurons were computed based on 40 s long simulations of the presynaptic networks. The Uniform Manifold Approximation and Projection (UMAP) algorithm, a dimensionality reduction technique , was then used to optimally project the presynaptic network onto a sphere such that the angle between presynaptic neurons with high STTCs was minimized. After this embedding step, the dendrites of the postsynaptic neurons were orthogonally projected onto the sphere. Finally, the following procedure was run until all connections were formed between pre- and post-synaptic neurons: (1) a postsynaptic dendrite segment was chosen randomly (with replacement) with a probability proportional to its surface area; (2) the presynaptic neuron closest on the spherical embedding was chosen and a connection formed.
To model suboptimal synapse placement, we randomly perturbed the spherical embedding before mapping the synapses. Each point in the embedding was perturbed by a distance along a randomly chosen bearing, where Uniform . Here, is what we refer to as the optimality index (Fig. 4e). By construction, when , the points on the sphere are not perturbed at all, while when , all the points on the sphere are perturbed by a distance sampled from the function . Consequently, for , the distribution of points on the sphere is uniformly random.
This procedure can be thought of as a model of dipole correlation that generalizes beyond dichotomous input. Alternatively, this procedure can be considered in terms of observations from recent
studies, which have reported that functionally related synaptic inputs cluster within individual dendritic branches, and that input from similar presynaptic populations target similar dendritic compartments in the postsynaptic population . These experimental observations hint at a more continuous mapping of synaptic input along dendrites than a strictly binary apical-basal compartment paradigm, which is precisely what is achieved when the above mapping algorithm is applied to a continuous presynaptic network topology, such as the planar subcritical network used in Fig. 5.

Mixed synaptic input

For modelling oscillatory input, we used a published formalism of rhythmogenesis, where counterphase sinusoidal inputs were applied on the apical and basal dendrites . Specifically, every synapse on the neuron received an inhomogeneous Poisson point process as input, with a rate function , where depends on whether the synapse is excitatory or inhibitory tunes the strength of the rhythm, and for apical dendritic synapses and for basal dendritic synapses. For simplicity, to model other rhythms, we generalized this formalism by defining the rate function of each synapse as , where if the synapse was an apical synapse and if the synapse was a basal synapse, for any time series with zero mean and unit variance. This methodology was simpler than modelling networks for each type of dynamic and embedding the synapses as described in the above section, but more importantly this methodology allowed us to make direct comparisons between the modelled EEG signals generated by different rate functions.

Experimental design and procedure

Following MNH Ethics Board approval, we recruited 16 American Society of Anesthesiologists (ASA) class I or II patients (18-65 years old) presenting for lumbar disk surgery as subjects for the study. All subjects gave written informed consent to participate in the study. The standards of care of the Canadian Anesthesiologists’ Society in regard to monitoring, equipment and care provider were rigorously applied. Gold cup electrodes (Fz, Cz, Pz, C3, C4, CP3, CP4, M2 as reference; FC1 as ground; impedance ) were glued to the scalp to obtain a continuous EEG recording, which was amplified with a band pass and digitized at 1024 Hz . For each participant, we obtained 2 min of recording during preoxygenation with eyes closed. The participant was then asked to hold an object ( 0.5 kg cylinder; 2.5 cm diameter and 15 cm long) in a vertical position with their dominant hand and to keep the eyes closed. Preoxygenation continued for another 2 min . Lidocaine was given to attenuate the discomfort caused by the propofol injection. All medications were given intravenously via a catheter placed on the non-dominant arm. Propofol was given at the rate of and maintained until the cylinder fell from the participant’s hand. Following LOC, gentle jaw lift was applied if needed to relieve airway obstruction. The ability of the participants to respond to loud verbal command was assessed 60 seconds after the fall of the object: all failed to response and remained immobile. The study was then terminated.

Data analysis

Two participants were excluded because of failure to comply with the instructions during induction. One kept talking, the other kept moving their dominant arm. The final data set was therefore based on 14 subjects ( 10 males; 12 right-handed). Artifacts in the data were removed following visual inspections of the time series. Spectrograms were computed with the multitaper method, using three tapers over 2 s windows, with 1.9 s overlap. Group averages were either computed as the average power spectral density across subjects with time aligned to LOC, or with time rescaled so that both the infusion onset and LOC were aligned across individuals. To rescale time, LOC-aligned time for each subject was scale by the latency from infusion to LOC.
Consequently, a rescaled time value of -1 is equivalent to the moment of propofol infusion onset and a rescaled time value of 0 is equivalent to the moment of LOC.

Estimated propofol concentration

For estimating the effect-site concentration of propofol for each subject, we used the Marsh model, a multicompartment pharmacokinetics model . We used a plasma to effect-site equilibration rate constant . Faster and slower values for would shift the estimated dose-response curve in Fig. 8f right and left, respectively, but would not be expected to qualitatively change our results.

Detrending EEG spectra

To detrend EEG spectra, we used a modified version of the FOOOF algorithm , whereby a background trend is fitted in addition to several Gaussian functions to account for oscillatory peaks. Peaks at 60 Hz due to noise were removed from spectra using MATLAB’s fillgaps function prior to fitting the spectral trend. The FOOOF algorithm provides two options for the background trend, or . Here, we wanted a biophysically interpretable background function, and therefore started with the sum of two Lorentzian functions (Eq. 1). This function is an exact analytical solution to the computational model of Gao et al. and has several benefits. Firstly, it provides exact fits to our simulations, which allowed us to investigate theoretical consequences of detrending EEG spectra. Secondly, the parameters are physiologically interpretable. and reflect the kinetics of GABARs and AMPARs (Fig. 1), while and reflect the amplitudes of inhibitory and excitatory contributions to the EEG signal. Thirdly, it is thought that the spectral exponent, , reflects the relative contribution of excitation to inhibition , i.e., it depends on the ratio of to (Fig. 1). However, we found here that this is not always the case (Fig. 6). Therefore, Eq. 1 makes fewer assumptions about its parameters than the two options provided by the FOOOF package.
For analyzing experimental data, we modified Eq. 1 to provide better fits to the data and reduce the chances of overfitting. In contrast to our simulations, we found that high frequency power plateaued in our data around where we would expect the influence of excitatory synaptic time scales to be exerted (Fig. 1d, f). We therefore replaced the second term in the equation with a constant term,
This constant term, , captures the fast excitatory time scales as well as any high frequency contributions from action potentials , muscle activity , and amplifier noise , which were not present in our simulations. Importantly, because this equation has physiologically interpretable parameters, with reflecting inhibitory synaptic time scales (Fig. 1d, e), we could constrain the range of to avoid overfitting. Specifically, we constrained to be greater than 10 ms and less than 75 ms when fitting propofol data, as we expected propofol to increase the physiological range of GABAR kinetics (Table S2).
This modified equation fit the EEG spectra at baseline conditions well, but following propofol infusion, the equation did not decay fast enough to capture the EEG spectra (Fig. S7). This was seemingly because the original equations oversimplified the kinetics of inhibitory synapses. Notably, Eq. 1 is an analytical solution for exponentially decaying synaptic responses, whereas real synaptic responses are characterized by a rise time and decay time: . It follows that a more accurate synaptic response function for the power spectrum is given by
where the first term is the analytical solution to the power spectrum of the difference of exponentials. is the risetime of inhibitory synaptic currents, which we fixed at to keep the number of fitting parameters low . Notably, if we fixed both and , physiologically plausible values , all our baseline data could be captured by simply changing and (Fig. S5a). Moreover, fitting Eq. 6 provided consistent and physiologically plausible estimates for both at baseline and following propofol infusion (Fig. 8e, f). Thus, Eq. 6 is biophysically motivated, physiologically interpretable, has only three parameters to fit, and captured our data well both at baseline and following the infusion of propofol (Fig. 8d; Fig. S5a-c).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

Computed EEG spectrograms for all subjects have been uploaded to Figshare (https://doi.org/10.6084/m9.figshare.24777990), along with all the simulation results required to reproduce our figures. Source data are provided with this paper.

Code availability

Code used to run simulations, analyze data, and generate manuscript figures has been deposited in Zenodo (https://doi.org/10.5281/ zenodo.10359818) and is also available on GitHub (github.com/niklasbrake/EEG_modelling).

References

  1. Berger, H. Über das elektrenkephalogramm des menschen. Arch. Psychiatr. Nervenkr. 87, 527-570 (1929).
  2. Steriade, M. Cellular substrates of brain rhythms. Electroencephalogr. Basic Princ. Clin. Appl. Relat. fields 5, 31-83 (2005).
  3. Nunez, P. L. & Srinivasan, R. Electric Fields of the Brain (Oxford Univ. Press, Oxford, 2006). https://doi.org/10.1093/acprof:oso/ 9780195050387.001.0001.
  4. Buzsáki, G., Anastassiou, C. A. & Koch, C. The origin of extracellular fields and currents – EEG, ECoG, LFP and spikes. Nat. Rev. Neurosci. 13, 407-420 (2012).
  5. Pritchard, W. S. The brain in fractal time: f-like power spectrum scaling of the human electroencephalogram. Int. J. Neurosci. 66, 119-129 (1992).
  6. Manning, J. R., Jacobs, J., Fried, I. & Kahana, M. J. Broadband shifts in local field potential power spectra are correlated with singleneuron spiking in humans. J. Neurosci. 29, 13613-13620 (2009).
  7. Miller, K. J., Sorensen, L. B., Ojemann, J. G. & Den Nijs, M. Power-law scaling in the brain surface electric potential. PLoS Comput. Biol. 5, e1000609 (2009).
  8. He, B. J. Scale-free brain activity: past, present, and future. Trends Cogn. Sci. 18, 480-487 (2014).
  9. Voytek, B. et al. Age-related changes in neural electrophysiological noise. J. Neurosci. 35, 13257-13265 (2015).
  10. Roche, K. J. et al. Electroencephalographic spectral power as a marker of cortical function and disease severity in girls with rett syndrome. J. Neurodev. Disord. 11, 15 (2019).
  11. Colombo, M. A. et al. The spectral exponent of the resting EEG indexes the presence of consciousness during unresponsiveness induced by propofol, xenon, and ketamine. Neuroimage 189, 631-644 (2019).
  12. Ouyang, G., Hildebrandt, A., Schmitz, F. & Herrmann, C. S. Decomposing alpha and brain activities reveals their differential associations with cognitive processing speed. Neuroimage 205, 116304 (2020).
  13. Lendner, J. D. et al. An electrophysiological marker of arousal level in humans. Elife 9, 1-29 (2020).
  14. Donoghue, T. et al. Parameterizing neural power spectra into periodic and aperiodic components. Nat. Neurosci. 23, 1655-1665 (2020).
  15. Bédard, C., Kröger, H. & Destexhe, A. Does the frequency scaling of brain signals reflect self-organized critical states? Phys. Rev. Lett. 97, 118102 (2006).
  16. Gao, R., Peterson, E. J. & Voytek, B. Inferring synaptic excitation/ inhibition balance from field potentials. Neuroimage 158, 70-78 (2017).
  17. Bak, P., Tang, C. & Wiesenfeld, K. Self-organized criticality: an explanation of the noise. Phys. Rev. Lett. 59, 381-384 (1987).
  18. Beggs, J. M. & Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167-11177 (2003).
  19. Priesemann, V. Spike avalanches in vivo suggest a driven, slightly subcritical brain state. Front. Syst. Neurosci. 8, 108 (2014).
  20. Chaudhuri, R., He, B. J. & Wang, X. J. Random recurrent networks near criticality capture the broadband power distribution of human ECoG dynamics. Cereb. Cortex 28, 3610-3622 (2018).
  21. Lombardi, F., Herrmann, H. J. & de Arcangelis, L. Balance of excitation and inhibition determines power spectrum in neuronal networks. Chaos Interdiscip. J. Nonlinear Sci. 27, 047402 (2017).
  22. Buzsáki, G. & Draguhn, A. Neuronal olscillations in cortical networks. Science 304, 1926-1929 (2004).
  23. Buzsáki, G. & Vöröslakos, M. Brain rhythms have come of age. Neuron 111, 922-926 (2023).
  24. Huang, Y., Parra, L. C. & Haufe, S. The New York head-a precise standardized volume conductor model for EEG source localization and tES targeting. Neuroimage 140, 150-162 (2016).
  25. Hagen, E. et al. Hybrid scheme for modeling local field potentials from point-neuron networks. Cereb. Cortex 26, 4461-4496 (2016).
  26. Næss, S. et al. Biophysically detailed forward modeling of the neural origin of eeg and meg signals. Neuroimage 225, 117467 (2021).
  27. Orser, B. A., Wang, L. Y., Pennefather, P. S. & MacDonald, J. F. Propofol modulates activation and desensitization of receptors in cultured murine hippocampal neurons. J. Neurosci. 14, 7747-7760 (1994).
  28. Kitamura, A., Marszalec, W., Yeh, J. Z. & Narahashi, T. Effects of halothane and propofol on excitatory and inhibitory synaptic transmission in rat cortical neurons. J. Pharmacol. Exp. Ther. 304, 162-171 (2003).
  29. Whittington, M. A., Jefferys, J. G. R. & Traub, R. D. Effects of intravenous anaesthetic agents on fast inhibitory oscillations in the rat hippocampus in vitro. Br. J. Pharmacol. 118, 1977-1986 (1996).
  30. Franks, N. P. General anaesthesia: from molecular targets to neuronal pathways of sleep and arousal. Nat. Rev. Neurosci. 9, 370-386 (2008).
  31. McInnes, L., Healy, J. & Melville, J. UMAP: uniform manifold approximation and projection for dimension reduction. Preprint at https://arxiv.org/abs/1802.03426 (2020).
  32. Wilting, J. & Priesemann, V. Between perfectly critical and fully irregular: a reverberating model captures and predicts cortical spike propagation. Cereb. Cortex 29, 2759-2770 (2019).
  33. Suryadi, Cheng, R.-K., Birkett, E., Jesuthasan, S. & Chew, L. Y. Dynamics and potential significance of spontaneous activity in the habenula. eneuro 9, ENEURO.0287-21.2022 (2022).
  34. Lombardi, F., Pepić, S., Shriki, O., Tkačik, G. & De Martino, D. Statistical modeling of adaptive neural networks explains co-existence of avalanches and oscillations in resting human brain. Nat. Comput. Sci. 3, 254-263 (2023).
  35. Guay, C. S. & Plourde, G. Handgrip dynamometry for continuous assessment of volitional control during induction of anesthesia: a prospective observational study. Can. J. Anesth. Can. d’Anesth.ésie 66, 48-56 (2019).
  36. Cummings, G. C. et al. Dose requirements of (Propofol, ‘Diprivan’) in a new formulation for induction of anaesthesia. Anaesthesia 39, 1168-1171 (1984).
  37. Marsh, B., White, M., Morton, N. & Kenny, G. N. C. Pharmacokinetic model driven infusion of propofol in children. Br. J. Anaesth. 67, 41-48 (1991).
  38. Purdon, P. L. et al. Electroencephalogram signatures of loss and recovery of consciousness from propofol. Proc. Natl Acad. Sci. USA 110, E1142-E1151 (2013).
  39. Li, J. & Shew, W. L. Tuning network dynamics from criticality to an asynchronous state. PLOS Comput. Biol. 16, e1008268 (2020).
  40. Zeraati, R., Engel, T. A. & Levina, A. A flexible bayesian framework for unbiased estimation of timescales. Nat. Comput. Sci. 2, 193-204 (2022).
  41. Gao, R., van den Brink, R. L., Pfeffer, T. & Voytek, B. Neuronal timescales are functionally dynamic and shaped by cortical microarchitecture. Elife 9, e61277 (2020).
  42. Reimann, M. W. et al. A biophysically detailed model of neocortical local field potentials predicts the critical role of active membrane currents. Neuron 79, 375-390 (2013).
  43. Suzuki, M. & Larkum, M. E. Dendritic calcium spikes are clearly detectable at the cortical surface. Nat. Commun. 8, 276 (2017).
  44. Petermann, T. et al. Spontaneous cortical activity in awake monkeys composed of neuronal avalanches. Proc. Natl Acad. Sci. USA 106, 15921-15926 (2009).
  45. Iacaruso, M. F., Gasler, I. T. & Hofer, S. B. Synaptic organization of visual space in primary visual cortex. Nature 547, 449-452 (2017).
  46. Scholl, B., Wilson, D. E. & Fitzpatrick, D. Local order within global disorder: synaptic architecture of visual space. Neuron 96, 1127-1138.e4 (2017).
  47. Kerlin, A. et al. Functional clustering of dendritic activity during decision-making. Elife 8, e46966 (2019).
  48. Ju, N. et al. Spatiotemporal functional organization of excitatory synaptic inputs onto macaque v1 neurons. Nat. Commun. 11, 697 (2020).
  49. Lafourcade, M. et al. Differential dendritic integration of long-range inputs in association cortex via subcellular changes in synaptic ampa-to-nmda receptor ratio. Neuron 110, 1532-1546.e4 (2022).
  50. Gugino, L. D. et al. Quantitative eeg changes associated with loss and return of consciousness in healthy adult volunteers anaesthetized with propofol or sevoflurane. Br. J. Anaesth. 87, 421-428 (2001).
  51. Murphy, M. et al. Propofol anesthesia and sleep: a high-density EEG study. Sleep 34, 283-291 (2011).
  52. Lewis, L. D. et al. Rapid fragmentation of neuronal networks at the onset of propofol-induced unconsciousness. Proc. Natl Acad. Sci. USA 109, E3377-E3386 (2012).
  53. Huupponen, E. et al. Electroencephalogram spindle activity during dexmedetomidine sedation and physiological sleep. Acta Anaesthesiol. Scand. 52, 289-294 (2008).
  54. Ma, J. & Leung, L. S. Limbic system participates in mediating the effects of general anesthetics. Neuropsychopharmacology 31, 1177-1192 (2006).
  55. Johnson, B. W., Sleigh, J. W., Kirk, I. J. & Williams, M. L. High-density EEG mapping during general anaesthesia with xenon and propofol: a pilot study. Anaesth. Intensive Care 31, 155-163 (2003).
  56. Amzica, F. & Steriade, M. Electrophysiological correlates of sleep delta waves. Electroencephalogr. Clin. Neurophysiol. 107, 69-83 (1998).
  57. Steriade, M. Corticothalamic resonance, states of vigilance and mentation. Neuroscience 101, 243-276 (2000).
  58. Le Masson, G., Renaud-Le Masson, S., Debay, D. & Bal, T. Feedback inhibition controls spike transfer in hybrid thalamic circuits. Nature 417, 854-858 (2002).
  59. Tagliazucchi, E. et al. Increased global functional connectivity correlates with LSD-induced ego dissolution. Curr. Biol. 26, 1043-1050 (2016).
  60. Toker, D. et al. Consciousness is supported by near-critical slow cortical electrodynamics. Proc. Natl Acad. Sci. USA 119, 1-12 (2022).
  61. Malmivuo, J. & Plonsey, R. Bioelectromagnetism (Oxford Univ. Press, Oxford, 1995).
  62. Palmer, L., Murayama, M. & Larkum, M. Inhibitory regulation of dendritic activity in vivo. Front. Neural Circuits 6, 26 (2012).
  63. lascone, D. M. et al. Whole-neuron synaptic mapping reveals spatially precise excitatory/inhibitory balance limiting dendritic and somatic spiking. Neuron 106, 566-578.e8 (2020).
  64. Karimi, A., Odenthal, J., Drawitsch, F., Boergens, K. M. & Helmstaedter, M. Cell-type specific innervation of cortical pyramidal cells at their apical dendrites. Elife 9, 1-23 (2020).
  65. Hagen, E., Næss, S., Ness, T. V. & Einevoll, G. T. Multimodal modeling of neural network activity: computing lfp, ecog, eeg, and meg signals with lfpy 2.0. Front. Neuroinform. 12, 92 (2018).
  66. Carnevale, N. T. & Hines, M. L. The NEURON Book (Cambridge University Press, 2006). https://doi.org/10.1017/ CBO9780511541612.
  67. Fonov, V., Evans, A., McKinstry, R., Almli, C. & Collins, D. Unbiased nonlinear average age-appropriate brain templates from birth to adulthood. Neuroimage 47, S102 (2009).
  68. Fonov, V. et al. Unbiased average age-appropriate atlases for pediatric studies. Neuroimage 54, 313-327 (2011).
  69. Carlo, C. N. & Stevens, C. F. Structural uniformity of neocortex, revisited. Proc. Natl Acad. Sci. USA 110, 1488-1493 (2013).
  70. Volgushev, M., Chauvette, S. & Timofeev, I. Long-range correlation of the membrane potential in neocortical neurons during slow oscillation. in Progress in Brain Research 181-199 (2011). https://doi. org/10.1016/B978-0-444-53839-0.00012-0.
  71. Einevoll, G. T., Kayser, C., Logothetis, N. K. & Panzeri, S. Modelling and analysis of local field potentials for studying the function of cortical circuits. Nat. Rev. Neurosci. 14, 770-785 (2013).
  72. Jones, S. R. et al. Quantitative analysis and biophysically realistic neural modeling of the MEG mu rhythm: rhythmogenesis and modulation of sensory-evoked responses. J. Neurophysiol. 102, 3554-3572 (2009).
  73. Studenova, A. A., Villringer, A. & Nikulin, V. V. Non-zero mean alpha oscillations revealed with computational model and empirical data. PLoS Comput. Biol. 18, e1010272 (2022).
  74. Cutts, C. S. & Eglen, S. J. Detecting pairwise correlations in spike trains: an objective comparison of methods and application to the study of retinal waves. J. Neurosci. 34, 14288-14303 (2014).
  75. Struys, M. M. R. F. et al. Comparison of plasma compartment versus two methods for effect compartment-controlled target-controlled infusion for propofol. Anesthesiology 92, 399-399 (2000).
  76. Muthukumaraswamy, S. D. High-frequency brain activity and muscle artifacts in MEG/EEG: a review and recommendations. Front. Hum. Neurosci. 7, 138 (2013).
  77. Sceniak, M. P. & Maclver, M. B. Slow mediated synaptic transmission in rat visual cortex. BMC Neurosci. 9, 8 (2008).
  78. Brake, N. et al. EEG data during propofol anesthesia and a biophysical model of the EEG spectral trend. figshare. https://doi.org/10. 6084/m9.figshare. 24777990 (2023).
  79. Brake, N. niklasbrake/EEG_modelling: Manuscript revisions (v1.0.0). Zenodo. https://zenodo.org/doi/10.5281/zenodo. 10359817 (2023).

Acknowledgements

This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) discovery grant (RGPIN-2019O4520) to A.K. N.B. was supported by the NSERC-CREATE in Complex Dynamics Graduate Scholarship and the Fonds de recherche du Québec
  • Nature et technologies (FRQNT) doctoral training scholarship. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Author contributions

Conceptualization: N.B., G.P. and A.K. Data curation: N.B. and G.P. Formal analysis: N.B. Funding acquisition: A.K. and G.P. Investigation: N.B., F.D., A.R., F.A., S.S. and G.P. Methodology: N.B. Project administration: A.K. and G.P. Software: N.B. Supervision: A.K. and G.P. Visualization: N.B. Writingoriginal draft: N.B. Writing—review and editing: N.B., A.K. and G.P.

Competing interests

The authors declare no competing interests.

Additional information

Supplementary information The online version contains
supplementary material available at
https://doi.org/10.1038/s41467-024-45922-8.
Correspondence and requests for materials should be addressed to Anmar Khadra or Gilles Plourde.
Peer review information Nature Communications thanks Richard Gao and Balazs Hangya for their contribution to the peer review of this work. A peer review file is available.
Reprints and permissions information is available at
http://www.nature.com/reprints
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/ licenses/by/4.0/.
© The Author(s) 2024
  1. ¹Quantiative Life Sciences PhD Program, McGill University, Montreal, Canada. Department of Physiology, McGill University, Montreal, Canada.
    Department of Anesthesia, McGill University, Montreal, Canada. School of Nursing, McGill University, Montreal, Canada.
    -e-mail: anmar.khadra@mcgill.ca; gilles.plourde@mcgill.ca