DOI: https://doi.org/10.31181/sor2120259
تاريخ النشر: 2024-08-28
اتخاذ القرار المتقدم القائم على الضبابية: طريقة كوداس الضبابية الخطية ديوفانتين لاختيار المتخصصين في اللوجستيات
معلومات المقال
تاريخ المقال:
استلم في الشكل المنقح 14 يوليو 2024
تم القبول في 19 أغسطس 2024
متاح على الإنترنت 28 أغسطس 2024
الكلمات المفتاحية:
الملخص
تتناول هذه الدراسة عدم اليقين الكامن في اتخاذ القرار البشري من خلال الاستفادة من المجموعات الضبابية، التي تم تقديمها لالتقاط عدم الدقة المرتبطة بالأفكار والأحكام البشرية بشكل أفضل. كامتداد للمجموعات الضبابية التقليدية، تم تطوير مجموعة الضبابية الخطية ديوفانتين (LDFS)، مما يوفر نهجًا أكثر مرونة من خلال تخفيف القيود الحالية على قيم الدرجات. لقد وجدت LDFS تطبيقات عبر مجالات مختلفة، مما يوضح تنوعها وفعاليتها. في هذه الدراسة، نستكشف تطبيق مجموعة الضبابية الخطية ديوفانتين ضمن إطار طريقة التقييم القائم على المسافة التراكمية (CODAS). تبرز طريقة CODAS لأنها تتضمن المسافات الإقليدية ومسافات التاكسي. يجب أن يأخذ اتخاذ القرار في الاعتبار ليس فقط المسافات المباشرة بين الحلول المثالية والبدائل ولكن أيضًا المسافات غير المباشرة. الهدف الرئيسي من هذا البحث هو اقتراح نهج جديد من خلال دمج طريقة CODAS مع LDFS لمعالجة مشاكل اتخاذ القرار المعقدة التي تتسم بعدم اليقين وعدم الدقة. لتوضيح الفائدة العملية للطريقة المقترحة، نطبقها على مثال عددي يتعلق باختيار متخصص لوجستيات، وهو قرار حاسم في تحسين اللوجستيات الطارئة. تتضمن الدراسة أيضًا دراسة حالة عن متخصص اللوجستيات، مما يبرز التطبيق العملي للطرق المناقشة. علاوة على ذلك، توفر هذه الدراسة تحليل حساسية شامل لأوزان المعلمات لتقييم متانة وموثوقية الطريقة المقترحة. تسلط النتائج الضوء على فعالية طريقة LDF CODAS في اتخاذ قرارات مستنيرة وموثوقة في ظل ظروف عدم اليقين، مما يمهد الطريق لتطبيقات مستقبلية في سيناريوهات اتخاذ القرار الأخرى.
1. المقدمة
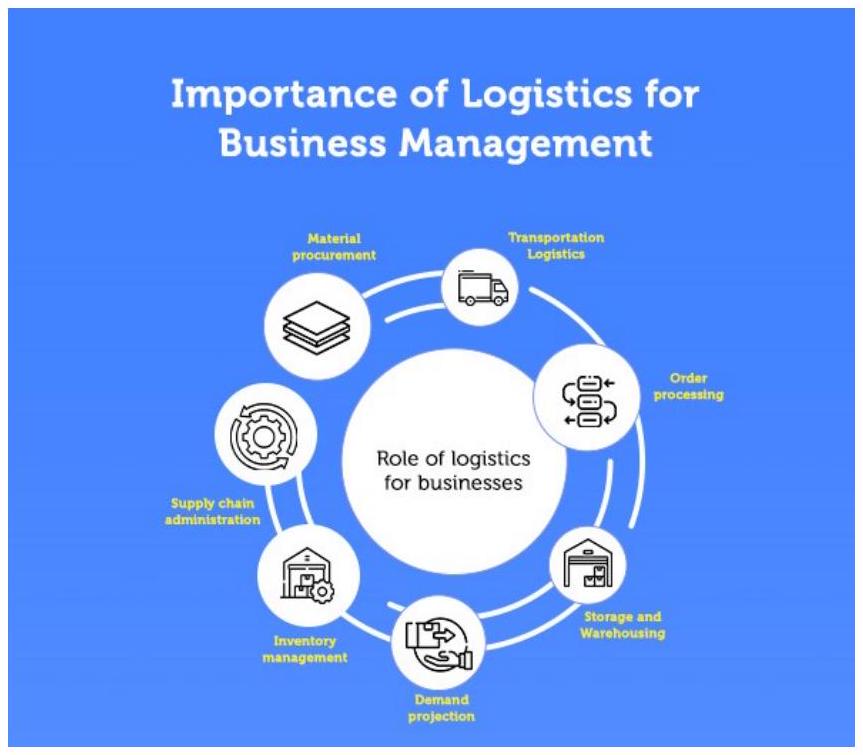
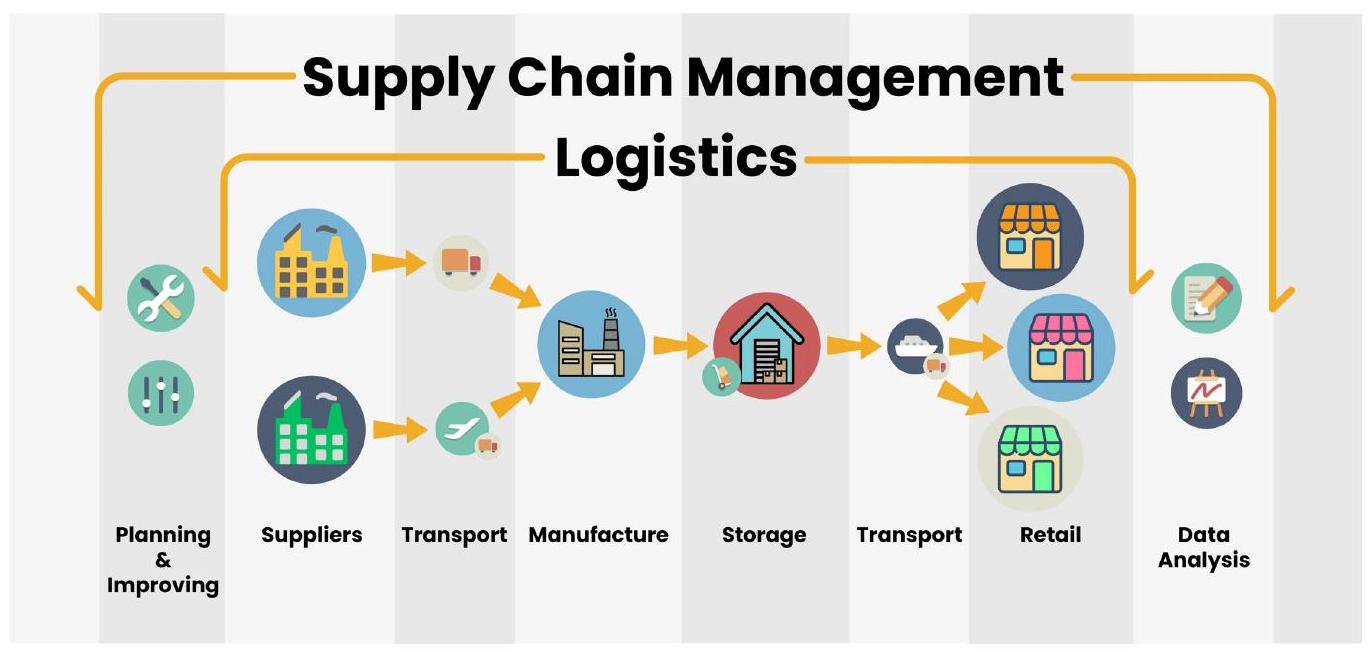
نظرًا لأنها تمكن من نقل المنتجات من الموردين إلى المصنعين، والبائعين أو الموزعين، و
مراجعة الأدبيات حول خصائص الاختيار
| المسمى الوظيفي | نهج التقييم | معايير الاختيار |
| [1] مهندس تحليل النظام | TOPSIS الضبابية | الاستقرار العاطفي، مهارات التواصل الشفوي، الشخصية، الخبرة السابقة، الثقة بالنفس |
| [2] مدير مشروع تكنولوجيا المعلومات والاتصالات | نهج التقييم اللغوي الضبابي | التعليم، الخبرة، معرفة الكمبيوتر، اللغة الأجنبية، العمر، الجنس، نوبة العمل وعدم التدخين |
| [3] تحليل النظام | IFS TOPSIS | القيادة، التحفيز، خبرة العمل، الكفاءة، المظهر، الإبداع، العمر ومهارات التواصل |
| [4] مدير المبيعات | IF-TOPSIS | مهارات التواصل الشفوي، الخبرة السابقة، الاستعداد العام، الرغبة، الثقة بالنفس والانطباع الأول |
| [5] مهندس | Fuzzy VIKOR | معايير المعرفة العامة والمهنية |
| [6] مدير المشروع | Fuzzy VIKOR | قدرة إدارة الموقع، المستوى الفني، مستوى القيادة، الصفات الشخصية والمهارات السياقية |
| [7] مدير المشروع | Fuzzy MCDM | المتطلبات الأساسية، مهارات إدارة المشاريع، مهارات الإدارة والمهارات الشخصية |
| [8] المدير التنفيذي للمعلومات | Fuzzy TOPSIS | المهارات الناعمة والفنية |
| [9] مدير الدعم | Fuzzy TOPSIS | الإبداع/الابتكار، حل المشكلات/اتخاذ القرار، إدارة النزاعات/التفاوض، التمكين/التفويض، التخطيط الاستراتيجي، مهارات العرض المحددة، مهارات التواصل، إدارة الفريق، إدارة التنوع، إدارة الذات، والخلفية التعليمية |
| [10] مدير الموارد البشرية | Fuzzy TOPSIS | الخصائص العلمية والنفسية والسلوكية والظاهرية، الخصائص الوظيفية والطبية |
| [11] محلل النظام | Fuzzy TOPSIS | الاستقرار العاطفي، مهارات التواصل الشفوي، الشخصية، الخبرة السابقة والثقة بالنفس |
| [12] موظف | Fuzzy TOPSIS | العلم والتعليم، السلوك والمظهر، النفس الشخصية، النشاط الوظيفي والمعايير الطبية |
1.1 مراجعة الأدبيات
بتطوير مجموعة LDF الغامضة المعقدة [20]. تم تطبيق عدة تقنيات تجميع أينشتاين لاستكشاف LDFS لمشاكل MCDM في أياريد لامبام[21]. يمكن أن تستخرج هذه المشغلات بيانات التقييم وتحدد الخيار الأمثل. بعد ذلك، ربط سايا أيوب[22] الميزات الجبرية بعلاقات LDF من خلال اتخاذ القرار. طور رياز وآخرون[23] على LDFS من خلال تقديم فكرة المجموعات الغامضة الناعمة لتطبيقها في معدات المناولة. لاختيار مقدمي خدمات اللوجستيات من الطرف الثالث، طور رياز وآخرون[24] مشغلات التجميع (AOs) التي استخدمت أعداد غامضة خطية (LDFNs) بترتيب الأولوية. تم اقتراح تطبيق مشغلات AOs الغامضة الخطية ذات الأولوية من أينشتاين من قبل فريد وآخرون[25].
لطريقة CODAS في سياق اختيار ERP من قبل H.Y. أيدوغموش وآخرون[55].
تم الإبلاغ عن دمج عدة تمديدات للأعداد الغامضة مع نهج CODAS تحت عدم اليقين، وفقًا للأدبيات. تركيز هذا العمل هو على التمديد الغامض الخطي لنهج CODAS، الذي لم يتم التحقيق فيه بعد في الأدبيات.
1.2 مساهمة هذا البحث
- يقدم هذا العمل إطارًا فريدًا لصنع القرار من خلال دمج مجموعة الأعداد الغامضة الخطية (LDFS) مع نهج CODAS.
- يعزز الأساليب التقليدية من خلال معالجة قضايا صنع القرار المعقدة التي تتسم بعدم اليقين وعدم الدقة.
- تم تقديم دراسة حالة تستخدم طريقة LDF CODAS المقترحة لتحسين اللوجستيات الطارئة عند اختيار متخصص لوجستي.
- لتقييم قوة وموثوقية الطريقة في الحالات العملية، يتضمن البحث تحليل حساسية شامل.
- يفتح البحث الباب لتطبيقات إضافية لتقنية LDF CODAS في مجموعة من سيناريوهات اتخاذ القرار متعددة المعايير.
2. المقدمات
التعريف 2.2. [17] مجموعة ضبابية خطية ديوفانتينية
-
-
. -
-
-
-
، حيث .
3. تقنية LDF-CODAS المقترحة
الخطوة 1: تجميع مصفوفة قرار LDF
الخطوة 2: تطبيع مصفوفة القرار كـ
الخطوة 4: تقييم الحل المثالي السلبي NIS بحيث
حيث
الخطوة 7: تحديد درجة التقييم
4. تحسين اللوجستيات الطارئة: دراسة حالة
1 بناء مصفوفة قرار LDF
2 تطبيع مصفوفة قرار LDF
3 الحصول على مصفوفة موزونة مطبوعة
4 تحديد الحل المثالي السلبي (NIS)
5 حساب المسافة الإقليدية ومسافة التاكسي
6 اشتقاق مصفوفة التقييم النسبي
7 حساب درجة التقييم
الشكل 3. تدفق خوارزمية LDF-CODAS
4.1 دور متخصص اللوجستيات
7. التخطيط للاستعداد: يعمل متخصصو اللوجستيات مسبقًا لوضع خطط واستراتيجيات استجابة طارئة شاملة. يتضمن ذلك تحديد المخاطر المحتملة، وتطوير بروتوكولات سلسلة الإمداد، ووضع خطط طوارئ لتمكين استجابة سريعة وفعالة خلال الكارثة.
2. تخصيص الموارد: يقومون بتحليل البيانات التاريخية واستخدام النمذجة التنبؤية لتحديد أفضل تخصيص للموارد بناءً على الطلبات المتوقعة خلال الأزمة. يساعد ذلك في ضمان نشر الموارد المناسبة في المواقع المناسبة في الوقت المناسب.
3. علاقات الموردين: من الضروري تطوير علاقات قوية مع الموردين الموثوقين. للحفاظ على تدفق مستمر من السلع الضرورية خلال الكوارث، يتفاوض متخصصو اللوجستيات على العقود ويشكلون شراكات مع الموردين.
4. إدارة المخزون: من الضروري الاحتفاظ بإمدادات كافية من الإمدادات الطارئة. يستخدم متخصصو اللوجستيات استراتيجيات إدارة المخزون لتتبع مستويات المخزون وإعادة تعبئة الإمدادات حسب الحاجة، مما يقلل من النقص والفائض.
5. التكامل التكنولوجي: لتبسيط عمليات اللوجستيات، يستخدمون حلول تكنولوجية مثل تتبع GPS، والمراقبة في الوقت الحقيقي، وبرامج إدارة المخزون. يتيح ذلك وعيًا أفضل بسلسلة الإمداد واتخاذ قرارات أسرع.
6. كفاءة النقل: يقوم متخصصو اللوجستيات بتحسين طرق النقل وأنماطها لتقليل أوقات التسليم والتكاليف. قد يخططون أيضًا لوضع الموارد مسبقًا في مواقع حيوية للسماح باستجابة سريعة.
7. الاتصال والتنسيق: يعد الاتصال الفعال والتنسيق مع الأطراف الأخرى، مثل الوكالات الحكومية، والمنظمات غير الحكومية، والحكومات المحلية، أمرًا حاسمًا لتحسين اللوجستيات. يقومون بإنشاء بروتوكولات الاتصال لتعزيز تبادل المعلومات والتعاون بسلاسة.
8. تحليل البيانات: باستخدام تحليل البيانات، يقوم متخصصو اللوجستيات بتحليل وتفسير البيانات في الوقت الحقيقي لاتخاذ قرارات مستنيرة بشأن تخصيص الموارد وتوزيعها. يتضمن ذلك تتبع أنماط الطلب، واختناقات النقل، واستخدام الموارد.
9. التحكم في التكاليف: إدارة النفقات بكفاءة هي جزء مهم من تحسين اللوجستيات الطارئة. يبحث متخصصو اللوجستيات عن طرق لتقليل التكاليف مع الحفاظ على جودة وفعالية الاستجابة. 10. ينظمون جلسات تدريبية وتمارين للفرق اللوجستية والمستجيبين لتحسين مهاراتهم واستعدادهم. تساعد التمارين المنتظمة في تحديد الفرص لتحسين إجراءات اللوجستيات.
10. التحسين المستمر: بعد كل استجابة للطوارئ، يقوم متخصصو اللوجستيات بإجراء تقييمات بعد العملية وجلسات تفريغ. تُستخدم نتائج هذه التقييمات لتعديل وتحسين استراتيجيات وإجراءات اللوجستيات الطارئة المستقبلية.
11. التخفيف من المخاطر: من الضروري تحديد المخاطر والضعف المحتملين في سلسلة التوريد. يقوم محترفو اللوجستيات بوضع تقنيات التخفيف من المخاطر استجابةً للعقبات مثل إغلاق الطرق، والكوارث الطبيعية، والمخاوف الأمنية.
4.2 الحاجة إلى متخصص لوجستي
متخصص لوجستي هو قرار استراتيجي له عواقب بعيدة المدى على تنافسية المنظمة، وربحيتها، وقدرتها على تلبية متطلبات سوق عالمي ديناميكي.
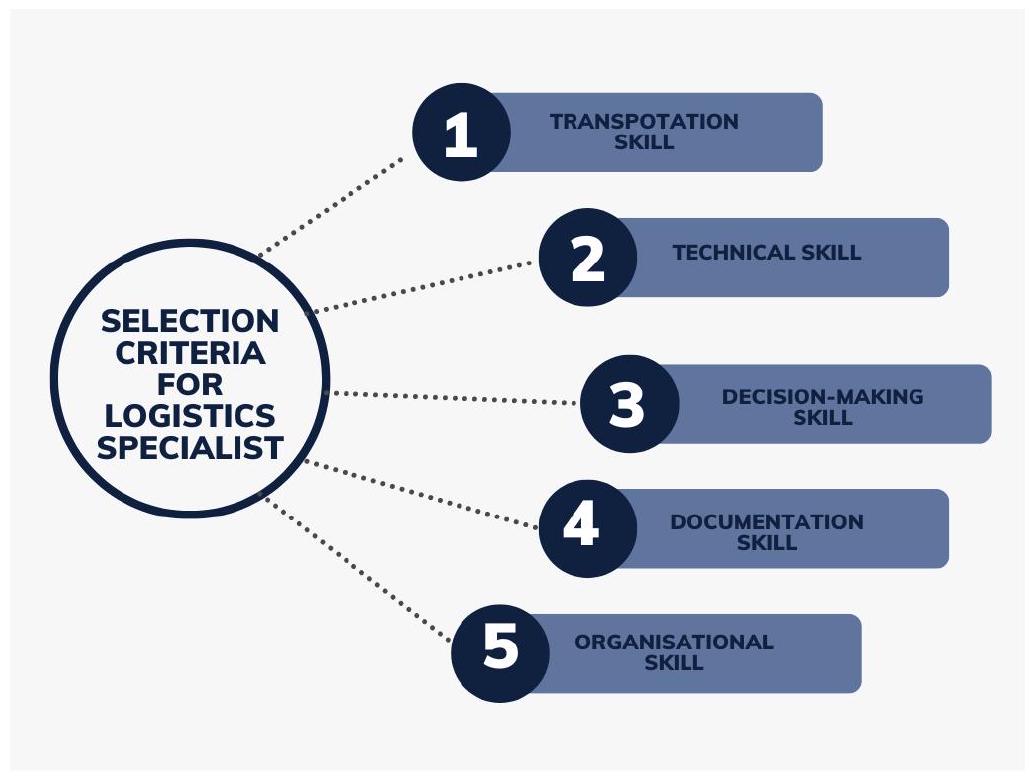
4.3 معايير اختيار المتخصص اللوجستي
4.4 الحساب الرياضي للنهج المقترح
4.4.1 وصف المشكلة
4.4.2 عملية اتخاذ القرار
- تم بناء مصفوفة قرار LDF كما يلي؛
- نظرًا لأن جميع المعايير من نفس النوع، فلا حاجة للتطبيع.
- تم حساب مصفوفة القرار الموزونة باستخدام الصيغة [Eq. (2)] كما يلي:
- لإيجاد NIS، يجب علينا إيجاد القيمة الدنيا لكل عمود ‘
- المسافة الإقليدية
المسافة الإقليدية
| البدائل |
|
|
|
|
0.1350 | 0.8232 |
|
|
0.2227 | 1.6410 |
|
|
0.1690 | 0.9770 |
|
|
0.2213 | 1.5940 |
|
|
0.2161 | 1.4106 |
|
|
0.2673 | 1.4923 |
|
|
0.2615 | 1.9229 |
- ذاكرة الوصول العشوائي
- يتم حساب درجات التقييم لكل بديل باستخدام المعادلة Eq. (11).
- ترتيب البدائل هو
4.5 تحليل الحساسية
الحالة 1: تم إعطاء تفضيل أعلى للمعايير
الحالة 2: تم إعطاء تفضيل أعلى للمعايير
الحالة 3: تم إعطاء تفضيل أعلى للمعايير
الحالة 4: تم إعطاء تفضيل أعلى للمعايير
من الواضح من النتائج أن الطريقة المقترحة حساسة لأوزان المعايير. ترتيب الأمر يتغير قليلاً أيضاً عندما نقوم بتعديل تفضيلات الوزن.
5. الخاتمة
مما يجعل هذه الطريقة مناسبة لجميع أنواع مجموعات البيانات. في هذه الدراسة، نحدد أفضل أخصائي لوجستي باستخدام طريقة CODAS، التي تتفوق من خلال دمج قياسين للمسافة، مما يؤدي إلى نتائج أكثر دقة. مع إطارها القابل للتكيف الذي يدير عدم الدقة والغموض، فإن تقنية LDF CODAS تحسن بشكل كبير من اتخاذ القرار – وهي ميزة حاسمة في الحالات المعقدة. يتم إثبات تأثيرها في العالم الحقيقي من خلال تنفيذها العملي في عملية اختيار أخصائي لوجستي، مما يعزز اتخاذ القرار التشغيلي والكفاءة. علاوة على ذلك، فإن قابلية توسيع النظام تعني أن لديه القدرة على أن يتم تطبيقه بشكل أوسع عبر العديد من الصناعات، مما يوفر أداة موثوقة لمشكلات اتخاذ القرار المستقبلية. يدعم دراسة الحساسية قوة طريقة LDF CODAS من خلال إظهار قدرتها على تحمل التغييرات في معلمات الإدخال دون المساس بالنتائج المتسقة. يوسع هذا العمل استخدام المجموعات الضبابية في اتخاذ القرار ويقدم أداة قوية لمزيد من التحقيق والتطبيقات في العالم الحقيقي في المجالات التي تحتاج إلى اتخاذ قرارات معقدة في مواجهة عدم اليقين. يمكن استخدام المعرفة التي تم جمعها من هذه الدراسة في مجالات متنوعة، مما يعزز المزيد من التحقيق وتحسين نماذج اتخاذ القرار المعتمدة على الضبابية. بينما تقدم نظريتنا العديد من المزايا، إلا أن لديها أيضًا بعض القيود. عندما تتجاوز قيم المعلمات المرجعية الواحد، فإن نظريتنا المقترحة غير قادرة على إدارة الوضع. أيضًا، عند التعامل مع كميات كبيرة من البيانات، قد يكون حساب النموذج المقترح مرهقًا. في المستقبل، سيتم استخدام عدة طرق MCDM مثل PROMTHEE وEDAS وVIKOR وTODIM وDEMATEL في مجالات متنوعة مثل الطب والزراعة والاقتصاد والمجتمع.
شكر وتقدير
تعارض المصالح
References
[2] Afshari, A., & Kowal, J. (2017). Decision Making Methods for the Selection of ICT Project Manager. Gospodarka Rynek Edukacja= Economy Market Education, 18(4), 19-28. https://doi.org/ 10.2139/ssrn. 3118075
[3] Bali, Ö., Gümüş, S., & Dağdeviren, M. (2013). A group madm method for personnel selection problem using delphi technique based on intuitionistic fuzzy sets. Journal of Management and Information Science, 1(1), 1-13.
[4] Boran, E., Genç, S., & Akay, D. (2011). Personnel selection based on intuitionistic fuzzy sets. Human Factors and Ergonomics in Manufacturing Service Industries, 21, 493-503. https://doi. org/10.1002/hfm. 20252
[5] Chen, C.-T., Pai, P.-F., & Wei Zhan, H. (2011). Applying linguistic vikor and knowledge map in personnel selection. Asia Pacific Management Review, 16(4), 491-502.
[6] Jafarnejad Chaghooshi, A., Arab, A., & Hosseini Dehshiri, S. J. (2016). A fuzzy hybrid approach for project manager selection. Decision Science Letters, 447-460. https://doi.org/10.5267/j. dsl.2016.1.001
[7] Dodangeh, J., Sorooshian, S., & Afshari, A. R. (2014). Linguistic Extension for Group Multicriteria Project Manager Selection. Journal of Applied Mathematics, 2014, 570398. https://doi.org/10. 1155/2014/570398
[8] Kelemenis, A., & Askounis, D. (2010). A new TOPSIS-based multi-criteria approach to personnel selection. Expert Systems with Applications, 37(7), 4999-5008. https://doi.org/10.1016/j.eswa. 2009.12.013
[9] Kelemenis, A., Ergazakis, K., & Askounis, D. (2011). Support managers selection using an extension of fuzzy TOPSIS. Expert Systems with Applications, 38(3), 2774-2782. https://doi.org/10. 1016/j.eswa.2010.08.068
[10] Nobari, S. M., & Zadeh, D. H. (2013). Designing a fuzzy model for decision support systems in the selection and recruitment process. African Journal of Business Management, 7(16), 1486. https://doi.org/10.5897/AJBM11.2803
[11] Mahdavi, I., Mahdavi-Amiri, N., Heidarzade, A., & Nourifar, R. (2008). Designing a model of fuzzy TOPSIS in multiple criteria decision making. Applied Mathematics and Computation, 206(2), 607-617. https://doi.org/10.1016/j.amc.2008.05.047
[12] Mammadova, M., & Jabrayilova, Z. (2014). Application of Fuzzy Optimization Method in DecisionMaking for Personnel Selection. Intelligent Control and Automation, 5(4), 190-204. https://doi. org/10.4236/ica.2014.54021
[13] Zadeh, L. (1965). Fuzzy sets. Information and Control, 8(3), 338-353. https://doi.org/10.1016/ Soo19-9958(65)90241-X
[14] Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87-96. https: //doi.org/10.1016/S0165-0114(86)80034-3
[15] Yager, R. R. (2014). Pythagorean Membership Grades in Multicriteria Decision Making. IEEE Transactions on Fuzzy Systems, 22(4), 958-965. https://doi.org/10.1109/TFUZZ.2013.2278989
[16] Yager, R. R. (2017). Generalized Orthopair Fuzzy Sets. IEEE Transactions on Fuzzy Systems, 25(5), 1222-1230. https://doi.org/10.1109/TFUZZ.2016.2604005
[17] Riaz, M., & Hashmi, M. R. (2019). Linear diophantine fuzzy set and its applications towards multi-attribute decision-making problems. Journal of Intelligent and Fuzzy Systems, 37(4), 54175439. https://doi.org/10.3233/jifs-190550
[18] Kannan, J., Jayakumar, V., Pethaperumal, M., & Kather Mohideen, A. B. (2024). An intensified linear diophantine fuzzy combined dematel framework for the assessment of climate crisis. Stochastic Environmental Research and Risk Assessment. https://doi.org/10.1007/s00477-023-02618-7
[19] Jeevitha, K., Garg, H., Vimala, J., Aljuaid, H., & Abdel-Aty, A.-H. (2023). Linear diophantine multifuzzy aggregation operators and its application in digital transformation. Journal of Intelligent Fuzzy Systems, 45(2), 3097-3107. https://doi.org/10.3233/JIFS-223844
[20] Jayakumar, V., Mohideen, A. B. K., Saeed, M. H., Alsulami, H., Hussain, A., & Saeed, M. (2023). Development of Complex Linear Diophantine Fuzzy Soft Set in Determining a Suitable AgriDrone for Spraying Fertilizers and Pesticides. IEEE Access, 11, 9031-9041. https://doi.org/10. 1109/ACCESS.2023.3239675
[21] Iampan, A., García, G. S., Riaz, M., Athar Farid, H. M., & Chinram, R. (2021). Linear diophantine fuzzy einstein aggregation operators for multi-criteria decision-making problems. Journal of Mathematics, 2021, 5548033. https://doi.org/10.1155/2021/5548033
[22] Ayub, S., Shabir, M., Riaz, M., Aslam, M., & Chinram, R. (2021). Linear diophantine fuzzy relations and their algebraic properties with decision making. Symmetry, 13(6), 945. https://doi. org/10.3390/sym13060945
[23] Riaz, M., Hashmi, M. R., Kalsoom, H., Pamucar, D., & Chu, Y.-M. (2020). Linear diophantine fuzzy soft rough sets for the selection of sustainable material handling equipment. Symmetry, 12(8), 1215. https://doi.org/10.3390/sym12081215
[24] Riaz, M., Farid, H. M. A., Aslam, M., Pamucar, D., & Bozanić, D. (2021). Novel approach for third-party reverse logistic provider selection process under linear diophantine fuzzy prioritized aggregation operators. Symmetry, 13(7), 1152. https://doi.org/10.3390/sym13071152
[25] Farid, H. M. A., Riaz, M., Khan, M. J., Kumam, P., & Sitthithakerngkiet, K. (2022). Sustainable thermal power equipment supplier selection by einstein prioritized linear diophantine fuzzy aggregation operators. AIMS Mathematics, 7(6), 11201-11242. https://doi.org/10.3934/math. 2022627
[26] Riaz, M., Farid, H. M. A., Wang, W., & Pamucar, D. (2022). Interval-valued linear diophantine fuzzy frank aggregation operators with multi-criteria decision-making. Mathematics, 10(11), 1811. https://doi.org/10.3390/math10111811
[27] Jayakumar, V., Kannan, J., Kausar, N., Deveci, M., & Wen, X. (2024). Multicriteria group decision making for prioritizing iot risk factors with linear diophantine fuzzy sets and marcos method. Granular Computing, 9(3), 56. https://doi.org/10.1007/s41066-024-00480-8
[28] Kannan, J., Jayakumar, V., Saeed, M., Alballa, T., Khalifa, H. A. E.-W., & Gomaa, H. G. (2024). Linear diophantine fuzzy clustering algorithm based on correlation coefficient and analysis on logistic efficiency of food products. IEEE Access, 12, 34889-34902. https://doi.org/10.1109/ access.2024.3371986
[29] Petchimuthu, S., Riaz, M., & Kamacı, H. (2022). Correlation coefficient measures and aggregation operators on interval-valued linear diophantine fuzzy sets and their applications. Computational and Applied Mathematics, 41, 409. https://doi.org/10.1007/s40314-022-02077-w
[30] Kannan, J., & Jayakumar, V. (2023). Sustainable method for tender selection using linear diophantine multi-fuzzy soft set. Communications Faculty Of Science University of Ankara Series A1 Mathematics and Statistics, 72(4), 976-991. https://doi.org/10.31801/cfsuasmas. 1255830
[31] Kannan, J., Jayakumar, V., Pethaperumal, M., & Shanmugam, N. S. (2024). Linear diophantine multi-fuzzy soft similarity measures: An analysis on alternative-fuel. Journal of Intelligent Fuzzy Systems, 1-13. https://doi.org/10.3233/jifs-219415
[32] Vimala, J., Garg, H., & Jeevitha, K. (2023). Prognostication of Myocardial Infarction Using Lattice Ordered Linear Diophantine Multi-fuzzy Soft Set. International Journal of Fuzzy Systems, 26, 44-59. https://doi.org/10.1007/s40815-023-01574-2
[33] Kannan, J., Jayakumar, V., & Saeid, A. B. (2024). Lattice algebraic structures on Idmfs domains. New Mathematics and Natural Computation, 1-21. https://doi.org/10.1142/s1793005725500218
[34] Jeevitha, K., Vimala, N. J., Banu, K. A., & Sri, S. N. (2024). Enhancing agricultural diagnostics through linear diophantine multi-fuzzy soft matrices with lattice implementation. Contemporary Mathematics, 2593-2618. https://doi.org/10.37256/cm.532O244387
[35] Sri, S., J, D., Kausar, N., Ozbilge, E., Ozbilge, E., & Pamucar, D. (2024). An mcdm approach on einstein aggregation operators under bipolar linear diophantine fuzzy hypersoft set. Heliyon, 10, e29863. https://doi.org/10.1016/j.heliyon.2024.e29863
[36] Pandipriya, A., J, D., & Begam, S. S. (2018). Lattice ordered interval-valued hesitant fuzzy soft sets in decision making problem. International Journal of Engineering Technology, 7(1.3), 5255. https://doi.org/10.14419/ijet.v7i1.3.9226
[37] Vimala, J., Mahalakshmi, P., Rahman, A. U., & Saeed, M. (2023). A customized TOPSIS method to rank the best airlines to fly during COVID-19 pandemic with q-rung orthopair multi-fuzzy soft information. Soft Computing, 27(20), 14571-14584. https://doi.org/10.1007/s00500-023-08976-2
[38] Pethaperumal, M., Jeyakumar, V., Kannan, J., & Banu, A. (2023). An algebraic analysis on exploring q-rung orthopair multi-fuzzy sets. Journal of Fuzzy Extension and Applications, 4(3), 235-245. https://doi.org/10.22105/jfea.2023.408513.1302
[39] Keshavarz-Ghorabaee, M., Zavadskas, E., Turskis, Z., & Antucheviciene, J. (2016). A new combinative distance-based assessment (codas) method for multi-criteria decision-making. Economic computation and economic cybernetics studies and research / Academy of Economic Studies, 50, 25-44.
[40] Keshavarz-Ghorabaee, M., Amiri, M., Zavadskas, E., Hooshmand, R., & Antucheviciene, J. (2017). Fuzzy extension of the codas method for multi-criteria market segment evaluation. Journal of Business Economics and Management, 18, 1-19. https: / / doi. org / 10. 3846/16111699. 2016. 1278559
[41] Panchal, D., Chatterjee, P., Shukla, R., Choudhury, T., & Tamosaitiene, J. (2017). Integrated fuzzy ahp-codas framework for maintenance decision in urea fertilizer industry. Economic Computation and Economic Cybernetics Studies and Research, 51(3), 179-196.
[42] Shetwan, A., Badi, I., & Abdulshahed, A. (2018). A case study of supplier selection for a steel making company in libya by using the combinative distance based assessment (codas) model. Decision Making: Applications in Management and Engineering, 1(1), 1-12. https://doi.org/10. 31181/dmame180101b
[43] Badi, I., Ballem, M., & Shetwan, A. (2018). Site selection of desalination plant in libya by using combinative distance-based assessment (codas) method. International Journal for Quality Research, 12(3), 609-624. https://doi.org/10.18421/IJQR12.03-04
[44] Boltürk, E. (2018). Pythagorean fuzzy codas and its application to supplier selection in a manufacturing firm. Journal of Enterprise Information Management, 3(4), 550-564. https://doi. org/10.1108/JEIM-01-2018-0020
[45] Boltürk, E., & Kahraman, C. (2018). Interval-valued intuitionistic fuzzy codas method and its application to wave energy facility location selection problem. Journal of Intelligent Fuzzy Systems, 35(4), 4865-4877. https://doi.org/10.3233/JIFS-18979
[46] Peng, X., & Garg, H. (2018). Algorithms for interval-valued fuzzy soft sets in emergency decision making based on wdba and codas with new information measure. Computers Industrial Engineering, 119, 439-452. https://doi.org/10.1016/j.cie.2018.04.001
[47] Mathew, M., & Sahu, S. (2018). Comparison of new multi-criteria decision making methods for material handling equipment selection. Management Science Letters, 8, 139-150. https: //doi.org/10.5267/j.msl.2018.1.004
[48] Pamucar, D., Badi, I., & Sanja, K. (2018). A novel approach for the selection of power-generation technology using a linguistic neutrosophic codas method: A case study in libya. Energies, 11(9), 2489. https://doi.org/10.3390/en11092489
[49] Yeni, F. B., & Özçelik, G. (2019). Interval-valued atanassov intuitionistic fuzzy codas method for multi criteria group decision making problems. Group Decision and Negotiation, 28. https: //doi.org/10.1007/s10726-018-9603-9
[50] Karaşan, A., Boltürk, E., & Kahraman, C. (2019). A novel neutrosophic codas method: Selection among wind energy plant locations. Journal of Intelligent and Fuzzy Systems, 36(2), 1491-1504. https://doi.org/10.3233/JIFS-181255
[51] Maghsoodi, A. I., Rasoulipanah, H., López, L. M., Liao, H., & Zavadskas, E. (2020). Integrating interval-valued multi-granular 2-tuple linguistic bwm-codas approach with target-based attributes: Site selection for a construction project. Computers Industrial Engineering, 139, 106147. https://doi.org/10.1016/j.cie.2019.106147
[52] Ijadi Maghsoodi, A., Maghsoodi, A., Poursoltan, P., Antucheviciene, J., & Turskis, Z. (2019). Dam construction material selection by implementing the integrated swara-codas approach with
target-based attributes. Archives of Civil and Mechanical Engineering, 19, 1194-1210. https: //doi.org/10.1016/j.acme.2019.06.010
[53] Seker, S. (2020). A novel interval-valued intuitionistic trapezoidal fuzzy combinative distancebased assessment (codas) method. Soft Computing, 24, 2287-2300. https://doi.org/10.1007/ s00500-019-04059-3
[54] Peng, X., & Ma, X. (2020). Pythagorean fuzzy multi-criteria decision making method based on codas with new score function. Journal of Intelligent and Fuzzy Systems, 38(3), 3307-3318. https://doi.org/10.3233/JIFS-190043
[55] Aydoğmuş, H., Kamber, E., & Kahraman, C. (2021). Erp selection using picture fuzzy codas method. Journal of Intelligent and Fuzzy Systems, 40(6), 11363-11373. https://doi.org/10. 3233/JIFS-202564
- *Corresponding author.
E-mail address: vimaljey@alagappauniversity.ac.in
DOI: https://doi.org/10.31181/sor2120259
Publication Date: 2024-08-28
Advanced Fuzzy-Based Decision-Making: The Linear Diophantine Fuzzy CODAS Method for Logistic Specialist Selection
ARTICLE INFO
Article history:
Received in revised form14 July 2024
Accepted 19 August 2024
Available online 28 August 2024
Keywords:
Abstract
This study addresses the inherent uncertainty in human decision-making by leveraging fuzzy sets, which were introduced to better capture the imprecision associated with human thoughts and judgments. As an extension to traditional fuzzy sets, the Linear Diophantine Fuzzy Set (LDFS) was developed, offering a more flexible approach by relaxing existing limitations on grade values. The LDFS has found applications across various fields, demonstrating its versatility and effectiveness. In this study, we explore the application of the Linear Diophantine Fuzzy Set within the framework of the Combinative Distance-based Assessment (CODAS) method. The CODAS method stands out because it incorporates Euclidean and Taxicab distances. Decision-making should consider not only the direct distances between ideal solutions and alternatives but also the indirect distances. The foremost objective of this research is to propose a novel approach by integrating the CODAS method with the LDFS to address complex decision-making problems characterized by uncertainty and imprecision. To illustrate the practical utility of the proposed method, we apply it to a numerical example involving the selection of a logistics specialist, a critical decision in emergency logistics optimization. The research also includes a case study on a logistics specialist, highlighting the practical application of the methods discussed. Furthermore, this study provides a comprehensive sensitivity analysis of the parameters’ weights to evaluate the robustness and reliability of the proposed method. The results highlight the effectiveness of the LDF CODAS method in making informed and reliable decisions under conditions of uncertainty, paving the way for future applications in other decisionmaking scenarios.
1. Introduction
As it enables the transfer of products from suppliers to manufacturers, sellers or distributors, and


Literature Review on Selection Charateristics
| Position | Evaluation Approach | Selection Criteria |
| [1] System analysis engineer | Fuzzy TOPSIS | Emotional steadiness, oral communication skills, personality, past experience, self-confidence |
| [2] ICT project manager | Fuzzy linguistic evaluation approach | Education, experience, computer knowledge, foreign language, age, gender, labor shift and non-smoker |
| [3] System analysis | IFS TOPSIS | Leadership, motivation, work experience, proficiency, appearance, creativity, age and communication skills |
| [4] Sales manager | IF-TOPSIS | Oral communication skills, past experience, general aptitude, willingness, self-confidence and first impression |
| [5] Engineer | Fuzzy VIKOR | General and professional knowledge criteria |
| [6] Project manager | Fuzzy VIKOR | Site management capacity, technical level,level of leadership, personal qualities and contextual competencies |
| [7] Project manager | Fuzzy MCDM | Basic requirements, project management skills, management skills and interpersonal skills |
| [8] CIO | Fuzzy TOPSIS | Soft and technical skills |
| [9] Support Manager | Fuzzy TOPSIS | Creativity/innovation, problem-solving/decision making, conflict management/negotiation, empowerment/delegation, strategic planning, specific presentation skills,communication skills, team management, diversity management, self-management, and educational background |
| [10] HR manager | Fuzzy TOPSIS | Scientific, psychological, behavioral and apparent characteristics, functional characteristics and medical |
| [11] System analyst | Fuzzy TOPSIS | Emotional steadiness, oral communication skills, personality, past experience and self-confidence |
| [12] Personnel | Fuzzy TOPSIS | Science and education, behavior and appearance, personal psychological, functional activity and medical criteria |
1.1 Literature Review
al.,built the complex LDF soft set [20]. Several Einstein aggregation techniques were applied to explore LDFS for MCDM problems in Aiyared Iampam[21]. These operators can extract rating data and identify the optimal choice. Subsequently, Saya Ayub[22] connected algebraic features with LDF relations through decision-making. Riaz et al.,[23] developed on LDFS by putting forth the idea of soft rough sets for application in material handling equipment. To choose third-party logistic service providers, Riaz et al.,[24] developed aggregation operators (AOs) that used linear Diophantine fuzzy numbers (LDFNs) in priority order. An application of Einstein prioritized linear Diophantine fuzzy AOs was proposed by Farid et al.,[25].
of the CODAS method is emphasized in the context of ERP selection by H.Y. Aydogmus et al., [55].
Several fuzzy number extensions have reportedly been combined with the CODAS approach under uncertainty, according to the literature. The focus of this work is on the linear Diophantine fuzzy extension of the CODAS approach, which has not yet been investigated in the literature.
1.2 Contribution of this research
- This work presents a unique framework for decision-making by combining the Linear Diophantine Fuzzy Set (LDFS) with the CODAS approach.
- It enhances conventional approaches by addressing intricate decision-making issues marked by uncertainty and imprecision.
- A case study is provided that utilizes the suggested LDF CODAS method for emergency logistics optimization when choosing a logistics specialist.
- To assess the method’s robustness and dependability in practical situations, the study involves a thorough sensitivity analysis.
- The study opens the door for additional LDF CODAS technique applications in a range of multicriteria decision-making scenarios.
2. Preliminaries
Definition 2.2. [17] A linear Diophantine fuzzy set
-
-
-
-
-
-
3. A Proposed LDF-CODAS Technique
Step 1: Assemble the LDF decision matrix
Step 2: Normalise the decision matrix as
Step 4: Evaluate the negative ideal solution NIS such that
where
Step 7: Determine the evaluation score
4. Optimization of Emergency Logistics: A Case study
1 Build a LDF Decision Matrix
2 Normalize the LDF Decision Matrix
3 Obtain Weighted Normalized Matrix
4 Determine the Negative Ideal Solution(NIS)
5 Compute Euclidean Distance and Taxicab Distance
6 Derive Relative Assessment Matrix
7 Compute the Evaluation Score
Fig. 3. LDF-CODAS Algorithmic Flow
4.1 Role of Logistics Specialist
7. Preparedness Planning: Logistics specialists work ahead of time to build thorough emergency response plans and tactics. This includes identifying potential risks, developing supply chain protocols, and developing contingency plans to enable a quick and effective response during a disaster.
2. Resource Allocation: They analyze historical data and utilize predictive modeling to identify the best resource allocation based on predicted demands during a crisis. This aids in ensuring that the appropriate resources are deployed to the appropriate locations at the appropriate time.
3. Supplier ties: It is critical to develop strong ties with dependable suppliers. To maintain a consistent flow of necessary commodities during catastrophes, logistics specialists negotiate contracts and form partnerships with suppliers.
4. Inventory Management: It is critical to keep an adequate supply of emergency supplies on hand. Inventory management strategies are used by logistics specialists to track stock levels and refill supplies as needed, minimizing shortages and surpluses.
5. technological Integration: To streamline logistics operations, they use technological solutions such as GPS tracking, real-time monitoring, and inventory management software. This enables better supply chain awareness and faster decision-making.
6. Transportation Efficiency: Logistics professionals optimize transportation routes and modes to reduce delivery times and costs. They may also plan for resource pre-positioning in crucial locations to allow speedy reaction.
7. Communication and Coordination: Effective communication and coordination with other stakeholders, such as government agencies, non-governmental organizations, and local governments, is crucial for optimizing logistics. They establish communication protocols to promote seamless information sharing and collaboration.
8. Data Analytics: Using data analytics, logistics specialists analyze and interpret real-time data to make informed decisions about resource allocation and distribution. This includes tracking demand patterns, transportation bottlenecks, and resource utilization.
9. Cost Control: Managing expenses efficiently is an important part of optimizing emergency logistics. Logistics specialists look for ways to cut costs while maintaining response quality and effectiveness. 10. They organize training sessions and disaster drills for logistical teams and responders to improve their skills and preparedness. Regular exercises aid in the identification of opportunities for improvement in logistics procedures.
10. Ongoing Improvement: Following each emergency response, logistics specialists undertake postoperation evaluations and debriefings. These evaluations’ findings are utilized to modify and improve future emergency logistics strategies and procedures.
11. Risk Mitigation: It is critical to identify potential risks and weaknesses in the supply chain. Logistics professionals devise risk-mitigation techniques in response to obstacles such as road closures, natural disasters, and security concerns.
4.2 The need for Logistics Specialist
a logistics specialist is a strategic decision with far-reaching consequences for an organization’s competitiveness, profitability, and ability to satisfy the demands of a dynamic global marketplace.
4.3 Selection Criteria for Logistic Specialist

4.4 Mathematical Computation of proposed approach
4.4.1 Description of the Problem
4.4.2 Decision-making Process
- The LDF decision matrix is constructed as below;
- Since all the criteria are of the same type, there is no need for normalization.
- The weighted decision matrix is computed by utilizing the formula [Eq. (2)] as follows:
- To find the NIS, we have to find the minimum value for each column ‘
- The Euclidean distance
Euclidean distance
| Alternatives |
|
|
|
|
0.1350 | 0.8232 |
|
|
0.2227 | 1.6410 |
|
|
0.1690 | 0.9770 |
|
|
0.2213 | 1.5940 |
|
|
0.2161 | 1.4106 |
|
|
0.2673 | 1.4923 |
|
|
0.2615 | 1.9229 |
- The RAM
- The Evaluation Scores of each alternative are computed by utilizing the formula Eq. (11).
- The rank of alternatives is
4.5 Sensitivity analysis
Case 1: The higher preference is given to the criteria
Case 2: The higher preference is given to the criteria
Case 3: The higher preference is given to the criteria
Case 4: The higher preference is given to the criteria
It is evident from the findings that the suggested method is sensitive to the criteria weights. The order’s rank also slightly varies as we adjust the weight preferences.
5. Conclusion
making this method suitable for all types of data sets. In this study, we identify the best logistics specialist using the CODAS method, which excels by incorporating two distance measures, leading to more accurate results. With its adaptable framework that manages imprecision and ambiguity, the LDF CODAS technique greatly improves decision-making-a critical feature for intricate situations. Its real-world impact is demonstrated by its practical implementation in the process of choosing a logistics specialist, which enhances operational decision-making and efficiency. Furthermore, the scalability of the system implies that it has the potential to be applied more widely across many industries, providing a trustworthy instrument for future decision-making difficulties. The sensitivity study supports the LDF CODAS method’s robustness by demonstrating its ability to tolerate changes in input parameters without compromising consistent results. This work expands the use of fuzzy sets in decision-making and presents a potent tool for further investigation and real-world applications in domains that need complex decision-making in the face of uncertainty. The knowledge gathered from this study can be used in various fields, promoting additional investigation and improvement of fuzzy-based decisionmaking models. As our theory offers numerous advantages, it also has certain limitations. When the reference parameter values add up to more than one, our proposed theory is unable to manage the situation. Also, while dealing with large amounts of data, the computation of the proposed model could be laborious. In the future, several MCDM methods such as PROMTHEE, EDAS, and VIKOR, TODIM, DEMATEL approaches will be employed in various fields such as medicine, agriculture, economics, and society.
Acknowledgement
Conflicts of Interest
References
[2] Afshari, A., & Kowal, J. (2017). Decision Making Methods for the Selection of ICT Project Manager. Gospodarka Rynek Edukacja= Economy Market Education, 18(4), 19-28. https://doi.org/ 10.2139/ssrn. 3118075
[3] Bali, Ö., Gümüş, S., & Dağdeviren, M. (2013). A group madm method for personnel selection problem using delphi technique based on intuitionistic fuzzy sets. Journal of Management and Information Science, 1(1), 1-13.
[4] Boran, E., Genç, S., & Akay, D. (2011). Personnel selection based on intuitionistic fuzzy sets. Human Factors and Ergonomics in Manufacturing Service Industries, 21, 493-503. https://doi. org/10.1002/hfm. 20252
[5] Chen, C.-T., Pai, P.-F., & Wei Zhan, H. (2011). Applying linguistic vikor and knowledge map in personnel selection. Asia Pacific Management Review, 16(4), 491-502.
[6] Jafarnejad Chaghooshi, A., Arab, A., & Hosseini Dehshiri, S. J. (2016). A fuzzy hybrid approach for project manager selection. Decision Science Letters, 447-460. https://doi.org/10.5267/j. dsl.2016.1.001
[7] Dodangeh, J., Sorooshian, S., & Afshari, A. R. (2014). Linguistic Extension for Group Multicriteria Project Manager Selection. Journal of Applied Mathematics, 2014, 570398. https://doi.org/10. 1155/2014/570398
[8] Kelemenis, A., & Askounis, D. (2010). A new TOPSIS-based multi-criteria approach to personnel selection. Expert Systems with Applications, 37(7), 4999-5008. https://doi.org/10.1016/j.eswa. 2009.12.013
[9] Kelemenis, A., Ergazakis, K., & Askounis, D. (2011). Support managers selection using an extension of fuzzy TOPSIS. Expert Systems with Applications, 38(3), 2774-2782. https://doi.org/10. 1016/j.eswa.2010.08.068
[10] Nobari, S. M., & Zadeh, D. H. (2013). Designing a fuzzy model for decision support systems in the selection and recruitment process. African Journal of Business Management, 7(16), 1486. https://doi.org/10.5897/AJBM11.2803
[11] Mahdavi, I., Mahdavi-Amiri, N., Heidarzade, A., & Nourifar, R. (2008). Designing a model of fuzzy TOPSIS in multiple criteria decision making. Applied Mathematics and Computation, 206(2), 607-617. https://doi.org/10.1016/j.amc.2008.05.047
[12] Mammadova, M., & Jabrayilova, Z. (2014). Application of Fuzzy Optimization Method in DecisionMaking for Personnel Selection. Intelligent Control and Automation, 5(4), 190-204. https://doi. org/10.4236/ica.2014.54021
[13] Zadeh, L. (1965). Fuzzy sets. Information and Control, 8(3), 338-353. https://doi.org/10.1016/ Soo19-9958(65)90241-X
[14] Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87-96. https: //doi.org/10.1016/S0165-0114(86)80034-3
[15] Yager, R. R. (2014). Pythagorean Membership Grades in Multicriteria Decision Making. IEEE Transactions on Fuzzy Systems, 22(4), 958-965. https://doi.org/10.1109/TFUZZ.2013.2278989
[16] Yager, R. R. (2017). Generalized Orthopair Fuzzy Sets. IEEE Transactions on Fuzzy Systems, 25(5), 1222-1230. https://doi.org/10.1109/TFUZZ.2016.2604005
[17] Riaz, M., & Hashmi, M. R. (2019). Linear diophantine fuzzy set and its applications towards multi-attribute decision-making problems. Journal of Intelligent and Fuzzy Systems, 37(4), 54175439. https://doi.org/10.3233/jifs-190550
[18] Kannan, J., Jayakumar, V., Pethaperumal, M., & Kather Mohideen, A. B. (2024). An intensified linear diophantine fuzzy combined dematel framework for the assessment of climate crisis. Stochastic Environmental Research and Risk Assessment. https://doi.org/10.1007/s00477-023-02618-7
[19] Jeevitha, K., Garg, H., Vimala, J., Aljuaid, H., & Abdel-Aty, A.-H. (2023). Linear diophantine multifuzzy aggregation operators and its application in digital transformation. Journal of Intelligent Fuzzy Systems, 45(2), 3097-3107. https://doi.org/10.3233/JIFS-223844
[20] Jayakumar, V., Mohideen, A. B. K., Saeed, M. H., Alsulami, H., Hussain, A., & Saeed, M. (2023). Development of Complex Linear Diophantine Fuzzy Soft Set in Determining a Suitable AgriDrone for Spraying Fertilizers and Pesticides. IEEE Access, 11, 9031-9041. https://doi.org/10. 1109/ACCESS.2023.3239675
[21] Iampan, A., García, G. S., Riaz, M., Athar Farid, H. M., & Chinram, R. (2021). Linear diophantine fuzzy einstein aggregation operators for multi-criteria decision-making problems. Journal of Mathematics, 2021, 5548033. https://doi.org/10.1155/2021/5548033
[22] Ayub, S., Shabir, M., Riaz, M., Aslam, M., & Chinram, R. (2021). Linear diophantine fuzzy relations and their algebraic properties with decision making. Symmetry, 13(6), 945. https://doi. org/10.3390/sym13060945
[23] Riaz, M., Hashmi, M. R., Kalsoom, H., Pamucar, D., & Chu, Y.-M. (2020). Linear diophantine fuzzy soft rough sets for the selection of sustainable material handling equipment. Symmetry, 12(8), 1215. https://doi.org/10.3390/sym12081215
[24] Riaz, M., Farid, H. M. A., Aslam, M., Pamucar, D., & Bozanić, D. (2021). Novel approach for third-party reverse logistic provider selection process under linear diophantine fuzzy prioritized aggregation operators. Symmetry, 13(7), 1152. https://doi.org/10.3390/sym13071152
[25] Farid, H. M. A., Riaz, M., Khan, M. J., Kumam, P., & Sitthithakerngkiet, K. (2022). Sustainable thermal power equipment supplier selection by einstein prioritized linear diophantine fuzzy aggregation operators. AIMS Mathematics, 7(6), 11201-11242. https://doi.org/10.3934/math. 2022627
[26] Riaz, M., Farid, H. M. A., Wang, W., & Pamucar, D. (2022). Interval-valued linear diophantine fuzzy frank aggregation operators with multi-criteria decision-making. Mathematics, 10(11), 1811. https://doi.org/10.3390/math10111811
[27] Jayakumar, V., Kannan, J., Kausar, N., Deveci, M., & Wen, X. (2024). Multicriteria group decision making for prioritizing iot risk factors with linear diophantine fuzzy sets and marcos method. Granular Computing, 9(3), 56. https://doi.org/10.1007/s41066-024-00480-8
[28] Kannan, J., Jayakumar, V., Saeed, M., Alballa, T., Khalifa, H. A. E.-W., & Gomaa, H. G. (2024). Linear diophantine fuzzy clustering algorithm based on correlation coefficient and analysis on logistic efficiency of food products. IEEE Access, 12, 34889-34902. https://doi.org/10.1109/ access.2024.3371986
[29] Petchimuthu, S., Riaz, M., & Kamacı, H. (2022). Correlation coefficient measures and aggregation operators on interval-valued linear diophantine fuzzy sets and their applications. Computational and Applied Mathematics, 41, 409. https://doi.org/10.1007/s40314-022-02077-w
[30] Kannan, J., & Jayakumar, V. (2023). Sustainable method for tender selection using linear diophantine multi-fuzzy soft set. Communications Faculty Of Science University of Ankara Series A1 Mathematics and Statistics, 72(4), 976-991. https://doi.org/10.31801/cfsuasmas. 1255830
[31] Kannan, J., Jayakumar, V., Pethaperumal, M., & Shanmugam, N. S. (2024). Linear diophantine multi-fuzzy soft similarity measures: An analysis on alternative-fuel. Journal of Intelligent Fuzzy Systems, 1-13. https://doi.org/10.3233/jifs-219415
[32] Vimala, J., Garg, H., & Jeevitha, K. (2023). Prognostication of Myocardial Infarction Using Lattice Ordered Linear Diophantine Multi-fuzzy Soft Set. International Journal of Fuzzy Systems, 26, 44-59. https://doi.org/10.1007/s40815-023-01574-2
[33] Kannan, J., Jayakumar, V., & Saeid, A. B. (2024). Lattice algebraic structures on Idmfs domains. New Mathematics and Natural Computation, 1-21. https://doi.org/10.1142/s1793005725500218
[34] Jeevitha, K., Vimala, N. J., Banu, K. A., & Sri, S. N. (2024). Enhancing agricultural diagnostics through linear diophantine multi-fuzzy soft matrices with lattice implementation. Contemporary Mathematics, 2593-2618. https://doi.org/10.37256/cm.532O244387
[35] Sri, S., J, D., Kausar, N., Ozbilge, E., Ozbilge, E., & Pamucar, D. (2024). An mcdm approach on einstein aggregation operators under bipolar linear diophantine fuzzy hypersoft set. Heliyon, 10, e29863. https://doi.org/10.1016/j.heliyon.2024.e29863
[36] Pandipriya, A., J, D., & Begam, S. S. (2018). Lattice ordered interval-valued hesitant fuzzy soft sets in decision making problem. International Journal of Engineering Technology, 7(1.3), 5255. https://doi.org/10.14419/ijet.v7i1.3.9226
[37] Vimala, J., Mahalakshmi, P., Rahman, A. U., & Saeed, M. (2023). A customized TOPSIS method to rank the best airlines to fly during COVID-19 pandemic with q-rung orthopair multi-fuzzy soft information. Soft Computing, 27(20), 14571-14584. https://doi.org/10.1007/s00500-023-08976-2
[38] Pethaperumal, M., Jeyakumar, V., Kannan, J., & Banu, A. (2023). An algebraic analysis on exploring q-rung orthopair multi-fuzzy sets. Journal of Fuzzy Extension and Applications, 4(3), 235-245. https://doi.org/10.22105/jfea.2023.408513.1302
[39] Keshavarz-Ghorabaee, M., Zavadskas, E., Turskis, Z., & Antucheviciene, J. (2016). A new combinative distance-based assessment (codas) method for multi-criteria decision-making. Economic computation and economic cybernetics studies and research / Academy of Economic Studies, 50, 25-44.
[40] Keshavarz-Ghorabaee, M., Amiri, M., Zavadskas, E., Hooshmand, R., & Antucheviciene, J. (2017). Fuzzy extension of the codas method for multi-criteria market segment evaluation. Journal of Business Economics and Management, 18, 1-19. https: / / doi. org / 10. 3846/16111699. 2016. 1278559
[41] Panchal, D., Chatterjee, P., Shukla, R., Choudhury, T., & Tamosaitiene, J. (2017). Integrated fuzzy ahp-codas framework for maintenance decision in urea fertilizer industry. Economic Computation and Economic Cybernetics Studies and Research, 51(3), 179-196.
[42] Shetwan, A., Badi, I., & Abdulshahed, A. (2018). A case study of supplier selection for a steel making company in libya by using the combinative distance based assessment (codas) model. Decision Making: Applications in Management and Engineering, 1(1), 1-12. https://doi.org/10. 31181/dmame180101b
[43] Badi, I., Ballem, M., & Shetwan, A. (2018). Site selection of desalination plant in libya by using combinative distance-based assessment (codas) method. International Journal for Quality Research, 12(3), 609-624. https://doi.org/10.18421/IJQR12.03-04
[44] Boltürk, E. (2018). Pythagorean fuzzy codas and its application to supplier selection in a manufacturing firm. Journal of Enterprise Information Management, 3(4), 550-564. https://doi. org/10.1108/JEIM-01-2018-0020
[45] Boltürk, E., & Kahraman, C. (2018). Interval-valued intuitionistic fuzzy codas method and its application to wave energy facility location selection problem. Journal of Intelligent Fuzzy Systems, 35(4), 4865-4877. https://doi.org/10.3233/JIFS-18979
[46] Peng, X., & Garg, H. (2018). Algorithms for interval-valued fuzzy soft sets in emergency decision making based on wdba and codas with new information measure. Computers Industrial Engineering, 119, 439-452. https://doi.org/10.1016/j.cie.2018.04.001
[47] Mathew, M., & Sahu, S. (2018). Comparison of new multi-criteria decision making methods for material handling equipment selection. Management Science Letters, 8, 139-150. https: //doi.org/10.5267/j.msl.2018.1.004
[48] Pamucar, D., Badi, I., & Sanja, K. (2018). A novel approach for the selection of power-generation technology using a linguistic neutrosophic codas method: A case study in libya. Energies, 11(9), 2489. https://doi.org/10.3390/en11092489
[49] Yeni, F. B., & Özçelik, G. (2019). Interval-valued atanassov intuitionistic fuzzy codas method for multi criteria group decision making problems. Group Decision and Negotiation, 28. https: //doi.org/10.1007/s10726-018-9603-9
[50] Karaşan, A., Boltürk, E., & Kahraman, C. (2019). A novel neutrosophic codas method: Selection among wind energy plant locations. Journal of Intelligent and Fuzzy Systems, 36(2), 1491-1504. https://doi.org/10.3233/JIFS-181255
[51] Maghsoodi, A. I., Rasoulipanah, H., López, L. M., Liao, H., & Zavadskas, E. (2020). Integrating interval-valued multi-granular 2-tuple linguistic bwm-codas approach with target-based attributes: Site selection for a construction project. Computers Industrial Engineering, 139, 106147. https://doi.org/10.1016/j.cie.2019.106147
[52] Ijadi Maghsoodi, A., Maghsoodi, A., Poursoltan, P., Antucheviciene, J., & Turskis, Z. (2019). Dam construction material selection by implementing the integrated swara-codas approach with
target-based attributes. Archives of Civil and Mechanical Engineering, 19, 1194-1210. https: //doi.org/10.1016/j.acme.2019.06.010
[53] Seker, S. (2020). A novel interval-valued intuitionistic trapezoidal fuzzy combinative distancebased assessment (codas) method. Soft Computing, 24, 2287-2300. https://doi.org/10.1007/ s00500-019-04059-3
[54] Peng, X., & Ma, X. (2020). Pythagorean fuzzy multi-criteria decision making method based on codas with new score function. Journal of Intelligent and Fuzzy Systems, 38(3), 3307-3318. https://doi.org/10.3233/JIFS-190043
[55] Aydoğmuş, H., Kamber, E., & Kahraman, C. (2021). Erp selection using picture fuzzy codas method. Journal of Intelligent and Fuzzy Systems, 40(6), 11363-11373. https://doi.org/10. 3233/JIFS-202564
- *Corresponding author.
E-mail address: vimaljey@alagappauniversity.ac.in
