المغناطيسية البديلة مع دوران غير متوازي Altermagnetism with non-collinear spins

المجلة: npj Quantum Materials، المجلد: 9، العدد: 1
DOI: https://doi.org/10.1038/s41535-024-00626-6
تاريخ النشر: 2024-01-22

المغناطيسية البديلة مع دوران غير متوازي

سانغ-ووك تشيونغ (د) وفاي-تينغ هوانغ (د

الملخص

يتم تقديم الألترمغناطيسية كفئة من الحالات المغناطيسية ذات الدوران المضاد “المتوازي” والتغيرات المتناوبة للهياكل المحلية حول الدورانات بطريقة تسمح بالتناظر الذي يتيح سلوكيات مغناطيسية حديدية نموذجية. يتبين أن الألترمغناطيسيات التي تظهر سلوكيات مغناطيسية حديدية دون أي اضطرابات خارجية (النوع الأول) تنتمي إلى مجموعة النقاط المغناطيسية الحديدية. يمكن أن تحتوي الألترمغناطيسيات الأخرى (النوع الثاني والنوع الثالث) على سلوكيات مغناطيسية حديدية فقط مع الاضطرابات الخارجية مثل التيار الكهربائي أو الضغط، والتي تحافظ على تناظر عكس الزمن-التماثل (PT). جميع أنواع الألترمغناطيسيات نفسها لديها كسر في تناظر PT. يمكن توسيع مفهوم الألترمغناطيسية لاستيعاب الدورانات غير المتوازية وتنوعات الهياكل المحلية المتعددة.

npj مواد الكم (2024)9:13؛https://doi.org/10.1038/s41535-024-00626-6

مقدمة

سبينترونيكس حيث تكون درجات حرية الدوران والشحنة مرتبطة ومتفاعلة من خلال تقاطع الحقول المترافقة (أي الحقول الكهربائية للدورانات والحقول المغناطيسية للشحنات) كانت منطقة بحث نشطة على مدى الثلاثة عقود الماضية منذ اكتشاف المقاومة المغناطيسية العملاقة. ، وقد تم تنفيذها بشكل جيد في الأجهزة الحقيقية. تقليديًا، تستخدم السبينترونيكس الفيرومغناطيسيات (الفيريمغناطيسيات) نظرًا لأن التلاعب واكتشاف هذه الحالات الفيرومغناطيسية (الفيريمغناطيسية) أمر سهل. لكن السبينترونيكس المضادة للمغناطيسية أصبح موضوعًا ذا أهمية كبيرة بسبب التلاعب النشط في الحالة المضادة للمغناطيسية وملامحها المغناطيسية من خلال تيارات الدوران والشحنة. يمكن أن تجسد المواد المضادة للمغناطيسية، بشكل عام، العديد من الميزات المثيرة للاهتمام المفيدة لتطبيقات السبينترونيك. لا تنتج حقولًا شاردة، لذا فهي قوية ضد الحقول المغناطيسية الخارجية وتجعلها مناسبة لتصغير الأجهزة، وتعرض ديناميات فائقة السرعة في نطاقات التيراهيرتز، وقادرة على توليد نقل جيد للتيار المغزلي مع أطوال انتشار مغزلي ميكرومترية.
المغناطيسات البديلة هي مغناطيسات ذات ترتيب مضاد مغناطيسي متوازي من نوع واحد من الدوران (أي، ‘دوران متناوب’)، وأيضًا في نفس الوقت مع ‘توجهات متناوبة للهياكل المحلية حول الدورانات، مما يحافظ على تناظر يمكّن من سلوكيات مغناطيسية حديدية (لحظة مغناطيسية صافية غير صفرية، تأثير هول الشاذ (AHE)، إلخ. بعبارة أخرى، في الألترماجنات، يتم تعويض لحظات المغناطيسية الدورانية بالكامل عندما يكون تفاعل الدوران-المدار (SOC) صفرًا، ولكن وجود تفاعل SOC غير الصفري، الذي يمكّن من الربط بين الدورانات والهياكل المحلية المتناوبة (مثل تنسيق الأكسجين حول الأيونات المغناطيسية)، يمكن أن يؤدي إلى لحظة مغناطيسية صافية غير صفرية وسلوكيات فيرومغناطيسية أخرى من خلال ‘لحظات المغناطيسية المدارية’ غير المعوضة.

المغناطيسية الحديدية مقابل المغناطيسية المضادة

من المدهش أن المغناطيسية المضادة ليست معرفة بشكل رسمي على الرغم من أن المصطلح قد تم استخدامه بشكل متكرر، لكن مجموعة النقاط المغناطيسية الحديدية معرفة بشكل جيد من حيث التناظر. المغنطة ( ) على قد انكسر مع دوران حر على طول (انظر المراجع. لتعريف رموز عمليات التناظر. جميع المجموعات النقطية المغناطيسية (MPGs) التي تنتمي إلى مجموعة النقاط الفيرومغناطيسية لديك، على الأقل، شيء مكسور مع دوران حر على طول أو المتطلبات ذات الصلة أو أي، لديها تناظر تشغيلي
تشابه (SOS) مع واحد وثلاثون (31) من مولدات الطاقة المغناطيسية الحديدية تضمين ، ، . لقد أخذنا في الاعتبار التماثلات التي تتماشى فقط مع تلك المتجهات الأساسية لأنظمة الإحداثيات البلورية التقليدية. يتم تقديم تلك المتجهات الأساسية في إعدادات 122 MPG. على سبيل المثال، نناقش التماثلات على طول ، و -الاتجاهات في MPGs الرباعية والسداسية، بينما فقط التماثلات على طول و تُعتبر الاتجاهات في MPGs المعينية في تحليل SOS الخاص بنا. حتى بالنسبة لتلك الهياكل السداسية والثلاثية، و -المحاور تُعرف بأنها متعامدة على بعضها البعض. الدوران يشمل كلا من (عكس اتجاه عقارب الساعة) و (في اتجاه عقارب الساعة)، مع علامات + و – . أي معايير تناظر مرتبطة بـ تنطبق بشكل متساوٍ على عملية و ، في الوقت نفسه. يمتد هذا المبدأ إلى و الدورات.
إنه تعريف صارم ولا ينتج عنه أي غموض لتعريف المغناطيسية الحديدية والمغناطيسية المضادة في المواد البلورية بهذه الطريقة: أي حالات مغناطيسية، تنتمي مجموعاتها النقطية إلى مجموعة النقاط المغناطيسية الحديدية، هي مغناطيسية حديدية؛ بخلاف ذلك، تكون مغناطيسية مضادة. . تظهر هذه المواد المغناطيسية الفيرومغناطيسية خصائص فيزيائية فريدة مثل العزم المغناطيسي الصافي غير الصفري، ودوران فاراداي البصري غير المتناظر، وتأثير هول الشاذ الخطي (AHE). (لاحظ أن هناك أربعة أنواع من تأثيرات هول الشاذ (تأثير هول الشاذ الحقيقي، وتأثير إتينغهاوزن، وتأثير نيرنست، وتأثير هول الحراري)، ومن حيث التناظر، هناك اختلاف طفيف بين المتطلبات لأربعة أنواع من تأثيرات هول الشاذ طالما يمكن أن يوجد التيار الكهربائي/الحراري المعني. إن الشرط لمراقبة كل من الظواهر المذكورة أعلاه هو نفسه شرط الانتماء إلى مجموعة النقاط الفيرومغناطيسية، لذا يمكن ملاحظة هذه التأثيرات ‘فقط’ في مجموعات النقاط الفيرومغناطيسية. كما تظهر الفيرومغناطيسات تأثيرات بيزومغناطيسية قطرية على طول اتجاهات العزم المغناطيسي الصافي وتأثيرات كير المغناطيسية البصرية (MOKEs)؛ ومع ذلك، يمكن أيضًا ملاحظة التأثير البيزومغناطيسي القطري وMOKE في بعض المواد المضادة للفيرومغناطيسات مع تماثلات مكسورة بشكل صحيح. . تنتمي المغناطيسات الفيرومغناطيسية البسيطة التي تشير جميع لحظات المغناطيس الأيونية في اتجاه واحد إلى مجموعات النقاط الفيرومغناطيسية، ولكن الحالات الفيريمغناطيسية، والمضادة الفيرومغناطيسية المائلة، والفيرومغناطيسية الضعيفة، أو الحالات الفيرومغناطيسية الضعيفة ذات اللحظات المغناطيسية الصافية غير الصفرية تنتمي أيضًا إلى مجموعة النقاط الفيرومغناطيسية. من أجل البساطة، سنصنف جميع المغناطيسات التي تنتمي إلى مجموعة النقاط الفيرومغناطيسية، ولكن لا تظهر البساطة.
الشكل 1 تصنيف حالات المغناطيسية المختلفة. جميع المواد الفيرومغناطيسية (الصندوق الأزرق) تنتمي إلى مجموعة النقاط الفيرومغناطيسية، وأي حالات مغناطيسية لا تنتمي إلى مجموعة النقاط الفيرومغناطيسية هي مضادة للفيرومغناطيسية (الصندوق الأخضر). جميع المواد الفيرومغناطيسية تظهر تأثير هول غير الخطي، ويمكن ملاحظة تأثير هول من الرتبة العالية في بعض المواد المضادة للفيرومغناطيسية، وجميع الحالات المغناطيسية التي تظهر تأثير هول من الرتبة الفردية لديها كسر في تناظر PT. مجموعات النقاط المغناطيسية ذات الصلة بالنوع الأول من الألترمغناطيسية المقترحة للدوران المتوازي موجودة داخل الدائرة المنقطة. تنتمي جميع الألترمغناطيسات من النوع الأول إلى مجموعة النقاط المغناطيسية الفيرومغناطيسية. يمكن أن تظهر جميع الألترمغناطيسات من النوع الثاني تأثير هول غير المتناظر من الرتبة الفردية العالية، بينما لا يمكن للألترمغناطيسات من النوع الثالث أن تظهر أي تأثير هول غير المتناظر على المحاور الرئيسية. تشير المنطقة الصفراء إلى الحالات غير المغناطيسية وغير المركزية، والتي لم يتم مناقشتها في هذا المنظور. تجدر الإشارة إلى أن ‘الألترمغناطيسية من النوع الأول’ هي مجموعة فرعية من ‘الفيرومغناطيسية’، و’الألترمغناطيسية من النوع الثاني’ هي مجموعة فرعية من ‘الأنتيفيرومغناطيسية مع تأثير هول غير المتناظر من الرتبة الفردية العالية’، و’الألترمغناطيسية من النوع الثالث’ هي مجموعة فرعية من ‘الأنتيفيرومغناطيسية بدون تناظر PT وتأثير هول غير المتناظر من الرتبة الفردية’؛ ومع ذلك، لا يمكن تحديد علاقات المجموعات الفرعية الدقيقة من تحليل التناظر وحده.
المغناطيسية الحديدية أو المغناطيسية الفيريمغناطيسية (التي تحتوي على لحظات غير متوازنة مع لحظات مغناطيسية أيونية مرتبة بشكل مضاد)، كـ ‘مغناطيسات حديدية ضعيفة’ نبرز أن المواد المضادة للمغناطيسية هي حالات مغناطيسية توجد في المواد الصلبة البلورية، والتي لا تنتمي إلى مجموعة النقاط المغناطيسية الحديدية.

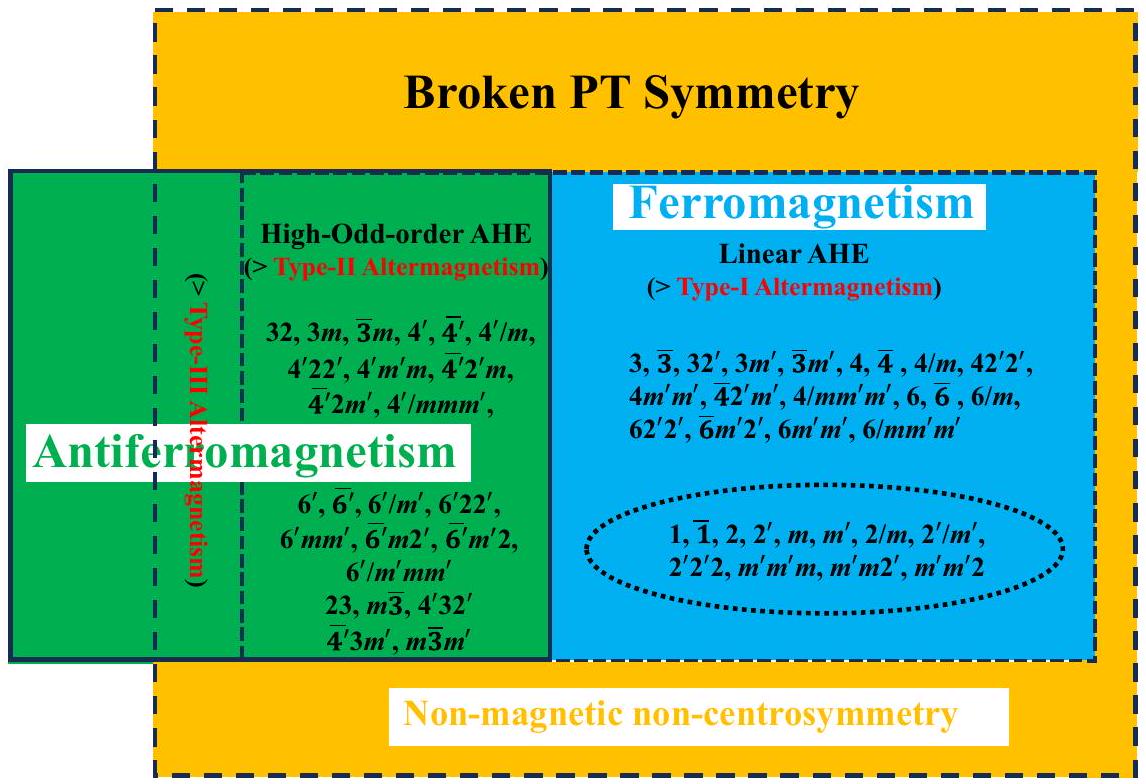
المغناطيسية البديلة من النوع الأول والنوع الثاني

تنكسر تناظر PT (P؛ التماثل، T؛ عكس الزمن، وPT؛ التماثل مضروبًا في عكس الزمن) في جميع الألترماجنات. الجانب الأساسي من الألترماجنات هو أنه عندما يتم تجاهل اقتران الدوران-المدار، فإن الزخم الزاوي للدوران في الألترماجنات يتم تعويضه بالكامل، لذا لا يوجد زخم زاوي صافي للدوران، ولكن الشبكة الدورانية مع التغيرات البلورية قد كسرت تناظر PT، لذا توجد ‘أنسجة دورانية في الإثارات’ و’زخم مغناطيسي صافي غير صفري من خلال اقتران الدوران-المدار في غياب الاضطرابات الخارجية أو تحت اضطرابات خارجية متناسقة مع PT’. لاحظ أن الشبكات البلورية للألترماجنات غالبًا ما تكون مركزية التماثل (أي، متناسقة مع PT)، ولكن يمكن أن تكون أيضًا غير مركزية التماثل (أي، تناظر PT مكسور). التأثير البارز لكسر تناظر PT هو خلق فيزياء مرتبطة بالمغناطيسية غير تافهة من خلال رفع ازدواجية كرامرز وإنتاج نطاقات إلكترونية ذات أنسجة دورانية، أي، اتجاهات دوران تعتمد على النطاق. لاحظ أن تناظر PT يمكن أن ينكسر بطرق ثلاث متميزة: [1] كسر P، ولكن عدم كسر T، [2] كسر T، ولكن عدم كسر P، و[3] كسر P، كسر T، وPT أيضًا مكسور إذا تم كسر P وT بطرق مختلفة. على سبيل المثال، الشرط الضروري لـ AHE من الرتبة الفردية، والذي يشمل الخطية ( -ترتيب) AHE، يتم كسر تناظر PT بالتحديد، يمكن أن يكون هناك نوعان مختلفان من الألترماجنات: النوع الأول لديه لحظة مغناطيسية صافية غير صفرية وسلوكيات مغناطيسية حديدية بدون اضطرابات خارجية، والنوع الثاني لديه لحظة مغناطيسية صافية صفرية ولا يظهر سلوكيات مغناطيسية حديدية بدون أي اضطرابات خارجية ولكنه يظهر لحظة مغناطيسية صافية غير صفرية وسلوكيات مغناطيسية حديدية في وجود اضطرابات خارجية متناظرة PT مثل تطبيق الكهرباء.
التيار الحراري، الإضاءة الضوئية أو الضغط. يتبين أن كل من المغناطيسات البديلة من النوع الأول والنوع الثاني لديها تماثل PT مكسور. لاحظ أن الاضطرابات الخارجية مثل التيارات الكهربائية/الحرارية المطبقة، الإضاءة الضوئية، أو الضغط لا تكسر تماثل PT بنفسها، ولكن، على سبيل المثال، الحقول الكهربائية أو الحقول المغناطيسية المطبقة تكسر تماثل PT. كما نؤكد أن الإعداد التجريبي بالكامل، الذي يجمع بين مغناطيس بديل من النوع الثاني مع تماثل PT المكسور واضطراب خارجي مع تماثل PT غير المكسور، لديه الآن SOS مع لذا يمكن أن تظهر سلوكيات مغناطيسية حديدية. الشكل 2أ-ج يوضح المغناطيسات البديلة من النوع الأول، ونسمي الهياكل المحلية ذات التناظر الثنائي المتناوب حول المغناطيسات كمديرين (موضحة كأهليلجات رمادية في الشكل 2). جميع المغناطيسات البديلة من النوع الأول تتبين أنها مغناطيسات حديدية ضعيفة. جميع MPGs للمغناطيسية البديلة مع المغناطيسات المتوازية المحددة في المرجع. تضمين ، و (داخل الدائرة المنقطة في الشكل 1). الألترماجنات في الشكل 2أ-ج لديها -نوع MPGs.
غالبًا ما تلعب الأنيسوتروبية المغناطيسية دورًا مهمًا في فهم المغناطيسية البديلة والمغناطيسية الضعيفة، بشكل عام. هناك ثلاث طرق مختلفة للحصول على الأنيسوتروبية المغناطيسية: الأنيسوتروبية أحادية الأيون، والتزاوج التبادلي غير المتناظر أو المتناظر، وأنيسوتروبية موتر g (أي، الحجم المعتمد على الاتجاه للعزم المغناطيسي الكلي). إن أصل العزم المغناطيسي الصافي في الألترماجنات في الشكل 2أ، ب هو أنيسوتروبي موتر g – بعبارة أخرى، فإن الدوران الحقيقي في تلك الحالات هو مضاد مغناطيسي بالكامل (أي، معوض بالكامل)، لكن تناظرها يسمح بوجود عزم مغناطيسي مداري صافي غير صفري من خلال SOC. العزم المائل الصافي في الشكل 2ج، حيث تكون لحظات الدوران النقية هي درجة بعيدة عن و المحاور، يعود إلى تفاعل دزيالوشينسكي-موريا (DM) (أي، اقتران تبادل غير متماثل)، بدلاً من أنيسوتروبية موتر g، الناتجة عن SOC. لاحظ أن كل من تفاعل دزيالوشينسكي-موريا وأنيسوتروبية موتر g تنشأ من SOC. الشكل 2b يتوافق، على سبيل المثال، مع حالة مغناطيسية ممكنة (ليست حالة الأرض) في وحالة مغناطيسية محتملة واحدة في ، وتمثل الشكل 2c المجال المغناطيسي
الشكل 2 معظم المغناطيسات البديلة من النوع الأول مع لحظة مغناطيسية صافية غير صفرية. تُظهر حالات مغناطيسية مختلفة مع اتجاهات مختلفة للهياكل المحلية حول أيونات مغناطيسية من نوع واحد (مديرين) واتجاهات/أحجام مختلفة للحظات المغناطيسية الأيونية ولحظاتها المغناطيسية الصافية ذات الصلة. يمثل ‘ التماثل التشغيلي المتشابه. الأسهم الزرقاء هي لحظات مغناطيسية، وتُظهر درجات الأزرق المختلفة للأسهم الزرقاء أحجام لحظات مغناطيسية أيونية مختلفة على الرغم من أنها من أيونات مغناطيسية متطابقة. يعرض الشكل ترتيبًا متناوبًا لاثنين من اتجاهات المدير المختلفة واثنين من اتجاهات الدوران المختلفة في سلسلة. يعرض ترتيبًا متناوبًا لاثنين من اتجاهات المديرين المختلفين واثنين من اتجاهات الدوران المختلفة على شبكة مربعة، ويظهر c ترتيبًا متناوبًا آخر لاثنين من المديرين واثنين من اتجاهات الدوران المختلفة على شبكة مربعة. يتم عرض ترتيب متناوب لثلاثة اتجاهات مديرين مختلفة وثلاثة اتجاهات دوران مختلفة على مثلث في d. يعرض e تكوين دوران في شبكة كاجومي مع -مرتبة الدوران وتتناسب مع الحالة المغناطيسية لـ . تصور ترتيبًا متناوبًا لثلاثة اتجاهات مختلفة للمخرج وثلاثة اتجاهات مختلفة للدوران على شبكة مثلثية ثلاثية. هذا هو نوع-II من الألترماجنات مع لحظات مغناطيسية صافية تساوي صفر. عرض حالات الألترمغناطيسية مع 3 اتجاهات مختلفة للمخرج و3 اتجاهات مختلفة للدوران في شبكة مثلثية ثلاثية التوزيع – كلا من المخرجات والدورات مائلان نحو الاتجاه الخارجي. تشير رؤوس الأسهم السوداء إلى ميل المخرج نحو الاتجاه الخارجي.
دولة من الحالة المغناطيسية لكل طبقة من أو ، والحالة المغناطيسية لـ .
المغناطيسات البديلة من النوع الثاني لا تمتلك عزم مغناطيسي صافٍ غير صفري ولا تظهر سلوكيات مشابهة للمغناطيسات الحديدية، لكنها لا تزال تتمتع بكسر في تناظر PT. مثال على المغناطيسات البديلة من النوع الثاني موضح في الشكل 3c مع عزم صافٍ يساوي صفر ولكن مع كسر في تناظر PT، والذي يتوافق مع الحالة المغناطيسية الأرضية لـ يتبين أنه . يبدو أن هذه المغناطيسات البديلة من النوع الثاني لا تزال قادرة على إظهار سلوك مشابه للمغناطيسات الحديدية في وجود تيار مطبق أو ضغط أحادي المحور (مع الحفاظ على تناظر PT). على سبيل المثال، يمكن تحفيز لحظة مغناطيسية صافية غير قطرية مع تيار كهربائي مطبق من رتبة زوجية، ويمكن تحفيز AHE في رتب فردية عالية. -, -ترتيب، إلخ.) مع تيار كهربائي مطبق، ويمكن أن يتم تحفيز لحظة صافية غير قطرية بواسطة إجهاد أحادي المحور. تشمل MPGs للـ AHE من الرتبة الفردية العالية، والتغنيد المغناطيسي الناتج عن التيار من الرتبة الزوجية غير القطرية، والبيزومغناطيسية غير القطرية، ، ، ، و (انظر المرجع. ). لاحظ أن الـ الحالة في الشكل 2ب، ج يمكن أن تظهر عزم مغناطيسي صافي على طول AHE الخطي مع التيار على (أو ) وجهد هول على طول (أو المغناطيسية البيزوالكتريكية غير القطرية مع إجهاد أحادي المحور على طول أو
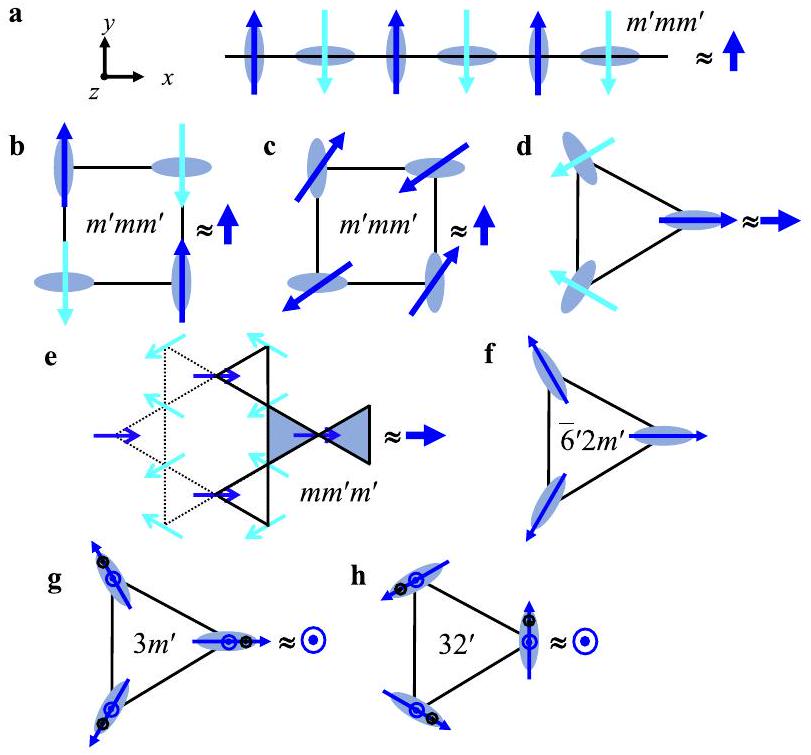
والمغنطة المستحثة على طول وأيضًا المغناطيسية البيزومترية القطرية على طول . الـ الحالة في الشكل 3c يمكن أن تظهر AHE من الرتبة الفردية العالية مع التيار على طول (أو ) وجهد القاعة على طول (أو التحفيز المغناطيسي الناتج عن التيار من الرتبة الزوجية مع التيار على طول أو والعزم الصافي المستحث على طول والمغناطيسية البيزوالكتريكية غير القطرية مع إجهاد أحادي المحور على طول أو والعزم الصافي المستحث على طول لاحظ أن الشكل 3d هو أيضًا نوع من المغناطيس البديل من النوع الثاني مع ، ويتوافق مع الذي يُعرف جيدًا بإظهار المغناطيسية الكهروضغطية غير القطرية .

تغيير المغناطيسية مع سبين غير متوازي

لا يجب أن يكون الألترمغناطيسية لها فقط مخرجان متناوبان وسبينات مضادة مغناطيسية متوازية (أي، اتجاهان للسبين). يمكن توسيع مفهوم الألترمغناطيسية ليشمل مخرجات متعددة (بشكل عام، معلمات هيكلية محلية مثل المخرجات، والكمية الزائفة، والاستقطابات الكهربائية، إلخ) وسبينات غير متوازية. أمثلة على الألترمغناطيسية بالتعريف الموسع وأيونات مغناطيسية من نوع واحد مدرجة في الشكل 2د-ز والشكل 3أ، ب. نؤكد أنه في جميع الحالات في الشكلين 2 و3، تكون لحظات السبين المغناطيسية النقية بدون تأثيرات التفاعل بين السبينات (SOC) متوازنة بالكامل. يتم عرض حالة ألترمغناطيسية مع 3 اتجاهات مخرجات مختلفة و3 اتجاهات سبين مختلفة على مثلث في الشكل 2د، وتكوين السبين في شبكة كاجومي مع يمكن اعتبار الدورانات المرتبة، الموضحة في الشكل 2e، كمزيج من حالة الشكل 2d وصورة المرآة لحالة الشكل 2d (المرآة المعنية عمودية على الـ -المحور). لاحظ أن نمط ربطة الفراشة (مثلثان رماديان) حول الأيونات المغناطيسية في الشكل 2e يعمل كمدير، ويمثل هذا الشكل 2e، على سبيل المثال، الحالة المغناطيسية في تظهر الشكل 2f نوع أحادي القطب ترتيب الدوران مع ترتيب متناوب لثلاثة اتجاهات مختلفة للمخرجين على شبكة مثلثية ثلاثية، والتي تتوافق مع MPG لـ تظهر الأشكال 2 ج، ح حالات مغناطيسية بديلة مع 3 اتجاهات مختلفة للمخرج و3 اتجاهات مختلفة للدوران في شبكة مثلثية ثلاثية الترتيب. الحالة في الشكل 2 ج مع (قطبي وفيرومغناطيسي) يتعلق، على سبيل المثال، بـ مرحلة في سداسي الأرض النادرة أو . حالة الشكل 2 هـ مع (كيرالي وفيرومغناطيسي) ذو صلة، على سبيل المثال، بحالة مغناطيسية مقترحة لكيرالي نؤكد أن الشبكات البلورية في الشكل 2a-c وe والشكل 3a-g هي مركزية التماثل (أي، متناسقة مع PT)، ولكن تلك الموجودة في الشكل و 3h، أنا غير مركزية (أي، تم كسر تناظر PT). الشكل 3a يصور حالة ألتيرمغناطيسية مع 4 اتجاهات مختلفة للمخرج و4 اتجاهات مختلفة للدوران في شبكة مربعة. جميع هذه الألتيرمغناطيسات الممتدة ذات الدورانات المعوضة بالكامل هي مغناطيسات ضعيفة، والتباين في موتر g والتفاعل DM الناتج عن SOC مسؤولان عن العزوم المغناطيسية الصافية في الشكل 2a وb وd وe و3a؛ والشكل 2c وg وh، على التوالي. لاحظ أنه عندما ينتج التباين في موتر g، الذي يكون عادةً صغيرًا جدًا، عزم مغناطيسي صافي صغير في، على سبيل المثال، الشكل 2a وb وd وe والشكل 3a. ومع ذلك، يمكن أن تكون التأثيرات الفيزيائية الأخرى الشبيهة بالمغناطيسات مثل AHE الخطية ودوران فاراداي كبيرة من خلال الآليات المرتبطة بانحناء بيري. بالإضافة إلى ذلك، نظرًا لأن العزوم المغناطيسية في الألتيرمغناطيسات من النوع المضاد للمغناطيسية، يمكن أن تكون الديناميات المغناطيسية للألتيرمغناطيسات سريعة مثل تلك الموجودة في المغناطيسات المضادة النموذجية. عندما يتم عكس العزم المغناطيسي الصافي في جميع الألتيرمغناطيسات (الممتدة) في الشكل 2a-h بواسطة، على سبيل المثال، مجالات مغناطيسية مطبقة، تدور جميع الدورانات بالكامل بواسطة أي أنه يحدث تبديل بين مجالات عكس الزمن، على الرغم من أن العزم المغناطيسي الصافي يمكن أن يكون صغيرًا جدًا ومعظم أجزاء العزوم المغناطيسية مرتبة بشكل مضاد. وبالتالي، يمكن أيضًا تبديل سلوكيات شبيهة بالفيرومغناطيسية مثل AHE الخطي وMOKE مع قلب العزوم المغناطيسية الصافية الصغيرة.
أخيرًا، نلاحظ هذه الجوانب المهمة: [1] ليس من الضروري أن يكون هناك نفس عدد اتجاهات المخرج واتجاهات الدوران من أجل المغناطيسية البديلة الممتدة، على الرغم من أن عدد اتجاهات المخرج (أو المتجهات الزائفة) وعدد اتجاهات الدوران في جميع أمثلة المغناطيسية البديلة (الممتدة) في الشكل 2.
الشكل 3 أنواع مختلفة من الألترماجنات وغير الألترماجنات. (أ) يُظهر حالة ألترماغنيتية بأربع اتجاهات مختلفة للمخرج وأربع اتجاهات مختلفة للدوران في شبكة مربعة، و يظهر حالة ألتيرمغناطيسية مع 3 اتجاهات مختلفة للمخرج و2 اتجاهات مختلفة للدوران في شبكة مربعة. يعرض الشكل c ترتيبًا متناوبًا لـ 2 اتجاهات مختلفة للمخرج و2 اتجاهات مختلفة للدوران في شبكة مربعة وليس مرتبطًا بأي لحظة مغناطيسية صافية. يشير إلى شبكات مربعة مكدسة من نوع AB مع اتجاهات مخرج ودوران متناوبة في طبقات مختلفة. يعرض e-g ترتيبات متناوبة لـ 3 اتجاهات مخرج مختلفة و3 اتجاهات دوران مختلفة على شبكة مثلثية مكدسة من نوع AB (أو شبكة خلوية مكونة من ستة عناصر). يظهر ترتيبات متناوبة من الإحداثيات الرباعية (رموز مثلثية) والإحداثيات الثمانية (رموز دائرية) ولحظات مغناطيسية لأعلى ولأسفل على شبكة العسل المكدسة. يكون أحد رؤوس كل إحداثية رباعية موجهًا دائمًا لأسفل. مرتبط بعزم مغناطيسي صاف غير صفري على طول لكن ليس له لحظة مغناطيسية صافية. يعرض j ترتيبات متناوبة من 4 اتجاهات مختلفة للمخرج و4 اتجاهات مختلفة للدوران على شبكة مستطيلة مكدسة من نوع AA. رؤوس الأسهم السوداء في و تشير إلى ميل المخرج خارج المستوى. يعرض ترتيبات متناوبة من 4 اتجاهات مختلفة للمخرجين و4 اتجاهات مختلفة للدوران في شبكة مربعة رباعية التكتل وليس مرتبطًا بأي لحظة مغناطيسية صافية. جميع الحالات المغناطيسية، باستثناء هي المغناطيسات البديلة مع كسر تناظر PT. هي مغناطيسات ألتيرماغنت من النوع-l مع لحظة مغناطيسية صافية غير صفرية، c-e و هي مغناطيسات بديلة من النوع الثاني ذات لحظات مغناطيسية صافية تساوي صفر. هو مغناطيس بديل من النوع الثالث مع لحظات مغناطيسية صافية صفرية وصفرية في تأثير هول غير الزوجي. هو نوع من المغناطيسات البديلة من النوع الثالث مع مغنطة مستحثة بواسطة تيار غير متساوي من الرتبة الفردية. هي غير المغناطيسات البديلة.
و 3a و c و d متطابقة. أحد الأمثلة هو الألترمغناطيس مع اتجاهي دوران و 3 اتجاهات مخرج في شبكة مربعة (انظر الشكل 3b)، حيث أن العزم المغناطيسي الصافي ناتج عن عدم التماثل في موتر g. [2] يمكن أيضًا تحقيق الألترمغناطيس من النوع الثاني مع مجموعة من 3 مخرجات و ترتيب الدوران كما هو موضح في الشكل 3e مع شبكة مثلثية ثلاثية مكدسة. هذا النوع الثاني من الألترمغناطيسية مع كسر تناظر PT يتوافق مع MPG لـ ، وليس مرتبطًا بأي لحظة مغناطيسية صافية، ولكنه يمكن أن يظهر، على سبيل المثال، تأثير هول غير العادي من الرتبة العالية والمغناطيسية البيزوكهربائية غير القطرية. من ناحية أخرى، فإن الحالات المغناطيسية في الشكل 3f و g مع شبكة مثلثية ثلاثية الطبقات، و3 موجهات، و ترتيب الدوران لديه تناظر PT غير مكسور، لذا لا يمكن أن يظهر أي نوع من السلوكيات الفيرومغناطيسية (المستحثة بواسطة التيار/الإجهاد)؛ على سبيل المثال، أي تأثير هول غير موجود. بدلاً من أن يقتصر على مجرد تبديل اتجاهات المخرجين أو المتجهات الزائفة، يمكن أن تشمل المغناطيسية البديلة الممتدة أنواعًا مختلفة من التبديلات في الهياكل المحلية ذات الصلة المحيطة بالدورانات. قد تشمل هذه التغييرات في مقادير المخرجين، تنسيق الأنيونات، أو اتجاه الهياكل القطبية المحلية. على سبيل المثال، توضح الأشكال 3h و i حالة مغناطيسية متوازية على شبكة عسلية مكدسة مع نوعين من تنسيق الأكسجين (مثلثات رمادية صغيرة: تنسيق رباعي السطوح؛ دوائر رمادية كبيرة: تنسيق ثماني السطوح). الحالة المغناطيسية في الشكل 3h مع هو نوع من المغناطيس البديل من النوع الأول يمكن أن يظهر تأثير هول الخطّي ويمثل الحالة المغناطيسية للقطب على النقيض,
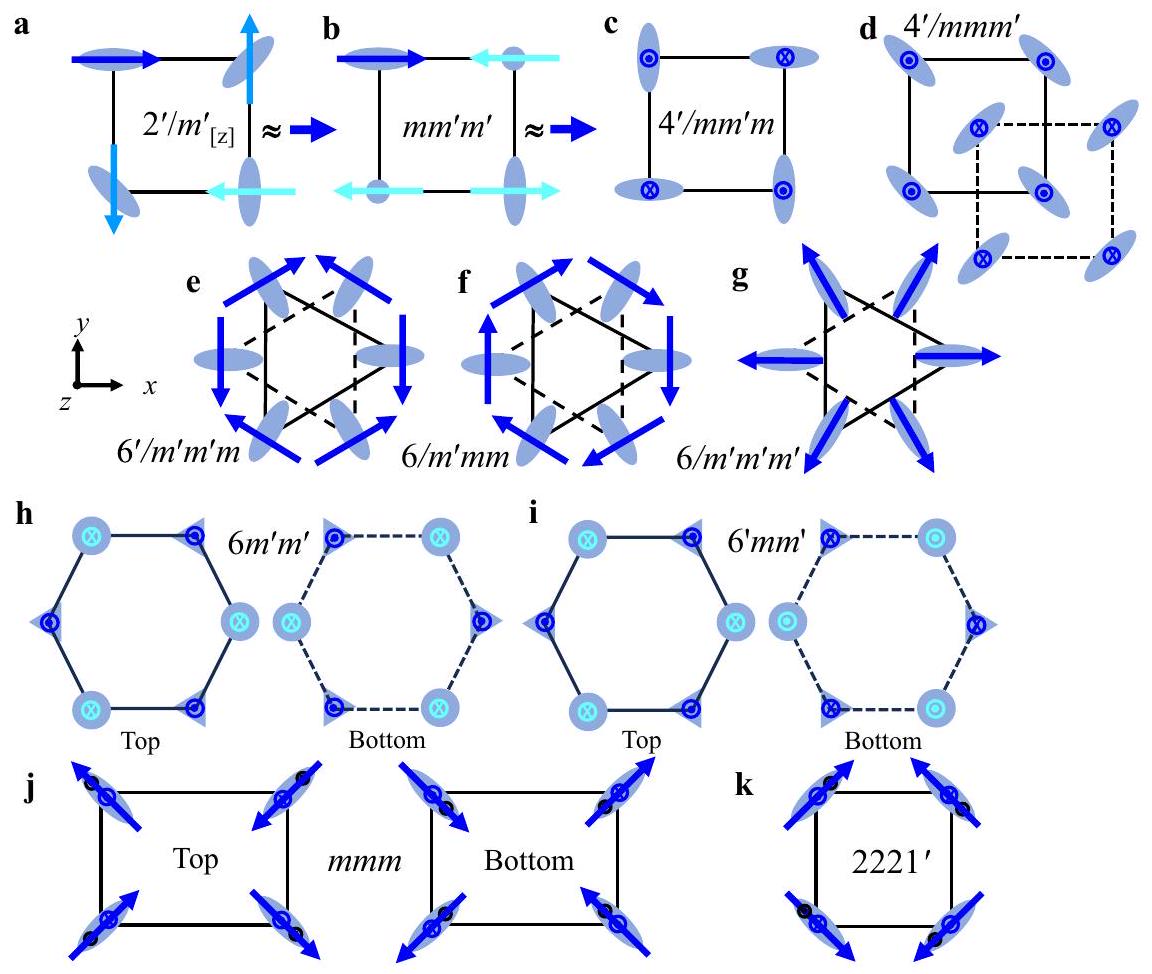
الحالة المغناطيسية في الشكل 3i مع يتبين أنه نوع من المغناطيس البديل من النوع الثاني، ويمثل الحالة المغناطيسية للقطب يمكن أن تظهر الحالة المغناطيسية في الشكل 3i AHE من الرتبة الفردية العالية مع التيار على طول وجهد القاعة على طول حتى ترتيب المغنطة الناتجة عن التيار مع التيار على طول والمغنطة المستحثة على طول المغناطيسية البيزوالكترونية غير القطرية مع الضغط على طول والمغنطة المستحثة على طول .
إليك ملخص قائمة بجميع الألترماجنات التي ناقشناها: (1) الألترماجنات من النوع الأول: MPG كما هو موضح في الشكل 2أ-ج، هـ و3ب؛ MPG في الشكل 2g؛ MPG 32′ في الشكل 2h؛ MPG في الشكل 3أ؛ MPG في الشكل 3h. (2) المغناطيسات البديلة من النوع الثاني: MPG في الشكل 2f؛ MPG في الشكل 3ج، د، MPG في الشكل 3 هـ، و MPG في الشكل 3 i.
لقد ناقشنا الألترا مغناطيسيات التي يمكن أن تظهر تأثير هول غير المتناظر من الرتبة الفردية – إما تأثير هول غير المتناظر الخطي مع لحظات مغناطيسية صافية غير صفرية (من الرتبة صفر) في الألترا مغناطيسيات من النوع الأول أو تأثير هول غير المتناظر من الرتبة الفردية العالية مع لحظات مغناطيسية مستحثة غير قطعية من الرتبة الزوجية في الألترا مغناطيسيات من النوع الثاني. ومع ذلك، فإن كسر تناظر PT يشمل أكثر من مجرد تأثير هول غير المتناظر من الرتبة الفردية. يمكن أن تكون هناك ألترا مغناطيسيات مع كسر تناظر PT، والتي لا تظهر تأثير هول غير المتناظر من الرتبة الفردية – يمكن أن تُطلق عليها الألترا مغناطيسيات من النوع الثالث. تشمل MPGs ذات الصلة ، ، ، ، و . يمكن أن تظهر هذه المغناطيسات البديلة من النوع الثالث بعض خصائص الدوران الأخرى-
ظواهر ذات صلة مثل المغنطة الناتجة عن التيار من الرتبة الفردية القطرية، المغنطة الناتجة عن التيار من الرتبة الفردية غير القطرية، التأثير الهول الكمي من الرتبة الزوجية، إلخ. أحد أمثلة المغناطيسات البديلة من النوع الثالث موضح في الشكل 3j (MPG mmm)، والذي لديه تماثل PT مكسور ولكنه لا يظهر أي من الظواهر المذكورة أعلاه، على الأقل، على طول أي محور رئيسي. ، و -محاور. مغنطة ناتجة عن تيار غير متساوي من الرتبة على طول يتطلب كسر . ميل في الغالون لديه غير منقطع ]، لذلك لا يظهر مغنطة ناتجة عن التيار من الرتبة الفردية القطرية على أي محور رئيسي ، و -محاور. ومع ذلك، فإن الحالة المغناطيسية في الشكل 3k (MPG 2221′ مع مجموعة النقاط البلورية 422) لم تنكسر وكسرت ، لذا تظهر مغنطة غير متساوية من النوع الغريب. أخيرًا، نلاحظ أننا ركزنا على سلوكيات المغناطيسية الحديدية للألترمغناطيسات إما في غياب الاضطرابات الخارجية أو في وجود تيار أو إجهاد؛ ومع ذلك، يمكن ربط أنسجة الدوران في الإثارات في الألترمغناطيسات بظواهر فيزيائية ناشئة أخرى ذات أنشطة دورانية مثل الموصلية الفائقة غير التافهة .

الاستنتاج

في الاقتراح الأصلي، تم التصريح ببيان قوي مثل ‘يجب اعتبار هذه المواد كأعضاء في فئة مغناطيسية ثالثة – الألترمغناطيسات – بجانب المغناطيسات الحديدية والمغناطيسات المضادة’ . ومع ذلك، من خلال اعتبارات التناظر، أظهرنا أنه بدلاً من فئة جديدة، فإن الألترمغناطيسية هي مفهوم عملي مفيد لتقديم كسر تناظر PT وسلوكيات شبيهة بالمغناطيسية الحديدية من خلال دمج التغيرات البلورية والدورانية. تمتلك الألترمغناطيسات الأصلية زوايا دوران ‘متوازية’ مع تعويض كامل، ولكن سلوكيات شبيهة بالمغناطيسية الحديدية مع زوايا دوران غير صفرية من خلال اقتران الدوران المداري مع تغيرين هيكليين متناوبين. لقد قمنا بتوسيع مفهوم الألترمغناطيسية لاستيعاب اتجاهات متعددة للمخرج (معلمات هيكلية، بشكل عام) واتجاهات الدوران، وتشتمل هذه الألترمغناطيسية الموسعة على حالات دوران ‘غير متوازية’. بالإضافة إلى ذلك، قمنا بتصنيف ثلاثة أنواع من الألترمغناطيسات؛ النوع-I-III. جميع الألترمغناطيسات من النوع-I، التي تظهر لحظة مغناطيسية صافية غير صفرية وسلوكيات شبيهة بالمغناطيسية الحديدية، تنتمي إلى مجموعة النقاط المغناطيسية الحديدية، وهي نوع من المغناطيسات الحديدية الضعيفة. جميع الألترمغناطيسات من النوع-II وIII، مع كسر تناظر PT ولحظات مغناطيسية صافية صفرية، يمكن أن تظهر سلوكيات شبيهة بالمغناطيسية الحديدية في وجود تيار أو إجهاد مطبق يكون متناسقًا مع PT. تظهر الألترمغناطيسات من النوع-II AHE من الرتبة الفردية العالية، ولكن الألترمغناطيسات من النوع-III لا تظهر أي AHE من الرتبة الفردية. تقدم هذه الأشكال المختلفة من الألترمغناطيسية فرصة مثيرة للاستفادة من المزايا التكميلية لكل من المغناطيسية الحديدية والمغناطيسية المضادة.
تاريخ الاستلام: 18 أكتوبر 2023؛ تاريخ القبول: 10 يناير 2024؛
تم النشر عبر الإنترنت: 22 يناير 2024

REFERENCES

  1. Baltz, V. et al. Antiferromagnetic spintronics. Rev. Mod. Phys. 90, 015005 (2018).
  2. Hirohata, A. et al. Review on spintronics: principles and device applications. J. Magn. Magn. Mater. 509, 166711 (2020).
  3. Jungwirth, T., Marti, X., Wadley, P. & Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 11, 231-241 (2016).
  4. Wolf, S. A. et al. Spintronics: a spin-based electronics vision for the future. Science 294, 1488-1495 (2001).
  5. Cheong, S.-W., Thompson, J. D. & Fisk, Z. Metamagnetism in . Phys. Rev. B 39, 4395-4398 (1989).
  6. Baibich, M. N. et al. Giant magnetoresistance of (001) magnetic superlattices. Phys. Rev. Lett. 61, 2472-2475 (1988).
  7. Fert, A. Nobel lecture: Origin, development, and future of spintronics Nobel lecture: origin, development, and future of spintronics. Rev. Mod. Phys. 80, 1517-1530 (2008).
  8. Binasch, G., Grünberg, P., Saurenbach, F. & Zinn, W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 39, 4828-4830 (1989).
  9. Šmejkal, L., MacDonald, A. H., Sinova, J., Nakatsuji, S. & Jungwirth, T. Anomalous Hall antiferromagnets. Nat. Rev. Mater. 7, 482-496 (2022).
  10. Šmejkal, L., Mokrousov, Y., Yan, B. & MacDonald, A. H. Topological antiferromagnetic spintronics. Nat. Phys. 14, 242-251 (2018).
  11. Wadley, P. et al. Electrical switching of an antiferromagnet. Science 351, 587-590 (2016).
  12. Chen, H., Niu, Q. & Macdonald, A. H. Anomalous Hall effect arising from noncollinear antiferromagnetism. Phys. Rev. Lett. 112, 017205 (2014).
  13. Kübler, J. & Felser, C. Non-collinear antiferromagnets and the anomalous Hall effect. Europhys. Lett. 108, 67001 (2014).
  14. Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212-215 (2015).
  15. Mazin, I. Editorial: Altermagnetism-a new punch line of fundamental magnetism. Phys. Rev. X 12, 040002 (2022).
  16. Šmejkal, L., Sinova, J. & Jungwirth, T. Emerging research landscape of altermagnetism. Phys. Rev. X 12, 040501 (2022).
  17. Šmejkal, L., Sinova, J. & Jungwirth, T. Beyond conventional ferromagnetism and antiferromagnetism: a phase with nonrelativistic spin and crystal rotation symmetry. Phys. Rev. X 12, 031042 (2022).
  18. Šmejkal, L. et al. Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets. Sci. Adv. 6, eaaz8809 (2020).
  19. McClarty, P. A. & Rau, J. G. Landau theory of altermagnetism. https://arxiv.org/abs/ 2308.04484 (2023).
  20. Hayami, S., Yanagi, Y. & Kusunose, H. Bottom-up design of spin-split and reshaped electronic band structures in antiferromagnets without spin-orbit coupling: Procedure on the basis of augmented multipoles. Phys. Rev. B 102, 144441 (2020).
  21. Gonzalez Betancourt, R. D. et al. Spontaneous anomalous Hall effect arising from an unconventional compensated magnetic phase in a semiconductor. Phys. Rev. Lett. 130, 036702 (2023).
  22. Cheong, S.-W. & Huang, F.-T. Trompe L’oeil Ferromagnetism: magnetic point group analysis. npj Quant. Mater. 8, 73 (2023).
  23. Cheong, S.-W., Huang, F.-T. & Minhyong, K. Linking emergent phenomena and broken symmetries through one-dimensional objects and their dot/cross products. Rep. Prog. Phys. 85, 124501 (2022).
  24. Birss, R. R. in Symmetry and Magnetism. 125-138 (North-Holland Pub. Co., 1964).
  25. Cheong, S.-W. SOS: symmetry-operational similarity. npj Quant. Mater. 4, 53 (2019).
  26. Cheong, S.-W. Trompe L’oeil Ferromagnetism. npj Quant. Mater. 5, 37 (2020).
  27. Gallego, S. V. et al. MAGNDATA: towards a database of magnetic structures. I.The commensurate case. J. Appl. Crystallogr. 49, 1750-1776 (2016).
  28. Landau, L. D. & Lifshitz, E. M. in Electrodynamics of Continuous Media, Vol. 8. (eds. Landau L. D. & Lifshitz E. M.) 130-179, Ch. V (Pergamon,1984).
  29. Shuvalov, L. A. Modern crystallography. IV. Physical properties of crystals. 1-46 (Springer England, 1989).
  30. Higo, T. et al. Large magneto-optical Kerr effect and imaging of magnetic octupole domains in an antiferromagnetic metal. Nat. Photonics 12, 73-78 (2018).
  31. Ikhlas, M. et al. Piezomagnetic switching of the anomalous Hall effect in an antiferromagnet at room temperature. Nat. Phys. 18, 1086-1093 (2022).
  32. Hohenberg, P. C. Existence of long-range order in one and two dimensions. Phys. Rev. 158, 383-386 (1967).
  33. Mermin, N. D. & Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 17, 1133-1136 (1966).
  34. Mazin, I. I. Altermagnetism in MnTe: origin, predicted manifestations, and routes to detwinning. Phys. Rev. B 107, L100418 (2023).
  35. Wang, H. et al. Giant anisotropic magnetoresistance and nonvolatile memory in canted antiferromagnet . Nat. Commun. 10, 2280 (2019).
  36. Kotegawa, H. et al. Large anomalous Hall effect and unusual domain switching in an orthorhombic antiferromagnetic material NbMnP. npj Quant. Mater. 8, 56 (2023).
  37. Disa, A. S. et al. Polarizing an antiferromagnet by optical engineering of the crystal field. Nat. Phys. 16, 937-941 (2020).
  38. Moriya, T. Piezomagnetism in . J. Phys. Chem. Solids 11, 73-77 (1959).
  39. Liu, J. & Balents, L. Anomalous Hall effect and topological defects in antiferromagnetic Weyl semimetals: . Phys. Rev. Lett. 119, 087202 (2017).
  40. Nayak, A. K. et al. Large anomalous Hall effect driven by a nonvanishing Berry curvature in the noncolinear antiferromagnet . Sci. Adv. 2, e1501870 (2016).
  41. Brown, P. J. & Chatterji, T. Neutron diffraction and polarimetric study of the magnetic and crystal structures of and . J. Phys. Condens. Matter 18, 10085-10096 (2006).
  42. Das, H., Wysocki, A. L., Geng, Y., Wu, W. & Fennie, C. J. Bulk magnetoelectricity in the hexagonal manganites and ferrites. Nat. Commun. 5, 2998 (2014).
  43. Du, K. et al. Vortex ferroelectric domains, large-loop weak ferromagnetic domains, and their decoupling in hexagonal (Lu, Sc)FeO3. npj Quant. Mater. 3, 33 (2018).
  44. Park, P. et al. Field-tunable toroidal moment and anomalous Hall effect in noncollinear antiferromagnetic Weyl semimetal TaS .npj Quant. Mater. 7, 42 (2022).
  45. Kurumaji, T., Ishiwata, S. & Tokura, Y. Diagonal magnetoelectric susceptibility and effect of Fe-doping in a polar ferrimagnet . Phys. Rev. B 95, 045142 (2016).
  46. Wang, Y. et al. Unveiling hidden ferrimagnetism and giant magnetoelectricity in polar magnet . Sci. Rep. 5, 12268 (2015).

الشكر والتقدير

نشكر جايرو سينا، ألان إتش. ماكدونالد، فاليري كيريوكين، وسونغ جون ليم على المناقشات المفيدة للغاية حول الألترمغناطيسية. تم دعم العمل في جامعة روتجرز من قبل وزارة الطاقة بموجب منحة رقم DOE: DE-FG02-07ER46382.

مساهمات المؤلفين

S.W.C. تصور وأشرف على المشروع. F.-T.H. أجرى تحليل مجموعة النقاط المغناطيسية. كتب S.W.C. الجزء المتبقي.

المصالح المتنافسة

يعلن المؤلفون عدم وجود مصالح متنافسة.

معلومات إضافية

يجب توجيه المراسلات والطلبات للحصول على المواد إلى سانغ-ووك تشيونغ.
معلومات إعادة الطبع والإذن متاحة على http://www.nature.com/ إعادة الطبع
ملاحظة الناشر: تظل Springer Nature محايدة فيما يتعلق بالمطالبات القضائية في الخرائط المنشورة والانتماءات المؤسسية.
الوصول المفتوح: هذه المقالة مرخصة بموجب رخصة المشاع الإبداعي للاستخدام والمشاركة والتكيف والتوزيع وإعادة الإنتاج في أي وسيلة أو تنسيق، طالما أنك تعطي الائتمان المناسب للمؤلفين الأصليين والمصدر، وتوفر رابطًا لرخصة المشاع الإبداعي، وتوضح ما إذا كانت هناك تغييرات قد أُجريت. الصور أو المواد الأخرى من طرف ثالث في هذه المقالة مشمولة في رخصة المشاع الإبداعي للمقالة، ما لم يُذكر خلاف ذلك في سطر الائتمان للمادة. إذا لم تكن المادة مشمولة في رخصة المشاع الإبداعي للمقالة واستخدامك المقصود غير مسموح به بموجب اللوائح القانونية أو يتجاوز الاستخدام المسموح به، ستحتاج إلى الحصول على إذن مباشرة من صاحب حقوق الطبع والنشر. لعرض نسخة من هذه الرخصة، قم بزيارة http:// creativecommons.org/licenses/by/4.0/.
© المؤلفون 2024
  1. مركز روتجرز للمواد الناشئة وقسم الفيزياء وعلم الفلك، جامعة روتجرز، بيسكاتاواي، نيو جيرسي 08854، الولايات المتحدة الأمريكية. البريد الإلكتروني: sangc@physics.rutgers.edu

Journal: npj Quantum Materials, Volume: 9, Issue: 1
DOI: https://doi.org/10.1038/s41535-024-00626-6
Publication Date: 2024-01-22

Altermagnetism with non-collinear spins

Sang-Wook Cheong (D) and Fei-Ting Huang (D

Abstract

Altermagnetism is introduced as a category of magnetic states with ‘collinear’ antiferromagnetic spins and alternating variations of local structures around spins in such a way that the symmetry allows typical ferromagnetic behaviors. Altermagnets exhibiting ferromagnetic behaviors without any external perturbations (type-l) turn out to belong to the ferromagnetic point group. Other altermagnets (type-II and type-III) can have ferromagnetic behaviors only with external perturbations such as electric current or stress, which conserve parity-time-reversal (PT) symmetry. All types of altermagnets themselves have broken PT symmetry. The concept of altermagnetism can be extended to accommodate non-collinear spins and multiple local-structure variations.

npj Quantum Materials (2024)9:13; https://doi.org/10.1038/s41535-024-00626-6

INTRODUCTION

Spintronics where spin and charge degrees of freedom are mutually coupled and manipulated through crossing conjugate fields (i.e., electric fields for spins and magnetic fields for charges) has been an active research area for the last three decades since the discovery of giant magnetoresistance , and has been well implemented in real devices. Traditionally, spintronics utilizes ferro-(ferri)magnets since the manipulation and detection of these ferro-(ferri)magnetic states are straightforward. But antiferromagnetic spintronics has become highly topical due to the active manipulation of the antiferromagnetic state and its magnetic textures via spin and charge currents. Antiferromagnetic materials, in general, could embody the numerous interesting features beneficial for spintronic applications : they produce no stray fields, so are robust against external magnetic fields and make them suitable for device miniaturization, display ultrafast dynamics in THz ranges, and are capable of generating good spincurrent transport with micrometer spin-diffusion lengths.
Altermagnets are magnets with collinear antiferroarrangement of one-kind spins (i.e., ‘alter’nating spins), and also simultaneously with ‘alter’nating orientations of local structures around spins, maintaining a symmetry that enables ferromagnetic behaviors (non-zero net magnetic moment, Anomalous Hall effect (AHE), etc. . In other words, in altermagnets, spin magnetic moments are fully compensated when spin-orbital coupling (SOC) is zero, but non-zero SOC, enabling coupling between spins and alternating local structures (such as oxygen coordination around magnetic ions), can result in a non-zero net magnetic moment and other ferromagnetic behaviors through uncompensated ‘orbital magnetic moments’.

FERROMAGNETISM VS. ANTIFERROMAGNETISM

Surprisingly, antiferromagnetism is not formally defined even though the term has been used frequently, but the ferromagnetic point group is well-defined in terms of symmetry. Magnetization ( ) along has broken with free rotation along (see refs. for the definition of symmetry operation notations. All magnetic point groups (MPGs), belonging to the ferromagnetic point group , do have, at least, broken with free rotation along or the relevant requirements along or , i.e., have symmetry operational
similarity (SOS) with . The thirty one (31) ferromagnetic MPGs include , , . We have considered symmetries that are along only those basis vectors of the conventional crystallographic coordinate systems. Those basis vectors are given in the settings of 122 MPGs . For example, we discuss the symmetries along the , and -directions in the tetragonal and cubic MPGs, while only symmetries along the and -directions in the orthorhombic MPGs are considered in our SOS analysis. Even for those hexagonal and trigonal structures, the and -axes are defined to be orthogonal to each other. The rotation encompasses both (counterclockwise) and (clockwise), with the + and – signs. Any symmetry criteria associated with are equally applicable to the operation of and , concurrently. This principle extends to and rotations.
It is rigorous and produces no ambiguity to define ferromagnetism and antiferromagnetism in crystalline materials in this manner: any magnetic states, whose MPGs belong to the ferromagnetic point group, are ferromagnetic; otherwise, antiferromagnetic . These ferromagnetic MPGs do exhibit unique physical properties such as non-zero net magnetic moment, nonreciprocal Faraday optical rotation, and linear anomalous Hall effect (AHE). (Note that there are four types of anomalous Hall effects (true anomalous Hall, Ettingshausen, Nernst, and thermal Hall effects), and in terms of symmetry, there is little difference among the requirements for four types of anomalous Hall effects as long as the relevant electric/thermal current can exist .) The requirement to observe each of the above phenomena is identical to that of belonging to the ferromagnetic point group, so these effects can be observed ‘only’ in ferromagnetic MPGs. Ferromagnets also exhibit diagonal piezomagnetic effects along the net magnetic moment directions and magneto-optical Kerr effects (MOKEs); however, the diagonal piezomagnetic effect and MOKE can be also observed in some antiferromagnets with properly broken symmetries . Simple ferromagnets with all ionic magnetic moments pointing one direction do belong to ferromagnetic point groups, but ferrimagnetic, canted antiferromagnetic, weak ferrimagnetism, or weak ferromagnetic states with non-zero net magnetic moments all also belong to the ferromagnetic point group. For the sake of simplicity, we will classify all magnets, belonging to the ferromagnetic point group, but not exhibiting simple
Fig. 1 Classification of various magnetic states. All ferromagnets (blue box) belong to the ferromagnetic point group, and any magnetic states that do not belong to the ferromagnetic point group are antiferromagnetic (green box). All ferromagnets exhibit linear AHE, high-oddorder AHE can be observed in certain antiferromagnets, and all magnetic states, exhibiting odd-order AHE, have broken PT symmetry. Magnetic point groups relevant to type-I altermagnetism proposed for collinear spins are inside of dashed circle , and all type-I altermagnets belong to the ferromagnetic point group. All type-II altermagnets can exhibit high-odd-order AHE, and type-III altermagnets cannot show any odd-order AHE along principal axes. The yellow area denotes non-magnetic and non-centrosymmetric states, which are not discussed in this perspective. Note that ‘type-I altermagnetism’ is a subset of ‘ferromagnetism’, ‘type-II altermagnetism’ is a subset of ‘antiferromagnetism with high-odd-order AHE’, and ‘type-III altermagnetism’ is a subset of ‘antiferromagnetism without PT symmetry and odd-order AHE’; however, their exact subset relationships cannot be identified from symmetry analysis alone.
ferromagnetism or ferrimagnetism (having uncompensated moments with antiferro-arranged multiple-kinds of ionic magnetic moments), as ‘weak ferromagnets . We highlight that antiferromagnets are magnetic states found in crystalline solids, which do not belong to the ferromagnetic point group.

TYPE-I AND TYPE-II ALTERMAGNETISM

PT symmetry (P; parity, T; time-reversal, and PT; parity times timereversal) is broken in all altermagnets. The essential aspect of altermagnets is when the spin-orbit coupling is ignored, the spin angular momenta in an altermagnet are fully compensated, so there is no net spin angular momentum, but the spin-lattice with crystallographic variations have broken PT symmetry, so there exists ‘spin textures in excitations’ and ‘non-zero net magnetic momentum through spin-orbit coupling in zero external perturbations or under PT-symmetric external perturbations’. Note that the crystallographic lattices of altermagnets are often centrosymmetric (i.e., PT-symmetric), but can be also non-centrosymmetric (i.e., PT symmetry broken). The prominent effect of PT symmetry breaking is to create non-trivial magnetism-related physics by lifting the Kramers’ degeneracy and producing spin-textured electronic bands, i.e., band-dependent spin directions. Note that PT symmetry can be broken in three distinct manners: [1] broken P, but unbroken T, [2] broken T, but unbroken P, and [3] broken P, broken T , and PT is also broken if P and T are broken in different ways. For example, the necessary condition for odd-order AHE, which includes linear ( -order) AHE, is broken PT symmetry . Precisely speaking, there can be two different types of altermagnets: type-l has the non-zero net magnetic moment and ferromagnetic behaviors without external perturbations, and typeII has zero net magnetic moment and no ferromagnetic behaviors without any external perturbations but exhibits non-zero net magnetic moment and ferromagnetic behaviors in the presence of external PT-symmetric perturbations such as applied electric/
thermal current, light illumination or stress. It turns out that both type-I and type-II altermagnets do have broken PT symmetry. Note that external perturbations such as applied electric/thermal currents, light illumination, or stress themselves do not break the PT symmetry, but, for example, applied electric fields or magnetic fields do break the PT symmetry. We also emphasize that the entire experimental set-up, combining a type-II altermagnet with the broken PT symmetry and an external perturbation with the unbroken PT symmetry, now has SOS with , so it can exhibit ferromagnetic behaviors. Figure 2a-c exemplify type-I altermagnets, and we call alternating 2-fold-symmetric local structures around spins as directors (shown as gray ellipsoids in Fig. 2). All type-I altermagnets turn out to be weak ferromagnets. All MPGs for altermagnetism with collinear spins identified in ref. include , and (inside of the dashed circle in Fig. 1). The altermagnets of Fig. 2a-c have -type MPGs.
Magnetic anisotropy often plays an important role in understanding altermagnetism and weak ferromagnetism, in general. There exist three different manners to have magnetic anisotropy: single-ion anisotropy, anisotropic symmetric or antisymmetric exchange coupling, and g-tensor anisotropy (i.e., the orientationdependent magnitude of the total magnetic moment) . The origin of net magnetic moment in altermagnets in Fig. 2a, b is g-tensor anisotropy-in other words, the true spins in those states are fully antiferromagnetic (i.e., fully compensated), but their symmetry allows non-zero net orbital magnetic moments through SOC. The net canted moment in Fig. 2c, where pure spin moments are degree away from the and axes, is due to the Dzyaloshinskii-Moriya (DM) interaction (i.e., antisymmetric exchange coupling), rather than g-tensor anisotropy, from SOC. Note that both Dzyaloshinskii-Moriya interaction and g-tensor anisotropy originate from SOC. Figure 2b corresponds to, for example, one possible magnetic state (not ground state) in and one possible magnetic state in , and Fig. 2c represents the magnetic
Fig. 2 Mostly type-I altermagnets with a non-zero net magnetic moment. Various magnetic states with different orientations of local structures around one-kind magnetic ions (directors) and different orientations/magnitudes of ionic magnetic moments and their relevant net magnetic moments are shown. ‘ ‘ represents symmetry operational similarity. Blue arrows are magnetic moments, and the different blue tones of the blue arrows represent the different magnitudes of ionic magnetic moments even though they are from identical magnetic ions. a displays an alternating arrangement of 2 different director orientations and 2 different spin orientations in a chain. displays an alternating arrangement of 2 different director orientations and 2 different spin orientations on a square lattice, and c shows another alternating arrangement of 2 directors and 2 different spin orientations on a square lattice. An alternating arrangement of 3 different director orientations and 3 different spin orientations on a triangle is displayed in d. e displays a spin configuration in a kagome lattice with -ordered spins and corresponds to the magnetic state of . depicts an alternating arrangement of 3 different director orientations and 3 different spin orientations on a trimerized triangular lattice. This is a type-II altermagnet with zero net magnetic moments. show altermagnetic states with 3 different director orientations and 3 different spin orientations in a trimerized triangular lattice-both directors and spins are tilted toward the out-of-plane direction. Black arrowheads denote out-of-plane director tilting.
state of , the magnetic state of each layer of or , and the magnetic state of .
Type-II altermagnets do not have non-zero net magnetic moment nor exhibit ferromagnet-like behaviors but still have broken PT symmetry. One example of type-II altermagnets is shown in Fig. 3c with zero net moments but the broken PT symmetry, which corresponds to . The magnetic ground state of turns out to be . It appears that these type-II altermagnets can still exhibit ferromagnet-like behavior in the presence of applied current or uniaxial stress (conserving the PT symmetry). For example, an off-diagonal net magnetic moment can be induced with even-order of applied electric current, AHE can be induced in high-odd-order ( -, -order, etc.) with applied electric current, and an off-diagonal net moment can be induced by uniaxial stress. MPGs for high-odd-order AHE, offdiagonal even-order current-induced magnetization, and an offdiagonal piezomagnetism, include , , , and (see ref. ). Note that the state in Fig. 2b, c can exhibit net magnetic moment along , linear AHE with current along (or ) and Hall voltage along (or , off-diagonal piezomagnetism with uniaxial stress along or
and induced magnetization along , and also diagonal piezomagnetism along . The state in Fig. 3c can exhibit high-odd-order AHE with current along (or ) and Hall voltage along (or ), even-order current-induced magnetization with current along or and induced net moment along , and off-diagonal piezomagnetism with uniaxial stress along or and induced net moment along . Note that Fig. 3d is also a type-ll altermagnet with , and corresponds to , which is well known to exhibit off-diagonal piezomagnetism .

ALTERMAGNETISM WITH NON-COLLINEAR SPINS

Altermagnetism does not have to have only 2 alternating directors and collinear antiferromagnetic spins (i.e., 2 spin orientations). One can expand the concept of altermagnetism to include multiple directors (in general, local structural parameters such as directors, pseudo-scalars, electric polarizations, etc.) and non-collinear spins. Examples of altermagnetism with the extended definition and onekind magnetic ions are listed in Fig. 2d-g and Fig. 3a, b. We emphasize that in all cases in Fig. 2 and 3, pure spin magnetic moments without SOC are fully compensated. An altermagnetic state with 3 different director orientations and 3 different spin orientations on a triangle is displayed in Fig. 2d, and the spin configuration in the Kagome lattice with -ordered spins, shown in Fig. 2e, can be considered as a combination of the Fig. 2d state and the mirror image of the Fig. 2d state (the relevant mirror is perpendicular to the -axis). Note that the butterfly tie pattern (two gray triangles) around magnetic ions in Fig. 2e acts as a director, and this Fig. 2e state represents, for example, the magnetic state in . Figure 2f depicts a monopole-type spin order with an alternating arrangement of 3 different director orientations on a trimerized triangular lattice, which corresponds to the MPG of . Figure 2 g , h shows altermagnetic states with 3 different director orientations and 3 different spin orientations in a trimerized triangular lattice. The Fig. 2 g state with (polar and ferromagnetic) is relevant to, for example, the phase in hexagonal rare earth) or . The Fig. 2 h state with (chiral and ferromagnetic) is relevant to, for example, a proposed magnetic state of chiral . We emphasize that the crystallographic lattices of Fig. 2a-c, e and Fig. 3a-g are centrosymmetric (i.e., PT-symmetric), but those of Fig. and 3h, i are non-centrosymmetric (i.e., PT symmetry broken). Figure 3a depicts an altermagnetic state with 4 different director orientations and 4 different spin orientations in a square lattice. All these extended altermagnets with fully compensated spins are weak ferromagnets, and g-tensor anisotropy and DM interaction from SOC is responsible for net magnetic moments in Fig. 2a, b, d, e and 3a; and Fig. 2c, g, h, respectively. Note that when g-tensor anisotropy, which is usually very small, produces a tiny net magnetic moment in, for example, Fig. 2a, b, d, e and Fig. 3a. However, other ferromagnet-like physical effects such as linear AHE and Faraday rotation can be significant through mechanisms associated with the Berry curvature. In addition, since the magnetic moments in the altermagnets are antiferro-type, the magnetic dynamics of altermagnets can be fast like that in typical antiferromagnets. When the net magnetic moment is reversed in all (extended) altermagnets in Fig. 2a-h by, for example, applied magnetic fields, the entire spins rotate by , i.e., there is a switching between time-reversal domains, even though the net magnetic moment can be very small and most parts of magnetic moments are antiferro-arranged. Thus, various ferromagnetic-like behaviors such as linear AHE and MOKE can also be switched with the flipping of the tiny net magnetic moments.
Finally, we note these important aspects: [1] it is not necessary to have the same number of director orientations and spin orientations for the extended altermagnetism, even though the number of director orientations (or pseudo-scalars) and that of spin orientations in all (extended) altermagnet examples in Fig. 2
Fig. 3 Various altermagnets and non-altermagnets. a depicts an altermagnetic state with 4 different director orientations and 4 different spin orientations in a square lattice, and shows an altermagnetic state with 3 different director orientations and 2 different spin orientations in a square lattice. c displays an alternating arrangement of 2 different director orientations and 2 different spin orientations in a square lattice and is not associated with any net magnetic moment. denotes AB -stacked square lattices with alternating director and spin orientations in different layers. e-g displays alternating arrangements of 3 different director orientations and 3 different spin orientations on an AB-stacked trimerized triangle lattice (or hexamerized honeycomb lattice). shows alternating arrangements of tetrahedral (triangular symbols) and octahedral (circular symbols) coordinates and up-down magnetic moments on the stacked honeycomb lattice. One apex of each tetrahedral coordinate is always pointing down. is associated with a non-zero net magnetic moment along , but has no net magnetic moment. j displays alternating arrangements of 4 different director orientations and 4 different spin orientations on an AA-stacked rectangular lattice. Black arrowheads in and denote out-of-plane director tilting. displays alternating arrangements of 4 different director orientations and 4 different spin orientations in a tetramerized square lattice and is not associated with any net magnetic moment. All the magnetic states, except are altermagnets with the broken PT symmetry. are type-l altermagnets with the non-zero net magnetic moment, c-e and are type-II altermagnets with zero net magnetic moments. is type-III altermagnets with zero net magnetic moments and zero odd-order AHE. is a type-III altermagnets with diagonal odd-order current-induced magnetization. are non-altermagnets.
and 3a, c, d are identical. One example is an altermagnet with 2 spin orientations with 3 director orientations in a square lattice (see Fig. 3b), whose net magnetic moment is due to g-tensor anisotropy. [2] Type-II altermagnetism can be also achieved with the combination of 3 directors and spin order as shown in Fig. 3e with stacked trimerized triangular lattice. This type-II altermagnet with the broken PT symmetry corresponds to the MPG of , and is not associated with any net magnetic moment, but can exhibit, for example, high-odd-order AHE and off-diagonal piezomagnetism. On the other hand, the magnetic states in Fig. 3f, g with stacked trimerized triangular lattice, 3 directors, and spin order have unbroken PT symmetry, so cannot exhibit any kind of (current/stress-induced) ferromagnetic behaviors; for example, any AHE is absent. [3] Instead of being limited to mere alternation of director orientations or pseudoscalars, extended altermagnetism can encompass various types of alternations in the relevant local structures surrounding spins. These may include changes in the magnitudes of directors, anion coordination, or the orientation of local polar structures. For example, Fig. 3h, i depict a collinear magnetic state on a stacked honeycomb lattice with two types of oxygen coordination (small gray triangles: tetrahedral coordination; large gray circles: octahedral coordination). The magnetic state in Fig. 3h with is a type-I altermagnet that can exhibit linear AHE and represents the magnetic state of polar . In contrast,
the magnetic state in Fig. 3i with turns out to be a type-II altermagnet, and represents the magnetic state of polar . The magnetic state in Fig. 3i can show high-oddorder AHE with current along and Hall voltage along , evenorder current-induced magnetization with current along and induced magnetization along , Off-diagonal piezomagnetism with stress along and induced magnetization along .
Here is the summary list of all altermagnets that we have discussed: (1) Type-I altermagnets: MPG as shown in Fig. 2a-c, e and 3b; MPG in Fig. 2g; MPG 32′ in Fig. 2h; MPG in Fig. 3a; MPG in Fig. 3h. (2) Type-II altermagnets: MPG in Fig. 2f; MPG in Fig. 3c, d, MPG in Fig. 3 e , and MPG in Fig. 3 i .
We have discussed altermagnets that can exhibit odd-order AHE-either linear AHE with non-zero (zeroth order) net magnetic moments in type-I altermagnets or high-odd-order AHE with offdiagonal even-order current-induced magnetic moments in type-II altermagnets. However, broken PT symmetry encompasses more than just odd-order AHE. There can be altermagnets with broken PT symmetry, which do not exhibit odd-order AHE-these can be coined type-III altermagnets. The relevant MPGs include , , , , and . These type-III altermagnets can exhibit some other spin-
relevant phenomena such as diagonal odd-order current-induced magnetization, off-diagonal odd-order current-induced magnetization, even-order AHE, etc. One example of type-III altermagnets is shown in Fig. 3j (MPG mmm), which has broken PT symmetry but does not exhibit any of the phenomena listed above, at least, along any principal , and -axes. Diagonal odd-order currentinduced magnetization along requires broken . The MPG has unbroken ], so does not show diagonal odd-order current-induced magnetization along any principal , and -axes. However, the magnetic state of Fig. 3k (MPG 2221′ with crystallographic point group 422) has unbroken and broken , so does exhibit diagonal odd-order current-induced magnetization. Finally, we note that we have focused on ferromagnetic behaviors of altermagnets either in no external perturbations or in the presence of current or strain; however, spin textures in excitations in altermagnets can be associated with other emerging physical phenomena with spin activities such as non-trivial superconductivity .

CONCLUSION

In the original proposal, a strong declaration like ‘these materials should be viewed as members of a third magnetic class-altermagnets-alongside ferromagnets and antiferromagnets’ was stated . However, through symmetry considerations, we have demonstrated that rather than a fresh class, altermagnetism is a practically useful concept to introduce PT symmetry breaking and consequential ferromagnetic-like behaviors by combining crystallographic and spin alternations. The original altermagnets have fully compensated ‘collinear’ spin angular momenta, but ferromagnet-like behaviors with non-zero orbital angular momenta through spin-orbital coupling with alternating two structural variations. We have extended the concept of altermagnetism to accommodate multiple director orientations (structural parameters, in general) and spin orientations, and this extended Altermagnetism includes ‘non-collinear’ spin states. In addition, we have classified three kinds of altermagnets; type-I-III. All type-I altermagnets, showing non-zero net magnetic moment and ferromagnetic-like behaviors, belong to the ferromagnetic point group, and are a kind of weak ferromagnets. All type-II & III altermagnets, with the broken PT symmetry and zero net magnetic moments, can exhibit ferromagnet-like behavior in the presence of applied current or stress which is PT-symmetric. Type-II altermagnets exhibit high-odd-order AHE, but type-III altermagnets do not show any odd-order AHE. These various forms of altermagnetism offer an intriguing opportunity to leverage complementary advantages of both ferromagnetism and antiferromagnetism.
Received: 18 October 2023; Accepted: 10 January 2024;
Published online: 22 January 2024

REFERENCES

  1. Baltz, V. et al. Antiferromagnetic spintronics. Rev. Mod. Phys. 90, 015005 (2018).
  2. Hirohata, A. et al. Review on spintronics: principles and device applications. J. Magn. Magn. Mater. 509, 166711 (2020).
  3. Jungwirth, T., Marti, X., Wadley, P. & Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 11, 231-241 (2016).
  4. Wolf, S. A. et al. Spintronics: a spin-based electronics vision for the future. Science 294, 1488-1495 (2001).
  5. Cheong, S.-W., Thompson, J. D. & Fisk, Z. Metamagnetism in . Phys. Rev. B 39, 4395-4398 (1989).
  6. Baibich, M. N. et al. Giant magnetoresistance of (001) magnetic superlattices. Phys. Rev. Lett. 61, 2472-2475 (1988).
  7. Fert, A. Nobel lecture: Origin, development, and future of spintronics Nobel lecture: origin, development, and future of spintronics. Rev. Mod. Phys. 80, 1517-1530 (2008).
  8. Binasch, G., Grünberg, P., Saurenbach, F. & Zinn, W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 39, 4828-4830 (1989).
  9. Šmejkal, L., MacDonald, A. H., Sinova, J., Nakatsuji, S. & Jungwirth, T. Anomalous Hall antiferromagnets. Nat. Rev. Mater. 7, 482-496 (2022).
  10. Šmejkal, L., Mokrousov, Y., Yan, B. & MacDonald, A. H. Topological antiferromagnetic spintronics. Nat. Phys. 14, 242-251 (2018).
  11. Wadley, P. et al. Electrical switching of an antiferromagnet. Science 351, 587-590 (2016).
  12. Chen, H., Niu, Q. & Macdonald, A. H. Anomalous Hall effect arising from noncollinear antiferromagnetism. Phys. Rev. Lett. 112, 017205 (2014).
  13. Kübler, J. & Felser, C. Non-collinear antiferromagnets and the anomalous Hall effect. Europhys. Lett. 108, 67001 (2014).
  14. Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212-215 (2015).
  15. Mazin, I. Editorial: Altermagnetism-a new punch line of fundamental magnetism. Phys. Rev. X 12, 040002 (2022).
  16. Šmejkal, L., Sinova, J. & Jungwirth, T. Emerging research landscape of altermagnetism. Phys. Rev. X 12, 040501 (2022).
  17. Šmejkal, L., Sinova, J. & Jungwirth, T. Beyond conventional ferromagnetism and antiferromagnetism: a phase with nonrelativistic spin and crystal rotation symmetry. Phys. Rev. X 12, 031042 (2022).
  18. Šmejkal, L. et al. Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets. Sci. Adv. 6, eaaz8809 (2020).
  19. McClarty, P. A. & Rau, J. G. Landau theory of altermagnetism. https://arxiv.org/abs/ 2308.04484 (2023).
  20. Hayami, S., Yanagi, Y. & Kusunose, H. Bottom-up design of spin-split and reshaped electronic band structures in antiferromagnets without spin-orbit coupling: Procedure on the basis of augmented multipoles. Phys. Rev. B 102, 144441 (2020).
  21. Gonzalez Betancourt, R. D. et al. Spontaneous anomalous Hall effect arising from an unconventional compensated magnetic phase in a semiconductor. Phys. Rev. Lett. 130, 036702 (2023).
  22. Cheong, S.-W. & Huang, F.-T. Trompe L’oeil Ferromagnetism: magnetic point group analysis. npj Quant. Mater. 8, 73 (2023).
  23. Cheong, S.-W., Huang, F.-T. & Minhyong, K. Linking emergent phenomena and broken symmetries through one-dimensional objects and their dot/cross products. Rep. Prog. Phys. 85, 124501 (2022).
  24. Birss, R. R. in Symmetry and Magnetism. 125-138 (North-Holland Pub. Co., 1964).
  25. Cheong, S.-W. SOS: symmetry-operational similarity. npj Quant. Mater. 4, 53 (2019).
  26. Cheong, S.-W. Trompe L’oeil Ferromagnetism. npj Quant. Mater. 5, 37 (2020).
  27. Gallego, S. V. et al. MAGNDATA: towards a database of magnetic structures. I.The commensurate case. J. Appl. Crystallogr. 49, 1750-1776 (2016).
  28. Landau, L. D. & Lifshitz, E. M. in Electrodynamics of Continuous Media, Vol. 8. (eds. Landau L. D. & Lifshitz E. M.) 130-179, Ch. V (Pergamon,1984).
  29. Shuvalov, L. A. Modern crystallography. IV. Physical properties of crystals. 1-46 (Springer England, 1989).
  30. Higo, T. et al. Large magneto-optical Kerr effect and imaging of magnetic octupole domains in an antiferromagnetic metal. Nat. Photonics 12, 73-78 (2018).
  31. Ikhlas, M. et al. Piezomagnetic switching of the anomalous Hall effect in an antiferromagnet at room temperature. Nat. Phys. 18, 1086-1093 (2022).
  32. Hohenberg, P. C. Existence of long-range order in one and two dimensions. Phys. Rev. 158, 383-386 (1967).
  33. Mermin, N. D. & Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 17, 1133-1136 (1966).
  34. Mazin, I. I. Altermagnetism in MnTe: origin, predicted manifestations, and routes to detwinning. Phys. Rev. B 107, L100418 (2023).
  35. Wang, H. et al. Giant anisotropic magnetoresistance and nonvolatile memory in canted antiferromagnet . Nat. Commun. 10, 2280 (2019).
  36. Kotegawa, H. et al. Large anomalous Hall effect and unusual domain switching in an orthorhombic antiferromagnetic material NbMnP. npj Quant. Mater. 8, 56 (2023).
  37. Disa, A. S. et al. Polarizing an antiferromagnet by optical engineering of the crystal field. Nat. Phys. 16, 937-941 (2020).
  38. Moriya, T. Piezomagnetism in . J. Phys. Chem. Solids 11, 73-77 (1959).
  39. Liu, J. & Balents, L. Anomalous Hall effect and topological defects in antiferromagnetic Weyl semimetals: . Phys. Rev. Lett. 119, 087202 (2017).
  40. Nayak, A. K. et al. Large anomalous Hall effect driven by a nonvanishing Berry curvature in the noncolinear antiferromagnet . Sci. Adv. 2, e1501870 (2016).
  41. Brown, P. J. & Chatterji, T. Neutron diffraction and polarimetric study of the magnetic and crystal structures of and . J. Phys. Condens. Matter 18, 10085-10096 (2006).
  42. Das, H., Wysocki, A. L., Geng, Y., Wu, W. & Fennie, C. J. Bulk magnetoelectricity in the hexagonal manganites and ferrites. Nat. Commun. 5, 2998 (2014).
  43. Du, K. et al. Vortex ferroelectric domains, large-loop weak ferromagnetic domains, and their decoupling in hexagonal (Lu, Sc)FeO3. npj Quant. Mater. 3, 33 (2018).
  44. Park, P. et al. Field-tunable toroidal moment and anomalous Hall effect in noncollinear antiferromagnetic Weyl semimetal TaS .npj Quant. Mater. 7, 42 (2022).
  45. Kurumaji, T., Ishiwata, S. & Tokura, Y. Diagonal magnetoelectric susceptibility and effect of Fe-doping in a polar ferrimagnet . Phys. Rev. B 95, 045142 (2016).
  46. Wang, Y. et al. Unveiling hidden ferrimagnetism and giant magnetoelectricity in polar magnet . Sci. Rep. 5, 12268 (2015).

ACKNOWLEDGEMENTS

We thank Jairo Sinova, Allan H. Macdonald, Valery Kiryukhin, and Seong Joon Lim for highly beneficial discussions on altermagnetism. The work at Rutgers University was supported by the DOE under Grant No. DOE: DE-FG02-07ER46382.

AUTHOR CONTRIBUTIONS

S.W.C. conceived and supervised the project. F.-T.H. conducted a magnetic point group analysis. S.W.C. wrote the remaining part.

COMPETING INTERESTS

The authors declare no competing interests.

ADDITIONAL INFORMATION

Correspondence and requests for materials should be addressed to Sang-Wook Cheong.
Reprints and permission information is available at http://www.nature.com/ reprints
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http:// creativecommons.org/licenses/by/4.0/.
© The Author(s) 2024
  1. Rutgers Center for Emergent Materials and Department of Physics and Astronomy, Rutgers University, Piscataway, NJ 08854, USA. email: sangc@physics.rutgers.edu