المغناطيسية الفيريمغناطيسية المعوضة بالكامل ثنائية الأبعاد Two-Dimensional Fully Compensated Ferrimagnetism

المجلة: Physical Review Letters، المجلد: 134، العدد: 11
DOI: https://doi.org/10.1103/physrevlett.134.116703
PMID: https://pubmed.ncbi.nlm.nih.gov/40192380
تاريخ النشر: 2025-03-18

المغناطيسية الفيريمغناطيسية المعوضة بالكامل ثنائية الأبعاد

يشن ليو، سان-دونغ قوه يونغبان لي وتشنغ تشينغ ليو مركز الفيزياء الكمومية، المختبر الرئيسي للهندسة البصرية الكمومية المتقدمة والقياس (MOE)، كلية الفيزياء، معهد بكين للتكنولوجيا، بكين 100081، الصين كلية الهندسة الإلكترونية، جامعة شيان للبريد والاتصالات، شيان 710121، الصين

الملخص

لقد كانت الإلكترونيات المغناطيسية المضادة لفترة طويلة موضوعًا لاهتمام بحثي مكثف، وقد أشعلت المقدمة الأخيرة للـ “ألتيرمغناطيسية” الحماس في هذا المجال. ومع ذلك، لم تحظَ الفيريمغناطيسية المعوضة بالكامل، التي تظهر انقسامًا في دوران الشريط ولكنها تتمتع بمغناطيسية صافية صفرية، بالاهتمام الكافي بعد. منذ التحضير التجريبي للمواد المغناطيسية ثنائية الأبعاد (2D) من نوع فان دير واهل في عام 2017، أصبحت المواد المغناطيسية ثنائية الأبعاد، بفضل قابليتها الكبيرة للتعديل، ساحة مهمة للإلكترونيات المغناطيسية. هنا، نوسع مفهوم الفيريمغناطيسية المعوضة بالكامل (fFIM) إلى بعدين ونقترح fFIM المعززة بالتعبئة ثنائية الأبعاد، ونظهر استقرارها وسهولة التلاعب بها، ونقدم ثلاث خطط تنفيذ ممكنة مع مواد مرشحة نموذجية لكل منها. تم تطوير نموذج بسيط للفيريمغناطيسيات المعوضة بالكامل ثنائية الأبعاد (fFIMs). تكشف المزيد من التحقيقات في الخصائص الفيزيائية لـ fFIMs ثنائية الأبعاد أنها لا تظهر فقط استجابة مغناطيسية بصرية كبيرة ولكنها أيضًا تظهر تيارات قطبية بالكامل وتأثير هول الشاذ في الحالات نصف المعدنية، مما يعرض خصائص كانت تقريبًا حصرية سابقًا للمواد الفيرومغناطيسية، مما يوسع بشكل كبير آفاق البحث والتطبيق لمواد الإلكترونيات المغناطيسية.

مقدمة.- تقليديًا، يمكن تصنيف المغناطيسية المتوازية إلى مغناطيسية حديدية، ومغناطيسية مضادة، ومغناطيسية مختلطة. في المغناطيسات الحديدية، تكون جميع اللحظات المغناطيسية متراصة في نفس الاتجاه مع مغنطة غير صفرية، وتكون النطاقات متباينة الدوران. في المغناطيسات المضادة التقليدية (cAFMs)، تكون اللحظات المغناطيسية مرتبة بشكل مضاد مع مغنطة صافية صفرية، وتكون النطاقات متساوية الدوران. ومع ذلك، فإن الطبيعة المتساوية للدوران في النطاقات الطاقية في cAFMs تلغي تأثير هول الشاذ (AHE) وتأثير المغناطيسية البصرية، مما يقيّد تطبيقاتها المحتملة [1]. تحتوي المغناطيسية المختلطة على لحظات مغناطيسية مضادة عادةً لا يمكنها إلغاء بعضها البعض تمامًا. مؤخرًا، تم اقتراح نوع جديد من المواد المغناطيسية، ما يسمى بالمغناطيسات البديلة، مع مغنطة صافية صفرية ونطاقات متباينة الدوران غير متساوية [2، 3]. بالمقارنة مع المواد المغناطيسية الحديدية، توفر المواد المغناطيسية ذات المغنطة الصفرية، مثل cAFMs والمغناطيسات البديلة، عدة مزايا، بما في ذلك الديناميات الفائقة السرعة، وغياب الحقول المتناثرة، وزيادة الاستقرار في وجود الحقول المغناطيسية [1]. ومع ذلك، فإن هذا التصنيف يتجاهل فئة هامة من المغنطة الصفرية الصافية، وهي المغناطيسية المختلطة المدفوعة بالكامل [3-6]، التي تم إصدارها لأول مرة بواسطة دي غروت وآخرون [4]. على عكس cFAMs والمغناطيسات البديلة، تحقق المغناطيسات المختلطة المدفوعة بالكامل (fFIMs) مغنطة صافية صفرية من خلال التعبئة المناسبة بدلاً من التماثل.
الدراسات السابقة حول fFIMs كانت محدودة على أنظمة ثلاثية الأبعاد (3D) ذات هياكل بلورية معقدة، مثل أكاسيد البيروفسكايت المزدوجة، ونظام هيوسلي، والمركبات العضوية [7-17]. علاوة على ذلك، لا تزال الأدلة التجريبية الواضحة لـ fFIMs بعيدة المنال. منذ تصنيعها التجريبي لـ [18] و [19] في عام 2017، الفاندر واهل المغناطيسي ثنائي الأبعاد
المواد (mvdW) ذات القابلية الممتازة للتعديل قد جذبت اهتمامًا هائلًا على الفور. حتى الآن، تم تخليق مجموعة أغنى من أنظمة المواد ثنائية الأبعاد (mvdW) [20-22]، بما في ذلك ، و ، إلخ. بالنظر إلى وفرة وقابلية ضبط المواد المغناطيسية ثنائية الأبعاد الممتازة، وحقيقة أن الفيريمغناطيسيات المعكوسة (fFIMs) تتمتع بميزة دمج انقسام دوران الشريط للمغناطيسية الحديدية مع عدم وجود مغناطيسية صافية في المغناطيسيات المعاكسة (cAFMs) ولكن تفتقر إلى تأكيد تجريبي واضح، فإن توسيع الفيريمغناطيسية المعوضة بالكامل إلى بعدين أمر ضروري للغاية وجذاب جداً.
في الرسالة، نقوم بتصور الفيريمغناطيسية المعوضة بالكامل المدفوعة بالتعبئة ثنائية الأبعاد (fFIM). تم تطوير نموذج بسيط يعتمد على الربط الضيق، ومن خلال حجج التناظر، تم إظهار الانتقال بين الفيريمغناطيسيات المعوضة بالكامل المدفوعة بالتعبئة ثنائية الأبعاد (fFIMs)، والمغناطيسات المعاكسة (cAFMs)، والمغناطيسات البديلة. استنادًا إلى التحليل النظري، نقترح ثلاث طرق قابلة للتطبيق لبناء الفيريمغناطيسيات المعوضة بالكامل باستخدام مواد mvdW ثنائية الأبعاد: بناء هيكل جانوس، إضافة جهد متناوب، واستخدام استبدال العناصر أو السبائك، كل منها مع مواد مرشحة نموذجية. على الرغم من عدم وجود مغنطة صافية، نجد أن الفيريمغناطيسيات المعوضة بالكامل يمكن أن تظهر تأثيرات مغناطيسية بصرية ملحوظة، مثل زوايا كير وفاراداي القابلة للرصد، وAHE، وتيارات مستقطبة بالكامل. ونصف معدني كمثال، نوضح أن الفيمات 2D لا تقوم فقط بالتنفيذ التجريبي بسهولة، بل تظهر أيضًا زوايا كير وفاراداي كبيرة وموصلية هول الشاذة (AHC).
تعويض كامل مفروض بالتعبئةالفيريمغناطيسية.في نوعي المغناطيسية المتوازية المدفوعة بالكامل، أي المغناطيسية المضادة التقليدية (cAFM) والمغناطيسية البديلة، تكون الشبكات المغناطيسية الفرعية مرتبطة بالتناظر، مثل من خلال تناظر الانعكاس المكاني. ) في cAFM ومن خلال rota-
الشكل 1. ثلاث فئات من المغناطيسية المتوازية المدفوعة بالكامل مع عدم وجود مغناطيسية صافية ). (a1) يتميز المغناطيسية المضادة التقليدية (cAFM) بشبكات مغناطيسية فرعية مترابطة بواسطة و ، الذي يتميز بتدهور كرامرز، كما هو موضح في (a2). هنا ، “ ، و هما الدوران الثنائي العمودي على محور الدوران، الانعكاس، والترجمة، على التوالي. (ب1) يتم ربط طبقتين مغناطيسيتين في الألترمغناطيسية (AM) بواسطة ، حيث يمثل دورانًا أو تناظرًا مرآتيًا. وهذا يؤدي إلى انقسام مغزلي غير متساوٍ، كما هو موضح في (b2). (c1) الفيريمغناطيسية المدفوعة بالكامل (fFIM)، حيث لا توجد علاقة تناظرية بين الطبقتين المغناطيسيتين، تظهر انقسامًا مغزليًا متساويًا (c2). إن عدم وجود مغنطة صافية في cAFM وAM مفروض بالتناظر، بينما في fFIM مفروض بالملء. في (a2)-(c2)، تمثل الأسطح الرمادية نطاقات مغزلية متساوية، والأسطح الحمراء والزرقاء تت correspond إلى نطاقات مغزلية لأعلى ولأسفل، على التوالي، والطائرة الخضراء تشير إلى مستوى فيرمي.
تناظر عكسي أو تناظر مرآة ( في المغناطيسية البديلة. لذلك، نسمي cAFM والمغناطيسية البديلة مغناطيسية خطية كاملة التعويض مفروضة بالتناظر، كما هو موضح في الأشكال 1(أ) و(ب). بالمقابل، لا يمكن ربط الشبكات المغناطيسية في fFIMs المفروضة بالتعبئة ثنائية الأبعاد من خلال أي تناظر، مما يؤدي إلى انقسام مغناطيسي شبيه بالفيرومغناطيسية، كما هو موضح في الشكل 1(ج). يتم إعطاء المغناطيسية الصافية في الفيريمغناطيسية المعتادة بواسطة
مع المغناطيسية بور، حيث و يمثل عدد الحالات المشغولة في قنوات الدوران لأعلى ولأسفل، على التوالي. طالما أن أيًا من قنوات الدوران تحتوي على فجوة، بغض النظر عما إذا كانت القناة الأخرى تحتوي على فجوة أم لا، وهو ما يتوافق مع حالات الفيريمغناطيسية العازلة وحالات الفيريمغناطيسية نصف المعدنية، يجب أن يكون المغنطة الصافية عددًا صحيحًا من مغنطيس بوهري. وذلك لأن العدد الإجمالي للإلكترونات هو عدد صحيح، وعدد الإلكترونات في القناة الموصلة أيضاً عدد صحيح، لذا فإن عدد الإلكترونات في قناة الدوران الأخرى هو أيضاً عدد صحيح. في هذه الحالة، العددان الصحيحان و هما عددان كميان جيدان يمكن استخدامهما للتسمية
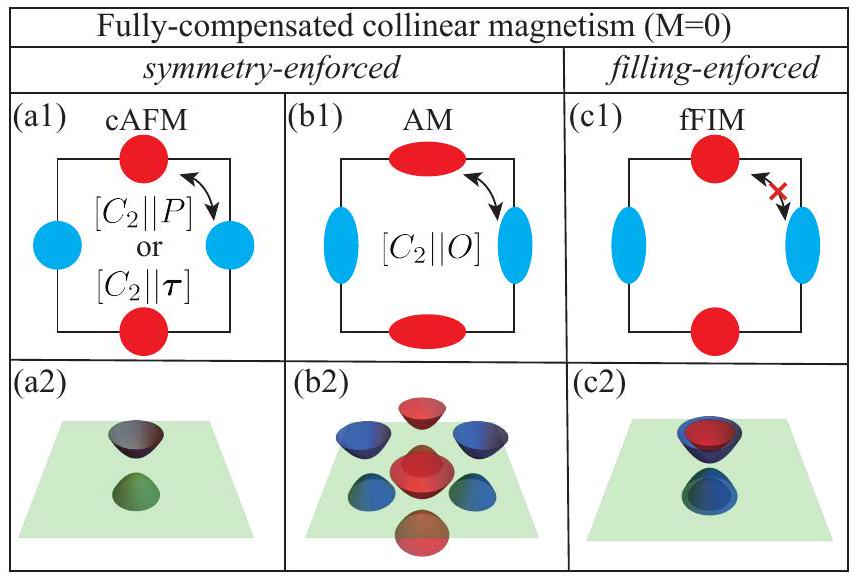
مغناطيسات فيري مختلفة. عندما يكون للنظام تعبئة مناسبة، أي، ، فإن المغناطيسية الصافية تساوي صفرًا تمامًا، مما يتوافق مع الفيريمغناطيسية المدعومة بالكامل (fFIM)، والتي نسميها fFIM المدعومة بالتعبئة. طالما أن الفجوة لم تُغلق، فإن الأعداد الثلاثة ، ، و لن تتغير، والأعداد الصحيحة لا تتغير بشكل مستمر، لذا , أي أن الخصائص المدفوعة بالكامل يتم الحفاظ عليها بدقة تحت الاضطرابات المعقولة. تعني الاضطرابات المعقولة هنا أنها لن تغلق الفجوة. يتم حماية fFIM المدفوع بالملء من خلال كوانتization الدوران المضمون للفجوة في قناة دوران واحدة، وهو مشابه لكيفية حماية الحالات الكمومية الطوبولوجية المستقرة من خلال فجوة طاقة كبيرة [24، 25]. نظرًا لأن fFIM المدفوع بالملء ليس مقيدًا بقيود التناظر، فإنه يظل قويًا للغاية تحت الحقول الخارجية، مثل الحقول الكهربائية والضغط، بغض النظر عما إذا كانت هذه الحقول تكسر التناظر.
نطور نموذجًا بسيطًا ثنائي الأبعاد لالتقاط cAFMs، والمغناطيسات البديلة، وfFIMs المدفوعة بالملء والتحول بينها. النموذج كما يلي
حيث تمثل القفزات بين الجيران الأقرب، 1،2 تشير إلى الشبكات الفرعية الموجودة في و ، على التوالي، و هما القفزات بين الجيران الأقرب، هو الجهد المتقطع، هو مشغل الدوران، و هو المغنطة. و هما المتجه الأقرب و متجهات الشبكة في الاتجاه. يتم توضيح هيكل الشبكة في الشكل 2(أ). نستخدم و و لتنظيم تناظر النظام، مما يتوافق مع الحالات الثلاث التالية من cAFMs، والمغناطيسات البديلة، وfFIMs المدفوعة بالملء.
عندما يكون و ، يمكن ربط الشبكات الفرعية ذات الدوران المعاكس من خلال الانعكاس . يقع مركز الانعكاس عند ( )، مما يبدل بين و . نظرًا لأن الشبكتين الفرعيتين لهما دوران معكوس، فإن النظام يمتلك تناظرًا مع دوران مزدوج عمودي على محور الدوران، مما يؤدي إلى تدهور كرامرز كما هو موضح في الشكل 2(ب).
عندما يكون و ، يتم كسر تناظر . ومع ذلك، يمكن ربط الشبكات الفرعية ذات المغنطة المعاكسة من خلال دوران مع المركز عند ( 0،0 )، مما يؤدي إلى و . وبالتالي، يمتلك النظام تناظرًا ، مما يؤدي إلى انقسام الدوران غير المتساوي المميز في المغناطيسات البديلة، كما هو موضح في الشكل 2(ج). من المثير للاهتمام، أن إدخال الجهد المتقطع (
على الشبكات الفرعية يكسر أي اتصال بينها من خلال التناظر. يؤدي تطبيق طاقات مختلفة على الموقعين إلى الشكل 2. نموذج بسيط لفئات المغناطيسية المتوازنة بالكامل، أي، المغناطيسية المضادة التقليدية (cAFM)، والمغناطيسية البديلة (AM)، وfFIM المدفوع بالملء. (أ) توضيح نموذجنا. (ب) عندما يكون
و ، يكون النظام cAFM مع تناظر . (ج) عندما يكون و ، يتم ربط الشبكات الفرعية ذات الدوران المعاكس بواسطة ، مما يحول النظام إلى AM مع انقسام دوران غير متساوي. (د) (هـ) تعيين و مع يرفع أي تناظر يربط بين شبكتين فرعيتين، يمكن أن يكون النظام fFIM. نظرًا لأن الفجوة في قناة دوران واحدة لم تغلق أبدًا، فإن IDOSs للدوران المعاكس هي أعداد صحيحة وتظل متساوية عند طاقة فيرمي مع ، مما يؤدي إلى مغنطة صافية صفرية. يتم عرض fFIM نصف المعدني في (هـ). يتم أخذ لـ (ب)-(هـ).
يمكن أن تجعل الشبكات الفرعية تعتبر مكونة من ذرات مغناطيسية مختلفة تمامًا أو نفس الذرات المغناطيسية في بيئات مختلفة. وبالتالي، لا يمكن أن يربط أي تناظر بين الشبكتين الفرعيتين، مما يؤدي إلى انقسام الدوران في النطاقات، كما هو موضح في الأشكال 2(د) و(هـ). على الرغم من أن الكثافات المتكاملة للحالات (IDOSs) لقناتي الدوران لا تتطابق عبر جميع الطاقات، إلا أنها متساوية ضمن فجوة النطاق لقناة دوران واحدة مع ، مما يحافظ على المغنطة الكلية صفرًا بالضبط. لاحظ أن fFIM المدفوع بالملء في الشكل 2(هـ) هو نصف معدن، يوصل فقط في قناة دوران واحدة. على الرغم من أن المناقشة أعلاه تستند إلى الشبكة الرباعية، فإن استنتاجاتنا عامة. نحن أيضًا نبني نموذجًا للشبكة السداسية (انظر المواد التكميلية (SM) [27] للتفاصيل).
خطط وتحقيقات المواد. – لكي يكون مادة fFIM، يجب أن تلبي المادة شرطين: (1) يجب أن يكون عدد الحالات المشغولة ذات الدوران المعاكس متساويًا، و(2) يجب ألا تكون هناك عمليات تناظر تربط بين الشبكات الفرعية ذات الدوران المعاكس. في هذا العمل، نقترح ثلاث طرق لبناء fFIMs: (1) هيكل جانوس، (2) جهد متقطع بواسطة حقل كهربائي خارجي أو ركيزة، و(3) استبدال عنصر أو سبائك.
الشكل 3. خطط التحقيق والمواد التمثيلية لمواد مغناطيسية ثنائية الأبعاد متوازنة بالكامل. (أ) الطبقة الثنائية من NiICl مع هيكل جانوس وبنيتها النطاقية، بالإضافة إلى IDOS. (ب) الهندسة وبنية النطاق للهيكل الثنائي الطبقات مع جهد متقطع قدره 0.5 eV. يتم عرض الجهد المتقطع للطبقات العليا والسفلى كخلفية خضراء وزرقاء. (ج) الهندسة وبنية النطاق لـ 2D ، حيث يستبدل ذرة Mo ذرة Cr. (د) الهندسة وبنية النطاق لـ تحت حقل كهربائي قدره Å. النظام هو نصف معدن، وتبقى IDOS متساوية عند طاقة فيرمي مع ، مما يؤدي إلى مغنطة صافية صفرية. يتم رسم الهندسة باستخدام برنامج VESTA [26]
(1) هيكل جانوس: يكسر هيكل جانوس التناظر الذي يربط بين الشبكتين الفرعيتين المغناطيسيتين عن طريق تغيير البيئة المحيطة بالذرات المغناطيسية ويولد حقل كهربائي عمودي مدمج. يُعرف هيكل جانوس هذا جيدًا في سياق ثنائي كبريتيد المعادن الانتقالية [28]. هنا، نأخذ هيكل جانوس NiICl كمثال [29،30]. يتم اشتقاقه عن طريق استبدال ذرات I في الطبقة العليا في [31] بذرات Cl مع كسر التناظر. يتم عرض الهندسة وبنية النطاق للطبقة الثنائية NiICl في الشكل 3(أ). على الرغم من أن هيكل جانوس في الطبقة الثنائية NiICl يكسر التناظر الذي عادة ما يقيد النظام إلى مغنطة صافية صفرية، كما تم مناقشته أعلاه، طالما أن أحد قنوات الدوران مكسورة، فإن العزم المغناطيسي الكلي للنظام يبقى صفرًا، مما يؤدي إلى fFIM.
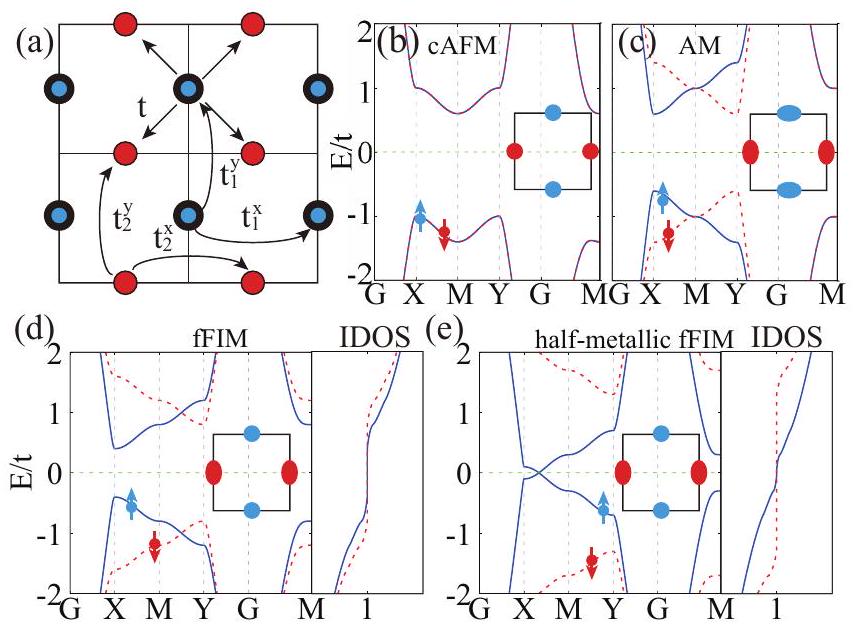
(2) الجهد المتقطع: من خلال تطبيق جهد متقطع، تم تقديمه بواسطة حقل كهربائي أو ركيزة، إلخ، على شبكتين فرعيتين مغناطيسيتين، يتم كسر التناظر الذي يربط بين الشبكتين الفرعيتين، مما يؤدي إلى انقسام الدوران، ويصبح النظام fFIM. من التحليل النظري أعلاه، يمكن رؤية أنه بينما يمكن أن يؤدي جهد متقطع صغير إلى fFIMs مكسورة، يمكن أن يؤدي جهد كبير إلى fFIMs نصف معدنية، كما هو موضح في الأشكال 2(د) و(هـ). على سبيل المثال، في الطبقة الثنائية المضادة المغناطيسية من النوع A التي تم إعدادها تجريبيًا [18]، عند تطبيق حقل كهربائي عمودي قدره Å، يحدث انقسام للدوران، وتبقى IDOSs للدوران لأعلى ولأسفل متساوية في الفجوة، كما هو موضح في الشكل 3(ب). بالمقابل، تحت حقل كهربائي عمودي قدره Å هو نصف معدن ويظهر نطاقات دوران لأعلى بدون فجوة ونطاقات دوران لأسفل بفجوة. كما هو موضح أعلاه، على الرغم من أن قناة الدوران لأعلى
الشكل 4. التأثير المغناطيسي البصري والتأثير الهالي الشاذ في fFIMs ثنائية الأبعاد. (أ) و(ب) تظهر زاوية كير وزاوية فاراداي للطبقة الثنائية من fFIM مع حقل كهربائي قدره 0.08 Å. و تمثل الزاوية والبيضاوية، على التوالي. (ج) (د) زاوية كير/AHC كدالة للتردد/طاقة فيرمي في نصف المعدني مع حقل كهربائي قدره 0.6 Å.
قناة الدوران لأعلى بدون فجوة، طالما أن قناة الدوران لأسفل مكسورة، يحتفظ النظام بـ ، وتكون الكثافة المتكاملة للحالات (IDOS) للدوران لأعلى متساوية مع IDOS للدوران لأسفل عند طاقة فيرمي، كما هو موضح في الشكل 3(د)، مما يوضح أن النظام يبقى متوازنًا بالكامل.
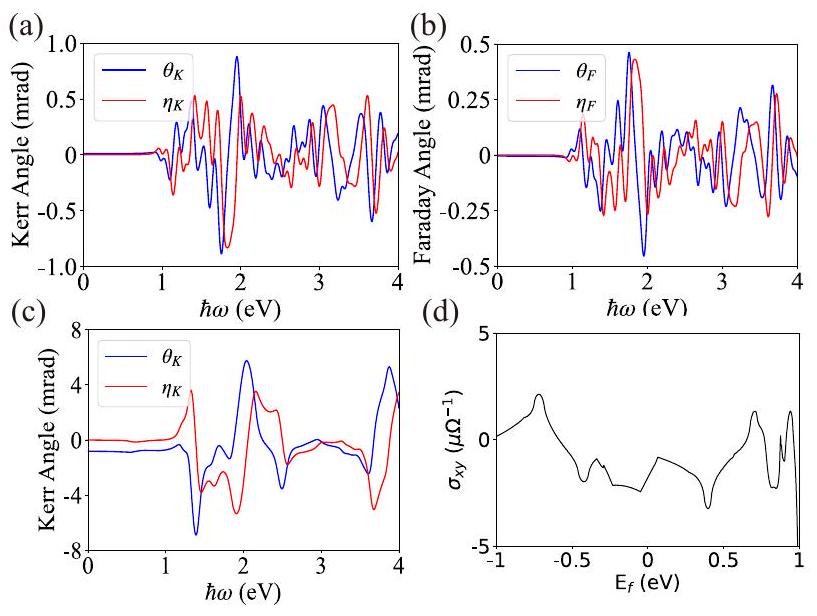
(3) استبدال عنصر أو سبائك: من خلال استبدال أو سبائك مع عنصر له نفس عدد الإلكترونات التكافؤية أو يختلف بعدد زوجي مقارنة بالذرة المغناطيسية الأصلية، مما يضمن توزيع هذه الإلكترونات بالتساوي عبر قناتي الدوران، يحتفظ النظام بـ ، مما يؤدي إلى مغنطة صافية صفرية. تم تقديم هذه الطريقة لأول مرة في الأنظمة ثلاثية الأبعاد [4] وتم تنفيذها بنجاح في سبائك هيوسلي [15، 32]. كمثال، نستبدل ذرات Cr المغناطيسية في مادة cAFM ثنائية الأبعاد بذرات Mo من نفس المجموعة في الجدول الدوري، مما يؤدي إلى المادة [33]. على الرغم من الحفاظ على مغنطة صافية صفرية، يظهر النظام انقسام دوران شبيه بالمغناطيسية، كما هو موضح في الشكل 3(ج).
تفاصيل أكثر عن طيف الفونون وحالات الأرض المغناطيسية للطبقة الثنائية NiICl، والطبقة الثنائية ، والطبقة الأحادية موجودة في SM [27].
الخصائص الفيزيائية. – تمتلك fFIMs مغنطة صافية صفرية، مما يجعل خصائصها المغناطيسية مشابهة لتلك الخاصة بـ cAFMs وبالتالي لا يمكن تمييزها عن cAFMs من خلال قياسات الحقل المغناطيسي الخارجي. ومع ذلك، تكشف أبحاثنا المتعمقة أن fFIMs تمتلك خصائص فيزيائية تختلف جوهريًا عن cAFMs ولكنها تشبه أنظمة الفيرومغناطيسية، مثل التأثير الهائل للانحراف الأيوني، وتأثيرات كير وفاراداي المغناطيسية البصرية، والتي يُعتقد تقليديًا أنها تحدث في…
تحدث فقط في الأنظمة الفيرومغناطيسية. لتأكيد هذه الخصائص الفيزيائية الجديدة، نعرض نتائجنا من حيث كل من النموذج الفعال والمواد التمثيلية. الفجوة المذكورة في fFIM و نصف معدني fFIM تُؤخذ كأمثلة. تم أيضًا حساب التأثير المغناطيسي البصري وAHE بواسطة نموذج الربط الضيق fFIM في SM [27].
تُعطى زوايا كير وفاراداي المغناطيسية الضوئية في الأنظمة ثنائية الأبعاد [34، 35] بواسطة
أين و تمثل زاوية الدوران والانحراف البيضاوي، على التوالي. و هي المكونات القطرية وغير القطرية لموتر التوصيل البصري، التي تقيس استجابة المادة لمجال كهرومغناطيسي مطبق. هو مقاومة الفراغ (تقريباً ) ، هو سمك البسيط، و هو السماحية الفراغية. معامل الانكسار للركيزة، الذي يُشار إليه بـ يُفترض أن تكون 1.5، وهو ما يتوافق مع معامل الانكسار لـ موتر التوصيلية البصرية يمكن حسابه بواسطة صيغة كوبو-غرينوود[36، 37]
هنا يمثل الفرق في الطاقة بين النطاقات و هو مشغل السرعة، يعرف على أنه ، حيث يمثل تردد الضوء و هو معامل التمويه، تم تعيينه إلى 0.05 إلكترون فولت في هذه الدراسة.
بينما الطبقة الثنائية النقية هو cAFM، الذي لا يظهر تأثيرات كير أو فاراداي، عندما يتم تطبيق جهد متداخل، يتم انتقال النظام إلى fFIM، مع زوايا كير وفاراداي الناتجة الموضحة في الأشكال 4 (أ) و (ب) على التوالي. الزاوية القصوى لكير قريبة من 1 مللي راديان، وهي من نفس ترتيب أحادية الطبقة. [18] ويتجاوز بكثير حد القياس للأجهزة الحالية، مما يدل على تأثير مغناطيسي بصري كبير.
مع وجود إمكانيات متدرجة كبيرة، يظهر سلوكًا نصف معدني، حيث إن قناة الدوران لأعلى فقط هي القابلة للتوصيل، مما يؤدي إلى تيار مستقطب بالكامل بشكل كبير. علاوة على ذلك، بسبب عدم وجود كل من تناظر الانعكاس الزمكاني وتناظر عكس الزمن، يمكن للنظام أن يظهر AHC غير صفري على الرغم من عدم وجود مغنطة صافية. يتم حساب AHC باستخدام الصيغة [38، 39]
زاوية كير ونتائج AHC لـ fFIM YI موضحة في الأشكال 4(c) و(d)، وزاوية فاراداي موضحة في SM [27]. على الرغم من عدم وجود مغنطة صافية عند طاقة فيرمي، fFIM تظهر زوايا كير غير الصفرية وAHC. النتائج النموذجية للمواد المذكورة أعلاه وحسابات النموذج الفعال العامة في SM توضح أن المواد ثنائية الأبعاد المدعومة بالملء fFIMs تظهر عمومًا تأثيرًا مغناطيسيًا بصريًا كبيرًا، كما أن المواد نصف المعدنية تظهر أيضًا تأثير هول الأنيون الملحوظ والتيار المستقطب بالكامل.
الخاتمة. – في الملخص، نقترح نوعًا جديدًا من المغناطيسات ثنائية الأبعاد المتوازية، يختلف عن cAFM والمغناطيسية البديلة، يُطلق عليه اسم fFIM المعزز بالتعبئة ثنائية الأبعاد، والذي يحقق مغنطة صافية صفرية من خلال التعبئة المناسبة بدلاً من التماثل. بفضل خلوه من قيود التماثل، نقدم ثلاث خطط عالمية لتحقيق fFIMs ثنائية الأبعاد: هياكل جانوس، الجهد المتناوب، والاستبدال العنصري أو السبائك. نوضح فعالية هذه الطرق باستخدام NiICl مع هيكل جانوس، ثنائي الطبقة. و تحت مجال كهربائي، و كمثال، تؤكد مغناطيسيتها الصفرية الصافية والانقسام الشريطي الشبيه بالمغناطيسات الحديدية من خلال حسابات DFT. نكشف أن fFIMs تظهر بعض الخصائص الفيزيائية التي تشبه المغناطيسات الحديدية بدلاً من cAFMs، مثل التأثير المغناطيسي البصري، وAHE، والتيارات المستقطبة بالكامل. على عكس الألترمغناطيسات، فإن الأشرطة في fFIMs المفروضة بالتعبئة لا تحتوي على انحلال مغزلي عند نقطة. يمكن تمييز fFIMs المعززة بالتعبئة تجريبيًا عن cAFMs، والألترماجنات، والفيروماغنتات من خلال التأثير المغناطيسي البصري، وARPES المعتمد على الدوران، وقياسات المغنطة المباشرة.
من خلال استخدام المخططات المقدمة في هذا العمل لتحقيق المواد المغناطيسية ثنائية الأبعاد المعززة بالملء، يمكن استخدام الفحص عالي الإنتاجية لتحديد العديد من المواد المرشحة. لا تعرض هذه المواد المغناطيسية ثنائية الأبعاد الخصائص الفيزيائية للمواد المغناطيسية الحديدية فحسب، بل تمتلك أيضًا مزايا المواد المضادة للمغناطيسية، إلى جانب القابلية الفطرية للتعديل للمواد ثنائية الأبعاد. ستجذب خصائصها الفيزيائية الرائعة، مثل التأثير المغناطيسي البصري وتأثير هول الأنواع، بالإضافة إلى التيارات المستقطبة بالكامل، اهتمامًا واسعًا ويمكن التحقق منها تجريبيًا بسهولة. إن غياب الحقول المغناطيسية المتناثرة في المواد المغناطيسية ثنائية الأبعاد يسمح بزيادة كبيرة في كثافة التخزين، مدعومًا بمزايا أخرى مثل ترددات الاستجابة العالية. تشير كل هذه المزايا إلى أن المواد المغناطيسية ثنائية الأبعاد المقترحة ستضخ حيوية جديدة وقوية في تطوير الإلكترونيات المغناطيسية.
الشكر.- العمل مدعوم من البرنامج الوطني الرئيسي للبحث والتطوير في الصين (رقم المنحة 2020YFA0308800)، وصندوق العلوم الوطنية في الصين (رقم المنحة 12374055)، وصندوق العلوم لمجموعات البحث الإبداعية من NSF (رقم المنحة 12321004).
  • ساهم هؤلاء المؤلفون بالتساوي في هذا العمل.
    ccliu@bit.edu.cn
    [1] V. بالتز، A. مانشون، M. تسوي، T. مورياما، T. أونو، وY. تسيركوفنياك، سبينترونيك مضاد للمغناطيسية، مراجعة الفيزياء الحديثة 90، 015005 (2018).
    [2] ل. شميكال، ج. سينوفا، وت. يونغويرث، المشهد البحثي الناشئ للـ ألترمغناطيسية، فيزي. ريف. إكس 12، 040501 (2022).
    [3] I. مازن ومحررو PRX، تحرير: المغناطيسية البديلة – سطر جديد في المغناطيسية الأساسية، فيزي. ريف. X 12، 040002 (2022).
    [4] هـ. فان لوكن و ر. أ. دي غروت، مضادات مغناطيسية نصف معدنية، فيزيكال ريفيو ليترز 74، 1171 (1995).
    [5] هـ. أكاي وم. أوجورا، أشباه الموصلات المضادة للمغناطيسية المخففة نصف المعدنية، فيزيكال ريفيو ليترز 97، 026401 (2006).
    [6] س. وورمهيل، هـ. س. كاندبال، ج. هـ. فيشر، و س. فيلزر، قواعد إلكترونات التكافؤ للتنبؤ بسلوك الفيريمغناطيسية المعوضة نصف المعدنية لمركبات هيوسلر ذات الاستقطاب المغناطيسي الكامل، مجلة الفيزياء: المادة المكثفة 18، 6171 (2006).
    [7] و. إ. بيكيت، بحث قائم على دالة كثافة الدوران للمواد المضادة للمغناطيسية نصف المعدنية، فيزي. ريف. ب 57، 10613 (1998).
    [8] ي.-م. نيي و إكس. هو، مغناطيس مضاد نصف معدني محتمل في كوبرات بيروفسكايت المدعومة بالثقوب كما تم التنبؤ به من خلال حسابات المبادئ الأولى، فيزي. ريف. ليت. 100، 117203 (2008).
    [9] ك. إ. سيفيرسكا، ج. أتشيسون، أ. جها، ك. إيسين، ر. سميث، س. ليني، ن. تيشرت، ج. أوبراين، ج. م. د. كوي، ب. ستامينوف، وك. رود، النظام المغناطيسي والنقل المغناطيسي في أفلام نصف معدنية مغناطيسية مكونة من mn y ru x ga، فيزيكس ريفيو ب 104، 064414 (2021).
    [10] م. إ. جامر، ي. ج. وانغ، ج. م. ستيفن، إ. ج. مك دونالد، أ. ج. غروتر، ج. إ. ستيربينسكي، د. أ. أرينا، ج. أ. بورشرز، ب. ج. كيربي، ل. هـ. لويس، ب. باربييليني، أ. بانسيل، ود. هييمان، المغناطيسية الفيريمغناطيسية المعوضة في سبيكة هويزلر ذات الزيرو مومنت فيزي. ريف. أبليد. 7، 064036 (2017).
    [11] م. زيتش، ك. رود، ن. ثياغاراجاه، ي.-س. لاو، د. بيتو، ج. م. د. كوي، س. سانفيتو، ك. ج. أوشيا، ج. أ. فيرغسون، د. أ. ماكلارين، و ت. آرتشر، تصميم مغناطيس نصف معدني مع تعويض كامل، فيزيكس ريفيو ب 93، 140202 (2016).
    [12] ج. كوي و م. فينكاتيسان، المغناطيسية نصف المعدنية: مثال على (مدعو)، J APPL PHYS 91، 8345 (2002).
    [13] إكس. هو، المغناطيس المضاد نصف المعدني كمادة محتملة لتكنولوجيا السبين، مواد متقدمة 24، 294 (2012).
    [14] ك. أوزدوغان، إ. شاشيوغلو، و إ. جالاناكيس، دراسة أولية للخصائص الإلكترونية والمغناطيسية لمركبات هيوسليير الفيريمغناطيسية ذات الـ 18 إلكترونًا في حالة التكافؤ والمُعوضة بالكامل: نموذج لمواد فلاتر الدوران، علوم المواد الحاسوبية 110، 77 (2015).
    [15] ر. ستينشوف، أ. ك. ناياك، ج. هـ. فيشر، ب. بالكي، س. أواردي، ي. سكورسكي، ت. ناكامورا، و ج. فيلزر، مغناطيسية فيري كاملة التعويض وعبور دوران الشبكة في المركب الهيوسلر نصف المعدني المراجعة الفيزيائية ب 95، 060410 (2017).
    [16] ك. فليشير، ن. ثياغاراجاه، ي.-س. لاو، د. بيتو، ك. بوريسوف، س. س. سميث، إ. ف. شفيتس، ج. م. د. كوي.
    كي. رود، تأثير كير المغناطيسي البصري في فيري مغناطيس ذو لحظة صفرية مستقطبة، فيزيكال ريفيو بي 98، 134445 (2018).
    [17] ت. كاوامورا، ك. يوشيمي، ك. هاشيموتو، أ. كوباياشي، و ت. ميساوا، الفيريمغناطيسيات المعوضة مع انقسام دوران ضخم في المركبات العضوية، فيز. ريف. ليت. 132، 156502 (2024).
    [18] ب. هوانغ، ج. كلارك، إ. نافارو-موراتالا، د. ر. كلاين، ر. تشينغ، ك. ل. سايلر، د. تشونغ، إ. شميتغال، م. أ. مكغواير، د. هـ. كوبدن، و. ياو، د. شياو، ب. جاريلو-هيريرو، و إكس. شو، المغناطيسية الحديدية المعتمدة على الطبقات في بلورة فان دير وولس حتى حد الطبقة الأحادية، ناتشر 546، 270 (2017).
    [19] سي. غونغ، ل. لي، ز. لي، هـ. جي، أ. ستيرن، ي. شيا، ت. كاو، و. باو، سي. وانغ، ي. وانغ، ز. كيو. كيو، ر. ج. كافا، س. ج. لوي، ج. شيا، و إكس. تشانغ، اكتشاف المغناطيسية الذاتية في بلورات فان دير فالس ثنائية الأبعاد، ناتشر 546، 265 (2017).
    [20] ي. دينغ، ي. يو، ي. سونغ، ج. تشانغ، ن. ز. وانغ، ز. سون، ي. يي، ي. ز. وو، س. وو، ج. تشو، ج. وانغ، إكس. هـ. تشين، وي. تشانغ، مغناطيسية حديدية قابلة للتعديل عند درجة حرارة الغرفة في الأبعاد الثنائية طبيعة 563، 94 (2018).
    [21] م. بونيلا، س. كوليكار، ي. ما، هـ. سي. دياز، ف. كالا باتيل، ر. داس، ت. إيغرز، هـ. ر. غوتيريز، م.-هـ. فهان، وم. باتزيل، مغناطيسية قوية عند درجة حرارة الغرفة. طبقات أحادية على الركائز من نوع فان دير فال، نات. نانو تكنولوج 13، 289 (2018).
    [22] ج. كلاين، ت. فام، ج. د. تومسن، ج. ب. كيرتس، ت. دينولين، م. لوركي، م. فلوريان، أ. شتاينهوف، ر. أ. ويسكونس، ج. لوكسا، ز. سوفر، ف. ياهنكي، ب. نارنج، و ف. م. روس، التحكم في الهيكل ونسيج الدوران في المغناطيس ذو الطبقات فان دير فالس CrSBr، نات كوميون 13، 5420 (2022).
    [23] ب. هوانغ، و.-ي. ليو، إكس.-سي. وو، س.-ز. لي، هـ. لي، ز. يانغ، و و.-ب. تشانغ، استقطاب وادي عفوي كبير ودرجة حرارة انتقال مغناطيسي عالية في ferrovalley ثنائي الأبعاد المستقر ، و Cl فيزي. ريف. ب 107، 045423 (2023).
    [24] ف. د. م. هالدين، نموذج لتأثير هال الكمي بدون مستويات لاندو: تحقيق في المادة المكثفة لـ “شذوذ التماثل”، فيزيكال ريفيو ليترز 61، 2015 (1988).
    [25] سي. إل. كاين وإي. جي. ميلي، ترتيب طوبولوجي وتأثير سبين كوانتي هول، مجلة مراجعة الفيزياء. 95، 146802 (2005).
    [26] ك. مومّا و ف. إيزومي، فيستا 3 للتصوير ثلاثي الأبعاد لبيانات البلورات والحجم والشكل، مجلة البلورات التطبيقية 44، 1272 (2011).
    [27] انظر المواد التكميلية لمزيد من المعلومات التفصيلية حول (I) نموذج الربط الضيق لشبكة مربعة fFIM، (II) التأثير المغناطيسي البصري الملحوظ وتأثير هول الشاذ في نموذج fFIM العام، (III) نموذج الربط الضيق لشبكة سداسية، و (IV) تفاصيل حساب المواد، والتي تشمل المراجع [18، 23، 30، 33-47].
    [28] أ.-ي. لو، هـ. زو، ج. شياو، س.-ب. تشو، ي. هان، م.-هـ. تشيو، س.-س. تشينغ، س.-و. يانغ، ك.-هـ. وي، ي. يانغ، ي. وانغ، د. سوكاراس، د. نوردلوند، ب. يانغ، د. أ. مولر، م.-ي. تشو، إكس. تشانغ، و ل.-ج. لي، طبقات أحادية من ثنائي كبريتيد المعادن الانتقالية، نات. نانو تكنولوجول 12، 744 (2017).
    [29] س.-د. قوه، ي.-ت. تشو، ك. كوين، وي.-س. أنغ، استجابة بيزوكهربائية كبيرة خارج المستوى في طبقة أحادية من النيكل المغناطيسي، رسائل الفيزياء التطبيقية 120، 232403 (2022).
    [30] ت. غوركان، ج. داس، ج. كابيجان، م. أكرم، ج. ف.
بارث، س. تونغاي، إ. أكتورك، أ. إرتين، و أ. س. بوتانا، تشكيل سكريمون في طبقات ثنائية الهاليد جانوس القائمة على النيكل: التفاعل بين الإحباط المغناطيسي وتفاعل دزيالوشينسكي-موريا، فيزيكال ريفيو ماتيير 7، 054006 (2023).
[31] ق. سونغ، ج. أ. أوكالييني، إ. إرجين، ب. إلياس، د. أموروسو، ب. باروني، ج. كابيغيان، ك. واتانابي، ت. تانيغوتشي، أ. س. بوتانا، س. بيكوزي، ن. جيديك، ور. كومن، دليل على وجود مادة متعددة ferroic ذات طبقة واحدة من فان دير فال، ناتشر 602، 601 (2022).
[32] س. سيمبوشي، ر. ي. أوميتسو، ي. كاواهito، و هـ. أكاي، نوع جديد من الفيريمغناطيس نصف المعدني المدعوم بالكامل، Sci Rep 12، 10687 (2022).
[33] ب. وانغ، د. وو، ك. تشانغ، و إكس. وو، كبريتيد المعادن الانتقالية الرباعية الأبعاد ثنائية الأبعاد Si أو Ge): شبه موصل ثنائي القطب مضاد مغناطيسي مع درجة حرارة نيل عالية، J. Phys. Chem. Lett. 13، 3850 (2022).
[34] م.-هـ. كيم، ج. أكباس، م.-هـ. يانغ، إ. أوكوبو، هـ. كريستين، د. ماندروس، م. أ. سكاربولا، أ. د. دوبون، ز. شليسينجر، ب. خليفة، وج. سيرني، تحديد موتر التوصيلية المغناطيسية المعقدة تحت تأثير الأشعة تحت الحمراء في الفيرومغناطيسيات المتنقلة من قياسات فاراداي وكير، فيزيكس ريفيو ب 75، 214416 (2007).
[35] ر. فالديز أغيلار، أ. ف. ستير، و. ليو، ل. س. بيلبرو، د. ك. جورج، ن. بانسال، ل. وو، ج. سيرني، أ. ج. ماركيلز، س. أوه، و ن. ب. أرمتيج، استجابة التيراهيرتز ودوران كير الضخم من حالات السطح للعازل الطوبولوجي فيزي. ريف. ليت. 108، 087403 (2012).
[36] هـ. إيبيرت، التأثيرات المغناطيسية الضوئية في أنظمة المعادن الانتقالية، تقرير تقدم في الفيزياء 59، 1665 (1996).
[37] C. Aversa و J. E. Sipe، الاستجابات البصرية غير الخطية للموصلات نصفية: نتائج مع تحليل بواسطة مقياس الطول، فيزي. ريف. ب 52، 14636 (1995).
[38] ي. ياو، ل. كلاينمان، أ. هـ. ماكدونالد، ج. سينوفا، ت. يونغويرث، د.-س. وانغ، إ. وانغ، و ق. نيو، حسابات من المبادئ الأولى للتوصيل غير العادي في الحديد المغناطيسي البارد bcc، فيزيكال ريفيو ليترز 92، 037204 (2004).
[39] إكس. وانغ، ج. ر. ييتس، آي. سوزا، و د. فاندربيلت، حساب من أول المبدأ للتوصيلية الغريبة باستخدام تقنيات وانير، فيزيكال ريفيو بي 74، 195118 (2006).
[40] ج. كريسه و ج. فورتسمولر، مخططات تكرارية فعالة لحسابات الطاقة الكلية من أولى المبادئ باستخدام مجموعة أساس الموجة المستوية، فيزي. ريف. ب 54، 11169 (1996).
[41] ج. ب. بيردو، ك. بورك، و م. إرنزرهوف، تقريب التدرج العام المبسط، فيزيكال ريفيو ليترز 77، 3865 (1996).
[42] أ. توغو، ف. أوبا، وإي. تانكا، حسابات من المبادئ الأولى للانتقال الفيروالاستيكي بين نوع الروتيل و -اكتب عند الضغوط العالية، مراجعة الفيزياء B 78، 134106 (2008).
[43] ن. مارزاري و د. فاندربيلت، دوال وانيير العامة المحلية بشكل أقصى لشرائط الطاقة المركبة، فيزي. ريف. ب 56، 12847 (1997).
[44] أ. أ. موستوفي، ج. ر. ييتس، ي.-س. لي، إ. سوزا، د. فاندربيلت، و ن. مارزاري، وانير90: أداة للحصول على دوال وانير المحلية بشكل أقصى، اتصالات فيزيائية حاسوبية 178، 685 (2008)، 0708.0650.
[45] I. سوزا، ن. مارزاري، و د. فاندربيلت، دوال وانيير المحلية بشكل أقصى للشرائط الطاقية المتشابكة، فيزي. ريف. ب 65، 035109 (2001).
[46] ك. س. بورش، د. ماندروس، وج. – ج. بارك، المغناطيسية في المواد ثنائية الأبعاد من نوع فان دير وولز، ناتشر 563، 47 (2018).
[47] م. كوكوتشوني و س. دي جيرونكولي، نهج الاستجابة الخطية لحساب التفاعل الفعال
معلمات في طريقة LDA+U، مراجعة الفيزياء B 71، 035105 (2005).

المواد التكميلية لـ “المغناطيسية الفيريمغناطيسية المعوضة بالكامل ثنائية الأبعاد”

يشن ليو ، سان-دونغ قوه ، يونغبان لي وتشنغ تشينغ ليو مركز الفيزياء الكمومية، المختبر الرئيسي للهندسة البصرية الكمومية المتقدمة والقياس (MOE)، كلية الفيزياء، معهد بكين للتكنولوجيا، بكين 100081، الصين و كلية الهندسة الإلكترونية، جامعة شيان للبريد والاتصالات، شيان 710121، الصين

تم تنظيم هذا المادة التكميلية في أربعة أقسام. في القسم الأول، نقدم تحليلًا أكثر تفصيلًا لنموذج الشبكة المربعة في النص الرئيسي. في القسم الثاني، نوضح أن الفيريمغناطيسات المعوضة بالكامل التي تفرضها التعبئة في بعدين (fFIM) تظهر عمومًا استجابات مغناطيسية بصرية ملحوظة وموصلية هول الشاذة (AHC) من خلال حساب هذه الخصائص في نموذج الربط الضيق العام. في القسم الثالث، نوضح كيفية تحويل الفيريمغناطيسات التقليدية إلى fFIM في نموذج سداسي. يوفر القسم الأخير حسابات DFT التفصيلية لـ ، و .

نموذج الربط الضيق لشبكة مربعة

في هذا القسم، نقدم تحليلًا أكثر تفصيلًا لنموذج الشبكة المربعة في النص الرئيسي. النموذج في النص الرئيسي هو
ه.س. ه.س. .
هنا هو الأقرب للقفز، و هي القفزات التالية الأقرب. هو الجهد المتقطع، و هو العزم المغناطيسي. هو أقرب متجه، و و هي متجهات الشبكة. ثم نقوم بتحويل هاميلتونيان إلى الفضاء المعكوس وندع لتبسيط المعادلة.
تتمتع الفرق بالشكل التالي
تشير الرموز ↑ و ↓ في النص العلوي إلى نطاقات الدوران لأعلى ولأسفل.
عندما تكون المعلمات مضبوطة على و ، يحافظ النظام على تناظر عكس الزمان والمكان. تحت هذه الحالة، تكون تعبيرات نطاقات الطاقة هي
حيث تكون نطاقات الطاقة متساوية في الدوران، وكثافة الحالات المتكاملة (IDOSs) أيضًا متساوية في الدوران، كما هو موضح في الشكل S1(a).
عندما تكون المعايير مضبوطة على و ، يتم كسر تناظر الزمن والزوجية، لكن تظل التناظرية، ويصبح النظام مغناطيسية بديلة. يتم تحديد نطاقات الطاقة بواسطة
الشكل S1. نموذج الربط الضيق، مع تغيير المعلمات التي تؤدي إلى المغناطيسية المضادة التقليدية (cAFM)، المغناطيسية البديلة (AM)، ونماذج المغناطيسية الفيريمغناطيسية المدفوعة بالكامل (fFIM). (أ) هيكل النطاق المتساوي للدوران لنموذج AFM (المعادلة S4) مع ، و . اللوحة اليمنى تظهر كثافة الحالة الداخلية المتجانسة للدوران لأعلى (باللون الأحمر) ولأسفل (باللون الأزرق). (ب) هيكل نطاق الانقسام الدوراني لنموذج AM (المعادلة S-5)، مع تعيين المعلمات كـ ، ، و . تظل قيم IDOS للدوران لأعلى ولأسفل متساوية. (ج) هيكل نطاق الانقسام الدوراني لنموذج fFIM (المعادلة S-6) مع تعيين المعلمات كـ ، و . يتم رفع تناظر IDOS للدوران لأعلى ولأسفل ولكنه يبقى متساويًا ضمن الفجوة. (د) هيكل النطاق نصف المعدني لنموذج fFIM، مع تعيين المعلمات كـ ، و قناة الدوران لأسفل بلا فجوة، بينما قناة الدوران لأعلى تحتوي على فجوة. إن كثافة حالات الدوران لأعلى ولأسفل متساوية عند طاقة فيرمي.
يمكن التحقق من أنه في صيغة نطاق الطاقة المعطاة بالمعادلة (S-5)، يمكننا ملاحظة . هذه المعادلة تنشأ من التناظر، الذي يحول و بالإضافة إلى الدوران من الدوران لأعلى إلى الدوران لأسفل. لذلك، فإن الشريحتين ذات الدوران المعاكس متصلتان من خلال التناظر. وبالتالي، تحافظ IDOSs على ازدواجية الدوران، كما هو موضح في الشكل S1 (ب).
علاوة على ذلك، عندما و تتحول نطاقات الطاقة إلى
ال تم كسر التناظر، لا يوجد تناظر يربط الشبكات الفرعية ذات الدوران المعاكس، ولا يوجد أي تناظر لضمان عدم وجود مغنطة إجمالية. ومع ذلك، إذا كان عدد حالات الدوران لأعلى المملوكة وحالات الشغل ذات الدوران لأسفل متساوية، يبقى إجمالي المغنطة صفرًا، مما يؤدي إلى fFIM. الهيكل الفرعي المقابل وIDOS موضحان في الشكل S1 (ج)، حيث تكون IDOSs للدوران لأعلى ولأسفل متساوية في الفجوة. إذا ظلت نطاقات الطاقة لقناة دوران واحدة مفصولة، فإن أو يبقى عدد صحيح ثابت. لذلك، حتى إذا أغلقت نطاقات قناة الدوران الأخرى، طالما أن العدد الإجمالي للحالات المشغولة يبقى دون تغيير، لا يزال ساريًا، حيث يحافظ على حالة fFIM. هذه الحالة، حيث يكون أحد قنوات الدوران معدنيًا والآخر عازلًا، تُعرف بنظام نصف معدني. هيكل النطاق وIDOS موضحان في الشكل S1 (د)، حيث تكون IDOS للدوران لأعلى ولأسفل متساوية عند طاقة فيرمي.

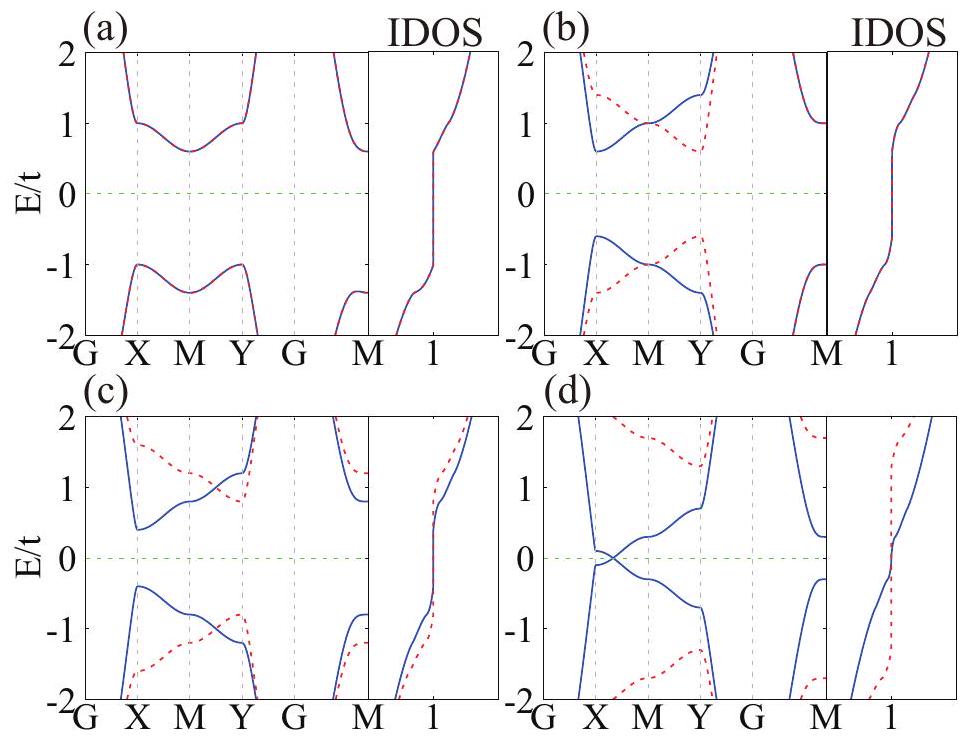
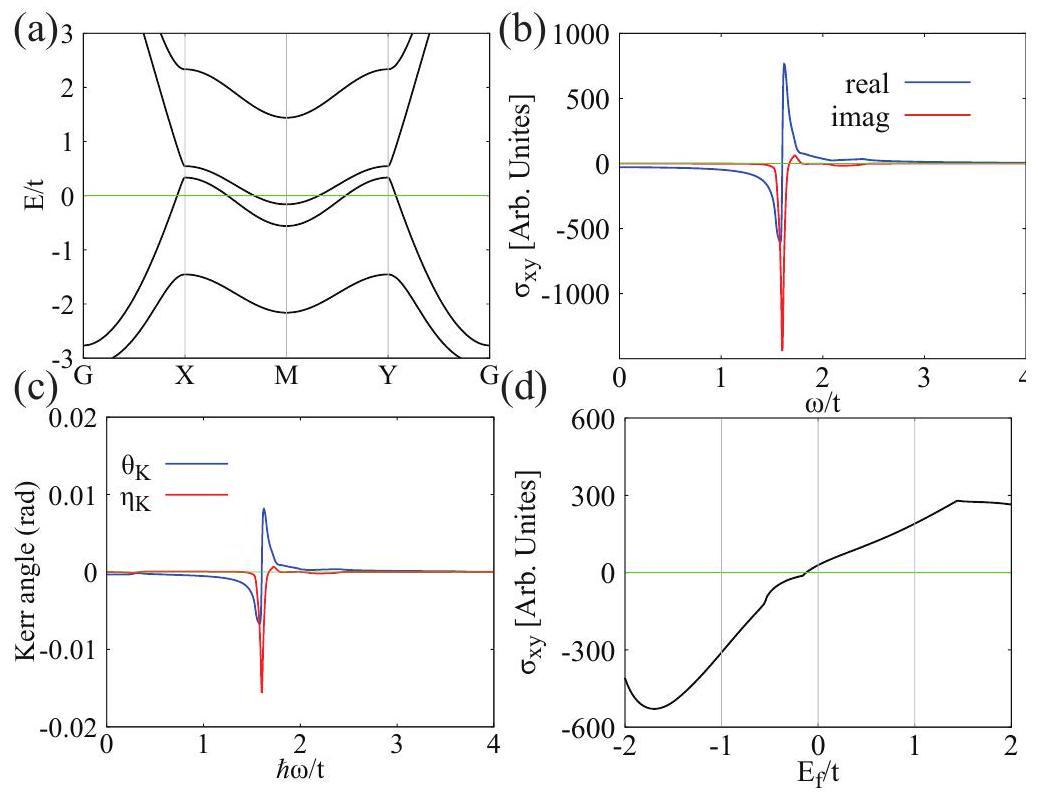
II. التأثير المغناطيسي البصري الملحوظ وتأثير هول الشاذ في نموذج FFIM العام

بعد ذلك، نستكشف المزيد من الخصائص الفيزيائية الجديدة لـ fFIMs بناءً على هذا النموذج. يتم إدخال تأثير Rashba SOC في النموذج، ويمكن كتابة هاميلتونيان على النحو التالي
الشكل S2. نطاقات الطاقة، زاوية كير، زاوية فاراداي، والتوصيلية الهول الشاذة للنموذج العام للفيريمغناطيسية المعوضة بالكامل. (أ) الهياكل النطاقية لهذا النموذج، مما يدل على الخصائص المعدنية. (ب) التوصيلية الهول البصرية كدالة لتردد الضوء، حيث تمثل الخطوط الحمراء (الزرقاء) الأجزاء الحقيقية (التخييلية) من . (ج) زاوية كير كدالة لتردد الضوء. و تمثل الزاوية والبيضاوية، على التوالي. (د) الموصلية الهولية الشاذة كدالة لطاقة فيرمي. الموصلية غير صفرية عند عدم وجود مغنطة صافية. المعلمات ثابتة كما هي ، و .
مع الهاميلتوني في الفضاء التبادلي هو
نركز على مرحلة معدنية مع ، و كما هو موضح في الشكل S2. هناك جيبان من الثقوب وجيب إلكتروني واحد في هيكل النطاق الخاص به في الشكل S2(a). هذا النموذج خالٍ من تناظر الانعكاس الزمني المكاني، ويظهر خصائص فيزيائية تشبه المغناطيسية مثل تأثير هول البصري، وتأثير كير المغناطيسي البصري، وتأثير هول الشاذ. صيغة حساب موصلية هول البصرية هي [1،2]
هنا و هي مشغلات السرعة، و يمثل الفرق في الطاقة بين النطاقات و ، حيث يمثل تردد الضوء و هو معامل التلطيخ، تم تعيينه إلى 0.05 إلكترون فولت في هذه الدراسة. الموصلية البصرية في قاعة نموذج المعادلة الهاميلتونية (S-7) موضح في الشكل S2(b). علاوة على ذلك، يمكننا استخدام نظام هول البصري ثنائي الأبعاد المقدم في [3،4].
أين و زاوية الدوران والانحراف البيضاوي، على التوالي. و هي المكونات القطرية وغير القطرية لموتر التوصيلية البصرية، التي تقيس استجابة المادة لمجال كهرومغناطيسي مطبق. هو مقاومة الفراغ (تقريبًا )، و هو السماحية الفراغية. هو سمك العينة ويتم تعيينه كـ 1 نانومتر للنموذج. معامل الانكسار للركيزة، المشار إليه بـ يُفترض أن تكون 1.5، وهو ما يتوافق مع معامل الانكسار لـ زاوية كير للنموذج موضحة في الشكل S2(c).
نظرًا لأن النظام معدني، يمكننا أيضًا حساب AHC، cuya fórmula es [5,6]
نحسب AHC كدالة لمستوى فيرمي كما هو موضح في الشكل S 2 (د). من الجدير بالذكر أنه عندما النموذج لديه مغنطة صافية صفرية، لكنه يمتلك AHC غير صفري.
الشكل S3. هيكل النطاق وكثافة الحالات المتكاملة (IDOS) للنموذج السداسي الموصوف بالمعادلة (S-12) مع تكوينات مختلفة للمعلمات. (أ) هيكل النطاق ذو التماثل الدوراني للنموذج في المعادلة (S-12). تُظهر اللوحة اليمنى IDOS للدوران لأعلى (أحمر) والدوران لأسفل (أزرق). (ب) هيكل النطاق مع انقسام الدوران للنموذج في المعادلة (S-6). تكون IDOS للدوران لأعلى والدوران لأسفل متساوية في الفجوة. (ج) هيكل النطاق للمعادلة (S-6) عندما النظام نصف معدني.

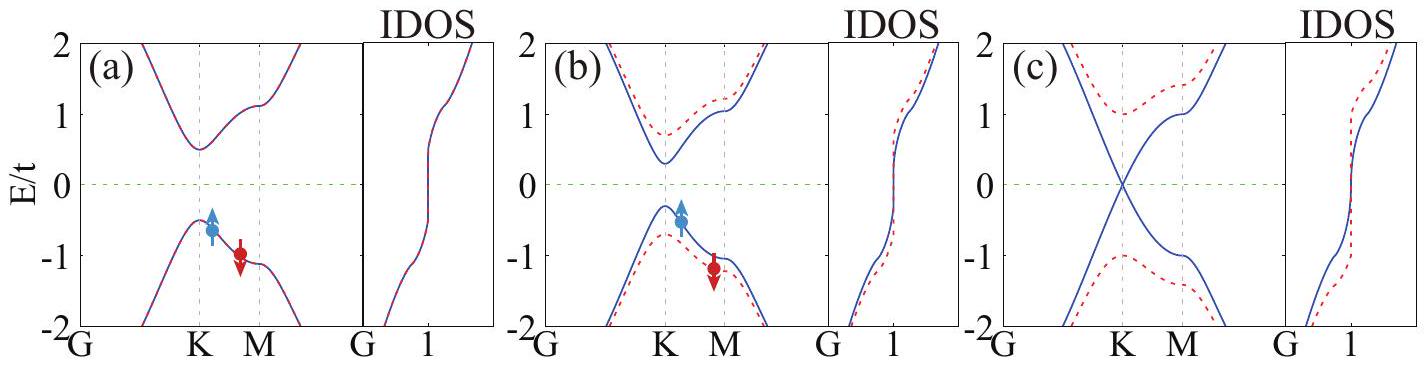
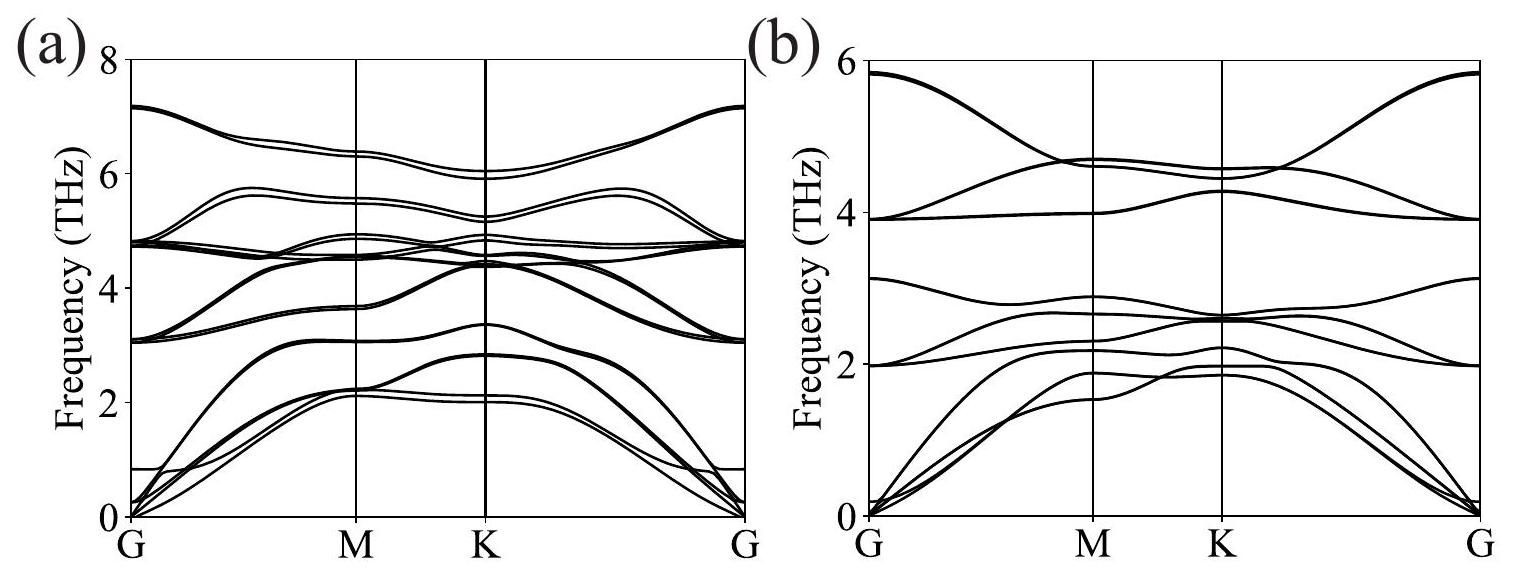
III. نموذج الربط الضيق لشبكة سداسية

بالنسبة للنموذج في شبكة سداسية، نبدأ بالنظر في نموذج سداسي مع مصطلح مضاد للمغناطيسية على الشبكة.
هنا، يمثل القفز بين الجيران الأقرب، هو مقدار العزم المغناطيسي في كل موقع، هو مشغل الدوران، و يمثل علامة معاكسة للدوران بين الشبكات الفرعية. تم تعيين الشبكتين كـ و في هذا النموذج، تمتلك الشبكتان الفرعيتان دورانًا متعاكسًا، ويمكن ربطهما من خلال تناظر الانعكاس. وبالتالي، يوجد في النظام تناظر عكسي للزمن. يتم إعطاء نطاقات الطاقة في هذا النموذج بواسطة
نطاقات الطاقة متساوية في الدوران، كما أن كثافات حالات السبين لأعلى ولأسفل متساوية أيضًا، كما هو موضح في الشكل S3(a). لكسر تماثل الانعكاس، نقدم جهدًا متناوبًا.
الآن، لم يعد بالإمكان ربط الشبكتين الفرعيتين بأي تناظر. وبالتالي، تصبح نطاقات الطاقة في النموذج
يتم عرض هيكل الفرقة في الشكل S3(b) مع انقسام الدوران. طالما أن ، تظل فجوة الطاقة مفتوحة، فإن IDOSs للدوران لأعلى ولأسفل تكون متساوية في الفجوة. لذلك، يبقى العزم المغناطيسي الصافي صفرًا، ويصبح النظام fFIM، كما هو موضح في الشكل S3(b). عندما ، قناة الدوران لأسفل بلا فجوة، ويصبح النظام نصف معدن fFIM، كما هو موضح في الشكل S3(c). ثم كما قناة الدوران لأسفل مرة أخرى محجوبة، ويعود النظام إلى fFIM.

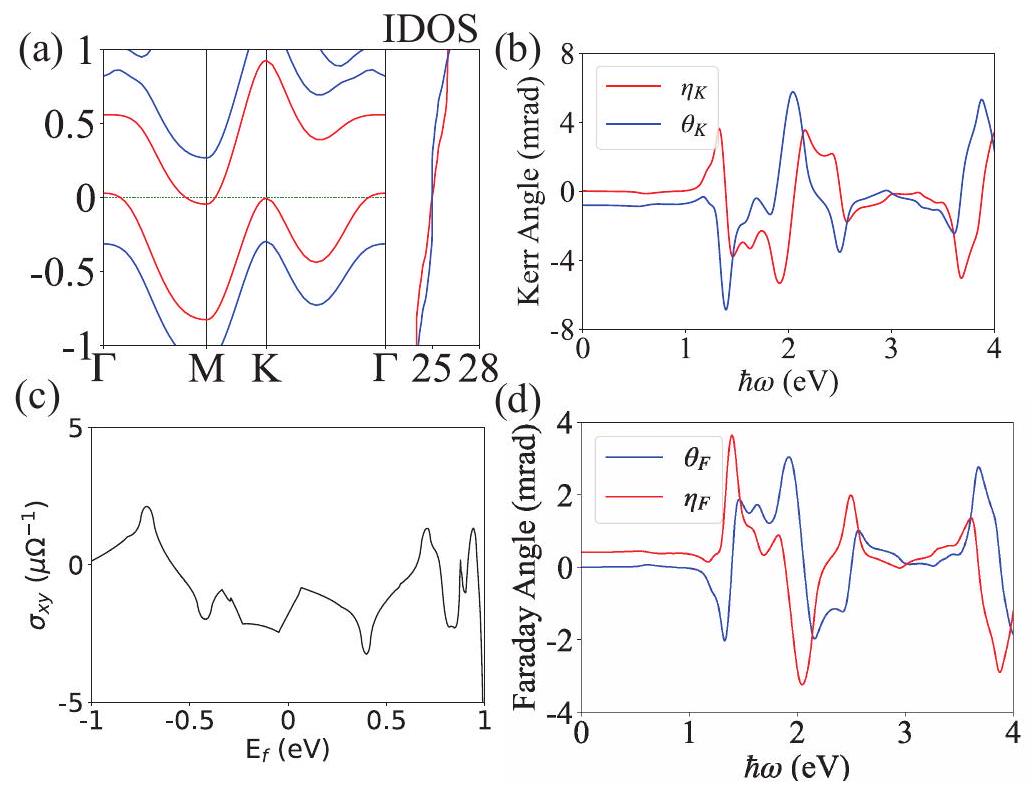
الرابع. حساب المواد

في هذا القسم، تفاصيل الحساب لـ ، و مقدمة.
الشكل S4. طيف الفونونات لثنائي الطبقة NiICl (أ) وثنائي الطبقة (ب).
تم استخدام حزمة محاكاة فيينا من الدرجة الأولى (VASP) [7] لحساب تحسين الهيكل وهياكل النطاق. تم اعتبار تقريب التدرج العام (GGA) مع تحقيق بيردو-بورك-إرنزرهوف (PBE) [8]. نستخدم معلمات EFIELD وIDIPOL وDIPOL وLDIPOL في VASP لأخذ الحقل الكهربائي في الاعتبار. تم إجراء حسابات الفونون باستخدام نظرية الاضطراب الوظيفي الكثافة كما هو مطبق في كود PHONOPY [9]. تم بناء نماذج الربط الضيق من الدرجة الأولى باستخدام كود WANNIER90 [10-12] لحساب الاستجابة المغناطيسية البصرية وموصلية هول الشاذة.
طبقة مزدوجة تم تخليقه [13، 14] وهو مادة مضادة للمغناطيسية بين الطبقات، ومعامل الشبكة هو Å، والمسافة بين الطبقات هي Åتم تعيين Hubbard U كـ لأوربيتال 3d لذرة الكروم، وتم تعيين المجال الكهربائي كـ Åعلى السلبية -محور. أ -تم استخدام الشبكة لهذه الحسابات.
NiICl ينتمي إلى شبكة سداسية مع مجموعة الفضاء P3m1 ويمتلك التناظر. بعد التحسين، ثابت الشبكة a هو Å، والمسافة بين الطبقات هي Å. شبكة k- يتم استخدامه في الحسابات. لأخذ في الاعتبار التفاعلات القوية بين الإلكترونات في مدارات Ni 3d، قمنا بتطبيق تصحيح هوبارد U مع في حساباتنا باستخدام نظرية الكثافة.
طبقة أحادية يتم الحصول عليه عن طريق استبدال ذرة الكروم بذرات الموليبدينوم في المادة الأحادية الطبقة المضادة للمغناطيسية تم تعيين مستوى هوبارد لعناصر الموليبدينوم والكروم إلى 4 إلكترون فولت. -شبكة تستخدم للاسترخاء الشبكي والحساب الذاتي المتسق.
طبقة ثنائية بتكديس AB هو مادة مضادة للمغناطيسية بين الطبقات، ومعامل الشبكة هو Å، والمسافة بين الطبقات هي Åتم تعيين Hubbard U كـ لمدار 3d لذرة اليوتبريوم، ويتم ضبط المجال الكهربائي على Åعلى السلبية -محور. أ -تم استخدام الشبكة لهذه الحسابات. هيكل النطاق، وزاوية كير، وزاوية فاراداي، وAHC موضحة في الشكل S5.
استقرار طبقة أحادية من NiICl [16]، طبقة أحادية [17] وطبقة أحادية [18] تم التحقق منها من خلال حسابات DFT على طيف الفونونات. استخدام سوبرسيل لثنائي الطبقة NiICl و سوبرسيل لطبقتين نحسب طيف الفونونات الخاص بهم، كما هو موضح في الشكل S4. لا تظهر هذه الأطياف أي ترددات تخيلية في منطقة بريلوين، مما يشير إلى الاستقرار الهيكلي لهذه المواد.
التكوينات الفيرومغناطيسية والفيرومغناطيسية المضادة للطبقة الأحادية ثنائي الطبقة NiICl ، وثنائي الطبقة كدالة للمعامل هوبارد U مدرجة في الجدول S1. ضمن نطاق معقول من معامل هوبارد U، فإن الحالات الأساسية لـ ثنائي الطبقة NiICl ، وثنائي الطبقة مضادة للمغناطيسية.
[1] C. Aversa و J. E. Sipe، الحساسية البصرية غير الخطية للموصلات نصفية: نتائج مع تحليل بواسطة مقياس الطول، فيزيكال ريفيو B 52، 14636 (1995).
[2] هـ. إيبيرت، التأثيرات المغناطيسية الضوئية في أنظمة المعادن الانتقالية، تقرير تقدم الفيزياء 59، 1665 (1996).
[3] م.-هـ. كيم، ج. أكباس، م.-هـ. يانغ، إ. أوكوبو، هـ. كريستين، د. ماندروس، م. أ. سكاربولا، أ. د. دوبون، ز. شليسينجر، ب. خليفة، وج. سيرني، تحديد موتر التوصيلية المغناطيسية المعقدة تحت الأشعة تحت الحمراء في الفيرومغناطيسيات المتنقلة من قياسات فاراداي وكير، فيزيكس ريفيو ب 75، 214416 (2007).
[4] ر. فالديز أغيلار، أ. ف. ستير، و. ليو، ل. س. بيلبرو، د. ك. جورج، ن. بانسال، ل. وو، ج. سيرني، أ. ج. ماركيلز، س. أوه، و
الشكل S5. هيكل النطاق، زاوية كير، زاوية فاراداي، والتوصيلية الهول الشاذة لفيريمغناطيس معوض بالكامل مفروض التعبئة ثنائي الأبعاد . (أ) هيكل النطاق وكثافة الحالة المتكاملة (IDOS). (ب) زاوية كير كدالة لتردد الضوء. و تمثل الزاوية والانحراف البيضاوي، على التوالي. (ج) الموصلية الهول الغير طبيعية كدالة لطاقة فيرمي . (د) زاوية فاراداي كدالة لتردد الضوء.
الجدول S1. الطاقة الكلية للنظام المغناطيسي الفيرومغناطيسي والمضاد للمغناطيسية طبقة أحادية، طبقة ثنائية NiICl، و طبقة ثنائية كدالة لـ Hubbard U. و هي الطاقة الكلية للنظام مع الترتيب المضاد للمغناطيس والترتيب المغناطيسي على التوالي. هو الفرق الكلي في الطاقة بين النظامين المغناطيسيين. عندما المادة هي مادة مضادة للمغناطيسية؛ وإلا فهي مادة مغناطيسية. في الجدول، يشير “-” إلى أن VASP غير قادر على التوصل إلى ترتيب مغناطيسي مطابق. تم تعيين قيمة هوبارد U للكروم والموليبدينوم كقيمة واحدة في .
نيكل
U (eV) 2 ٣ ٤ ٥
إ -17.713227 -16.865274 -16.077713 -15.348955
-17.714349 -16.864369 -16.073680 -15.341357
0.001122 -0.000905 -0.004033 -0.007598
U (eV) 1 2 ٣ ٤
إ -64.108138 -62.529771 -61.062467 -59.686118
– -61.917934 -60.410827 -58.999141
– -0.611837 -0.65164 -0.686977
U (eV) 0 1 2 ٣
-27.797280 -26.962275 -26.161623 -25.395336
-27.797266 -26.962107 -26.161330 -25.394878
-0.000014 -0.000168 -0.000293 -0.000458
N. P. أرمتيج، استجابة التيراهيرتز ودوران كير الضخم من حالات السطح للعازل الطوبولوجي فيزي. ريف. ليت. 108، 087403 (2012).
[5] ي. ياو، ل. كلاينمان، أ. هـ. ماكدونالد، ج. سينوفا، ت. يونغويرث، د.-س. وانغ، إ. وانغ، و ق. نيو، حسابات من المبادئ الأولى للتوصيل غير العادي في الحديد المغناطيسي البسيط bcc، فيزيكال ريفيو ليترز 92، 037204 (2004).
[6] إكس. وانغ، ج. ر. ييتس، آي. سوزا، ود. فاندربيلت، حساب من أول المبدأ للتوصيلية الغريبة باستخدام تقنيات وانير، فيزيكال ريفيو بي 74، 195118 (2006).
[7] ج. كريس وج. فورتسمولر، مخططات تكرارية فعالة لحسابات الطاقة الكلية من أولى المبادئ باستخدام مجموعة أساس الموجة المسطحة، فيزي. ريف. ب 54، 11169 (1996).
[8] ج. ب. بيرديو، ك. بورك، و م. إرنزرهوف، تقريب التدرج العام المبسط، فيزيكال ريفيو ليترز 77، 3865 (1996).
[9] أ. توغو، ف. أوبا، وإي. تانكا، حسابات من المبادئ الأولى للانتقال الفيروالاستيكي بين نوع الروتيل و –
اكتب عند الضغوط العالية، مراجعة الفيزياء B 78، 134106 (2008).
[10] ن. مارزاري و د. فاندربيلت، دوال وانيير العامة المحلية بشكل أقصى للشرائط الطاقية المركبة، فيزي. ريف. ب 56، 12847 (1997).
[11] أ. أ. موستوفي، ج. ر. ييتس، ي.-س. لي، إ. سوزا، د. فاندربيلت، و ن. مارزاري، وانير90: أداة للحصول على دوال وانير المحلية بشكل أقصى، اتصالات فيزيائية حاسوبية 178، 685 (2008)، 0708.0650.
[12] I. سوزا، ن. مارزاري، و د. فاندربيلت، دوال وانيير المحلية بشكل أقصى للشرائط الطاقية المتشابكة، فيزي. ريف. ب 65، 035109 (2001).
[13] ك. س. بورش، د. ماندروس، وج. – ج. بارك، المغناطيسية في المواد ثنائية الأبعاد من فان دير وولز، ناتشر 563، 47 (2018).
[14] ب. هوانغ، ج. كلارك، إ. نافارو-موراتالا، د. ر. كلاين، ر. تشينغ، ك. ل. سييلر، د. تشونغ، إ. شميتغال، م. أ. مكغواير، د. هـ. كوبدن، و. ياو، د. شياو، ب. جاريلو-هيريرو، و إكس. شو، المغناطيسية الحديدية المعتمدة على الطبقات في بلورة فان دير وولس حتى حد الطبقة الواحدة، ناتشر 546، 270 (2017).
[15] م. كوكوتشوني و س. دي جيرونكولي، نهج الاستجابة الخطية لحساب معلمات التفاعل الفعالة في طريقة LDA+U، مراجعة الفيزياء B 71، 035105 (2005).
[16] ت. غوركان، ج. داس، ج. كابيجان، م. أكرم، ج. ف. بارث، س. تونغاي، إ. أكتورك، أ. إرتين، و أ. س. بوتانا، تشكيل سكريمون في طبقات ثنائية الهاليد جانوس القائمة على النيكل: التفاعل بين الإحباط المغناطيسي وتفاعل دزيالوشينسكي-موريا، فيزيكس ريفيو ماتيير 7، 054006 (2023).
[17] ب. وانغ، د. وو، ك. تشانغ، و إكس. وو، كبريتيد المعادن الانتقالية الرباعية الأبعاد ثنائي الأبعاد (A = C، Si، أو Ge): شبه موصل ثنائي القطب مضاد مغناطيسي مع درجة حرارة نيل عالية، J. Phys. Chem. Lett. 13، 3850 (2022).
[18] ب. هوانغ، و.-ي. ليو، إكس.-سي. وو، س.-ز. لي، هـ. لي، ز. يانغ، و و.-ب. تشانغ، استقطاب وادي عفوي كبير ودرجة حرارة انتقال مغناطيسي عالية في ferrovalley ثنائي الأبعاد المستقر ، و Cl فيزي. ريف. ب 107، 045423 (2023).
    • ساهم هؤلاء المؤلفون بالتساوي في هذا العمل.
      ccliu@bit.edu.cn

Journal: Physical Review Letters, Volume: 134, Issue: 11
DOI: https://doi.org/10.1103/physrevlett.134.116703
PMID: https://pubmed.ncbi.nlm.nih.gov/40192380
Publication Date: 2025-03-18

Two-dimensional fully-compensated Ferrimagnetism

Yichen Liu, San-Dong Guo, Yongpan Li, and Cheng-Cheng Liu Centre for Quantum Physics, Key Laboratory of Advanced Optoelectronic Quantum Architecture and Measurement (MOE), School of Physics, Beijing Institute of Technology, Beijing 100081, China School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China

Abstract

Antiferromagnetic spintronics has long been a subject of intense research interest, and the recent introduction of altermagnetism has further ignited enthusiasm in the field. However, fullycompensated ferrimagnetism, which exhibits band spin splitting but zero net magnetization, has yet to receive enough attention. Since the experimental preparation of two-dimensional (2D) magnetic van der Waals (vdW) materials in 2017, 2D magnetic materials, thanks to their super tunability, have quickly become an important playground for spintronics. Here, we extend the concept of fully-compensated ferrimagnetism (fFIM) to two dimensions and propose 2D filling-enforced fFIM, demonstrate its stability and ease of manipulation, and present three feasible realization schemes with respective exemplary candidate materials. A simple model for 2D fully-compensated ferrimagnets (fFIMs) is developed. Further investigation of 2D fFIMs’ physical properties reveals that they not only exhibit significant magneto-optical response but also show fully spin-polarized currents and the anomalous Hall effect in the half-metallic states, displaying characteristics previously almost exclusive to ferromagnetic materials, greatly broadening the research and application prospects of spintronic materials.

Introduction.- Traditionally, collinear magnetism can be classified into ferromagnetism, antiferromagnetism, and ferrimagnetism. In ferromagnets, all magnetic moments are aligned in the same direction with non-zero magnetization, and the bands are spin-splitting. In conventional antiferromagnets (cAFMs), the magnetic moments are arranged antiparallel with zero net magnetization, and the bands are spin-degenerate. However, the spin-degenerate nature of the energy bands in cAFMs eliminates the anomalous Hall effect (AHE) and magneto-optical effect, thereby restricting their potential applications [1]. Ferrimagnetism has antiparallel magnetic moments that usually cannot completely cancel each other out. Recently, a new type of magnetic material, the so-called altermagnets, with zero net magnetization and anisotropic spin-splitting bands, was proposed[2, 3]. Compared to ferromagnetic materials, magnetic materials with null magnetization, such as cAFMs and altermagnets, offer several advantages, including ultrafast dynamics, the absence of stray fields, and enhanced stability in the presence of magnetic fields [1]. However, this classification overlooks a significant class of zero net magnetization, the fullycompensated ferrimagnetism [3-6], which is firstly issued by de Groot et al. [4]. Unlike cFAMs and altermagnets, fully-compensated ferrimagnets (fFIMs) achieve zero net magnetization through appropriate filling instead of symmetry.
Previous studies on fFIMs have been limited to three-dimensional (3D) systems with sophisticated crystal structures, such as the double perovskite oxides, Heusler system, and organic compound [7-17]. Moreover, clear experimental evidence for fFIMs remains elusive. Since the experimental fabrication of [18] and [19] in 2017, 2D magnetic van der Waals
(mvdW) materials with excellent adjustability have immediately attracted tremendous interest. So far, a richer variety of 2D mvdW material systems have been synthesized[20-22], including , and , etc. Considering the abundance and excellent tunability of 2D magnetic materials and the fact that fFIMs have the advantage of combining the band spin splitting of ferromagnetism with a zero net magnetization in cAFMs but lack of clear experimental confirmation, extending fully-compensated ferrimagnetism to two dimensions is highly necessary and very attractive.
In the Letter, we conceptualize the 2D fillingenforced fully-compensated ferrimagnetism (fFIM). A simple tight-binding model is developed, and by symmetry arguments, the transition between 2D filling-enforced fFIMs, cAFMs, and altermagnets is shown. Based on theoretical analysis, we propose three feasible approaches to constructing fFIMs using 2D mvdW materials: Constructing Janus structure, adding staggered potential, and using element substitution or alloying, each with exemplary candidate materials. Despite having null net magnetization, we find that fFIMs can exhibit remarkable magneto-optical effects, such as observable Kerr and Faraday angles, AHE, and fully spin-polarized currents. Taking classic 2D mvdW materials and half-metallic [23] as examples, we show that 2D fFIMs not only readily implement experimentally but also display significant Kerr and Faraday angles and anomalous Hall conductivity (AHC).
Filling-enforced fully-compensated ferrimagnetism.In the two kinds of fully-compensated collinear magnetism, i.e., conventional antiferromagnetism (cAFM) and altermagnetism, the magnetic sublattices are connected by symmetry, such as through the spatial inversion symmetry ( ) in cAFM and through rota-
FIG. 1. Three categories of fully-compensated collinear magnetism with null net magnetization ( ). (a1) Conventional antiferromagnetism (cAFM) is characterized by magnetic sublattices that are interconnected by and , featuring Kramers degeneracy, as shown in (a2). Here , , and are the two-fold rotation perpendicular to the spin axis, inversion, and translation, respectively. (b1) Two magnetic sublattices in altermagnetism (AM) are connected by , where represents a rotation or mirror symmetry. This results in anisotropic spin splitting, as depicted in (b2). (c1) Fully-compensated ferrimagnetism (fFIM), in which the two magnetic sublattices have no symmetry connection, exhibits isotropic spin splitting (c2). The zero net magnetization in cAFM and AM is symmetry-enforced, while in fFIM is filling-enforced. In (a2)-(c2), the gray surfaces represent spin-degenerate bands, the red and blue surfaces correspond to spin-up and spin-down bands, respectively, and the green plane indicates the Fermi level.
tional or mirror symmetry ( ) in altermagnetism. We thus call cAFM and altermagnetism symmetry-enforced fully-compensated collinear magnetism, as illustrated in Figs. 1(a) and (b). In contrast, the magnetic sublattices in 2D filling-enforced fFIMs cannot be connected through any symmetry, resulting in ferromagnetic-like spin splitting, as shown in Fig. 1(c). The net magnetization in usual ferrimagnetism is given by
with the Bohr magneton, where and represent the number of occupied states in the spin-up and spin-down channels, respectively. As long as any one of the spin channels is gapped, regardless of whether the other spin channel has a gap or not, which corresponds to insulating ferrimagnetic states and half-metallic ferrimagnetic states, the net magnetization must be an integer Bohr magneton. This is because the total number of electrons is an integer, and the number of electrons in the gapped channel is also an integer, so the number of electrons in the other spin channel is an integer, too. In this case, the two integers and are two good quantum numbers that can be used to label
different ferrimagnets. When the system has an appropriate filling, i.e., , the net magnetization is strictly zero, corresponding to the fully-compensated ferrimagnetism (fFIM), which we call filling-enforced fFIM. As long as the gap is not closed, the three integers , , and will not change, and integers do not change continuously, so , that is, the fully-compensated characteristic is strictly maintained under reasonable perturbations. The reasonable perturbations here mean that they will not close the gap. Such filling-enforced fFIM is protected by the gap-guaranteed spin quantization in one spin channel, which is similar to how stable topological quantum states are protected by a bulk energy gap [24, 25]. Since the filling-enforced fFIM is not limited by symmetry constraints, it remains highly robust under external fields, such as electric fields and stress, regardless of whether these fields break the symmetry.
We develop a simple 2D model to capture cAFMs, altermagnets, and filling-enforced fFIMs and the transformation between them. The model is as follows
where represents the nearest-neighbor hopping, 1,2 denotes the sublattices located at and , respectively, and are the next-nearest-neighbor hopping, is the staggered potential, is the spin operator, and is the magnetization. and are the nearest vector and direction lattice vectors. The lattice structure is illustrated in Fig. 2(a). We use , , and to regulate the symmetry of the system, corresponding to the following three cases of respective cAFMs, altermagnets, and filling-enforced fFIMs.
When and , the sublattices with opposite spin can be connected through inversion . The inversion center is located at ( ), swapping with . Since the two sublattices have opposite spin, the system possesses symmetry with a twofold rotation perpendicular to the spin axis, resulting in Kramers degeneracy as illustrated in Fig. 2(b).
When and , the symmetry is broken. However, the sublattices with opposite magnetization can be connected through a rotation with the center at ( 0,0 ), resulting in and . Thus, the system possesses symmetry, inducing the hallmark anisotropic -wave spin splitting in altermagnets, as depicted in Fig. 2(c).
Interestingly, introducing the staggered potential ( on sublattices breaks any connection between them by symmetry. Applying different onsite energies to the two
FIG. 2. A simple model for the three categories of fullycompensated collinear magnetism, i.e., conventional antiferromagnetism (cAFM), altermagnetism (AM), and fillingenforced fully-compensated ferrimagnetism (fFIM). (a) The illustration of our model. (b) When and , the system is cAFM with symmetry. (c) When and , the opposite spin sublattices are connected by , transforming the system into AM with anistropic spin splitting. (d) (e) Setting and with lift any symmetry that connects two sublattices, the system can be fFIM. Since the gap in one spin channel has never closed, the IDOSs of opposite spins are integer and remain equal at Fermi energy with , resulting in a zero net magnetization. The halfmetallic fFIM is shown in (e). is taken for (b)-(e).
sublattices can make them be considered composed of entirely different magnetic atoms or the same magnetic atoms under different environments. Consequently, no symmetry can connect the two sublattices, resulting in the spin splitting in bands, as shown in Figs. 2(d) and (e). Although the integrated densities of states (IDOSs) for two spin channels do not coincide across all energies, they are the same within the band gap of one spin channel with , thereby keeping the total magnetization zero exactly. Notice that the filling-enforced fFIM in Fig. 2(e) is a half metal, conducting only in one spin channel. Although the above discussion is based on the tetragonal lattice, our conclusions are general. We also build a model for the hexagonal lattice (see Supplementary Material (SM) [27] for details).
Realizaiton schemes and materials. – To be an fFIM, a material must satisfy two conditions: (1) the number of occupied states with opposite spins must be equal, and (2) there should be no symmetry operations that connect the opposite spin sublattices. In this work, we propose three methods to construct fFIMs: (1) Janus structure, (2) staggered potential by external electric field or substrate, and (3) elemental substitution or alloying.
FIG. 3. Realization schemes and representative materials of 2D fully-compensated ferromagnetic materials. (a) The bilayer of NiICl with Janus structure and its band structure, as well as IDOS. (b) The geometry and band structure of bilayer structure with a staggered potential of 0.5 eV . The staggered potential of the upper and lower layers is shown as the green and blue background. (c) The geometry and band structure of 2D , where the Mo atom replaces the Cr atom. (d) The geometry and band structure of under Å electric field. The system is half metal, and IDOS remains equal at Fermi energy with , leading to a zero net magnetization. The geometry is plotted using VESTA software [26]
(1) Janus structure: The Janus structure breaks the symmetry connecting the two magnetic sublattices by altering the environment surrounding the magnetic atoms and induces a built-in vertical electric field. Such Janus structure is well known in the context of transition metal dichalcogenides [28]. Here, we take the Janus structure NiICl as an example [29,30]. It is derived by replacing the top layer I atoms in as-prepared [31] by Cl atoms with the inversion symmetry broken. The geometry and band structure of the bilayer NiICl are shown in Fig. 3(a). Although the Janus structure in the bilayer NiICl breaks the symmetry that typically restricts the system to zero net magnetization, as discussed above, as long as one of the spin channels is gapped, the total magnetic moment of the system remains zero, resulting in a fFIM.
(2) Staggered potential: By applying a staggered potential, introduced by an electric field or substrate, etc., to two magnetic sublattices, the symmetry connecting the two sublattices is broken, leading to spin splitting, and the system becomes a fFIM. From the above theoretical analysis, it can be seen that while a small staggered potential can induce gapped fFIMs, a large one can induce half-metallic fFIMs, as shown in Figs. 2(d) and (e). For example, in experimentally-prepared A-type antiferromagnetic bilayer [18], when a perpendicular electric field of Å is applied, spin splitting occurs, and the spin-up and spin-down IDOSs remain equal in the gap, as shown in Fig. 3(b). In contrast, under a perpendicular electric field of Å is a half metal and exhibits gapless spin-up bands and gapped spin-down bands. As described above, although the spin-
FIG. 4. Magneto-optical effect and anomalous Hall effect in 2D fully-compensated ferrimagnets. (a) and (b) show the Kerr angle and Faraday angle of fFIM bilayer with a 0.08 Å electric field. and represent the angle and ellipticity, respectively. (c) (d) The Kerr angle/AHC as a function of frequency/Fermi energy in half-metallic with a 0.6 Å electric field.
up channel is gapless, as long as the spin-down channel is gapped, the system maintains , and the spinup integrated density of states (IDOS) is equal to the spin-down IDOS at the Fermi energy, as shown in Fig. 3(d), demonstrating that the system remains fully compensated.
(3) Elemental substitution or alloying: By substituting or alloying with an element that either has the same number of valence electrons or differs by an even number compared with the original magnetic atom, ensuring these electrons are evenly distributed across both spin channels, the system maintains , resulting in zero net magnetization. This method was first introduced in 3D systems [4] and successfully implemented in Heusler alloys [15, 32]. As an example, we replace the magnetic Cr atoms in the 2D cAFM material with Mo atoms from the same group in the periodic table, resulting in the material [33]. Despite maintaining zero net magnetization, the system exhibits ferromagnetic-like spin splitting, as illustrated in Fig. 3(c).
More details on the phonon spectra and magnetic ground states of bilayer NiICl , bilayer , and monolayer are given in SM [27].
Physical properties. – fFIMs have zero net magnetization, making their magnetic properties similar to those of cAFMs and thus indistinguishable from cAFMs through external magnetic field measurements. However, our indepth research reveals that fFIMs possess physical properties fundamentally different from cAFMs but more like ferromagnetic systems, such as the remarkable AHE, magneto-optical Kerr and Faraday effects, and fully spinpolarized currents, which are traditionally believed to oc-
cur only in ferromagnetic systems. To confirm these novel physical properties, we demonstrate our results in terms of both the effective model and representative materials. The above gapped fFIM and half-metallic fFIM are taken as examples. The magneto-optical effect and AHE are also calculated by our fFIM tight-binding model in SM [27].
The magneto-optical Kerr and Faraday angles in 2D systems [34, 35] are given by
where and represent the rotation angle and ellipticity, respectively. and are the diagonal and offdiagonal components of the optical conductivity tensor, quantifying the material’s response to an applied electromagnetic field. is the impedance of free space (approximately ), is the thickness of the simple, and is the vacuum permittivity. The refractive index of the substrate, denoted as , is assumed to be 1.5 , which corresponds to the refractive index of . The optical conductivity tensor can be calculated by Kubo-Greenwood formula[36, 37]
Here represents the energy difference between bands and is the velocity operator, defined as , where represents the frequency of the light and is the smearing parameter, set to 0.05 eV in this study.
While the pristine bilayer is cAFM , exhibiting no Kerr or Faraday effects, when a staggered potential is applied, the system is transited to an fFIM, with the resulting Kerr and Faraday angles shown in Figs. 4(a) and (b), respectively. The maximum Kerr angle is close to 1 mrad , which is of the same order as that of monolayer [18] and far exceeds the measurement limit of current equipment, demonstrating a significant magnetooptical effect.
With a large staggered potential, exhibits halfmetallic behavior, with only the spin-up channel being conductive, resulting in a significantly fully spinpolarized current. Furthermore, due to the lack of both space-time inversion symmetry and time-reversal symmetry, the system can display a nonzero AHC despite having zero net magnetization. The AHC is calculated using the formula [38, 39]
The Kerr angle and AHC results for fFIM YI are shown in Figs. 4(c) and (d), and the Faraday angle is shown in SM [27]. Despite zero net magnetization at the Fermi energy, fFIM exhibits nonzero Kerr angle and AHC . The typical material results above and the general effective model calculations in SM demonstrate that 2D filling-enforced fFIMs generally display a significant magneto-optical effect, and the half-metallic ones also show remarkable AHE and fully spin-polarized current.
Conclusion. – In summary, we propose a new type of 2D collinear magnets, distinct from cAFM and altermagnetism, termed 2D filling-enforced fFIM, which achieves zero net magnetization through appropriate filling instead of symmetry. Thanks to being free of symmetry constraints, we put forward three universal schemes to realize 2D fFIMs: Janus structures, staggered potential, and elemental substitution or alloying. We demonstrate the effectiveness of these methods using NiICl with Janus structure, bilayer and under an electric field, and as examples, confirming their zero net magnetization and ferromagnetic-like band spin splitting through DFT calculations. We reveal that fFIMs display some physical properties that are similar to ferromagnets rather than cAFMs, such as magneto-optical effect, AHE, and fully spin-polarized currents. In contrast to altermagnets, the bands of filling-enforced fFIMs have no spin degeneracy at the point. Filling-enforced fFIMs are experimentally distinguishable from cAFMs, altermagnets, and ferromagnets through magneto-optical effect, spin-resolved ARPES, and direct magnetization measurements.
By utilizing the schemes presented in this work to achieve 2D filling-enforced fFIMs, high-throughput screening can be employed to identify numerous candidate materials. These 2D fFIMs not only exhibit the physical properties of ferromagnetic materials but also possess the advantages of antiferromagnetic materials, along with the inherent tunability of 2D materials. Their remarkable physical properties, such as magneto-optical effect and AHE, as well as fully spin-polarized currents, will undoubtedly attract broad interest and are readily verified experimentally. The absence of stray magnetic fields in the 2D fFIMs allows for a significant increase in storage density, complemented by other benefits such as high response frequencies. All these merits indicate that our proposed 2D fFIMs will inject new and strong vitality into the development of spintronics.
Acknowledgments.-The work is supported by the National Key R&D Program of China (Grant No. 2020YFA0308800), the NSF of China (Grant No. 12374055), and the Science Fund for Creative Research Groups of NSFC (Grant No. 12321004).
  • These authors contributed equally to this work.
    ccliu@bit.edu.cn
    [1] V. Baltz, A. Manchon, M. Tsoi, T. Moriyama, T. Ono, and Y. Tserkovnyak, Antiferromagnetic spintronics, Rev. Mod. Phys. 90, 015005 (2018).
    [2] L. Šmejkal, J. Sinova, and T. Jungwirth, Emerging research landscape of altermagnetism, Phys. Rev. X 12, 040501 (2022).
    [3] I. Mazin and The PRX Editors, Editorial: Altermagnetism-a new punch line of fundamental magnetism, Phys. Rev. X 12, 040002 (2022).
    [4] H. van Leuken and R. A. de Groot, Half-metallic antiferromagnets, Phys. Rev. Lett. 74, 1171 (1995).
    [5] H. Akai and M. Ogura, Half-metallic diluted antiferromagnetic semiconductors, Phys. Rev. Lett. 97, 026401 (2006).
    [6] S. Wurmehl, H. C. Kandpal, G. H. Fecher, and C. Felser, Valence electron rules for prediction of half-metallic compensated-ferrimagnetic behaviour of heusler compounds with complete spin polarization, J. Phys.: Condens. Matter 18, 6171 (2006).
    [7] W. E. Pickett, Spin-density-functional-based search for half-metallic antiferromagnets, Phys. Rev. B 57, 10613 (1998).
    [8] Y.-m. Nie and X. Hu, Possible half metallic antiferromagnet in a hole-doped perovskite cuprate predicted by first-principles calculations, Phys. Rev. Lett. 100, 117203 (2008).
    [9] K. E. Siewierska, G. Atcheson, A. Jha, K. Esien, R. Smith, S. Lenne, N. Teichert, J. O’Brien, J. M. D. Coey, P. Stamenov, and K. Rode, Magnetic order and magnetotransport in half-metallic ferrimagnetic mn y ru x ga thin films, Phys. Rev. B 104, 064414 (2021).
    [10] M. E. Jamer, Y. J. Wang, G. M. Stephen, I. J. McDonald, A. J. Grutter, G. E. Sterbinsky, D. A. Arena, J. A. Borchers, B. J. Kirby, L. H. Lewis, B. Barbiellini, A. Bansil, and D. Heiman, Compensated ferrimagnetism in the zero-moment heusler alloy , Phys. Rev. Appl. 7, 064036 (2017).
    [11] M. Žic, K. Rode, N. Thiyagarajah, Y.-C. Lau, D. Betto, J. M. D. Coey, S. Sanvito, K. J. O’Shea, C. A. Ferguson, D. A. MacLaren, and T. Archer, Designing a fully compensated half-metallic ferrimagnet, Phys. Rev. B 93, 140202 (2016).
    [12] J. Coey and M. Venkatesan, Half-metallic ferromagnetism:: Example of (invited), J APPL PHYS 91, 8345 (2002).
    [13] X. Hu, Half-metallic antiferromagnet as a prospective material for spintronics, Adv Mater 24, 294 (2012).
    [14] K. Özdoğan, E. Şaşıoğlu, and I. Galanakis, Ab-initio investigation of electronic and magnetic properties of the 18 -valence-electron fully-compensated ferrimagnetic (crv)xz heusler compounds: A prototype for spin-filter materials, Comput. Mater. Sci 110, 77 (2015).
    [15] R. Stinshoff, A. K. Nayak, G. H. Fecher, B. Balke, S. Ouardi, Y. Skourski, T. Nakamura, and C. Felser, Completely compensated ferrimagnetism and sublattice spin crossing in the half-metallic heusler compound , Physical Review B 95, 060410 (2017).
    [16] K. Fleischer, N. Thiyagarajah, Y.-C. Lau, D. Betto, K. Borisov, C. C. Smith, I. V. Shvets, J. M. D. Coey, and
    K. Rode, Magneto-optic kerr effect in a spin-polarized zero-moment ferrimagnet, Phys. Rev. B 98, 134445 (2018).
    [17] T. Kawamura, K. Yoshimi, K. Hashimoto, A. Kobayashi, and T. Misawa, Compensated ferrimagnets with colossal spin splitting in organic compounds, Phys. Rev. Lett. 132, 156502 (2024).
    [18] B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. JarilloHerrero, and X. Xu, Layer-dependent ferromagnetism in a van Der Waals crystal down to the monolayer limit, Nature 546, 270 (2017).
    [19] C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia, and X. Zhang, Discovery of intrinsic ferromagnetism in two-dimensional van Der Waals crystals, Nature 546, 265 (2017).
    [20] Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu, J. Zhu, J. Wang, X. H. Chen, and Y. Zhang, Gate-tunable room-temperature ferromagnetism in two-dimensional , Nature 563, 94 (2018).
    [21] M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M.-H. Phan, and M. Batzill, Strong room-temperature ferromagnetism in monolayers on van Der Waals Substrates, Nat. Nanotechnol 13, 289 (2018).
    [22] J. Klein, T. Pham, J. D. Thomsen, J. B. Curtis, T. Denneulin, M. Lorke, M. Florian, A. Steinhoff, R. A. Wiscons, J. Luxa, Z. Sofer, F. Jahnke, P. Narang, and F. M. Ross, Control of structure and spin texture in the van Der Waals layered magnet CrSBr, Nat Commun 13, 5420 (2022).
    [23] B. Huang, W.-Y. Liu, X.-C. Wu, S.-Z. Li, H. Li, Z. Yang, and W.-B. Zhang, Large spontaneous valley polarization and high magnetic transition temperature in stable twodimensional ferrovalley , and Cl , Phys. Rev. B 107, 045423 (2023).
    [24] F. D. M. Haldane, Model for a quantum hall effect without landau levels: Condensed-matter realization of the “parity anomaly”, Phys. Rev. Lett. 61, 2015 (1988).
    [25] C. L. Kane and E. J. Mele, topological order and the quantum spin hall effect, Phys. Rev. Lett. 95, 146802 (2005).
    [26] K. Momma and F. Izumi, Vesta 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr 44, 1272 (2011).
    [27] See Supplemental Material for more detailed information on (I) Square lattice fFIM tight-binding model, (II) The remarkable magneto-optical effect and anomalous Hall effect in general fFIM model, (III) Hexagonal lattice tight-binding model, and (IV) Materials calculation details, which includes Refs.[18, 23, 30, 33-47].
    [28] A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M.-Y. Chou, X. Zhang, and L.-J. Li, Janus monolayers of transition metal dichalcogenides, Nat. Nanotechnol 12, 744 (2017).
    [29] S.-D. Guo, Y.-T. Zhu, K. Qin, and Y.-S. Ang, Large out-of-plane piezoelectric response in ferromagnetic monolayer nicli, Applied Physics Letters 120, 232403 (2022).
    [30] T. Gorkan, J. Das, J. Kapeghian, M. Akram, J. V.
Barth, S. Tongay, E. Akturk, O. Erten, and A. S. Botana, Skyrmion formation in ni-based janus dihalide monolayers: Interplay between magnetic frustration and dzyaloshinskii-moriya interaction, Phys. Rev. Mater 7, 054006 (2023).
[31] Q. Song, C. A. Occhialini, E. Ergeçen, B. Ilyas, D. Amoroso, P. Barone, J. Kapeghian, K. Watanabe, T. Taniguchi, A. S. Botana, S. Picozzi, N. Gedik, and R. Comin, Evidence for a single-layer van Der Waals multiferroic, Nature 602, 601 (2022).
[32] S. Semboshi, R. Y. Umetsu, Y. Kawahito, and H. Akai, A new type of half-metallic fully compensated ferrimagnet, Sci Rep 12, 10687 (2022).
[33] P. Wang, D. Wu, K. Zhang, and X. Wu, Two-dimensional quaternary transition metal sulfide , Si , or Ge ): A bipolar antiferromagnetic semiconductor with a high Néel temperature, J. Phys. Chem. Lett. 13, 3850 (2022).
[34] M.-H. Kim, G. Acbas, M.-H. Yang, I. Ohkubo, H. Christen, D. Mandrus, M. A. Scarpulla, O. D. Dubon, Z. Schlesinger, P. Khalifah, and J. Cerne, Determination of the infrared complex magnetoconductivity tensor in itinerant ferromagnets from faraday and kerr measurements, Phys. Rev. B 75, 214416 (2007).
[35] R. Valdés Aguilar, A. V. Stier, W. Liu, L. S. Bilbro, D. K. George, N. Bansal, L. Wu, J. Cerne, A. G. Markelz, S. Oh, and N. P. Armitage, Terahertz response and colossal kerr rotation from the surface states of the topological insulator , Phys. Rev. Lett. 108, 087403 (2012).
[36] H. Ebert, Magneto-optical effects in transition metal systems, Rep. Prog. Phys. 59, 1665 (1996).
[37] C. Aversa and J. E. Sipe, Nonlinear optical susceptibilities of semiconductors: Results with a length-gauge analysis, Phys. Rev. B 52, 14636 (1995).
[38] Y. Yao, L. Kleinman, A. H. MacDonald, J. Sinova, T. Jungwirth, D.-s. Wang, E. Wang, and Q. Niu, First principles calculation of anomalous hall conductivity in ferromagnetic bcc Fe, Phys. Rev. Lett. 92, 037204 (2004).
[39] X. Wang, J. R. Yates, I. Souza, and D. Vanderbilt, Ab initio calculation of the anomalous hall conductivity by wannier interpolation, Phys. Rev. B 74, 195118 (2006).
[40] G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B 54, 11169 (1996).
[41] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett. 77, 3865 (1996).
[42] A. Togo, F. Oba, and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and -Type at high pressures, Physical Review B 78, 134106 (2008).
[43] N. Marzari and D. Vanderbilt, Maximally localized generalized wannier functions for composite energy bands, Phys. Rev. B 56, 12847 (1997).
[44] A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt, and N. Marzari, Wannier90: A tool for obtaining maximally-localised wannier functions, Comput Phys Commun 178, 685 (2008), 0708.0650.
[45] I. Souza, N. Marzari, and D. Vanderbilt, Maximally localized wannier functions for entangled energy bands, Phys. Rev. B 65, 035109 (2001).
[46] K. S. Burch, D. Mandrus, and J.-G. Park, Magnetism in two-dimensional van Der Waals materials, Nature 563, 47 (2018).
[47] M. Cococcioni and S. de Gironcoli, Linear response approach to the calculation of the effective interaction pa-
rameters in the LDA+U method, Physical Review B 71, 035105 (2005).

Supplementary material for “Two-dimensional fully-compensated Ferrimagnetism”

Yichen Liu , San-Dong Guo , Yongpan Li , and Cheng-Cheng Liu Centre for Quantum Physics, Key Laboratory of Advanced Optoelectronic Quantum Architecture and Measurement (MOE), School of Physics, Beijing Institute of Technology, Beijing 100081, China and School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China

This supplementary material is organized into four sections. In the first section, we give a more detailed analysis of the square lattice model in the main text. In the second section, we demonstrate that 2D filling-enforced fully-compensated ferrimagnets (fFIM) generally exhibit remarkable magneto-optical responses and anomalous Hall conductivity (AHC) by calculating these properties in a general tight-binding model. In the third section, we show how to convert traditional antiferromagnets into fFIM in a hexagonal model. The last section provides the detailed DFT calculations of , and .

I. SQUARE LATTICE TIGHT-BINDING MODEL

In this section, we give a more detailed analysis of the square lattice model in the main text. The model in the main text is
h.c. h.c. .
Here is the nearest hopping, and are the next-nearest hopping. is the staggered potential, and is the magnetic moment. is the nearest vector, and and are the lattice vector. Then we transform the Hamiltonian into the reciprocal space and let to simplify the formula.
The bands have the following form
The ↑ and ↓ in the superscript correspond to the spin-up and spin-down bands.
When the parameters are set to and , the system maintains space-time inversion symmetry. Under this condition, the expression of energy bands are
where energy bands are spin-degenerate, and the integrated density of states (IDOSs) are also spin-degenerate, as shown in Fig. S1(a).
When the parameters set to and , the parity-time symmetry is broken, but the symmetry is remained, and the system becomes altermagnetism. The energy bands are given by
FIG. S1. Tight binding model, with varying parameters yielding the conventional antiferromagnetism (cAFM), altermagnetism (AM), and fully-compensated ferrimagnetism models (fFIM). (a) The spin-degenerate band structure of the AFM model (Eq. S4) with , and . The right panel shows the spin-degenerate spin-up (red) and spin-down (blue) IDOS. (b) The spin-splitting band structure of the AM model (Eq. S-5), with parameters set as , , and . The spin-up and spin-down IDOSs remain equal. (c) The spin-splitting band structure of the fFIM model ( Eq. S-6) with parameters set as , and . The spin-up and spin-down IDOS degeneracy is lifted but remains equal within the gap. (d) The half-metal band structure of the fFIM model, with parameters set as , and . The spin-down channel is gapless, while the spin-up channel is gapped. The spin-up and spin-down IDOSs are equal at the Fermi energy.
It can be verified that in the energy band formula given by Eq. (S-5), we can observe . This equation originates from the symmetry, which transforms and as well as spin up to spin down. Therefore, the two bands with opposite spins are connected through the symmetry. Thus the IDOSs maintain spin-degeneracy, as shown in Fig. S1 (b).
Furthermore, when and , the energy bands become
The symmetry is broken, there is no symmetry to connect sublattices of opposite spins, nor is there any symmetry to ensure zero total magnetization. However, if the number of spin-up occupied states and spin-down occupied states are equal, the total magnetization remains zero, resulting in a fFIM. The corresponding band structure and IDOS are shown in Fig. S1 (c), where the spin-up and spin-down IDOSs are equal in the gap. If the energy bands for one spin channel remain gapped, the corresponding or stays a constant integer. Therefore, even if the other spin channel’s bands close, as long as the total number of occupied states remains unchanged, still holds, maintaining the fFIM state. This situation, where one spin channel is metallic and the other is insulating, is known as a half-metal system. The band structure and IDOS are shown in Fig. S1 (d), where the spin-up and spin-down IDOSs are equal at Fermi energy.

II. THE REMARKABLE MAGNETO-OPTICAL EFFECT AND ANOMALOUS HALL EFFECT IN GENERAL FFIM MODEL

Next, we further explore the novel physical properties of fFIMs based on this model. The Rashba SOC effect is introduced to the model, and the Hamiltonian can be written as
FIG. S2. The energy bands, Kerr angle, Faraday angle, and anomalous Hall conductivity of the general model of fullycompensated ferrimagnetism. (a) The band structures of this model, indicating metallic properties. (b) The optical Hall conductivity as a function of the light frequency, where the red (blue) lines represent the real (imaginary) parts of . (c) The Kerr angle as a function of the light frequency. and represent the angle and ellipticity, respectively. (d) The anomalous Hall conductivity as a function of the Fermi energy. The conductivity is nonzero at zero net magnetization. The parameters are fixed as , and .
with . The Hamiltonian in reciprocal space is
We focus on a metallic phase with , and , as shown in Fig. S2. There are two hole pockets and one electron pocket in its band structure in Fig. S2(a). This model is free of space-time inversion symmetry, exhibiting ferromagnetic-like physical properties such as optical Hall effect, magneto-optical Kerr effect, and anomalous Hall effect. The calculation formula of optical Hall conductivity is [1,2]
Here and are the velocity operators, and represents the energy difference between bands and , where represents the frequency of the light and is the smearing parameter, set to 0.05 eV in this study. The optical Hall conductivity of the model with Hamiltonian Eq. (S-7) is shown in Fig. S2(b). Furthermore, we can use the optical Hall two-dimensional system given by [3,4]
where and are the rotation angle and ellipticity, respectively. and are the diagonal and off-diagonal components of the optical conductivity tensor, quantifying the material’s response to an applied electromagnetic field. is the impedance of free space (approximately ), and is the vacuum permittivity. is the thickness of the sample and is set as 1 nm for the model. The refractive index of the substrate, denoted as , is assumed to be 1.5 , which corresponds to the refractive index of . The Kerr angle of the model is illustrated in Fig. S2(c).
Since the system is metallic, we can also calculate AHC, whose formula is [5,6]
We calculate the AHC as a function of Fermi level , as shown in Fig. S 2 (d). It is worth noting that when , the model has zero net magnetization, but it has non-zero AHC.
FIG. S3. Band structure and integrated density of states (IDOS) for the hexagonal model described by Eq. (S-12) with various parameter configurations. (a) The spin-degeneracy band structure of the model of Eq. (S-12). The right panel shows the spin-up (red) and spin-down (blue) IDOS. (b) The spin-splitting band structure of the model of Eq. (S-6). The spin-up and spin-down IDOSs are degenerate in the gap. (c) The band structure of Eq. (S-6) when . The system is a half metal.

III. HEXAGONAL LATTICE TIGHT-BINDING MODEL

For the model in a hexagonal lattice, we begin by considering a hexagonal model with an antiferromagnetic term on the lattice
Here, represents the nearest-neighbor hopping, is the magnitude of the magnetic moment on each site, is the spin operator, and represents an opposite sign of spins between sublattices. The two lattice is set as and . In this model, the two sublattices possess opposite spins, and can be connected through inversion symmetry. Thus the system exists parity-time reversal symmetry. The energy bands of this model are given by
Energy bands are spin degenerate, and spin-up and spin-down IDOSs are also degenerate, as illustrated in Fig. S3(a). To break the inversion symmetry, we introduce a staggered potential
Now, the two sublattices can no longer be related by any symmetry. Consequently, the energy bands of the model become
The band structure is shown in Fig. S3(b) with spin splitting. As long as , the energy gap remains open, then the spin-up and spin-down IDOSs are equal in the gap. Therefore, the net magnetic moment maintains zero, and the system becomes a fFIM, as shown in Fig. S3(b). When , the spin-down channel is gapless, and the system becomes a half-metal fFIM, as shown in Fig. S3(c). Then as , the spin-down channel is gapped again, and the system returns to a fFIM.

IV. MATERIALS CALCULATION

In this section, the calculation details for , and are provided.
FIG. S4. The phonon spectra of bilayer NiICl (a) and bilayer (b).
The first-principles calculation of structure optimization and band structures are using Vienna ab initio simulation package(VASP)[7]. The generalized gradient approximation (GGA) with Perdew-Burke-Ernzerhof (PBE)[8] realization is considered. We use the EFIELD, IDIPOL, DIPOL, and LDIPOL parameters in VASP to account for the electric field. The phonon calculations were performed using density functional perturbation theory as implemented in the PHONOPY code [9]. The ab initio tight-binding models are constructed using the WANNIER90 code [10-12] to calculate the magneto-optical response and anomalous Hall conductivity.
Bilayer has been synthesized [13, 14] and is an interlayer antiferromagnetic material, the lattice parameter is Å, and the interlayer distance is Å. The Hubbard U is set as for the 3d orbital of Cr atom, and the Electric field is set as Å along negative -axis. A -mesh was utilized for these calculations.
NiICl belongs to a hexagonal lattice with the space group P3m1 and possesses symmetry. After optimization, the lattice constant a is Å, and the interlayer distance is Å. A k-mesh of is employed for the calculations. To account for strong electron correlations in the Ni 3d orbitals, we applied the Hubbard U correction with in our DFT calculations.
Monolayer is obtained by replacing the Cr atom with Mo atoms in the monolayer antiferromagnetic material . The Hubbard U of Mo and Cr elements are set as 4 eV . The -mesh is used for lattice relaxation and self-consistent calculation.
AB-stacking bilayer is an interlayer antiferromagnetic material, the lattice parameter is Å, and the interlayer distance is Å. The Hubbard U is set as for the 3 d orbital of Y atom, and the electric field is set as Å along negative -axis. A -mesh is utilized for these calculations. The band structure, Kerr angle, Faraday angle, and AHC are shown in Fig. S5.
The stability of monolayer NiICl [16], monolayer [17] and monolayer [18] have been verified through DFT calculations on the phonon spectra. Employing a supercell for bilayer NiICl and a supercell for bilayer , we calculate their phonon spectra, as shown in Fig. S4. These spectra exhibit no imaginary frequencies in the Brillouin zone, indicating the structural stability of these materials.
The ferromagnetic and antiferromagnetic configurations of monolayer , bilayer NiICl , and bilayer as a function of Hubbard U are listed in Table. S1 Within a reasonable range of the Hubbard U parameter, the ground states of , bilayer NiICl , and bilayer are antiferromagnetic.
[1] C. Aversa and J. E. Sipe, Nonlinear optical susceptibilities of semiconductors: Results with a length-gauge analysis, Phys. Rev. B 52, 14636 (1995).
[2] H. Ebert, Magneto-optical effects in transition metal systems, Rep. Prog. Phys. 59, 1665 (1996).
[3] M.-H. Kim, G. Acbas, M.-H. Yang, I. Ohkubo, H. Christen, D. Mandrus, M. A. Scarpulla, O. D. Dubon, Z. Schlesinger, P. Khalifah, and J. Cerne, Determination of the infrared complex magnetoconductivity tensor in itinerant ferromagnets from faraday and kerr measurements, Phys. Rev. B 75, 214416 (2007).
[4] R. Valdés Aguilar, A. V. Stier, W. Liu, L. S. Bilbro, D. K. George, N. Bansal, L. Wu, J. Cerne, A. G. Markelz, S. Oh, and
FIG. S5. The band structure, Kerr angle, Faraday angle, and anomalous Hall conductivity of 2D filling-enforced fullycompensated ferrimagnet . (a) Band structure and integrated density of states (IDOS). (b) The Kerr angle as a function of light frequency. and represent the angle and ellipticity, respectively. (c) The anomalous Hall conductivity as a function of Fermi energy . (d) The Faraday angle as a function of light frequency.
TABLE S1. The total energy of the ferromagnetic and antiferromagnetic order of monolayer, NiICl bilayer, and bilayer as a function of Hubbard U. and are the total energy of the system with the antiferromagnetic and ferromagnetic order respectively. The is the total energy difference between the two magnetic orders. When , the material is an antiferromagnet; otherwise, it is a ferromagnet. In the table, “-” indicates that VASP is unable to converge to the corresponding magnetic order. The Hubbard U of Cr and Mo are set as the same value in .
NiICl
U (eV) 2 3 4 5
E -17.713227 -16.865274 -16.077713 -15.348955
-17.714349 -16.864369 -16.073680 -15.341357
0.001122 -0.000905 -0.004033 -0.007598
U (eV) 1 2 3 4
E -64.108138 -62.529771 -61.062467 -59.686118
– -61.917934 -60.410827 -58.999141
– -0.611837 -0.65164 -0.686977
U (eV) 0 1 2 3
-27.797280 -26.962275 -26.161623 -25.395336
-27.797266 -26.962107 -26.161330 -25.394878
-0.000014 -0.000168 -0.000293 -0.000458
N. P. Armitage, Terahertz response and colossal kerr rotation from the surface states of the topological insulator , Phys. Rev. Lett. 108, 087403 (2012).
[5] Y. Yao, L. Kleinman, A. H. MacDonald, J. Sinova, T. Jungwirth, D.-s. Wang, E. Wang, and Q. Niu, First principles calculation of anomalous hall conductivity in ferromagnetic bcc Fe, Phys. Rev. Lett. 92, 037204 (2004).
[6] X. Wang, J. R. Yates, I. Souza, and D. Vanderbilt, Ab initio calculation of the anomalous hall conductivity by wannier interpolation, Phys. Rev. B 74, 195118 (2006).
[7] G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B 54, 11169 (1996).
[8] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett. 77, 3865 (1996).
[9] A. Togo, F. Oba, and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and –
Type at high pressures, Physical Review B 78, 134106 (2008).
[10] N. Marzari and D. Vanderbilt, Maximally localized generalized wannier functions for composite energy bands, Phys. Rev. B 56, 12847 (1997).
[11] A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt, and N. Marzari, Wannier90: A tool for obtaining maximallylocalised wannier functions, Comput Phys Commun 178, 685 (2008), 0708.0650.
[12] I. Souza, N. Marzari, and D. Vanderbilt, Maximally localized wannier functions for entangled energy bands, Phys. Rev. B 65, 035109 (2001).
[13] K. S. Burch, D. Mandrus, and J.-G. Park, Magnetism in two-dimensional van Der Waals materials, Nature 563, 47 (2018).
[14] B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero, and X. Xu, Layer-dependent ferromagnetism in a van Der Waals crystal down to the monolayer limit, Nature 546, 270 (2017).
[15] M. Cococcioni and S. de Gironcoli, Linear response approach to the calculation of the effective interaction parameters in the LDA+U method, Physical Review B 71, 035105 (2005).
[16] T. Gorkan, J. Das, J. Kapeghian, M. Akram, J. V. Barth, S. Tongay, E. Akturk, O. Erten, and A. S. Botana, Skyrmion formation in ni-based janus dihalide monolayers: Interplay between magnetic frustration and dzyaloshinskii-moriya interaction, Phys. Rev. Mater 7, 054006 (2023).
[17] P. Wang, D. Wu, K. Zhang, and X. Wu, Two-dimensional quaternary transition metal sulfide (A = C, Si, or Ge): A bipolar antiferromagnetic semiconductor with a high Néel temperature, J. Phys. Chem. Lett. 13, 3850 (2022).
[18] B. Huang, W.-Y. Liu, X.-C. Wu, S.-Z. Li, H. Li, Z. Yang, and W.-B. Zhang, Large spontaneous valley polarization and high magnetic transition temperature in stable two-dimensional ferrovalley , and Cl , Phys. Rev. B 107, 045423 (2023).