أخذ العينات
حجم العينة
تقنية أخذ العينات
حسابات حجم العينة
جدول حجم العينة
عملية أخذ العينات
أخذ العينات الاحتمالية
أخذ العينات غير الاحتمالية
البحث الكمي
مستوى الثقة
هامش الخطأ
حجم السكان
حجم التأثير
الصلاحية
الموثوقية
البحث الاستقصائي
تصميم الدراسة

ستكون الدراسة التجريبية دقيقة وصحيحة عندما يتم اختيار تقنية العينة المناسبة بعناية. تتضمن تقنية أخذ العينات اختيار مجموعة فرعية من السكان الأكبر وهي جوهر البحث، حيث تعتمد طبيعة وقابلية تعميم النتائج على ذلك [1]. يعتمد نجاح أي دراسة على ملاءمة طريقة أخذ العينات.

تستند مبررات منهجيات أخذ العينات إلى قدرة هذه الإجراءات على استنتاج خصائص حول السكان دون التوقع غير الواقعي المتأصل في تقييم مجموعة كاملة. هذا مهم وضروري جداً في الحالات التي يصبح فيها التعداد الكامل مستحيلاً لسكان معينين بسبب قضايا تشغيلية مثل الوقت، والموارد، أو قيود الوصول. ستلتقط العينة المختارة بشكل صحيح وتعزز الصلاحية الخارجية وقابلية تعميم النتائج [2].

تقسم بشكل عام إلى قسمين: الاحتمالية وغير الاحتمالية
أخذ العينات [1،3]. تشمل أخذ العينات الاحتمالية أخذ العينات العشوائية الأساسية، وأخذ العينات الطبقية، وأخذ العينات العنقودية، حيث تعتمد طرق الاختيار على عملية العشوائية كعملية تعزيز لتقليل التحيز في الاختيار. تتمتع هذه الطرق بمبادئ إحصائية سليمة وعادة ما يتم اعتمادها عندما يكون الهدف هو التعميم. تشمل طرق أخذ العينات غير الاحتمالية أخذ العينات المريحة وأخذ العينات الهادفة كلما لم يكن الاختيار العشوائي ممكنًا أو عمليًا. قد تكون هذه مريحة لأغراض عملية، لكنها ستؤدي بسرعة إلى تحيزات في العينة التي ستؤثر بعد ذلك على تعميم النتائج [4].

يرتبط اختيار طريقة أخذ العينات ارتباطًا وثيقًا ببعض الأهداف البحثية المحددة، وبعض الخصائص الديموغرافية للسكان المستهدفين، وبعض القيود المنهجية للدراسة. يرتبط الاختيار الصحيح لتقنية أخذ العينات ارتباطًا كبيرًا بالصلاحية وقابلية تعميم نتائج الدراسة. يتطلب ذلك معرفة واسعة بإجراءات أخذ العينات المختلفة وعواقبها من جانب الباحث الذي ينوي أن يكون صحيحًا منهجيًا.

حاولت المقالة مناقشة مختلف الأساليب لأخذ العينات في

منهجية البحث، وتحديد حسابات حجم العينة الأكثر ملاءمة حتى يتمكن الباحث من اختيار الأنسب لوضع بحث معين. ستسعى هذه الورقة إلى إلقاء نظرة قريبة على مزايا وعيوب الإجراءات المختلفة لأخذ العينات في تعزيز أفضل ممارسات البحث وتعزيز الصلاحية التجريبية.

تعتبر عملية أخذ العينات واحدة من أهم أجزاء منهجية البحث، والتي من خلالها يتم ضمان دقة وصلاحية النتائج من الدراسة [5]. تبدأ هذه العملية بتحديد السكان المستهدفين، الذين يمكن أن يكونوا مجموعة كاملة من الأشخاص أو الكيانات المتعلقة بسؤال البحث. من المهم جدًا تحديد بوضوح ودقة ما يشكل السكان للتأكد من أن العينة تصف المجموعة قيد الدراسة. يعني السكان التعريف الذي يجب أن يعكس سمة مثل المتغيرات الديموغرافية، والموقع الجغرافي، وأي سمة أخرى قد تكون ذات صلة بالبحث.

بعد تحديد السكان، تكون العملية التالية هي اختيار طريقة أخذ عينات مناسبة. نظرًا لأهداف البحث والموارد والحاجة إلى التعميم، يجب على الباحثين الاختيار بين طرق أخذ العينات الاحتمالية وغير الاحتمالية. عادةً ما تشمل مبررات التفضيل، إذا كان الهدف هو إجراء استنتاجات حول السكان، الطرق التالية لأخذ العينات الاحتمالية: أخذ العينات العشوائية البسيطة، وأخذ العينات الطبقية، وأخذ العينات العنقودية، وأخذ العينات النظامية. تعتبر أخذ العينات المريحة، وأخذ العينات الهادفة، وأخذ العينات الثلجية بعض الطرق التي يتم اعتمادها عادةً في طرق أخذ العينات غير الاحتمالية للدراسات الاستكشافية أو عندما لا يكون السكان متاحين.

بمجرد تنفيذ اختيار خطة أخذ العينات، يجب على الباحث تحديد حجم هذه العينة، ويعتبر ذلك أمرًا حيويًا لموثوقية النتائج. عند حساب حجم العينة، قد تكون عدة عوامل مهمة: حجم السكان، وحجم التأثير المتوقع، ومستوى الثقة، وهامش الخطأ. يمكن تحقيق ذلك بمساعدة تقنيات أو أدوات إحصائية لتجنب الحصول على عينة صغيرة جدًا قد تؤدي إلى نتائج غير موثوقة، أو كبيرة جدًا حيث سيتم إهدار الموارد.

يشير اختيار أخذ العينات إلى المرحلة التي ستحدد فيها طريقة أخذ العينات المختارة من يجب أن يشكل دراسة في السكان. يمكن القيام بذلك من خلال توليد أرقام عشوائية أو طرق اختيار منهجية في حالة أخذ العينات الاحتمالية. في أخذ العينات غير الاحتمالية، قد يتعلق الأمر بالحالات القابلة للوصول أو الحالات المحددة ذات الصلة بالدراسة المعنية.

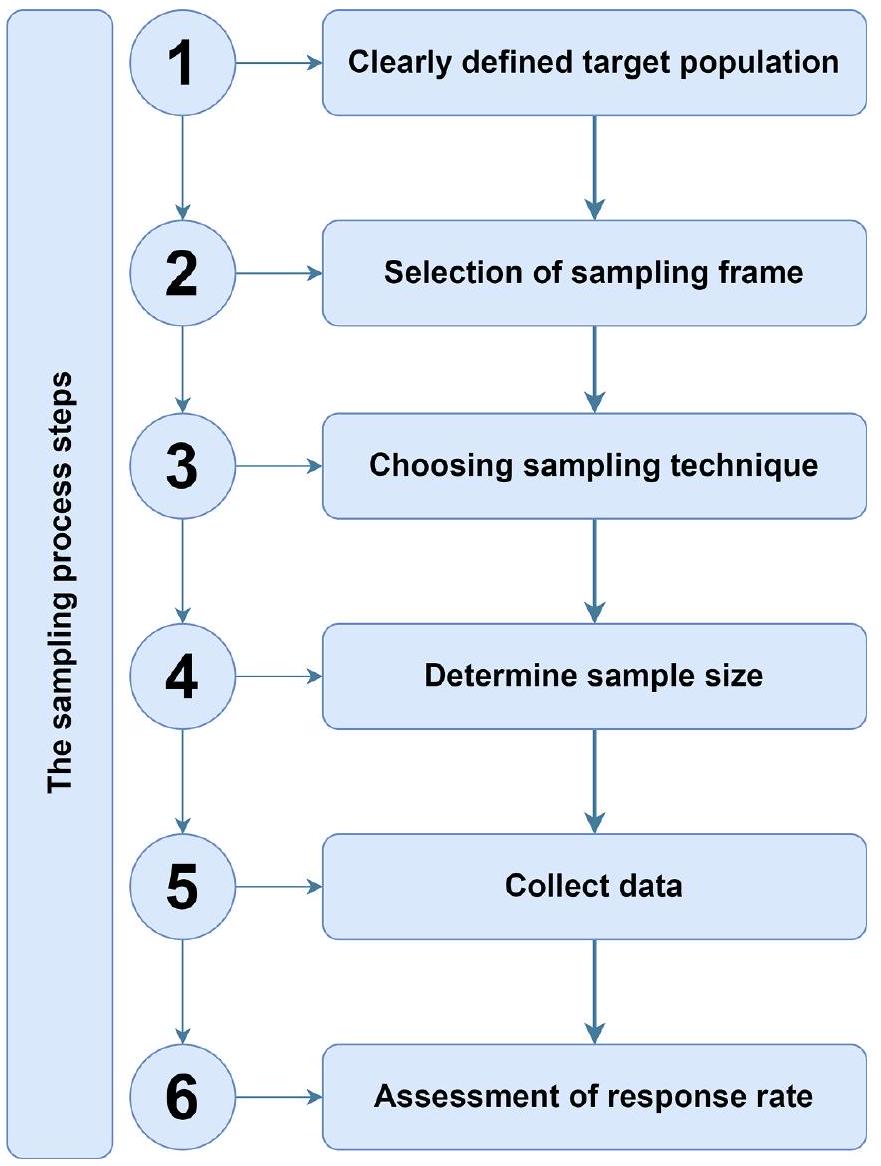
أخيرًا، يجب على الباحث تحليل البيانات المستمدة من العينة، مع الأخذ في الاعتبار أنه لا يمكن استخلاص أي استنتاج إذا لم يتم النظر في إجراء أخذ العينات. بعبارة أخرى، يجب أن يكون في الاعتبار مدى تحيز العينة، أو أين تكمن القيود وما إذا كان التعميم على السكان بأكمله ممكنًا. ستساعد خطة أخذ عينات رسمية الباحث في تعزيز صلاحية وموثوقية النتائج، وبالتالي دقة وموضوعية استنتاجاته. يتم تقديم خطوات عملية أخذ العينات في الشكل 1.

التمييز بين العينة العشوائية والعينة غير العشوائية هو استراتيجيتان مختلفتان تعتمد عليهما الأبحاث لاختيار المشاركين [6]. لكل منهما مزايا وعيوب خاصة بها. تضمن العينة العشوائية أن كل موضوع من السكان يحمل احتمالًا معروفًا وغير صفري للاختيار. يقلل العشوائية في هذا التصميم من التحيز في الاختيار ويجعل العينة تمثل السكان ككل. توفر العينة العشوائية للباحث فرصة لإجراء تعميمات من العينة إلى السكان وتقدير خطأ العينة بمقياس من الثقة. تشمل أمثلة التقنيات التي تندرج تحت هذه الفئة العينة العشوائية البسيطة، والعينة الطبقية، وعينة المجموعات. بينما تكون العينة العشوائية دقيقة، إلا أنها تميل إلى أن تكون

مرهقة وتتطلب الكثير من الوقت والموارد، خاصة عندما يكون عدد السكان المستهدف كبيرًا جدًا أو متشتتًا، حيث إنها تعتمد على قائمة مفصلة بالسكان ويجب أن يتم الاختيار باستخدام إجراء معقد.

على العكس، تشمل العينة غير العشوائية عدم وجود عشوائية؛ لذلك، لا يحمل جميع الموضوعات في السكان احتمالًا متساويًا أو معروفًا للاختيار. يُستخدم هذا بشكل أساسي عندما لا يكون من الممكن للباحثين الوصول إلى جميع السكان أو عندما تكون الموارد والوقت محدودة. تشمل بعض طرق أخذ العينات غير العشوائية أخذ العينات المريحة، وأخذ العينات الهادفة، وأخذ العينات المتساقطة، حيث يعتمد الأمر على حكم الباحث أو توفر المشاركين. هذه الطريقة الأخيرة، على الرغم من كونها أسرع وأقل تكلفة وأسهل في التنفيذ، تحمل خطر التحيز في الاختيار – أي أن العينة المختارة قد تحتوي في النهاية على تمثيل زائد أو ناقص لمجموعات. لذلك، فإن نتائج أخذ العينات غير العشوائية لها عمومًا قابلية تعميم محدودة على السكان بشكل عام، ولا يمكن إجراء الاستدلال الإحصائي بثقة. ومع ذلك، فهي مفيدة جدًا في الأبحاث الاستكشافية والدراسات النوعية، حيث يكون الهدف هو دراسة بعض تلك المجموعات الفرعية التي يصعب الوصول إليها بدلاً من تمثيل السكان ككل.

عندما تتطلب حالة البحث درجة عالية من الدقة والتعميم للنتائج على السكان ككل، يُفضل استخدام العينة العشوائية. فقط في الدراسات الصغيرة أو الاستكشافية يمكن للمرء اللجوء إلى العينة غير العشوائية عندما تكون القيود اللوجستية أو مجموعات التركيز أكثر أهمية من التمثيل. لكل من التقنيتين مكان في البحث، لكن اختيار واحدة أو أخرى يعتمد على أهداف البحث والموارد والاحتياجات المتعلقة بالموثوقية الإحصائية. 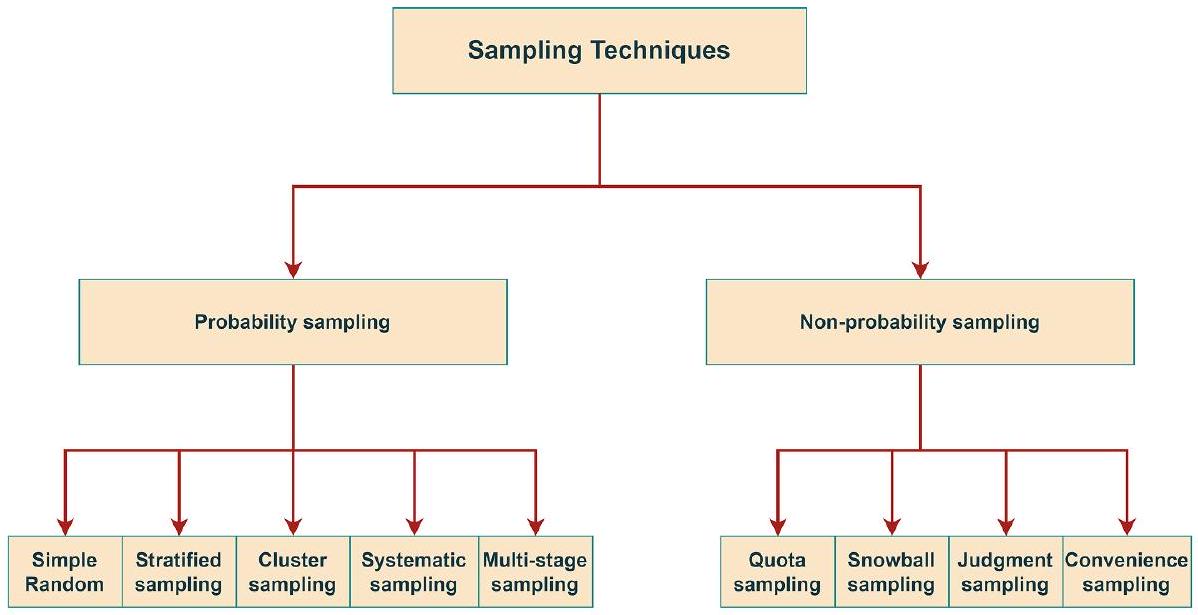يلخص الشكل 2 والجدول 1 تقنيات أخذ العينات العشوائية وغير العشوائية بالتفصيل، مع عدد من المزايا والعيوب المرتبطة بكل تقنية. يجب أن يكون هذا مفيدًا في تمكين الباحث من اختيار

طريقة أخذ العينات الأنسب لدراساته.

العينة العشوائية البسيطة، على الرغم من كونها أساسية جدًا، هي طريقة فعالة لضمان أن كل عضو من السكان سيكون له فرصة للاختيار. بعد تعريف وتجميع قائمة كاملة من الأعضاء الذين يشكلون السكان، يتم تحديد حجم العينة، ثم يبدأ الاختيار العشوائي الفعلي باستخدام مولد أرقام عشوائية أو سحب القرعة. هذه الطريقة ذات قيمة عالية لأنها تقلل من التحيز في الاختيار، على الرغم من أنها قد تكون متطلبة جدًا من حيث اللوجستيات، خاصة عندما يكون عدد السكان كبيرًا أو متشتتًا.

في أخذ العينات الطبقية، يتم تقسيم السكان إلى مجموعات متميزة، تُعرف عادةً بالطبقات، بناءً على فئات موحدة مثل العمر أو الجنس أو التعليم. ثم يتم أخذ عينات عشوائية من كل طبقة لاشتقاق عينة تمثل النطاق الكامل من الفئات. سيزيد هذا من دقة التقديرات، نظرًا لأن كل مجموعة فرعية ممثلة بشكل جيد، مما يجعل هذه الطريقة أكثر ملاءمة للسكان حيث توجد تباينات كبيرة في الخصائص الرئيسية. ومع ذلك، من الصعب تشكيل الطبقات بشكل ذي معنى إذا لم يكن هناك معرفة تفصيلية بالسكان.

أخذ العينات العنقودية هي طريقة لتبسيط عملية جمع البيانات حيث يتم تقسيم السكان إلى عنقود، قد تكون مواقع جغرافية أو مؤسسات، ويتم أخذ اختيار عشوائي من هذه للدراسة. سيتم تضمين جميع الأعضاء في العناقيد المختارة في العينة. ستكون هذه الطريقة مفيدة جدًا في الدراسات الكبيرة حيث سيكون من غير العملي تجميع قائمة كاملة من السكان. على الرغم من أن أخذ العينات العنقودية غير مكلف، إلا أنه قد يقدم تحيزات إذا كانت العناقيد المختارة ليست نموذجية للسكان بشكل عام.

في أخذ العينات النظامية، يتم اختيار كل فرد بطريقة مستمرة من قائمة السكان، بدءًا من نقطة عشوائية. إنها فعالة وسهلة التنفيذ إلى حد ما لأنها تعتمد على فترة أخذ عينات منتظمة. قد تكون أخذ العينات النظامية متحيزة، ومع ذلك، إذا كان هناك نمط متأصل في السكان يتزامن مع فترة أخذ العينات.

في أخذ العينات متعددة المراحل، يتم تقسيم السكان إلى عدد من المراحل أو المستويات. على سبيل المثال، في أخذ العينات العنقودية – شكل معقد من
أخذ العينات متعددة المراحل – يتم تقسيم السكان إلى عناقيد كبيرة (على سبيل المثال، مناطق أو مؤسسات)، يتم منها سحب عينات عشوائية إضافية في مراحل متعاقبة. بمجرد اختيار المناطق الجغرافية، على سبيل المثال، يمكن اختيار عينة عشوائية من الأفراد داخل كل منطقة. تعتبر الطبقات المتدرجة مفيدة في الدراسات الكبيرة لتقليل حجم العينة بشكل منهجي من خلال تضييق نطاق السكان الواسع أو المتشتت. بينما قد يوفر ذلك التكاليف والوقت، هناك خطر زيادة خطأ العينة في كل مرحلة من عملية الاختيار، إذا لم تكن العينة في كل مستوى تمثل.

من بين الطرق المختلفة لجمع البيانات، تتضمن أخذ العينات المريحة سحب عينات من تلك الجزء من السكان الذي يجد الباحث أنه الأكثر وصولًا [2]. هذه طريقة سريعة ورخيصة لجمع البيانات عندما يكون الوقت أو الموارد محدودة. ومع ذلك، في معظم الحالات، تقدم هذه الطريقة تحيزًا، حيث قد لا تكون العينة تمثيلية وبالتالي لن يكون من الممكن تعميم النتائج على بقية السكان.

في أخذ العينات الهادفة، المعروف أيضًا بأخذ العينات الحكمية أو الخبيرة، يتم اختيار المشاركين بناءً على حكم الباحث الذي يقرر من سيكون الأكثر فائدة للبيانات المطلوبة [2]. يُستخدم هذا عادةً في الأبحاث التي تتطلب أشخاصًا معينين يتمتعون بخصائص أو خبرات محددة. على الرغم من أن هذه الطريقة يمكن أن تؤدي إلى رؤى عميقة جدًا، إلا أنها تحمل خطرًا عاليًا جدًا من التحيز من جانب الباحث وقد لا تمثل السكان ككل.

تُستخدم أخذ العينات المتساقطة عندما يتم دراسة السكان المخفيين أو صعب الوصول إليهم. في هذه الحالة، يُطلب من المشاركين إحالة أولئك الذين يتناسبون أيضًا مع معايير المشاركين في الدراسة، مما يجعل شبكة من الإحالات. هذه التقنية مفيدة في الأبحاث الاستكشافية. ومع ذلك، تم انتقادها لأنها تؤدي إلى عينات متحيزة لأن العينات تصبح متجانسة مع مرور الوقت بسبب الشبكات الاجتماعية.

تشير أخذ العينات الحصصية إلى العملية التي يتم من خلالها تقسيم السكان إلى مجموعات فرعية متبادلة حصرية يتم من خلالها اختيار المشاركين، مما يضمن ملء حصص معينة داخل كل مجموعة فرعية. تضمن الحصص وجود خصائص معينة من السكان داخل العينة؛ ومع ذلك، يبقى الاختيار الفعلي داخل المجموعة الفرعية غير عشوائي، وبالتالي متحيز وعينة أقل تمثيلاً.

تحديد حجم العينة أمر حيوي في البحث للحصول على نتائج صالحة وموثوقة [7،8]. في تقدير متوسطات أو نسب السكان، يضمن تطبيق الصيغة الصحيحة أن العينة المأخوذة تمثل السكان وتقلل من الخطأ [9].

من بين جميع الصيغ المستخدمة في البحث، ربما الأكثر شيوعًا هي لتقدير نسبة السكان [10]. صيغة شائعة الاستخدام هي:

حيث.

تُطبق هذه الصيغة عندما يكون الباحث مهتمًا بنسبة السكان الذين لديهم سمة معينة، مثل نسبة المدخنين أو الناخبين. كلما كان حجم العينة أكبر، قلل من هامش الخطأ E وبالتالي يوفر تقديرًا أقرب إلى الواقع.

الصيغة لحجم العينة في الدراسات المصممة لتقدير متوسط السكان، مثل متوسط الدخل أو الطول، هي كما يلي:

حيث.

هذه صيغة مهمة عندما يعمل المرء مع متغيرات مستمرة. كلما زاد التشتت في السكان، ، كلما كان حجم العينة أكبر الذي سيكون مطلوبًا للحصول على تقدير دقيق. وبالمثل، كلما كان هامش الخطأ أصغر، أو كلما كان مستوى الثقة أعلى، كلما كان حجم العينة أكبر المطلوب.

تُستخدم صيغة كوخران عادةً عندما يكون السكان كبيرين أو غير محدودين وتطبق على كل من النسب والمتوسطات [11]. الصيغة العامة للحساب:

حيث.

تُطبق صيغة كوخران على نطاق واسع عندما يتم استخدام استطلاع أو دراسة مقطعية، حيث يتوقع الباحث أن يكون السكان كبيرين.

إذا كان حجم السكان صغيرًا – أي محدودًا – يجب تعديل حجم العينة بواسطة تصحيح السكان المحدود. يتم ذلك بالطريقة التالية:

حيث.

سيعدل هذا حجم العينة، خاصة عندما يكون السكان صغيرين، للحفاظ على دقة النتائج دون الإفراط في أخذ العينات.

تُستخدم العينة الطبقية عندما يمكن تقسيم السكان إلى مجموعات فرعية متميزة، أو طبقات، مثل مجموعة العمر، الجنس، أو مستوى التعليم. يمكن تحديد حجم العينة لكل طبقة باستخدام التخصيص النسبي:

حيث.

سيضمن ذلك أن العينة تمثل جميع المجموعات الفرعية في السكان المعنيين. تعتبر العينة العشوائية الطبقية مفيدة في حالة تكون فيها المجموعات الفرعية مختلفة جدًا عن بعضها البعض.

صيغة ياماني، 1967، هي واحدة من الطرق الشائعة في أبحاث الاستطلاع المستخدمة لتقدير حجم عينة مناسب لأي سكان معين مع مراعاة الدقة والعملية [12]. تقرب هذه الصيغة حجم العينة بناءً على الحجم الكلي للسكان وهامش الخطأ المطلوب. لاستخدام هذه الطريقة، تعتبر مستويات الثقة؛ على الرغم من أنه يمكن تعديلها باستخدام مستويات ثقة أخرى.

صيغة حساب حجم العينة وفقًا لياماني هي:

أين.

إحدى الوسائل الشائعة لتخفيف العبء الحسابي في تحديد حجم العينة هي من خلال استخدام الجداول المحسوبة مسبقًا. توفر هذه الجداول عمومًا تقديرات لحجم العينة لقيم محسوبة مسبقًا لهامش الخطأ، E؛ مستوى الثقة، Z؛ والنسبة المقدرة، p. توفر هذه الجداول نقاط مرجعية سريعة للباحثين الذين قد يرغبون في تقدير حجم العينة المطلوب لدقة معينة دون الحاجة بالضرورة إلى حساب صيغ معقدة (الجداول 2 و 3).

يتم تحديد حجم العينة في أي دراسة من خلال عدد من العوامل. أولاً، هناك حجم السكان الذين سيتم سحب العينة منهم؛ قد تتطلب السكان الأكبر نهجًا مختلفًا عن الأصغر. ثانيًا، يؤثر مستوى الثقة المطلوب بشكل كبير على حجم العينة؛ كلما زاد مستوى الثقة – 95 في المئة مقارنة بـ 90 في المئة، على سبيل المثال – كان يجب أن يكون حجم العينة أكبر. تشمل الاعتبارات المهمة الأخرى هامش الخطأ – حيث يرتبط الهامش الأصغر بحجم عينات أكبر لضمان أن تكون النتائج دالة على المعلمات الحقيقية في السكان. قد تؤثر التباين داخل السكان أيضًا على حجم العينة؛ كلما زاد التباين، زاد عدد المشاركين، بشكل عام، الذي سيتعين على المرء جمعه لتغطية النطاق. من المهم أيضًا النظر في حجم التأثير والقوة الإحصائية: مع أحجام تأثير أصغر ومستويات عالية من القوة، تكون العينات الأكبر مطلوبة لاكتشاف الفروق ذات الدلالة. أي تصميم دراسة – مقطعي، طولي، أو تجريبي – سيحدد أيضًا متطلبات حجم العينة. أخيرًا، قد يكون معدل التسرب المتوقع – على سبيل المثال، عدد المتسربين أو عدم الاستجابات – هو السبب في تعديل حجم العينة الأولي لضمان عدد كافٍ من المشاركين لإكمال الدراسة. ستؤدي العوامل المذكورة، إذا تم النظر فيها بعناية، إلى حجم عينة كافٍ ليس فقط لدعم

المصدر (Gill et al., 2010) [13].

المصدر (Gill et al., 2010) [13].

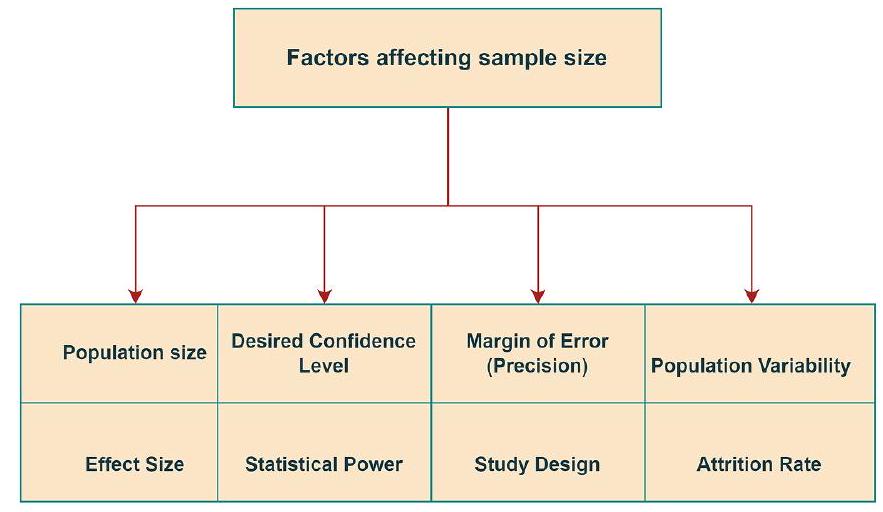
أهداف الدراسة ولكن أيضًا إنتاج نتائج ذات دلالة إحصائية. العوامل المؤثرة على حجم العينة موضحة في الشكل 3.

تعتمد دقة المنهجية في البحث على اختيار تقنيات أخذ العينات المناسبة وحساب حجم العينة المناسب. تعتبر أخذ العينات الاحتمالية، مثل أخذ العينات الطبقية وأخذ العينات العنقودية، أساسية في الدراسات التي تهدف إلى إجراء استنتاجات ذات دلالة إحصائية حول السكان الأوسع. بالمقابل، تقدم طرق أخذ العينات غير الاحتمالية طرقًا عملية عند إجراء أبحاث استكشافية أو عندما لا يمكن الوصول إلى كامل السكان. يعد الحساب الدقيق لحجم العينة خطوة مهمة جدًا في أي مشروع بحثي. يؤثر هذا العامل بشكل كبير على القوة الإحصائية ودقة الاستنتاجات التي يمكن استخلاصها من أي دراسة. لا يمكن أن تؤدي العينات الصغيرة إلى نتائج حاسمة، بينما العينات الكبيرة جدًا تعتبر مضيعة لأنها لن تضيف شيئًا إلى صحة الدراسة. تظل مستويات الثقة، وهامش الخطأ، وحجم التأثيرات من بين العوامل الرئيسية التي تساعد الباحثين على ضمان أن تصاميم أبحاثهم تسهل الحصول على نتائج قوية. في هذا الصدد، تشمل الإرشادات المنهجية طرقًا يمكن للباحث من خلالها المساهمة في تقدم المعرفة العلمية من خلال إعداد أعمال سيشير إليها باحثون آخرون كأساس لسنوات قادمة. نأمل أن يضع هذا الدليل معيارًا فيما يتعلق بمنهجية البحث وبالتالي يعمل كنقطة مرجعية للعلماء الملتزمين بإنتاج أعمال بأعلى المعايير التجريبية والنظرية، بهدف نهائي يتمثل في زيادة التأثير وإمكانية الاقتباس من الأبحاث على مستوى عالمي.

لم يكن من الضروري الحصول على موافقة أخلاقية، حيث أن الدراسة التي تم إجراؤها لم تتضمن أي مخاوف أو قضايا أخلاقية.

لم يتلقَ هذا المقال أي دعم مالي.

لم يتم استخدام أي بيانات في البحث الموصوف في هذه المقالة.

سيروان خالد أحمد: التصور، تنظيم البيانات، الإشراف، الكتابة – المسودة الأصلية.

يعلن المؤلفون أنهم ليس لديهم أي تضارب مالي معروف
المصالح أو العلاقات الشخصية التي قد تكون بدت وكأنها تؤثر على العمل المبلغ عنه في هذه الورقة.

شكرًا لجميع المراجعين الأقران والمحررين على آرائهم واقتراحاتهم ودعمهم لهذا البحث.

[1] Elfil M, Negida A. Sampling methods in clinical research; an educational review. Emerg (Tehran, Iran) 2017;5:e52. https://sid.ir/paper/339768/en.
[2] Andrade C. The inconvenient truth about convenience and purposive samples. Indian J Psychol Med 2020;43:86-8. https://doi.org/10.1177/ 0253717620977000.
[3] Shorten A, Moorley C. Selecting the sample. Evid Base Nurs 2014;17:32-3. https:// doi.org/10.1136/eb-2014-101747.
[4] Rahman MM. Sample size determination for survey research and non-probability sampling techniques: a review and set of recommendations. J Entrep Bus Econ

2023;11(1 11):42-62. https://www.scientificia.com/index.php/JEBE/article/view ?path=.
[5] Suresh K, V Thomas S, Suresh G. Design, data analysis and sampling techniques for clinical research. Ann Indian Acad Neurol 2011;14:287-90. https://doi.org/ 10.4103/0972-2327.91951.
[6] Taherdoost H. Sampling methods in research methodology; how to choose a sampling technique for research. Int J Acad Res Manag 2016;5:18-27.
[7] Krejcie R, Morgan D. Determining sample size for research activities. Educ Psychol Meas 1970;30:607-10. https://doi.org/10.1177/001316447003000308.
[8] Altman DG. Practical statistics for medical research. first ed. New York: Chapman and Hall/CRC; 1990. https://doi.org/10.1201/9780429258589.
[9] Rodríguez del Águila MM, González-Ramírez AR. Sample size calculation. Allergol Immunopathol 2014;42:485-92. https://doi.org/10.1016/j.aller.2013.03.008.
[10] Daniel WW, Cross CL. Biostatistics: a foundation for analysis in the health sciences. tenth ed. New York, NY, USA: John Wiley & Sons; 2018.
[11] Cochran WG. Sampling techniques. second ed. Inc, New York: ohn Wiley and Sons; 1963.
[12] Yamane T. Statistics: an introductory analysis. second ed. New York: Harper and Row; 1967.
[13] Gill J, Johnson P. Research methods for managers. Sage; 2010.

Sampling
Sample size
Sampling technique
Sample size calculations
Sample size table
Sampling process
Probability sampling
Non-probability sampling
Quantitative research
Confidence level
Margin error
Population size
Effect size
Validity
Reliability
Survey research
Study design

The empirical study will be accurate and valid when the proper sample technique will be cautiously selected. Sampling technique involve the selection of a subset from the larger population and are core to research, since through sampling, the nature and generalizability of findings depend on it [1]. The success of any study would depend upon the appropriateness of the sampling method.

The rationale for sampling methodologies is the capability of such procedures to infer characteristics about populations without the unrealistic expectation inherent in evaluating an entire group. This is very important and necessary in cases where complete enumeration becomes impossible for a given population due to such operational issues as time, resources, or access restrictions. A properly chosen sample would capture and enhance the external validity and generalizability of the findings [2].

It is generally divided into two: probability and non-probability
sampling [1,3]. Probability sampling includes basic random sampling, stratified sampling, and cluster sampling, where methods of selection depend on the randomization process as a strengthening process to reduce selection bias. These methods boast of sound statistical tenets and are usually adopted when generalization is intended. Non-probability sampling methods include convenience and purposive sampling whenever random selection is not feasible or practical. These may be convenient for practical purposes, but they will rapidly lead to biases in the sample that then will affect the generalization of results [4].

The selection of the sampling method is intrinsically identified with a few specific research goals, some demographic features of the target population, and some methodological limitations of the study. Proper selection of sampling technique bears great relevance to the validity and generalization of the study outcomes. This calls for wide-ranging acquaintance with different sampling procedures and their consequences on the part of the researcher who intends to be methodologically correct.

The article tried to discuss various approaches to sampling in

research methodology, and determine the most appropriate sample size calculations so that the researcher may choose the best fit for a particular research situation. This paper will attempt to give a close look at the pros and cons of the different procedures of sampling in promoting best practices of research and enhancing empirical validity.

The sampling process is one of the most important parts of the research methodology, through which accuracy and validity of findings from a study are guaranteed [5]. This process starts with the identification of a target population, which could be a total group of persons or entities relating to the research question. Defining clearly and properly what constitutes a population is highly important to make sure that the sample describes the group under study. Population means the definition that should reflect such an attribute like demographic variables, geographic location, and every other feature which could be relevant for research.

Having defined the population, the next process is the choice of a suitable sampling method. In view of research goals and resources and a need for generalization, researchers have to choose between probability and non-probability sampling methods. The justification for preference, if the objective is to make inferences about the population, normally includes the following probability sampling methods: simple random sampling, stratified sampling, cluster sampling, and systematic sampling. Convenience sampling, purposive sampling, and snowball sampling are some of the methods generally adopted in non-probability methods for exploratory studies or when the population is not accessible.

Once the selection of a sampling plan is effected, the size of this sample has to be determined by the researcher, and this is taken as vital for the reliability of the results. In calculating sample size, several factors may be important: the size of the population, the effect size one expects, the confidence level, and the margin of error. This can be achieved with the help of statistical techniques or tools in order not to have too small a sample that would yield untrustworthy results, or too large in which case resources will be wasted.

Sampling selection refers to the stage where the chosen sampling method will decide who or which units in the population should constitute a study. This could be done through random number generation or systematic selection methods in the case of probability sampling. In non-probability sampling, it could be related to accessible or particular cases that are relevant to the study at hand.

Finally, the researcher must analyze the data obtained from the sample, taking into consideration that no conclusion can be made if the sampling procedure is not considered. In other words, it is to have in mind how biased the sample can be, or where the limitation is and whether generalization to the whole population is feasible. A formal sampling plan will enable the researcher to enhance the validity and reliability of the results and, therefore the accuracy and meaningfulness of his conclusions. Steps of Sampling process are presented in Fig. 1.

Differentiating between the two, probability sampling and nonprobability sampling are mainly two different strategies adopted in research for the selection of participants [6]. Each has its own advantages and disadvantages. Probability sampling assures that every subject from the population carries a known, nonzero possibility of selection. The randomization in this design reduces selection bias and makes the sample representative of the population as a whole. Probability sampling provides the researcher with the chance to make generalizations from the sample to the population and estimate the sampling error with a measure of confidence. Examples of techniques falling under this category include simple random sampling, stratified sampling, and cluster sampling. While probability sampling is accurate, it tends to be

cumbersome and requires much time and resources, especially when the base of the population being targeted is very large or scattered since it is based on a detailed listing of the population and selections must be done using a complex procedure.

On the contrary, non-probability sampling encompasses no randomization; therefore, not all subjects in the population carry an equal or known probability of selection. This is mainly used when it is not possible for the researchers to reach the entire population or when the resources and time are limited. Some of the non-probability sampling methods include convenience sampling, purposive sampling, and snowball sampling, in which the judgment of the researcher or the availability of participants is depended on. This latter method, while faster, inexpensive, and easier to carry out, has the liability of selection bias-that is, the sample chosen may eventually contain overrepresentation or underrepresentation of groups. Results from nonprobability sampling therefore have limited generalizability to the population-at-large, and statistical inference cannot be carried out as confidently. It is, however, very useful in exploratory research, qualitative studies, and where the intention is to study some of those difficult-to-reach subgroups rather than to represent the whole population.

Where the research situation calls for a high degree of accuracy and generalization of results to the whole population, the preference is for probability sampling. Only in small-scale or exploratory studies can one resort to non-probability sampling when logistical constraints or focus groups turn out to be more important than representativeness. Both techniques have a place in research, but the choice of one or the other depends upon research objectives, resources, and needs regarding statistical reliability. Fig. 2 and Table 1 summarize probability and nonprobability sampling techniques in detail, together with a number of advantages and disadvantages associated with each technique. This should be helpful in enabling the researcher to choose the most

appropriate sampling method for their studies.

The simple random sample, although very basic, is an effective method of ensuring that every single member of the population will have a chance of being selected. Following definition and compilation of a complete list of members constituting the population, the defining of the sample size, then the actual random selection using a random number generator or drawing of lots commences. This is highly valued because it reduces selection bias, although it might be very demanding in logistics, especially when the population is so big or dispersed.

In stratified sampling, the population would be divided into distinct groups, commonly known as strata, based on uniform categories such as age, sex, or education. Random samples would then be taken from each stratum to derive a sample representative of the entire range of categories. This will increase the accuracy of the estimates, given that every subgroup is well-represented, thereby making this method more suitable for populations where great variability in key characteristics exists. However, it is difficult to meaningfully form strata if detailed knowledge of the population does not exist.

Cluster sampling is a method of simplifying the process of data collection whereby a population is divided into clusters, which may be geographic locations or institutions, and a random selection is taken from these for study. All members in the selected clusters will then be included in the sample. It will be very useful in large-scale studies where compiling a complete list of the population would be highly impractical. Though cluster sampling is inexpensive, it might introduce biases if the selected clusters are not typical of the overall population.

In systematic sampling, every individual is chosen in a continuous manner from a population list, starting from a random point. It is efficient and quite easy to conduct because it is based on a regular sampling interval. Systematic sampling may be biased, however, if there is an inherent pattern in the population that coincides with the sampling interval.

In multi-stage sampling, a population is divided into a number of stages or levels. For example, in cluster sampling – a complicated form of
multi-stage sampling – populations are divided into large clusters (for instance, regions or institutions), from which further random samples are drawn in successive stages. Once geographic areas are selected, for example, a random sample of individuals within each area could be selected. The stepwise stratification is useful in large-scale studies to systematically reduce the sample size by narrowing down through vast or dispersed populations. While this may save costs and time, there is a risk of increased sampling error at each stage in the selection process, if the sampling at each level is not representative.

Of the various methods of data collection, convenience sampling involves drawing samples from that portion of the population which the researcher finds most accessible [2]. This is a fast and cheap method of collecting data when either time or resources are in short supply. However, in most instances, this method introduces bias, since the sample may not be representative and thus generalization of the findings to the rest of the population will not be possible.

In purposive sampling, also known as judgmental or expert sampling, the participants are selected based on the judgment of the researcher who decides who will be most useful for the data required [2]. This is normally used in research requiring certain people with some specific characteristics or expertise. Though the method can result in very profound insights, it carries a very high risk of bias on the part of the researcher and may not represent the whole population.

Snowball sampling is utilized when one is studying hidden or hard-to-reach populations. In this case, participants are required to refer those that also fit the criteria for study participants, making a network of referrals. This technique is useful in exploratory research. However, it has been criticized to lead to biased samples because samples get homogeneous over time due to social networks.

Quota sampling refers to the process whereby the population is divided into mutually exclusive subgroups from which participants are selected, ensuring that certain quotas within each subgroup are filled. Quotas ensure that certain characteristics of the population exist within the sample; however, the actual selection within the subgroup remains non-random, hence biased and a less representative sample.

The sample size determination is vital in research for valid and reliable results [7,8]. In the estimation of population means or proportions, applying the correct formula ensures that the sample taken represents the population and minimizes error [9].

Among all formulas used in research, perhaps the most common is for estimating a population proportion [10]. A commonly used formula is:

Where.

This formula is applied when a researcher is interested in the proportion of a population with a particular attribute, such as the percentage of smokers or voters. A larger sample size reduces the margin of error E and hence provides an estimate closer to actuality.

The formula for sample size in studies designed to estimate a population mean, such as average income or height, is given by:

Where.

This is an important formula when one is working with continuous variables. The greater the dispersion in the population, , the larger the sample that will be needed in order to have an accurate estimate. Similarly, the smaller the margin of error, or the higher confidence level, the greater the sample size needed.

Cochran’s formula is normally used when the population is large or infinite and applies to both proportions and means [11]. The general formula for the calculation:

Where.

Cochran’s formula is widely applied when a survey or a crosssectional study is used, in which the researcher expects the population to be large.

If the size of the population is small-that is, finite-the sample size has to be adjusted by the finite population correction. This is done in the following manner:

Where.

This will adjust the sample size, especially when the population is small, to retain precision of results without over-sampling.

Stratified sampling is used when a population can be divided into distinct subgroups, or strata, such as age group, gender, or level of education. The sample size for each stratum can be determined by the use of proportional allocation:

Where.

This would ensure that the sample is representative of all subgroups in the population of interest. Stratified random sampling is useful in a situation where the subgroups are very different from one another.

Yamane’s formula, 1967, is one of the common methods in survey research used to estimate an appropriate sample size for any given population with concern for precision and practicality [12]. This formula approximates the sample size based on the total size of a population and desired margin of error. For using this method, confidence levels are considered; although it can be modified using other confidence levels.

The formula for Yamane’s sample size calculation is:

Where.

One common means of easing the computational burden in determining sample size is through the use of precalculated tables. These tables generally provide sample size estimates for precalculated values of the margin of error, E; confidence level, Z; and estimated proportion, p. Such tables provide quick reference points for researchers who may want to estimate a required sample size for a certain accuracy without necessarily having to compute complicated formulae (Tables 2 and 3).

The sample size of any study is determined by a number of factors. First, there is the size of the population from which the sample is to be drawn; larger populations may require a different approach than smaller ones. Second, the desired confidence level significantly influences sample size; the higher the confidence level-95 percent compared to 90 percent, for example-the larger the sample size must be. Other important considerations include margin of error-smaller margins are associated with larger sample sizes to ensure findings indicative of true parameters in a population. The variability within the population might also affect sample size; the larger the variability, the more participants, generally speaking, one will have to capture the range in. It is equally important to look at the effect size and statistical power: with smaller effect sizes and high levels of power, larger samples are needed to detect meaningful differences. Any study design-cross-sectional, longitudinal, or experimental-will further stipulate sample size requirements. Lastly, the expected attrition rate-for example, the number of dropouts or non-responses-may be the reason for an adjustment of the initial sample size to ensure a sufficient number of participants complete the study. The said factors, if considered with due deliberation, will lead a researcher to such a sample size that is sufficient not only to support the

Source (Gill et al., 2010) [13].

Source (Gill et al., 2010) [13].

objectives of the study but also produce results which are statistically significant. The factors affecting sample size are illustrated in Fig. 3.

The precision of methodology in research depends on the selection of proper sampling techniques and calculation of an adequately powered sample size. Probability sampling, for example, stratified and cluster sampling, is thus fundamental in those studies that tend to make statistically significant inferences about the wider population. By contrast, non-probability sampling methods offer pragmatic ways when one conducts exploratory research or where full population access cannot be made. Precise calculation of sample size is a very important step in any research project. This factor has a great bearing on the statistical power and the precision of conclusions that may be drawn from any study. Undersized samples cannot yield conclusive results, whereas samples that are too big are wasteful because they will add nothing to the validity of the study. Confidence level, margin of error, and size of effects remain some of the key determinants that help researchers ensure their research designs facilitate strong findings. In that respect, the methodological guidelines include ways a researcher can contribute to the advance of scientific knowledge by setting up works that other researchers will refer to as foundational many years to come. This guide hopefully sets a benchmark with regard to research methodology and thus serves as a reference point for scholars committed to the production of work of the highest empirical and theoretical standards, with an ultimate aim of globally increasing the impact and citation potential of the research.

The ethical approval was not required, as the study conducted did not involve any ethical concerns or issues.

This article did not receive any financial support.

No data were used in the research described in this article.

Sirwan Khalid Ahmed: Conceptualization, Data curation, Supervision, Writing – original draft.

The authors declare that they have no known competing financial
interests or personal relationships that could have appeared to influence the work reported in this paper.

Thanks to all the peer reviewers and editors for their opinions and suggestions and for their support of this research.

[1] Elfil M, Negida A. Sampling methods in clinical research; an educational review. Emerg (Tehran, Iran) 2017;5:e52. https://sid.ir/paper/339768/en.
[2] Andrade C. The inconvenient truth about convenience and purposive samples. Indian J Psychol Med 2020;43:86-8. https://doi.org/10.1177/ 0253717620977000.
[3] Shorten A, Moorley C. Selecting the sample. Evid Base Nurs 2014;17:32-3. https:// doi.org/10.1136/eb-2014-101747.
[4] Rahman MM. Sample size determination for survey research and non-probability sampling techniques: a review and set of recommendations. J Entrep Bus Econ

2023;11(1 11):42-62. https://www.scientificia.com/index.php/JEBE/article/view ?path=.
[5] Suresh K, V Thomas S, Suresh G. Design, data analysis and sampling techniques for clinical research. Ann Indian Acad Neurol 2011;14:287-90. https://doi.org/ 10.4103/0972-2327.91951.
[6] Taherdoost H. Sampling methods in research methodology; how to choose a sampling technique for research. Int J Acad Res Manag 2016;5:18-27.
[7] Krejcie R, Morgan D. Determining sample size for research activities. Educ Psychol Meas 1970;30:607-10. https://doi.org/10.1177/001316447003000308.
[8] Altman DG. Practical statistics for medical research. first ed. New York: Chapman and Hall/CRC; 1990. https://doi.org/10.1201/9780429258589.
[9] Rodríguez del Águila MM, González-Ramírez AR. Sample size calculation. Allergol Immunopathol 2014;42:485-92. https://doi.org/10.1016/j.aller.2013.03.008.
[10] Daniel WW, Cross CL. Biostatistics: a foundation for analysis in the health sciences. tenth ed. New York, NY, USA: John Wiley & Sons; 2018.
[11] Cochran WG. Sampling techniques. second ed. Inc, New York: ohn Wiley and Sons; 1963.
[12] Yamane T. Statistics: an introductory analysis. second ed. New York: Harper and Row; 1967.
[13] Gill J, Johnson P. Research methods for managers. Sage; 2010.