DOI: https://doi.org/10.1186/s13663-024-00760-7
تاريخ النشر: 2024-01-22
تحليل مقارن لنماذج كلاسيكية وكابوتو لانتشار COVID-19: تقييم التطعيم والاستقرار
الملخص
تستخدم عدة نماذج وبائية مشغل التفاضل من الدرجة الكسرية كابوتو دون تحديد أهميته. تتحقق هذه الدراسة من نموذج وبائي من نوع SAIVR يعتمد على مشغل كابوتو. COVID-19 يقتل. العدوى تضعف الجهاز المناعي. يصف مشغل كابوتو الكسرية تطعيم COVID-19. يتم تحديد الخصائص الأساسية للنظام باستخدام حساب التفاضل الكسرية. شمل تحليلنا استقرار النظام الكسرية وفقًا لمبدأ هايرز-أولام-راسياس والحالات المستقرة. يتم استكشاف تفرد ووجود حلول نظام كابوتو الكسرية. تحدد طريقة المربعات الصغرى معلمات النظام. مشغل كابوتو من الدرجة الكسرية
1 المقدمة
تمت محاكاة عددية وتجريبية للنموذج الرياضي الذي تم صياغته. تم توسيع النموذج الرياضي لتفشي الكوليرا الذي طوره المؤلف في [28] والتحقيق فيه من قبل جافيدي وآخرين [29] لالتقاط المشتق من الدرجة الكسرية كابوتو. في [30]، قام المؤلف بفحص الاستقرار غير المتجانس لبعض النماذج الوبائية البسيطة (SIS، SIR، SIRS)، بالإضافة إلى الأمراض المعروفة التي تنقلها النواقل روس في سياق كابوتو باستخدام دوال ليابونوف من نوع فولتيرا.
2 الصياغة الرياضية
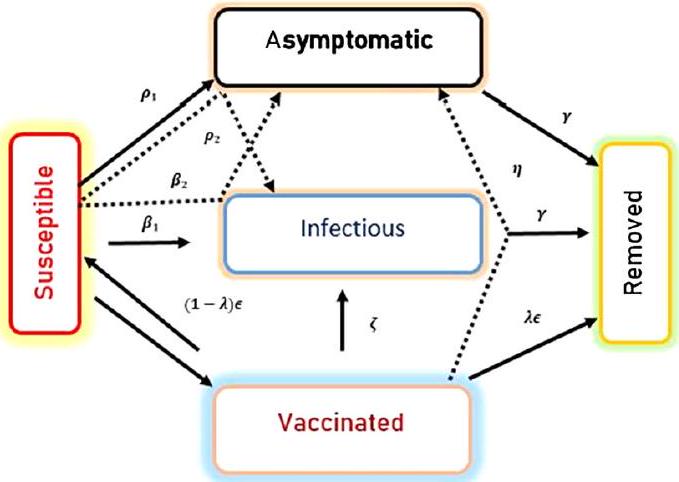
تسجيل الظواهر المتعلقة باللاتمحورية أكثر من المشتقات ذات الرتبة الصحيحة. لذلك، تم استخدام المشتقات الكسرية المستندة إلى الأوبئة أيضًا لمعالجة بعض الاتجاهات الوبائية. بشكل عام، لا ينتج هذا النموذج الأساسي/الكلاسيكي نتائج كافية أو مرضية، كما يتضح من فشل المعادلات التفاضلية الكلاسيكية من الرتبة الأولى في إعادة إنتاج البيانات الإحصائية التي تم جمعها خلال وباء حقيقي للمرض بدقة. في عملنا، استكشفنا مجموعة أكثر دقة وتعقيدًا من المعادلات التفاضلية الكسرية في محاولة لتحقيق نتائج أفضل تتماشى أكثر مع الواقع.
3 لماذا نموذج COVID-19 مع مشغل كابوتو؟
- لأنه من المعروف أن الأمراض المعدية تحتوي على مكونات وراثية، فإن البدائل الأكثر ملاءمة لنمذجة الأمراض المعدية هي المشغلين من الرتبة الكسرية الذين يمكن أن يحافظوا على ذاكرة الأنظمة المعنية [44]. بهذه الطريقة، يعتبر مشغل كابوتو الخيار الأفضل لاستبدال المشتق الزمني من الرتبة الصحيحة في نموذج COVID-19 الذي يتم الحديث عنه حاليًا.
- استبدال
بـ في صيغة كوشي للتكامل المتكرر ينتج عنه صيغة التكامل المعروفة ريمان-ليوفيلي، التي كانت أساسًا لتطوير العديد من الطرق العددية لحل المعادلات التفاضلية العادية والجزئية الكسرية. - استخدمت الأعمال الحديثة بنجاح مراجعة كابوتو للنماذج الوبائية التقليدية، التي تم اقترانها بتفاصيل تتعلق بوجود حل واحد ودراسة استقرار النظام [45]. في ذلك الجزء، تم استخدام المحاكاة لإظهار لماذا يعتبر متغير كابوتو أفضل من النموذج القياسي (الكلاسيكي: المشتقات من الرتبة الصحيحة).
- تظهر الأبحاث الوبائية المنشورة مؤخرًا [46] أن النماذج القديمة فشلت في حساب الديناميات المعقدة وغير القابلة للتنبؤ لانتشار العدوى. بدلاً من ذلك، استخدمنا بيانات فعلية تتعلق بالوباء، إلى حد كبير من مصادر موثوقة مثل منظمة الصحة العالمية والمقالات المنشورة علميًا، لتأكيد وت corroborate حسابات كابوتو. لتوضيح الرقم التناسلي الأساسي، الذي يصف العدد النموذجي للحالات الثانوية المصابة الناتجة عندما يدخل فرد معدٍ إلى فئة قابلة تمامًا للإصابة، يمكننا استخدام مشغل كابوتو التفاضلي لتحليل سلوك المرض تحت قيم مختلفة للمعلمات البيولوجية.
- أخيرًا، باستخدام مشغل من الرتبة الكسرية لأي نموذج فيزيائي أو بيولوجي، يمكن للمرء التحقق من عدم وجود معنى فيزيائي أو هندسي للمعامل الكسرية
مع الأخذ في الاعتبار أنه لا يوجد معنى فيزيائي أو هندسي حتى للمشتقات من الرتبة الصحيحة، مثل المعادلة التفاضلية من الرتبة الرابعة لانحراف شعاع [47] حيث لا يحمل المشتق الرابع نفسه أي معنى.
4 أفضل ملاءمة للمعلمات البيولوجية
| المعلمة | الشرح | (كابوتو) | (كلاسيكي) | المصدر |
|
|
معدل تعرض الأفراد للأعراض |
|
|
ملائم |
|
|
من الرتبة الكسرية |
|
1 | ملائم |
|
|
معدل العدوى غير المصابة | 0.002 | 0.02 | ثابت |
|
|
معدل العدوى للأفراد غير المصابين | 0.005 | 0.01 | ثابت |
|
|
معدل العدوى المصابة | 0.005 | 0.005 | ثابت |
|
|
معدل الإزالة | 1/9 | 1/12 | ثابت |
|
|
معدل الأفراد الملقحين (غير المناعيين) | 0.02 | 0.5 | ثابت |
|
|
معدل الانتقال الذي يتواصل فيه الأفراد غير المصابين ويعدون الأفراد الملقحين (لكنهم لا يزالون غير المناعيين) | 0.05 | 0.05 | ثابت |
|
|
معدل التطعيم للجرعة الأولى | 0.01 | 0.01 | ثابت |
|
|
فعالية اللقاح | 0.05 | 0.002 | ثابت |
|
|
المناعة والانتقال إلى قسم الإزالة | 0.02 | 0.02 | ثابت |
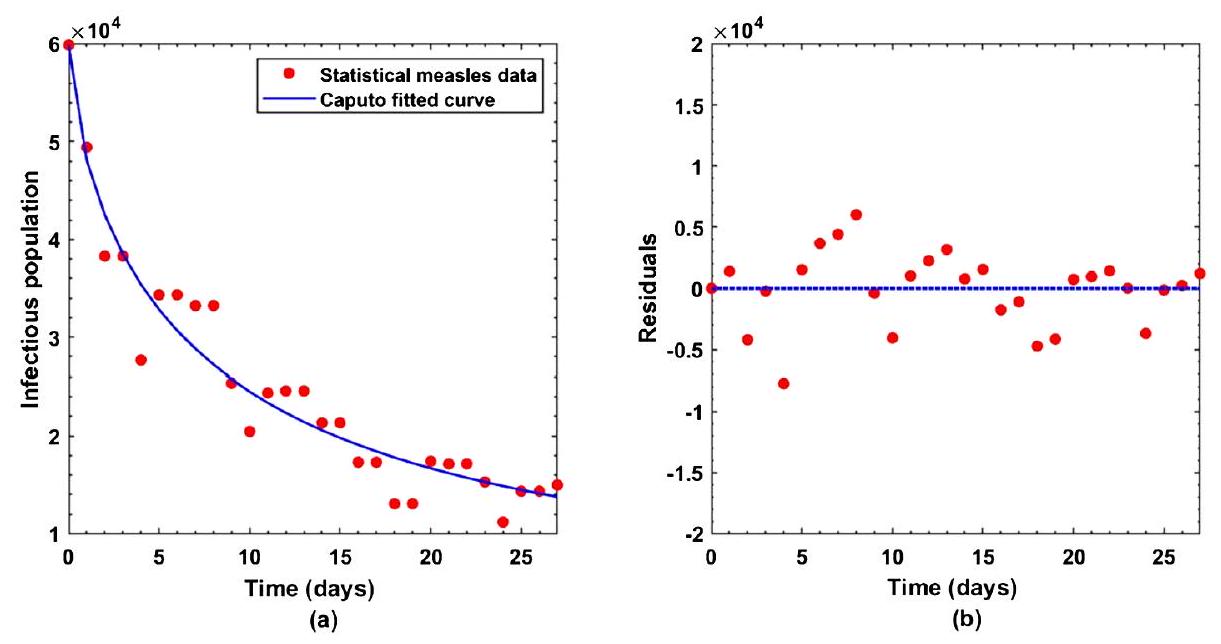

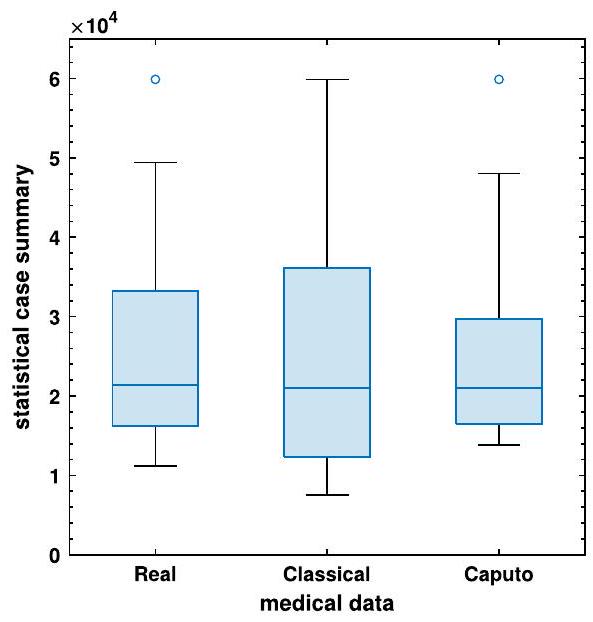
5 تحليل ملخص
5.1 نتائج الوجود والحصرية
5.2 وجود الحل
5.3 تفرد الحل
5.4 استقرار هايرز-أولام-راسياس
-
-
-
6 النتائج العددية من المحاكاة
بالنسبة لنموذج COVID-19 الذي تم اختياره ليتم تشغيله بواسطة مشغل كابوتو، هناك العديد من المعلمات الحاسمة التي تحتاج قيمها إلى اهتمام دقيق لتحديد ما إذا كانت
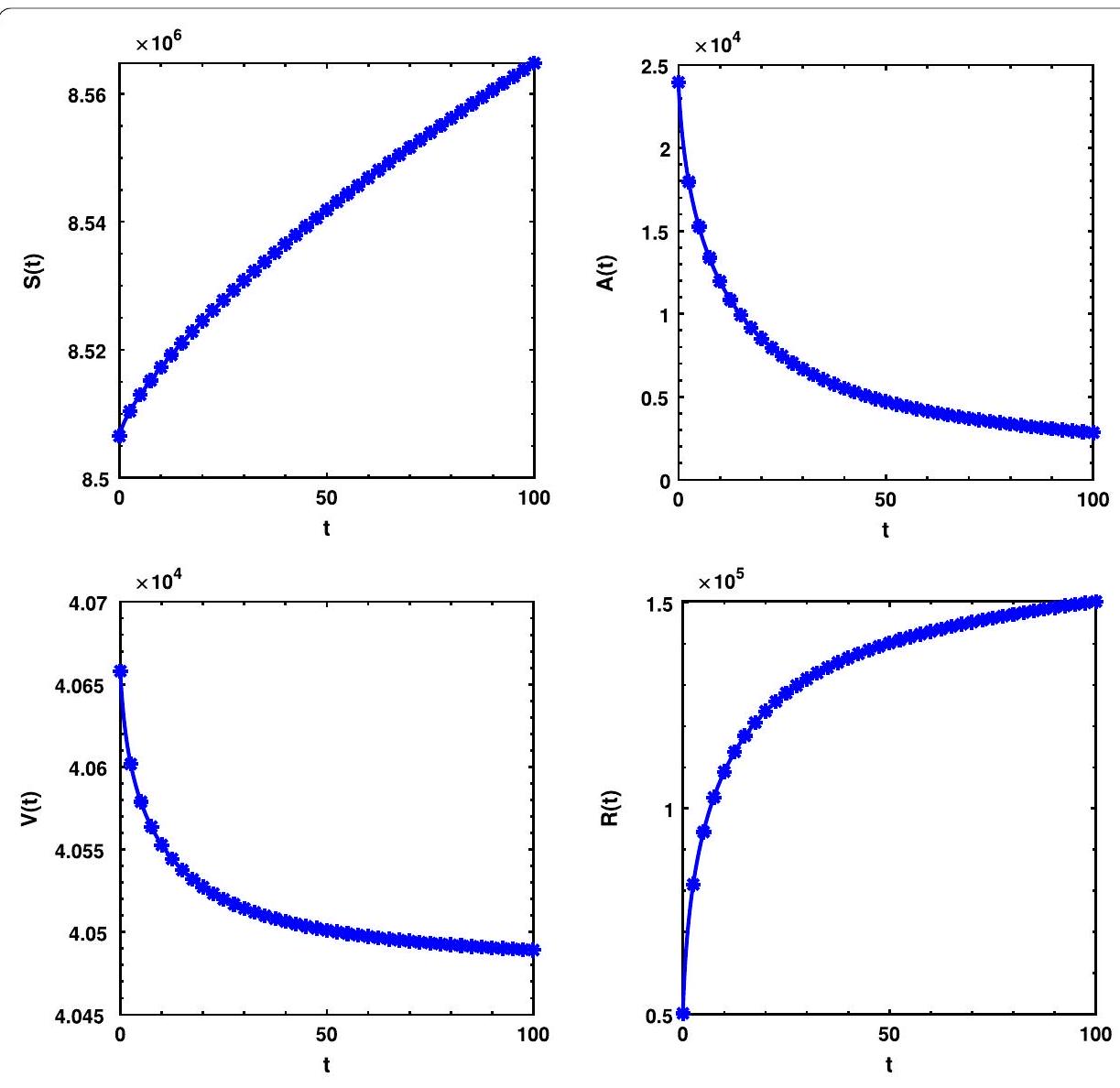


6.1 أثر الذاكرة والسمات الوراثية
7 الخاتمة
الشكر والتقدير
التمويل
الإعلانات
موافقة الأخلاقيات والموافقة على المشاركة
الموافقة على النشر
المصالح المتنافسة
مساهمات المؤلفين
تفاصيل المؤلف
تم الاستلام: 22 أغسطس 2023 تم القبول: 3 يناير 2024 تم النشر عبر الإنترنت: 22 يناير 2024
References
- Al-Shomrani, M.M., Musa, S.S., Yusuf, A.: Unfolding the transmission dynamics of monkeypox virus: an epidemiological modelling analysis. Mathematics 11(5), 1121 (2023)
- Jamil, S., Farman, M., Akgül, A., Saleem, M.U., Hincal, E., El Din, S.M.: Fractional order age dependent Covid-19 model: an equilibria and quantitative analysis with modeling. Results Phys. 53, 106928 (2023)
- Yao, S.W., Farman, M., Akgül, A., Nisar, K.S., Amin, M., Saleem, M.U., Inc, M.: Simulations and analysis of COVID-19 as a fractional model with different kernels. Fractals 31, 2340051 (2023)
- Zarin, R., Khan, M., Khan, A., Yusuf, A.: Deterministic and fractional analysis of a newly developed dengue epidemic model. Waves Random Complex Media, 1-34 (2023). https://doi.org/10.1080/17455030.2023.2226765
- Partohaghighi, M., Yusuf, A., Alshomrani, A.S., Sulaiman, T.A., Baleanu, D.: Fractional hyper-chaotic system with complex dynamics and high sensitivity: applications in engineering. Int. J. Mod. Phys. B, 2450012 (2023). https://doi.org/10.1142/S0217979224500127
- Liu, P., Rahman, M.U., Din, A.: Fractal fractional based transmission dynamics of COVID-19 epidemic model. Comput. Methods Biomech. Biomed. Eng. 25(16), 1852-1869 (2022)
- Liu, P., Huang, X., Zarin, R., Cui, T., Din, A.: Modeling and numerical analysis of a fractional order model for dual variants of SARS-CoV-2. Alex. Eng. J. 65, 427-442 (2023)
- Atede, A.O., Omame, A., Inyama, S.C.: A fractional order vaccination model for COVID-19 incorporating environmental transmission: a case study using Nigerian data. Bull. Biomath. 1(1), 78-110 (2023)
- Din, A., Li, Y., Khan, F.M., Khan, Z.U., Liu, P.: On analysis of fractional order mathematical model of hepatitis B using Atangana-Baleanu Caputo (ABC) derivative. Fractals 30(01), 2240017 (2022)
- Din, A., Li, Y., Yusuf, A., Ali, A.I.: Caputo type fractional operator applied to hepatitis B system. Fractals 30(01), 2240023 (2022)
- Liu, P., Din, A., Zarin, R.: Numerical dynamics and fractional modeling of hepatitis B virus model with non-singular and non-local kernels. Results Phys. 39, 105757 (2022)
- Arif, M., Di Persio, L., Kumam, P., Watthayu, W., Akgül, A.: Heat transfer analysis of fractional model of couple stress Casson tri-hybrid nanofluid using dissimilar shape nanoparticles in blood with biomedical applications. Sci. Rep. 13(1), 4596 (2023)
- Xu, C., Liu, Z., Pang, Y., Akgül, A.: Stochastic analysis of a COVID-19 model with effects of vaccination and different transition rates: real data approach. Chaos Solitons Fractals 170, 113395 (2023)
- Memon, Z., Qureshi, S., Memon, B.R.: Assessing the role of quarantine and isolation as control strategies for COVID-19 outbreak: a case study. Chaos Solitons Fractals 144, 110655 (2021)
- Du, M., Wang, Z., Hu, H.: Measuring memory with the order of fractional derivative. Sci. Rep. 3(1), 3431 (2013)
- Petráš, I., Terpák, J.: Fractional calculus as a simple tool for modeling and analysis of long memory process in industry. Mathematics 7(6), 511 (2019)
- Mohammadi, F., Moradi, L., Baleanu, D., Jajarmi, A.: A hybrid functions numerical scheme for fractional optimal control problems: application to nonanalytic dynamic systems. J. Vib. Control 24(21), 5030-5043 (2018)
- Rezapour, S., Etemad, S., Mohammadi, H.: A mathematical analysis of a system of Caputo-Fabrizio fractional differential equations for the anthrax disease model in animals. Adv. Differ. Equ. 2020(1), 481 (2020)
- Githire, G.T.O., Kimathi, G., Wainaina, M.: Analysis of transmission dynamics of anthrax in animals: a modeling approach. J. Sci. Res. Rep. 23(1), 1-9 (2019)
- Naik, P.A., Owolabi, K.M., Yavuz, M., Zu, J.: Chaotic dynamics of a fractional order HIV-1 model involving AIDS-related cancer cells. Chaos Solitons Fractals 140, 110272 (2020)
- Ullah, I., Ahmad, S., ur Rahman, M., Arfan, M.: Investigation of fractional order tuberculosis (TB) model via Caputo derivative. Chaos Solitons Fractals 142, 110479 (2021)
- Atangana, A., Qureshi, S.: Mathematical modeling of an autonomous nonlinear dynamical system for malaria transmission using Caputo derivative. In: Fractional Order Analysis: Theory, Methods and Applications, pp. 225-252 (2020)
- Diethelm, K.: A fractional calculus based model for the simulation of an outbreak of dengue fever. Nonlinear Dyn. 71(4), 613-619 (2013)
- Khan, M.A., Ullah, S., Farhan, M.: The dynamics of Zika virus with Caputo fractional derivative. AIMS Math. 4(1), 134-146 (2019)
- Tulu, T.W., Tian, B., Wu, Z.: Modeling the effect of quarantine and vaccination on Ebola disease. Adv. Differ. Equ. 2017(1), 178 (2017)
- Danane, J., Allali, K., Hammouch, Z.: Mathematical analysis of a fractional differential model of HBV infection with antibody immune response. Chaos Solitons Fractals 136, 109787 (2020)
- El-Saka, H.A.A.: Backward bifurcations in fractional-order vaccination models. J. Egypt. Math. Soc. 23(1), 49-55 (2015)
- Codeço, C.T.: Endemic and epidemic dynamics of cholera: the role of the aquatic reservoir. BMC Infect. Dis. 1(1), 1-14 (2001)
- Javidi, M., Ahmad, B.: A study of a fractional-order cholera model. Appl. Math. Inf. Sci. 8(5), 2195 (2014)
- Vargas-De-León, C.: Volterra-type Lyapunov functions for fractional-order epidemic systems. Commun. Nonlinear Sci. Numer. Simul. 24(1-3), 75-85 (2015)
- Özalp, N., Demirci, E.: A fractional order SEIR model with vertical transmission. Math. Comput. Model. 54(1-2), 1-6 (2011)
- Rezapour, S., Mohammadi, H., Jajarmi, A.: A new mathematical model for Zika virus transmission. Adv. Differ. Equ. 2020(1), 589 (2020)
- Qureshi, S.: Periodic dynamics of rubella epidemic under standard and fractional Caputo operator with real data from Pakistan. Math. Comput. Simul. 178, 151-165 (2020)
- Al-Deiakeh, R., Al-Smadi, M., Yusuf, A., Al-Omari, S., Momani, S.: Explicit solutions for fractional Chaffee-Infante reaction-diffusion coupled hierarchy system with conservation laws. Math. Methods Appl. Sci. 46, 12777-12793 (2023)
- Pinto, C.M., Carvalho, A.R.: The role of synaptic transmission in a HIV model with memory. Appl. Math. Comput. 292, 76-95 (2017)
- Naik, P.A., Yavuz, M., Qureshi, S., Zu, J., Townley, S.: Modeling and analysis of COVID-19 epidemics with treatment in fractional derivatives using real data from Pakistan. Eur. Phys. J. Plus 135(10), 1-42 (2020)
- Peter, O.J., Shaikh, A.S., Ibrahim, M.O., Nisar, K.S., Baleanu, D., Khan, I., Abioye, A.I.: Analysis and dynamics of fractional order mathematical model of COVID-19 in Nigeria using Atangana-Baleanu operator. Comput. Mater. Continua 66(2), 1823-1848 (2021)
- Baleanu, D., Mohammadi, H., Rezapour, S.: A fractional differential equation model for the COVID-19 transmission by using the Caputo-Fabrizio derivative. Adv. Differ. Equ. 2020(1), 299 (2020)
- Chen, T.M., Rui, J., Wang, Q.P., Zhao, Z.Y., Cui, J.A., Yin, L.: A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 9(1), 1-8 (2020)
- Baba, I.A., Nasidi, B.A.: Fractional order epidemic model for the dynamics of novel COVID-19. Alex. Eng. J. 60(1), 537-548 (2021)
- Faridi, W.A., Asjad, M.I., Jhangeer, A., Yusuf, A., Sulaiman, T.A.: The weakly non-linear waves propagation for Kelvin-Helmholtz instability in the magnetohydrodynamics flow impelled by fractional theory. Opt. Quantum Electron. 55(2), 172 (2023)
- Angeli, M., Neofotistos, G., Mattheakis, M., Kaxiras, E.: Modeling the effect of the vaccination campaign on the COVID-19 pandemic. Chaos Solitons Fractals 154, 111621 (2022)
- Coronel-Escamilla, A., Gomez-Aguilar, J.F., Stamova, I., Santamaria, F.: Fractional order controllers increase the robustness of closed-loop deep brain stimulation systems. Chaos Solitons Fractals 140, 110149 (2020)
- Pinto, C.M., Carvalho, A.R.: Diabetes mellitus and TB co-existence: clinical implications from a fractional order modelling. Appl. Math. Model. 68, 219-243 (2019)
- Zeb, A., Atangana, A., Khan, Z.A., Djillali, S.: A robust study of a piecewise fractional order COVID-19 mathematical model. Alex. Eng. J. 61(7), 5649-5665 (2022)
- Baba, I.A., Rihan, F.A.: A fractional-order model with different strains of COVID-19. Phys. A, Stat. Mech. Appl. 603, 127813 (2022)
- Bonanno, G., Di Bella, B., O’Regan, D.: Non-trivial solutions for nonlinear fourth-order elastic beam equations. Comput. Math. Appl. 62(4), 1862-1869 (2011)
- Diethelm, K., Ford, N.J., Freed, A.D.: A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 29(1), 3-22 (2002)
- Diethelm, K., Ford, N.J., Freed, A.D.: Detailed error analysis for a fractional Adams method. Numer. Algorithms 36(1), 31-52 (2004)
- Garrappa, R.: Numerical solution of fractional differential equations: a survey and a software tutorial. Mathematics 6(2), 16 (2018)
- Ahmed, I., Akgül, A., Jarad, F., Kumam, P., Nonlaopon, K.: A Caputo-Fabrizio fractional-order cholera model and its sensitivity analysis. Math. Model. Numer. Simul. Appl. 3(2), 170-187 (2023)
- Liu, F., Zhuang, P., Liu, Q.: Numerical methods of fractional partial differential equations and applications (2015)
- Özköse, F.: Long-term side effects: a mathematical modeling of COVID-19 and stroke with real data. Fractal Fract. 7(10), 719 (2023)
- Yavuz, M., Özköse, F., Susam, M., Kalidass, M.: A new modeling of fractional-order and sensitivity analysis for hepatitis-B disease with real data. Fractal Fract. 7(2), 165 (2023)
ملاحظة الناشر
- *المراسلة:
a.tassaddiq@mu.edu.sa¹قسم العلوم الأساسية والإنسانية، كلية علوم الحاسوب والمعلومات، جامعة المجمعة، المجمعة، 11952، المملكة العربية السعودية
القائمة الكاملة لمعلومات المؤلف متاحة في نهاية المقالة - © المؤلفون 2024. الوصول المفتوح، هذه المقالة مرخصة بموجب رخصة المشاع الإبداعي للاستخدام والمشاركة والتكيف والتوزيع وإعادة الإنتاج في أي وسيلة أو صيغة، طالما أنك تعطي الائتمان المناسب للمؤلفين الأصليين والمصدر، وتوفر رابطًا لرخصة المشاع الإبداعي، وتوضح ما إذا كانت هناك تغييرات قد تم إجراؤها. الصور أو المواد الأخرى من طرف ثالث في هذه المقالة مشمولة في رخصة المشاع الإبداعي للمقالة، ما لم يُشار إلى خلاف ذلك في سطر الائتمان للمادة. إذا لم تكن المادة مشمولة في رخصة المشاع الإبداعي للمقالة واستخدامك المقصود غير مسموح به بموجب اللوائح القانونية أو يتجاوز الاستخدام المسموح به، ستحتاج إلى الحصول على إذن مباشرة من صاحب حقوق الطبع والنشر. لعرض نسخة من هذه الرخصة، قم بزيارة http://creativecommons.org/licenses/by/4.0/.
DOI: https://doi.org/10.1186/s13663-024-00760-7
Publication Date: 2024-01-22
Comparative analysis of classical and Caputo models for COVID-19 spread: vaccination and stability assessment
Abstract
Several epidemiological models use the Caputo fractional-order differential operator without establishing its significance. This study verifies a Caputo operator-based fractional-order epidemiological model of the SAIVR type. COVID-19 kills. Infection weakens the immune system. The fractional Caputo operator describes COVID-19 immunization. Fundamental system characteristics are determined using fractional calculus. Our analysis included the fractional system’s Hyers-Ulam-Rassias stability and stable states. The uniqueness and existence of fractional Caputo system solutions are explored. The least-squares approach determines system parameters. The Caputo fractional-order
1 Introduction
itative and numerical simulations of the formulated mathematical model. The mathematical model of the cholera outbreak that the author developed in [28] was extended and investigated by Javidi et al. [29] to capture the Caputo fractional-order derivative. In [30], the author examined the uniform asymptotic stability of a few simple epidemic models (SIS, SIR, SIRS), as well as the well-known Ross vector-borne diseases in the Caputo sense using Lyapunov functions of the Volterra type.
2 Mathematical formulation

scribing phenomena related to non-locality than integer-order derivatives. Therefore, epidemic-based fractional derivatives have also been employed to address some epidemic tendencies. In general, this basic/classical model does not yield adequate or satisfactory results, as demonstrated by the failure of the classical first-order differential equations to accurately reproduce the statistical data collected during an actual epidemic of the disease. In our work, we have explored a more precise and intricate set of fractional differential equations in an effort to achieve better findings that are more in line with reality.
3 Why COVID-19 model with the Caputo operator?
- Because it is common knowledge that infectious diseases contain hereditary components, the most appropriate alternatives for modeling infectious diseases are fractional-order operators that can potentially preserve the memory of the systems being considered [44]. In this way, the Caputo operator is the best choice to replace the integer-order time derivative in the COVID-19 model that is currently being talked about.
- Substituting
- Recent works have successfully used Caputo’s revision of traditional epidemiological models, which are paired with particulars regarding the existence of a single solution and a study of the system’s stability [45]. In that part, simulations were used to show why the Caputo variant is better than the standard (classical: integer-order derivatives) one.
- Epidemiological research published recently [46] demonstrates that older models failed to account for the complex and unpredictable dynamics of an infection’s spread. Instead, we used actual data regarding the outbreak, largely from reputable sources like the World Health Organization and scientifically published articles, to confirm and corroborate the Caputo accounts. To further clarify the basic reproductive number, which describes the typical number of secondary infected cases produced when an infectious individual enters a completely susceptible class, we can use Caputo’s differential operator to analyze the disease’s behavior under different values for biological parameters.
- Finally, using a fractional-order operator for any physical or biological model, one can verify that there is no physical or geometrical meaning of the fractional parameter
4 Best fitting of biological parameters
| Parameter | Explanation | (Caputo) | (Classical) | Source |
|
|
the rate at which individuals are exposed to symptomatic |
|
|
fitted |
|
|
fractional-order |
|
1 | fitted |
|
|
asymptomatic infection rate | 0.002 | 0.02 | fixed |
|
|
the rate at which individuals are infected to asymptomatic | 0.005 | 0.01 | fixed |
|
|
symptomatic infection rate | 0.005 | 0.005 | fixed |
|
|
the removal rate | 1/9 | 1/12 | fixed |
|
|
the rate at which a vaccinated (not immune) | 0.02 | 0.5 | fixed |
|
|
the transmission rate at which asymptomatic individual comes into contact and infects vaccinated (but still not immune) individuals | 0.05 | 0.05 | fixed |
|
|
the first shot vaccination rate | 0.01 | 0.01 | fixed |
|
|
the vaccine efficacy | 0.05 | 0.002 | fixed |
|
|
immunity and moving to the removed compartment | 0.02 | 0.02 | fixed |



5 Abstract analysis
5.1 Existence and uniqueness results
5.2 Existence of the solution
5.3 Uniqueness of the solution
5.4 Hyers-Ulam-Rassias stability
-
-
-
6 Numerical results from simulations
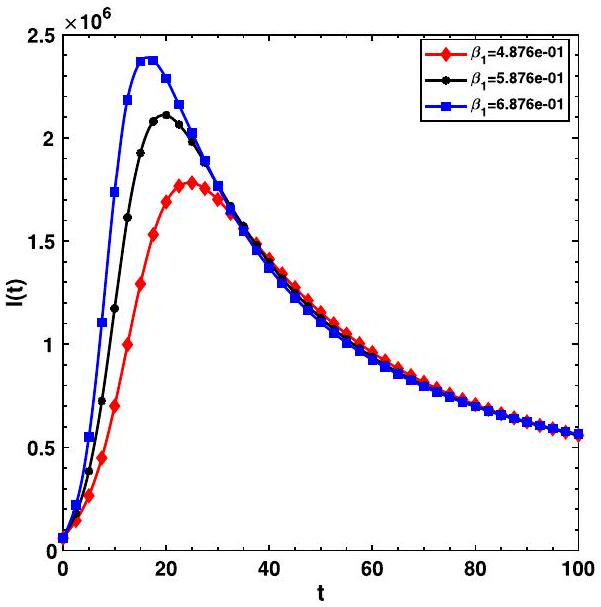
For the COVID-19 model selected to be operated on by the Caputo operator, there are many crucial parameters whose values need careful attention to determine whether they




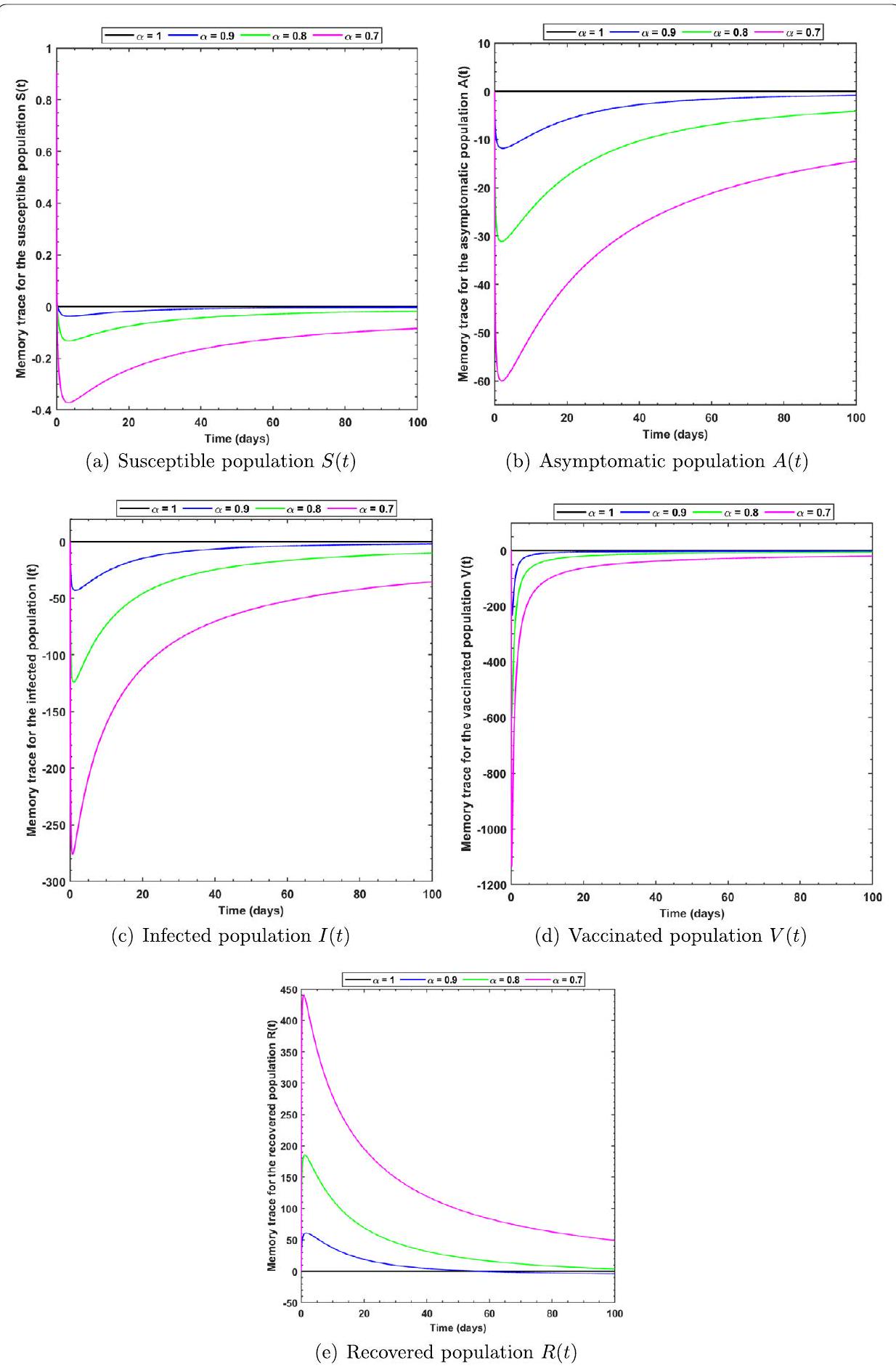
6.1 Memory trace and hereditary traits

7 Conclusion
Acknowledgements
Funding
Declarations
Ethics approval and consent to participate
Consent for publication
Competing interests
Author contributions
Author details
Received: 22 August 2023 Accepted: 3 January 2024 Published online: 22 January 2024
References
- Al-Shomrani, M.M., Musa, S.S., Yusuf, A.: Unfolding the transmission dynamics of monkeypox virus: an epidemiological modelling analysis. Mathematics 11(5), 1121 (2023)
- Jamil, S., Farman, M., Akgül, A., Saleem, M.U., Hincal, E., El Din, S.M.: Fractional order age dependent Covid-19 model: an equilibria and quantitative analysis with modeling. Results Phys. 53, 106928 (2023)
- Yao, S.W., Farman, M., Akgül, A., Nisar, K.S., Amin, M., Saleem, M.U., Inc, M.: Simulations and analysis of COVID-19 as a fractional model with different kernels. Fractals 31, 2340051 (2023)
- Zarin, R., Khan, M., Khan, A., Yusuf, A.: Deterministic and fractional analysis of a newly developed dengue epidemic model. Waves Random Complex Media, 1-34 (2023). https://doi.org/10.1080/17455030.2023.2226765
- Partohaghighi, M., Yusuf, A., Alshomrani, A.S., Sulaiman, T.A., Baleanu, D.: Fractional hyper-chaotic system with complex dynamics and high sensitivity: applications in engineering. Int. J. Mod. Phys. B, 2450012 (2023). https://doi.org/10.1142/S0217979224500127
- Liu, P., Rahman, M.U., Din, A.: Fractal fractional based transmission dynamics of COVID-19 epidemic model. Comput. Methods Biomech. Biomed. Eng. 25(16), 1852-1869 (2022)
- Liu, P., Huang, X., Zarin, R., Cui, T., Din, A.: Modeling and numerical analysis of a fractional order model for dual variants of SARS-CoV-2. Alex. Eng. J. 65, 427-442 (2023)
- Atede, A.O., Omame, A., Inyama, S.C.: A fractional order vaccination model for COVID-19 incorporating environmental transmission: a case study using Nigerian data. Bull. Biomath. 1(1), 78-110 (2023)
- Din, A., Li, Y., Khan, F.M., Khan, Z.U., Liu, P.: On analysis of fractional order mathematical model of hepatitis B using Atangana-Baleanu Caputo (ABC) derivative. Fractals 30(01), 2240017 (2022)
- Din, A., Li, Y., Yusuf, A., Ali, A.I.: Caputo type fractional operator applied to hepatitis B system. Fractals 30(01), 2240023 (2022)
- Liu, P., Din, A., Zarin, R.: Numerical dynamics and fractional modeling of hepatitis B virus model with non-singular and non-local kernels. Results Phys. 39, 105757 (2022)
- Arif, M., Di Persio, L., Kumam, P., Watthayu, W., Akgül, A.: Heat transfer analysis of fractional model of couple stress Casson tri-hybrid nanofluid using dissimilar shape nanoparticles in blood with biomedical applications. Sci. Rep. 13(1), 4596 (2023)
- Xu, C., Liu, Z., Pang, Y., Akgül, A.: Stochastic analysis of a COVID-19 model with effects of vaccination and different transition rates: real data approach. Chaos Solitons Fractals 170, 113395 (2023)
- Memon, Z., Qureshi, S., Memon, B.R.: Assessing the role of quarantine and isolation as control strategies for COVID-19 outbreak: a case study. Chaos Solitons Fractals 144, 110655 (2021)
- Du, M., Wang, Z., Hu, H.: Measuring memory with the order of fractional derivative. Sci. Rep. 3(1), 3431 (2013)
- Petráš, I., Terpák, J.: Fractional calculus as a simple tool for modeling and analysis of long memory process in industry. Mathematics 7(6), 511 (2019)
- Mohammadi, F., Moradi, L., Baleanu, D., Jajarmi, A.: A hybrid functions numerical scheme for fractional optimal control problems: application to nonanalytic dynamic systems. J. Vib. Control 24(21), 5030-5043 (2018)
- Rezapour, S., Etemad, S., Mohammadi, H.: A mathematical analysis of a system of Caputo-Fabrizio fractional differential equations for the anthrax disease model in animals. Adv. Differ. Equ. 2020(1), 481 (2020)
- Githire, G.T.O., Kimathi, G., Wainaina, M.: Analysis of transmission dynamics of anthrax in animals: a modeling approach. J. Sci. Res. Rep. 23(1), 1-9 (2019)
- Naik, P.A., Owolabi, K.M., Yavuz, M., Zu, J.: Chaotic dynamics of a fractional order HIV-1 model involving AIDS-related cancer cells. Chaos Solitons Fractals 140, 110272 (2020)
- Ullah, I., Ahmad, S., ur Rahman, M., Arfan, M.: Investigation of fractional order tuberculosis (TB) model via Caputo derivative. Chaos Solitons Fractals 142, 110479 (2021)
- Atangana, A., Qureshi, S.: Mathematical modeling of an autonomous nonlinear dynamical system for malaria transmission using Caputo derivative. In: Fractional Order Analysis: Theory, Methods and Applications, pp. 225-252 (2020)
- Diethelm, K.: A fractional calculus based model for the simulation of an outbreak of dengue fever. Nonlinear Dyn. 71(4), 613-619 (2013)
- Khan, M.A., Ullah, S., Farhan, M.: The dynamics of Zika virus with Caputo fractional derivative. AIMS Math. 4(1), 134-146 (2019)
- Tulu, T.W., Tian, B., Wu, Z.: Modeling the effect of quarantine and vaccination on Ebola disease. Adv. Differ. Equ. 2017(1), 178 (2017)
- Danane, J., Allali, K., Hammouch, Z.: Mathematical analysis of a fractional differential model of HBV infection with antibody immune response. Chaos Solitons Fractals 136, 109787 (2020)
- El-Saka, H.A.A.: Backward bifurcations in fractional-order vaccination models. J. Egypt. Math. Soc. 23(1), 49-55 (2015)
- Codeço, C.T.: Endemic and epidemic dynamics of cholera: the role of the aquatic reservoir. BMC Infect. Dis. 1(1), 1-14 (2001)
- Javidi, M., Ahmad, B.: A study of a fractional-order cholera model. Appl. Math. Inf. Sci. 8(5), 2195 (2014)
- Vargas-De-León, C.: Volterra-type Lyapunov functions for fractional-order epidemic systems. Commun. Nonlinear Sci. Numer. Simul. 24(1-3), 75-85 (2015)
- Özalp, N., Demirci, E.: A fractional order SEIR model with vertical transmission. Math. Comput. Model. 54(1-2), 1-6 (2011)
- Rezapour, S., Mohammadi, H., Jajarmi, A.: A new mathematical model for Zika virus transmission. Adv. Differ. Equ. 2020(1), 589 (2020)
- Qureshi, S.: Periodic dynamics of rubella epidemic under standard and fractional Caputo operator with real data from Pakistan. Math. Comput. Simul. 178, 151-165 (2020)
- Al-Deiakeh, R., Al-Smadi, M., Yusuf, A., Al-Omari, S., Momani, S.: Explicit solutions for fractional Chaffee-Infante reaction-diffusion coupled hierarchy system with conservation laws. Math. Methods Appl. Sci. 46, 12777-12793 (2023)
- Pinto, C.M., Carvalho, A.R.: The role of synaptic transmission in a HIV model with memory. Appl. Math. Comput. 292, 76-95 (2017)
- Naik, P.A., Yavuz, M., Qureshi, S., Zu, J., Townley, S.: Modeling and analysis of COVID-19 epidemics with treatment in fractional derivatives using real data from Pakistan. Eur. Phys. J. Plus 135(10), 1-42 (2020)
- Peter, O.J., Shaikh, A.S., Ibrahim, M.O., Nisar, K.S., Baleanu, D., Khan, I., Abioye, A.I.: Analysis and dynamics of fractional order mathematical model of COVID-19 in Nigeria using Atangana-Baleanu operator. Comput. Mater. Continua 66(2), 1823-1848 (2021)
- Baleanu, D., Mohammadi, H., Rezapour, S.: A fractional differential equation model for the COVID-19 transmission by using the Caputo-Fabrizio derivative. Adv. Differ. Equ. 2020(1), 299 (2020)
- Chen, T.M., Rui, J., Wang, Q.P., Zhao, Z.Y., Cui, J.A., Yin, L.: A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 9(1), 1-8 (2020)
- Baba, I.A., Nasidi, B.A.: Fractional order epidemic model for the dynamics of novel COVID-19. Alex. Eng. J. 60(1), 537-548 (2021)
- Faridi, W.A., Asjad, M.I., Jhangeer, A., Yusuf, A., Sulaiman, T.A.: The weakly non-linear waves propagation for Kelvin-Helmholtz instability in the magnetohydrodynamics flow impelled by fractional theory. Opt. Quantum Electron. 55(2), 172 (2023)
- Angeli, M., Neofotistos, G., Mattheakis, M., Kaxiras, E.: Modeling the effect of the vaccination campaign on the COVID-19 pandemic. Chaos Solitons Fractals 154, 111621 (2022)
- Coronel-Escamilla, A., Gomez-Aguilar, J.F., Stamova, I., Santamaria, F.: Fractional order controllers increase the robustness of closed-loop deep brain stimulation systems. Chaos Solitons Fractals 140, 110149 (2020)
- Pinto, C.M., Carvalho, A.R.: Diabetes mellitus and TB co-existence: clinical implications from a fractional order modelling. Appl. Math. Model. 68, 219-243 (2019)
- Zeb, A., Atangana, A., Khan, Z.A., Djillali, S.: A robust study of a piecewise fractional order COVID-19 mathematical model. Alex. Eng. J. 61(7), 5649-5665 (2022)
- Baba, I.A., Rihan, F.A.: A fractional-order model with different strains of COVID-19. Phys. A, Stat. Mech. Appl. 603, 127813 (2022)
- Bonanno, G., Di Bella, B., O’Regan, D.: Non-trivial solutions for nonlinear fourth-order elastic beam equations. Comput. Math. Appl. 62(4), 1862-1869 (2011)
- Diethelm, K., Ford, N.J., Freed, A.D.: A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 29(1), 3-22 (2002)
- Diethelm, K., Ford, N.J., Freed, A.D.: Detailed error analysis for a fractional Adams method. Numer. Algorithms 36(1), 31-52 (2004)
- Garrappa, R.: Numerical solution of fractional differential equations: a survey and a software tutorial. Mathematics 6(2), 16 (2018)
- Ahmed, I., Akgül, A., Jarad, F., Kumam, P., Nonlaopon, K.: A Caputo-Fabrizio fractional-order cholera model and its sensitivity analysis. Math. Model. Numer. Simul. Appl. 3(2), 170-187 (2023)
- Liu, F., Zhuang, P., Liu, Q.: Numerical methods of fractional partial differential equations and applications (2015)
- Özköse, F.: Long-term side effects: a mathematical modeling of COVID-19 and stroke with real data. Fractal Fract. 7(10), 719 (2023)
- Yavuz, M., Özköse, F., Susam, M., Kalidass, M.: A new modeling of fractional-order and sensitivity analysis for hepatitis-B disease with real data. Fractal Fract. 7(2), 165 (2023)
Publisher’s Note
- *Correspondence:
a.tassaddiq@mu.edu.sa¹Department of Basic Sciences and Humanities, College of Computer and Information Sciences, Majmaah University, Al-Majmaah, 11952, Saudi Arabia
Full list of author information is available at the end of the article - © The Author(s) 2024. Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
