تفضيل قوي للطاقة المظلمة الديناميكية في قياسات DESI BAO وSN Robust preference for Dynamical Dark Energy in DESI BAO and SN measurements

المجلة: Journal of Cosmology and Astroparticle Physics، المجلد: 2024، العدد: 10
DOI: https://doi.org/10.1088/1475-7516/2024/10/035
تاريخ النشر: 2024-10-01

تفضيل قوي للطاقة المظلمة الديناميكية في قياسات DESI BAO وSN

ويليام جياري، مهدي نجفي، سوبريا بان، إليونورا دي فالنتينو، جواد تي. فيروزجائي مدرسة الرياضيات والإحصاء، جامعة شيفيلد، طريق هونسفيلد، شيفيلد S3 7RH، المملكة المتحدة قسم الفيزياء، جامعة ك.ن. توسي للتكنولوجيا، صندوق بريد 15875-4416، طهران، إيران مختبر PDAT، قسم الفيزياء، جامعة ك.ن. توسي للتكنولوجيا، صندوق بريد 15875-4416، طهران، إيران قسم الرياضيات، جامعة الرئاسة، 86/1 شارع الكلية، كولكاتا 700073، الهند معهد علوم الأنظمة، جامعة دوربان للتكنولوجيا، صندوق بريد 1334، دوربان 4000، جمهورية جنوب أفريقيا مدرسة الفيزياء، معهد الأبحاث في العلوم الأساسية (IPM)، صندوق بريد 193955531، طهران، إيرانالبريد الإلكتروني: w.giare@sheffield.ac.uk، mahdinajafi12676@yahoo.com، supriya.maths@presiuniv.ac.in، e.divalentino@sheffield.ac.uk، firouzjaee@kntu.ac.ir

الملخص

تظهر قياسات تذبذبات الصوت الباريونية (BAO) الأخيرة التي أصدرتها DESI، عند دمجها مع بيانات الخلفية الكونية الميكروية (CMB) من بلانك وعينتين مختلفتين من المستعرات العظمى من النوع Ia (بانثيون-بلس و DESY5) تفضيلًا للطاقة المظلمة الديناميكية (DDE) التي تتميز بمعادلة حالة شبيهة بالكيان الحاضر التي عبرت إلى نظام الشبح في الماضي. فرضية أساسية لهذه النتيجة هي افتراض معلمة خطية لتشيفالييه-بولارسكي-ليندر (CPL) لوصف تطور معادلة حالة الطاقة المظلمة (EoS). في هذه الورقة، نختبر ما إذا كان هذا الافتراض يؤثر على النتائج وإلى أي مدى. لمنع توسيع الشكوك في استنتاج المعلمات الكونية وتسهيل المقارنة المباشرة مع حالة CPL الأساسية، نركز على 4 نماذج بديلة معروفة جيدًا تتكون، تمامًا مثل CPL، من معلمين حرين فقط: معادلة حالة الطاقة المظلمة الحالية ( ) ومعلمة تقيس تطورها الديناميكي ( ). نوضح أن التفضيل للطاقة المظلمة الديناميكية يظل قويًا بغض النظر عن المعلمة: تظل باستمرار في نظام الكيان، بينما تشير باستمرار إلى تفضيل لتطور ديناميكي نحو نظام الشبح. هذه النزعة تعزز بشكل كبير بواسطة قياسات SN من DESY5. من خلال مقارنة أفضل ملاءمة التي تم الحصول عليها ضمن كل نموذج DDE، نلاحظ أن المعلمة الخطية CPL ليست الحالة الأكثر ملاءمة. من بين النماذج المدروسة، تؤدي معادلة الحالة المقترحة من باربوزا وألكانيز باستمرار إلى تحسين كبير.

المحتويات

1 المقدمة ….. 1
2 نماذج الطاقة المظلمة الديناميكية ….. 5
2.1 معلمة تشيفالييه-بولارسكي-ليندر ….. 5
2.2 المعلمة الأسية ….. 6
2.3 معلمة جاسيال-باجلا-بادمانابهان ….. 6
2.4 المعلمة اللوغاريتمية ….. 6
2.5 معلمة باربوزا-ألكانيز ….. 7
3 الطرق ….. 7
3.1 التحليلات الإحصائية ….. 7
3.2 مجموعات البيانات ….. 8
4 النتائج ….. 9
4.1 النتائج لمعلمة CPL ….. 10
4.2 النتائج للمعلمة الأسية ….. 11
4.3 النتائج لمعلمة JBP ….. 13
4.4 النتائج للمعلمة اللوغاريتمية ….. 15
4.5 النتائج للمعلمة BA ….. 17
5 المناقشات والاستنتاجات ….. 18
A معادلة الحالة، انزياح المحور، وعبور الشبح عبر النماذج المختلفة ….. 21

1 المقدمة

واحدة من أكثر الاكتشافات إثارة للاهتمام وغير المتوقعة في العقود الثلاثة الماضية هي أن الكون يمر بمرحلة تسارع في التوسع. تم طرح هذا لأول مرة في عام 1998 من خلال ملاحظات المستعرات العظمى من النوع Ia البعيدة [1، 2]، ومنذ ذلك الحين تم تأكيده من خلال مجموعة واسعة من الأدلة الأخرى [3-45، 45-62].
نظرًا لأن جميع القوى والمكونات المعروفة في الطبيعة ستؤدي إلى تباطؤ معدل توسع الكون، فإن التسارع نفسه يتطلب آلية فيزيائية تتجاوز النموذج القياسي للتفاعلات الأساسية، قادرة على مواجهة التباطؤ، مما يؤدي بدلاً من ذلك إلى مرحلة من الطاقة المظلمة (DE) حيث يتميز الديناميكية بالضغط السلبي مع معادلة حالة فعالة (EoS) ، وهي حالة تتبع مباشرة من المعادلة الثانية لفريدمان (المعروفة أيضًا بمعادلة التسارع) [75-82].
في الإطار النظري الموصوف بواسطة النموذج القياسي للطاقة المظلمة، يتم تمثيل DE بواسطة مصطلح ثابت كوني إيجابي ( ) في معادلة أينشتاين مع كثافة طاقتها التي تشكل الغالبية العظمى من ميزانية طاقة الكون. على الرغم من بساطتها الظاهرة، فإن هذه التفسير ليست خالية من المشاكل والمحدودات المفاهيمية [75، 78، 83-92]. أولاً، إدخال مكون ثابت كوني إيجابي في
معادلات مجال الجاذبية الموصوفة بواسطة النسبية العامة (GR) يعني العيش في كون ديسيتير غير متناهي، مما يبدو أنه يتعارض مع العديد من النظريات/النماذج للجاذبية الكمومية التي تقترح بدلاً من ذلك كونًا غير متناهي مضادًا للديسيتير [93-97]. ثانيًا، يبدو من الطبيعي تمامًا التساؤل عما جعلنا محظوظين للعيش بالضبط في الحقبة الكونية عندما أصبح مثل هذا المكون الثابت ليس فقط ذا صلة ولكن حتى مهيمنًا مقارنة بمساهمات أخرى مثل المادة، مما يغير تاريخ توسع الكون بشكل بارز لدرجة أنه سمح لنا بأن نكون على دراية بوجوده وآثاره [82، 98-100]. أخيرًا، والأهم من ذلك، عندما يتعلق الأمر بالتفسيرات الفيزيائية، فإن أي شيء يساهم في كثافة طاقة الفراغ يتصرف كما لو كان ثابتًا كونيًا، مما يجمع ضمن موتر الطاقة-الزخم كـ بسبب عدم انحياز لورنتز. بناءً على حسابات نظرية الحقل الكمومي القياسية، من المتوقع أن تكون مساهمة كثافة الطاقة عند النقطة الصفرية هي ، والتي، اعتمادًا على مقياس قطع الطول الموجي فوق البنفسجي، توجد في مكان ما بين إلى أوامر من حيث الحجم أكبر مما يتم استنتاجه من البيانات الكونية [83]. وهذا يؤدي إلى واحدة من أكبر الخلافات بين التوقعات النظرية والملاحظات، مما يتطلب مستوى من الضبط الدقيق يبدو أنه يتجاوز ما يمكن أن تشرحه أي نظريات حالية بشكل واقعي [78،83،101-103]. نتيجة لذلك، من منظور نظري، تظل طبيعة DE واحدة من أكبر الألغاز في الفيزياء الحديثة، مما يحافظ على اهتمام بحثي كبير في مجتمع الفيزياء عالية الطاقة.
من منظور ملاحظي، أدى التحقيق في طبيعة DE إلى إثارة اهتمام بحثي قابل للمقارنة مع ذلك المدفوع بالمشاكل النظرية المحيطة بتفسيرها الفيزيائي [143، 165، 168-268]. أدت الملاحظات المتزايدة الدقة للإشعاع الخلفي الكوني الميكروي (CMB)، التي تم الحصول عليها من تجارب مثل WMAP [20، 21]، ومؤخراً، القمر الصناعي بلانك [39، 40]، بالإضافة إلى تلسكوب أتاكاما لعلم الكونيات (ACT) [43، 44، 56، 269] وتلسكوب القطب الجنوبي (SPT) [51، 270، 271]، إلى توفير قياسات دقيقة للغاية لطيف القوة الزاوي للحرارة والقطبية، مما يكشف عن لقطة دقيقة للكون عند سطح التشتت الأخير في الوقت نفسه، أدى التقدم في علم الفلك الرصدي وعلم الفلك إلى سلسلة من الاستطلاعات الحالية التي تهدف إلى تحديد خصائص الكون عند انزياح منخفض من خلال مجموعة متعددة من الأدلة، بما في ذلك – ولكن لا تقتصر على – تذبذبات الصوت الباريونية (BAO) وقياسات المستعرات العظمى من النوع Ia (SN). لقد أدت هذه الجهود الجماعية إلى عصر جديد من علم الكونيات الدقيق، مما سمح في النهاية بدقة على مستوى النسبة المئوية في استنتاج المعلمات الكونية وتمكين اختبارات دقيقة للفيزياء داخل وخارج إطار CDM [289-291].
على الرغم من هذه الإنجازات الملحوظة، ليس من المبالغة أن نقول إنه في وقت كتابة هذا، فإن الملاحظات غير حاسمة بشأن الطبيعة الفيزيائية للطاقة المظلمة. بينما تبدو الانحرافات البعيدة عن النموذج القياسي CDM مقيدة بشدة [292]، تظل العديد من
الأطر النظرية البديلة والطرق الظاهرة التي تتميز بفيزياء جديدة في القطاع المظلم من النموذج على الأقل قابلة للتصديق.
محاولين تلخيص نقاش معقد للغاية، يمكننا الالتزام بمبدأ شفرة أوكام وبدء التفكير في واحدة من أبسط الفرضيات بخلاف الثابت الكوني. وهذا يتضمن افتراض أن الطاقة المظلمة يمكن نمذجتها كسائل عام ذو معادلة حالة ثابتة. بترك كمعامل حر في النموذج النظري، يمكن للملاحظات الكونية تقييد الانحرافات عن قيمة الثابت الكوني. في هذا الصدد، قد يتكهن المرء بوجود تفضيل لمكون طاقة مظلمة شبيه بالشبح عند التركيز حصريًا على بيانات إشعاع الخلفية الكونية الميكروي (CMB) من بلانك. ) [40، 245]. ومع ذلك، كما هو موثق بشكل واسع في الأدبيات، فإن هذا التفضيل لم يتم تأكيده من خلال تجارب CMB المستقلة مثل ACT وSPT [44، 51، 271، 340]، والأهم من ذلك – أنه يفتقر إلى دعم متسق من ملاحظات الكون المحلي. عند الجمع بين وبيانات SN معًا، لا انحراف مقنع عن يُرى، مما قد يعزز تفسير الثابت الكوني [245].
ومع ذلك، يمكن للمرء أن يجادل بأن البساطة قد لا تكون دائمًا من خصائص الطبيعة. من خلال دفع هذا النهج إلى الأمام، يمكننا تخفيف افتراض وجود معادلة حالة ثابتة والنظر في نماذج حيث يتغير مع توسع الكون – هنا وبعد ذلك يعرف بالطاقة المظلمة الديناميكية (DDE). لقد خضعت هذه الإمكانية، جنبًا إلى جنب مع مختلف التصورات الفيزيائية المقترحة، لاختبارات واسعة؛ انظر، على سبيل المثال، المراجع [194، 195، 313، 319، 341-353]. من منظور رصدي، فإن بيانات إشعاع الخلفية الكونية (CMB) وحدها لديها قدرة محدودة على تقييد نماذج DDE بسبب التأثيرات الضئيلة المتبقية في عصر سطح التشتت الأخير وزيادة عدد المعلمات الكونية [354-356]. حتى في التوصيفات البسيطة التي تهدف إلى تقليل عدد درجات الحرية الحرة، تنتج تجارب إشعاع الخلفية الكونية قيودًا تكون عادةً واسعة جدًا لتوفير نتائج مفيدة. لذلك، تكتسب ملاحظات الكون المحلي أهمية أساسية.
تُعَدُّ الإصدارات الأخيرة من بيانات BAO من أداة الطيف الضوئي للطاقة المظلمة (DESI) [58، 59] نقطة تحول مهمة في دراسة نماذج الطاقة المظلمة المتغيرة، وكذلك – وإن كان بدرجة أقل – قياسات وحدات المسافة من انفجار النجوم (SN) من تجميع Union3 [357] أولاً، ومؤخراً من الملاحظات التي استمرت خمس سنوات من مسح الطاقة المظلمة (DESY5) [60-62]. قبل هذه البيانات المحدثة، لم يظهر أي تفضيل كبير لصالح نماذج الطاقة المظلمة المتغيرة، بالتأكيد ليس بالقدر المطلوب لتحدي تفسير الثابت الكوني الأساسي [292]. ومن المثير للاهتمام، عندما يتم دمج ملاحظات BAO من DESI مع بيانات CMB من بلانك وقياسات وحدات المسافة من SN (سواء من كتالوج Pantheon-plus [55، 358]، أو تجميع Union3 [357]، أو DESY5 [60-62])، فإنها تنتج مؤشرات قوية لصالح الطاقة المظلمة المتغيرة. على وجه التحديد، ضمن التمثيل الخطي لبارامتر Chevallier-Polarski-Linder (CPL) لمعادلة حالة الطاقة المظلمة، [170,172] – حيث يمثل معادلة الحالة الحالية DE يقيس التطور الديناميكي – نلاحظ تفضيلًا لـ و في
مستوى إحصائي يتراوح بين 2.5 و ، اعتمادًا على التركيبة المحددة من بيانات SN المستخدمة [336].
بشكل غير متوقع، أدت هذه النتائج إلى تسخين النقاشات الأخيرة، مما أثار العديد من إعادة التحليلات وإعادة التفسيرات [59، 253، 264، 266، 267، 359-375]. كما أن “المطالبات الاستثنائية تتطلب أدلة استثنائية”، فإننا بالتأكيد ننصح ونتوخى الحذر. ومع ذلك، حتى مع الأخذ في الاعتبار جميع التحذيرات والقيود المحتملة المحيطة بالإصدار الأول لبيانات DESI، فإنه من غير القابل للإنكار أن هناك تفضيلاً إحصائيًا عاليًا لصالح DDE يحمل اهتمامًا جوهريًا – إذا تم تأكيد ذلك، فسيكون هذا بمثابة أول دليل ملموس على فيزياء جديدة تتجاوز النموذج القياسي لعلم الكون.
نظرًا للتداعيات المحتملة لهذه النتيجة، من الطبيعي التساؤل عن قوتها. باستثناء أي مشكلات منهجية محتملة في هذه البيانات نحن نفحص ما إذا كان و إلى أي مدى قد يؤثر افتراض معلمة خطية لمعادلة الحالة للطاقة المظلمة على النتائج الحالية. على الرغم من أن معلمة CPL قد تم إثبات أنها تتطابق مع تطور الخلفية للمسافات الناتجة عن معادلات الحركة الدقيقة للطاقة المظلمة بدقة تقارب للنماذج الكونية القابلة للتطبيق على نطاق واسع من الفيزياء، بما في ذلك الحقول السلمية، والجاذبية المعدلة، والانتقالات الطورية (انظر، على سبيل المثال، المراجع [172، 378])، تم اقتراح معلمات أخرى على مر السنين (التي قد تنحرف عن CPL في كل من و تظل هذه النماذج البديلة مسموح بها وفقًا للملاحظات الحالية. يمكن أن يمثل اختبار هذه النماذج البديلة ضد بيانات جديدة بالتأكيد تمرينًا مفيدًا لتسليط الضوء على الدور الذي تلعبه المعايرة نفسها. وللإنصاف، فقد بدأت العملية بالفعل مع عدة مجموعات مستقلة تشارك بنشاط في هذا النشاط [364، 379-384].
نظرًا للعدد الهائل من المعلمات المقترحة على مر السنين والتي تم تحليلها مؤخرًا فيما يتعلق ببيانات DESI، هناك بعض التحذيرات التي يجب أخذها في الاعتبار. أولاً وقبل كل شيء، غالبًا ما تقدم المعلمات البديلة معلمات إضافية مقارنةً بـ CPL. هذه ميزة وعيب في آن واحد: من ناحية، فإن الأخذ في الاعتبار المزيد من درجات الحرية يسمح بمزيد من المرونة في . من ناحية أخرى، فإن هذا يعني عادةً تخفيف القوة التقييدية العامة بسبب التأثيرات المجمعة للازدواجيات والارتباطات بين المعلمات. ثانيًا، قد تختلف التفسيرات الفيزيائية للمعلمات المعنية عن تلك المستخدمة في نموذج CPL. وهذا يزيد من تعقيد مقارنة النتائج، مما يجعل من الصعب استخلاص إرشادات عامة حول التفضيل نحو DDE.
لتجاوز هذه الصعوبات، في هذه المقالة، نقوم باختبار نماذج DDE مختلفة مع السماح بمقارنة عادلة للنتائج. نحن نركز اهتمامنا على خمسة نماذج معروفة جيدًا تلبي المعايير التالية: (i) تتكون من معلمين لوصف تطور و ; (ii) يحتفظ هذان المعلمان بنفس المعنى الفيزيائي كما في معلمة CPL؛ (iii) لنفس تركيبات الأزواج الشكل الناتج من ينحرف عن CPL إما بالقرب من الحقبة الحالية أو في الماضي، اعتمادًا على الحالة المحددة.
الورقة منظمة على النحو التالي. في القسم 2، نعرض الإعداد النظري لمعادلات الجاذبية ونقترح معلمات الطاقة المظلمة التي نرغب في دراستها. في القسم 3، نصف البيانات الرصدية والمنهجية لتقييد معلمات الطاقة المظلمة المقترحة. في القسم 4، نقدم القيود على السيناريوهات الناتجة للطاقة المظلمة. أخيرًا، في القسم 5، نستخلص استنتاجاتنا العامة.

2 نماذج الطاقة المظلمة الديناميكية

إن اعتبار مكون DDE في النماذج الكونية يُحدث تغييرات في كل من الديناميات الخلفية وديناميات الاضطرابات الكونية.
التركيز على كوزمولوجيا فريدمان-ليمتر-روبرتسون-وكر المسطحة والنماذج حيث معادلة الحالة للطاقة المظلمة يمكن وصفه بدالة مستمرة لعامل المقياس، وتقرأ المعادلة الأولى لفريدمان
هنا هو معامل هابل، والنقطة تشير إلى المشتق بالنسبة للزمن الفيزيائي تشير الصيغة الفرعية 0 إلى الكميات التي يتم تقييمها في الوقت الحاضر بينما ، و هي كثافات الطاقة في الإشعاع، والمادة، والطاقة المظلمة، على التوالي.
عندما يتعلق الأمر بالاضطرابات الكونية، يتطلب عدم التماثل في نظرية النسبية العامة تثبيت مقياس. في مقياس التزامن، يُقرأ عنصر الخط [385]
أين هو الزمن المتناظر، و هي الجزء المكاني غير المضطرب والمضطرب من موترات المترية. بالنسبة لمكون سائل المعادلات التي تحكم الاضطرابات الكثافة غير البعدية وانحراف الـ سرعة السائل “-ث” في فضاء فورييه هي [385]:
حيث تشير الرموز المميزة إلى المشتق بالنسبة للزمن المتناغم هو اضطراب المقياس المتزامن المعتاد، هو معامل هابل المتناظر، هو عدد الموجة في فضاء فورييه، يمثل الإجهاد غير المتجانس لـ -السائل، و يمثل سرعة الصوت الأديباتيكية لـ -السائل المحدد على أنه في هذا العمل، نثبت سرعة الصوت المربعة لمكون الطاقة المظلمة في إطار السكون. كما هو متوقع على نطاق واسع بالنسبة لأبسط نماذج الديناميكا الديناميكية المستندة إلى حقل عددي خفيف مرتبط بشكل طفيف مع حد حركي قياسي.
بعد أن قمنا بتحديد الخلفية وديناميات الاضطراب، نقوم الآن بإدراج ووصف النماذج الخمسة المختلفة ذات المعاملين المستخدمين لـ .

2.1 بارامترية شيفالييه-بولارسكي-ليندر

يمكن اعتبار النموذج المقترح من قبل شيفالييه، بولارسكي وليندر [170،172] (CPL فيما بعد) كمعيار أساسي يُستخدم في معظم التحليلات التي تركز على DDE، بما في ذلك هذا العمل. في هذا السيناريو، تقرأ معادلة الحالة للطاقة المظلمة
كما ذُكر بالفعل في المقدمة، تشمل مزاياه فضاء الطور ثنائي الأبعاد القابل للإدارة، والحد من سلوك الانزياح الأحمر الخطي عند الانزياح الأحمر المنخفض، والسلوك المحدود عند الانزياح الأحمر العالي، والدقة العالية في إعادة بناء معادلات حالة مختلف الحقول الاسكالر والعلاقات الناتجة بين المسافة والانزياح الأحمر حتى الدقة، والحساسية الجيدة للبيانات الملاحظة، وتفسير فيزيائي بسيط. وينشأ الأخير من تمثيله كامتداد تايلور لـ حول العصر الحالي حتى الطلب الأول: و الذي هو معامل الحد الديناميكي.

2.2 التمثيل الأسي

كخطوة تالية، نعتبر الشكل الأسّي لمعادلة الحالة DE [386، 387]
حتى الرتبة الأولى من توسع تايلور، فإن هذا الوصف يتقلص إلى معلمة CPL حول . ومع ذلك، كما تبتعد كثيرًا عن 1، يمكن أن يقدم الأس من (الانحرافات الصغيرة) عن نظام CPL الخطي دون زيادة أبعاد فضاء المعلمات [259].

2.3 معلمة جسال-باجلا-بادمانابهان

المعلمة الثالثة التي تم دراستها في هذا العمل هي النموذج المقترح من قبل جسال-باجلا بادمانابان في المرجع [178] (JBP فيما بعد). في هذه الحالة، معادلة الحالة للطاقة المظلمة هي
يتميز بمجموع حد خطي وحد تربيعي في عامل المقياس. عندما قريب من 1، المصطلح يصبح قابلاً للمقارنة مع مما يؤدي إلى اختلافات متوقعة عند الانزياح الأحمر المنخفض مقارنة بـ CPL.

2.4 التمثيل اللوغاريتمي

نعتبر الشكل اللوغاريتمي التالي لمعادلة الحالة:
حسب أفضل معرفتنا، تم تقديم هذه المعلمة في الأصل من قبل ج. إيفستاثيو في المرجع [169] لالتقاط سلوك فئة واسعة من نماذج الحقل الاسكالر المحتمل للطاقة المظلمة عند الانزياح الأحمر المنخفض. . هنا، مع قدر معقول من الشجاعة وبعد إجراء اختبارات استقرار شاملة، نمد هذا التوصيف حتى من حيث المبدأ، بالنسبة لبعض تركيبات المعلمات، يمكن أن ينمو الحد اللوغاريتمي في القيمة المطلقة ويتسبب في عدم الاستقرار. ومع ذلك، نظرًا للقيود الحالية على البيانات والنمو البطيء اللوغاريتمي
معامل سابق
[0.005, 0.1]
[0.01, 0.99]
[1.61, 3.91]
[0.8, 1.2]
[0.01، 0.8]
[0.5, 10]
[-3,1]
[-3, 2]
الجدول 1. النطاقات للتوزيعات السابقة المسطحة المفروضة على المعلمات الكونية الحرة في التحليل.
النمو، هذا ليس هو الحال. نجد أن المعاملات يمكن توسيعها بأمان إلى انزياح أحمر عالٍ لأن مساهمة الطاقة المظلمة تظل ضئيلة إلى حد كبير مقارنةً بالمكونات الأخرى في ميزانية طاقة الكون.

2.5 باربوزا-ألكانيز التماثل

النموذج الأخير (ولكن كما سنرى، ليس الأقل) المعني في تحليلنا هو الذي اقترحه باربوزا وألكانيز في المرجع [181] (المشار إليه بـ BA فيما بعد). في هذه الحالة، يتميز معادلة الحالة للطاقة المظلمة بالشكل الوظيفي التالي:
تظهر هذه المعاملات سلوكًا خطيًا عند الانزياحات الحمراء المنخفضة وتظل جيدة التصرف كما مع السماح بالانحرافات عن سيناريو CPL الأساسي.

3 طرق

في هذا القسم، نصف المنهجيات الإحصائية ومجموعات البيانات الملاحظة المستخدمة في تحليلنا.

3.1 التحليلات الإحصائية

يمكن وصف الكوزمولوجيا الناتجة عن جميع نماذج DDE الخمسة المذكورة في القسم 2 بـ 8 معلمات حرة: كثافة الطاقة الباريونية الفيزيائية كثافة طاقة المادة المظلمة الباردة الفيزيائية سعة الطيف السكالاري البدائي مؤشره الطيفي عمق البصريات لإعادة التأين حجم الزاوية لأفق الصوت والمعلمان الحرّان اللذان يصفان قطاع الطاقة المظلمة – أي القيمة الحالية لمعادلة الحالة للطاقة المظلمة والمعامل الذي يصف تطوره الديناميكي لمقارنة التنبؤات النظرية مع الملاحظات، نقوم بتنفيذ هذه النماذج في خمسة إصدارات معدلة مختلفة من الشيفرة الكونية المتاحة للجمهور CAMB [388، 389] ونستكشف التوزيعات الخلفية لمساحة المعلمات ذات الأبعاد الثمانية من خلال إجراء سلسلة ماركوف مونت كارلو (MCMC).
تحليلات عبر العينة المتاحة للجمهور Cobaya [390، 391] التي تستخدم تنفيذ تسلسل سرعة السحب السريع [392]. يتم تقييم تقارب سلاسل MCMC المولدة عبر معلمة جيلمان-روبين [393]. لجميع النماذج ومجموعات البيانات، نحتاج إلى لكي تعتبر السلاسل متقاربة. في الجدول 1، نقدم نطاقات الأوليات المسطحة التي تُترك فيها المعلمات لتتغير بحرية.

3.2 مجموعات البيانات

مجموعة البيانات المعنية في تحليلاتنا هي:
  • بلانك: قياسات تباين درجة حرارة إشعاع الخلفية الكونية الميكروي (CMB) واستقطاب طيف القوة، وطيف القوة المتقاطع، ومزيج طيف قوة عدسات ACT وبلانك. جميع احتمالات CMB المستخدمة في هذا العمل مدرجة أدناه:
    (ط) قياسات طيف الطاقة لعدم تجانس درجة الحرارة والاستقطاب، ، ، و ، على مقاييس صغيرة ( )، التي تم الحصول عليها من احتمال بلانك بليك [40، 394]؛
    (ii) قياسات طيف التباينات في درجة الحرارة، على نطاق واسع )، التي تم الحصول عليها من خلال احتمال قائد بلانك [40، 394]؛
    (iii) قياسات طيف استقطاب وضعية E، على نطاق واسع 30)، تم الحصول عليها بواسطة محاكاة بلانك SimAll [40، 394]؛
    (رابعاً) إعادة بناء طيف إمكانيات العدسة، الذي تم الحصول عليه من إصدار بيانات Planck PR4 NPIPE [395] المستخدم بالاقتران مع احتمالية عدسة ACT-DR6 [56، 269].
  • DESI: قياسات تذبذبات الصوت الباريونية (BAO) المستخرجة من ملاحظات المجرات والكوازارات [58]، وليمين- [396] مؤشرات من السنة الأولى من الملاحظات باستخدام أداة الطيف الضوئي للطاقة المظلمة (DESI). تشمل هذه القياسات المسافة المتحركة العرضية، أفق هابل، والمسافة المتوسطة الزاوية كما هو ملخص في الجدول I من المرجع [336].
  • بانثيون بلس: قياسات معاملات المسافة لـ 1701 منحنى ضوئي لـ 1550 سوبرنوفا من النوع Ia تم تأكيدها طيفياً، مستمدة من ثمانية عشر مسحاً مختلفاً، تم جمعها من عينة بانثيون بلس [55، 358].
  • DESY5: قياسات معاملات المسافة لـ 1635 سوبرنوفا من النوع Ia تغطي نطاق الانزياح الأحمر من التي تم جمعها خلال السنوات الخمس الكاملة من برنامج سوبرنوفا لاستطلاع الطاقة المظلمة (DES) [60-62]، بالإضافة إلى 194 سوبرنوفا منخفضة الانزياح الأحمر في نطاق الانزياح الأحمر من التي تتشارك مع عينة بانثيون بلس [55، 358].
نختتم هذا القسم بملاحظة أخيرة. تركز تحليلاتنا على عينتين من نوع Ia من المستعرات الأعظمية: PantheonPlus وDESY5، مع استبعاد عينة Union3. كما تم تسليط الضوء في ورقة DESI [336]، من بين هذه العينات الثلاث، تنتج PantheonPlus (التي تستخدم مستعرات أعظمية مؤكدة طيفياً) أقل تفضيل، ولكنه ذو دلالة، لنموذج DDE، حيث تنحرف بـ
حول من سيناريو الثابت الكوني. بالمقابل، يظهر DESY5 (الذي يستخدم الفوتومترية) أكبر تحول نحو DDE، عند تظهر عينة Union3 (التي تستخدم أيضًا SN المؤكدة طيفيًا) تفضيلًا لـ DDE حول ، تقع بين PantheonPlus و DESY5. على الرغم من أن Union3 يوفر تأكيدًا قيمًا لهذه النتائج، هنا نركز على العينتين اللتين تمثلان أصغر وأكبر انحرافات عن الثابت الكوني.

4 نتائج

في هذا القسم، نقدم القيود الرصدية على النماذج الخمسة لـ DDE التي تم النظر فيها في هذه المقالة. نناقش النتائج نموذجًا تلو الآخر، مختبرين كل حالة ضد ثلاث مجموعات بيانات مختلفة: Planck + DESI، Planck + DESI + PantheonPlus، و Planck + DESI + DESY5. لا نخفى أن العدد الكبير من النماذج التي تم تحليلها وتشابه النتائج التي تم الحصول عليها قد يجعل المناقشة التالية تبدو متكررة بعض الشيء (على الرغم من أنها ضرورية). لذلك، يمكن للقراء المهتمين بنتائج نماذج معينة العثور على القيود العددية، والارتباطات ثنائية الأبعاد، ودوال التوزيع الخلفي أحادية الأبعاد للمعلمات الرئيسية كما يلي:
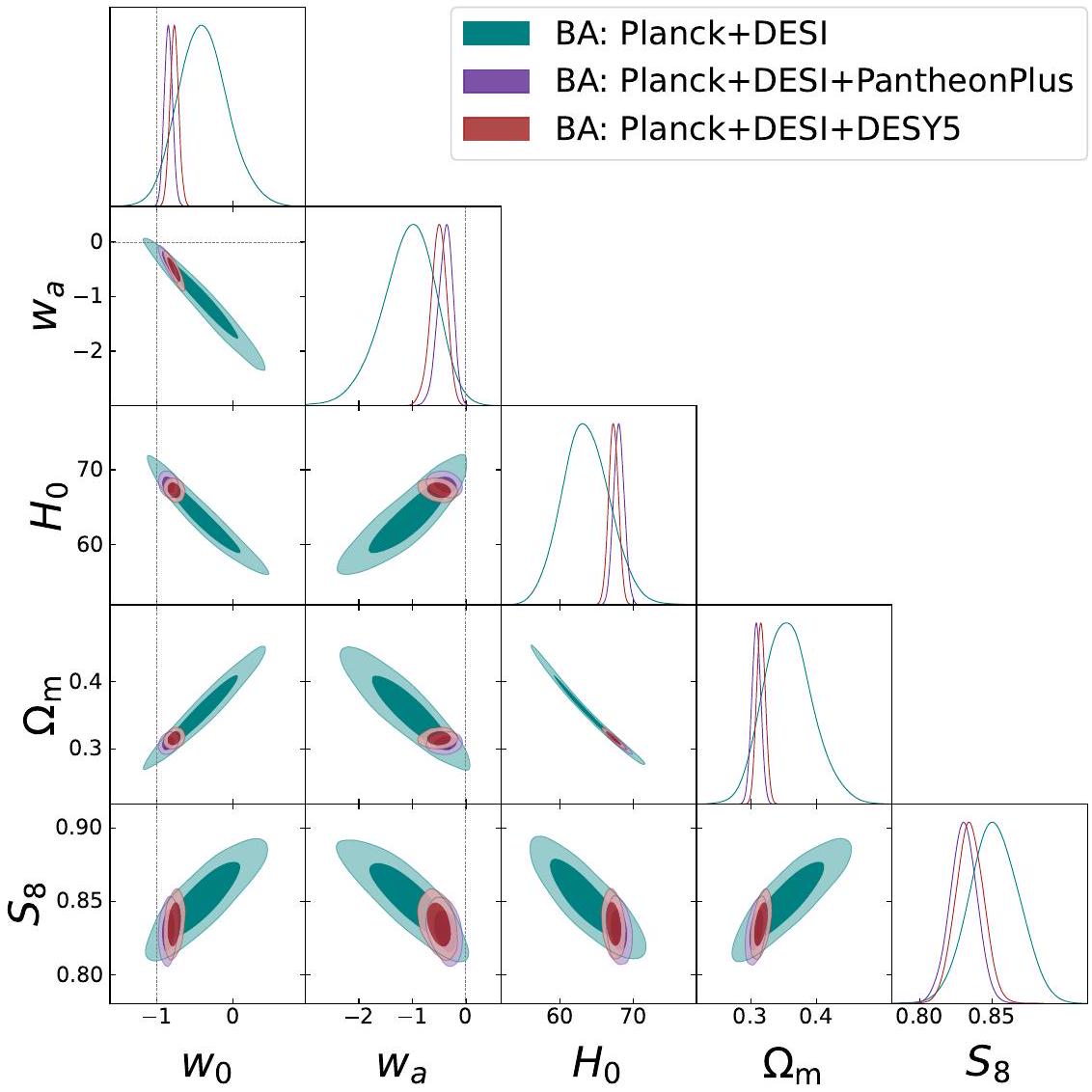
  • الجدول 2 والشكل 1 يلخصان القيود العددية وارتباطات المعلمات لحالة CPL الأساسية (2.5). النتائج لهذه الحالة مفصلة في القسم 4.1.
  • تقدم الجدول 3 والشكل 2 النتائج للمعامل الأسي (2.6)، الذي تم مناقشته في القسم 4.2.
  • توفر الجدول 4 والشكل 3 النتائج لنموذج JBP EoS (2.7)، الذي تم مناقشته في القسم 4.3.
  • تلخص الجدول 5 والشكل 4 النتائج للمعلمة اللوغاريتمية (2.8)، المفصلة في القسم 4.4.
  • تقدم الجدول 6 والشكل 5 النتائج للمعلمة BA (2.9)، التي تم مناقشتها في القسم 4.5.
على العكس، يمكن للقراء المهتمين بنظرة شاملة على النتائج وتفسيرها وآثارها الرجوع مباشرة إلى القسم 5. بدلاً من ذلك، يتم تقديم مناقشة شاملة لسلوك EoS المستنتج من مجموعات البيانات المختلفة المستخدمة في التحليل عبر نماذج متنوعة، بالإضافة إلى القيود على الكميات الحاسمة التي تساعد في تفسير النتائج التي تم مناقشتها في هذا القسم – مثل انزياح المحور (أي الانزياحات التي يتم فيها تقييد معادلة الحالة بشكل أفضل بواسطة البيانات الحالية) وعبور الشبح – في الملحق A ويتم تلخيصها في الشكل 7 والجدول 7. يمكن للقراء المهتمين الرجوع إلى هذا الملحق لمزيد من التفاصيل.

4.1 نتائج المعلمة CPL

تُعطى القيود العددية التي تم الحصول عليها من خلال اعتماد معلمة CPL الأساسية في الجدول 2. يعرض الشكل 1 المعلمات الرئيسية التي تميز هذا النموذج (أي، القيمة الحالية لـ EoS والمعلمة التي تحدد تطورها مع الانزياح ) بالإضافة إلى ارتباطاتها مع معلمات كونية أخرى ذات أهمية جوهرية لتاريخ التوسع في الكون في الأوقات المتأخرة مثل ثابت هابل ، وكثافة الطاقة الكونية الحالية ، ومعلمة تجمع المادة .
معلمة Planck+DESI Planck + DESI + PantheonPlus Planck+DESI+DESY5
-6.8 -8.4 -15.2
الجدول 2. معلمة CPL (2.5) – قيود CL على المعلمات الكونية الحرة والمشتقة لثلاث مجموعات بيانات مختلفة مفصلة في القسم 3. تشير القيم السلبية لـ إلى تحسين في التوافق مع البيانات مقارنة بـ .
نستعيد جميع النتائج التي تم مناقشتها في ورقة إصدار DESI الأخيرة [336]. بالنسبة لـ Planck+DESI، تفضل القيود وجود EoS كوانتية حالية مع عند مما يظهر تحولًا ملحوظًا بعيدًا عن . من ناحية أخرى، يوفر تلميحات عن تطور ديناميكي نحو نظام الشبح.
يؤدي إضافة PantheonPlus إلى تحسين القيود على فضاء المعلمات بشكل كبير، مما يقلل من أشرطة الخطأ على معلمات DE بمقدار يصل إلى 5 مرات. على الرغم من أن يتحول نحو -1، إلا أنه يبقى بشكل صارم في نظام الكوانتية: . يتماشى مع نتائج DESI 2024 [59]، حيث تزداد القيمة المتوسطة لـ مقارنة بـ Planck + DESI، الآن تقرأ . هذا يعزز الأدلة على وجود مكون DDE شبيه بالشبح في الماضي بحوالي ، انظر أيضًا الشكل 1.
عند استبدال PantheonPlus بـ DESY5 نوع Ia SN، نلاحظ تحولًا قدره بعيدًا عن -1، مما يؤدي إلى . هذا يضع في عمق نظام الكوانتية، انظر أيضًا الشكل 1. بالمثل، وُجد أن غير صفري عند دلالة إحصائية عالية. وبالتالي، تبقى الأدلة على DDE أقوى في حالة Planck + DESI + DESY5 مقارنة بـ Planck + DESI + PantheonPlus، وتخرج حالة الثابت الكوني بعيدًا عن حدود الاحتمالية المشتركة في المستوى، كما هو موضح في الشكل 1.
الشكل 1. معلمة CPL (2.5) – توزيعات خلفية أحادية الأبعاد وحدود هامشية ثنائية الأبعاد للمعلمات الرئيسية كما تم الحصول عليها من مجموعات بيانات Planck + DESI وPlanck + DESI + PantheonPlus وPlanck + DESI + DESY5.

4.2 نتائج المعلمة الأسية

نقدم القيود التي تم الحصول عليها من خلال افتراض معلمة أسية لـ EoS DE في الجدول 3. في الشكل 2، نعرض وظائف توزيع الخلفية أحادية الأبعاد وحدود هامشية ثنائية الأبعاد للمعلمات الكونية الرئيسية.
كما هو معتاد، نختبر النموذج ضد ثلاث مجموعات بيانات مختلفة تتضمن قياسات DESI BAO. مع التركيز على مجموعة Planck + DESI الدنيا، نجد – تختلف بشكل كبير عن -1 وعميق في نظام الكوانتية. بالمثل، قريب من بعيدًا عن الحالة غير الديناميكية ، مما يعزز تفضيل Planck + DESI لـ DDE.
تدعم إضافة قياسات PantheonPlus SN هذا التفضيل: تضيّق القيود على في نظام الكوانتية، مبتعدة عن بأكثر من . بالإضافة إلى ذلك، وُجد أن غير صفري عند أكثر من . بشكل عام، توفر Planck + DESI + PantheonPlus أدلة على DDE مع EoS الحالية في نظام الكوانتية وتطور ديناميكي يتجاوز نظام الشبح، كما هو موضح بوضوح في الشكل 2.
عندما نركز على مجموعة بيانات Planck + DESI + DESY 5، تصبح الأدلة على DDE أكثر وضوحًا بشكل ملحوظ. تبقى بشكل صارم في نظام الكوانتية
معلمة Planck+DESI Planck + DESI + PantheonPlus Planck+DESI+DESY5
-6.9 -7.8 -15.2
الجدول 3. معلمة أسية (2.6) – قيود CL على المعلمات الكونية الحرة والمشتقة لثلاث مجموعات بيانات مختلفة مفصلة في القسم 3. تشير القيم السلبية لـ إلى تحسين في التوافق مع البيانات مقارنة بـ .
نظام، بينما هو بعيدًا عن السيناريو غير الديناميكي ؛ انظر مرة أخرى الشكل 2.
بشكل عام، من حيث القيود على المعلمات الكونية، تتفق هذه النتائج مع تلك المستمدة من معلمة CPL في القسم السابق، مما يبرز مرونة الأدلة على DDE ويخفف من المخاوف بشأن الاعتماد على النموذج لهذه النتائج الخاصة.
الشكل 2. معلمة أسية (2.6) – توزيعات خلفية أحادية الأبعاد وحدود هامشية ثنائية الأبعاد للمعلمات الرئيسية كما تم الحصول عليها من مجموعات بيانات Planck + DESI وPlanck + DESI + PantheonPlus وPlanck + DESI + DESY5.

4.3 نتائج معلمة JBP

تُعطى القيود العددية لمعلمة JBP في الجدول 4، بينما تُظهر حدود الاحتمالية الهامشية للمعلمات المعتادة في الشكل 3.
عند النظر في Planck + DESI، على عكس المعلمات الأخرى الموصوفة حتى الآن (مثل CPL والشكل الأسّي)، تبقى غير محدودة ويمكن اشتقاق حد أعلى لـ عند . على العكس، تبقى في نظام الكوانتية ( )، مما يؤكد الاتجاه العام نحو وجود EoS كوانتية حالية.
عند النظر في PantheonPlus بالاشتراك مع Planck وDESI، نحصل على – غير صفري عند أكثر من . بالإضافة إلى ذلك، يتم تضييق القيود على 0.086 ضمن جزء الكوانتية من فضاء المعلمات كما هو موضح في الشكل 3. وبالتالي، يتم تأكيد الأدلة على DDE لهذه المعلمة أيضًا.
أخيرًا، نستبدل PantheonPlus بقياسات SN من نوع DESY5. في هذه الحالة، نحصل على و ، مما يؤكد أن الأدلة على DDE تصبح أكثر وضوحًا مع DESY5. تصل هذه الأدلة إلى دلالة إحصائية . ومع ذلك، عند مقارنة الشكل 3 مع الرسوم البيانية المثلثية الخاصة بالمعلمات الأخرى، نلاحظ أنه بالنسبة لهذا النموذج، تبقى الشكوك أوسع بكثير، خاصة بالنسبة للمعلمات التي تصف EoS DE. يمكن تفسير ذلك من حيث التطور الغريب لـ
معلمة Planck+DESI Planck + DESI + PantheonPlus Planck+DESI+DESY5
< 0.648
-5.6 -6.4 -16.0
الجدول 4. معلمة JBP (2.7) – قيود CL و حدود CL العليا على المعلمات الكونية الحرة والمشتقة لثلاث مجموعات بيانات مختلفة مفصلة في القسم 3. تشير القيم السلبية لـ إلى تحسين في التوافق مع البيانات مقارنة بـ .
EoS DE التي تم الحصول عليها في هذا النموذج. كما تم مناقشته بالتفصيل في الملحق A، فإن معلمة JBP تقدم ظاهرة أكثر تفصيلاً فيما يتعلق بتطور EoS DE. بسبب طبيعتها التربيعية في عامل المقياس، يتجاوز تطور EoS ضمن معلمة JBP مرتين. عند الانزياح المنخفض، يتصرف بشكل مشابه للمعلمات الأخرى؛ ومع ذلك، بعد الانتقال الأول من الكوانتية إلى الشبح، يقترب من قيمة دنيا حول قبل أن يرتفع مرة أخرى، مما يؤدي إلى عبور ثانٍ من الشبح إلى الكوانتية عند . يتناقض هذا السلوك مع النماذج الأخرى، حيث تبقى EoS ضمن نظام الشبح. كما هو موضح بالتفصيل في الملحق A، فإن التفاعل بين سلوكيات الانزياح المنخفض والعالي يؤدي إلى وجود انزياحين محوريين مختلفين عند الانزياحات المنخفضة والعالية . قد يساهم هذا التفاعل في إمالة حدود الاحتمالية ثنائية الأبعاد في و الطائرة، كما هو موضح في الشكل 3 (انظر أيضًا الشكل 6 للمقارنات مع نماذج أخرى). بالإضافة إلى ذلك، قد تشير الزيادة في عدم اليقين عند الانزياح الأحمر المنخفض إلى أن هذه الظاهرة ليست مثالية لتناسب جميع البيانات بشكل متسق عبر الانزياح الأحمر المنخفض والعالي. يتم تأكيد هذه القلق عند مقارنة الفروق بين أفضل ملاءمة تم الحصول عليها ضمن كل نموذج DDE وأفضل ملاءمة تم الحصول عليه ضمن . في الواقع، هذا النموذج يؤدي باستمرار إلى أصغر تحسين على CDM عبر جميع مجموعات البيانات ونماذج DDE. لمزيد من التفاصيل، نشير إلى الملحق A.
الشكل 3. معلمات JBP (2.7) – التوزيعات البعدية الواحدة والتجاويف المهمشة ثنائية الأبعاد للمعلمات الرئيسية كما تم الحصول عليها من مجموعات بيانات Planck + DESI و Planck + DESI + PantheonPlus و Planck + DESI + DESY5.

4.4 النتائج للمعايرة اللوغاريتمية

الجدول 5 يلخص القيود على النموذج حيث يتم وصف معادلة الحالة للطاقة المظلمة بواسطة المعايرة اللوغاريتمية. الشكل 4 يعرض الخطوط الهامشية المعتادة على المعلمات ذات الصلة.
بدءًا من بلانك + ديزي، مقتصر على نظام الجوهر عند أكثر من بينما مقيد بأن يكون مختلفًا عن الصفر بأكثر من – تأكيد مرة أخرى على تفضيل DDE في بلانك + DESI.
عندما يتم إضافة PantheonPlus إلى Planck + DESI، نجد ؛ أي، تم تحويله نحو على الرغم من أن أشرطة الخطأ أصغر بعامل 5. ومع ذلك، أيضًا في هذه المعلمة، يفضل أن يكون في نظام الجوهر، باستثناء أكثر من . وبالمثل، النتيجة على يؤكد التفضيل العام لـ DDE، انظر الشكل 4.
بالنظر إلى DESY5 بدلاً من PantheonPlus، القيود على و تغيير إلى و على التوالي. ونتيجة لذلك، يبقى في نظام الجوهر بأكثر من بينما يُوجد أنه غير صفري تقريبًا من الجدير بالذكر أن أدلة DDE تكون أكثر وضوحًا باستمرار في وجود DESY5 مقارنة بـ PantheonPlus، انظر الشكل 4.
معامل بلانك + ديزي بلانك + ديزي + بانثيون بلس بلانك + ديزي + ديزي 5
-6.5 -9.3 -14.8
الجدول 5. المعايرة اللوغاريتمية (2.8) – قيود CL على المعلمات الكونية الحرة والمشتقة لثلاث مجموعات بيانات مختلفة مفصلة في القسم 3. القيم السلبية لـ تشير إلى تحسين في التوافق مع البيانات مقارنة بـ .
الشكل 4. المعايرة اللوغاريتمية (2.8) – التوزيعات الخلفية أحادية البعد والكونتوريات المهمشة ثنائية الأبعاد للمعلمات الرئيسية كما تم الحصول عليها من مجموعات بيانات Planck + DESI وPlanck + DESI + PantheonPlus وPlanck + DESI + DESY 5.

4.5 نتائج التوصيف BA

تُعطى القيود الرصدية للنموذج الأخير الذي تم تحليله في هذا العمل – معلمة BA – في الجدول 6. كما هو معتاد، نوضح الارتباطات بين المعلمات الكونية الرئيسية في الشكل 5.
معامل بلانك + ديزي بلانك + ديزي + بانثيون بلس بلانك + ديزي + ديزي 5
-8.7 -9.4 -16.2
الجدول 6. بارامترية BA (2.9) – قيود CL على المعلمات الكونية الحرة والمشتقة لثلاث مجموعات بيانات مختلفة مفصلة في القسم 3. القيم السلبية لـ تشير إلى تحسين في التوافق مع البيانات مقارنة بـ .
بدمج بلانك مع ديزي، نحصل على يقترب من وحوالي بعيد عن . بالإضافة إلى ذلك، يختلف بشكل كبير عن مؤكداً التفضيل لـ DDE بطريقة مشابهة للمعلمات الأخرى التي تم مناقشتها في جميع أنحاء المخطوطة.
إدراج بانثيون بلس يعطي (عميق في نظام الجوهر) و (غير صفري عند أكثر من لذا، بالنسبة لـ Planck + DESI + PantheonPlus، تشير الأدلة بوضوح إلى وجود طاقة مظلمة ديناميكية، وهو ما يتماشى مع جميع التوصيفات الأخرى الموصوفة حتى الآن.
في حالة بلانك + ديزي + ديزي يبتعد أكثر عن -1، مما يعزز التفضيل لنموذج الطاقة الكامنة. يُوجد أنه غير صفري في أكثر من كما هو موضح في الشكل 5.
من المثير للاهتمام أنه عند مقارنة الفرق بين أفضل ملاءمة تم الحصول عليها ضمن كل نموذج DDE وأفضل ملاءمة تم الحصول عليه ضمن CDM، هذا النموذج يؤدي باستمرار إلى أكبر تحسين. CDM عبر جميع مجموعات البيانات الثلاث التي تم تحليلها. إنه يؤدي بشكل أفضل من معلمة CPL، كما يتضح من مقارنة السطر الأخير في الجدول 2 والسطر الأخير في الجدول 6. كما تم مناقشته في الملحق A، عند مقارنة تطور EoS المستنتج في هذا النموذج مع الحالات الأخرى التي تم تحليلها حتى الآن، نجد أنه عند الانزياح الأحمر المنخفض يتصرف بشكل مشابه لمعلمة CPL. تظهر الاختلافات الأكثر وضوحًا عند . في جميع النماذج، تنتقل معادلة الحالة (EoS) بعمق إلى القيم الشبحية (باستثناء نموذج JBP، حيث يُجبر على الارتفاع مرة أخرى نحو قيم تشبه الكوانتس). بالمقابل، ضمن نموذج BA، لا يميل نحو قيم سلبية للغاية عند بينما تظل شبحًا، تستقر على هضبة مميزة، شبه مسطحة.
الشكل 5. معلمات BA (2.9) – توزيعات خلفية أحادية الأبعاد وكونتور ثنائي الأبعاد مُهمش للمعلمات الرئيسية كما تم الحصول عليها من مجموعات بيانات Planck + DESI وPlanck + DESI + PantheonPlus وPlanck + DESI + DESY 5.

5 المناقشات والاستنتاجات

تشير قياسات DESI BAO الأخيرة، عند دمجها مع بيانات CMB من بلانك وعينتين من المستعرات الأعظمية من النوع Ia (بانثيون-بلس وDESY5)، إلى تفضيل معادلة حالة شبيهة بالجوهر في الوقت الحاضر التي عبرت إلى نظام الشبح في الماضي. تتراوح الأهمية الإحصائية لهذا التفضيل للطاقة المظلمة الديناميكية بين و ، اعتمادًا على تركيبات البيانات المحددة التي تم تحليلها. إن الفرضية الأساسية لهذه النتيجة هي استخدام معلمة شيفالييه-بولارسكي-ليندر (CPL) لوصف تطور الانزياح الأحمر لمعادلة الحالة. على الرغم من مزاياها العديدة – مثل التقاط السلوك الفعال لمجموعة واسعة من النماذج تصل إلى الدقة – تفرض معلمة CPL تطور معادلة الحالة ليكون خطيًا في عامل المقياس.
في هذه الورقة، اختبرنا ما إذا كانت و إلى أي مدى تعتمد تفضيلات معادلة الحالة للجوهر الحالي التي تتطور نحو نظام الشبح على التوصيف المعتمد لوصف سلوكها الديناميكي. لتجنب توسيع الشكوك في المعلمات الكونية وتسهيل المقارنة المباشرة مع حالة CPL الأساسية، ركزنا على بعض النماذج البديلة المعروفة: التوصيف الأسي، وجاسال-باجلا-بادمانابان، والتوصيف اللوغاريتمي، وتوصيف باربوزا-ألكانيز لمعادلة الحالة. مثل الـ CPL
نموذج، تتكون جميع هذه المعلمات من اثنين فقط من المعلمات الحرة: القيمة الحالية لمعادلة الحالة ( ) ومعامل يحدد تطوره الديناميكي ( ومع ذلك، فإنها تسمح بالانحرافات عن السلوك الخطي عند كل من الانزياحات الحمراء العالية والمنخفضة. لذلك، بالنظر إلى نفس الزوج من القيم تُحصل على تاريخيات توسع مختلفة في أوقات متأخرة ضمن النماذج الأربعة، مما يؤثر على الملاحظات الكونية بشكل مختلف.
لتقييم ما إذا كانت هناك تفضيل لمكون طاقة مظلمة ديناميكية يتميز بـ و تظل توقعات قوية للبيانات، قمنا باختبار هذه النماذج ضد أحدث الملاحظات ذات الانزياح الأحمر العالي والمنخفض: قياسات الخلفية الكونية الميكروية من بلانك 2018، BAO من DESI، بالإضافة إلى قياسات سوبرنوفا من PantheonPlus وDESY5. بالنسبة لجميع تركيبات مجموعات البيانات المستكشفة – أي، بلانك + DESI، بلانك + DESI + PantheonPlus، وبلانك + DESI + DESY. نجد أن تظل باستمرار في نظام الجوهر. بالإضافة إلى ذلك، القيود على تشير باستمرار إلى تفضيل لتطور ديناميكي عبر إلى نظام الشبح ( لذلك، تؤكد نتائجنا نتائج DESI، بغض النظر عن التوصيف المعتمد لوصف ديناميات قطاع الطاقة المظلمة.
من الجدير بالذكر أن هناك دلائل مقنعة على تطور ديناميكي لمعادلة الحالة حتى مع استخدام بيانات بلانك + ديزي فقط. كما يتضح بوضوح في الشكل 6 – الذي يلخص النتائج للنماذج المختلفة – الزوج و (المتوافق مع نموذج الثابت الكوني القياسي لتشكيل البنية، CDM) دائمًا يقع خارج خط مستوى الثقة.
ومع ذلك، فإن الخطوة الحقيقية للأمام من حيث التفضيل للطاقة المظلمة الديناميكية تأتي عندما نأخذ في الاعتبار المستعرات العظمى من النوع Ia. بما في ذلك قياسات معدل المسافة التي تم جمعها من كتالوج PantheonPlus، فإن أشرطة الخطأ على و تضيق بمقدار 5 مرات مقارنةً بـ Planck + DESI فقط. تتقلص الحدود على بشكل كبير داخل جزء الكوانتس ، بينما تقلص الحدود على بشكل كبير داخل منطقة . استبدال بيانات PantheonPlus ببيانات DESY5 SN، يصبح التفضيل للطاقة المظلمة الديناميكية أكثر أهمية بشكل كبير، إلى درجة أنه ليس من المبالغة الإشارة إليها كدليل بدلاً من مجرد تفضيل. يتم توضيح ذلك مرة أخرى بوضوح في الشكل 6: بالنسبة لجميع النماذج، تتحرك القيود بعيدًا عن الثابت الكوني، الذي يقع دائمًا خارج حدود الاحتمالية المارجة لـ .
للوهلة الأولى، يكشف الشكل 6 أيضًا أن الحدود في مستوى تظهر اتجاهات مشابهة لجميع التخصيصات الأربعة (بما في ذلك حالة CPL الأساسية)، خاصة عندما يتم تضمين قياسات SN في التحليل. هذا يبرز في الوقت نفسه القوة الجوهرية للتفضيل للطاقة المظلمة الديناميكية كما أبلغت عنها قياسات DESI BAO وSN ومرونتها ضد تخصيصات مختلفة. بالنظر إلى هذه النتائج، هناك أساس قوي للاستنتاج بأن اختيار التخصيص له تأثير ضئيل.
وأخيرًا، قمنا بفحص المقاييس الإحصائية لتحديد مدى نجاح التخصيصات المختلفة التي تم تحليلها في هذه الدراسة في تفسير الملاحظات. على وجه التحديد، لكل نموذج وتركيبة بيانات، نبلغ عن الفرق بين أفضل ملاءمة التي تم الحصول عليها ضمن كل نموذج للطاقة المظلمة الديناميكية وأفضل ملاءمة التي تم الحصول عليها ضمن .
الشكل 6. ملخص الرسم البياني – الحدود المارجة ثنائية الأبعاد في مستوى ( ) لجميع النماذج ومجموعات البيانات التي تم تحليلها في هذه الدراسة.
مرة أخرى، تظهر جميع النماذج اتجاهات مشابهة: بالنسبة لـ Planck + DESI، نلاحظ باستمرار تحسينًا في الملاءمة على ، مع يتراوح من -5.6 إلى -8.7، اعتمادًا على النموذج المحدد. يتم تعزيز هذا التحسين في الملاءمة بشكل أكبر عند تضمين قياسات PantheonPlus SN (يتراوح من -6.4 إلى -9.4) ويزداد بشكل كبير –
حتى بمقدار عند اعتماد بيانات DESY5 SN (في هذه الحالة، يتراوح من -14.8 إلى -16.2). يتبع هذا الاتجاه التفضيل العام للطاقة المظلمة الديناميكية الذي تم مناقشته حتى الآن. من المثير للاهتمام أن تخصيص CPL الخطي ليس أبدًا النموذج الأفضل ملاءمة. المعادلة الحركية المقترحة من قبل Barboza-Alcaniz، المعطاة بالمعادلة (2.9)، تؤدي باستمرار إلى تحسين كبير في على CDM عبر جميع تركيبات البيانات الثلاثة التي تم تحليلها. على العكس من ذلك، يظهر تخصيص Jassal-Bagla-Padmanabhan، المعطى بالمعادلة (2.7)، أقل تحسين في الملاءمة مقارنةً بـ بين النماذج المدروسة. الاستثناء الوحيد هو لـ Planck + DESI + DESY5، حيث يشير إلى ملاءمة أفضل لهذه المجموعة من البيانات مقارنةً بـ CPL، والتخصيصات اللوغاريتمية، والتخصيصات الأسية، على الرغم من أنه لا يزال أقل مقارنةً بنموذج Barboza-Alcaniz. لمزيد من المناقشة والتفسير الفيزيائي للسلوكيات الظاهرة المختلفة للنماذج التي تم تحليلها حتى الآن، نشير إلى الملحق A. على وجه التحديد، يقدم الشكل 7 قيودًا على تطور المعادلة الحركية بالنسبة للانزياح الأحمر، كما تم استنتاجه من مجموعات بيانات مختلفة عبر جميع النماذج. يوفر الجدول 7 قيودًا على خصائص مهمة أخرى، مثل الانزياح المحوري، والقيم المقابلة (والشكوك) للمعادلة الحركية، وحقبة الانتقال من الكوانتس إلى الشبح. بشكل عام، تدعم هذه النتائج الاستنتاجات الرئيسية بشأن مرونة تفضيل DESI وSN للطاقة المظلمة المتطورة، بينما تشير إلى أن البيانات الحالية تقترب من دقة قد تعزز فهمنا لطبيعتها الفيزيائية، إذا أكدت الاستطلاعات والإصدارات المستقبلية من البيانات هذه النتائج.

شكر وتقدير

يشكر المؤلفون المحكم على العديد من التعليقات المهمة التي حسنت المخطوطة. يعترف W.G. بالدعم من اتحاد لانكستر-شيفيلد للفيزياء الأساسية من خلال منحة مجلس العلوم والتكنولوجيا (STFC) ST/X000621/1. يعترف S.P. بالدعم المالي من قسم العلوم والتكنولوجيا (DST)، حكومة الهند بموجب خطة “صندوق تحسين بنية العلوم والتكنولوجيا (FIST)” (رقم الملف SR/FST/MS-I/2019/41). يعترف E.D.V بالدعم من الجمعية الملكية من خلال زمالة أبحاث دوروثي هودجكين من الجمعية الملكية. تستند هذه المقالة إلى عمل من عمل COST Action CA21136 “معالجة التوترات الملاحظة في علم الكونيات مع الأنظمة والفيزياء الأساسية” (CosmoVerse)، المدعوم من COST (التعاون الأوروبي في العلوم والتكنولوجيا).

معادلة الحالة، الانزياح المحوري، وعبور الشبح عبر النماذج المختلفة

في هذه المقالة، أكدنا على مرونة النتائج التي قدمتها مؤخرًا تعاون DESI، موضحين أن بيانات DESI BAO، بالاشتراك مع ملاحظات CMB من Planck وكتالوجين مختلفين من قياسات معدل المسافة SN (أي PantheonPlus وDESY5)، تشير باستمرار إلى تفضيل للطاقة المظلمة الديناميكية عبر تخصيصات مختلفة للمعادلة الحركية. بينما كان الهدف الأساسي هو تأكيد أن هذا التفضيل يبقى مستقرًا بغض النظر عن نموذج الطاقة المظلمة الديناميكية المحدد، ظهرت اختلافات طفيفة عبر الحالات الخمس التي تم تحليلها، مما يستدعي مزيدًا من التحقيق. في هذا الملحق، نستكشف هذه الاختلافات بمزيد من التفصيل، بهدف تقديم تفسير فيزيائي أقوى للنتائج المقدمة في المخطوطة. بالنسبة لجميع النماذج الخمس، نعيد بناء تطور المعادلة الحركية مع الانزياح الأحمر، ، بناءً على القيود المفروضة على و المستنتجة من مجموعات بيانات Planck + DESI + PantheonPlus وPlanck + DESI + DESY5. في الشكل 7، نقدم القيمة المتوسطة لـ (المتقطع
نموذج مجموعة البيانات
CPL Planck+DESI+PantheonPlus 0.27
Planck+DESI+DESY5 0.25
أسية Planck+DESI+PantheonPlus 0.21
Planck+DESI+DESY5 0.22
JBP Planck+DESI+PantheonPlus 0.21
4.6
Planck+DESI+DESY5 0.21
4.7
لوغاريتمي Planck+DESI+PantheonPlus 0.29
Planck+DESI+DESY5 0.26
BA Planck+DESI+PantheonPlus 0.28
Planck+DESI+DESY5 0.28
الجدول 7. قيود عند على الانزياح المحوري ، القيمة المقابلة لـ ، والانزياح الأحمر حيث تعبر المعادلة الحركية عن حدود الشبح، لمجموعات بيانات Planck + DESI + PantheonPlus وPlanck + DESI + DESY 5.
الخطوط)، جنبًا إلى جنب مع شكوكها عند (المناطق الداكنة) و (المناطق الفاتحة) CL، عبر نطاق الانزياح الأحمر لجميع النماذج وتركيبات البيانات. من الشكل المعاد بناؤه لـ ، نستخرج معلومات حاسمة تساعد في مقارنة النماذج المختلفة وتوضيح النتائج المقدمة في المخطوطة. على وجه التحديد، في الجدول 7، نقدم النتائج لـ:
(ط) الانزياح المحوري والقيمة المقابلة للمعادلة الحركية، ، التي تشير إلى الانزياح الأحمر وقيمة المعادلة الحركية التي يتم فيها تقييد بشكل أفضل من قبل مجموعتي البيانات عبر النماذج الخمس؛
(2) الانزياح الأحمر عندما تعبر المعادلة الحركية عن حدود الشبح (أي، )، مما يخبرنا متى يحدث عبور الشبح، جنبًا إلى جنب مع شكوكها المقابلة.
بدءًا من نموذج CPL الأساسي كحالة مرجعية، نلخص الميزات الرئيسية والاختلافات عبر النماذج المختلفة.
الشكل 7. تطور لـ عبر جميع نماذج الطاقة المظلمة الديناميكية، المستنتجة من CMB + DESI + PantheonPlus (الألواح اليسرى) وCMB + DESI + DESY5 (الألواح اليمنى). تمثل الخطوط المتقطعة القيم المتوسطة، بينما تشير المناطق المظللة الداكنة والفاتحة إلى الشكوك في و على التوالي.
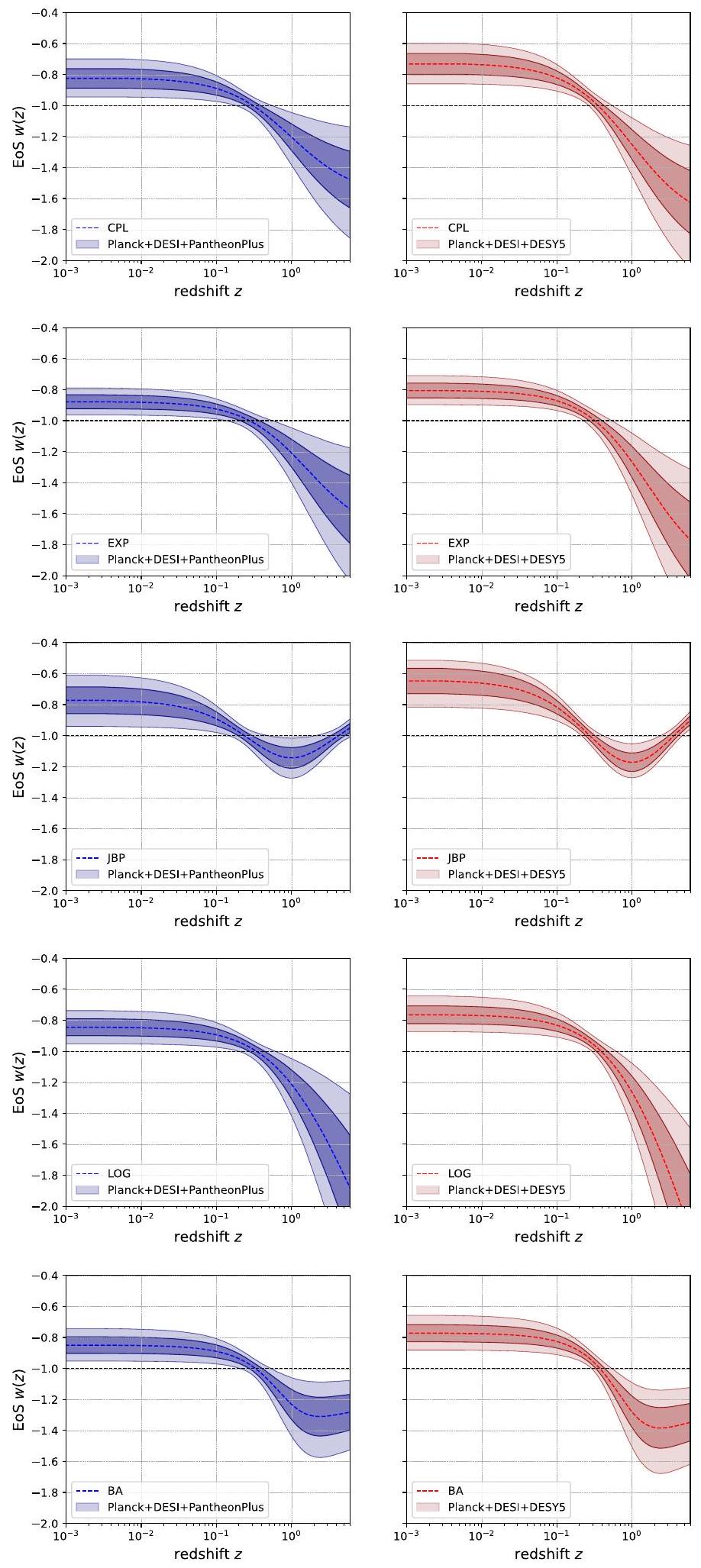
  • أسية: كما يتضح عند مقارنة الألواح العلوية مع تلك في الصف الثاني من الأعلى في الشكل 7، من منظور ظاهري، يشبه التخصيص الأسّي نموذج CPL عن كثب. تم تسليط الضوء على هذه الشبه بالفعل في النص الرئيسي عند مقارنة التحسين في على CDM (الذي يشبه إلى حد كبير كلا السيناريوهين). يتم دعم الاتفاق في التوقعات بشكل أكبر من خلال الجدول 7. الاختلاف الملحوظ الوحيد بين النماذج هو الانزياح المحوري الأصغر قليلاً في المعلمة الأسية. ومع ذلك، فإن معادلة الحالة عند هذه النقطة المحورية مقيدة بدقة مماثلة. بالإضافة إلى ذلك، فإن التنبؤات المتعلقة بالانزياح الأحمر لعبور الشبح تتفق ضمن انحراف معياري واحد لكل من Planck + DESI + PantheonPlus و Planck + DESI + DESY 5.
  • JBP: من بين النماذج الخمسة التي تم تحليلها، تقدم معلمة JBP ظاهرة أكثر دقة فيما يتعلق بتطور معادلة الحالة للطاقة المظلمة. كما هو موضح في الألواح الثالثة من الأعلى في الشكل 7، بسبب طبيعته التربيعية في عامل المقياس، يتقاطع تطور معادلة الحالة ضمن معلمة JBP مرتين. عند الانزياح الأحمر المنخفض جداً، يتصرف بشكل مشابه للنماذج الأخرى، ويبقى ضمن منطقة الكوانتس، على الرغم من وجود عدم يقين أكبر مقارنة بالنماذج الأخرى. يُقدّر أن الانتقال الأول من الكوانتس إلى الشبح يحدث عند لـ Planck + DESI + PantheonPlus (Planck + DESI + DESY5) عند CL. بعد هذا الانتقال، يقترب من قيمة دنيا حوالي قبل أن يرتفع نحو قيم أقل سلبية. في النهاية، يحدث عبور ثانٍ من الشبح إلى الكوانتس عند ( ) لـ Planck+DESI+PantheonPlus (Planck+DESI+DESY5)، كلاهما عند CL. يتناقض هذا السلوك مع النماذج الأخرى، حيث تبقى معادلة الحالة ضمن نظام الشبح، وغالباً ما تميل نحو قيم أكثر سلبية عند الانزياح الأحمر العالي. في المقابل، ضمن نموذج JBP، لا يمكن لمعادلة الحالة الانتقال نحو قيم (أكثر) شبحية ولكن تُجبر على الانتقال مرة أخرى نحو قيم أقل سلبية عند . يتم أيضاً عكس العبور المزدوج للنظم الذي تحقق ضمن هذه المعلمة في مقياس المحور الذي يتم فيه تقييد معادلة الحالة بشكل جيد بواسطة البيانات. في الجدول 7، نميز بين نظامين مختلفين: نطاق الانزياح الأحمر (الذي يلتقط أول عبور من الكوانتس إلى الشبح) والنطاق (الذي يغطي ثاني عبور من الشبح إلى الكوانتس). في هذين المنطقتين، نحدد انزياحين حمر متميزين: الأول عند والثاني عند . في كلا الحالتين (ولكلا مجموعتي البيانات)، يتم تقييد معادلة الحالة ضمن نفس الحد الأدنى من الخطأ. هذا يؤكد أنه، ضمن هذا النموذج، بسبب الشكل الوظيفي لمعادلة الحالة، فإن القيود عند الانزياح الأحمر المنخفض (أي، حوالي ) تحدد أيضاً سلوك المعلمة عند الانزياحات الحمراء الأعلى. يمكن أن تساهم التفاعلات بين سلوكيات الانزياح الأحمر المنخفض والعالي، كما تم تسليط الضوء عليه بواسطة الانزياحات الحمراء المحورية، في زيادة عدم اليقين عند الانزياح الأحمر المنخفض وإمالة حدود الاحتمالية التي تظهر في الشكل 6. كما تم مناقشته في المخطوطة الرئيسية، يقدم هذا النموذج تحسينات متواضعة نسبياً في الملاءمة مقارنةً ، خاصة في مجموعات البيانات التي تغطي ، حيث تصبح انحرافات النموذج عن الآخرين أكثر وضوحاً.
  • لوغاريتمي: عندما يتعلق الأمر بالمعلمة اللوغاريتمية، فإن سلوك لـ ، كما هو موضح في اللوحة الرابعة من الشكل 7، مشابه لذلك لنماذج CPL والأسية. ينعكس هذا أيضاً في القيم التي استنتجناها لـ و ، جميعها ملخصة في الجدول 7 ومتوافقة مع تلك النماذج. ومع ذلك، نلاحظ أنه عند ، تُجبر معادلة الحالة على النزول إلى قيم شبحية عميقة، ويكون الانحدار نحو هذه القيم السلبية جداً أكثر حدة من حالات CPL والأسية. ويرجع ذلك إلى أنه عند ، يقترب عامل المقياس من قيم صغيرة (يتجه نحو )، مما يتسبب في انخفاض إلى قيم سلبية بسرعة كبيرة. يمكن أن يؤدي هذا الانخفاض المفاجئ في لـ إلى تغييرات
    في الملاءمة للبيانات التي تمتد عبر ، والتي تغطيها ملاحظات BAO وSN، مما يؤدي إلى الاختلافات في في الملاءمة التي تم مناقشتها في المخطوطة.
  • BA: وأخيراً وليس آخراً، يتم تقديم تطور الذي تم الحصول عليه لنموذج BA في اللوحة السفلية من الشكل 7. كما جادلنا في المخطوطة، يوفر هذا النموذج أكبر تحسين في الملاءمة مقارنةً بـ CDM عبر جميع مجموعات البيانات التي تم تحليلها في هذه الدراسة. لذلك، من المثير للاهتمام فحص ما هو مختلف في تطور معادلة الحالة مقارنة بالنماذج الأخرى. عند النظر إلى الجزء المنخفض الانزياح الأحمر من معادلة الحالة، نرى أن النموذج يتصرف بشكل مشابه جداً لـ CPL (وأقاربه). ومع ذلك، بالنسبة للانزياح الأحمر المحوري، نحصل على ، أكبر قليلاً من أي نموذج آخر، بينما تأخذ قيم متوافقة مع الحالات الأخرى. نقدر أن الانتقال من الكوانتس إلى الشبح يحدث عند لـ Planck + DESI + PantheonPlus (Planck + DESI + DESY 5) عند CL. يحدث الاختلاف الأكثر وضوحاً في معادلة الحالة عند . في جميع النماذج الأخرى التي تم دراستها حتى الآن، إما أن انتقلت معادلة الحالة بعمق إلى قيم شبحية (تتميز بأشكال وظيفية أكثر أو أقل حدة لـ ) أو كانت مجبرة على الزيادة مرة أخرى نحو قيم شبيهة بالكوانتس في نموذج JBP. بالإشارة إلى اللوحة السفلية من الشكل 7، نلاحظ أنه بالنسبة لـ ، يبقى تطور في نموذج BA شبحياً ولكنه لا يميل نحو قيم سلبية جداً. بدلاً من ذلك، تستقر على نوع من الهضبة الثانية التي تميز نموذج BA.

References

[1] Supernova Search Team collaboration, Observational evidence from supernovae for an accelerating universe and a cosmological constant, Astron. J. 116 (1998) 1009 [astro-ph/9805201].
[2] Supernova Cosmology Project collaboration, Measurements of and from 42 High Redshift Supernovae, Astrophys. J. 517 (1999) 565 [astro-ph/9812133].
[3] Supernova Search Team collaboration, The farthest known supernova: support for an accelerating universe and a glimpse of the epoch of deceleration, Astrophys. J. 560 (2001) 49 [astro-ph/0104455].
[4] SDSS collaboration, Cosmological parameters from SDSS and WMAP, Phys. Rev. D 69 (2004) 103501 [astro-ph/0310723].
[5] SDSS collaboration, Physical evidence for dark energy, astro-ph/0307335.
[6] Supernova Search Team collaboration, Cosmological results from high-z supernovae, Astrophys. J. 594 (2003) 1 [astro-ph/0305008].
[7] Supernova Cosmology Project collaboration, New constraints on Omega(M), Omega(lambda), and from an independent set of eleven high-redshift supernovae observed with HST, Astrophys. J. 598 (2003) 102 [astro-ph/0309368].
[8] SDSS collaboration, Cosmological parameter analysis including SDSS Ly-alpha forest and galaxy bias: Constraints on the primordial spectrum of fluctuations, neutrino mass, and dark energy, Phys. Rev. D 71 (2005) 103515 [astro-ph/0407372].
[9] B. Feng, X.-L. Wang and X.-M. Zhang, Dark energy constraints from the cosmic age and supernova, Phys. Lett. B 607 (2005) 35 [astro-ph/0404224].
[10] Supernova Search Team collaboration, Type Ia supernova discoveries at from the Hubble Space Telescope: Evidence for past deceleration and constraints on dark energy evolution, Astrophys. J. 607 (2004) 665 [astro-ph/0402512].
[11] SNLS collaboration, The Supernova Legacy Survey: Measurement of and from the first year data set, Astron. Astrophys. 447 (2006) 31 [astro-ph/0510447].
[12] SDSS collaboration, Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies, Astrophys. J. 633 (2005) 560 [astro-ph/0501171].
[13] D.J. Eisenstein, H.-j. Seo, E. Sirko and D. Spergel, Improving Cosmological Distance Measurements by Reconstruction of the Baryon Acoustic Peak, Astrophys. J. 664 (2007) 675 [astro-ph/0604362].
[14] SDSS collaboration, Cosmological Constraints from the SDSS Luminous Red Galaxies, Phys. Rev. D 74 (2006) 123507 [astro-ph/0608632].
[15] V. Sahni and A. Starobinsky, Reconstructing Dark Energy, Int. J. Mod. Phys. D 15 (2006) 2105 [astro-ph/0610026].
[16] ESSENCE collaboration, Observational Constraints on the Nature of the Dark Energy: First Cosmological Results from the ESSENCE Supernova Survey, Astrophys. J. 666 (2007) 694 [astro-ph/0701041].
[17] A. Vikhlinin et al., Chandra Cluster Cosmology Project III: Cosmological Parameter Constraints, Astrophys. J. 692 (2009) 1060 [0812.2720].
[18] D. Stern, R. Jimenez, L. Verde, M. Kamionkowski and S.A. Stanford, Cosmic Chronometers: Constraining the Equation of State of Dark Energy. I: H(z) Measurements, JCAP 02 (2010) 008 [0907.3149].
[19] B.D. Sherwin et al., Evidence for dark energy from the cosmic microwave background alone using the Atacama Cosmology Telescope lensing measurements, Phys. Rev. Lett. 107 (2011) 021302 [1105.0419].
[20] WMAP collaboration, Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results, Astrophys. J. Suppl. 208 (2013) 20 [1212.5225].
[21] WMAP collaboration, Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results, Astrophys. J. Suppl. 208 (2013) 19 [1212.5226].
[22] BOSS collaboration, The Baryon Oscillation Spectroscopic Survey of SDSS-III, Astron. J. 145 (2013) 10 [1208.0022].
[23] Astro-WISE, KiDS collaboration, The Kilo-Degree Survey, Exper. Astron. 35 (2013) 25 [1206. 1254].
[24] BOSS collaboration, The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples, Mon. Not. Roy. Astron. Soc. 441 (2014) 24 [1312.4877].
[25] D.H. Weinberg, M.J. Mortonson, D.J. Eisenstein, C. Hirata, A.G. Riess and E. Rozo, Observational Probes of Cosmic Acceleration, Phys. Rept. 530 (2013) 87 [1201.2434].
[26] BOSS collaboration, The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Testing gravity with redshift-space distortions using the power spectrum multipoles, Mon. Not. Roy. Astron. Soc. 443 (2014) 1065 [1312.4611].
[27] BOSS collaboration, Baryon acoustic oscillations in the Lyo forest of BOSS DR11 quasars, Astron. Astrophys. 574 (2015) A59 [1404. 1801].
[28] SDSS collaboration, Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples, Astron. Astrophys. 568 (2014) A22 [1401.4064].
[29] BOSS collaboration, Cosmological implications of baryon acoustic oscillation measurements, Phys. Rev. D 92 (2015) 123516 [1411.1074].
[30] A.J. Ross, L. Samushia, C. Howlett, W.J. Percival, A. Burden and M. Manera, The clustering of the SDSS DR7 main Galaxy sample – I. A 4 per cent distance measure at , Mon. Not. Roy. Astron. Soc. 449 (2015) 835 [1409.3242].
[31] M. Moresco, L. Pozzetti, A. Cimatti, R. Jimenez, C. Maraston, L. Verde et al., A measurement of the Hubble parameter at : direct evidence of the epoch of cosmic re-acceleration, JCAP 05 (2016) 014 [1601.01701].
[32] M. Moresco, R. Jimenez, L. Verde, A. Cimatti, L. Pozzetti, C. Maraston et al., Constraining the time evolution of dark energy, curvature and neutrino properties with cosmic chronometers, JCAP 12 (2016) 039 [1604.00183].
[33] D. Rubin and B. Hayden, Is the expansion of the universe accelerating? All signs point to yes, Astrophys. J. Lett. 833 (2016) L30 [1610.08972].
[34] BOSS collaboration, The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: cosmological analysis of the DR12 galaxy sample, Mon. Not. Roy. Astron. Soc. 470 (2017) 2617 [1607.03155].
[35] DES collaboration, The Dark Energy Survey: more than dark energy – an overview, Mon. Not. Roy. Astron. Soc. 460 (2016) 1270 [1601.00329].
[36] B.S. Haridasu, V.V. Luković, R. D’Agostino and N. Vittorio, Strong evidence for an accelerating universe, Astron. Astrophys. 600 (2017) L1 [1702.08244].
[37] DES collaboration, Dark Energy Survey Year 1 results: Cosmological constraints from cosmic shear, Phys. Rev. D 98 (2018) 043528 [1708.01538].
[38] Pan-STARRS1 collaboration, The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample, Astrophys. J. 859 (2018) 101 [1710.00845].
[39] Planck collaboration, Planck 2018 results. I. Overview and the cosmological legacy of Planck, Astron. Astrophys. 641 (2020) A1 [1807.06205].
[40] Planck collaboration, Planck 2018 results. VI. Cosmological parameters, Astron. Astrophys. 641 (2020) A6 [1807.06209].
[41] A. Gómez-Valent, Quantifying the evidence for the current speed-up of the Universe with low and intermediate-redshift data. A more model-independent approach, JCAP 05 (2019) 026 [1810.02278].
[42] Y. Yang and Y. Gong, The evidence of cosmic acceleration and observational constraints, JCAP 06 (2020) 059 [1912.07375].
[43] ACT collaboration, The Atacama Cosmology Telescope: a measurement of the Cosmic Microwave Background power spectra at 98 and 150 GHz, JCAP 12 (2020) 045 [2007.07289].
[44] ACT collaboration, The Atacama Cosmology Telescope: DR4 Maps and Cosmological Parameters, JCAP 12 (2020) 047 [2007.07288].
[45] EBOSS collaboration, Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory, Phys. Rev. D 103 (2021) 083533 [2007.08991].
[46] S. Nadathur, W.J. Percival, F. Beutler and H. Winther, Testing Low-Redshift Cosmic Acceleration with Large-Scale Structure, Phys. Rev. Lett. 124 (2020) 221301 [2001.11044].
[47] B.M. Rose, D. Rubin, A. Cikota, S.E. Deustua, S. Dixon, A. Fruchter et al., Evidence for Cosmic Acceleration is Robust to Observed Correlations Between Type Ia Supernova Luminosity and Stellar Age, Astrophys. J. Lett. 896 (2020) L4 [2002. 12382].
[48] E. Di Valentino, S. Gariazzo, O. Mena and S. Vagnozzi, Soundness of Dark Energy properties, JCAP 07 (2020) 045 [2005. 02062].
[49] KIDS collaboration, KiDS-1000 Cosmology: Cosmic shear constraints and comparison between two point statistics, Astron. Astrophys. 645 (2021) A104 [2007.15633].
[50] KiDS collaboration, KiDS-1000 Cosmology: Constraints beyond flat , Astron. Astrophys. 649 (2021) A88 [2010.16416].
[51] SPT-3G collaboration, Measurements of the -mode polarization and temperature- -mode correlation of the CMB from SPT-3G 2018 data, Phys. Rev. D 104 (2021) 022003 [2101.01684].
[52] DES collaboration, Dark Energy Survey Year 3 results: Cosmological constraints from galaxy clustering and weak lensing, Phys. Rev. D 105 (2022) 023520 [2105.13549].
[53] M. Moresco et al., Unveiling the Universe with emerging cosmological probes, Living Rev. Rel. 25 (2022) 6 [2201.07241].
[54] DES collaboration, Dark Energy Survey Year 3 results: Constraints on extensions to CDM with weak lensing and galaxy clustering, Phys. Rev. D 107 (2023) 083504 [2207.05766].
[55] D. Brout et al., The Pantheon + Analysis: Cosmological Constraints, Astrophys. J. 938 (2022) 110 [2202.04077].
[56] ACT collaboration, The Atacama Cosmology Telescope: DR6 Gravitational Lensing Map and Cosmological Parameters, Astrophys. J. 962 (2024) 113 [2304.05203].
[57] Kilo-Degree Survey, Dark Energy Survey collaboration, DES Y3 + KiDS-1000: Consistent cosmology combining cosmic shear surveys, Open J. Astrophys. 6 (2023) 2305.17173 [2305.17173].
[58] DESI collaboration, DESI 2024 III: Baryon Acoustic Oscillations from Galaxies and Quasars, 2404.03000.
[59] DESI collaboration, DESI 2024: Constraints on Physics-Focused Aspects of Dark Energy using DESI DR1 BAO Data, 2405.13588.
[60] DES collaboration, The Dark Energy Survey: Cosmology Results With New High-redshift Type Ia Supernovae Using The Full 5-year Dataset, 2401.02929.
[61] DES collaboration, The Dark Energy Survey Supernova Program: Light curves and 5-Year data release, 2406.05046.
[62] DES collaboration, The Dark Energy Survey Supernova Program: Cosmological Analysis and Systematic Uncertainties, 2401.02945.
[63] T. Buchert, On average properties of inhomogeneous fluids in general relativity. 1. Dust cosmologies, Gen. Rel. Grav. 32 (2000) 105 [gr-qc/9906015].
[64] T. Buchert, On average properties of inhomogeneous fluids in general relativity: Perfect fluid cosmologies, Gen. Rel. Grav. 33 (2001) 1381 [gr-qc/0102049].
[65] T. Buchert, Dark Energy from Structure: A Status Report, Gen. Rel. Grav. 40 (2008) 467 [0707.2153].
[66] P. Hunt and S. Sarkar, Constraints on large scale inhomogeneities from WMAP-5 and SDSS: confrontation with recent observations, Mon. Not. Roy. Astron. Soc. 401 (2010) 547 [0807.4508].
[67] J.T. Nielsen, A. Guffanti and S. Sarkar, Marginal evidence for cosmic acceleration from Type Ia supernovae, Sci. Rep. 6 (2016) 35596 [1506.01354].
[68] I. Tutusaus, B. Lamine, A. Dupays and A. Blanchard, Is cosmic acceleration proven by local cosmological probes?, Astron. Astrophys. 602 (2017) A73 [1706.05036].
[69] L.H. Dam, A. Heinesen and D.L. Wiltshire, Apparent cosmic acceleration from type Ia supernovae, Mon. Not. Roy. Astron. Soc. 472 (2017) 835 [1706.07236].
[70] J. Colin, R. Mohayaee, M. Rameez and S. Sarkar, Evidence for anisotropy of cosmic acceleration, Astron. Astrophys. 631 (2019) L13 [1808.04597].
[71] C. Desgrange, A. Heinesen and T. Buchert, Dynamical spatial curvature as a fit to type Ia supernovae, Int. J. Mod. Phys. D 28 (2019) 1950143 [1902.07915].
[72] S.M. Koksbang, Towards statistically homogeneous and isotropic perfect fluid universes with cosmic backreaction, Class. Quant. Grav. 36 (2019) 185004 [1907.08681].
[73] S.M. Koksbang, Another look at redshift drift and the backreaction conjecture, JCAP 10 (2019) 036 [1909. 13489].
[74] A. Heinesen, Reconciling a decelerating Universe with cosmological observations, Phys. Rev. D 107 (2023) L101301 [2212.05568].
[75] V. Sahni and A.A. Starobinsky, The Case for a positive cosmological Lambda term, Int. J. Mod. Phys. D 9 (2000) 373 [astro-ph/9904398].
[76] S.M. Carroll, The Cosmological constant, Living Rev. Rel. 4 (2001) 1 [astro-ph/0004075].
[77] P.J.E. Peebles and B. Ratra, The Cosmological Constant and Dark Energy, Rev. Mod. Phys. 75 (2003) 559 [astro-ph/0207347].
[78] T. Padmanabhan, Cosmological constant: The Weight of the vacuum, Phys. Rept. 380 (2003) 235 [hep-th/0212290].
[79] E.J. Copeland, M. Sami and S. Tsujikawa, Dynamics of dark energy, Int. J. Mod. Phys. D 15 (2006) 1753 [hep-th/0603057].
[80] R.R. Caldwell and M. Kamionkowski, The Physics of Cosmic Acceleration, Ann. Rev. Nucl. Part. Sci. 59 (2009) 397 [0903.0866].
[81] M. Li, X.-D. Li, S. Wang and Y. Wang, Dark Energy, Commun. Theor. Phys. 56 (2011) 525 [1103.5870].
[82] J. Martin, Everything You Always Wanted To Know About The Cosmological Constant Problem (But Were Afraid To Ask), Comptes Rendus Physique 13 (2012) 566 [1205.3365].
[83] S. Weinberg, The Cosmological Constant Problem, Rev. Mod. Phys. 61 (1989) 1.
[84] L.M. Krauss and M.S. Turner, The Cosmological constant is back, Gen. Rel. Grav. 27 (1995) 1137 [astro-ph/9504003].
[85] S. Weinberg, The Cosmological constant problems, 2, 2000.
[86] V. Sahni, The Cosmological constant problem and quintessence, Class. Quant. Grav. 19 (2002) 3435 [astro-ph/0202076].
[87] J. Yokoyama, Issues on the cosmological constant, 5, 2003.
[88] S. Nobbenhuis, Categorizing different approaches to the cosmological constant problem, Found. Phys. 36 (2006) 613 [gr-qc/0411093].
[89] C.P. Burgess, The Cosmological Constant Problem: Why it’s hard to get Dark Energy from Micro-physics, 2015. 10.1093/acprof:oso/9780198728856.003.0004.
[90] A. Joyce, B. Jain, J. Khoury and M. Trodden, Beyond the Cosmological Standard Model, Phys. Rept. 568 (2015) 1 [1407.0059].
[91] P. Bull et al., Beyond CDM: Problems, solutions, and the road ahead, Phys. Dark Univ. 12 (2016) 56 [1512.05356].
[92] B. Wang, E. Abdalla, F. Atrio-Barandela and D. Pavon, Dark Matter and Dark Energy Interactions: Theoretical Challenges, Cosmological Implications and Observational Signatures, Rept. Prog. Phys. 79 (2016) 096901 [1603.08299].
[93] R. Brustein and P.J. Steinhardt, Challenges for superstring cosmology, Phys. Lett. B 302 (1993) 196 [hep-th/9212049].
[94] E. Witten, The Cosmological constant from the viewpoint of string theory, 3, 2000.
[95] S. Kachru, R. Kallosh, A.D. Linde and S.P. Trivedi, De Sitter vacua in string theory, Phys. Rev. D 68 (2003) 046005 [hep-th/0301240].
[96] J. Polchinski, The Cosmological Constant and the String Landscape, 3, 2006.
[97] U.H. Danielsson and T. Van Riet, What if string theory has no de Sitter vacua?, Int. J. Mod. Phys. D 27 (2018) 1830007 [1804.01120].
[98] I. Zlatev, L.-M. Wang and P.J. Steinhardt, Quintessence, cosmic coincidence, and the cosmological constant, Phys. Rev. Lett. 82 (1999) 896 [astro-ph/9807002].
[99] D. Pavon and W. Zimdahl, Holographic dark energy and cosmic coincidence, Phys. Lett. B 628 (2005) 206 [gr-qc/0505020].
[100] H.E.S. Velten, R.F. vom Marttens and W. Zimdahl, Aspects of the cosmological “coincidence problem”, Eur. Phys. J. C 74 (2014) 3160 [1410.2509].
[101] A.D. Dolgov, The Problem of vacuum energy and cosmology, 6, 1997.
[102] N. Straumann, The Mystery of the cosmic vacuum energy density and the accelerated expansion of the universe, Eur. J. Phys. 20 (1999) 419 [astro-ph/9908342].
[103] J. Sola, Cosmological constant and vacuum energy: old and new ideas, J. Phys. Conf. Ser. 453 (2013) 012015 [1306.1527].
[104] L. Amendola, Coupled quintessence, Phys. Rev. D 62 (2000) 043511 [astro-ph/9908023].
[105] A.Y. Kamenshchik, U. Moschella and V. Pasquier, An Alternative to quintessence, Phys. Lett. (2001) 265 [gr-qc/0103004].
[106] S. Capozziello, Curvature quintessence, Int. J. Mod. Phys. D 11 (2002) 483 [gr-qc/0201033].
[107] M.C. Bento, O. Bertolami and A.A. Sen, Generalized Chaplygin gas, accelerated expansion and dark energy matter unification, Phys. Rev. D 66 (2002) 043507 [gr-qc/0202064].
[108] G. Mangano, G. Miele and V. Pettorino, Coupled quintessence and the coincidence problem, Mod. Phys. Lett. A 18 (2003) 831 [astro-ph/0212518].
[109] G.R. Farrar and P.J.E. Peebles, Interacting dark matter and dark energy, Astrophys. J. 604 (2004) 1 [astro-ph/0307316].
[110] J. Khoury and A. Weltman, Chameleon fields: Awaiting surprises for tests of gravity in space, Phys. Rev. Lett. 93 (2004) 171104 [astro-ph/0309300].
[111] M. Li, A Model of holographic dark energy, Phys. Lett. B 603 (2004) 1 [hep-th/0403127].
[112] L. Amendola, R. Gannouji, D. Polarski and S. Tsujikawa, Conditions for the cosmological viability of dark energy models, Phys. Rev. D 75 (2007) 083504 [gr-qc/0612180].
[113] W. Hu and I. Sawicki, Models of Cosmic Acceleration that Evade Solar-System Tests, Phys. Rev. D 76 (2007) 064004 [0705.1158].
[114] G. Cognola, E. Elizalde, S. Nojiri, S.D. Odintsov, L. Sebastiani and S. Zerbini, A Class of viable modified gravities describing inflation and the onset of accelerated expansion, Phys. Rev. D 77 (2008) 046009 [0712.4017].
[115] S. Nojiri, S.D. Odintsov, M. Sasaki and Y.-l. Zhang, Screening of cosmological constant in non-local gravity, Phys. Lett. B 696 (2011) 278 [1010.5375].
[116] Y.-l. Zhang and M. Sasaki, Screening of cosmological constant in non-local cosmology, Int. J. Mod. Phys. D 21 (2012) 1250006 [1108.2112].
[117] M. Rinaldi, Higgs Dark Energy, Class. Quant. Grav. 32 (2015) 045002 [1404.0532].
[118] O. Luongo and H. Quevedo, A Unified Dark Energy Model from a Vanishing Speed of Sound with Emergent Cosmological Constant, Int. J. Mod. Phys. D 23 (2014) 1450012.
[119] M. Rinaldi, Dark energy as a fixed point of the Einstein Yang-Mills Higgs Equations, JCAP 10 (2015) 023 [1508.04576].
[120] A. De Felice, L. Heisenberg, R. Kase, S. Mukohyama, S. Tsujikawa and Y.-l. Zhang, Cosmology in generalized Proca theories, JCAP 06 (2016) 048 [1603.05806].
[121] T. Josset, A. Perez and D. Sudarsky, Dark Energy from Violation of Energy Conservation, Phys. Rev. Lett. 118 (2017) 021102 [1604.04183].
[122] C. Burrage and J. Sakstein, A Compendium of Chameleon Constraints, JCAP 11 (2016) 045 [1609.01192].
[123] L. Sebastiani, S. Vagnozzi and R. Myrzakulov, Mimetic gravity: a review of recent developments and applications to cosmology and astrophysics, Adv. High Energy Phys. 2017 (2017) 3156915 [1612.08661].
[124] S. Nojiri, S.D. Odintsov and V.K. Oikonomou, Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution, Phys. Rept. 692 (2017) 1 [1705.11098].
[125] C. Burrage and J. Sakstein, Tests of Chameleon Gravity, Living Rev. Rel. 21 (2018) 1 [1709.09071].
[126] S. Capozziello, R. D’Agostino and O. Luongo, Cosmic acceleration from a single fluid description, Phys. Dark Univ. 20 (2018) 1 [1712.04317].
[127] D. Benisty and E.I. Guendelman, Unified dark energy and dark matter from dynamical spacetime, Phys. Rev. D 98 (2018) 023506 [1802.07981].
[128] A. Casalino, M. Rinaldi, L. Sebastiani and S. Vagnozzi, Mimicking dark matter and dark energy in a mimetic model compatible with GW170817, Phys. Dark Univ. 22 (2018) 108 [1803.02620].
[129] W. Yang, S. Pan, E. Di Valentino, R.C. Nunes, S. Vagnozzi and D.F. Mota, Tale of stable interacting dark energy, observational signatures, and the tension, JCAP 09 (2018) 019 [1805.08252].
[130] E.N. Saridakis, K. Bamba, R. Myrzakulov and F.K. Anagnostopoulos, Holographic dark energy through Tsallis entropy, JCAP 12 (2018) 012 [1806.01301].
[131] L. Visinelli and S. Vagnozzi, Cosmological window onto the string axiverse and the supersymmetry breaking scale, Phys. Rev. D 99 (2019) 063517 [1809.06382].
[132] D. Langlois, Dark energy and modified gravity in degenerate higher-order scalar-tensor (DHOST) theories: A review, Int. J. Mod. Phys. D 28 (2019) 1942006 [1811.06271].
[133] D. Benisty, E. Guendelman and Z. Haba, Unification of dark energy and dark matter from diffusive cosmology, Phys. Rev. D 99 (2019) 123521 [1812.06151].
[134] K. Boshkayev, R. D’Agostino and O. Luongo, Extended logotropic fluids as unified dark energy models, Eur. Phys. J. C 79 (2019) 332 [1901.01031].
[135] J.J. Heckman, C. Lawrie, L. Lin, J. Sakstein and G. Zoccarato, Pixelated Dark Energy, Fortsch. Phys. 67 (2019) 1900071 [1901.10489].
[136] R. D’Agostino, Holographic dark energy from nonadditive entropy: cosmological perturbations and observational constraints, Phys. Rev. D 99 (2019) 103524 [1903.03836].
[137] U. Mukhopadhyay, D. Majumdar and D. Adak, Evolution of Dark Energy Perturbations for Slotheon Field and Power Spectrum, Eur. Phys. J. C 80 (2020) 593 [1903.08650].
[138] U. Mukhopadhyay and D. Majumdar, Swampland criteria in the slotheon field dark energy, Phys. Rev. D 100 (2019) 024006 [1904.01455].
[139] U. Mukhopadhyay, A. Paul and D. Majumdar, Addressing the high- problem in pseudo-Nambu-Goldstone boson dark energy models with dark matter-dark energy interaction, Eur. Phys. J. C 80 (2020) 904 [1909.03925].
[140] S. Vagnozzi, L. Visinelli, O. Mena and D.F. Mota, Do we have any hope of detecting scattering between dark energy and baryons through cosmology?, Mon. Not. Roy. Astron. Soc. 493 (2020) 1139 [1911.12374].
[141] O. Akarsu, J.D. Barrow, L.A. Escamilla and J.A. Vazquez, Graduated dark energy: Observational hints of a spontaneous sign switch in the cosmological constant, Phys. Rev. 101 (2020) 063528 [1912.08751].
[142] E.N. Saridakis, Barrow holographic dark energy, Phys. Rev. D 102 (2020) 123525 [2005.04115].
[143] Ruchika, S.A. Adil, K. Dutta, A. Mukherjee and A.A. Sen, Observational constraints on axion(s) dark energy with a cosmological constant, Phys. Dark Univ. 40 (2023) 101199 [2005.08813].
[144] S.D. Odintsov, V.K. Oikonomou and T. Paul, From a Bounce to the Dark Energy Era with Gravity, Class. Quant. Grav. 37 (2020) 235005 [2009.09947].
[145] S.D. Odintsov, V.K. Oikonomou, F.P. Fronimos and K.V. Fasoulakos, Unification of a Bounce with a Viable Dark Energy Era in Gauss-Bonnet Gravity, Phys. Rev. D 102 (2020) 104042 [2010. 13580].
[146] V.K. Oikonomou, Unifying inflation with early and late dark energy epochs in axion gravity, Phys. Rev. D 103 (2021) 044036 [2012.00586].
[147] V.K. Oikonomou, Rescaled Einstein-Hilbert Gravity from Gravity: Inflation, Dark Energy and the Swampland Criteria, Phys. Rev. D 103 (2021) 124028 [2012.01312].
[148] S. Vagnozzi, L. Visinelli, P. Brax, A.-C. Davis and J. Sakstein, Direct detection of dark energy: The XENON1T excess and future prospects, Phys. Rev. D 104 (2021) 063023 [2103.15834].
[149] R. Solanki, S.K.J. Pacif, A. Parida and P.K. Sahoo, Cosmic acceleration with bulk viscosity in modified gravity, Phys. Dark Univ. 32 (2021) 100820 [2105.00876].
[150] E.N. Saridakis, Do we need soft cosmology?, Phys. Lett. B 822 (2021) 136649 [2105.08646].
[151] S. Arora, S.K.J. Pacif, A. Parida and P.K. Sahoo, Bulk viscous matter and the cosmic acceleration of the universe in gravity, JHEAp 33 (2022) 1 [2106.00491].
[152] S. Capozziello, R. D’Agostino and O. Luongo, Thermodynamic parametrization of dark energy, Phys. Dark Univ. 36 (2022) 101045 [2202.03300].
[153] S.A. Narawade, L. Pati, B. Mishra and S.K. Tripathy, Dynamical system analysis for accelerating models in non-metricity gravity, Phys. Dark Univ. 36 (2022) 101020 [2203. 14121].
[154] R. D’Agostino, O. Luongo and M. Muccino, Healing the cosmological constant problem during inflation through a unified quasi-quintessence matter field, Class. Quant. Grav. 39 (2022) 195014 [2204.02190].
[155] V.K. Oikonomou and I. Giannakoudi, A panorama of viable gravity dark energy models, Int. J. Mod. Phys. D 31 (2022) 2250075 [2205.08599].
[156] A. Belfiglio, R. Giambò and O. Luongo, Alleviating the cosmological constant problem from particle production, Class. Quant. Grav. 40 (2023) 105004 [2206.14158].
[157] G.G. Luciano and J. Giné, Generalized interacting Barrow Holographic Dark Energy: Cosmological predictions and thermodynamic considerations, Phys. Dark Univ. 41 (2023) 101256 [2210.09755].
[158] S.A. Kadam, J. Levi Said and B. Mishra, Accelerating cosmological models in gravitational theory, Int. J. Geom. Meth. Mod. Phys. 20 (2023) 2350083 [2210.17075].
[159] Y.C. Ong, An Effective Sign Switching Dark Energy: Lotka-Volterra Model of Two Interacting Fluids, Universe 9 (2023) 437 [2212.04429].
[160] A. Bernui, E. Di Valentino, W. Giarè, S. Kumar and R.C. Nunes, Exploring the Ho tension and the evidence for dark sector interactions from 2D BAO measurements, Phys. Rev. D 107 (2023) 103531 [2301.06097].
[161] G.G. Luciano, Saez-Ballester gravity in Kantowski-Sachs Universe: A new reconstruction paradigm for Barrow Holographic Dark Energy, Phys. Dark Univ. 41 (2023) 101237 [2301.12488].
[162] L. Giani and O.F. Piattella, Induced non-local cosmology, Phys. Dark Univ. 40 (2023) 101219 [2302.06762].
[163] A. Belfiglio, Y. Carloni and O. Luongo, Particle production from non-minimal coupling in a symmetry breaking potential transporting vacuum energy, Phys. Dark Univ. 44 (2024) 101458 [2307.04739].
[164] E. Frion, D. Camarena, L. Giani, T. Miranda, D. Bertacca, V. Marra et al., Bayesian analysis of a Unified Dark Matter model with transition: can it alleviate the tension?, 2307.06320.
[165] S.A. Adil, U. Mukhopadhyay, A.A. Sen and S. Vagnozzi, Dark energy in light of the early JWST observations: case for a negative cosmological constant?, JCAP 10 (2023) 072 [2307.12763].
[166] S. Halder, S. Pan, P.M. Sá and T. Saha, Coupled phantom cosmological model motivated by the warm inflationary paradigm, 2407.15804.
[167] H. Fischer, C. Käding and M. Pitschmann, Screened Scalar Fields in the Laboratory and the Solar System, Universe 10 (2024) 297 [2405.14638].
[168] A.R. Cooray and D. Huterer, Gravitational lensing as a probe of quintessence, Astrophys. J. Lett. 513 (1999) L95 [astro-ph/9901097].
[169] G. Efstathiou, Constraining the equation of state of the universe from distant type Ia supernovae and cosmic microwave background anisotropies, Mon. Not. Roy. Astron. Soc. 310 (1999) 842 [astro-ph/9904356].
[170] M. Chevallier and D. Polarski, Accelerating universes with scaling dark matter, Int. J. Mod. Phys. D 10 (2001) 213 [gr-qc/0009008].
[171] A. Melchiorri, L. Mersini-Houghton, C.J. Odman and M. Trodden, The State of the dark energy equation of state, Phys. Rev. D 68 (2003) 043509 [astro-ph/0211522].
[172] E.V. Linder, Exploring the expansion history of the universe, Phys. Rev. Lett. 90 (2003) 091301 [astro-ph/0208512].
[173] C. Wetterich, Phenomenological parameterization of quintessence, Phys. Lett. B 594 (2004) 17 [astro-ph/0403289].
[174] B. Feng, M. Li, Y.-S. Piao and X. Zhang, Oscillating quintom and the recurrent universe, Phys. Lett. B 634 (2006) 101 [astro-ph/0407432].
[175] J.-Q. Xia, B. Feng and X.-M. Zhang, Constraints on oscillating quintom from supernova, microwave background and galaxy clustering, Mod. Phys. Lett. A 20 (2005) 2409 [astro-ph/0411501].
[176] S. Hannestad and E. Mortsell, Cosmological constraints on the dark energy equation of state and its evolution, JCAP 09 (2004) 001 [astro-ph/0407259].
[177] Y.-g. Gong and Y.-Z. Zhang, Probing the curvature and dark energy, Phys. Rev. D 72 (2005) 043518 [astro-ph/0502262].
[178] H.K. Jassal, J.S. Bagla and T. Padmanabhan, Observational constraints on low redshift evolution of dark energy: How consistent are different observations?, Phys. Rev. D 72 (2005) 103503 [astro-ph/0506748].
[179] S. Nesseris and L. Perivolaropoulos, Comparison of the legacy and gold snia dataset constraints on dark energy models, Phys. Rev. D 72 (2005) 123519 [astro-ph/0511040].
[180] D.-J. Liu, X.-Z. Li, J. Hao and X.-H. Jin, Revisiting the parametrization of Equation of State of Dark Energy via SNIa Data, Mon. Not. Roy. Astron. Soc. 388 (2008) 275 [0804.3829].
[181] E.M. Barboza, Jr. and J.S. Alcaniz, A parametric model for dark energy, Phys. Lett. B 666 (2008) 415 [0805.1713].
[182] J.-Z. Ma and X. Zhang, Probing the dynamics of dark energy with novel parametrizations, Phys. Lett. B 699 (2011) 233 [1102.2671].
[183] I. Sendra and R. Lazkoz, SN and BAO constraints on (new) polynomial dark energy parametrizations: current results and forecasts, Mon. Not. Roy. Astron. Soc. 422 (2012) 776 [1105.4943].
[184] A. De Felice, S. Nesseris and S. Tsujikawa, Observational constraints on dark energy with a fast varying equation of state, JCAP 05 (2012) 029 [1203.6760].
[185] H. Li and X. Zhang, Constraining dynamical dark energy with a divergence-free parametrization in the presence of spatial curvature and massive neutrinos, Phys. Lett. B 713 (2012) 160 [1202.4071].
[186] C.-J. Feng, X.-Y. Shen, P. Li and X.-Z. Li, A New Class of Parametrization for Dark Energy without Divergence, JCAP 09 (2012) 023 [1206.0063].
[187] J. Magaña, V.H. Cárdenas and V. Motta, Cosmic slowing down of acceleration for several dark energy parametrizations, JCAP 10 (2014) 017 [1407.1632].
[188] G. Pantazis, S. Nesseris and L. Perivolaropoulos, Comparison of thawing and freezing dark energy parametrizations, Phys. Rev. D 93 (2016) 103503 [1603.02164].
[189] E. Di Valentino, A. Melchiorri and J. Silk, Reconciling Planck with the local value of in extended parameter space, Phys. Lett. B 761 (2016) 242 [1606.00634].
[190] W. Yang, S. Pan and A. Paliathanasis, Latest astronomical constraints on some non-linear parametric dark energy models, Mon. Not. Roy. Astron. Soc. 475 (2018) 2605 [1708.01717].
[191] S. Pan, E.N. Saridakis and W. Yang, Observational Constraints on Oscillating Dark-Energy Parametrizations, Phys. Rev. D 98 (2018) 063510 [1712.05746].
[192] E. Mörtsell and S. Dhawan, Does the Hubble constant tension call for new physics?, JCAP 09 (2018) 025 [1801.07260].
[193] K. Dutta, Ruchika, A. Roy, A.A. Sen and M.M. Sheikh-Jabbari, Beyond with low and high redshift data: implications for dark energy, Gen. Rel. Grav. 52 (2020) 15 [1808.06623].
[194] W. Yang, S. Pan, E. Di Valentino and E.N. Saridakis, Observational constraints on dynamical dark energy with pivoting redshift, Universe 5 (2019) 219 [1811.06932].
[195] W. Yang, S. Pan, E. Di Valentino, E.N. Saridakis and S. Chakraborty, Observational constraints on one-parameter dynamical dark-energy parametrizations and the tension, Phys. Rev. D 99 (2019) 043543 [1810.05141].
[196] X. Li and A. Shafieloo, A Simple Phenomenological Emergent Dark Energy Model can Resolve the Hubble Tension, Astrophys. J. Lett. 883 (2019) L3 [1906.08275].
[197] S. Vagnozzi, New physics in light of the tension: An alternative view, Phys. Rev. (2020) 023518 [1907.07569].
[198] L. Visinelli, S. Vagnozzi and U. Danielsson, Revisiting a negative cosmological constant from low-redshift data, Symmetry 11 (2019) 1035 [1907. 07953].
[199] E. Di Valentino, A. Melchiorri, O. Mena and S. Vagnozzi, Interacting dark energy in the early 2020s: A promising solution to the and cosmic shear tensions, Phys. Dark Univ. 30 (2020) 100666 [1908.04281].
[200] K. Dutta, A. Roy, Ruchika, A.A. Sen and M.M. Sheikh-Jabbari, Cosmology with low-redshift observations: No signal for new physics, Phys. Rev. D 100 (2019) 103501 [1908.07267].
[201] E. Di Valentino, A. Melchiorri, O. Mena and S. Vagnozzi, Nonminimal dark sector physics and cosmological tensions, Phys. Rev. D 101 (2020) 063502 [1910.09853].
[202] S. Pan, W. Yang, E. Di Valentino, A. Shafieloo and S. Chakraborty, Reconciling tension in a six parameter space?, JCAP 06 (2020) 062 [1907.12551].
[203] E.M. Teixeira, A. Nunes and N.J. Nunes, Disformally Coupled Quintessence, Phys. Rev. D 101 (2020) 083506 [1912.13348].
[204] E.M. Teixeira, A. Nunes and N.J. Nunes, Conformally Coupled Tachyonic Dark Energy, Phys. Rev. D 100 (2019) 043539 [1903.06028].
[205] M. Martinelli, N.B. Hogg, S. Peirone, M. Bruni and D. Wands, Constraints on the interacting vacuum-geodesic CDM scenario, Mon. Not. Roy. Astron. Soc. 488 (2019) 3423 [1902.10694].
[206] M. Zumalacarregui, Gravity in the Era of Equality: Towards solutions to the Hubble problem without fine-tuned initial conditions, Phys. Rev. D 102 (2020) 023523 [2003.06396].
[207] N.B. Hogg, M. Bruni, R. Crittenden, M. Martinelli and S. Peirone, Latest evidence for a late time vacuum-geodesic CDM interaction, Phys. Dark Univ. 29 (2020) 100583 [2002.10449].
[208] G. Alestas, L. Kazantzidis and L. Perivolaropoulos, tension, phantom dark energy, and cosmological parameter degeneracies, Phys. Rev. D 101 (2020) 123516 [2004.08363].
[209] E. Di Valentino, A. Mukherjee and A.A. Sen, Dark Energy with Phantom Crossing and the Tension, Entropy 23 (2021) 404 [2005. 12587].
[210] G. Alestas, L. Kazantzidis and L. Perivolaropoulos, phantom transition at as a resolution of the Hubble tension, Phys. Rev. D 103 (2021) 083517 [2012.13932].
[211] M. Rezaei, T. Naderi, M. Malekjani and A. Mehrabi, A Bayesian comparison between and phenomenologically emergent dark energy models, Eur. Phys. J. C 80 (2020) 374 [2004.08168].
[212] D. Perkovic and H. Stefancic, Barotropic fluid compatible parametrizations of dark energy, Eur. Phys. J. C 80 (2020) 629 [2004.05342].
[213] H.B. Benaoum, W. Yang, S. Pan and E. Di Valentino, Modified emergent dark energy and its astronomical constraints, Int. J. Mod. Phys. D 31 (2022) 2250015 [2008.09098].
[214] S. Kumar, Remedy of some cosmological tensions via effective phantom-like behavior of interacting vacuum energy, Phys. Dark Univ. 33 (2021) 100862 [2102.12902].
[215] S. Vagnozzi, F. Pacucci and A. Loeb, Implications for the Hubble tension from the ages of the oldest astrophysical objects, JHEAp 36 (2022) 27 [2105.10421].
[216] L.A. Escamilla and J.A. Vazquez, Model selection applied to reconstructions of the Dark Energy, Eur. Phys. J. C 83 (2023) 251 [2111.10457].
[217] S. Bag, V. Sahni, A. Shafieloo and Y. Shtanov, Phantom Braneworld and the Hubble Tension, Astrophys. J. 923 (2021) 212 [2107.03271].
[218] A. Theodoropoulos and L. Perivolaropoulos, The Hubble Tension, the M Crisis of Late Time H(z) Deformation Models and the Reconstruction of Quintessence Lagrangians, Universe 7 (2021) 300 [2109.06256].
[219] G. Alestas, D. Camarena, E. Di Valentino, L. Kazantzidis, V. Marra, S. Nesseris et al., Late-transition versus smooth -deformation models for the resolution of the Hubble crisis, Phys. Rev. D 105 (2022) 063538 [2110.04336].
[220] A.A. Sen, S.A. Adil and S. Sen, Do cosmological observations allow a negative ?, Mon. Not. Roy. Astron. Soc. 518 (2022) 1098 [2112.10641].
[221] W. Yang, E. Di Valentino, S. Pan, A. Shafieloo and X. Li, Generalized emergent dark energy model and the Hubble constant tension, Phys. Rev. D 104 (2021) 063521 [2103.03815].
[222] N.B. Hogg and M. Bruni, Shan-Chen interacting vacuum cosmology, Mon. Not. Roy. Astron. Soc. 511 (2022) 4430 [2109.08676].
[223] N. Roy, S. Goswami and S. Das, Quintessence or phantom: Study of scalar field dark energy models through a general parametrization of the Hubble parameter, Phys. Dark Univ. 36 (2022) 101037 [2201.09306].
[224] L. Heisenberg, H. Villarrubia-Rojo and J. Zosso, Simultaneously solving the H0 and tensions with late dark energy, Phys. Dark Univ. 39 (2023) 101163 [2201.11623].
[225] A. Chudaykin, D. Gorbunov and N. Nedelko, Exploring CDM extensions with SPT-3G and Planck data: evidence for neutrino masses and implications of extended dark energy models for cosmological tensions, 2203.03666.
[226] O. Akarsu, S. Kumar, E. Özülker, J.A. Vazquez and A. Yadav, Relaxing cosmological tensions with a sign switching cosmological constant: Improved results with Planck, BAO, and Pantheon data, Phys. Rev. D 108 (2023) 023513 [2211.05742].
[227] F.B.M.d. Santos, Updating constraints on phantom crossing f gravity, JCAP 06 (2023) 039 [2211.16370].
[228] T. Schiavone, G. Montani and F. Bombacigno, gravity in the Jordan frame as a paradigm for the Hubble tension, Mon. Not. Roy. Astron. Soc. 522 (2023) L72 [2211.16737].
[229] C. van de Bruck, G. Poulot and E.M. Teixeira, Scalar field dark matter and dark energy: a hybrid model for the dark sector, JCAP 07 (2023) 019 [2211.13653].
[230] E. Ozulker, Is the dark energy equation of state parameter singular?, Phys. Rev. D 106 (2022) 063509 [2203.04167].
[231] E.M. Teixeira, B.J. Barros, V.M.C. Ferreira and N. Frusciante, Dissecting kinetically coupled quintessence: phenomenology and observational tests, JCAP 11 (2022) 059 [2207.13682].
[232] I. Ben-Dayan and U. Kumar, Emergent Unparticles Dark Energy can restore cosmological concordance, JCAP 12 (2023) 047 [2302.00067].
[233] M. Ballardini, A.G. Ferrari and F. Finelli, Phantom scalar-tensor models and cosmological tensions, JCAP 04 (2023) 029 [2302.05291].
[234] W. Yang, W. Giarè, S. Pan, E. Di Valentino, A. Melchiorri and J. Silk, Revealing the effects of curvature on the cosmological models, Phys. Rev. D 107 (2023) 063509 [2210.09865].
[235] J. de Cruz Perez and J. Sola Peracaula, Running vacuum in Brans Dicke theory: A possible cure for the and H0 tensions, Phys. Dark Univ. 43 (2024) 101406 [2302.04807].
[236] T. Patil, Ruchika and S. Panda, Coupled quintessence scalar field model in light of observational datasets, JCAP 05 (2024) 033 [2307.03740].
[237] Y. Zhai, W. Giarè, C. van de Bruck, E. Di Valentino, O. Mena and R.C. Nunes, A consistent view of interacting dark energy from multiple CMB probes, JCAP 07 (2023) 032 [2303.08201].
[238] S.A. Adil, O. Akarsu, E. Di Valentino, R.C. Nunes, E. Özülker, A.A. Sen et al., Omnipotent dark energy: A phenomenological answer to the Hubble tension, Phys. Rev. D 109 (2024) 023527 [2306.08046].
[239] G. Montani, M. De Angelis, F. Bombacigno and N. Carlevaro, Metric gravity with dynamical dark energy as a scenario for the Hubble tension, Mon. Not. Roy. Astron. Soc. 527 (2023) L156 [2306.11101].
[240] O. Akarsu, E. Di Valentino, S. Kumar, R.C. Nunes, J.A. Vazquez and A. Yadav, model: A promising scenario for alleviation of cosmological tensions, 2307. 10899.
[241] S. Vagnozzi, Seven Hints That Early-Time New Physics Alone Is Not Sufficient to Solve the Hubble Tension, Universe 9 (2023) 393 [2308.16628].
[242] O. Avsajanishvili, G.Y. Chitov, T. Kahniashvili, S. Mandal and L. Samushia, Observational Constraints on Dynamical Dark Energy Models, Universe 10 (2024) 122 [2310.16911].
[243] L. Giani, C. Howlett, K. Said, T. Davis and S. Vagnozzi, An effective description of Laniakea: impact on cosmology and the local determination of the Hubble constant, JCAP (2024) 071 [2311.00215].
[244] R. Lazkoz, V. Salzano, L. Fernandez-Jambrina and M. Bouhmadi-López, Ripped : An observational contender to the consensus cosmological model, Phys. Dark Univ. 45 (2024) 101511 [2311.10526].
[245] L.A. Escamilla, W. Giarè, E. Di Valentino, R.C. Nunes and S. Vagnozzi, The state of the dark energy equation of state circa 2023, JCAP 05 (2024) 091 [2307.14802].
[246] L.A. Escamilla, O. Akarsu, E. Di Valentino and J.A. Vazquez, Model-independent reconstruction of the interacting dark energy kernel: Binned and Gaussian process, JCAP 11 (2023) 051 [2305.16290].
[247] M. Rezaei, S. Pan, W. Yang and D.F. Mota, Evidence of dynamical dark energy in a non-flat universe: current and future observations, JCAP 01 (2024) 052 [2305.18544].
[248] E.M. Teixeira, R. Daniel, N. Frusciante and C. van de Bruck, Forecasts on interacting dark energy with standard sirens, Phys. Rev. D 108 (2023) 084070 [2309.06544].
[249] M. Forconi, W. Giarè, O. Mena, Ruchika, E. Di Valentino, A. Melchiorri et al., A double take on early and interacting dark energy from JWST, JCAP 05 (2024) 097 [2312.11074].
[250] M. Sebastianutti, N.B. Hogg and M. Bruni, The interacting vacuum and tensions: A comparison of theoretical models, Phys. Dark Univ. 46 (2024) 101546 [2312.14123].
[251] W.J. Wolf and P.G. Ferreira, Underdetermination of dark energy, Phys. Rev. D 108 (2023) 103519 [2310.07482].
[252] W. Giarè, E. Di Valentino, E.V. Linder and E. Specogna, Testing -attractor quintessential inflation against CMB and low-redshift data, 2402.01560.
[253] W. Giarè, M.A. Sabogal, R.C. Nunes and E. Di Valentino, Interacting Dark Energy after DESI Baryon Acoustic Oscillation measurements, 2404.15232.
[254] W. Giarè, Y. Zhai, S. Pan, E. Di Valentino, R.C. Nunes and C. van de Bruck, Tightening the reins on non-minimal dark sector physics: Interacting Dark Energy with dynamical and non-dynamical equation of state, 2404.02110.
[255] N. Menci, S.A. Adil, U. Mukhopadhyay, A.A. Sen and S. Vagnozzi, Negative cosmological constant in the dark energy sector: tests from JWST photometric and spectroscopic observations of high-redshift galaxies, 2401.12659.
[256] O. Akarsu, E.O. Colgáin, A.A. Sen and M.M. Sheikh-Jabbari, Tensions: Localising Missing Physics through Consistency Checks, 2402.04767.
[257] E.M. Teixeira, Illuminating the Dark Sector: Searching for new interactions between dark matter and dark energy, 1, 2024.
[258] D. Benisty, S. Pan, D. Staicova, E. Di Valentino and R.C. Nunes, Late-Time constraints on Interacting Dark Energy: Analysis independent of and .
[259] M. Najafi, S. Pan, E. Di Valentino and J.T. Firouzjaee, Dynamical dark energy confronted with multiple CMB missions, Phys. Dark Univ. 45 (2024) 101539.
[260] H. Moshafi, A. Talebian, E. Yusofi and E. Di Valentino, Observational constraints on the dark energy with a quadratic equation of state, Phys. Dark Univ. 45 (2024) 101524 [2403.02000].
[261] E. Silva, U. Zúñiga Bolaño, R.C. Nunes and E. Di Valentino, Non-Linear Matter Power Spectrum Modeling in Interacting Dark Energy Cosmologies, 2403. 19590.
[262] M. Reyhani, M. Najafi, J.T. Firouzjaee and E. Di Valentino, Structure formation in various dynamical dark energy scenarios, Phys. Dark Univ. 44 (2024) 101477 [2403. 15202].
[263] L.A. Escamilla, S. Pan, E. Di Valentino, A. Paliathanasis, J.A. Vázquez and W. Yang, Oscillations in the Dark?, 2404.00181.
[264] H. Wang, G. Ye and Y.-S. Piao, Impact of evolving dark energy on the search for primordial gravitational waves, 2407.11263.
[265] G. Montani, N. Carlevaro and M. De Angelis, Modified gravity in the presence of matter creation in the late Universe: alleviation of the Hubble tension, 2407.12409.
[266] T.-N. Li, P.-J. Wu, G.-H. Du, S.-J. Jin, H.-L. Li, J.-F. Zhang et al., Constraints on interacting dark energy models from the DESI BAO and DES supernovae data, 2407.14934.
[267] Y. Yang, X. Ren, Q. Wang, Z. Lu, D. Zhang, Y.-F. Cai et al., Quintom cosmology and modified gravity after DESI 2024, 2404.19437.
[268] S. Dwivedi and M. Högås, 2D BAO vs 3D BAO: solving the Hubble tension with alternative cosmological models, 2407.04322.
[269] ACT collaboration, The Atacama Cosmology Telescope: A Measurement of the DR6 CMB Lensing Power Spectrum and Its Implications for Structure Growth, Astrophys. J. 962 (2024) 112 [2304. 05202].
[270] SPT-3G collaboration, SPT-3G: A Next-Generation Cosmic Microwave Background Polarization Experiment on the South Pole Telescope, Proc. SPIE Int. Soc. Opt. Eng. 9153 (2014) 91531P [1407. 2973].
[271] SPT-3G collaboration, Measurement of the CMB temperature power spectrum and constraints on cosmology from the SPT-3G 2018 TT, TE, and EE dataset, Phys. Rev. D 108 (2023) 023510 [2212.05642].
[272] A. Lewis and A. Challinor, Weak gravitational lensing of the CMB, Phys. Rept. 429 (2006) 1 [astro-ph/0601594].
[273] W. Giarè, E. Di Valentino, A. Melchiorri and O. Mena, New cosmological bounds on hot relics: axions and neutrinos, Mon. Not. Roy. Astron. Soc. 505 (2021) 2703 [2011.14704].
[274] E. Di Valentino and A. Melchiorri, Neutrino Mass Bounds in the Era of Tension Cosmology, Astrophys. J. Lett. 931 (2022) L18 [2112.02993].
[275] F. D’Eramo, E. Di Valentino, W. Giarè, F. Hajkarim, A. Melchiorri, O. Mena et al., Cosmological bound on the QCD axion mass, redux, JCAP 09 (2022) 022 [2205.07849].
[276] E. Di Valentino, S. Gariazzo, W. Giarè, A. Melchiorri, O. Mena and F. Renzi, Novel model-marginalized cosmological bound on the QCD axion mass, Phys. Rev. D 107 (2023) 103528 [2212.11926].
[277] W. Giarè, O. Mena and E. Di Valentino, Lensing impact on cosmic relics and tensions, Phys. Rev. D 108 (2023) 103539 [2307.14204].
[278] Planck collaboration, Planck 2018 results. VIII. Gravitational lensing, Astron. Astrophys. 641 (2020) A8 [1807.06210].
[279] G. Ye, J.-Q. Jiang and Y.-S. Piao, Shape of CMB lensing in the early dark energy cosmology, Phys. Rev. D 108 (2023) 063512 [2305.18873].
[280] ACT, DES collaboration, Cosmology from cross-correlation of ACT-DR4 CMB lensing and DES-Y3 cosmic shear, Mon. Not. Roy. Astron. Soc. 528 (2024) 2112 [2309.04412].
[281] ACT, DES collaboration, Cosmological constraints from the tomography of DES-Y3 galaxies with CMB lensing from ACT DR4, JCAP 01 (2024) 033 [2306.17268].
[282] ACT, DESI collaboration, The Atacama Cosmology Telescope DR6 and DESI: Structure formation over cosmic time with a measurement of the cross-correlation of CMB Lensing and Luminous Red Galaxies, 2407.04606.
[283] N. Sailer et al., Cosmological constraints from the cross-correlation of DESI Luminous Red Galaxies with CMB lensing from Planck PR4 and ACT DR6, 2407.04607.
[284] ACT collaboration, The Atacama Cosmology Telescope: DR6 Gravitational Lensing and SDSS BOSS cross-correlation measurement and constraints on gravity with the statistic, 2405.12795.
[285] EUCLID collaboration, Euclid Definition Study Report, 1110.3193.
[286] LSST collaboration, LSST: from Science Drivers to Reference Design and Anticipated Data Products, Astrophys. J. 873 (2019) 111 [0805.2366].
[287] D. Spergel et al., Wide-Field InfraRed Survey Telescope-Astrophysics Focused Telescope Assets WFIRST-AFTA Final Report, 1305.5422.
[288] SKA collaboration, Cosmology with Phase 1 of the Square Kilometre Array: Red Book 2018: Technical specifications and performance forecasts, Publ. Astron. Soc. Austral. 37 (2020) e007 [1811.02743].
[289] E. Di Valentino, O. Mena, S. Pan, L. Visinelli, W. Yang, A. Melchiorri et al., In the realm of the Hubble tension-a review of solutions, Class. Quant. Grav. 38 (2021) 153001 [2103.01183].
[290] L. Perivolaropoulos and F. Skara, Challenges for CDM: An update, New Astron. Rev. 95 (2022) 101659 [2105.05208].
[291] E. Abdalla et al., Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies, JHEAp 34 (2022) 49 [2203.06142].
[292] S. Gariazzo, W. Giarè, O. Mena and E. Di Valentino, How robust are the parameter constraints extending the CDM model?, 2404.11182.
[293] R. Bean and A. Melchiorri, Current constraints on the dark energy equation of state, Phys. Rev. D 65 (2002) 041302 [astro-ph/0110472].
[294] S. Hannestad and E. Mortsell, Probing the dark side: Constraints on the dark energy equation of state from CMB, large scale structure and Type Ia supernovae, Phys. Rev. D 66 (2002) 063508 [astro-ph/0205096].
[295] N. Said, C. Baccigalupi, M. Martinelli, A. Melchiorri and A. Silvestri, New Constraints On The Dark Energy Equation of State, Phys. Rev. D 88 (2013) 043515 [1303.4353].
[296] D.L. Shafer and D. Huterer, Chasing the phantom: A closer look at Type Ia supernovae and the dark energy equation of state, Phys. Rev. D 89 (2014) 063510 [1312.1688].
[297] X. Zhang, Impacts of dark energy on weighing neutrinos after Planck 2015, Phys. Rev. D 93 (2016) 083011 [1511.02651].
[298] Y.-Y. Xu and X. Zhang, Comparison of dark energy models after Planck 2015, Eur. Phys. J. (2016) 588 [1607.06262].
[299] S. Wang, Y.-F. Wang, D.-M. Xia and X. Zhang, Impacts of dark energy on weighing neutrinos: mass hierarchies considered, Phys. Rev. D 94 (2016) 083519 [1608.00672].
[300] S. Vagnozzi, E. Giusarma, O. Mena, K. Freese, M. Gerbino, S. Ho et al., Unveiling secrets with cosmological data: neutrino masses and mass hierarchy, Phys. Rev. D 96 (2017) 123503 [1701.08172].
[301] X. Zhang, Weighing neutrinos in dynamical dark energy models, Sci. China Phys. Mech. Astron. 60 (2017) 060431 [1703.00651].
[302] L. Feng, J.-F. Zhang and X. Zhang, Searching for sterile neutrinos in dynamical dark energy cosmologies, Sci. China Phys. Mech. Astron. 61 (2018) 050411 [1706.06913].
[303] D. Wang, Dark Energy Constraints in light of Pantheon SNe Ia, BAO, Cosmic Chronometers and CMB Polarization and Lensing Data, Phys. Rev. D 97 (2018) 123507 [1801.02371].
[304] T. Sprenger, M. Archidiacono, T. Brinckmann, S. Clesse and J. Lesgourgues, Cosmology in the era of Euclid and the Square Kilometre Array, JCAP 02 (2019) 047 [1801.08331].
[305] V. Poulin, K.K. Boddy, S. Bird and M. Kamionkowski, Implications of an extended dark energy cosmology with massive neutrinos for cosmological tensions, Phys. Rev. D 97 (2018) 123504 [1803.02474].
[306] S. Roy Choudhury and A. Naskar, Strong Bounds on Sum of Neutrino Masses in a 12 Parameter Extended Scenario with Non-Phantom Dynamical Dark Energy with CPL parameterization, Eur. Phys. J. C 79 (2019) 262 [1807.02860].
[307] DES collaboration, Dark Energy Survey Year 1 Results: Constraints on Extended Cosmological Models from Galaxy Clustering and Weak Lensing, Phys. Rev. D 99 (2019) 123505 [1810.02499].
[308] D. Wang, Exploring new physics beyond the standard cosmology with Dark Energy Survey Year 1 Data, Phys. Dark Univ. 32 (2021) 100810 [1904.00657].
[309] S. Roy Choudhury and S. Hannestad, Updated results on neutrino mass and mass hierarchy from cosmology with Planck 2018 likelihoods, JCAP 07 (2020) 037 [1907.12598].
[310] A. Chudaykin, K. Dolgikh and M.M. Ivanov, Constraints on the curvature of the Universe and dynamical dark energy from the Full-shape and BAO data, Phys. Rev. D 103 (2021) 023507 [2009. 10106].
[311] G. D’Amico, L. Senatore and P. Zhang, Limits on wCDM from the EFTofLSS with the PyBird code, JCAP 01 (2021) 006 [2003.07956].
[312] S. Vagnozzi, A. Loeb and M. Moresco, Eppur è piatto? The Cosmic Chronometers Take on Spatial Curvature and Cosmic Concordance, Astrophys. J. 908 (2021) 84 [2011.11645].
[313] W. Yang, E. Di Valentino, S. Pan, Y. Wu and J. Lu, Dynamical dark energy after Planck CMB final release and tension, Mon. Not. Roy. Astron. Soc. 501 (2021) 5845 [2101.02168].
[314] E. Di Valentino, A combined analysis of the late time direct measurements and the impact on the Dark Energy sector, Mon. Not. Roy. Astron. Soc. 502 (2021) 2065 [2011.00246].
[315] S. Brieden, H. Gil-Marín and L. Verde, Model-agnostic interpretation of 10 billion years of cosmic evolution traced by BOSS and eBOSS data, JCAP 08 (2022) 024 [2204.11868].
[316] C. Grillo, P. Rosati, S.H. Suyu, G.B. Caminha, A. Mercurio and A. Halkola, On the accuracy of time-delay cosmography in the Frontier Fields Cluster MACS J1149.5+2223 with supernova Refsdal, Astrophys. J. 898 (2020) 87 [2001. 02232].
[317] S. Cao, J. Ryan and B. Ratra, Cosmological constraints from Hii starburst galaxy, quasar angular size, and other measurements, Mon. Not. Roy. Astron. Soc. 509 (2022) 4745 [2109.01987].
[318] M. Zhang, B. Wang, P.-J. Wu, J.-Z. Qi, Y. Xu, J.-F. Zhang et al., Prospects for Constraining Interacting Dark Energy Models with 21 cm Intensity Mapping Experiments, Astrophys. J. 918 (2021) 56 [2102.03979].
[319] E.O. Colgáin, M.M. Sheikh-Jabbari and L. Yin, Can dark energy be dynamical?, Phys. Rev. D 104 (2021) 023510 [2104.01930].
[320] Y.-P. Teng, W. Lee and K.-W. Ng, Constraining the dark-energy equation of state with cosmological data, Phys. Rev. D 104 (2021) 083519 [2105.02667].
[321] C. Krishnan, R. Mohayaee, E.O. Colgáin, M.M. Sheikh-Jabbari and L. Yin, Does Hubble tension signal a breakdown in FLRW cosmology?, Class. Quant. Grav. 38 (2021) 184001 [2105.09790].
[322] R.C. Nunes and S. Vagnozzi, Arbitrating the S8 discrepancy with growth rate measurements from redshift-space distortions, Mon. Not. Roy. Astron. Soc. 505 (2021) 5427 [2106.01208].
[323] R.C. Bernardo, D. Grandón, J. Said Levi and V.H. Cárdenas, Parametric and nonparametric methods hint dark energy evolution, Phys. Dark Univ. 36 (2022) 101017 [2111.08289].
[324] G. Bargiacchi, M. Benetti, S. Capozziello, E. Lusso, G. Risaliti and M. Signorini, Quasar cosmology: dark energy evolution and spatial curvature, Mon. Not. Roy. Astron. Soc. 515 (2022) 1795 [2111.02420].
[325] A. Semenaite, A.G. Sánchez, A. Pezzotta, J. Hou, A. Eggemeier, M. Crocce et al., Beyond constraints from the full shape clustering measurements from BOSS and eBOSS, Mon. Not. Roy. Astron. Soc. 521 (2023) 5013 [2210.07304].
[326] P. Carrilho, C. Moretti and A. Pourtsidou, Cosmology with the EFTofLSS and BOSS: dark energy constraints and a note on priors, JCAP 01 (2023) 028 [2207.14784].
[327] D. Wang, Pantheon + constraints on dark energy and modified gravity: An evidence of dynamical dark energy, Phys. Rev. D 106 (2022) 063515 [2207.07164].
[328] M. Koussour, S.K.J. Pacif, M. Bennai and P.K. Sahoo, A New Parametrization of Hubble Parameter in Gravity, Fortsch. Phys. 71 (2023) 2200172 [2208.04723].
[329] R.C. Bernardo, D. Grandón, J. Levi Said and V.H. Cárdenas, Dark energy by natural evolution: Constraining dark energy using Approximate Bayesian Computation, Phys. Dark Univ. 40 (2023) 101213 [2211.05482].
[330] S.A. Narawade and B. Mishra, Phantom Cosmological Model with Observational Constraints in Gravity, Annalen Phys. 535 (2023) 2200626 [2211.09701].
[331] W.-T. Hou, J.-Z. Qi, T. Han, J.-F. Zhang, S. Cao and X. Zhang, Prospects for constraining interacting dark energy models from gravitational wave and gamma ray burst joint observation, JCAP 05 (2023) 017 [2211.10087].
[332] S. Kumar, R.C. Nunes, S. Pan and P. Yadav, New late-time constraints on gravity, Phys. Dark Univ. 42 (2023) 101281 [2301.07897].
[333] R. Bhagat, S.A. Narawade and B. Mishra, Weyl type gravity observational constrained cosmological models, Phys. Dark Univ. 41 (2023) 101250 [2305. 01659].
[334] A. Mussatayeva, N. Myrzakulov and M. Koussour, Cosmological constraints on dark energy in f(Q) gravity: A parametrized perspective, Phys. Dark Univ. 42 (2023) 101276 [2307.00281].
[335] N.B. Hogg, Constraints on dark energy from TDCOSMO & SLACS lenses, Mon. Not. Roy. Astron. Soc. 528 (2024) L95 [2310.11977].
[336] DESI collaboration, DESI 2024 VI: Cosmological Constraints from the Measurements of Baryon Acoustic Oscillations, 2404.03002.
[337] L. Verde, T. Treu and A.G. Riess, Tensions between the Early and the Late Universe, Nature Astron. 3 (2019) 891 [1907. 10625].
[338] J.-P. Hu and F.-Y. Wang, Hubble Tension: The Evidence of New Physics, Universe 9 (2023) 94 [2302.05709].
[339] W. Giarè, Inflation, the Hubble tension, and early dark energy: An alternative overview, Phys. Rev. D 109 (2024) 123545 [2404.12779].
[340] W. Giarè, CMB Anomalies and the Hubble Tension, 2305. 16919.
[341] R. Mainini, A.V. Maccio, S.A. Bonometto and A. Klypin, Modeling dynamical dark energy, Astrophys. J. 599 (2003) 24 [astro-ph/0303303].
[342] U. Alam, V. Sahni and A.A. Starobinsky, The Case for dynamical dark energy revisited, JCAP 06 (2004) 008 [astro-ph/0403687].
[343] J. Sola and H. Stefancic, Dynamical dark energy or variable cosmological parameters?, Mod. Phys. Lett. A 21 (2006) 479 [astro-ph/0507110].
[344] I. Antoniadis, P.O. Mazur and E. Mottola, Cosmological dark energy: Prospects for a dynamical theory, New J. Phys. 9 (2007) 11 [gr-qc/0612068].
[345] G.-B. Zhao, R.G. Crittenden, L. Pogosian and X. Zhang, Examining the evidence for dynamical dark energy, Phys. Rev. Lett. 109 (2012) 171301 [1207.3804].
[346] J. Solà Peracaula, J. de Cruz Pérez and A. Gómez-Valent, Dynamical dark energy vs. const in light of observations, EPL 121 (2018) 39001 [1606.00450].
[347] J. Sola, A. Gomez-Valent and J. de Cruz Pérez, Dynamical dark energy: scalar fields and running vacuum, Mod. Phys. Lett. A 32 (2017) 1750054 [1610.08965].
[348] G.-B. Zhao et al., Dynamical dark energy in light of the latest observations, Nature Astron. 1 (2017) 627 [1701.08165].
[349] W. Yang, N. Banerjee and S. Pan, Constraining a dark matter and dark energy interaction scenario with a dynamical equation of state, Phys. Rev. D 95 (2017) 123527 [1705.09278].
[350] J. Sola Peracaula, A. Gomez-Valent and J. de Cruz Pérez, Signs of Dynamical Dark Energy in Current Observations, Phys. Dark Univ. 25 (2019) 100311 [1811.03505].
[351] S. Pan, W. Yang, E. Di Valentino, E.N. Saridakis and S. Chakraborty, Interacting scenarios with dynamical dark energy: Observational constraints and alleviation of the tension, Phys. Rev. D 100 (2019) 103520 [1907.07540].
[352] C. Escamilla-Rivera and A. Nájera, Dynamical dark energy models in the light of gravitational-wave transient catalogues, JCAP 03 (2022) 060 [2103.02097].
[353] Z.-W. Zhao, Z.-X. Li, J.-Z. Qi, H. Gao, J.-F. Zhang and X. Zhang, Cosmological parameter estimation for dynamical dark energy models with future fast radio burst observations, Astrophys. J. 903 (2020) 83 [2006.01450].
[354] E. Di Valentino, A. Melchiorri, E.V. Linder and J. Silk, Constraining Dark Energy Dynamics in Extended Parameter Space, Phys. Rev. D 96 (2017) 023523 [1704.00762].
[355] E. Di Valentino, A. Melchiorri and J. Silk, Cosmological constraints in extended parameter space from the Planck 2018 Legacy release, JCAP 01 (2020) 013 [1908.01391].
[356] E. Di Valentino, W. Giarè, A. Melchiorri and J. Silk, Health checkup test of the standard cosmological model in view of recent cosmic microwave background anisotropies experiments, Phys. Rev. D 106 (2022) 103506 [2209.12872].
[357] D. Rubin et al., Union Through UNITY: Cosmology with 2,000 SNe Using a Unified Bayesian Framework, 2311.12098.
[358] D. Scolnic et al., The Pantheon + Analysis: The Full Data Set and Light-curve Release, Astrophys. J. 938 (2022) 113 [2112.03863].
[359] M. Cortês and A.R. Liddle, Interpreting DESI’s evidence for evolving dark energy, 2404.08056.
[360] V. Patel and L. Amendola, Comments on the prior dependence of the DESI results, 2407.06586.
[361] L. Orchard and V.H. Cárdenas, Probing Dark Energy Evolution Post-DESI 2024, 2407.05579.
[362] G. Liu, Y. Wang and W. Zhao, Impact of LRG1 and LRG2 in DESI 2024 BAO data on dark energy evolution, 2407.04385.
[363] A. Chudaykin and M. Kunz, Modified gravity interpretation of the evolving dark energy in light of DESI data, 2407. 02558.
[364] A. Notari, M. Redi and A. Tesi, Consistent Theories for the DESI dark energy fit, 2406.08459.
[365] I.D. Gialamas, G. Hütsi, K. Kannike, A. Racioppi, M. Raidal, M. Vasar et al., Interpreting DESI 2024 BAO: late-time dynamical dark energy or a local effect?, 2406.07533.
[366] H. Wang, Z.-Y. Peng and Y.-S. Piao, Can recent DESI BAO measurements accommodate a negative cosmological constant?, 2406.03395.
[367] H. Wang and Y.-S. Piao, Dark energy in light of recent DESI BAO and Hubble tension, 2404.18579.
[368] Y. Carloni, O. Luongo and M. Muccino, Does dark energy really revive using DESI 2024 data?, 2404. 12068.
[369] E.O. Colgáin, M.G. Dainotti, S. Capozziello, S. Pourojaghi, M.M. Sheikh-Jabbari and D. Stojkovic, Does DESI 2024 Confirm CDM?, 2404.08633.
[370] Y. Tada and T. Terada, Quintessential interpretation of the evolving dark energy in light of DESI observations, Phys. Rev. D 109 (2024) L121305 [2404.05722].
[371] W. Yin, Cosmic clues: DESI, dark energy, and the cosmological constant problem, JHEP 05 (2024) 327 [2404.06444].
[372] O. Luongo and M. Muccino, Model independent cosmographic constraints from DESI 2024, 2404.07070.
[373] C.-G. Park, J. de Cruz Perez and B. Ratra, Using non-DESI data to confirm and strengthen the DESI 2024 spatially-flat CDM cosmological parameterization result, 2405.00502.
[374] D. Shlivko and P.J. Steinhardt, Assessing observational constraints on dark energy, Phys. Lett. B 855 (2024) 138826 [2405.03933].
[375] G. Ye, M. Martinelli, B. Hu and A. Silvestri, Non-minimally coupled gravity as a physically viable fit to DESI 2024 BAO, 2407.15832.
[376] Z. Wang, S. Lin, Z. Ding and B. Hu, The role of LRG1 and LRG2’s monopole in inferring the DESI 2024 BAO cosmology, 2405.02168.
[377] D. Naredo-Tuero, M. Escudero, E. Fernández-Martínez, X. Marcano and V. Poulin, Living at the Edge: A Critical Look at the Cosmological Neutrino Mass Bound, 2407.13831.
[378] R. de Putter and E.V. Linder, Calibrating Dark Energy, JCAP 10 (2008) 042 [0808.0189].
[379] A. Hernández-Almada, M.L. Mendoza-Martínez, M.A. García-Aspeitia and V. Motta, Phenomenological emergent dark energy in the light of DESI Data Release 1, 2407. 09430.
[380] S. Pourojaghi, M. Malekjani and Z. Davari, Cosmological constraints on dark energy parametrizations after DESI 2024: Persistent deviation from standard CDM cosmology, 2407.09767.
[381] O.F. Ramadan, J. Sakstein and D. Rubin, DESI Constraints on Exponential Quintessence, 2405.18747.
[382] K.V. Berghaus, J.A. Kable and V. Miranda, Quantifying Scalar Field Dynamics with DESI 2024 Y1 BAO measurements, 2404.14341.
[383] F.J. Qu, K.M. Surrao, B. Bolliet, J.C. Hill, B.D. Sherwin and H.T. Jense, Accelerated inference on accelerated cosmic expansion: New constraints on axion-like early dark energy with DESI BAO and ACT DR6 CMB lensing, 2404.16805.
[384] P. Adolf, M. Hirsch, S. Krieg, H. Päs and M. Tabet, Fitting the DESI BAO Data with Dark Energy Driven by the Cohen-Kaplan-Nelson Bound, 2406.09964.
[385] C.-P. Ma and E. Bertschinger, Cosmological perturbation theory in the synchronous and conformal Newtonian gauges, Astrophys. J. 455 (1995) 7 [astro-ph/9506072].
[386] N. Dimakis, A. Karagiorgos, A. Zampeli, A. Paliathanasis, T. Christodoulakis and P.A. Terzis, General Analytic Solutions of Scalar Field Cosmology with Arbitrary Potential, Phys. Rev. D 93 (2016) 123518 [1604.05168].
[387] S. Pan, W. Yang and A. Paliathanasis, Imprints of an extended Chevallier-Polarski-Linder parametrization on the large scale of our universe, Eur. Phys. J. C 80 (2020) 274 [1902.07108].
[388] A. Lewis, A. Challinor and A. Lasenby, Efficient computation of CMB anisotropies in closed FRW models, Astrophys. J. 538 (2000) 473 [astro-ph/9911177].
[389] C. Howlett, A. Lewis, A. Hall and A. Challinor, CMB power spectrum parameter degeneracies in the era of precision cosmology, JCAP (2012) 027 [1201.3654].
[390] A. Lewis and S. Bridle, Cosmological parameters from CMB and other data: A Monte Carlo approach, Phys. Rev. D 66 (2002) 103511 [astro-ph/0205436].
[391] A. Lewis, Efficient sampling of fast and slow cosmological parameters, Phys. Rev. D 87 (2013) 103529 [1304.4473].
[392] R.M. Neal, Taking Bigger Metropolis Steps by Dragging Fast Variables, ArXiv Mathematics e-prints (2005) [math/0502099].
[393] A. Gelman and D.B. Rubin, Inference from Iterative Simulation Using Multiple Sequences, Statist. Sci. 7 (1992) 457.
[394] Planck collaboration, Planck 2018 results. V. CMB power spectra and likelihoods, Astron. Astrophys. 641 (2020) A5 [1907.12875].
[395] J. Carron, M. Mirmelstein and A. Lewis, CMB lensing from Planck PR4 maps, JCAP 09 (2022) 039 [2206.07773].
[396] DESI collaboration, DESI 2024 IV: Baryon Acoustic Oscillations from the Lyman Alpha Forest, 2404.03001.
[397] D. Huterer and M.S. Turner, Probing the dark energy: Methods and strategies, Phys. Rev. D 64 (2001) 123527 [astro-ph/0012510].
[398] A. Albrecht et al., Report of the Dark Energy Task Force, astro-ph/0609591.
  1. Corresponding author.
  2. For a few caveats, objections, and discussions surrounding this conclusion raised over the years, see Refs. [63-74].
  3. This diffuse interest is reflected in the wide range of models – both within and beyond the standard cosmological constant – that have been proposed over the years. These include, for example, new (ultra)light fields and modifications to gravity. With no claims to completeness see, e.g., Refs. [92, 104-167].
    Notably, the gravitational deflection, or lensing, experienced by CMB photons due to their interactions with the large-scale structure of the Universe imprints a distinctive non-Gaussian four-point correlation function (trispectrum) in both temperature and polarization anisotropies [272]. This signal provides complementary information about late-time processes affecting structure formation, from neutrinos and thermal relics [273-277] to dark energy and its dynamical properties [56, 278-284].
    Excitingly, upcoming Stage-IV astronomical surveys such as future data releases from DESI, Euclid [285], the Large Synoptic Survey Telescope (LSST) [286], the Wide-Field InfraRed Survey Telescope (WFIRST) [287], and the Square Kilometre Array (SKA) [288], are expected to improve upon current sensitivity and are forecasted to constrain DE parameters to near-percent precision, offering new insights into the dark sector of the Universe.
  4. See, e.g., Refs [32, 38, 40, 45, 50, 53, 54, 215, 245, 293-336] for recent and not-so-recent discussions and constraints on the DE EoS from a variety of astrophysical and cosmological probes.
    In recent years, the possibility that the DE EoS can be phantom in nature has gained substantial interest, as in principle a shift of towards could already be enough to address the well-known Hubble tension [289-291, 337, 338] – see, e.g., Refs. [197, 339] for an overview, as well as for caveats surrounding this possibility.
    This difficulty is often referred to as geometrical degeneracy. At its core, the problem is that different combinations of late-time cosmic parameters can be adjusted in such a way that the acoustic angular scale – determined by the ratio of the comoving sound horizon at recombination to the comoving distance to last scattering – remains constant if both quantities change proportionally. Consequently, measurements based solely on this scale cannot provide strong constraints on (dynamical) DE parameters by themselves, unless perturbation-level effects and late-time data are also incorporated to break this degeneracy.
  5. As argued in various recent works, the DESI BAO measurement at (which is in tension with Planck) can play a crucial role in deriving many of the DESI signals for new physics, partially including the preference for DDE [369, 376, 377].
  6. To address this problem, in Ref. [313], some of us adopted flat priors , thus removing positive values of a priori. In this work, we have performed additional stability tests, which revealed that numerical instabilities arise only when CMB data are considered on their own (we do not report these results for any of the models under study, as they are not informative). Without late-time data, DE parameters remain essentially unconstrained, and can acquire large positive values. Despite the logarithmic nature of the equation of state, for these values, the DE energy density does not remain negligible in the early Universe, triggering warnings and errors in the Boltzmann solver code CAMB [388, 389]. In contrast, when late-time data are included, the DE parameters are significantly constrained in the region , and no large positive values are allowed. As a result, in the allowed region of parameter space, the DE energy density remains negligible at early times and does not affect early Universe cosmology.
  7. The NPIPE lensing map [395] covers CMB angular scales in the range using the quadratic estimator and re-processing Planck time-ordered data with several improvements, including around more data compared to the plik-lensing likelihood. Notice also that NPIPE and ACT-DR6 measurements explore distinct angular scales, as ACT uses only CMB multipoles and has only partial overlap with the sky fraction used in the Planck analysis [269]. Additionally they have different noise levels and instrument-related systematics. Therefore they can be regarded as nearly independent lensing measurements.
  8. Hereafter, constraints will always be quoted at CL unless otherwise specified.
  9. See, e.g., Refs [397, 398] for discussions on the importance of the pivot redshift.
    Note that the features presented in this appendix for the CPL model have been discussed in detail by the DESI collaboration – see, e.g., Sec. 5.2 of Ref. [336]. As we essentially recover all of the DESI results, we omit further discussion of the CPL model here.

Journal: Journal of Cosmology and Astroparticle Physics, Volume: 2024, Issue: 10
DOI: https://doi.org/10.1088/1475-7516/2024/10/035
Publication Date: 2024-10-01

Robust Preference for Dynamical Dark Energy in DESI BAO and SN Measurements

William Giarè, Mahdi Najafi, Supriya Pan, Eleonora Di Valentino, Javad T. Firouzjaee School of Mathematics and Statistics, University of Sheffield, Hounsfield Road, Sheffield S3 7RH, United Kingdom Department of Physics, K.N. Toosi University of Technology, P.O. Box 15875-4416, Tehran, Iran PDAT Laboratory, Department of Physics, K.N. Toosi University of Technology, P.O. Box 15875-4416, Tehran, Iran Department of Mathematics, Presidency University, 86/1 College Street, Kolkata 700073, India Institute of Systems Science, Durban University of Technology, PO Box 1334, Durban 4000, Republic of South Africa School of Physics, Institute for Research in Fundamental Sciences (IPM), P.O. Box 193955531, Tehran, IranE-mail: w.giare@sheffield.ac.uk, mahdinajafi12676@yahoo.com, supriya.maths@presiuniv.ac.in, e.divalentino@sheffield.ac.uk, firouzjaee@kntu.ac.ir

Abstract

Recent Baryon Acoustic Oscillation (BAO) measurements released by DESI, when combined with Cosmic Microwave Background (CMB) data from Planck and two different samples of Type Ia supernovae (Pantheon-Plus and DESY5) reveal a preference for Dynamical Dark Energy (DDE) characterized by a present-day quintessence-like equation of state that crossed into the phantom regime in the past. A core ansatz for this result is assuming a linear Chevallier-Polarski-Linder (CPL) parameterization to describe the evolution of the DE equation of state (EoS). In this paper, we test if and to what extent this assumption impacts the results. To prevent broadening uncertainties in cosmological parameter inference and facilitate direct comparison with the baseline CPL case, we focus on 4 alternative well-known models that, just like CPL, consist of only two free parameters: the present-day DE EOS ( ) and a parameter quantifying its dynamical evolution ( ). We demonstrate that the preference for DDE remains robust regardless of the parameterization: consistently remains in the quintessence regime, while consistently indicates a preference for a dynamical evolution towards the phantom regime. This tendency is significantly strengthened by DESY5 SN measurements. By comparing the best-fit obtained within each DDE model, we notice that the linear CPL parameterization is not the best-fitting case. Among the models considered, the EoS proposed by Barboza and Alcaniz consistently leads to the most significant improvement.

Contents

1 Introduction ….. 1
2 Dynamical Dark Energy Models ….. 5
2.1 Chevallier-Polarski-Linder parametrization ….. 5
2.2 Exponential parametrization ….. 6
2.3 Jassal-Bagla-Padmanabhan parametrization ….. 6
2.4 Logarithmic parametrization ….. 6
2.5 Barboza-Alcaniz parametrization ….. 7
3 Methods ….. 7
3.1 Statistical Analyses ….. 7
3.2 Datasets ….. 8
4 Results ….. 9
4.1 Results for the CPL parameterization ….. 10
4.2 Results for the Exponential parametrization ….. 11
4.3 Results for the JBP parametrization ….. 13
4.4 Results for the Logarithmic parametrization ….. 15
4.5 Results for the BA parametrization ….. 17
5 Discussions and Conclusions ….. 18
A Equation of State, pivot redshift, and phantom crossing across the different models ….. 21

1 Introduction

One of the most undoubtedly fascinating and unforeseen discoveries of the past three decades is that the Universe is undergoing an accelerated phase of expansion. This was first argued in 1998 through observations of distant Type Ia Supernovae [1, 2], and has since been corroborated by a wide variety of other probes [3-45, 45-62].
Since all known forces and components in nature would decelerate the expansion rate of the Universe, acceleration itself requires a physical mechanism beyond the Standard Model of fundamental interactions, able to counteract deceleration, inducing instead a Dark Energy (DE) phase where the dynamics is characterized by negative pressure with an effective Equation of State (EoS) , a condition that directly follows from the second Friedmann equation (also known as the acceleration equation) [75-82].
In the theoretical framework described by the standard model of cosmology, DE is parametrized by a positive cosmological constant term ( ) in the Einstein equation with its energy density comprising the vast majority of the Universe’s energy budget. Despite its apparent simplicity, this interpretation is not free from conceptual problems and limitations [75, 78, 83-92]. Foremost, plugging a positive cosmological constant component into the
gravitational field equations described by General Relativity (GR) implies living in an asymptotically de Sitter universe, which seems to contrast with several theories/models of quantum gravity proposing instead an asymptotically anti-de Sitter universe [93-97]. Secondly, it seems quite natural to question what made us so lucky to live precisely in the cosmic epoch when such a constant component came to be not only relevant but even dominant compared to other contributions such as matter, altering the expansion history of the Universe so prominently as to allow us to become easily aware of its existence and implications [82, 98-100]. Finally, and most importantly, when it comes to the physical interpretations, anything that contributes to the energy density of the vacuum behaves akin to a cosmological constant, summing up within the energy-momentum tensor as due to Lorentz invariance. Based on standard quantum field theory calculations, one would expect a zero-point energy density contribution of , which, depending on the ultraviolet wavelength cutoff scale, is found to be somewhere between to orders of magnitude larger than what is inferred by cosmological data [83]. This leads to one of the biggest disagreements between theoretical predictions and observations, arguably requiring a level of fine-tuning that appears to be well beyond what any current theories can realistically explain [78,83,101-103]. As a result, from a theoretical perspective, the nature of DE remains one of the biggest puzzles in modern physics, sustaining significant research interest in the high-energy physics community.
From an observational standpoint, investigating the nature of DE has sparked research interest comparable to that driven by the theoretical problems surrounding its physical interpretation [143, 165, 168-268]. Increasingly precise observations of the Cosmic Microwave Background (CMB) radiation, obtained from experiments such as WMAP [20, 21] and, more recently, the Planck satellite [39, 40], as well as the Atacama Cosmology Telescope (ACT) [43, 44, 56, 269] and the South Pole Telescope (SPT) [51, 270, 271], have provided extremely accurate measurements of the angular power spectra of temperature and polarization anisotropies, revealing a precise snapshot of the Universe at the last scattering surface Concurrently, progress in observational astronomy and astrophysics has culminated in a series of present surveys aimed at determining the properties of the Universe at low redshift through a multitude of probes, including – but not limited to – Baryon Acoustic Oscillations (BAO) and Type Ia Supernovae (SN) measurements. These collective efforts have ushered in a new era of precision cosmology, eventually allowing percentage-level precision in cosmological parameter inference and enabling precise tests of physics within and beyond the CDM framework [289-291].
Despite these remarkable achievements, it is no exaggeration to say that at the time of writing, observations are inconclusive about the physical nature of DE. While too faraway deviations from the canonical CDM model appear severely constrained [292], several
alternative theoretical frameworks and phenomenological avenues featuring new physics in the dark sector of the model remain at the very least plausible.
Trying to summarize an otherwise very articulated debate, we can adhere to Occam’s razor principle and start considering one of the simplest hypotheses beyond the cosmological constant. This involves assuming that DE can be modeled as a generic fluid with a constant EoS, . By leaving as a free parameter in the theoretical model, cosmological observations can constrain deviations from the cosmological constant value In this regard, focusing exclusively on the Planck CMB data one might speculate about a preference for a phantom-like DE component ( ) [40, 245]. However, as extensively documented in the literature, this preference is not confirmed by independent CMB experiments such as ACT and SPT [44, 51, 271, 340], and – most importantly – it lacks consistent support from observations of the local universe. When combining and SN data altogether, no convincing deviation from is seen, possibly lending weight to the cosmological constant interpretation [245].
However, one may argue that simplicity may not always be a prerogative of nature. Pushing this approach forward, we can relax the assumption of a constant EoS and consider models where varies with the universe’s expansion – here and after known as Dynamical Dark Energy (DDE). This possibility, along with the various proposed physical realizations, has also undergone extensive testing; see, e.g., Refs. [194, 195, 313, 319, 341-353]. From an observational standpoint, CMB data alone have limited capacity to constrain DDE models due to minimal effects left at the epoch of the last scattering surface and the increased number of cosmological parameters [354-356]. Even in simple parametrizations aimed at minimizing the number of free degrees of freedom, CMB experiments produce constraints that are typically too broad to provide informative results. Therefore, local universe observations acquire primary importance.
A significant turning point in the study of DDE models is marked by the very recent BAO release from the Dark Energy Spectroscopic Instrument (DESI) [58, 59], and – albeit to a lesser extent – by SN distance moduli measurements from the Union3 compilation [357] first and, more recently, from the five-year observations of the Dark Energy Survey (DESY5) [60-62]. Before these updated data, no significant preference had ever emerged in favor of DDE models, certainly not to the extent required to challenge the baseline cosmological constant interpretation [292]. Excitingly, when DESI BAO observations are combined with Planck CMB data and SN distance moduli measurements (whether from the Pantheon-plus catalog [55, 358], the Union3 compilation [357], or DESY5 [60-62]), they produce strong indications for DDE. Specifically, within the linear Chevallier-Polarski-Linder (CPL) parameterization of the DE EoS, [170,172] – where represents the present-day DE EoS and quantifies the dynamical evolution – we observe a preference for and at
a statistical level ranging between 2.5 and , depending on the specific combination of SN data used [336].
Unexpectedly, these results have heated up the recent debate, fueling a multitude of re-analyses and re-interpretations [59, 253, 264, 266, 267, 359-375]. As “extraordinary claims require extraordinary evidence”, we certainly advise and exercise caution. However, even taking in mind all the possible caveats and limitations surrounding the first DESI data release, it is undeniable that a high statistical preference for DDE holds intrinsic interest – if confirmed, this would represent the first concrete evidence of new physics beyond the standard model of cosmology.
Given the potential implications of this result, it is natural to question its robustness. Barring any possible systematic issues in these datasets , we examine if and to what extent assuming a linear parameterization for the DE EoS might impact the current findings. Although the CPL parameterization has been demonstrated to match the background evolution of distances arising from exact DE equations of motion to an accuracy of approximately for viable cosmologies over a wide range of physics, including scalar fields, modified gravity, and phase transitions (see, e.g., Refs. [172, 378]), other parameterizations proposed over the years (which may deviate from CPL at both and ) remain allowed by current observations. Testing these alternative models against new data can certainly represent a useful exercise to shed light on the role played by the parameterization itself. To be fair, the process has already begun with several independent groups actively engaged in this activity [364, 379-384].
Given the vast number of parameterizations proposed over the years and recently analyzed in relation to the DESI data, a few warnings are in order. First and foremost, alternative parameterizations often introduce extra parameters compared to CPL. This is both a blessing and a curse: on the one hand, accounting for more degrees of freedom allows more flexibility in . On the other hand, this typically implies relaxing the overall constraining power due to the combined effects of degeneracies and correlations among parameters. Secondly, the physical interpretations of the parameters involved may differ from the two employed in the CPL model. This further compounds the comparison of the results, making it difficult to derive general guidelines on the preference towards DDE.
To overcome these difficulties, in this article, we test different DDE models while allowing for a fair comparison of the results. We restrict our attention to five well-known parameterizations that satisfy the following criteria: (i) they consist of two parameters to describe the evolution of and ; (ii) these two parameters retain the same physical meaning as in the CPL parameterization; (iii) for the same combinations of pairs , the resulting shape of deviates from CPL either near the present epoch or in the past, depending on the specific case.
The paper is organized as follows. In Sec. 2 we sketch the theoretical set-up of the gravitational equations and propose the DE parametrizations we wish to study. In Sec. 3 we describe the observational data and the methodology to constrain the proposed DE parametrizations. In Sec. 4 we present the constraints on the resulting DE scenarios. Finally, in Sec. 5 we draw our general conclusions.

2 Dynamical Dark Energy Models

Considering a DDE component in cosmological models produces changes both in the background dynamics and in the dynamics of cosmological perturbations.
Focusing on flat Friedmann-Lemaitre-Robertson-Walker cosmology and models where the DE EoS can be described by a continuous function of the scale factor, the first Friedman equation reads
Here is the Hubble parameter, the dot denotes the derivative with respect to physical time , the subscript 0 indicates quantities evaluate at present while , and are the energy densities in radiation, matter, and DE, respectively.
When it comes to cosmological perturbations, diffeomorphism invariance of GR requires fixing a gauge. In the synchronous gauge, the line element reads [385]
where is the conformal time, and are the unperturbed and perturbed spatial part of the metric tensors. For a fluid component , the equations governing the dimensionless density perturbations and the divergence of the -th fluid velocity in the Fourier space are [385]:
where the primes denote the derivative with respect to conformal time is the usual synchronous gauge metric perturbation, is the conformal Hubble parameter, is the wavenumber in Fourier space, stands for the anisotropic stress of the -th fluid, and represents the adiabatic sound speed of the -th fluid defined as . In this work, we fix the squared sound speed of the DE component in the rest frame as broadly expected for the simplest DE models based on a single light minimally coupled scalar field with a canonical kinetic term.
Having outlined the background and perturbation dynamics, we now list and describe the five different two-parameter models employed for .

2.1 Chevallier-Polarski-Linder parametrization

The model proposed by Chevallier, Polarski and Linder [170,172] (CPL hereafter) can be regarded as the baseline parameterization used in most analyses focusing on DDE, including this work. In this scenario, the DE EoS reads
As already mentioned in the introduction, its advantages include a manageable 2-dimensional phase space, reduction to linear redshift behavior at low redshift, bounded behavior at high redshift, high accuracy in reconstructing various scalar field equations of state and the resulting distance-redshift relations up to accuracy, good sensitivity to observational data, and a straightforward physical interpretation. The latter arises from its representation as the Taylor expansion of around the present epoch up to the first order: and which is the coefficient for the dynamical term.

2.2 Exponential parametrization

As a next step, we consider the exponential form for the DE EoS [386, 387]
Up to the first order of the Taylor expansion, this description reduces to the CPL parameterization around . However, as moves far away from 1 , the exponential from can introduce (small) deviations from the linear CPL regime without increasing the dimensionality of the parameter space [259].

2.3 Jassal-Bagla-Padmanabhan parametrization

The third parameterization studied in this work is the model proposed by Jassal-BaglaPadmanabhan in Ref. [178] (JBP hereafter). In this case the DE EoS is
It is characterized by the sum of a linear and a quadratic term in the scale factor. When is close to 1 , the term becomes comparable to , thereby leading to expected differences at low redshift compared to CPL.

2.4 Logarithmic parametrization

We consider the following logarithmic form for the EoS:
To the best of our knowledge, this parameterization was originally introduced by G. Efstathiou in Ref. [169] to capture the behaviour of a wide class of potential scalar field models of DE at low redshift . Here, with a fair amount of courage and following thorough stability tests, we extend this parameterization all the way up to . In principle, for some combinations of parameters, the logarithmic term can actually grow in absolute value and cause instabilities. However, given the current data constraints and the slow logarithmic
Parameter Prior
[0.005, 0.1]
[0.01, 0.99]
[1.61, 3.91]
[0.8, 1.2]
[0.01, 0.8]
[0.5, 10]
[-3,1]
[-3, 2]
Table 1. Ranges for the flat prior distributions imposed on the free cosmological parameters in the analysis.
growth, this is not the case. We find that the parameterization can be safely extended to high redshift because the DE contribution remains largely negligible compared to other components in the Universe’s energy budget.

2.5 Barboza-Alcaniz parametrization

The last (but as we shall see, not least) model involved in our analysis is the one proposed by Barboza and Alcaniz in Ref. [181] (referred to as BA hereafter). In this case, the DE EoS is characterized by the following functional form:
This parameterization shows a linear behavior at low redshifts and remains well-behaved as , while allowing for deviations from the baseline CPL scenario.

3 Methods

In this section, we describe the statistical methodologies and observational datasets employed in our analysis.

3.1 Statistical Analyses

The cosmology resulting from all the five DDE models listed in Sec. 2 can be characterized by 8 free parameters: the physical baryon energy density , the physical cold dark matter energy density , the amplitude of the primordial scalar spectrum , its spectral index , the optical depth to reionization , the angular size of the sound horizon , and the two free parameters describing the DE sector – i.e., the present-day value of the DE EoS and the parameter describing its dynamical evolution . To compare the theoretical predictions against observations, we implement these models in five different modified versions of the publicly available cosmological code CAMB [388, 389] and explore the posterior distributions of the 8 -dimensional parameter space by performing Markov Chain Monte Carlo (MCMC)
analyses via the publicly available sampler Cobaya [390, 391] that employs the fast dragging speed hierarchy implementation [392]. The convergence of the generated MCMC chains is assessed via the Gelman-Rubin parameter [393]. For all models and datasets, we require for the chains to be considered converged. In Tab. 1, we present the flat prior ranges on which the parameters are left to freely vary.

3.2 Datasets

The datasets involved in our analyses are:
  • Planck: Measurements of the Planck CMB temperature anisotropy and polarization power spectra, their cross-spectra, and the combination of the ACT and Planck lensing power spectrum. All CMB likelihoods employed in this work are listed below:
    (i) Measurements of the power spectra of temperature and polarization anisotropies, , , and , at small scales ( ), obtained by the Planck plik likelihood [40, 394];
    (ii) Measurements of the spectrum of temperature anisotropies, , at large scales ), obtained by the Planck Commander likelihood [40, 394];
    (iii) Measurements of the spectrum of E-mode polarization, , at large scales 30), obtained by the Planck SimAll likelihood [40, 394];
    (iv) Reconstruction of the spectrum of the lensing potential, obtained by the Planck PR4 NPIPE data release [395] used in combination with ACT-DR6 lensing likelihood [56, 269].
  • DESI: Baryon acoustic oscillations (BAO) measurements extracted by observations of galaxies & quasars [58], and Lyman- [396] tracers from the first year of observations using the Dark Energy Spectroscopic Instrument (DESI). These include measurements of the transverse comoving distance, the Hubble horizon, and the angle-averaged distance as summarized in Tab. I of Ref. [336].
  • PantheonPlus: Distance moduli measurements of 1701 light curves of 1550 spectroscopically confirmed type Ia SN sourced from eighteen different surveys, gathered from the Pantheon-plus sample [55, 358].
  • DESY5: Distance moduli measurements of 1635 Type Ia SN covering the redshift range of that have been collected during the full five years of the Dark Energy Survey (DES) Supernova Program [60-62], along with 194 low-redshift SN in the redshift range of which are in common with the Pantheon-plus sample [55, 358].
We conclude this subsection with a final remark. Our analysis focuses on two samples of Type-Ia SN: PantheonPlus and DESY5, excluding the Union3 sample. As highlighted in the DESI paper [336], among these three SN samples, PantheonPlus (which uses spectroscopically confirmed SN) produces the smallest, yet significant, preference for DDE, deviating by
about from the cosmological constant scenario. In contrast, DESY5 (which uses photometry) shows the largest shift towards DDE, at . The Union3 sample (which also uses spectroscopically confirmed SN ) shows a preference for DDE around , falling between PantheonPlus and DESY5. Although Union3 provides valuable confirmation of these results, here we focus on the two samples that represent the smallest and largest deviations from the cosmological constant.

4 Results

In this section, we present the observational constraints on the five DDE models considered in this article. We discuss the results model by model, testing each case against three different data combinations: Planck + DESI, Planck + DESI + PantheonPlus, and Planck + DESI + DESY5. We make no secret that due to the large number of analyzed models and the similarity of the results obtained, the following discussion may appear somewhat repetitive (though necessary). Therefore, readers interested in the results of specific models can find the numerical constraints, two-dimensional correlations, and one-dimensional posterior distribution functions of key parameters as follows:
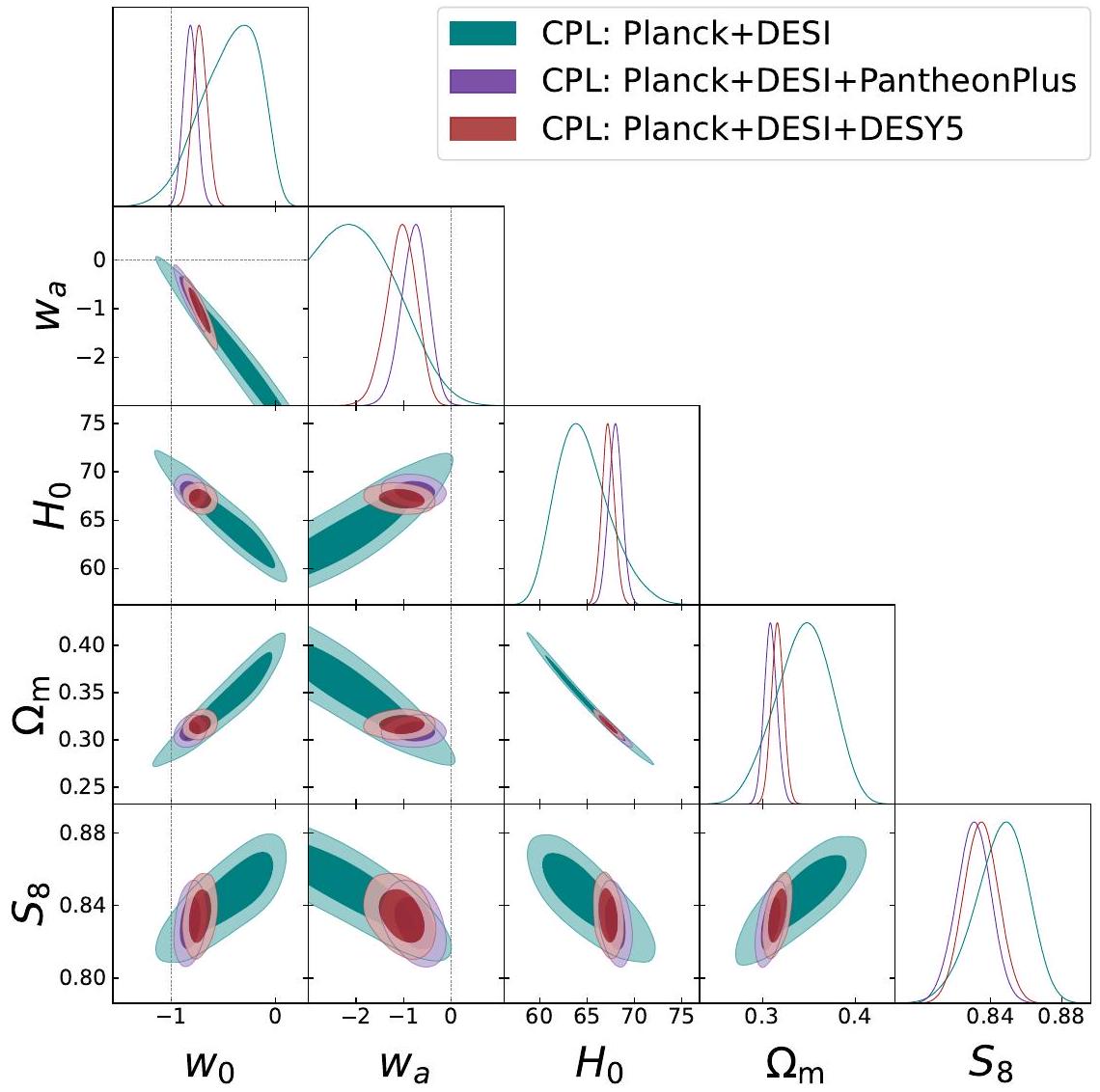
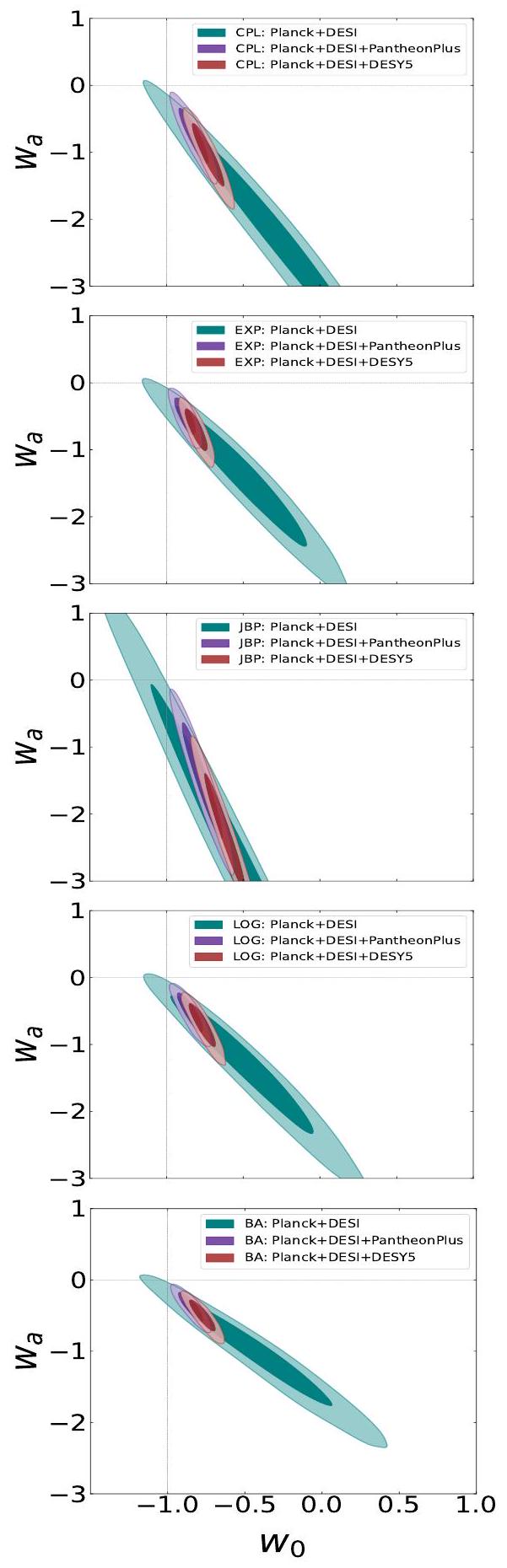
  • Table 2 and Figure 1 summarize the numerical constraints and parameter correlations for the baseline CPL case (2.5). The results for this case are detailed in Sec. 4.1.
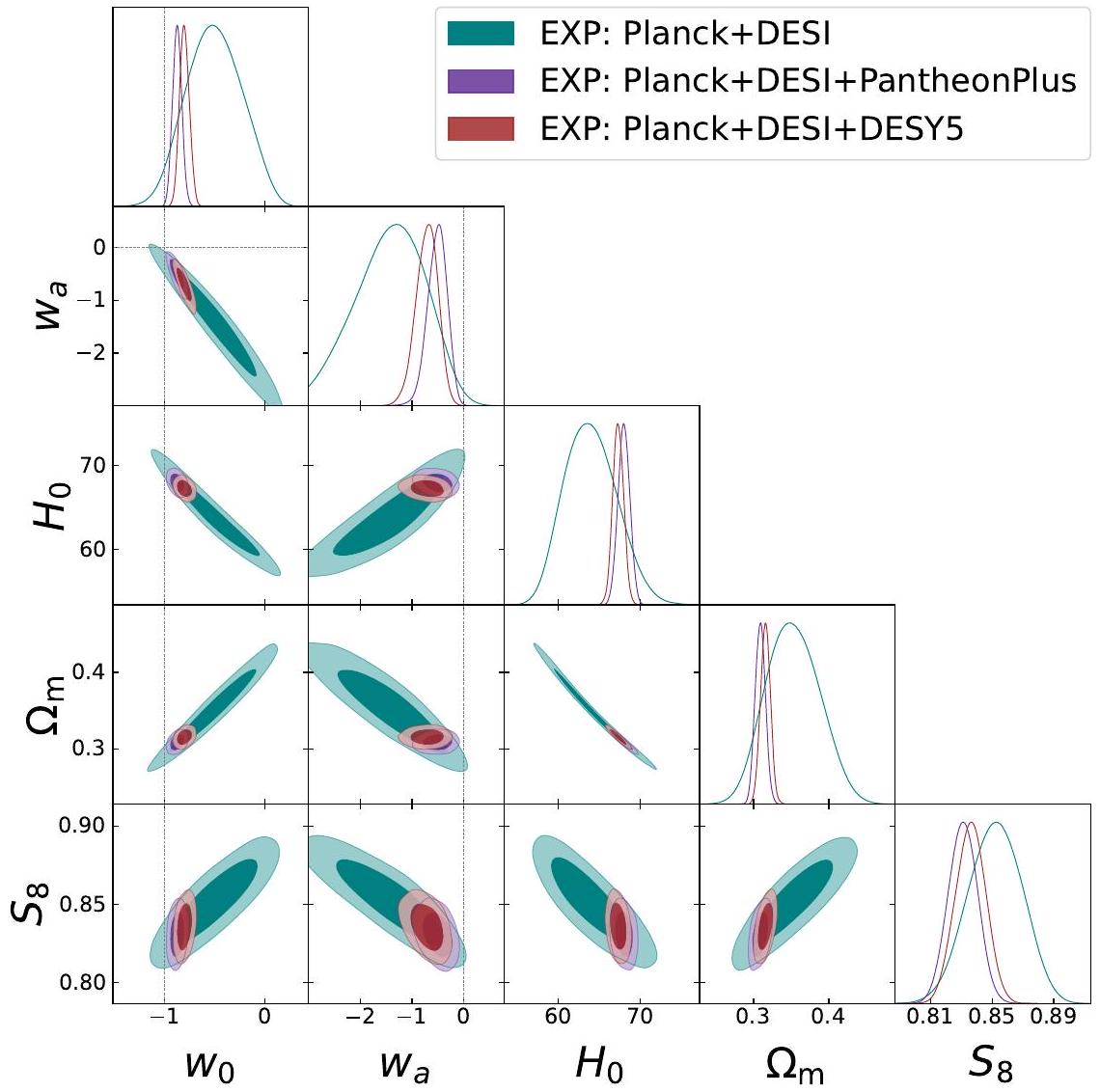
  • Table 3 and Figure 2 present the results for the exponential parameterization (2.6), discussed in Sec. 4.2.
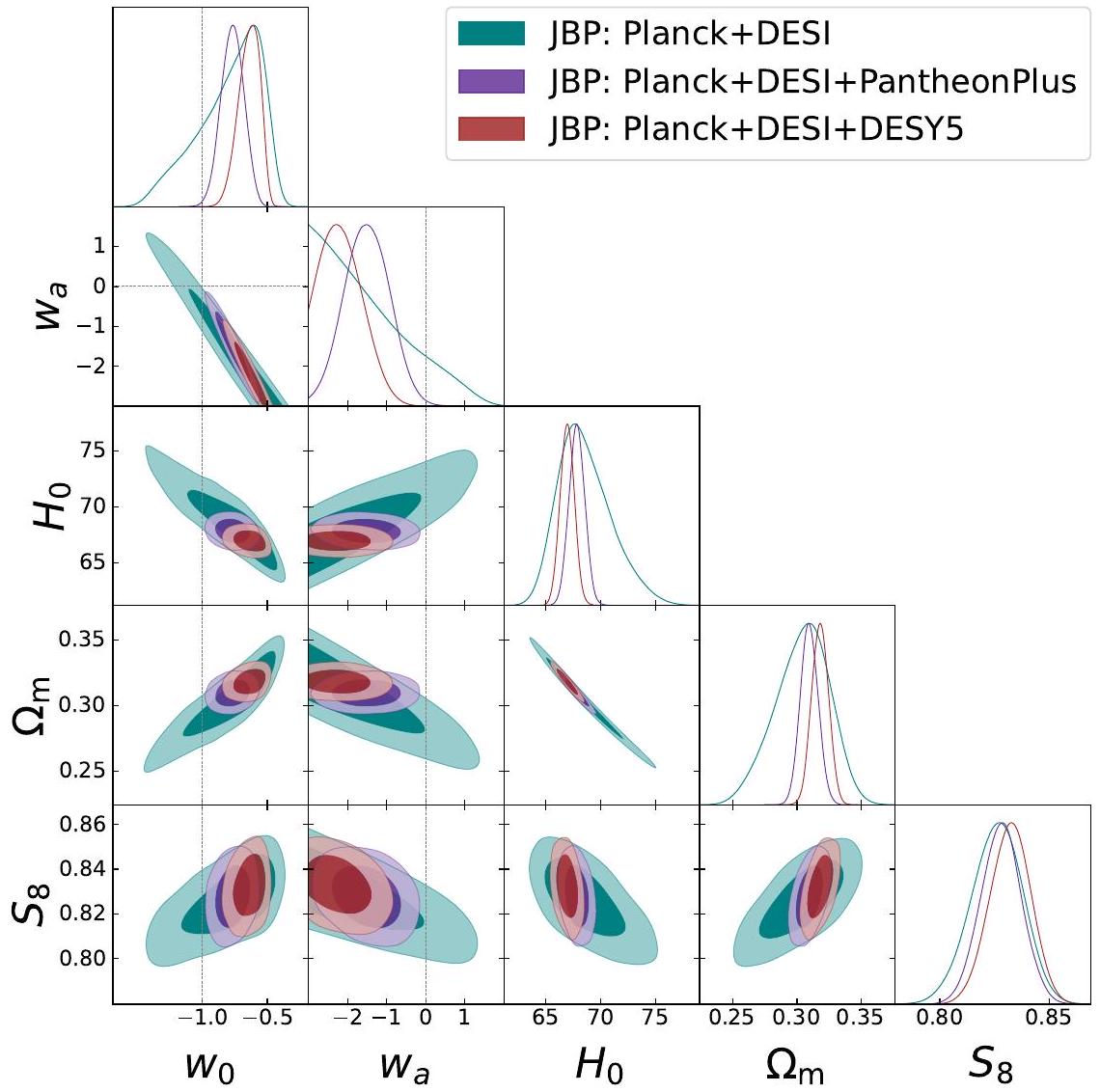
  • Table 4 and Figure 3 provide the results for the JBP EoS (2.7), discussed in Sec. 4.3.
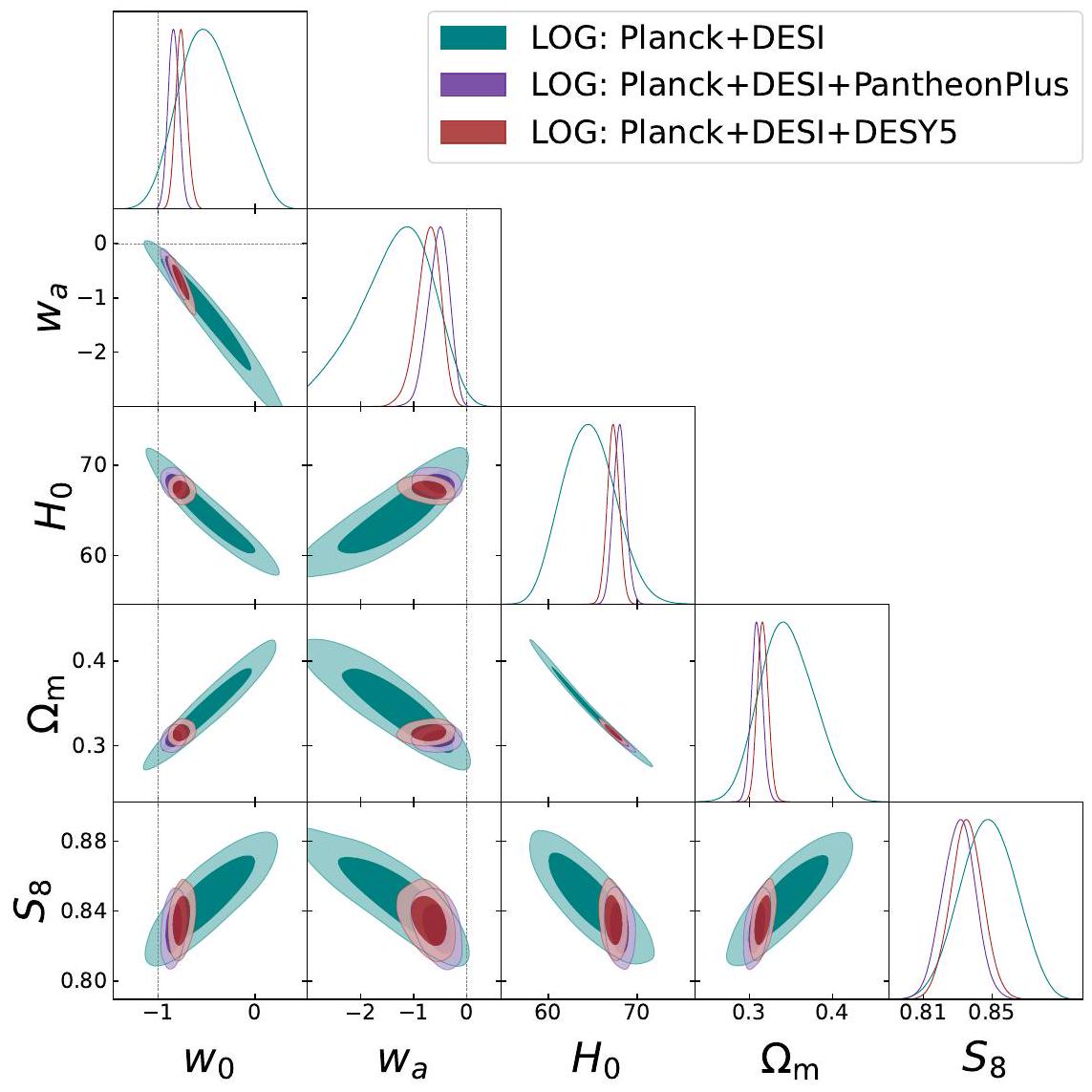
  • Table 5 and Figure 4 summarize the results for the logarithmic parameterization (2.8), detailed in Sec. 4.4.
  • Table 6 and Figure 5 present the results for the BA parameterization (2.9), discussed in Sec. 4.5.
Conversely, readers interested in a comprehensive overview of the results, their interpretation, and implications can refer directly to Sec. 5. Instead, a comprehensive discussion of the behavior of the EoS inferred from the different datasets employed in the analysis across various models, as well as constraints on crucial quantities that aid in interpreting the results discussed in this section – such as the pivot redshift (i.e., the redshifts where the equation of state is better constrained by current data) and phantom crossing – is presented in Appendix A and summarized in Fig. 7 and Tab. 7. Interested readers can refer to this appendix for further details.

4.1 Results for the CPL parameterization

The numerical constraints obtained by adopting a baseline CPL parametrization are given in Tab. 2. Fig. 1 displays key parameters that characterize this model (i.e., the presentday value of the EoS and the parameter quantifying its redshift evolution ) as well as their correlations with other cosmological parameters of intrinsic interest for the late-time expansion history of the Universe such as the Hubble constant , the present-day matter fractional energy density , and the matter clustering parameter .
Parameter Planck+DESI Planck + DESI + PantheonPlus Planck+DESI+DESY5
-6.8 -8.4 -15.2
Table 2. CPL Parametrization (2.5) – CL constraints on the free and derived cosmological parameters for 3 different data combinations detailed in Sec. 3. Negative values of indicate an improvement in the fit to the data compared to .
We recover all the results discussed in the recent DESI release paper [336]. For Planck+DESI, the constraints favor a present-day quintessence EoS with at showing a notable shift away from . On the other hand, provides hints of dynamical evolution towards the phantom regime.
The addition of PantheonPlus significantly refines the constraints on the parameter space, reducing the error bars on the DE parameters by up to a factor of 5 . Although shifts towards -1 , it remains strictly in the quintessence regime: . Consistent with DESI 2024 findings [59], the mean value of increases compared to Planck + DESI, now reading . This boosts the evidence for a past phantom-like DDE component to approximately , see also Fig. 1.
When replacing PantheonPlus with DESY5 type Ia SN, we observe a shift of away from -1 , resulting in . This places deep in the quintessence regime, see also Fig. 1. Similarly, is found to be non-zero at high statistical significance. Thus, the evidence for DDE remains stronger in the Planck + DESI + DESY5 case compared to Planck + DESI + PantheonPlus, and the cosmological constant case falls well outside the joint probability contours in the plane, as seen in Fig. 1.
Figure 1. CPL parametrization (2.5) – one-dimensional posterior distributions and twodimensional marginalized contours for the main key parameters as obtained from the Planck + DESI, Planck + DESI + PantheonPlus, and Planck + DESI + DESY5 dataset combinations.

4.2 Results for the Exponential parametrization

We present the constraints obtained by assuming an exponential parametrization for the DE EoS in Tab. 3. In Fig. 2, we show the one-dimensional posterior distribution functions and the two-dimensional marginalized contours for the key cosmic parameters.
As usual, we test the model against three different combinations of data involving the DESI BAO measurements. Focusing on the minimal Planck + DESI combination, we find – significantly different from -1 and deep in the quintessence regime. Similarly, is almost away from the non-dynamical case, lending weight to the Planck + DESI preference for DDE.
The addition of PantheonPlus SN measurements reinforces this preference: the constraints on shrink in the quintessence regime, deviating from by more than . Additionally, is found to be non-zero at more than . Overall, Planck + DESI + PantheonPlus provides evidence for DDE with the present-day EoS in the quintessence regime and a dynamical evolution that crosses into the phantom regime, as clearly shown in Fig. 2.
When we focus on the Planck + DESI + DESY 5 data combination, the evidence for DDE becomes significantly more pronounced. remains strictly in the quintessence
Parameter Planck+DESI Planck + DESI + PantheonPlus Planck+DESI+DESY5
-6.9 -7.8 -15.2
Table 3. Exponential Parametrization (2.6) – CL constraints on the free and derived cosmological parameters for 3 different data combinations detailed in Sec. 3. Negative values of indicate an improvement in the fit to the data compared to .
regime, while is away from the non-dynamical scenario; see again Fig. 2.
Overall, in terms of constraints on cosmic parameters, these results are in agreement with those derived for the CPL parametrization in the previous section, underscoring the resilience of the evidence for DDE and relieving concerns about dependence on the model for these particular results.
Figure 2. Exponential parameterization (2.6) – one-dimensional posterior distributions and twodimensional marginalized contours for the main key parameters as obtained from the Planck + DESI, Planck + DESI + PantheonPlus, and Planck + DESI + DESY5 dataset combinations.

4.3 Results for the JBP parametrization

The numerical constraints for the JBP parametrization are given in Tab. 4, while the marginalized probability contours for the usual parameters are shown in Fig. 3.
When considering Planck + DESI, unlike the other parametrizations described so far (e.g., CPL and exponential form), remains unbounded and an upper limit can be derived at . Conversely, remains in the quintessence regime ( ), confirming the overall tendency for a present-day quintessence EoS.
When considering PantheonPlus in combination with Planck and DESI, we get – non-null at more than . Additionally, the constraints on 0.086 are narrowed down within the quintessence portion of the parameter space as seen in Fig. 3. Thus, effectively, evidence of DDE is confirmed for this parametrization as well.
Finally, we replace PantheonPlus with DESY5 SN measurements. In this case, we obtain and , confirming that the evidence of DDE becomes much more pronounced with DESY5. This evidence reaches a statistical significance . Having said that, comparing Fig. 3 with the respective triangular plots of the other parameterizations, we notice that for this model, the uncertainties remain much broader, especially for the parameters describing DE EoS. This can be explained in terms of the peculiar evolution of the
Parameter Planck+DESI Planck + DESI + PantheonPlus Planck+DESI+DESY5
< 0.648
-5.6 -6.4 -16.0
Table 4. JBP parametrization (2.7) – CL constraints and CL upper limits on the free and derived cosmological parameters for 3 different data combinations detailed in Sec. 3. Negative values of indicate an improvement in the fit to the data compared to .
DE EoS obtained in this model. As discussed in detail in Appendix A, among the five models analyzed, the JBP parameterization presents a more articulated phenomenology regarding the evolution of the DE EoS. Due to its quadratic nature in the scale factor, the evolution of the EoS within the JBP parameterization crosses twice. At low redshift, it behaves similarly to the other parameterizations; however, after the first quintessence-to-phantom transition, approaches a minimum value around before rising again, leading to a second phantom-to-quintessence crossing at . This behavior contrasts with other models, where the EoS remains within the phantom regime. As detailed in Appendix A, the interplay between low and high redshift behaviors results in two different pivot redshifts at low and high . This interplay may contribute to tilting the 2-D probability contours in the and plane, as shown in Fig. 3 (see also Fig. 6 for comparisons with other models). Additionally, the increased uncertainties at low redshift might suggest that this phenomenology is not ideal for consistently fitting all the data across low and high redshift. This concern is confirmed when comparing the differences between the best-fit obtained within each DDE model and the best-fit obtained within . Indeed, this model consistently leads to the smallest improvement over CDM across all datasets and DDE models. For more details, we refer to Appendix A.
Figure 3. JBP parametrization (2.7) – one-dimensional posterior distributions and twodimensional marginalized contours for the main key parameters as obtained from the Planck + DESI, Planck + DESI + PantheonPlus, and Planck + DESI + DESY5 dataset combinations.

4.4 Results for the Logarithmic parametrization

Tab. 5 summarizes the constraints on the model where the DE EoS is described by the logarithmic parametrization. Fig. 4 displays the usual marginalized contours on relevant parameters.
Starting with Planck + DESI, is confined to the quintessence regime at more than , while is constrained to be different from zero at more than – confirming once more the preference for DDE in Planck + DESI.
When PantheonPlus is added to Planck + DESI, we find ; i.e., shifted towards although with error bars smaller by a factor of 5 . However, also in this parameterization, is preferred to be in the quintessence regime, excluding at more than . Similarly, the result on confirms the overall preference for DDE, see Fig. 4.
Considering DESY5 in place of PantheonPlus, the constraints on and change to and , respectively. As a result, remains in the quintessence regime at more than , while is found to be non-zero at almost . It is noteworthy that the evidence of DDE is consistently more pronounced in the presence of DESY5 compared to PantheonPlus, see Fig. 4.
Parameter Planck+DESI Planck + DESI + PantheonPlus Planck+DESI+DESY5
-6.5 -9.3 -14.8
Table 5. Logarithmic parametrization (2.8) – CL constraints on the free and derived cosmological parameters for 3 different data combinations detailed in Sec. 3. Negative values of indicate an improvement in the fit to the data compared to .
Figure 4. Logarithmic parametrization (2.8) – one-dimensional posterior distributions and twodimensional marginalized contours for the main key parameters as obtained from the Planck + DESI, Planck + DESI + PantheonPlus, and Planck + DESI + DESY 5 dataset combinations.

4.5 Results for the BA parametrization

The observational constraints for the last model analyzed in this work – the BA parametrization – are given in Tab. 6. As usual, we illustrate the correlations among the key cosmic parameters in Fig. 5.
Parameter Planck+DESI Planck + DESI + PantheonPlus Planck+DESI+DESY5
-8.7 -9.4 -16.2
Table 6. BA parametrization (2.9) – CL constraints on the free and derived cosmological parameters for 3 different data combinations detailed in Sec. 3. Negative values of indicate an improvement in the fit to the data compared to .
Combining Planck with DESI, we get , approaching and approximately away from . Additionally, is significantly different from , confirming the preference for DDE in a similar fashion to other parameterizations discussed throughout the manuscript.
The inclusion of PantheonPlus gives (deep in the quintessence regime) and (non-zero at more than ). Thus, for Planck + DESI + PantheonPlus, evidence of dynamical dark energy is clearly indicated, consistent with all the other parameterizations described so far.
In the case of Planck + DESI + DESY shifts further away from -1 , strengthening the preference for a quintessence EoS. Meanwhile, is found to be non-zero at more than , as visualized in Fig. 5.
Interestingly, when comparing the difference between the best-fit obtained within each DDE model and the best-fit obtained within CDM, this model consistently leads to the most significant improvement over CDM across all three data combinations analyzed. It performs better than the CPL parameterization, as seen by comparing the last line in Tab. 2 and the last line in Tab. 6. As discussed in Appendix A, when comparing the evolution of the EoS inferred in this model with the other cases analyzed so far, we find that at low redshift it behaves similarly to the CPL parameterization. The most notable differences emerge at . In all models, the EoS moves deeply into phantom values (except for the JBP model, where it is compelled to rise back towards quintessence-like values). In contrast, within the BA model, does not trend towards very negative values at . While it remains phantom, it stabilizes on a distinctive, nearly flat plateau.
Figure 5. BA parametrization (2.9) – one-dimensional posterior distributions and twodimensional marginalized contours for the main key parameters as obtained from the Planck + DESI, Planck + DESI + PantheonPlus, and Planck + DESI + DESY 5 dataset combinations.

5 Discussions and Conclusions

The recent DESI BAO measurements, when combined with CMB data from Planck and two samples of Type Ia supernovae (Pantheon-Plus and DESY5), reveal a preference for a present-day quintessence-like equation of state that crossed into the phantom regime in the past. The statistical significance of this preference for dynamic dark energy ranges between and , depending on the specific data combinations analyzed. A core ansatz for this result is the use of the Chevallier-Polarski-Linder (CPL) parameterization to describe the redshift evolution of the equation of state. Despite its several advantages – such as capturing the effective behavior of a wide range of models with up to accuracy – the CPL parameterization forces the evolution of the equation of state to be linear in the scale factor.
In this paper, we tested whether and to what extent the preference for a present-day quintessence equation of state that evolves towards the phantom regime depends on the parameterization adopted to describe its dynamical behavior. To avoid broadening uncertainties in cosmological parameters and facilitate direct comparison with the baseline CPL case, we focused on some well-known alternative models: the exponential, Jassal-Bagla-Padmanabhan, logarithmic, and Barboza-Alcaniz parameterizations for the equation of state. Like the CPL
model, all these parameterizations consist of only two free parameters: the present-day value of the equation of state ( ) and a parameter quantifying its dynamical evolution ( ). However, they allow for deviations from linear behavior at both high and low redshifts. Therefore, given the same pair of values , different late-time expansion histories are obtained within the four models, thereby affecting cosmological observables differently.
To assess whether the preference for a dynamical dark energy component characterized by and remains a robust prediction of the data, we tested these models against the most recent high and low redshift observations: the Planck 2018 CMB measurements, DESI BAO, as well as PantheonPlus and DESY5 SN measurements. For all the dataset combinations explored – i.e., Planck + DESI, Planck + DESI + PantheonPlus, and Planck + DESI + DESY we find that consistently remains in the quintessence regime. Additionally, the constraints on consistently indicate a preference for a dynamical evolution that crossed into the phantom regime ( ). Therefore, our findings confirm the DESI results, regardless of the parameterization adopted to describe the dynamics of the dark energy sector.
Notably, convincing hints of a dynamical evolution of the equation of state are found even with just Planck + DESI. As clearly seen in Fig. 6 – which summarizes the results for the different models – the pair and (corresponding to the standard cosmological constant model of structure formation, CDM) always falls outside the confidence level contour.
However, the real step forward in terms of preference for dynamical dark energy comes when we consider Type Ia supernovae. Including distance moduli measurements gathered from the PantheonPlus catalog, the error bars on and tighten by a factor of 5 compared to Planck + DESI alone. The contours on significantly shrink within the quintessence portion of the parameter space , while the contours on significantly reduce within the region. Replacing PantheonPlus data with DESY5 SN measurements, the preference for dynamical dark energy becomes substantially more significant, to the point where it is not an exaggeration to refer to it as evidence rather than mere preference. This is again clearly illustrated in Fig. 6: for all models, the constraints shift further away from a cosmological constant, which always falls well outside the marginalized probability contours.
At first glance, Fig. 6 also reveals that the contours in the plane show similar trends for all four parameterizations (including the baseline CPL case), especially when SN measurements are included in the analysis. This simultaneously underscores the intrinsic robustness of the preference for dynamical dark energy as reported by the DESI BAO and SN measurements and its resilience against different parameterizations. Given these results, there is solid ground to conclude that the choice of parameterization has a minimal impact.
Last but not least, we examined statistical metrics to quantify the extent to which the different parameterizations analyzed in this study are successful in explaining observations. Specifically, for each model and data combination, we report the difference between the bestfit obtained within each dynamical dark energy model and the best-fit obtained within .
Figure 6. Summary Plot – two-dimensional marginalized contours in the ( ) plane for all models and datasets analyzed in this study.
Once more, all models exhibit similar trends: for Planck + DESI, we consistently observe an improvement in the fit over , with ranging from -5.6 to -8.7 , depending on the specific model. This improvement in the fit is further enhanced when PantheonPlus SN measurements are included ( ranges from -6.4 to -9.4 ) and is substantially increased –
by up to a factor of when adopting DESY5 SN data (in this case, ranges from -14.8 to -16.2 ). This trend follows the overall preference for dynamical dark energy discussed thus far. Interestingly, the linear CPL parameterization is never the best-fitting model. The equation of state proposed by Barboza-Alcaniz, given by Eq. (2.9), consistently leads to the most significant improvement in over CDM across all three data combinations analyzed. Conversely, the Jassal-Bagla-Padmanabhan parameterization, given by Eq. (2.7), shows the smallest improvement in fit compared to among the models considered. The only exception is for Planck + DESI + DESY5, where indicates a better fit to this dataset compared to the CPL, logarithmic, and exponential parameterizations, although it is still smaller compared to the Barboza-Alcaniz model. For further discussion and physical interpretation of the different phenomenological behaviors of the models analyzed so far, we refer to Appendix A. Specifically, Fig. 7 presents constraints on the evolution of the equation of state with respect to redshift, as inferred from various datasets across all models. Tab. 7 provides constraints on other important properties, such as the pivot redshift, the corresponding values (and uncertainties) of the equation of state, and the epoch of the quintessence-to-phantom transition. Overall, these results support the main conclusions regarding the resilience of the DESI and SN preference for evolving dark energy, while suggesting that current data are approaching a precision that could enhance our understanding of its physical nature, should future surveys and data releases confirm these findings.

Acknowledgments

The authors thank the referee for many important comments that improved the manuscript. W.G. acknowledges support from the Lancaster-Sheffield Consortium for Fundamental Physics through the Science and Technology Facilities Council (STFC) grant ST/X000621/1. S.P. acknowledges the financial support from the Department of Science and Technology (DST), Govt. of India under the Scheme “Fund for Improvement of S&T Infrastructure (FIST)” (File No. SR/FST/MS-I/2019/41). E.D.V acknowledges support from the Royal Society through a Royal Society Dorothy Hodgkin Research Fellowship. This article is based upon work from the COST Action CA21136 “Addressing observational tensions in cosmology with systematics and fundamental physics” (CosmoVerse), supported by COST (European Cooperation in Science and Technology).

A Equation of State, pivot redshift, and phantom crossing across the different models

In this article, we have emphasized the resilience of the results recently delivered by the DESI collaboration, showing that DESI BAO data, in combination with Planck CMB observations and two different catalogs of SN distance moduli measurements (i.e., PantheonPlus and DESY5), consistently indicate a preference for DDE across various parameterizations of the EoS. While the primary goal was to confirm that this preference remains stable regardless of the specific DDE model, minor differences have emerged across the five cases analyzed, warranting further investigation. In this appendix, we explore these differences in more detail, aiming to provide a stronger physical interpretation of the results presented in the manuscript. For all five models, we reconstruct the evolution of the EoS with redshift, , based on the constraints on and inferred from the Planck + DESI + PantheonPlus and Planck + DESI + DESY5 datasets. In Fig. 7, we present the mean value of (dashed
Model Dataset
CPL Planck+DESI+PantheonPlus 0.27
Planck+DESI+DESY5 0.25
Exponential Planck+DESI+PantheonPlus 0.21
Planck+DESI+DESY5 0.22
JBP Planck+DESI+PantheonPlus 0.21
4.6
Planck+DESI+DESY5 0.21
4.7
Logarithmic Planck+DESI+PantheonPlus 0.29
Planck+DESI+DESY5 0.26
BA Planck+DESI+PantheonPlus 0.28
Planck+DESI+DESY5 0.28
Table 7. Constraints at on the pivot redshift , the corresponding value of the , and the redshift where the EoS crosses the phantom divide, for Planck + DESI + PantheonPlus and Planck + DESI + DESY 5 .
lines), along with its uncertainties at the (dark regions) and (light regions) CL, across the redshift range for all models and both data combinations. From the reconstructed shape of , we extract crucial information that helps compare the different models and clarify the results presented in the manuscript. Specifically, in Tab. 7, we present the results for:
(i) the pivot redshift and the corresponding value of the EoS, , which indicate the redshift and the EoS value at which is best constrained by the two datasets across the five models;
(ii) the redshift when the EoS crosses the phantom divide (i.e., ), informing us of when the phantom crossing occurs, along with their respective uncertainties.
Starting from the baseline CPL model as the reference case, we summarize the main features and differences across the various models.
Figure 7. Evolution of for across all DDE models, inferred from CMB + DESI + PantheonPlus (left panels) and CMB + DESI + DESY5 (right panels). The dashed lines represent the mean values, while the dark and light shaded regions indicate the and uncertainties, respectively.
  • Exponential: As seen when comparing the top panels with those in the second row from the top in Fig. 7, from a phenomenological perspective, the exponential parameterization closely resembles the CPL model. This similarity was already highlighted in the main text when comparing the improvement in over CDM (which is quite similar for both scenarios). The agreement in predictions is further supported by Tab. 7. The only noticeable difference between the models is a slightly smaller pivot redshift in the exponential parameterization. However, the EoS at this pivot is constrained with comparable precision. Additionally, the predictions regarding the redshift of the phantom crossing agree within one standard deviation for both Planck + DESI + PantheonPlus and Planck + DESI + DESY 5 .
  • JBP: Among the five models analyzed, the JBP parameterization presents a more nuanced phenomenology regarding the evolution of the DE EoS. As shown in the third panels from the top in Fig. 7, due to its quadratic nature in the scale factor, the evolution of the EoS within the JBP parameterization crosses twice. At very low redshift, it behaves similarly to the other parameterizations, remaining within the quintessence region , albeit with larger uncertainties compared to the other models. The first quintessence-to-phantom transition is estimated to occur at for Planck + DESI + PantheonPlus (Planck + DESI + DESY5) at CL. After this transition, approaches a minimum value around before rising towards less negative values. Eventually, a second phantom-to-quintessence crossing occurs at ( ) for Planck+DESI+PantheonPlus (Planck+DESI+DESY5), both at CL. This behavior contrasts with other models, where the EoS remains within the phantom regime, often trending towards more negative values at high redshift. In contrast, within the JBP model, the EoS cannot move towards (more) phantom values but is compelled to transition back towards less negative values at . The double crossing of regimes achieved within this parameterization is also reflected in the pivot scale , at which the EoS is well constrained by data. In Tab. 7, we distinguish between two different regimes: the redshift range (capturing the first quintessence-to-phantom crossing) and the range (covering the second phantom-to-quintessence crossing). In these two regions, we identify two distinct pivot redshifts: the first at and the second at . In both cases (and for both datasets), the EoS is constrained within the same minimal error. This confirms that, within this model, due to the functional form of the EoS, constraints at low redshift (i.e., around ) also dictate the behavior of the parameterization at higher redshifts. The interplay between low and high redshift behaviors, as highlighted by the two pivot redshifts, could contribute to the increased uncertainties at low redshift and the tilting of the probability contours seen in Fig. 6. As discussed in the main manuscript, this model offers relatively modest improvements in the fit compared to , particularly in datasets covering , where the model’s deviations from the others become more pronounced.
  • Logarithmic: When it comes to the logarithmic parameterization, the behavior of for , shown in the fourth panel of Fig. 7, is similar to that of the CPL and exponential models. This is also reflected in the values we inferred for , and , all summarized in Tab. 7 and consistent with those models. However, we observe that at , the EoS is forced down into deep phantom values, and the descent towards these very negative values is steeper than in the CPL and exponential cases. This is due to the fact that at , the scale factor approaches small values (moving towards ), causing to decrease to negative values quite rapidly. This sudden decline in for can lead to changes
    in the fit to data spanning , which is covered by BAO and SN observations, resulting in the differences in the of the fit discussed in the manuscript.
  • BA: Last but not least, the evolution of obtained for the BA model is presented in the bottom panel of Fig. 7. As we argued in the manuscript, this model provides the most significant improvement in the fit over CDM across all datasets analyzed in this study. Therefore, it is interesting to examine what is different in the evolution of the EoS compared to the other models. Looking at the low-redshift part of the EoS, we see that the model behaves very similarly to CPL (and its relatives). However, for the pivot redshift, we obtain , slightly larger than in any other model, while takes values consistent with the other cases. We estimate the quintessence-to-phantom transition to occur at for Planck + DESI + PantheonPlus (Planck + DESI + DESY 5 ) at CL. The most noticeable difference in the EoS occurs at . In all other models studied so far, the EoS either moved deeply into phantom values (characterized by more or less steep functional forms of ) or was compelled to increase back towards quintessence-like values in the JBP model. Referring to the bottom panel of Fig. 7, we observe that for , the evolution of in the BA model remains phantom but does not trend towards very negative values. Instead, stabilizes on a sort of second plateau that is distinctive of the BA model.

References

[1] Supernova Search Team collaboration, Observational evidence from supernovae for an accelerating universe and a cosmological constant, Astron. J. 116 (1998) 1009 [astro-ph/9805201].
[2] Supernova Cosmology Project collaboration, Measurements of and from 42 High Redshift Supernovae, Astrophys. J. 517 (1999) 565 [astro-ph/9812133].
[3] Supernova Search Team collaboration, The farthest known supernova: support for an accelerating universe and a glimpse of the epoch of deceleration, Astrophys. J. 560 (2001) 49 [astro-ph/0104455].
[4] SDSS collaboration, Cosmological parameters from SDSS and WMAP, Phys. Rev. D 69 (2004) 103501 [astro-ph/0310723].
[5] SDSS collaboration, Physical evidence for dark energy, astro-ph/0307335.
[6] Supernova Search Team collaboration, Cosmological results from high-z supernovae, Astrophys. J. 594 (2003) 1 [astro-ph/0305008].
[7] Supernova Cosmology Project collaboration, New constraints on Omega(M), Omega(lambda), and from an independent set of eleven high-redshift supernovae observed with HST, Astrophys. J. 598 (2003) 102 [astro-ph/0309368].
[8] SDSS collaboration, Cosmological parameter analysis including SDSS Ly-alpha forest and galaxy bias: Constraints on the primordial spectrum of fluctuations, neutrino mass, and dark energy, Phys. Rev. D 71 (2005) 103515 [astro-ph/0407372].
[9] B. Feng, X.-L. Wang and X.-M. Zhang, Dark energy constraints from the cosmic age and supernova, Phys. Lett. B 607 (2005) 35 [astro-ph/0404224].
[10] Supernova Search Team collaboration, Type Ia supernova discoveries at from the Hubble Space Telescope: Evidence for past deceleration and constraints on dark energy evolution, Astrophys. J. 607 (2004) 665 [astro-ph/0402512].
[11] SNLS collaboration, The Supernova Legacy Survey: Measurement of and from the first year data set, Astron. Astrophys. 447 (2006) 31 [astro-ph/0510447].
[12] SDSS collaboration, Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies, Astrophys. J. 633 (2005) 560 [astro-ph/0501171].
[13] D.J. Eisenstein, H.-j. Seo, E. Sirko and D. Spergel, Improving Cosmological Distance Measurements by Reconstruction of the Baryon Acoustic Peak, Astrophys. J. 664 (2007) 675 [astro-ph/0604362].
[14] SDSS collaboration, Cosmological Constraints from the SDSS Luminous Red Galaxies, Phys. Rev. D 74 (2006) 123507 [astro-ph/0608632].
[15] V. Sahni and A. Starobinsky, Reconstructing Dark Energy, Int. J. Mod. Phys. D 15 (2006) 2105 [astro-ph/0610026].
[16] ESSENCE collaboration, Observational Constraints on the Nature of the Dark Energy: First Cosmological Results from the ESSENCE Supernova Survey, Astrophys. J. 666 (2007) 694 [astro-ph/0701041].
[17] A. Vikhlinin et al., Chandra Cluster Cosmology Project III: Cosmological Parameter Constraints, Astrophys. J. 692 (2009) 1060 [0812.2720].
[18] D. Stern, R. Jimenez, L. Verde, M. Kamionkowski and S.A. Stanford, Cosmic Chronometers: Constraining the Equation of State of Dark Energy. I: H(z) Measurements, JCAP 02 (2010) 008 [0907.3149].
[19] B.D. Sherwin et al., Evidence for dark energy from the cosmic microwave background alone using the Atacama Cosmology Telescope lensing measurements, Phys. Rev. Lett. 107 (2011) 021302 [1105.0419].
[20] WMAP collaboration, Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results, Astrophys. J. Suppl. 208 (2013) 20 [1212.5225].
[21] WMAP collaboration, Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results, Astrophys. J. Suppl. 208 (2013) 19 [1212.5226].
[22] BOSS collaboration, The Baryon Oscillation Spectroscopic Survey of SDSS-III, Astron. J. 145 (2013) 10 [1208.0022].
[23] Astro-WISE, KiDS collaboration, The Kilo-Degree Survey, Exper. Astron. 35 (2013) 25 [1206. 1254].
[24] BOSS collaboration, The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples, Mon. Not. Roy. Astron. Soc. 441 (2014) 24 [1312.4877].
[25] D.H. Weinberg, M.J. Mortonson, D.J. Eisenstein, C. Hirata, A.G. Riess and E. Rozo, Observational Probes of Cosmic Acceleration, Phys. Rept. 530 (2013) 87 [1201.2434].
[26] BOSS collaboration, The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Testing gravity with redshift-space distortions using the power spectrum multipoles, Mon. Not. Roy. Astron. Soc. 443 (2014) 1065 [1312.4611].
[27] BOSS collaboration, Baryon acoustic oscillations in the Lyo forest of BOSS DR11 quasars, Astron. Astrophys. 574 (2015) A59 [1404. 1801].
[28] SDSS collaboration, Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples, Astron. Astrophys. 568 (2014) A22 [1401.4064].
[29] BOSS collaboration, Cosmological implications of baryon acoustic oscillation measurements, Phys. Rev. D 92 (2015) 123516 [1411.1074].
[30] A.J. Ross, L. Samushia, C. Howlett, W.J. Percival, A. Burden and M. Manera, The clustering of the SDSS DR7 main Galaxy sample – I. A 4 per cent distance measure at , Mon. Not. Roy. Astron. Soc. 449 (2015) 835 [1409.3242].
[31] M. Moresco, L. Pozzetti, A. Cimatti, R. Jimenez, C. Maraston, L. Verde et al., A measurement of the Hubble parameter at : direct evidence of the epoch of cosmic re-acceleration, JCAP 05 (2016) 014 [1601.01701].
[32] M. Moresco, R. Jimenez, L. Verde, A. Cimatti, L. Pozzetti, C. Maraston et al., Constraining the time evolution of dark energy, curvature and neutrino properties with cosmic chronometers, JCAP 12 (2016) 039 [1604.00183].
[33] D. Rubin and B. Hayden, Is the expansion of the universe accelerating? All signs point to yes, Astrophys. J. Lett. 833 (2016) L30 [1610.08972].
[34] BOSS collaboration, The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: cosmological analysis of the DR12 galaxy sample, Mon. Not. Roy. Astron. Soc. 470 (2017) 2617 [1607.03155].
[35] DES collaboration, The Dark Energy Survey: more than dark energy – an overview, Mon. Not. Roy. Astron. Soc. 460 (2016) 1270 [1601.00329].
[36] B.S. Haridasu, V.V. Luković, R. D’Agostino and N. Vittorio, Strong evidence for an accelerating universe, Astron. Astrophys. 600 (2017) L1 [1702.08244].
[37] DES collaboration, Dark Energy Survey Year 1 results: Cosmological constraints from cosmic shear, Phys. Rev. D 98 (2018) 043528 [1708.01538].
[38] Pan-STARRS1 collaboration, The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample, Astrophys. J. 859 (2018) 101 [1710.00845].
[39] Planck collaboration, Planck 2018 results. I. Overview and the cosmological legacy of Planck, Astron. Astrophys. 641 (2020) A1 [1807.06205].
[40] Planck collaboration, Planck 2018 results. VI. Cosmological parameters, Astron. Astrophys. 641 (2020) A6 [1807.06209].
[41] A. Gómez-Valent, Quantifying the evidence for the current speed-up of the Universe with low and intermediate-redshift data. A more model-independent approach, JCAP 05 (2019) 026 [1810.02278].
[42] Y. Yang and Y. Gong, The evidence of cosmic acceleration and observational constraints, JCAP 06 (2020) 059 [1912.07375].
[43] ACT collaboration, The Atacama Cosmology Telescope: a measurement of the Cosmic Microwave Background power spectra at 98 and 150 GHz, JCAP 12 (2020) 045 [2007.07289].
[44] ACT collaboration, The Atacama Cosmology Telescope: DR4 Maps and Cosmological Parameters, JCAP 12 (2020) 047 [2007.07288].
[45] EBOSS collaboration, Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory, Phys. Rev. D 103 (2021) 083533 [2007.08991].
[46] S. Nadathur, W.J. Percival, F. Beutler and H. Winther, Testing Low-Redshift Cosmic Acceleration with Large-Scale Structure, Phys. Rev. Lett. 124 (2020) 221301 [2001.11044].
[47] B.M. Rose, D. Rubin, A. Cikota, S.E. Deustua, S. Dixon, A. Fruchter et al., Evidence for Cosmic Acceleration is Robust to Observed Correlations Between Type Ia Supernova Luminosity and Stellar Age, Astrophys. J. Lett. 896 (2020) L4 [2002. 12382].
[48] E. Di Valentino, S. Gariazzo, O. Mena and S. Vagnozzi, Soundness of Dark Energy properties, JCAP 07 (2020) 045 [2005. 02062].
[49] KIDS collaboration, KiDS-1000 Cosmology: Cosmic shear constraints and comparison between two point statistics, Astron. Astrophys. 645 (2021) A104 [2007.15633].
[50] KiDS collaboration, KiDS-1000 Cosmology: Constraints beyond flat , Astron. Astrophys. 649 (2021) A88 [2010.16416].
[51] SPT-3G collaboration, Measurements of the -mode polarization and temperature- -mode correlation of the CMB from SPT-3G 2018 data, Phys. Rev. D 104 (2021) 022003 [2101.01684].
[52] DES collaboration, Dark Energy Survey Year 3 results: Cosmological constraints from galaxy clustering and weak lensing, Phys. Rev. D 105 (2022) 023520 [2105.13549].
[53] M. Moresco et al., Unveiling the Universe with emerging cosmological probes, Living Rev. Rel. 25 (2022) 6 [2201.07241].
[54] DES collaboration, Dark Energy Survey Year 3 results: Constraints on extensions to CDM with weak lensing and galaxy clustering, Phys. Rev. D 107 (2023) 083504 [2207.05766].
[55] D. Brout et al., The Pantheon + Analysis: Cosmological Constraints, Astrophys. J. 938 (2022) 110 [2202.04077].
[56] ACT collaboration, The Atacama Cosmology Telescope: DR6 Gravitational Lensing Map and Cosmological Parameters, Astrophys. J. 962 (2024) 113 [2304.05203].
[57] Kilo-Degree Survey, Dark Energy Survey collaboration, DES Y3 + KiDS-1000: Consistent cosmology combining cosmic shear surveys, Open J. Astrophys. 6 (2023) 2305.17173 [2305.17173].
[58] DESI collaboration, DESI 2024 III: Baryon Acoustic Oscillations from Galaxies and Quasars, 2404.03000.
[59] DESI collaboration, DESI 2024: Constraints on Physics-Focused Aspects of Dark Energy using DESI DR1 BAO Data, 2405.13588.
[60] DES collaboration, The Dark Energy Survey: Cosmology Results With New High-redshift Type Ia Supernovae Using The Full 5-year Dataset, 2401.02929.
[61] DES collaboration, The Dark Energy Survey Supernova Program: Light curves and 5-Year data release, 2406.05046.
[62] DES collaboration, The Dark Energy Survey Supernova Program: Cosmological Analysis and Systematic Uncertainties, 2401.02945.
[63] T. Buchert, On average properties of inhomogeneous fluids in general relativity. 1. Dust cosmologies, Gen. Rel. Grav. 32 (2000) 105 [gr-qc/9906015].
[64] T. Buchert, On average properties of inhomogeneous fluids in general relativity: Perfect fluid cosmologies, Gen. Rel. Grav. 33 (2001) 1381 [gr-qc/0102049].
[65] T. Buchert, Dark Energy from Structure: A Status Report, Gen. Rel. Grav. 40 (2008) 467 [0707.2153].
[66] P. Hunt and S. Sarkar, Constraints on large scale inhomogeneities from WMAP-5 and SDSS: confrontation with recent observations, Mon. Not. Roy. Astron. Soc. 401 (2010) 547 [0807.4508].
[67] J.T. Nielsen, A. Guffanti and S. Sarkar, Marginal evidence for cosmic acceleration from Type Ia supernovae, Sci. Rep. 6 (2016) 35596 [1506.01354].
[68] I. Tutusaus, B. Lamine, A. Dupays and A. Blanchard, Is cosmic acceleration proven by local cosmological probes?, Astron. Astrophys. 602 (2017) A73 [1706.05036].
[69] L.H. Dam, A. Heinesen and D.L. Wiltshire, Apparent cosmic acceleration from type Ia supernovae, Mon. Not. Roy. Astron. Soc. 472 (2017) 835 [1706.07236].
[70] J. Colin, R. Mohayaee, M. Rameez and S. Sarkar, Evidence for anisotropy of cosmic acceleration, Astron. Astrophys. 631 (2019) L13 [1808.04597].
[71] C. Desgrange, A. Heinesen and T. Buchert, Dynamical spatial curvature as a fit to type Ia supernovae, Int. J. Mod. Phys. D 28 (2019) 1950143 [1902.07915].
[72] S.M. Koksbang, Towards statistically homogeneous and isotropic perfect fluid universes with cosmic backreaction, Class. Quant. Grav. 36 (2019) 185004 [1907.08681].
[73] S.M. Koksbang, Another look at redshift drift and the backreaction conjecture, JCAP 10 (2019) 036 [1909. 13489].
[74] A. Heinesen, Reconciling a decelerating Universe with cosmological observations, Phys. Rev. D 107 (2023) L101301 [2212.05568].
[75] V. Sahni and A.A. Starobinsky, The Case for a positive cosmological Lambda term, Int. J. Mod. Phys. D 9 (2000) 373 [astro-ph/9904398].
[76] S.M. Carroll, The Cosmological constant, Living Rev. Rel. 4 (2001) 1 [astro-ph/0004075].
[77] P.J.E. Peebles and B. Ratra, The Cosmological Constant and Dark Energy, Rev. Mod. Phys. 75 (2003) 559 [astro-ph/0207347].
[78] T. Padmanabhan, Cosmological constant: The Weight of the vacuum, Phys. Rept. 380 (2003) 235 [hep-th/0212290].
[79] E.J. Copeland, M. Sami and S. Tsujikawa, Dynamics of dark energy, Int. J. Mod. Phys. D 15 (2006) 1753 [hep-th/0603057].
[80] R.R. Caldwell and M. Kamionkowski, The Physics of Cosmic Acceleration, Ann. Rev. Nucl. Part. Sci. 59 (2009) 397 [0903.0866].
[81] M. Li, X.-D. Li, S. Wang and Y. Wang, Dark Energy, Commun. Theor. Phys. 56 (2011) 525 [1103.5870].
[82] J. Martin, Everything You Always Wanted To Know About The Cosmological Constant Problem (But Were Afraid To Ask), Comptes Rendus Physique 13 (2012) 566 [1205.3365].
[83] S. Weinberg, The Cosmological Constant Problem, Rev. Mod. Phys. 61 (1989) 1.
[84] L.M. Krauss and M.S. Turner, The Cosmological constant is back, Gen. Rel. Grav. 27 (1995) 1137 [astro-ph/9504003].
[85] S. Weinberg, The Cosmological constant problems, 2, 2000.
[86] V. Sahni, The Cosmological constant problem and quintessence, Class. Quant. Grav. 19 (2002) 3435 [astro-ph/0202076].
[87] J. Yokoyama, Issues on the cosmological constant, 5, 2003.
[88] S. Nobbenhuis, Categorizing different approaches to the cosmological constant problem, Found. Phys. 36 (2006) 613 [gr-qc/0411093].
[89] C.P. Burgess, The Cosmological Constant Problem: Why it’s hard to get Dark Energy from Micro-physics, 2015. 10.1093/acprof:oso/9780198728856.003.0004.
[90] A. Joyce, B. Jain, J. Khoury and M. Trodden, Beyond the Cosmological Standard Model, Phys. Rept. 568 (2015) 1 [1407.0059].
[91] P. Bull et al., Beyond CDM: Problems, solutions, and the road ahead, Phys. Dark Univ. 12 (2016) 56 [1512.05356].
[92] B. Wang, E. Abdalla, F. Atrio-Barandela and D. Pavon, Dark Matter and Dark Energy Interactions: Theoretical Challenges, Cosmological Implications and Observational Signatures, Rept. Prog. Phys. 79 (2016) 096901 [1603.08299].
[93] R. Brustein and P.J. Steinhardt, Challenges for superstring cosmology, Phys. Lett. B 302 (1993) 196 [hep-th/9212049].
[94] E. Witten, The Cosmological constant from the viewpoint of string theory, 3, 2000.
[95] S. Kachru, R. Kallosh, A.D. Linde and S.P. Trivedi, De Sitter vacua in string theory, Phys. Rev. D 68 (2003) 046005 [hep-th/0301240].
[96] J. Polchinski, The Cosmological Constant and the String Landscape, 3, 2006.
[97] U.H. Danielsson and T. Van Riet, What if string theory has no de Sitter vacua?, Int. J. Mod. Phys. D 27 (2018) 1830007 [1804.01120].
[98] I. Zlatev, L.-M. Wang and P.J. Steinhardt, Quintessence, cosmic coincidence, and the cosmological constant, Phys. Rev. Lett. 82 (1999) 896 [astro-ph/9807002].
[99] D. Pavon and W. Zimdahl, Holographic dark energy and cosmic coincidence, Phys. Lett. B 628 (2005) 206 [gr-qc/0505020].
[100] H.E.S. Velten, R.F. vom Marttens and W. Zimdahl, Aspects of the cosmological “coincidence problem”, Eur. Phys. J. C 74 (2014) 3160 [1410.2509].
[101] A.D. Dolgov, The Problem of vacuum energy and cosmology, 6, 1997.
[102] N. Straumann, The Mystery of the cosmic vacuum energy density and the accelerated expansion of the universe, Eur. J. Phys. 20 (1999) 419 [astro-ph/9908342].
[103] J. Sola, Cosmological constant and vacuum energy: old and new ideas, J. Phys. Conf. Ser. 453 (2013) 012015 [1306.1527].
[104] L. Amendola, Coupled quintessence, Phys. Rev. D 62 (2000) 043511 [astro-ph/9908023].
[105] A.Y. Kamenshchik, U. Moschella and V. Pasquier, An Alternative to quintessence, Phys. Lett. (2001) 265 [gr-qc/0103004].
[106] S. Capozziello, Curvature quintessence, Int. J. Mod. Phys. D 11 (2002) 483 [gr-qc/0201033].
[107] M.C. Bento, O. Bertolami and A.A. Sen, Generalized Chaplygin gas, accelerated expansion and dark energy matter unification, Phys. Rev. D 66 (2002) 043507 [gr-qc/0202064].
[108] G. Mangano, G. Miele and V. Pettorino, Coupled quintessence and the coincidence problem, Mod. Phys. Lett. A 18 (2003) 831 [astro-ph/0212518].
[109] G.R. Farrar and P.J.E. Peebles, Interacting dark matter and dark energy, Astrophys. J. 604 (2004) 1 [astro-ph/0307316].
[110] J. Khoury and A. Weltman, Chameleon fields: Awaiting surprises for tests of gravity in space, Phys. Rev. Lett. 93 (2004) 171104 [astro-ph/0309300].
[111] M. Li, A Model of holographic dark energy, Phys. Lett. B 603 (2004) 1 [hep-th/0403127].
[112] L. Amendola, R. Gannouji, D. Polarski and S. Tsujikawa, Conditions for the cosmological viability of dark energy models, Phys. Rev. D 75 (2007) 083504 [gr-qc/0612180].
[113] W. Hu and I. Sawicki, Models of Cosmic Acceleration that Evade Solar-System Tests, Phys. Rev. D 76 (2007) 064004 [0705.1158].
[114] G. Cognola, E. Elizalde, S. Nojiri, S.D. Odintsov, L. Sebastiani and S. Zerbini, A Class of viable modified gravities describing inflation and the onset of accelerated expansion, Phys. Rev. D 77 (2008) 046009 [0712.4017].
[115] S. Nojiri, S.D. Odintsov, M. Sasaki and Y.-l. Zhang, Screening of cosmological constant in non-local gravity, Phys. Lett. B 696 (2011) 278 [1010.5375].
[116] Y.-l. Zhang and M. Sasaki, Screening of cosmological constant in non-local cosmology, Int. J. Mod. Phys. D 21 (2012) 1250006 [1108.2112].
[117] M. Rinaldi, Higgs Dark Energy, Class. Quant. Grav. 32 (2015) 045002 [1404.0532].
[118] O. Luongo and H. Quevedo, A Unified Dark Energy Model from a Vanishing Speed of Sound with Emergent Cosmological Constant, Int. J. Mod. Phys. D 23 (2014) 1450012.
[119] M. Rinaldi, Dark energy as a fixed point of the Einstein Yang-Mills Higgs Equations, JCAP 10 (2015) 023 [1508.04576].
[120] A. De Felice, L. Heisenberg, R. Kase, S. Mukohyama, S. Tsujikawa and Y.-l. Zhang, Cosmology in generalized Proca theories, JCAP 06 (2016) 048 [1603.05806].
[121] T. Josset, A. Perez and D. Sudarsky, Dark Energy from Violation of Energy Conservation, Phys. Rev. Lett. 118 (2017) 021102 [1604.04183].
[122] C. Burrage and J. Sakstein, A Compendium of Chameleon Constraints, JCAP 11 (2016) 045 [1609.01192].
[123] L. Sebastiani, S. Vagnozzi and R. Myrzakulov, Mimetic gravity: a review of recent developments and applications to cosmology and astrophysics, Adv. High Energy Phys. 2017 (2017) 3156915 [1612.08661].
[124] S. Nojiri, S.D. Odintsov and V.K. Oikonomou, Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution, Phys. Rept. 692 (2017) 1 [1705.11098].
[125] C. Burrage and J. Sakstein, Tests of Chameleon Gravity, Living Rev. Rel. 21 (2018) 1 [1709.09071].
[126] S. Capozziello, R. D’Agostino and O. Luongo, Cosmic acceleration from a single fluid description, Phys. Dark Univ. 20 (2018) 1 [1712.04317].
[127] D. Benisty and E.I. Guendelman, Unified dark energy and dark matter from dynamical spacetime, Phys. Rev. D 98 (2018) 023506 [1802.07981].
[128] A. Casalino, M. Rinaldi, L. Sebastiani and S. Vagnozzi, Mimicking dark matter and dark energy in a mimetic model compatible with GW170817, Phys. Dark Univ. 22 (2018) 108 [1803.02620].
[129] W. Yang, S. Pan, E. Di Valentino, R.C. Nunes, S. Vagnozzi and D.F. Mota, Tale of stable interacting dark energy, observational signatures, and the tension, JCAP 09 (2018) 019 [1805.08252].
[130] E.N. Saridakis, K. Bamba, R. Myrzakulov and F.K. Anagnostopoulos, Holographic dark energy through Tsallis entropy, JCAP 12 (2018) 012 [1806.01301].
[131] L. Visinelli and S. Vagnozzi, Cosmological window onto the string axiverse and the supersymmetry breaking scale, Phys. Rev. D 99 (2019) 063517 [1809.06382].
[132] D. Langlois, Dark energy and modified gravity in degenerate higher-order scalar-tensor (DHOST) theories: A review, Int. J. Mod. Phys. D 28 (2019) 1942006 [1811.06271].
[133] D. Benisty, E. Guendelman and Z. Haba, Unification of dark energy and dark matter from diffusive cosmology, Phys. Rev. D 99 (2019) 123521 [1812.06151].
[134] K. Boshkayev, R. D’Agostino and O. Luongo, Extended logotropic fluids as unified dark energy models, Eur. Phys. J. C 79 (2019) 332 [1901.01031].
[135] J.J. Heckman, C. Lawrie, L. Lin, J. Sakstein and G. Zoccarato, Pixelated Dark Energy, Fortsch. Phys. 67 (2019) 1900071 [1901.10489].
[136] R. D’Agostino, Holographic dark energy from nonadditive entropy: cosmological perturbations and observational constraints, Phys. Rev. D 99 (2019) 103524 [1903.03836].
[137] U. Mukhopadhyay, D. Majumdar and D. Adak, Evolution of Dark Energy Perturbations for Slotheon Field and Power Spectrum, Eur. Phys. J. C 80 (2020) 593 [1903.08650].
[138] U. Mukhopadhyay and D. Majumdar, Swampland criteria in the slotheon field dark energy, Phys. Rev. D 100 (2019) 024006 [1904.01455].
[139] U. Mukhopadhyay, A. Paul and D. Majumdar, Addressing the high- problem in pseudo-Nambu-Goldstone boson dark energy models with dark matter-dark energy interaction, Eur. Phys. J. C 80 (2020) 904 [1909.03925].
[140] S. Vagnozzi, L. Visinelli, O. Mena and D.F. Mota, Do we have any hope of detecting scattering between dark energy and baryons through cosmology?, Mon. Not. Roy. Astron. Soc. 493 (2020) 1139 [1911.12374].
[141] O. Akarsu, J.D. Barrow, L.A. Escamilla and J.A. Vazquez, Graduated dark energy: Observational hints of a spontaneous sign switch in the cosmological constant, Phys. Rev. 101 (2020) 063528 [1912.08751].
[142] E.N. Saridakis, Barrow holographic dark energy, Phys. Rev. D 102 (2020) 123525 [2005.04115].
[143] Ruchika, S.A. Adil, K. Dutta, A. Mukherjee and A.A. Sen, Observational constraints on axion(s) dark energy with a cosmological constant, Phys. Dark Univ. 40 (2023) 101199 [2005.08813].
[144] S.D. Odintsov, V.K. Oikonomou and T. Paul, From a Bounce to the Dark Energy Era with Gravity, Class. Quant. Grav. 37 (2020) 235005 [2009.09947].
[145] S.D. Odintsov, V.K. Oikonomou, F.P. Fronimos and K.V. Fasoulakos, Unification of a Bounce with a Viable Dark Energy Era in Gauss-Bonnet Gravity, Phys. Rev. D 102 (2020) 104042 [2010. 13580].
[146] V.K. Oikonomou, Unifying inflation with early and late dark energy epochs in axion gravity, Phys. Rev. D 103 (2021) 044036 [2012.00586].
[147] V.K. Oikonomou, Rescaled Einstein-Hilbert Gravity from Gravity: Inflation, Dark Energy and the Swampland Criteria, Phys. Rev. D 103 (2021) 124028 [2012.01312].
[148] S. Vagnozzi, L. Visinelli, P. Brax, A.-C. Davis and J. Sakstein, Direct detection of dark energy: The XENON1T excess and future prospects, Phys. Rev. D 104 (2021) 063023 [2103.15834].
[149] R. Solanki, S.K.J. Pacif, A. Parida and P.K. Sahoo, Cosmic acceleration with bulk viscosity in modified gravity, Phys. Dark Univ. 32 (2021) 100820 [2105.00876].
[150] E.N. Saridakis, Do we need soft cosmology?, Phys. Lett. B 822 (2021) 136649 [2105.08646].
[151] S. Arora, S.K.J. Pacif, A. Parida and P.K. Sahoo, Bulk viscous matter and the cosmic acceleration of the universe in gravity, JHEAp 33 (2022) 1 [2106.00491].
[152] S. Capozziello, R. D’Agostino and O. Luongo, Thermodynamic parametrization of dark energy, Phys. Dark Univ. 36 (2022) 101045 [2202.03300].
[153] S.A. Narawade, L. Pati, B. Mishra and S.K. Tripathy, Dynamical system analysis for accelerating models in non-metricity gravity, Phys. Dark Univ. 36 (2022) 101020 [2203. 14121].
[154] R. D’Agostino, O. Luongo and M. Muccino, Healing the cosmological constant problem during inflation through a unified quasi-quintessence matter field, Class. Quant. Grav. 39 (2022) 195014 [2204.02190].
[155] V.K. Oikonomou and I. Giannakoudi, A panorama of viable gravity dark energy models, Int. J. Mod. Phys. D 31 (2022) 2250075 [2205.08599].
[156] A. Belfiglio, R. Giambò and O. Luongo, Alleviating the cosmological constant problem from particle production, Class. Quant. Grav. 40 (2023) 105004 [2206.14158].
[157] G.G. Luciano and J. Giné, Generalized interacting Barrow Holographic Dark Energy: Cosmological predictions and thermodynamic considerations, Phys. Dark Univ. 41 (2023) 101256 [2210.09755].
[158] S.A. Kadam, J. Levi Said and B. Mishra, Accelerating cosmological models in gravitational theory, Int. J. Geom. Meth. Mod. Phys. 20 (2023) 2350083 [2210.17075].
[159] Y.C. Ong, An Effective Sign Switching Dark Energy: Lotka-Volterra Model of Two Interacting Fluids, Universe 9 (2023) 437 [2212.04429].
[160] A. Bernui, E. Di Valentino, W. Giarè, S. Kumar and R.C. Nunes, Exploring the Ho tension and the evidence for dark sector interactions from 2D BAO measurements, Phys. Rev. D 107 (2023) 103531 [2301.06097].
[161] G.G. Luciano, Saez-Ballester gravity in Kantowski-Sachs Universe: A new reconstruction paradigm for Barrow Holographic Dark Energy, Phys. Dark Univ. 41 (2023) 101237 [2301.12488].
[162] L. Giani and O.F. Piattella, Induced non-local cosmology, Phys. Dark Univ. 40 (2023) 101219 [2302.06762].
[163] A. Belfiglio, Y. Carloni and O. Luongo, Particle production from non-minimal coupling in a symmetry breaking potential transporting vacuum energy, Phys. Dark Univ. 44 (2024) 101458 [2307.04739].
[164] E. Frion, D. Camarena, L. Giani, T. Miranda, D. Bertacca, V. Marra et al., Bayesian analysis of a Unified Dark Matter model with transition: can it alleviate the tension?, 2307.06320.
[165] S.A. Adil, U. Mukhopadhyay, A.A. Sen and S. Vagnozzi, Dark energy in light of the early JWST observations: case for a negative cosmological constant?, JCAP 10 (2023) 072 [2307.12763].
[166] S. Halder, S. Pan, P.M. Sá and T. Saha, Coupled phantom cosmological model motivated by the warm inflationary paradigm, 2407.15804.
[167] H. Fischer, C. Käding and M. Pitschmann, Screened Scalar Fields in the Laboratory and the Solar System, Universe 10 (2024) 297 [2405.14638].
[168] A.R. Cooray and D. Huterer, Gravitational lensing as a probe of quintessence, Astrophys. J. Lett. 513 (1999) L95 [astro-ph/9901097].
[169] G. Efstathiou, Constraining the equation of state of the universe from distant type Ia supernovae and cosmic microwave background anisotropies, Mon. Not. Roy. Astron. Soc. 310 (1999) 842 [astro-ph/9904356].
[170] M. Chevallier and D. Polarski, Accelerating universes with scaling dark matter, Int. J. Mod. Phys. D 10 (2001) 213 [gr-qc/0009008].
[171] A. Melchiorri, L. Mersini-Houghton, C.J. Odman and M. Trodden, The State of the dark energy equation of state, Phys. Rev. D 68 (2003) 043509 [astro-ph/0211522].
[172] E.V. Linder, Exploring the expansion history of the universe, Phys. Rev. Lett. 90 (2003) 091301 [astro-ph/0208512].
[173] C. Wetterich, Phenomenological parameterization of quintessence, Phys. Lett. B 594 (2004) 17 [astro-ph/0403289].
[174] B. Feng, M. Li, Y.-S. Piao and X. Zhang, Oscillating quintom and the recurrent universe, Phys. Lett. B 634 (2006) 101 [astro-ph/0407432].
[175] J.-Q. Xia, B. Feng and X.-M. Zhang, Constraints on oscillating quintom from supernova, microwave background and galaxy clustering, Mod. Phys. Lett. A 20 (2005) 2409 [astro-ph/0411501].
[176] S. Hannestad and E. Mortsell, Cosmological constraints on the dark energy equation of state and its evolution, JCAP 09 (2004) 001 [astro-ph/0407259].
[177] Y.-g. Gong and Y.-Z. Zhang, Probing the curvature and dark energy, Phys. Rev. D 72 (2005) 043518 [astro-ph/0502262].
[178] H.K. Jassal, J.S. Bagla and T. Padmanabhan, Observational constraints on low redshift evolution of dark energy: How consistent are different observations?, Phys. Rev. D 72 (2005) 103503 [astro-ph/0506748].
[179] S. Nesseris and L. Perivolaropoulos, Comparison of the legacy and gold snia dataset constraints on dark energy models, Phys. Rev. D 72 (2005) 123519 [astro-ph/0511040].
[180] D.-J. Liu, X.-Z. Li, J. Hao and X.-H. Jin, Revisiting the parametrization of Equation of State of Dark Energy via SNIa Data, Mon. Not. Roy. Astron. Soc. 388 (2008) 275 [0804.3829].
[181] E.M. Barboza, Jr. and J.S. Alcaniz, A parametric model for dark energy, Phys. Lett. B 666 (2008) 415 [0805.1713].
[182] J.-Z. Ma and X. Zhang, Probing the dynamics of dark energy with novel parametrizations, Phys. Lett. B 699 (2011) 233 [1102.2671].
[183] I. Sendra and R. Lazkoz, SN and BAO constraints on (new) polynomial dark energy parametrizations: current results and forecasts, Mon. Not. Roy. Astron. Soc. 422 (2012) 776 [1105.4943].
[184] A. De Felice, S. Nesseris and S. Tsujikawa, Observational constraints on dark energy with a fast varying equation of state, JCAP 05 (2012) 029 [1203.6760].
[185] H. Li and X. Zhang, Constraining dynamical dark energy with a divergence-free parametrization in the presence of spatial curvature and massive neutrinos, Phys. Lett. B 713 (2012) 160 [1202.4071].
[186] C.-J. Feng, X.-Y. Shen, P. Li and X.-Z. Li, A New Class of Parametrization for Dark Energy without Divergence, JCAP 09 (2012) 023 [1206.0063].
[187] J. Magaña, V.H. Cárdenas and V. Motta, Cosmic slowing down of acceleration for several dark energy parametrizations, JCAP 10 (2014) 017 [1407.1632].
[188] G. Pantazis, S. Nesseris and L. Perivolaropoulos, Comparison of thawing and freezing dark energy parametrizations, Phys. Rev. D 93 (2016) 103503 [1603.02164].
[189] E. Di Valentino, A. Melchiorri and J. Silk, Reconciling Planck with the local value of in extended parameter space, Phys. Lett. B 761 (2016) 242 [1606.00634].
[190] W. Yang, S. Pan and A. Paliathanasis, Latest astronomical constraints on some non-linear parametric dark energy models, Mon. Not. Roy. Astron. Soc. 475 (2018) 2605 [1708.01717].
[191] S. Pan, E.N. Saridakis and W. Yang, Observational Constraints on Oscillating Dark-Energy Parametrizations, Phys. Rev. D 98 (2018) 063510 [1712.05746].
[192] E. Mörtsell and S. Dhawan, Does the Hubble constant tension call for new physics?, JCAP 09 (2018) 025 [1801.07260].
[193] K. Dutta, Ruchika, A. Roy, A.A. Sen and M.M. Sheikh-Jabbari, Beyond with low and high redshift data: implications for dark energy, Gen. Rel. Grav. 52 (2020) 15 [1808.06623].
[194] W. Yang, S. Pan, E. Di Valentino and E.N. Saridakis, Observational constraints on dynamical dark energy with pivoting redshift, Universe 5 (2019) 219 [1811.06932].
[195] W. Yang, S. Pan, E. Di Valentino, E.N. Saridakis and S. Chakraborty, Observational constraints on one-parameter dynamical dark-energy parametrizations and the tension, Phys. Rev. D 99 (2019) 043543 [1810.05141].
[196] X. Li and A. Shafieloo, A Simple Phenomenological Emergent Dark Energy Model can Resolve the Hubble Tension, Astrophys. J. Lett. 883 (2019) L3 [1906.08275].
[197] S. Vagnozzi, New physics in light of the tension: An alternative view, Phys. Rev. (2020) 023518 [1907.07569].
[198] L. Visinelli, S. Vagnozzi and U. Danielsson, Revisiting a negative cosmological constant from low-redshift data, Symmetry 11 (2019) 1035 [1907. 07953].
[199] E. Di Valentino, A. Melchiorri, O. Mena and S. Vagnozzi, Interacting dark energy in the early 2020s: A promising solution to the and cosmic shear tensions, Phys. Dark Univ. 30 (2020) 100666 [1908.04281].
[200] K. Dutta, A. Roy, Ruchika, A.A. Sen and M.M. Sheikh-Jabbari, Cosmology with low-redshift observations: No signal for new physics, Phys. Rev. D 100 (2019) 103501 [1908.07267].
[201] E. Di Valentino, A. Melchiorri, O. Mena and S. Vagnozzi, Nonminimal dark sector physics and cosmological tensions, Phys. Rev. D 101 (2020) 063502 [1910.09853].
[202] S. Pan, W. Yang, E. Di Valentino, A. Shafieloo and S. Chakraborty, Reconciling tension in a six parameter space?, JCAP 06 (2020) 062 [1907.12551].
[203] E.M. Teixeira, A. Nunes and N.J. Nunes, Disformally Coupled Quintessence, Phys. Rev. D 101 (2020) 083506 [1912.13348].
[204] E.M. Teixeira, A. Nunes and N.J. Nunes, Conformally Coupled Tachyonic Dark Energy, Phys. Rev. D 100 (2019) 043539 [1903.06028].
[205] M. Martinelli, N.B. Hogg, S. Peirone, M. Bruni and D. Wands, Constraints on the interacting vacuum-geodesic CDM scenario, Mon. Not. Roy. Astron. Soc. 488 (2019) 3423 [1902.10694].
[206] M. Zumalacarregui, Gravity in the Era of Equality: Towards solutions to the Hubble problem without fine-tuned initial conditions, Phys. Rev. D 102 (2020) 023523 [2003.06396].
[207] N.B. Hogg, M. Bruni, R. Crittenden, M. Martinelli and S. Peirone, Latest evidence for a late time vacuum-geodesic CDM interaction, Phys. Dark Univ. 29 (2020) 100583 [2002.10449].
[208] G. Alestas, L. Kazantzidis and L. Perivolaropoulos, tension, phantom dark energy, and cosmological parameter degeneracies, Phys. Rev. D 101 (2020) 123516 [2004.08363].
[209] E. Di Valentino, A. Mukherjee and A.A. Sen, Dark Energy with Phantom Crossing and the Tension, Entropy 23 (2021) 404 [2005. 12587].
[210] G. Alestas, L. Kazantzidis and L. Perivolaropoulos, phantom transition at as a resolution of the Hubble tension, Phys. Rev. D 103 (2021) 083517 [2012.13932].
[211] M. Rezaei, T. Naderi, M. Malekjani and A. Mehrabi, A Bayesian comparison between and phenomenologically emergent dark energy models, Eur. Phys. J. C 80 (2020) 374 [2004.08168].
[212] D. Perkovic and H. Stefancic, Barotropic fluid compatible parametrizations of dark energy, Eur. Phys. J. C 80 (2020) 629 [2004.05342].
[213] H.B. Benaoum, W. Yang, S. Pan and E. Di Valentino, Modified emergent dark energy and its astronomical constraints, Int. J. Mod. Phys. D 31 (2022) 2250015 [2008.09098].
[214] S. Kumar, Remedy of some cosmological tensions via effective phantom-like behavior of interacting vacuum energy, Phys. Dark Univ. 33 (2021) 100862 [2102.12902].
[215] S. Vagnozzi, F. Pacucci and A. Loeb, Implications for the Hubble tension from the ages of the oldest astrophysical objects, JHEAp 36 (2022) 27 [2105.10421].
[216] L.A. Escamilla and J.A. Vazquez, Model selection applied to reconstructions of the Dark Energy, Eur. Phys. J. C 83 (2023) 251 [2111.10457].
[217] S. Bag, V. Sahni, A. Shafieloo and Y. Shtanov, Phantom Braneworld and the Hubble Tension, Astrophys. J. 923 (2021) 212 [2107.03271].
[218] A. Theodoropoulos and L. Perivolaropoulos, The Hubble Tension, the M Crisis of Late Time H(z) Deformation Models and the Reconstruction of Quintessence Lagrangians, Universe 7 (2021) 300 [2109.06256].
[219] G. Alestas, D. Camarena, E. Di Valentino, L. Kazantzidis, V. Marra, S. Nesseris et al., Late-transition versus smooth -deformation models for the resolution of the Hubble crisis, Phys. Rev. D 105 (2022) 063538 [2110.04336].
[220] A.A. Sen, S.A. Adil and S. Sen, Do cosmological observations allow a negative ?, Mon. Not. Roy. Astron. Soc. 518 (2022) 1098 [2112.10641].
[221] W. Yang, E. Di Valentino, S. Pan, A. Shafieloo and X. Li, Generalized emergent dark energy model and the Hubble constant tension, Phys. Rev. D 104 (2021) 063521 [2103.03815].
[222] N.B. Hogg and M. Bruni, Shan-Chen interacting vacuum cosmology, Mon. Not. Roy. Astron. Soc. 511 (2022) 4430 [2109.08676].
[223] N. Roy, S. Goswami and S. Das, Quintessence or phantom: Study of scalar field dark energy models through a general parametrization of the Hubble parameter, Phys. Dark Univ. 36 (2022) 101037 [2201.09306].
[224] L. Heisenberg, H. Villarrubia-Rojo and J. Zosso, Simultaneously solving the H0 and tensions with late dark energy, Phys. Dark Univ. 39 (2023) 101163 [2201.11623].
[225] A. Chudaykin, D. Gorbunov and N. Nedelko, Exploring CDM extensions with SPT-3G and Planck data: evidence for neutrino masses and implications of extended dark energy models for cosmological tensions, 2203.03666.
[226] O. Akarsu, S. Kumar, E. Özülker, J.A. Vazquez and A. Yadav, Relaxing cosmological tensions with a sign switching cosmological constant: Improved results with Planck, BAO, and Pantheon data, Phys. Rev. D 108 (2023) 023513 [2211.05742].
[227] F.B.M.d. Santos, Updating constraints on phantom crossing f gravity, JCAP 06 (2023) 039 [2211.16370].
[228] T. Schiavone, G. Montani and F. Bombacigno, gravity in the Jordan frame as a paradigm for the Hubble tension, Mon. Not. Roy. Astron. Soc. 522 (2023) L72 [2211.16737].
[229] C. van de Bruck, G. Poulot and E.M. Teixeira, Scalar field dark matter and dark energy: a hybrid model for the dark sector, JCAP 07 (2023) 019 [2211.13653].
[230] E. Ozulker, Is the dark energy equation of state parameter singular?, Phys. Rev. D 106 (2022) 063509 [2203.04167].
[231] E.M. Teixeira, B.J. Barros, V.M.C. Ferreira and N. Frusciante, Dissecting kinetically coupled quintessence: phenomenology and observational tests, JCAP 11 (2022) 059 [2207.13682].
[232] I. Ben-Dayan and U. Kumar, Emergent Unparticles Dark Energy can restore cosmological concordance, JCAP 12 (2023) 047 [2302.00067].
[233] M. Ballardini, A.G. Ferrari and F. Finelli, Phantom scalar-tensor models and cosmological tensions, JCAP 04 (2023) 029 [2302.05291].
[234] W. Yang, W. Giarè, S. Pan, E. Di Valentino, A. Melchiorri and J. Silk, Revealing the effects of curvature on the cosmological models, Phys. Rev. D 107 (2023) 063509 [2210.09865].
[235] J. de Cruz Perez and J. Sola Peracaula, Running vacuum in Brans Dicke theory: A possible cure for the and H0 tensions, Phys. Dark Univ. 43 (2024) 101406 [2302.04807].
[236] T. Patil, Ruchika and S. Panda, Coupled quintessence scalar field model in light of observational datasets, JCAP 05 (2024) 033 [2307.03740].
[237] Y. Zhai, W. Giarè, C. van de Bruck, E. Di Valentino, O. Mena and R.C. Nunes, A consistent view of interacting dark energy from multiple CMB probes, JCAP 07 (2023) 032 [2303.08201].
[238] S.A. Adil, O. Akarsu, E. Di Valentino, R.C. Nunes, E. Özülker, A.A. Sen et al., Omnipotent dark energy: A phenomenological answer to the Hubble tension, Phys. Rev. D 109 (2024) 023527 [2306.08046].
[239] G. Montani, M. De Angelis, F. Bombacigno and N. Carlevaro, Metric gravity with dynamical dark energy as a scenario for the Hubble tension, Mon. Not. Roy. Astron. Soc. 527 (2023) L156 [2306.11101].
[240] O. Akarsu, E. Di Valentino, S. Kumar, R.C. Nunes, J.A. Vazquez and A. Yadav, model: A promising scenario for alleviation of cosmological tensions, 2307. 10899.
[241] S. Vagnozzi, Seven Hints That Early-Time New Physics Alone Is Not Sufficient to Solve the Hubble Tension, Universe 9 (2023) 393 [2308.16628].
[242] O. Avsajanishvili, G.Y. Chitov, T. Kahniashvili, S. Mandal and L. Samushia, Observational Constraints on Dynamical Dark Energy Models, Universe 10 (2024) 122 [2310.16911].
[243] L. Giani, C. Howlett, K. Said, T. Davis and S. Vagnozzi, An effective description of Laniakea: impact on cosmology and the local determination of the Hubble constant, JCAP (2024) 071 [2311.00215].
[244] R. Lazkoz, V. Salzano, L. Fernandez-Jambrina and M. Bouhmadi-López, Ripped : An observational contender to the consensus cosmological model, Phys. Dark Univ. 45 (2024) 101511 [2311.10526].
[245] L.A. Escamilla, W. Giarè, E. Di Valentino, R.C. Nunes and S. Vagnozzi, The state of the dark energy equation of state circa 2023, JCAP 05 (2024) 091 [2307.14802].
[246] L.A. Escamilla, O. Akarsu, E. Di Valentino and J.A. Vazquez, Model-independent reconstruction of the interacting dark energy kernel: Binned and Gaussian process, JCAP 11 (2023) 051 [2305.16290].
[247] M. Rezaei, S. Pan, W. Yang and D.F. Mota, Evidence of dynamical dark energy in a non-flat universe: current and future observations, JCAP 01 (2024) 052 [2305.18544].
[248] E.M. Teixeira, R. Daniel, N. Frusciante and C. van de Bruck, Forecasts on interacting dark energy with standard sirens, Phys. Rev. D 108 (2023) 084070 [2309.06544].
[249] M. Forconi, W. Giarè, O. Mena, Ruchika, E. Di Valentino, A. Melchiorri et al., A double take on early and interacting dark energy from JWST, JCAP 05 (2024) 097 [2312.11074].
[250] M. Sebastianutti, N.B. Hogg and M. Bruni, The interacting vacuum and tensions: A comparison of theoretical models, Phys. Dark Univ. 46 (2024) 101546 [2312.14123].
[251] W.J. Wolf and P.G. Ferreira, Underdetermination of dark energy, Phys. Rev. D 108 (2023) 103519 [2310.07482].
[252] W. Giarè, E. Di Valentino, E.V. Linder and E. Specogna, Testing -attractor quintessential inflation against CMB and low-redshift data, 2402.01560.
[253] W. Giarè, M.A. Sabogal, R.C. Nunes and E. Di Valentino, Interacting Dark Energy after DESI Baryon Acoustic Oscillation measurements, 2404.15232.
[254] W. Giarè, Y. Zhai, S. Pan, E. Di Valentino, R.C. Nunes and C. van de Bruck, Tightening the reins on non-minimal dark sector physics: Interacting Dark Energy with dynamical and non-dynamical equation of state, 2404.02110.
[255] N. Menci, S.A. Adil, U. Mukhopadhyay, A.A. Sen and S. Vagnozzi, Negative cosmological constant in the dark energy sector: tests from JWST photometric and spectroscopic observations of high-redshift galaxies, 2401.12659.
[256] O. Akarsu, E.O. Colgáin, A.A. Sen and M.M. Sheikh-Jabbari, Tensions: Localising Missing Physics through Consistency Checks, 2402.04767.
[257] E.M. Teixeira, Illuminating the Dark Sector: Searching for new interactions between dark matter and dark energy, 1, 2024.
[258] D. Benisty, S. Pan, D. Staicova, E. Di Valentino and R.C. Nunes, Late-Time constraints on Interacting Dark Energy: Analysis independent of and .
[259] M. Najafi, S. Pan, E. Di Valentino and J.T. Firouzjaee, Dynamical dark energy confronted with multiple CMB missions, Phys. Dark Univ. 45 (2024) 101539.
[260] H. Moshafi, A. Talebian, E. Yusofi and E. Di Valentino, Observational constraints on the dark energy with a quadratic equation of state, Phys. Dark Univ. 45 (2024) 101524 [2403.02000].
[261] E. Silva, U. Zúñiga Bolaño, R.C. Nunes and E. Di Valentino, Non-Linear Matter Power Spectrum Modeling in Interacting Dark Energy Cosmologies, 2403. 19590.
[262] M. Reyhani, M. Najafi, J.T. Firouzjaee and E. Di Valentino, Structure formation in various dynamical dark energy scenarios, Phys. Dark Univ. 44 (2024) 101477 [2403. 15202].
[263] L.A. Escamilla, S. Pan, E. Di Valentino, A. Paliathanasis, J.A. Vázquez and W. Yang, Oscillations in the Dark?, 2404.00181.
[264] H. Wang, G. Ye and Y.-S. Piao, Impact of evolving dark energy on the search for primordial gravitational waves, 2407.11263.
[265] G. Montani, N. Carlevaro and M. De Angelis, Modified gravity in the presence of matter creation in the late Universe: alleviation of the Hubble tension, 2407.12409.
[266] T.-N. Li, P.-J. Wu, G.-H. Du, S.-J. Jin, H.-L. Li, J.-F. Zhang et al., Constraints on interacting dark energy models from the DESI BAO and DES supernovae data, 2407.14934.
[267] Y. Yang, X. Ren, Q. Wang, Z. Lu, D. Zhang, Y.-F. Cai et al., Quintom cosmology and modified gravity after DESI 2024, 2404.19437.
[268] S. Dwivedi and M. Högås, 2D BAO vs 3D BAO: solving the Hubble tension with alternative cosmological models, 2407.04322.
[269] ACT collaboration, The Atacama Cosmology Telescope: A Measurement of the DR6 CMB Lensing Power Spectrum and Its Implications for Structure Growth, Astrophys. J. 962 (2024) 112 [2304. 05202].
[270] SPT-3G collaboration, SPT-3G: A Next-Generation Cosmic Microwave Background Polarization Experiment on the South Pole Telescope, Proc. SPIE Int. Soc. Opt. Eng. 9153 (2014) 91531P [1407. 2973].
[271] SPT-3G collaboration, Measurement of the CMB temperature power spectrum and constraints on cosmology from the SPT-3G 2018 TT, TE, and EE dataset, Phys. Rev. D 108 (2023) 023510 [2212.05642].
[272] A. Lewis and A. Challinor, Weak gravitational lensing of the CMB, Phys. Rept. 429 (2006) 1 [astro-ph/0601594].
[273] W. Giarè, E. Di Valentino, A. Melchiorri and O. Mena, New cosmological bounds on hot relics: axions and neutrinos, Mon. Not. Roy. Astron. Soc. 505 (2021) 2703 [2011.14704].
[274] E. Di Valentino and A. Melchiorri, Neutrino Mass Bounds in the Era of Tension Cosmology, Astrophys. J. Lett. 931 (2022) L18 [2112.02993].
[275] F. D’Eramo, E. Di Valentino, W. Giarè, F. Hajkarim, A. Melchiorri, O. Mena et al., Cosmological bound on the QCD axion mass, redux, JCAP 09 (2022) 022 [2205.07849].
[276] E. Di Valentino, S. Gariazzo, W. Giarè, A. Melchiorri, O. Mena and F. Renzi, Novel model-marginalized cosmological bound on the QCD axion mass, Phys. Rev. D 107 (2023) 103528 [2212.11926].
[277] W. Giarè, O. Mena and E. Di Valentino, Lensing impact on cosmic relics and tensions, Phys. Rev. D 108 (2023) 103539 [2307.14204].
[278] Planck collaboration, Planck 2018 results. VIII. Gravitational lensing, Astron. Astrophys. 641 (2020) A8 [1807.06210].
[279] G. Ye, J.-Q. Jiang and Y.-S. Piao, Shape of CMB lensing in the early dark energy cosmology, Phys. Rev. D 108 (2023) 063512 [2305.18873].
[280] ACT, DES collaboration, Cosmology from cross-correlation of ACT-DR4 CMB lensing and DES-Y3 cosmic shear, Mon. Not. Roy. Astron. Soc. 528 (2024) 2112 [2309.04412].
[281] ACT, DES collaboration, Cosmological constraints from the tomography of DES-Y3 galaxies with CMB lensing from ACT DR4, JCAP 01 (2024) 033 [2306.17268].
[282] ACT, DESI collaboration, The Atacama Cosmology Telescope DR6 and DESI: Structure formation over cosmic time with a measurement of the cross-correlation of CMB Lensing and Luminous Red Galaxies, 2407.04606.
[283] N. Sailer et al., Cosmological constraints from the cross-correlation of DESI Luminous Red Galaxies with CMB lensing from Planck PR4 and ACT DR6, 2407.04607.
[284] ACT collaboration, The Atacama Cosmology Telescope: DR6 Gravitational Lensing and SDSS BOSS cross-correlation measurement and constraints on gravity with the statistic, 2405.12795.
[285] EUCLID collaboration, Euclid Definition Study Report, 1110.3193.
[286] LSST collaboration, LSST: from Science Drivers to Reference Design and Anticipated Data Products, Astrophys. J. 873 (2019) 111 [0805.2366].
[287] D. Spergel et al., Wide-Field InfraRed Survey Telescope-Astrophysics Focused Telescope Assets WFIRST-AFTA Final Report, 1305.5422.
[288] SKA collaboration, Cosmology with Phase 1 of the Square Kilometre Array: Red Book 2018: Technical specifications and performance forecasts, Publ. Astron. Soc. Austral. 37 (2020) e007 [1811.02743].
[289] E. Di Valentino, O. Mena, S. Pan, L. Visinelli, W. Yang, A. Melchiorri et al., In the realm of the Hubble tension-a review of solutions, Class. Quant. Grav. 38 (2021) 153001 [2103.01183].
[290] L. Perivolaropoulos and F. Skara, Challenges for CDM: An update, New Astron. Rev. 95 (2022) 101659 [2105.05208].
[291] E. Abdalla et al., Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies, JHEAp 34 (2022) 49 [2203.06142].
[292] S. Gariazzo, W. Giarè, O. Mena and E. Di Valentino, How robust are the parameter constraints extending the CDM model?, 2404.11182.
[293] R. Bean and A. Melchiorri, Current constraints on the dark energy equation of state, Phys. Rev. D 65 (2002) 041302 [astro-ph/0110472].
[294] S. Hannestad and E. Mortsell, Probing the dark side: Constraints on the dark energy equation of state from CMB, large scale structure and Type Ia supernovae, Phys. Rev. D 66 (2002) 063508 [astro-ph/0205096].
[295] N. Said, C. Baccigalupi, M. Martinelli, A. Melchiorri and A. Silvestri, New Constraints On The Dark Energy Equation of State, Phys. Rev. D 88 (2013) 043515 [1303.4353].
[296] D.L. Shafer and D. Huterer, Chasing the phantom: A closer look at Type Ia supernovae and the dark energy equation of state, Phys. Rev. D 89 (2014) 063510 [1312.1688].
[297] X. Zhang, Impacts of dark energy on weighing neutrinos after Planck 2015, Phys. Rev. D 93 (2016) 083011 [1511.02651].
[298] Y.-Y. Xu and X. Zhang, Comparison of dark energy models after Planck 2015, Eur. Phys. J. (2016) 588 [1607.06262].
[299] S. Wang, Y.-F. Wang, D.-M. Xia and X. Zhang, Impacts of dark energy on weighing neutrinos: mass hierarchies considered, Phys. Rev. D 94 (2016) 083519 [1608.00672].
[300] S. Vagnozzi, E. Giusarma, O. Mena, K. Freese, M. Gerbino, S. Ho et al., Unveiling secrets with cosmological data: neutrino masses and mass hierarchy, Phys. Rev. D 96 (2017) 123503 [1701.08172].
[301] X. Zhang, Weighing neutrinos in dynamical dark energy models, Sci. China Phys. Mech. Astron. 60 (2017) 060431 [1703.00651].
[302] L. Feng, J.-F. Zhang and X. Zhang, Searching for sterile neutrinos in dynamical dark energy cosmologies, Sci. China Phys. Mech. Astron. 61 (2018) 050411 [1706.06913].
[303] D. Wang, Dark Energy Constraints in light of Pantheon SNe Ia, BAO, Cosmic Chronometers and CMB Polarization and Lensing Data, Phys. Rev. D 97 (2018) 123507 [1801.02371].
[304] T. Sprenger, M. Archidiacono, T. Brinckmann, S. Clesse and J. Lesgourgues, Cosmology in the era of Euclid and the Square Kilometre Array, JCAP 02 (2019) 047 [1801.08331].
[305] V. Poulin, K.K. Boddy, S. Bird and M. Kamionkowski, Implications of an extended dark energy cosmology with massive neutrinos for cosmological tensions, Phys. Rev. D 97 (2018) 123504 [1803.02474].
[306] S. Roy Choudhury and A. Naskar, Strong Bounds on Sum of Neutrino Masses in a 12 Parameter Extended Scenario with Non-Phantom Dynamical Dark Energy with CPL parameterization, Eur. Phys. J. C 79 (2019) 262 [1807.02860].
[307] DES collaboration, Dark Energy Survey Year 1 Results: Constraints on Extended Cosmological Models from Galaxy Clustering and Weak Lensing, Phys. Rev. D 99 (2019) 123505 [1810.02499].
[308] D. Wang, Exploring new physics beyond the standard cosmology with Dark Energy Survey Year 1 Data, Phys. Dark Univ. 32 (2021) 100810 [1904.00657].
[309] S. Roy Choudhury and S. Hannestad, Updated results on neutrino mass and mass hierarchy from cosmology with Planck 2018 likelihoods, JCAP 07 (2020) 037 [1907.12598].
[310] A. Chudaykin, K. Dolgikh and M.M. Ivanov, Constraints on the curvature of the Universe and dynamical dark energy from the Full-shape and BAO data, Phys. Rev. D 103 (2021) 023507 [2009. 10106].
[311] G. D’Amico, L. Senatore and P. Zhang, Limits on wCDM from the EFTofLSS with the PyBird code, JCAP 01 (2021) 006 [2003.07956].
[312] S. Vagnozzi, A. Loeb and M. Moresco, Eppur è piatto? The Cosmic Chronometers Take on Spatial Curvature and Cosmic Concordance, Astrophys. J. 908 (2021) 84 [2011.11645].
[313] W. Yang, E. Di Valentino, S. Pan, Y. Wu and J. Lu, Dynamical dark energy after Planck CMB final release and tension, Mon. Not. Roy. Astron. Soc. 501 (2021) 5845 [2101.02168].
[314] E. Di Valentino, A combined analysis of the late time direct measurements and the impact on the Dark Energy sector, Mon. Not. Roy. Astron. Soc. 502 (2021) 2065 [2011.00246].
[315] S. Brieden, H. Gil-Marín and L. Verde, Model-agnostic interpretation of 10 billion years of cosmic evolution traced by BOSS and eBOSS data, JCAP 08 (2022) 024 [2204.11868].
[316] C. Grillo, P. Rosati, S.H. Suyu, G.B. Caminha, A. Mercurio and A. Halkola, On the accuracy of time-delay cosmography in the Frontier Fields Cluster MACS J1149.5+2223 with supernova Refsdal, Astrophys. J. 898 (2020) 87 [2001. 02232].
[317] S. Cao, J. Ryan and B. Ratra, Cosmological constraints from Hii starburst galaxy, quasar angular size, and other measurements, Mon. Not. Roy. Astron. Soc. 509 (2022) 4745 [2109.01987].
[318] M. Zhang, B. Wang, P.-J. Wu, J.-Z. Qi, Y. Xu, J.-F. Zhang et al., Prospects for Constraining Interacting Dark Energy Models with 21 cm Intensity Mapping Experiments, Astrophys. J. 918 (2021) 56 [2102.03979].
[319] E.O. Colgáin, M.M. Sheikh-Jabbari and L. Yin, Can dark energy be dynamical?, Phys. Rev. D 104 (2021) 023510 [2104.01930].
[320] Y.-P. Teng, W. Lee and K.-W. Ng, Constraining the dark-energy equation of state with cosmological data, Phys. Rev. D 104 (2021) 083519 [2105.02667].
[321] C. Krishnan, R. Mohayaee, E.O. Colgáin, M.M. Sheikh-Jabbari and L. Yin, Does Hubble tension signal a breakdown in FLRW cosmology?, Class. Quant. Grav. 38 (2021) 184001 [2105.09790].
[322] R.C. Nunes and S. Vagnozzi, Arbitrating the S8 discrepancy with growth rate measurements from redshift-space distortions, Mon. Not. Roy. Astron. Soc. 505 (2021) 5427 [2106.01208].
[323] R.C. Bernardo, D. Grandón, J. Said Levi and V.H. Cárdenas, Parametric and nonparametric methods hint dark energy evolution, Phys. Dark Univ. 36 (2022) 101017 [2111.08289].
[324] G. Bargiacchi, M. Benetti, S. Capozziello, E. Lusso, G. Risaliti and M. Signorini, Quasar cosmology: dark energy evolution and spatial curvature, Mon. Not. Roy. Astron. Soc. 515 (2022) 1795 [2111.02420].
[325] A. Semenaite, A.G. Sánchez, A. Pezzotta, J. Hou, A. Eggemeier, M. Crocce et al., Beyond constraints from the full shape clustering measurements from BOSS and eBOSS, Mon. Not. Roy. Astron. Soc. 521 (2023) 5013 [2210.07304].
[326] P. Carrilho, C. Moretti and A. Pourtsidou, Cosmology with the EFTofLSS and BOSS: dark energy constraints and a note on priors, JCAP 01 (2023) 028 [2207.14784].
[327] D. Wang, Pantheon + constraints on dark energy and modified gravity: An evidence of dynamical dark energy, Phys. Rev. D 106 (2022) 063515 [2207.07164].
[328] M. Koussour, S.K.J. Pacif, M. Bennai and P.K. Sahoo, A New Parametrization of Hubble Parameter in Gravity, Fortsch. Phys. 71 (2023) 2200172 [2208.04723].
[329] R.C. Bernardo, D. Grandón, J. Levi Said and V.H. Cárdenas, Dark energy by natural evolution: Constraining dark energy using Approximate Bayesian Computation, Phys. Dark Univ. 40 (2023) 101213 [2211.05482].
[330] S.A. Narawade and B. Mishra, Phantom Cosmological Model with Observational Constraints in Gravity, Annalen Phys. 535 (2023) 2200626 [2211.09701].
[331] W.-T. Hou, J.-Z. Qi, T. Han, J.-F. Zhang, S. Cao and X. Zhang, Prospects for constraining interacting dark energy models from gravitational wave and gamma ray burst joint observation, JCAP 05 (2023) 017 [2211.10087].
[332] S. Kumar, R.C. Nunes, S. Pan and P. Yadav, New late-time constraints on gravity, Phys. Dark Univ. 42 (2023) 101281 [2301.07897].
[333] R. Bhagat, S.A. Narawade and B. Mishra, Weyl type gravity observational constrained cosmological models, Phys. Dark Univ. 41 (2023) 101250 [2305. 01659].
[334] A. Mussatayeva, N. Myrzakulov and M. Koussour, Cosmological constraints on dark energy in f(Q) gravity: A parametrized perspective, Phys. Dark Univ. 42 (2023) 101276 [2307.00281].
[335] N.B. Hogg, Constraints on dark energy from TDCOSMO & SLACS lenses, Mon. Not. Roy. Astron. Soc. 528 (2024) L95 [2310.11977].
[336] DESI collaboration, DESI 2024 VI: Cosmological Constraints from the Measurements of Baryon Acoustic Oscillations, 2404.03002.
[337] L. Verde, T. Treu and A.G. Riess, Tensions between the Early and the Late Universe, Nature Astron. 3 (2019) 891 [1907. 10625].
[338] J.-P. Hu and F.-Y. Wang, Hubble Tension: The Evidence of New Physics, Universe 9 (2023) 94 [2302.05709].
[339] W. Giarè, Inflation, the Hubble tension, and early dark energy: An alternative overview, Phys. Rev. D 109 (2024) 123545 [2404.12779].
[340] W. Giarè, CMB Anomalies and the Hubble Tension, 2305. 16919.
[341] R. Mainini, A.V. Maccio, S.A. Bonometto and A. Klypin, Modeling dynamical dark energy, Astrophys. J. 599 (2003) 24 [astro-ph/0303303].
[342] U. Alam, V. Sahni and A.A. Starobinsky, The Case for dynamical dark energy revisited, JCAP 06 (2004) 008 [astro-ph/0403687].
[343] J. Sola and H. Stefancic, Dynamical dark energy or variable cosmological parameters?, Mod. Phys. Lett. A 21 (2006) 479 [astro-ph/0507110].
[344] I. Antoniadis, P.O. Mazur and E. Mottola, Cosmological dark energy: Prospects for a dynamical theory, New J. Phys. 9 (2007) 11 [gr-qc/0612068].
[345] G.-B. Zhao, R.G. Crittenden, L. Pogosian and X. Zhang, Examining the evidence for dynamical dark energy, Phys. Rev. Lett. 109 (2012) 171301 [1207.3804].
[346] J. Solà Peracaula, J. de Cruz Pérez and A. Gómez-Valent, Dynamical dark energy vs. const in light of observations, EPL 121 (2018) 39001 [1606.00450].
[347] J. Sola, A. Gomez-Valent and J. de Cruz Pérez, Dynamical dark energy: scalar fields and running vacuum, Mod. Phys. Lett. A 32 (2017) 1750054 [1610.08965].
[348] G.-B. Zhao et al., Dynamical dark energy in light of the latest observations, Nature Astron. 1 (2017) 627 [1701.08165].
[349] W. Yang, N. Banerjee and S. Pan, Constraining a dark matter and dark energy interaction scenario with a dynamical equation of state, Phys. Rev. D 95 (2017) 123527 [1705.09278].
[350] J. Sola Peracaula, A. Gomez-Valent and J. de Cruz Pérez, Signs of Dynamical Dark Energy in Current Observations, Phys. Dark Univ. 25 (2019) 100311 [1811.03505].
[351] S. Pan, W. Yang, E. Di Valentino, E.N. Saridakis and S. Chakraborty, Interacting scenarios with dynamical dark energy: Observational constraints and alleviation of the tension, Phys. Rev. D 100 (2019) 103520 [1907.07540].
[352] C. Escamilla-Rivera and A. Nájera, Dynamical dark energy models in the light of gravitational-wave transient catalogues, JCAP 03 (2022) 060 [2103.02097].
[353] Z.-W. Zhao, Z.-X. Li, J.-Z. Qi, H. Gao, J.-F. Zhang and X. Zhang, Cosmological parameter estimation for dynamical dark energy models with future fast radio burst observations, Astrophys. J. 903 (2020) 83 [2006.01450].
[354] E. Di Valentino, A. Melchiorri, E.V. Linder and J. Silk, Constraining Dark Energy Dynamics in Extended Parameter Space, Phys. Rev. D 96 (2017) 023523 [1704.00762].
[355] E. Di Valentino, A. Melchiorri and J. Silk, Cosmological constraints in extended parameter space from the Planck 2018 Legacy release, JCAP 01 (2020) 013 [1908.01391].
[356] E. Di Valentino, W. Giarè, A. Melchiorri and J. Silk, Health checkup test of the standard cosmological model in view of recent cosmic microwave background anisotropies experiments, Phys. Rev. D 106 (2022) 103506 [2209.12872].
[357] D. Rubin et al., Union Through UNITY: Cosmology with 2,000 SNe Using a Unified Bayesian Framework, 2311.12098.
[358] D. Scolnic et al., The Pantheon + Analysis: The Full Data Set and Light-curve Release, Astrophys. J. 938 (2022) 113 [2112.03863].
[359] M. Cortês and A.R. Liddle, Interpreting DESI’s evidence for evolving dark energy, 2404.08056.
[360] V. Patel and L. Amendola, Comments on the prior dependence of the DESI results, 2407.06586.
[361] L. Orchard and V.H. Cárdenas, Probing Dark Energy Evolution Post-DESI 2024, 2407.05579.
[362] G. Liu, Y. Wang and W. Zhao, Impact of LRG1 and LRG2 in DESI 2024 BAO data on dark energy evolution, 2407.04385.
[363] A. Chudaykin and M. Kunz, Modified gravity interpretation of the evolving dark energy in light of DESI data, 2407. 02558.
[364] A. Notari, M. Redi and A. Tesi, Consistent Theories for the DESI dark energy fit, 2406.08459.
[365] I.D. Gialamas, G. Hütsi, K. Kannike, A. Racioppi, M. Raidal, M. Vasar et al., Interpreting DESI 2024 BAO: late-time dynamical dark energy or a local effect?, 2406.07533.
[366] H. Wang, Z.-Y. Peng and Y.-S. Piao, Can recent DESI BAO measurements accommodate a negative cosmological constant?, 2406.03395.
[367] H. Wang and Y.-S. Piao, Dark energy in light of recent DESI BAO and Hubble tension, 2404.18579.
[368] Y. Carloni, O. Luongo and M. Muccino, Does dark energy really revive using DESI 2024 data?, 2404. 12068.
[369] E.O. Colgáin, M.G. Dainotti, S. Capozziello, S. Pourojaghi, M.M. Sheikh-Jabbari and D. Stojkovic, Does DESI 2024 Confirm CDM?, 2404.08633.
[370] Y. Tada and T. Terada, Quintessential interpretation of the evolving dark energy in light of DESI observations, Phys. Rev. D 109 (2024) L121305 [2404.05722].
[371] W. Yin, Cosmic clues: DESI, dark energy, and the cosmological constant problem, JHEP 05 (2024) 327 [2404.06444].
[372] O. Luongo and M. Muccino, Model independent cosmographic constraints from DESI 2024, 2404.07070.
[373] C.-G. Park, J. de Cruz Perez and B. Ratra, Using non-DESI data to confirm and strengthen the DESI 2024 spatially-flat CDM cosmological parameterization result, 2405.00502.
[374] D. Shlivko and P.J. Steinhardt, Assessing observational constraints on dark energy, Phys. Lett. B 855 (2024) 138826 [2405.03933].
[375] G. Ye, M. Martinelli, B. Hu and A. Silvestri, Non-minimally coupled gravity as a physically viable fit to DESI 2024 BAO, 2407.15832.
[376] Z. Wang, S. Lin, Z. Ding and B. Hu, The role of LRG1 and LRG2’s monopole in inferring the DESI 2024 BAO cosmology, 2405.02168.
[377] D. Naredo-Tuero, M. Escudero, E. Fernández-Martínez, X. Marcano and V. Poulin, Living at the Edge: A Critical Look at the Cosmological Neutrino Mass Bound, 2407.13831.
[378] R. de Putter and E.V. Linder, Calibrating Dark Energy, JCAP 10 (2008) 042 [0808.0189].
[379] A. Hernández-Almada, M.L. Mendoza-Martínez, M.A. García-Aspeitia and V. Motta, Phenomenological emergent dark energy in the light of DESI Data Release 1, 2407. 09430.
[380] S. Pourojaghi, M. Malekjani and Z. Davari, Cosmological constraints on dark energy parametrizations after DESI 2024: Persistent deviation from standard CDM cosmology, 2407.09767.
[381] O.F. Ramadan, J. Sakstein and D. Rubin, DESI Constraints on Exponential Quintessence, 2405.18747.
[382] K.V. Berghaus, J.A. Kable and V. Miranda, Quantifying Scalar Field Dynamics with DESI 2024 Y1 BAO measurements, 2404.14341.
[383] F.J. Qu, K.M. Surrao, B. Bolliet, J.C. Hill, B.D. Sherwin and H.T. Jense, Accelerated inference on accelerated cosmic expansion: New constraints on axion-like early dark energy with DESI BAO and ACT DR6 CMB lensing, 2404.16805.
[384] P. Adolf, M. Hirsch, S. Krieg, H. Päs and M. Tabet, Fitting the DESI BAO Data with Dark Energy Driven by the Cohen-Kaplan-Nelson Bound, 2406.09964.
[385] C.-P. Ma and E. Bertschinger, Cosmological perturbation theory in the synchronous and conformal Newtonian gauges, Astrophys. J. 455 (1995) 7 [astro-ph/9506072].
[386] N. Dimakis, A. Karagiorgos, A. Zampeli, A. Paliathanasis, T. Christodoulakis and P.A. Terzis, General Analytic Solutions of Scalar Field Cosmology with Arbitrary Potential, Phys. Rev. D 93 (2016) 123518 [1604.05168].
[387] S. Pan, W. Yang and A. Paliathanasis, Imprints of an extended Chevallier-Polarski-Linder parametrization on the large scale of our universe, Eur. Phys. J. C 80 (2020) 274 [1902.07108].
[388] A. Lewis, A. Challinor and A. Lasenby, Efficient computation of CMB anisotropies in closed FRW models, Astrophys. J. 538 (2000) 473 [astro-ph/9911177].
[389] C. Howlett, A. Lewis, A. Hall and A. Challinor, CMB power spectrum parameter degeneracies in the era of precision cosmology, JCAP (2012) 027 [1201.3654].
[390] A. Lewis and S. Bridle, Cosmological parameters from CMB and other data: A Monte Carlo approach, Phys. Rev. D 66 (2002) 103511 [astro-ph/0205436].
[391] A. Lewis, Efficient sampling of fast and slow cosmological parameters, Phys. Rev. D 87 (2013) 103529 [1304.4473].
[392] R.M. Neal, Taking Bigger Metropolis Steps by Dragging Fast Variables, ArXiv Mathematics e-prints (2005) [math/0502099].
[393] A. Gelman and D.B. Rubin, Inference from Iterative Simulation Using Multiple Sequences, Statist. Sci. 7 (1992) 457.
[394] Planck collaboration, Planck 2018 results. V. CMB power spectra and likelihoods, Astron. Astrophys. 641 (2020) A5 [1907.12875].
[395] J. Carron, M. Mirmelstein and A. Lewis, CMB lensing from Planck PR4 maps, JCAP 09 (2022) 039 [2206.07773].
[396] DESI collaboration, DESI 2024 IV: Baryon Acoustic Oscillations from the Lyman Alpha Forest, 2404.03001.
[397] D. Huterer and M.S. Turner, Probing the dark energy: Methods and strategies, Phys. Rev. D 64 (2001) 123527 [astro-ph/0012510].
[398] A. Albrecht et al., Report of the Dark Energy Task Force, astro-ph/0609591.
  1. Corresponding author.
  2. For a few caveats, objections, and discussions surrounding this conclusion raised over the years, see Refs. [63-74].
  3. This diffuse interest is reflected in the wide range of models – both within and beyond the standard cosmological constant – that have been proposed over the years. These include, for example, new (ultra)light fields and modifications to gravity. With no claims to completeness see, e.g., Refs. [92, 104-167].
    Notably, the gravitational deflection, or lensing, experienced by CMB photons due to their interactions with the large-scale structure of the Universe imprints a distinctive non-Gaussian four-point correlation function (trispectrum) in both temperature and polarization anisotropies [272]. This signal provides complementary information about late-time processes affecting structure formation, from neutrinos and thermal relics [273-277] to dark energy and its dynamical properties [56, 278-284].
    Excitingly, upcoming Stage-IV astronomical surveys such as future data releases from DESI, Euclid [285], the Large Synoptic Survey Telescope (LSST) [286], the Wide-Field InfraRed Survey Telescope (WFIRST) [287], and the Square Kilometre Array (SKA) [288], are expected to improve upon current sensitivity and are forecasted to constrain DE parameters to near-percent precision, offering new insights into the dark sector of the Universe.
  4. See, e.g., Refs [32, 38, 40, 45, 50, 53, 54, 215, 245, 293-336] for recent and not-so-recent discussions and constraints on the DE EoS from a variety of astrophysical and cosmological probes.
    In recent years, the possibility that the DE EoS can be phantom in nature has gained substantial interest, as in principle a shift of towards could already be enough to address the well-known Hubble tension [289-291, 337, 338] – see, e.g., Refs. [197, 339] for an overview, as well as for caveats surrounding this possibility.
    This difficulty is often referred to as geometrical degeneracy. At its core, the problem is that different combinations of late-time cosmic parameters can be adjusted in such a way that the acoustic angular scale – determined by the ratio of the comoving sound horizon at recombination to the comoving distance to last scattering – remains constant if both quantities change proportionally. Consequently, measurements based solely on this scale cannot provide strong constraints on (dynamical) DE parameters by themselves, unless perturbation-level effects and late-time data are also incorporated to break this degeneracy.
  5. As argued in various recent works, the DESI BAO measurement at (which is in tension with Planck) can play a crucial role in deriving many of the DESI signals for new physics, partially including the preference for DDE [369, 376, 377].
  6. To address this problem, in Ref. [313], some of us adopted flat priors , thus removing positive values of a priori. In this work, we have performed additional stability tests, which revealed that numerical instabilities arise only when CMB data are considered on their own (we do not report these results for any of the models under study, as they are not informative). Without late-time data, DE parameters remain essentially unconstrained, and can acquire large positive values. Despite the logarithmic nature of the equation of state, for these values, the DE energy density does not remain negligible in the early Universe, triggering warnings and errors in the Boltzmann solver code CAMB [388, 389]. In contrast, when late-time data are included, the DE parameters are significantly constrained in the region , and no large positive values are allowed. As a result, in the allowed region of parameter space, the DE energy density remains negligible at early times and does not affect early Universe cosmology.
  7. The NPIPE lensing map [395] covers CMB angular scales in the range using the quadratic estimator and re-processing Planck time-ordered data with several improvements, including around more data compared to the plik-lensing likelihood. Notice also that NPIPE and ACT-DR6 measurements explore distinct angular scales, as ACT uses only CMB multipoles and has only partial overlap with the sky fraction used in the Planck analysis [269]. Additionally they have different noise levels and instrument-related systematics. Therefore they can be regarded as nearly independent lensing measurements.
  8. Hereafter, constraints will always be quoted at CL unless otherwise specified.
  9. See, e.g., Refs [397, 398] for discussions on the importance of the pivot redshift.
    Note that the features presented in this appendix for the CPL model have been discussed in detail by the DESI collaboration – see, e.g., Sec. 5.2 of Ref. [336]. As we essentially recover all of the DESI results, we omit further discussion of the CPL model here.