DOI: https://doi.org/10.1038/s41598-024-57772-x
PMID: https://pubmed.ncbi.nlm.nih.gov/38528081
تاريخ النشر: 2024-03-25
افتح
توقع التوزيع الحراري في زعنفة متموجة متحركة باستخدام طريقة جديدة لتدريب الشبكات العصبية المستنيرة بالفيزياء
الملخص
تستخدم الزعانف على نطاق واسع في العديد من التطبيقات الصناعية، بما في ذلك المبادلات الحرارية. تستفيد من تكلفة تصميم اقتصادية نسبياً، وهي خفيفة الوزن، وصغيرة الحجم جداً. وبالتالي، تبحث هذه الدراسة في تأثير هيكل الزعنفة المتموجة المعرضة لتأثيرات الحمل الحراري مع توليد حرارة داخلية. يتم وصف توزيع الحرارة، الذي يعتبر حالة مستقرة في بعد واحد، من خلال تنفيذ فريد لشبكة عصبية مستنيرة بالفيزياء (PINN) كجزء من استراتيجيات الذكاء الاصطناعي لتحليل انتقال الحرارة في زعنفة متموجة متدفقة. تستكشف هذه الأبحاث الجديدة استخدام PINNs لفحص تأثير عدم خطية معادلة الحرارة وظروف الحدود من خلال تغيير المعلمات الفائقة للهندسة. يتم تقليل المعادلة التفاضلية العادية غير الخطية (ODE) المتعلقة بانتقال الحرارة إلى شكل غير بعدي باستخدام المتغيرات غير البعدية لتبسيط المشكلة. علاوة على ذلك، يتم تنفيذ طريقة رانج-كوتا فيلبيرغ من الرتبة الرابعة والخامسة (RKF-45) لتقييم المعادلات المبسطة عددياً. للتنبؤ بخصائص انتقال الحرارة في الزعنفة المتموجة، تم إنشاء نموذج متقدم للشبكة العصبية دون استخدام نهج تقليدي قائم على البيانات، مع القدرة على حل ODEs بشكل صريح من خلال دمج دالة خسارة تعتمد على متوسط مربع الخطأ. تكشف النتائج التي تم الحصول عليها أن زيادة متغير الموصلية الحرارية تزيد من توزيع الحرارة. في المقابل، يتسبب انخفاض في ملف درجة الحرارة بسبب الزيادة في قيم المتغيرات الموصلة-الحمل.
قائمة الرموز
Nc معامل الحمل-التوصيل
|
|
معامل توليد الحرارة الداخلي (غير بعدي) |
|
|
إزاحة طور الموجة السطحية |
|
|
درجة الحرارة المحيطة |
|
|
معامل الموصلية الحرارية |
|
|
معدل توليد الحرارة الداخلي (غير بعدي) |
|
|
الطول الكلي للقوس الزعنفة المتموجة |
|
|
معامل توليد الحرارة |
|
|
درجة الحرارة عند قاعدة الزعنفة |
|
|
نصف ارتفاع قاعدة الزعنفة |
|
|
توليد الحرارة |
|
|
عدد الموجات |
|
|
مساحة سطح الزعنفة |
|
|
درجة الحرارة غير البعدية |
| ك | الموصلية الحرارية |
| H | نصف ارتفاع الزعنفة |
|
|
معامل انتقال الحرارة المتدفقة |
|
|
مساحة المقطع العرضي للزعنفة |
| T | درجة الحرارة |
|
|
عرض الزعنفة |
|
|
معامل تغير الموصلية الحرارية |
الرمز الفرعي
إطالة مسار التدفق، وتعزيز مساحة سطح نقل الحرارة، وإنشاء تجاعيد فعالة تسبب دوامات لخلط الهواء البارد. يسمح الشكل المستمر للزعانف المتموجة بالعمل المستمر لتحمل الظروف المحيطة غير المواتية، حتى لو كان انتقال الحرارة للزعانف المتموجة أقل من الأسطح المتقطعة مثل الزعانف ذات الشفرات أو الشقوق. أبلغ ليو وآخرون.
- معدلات نقل الحرارة المتدفقة والتقلبات الحرارية الديناميكية في الزعنفة المتموجة.
- تأثير توليد الحرارة الداخلية على التغير الحراري للزعانف المتموجة.
- حل نموذج نقل الحرارة المطور مع تطبيق PINN.
- دقة PINN المطبقة في حل معادلات نقل الحرارة غير الخطية.
صياغة المشكلة
- يفترض أن الزعنفة تنقل الحرارة مع البيئة المحيطة التي لها درجة حرارة ثابتة
من خلال الحمل الحراري. - يحدث نقل الحرارة من السطح الممتد إلى السائل المجاور في حالة مستقرة.
- يفترض أن الموصلية الحرارية وتوليد الحرارة الداخلية ومعامل نقل الحرارة بالحمل تعتمد على درجة الحرارة.
- يعتبر المحور السيني على طول الطول الكلي للزعانف، في البداية عند سطحها الأساسي.
- مقاومة الحرارة عند نقطة التفاعل بين الزعنفة والجدار غير مهمة.
- يتم اعتبار درجة حرارة السائل المجاور
ودرجة حرارة قاعدة الزعنفة ثوابت. - نظرًا لأن سمك الزعنفة صغير بالنسبة للقياسات المتبقية، يمكن تقريب توزيع درجة الحرارة في الزعنفة كدالة تعتمد فقط على إحداثيات الطول.
تم تصميم سطح الزعنفة بشكل متموج على طول محورها الطولي. تم تصميم هيكل الزعنفة المتموجة على شكل منحنى جيب مع (براكاش وآخرون.
علاوة على ذلك، يتم تمثيل الموصلية الحرارية وتوليد الحرارة الداخلية ومعامل نقل الحرارة بالحمل رياضيًا على النحو التالي
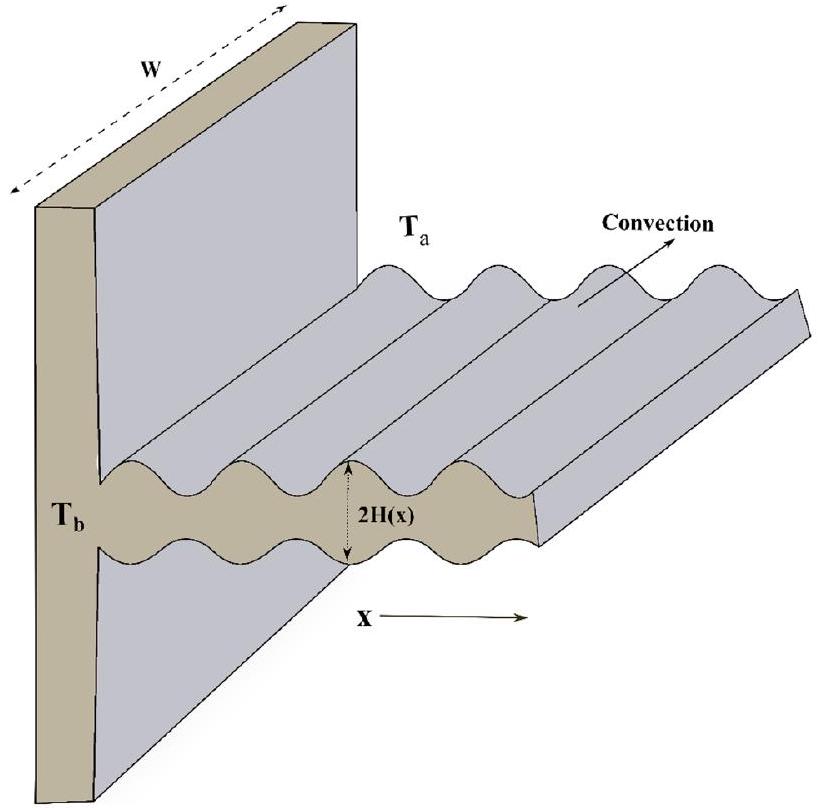
بالنظر إلى الفرضيات المذكورة أعلاه، يتم التعبير عن المعادلة الحاكمة على النحو التالي (بورنيما وآخرون.
عند طرف الزعنفة:
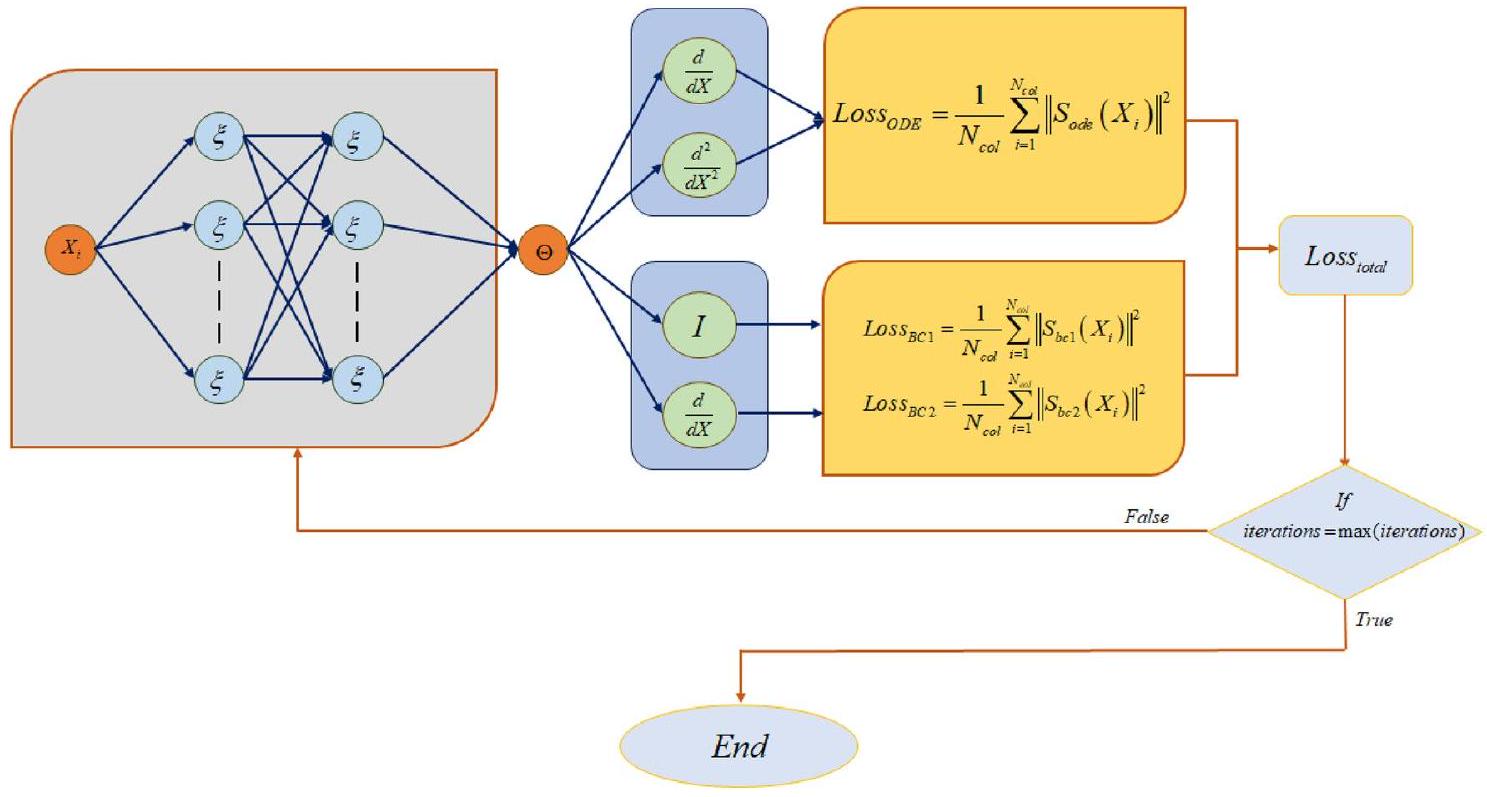
الشبكات العصبية المدعومة بالفيزياء (PINNs)
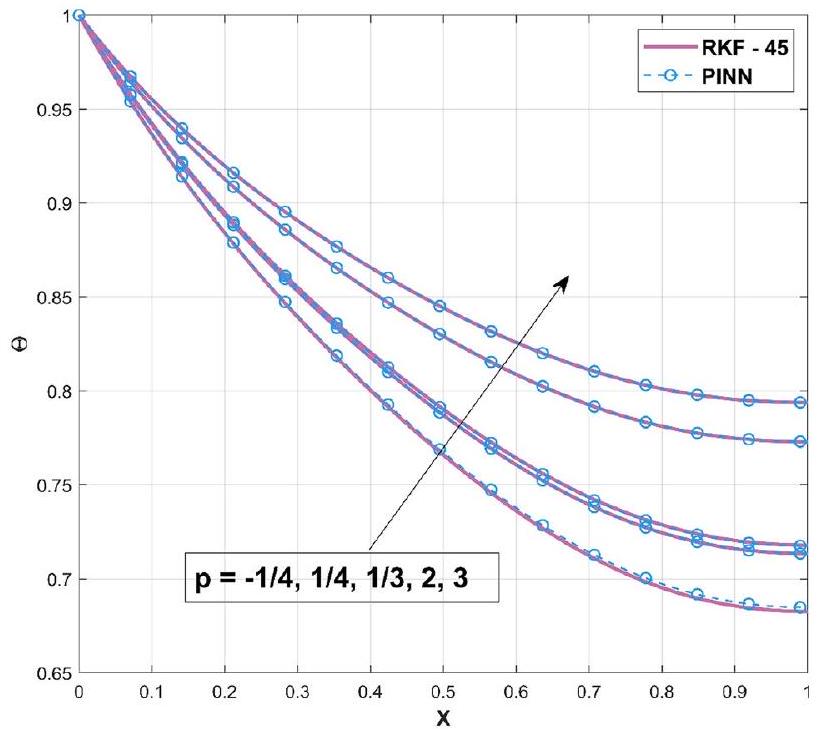
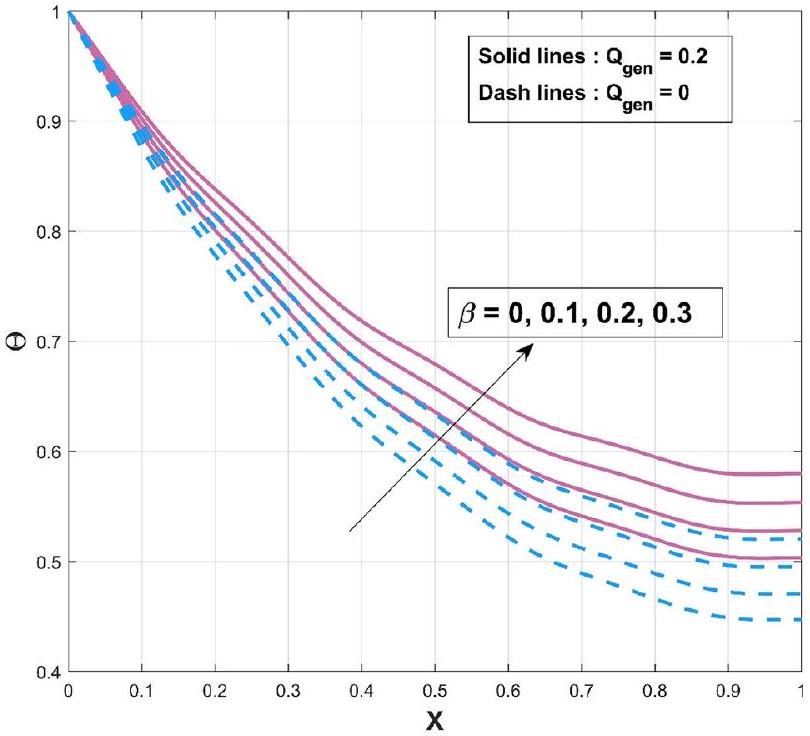
النتائج والمناقشة



| ب | إكس |
|
||
| بين | RKF-45 | خطأ | ||
| -1/4 | 0 | 1.000007 | 1.000000 | 7.62939E-06 |
| 0.2 | 0.883129 | 0.883691 | 0.000561046 | |
| 0.4 | 0.798810 | 0.799922 | 0.001111697 | |
| 0.6 | 0.734608 | 0.736249 | 0.001640231 | |
| 0.8 | 0.694266 | 0.696286 | 0.002019562 | |
| 1 | 0.682647 | 0.684796 | 0.002148474 | |
| 1/4 | 0 | 0.999951 | 1.000000 |
|
| 0.2 | 0.892658 | 0.892695 |
|
|
| 0.4 | 0.816564 | 0.816588 |
|
|
| 0.6 | 0.759252 | 0.759288 | ٣.٥٦٣٠٦ × ١٠^-٥ | |
| 0.8 | 0.723614 | 0.723627 |
|
|
| 1 | 0.713446 | 0.71347 |
|
|
| 1/3 | 0 | 1.000108 | 1.000000 | 0.000108004 |
| 0.2 | 0.894164 | 0.893973 | 0.000191383 | |
| 0.4 | 0.819222 | 0.818943 | 0.000279093 | |
| 0.6 | 0.762864 | 0.76253 | 0.000334411 | |
| 0.8 | 0.727856 | 0.727461 | 0.000395874 | |
| 1 | 0.717921 | 0.717487 | 0.000434257 | |
| 2 | 0 | 0.999963 | 1.000000 |
|
| 0.2 | 0.912096 | 0.912148 | 5.16784E-05 | |
| 0.4 | 0.852048 | 0.85211 |
|
|
| 0.6 | 0.807671 | 0.807757 | 0.0000852146 | |
| 0.8 | 0.780521 | 0.780621 | 0.000099786 | |
| 1 | 0.772955 | 0.773073 | 0.000117642 | |
| ٣ | 0 | 0.999983 | 1.000000 |
|
| 0.2 | 0.919179 | 0.919204 |
|
|
| 0.4 | 0.864789 | 0.864811 |
|
|
| 0.6 | 0.824819 | 0.824861 |
|
|
| 0.8 | 0.800506 | 0.800555 |
|
|
| 1 | 0.793797 | 0.793862 |
|
|
الخاتمة
| إن سي |
|
|
|
|
|
خالد
|
0.886819 | 0.648054 |
| بين | 0.886754 | 0.648013 | |
| خطأ |
|
|
|
- زيادة في متغير الموصلية الحرارية تؤدي إلى زيادة في تباين درجة الحرارة في الزعنفة المتموجة.
- يلاحظ انخفاض في التغير الحراري مع زيادة في معامل الحمل الحراري والتوصيل.
- تؤدي المستويات المرتفعة من معلمة توليد الحرارة الداخلية إلى تعزيز التشتت الحراري في الزعنفة ذات الشكل الموجي.
- الملف الحراري للزعنفة المتموجة يتزايد مع ارتفاع مؤشر معلمة عملية الحمل الحراري.
- وفقًا للنتائج، أظهر الشبكة العصبية المعتمدة على الفيزياء (PINN) توافقًا ملحوظًا مع النتائج العددية خلال التدريب. وقد تفوقت الشبكة، المعززة بالخصائص المصممة، في التقاط الفيزياء الأساسية للمشكلة. ونتيجة لذلك، تفوقت على الشبكات العصبية التقليدية في قدرتها على تقديم توقعات دقيقة خارج بيئة التدريب.
- تجمع خصائص النمذجة التقليدية المعتمدة على الفيزياء مع القدرة على التكيف والتعلم لشبكة الأعصاب المعتمدة على الفيزياء. إنها توفر حلاً دقيقًا وفعالًا، مما يقلل من الحاجة إلى مجموعات بيانات ضخمة ويقلل من التكاليف الحاسوبية مع الحفاظ على دقة عالية من خلال تضمين المعادلات الحاكمة بشكل صريح في بنية الشبكة العصبية.
توفر البيانات
نُشر على الإنترنت: 25 مارس 2024
References
- Prasannakumara, B. C. & Shashikumar, N. S. Boundary layer flow and heat transfer of nanofluid with fluid particle suspension over a nonlinear stretching sheet in the presence of thermal radiation. J. Nanofluids 6, 487-495 (2017).
- Prasannakumara, B. C., Shashikumar, N. S. & Venkatesh, P. Boundary Layer Flow and Heat Transfer of fluid particle suspension with nanoparticles over a nonlinear stretching sheet embedded in a porous medium. Nonlinear Eng. 6, 179-190 (2017).
- Prasannakumara, B. C., Shashikumar, N. S. & Archana, N. S. Three-dimensional boundary layer flow and heat transfer of a dusty fluid towards a stretching sheet with convective boundary conditions. J. Comput. Appl. Res. Mech. Eng. 8, 25-38 (2018).
- Muhammad, T. et al. Significance of darcy-forchheimer porous medium in nanofluid through carbon nanotubes. Commun. Theor. Phys. 70, 361 (2018).
- Shashikumar, N. S., Gireesha, B. J., Mahanthesh, B. & Prasannakumara, B. C. Brinkman-Forchheimer flow of SWCNT and MWCNT magneto-nanoliquids in a microchannel with multiple slips and Joule heating aspects. Multidiscip. Model. Mater. Struct. 14, 769-786 (2018).
- Souayeh, B. et al. Slip flow and radiative heat transfer behavior of Titanium alloy and ferromagnetic nanoparticles along with suspension of dusty fluid. J. Mol. Liq. 290, 111223 (2019).
- Madhu, M., Shashikumar, N. S., Gireesha, B. J. & Kishan, N. Second law analysis of Powell-Eyring fluid flow through an inclined microchannel with thermal radiation. Phys. Scr. 94, 125205 (2019).
- Shashikumar, N. S., Macha, M., Gireesha, B. J. & Kishan, N. Finite element analysis of micropolar nanofluid flow through an inclined microchannel with thermal radiation. Multidiscip. Model. Mater. Struct. 16, 1521-1538 (2020).
- Riasat, S., Ramzan, M., Kadry, S. & Chu, Y.-M. Significance of magnetic Reynolds number in a three-dimensional squeezing Darcy-Forchheimer hydromagnetic nanofluid thin-film flow between two rotating disks. Sci. Rep. 10, 17208 (2020).
- Shashikumar, N. S., Madhu, M., Sindhu, S., Gireesha, B. J. & Kishan, N. Thermal analysis of MHD Williamson fluid flow through a microchannel. Int. Commun. Heat Mass Transfer 127, 105582 (2021).
- Madhu, M., Shashikumar, N. S., Gireesha, B. J. & Kishan, N. Thermal analysis of MHD powell-eyring fluid flow through a vertical microchannel. Int. J. Ambient Energy 43, 4454-4462 (2022).
- Madhu, M., Shashikumar, N. S., Gireesha, B. J. & Kishan, N. Second law analysis of MHD third-grade fluid flow through the microchannel. Pramana J. Phys. 95, 4 (2021).
- Shashikumar, N. et al. Entropy generation analysis of radiative Williamson fluid flow in an inclined microchannel with multiple slip and convective heating boundary effects. In Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering 09544089211049863 (2021) doi:https://doi.org/10.1177/09544089211049863.
- Mahanthesh, B., Shashikumar, N. S. & Lorenzini, G. Heat transfer enhancement due to nanoparticles, magnetic field, thermal and exponential space-dependent heat source aspects in nanoliquid flow past a stretchable spinning disk. J. Therm. Anal. Calorim. 145, 3339-3347 (2021).
15 Gireesha, B. J., Prasannakumara, B. C., Umeshaiah, M. & Shashikumar, N. S. Three dimensional boundary layer flow of MHD maxwell nanofluid over a non-linearly stretching sheet with nonlinear thermal radiation. J. Appl. Nonlinear Dyn. 10, 263-277 (2021). - Souayeh, B., Yasin, E., Alam, M. W. & Hussain, S. G. Numerical simulation of magnetic dipole flow over a stretching sheet in the presence of non-uniform heat source/sink. Front Energy Res. https://doi.org/10.3389/fenrg.2021.767751 (2021).
17 Madhu, M., Shashikumar, N. S., Gireesha, B. J. & Kishan, N. Entropy generation analysis of MHD micropolar nanofluid flow through a micro channel. Discontin. Nonlinear. Complex. 11, 569-582 (2022). - Shashikumar, N. S., Sindhu, S., Madhu, M. & Gireesha, B. J. Second law analysis of MHD Carreau fluid flow through a microchannel with thermal radiation. Waves Random Complex Media https://doi.org/10.1080/17455030.2022.2060532 (2022).
- Madhu, M., Shashikumar, N. S., Thriveni, K., Gireesha, B. J. & Mahanthesh, B. Irreversibility analysis of the MHD Williamson fluid flow through a microchannel with thermal radiation. Waves Random Complex Media https://doi.org/10.1080/17455030.2022. 2111473 (2022).
- Ramesh, G. K., Madhukesh, J. K., Aly, E. H. & Pop, I. Modified Buongiorno’s model for biomagnetic hybrid nanoliquid past a permeable moving thin needle. Int. J. Num. Methods Heat Fluid Flow 32, 3551-3578 (2022).
- Alsulami, M. D., Naveen Kumar, R., Punith Gowda, R. J. & Prasannakumara, B. C. Analysis of heat transfer using Local thermal non-equilibrium conditions for a non-Newtonian fluid flow containing Ti6Al4V and AA7075 nanoparticles in a porous media. ZAMM J. Appl. Math Mech. Z Angewandte Math. Mech. 103, e202100360 (2023).
- Alhowaity, A. et al. Non-Fourier energy transmission in power-law hybrid nanofluid flow over a moving sheet. Sci Rep 12, 10406 (2022).
- Souayeh, B. Simultaneous features of CC heat flux on dusty ternary nanofluid (Graphene + Tungsten Oxide + Zirconium Oxide) through a magnetic field with slippery condition. Mathematics 11, 554 (2023).
- Ramesh, G. K., Madhukesh, J. K., Khan, U., Hussain, S. M. & Galal, A. M. Inspection of hybrid nanoparticles flow across a nonlinear/linear stretching surface when heat sink/source and thermophoresis particle deposition impacts are significant. Int. J. Mod. Phys. B 37, 2350008 (2023).
- Mahabaleshwar, U. S., Vanitha, G. P. & Souayeh, B. A study of casson viscous gas flows and heat transfer across a linear stretching/ shrinking sheet by considering induced slip, mass transpiration, inclined magnetic force, and radiation effect. BioNanoScience 13, 1052-1063 (2023).
- Dinesh Kumar, M. et al. Analysis of dynamical assisting and opposing flow characteristics of darcy surface-filled ternary nanoparticles and fourier flux: Artificial neural network and levenberg method. J. Circuit. Syst. Comp. https://doi.org/10.1142/S0218 126624400012 (2024).
- Alqahtani, A. M., Bilal, M., Ali, A., Alsenani, T. R. & Eldin, S. M. Numerical solution of an electrically conducting spinning flow of hybrid nanofluid comprised of silver and gold nanoparticles across two parallel surfaces. Sci. Rep. 13, 7180 (2023).
- Nagaraja, K. V. et al. Heat and mass transfer analysis of assisting and opposing radiative flow conveying ternary hybrid nanofluid over an exponentially stretching surface. Sci. Rep. 13, 14795 (2023).
- Alfannakh, H. & Souayeh, B. Computational assessment of
30 Karthik, K. et al. Impacts of thermophoretic deposition and thermal radiation on heat and mass transfer analysis of ternary nanofluid flow across a wedge. Int. J. Model. Simul. https://doi.org/10.1080/02286203.2023.2298234 (2024). - Madhukesh, J. K. et al. A model development for thermal and solutal transport analysis of non-newtonian nanofluid flow over a riga surface driven by a waste discharge concentration. Water 15, 2879 (2023).
- Sharma, R. P., Madhukesh, J. K., Shukla, S., Gamaoun, F. & Prasannakumara, B. C. Numerical study of the thermophoretic velocity of ternary hybrid nanofluid in a microchannel bounded by the two parallel permeable flat plates. J. Therm. Anal. Calorim. 148, 14069-14080 (2023).
- Madhura, K. R., Babitha, Kalpana, G. & Makinde, O. D. Thermal performance of straight porous fin with variable thermal conductivity under magnetic field and radiation effects. Heat Transf. 49, 5002-5019 (2020).
- Abukhaled, M. & Khuri, S. A. Efficient numerical treatment of a conductive-radiative fin with temperature-dependent thermal conductivity and surface emissivity. Int. J. Comput. Methods Eng. Sci. Mech. 21, 159-168 (2020).
- Sarwe, D. U. & Kulkarni, V. S. Thermal behaviour of annular hyperbolic fin with temperature dependent thermal conductivity by differential transformation method and Pade approximant. Phys. Scr. 96, 105213 (2021).
- Wang, K.-J. & Shi, F. A new fractal model of the convective-radiative fins with temperature-dependent thermal conductivity. Therm. Sci. 207-207 (2022).
- Kumar, R. S. V., Jagadeesha, K. C. & Prasannakumara, B. C. Heat transfer and thermal analysis in a semi-spherical fin with temperature-variant thermal properties: an application of Probabilists’ Hermite collocation method. Waves Random Complex Media https://doi.org/10.1080/17455030.2023.2198031 (2023).
- Liu, X., Wang, M., Liu, H., Chen, W. & Qian, S. Numerical analysis on heat transfer enhancement of wavy fin-tube heat exchangers for air-conditioning applications. Appl. Therm. Eng. 199, 117597 (2021).
- Song, K. et al. Thermal-hydraulic characteristic of a novel wavy fin-and-circle tube heat exchanger with concave curved vortex generators. Int. J. Heat Mass Transf. 194, 123023 (2022).
- Kumar, C. et al. Analysis of heat transfer behavior of porous wavy fin with radiation and convection by using a machine learning technique. Symmetry 15, 1601 (2023).
- Sharma, A., Ding, C., Chul Kim, S. & Chauhan, R. Investigation and optimization of solidification performance of concentration tube type latent heat storage unit with herringbone wavy fin designs. Appl. Therm. Eng. 222, 119924 (2023).
- Kumar, R. S. V., Alsulami, M. D., Sarris, I. E., Sowmya, G. & Gamaoun, F. Stochastic Levenberg-Marquardt neural network implementation for analyzing the convective heat transfer in a wavy fin. Mathematics 11, 2401 (2023).
- Das, R. & Kundu, B. Simultaneous estimation of heat generation and magnetic field in a radial porous fin from surface temperature information. Int. Commun. Heat Mass Transf. 127, 105497 (2021).
- Din, Z. U., Ali, A., De la Sen, M. & Zaman, G. Entropy generation from convective-radiative moving exponential porous fins with variable thermal conductivity and internal heat generations. Sci. Rep. 12, 1791 (2022).
- Venkitesh, V. & Mallick, A. Thermal analysis of a convective-conductive-radiative annular porous fin with variable thermal parameters and internal heat generation. J. Therm. Anal. Calorim. 147, 1519-1533 (2022).
- Kaur, P. & Singh, S. Convective radiative moving fin with temperature-dependent thermal conductivity, internal heat generation and heat transfer coefficient. Pramana J. Phys. 96, 216 (2022).
- Gireesha, B. J., Pavithra, C. G. & Keerthi, M. L. Semianalytical investigation on heat transfer in porous fins with temperaturedependent thermal conductivity via the homotopy perturbation Sumudu transform approach. Heat Transf. 53, 610-645 (2024).
- Ji, W., Qiu, W., Shi, Z., Pan, S. & Deng, S. Stiff-PINN: Physics-Informed neural network for stiff chemical kinetics. J. Phys. Chem. A 125, 8098-8106 (2021).
- Berkhahn, S. & Ehrhardt, M. A physics-informed neural network to model COVID-19 infection and hospitalization scenarios. Adv. Cont. Discr. Mod. 2022, 61 (2022).
- Chiu, P.-H., Wong, J. C., Ooi, C., Dao, M. H. & Ong, Y.-S. CAN-PINN: A fast physics-informed neural network based on coupled-automatic-numerical differentiation method. Comput. Methods Appl. Mech. Eng. 395, 114909 (2022).
- Bararnia, H. & Esmaeilpour, M. On the application of physics informed neural networks (PINN) to solve boundary layer thermalfluid problems. Int. Commun. Heat Mass Transf. 132, 105890 (2022).
- Prakash, S. B. et al. Investigation of the thermal analysis of a wavy fin with radiation impact: an application of extreme learning machine. Phys. Scr. 99, 015225 (2023).
- Poornima, B. S. et al. Evolutionary computing for the radiative-convective heat transfer of a wetted wavy fin using a genetic algorithm-based neural network. Biomimetics 8, 574 (2023).
- Khaled, A. A. Thermal performance of six different types of wavy-fins. Int. J. Num. Methods Heat Fluid Flow 25, 892-911 (2015).
- Ramesh, G. K., Manohar, G. R., Madhukesh, J. K., Venkatesh, P. & Gireesha, B. J. Thermal aspects of a radiative-convective semispherical porous fin of functionally graded material. Eur. Phys. J. Plus 139, 97 (2024).
- Madhu, J., Baili, J., Kumar, R. N., Prasannakumara, B. C. & Gowda, R. J. P. Multilayer neural networks for studying three-dimensional flow of non-Newtonian fluid flow with the impact of magnetic dipole and gyrotactic microorganisms. Phys. Scr. 98, 115228 (2023).
- Khan, M. I. et al. Neural artificial networking for nonlinear Darcy-Forchheimer nanofluidic slip flow. Appl. Nanosci. 13, 3767-3786 (2023).
- Punith Gowda, R. J., ChandrappaPrasannakumara, B., Shehzad, S. A. & Sahar, F. Blasius and Sakiadis flow of titania-copper-water based hybrid nanofluid flow: An artificial neural network modeling. Sci. Iran. https://doi.org/10.24200/sci.2023.61937.7566 (2023).
- Shoaib, M. et al. Intelligent backpropagated neural networks application on Darcy-Forchheimer ferrofluid slip flow system. Int. Commun. Heat Mass Transf. 129, 105730 (2021).
شكر وتقدير
مساهمات المؤلفين
المصالح المتنافسة
معلومات إضافية
معلومات إعادة الطبع والتصاريح متاحة علىwww.nature.com/reprints.
ملاحظة الناشر: تظل شركة سبرينجر ناتشر محايدة فيما يتعلق بالمطالبات القضائية في الخرائط المنشورة والانتماءات المؤسسية.
© المؤلفون 2024
DOI: https://doi.org/10.1038/s41598-024-57772-x
PMID: https://pubmed.ncbi.nlm.nih.gov/38528081
Publication Date: 2024-03-25
OPEN
Predicting the thermal distribution in a convective wavy fin using a novel training physics-informed neural network method
Abstract
Fins are widely used in many industrial applications, including heat exchangers. They benefit from a relatively economical design cost, are lightweight, and are quite miniature. Thus, this study investigates the influence of a wavy fin structure subjected to convective effects with internal heat generation. The thermal distribution, considered a steady condition in one dimension, is described by a unique implementation of a physics-informed neural network (PINN) as part of machine-learning intelligent strategies for analyzing heat transfer in a convective wavy fin. This novel research explores the use of PINNs to examine the effect of the nonlinearity of temperature equation and boundary conditions by altering the hyperparameters of the architecture. The non-linear ordinary differential equation (ODE) involved with heat transfer is reduced into a dimensionless form utilizing the nondimensional variables to simplify the problem. Furthermore, Runge-Kutta Fehlberg’s fourth-fifth order (RKF-45) approach is implemented to evaluate the simplified equations numerically. To predict the wavy fin’s heat transfer properties, an advanced neural network model is created without using a traditional data-driven approach, the ability to solve ODEs explicitly by incorporating a mean squared error-based loss function. The obtained results divulge that an increase in the thermal conductivity variable upsurges the thermal distribution. In contrast, a decrease in temperature profile is caused due to the augmentation in the convective-conductive variable values.
List of symbols
Nc Convection-conduction parameter
|
|
Internal heat generation parameter (dimensionless) |
|
|
Surface wave phase shift |
|
|
Ambient temperature |
|
|
Thermal conductivity parameter |
|
|
Internal heat generating rate (dimensionless) |
|
|
Wavy fin total arc length |
|
|
Parameter of heat generation |
|
|
Temperature at the fin’s base |
|
|
Fin base half height |
|
|
Heat generation |
|
|
Wave number |
|
|
Fin surface area |
|
|
Non-dimensional temperature |
| K | Thermal conductivity |
| H | Fin half height |
|
|
Convective heat transfer coefficient |
|
|
Fin cross-sectional area |
| T | Temperature |
|
|
Fin’s width |
|
|
Thermal conductivity variation parameter |
Subscript
prolonging the flow route, strengthening the heat transmission surface area, and creating efficient corrugations that cause vortices to mix with the cooling air. The continuous fin shape of wavy fins allows the consistent operation to withstand unfavourable ambient circumstances, even if the heat transmission of wavy fins is inferior to interrupted surfaces like louvre or slit fins. Liu et al.
- Convective heat transfer rates and dynamic thermal fluctuations in a wavy fin.
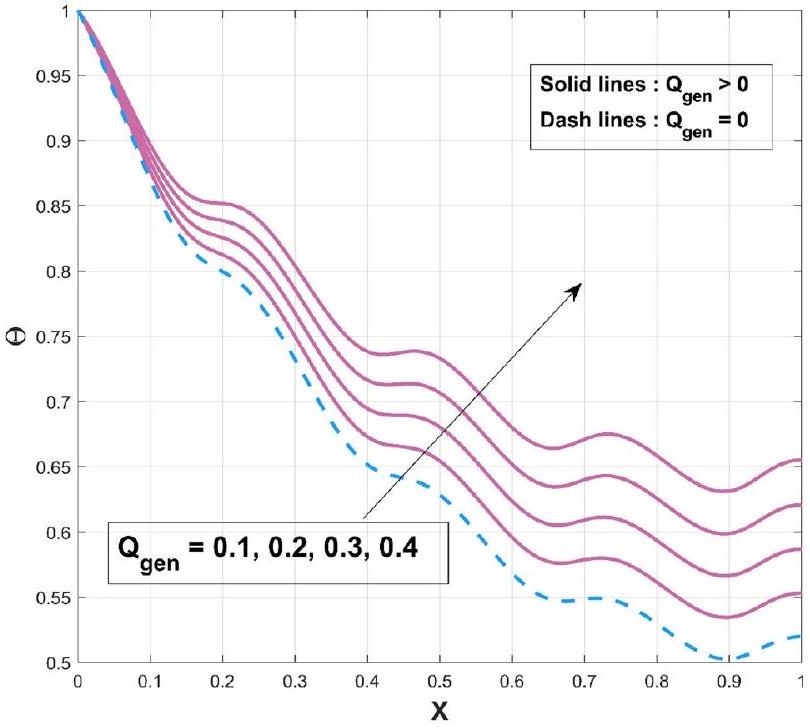
- Influence of internal heat generation on the thermal variation of the wavy fin.
- Solution of the developed heat transfer model with the application of PINN.
- Precision of the applied PINN in solving the heat transfer nonlinear equations.
Formulation of the problem
- The fin is presumed to transmit heat with the surrounding environment having conatant temperature
- Transfer of heat from the extended surface to the adjacent fluid occurs in a steady state.
- The thermal conductivity, internal heat generation and convective heat transfer coefficient are supposed to be temperature-dependent.
- The x -axis is regarded along the overall length of the fin, initially at its primary surface.
- The heat resistance at the point of interacting between the fin and the wall is insignificant.
- The temperature of the adjacent fluid
- Since the fin thickness is small in regard to the remaining measurements, the temperature distribution throughout the fin can be approximated as a function of only the length coordinate.
The fin surface has been wavy along its longitudinal axis. The wavy fin structure is designed in the shape of a sine curve with (Prakash et al.
Further, the thermal conductivity, internal heat generation and the convective heat transfer coefficient are mathematically denoted as

Considering the aforesaid-stated premises, the governing equation is expressed as follows (Poornima et al.
At fin’s tip:
Physics-informed neural networks (PINNs)

Results and discussion








| p | X |
|
||
| PINN | RKF-45 | Error | ||
| -1/4 | 0 | 1.000007 | 1.000000 | 7.62939E-06 |
| 0.2 | 0.883129 | 0.883691 | 0.000561046 | |
| 0.4 | 0.798810 | 0.799922 | 0.001111697 | |
| 0.6 | 0.734608 | 0.736249 | 0.001640231 | |
| 0.8 | 0.694266 | 0.696286 | 0.002019562 | |
| 1 | 0.682647 | 0.684796 | 0.002148474 | |
| 1/4 | 0 | 0.999951 | 1.000000 |
|
| 0.2 | 0.892658 | 0.892695 |
|
|
| 0.4 | 0.816564 | 0.816588 |
|
|
| 0.6 | 0.759252 | 0.759288 | 3.56306E-05 | |
| 0.8 | 0.723614 | 0.723627 |
|
|
| 1 | 0.713446 | 0.71347 |
|
|
| 1/3 | 0 | 1.000108 | 1.000000 | 0.000108004 |
| 0.2 | 0.894164 | 0.893973 | 0.000191383 | |
| 0.4 | 0.819222 | 0.818943 | 0.000279093 | |
| 0.6 | 0.762864 | 0.76253 | 0.000334411 | |
| 0.8 | 0.727856 | 0.727461 | 0.000395874 | |
| 1 | 0.717921 | 0.717487 | 0.000434257 | |
| 2 | 0 | 0.999963 | 1.000000 |
|
| 0.2 | 0.912096 | 0.912148 | 5.16784E-05 | |
| 0.4 | 0.852048 | 0.85211 |
|
|
| 0.6 | 0.807671 | 0.807757 | 8.52146E-05 | |
| 0.8 | 0.780521 | 0.780621 | 9.9786E-05 | |
| 1 | 0.772955 | 0.773073 | 0.000117642 | |
| 3 | 0 | 0.999983 | 1.000000 |
|
| 0.2 | 0.919179 | 0.919204 |
|
|
| 0.4 | 0.864789 | 0.864811 |
|
|
| 0.6 | 0.824819 | 0.824861 |
|
|
| 0.8 | 0.800506 | 0.800555 |
|
|
| 1 | 0.793797 | 0.793862 |
|
|
Conclusion
| Nc |
|
|
|
|
|
Khaled
|
0.886819 | 0.648054 |
| PINN | 0.886754 | 0.648013 | |
| Error |
|
|
|
- An increase in the thermal conductivity variable upsurges the temperature variation in the wavy fin.
- A decrease in the thermal variation is observed for an augmentation in the convective-conductive parameter.
- Elevated scales of internal heat generation parameter promote thermal dispersal in the wavy profiled fin.
- The thermal profile of the wavy fin proliferates with an escalation in the index of the convective process parameter.
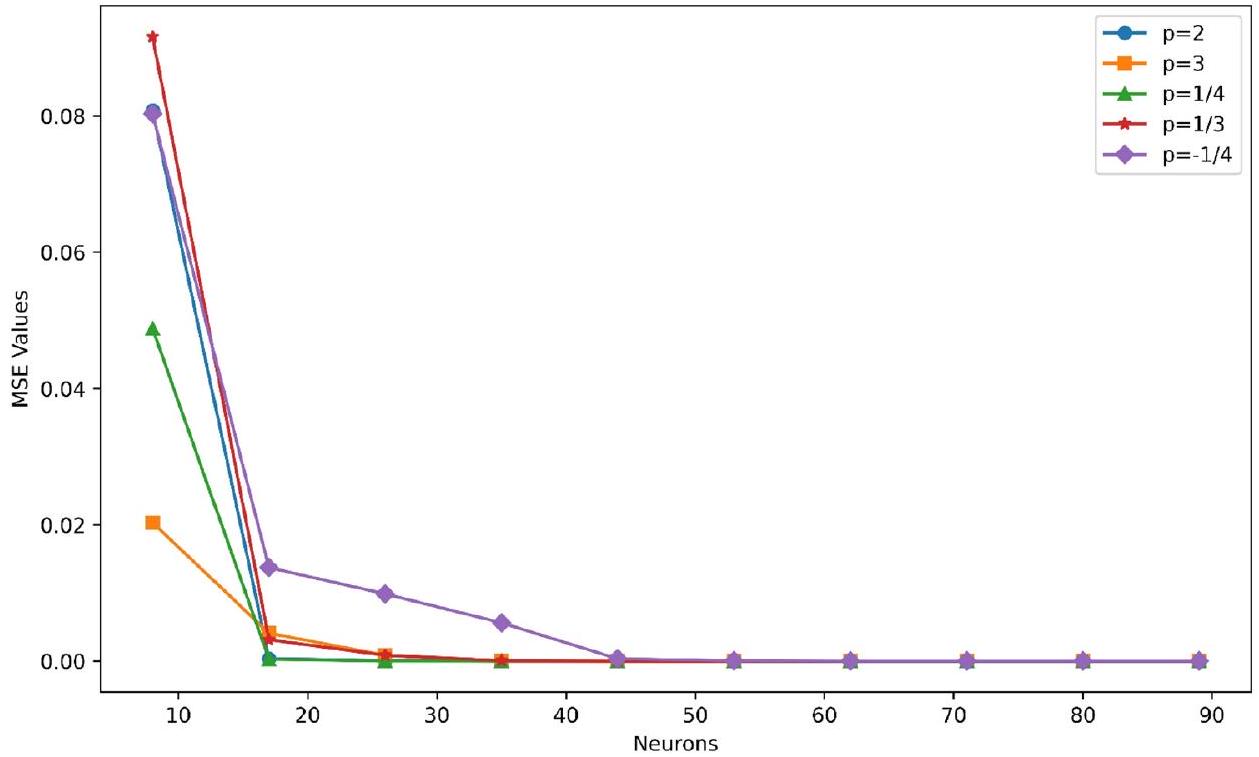
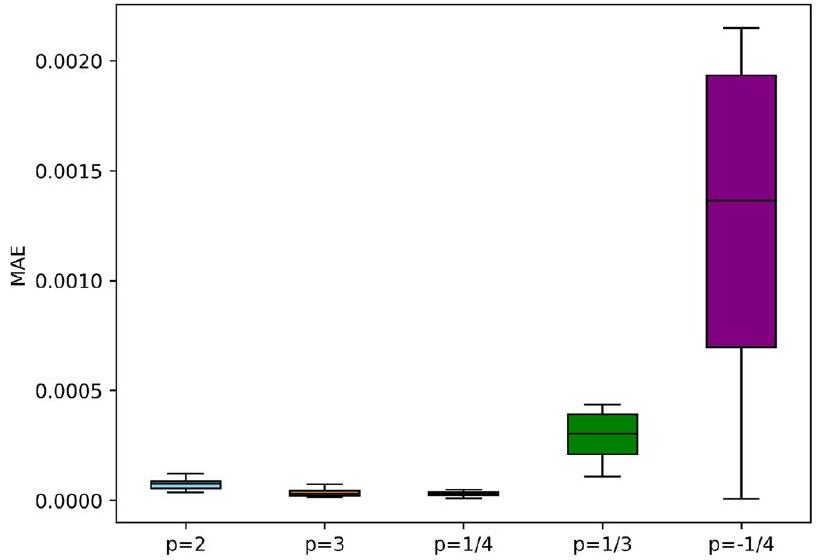
- According to the findings, the PINN displayed commendable alignment with numerical results in the training. The PINN, enhanced with designed characteristics, excelled at capturing the problem’s underlying physics. As a result, it outperformed typical neural networks in its capacity to make exact predictions outside of the training environment.
- The characteristics of traditional physics-based modelling are combined with the adaptability and learning capabilities of the PINN. It provides a precise and effective solution, decreasing the requirement for enormous data sets and minimizing the computational costs while retaining high accuracy by explicitly embedding the governing equations into the neural network architecture.
Data availability
Published online: 25 March 2024
References
- Prasannakumara, B. C. & Shashikumar, N. S. Boundary layer flow and heat transfer of nanofluid with fluid particle suspension over a nonlinear stretching sheet in the presence of thermal radiation. J. Nanofluids 6, 487-495 (2017).
- Prasannakumara, B. C., Shashikumar, N. S. & Venkatesh, P. Boundary Layer Flow and Heat Transfer of fluid particle suspension with nanoparticles over a nonlinear stretching sheet embedded in a porous medium. Nonlinear Eng. 6, 179-190 (2017).
- Prasannakumara, B. C., Shashikumar, N. S. & Archana, N. S. Three-dimensional boundary layer flow and heat transfer of a dusty fluid towards a stretching sheet with convective boundary conditions. J. Comput. Appl. Res. Mech. Eng. 8, 25-38 (2018).
- Muhammad, T. et al. Significance of darcy-forchheimer porous medium in nanofluid through carbon nanotubes. Commun. Theor. Phys. 70, 361 (2018).
- Shashikumar, N. S., Gireesha, B. J., Mahanthesh, B. & Prasannakumara, B. C. Brinkman-Forchheimer flow of SWCNT and MWCNT magneto-nanoliquids in a microchannel with multiple slips and Joule heating aspects. Multidiscip. Model. Mater. Struct. 14, 769-786 (2018).
- Souayeh, B. et al. Slip flow and radiative heat transfer behavior of Titanium alloy and ferromagnetic nanoparticles along with suspension of dusty fluid. J. Mol. Liq. 290, 111223 (2019).
- Madhu, M., Shashikumar, N. S., Gireesha, B. J. & Kishan, N. Second law analysis of Powell-Eyring fluid flow through an inclined microchannel with thermal radiation. Phys. Scr. 94, 125205 (2019).
- Shashikumar, N. S., Macha, M., Gireesha, B. J. & Kishan, N. Finite element analysis of micropolar nanofluid flow through an inclined microchannel with thermal radiation. Multidiscip. Model. Mater. Struct. 16, 1521-1538 (2020).
- Riasat, S., Ramzan, M., Kadry, S. & Chu, Y.-M. Significance of magnetic Reynolds number in a three-dimensional squeezing Darcy-Forchheimer hydromagnetic nanofluid thin-film flow between two rotating disks. Sci. Rep. 10, 17208 (2020).
- Shashikumar, N. S., Madhu, M., Sindhu, S., Gireesha, B. J. & Kishan, N. Thermal analysis of MHD Williamson fluid flow through a microchannel. Int. Commun. Heat Mass Transfer 127, 105582 (2021).
- Madhu, M., Shashikumar, N. S., Gireesha, B. J. & Kishan, N. Thermal analysis of MHD powell-eyring fluid flow through a vertical microchannel. Int. J. Ambient Energy 43, 4454-4462 (2022).
- Madhu, M., Shashikumar, N. S., Gireesha, B. J. & Kishan, N. Second law analysis of MHD third-grade fluid flow through the microchannel. Pramana J. Phys. 95, 4 (2021).
- Shashikumar, N. et al. Entropy generation analysis of radiative Williamson fluid flow in an inclined microchannel with multiple slip and convective heating boundary effects. In Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering 09544089211049863 (2021) doi:https://doi.org/10.1177/09544089211049863.
- Mahanthesh, B., Shashikumar, N. S. & Lorenzini, G. Heat transfer enhancement due to nanoparticles, magnetic field, thermal and exponential space-dependent heat source aspects in nanoliquid flow past a stretchable spinning disk. J. Therm. Anal. Calorim. 145, 3339-3347 (2021).
15 Gireesha, B. J., Prasannakumara, B. C., Umeshaiah, M. & Shashikumar, N. S. Three dimensional boundary layer flow of MHD maxwell nanofluid over a non-linearly stretching sheet with nonlinear thermal radiation. J. Appl. Nonlinear Dyn. 10, 263-277 (2021). - Souayeh, B., Yasin, E., Alam, M. W. & Hussain, S. G. Numerical simulation of magnetic dipole flow over a stretching sheet in the presence of non-uniform heat source/sink. Front Energy Res. https://doi.org/10.3389/fenrg.2021.767751 (2021).
17 Madhu, M., Shashikumar, N. S., Gireesha, B. J. & Kishan, N. Entropy generation analysis of MHD micropolar nanofluid flow through a micro channel. Discontin. Nonlinear. Complex. 11, 569-582 (2022). - Shashikumar, N. S., Sindhu, S., Madhu, M. & Gireesha, B. J. Second law analysis of MHD Carreau fluid flow through a microchannel with thermal radiation. Waves Random Complex Media https://doi.org/10.1080/17455030.2022.2060532 (2022).
- Madhu, M., Shashikumar, N. S., Thriveni, K., Gireesha, B. J. & Mahanthesh, B. Irreversibility analysis of the MHD Williamson fluid flow through a microchannel with thermal radiation. Waves Random Complex Media https://doi.org/10.1080/17455030.2022. 2111473 (2022).
- Ramesh, G. K., Madhukesh, J. K., Aly, E. H. & Pop, I. Modified Buongiorno’s model for biomagnetic hybrid nanoliquid past a permeable moving thin needle. Int. J. Num. Methods Heat Fluid Flow 32, 3551-3578 (2022).
- Alsulami, M. D., Naveen Kumar, R., Punith Gowda, R. J. & Prasannakumara, B. C. Analysis of heat transfer using Local thermal non-equilibrium conditions for a non-Newtonian fluid flow containing Ti6Al4V and AA7075 nanoparticles in a porous media. ZAMM J. Appl. Math Mech. Z Angewandte Math. Mech. 103, e202100360 (2023).
- Alhowaity, A. et al. Non-Fourier energy transmission in power-law hybrid nanofluid flow over a moving sheet. Sci Rep 12, 10406 (2022).
- Souayeh, B. Simultaneous features of CC heat flux on dusty ternary nanofluid (Graphene + Tungsten Oxide + Zirconium Oxide) through a magnetic field with slippery condition. Mathematics 11, 554 (2023).
- Ramesh, G. K., Madhukesh, J. K., Khan, U., Hussain, S. M. & Galal, A. M. Inspection of hybrid nanoparticles flow across a nonlinear/linear stretching surface when heat sink/source and thermophoresis particle deposition impacts are significant. Int. J. Mod. Phys. B 37, 2350008 (2023).
- Mahabaleshwar, U. S., Vanitha, G. P. & Souayeh, B. A study of casson viscous gas flows and heat transfer across a linear stretching/ shrinking sheet by considering induced slip, mass transpiration, inclined magnetic force, and radiation effect. BioNanoScience 13, 1052-1063 (2023).
- Dinesh Kumar, M. et al. Analysis of dynamical assisting and opposing flow characteristics of darcy surface-filled ternary nanoparticles and fourier flux: Artificial neural network and levenberg method. J. Circuit. Syst. Comp. https://doi.org/10.1142/S0218 126624400012 (2024).
- Alqahtani, A. M., Bilal, M., Ali, A., Alsenani, T. R. & Eldin, S. M. Numerical solution of an electrically conducting spinning flow of hybrid nanofluid comprised of silver and gold nanoparticles across two parallel surfaces. Sci. Rep. 13, 7180 (2023).
- Nagaraja, K. V. et al. Heat and mass transfer analysis of assisting and opposing radiative flow conveying ternary hybrid nanofluid over an exponentially stretching surface. Sci. Rep. 13, 14795 (2023).
- Alfannakh, H. & Souayeh, B. Computational assessment of
30 Karthik, K. et al. Impacts of thermophoretic deposition and thermal radiation on heat and mass transfer analysis of ternary nanofluid flow across a wedge. Int. J. Model. Simul. https://doi.org/10.1080/02286203.2023.2298234 (2024). - Madhukesh, J. K. et al. A model development for thermal and solutal transport analysis of non-newtonian nanofluid flow over a riga surface driven by a waste discharge concentration. Water 15, 2879 (2023).
- Sharma, R. P., Madhukesh, J. K., Shukla, S., Gamaoun, F. & Prasannakumara, B. C. Numerical study of the thermophoretic velocity of ternary hybrid nanofluid in a microchannel bounded by the two parallel permeable flat plates. J. Therm. Anal. Calorim. 148, 14069-14080 (2023).
- Madhura, K. R., Babitha, Kalpana, G. & Makinde, O. D. Thermal performance of straight porous fin with variable thermal conductivity under magnetic field and radiation effects. Heat Transf. 49, 5002-5019 (2020).
- Abukhaled, M. & Khuri, S. A. Efficient numerical treatment of a conductive-radiative fin with temperature-dependent thermal conductivity and surface emissivity. Int. J. Comput. Methods Eng. Sci. Mech. 21, 159-168 (2020).
- Sarwe, D. U. & Kulkarni, V. S. Thermal behaviour of annular hyperbolic fin with temperature dependent thermal conductivity by differential transformation method and Pade approximant. Phys. Scr. 96, 105213 (2021).
- Wang, K.-J. & Shi, F. A new fractal model of the convective-radiative fins with temperature-dependent thermal conductivity. Therm. Sci. 207-207 (2022).
- Kumar, R. S. V., Jagadeesha, K. C. & Prasannakumara, B. C. Heat transfer and thermal analysis in a semi-spherical fin with temperature-variant thermal properties: an application of Probabilists’ Hermite collocation method. Waves Random Complex Media https://doi.org/10.1080/17455030.2023.2198031 (2023).
- Liu, X., Wang, M., Liu, H., Chen, W. & Qian, S. Numerical analysis on heat transfer enhancement of wavy fin-tube heat exchangers for air-conditioning applications. Appl. Therm. Eng. 199, 117597 (2021).
- Song, K. et al. Thermal-hydraulic characteristic of a novel wavy fin-and-circle tube heat exchanger with concave curved vortex generators. Int. J. Heat Mass Transf. 194, 123023 (2022).
- Kumar, C. et al. Analysis of heat transfer behavior of porous wavy fin with radiation and convection by using a machine learning technique. Symmetry 15, 1601 (2023).
- Sharma, A., Ding, C., Chul Kim, S. & Chauhan, R. Investigation and optimization of solidification performance of concentration tube type latent heat storage unit with herringbone wavy fin designs. Appl. Therm. Eng. 222, 119924 (2023).
- Kumar, R. S. V., Alsulami, M. D., Sarris, I. E., Sowmya, G. & Gamaoun, F. Stochastic Levenberg-Marquardt neural network implementation for analyzing the convective heat transfer in a wavy fin. Mathematics 11, 2401 (2023).
- Das, R. & Kundu, B. Simultaneous estimation of heat generation and magnetic field in a radial porous fin from surface temperature information. Int. Commun. Heat Mass Transf. 127, 105497 (2021).
- Din, Z. U., Ali, A., De la Sen, M. & Zaman, G. Entropy generation from convective-radiative moving exponential porous fins with variable thermal conductivity and internal heat generations. Sci. Rep. 12, 1791 (2022).
- Venkitesh, V. & Mallick, A. Thermal analysis of a convective-conductive-radiative annular porous fin with variable thermal parameters and internal heat generation. J. Therm. Anal. Calorim. 147, 1519-1533 (2022).
- Kaur, P. & Singh, S. Convective radiative moving fin with temperature-dependent thermal conductivity, internal heat generation and heat transfer coefficient. Pramana J. Phys. 96, 216 (2022).
- Gireesha, B. J., Pavithra, C. G. & Keerthi, M. L. Semianalytical investigation on heat transfer in porous fins with temperaturedependent thermal conductivity via the homotopy perturbation Sumudu transform approach. Heat Transf. 53, 610-645 (2024).
- Ji, W., Qiu, W., Shi, Z., Pan, S. & Deng, S. Stiff-PINN: Physics-Informed neural network for stiff chemical kinetics. J. Phys. Chem. A 125, 8098-8106 (2021).
- Berkhahn, S. & Ehrhardt, M. A physics-informed neural network to model COVID-19 infection and hospitalization scenarios. Adv. Cont. Discr. Mod. 2022, 61 (2022).
- Chiu, P.-H., Wong, J. C., Ooi, C., Dao, M. H. & Ong, Y.-S. CAN-PINN: A fast physics-informed neural network based on coupled-automatic-numerical differentiation method. Comput. Methods Appl. Mech. Eng. 395, 114909 (2022).
- Bararnia, H. & Esmaeilpour, M. On the application of physics informed neural networks (PINN) to solve boundary layer thermalfluid problems. Int. Commun. Heat Mass Transf. 132, 105890 (2022).
- Prakash, S. B. et al. Investigation of the thermal analysis of a wavy fin with radiation impact: an application of extreme learning machine. Phys. Scr. 99, 015225 (2023).
- Poornima, B. S. et al. Evolutionary computing for the radiative-convective heat transfer of a wetted wavy fin using a genetic algorithm-based neural network. Biomimetics 8, 574 (2023).
- Khaled, A. A. Thermal performance of six different types of wavy-fins. Int. J. Num. Methods Heat Fluid Flow 25, 892-911 (2015).
- Ramesh, G. K., Manohar, G. R., Madhukesh, J. K., Venkatesh, P. & Gireesha, B. J. Thermal aspects of a radiative-convective semispherical porous fin of functionally graded material. Eur. Phys. J. Plus 139, 97 (2024).
- Madhu, J., Baili, J., Kumar, R. N., Prasannakumara, B. C. & Gowda, R. J. P. Multilayer neural networks for studying three-dimensional flow of non-Newtonian fluid flow with the impact of magnetic dipole and gyrotactic microorganisms. Phys. Scr. 98, 115228 (2023).
- Khan, M. I. et al. Neural artificial networking for nonlinear Darcy-Forchheimer nanofluidic slip flow. Appl. Nanosci. 13, 3767-3786 (2023).
- Punith Gowda, R. J., ChandrappaPrasannakumara, B., Shehzad, S. A. & Sahar, F. Blasius and Sakiadis flow of titania-copper-water based hybrid nanofluid flow: An artificial neural network modeling. Sci. Iran. https://doi.org/10.24200/sci.2023.61937.7566 (2023).
- Shoaib, M. et al. Intelligent backpropagated neural networks application on Darcy-Forchheimer ferrofluid slip flow system. Int. Commun. Heat Mass Transf. 129, 105730 (2021).
Acknowledgements
Author contributions
Competing interests
Additional information
Reprints and permissions information is available at www.nature.com/reprints.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
© The Author(s) 2024
