طريقة تشيبيشيف بيتروف-غاليركين للمعادلات التكاملية التفاضلية غير الخطية ذات النواة ذات التفرد المعتدل Chebyshev Petrov–Galerkin method for nonlinear time-fractional integro-differential equations with a mildly singular kernel

المجلة: Journal of Applied Mathematics and Computing، المجلد: 71، العدد: 3
DOI: https://doi.org/10.1007/s12190-025-02371-w
تاريخ النشر: 2025-01-23

طريقة تشيبيشيف بيتروف-غاليركين للمعادلات التكاملية التفاضلية غير الخطية ذات النواة ذات التفرد المعتدل

ي. ح. يسري (د) ⋅ أ. ج. عطاء (د)

تاريخ الاستلام: 29 أكتوبر 2024 / تاريخ المراجعة: 3 يناير 2025 / تاريخ القبول: 5 يناير 2025 /
تم النشر على الإنترنت: 23 يناير 2025
© المؤلفون 2025

الملخص

في هذه الورقة، يتم تقديم نهج جديد للمعادلات الجزئية التكاملية غير الخطية ذات الفواصل الزمنية مع نوى ضعيفة التفرد (TFPIDE). تنتج الطريقة المقترحة حلاً طيفياً شبه تحليلي باستخدام كثيرات حدود تشيبيشيف من النوع الأول المنقولة (SCP1K) كدوال أساسية. لتلبية متطلبات البداية والحدود المتجانسة، يجب اختيار مجموعة مناسبة من الدوال الأساسية. ثم يتم العثور على معاملات التوسع المجهولة باستخدام تقنية بيتروف-غاليركين. من المثير للاهتمام، أننا نحصل على معادلات دقيقة لكل من عناصر المصفوفات ذات الصلة. تتبع هذه المصفوفات نمطًا واضحًا يسهل إجراء عملية الانعكاس ويسمح بحل المشكلة الجبرية الناتجة عن تقنية بيتروف-غاليركين. تسهم هذه الدراسة في فهم أفضل لجدوى النهج من خلال فحص شامل للتقارب وتحليل الخطأ. توضح الأمثلة العددية قابلية التطبيق والدقة والكفاءة للطريقة المقترحة، مدعومة بمقارنات مع الأبحاث السابقة. تظهر النتائج مدى فعالية هذه الطريقة في حل المعادلات الجزئية التكاملية ذات الفواصل الزمنية، مما يبرز أهميتها كمساهمة مفيدة في مجال المعرفة في هذا المجال.

الكلمات الرئيسية: المعادلة الجزئية التكاملية غير الخطية ذات الفواصل الزمنية مع نواة ضعيفة التفرد • كثيرات حدود تشيبيشيف من النوع الأول • طريقة بيتروف-غاليركين ⋅ تحليل الخطأ
تصنيف موضوع الرياضيات 35R09 33D50

1 المقدمة

تعتبر الطرق الطيفية، المعروفة بدقتها وكفاءتها في مجموعة واسعة من التطبيقات، عنصرًا رئيسيًا في الحلول العددية لمعادلات التفاضل. لقد أظهر خوارزمية جاكوب-غاليركين نجاحًا كبيرًا في حل المعادلات التفاضلية الجزئية الزمنية ثنائية الأبعاد التي تواجهها الفيزياء [1]. تعتبر مخططات جاكوب-رومانوفكسي الطيفية، التي تم تصميمها خصيصًا للتعامل مع المعادلات التفاضلية عالية الرتبة، نهجًا آخر تم التحقيق فيه. لقد تم إثبات فعاليتها في الرياضيات العددية التطبيقية [2]. عند معالجة المعادلات التفاضلية الجزئية ذات الفواصل الزمنية، يثبت نهج تشيبيشيف بيتروف-غاليركين، المقدم في [3]، فائدته في معادلات الحرارة في ظروف غير محلية. تعتبر الاستراتيجية الواعدة الأخرى لمعادلات بورجرز غير الخطية ذات الفواصل الزمنية هي نهج الطيفي المودالي لتشيبيشيف بيتروف-غاليركين [4]. يوفر التحقيق في مخططات تشيبيشيف-غاليركين الصريحة استراتيجية حل فعالة لمعادلة الانتشار ذات الفواصل الزمنية [5]. تم تقديم تطبيقات ناجحة لأساليب تشيبيشيف التقدمية المنقولة لمشاكل التلغراف الخطية أحادية البعد في [6]. بالإضافة إلى ذلك، تم إثبات فعالية تقنية جاكوب التشغيلية النسبية في الرياضيات الحديثة من خلال استكشافها لمعادلات تحت الانتشار ذات الفواصل الزمنية على مجالات شبه لانهائية [7]. تم تطوير وتنفيذ خوارزمية تجميع فيجر-كوادرات من قبل يسري وعطاء [8] لحل المعادلات التكاملية التفاضلية باستخدام كثيرات حدود فيبوناتشي. بشكل جماعي، تقدم هذه التقنيات الطيفية بشكل كبير الحلول العددية لأشكال مختلفة من المعادلات التفاضلية [9-12].
تعتبر طريقة بيتروف-غاليركين الطيفية منهجية قوية ومتعددة الاستخدامات لحل مجموعة واسعة من المعادلات التفاضلية الصعبة. لقد أثبتت هذه الطريقة، التي تعتمد على اختيار دوال أساسية بعناية، أنها حاسمة في تقديم حلول دقيقة لمجموعة واسعة من النماذج الرياضية، بما في ذلك [13-16].
تتميز كثيرات حدود تشيبيشيف من النوع الأول بين مجموعة دوال الأساس بأنها مفيدة جدًا في الطرق الطيفية، مما يزيد بشكل كبير من دقة وكفاءة الحلول العددية. تعتبر هذه كثيرات الحدود ركيزة في مجال التقنيات الطيفية بسبب توافقيتها وخصائصها الطيفية [17-19]. إن تطبيقها الواسع عبر عدة مجالات علمية وتقنية يشهد على قابليتها وفعاليتها [20،21].
مؤخراً، تم التحقيق في العديد من التقنيات العددية لحل المعادلات التفاضلية التكاملية ذات الرتبة الكسرية. في مقال نُشر في مجلة الفراكتال والفواصل، قدم أكرم وآخرون [22] حلولًا عددية لمعادلة تفاضلية تكاملية غير خطية ذات رتبة كسرية مع نواة ضعيفة التفرد. بالمثل، في المجلة الصينية للفيزياء، قدم لو وآخرون [23] استراتيجية لحل معادلات مماثلة. تجمع هذه التقنية بين تحويل لابلاس ومنهج النواة القابلة للحل. بالإضافة إلى ذلك، وصفت هليوون نهجًا فعالًا باستخدام المنحنيات لحل المعادلات التكاملية التفاضلية ذات الفواصل الزمنية من قبل عباس وآخرون [24].
نركز على الموضوع الصعب للمعادلات التفاضلية التكاملية غير الخطية ذات الفواصل الزمنية التي تتميز بنوى ضعيفة التفرد في إطار بحثنا. يبدو أن طريقة بيتروف-غاليركين، المحسنة من خلال الاستخدام المدروس لكثيرات حدود تشيبيشيف من النوع الأول، هي حل قابل للتطبيق لمواجهة صعوبات هذه المعادلات. باستخدام التأثير التآزري لهذين الطريقتين، يمكن
إنشاء نهج قوي ودقيق للحل لمعادلات التفاضل التكاملية غير الخطية ذات الفواصل الزمنية مع نوى ضعيفة التفرد.
عند بدء تحقيقنا، هدفنا هو تقديم فهم شامل للمنهجية المقترحة. توفر الأقسام التالية وصفًا مفصلًا لخوارزمية بيتروف-غاليركين، بما في ذلك شرح لمبادئها الأساسية وقائمة بتطبيقاتها في حل المشكلات التفاضلية [25]. في الوقت نفسه، نشرح كيف تعمل كثيرات حدود تشيبيشيف من النوع الأول في الطرق الطيفية وكيف يمكن استخدامها لتحسين دقة وكفاءة الحلول العددية.
يركز بحثنا على المشكلات التي تقدمها المعادلات التفاضلية التكاملية غير الخطية ذات الفواصل الزمنية مع نوى ضعيفة التفرد. تمثل هذه الفئة من المعادلات منطقة حاسمة حيث تفشل الطرق التقليدية في حلها. يحاول نهجنا المقترح، الذي يجمع بعناية بين خوارزمية بيتروف-غاليركين وكثيرات حدود تشيبيشيف من النوع الأول، التغلب على هذه العوائق وتقديم إطار موثوق لاشتقاق إجابات دقيقة لهذه الحسابات الصعبة [26، 27].
ستوفر الأقسام التالية شرحًا شاملاً لنهجنا، بما في ذلك كيفية تطوير وتطبيق خوارزمية بيتروف-غاليركين، وما يميز كثيرات حدود تشيبيشيف من النوع الأول، وكيف يتم استخدامها جميعًا في سياق المعادلات التفاضلية التكاملية غير الخطية ذات الفواصل الزمنية. من خلال إجراء فحص شامل وتقديم عدة أمثلة عددية ومقارنات مع الدراسات السابقة، نهدف إلى إظهار فعالية نهجنا المقترح.
أصبح القارئ أخيرًا جاهزًا لتحليل شامل لكثيرات حدود تشيبيشيف من النوع الأول، وطريقة بيتروف-غاليركين، وتطبيقها في حل المعادلات التفاضلية التكاملية غير الخطية ذات الفواصل الزمنية مع نوى ضعيفة التفرد بفضل هذه المقدمة المطولة. تستكشف الأقسام التالية تعقيدات الطريقة المقترحة، مقدمة شرحًا شاملاً لنهجنا وأهميته في إنشاء حلول عددية لنماذج معقدة.
يمكن تلخيص الأهداف الرئيسية لهذه الدراسة كما يلي.
  • لتجنب العقبات الكامنة، تقديم طريقة جديدة لحل الفئة المعطاة من المعادلات من خلال دمج SCP1K باستخدام خوارزمية بيتروف-غاليركين.
  • فحص نهج بيتروف-غاليركين بدقة، موضحًا نظرياته الأساسية وتقديم قائمة بالمشكلات التفاضلية المختلفة التي يمكنه حلها.
  • تحديد دالة الأساس لـ SCP1K في الطرق الطيفية، مع تسليط الضوء على مرونتها في تعزيز دقة وكفاءة الحلول العددية.
  • قم بالتحقيق بعناية في الطريقة المقترحة باستخدام تحليل الأخطاء لتسليط الضوء على صحتها وموثوقيتها.
  • عرض أمثلة عددية ومقارنات مع الدراسات السابقة لإظهار الدقة والقابلية للتطبيق وفعالية النهج الموصى به.
    حسب أفضل معرفتنا، يمكن سرد المساهمة الرئيسية والجدة في هذه الورقة في النقاط التالية:
  • يتم تقديم خلفية نظرية جديدة لمجموعات SCP1K المعدلة.
  • إنشاء مصفوفات تشغيلية جديدة للمشتقات الصحيحة والكسريّة لهذه الحدود. تُعتبر هذه المصفوفات أدوات مهمة لمعالجة TFPIDE.
  • دراسة حدود الخطأ جديدة.
مزايا النهج المقدم هي كما يلي:
  • من خلال اختيار المجموعات المعدلة من SCP1K كدوال أساسية، فإن بعض الحدود من الأوضاع المحتفظ بها تجعل من الممكن إنتاج تقريبات بدقة ممتازة.
  • يتطلب الحصول على الحل التقريبي المطلوب حسابات أقل.
الورقة منظمة على النحو التالي: في القسم 2، يتم تقديم ملخص لمشتق كابوتو الكسري والتعاريف والصيغ ذات الصلة المرتبطة بـ SCP1K. يقدم القسم 3 تقنية عددية لحل TFPIDE غير الخطية باستخدام طريقة بيتروف-غاليركين الطيفية. يتم مناقشة تحليل الخطأ للتوسع المزدوج المقترح في القسم 4. يوفر القسم 5 أمثلة عددية لتوضيح النتائج النظرية. أخيرًا، يحتوي القسم 6 على الاستنتاجات.

2 المقدمات

الهدف الرئيسي من هذا القسم هو تقديم نظرة عامة على مشتق كابوتو الكسري. علاوة على ذلك، بعض العلاقات والخصائص الأساسية لـ SCP1K.

2.1 مشتق كابوتو الكسري

التعريف 1 [28] المشتق الكسرى من نوع كابوتو من الرتبة يتم تعريفه على أنه:
أين .
الخصائص التالية مُرضية من قبل المشغل لـ ،
أين هي دالة السقف و .

2.2 متعددة الحدود الشيفية من النوع الأول المنقولة

حدد الـ كـ:
الذي يفي بعلاقة التعامد التالية صالح: [29]
أين ،
و
علاقة التكرار لـ هو
أين .
علاوة على ذلك، شكل القوة وعلاقات الانعكاس لـ هم [29]
أين
اللمّا 1 [30] الصيغة التالية للربط بين كثيرات الحدود من النوع الأول من شبيشيف صحيحة:
أين هو متعدد الحدود الشيفي من النوع الثاني المنزاح وهو متعامد وفقًا للعلاقة التالية [4]:
اللمّا 2 [30] الصيغة الخطية التالية صحيحة:

3 النظام العددي

اعتبر ما يلي من TFPIDE غير الخطي:
بافتراض أن الشروط الابتدائية والحدودية هي كما يلي:
أين هو مصطلح المصدر.

3.1 دوال الأساس

افترض أن
علاقات التعامد في المعادلتين (14) و (15) هي:
و
أين كما هو موضح في (5).
النظرية 1 الصيغ التكاملية الثلاثة المفيدة التالية صحيحة:
(أ) ،
(ب) ،
أين
برهان الجزء (أ)، لدينا
ومن (9)، لدينا
الآن، بتطبيق اللمّة 2 واستخدام علاقة التعامد (4)، نحصل على النتيجة المطلوبة.
بالنسبة للجزء (ب)، لدينا
باستخدام علاقة الخطية
نحن نحصل على
الذي ينتج
باستخدام اللمّا 1، لدينا
باستخدام علاقة التعامد (16) جنبًا إلى جنب مع علاقة التعامد (11)، يتم الحصول على النتيجة المطلوبة.
الدليل للجزء (ج) يتقدم من خلال الالتزام بنفس الخطوات الموضحة في دليل الجزء (ب).
النظرية 2 الصيغتين التكاملتين المفيدتين التاليتين معطاة بواسطة
أين
و
الدليل استنادًا إلى النظرية 3 في [29]، المشتق الكسرى لـ يمكن كتابته كـ
الآن,
يمكن إعادة كتابته بعد التقييم والتبسيط في الجانب الأيمن من المعادلة الأخيرة للحصول على
أين مُعرَّف في (25).
بموجب النظرية 2 في [29]، يمكن كتابة التكامل التالي على النحو التالي
الآن,
يمكن إعادة كتابته بعد التقييم والتبسيط في الجانب الأيمن من المعادلة الأخيرة للحصول على
هذا يكمل إثبات هذا النظرية.

3.2 حل بيتروف-غاليركين لمعادلة TFPIDE غير الخطية

الآن، عرّف
ثم، أي دالة يمكن توسيعه كـ
المتبقي يمكن كتابة المعادلة (12) على النحو التالي
أحد أهم مزايا استخدام طريقة بتروف-غاليركين هو مرونتها في اختيار دوال الاختبار، بحيث يمكننا اختيار مجموعة مناسبة من الدوال التي لا تشبه مجموعة الدوال الأساسية.
الآن، اختر دالة الاختبار لتكون:
الآن، تُستخدم طريقة بيتروف-غاليركين للعثور على بحيث
أين يمكن إعادة كتابة المعادلة (36) على النحو التالي
بشكل آخر، المعادلة السابقة مكتوبة كـ
أين
ملاحظة 1 العناصر و مقدمة في النظريتين 1 و 2.
ملاحظة 2 المعادلة (38) تولد نظام من المعادلات الجبرية غير الخطية في معاملات التوسع المجهولة والتي يمكن حلها باستخدام طريقة نيوتن التكرارية.
ملاحظة 3 التحويل التالي
أين من الضروري جدًا تحويل (12) مع شروط ابتدائية وحدودية غير متجانسة
إلى المعادلة في (12) مع شروط حدودية وبدائية متجانسة.

4 تحليل الأخطاء

في هذا القسم، يتم إجراء تحليل للخطأ للطريقة المقترحة. يثبت اللمّة 3 أن دالة معبرًا عنه كسلسلة مزدوجة من حيث دوال الأساس و يتقارب بشكل موحد إلى الدالة ويقدم حدًا تقاربيًا على معاملات التوسع. استنادًا إلى ذلك، يمتد النظرية 3 إلى نتيجة لدالة موزونة. ، والذي يتم توسيعه بشكل مشابه في قاعدة جديدة. يعتمد إثبات النظرية 3 على نتائج اللمحة 3 لإثبات التقارب المنتظم وحدود تقارب مماثلة لمعاملات التوسع. أخيرًا، تستنتج النظرية 4 تقدير خطأ الاقتطاع لتوسع السلسلة من ، مما يظهر أن الخطأ يتناقص مع ، حيث هو معامل الاقتطاع. يستخدم الإثبات حدودًا على دوال الأساس الجديدة ونتائج سابقة من الأدبيات.
اللمّا 3 [31] اعتبر الدالة ، حيث بحيث أن و مقيدون لبعض و يتم توسيعه كـ
السلسلة أعلاه تتقارب بشكل موحد إلى علاوة على ذلك، فإن معاملات التمدد في (42) تلبي:
النظرية 3 اعتبر الدالة بحيث أن و مقيدون لبعض و يتم توسيعه كـ
السلسلة أعلاه تتقارب بشكل موحد إلى علاوة على ذلك، فإن معاملات التوسع في (44) تلبي:
برهان باستخدام تعريف دالة الأساس في المعادلتين (14) و (15)، يمكننا كتابة
الآن، تتيح لنا Lemma3 الحصول على المتباينة التالية
النظرية 4: تقدير خطأ الاقتطاع التالي صالح
الدليل يمكن الحصول على دليل هذا theorem بسهولة بعد استخدام خطوات مشابهة كما في [31]، جنبًا إلى جنب مع عدمين و .

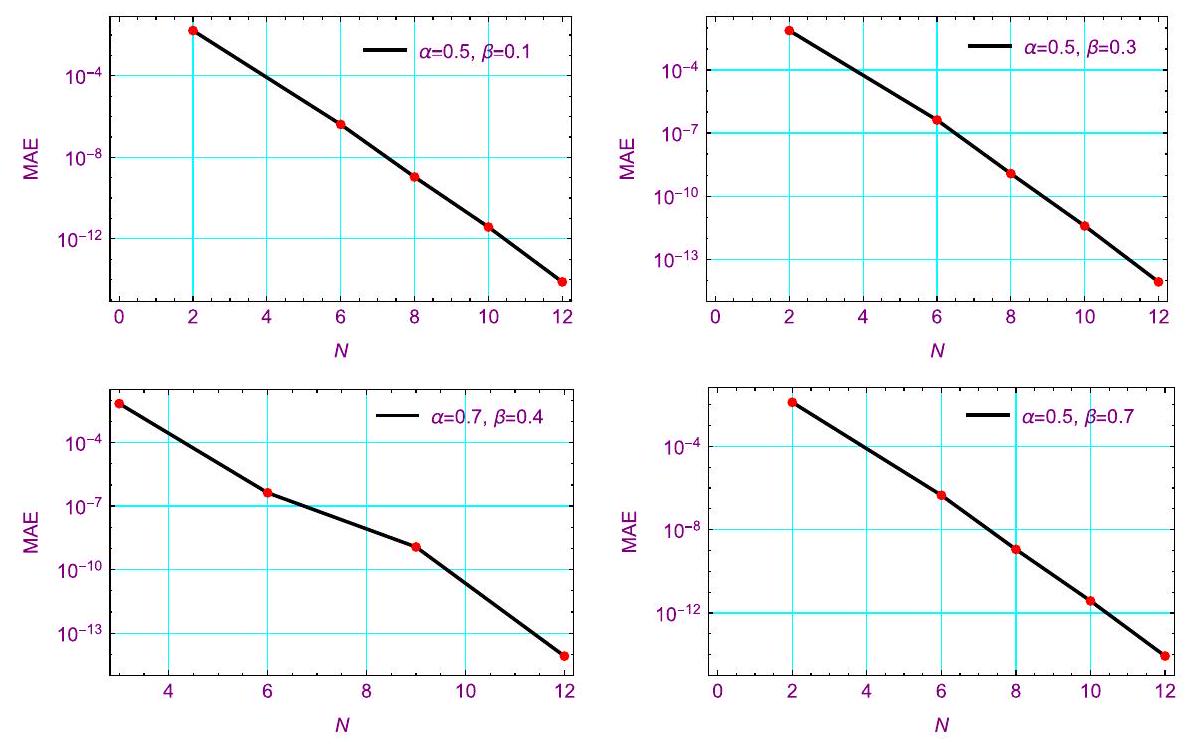
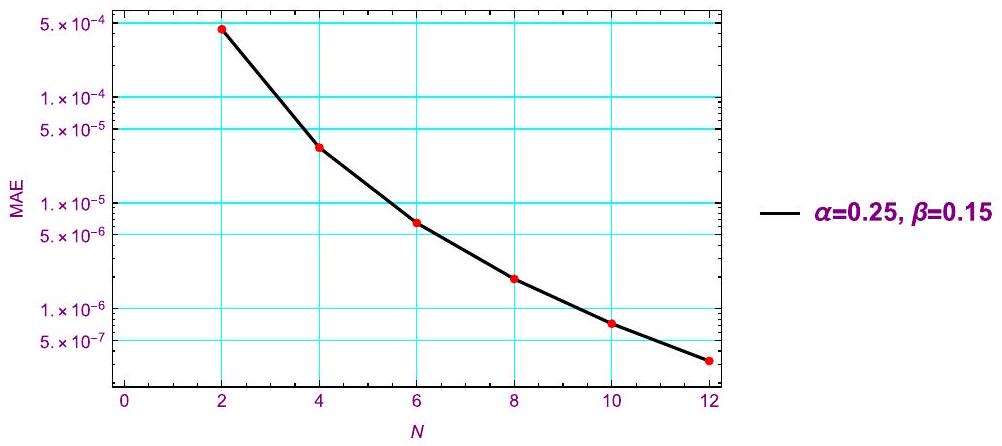
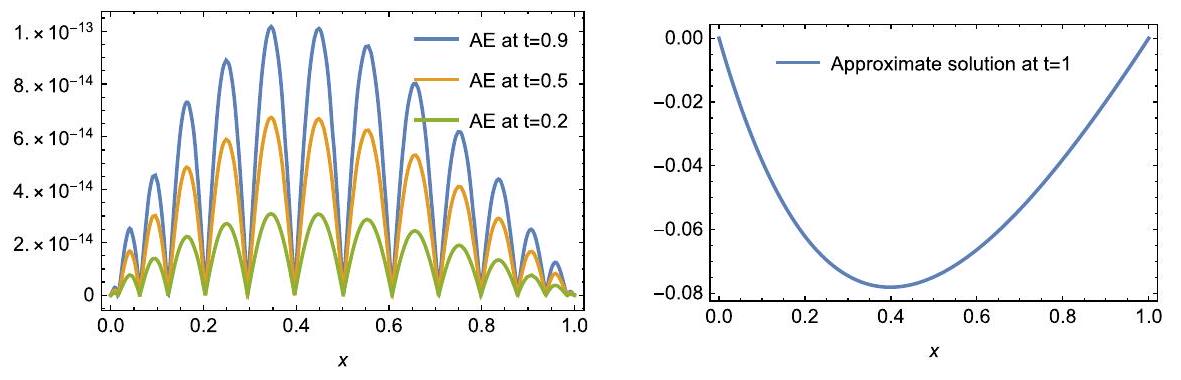
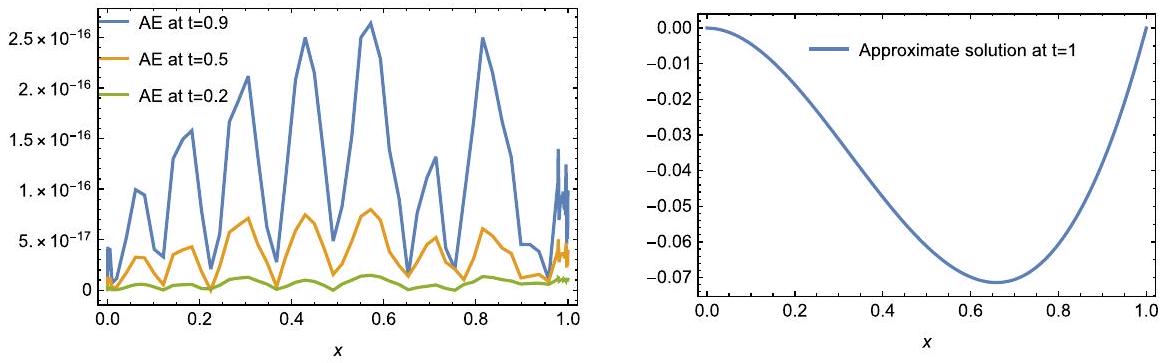
5 أمثلة توضيحية

مثال 1 [32] اعتبر TFPIDE غير الخطي التالي
بالإضافة إلى الشروط الابتدائية والحدودية التالية:
الجدول 1 مقارنة بـ -خطأ في المثال 1 عند
طريقتنا في الطريقة في [32]
الجدول 2 وقت وحدة المعالجة المركزية لنتائجنا في الجدول 1
١٤٠.٩٥٣ ١٣٣.٦٢٦ 131.668 ١٣٢٫٦٨٩
الشكل 1 متوسط الخطأ المطلق في المثال 1
أين
الحل الدقيق لهذه المشكلة هو في الجدول 1، نقدم مقارنة لـ -خطأ بين طريقتنا والطريقة في [32] عند قيم مختلفة من و تظهر الجدول 2 الوقت المستغرق لوحدة المعالجة المركزية في نتائجنا في الجدول 1. توضح الشكل 1 الحد الأقصى للخطأ المطلق (MAE) عند قيم مختلفة من و عند قيم مختلفة من
الجدول 3 مقارنة لـ -خطأ في المثال 2 عند
طريقتنا في الطريقة في [32]
الجدول 4 وقت وحدة المعالجة المركزية لنتائجنا في الجدول 3
١٤٥.٩٠٨ 141.503 ١٣٩٫٧٦٨ ١٤٤.١٥٢
. تشير هذه الرقم إلى ميزة طريقتنا في الحصول على MAE عند القيم الصغيرة لـ .
مثال 2 [32] اعتبر TFPIDE غير الخطي التالي
بالإضافة إلى الشروط الابتدائية والحدودية التالية:
أين
الحل الدقيق لهذه المشكلة هو في الجدول 3، نقدم مقارنة لـ -خطأ بين طريقتنا والطريقة في [32] عند قيم مختلفة من و يوضح الجدول 4 الوقت المستغرق لوحدة المعالجة المركزية في نتائجنا في الجدول 3. يوضح الشكل 2 متوسط الخطأ المطلق (MAE) عند و عند قيم مختلفة من . تشير هذه الرقم إلى ميزة طريقتنا في الحصول على MAE عند القيم الصغيرة لـ .
الشكل 2 متوسط الخطأ المطلق في المثال 2
المثال 3 [32] اعتبر ما يلي TFPIDE غير الخطي
بالإضافة إلى الشروط الابتدائية والحدودية التالية:
أين
الحل الدقيق لهذه المشكلة هو في الجدول 5، نقدم مقارنة لـ -خطأ بين طريقتنا والطريقة في [32] عند قيم مختلفة من و تظهر الجدول 6 الوقت المستغرق لوحدة المعالجة المركزية لنتائجنا في الجدول 5. توضح الشكل 3 الخطأ المطلق عند قيم مختلفة من (يسار) والحل التقريبي عند (يمين) عند و . تشير هذه الصورة إلى ميزة طريقتنا في الحصول على MAE عند القيم الصغيرة لـ .
الجدول 5 مقارنة بـ -خطأ المثال 3
طريقتنا في الطريقة في [32]
الجدول 6 وقت وحدة المعالجة المركزية لنتائجنا في الجدول 5
234.892 231.752 234.892 238.262
الشكل 3 AE عند قيم مختلفة من (يسار) والحل التقريبي عند (يمين) عند و من المثال 3
المثال 4 اعتبر المعادلة غير الخطية TFPIDE التالية
بالإضافة إلى الشروط الأولية والحدودية التالية:
حيث
الشكل 4 AE عند قيم مختلفة من (يسار) والحل التقريبي عند (يمين) عند و من المثال 4
الشكل 5 AE عند قيم مختلفة من عند (يسار) و (يمين) عند من المثال 4
الجدول 7 AE من المثال 4 عند
طريقتنا عند
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
الحل الدقيق لهذه المشكلة هو . الشكل 4 يوضح AE عند قيم مختلفة من (يسار) والحل التقريبي عند (يمين) عند 0.7 و . الشكل 5 يوضح AE عند قيم مختلفة من عند (يسار) و (يمين) عند . الجدول 7، يقدم AE عند عندما و عند قيم مختلفة من .

6 ملاحظات ختامية

في الختام، قدمت هذه الورقة نهجًا جديدًا وفعالًا لمعالجة TFPIDE. لقد أظهرت المنهجية المقترحة، التي تعتمد على SCP1K كدوال أساسية، قدرتها على إنتاج حلول شبه تحليلية طيفية. يضمن الاختيار الدقيق لمجموعة مناسبة من الدوال الأساسية تلبية الشروط الأولية والحدودية المتجانسة. كانت الاستفادة من تقنية بيتروف-غاليركين في تحديد معاملات التوسع المجهولة عنصرًا رئيسيًا في نهجنا. من الجدير بالذكر بشكل خاص الدقة التي تم تحقيقها في الحصول على معادلات صريحة لكل عنصر من العناصر المعنية. تظهر هذه المصفوفات نمطًا واضحًا، مما يسهل عملية الانعكاس ويمكّن من حل المشكلة الجبرية الناتجة عن تقنية بيتروف-غاليركين. تسهم هذه العمل بشكل كبير في تعزيز فهمنا لموثوقية هذا النهج. توفر الفحوصات الدقيقة للتقارب وتحليلات الخطأ رؤى قيمة حول متانة المنهجية المقترحة. تؤكد الأمثلة العددية المقدمة على قابلية التطبيق والدقة والكفاءة للتقنية المقترحة، مما يقدم عرضًا عمليًا لفعاليتها مقارنةً بالأبحاث السابقة. تؤكد النتائج على كفاءة الطريقة في حل المعادلات الجزئية التكاملية الزمنية، مما يبرز مساهمتها القيمة في مجموعة المعرفة الحالية في هذا المجال المتخصص. بينما نختتم، يقف النهج المقدم كإضافة ملحوظة إلى ترسانة المنهجيات لمعالجة المشكلات الرياضية الصعبة، واعدًا بتقدم مستمر في مجال الحلول العددية للمعادلات التفاضلية. كعمل مستقبلي متوقع، نهدف إلى استخدام النتائج النظرية المطورة في هذه الورقة جنبًا إلى جنب مع طرق طيفية مناسبة لمعالجة بعض المشكلات الأخرى. تم كتابة جميع الأكواد وتصحيحها بواسطة Mathematica 11 على محطة العمل HP Z420، المعالج: Intel (R) Xeon(R) CPU E5-1620 v2 – 3. رام DDR3، و512 جيجابايت من التخزين.
الشكر غير قابل للتطبيق.
مساهمات المؤلفين ساهم YHY وAGA بالتساوي في العمل.
التمويل تم توفير تمويل الوصول المفتوح من قبل هيئة تمويل العلوم والتكنولوجيا والابتكار (STDF) بالتعاون مع البنك المصري للمعرفة (EKB). لا تتلقى هذه البحث أي تمويل.
توفر البيانات لا توجد بيانات مرتبطة بهذه البحث.

الإعلانات

تضارب المصالح يعلن المؤلفون أنهم ليس لديهم تضارب في المصالح.
موافقة الأخلاقيات والموافقة على المشاركة غير قابلة للتطبيق.
الوصول المفتوح هذه المقالة مرخصة بموجب رخصة المشاع الإبداعي للاستخدام والمشاركة والتكيف والتوزيع وإعادة الإنتاج في أي وسيلة أو شكل، طالما أنك تعطي الائتمان المناسب للمؤلفين الأصليين والمصدر، وتوفر رابطًا لرخصة المشاع الإبداعي، وتوضح ما إذا كانت هناك تغييرات قد تم إجراؤها. الصور أو المواد الأخرى من طرف ثالث في هذه المقالة مشمولة في رخصة المشاع الإبداعي للمقالة، ما لم يُشار إلى خلاف ذلك في سطر ائتمان للمادة. إذا لم تكن المادة مشمولة في رخصة المشاع الإبداعي للمقالة واستخدامك المقصود غير مسموح به
بموجب اللوائح القانونية أو يتجاوز الاستخدام المسموح به، ستحتاج إلى الحصول على إذن مباشرة من صاحب حقوق الطبع والنشر. لعرض نسخة من هذه الرخصة، قم بزيارةhttp://creativecommons.org/licenses/by/4.0/.

References

  1. Ghanbari, F., Ghanbari, K., Mokhtary, P.: Generalized Jacobi-Galerkin method for nonlinear fractional differential algebraic equations. Comput. Appl. Math. 37, 5456-5475 (2018)
  2. Zaky, M.A., Abo-Gabal, H., Hafez, R.M., Doha, E.H.: Computational and theoretical aspects of Romanovski-Bessel polynomials and their applications in spectral approximations. Numer. Algor. 89, 1-35 (2022)
  3. Youssri, Y.H., Ismail, M., Atta, A.G.: Chebyshev Petrov-Galerkin procedure for the time-fractional heat equation with nonlocal conditions. Phys. Scr. 99(1), 015251 (2024)
  4. Youssri, Y.H., Atta, A.G.: Modal spectral Tchebyshev Petrov-Galerkin stratagem for the time-fractional nonlinear Burgers’ equation. Iran. J. Numer. Anal. Optim. 14(1), 1 (2024)
  5. Moustafa, M., Youssri, Y.H., Atta, A.G.: Explicit Chebyshev-Galerkin scheme for the time-fractional diffusion equation. Int. J. Mod. Phys. C 35(1), 2450002 (2024)
  6. Atta, A.G., Youssri, Y.H.: Shifted second-kind Chebyshev spectral collocation-based technique for time-fractional KdV-Burgers’ equation. Iran. J. Math. Chem. 14(4), 207-224 (2023)
  7. Hafez, R.M., Youssri, Y.H., Atta, A.G.: Jacobi rational operational approach for time-fractional subdiffusion equation on a semi-infinite domain. Contemp. Math. 4(4), 853-876 (2023)
  8. Youssri, Y.H., Atta, A.G.: Fejér-Quadrature collocation algorithm for solving fractional integrodifferential equations via Fibonacci polynomials. Contemp. Math. 5(1), 296-308 (2024)
  9. Zheng, W., Chen, Y., Zhou, J.: A Legendre spectral method for multidimensional partial Volterra integro-differential equations. J. Comput. Appl. Math. 436, 115302 (2024)
  10. Tu, H., Wang, Y., Zhang, Y., Liao, H., Liu, W.: Parallel numerical simulation of weakly range-dependent ocean acoustic waveguides by adiabatic modes based on a spectral method. Phys. Fluids 35(1), 017119 (2023)
  11. Tu, H., Wang, Y., Yang, C., Liu, W., Wang, X.: A Chebyshev-Tau spectral method for coupled modes of underwater sound propagation in range-dependent ocean environments. Phys. Fluids 35(3), 037113 (2023)
  12. Konoplya, R.A., Zhidenko, A.: Bernstein spectral method for quasinormal modes of a generic black hole spacetime and application to instability of dilaton-de Sitter solution. Phys. Rev. D. 107(4), 044009 (2023)
  13. Youssri, Y.H., Atta, A.G.: Radical Petrov-Galerkin approach for the time-fractional KdV-Burgers’ equation. Math. Comput. Appl. 29(6), 107 (2024)
  14. Youssri, Y.H., Atta, A.G., Abu Waar, Z.Y., Moustafa, M.O.: Petrov-Galerkin method for small deflections in fourth-order beam equations in civil engineering. Nonlinear Eng. 13(1), 20240022 (2024)
  15. Kharazmi, E., Zayernouri, M., Em Karniadakis, G.: A Petrov-Galerkin spectral element method for fractional elliptic problems. Comput. Methods Appl. Mech. Eng. 324, 512-536 (2017)
  16. Hafez, R.M., Zaky, M.A., Hendy, A.S.: A novel spectral Galerkin/Petrov-Galerkin algorithm for the multi-dimensional space-time fractional advection-diffusion-reaction equations with nonsmooth solutions. Math. Comput. Simul. 190, 678-690 (2021)
  17. Wang, M., Au, F.T.K.: Precise integration methods based on the Chebyshev polynomial of the first kind. Earthq. Eng. Eng. Vib. 7(2), 207-216 (2008)
  18. Ahmed, H.M.: Numerical Solutions for Singular Lane-Emden Equations Using Shifted Chebyshev Polynomials of the First Kind. Contemp. Math. 4, 132-149 (2023)
  19. Abd-Elhameed, W.M., Youssri, Y.H., Atta, A.G.: Tau algorithm for fractional delay differential equations utilizing seventh-kind Chebyshev polynomials. J. Math. Model. 12, 277-299 (2024)
  20. Lebedev, V.I., Finogenov, S.A.: Some algorithms for computing Chebyshev normalized first-kind polynomials by roots. Russ. J. Numer. Anal. Math. Model. 20(4), 353-363 (2005)
  21. Shoukralla, E.S.: Application of Chebyshev polynomials of the second kind to the numerical solution of weakly singular Fredholm integral equations of the first kind. IAENG Int. J. Appl. Math. 51(1), 1-16 (2021)
  22. Akram, T., Ali, Z., Rabiei, F., Shah, K., Kumam, P.: A numerical study of nonlinear fractional order partial integro-differential equation with a weakly singular kernel. Fract. Fract. 5(3), 85 (2021)
  23. Loh, J.R., Phang, C., Tay, K.G.: New method for solving fractional partial integro-differential equations by combination of Laplace transform and resolvent kernel method. Chin. J. Phys. 67, 666-680 (2020)
  24. Abbas, M., Aslam, S., Abdullah, F.A., Riaz, M.B., Gepreel, K.A.: An efficient spline technique for solving time-fractional integro-differential equations. Heliyon 9(9), e19307 (2023)
  25. Atta, A.G., Abd-Elhameed, W.M., Moatimid, G.M., Youssri, Y.H.: Modal shifted fifth-kind Chebyshev Tau integral approach for solving heat conduction equation. Fract. Fract. 6(11), 619 (2022)
  26. Abdelghany, E.M., Abd-Elhameed, W.M., Moatimid, G.M., Youssri, Y.H., Atta, A.G.: A tau approach for solving time-fractional heat equation based on the shifted sixth-kind Chebyshev polynomials. Symmetry 15(3), 594 (2023)
  27. Atta, A.G., Abd-Elhameed, W.M., Moatimid, G.M., Youssri, Y.H.: Novel spectral schemes to fractional problems with nonsmooth solutions. Math. Methods Appl. Sci. 46(13), 14745-14764 (2023)
  28. Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Elsevier, San Diego (1998)
  29. Atta, A.G., Youssri, Y.H.: Advanced shifted first-kind Chebyshev collocation approach for solving the nonlinear time-fractional partial integro-differential equation with a weakly singular kernel. Comput. Appl. Math. 41(8), 381 (2022)
  30. Mason, J.C., Handscomb, D.C.: Chebyshev Polynomials. Chapman and Hall, New York (2002)
  31. Youssri, Y.H., Atta, A.G.: Double Tchebyshev spectral Tau algorithm for solving KdV equation, with soliton application. In: Solitons, pp. 451-467. Springer (2022)
  32. Alavi, J., Aminikhah, H.: An efficient parametric finite difference and orthogonal spline approximation for solving the weakly singular nonlinear time-fractional partial integro-differential equation. Comput. Appl. Math. 42(8), 350 (2023)
Publisher’s Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
  1. Y. H. Youssri
    youssri@cu.edu.eg
    A. G. Atta
    ahmed_gamal@edu.asu.edu.eg
    1 Department of Mathematics, Faculty of Science, Cairo University, Giza 12613, Egypt
    2 Department of Mathematics, Faculty of Education, Ain Shams University, Roxy, Cairo 11341, Egypt

Journal: Journal of Applied Mathematics and Computing, Volume: 71, Issue: 3
DOI: https://doi.org/10.1007/s12190-025-02371-w
Publication Date: 2025-01-23

Chebyshev Petrov-Galerkin method for nonlinear time-fractional integro-differential equations with a mildly singular kernel

Y. H. Youssri (D) ⋅ A. G. Atta (D)

Received: 29 October 2024 / Revised: 3 January 2025 / Accepted: 5 January 2025 /
Published online: 23 January 2025
© The Author(s) 2025

Abstract

In this paper, a new approach to time-fractional partial integro-differential equations with weakly singular kernels (TFPIDE) is presented. The suggested method produces a spectral semi-analytic solution by using shifted first-kind Chebyshev polynomials (SCP1K) as basis functions. To satisfy homogeneous beginning and boundary requirements, a suitable collection of basis functions should be chosen. The unknown expansion coefficients are then found using the Petrov-Galerkin technique. Interestingly, we obtain precise equations for each of the related matrices’ elements. These matrices follow a clear pattern that facilitates the inversion procedure and allows the algebraic problem generated by the Petrov-Galerkin technique to be solved. The work contributes to a better knowledge of the dependability of the approach by thoroughly examining convergence and error analysis. Numerical examples demonstrate the applicability, accuracy, and efficiency of the suggested technique, supplemented by comparisons with previous research. The outcomes demonstrate how well this method works for solving time fractional partial integro-differential equations, highlighting its importance as a useful contribution to the body of knowledge in the area.

Keywords Nonlinear time-fractional partial integro-differential equation with weakly singular kernel • First-kind Chebyshev polynomials • Petrov-Galerkin method ⋅ Error analysis
Mathematics Subject Classification 35R09 33D50

1 Introduction

Spectral methods which are well-known for their accuracy and efficiency in a wide range of applications-are a major component of differential equation numerical solutions. The Jacobi-Galerkin algorithm has demonstrated considerable success in solving two-dimensional time-dependent partial differential equations encountered in physics [1]. Romanovski-Jacobi spectral schemes, which are specifically designed to handle high-order differential equations, are another approach that has been investigated. Their efficacy in applied numerical mathematics has been demonstrated [2]. Addressing time-fractional partial differential equations, the Chebyshev Petrov-Galerkin approach, given in [3], establishes its usefulness in heat equations with nonlocal circumstances. Another promising strategy for time-fractional nonlinear Burgers’ equations is the modal spectral Tchebyshev Petrov-Galerkin approach [4]. Investigating explicit Chebyshev-Galerkin schemes provides an effective solution strategy for the time-fractional diffusion equation [5]. Successful applications of advanced shifted Chebyshev tau approaches to linear one-dimensional hyperbolic telegraph-type problems are presented in [6]. Additionally, the effectiveness of the Jacobi rational operational technique in modern mathematics is demonstrated by exploring it for time-fractional sub-diffusion equations on semi-infinite domains [7]. The Fejér-quadrature collocation algorithm is developed and implemented by Youssri and Atta [8] to solve fractional integro-differential equations using Fibonacci polynomials. Collectively, these spectral techniques significantly advance numerical solutions for various differential equation forms [9-12].
The Petrov-Galerkin spectral approach is a powerful and versatile methodology for solving a wide range of difficult differential equations. This method, which is based on carefully selecting basis functions, has proven critical in giving precise solutions for a wide range of mathematical models, including [13-16].
First-kind Chebyshev polynomials stand out among the armor of basis functions as being very useful in spectral approaches, greatly increasing the accuracy and efficiency of numerical solutions. These polynomials are a mainstay in the field of spectral techniques due to their orthogonality and spectral characteristics [17-19]. Their extensive application across several scientific and technical fields attests to their adaptability and effectiveness [20,21].
Recently, numerous numerical techniques for solving fractional-order partial integro-differential equations have been investigated. In an article published in the Fractal and Fractional journal, Akram et al. [22] presented numerical solutions for a nonlinear fractional-order partial integro-differential equation with a weakly singular kernel. Similarly, in the Chinese Journal of Physics, Loh et al. [23] presented a strategy for resolving comparable equations. This technique combines the Laplace transform with the resolvent kernel approach. Additionally, Heliyon described an efficient spline approach for solving time-fractional integro-differential equations by Abbas et al. [24].
We concentrate on the difficult topic of weakly singular kernel-characterized nonlinear time-fractional partial integro-differential equations in the framework of our research. The Petrov-Galerkin method, improved by the deliberate employment of first-kind Chebyshev polynomials, appears to be a viable solution to solving the difficulties of these equations. Using the synergistic impact of these two methods, it is
possible to create a strong and exact solution approach for nonlinear time-fractional partial integro-differential equations with weakly singular kernels.
As we begin our inquiry, our goal is to provide a complete understanding of the proposed methodology. The next sections provide an in-depth description of the Petrov-Galerkin algorithm, including an explanation of its underlying principles and a list of its applications in differential problem resolution [25]. Simultaneously, we explain how first-kind Chebyshev polynomials work in spectral approaches and how they can be used to improve the precision and efficacy of numerical solutions.
Our research focuses on the problems that nonlinear time-fractional partial integrodifferential equations with weakly singular kernels provide. This class of equations represents a critical area where typical methods of solving them fail. Our proposed approach, which carefully combines the Petrov-Galerkin algorithm with first-kind Chebyshev polynomials, tries to overcome these shortcomings and provide a dependable framework for deriving accurate answers to these difficult calculations [26, 27].
The sections that follow will provide a thorough explanation of our approach, including how the Petrov-Galerkin algorithm is developed and applied, what distinguishes first-kind Chebyshev polynomials, and how they are all used in the context of nonlinear time-fractional partial integro-differential equations. By conducting a thorough examination and providing several numerical examples and comparisons to previous studies, we want to show the effectiveness of our suggested approach.
The reader is finally ready for a thorough analysis of first-kind Chebyshev polynomials, the Petrov-Galerkin method, and their application to the solution of nonlinear time-fractional partial integro-differential equations with weakly singular kernels thanks to this extended introduction. The ensuing sections explore the complexities of the suggested method, offering a thorough explanation of our approach and its importance in the creation of numerical solutions for intricate models.
The main goals of this study may be summed up as follows.
  • To avoid inherent obstacles, provide a novel method for resolving the given class of equations by integrating SCP1K using the Petrov-Galerkin algorithm.
  • Examine the Petrov-Galerkin approach thoroughly, outlining its basic theories and presenting a list of the various differential problems it may solve.
  • Define the basis function of SCP1K in spectral approaches, highlighting their flexibility in enhancing the accuracy and efficiency of numerical solutions.
  • Carefully investigate the suggested method using error analysis to shed light on its correctness and dependability.
  • Exhibit numerical examples and comparisons with earlier studies to demonstrate the precision, applicability, and efficacy of the recommended approach.
    To the best of our knowledge, the main contribution and novelty of this paper can be listed in the following points:
  • A new theoretical background to the modified sets of SCP1K are presented.
  • Establishing new operational matrices of integer and fractional derivatives for these polynomials. These matrices are considered important tools for treating TFPIDE.
  • The study of the error bound is new.
The advantages of the presented approach are as follows:
  • By choosing the modified sets of SCP1K as basis functions, a few terms of the retained modes make it possible to produce approximations with excellent precision.
  • Less calculation is required to obtain the desired approximate solution.
The paper is organized as follows: In Sect. 2, a summary of the Caputo fractional derivative and relevant definitions and formulas associated with the SCP1K are presented. Section 3 introduces a numerical technique for solving the nonlinear TFPIDE using the spectral Petrov-Galerkin method. The error analysis of the proposed double expansion is discussed in Sect.4. Section 5 provides numerical examples to illustrate the theoretical results. Lastly, Sect. 6 contains the conclusions.

2 Preliminaries

The principle aim of this sectionis to provide an overview of the Caputo fractional derivative. Furthermore, some essential relations and properties of SCP1K.

2.1 Caputo fractional derivative

Definition 1 [28] The Caputo fractional derivative of order is defined as:
where .
The following properties are satisfied by the operator for ,
where is the ceiling function and .

2.2 Shifted first-kind Chebyshev polynomials

Define the as:
that satisfy the following orthogonality relation is valid: [29]
where ,
and
The recurrence relation of is
where .
Moreover, the power form and inversion relations of are [29]
where
Lemma 1 [30] The following connection formula between first-kind Chebyshev polynomials is valid:
where is the shifted second-kind Chebyshev polynomial and is orthogonal according to the following relation [4]:
Lemma 2 [30] The following linearization formula is valid:

3 The numerical scheme

Consider the following nonlinear TFPIDE:
assuming that the initial and boundary conditions are as follows:
where is the source term.

3.1 Basis functions

Assume that
The orthogonality relations of Eqs. (14) and (15) are:
and
where is as given in (5).
Theorem 1 The following three useful integral formulas are valid:
(a) ,
(b) ,
where
Proof For part (a), we have
and from (9), we have
Now, applying Lemma 2 and using the orthogonality relation (4), we obtain the desired result.
For part (b), we have
Using the linearization relation
we get
which yields
Using Lemma 1, we have
Using the orthogonality relation (16) along with the orthogonality relation (11), the desired result is obtained.
The proof for Part (c) proceeds by adhering to the same steps outlined in the proof of Part (b).
Theorem 2 the following two useful integral formulas are given by
where
and
Proof Based on Theorem 3 in [29], the fractional derivative of can be written as
Now,
that can be rewritten after evaluating and simplifying , in the right-hand side of the last equation to get
where is defined in (25).
By virtue of Theorem 2 in [29], the following integral can be written as
Now,
that can be rewritten after evaluating and simplifying , in the right-hand side of the last equation to get
This completes the proof of this theorem.

3.2 Petrov-Galerkin solution for nonlinear TFPIDE

Now, define
then, any function can be expanded as
The residual of Eq. (12) can be written as
One of the most important advantages of using Petrov-Galerkin method is its flexibility in choosing test functions, so we can choose the appropriate set of functions that is not similar to the set of basis functions.
Now, choose the test function to be:
Now, the Petrov-Galerkin method is used to find such that
where . Equation (36) can be rewritten as
in another form, the previous equation written as
where
Remark 1 The elements and are given in Theorems 1 and 2.
Remark 2 Equation (38), generates system of nonlinear algebraic equations in the unknown expansion coefficients , which can be solved using Newton’s iterative method.
Remark 3 The following transformation
where , is very essential to convert (12) with non-homogeneous initial and boundary conditions
to the equation in (12) with homogeneous boundary and initial conditions.

4 Error analysis

In this section, an error analysis for the proposed method is conducted. Lemma 3 establishes that a function expressed as a double series in terms of basis functions and converges uniformly to the function and provides an asymptotic bound on the expansion coefficients. Building upon this, Theorem 3 extends the result to a weighted function , which is similarly expanded in a new basis. The proof of Theorem 3 leverages the results of Lemma 3 to establish uniform convergence and a similar asymptotic bound for the coefficients of the expansion. Finally, Theorem 4 derives a truncation error estimate for the series expansion of , showing that the error decreases as , where is the truncation parameter. The proof utilizes bounds on the new basis functions and prior results from the literature.
Lemma 3 [31] Consider the function , where , such that and are bounded for some and is expanded as
The above series is uniformly convergent to . Moreover, the expansion coefficients in (42) satisfy:
Theorem 3 Consider the function , such that and are bounded for some and is expanded as
The above series is uniformly convergent to . Moreover, the expansion coefficients in (44) satisfy:
Proof With the aid of the definition of basis function in Eqs. (14) and (15), we can write
Now, Lemma3 enables us to get the following inequality
Theorem 4 The following truncation error estimate is valid
Proof The proof of this theorem can be easily obtained after using similar steps as in [31], along with the two inequality and .

5 Illustrative examples

Example 1 [32] Consider the following nonlinear TFPIDE
along with the following initial and boundary conditions:
Table 1 Comparison of -error of Example 1at
Our method at Method in [32]
Table 2 CPU time of our results in Table 1
140.953 133.626 131.668 132.689
Fig. 1 The MAE of Example 1
where
The exact solution of this problem is . In Table 1, we give a comparison of -error between our method and method in [32] at different values of and . Table 2 shows the CPU time used of our results in Table 1. Figure 1 shows the maximum absolute error (MAE) at different values of and at different values of
Table 3 Comparison of -error of Example 2at
Our method at Method in [32]
Table 4 CPU time of our results in Table 3
145.908 141.503 139.768 144.152
. This figure indicates the advantage of our method for obtaining the MAE at small values of .
Example 2 [32] Consider the following nonlinear TFPIDE
along with the following initial and boundary conditions:
where
The exact solution of this problem is . In Table 3, we give a comparison of -error between our method and method in [32] at different values of and . Table 4 shows the CPU time used of our results in Table 3. Figure 2 shows the MAE at and at different values of . This figure indicates the advantage of our method for obtaining the MAE at small values of .
Fig. 2 The MAE of Example 2
Example 3 [32] Consider the following nonlinear TFPIDE
along with the following initial and boundary conditions:
where
The exact solution of this problem is . In Table 5, we give a comparison of -error between our method and method in [32] at different values of and . Table 6 shows the CPU time used of our results in Table 5. Figure 3 shows the AE at different values of (left) and approximate solution at (right) at and . This figure indicates the advantage of our method for obtaining the MAE at small values of .
Table 5 Comparison of -error of Example 3
Our method at Method in [32]
Table 6 CPU time of our results in Table 5
234.892 231.752 234.892 238.262
Fig. 3 The AE at different values of (left) and approximate solution at (right) at and of Example3
Example 4 Consider the following nonlinear TFPIDE
along with the following initial and boundary conditions:
where
Fig. 4 The AE at different values of (left) and approximate solution at (right) at and of Example 4
Fig. 5 The AE at different values of at (left) and (right) at of Example 4
Table 7 AE of Example 4 at
Our method at
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
The exact solution of this problem is . Figure 4 shows the AE at different values of (left) and approximate solution at (right) at 0.7 and . Figure 5 shows the AE at different values of at (left) and (right) at . Table 7, presents the AE at when and at different values of .

6 Concluding remarks

In conclusion, this paper has introduced a novel and effective approach to address TFPIDE. The proposed methodology, relying on SCP1K as basis functions, has demonstrated its capability to produce spectral semi-analytic solutions. The careful selection of a suitable collection of basis functions ensures the satisfaction of homogeneous initial and boundary conditions. The utilization of the Petrov-Galerkin technique in determining unknown expansion coefficients has been a key component of our approach. Particularly noteworthy is the precision achieved in obtaining explicit equations for each element of the involved matrices. These matrices exhibit a discernible pattern, streamlining the inversion process and enabling the solution of the algebraic problem generated by the Petrov-Galerkin technique. The work contributes significantly to enhancing our understanding of the reliability of this approach. Thorough examinations of convergence and error analyses provide valuable insights into the robustness of the proposed methodology. The presented numerical examples further validate the applicability, accuracy, and efficiency of the suggested technique, offering a practical demonstration of its effectiveness in comparison with previous research. The outcomes underscore the method’s proficiency in solving time fractional partial integro-differential equations, emphasizing its valuable contribution to the existing body of knowledge in this specialized area. As we conclude, the presented approach stands as a noteworthy addition to the arsenal of methodologies for tackling challenging mathematical problems, promising continued advancements in the field of numerical solutions for differential equations. As an expected future work, we aim to employ the developed theoretical results in this paper along with suitable spectral methods to treat some other problems. All codes were written and debugged by Mathematica 11 on HP Z420 Workstation, Processor: Intel (R) Xeon(R) CPU E5-1620 v2 – 3. Ram DDR3, and 512 GB storage.
Acknowledgements Not applicable.
Author Contributions YHY and AGA contributed equally to the work.
Funding Open access funding provided by The Science, Technology amp; Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB). This research receives no funding.
Data availability No data associated with this research.

Declarations

Conflict of interest The authors declare that they have no conflict of interest.
Ethics approval and consent to participate Not applicable.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted
by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

References

  1. Ghanbari, F., Ghanbari, K., Mokhtary, P.: Generalized Jacobi-Galerkin method for nonlinear fractional differential algebraic equations. Comput. Appl. Math. 37, 5456-5475 (2018)
  2. Zaky, M.A., Abo-Gabal, H., Hafez, R.M., Doha, E.H.: Computational and theoretical aspects of Romanovski-Bessel polynomials and their applications in spectral approximations. Numer. Algor. 89, 1-35 (2022)
  3. Youssri, Y.H., Ismail, M., Atta, A.G.: Chebyshev Petrov-Galerkin procedure for the time-fractional heat equation with nonlocal conditions. Phys. Scr. 99(1), 015251 (2024)
  4. Youssri, Y.H., Atta, A.G.: Modal spectral Tchebyshev Petrov-Galerkin stratagem for the time-fractional nonlinear Burgers’ equation. Iran. J. Numer. Anal. Optim. 14(1), 1 (2024)
  5. Moustafa, M., Youssri, Y.H., Atta, A.G.: Explicit Chebyshev-Galerkin scheme for the time-fractional diffusion equation. Int. J. Mod. Phys. C 35(1), 2450002 (2024)
  6. Atta, A.G., Youssri, Y.H.: Shifted second-kind Chebyshev spectral collocation-based technique for time-fractional KdV-Burgers’ equation. Iran. J. Math. Chem. 14(4), 207-224 (2023)
  7. Hafez, R.M., Youssri, Y.H., Atta, A.G.: Jacobi rational operational approach for time-fractional subdiffusion equation on a semi-infinite domain. Contemp. Math. 4(4), 853-876 (2023)
  8. Youssri, Y.H., Atta, A.G.: Fejér-Quadrature collocation algorithm for solving fractional integrodifferential equations via Fibonacci polynomials. Contemp. Math. 5(1), 296-308 (2024)
  9. Zheng, W., Chen, Y., Zhou, J.: A Legendre spectral method for multidimensional partial Volterra integro-differential equations. J. Comput. Appl. Math. 436, 115302 (2024)
  10. Tu, H., Wang, Y., Zhang, Y., Liao, H., Liu, W.: Parallel numerical simulation of weakly range-dependent ocean acoustic waveguides by adiabatic modes based on a spectral method. Phys. Fluids 35(1), 017119 (2023)
  11. Tu, H., Wang, Y., Yang, C., Liu, W., Wang, X.: A Chebyshev-Tau spectral method for coupled modes of underwater sound propagation in range-dependent ocean environments. Phys. Fluids 35(3), 037113 (2023)
  12. Konoplya, R.A., Zhidenko, A.: Bernstein spectral method for quasinormal modes of a generic black hole spacetime and application to instability of dilaton-de Sitter solution. Phys. Rev. D. 107(4), 044009 (2023)
  13. Youssri, Y.H., Atta, A.G.: Radical Petrov-Galerkin approach for the time-fractional KdV-Burgers’ equation. Math. Comput. Appl. 29(6), 107 (2024)
  14. Youssri, Y.H., Atta, A.G., Abu Waar, Z.Y., Moustafa, M.O.: Petrov-Galerkin method for small deflections in fourth-order beam equations in civil engineering. Nonlinear Eng. 13(1), 20240022 (2024)
  15. Kharazmi, E., Zayernouri, M., Em Karniadakis, G.: A Petrov-Galerkin spectral element method for fractional elliptic problems. Comput. Methods Appl. Mech. Eng. 324, 512-536 (2017)
  16. Hafez, R.M., Zaky, M.A., Hendy, A.S.: A novel spectral Galerkin/Petrov-Galerkin algorithm for the multi-dimensional space-time fractional advection-diffusion-reaction equations with nonsmooth solutions. Math. Comput. Simul. 190, 678-690 (2021)
  17. Wang, M., Au, F.T.K.: Precise integration methods based on the Chebyshev polynomial of the first kind. Earthq. Eng. Eng. Vib. 7(2), 207-216 (2008)
  18. Ahmed, H.M.: Numerical Solutions for Singular Lane-Emden Equations Using Shifted Chebyshev Polynomials of the First Kind. Contemp. Math. 4, 132-149 (2023)
  19. Abd-Elhameed, W.M., Youssri, Y.H., Atta, A.G.: Tau algorithm for fractional delay differential equations utilizing seventh-kind Chebyshev polynomials. J. Math. Model. 12, 277-299 (2024)
  20. Lebedev, V.I., Finogenov, S.A.: Some algorithms for computing Chebyshev normalized first-kind polynomials by roots. Russ. J. Numer. Anal. Math. Model. 20(4), 353-363 (2005)
  21. Shoukralla, E.S.: Application of Chebyshev polynomials of the second kind to the numerical solution of weakly singular Fredholm integral equations of the first kind. IAENG Int. J. Appl. Math. 51(1), 1-16 (2021)
  22. Akram, T., Ali, Z., Rabiei, F., Shah, K., Kumam, P.: A numerical study of nonlinear fractional order partial integro-differential equation with a weakly singular kernel. Fract. Fract. 5(3), 85 (2021)
  23. Loh, J.R., Phang, C., Tay, K.G.: New method for solving fractional partial integro-differential equations by combination of Laplace transform and resolvent kernel method. Chin. J. Phys. 67, 666-680 (2020)
  24. Abbas, M., Aslam, S., Abdullah, F.A., Riaz, M.B., Gepreel, K.A.: An efficient spline technique for solving time-fractional integro-differential equations. Heliyon 9(9), e19307 (2023)
  25. Atta, A.G., Abd-Elhameed, W.M., Moatimid, G.M., Youssri, Y.H.: Modal shifted fifth-kind Chebyshev Tau integral approach for solving heat conduction equation. Fract. Fract. 6(11), 619 (2022)
  26. Abdelghany, E.M., Abd-Elhameed, W.M., Moatimid, G.M., Youssri, Y.H., Atta, A.G.: A tau approach for solving time-fractional heat equation based on the shifted sixth-kind Chebyshev polynomials. Symmetry 15(3), 594 (2023)
  27. Atta, A.G., Abd-Elhameed, W.M., Moatimid, G.M., Youssri, Y.H.: Novel spectral schemes to fractional problems with nonsmooth solutions. Math. Methods Appl. Sci. 46(13), 14745-14764 (2023)
  28. Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Elsevier, San Diego (1998)
  29. Atta, A.G., Youssri, Y.H.: Advanced shifted first-kind Chebyshev collocation approach for solving the nonlinear time-fractional partial integro-differential equation with a weakly singular kernel. Comput. Appl. Math. 41(8), 381 (2022)
  30. Mason, J.C., Handscomb, D.C.: Chebyshev Polynomials. Chapman and Hall, New York (2002)
  31. Youssri, Y.H., Atta, A.G.: Double Tchebyshev spectral Tau algorithm for solving KdV equation, with soliton application. In: Solitons, pp. 451-467. Springer (2022)
  32. Alavi, J., Aminikhah, H.: An efficient parametric finite difference and orthogonal spline approximation for solving the weakly singular nonlinear time-fractional partial integro-differential equation. Comput. Appl. Math. 42(8), 350 (2023)
Publisher’s Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
  1. Y. H. Youssri
    youssri@cu.edu.eg
    A. G. Atta
    ahmed_gamal@edu.asu.edu.eg
    1 Department of Mathematics, Faculty of Science, Cairo University, Giza 12613, Egypt
    2 Department of Mathematics, Faculty of Education, Ain Shams University, Roxy, Cairo 11341, Egypt