تم الاستلام في 15 أبريل 2024
استلمت في شكل منقح 22 أغسطس 2024
تم القبول في 30 أغسطس 2024
متاح على الإنترنت 1 سبتمبر 2024

أوزان المعايير؛ TOPSIS؛ MCDA؛ MCDM؛ SITW

تحليل القرار متعدد المعايير (MCDA) هو مجال بحث يركز على الحلول العملية لمشاكل اتخاذ القرار المعقدة، والتي تكون شائعة في مجالات متنوعة مثل اللوجستيات [1،2]، إدارة-

تُستخدم أدوات تحليل القرار المتعدد (MCDA) لدعم عملية اتخاذ القرار في الحالات التي توجد فيها معايير متعارضة متعددة، مما يتحدى الأساليب التحليلية التقليدية. تقدم أدوات MCDA طريقة منظمة ومنهجية لتحليل القرارات، مع الأخذ في الاعتبار تنوع المعايير وتفضيلات صانعي القرار.

في قضايا تحليل القرار متعدد المعايير، غالبًا ما تتطلب مشاكل اتخاذ القرار المعقدة مشاركة الخبراء. إن مشاركتهم ضرورية في تحديد نماذج متعددة المعايير نظرًا لتنوع جوانب اتخاذ القرار. تُستخدم طرق مختلفة للتعبير عن معرفتهم لاستخراج معرفة الخبير في نموذج القرار، والتي يمكن تطبيقها اعتمادًا على سياق المشكلة. إحدى الطرق الشائعة هي المقارنات الثنائية لنقاط المرجعية، التي تسمح بالتقييم النسبي للميزات البديلة.

ومع ذلك، فإن أوزان المعايير هي الطريقة الأكثر تقليدية لنقل المعرفة الخبرائية في سياق تحليل القرار متعدد المعايير. تتضمن هذه التقنية تخصيص وزن لكل معيار يعكس أهميته في سياق القرار الذي سيتم اتخاذه. يمكن للخبراء تحديد هذه الأوزان، وتقييم خبراتهم، وتحليل البيانات.

بمجرد أن يقوم الخبير بتطوير نموذج محدد، قد تكون هناك مشاكل محتملة مرتبطة بفقدان معلمات النموذج أو عدم توفر الخبير. وهذا صحيح بشكل خاص في المشاريع طويلة الأمد أو الحالات التي قد يكون فيها الخبير غير متاح لأسباب مختلفة، مثل ضيق الوقت، أو تغيير الوظيفة، أو التزامات أخرى. من أجل معالجة مشكلة نقص المعرفة الخبيرة، يتم استخدام تقنيات لتحديد الأوزان بناءً على مقاييس المعلومات التي تسمح بتحديد أوزان المعايير بشكل موضوعي دون الحاجة إلى إشراك خبير في كل مرحلة من مراحل التحليل. واحدة من هذه التقنيات هي تحديد أوزان المعايير باستخدام الإنتروبيا أو الانحراف المعياري.

ومع ذلك، تركز الأساليب المعتمدة على مقاييس المعلومات بشكل أساسي على تحليل بيانات المدخلات. في بعض الحالات، قد يكون من المفيد استخدام عينات التقييم المتاحة بالفعل لتحسين النموذج. وهذا يثير إمكانية تحديد الأوزان العشوائية (SITW) [15]، وهي نهج مبتكر يستخدم الآلية الأساسية لتقنية MCDA المختارة وتقنيات التحسين لاختيار أوزان المعايير لتحقيق تصنيفات قريبة قدر الإمكان من العينات التي تم تقييمها بالفعل.

لذلك، تقارن هذه الدراسة بين الطرق المعتمدة على المعلومات، مثل الإنتروبيا والانحراف المعياري، مع طريقة التعرف العشوائي على الوزن (SITW) في إعادة تحديد الوظائف الطبية لـ TRI. كانت الدراسة تهدف إلى تقييم فعالية هذه الطرق تحت سيناريوهات مختلفة، مع الأخذ في الاعتبار أعدادًا مختلفة من البدائل. تم اعتماد الوظيفة الطبية لـ TRI كمعيار، مما يسمح بمقارنة النتائج وتحديد أفضل الاستراتيجيات. تم إجراء الدراسة لأعداد مختلفة من البدائل لفهم في أي الحالات تكون الطرق أكثر فائدة وفعالية. لتحقيق هذه الغاية، تم استخدام معامل الارتباط الموزون لسبيرمان. ) تم استخدامه لمقارنة تشابه الترتيبات التي تم إنشاؤها بواسطة كل طريقة.

يتم تنظيم بقية المقال على النحو التالي. القسم 2 يقدم الأساسيات المتعلقة بالطرق التي تم استخدامها في الدراسة. القسم 3 يقدم البحث والنتائج التي تم الحصول عليها منه وتحليلات النتائج. القسم 4 يقدم الاستنتاجات.

تعمل تقنية تفضيل الطلب بناءً على التشابه مع حل مثالي (TOPSIS) ضمن إطار منظم يدور حول نقاط مرجعية، مستخدمة نهجًا منطقيًا لتقييم البدائل. في جوهر هذه الطريقة توجد نقطتان مرجعيتان حاسمتان: الحل المثالي الإيجابي (PIS) والحل المثالي السلبي (NIS). تنفذ TOPSIS عملية التقييم من خلال قياس قرب البدائل من هذه النقاط المرجعية. يمكن توضيح الإجراء الكامل لـ TOPSIS.
كما يلي، تشمل عدة خطوات رئيسية:
الخطوة 1. قم بتطبيع مصفوفة القرار باستخدام تطبيع الحد الأدنى والحد الأقصى. يتم تطبيع قيم معايير نوع الفائدة باستخدام المعادلة (1)، بينما يتم تطبيع قيم معايير نوع التكلفة باستخدام المعادلة (2).

الخطوة 2. حساب مصفوفة قرار موزونة طبيعية بواسطة المعادلة (3):

الخطوة 3. تحديد الحلول المثالية الإيجابية والسلبية لمشكلة اتخاذ القرار المحددة باستخدام المعادلة (4):


أين يمثل معايير نوع الربح و لنوع التكلفة.
الخطوة 4. حساب المسافات الإيجابية والسلبية باستخدام المسافة الإقليدية ذات الأبعاد مع المعادلة (5):

الخطوة 5. حساب القرب النسبي من الحل المثالي بواسطة المعادلة (6):

تستند طريقة وزن الإنتروبيا إلى مقياس عدم اليقين المعلوماتي لشانون، مما يوفر فوائد مثل تقليل المخاطر وزيادة الكفاءة [14]. يمكن توضيح منهجية أوزان الإنتروبيا من خلال الخطوات التالية:

الخطوة 1. تطبيع مصفوفة القرار ، حيث هو عدد البدائل، هو عدد المعايير. يمكن تمثيل هذا التطبيع بالمعادلة (7).

الخطوة 2. حساب مقياس الإنتروبيا لكل معيار وفقًا للمعادلة (8).

الخطوة 3. اشتقاق الأوزان بناءً على الإنتروبيا المحسوبة لكل معيار وفقًا للمعادلة (9).

تستند طريقة وزن الانحراف المعياري إلى المقياس الإحصائي للانحراف المعياري. حيث تعطي أوزانًا صغيرة لمعيار له قيم مشابهة عبر المتغيرات [14]. يمكن تقديم هذه الطريقة في خطوتين:

الخطوة 1. احسب مقياس الانحراف المعياري لجميع المعايير وفقًا للمعادلة (10).

أين هو القيمة من مصفوفة القرار لـ بديل و معيار.
الخطوة 2. اشتق الأوزان بناءً على قيم مقياس الانحراف المعياري باستخدام المعادلة (11).

ستقدم هذه القسم طريقة لإعادة تحديد الأوزان تُسمى التعرف العشوائي على الأوزان (SITW)، باستخدام تقنية تحسين عشوائية تُعرف باسم تحسين سرب الجسيمات (PSO). تم اقتراح طريقة SITW في البداية في الدراسة التي أجراها [15] كحل للتحدي المتمثل في محدودية توفر بيانات الإدخال المتعلقة بالأوزان، والتي تعتبر محورية للعديد من منهجيات تحليل القرار المتعدد (MCDA). من خلال الاستفادة من الطرق العشوائية المصممة لمهام التحسين، يصبح من الممكن تحديد الأوزان المثلى التي تسهل إعادة تحديد نماذج MCDA لاحقًا. ضمن نطاق هذه الدراسة، التي تركز حصريًا على نهج PSO، يمكن توضيح طريقة SITW من خلال الخطوات التالية:
الخطوة 1. اختر مجموعة بيانات. يجب أن تحتوي مجموعة البيانات على متجهات المعايير ( )، متجه أنواع المعايير ( )، و متجه الترتيب ( ).
الخطوة 2. اختر طريقة تحسين عشوائية. في هذه الخطوة، اختر طريقة عشوائية لحل مشكلة التحسين وحدد معلماتها. في هذه الورقة، تم اختيار تحسين سرب الجسيمات (PSO) كطريقة تحسين عشوائية، ويمكن تقديم خوارزميتها على النحو التالي:

Algorithm 1 Particle Swarm Optimization (PSO)
    Input: $f, N, D,[a, b]$, max_iterations $, w, c_{1}, c_{2}$
    Initialize $X, V, P, P_{text {value }}, G, G_{text {value }}$
    for iteration $leftarrow 1$ to max_iterations do
        for each particle $i$ do
            Update velocity and position
            Clip position to within bounds
            Evaluate objective function
            if $f_{i}>P_{text {value }}[i]$ then
                Update personal best
            end if
        end for
        Update global best
        if convergence_criteria_met() then
            break
        end if
    end for
    Output: $G, G_{text {value }}$

الخطوة 3. تدريب النموذج. يتم تدريب النموذج باستخدام خوارزمية التحسين العشوائي ودالة الملاءمة، والتي يمكن تمثيلها كما يلي:

Algorithm 2 Fitness Function
    procedure Fitness(solutions):
        solutions $leftarrow$ solutions/sum(solutions)
        preference $leftarrow$ base $(C$, solutions,$T)$
        return rw(base.rank(preference), $R$ )
    end procedure

معامل ارتباط سبيرمان المرجح )، الذي تم تقديمه بواسطة [18]، يبني على معامل سبيرمان التقليدي من خلال دمج الأوزان. هذه الأوزان تعزز بشكل استراتيجي تأثير تغييرات الترتيب في المقدمة، مما يؤثر على قيمة الارتباط النهائية. تتضمن عملية حساب هذا الارتباط ترتيبين، كل منهما بحجم ، حيث يمثل المركز في الترتيب الأول و يشير إلى الموقع في الترتيب الثاني (12). الناتج يتراوح معامل الارتباط بين -1 و 1. تشير القيمة 1 إلى تصنيفات متطابقة، بينما تشير القيمة -1 إلى تصنيفات معكوسة، وتشير القيمة 0 إلى تصنيفات غير مرتبطة. من خلال تخصيص درجات متفاوتة من الأهمية لمواقع التصنيف المختلفة، تقدم هذه الطريقة منظورًا دقيقًا. يتم تعريف المعامل رسميًا كما في المعادلة (12):

تقوم هذه الدراسة بمقارنة طرق الوزن الموضوعي مع تقنية التعرف العشوائي على الأوزان (SITW) في سياق تحديد نماذج تحليل القرار متعدد المعايير (MCDA).
تم استخدام طريقة MCDA الكلاسيكية، المعروفة باسم TOPSIS، لإنشاء تصنيفات للبدائل المحددة مسبقًا وأوزان المعايير. تم الحصول على طرق MCDA المطبقة في هذه الدراسة من مكتبة pymcdm [19]. تم استخدام معامل الارتباط الموزون لسبيرمان كمقياس لتقييم دقة ملاءمة نماذج MCDA. كانت دالة المعايير المستخدمة في هذه الدراسة هي مؤشر خطر الانسداد القلبي (TRI)، المصمم لتقييم المرضى الذين يعانون من قصور التاجي الحاد. كانت دالة TRI بمثابة معيار لتقييم فعالية أساليب اختيار الأوزان المختلفة. التعبير عن دالة TRI هو كما يلي:

أين هو عمر المريض، هو عدد ضربات القلب في الدقيقة، و هو ضغط الدم الانقباضي المقاس بالملليمترات من عمود الزئبق.

في هذه الدراسة، تم استخدام مجموعات بديلة تم توليدها عشوائيًا لثلاثة معايير تتوافق مع المعلمات التالية لدالة TRI، أي، معدل ضربات القلب (العمر)، و (ضغط الدم الانقباضي). لتحديد هذه المجموعات، يتم تعريف فترات المعايير على النحو التالي: ينتمي إلى الفترة [60,100]، ينتمي إلى الفترة [40,60]، و ينتمي إلى الفترة [90، 180]. استنادًا إلى المنهجية المقدمة في الورقة [20]، تم إنشاء مجموعة مثال من 10 بدائل، كما هو موضح في الجدول 1.

لأغراض الدراسة، سيكون التركيز على فحص ثلاث طرق لاختيار الأوزان: طريقة الإنتروبيا، وطريقة الانحراف المعياري، وطريقة التعرف العشوائي على الأوزان (SITW). نظرًا لأن طريقة SITW تحتاج إلى عينات تم تقييمها مسبقًا لآلية الوزن الخاصة بها، تم اتخاذ قرار باستخدام 160 بديلًا تم إنشاؤها عشوائيًا، وتم اشتقاق تقييماتها من دالة TRI. نظرًا لأن طريقة SITW تعتمد على الترتيبات، تم تحويل التقييمات المشتقة من دالة TRI إلى ترتيبات. بالنسبة لطريقة SITW، تم استخدام TOPSIS كطريقة أساسية، بينما تم استخدام تحسين سرب الجسيمات (PSO) كطريقة تحسين. بالنسبة لإعادة تحديد الأوزان، تم تعيين معلمات PSO كإعدادات افتراضية من مكتبة MEALPY [21]. بالمقابل، تم تعديل معلمين، وهما: عدد العصور – 1000 وعدد الجسيمات – 100. بالنسبة لنهج SITW، تم تحديد الأوزان التالية: و من ناحية أخرى، يتم عرض عملية تحسين مسار دالة اللياقة في الشكل 1.

بمجرد الحصول على أوزان المعايير باستخدام نهج SITW، تم مقارنتها بنهج الأوزان المتساوية. في هذه الحالة، تم استخدام طريقة TOPSIS لنقل الأوزان ومصفوفات القرار للحصول على الترتيبات. تم إجراء هذه الدراسة على 1000 مجموعة عشوائية تحتوي على بدائل. معامل الارتباط الموزون لسبيرمان ( ) تم استخدامه لمقارنة الترتيبات الناتجة من طريقة TOPSIS ومنهج TRI المرجعي.

يوضح الشكل 2 مقارنة بين تصنيفات المراجع باستخدام نهج SITW-TOPSIS ونهج TOPSIS لعشرة بدائل تم توليدها عشوائيًا 1,000 مرة. يمكن ملاحظة أن نهج SITW-TOPSIS يؤدي بشكل أفضل بكثير من نهج TOPSIS الكلاسيكي مع أوزان متساوية. نطاق قيم المعاملات التي تم الحصول عليها لنهج SITW-TOPSIS هو [0.74، 1.0]. بالمقابل، نطاق قيم المعاملات لطريقة TOPSIS مع أوزان متساوية هي [ . بالمقابل، فإن التجميع الأكثر قوة لكلا النهجين المدروسين من المعامل يأتي من النطاق .

الشكل 3 يقارن بين الترتيبات المرجعية مع نهجي SITW-TOPSIS وTOPSIS لـ 25 بديلاً تم توليدها عشوائيًا 1000 مرة. تم ملاحظة تحسين كبير في جودة الترتيب لطريقة TOPSIS باستخدام أوزان متساوية في هذا التحليل. ومع ذلك، فإن نهج SITW-TOPSIS يحقق نتائج أعلى بشكل ملحوظ. قيم المعاملات في الحالات التي تحقق فيها طريقة TOPSIS باستخدام أوزان متساوية قيمًا أقل بشكل ملحوظ. ومع ذلك، في معظم الحالات، تحقق الطريقتان نتائج عالية بشكل متساوٍ. قيم المعاملات في النطاق من 0.96 إلى 0.98. ومن الجدير بالذكر أن معظم القيم التي تم الحصول عليها أصغر بكثير من تلك الخاصة بالبدائل العشرة. ومع ذلك، فإن الانحراف المعياري لكل من الطريقتين أيضًا أقل.

الشكل 4 يقارن التصنيفات المرجعية مع نهجي SITW-TOPSIS وTOPSIS لـ 50 بديل تم توليدها عشوائيًا 1,000 مرة. كلا النهجين يؤديان بشكل جيد جدًا في الرسم البياني ثنائي الأبعاد، حيث يحددان نماذج TOPSIS القريبة من عكس دالة TRI. ومع ذلك، هناك اتجاه ملحوظ يتمثل في أن التصنيفات التي تم الحصول عليها من كلا النهجين تنخفض مع زيادة عدد البدائل. ومن الجدير بالذكر أيضًا أن أعلى تم الحصول على قيم طرق SITW-TOPSIS وTOPSIS مع أوزان متساوية من 0.96 إلى 0.98. ومع ذلك، مرة أخرى، كان النطاق العام المقبول تقلصت القيم للطرق، حيث تتراوح بين 0.97 إلى 1.0 لطريقة SITW-TOPSIS و0.92 إلى 1.0 لطريقة TOPSIS مع الأوزان المتساوية.

بالإضافة إلى مقارنة نهج TOPSIS الكلاسيكي مع الأوزان المتساوية ونهج SITW-TOPIS، تم تحليل طرق الوزن الموضوعي. كما في الدراسة السابقة، تم سحب 1000 مصفوفة قرار تحتوي على 5، 10، 15، 25، 50 بديل بشكل عشوائي. تقارن الرسوم البيانية في الشكل 5 المقارنة. عند تحليل المقارنة العامة، كان نهج SITW-TOPIS هو الأفضل في التعامل مع مشكلة تحديد النموذج المرجعي، أي TRI. أظهر أعلى متوسطات لأحجام مصفوفات القرار المختبرة وأقل عدد من القيم الشاذة مقارنة ببقية النهج المختبرة. كانت الأوزان المتساوية جيدة بنفس القدر في حالة تحديد نماذج TOPSIS التي تشبه النموذج المرجعي TRI. ومع ذلك، بالنسبة لتحديد نماذج TOPSIS باستخدام أوزان تعتمد على مقاييس المعلومات، أي، الإنتروبيا والانحراف المعياري، قد يكون رسم طريقة TRI أكثر فعالية. في الغالب، كانت قيم كلا النهجين تتجمع لأحجام عدد البدائل المختبرة حول قيمة والذي لا يدل على دقة عالية في التعرف.

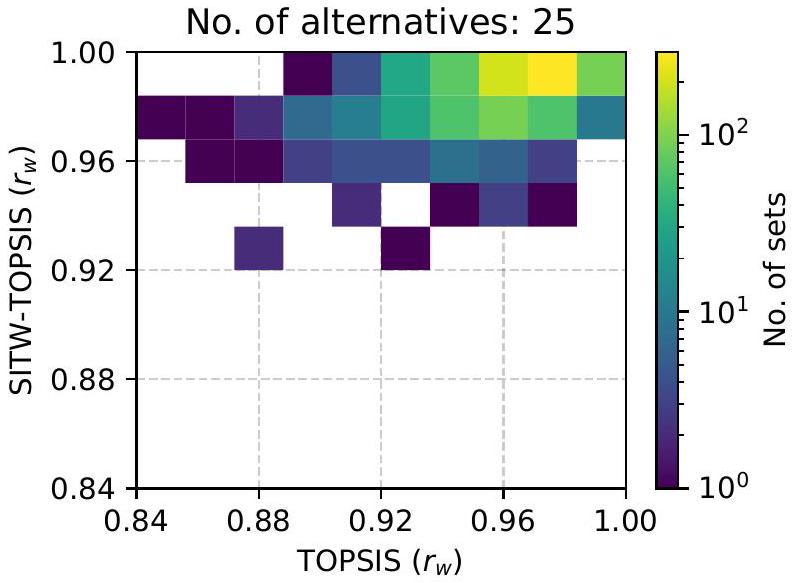
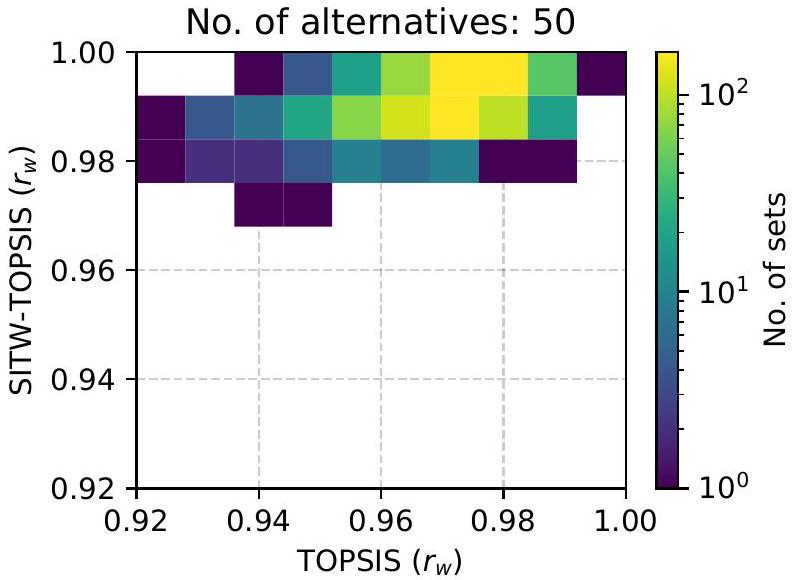
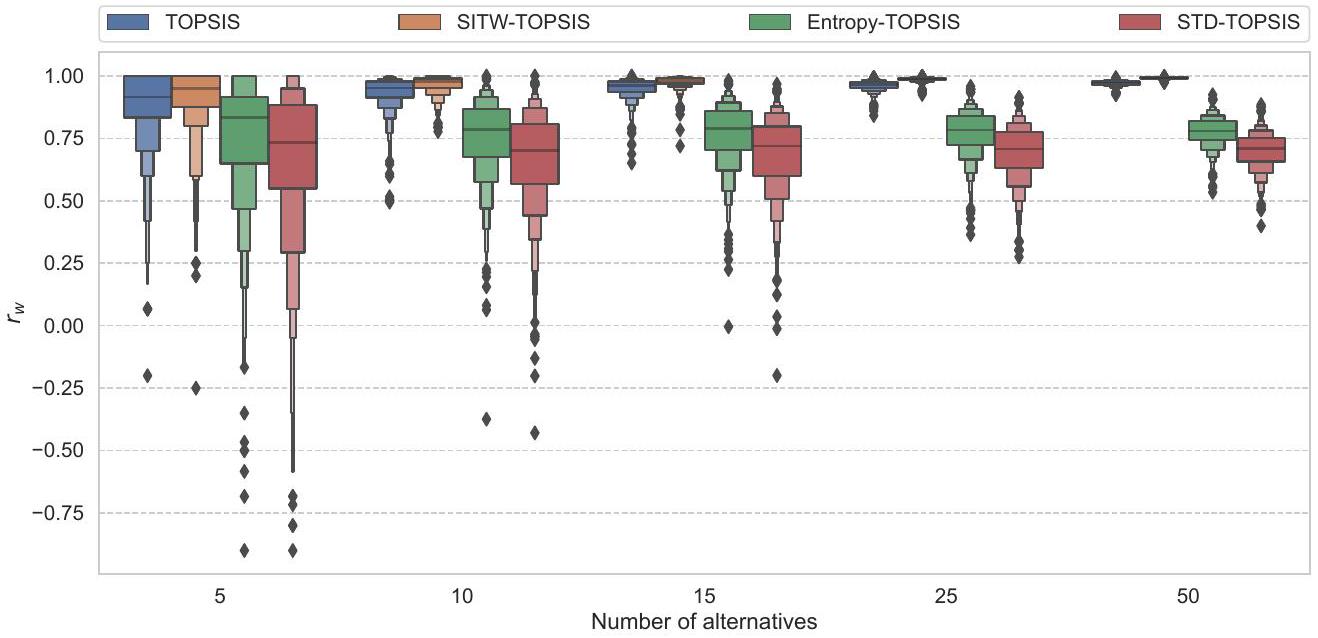
تقدم الجدول 2 إحصائيات مقارنة مفصلة لأساليب TOPSIS باستخدام أوزان مختلفة مع دالة TRI المرجعية. بالنسبة لطريقة Entropy-TOPSIS، يمكن ملاحظة أنه بالنسبة للمجموعات التي تحتوي على 25 و 50 بديلاً، تتأرجح قيم معامل rw حول 0.77 و 0.78، مما يشير إلى فعالية معتدلة لهذه الطريقة في تحديد النماذج. ومع ذلك، فإن الانحراف المعياري لهذه القيم مرتفع نسبيًا، مما قد يشير إلى بعض التباين في فعالية هذه الطريقة اعتمادًا على مجموعة البيانات المحددة. من ناحية أخرى، بالنسبة لطريقة SITW-TOPSIS، نلاحظ قيمًا أعلى بكثير لمعامل rw، خاصةً للمجموعات الأكبر. بالنسبة لمجموعة بيانات تحتوي على 50 بديلاً، تتجاوز القيمة المتوسطة لـ rw 0.99، مما يشير إلى أن هذه الطريقة فعالة للغاية في تحديد النماذج. بالإضافة إلى ذلك، فإن الانحراف المعياري لهذه الطريقة منخفض نسبيًا، مما يشير إلى استقرار نتائجها. وبالمثل، بالنسبة لطريقة STD-TOPSIS، تظهر قيم rw أيضًا اتجاهًا متزايدًا مع زيادة عدد البدائل، حيث تصل إلى قيمة متوسطة تبلغ حوالي 0.70 لمجموعة تحتوي على 50 بديلاً. ومع ذلك، مقارنةً بطريقة SITW-TOPSIS، فإن القيم المتوسطة لـ rw أقل، مما قد يشير إلى أن هذه الطريقة أقل فعالية في تحديد النماذج.

تم إجراء دراسة حول تحديد الأوزان في نماذج تحليل القرار متعدد المعايير (MCDA) في هذا التحليل المرجعي. تم استخدام وظيفة TRI لتقييم المرضى الذين يعانون من قصور التاج الحاد كنموذج مرجعي. كانت الأساليب التي تم تقييمها: TOPSIS (استخدام أوزان متساوية)، SITW-TOPSIS، Entropy-TOPSIS، وSTD-TOPSIS. أشارت نتائج الدراسة إلى أن أفضل طريقة لتحديد أوزان المعايير المتعددة هي طريقة SITW-TOPSIS. تستخدم هذه الطريقة معلومات من البدائل التي تم تقييمها سابقًا، مما يسمح بتطابق أفضل للأوزان مقارنة بالأساليب المعتمدة على مقاييس المعلومات. أكدت التحليل على الأداء العالي لطريقة SITW-TOPSIS والأداء المعتدل لطريقتي Entropy-TOPSIS وSTD-TOPSIS.

ستحتاج الأبحاث المستقبلية إلى التركيز على تحليل أوسع للنهج المختارة مع نماذج مرجعية مختلفة. في هذه الحالة، يمكن استخدام نموذج المرجعية الضبابية أو وظائف مرجعية أخرى. بالإضافة إلى ذلك، يجب توسيع هذه الدراسة لتشمل حالات مع عدم اليقين.

تم دعم العمل من قبل المركز الوطني للعلوم في بولندا، رقم القرار UMO-2021/41/B/HS4/O1296.

يعلن المؤلفون عدم وجود أي تضارب في المصالح.

[1] Özceylan, E., Çetinkaya, C., Erbaş, M., & Kabak, M. (2016). Logistic performance evaluation of provinces in Turkey: A GIS-based multi-criteria decision analysis. Transportation Research Part A: Policy and Practice, 94, 323-337. https://doi.org/10.1016/j.tra.2016.09.020
[2] Longaray, A., Ensslin, L., Ensslin, S., Alves, G., Dutra, A., & Munhoz, P. (2018). Using MCDA to evaluate the performance of the logistics process in public hospitals: the case of a Brazilian teaching hospital. International Transactions in Operational Research, 25(1), 133-156. https: //doi.org/10.1111/itor. 12387
[3] Uhde, B., Andreas Hahn, W., Griess, V. C., & Knoke, T. (2015). Hybrid MCDA methods to integrate multiple ecosystem services in forest management planning: a critical review. Environmental management, 56, 373-388. https://doi.org/10.1007/s00267-015-0503-3
[4] Wątróbski, J., & Jankowski, J. (2016). Guideline for MCDA method selection in production management area. New Frontiers in Information and Production Systems Modelling and Analysis: Incentive Mechanisms, Competence Management, Knowledge-based Production, 119-138. https://doi.org/10.1007/978-3-319-23338-3_6
[5] Angelis, A., & Kanavos, P. (2017). Multiple criteria decision analysis (MCDA) for evaluating new medicines in health technology assessment and beyond: the advance value framework. Social Science & Medicine, 188, 137-156. https://doi.org/10.1016/j.socscimed.2017.06.024
[6] Badia, X., Chugani, D., Abad, M. R., Arias, P., Guillén-Navarro, E., Jarque, I., Posada, M., Vitoria, I., & Poveda, J. L. (2019). Development and validation of an MCDA framework for evaluation and decision-making of orphan drugs in Spain. Expert Opinion on Orphan Drugs, 7(7-8), 363372. https://doi.org/10.1080/21678707.2019.1652163
[7] Deshpande, P. C., Skaar, C., Brattebø, H., & Fet, A. M. (2020). Multi-criteria decision analysis (MCDA) method for assessing the sustainability of end-of-life alternatives for waste plastics: A case study of Norway. Science of the total environment, 719, 137353. https://doi.org/10.1016/ j.scitotenv.2020.137353
[8] Puška, A., Stević, Ž., & Pamučar, D. (2022). Evaluation and selection of healthcare waste incinerators using extended sustainability criteria and multi-criteria analysis methods. Environment, Development and Sustainability, 1-31. https://doi.org/10.1007/s10668-021-01902-2
[9] Colapinto, C., Jayaraman, R., Ben Abdelaziz, F., & La Torre, D. (2020). Environmental sustainability and multifaceted development: multi-criteria decision models with applications. Annals of Operations Research, 293(2), 405-432. https://doi.org/10.1007/s10479-019-03403-y
[10] Lahdelma, R., Miettinen, K., & Salminen, P. (2005). Reference point approach for multiple decision makers. European Journal of Operational Research, 164(3), 785-791. https://doi.org/10. 1016/j.ejor.2004.01.030
[11] Hatefi, S., & Torabi, S. A. (2010). A common weight MCDA-DEA approach to construct composite indicators. Ecological Economics, 70(1), 114-120. https://doi.org/10.1016/j.ecolecon.2010. 08.014
[12] Zborowski, M., & Chmielarz, W. (2023). Sensitivity analysis of the criteria weights used in selected MCDA methods in the multi-criteria assessment of banking services in Poland in 2022. 2023 18th Conference on Computer Science and Intelligence Systems (FedCSIS), 1217-1222. https: //doi.org/10.15439/2023F3745
[13] Martin, T. G., Burgman, M. A., Fidler, F., Kuhnert, P. M., Low-Choy, S., McBride, M., & Mengersen, K. (2012). Eliciting expert knowledge in conservation science. Conservation Biology, 26(1), 2938. https://doi.org/10.1111/j.1523-1739.2011.01806.x
[14] Paradowski, B., Shekhovtsov, A., Bączkiewicz, A., Kizielewicz, B., & Sałabun, W. (2021). Similarity Analysis of Methods for Objective Determination of Weights in Multi-Criteria Decision Support Systems. Symmetry, 13(10), 1874. https://doi.org/10.3390/sym13101874
[15] Kizielewicz, B., Paradowski, B., Więckowski, J., & Sałabun, W. (2022). Identification of weights in multi-cteria decision problems based on stochastic optimization. AMCIS 2022 Proceedings, (17). https://aisel.aisnet.org/amcis2O22/sig_odis/sig_odis/17
[16] Yoon, K. P., & Kim, W. K. (2017). The behavioral TOPSIS. Expert Systems with Applications, 89, 266-272. https://doi.org/10.1016/j.eswa.2017.07.045
[17] Kizielewicz, B., Więckowski, J., & Wątrobski, J. (2021). A study of different distance metrics in the TOPSIS method. Intelligent Decision Technologies: Proceedings of the 13th KES-IDT 2021 Conference, 275-284. https://doi.org/10.1007/978-981-16-2765-1_23
[18] Dancelli, L., Manisera, M., & Vezzoli, M. (2013). On two classes of Weighted Rank Correlation measures deriving from the Spearman’s . In Statistical models for data analysis (pp. 107-114). Springer. https://doi.org/10.1007/978-3-319-00032-9_13
[19] Kizielewicz, B., Shekhovtsov, A., & Sałabun, W. (2023). pymcdm-The universal library for solving multi-criteria decision-making problems. SoftwareX, 22, 101368. https://doi.org/10.1016/j. softx.2023.101368
[20] Sałabun, W., & Piegat, A. (2017). Comparative analysis of MCDM methods for the assessment of mortality in patients with acute coronary syndrome. Artificial Intelligence Review, 48, 557571. https://doi.org/10.1007/s10462-016-9511-9
[21] Van Thieu, N., & Mirjalili, S. (2023). MEALPY: An open-source library for latest meta-heuristic algorithms in Python. Journal of Systems Architecture, 139, 102871. https://doi.org/10.1016/j. sysarc.2023.102871

Received 15 April 2024
Received in revised form22 August 2024
Accepted 30 August 2024
Available online 1 September 2024

Criteria weights; TOPSIS; MCDA; MCDM; SITW

Multi-Criteria Decision Analysis (MCDA) is a research area that focuses on the practical solution of complex decision-making problems, which is common in diverse fields such as logistics [1,2], manage-

ment [3, 4], medicine [5, 6], and sustainability [7, 8]. MCDA tools are used to support the decisionmaking process in situations where there are multiple conflicting criteria, challenging traditional analytical methods. MCDA tools offer a structured and systematic way to analyze decisions, considering the diversity of criteria and decision makers’ preferences.

In multi-criteria decision analysis issues, complex decision-making problems often require the involvement of experts. Their participation is essential in identifying multi-criteria models due to the diversity of decision-making aspects [5,9]. Various methods of expressing their knowledge are used to extrude the expert’s knowledge into the decision model, which can be applied depending on the context of the problem. One popular approach is pairwise comparisons of reference points, which allow relative evaluation of alternative features [10].

However, criterion weights are the most classic method of transferring expert knowledge in the context of multi-criteria decision analysis [11,12]. This technique involves assigning each criterion a weight that reflects its importance in the context of the decision to be made. Experts can determine these weights, assess their experience, and analyze the data.

Once an expert has developed an identified model, potential problems may be associated with loss of model parameters or lack of expert availability. This is especially true in long-term projects or situations where the expert may be unavailable for various reasons, such as time constraints, employment change, or other commitments. In order to address the problem of lack of expert knowledge [13], techniques are being used to determine weights based on measures of information that allow criteria weights to be determined objectively without involving an expert in each stage of the analysis. One such technique is the determination of criterion weights using entropy or standard deviation [14].

However, methods based on measures of information mainly focus on analyzing input data. In some cases, it may be beneficial to use assessment samples that are already available to optimize the model. This raises the possibility of Stochastic Identification of Weights (SITW) [15], an innovative approach that uses the underlying mechanism of the selected MCDA technique and optimization techniques to select criteria weights to achieve rankings as close as possible to samples that have already been evaluated.

Therefore, this study compares information-based methods, such as Entropy and STD, with the Stochastic Identification of Weight (SITW) method in re-identifying TRI medical functions. The study aimed to evaluate the effectiveness of these methods under different scenarios, considering different numbers of alternatives. The medical function of TRI was adopted as a benchmark, allowing for a comparison of results and identifying the best strategies. The study was conducted for different numbers of alternatives to understand in which cases the methods are more beneficial and effective. To this end, Spearman’s weighted correlation coefficient ( ) was used to compare the similarity of the rankings generated by each method.

The rest of the article is organized as follows. Section 2 presents preliminaries related to the methods that were used in the study. Section 3 presents the research, the results obtained from it, and analyses of the results. Section 4 presents the conclusions.

The Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) functions within a structured framework revolving around reference points, employing a logical approach to assess alternatives [16,17]. At the core of this method lie two critical reference points: the Positive Ideal Solution (PIS) and the Negative Ideal Solution (NIS). TOPSIS executes the evaluation process by gauging the proximity of alternatives to these reference points. The entire procedure of TOPSIS can be delineated
as follows, encompassing several key steps:
Step 1. Normalize the decision matrix by using min-max normalization. The values of benefit type criteria are normalized using the Eq. (1), while the values of cost type criteria are normalized using the Eq. (2).

Step 2. Calculation of a weighted normalized decision matrix by Eq. (3):

Step 3. Identification of the Positive and Negative Ideal Solutions for a defined decision-making problem with Eq. (4):


where stands for profit type criteria and for cost type.
Step 4. Calculation of the Positive and Negative Distances using the -dimensional Euclidean distance with Eq. (5):

Step 5. Calculation of the relative closeness to the Ideal Solution by Eq. (6):

The entropy weighting approach derives from Shannon’s information uncertainty measure, offering benefits such as risk reduction and efficiency enhancement [14]. The methodology of entropy weights can be outlined through the following steps:

Step 1. Normalization of the decision matrix , where is the number of alternatives, is the number of criteria. This normalization can be represented by the Eq. (7).

Step 2. Calculation of the entropy measure for each criterion according to the Eq. (8).

Step 3. Derive weights based on the calculated entropy for each criterion by Eq. (9).

The standard deviation weighting method is based on the statistical measure of standard deviation. It assigns small weights to a criterion that has similar values across variants [14]. This method can be presented in two steps:

Step 1. Calculate the standard deviation measure for all criteria according to the Eq. (10).

where is the value from the decision matrix for alternative and criterion.
Step 2. Derive the weights based on the values of the standard deviation measure with Eq. (11).

This section will introduce a method for re-identifying weights called Stochastic Identification of Weights (SITW), employing a stochastic optimization technique known as Particle Swarm Optimization (PSO). The SITW method was initially proposed in the study by [15] as a solution to the challenge of limited input data availability concerning weights, which are pivotal for many MCDA methodologies. By leveraging stochastic methods tailored for optimization tasks, it becomes feasible to determine optimal weights facilitating the subsequent re-identification of MCDA models. Within the scope of this study, which exclusively concentrates on the PSO approach, the SITW method can be delineated through the following steps:
Step 1. Select a dataset. The dataset should contain criteria vectors ( ), a criteria types vector ( ), and a ranking vector ( ).
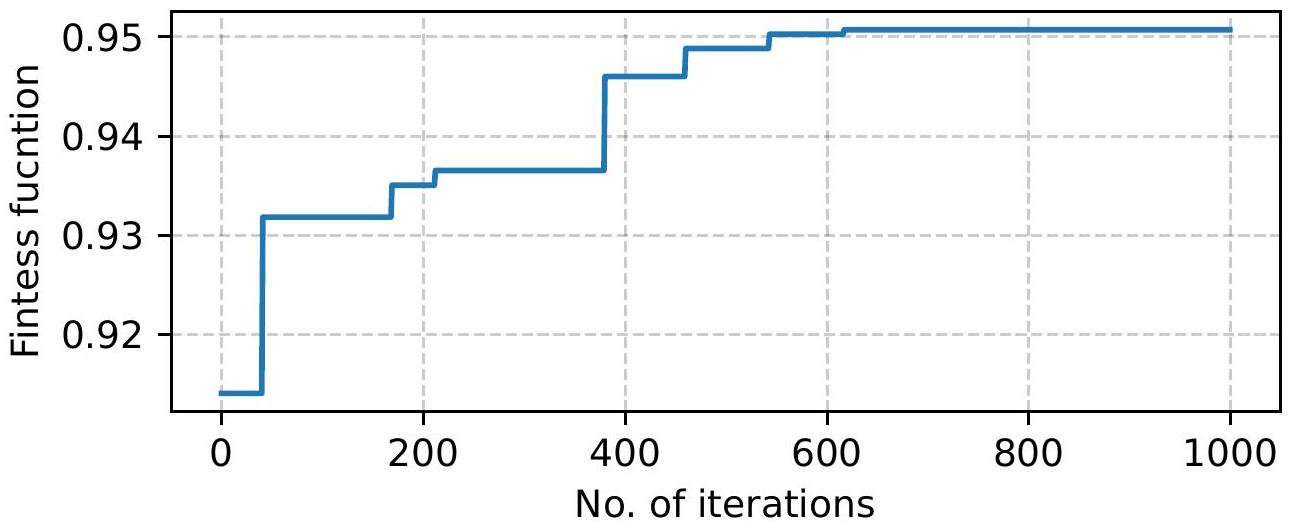
Step 2. Select a stochastic optimization method. In this step, choose a stochastic method for solving the optimization problem and select its parameters. In this paper, Particle swarm optimization (PSO) was selected as the stochastic optimization method, whose algorithm can be presented as follows:

Algorithm 1 Particle Swarm Optimization (PSO)
    Input: $f, N, D,[a, b]$, max_iterations $, w, c_{1}, c_{2}$
    Initialize $X, V, P, P_{text {value }}, G, G_{text {value }}$
    for iteration $leftarrow 1$ to max_iterations do
        for each particle $i$ do
            Update velocity and position
            Clip position to within bounds
            Evaluate objective function
            if $f_{i}>P_{text {value }}[i]$ then
                Update personal best
            end if
        end for
        Update global best
        if convergence_criteria_met() then
            break
        end if
    end for
    Output: $G, G_{text {value }}$

Step 3. Model training. Training the model is done using the stochastic optimization algorithm and the fitness function, which can be represented as follows:

Algorithm 2 Fitness Function
    procedure Fitness(solutions):
        solutions $leftarrow$ solutions/sum(solutions)
        preference $leftarrow$ base $(C$, solutions,$T)$
        return rw(base.rank(preference), $R$ )
    end procedure

The Weighted Spearman’s correlation coefficient ( ), introduced by [18], builds upon the conventional Spearman coefficient by incorporating weights. These weights strategically amplify the influence of ranking changes at the forefront, thereby impacting the final correlation value. This correlation computation involves two rankings, each of size , where represents the position in the first ranking and denotes the position in the second ranking (12). The resulting correlation coefficient ranges from -1 to 1 . A value of one indicates identical rankings, minus one suggests reversed rankings, and zero signifies uncorrelated rankings. By assigning varying degrees of importance to different ranking positions, this method offers a nuanced perspective. The coefficient is formally defined as Eq. (12):

This research compares objective weighting methods with the Stochastic Identification of Weights (SITW) technique in the context of identifying multi-criteria decision analysis (MCDA) models. The
classic MCDA method, known as TOPSIS, was employed to generate rankings for predefined alternatives and criterion weights. The MCDA methods implemented in this investigation were sourced from the pymcdm library [19]. Spearman’s weighted correlation coefficient served as a metric to assess the fitting accuracy of the MCDA models. The benchmark function utilized in this study was the Thrombolysis In Myocardial Infarction Risk Index (TRI), designed to evaluate patients with acute coronary insufficiency. The TRI function served as a benchmark to evaluate the effectiveness of various weight selection approaches. The expression for the TRI function is as follows:

where is the patient’s age, is the number of heartbeats per minute, and is the systolic blood pressure measured in millimeters of mercury column.

For this study, randomly generated sets of alternatives were used for three criteria that corresponded to the following parameters of the TRI function, i.e., (heart rate), (age), and (systolic blood pressure). To determine these sets, criterion intervals are defined as follows: belongs to the interval [60,100], belongs to the interval [40,60], and belongs to the interval [90,180]. Based on the methodology presented in the paper [20], an example set of 10 alternatives was generated, shown in the Table 1.

For study purposes, the focus will be on examining three weight selection methods: the Entropy method, the STD method, and the Stochastic Identification of Weights (SITW) method. Since the SITW method needs previously evaluated samples for its weighting mechanism, it was decided to use 160 randomly generated alternatives, and their evaluations were derived from the TRI function. Since the SITW method is based on rankings, the ratings derived from the TRI function were converted to rankings. For the SITW method, TOPSIS was used as the base method, while Particle Swarm Optimization (PSO) was used as the optimization method. For the re-identification of the weights, the PSO parameters were set as default settings from the MEALPY library [21]. In contrast, two parameters were modified, i.e., the number of epochs – 1000 and the number of particles – 100. For the SITW approach, the following weights were identified: and . On the other hand, the optimization process concerning the course of the fitness function is presented in Figure 1.

Once the criterion weights were obtained using the SITW approach, they were contrasted with the equal weights approach. In this case, the TOPSIS method was used to transfer weights and decision matrices to obtain rankings. This study was conducted on 1000 random sets containing alternatives. Spearman’s weighted correlation coefficient ( ) was used to compare the resulting rankings from the TOPSIS method and the TRI reference approach.

A comparison of reference rankings with the SITW-TOPSIS and TOPSIS approaches for 10 alternatives randomly generated 1,000 times is shown in Figure 2. It can be observed that the SITW-TOPSIS approach performs much better than the classical TOPSIS approach with equal weights. The range of obtained coefficient values for the SITW-TOPSIS approach is [0.74, 1.0]. In contrast, the range of coefficient values for the TOPSIS approach with equal weights is [ ]. In contrast, the most robust clustering for both studied approaches of the coefficient comes from the range .

Figure 3 compares reference rankings with the SITW-TOPSIS and TOPSIS approaches for 25 alternatives randomly generated 1000 times. A significant improvement in the ranking quality of the TOPSIS method using equal weights was observed in this analysis. Nevertheless, the SITW-TOPSIS approach achieves significantly higher coefficient values in cases where TOPSIS using equal weights achieves them significantly lower. Nevertheless, in most cases, both approaches achieve equally high coefficient values in the range of 0.96 to 0.98 . Notably, most of the values obtained are significantly smaller than those of the 10 alternatives. Nevertheless, the standard deviation for both approaches is also more minor.

Figure 4 compares reference rankings with the SITW-TOPSIS and TOPSIS approaches for 50 alternatives randomly generated 1,000 times. Both approaches perform very well in two-dimensional histogram, identifying TOPSIS models close to reflecting the TRI function. Nevertheless, there is a noticeable trend that the rankings obtained from both approaches decrease as the number of alternatives increases. It is also worth noting that the highest values for the SITW-TOPSIS and TOPSIS approaches with equal weights were obtained from 0.96 to 0.98 . However, again, the overall range of accepted values narrowed for the approaches, where it is 0.97 to 1.0 for SITW-TOPSIS and 0.92 to 1.0 for TOPSIS with equal weights.

In addition to comparing the classic TOPSIS approach with equal weights and the SITW-TOPIS approach, objective weighting methods were analyzed. As in the previous study, 1000 decision matrices containing 5, 10, 15, 25, 50 alternatives were randomly drawn. The box plots in Figure 5 compare the comparison. Analyzing the overall comparison, the SITW-TOPIS approach coped best with the problem of identifying the reference model, i.e., TRI. It showed the highest averages for the tested decision matrix sizes and fewer outliers than the rest of the tested approaches. Equal weights did equally well in the case of identifying TOPSIS models that are close in similarity to the reference TRI model. However, for the identification of TOPSIS models using weights based on measures of information, i.e., Entropy and Standard Deviation, mapping the TRI method could have been more effective. Mostly, the values of both of these approaches clustered for the tested sizes of the number of alternatives around the value of , which does not indicate high identification accuracy.

Table 2 presents detailed comparative statistics of TOPSIS approaches using different weights with the reference TRI function. For the Entropy-TOPSIS method, it can be seen that for sets containing 25 and 50 alternatives, the values of the rw coefficient oscillate around 0.77 and 0.78 , suggesting the moderate effectiveness of this method in identifying models. However, the standard deviation of these values is relatively high, which may indicate some variability in the effectiveness of this method depending on the specific dataset. For the SITW-TOPSIS method, on the other hand, we observe significantly higher values of the rw coefficient, especially for larger datasets. For a dataset containing 50 alternatives, the average rw value exceeds 0.99 , indicating that this method is highly effective in identifying models. In addition, the standard deviation for this method is relatively low, suggesting the stability of its results. Similarly, for the STD-TOPSIS method, the rw values also show an increasing trend with the increasing number of alternatives, reaching an average value of about 0.70 for a set containing 50 alternatives. However, compared to the SITW-TOPSIS method, the average rw values are lower, which may indicate that this method is less effective in identifying models.

A study on the identification of weights in multi-criteria decision analysis (MCDA) models was conducted in this benchmark analysis. The TRI function for evaluating patients with acute coronary insufficiency was used as the reference model. The evaluated approaches were: TOPSIS (use of equal weights), SITW-TOPSIS, Entropy-TOPSIS, and STD-TOPSIS. The study results indicated that the best approach for identifying multi-criteria weights is the SITW-TOPSIS method. It uses information from previously evaluated alternatives, which allows better matching of weights compared to approaches based on measures of information. The analysis confirmed the high performance of the SITW-TOPSIS method and the moderate performance of the Entropy-TOPSIS and STD-TOPSIS methods.

Future research would need to focus around a broader analysis of selected approaches with different reference models. In this case, the Fuzzy Reference Model or other benchmark functions could be used. In addition, this study would need to be expanded to include cases with uncertainty.

The work was supported by the National Science Centre, Poland, Decision number UMO-2021/41/B/HS4/O1296.

The authors declare no conflicts of interest.

[1] Özceylan, E., Çetinkaya, C., Erbaş, M., & Kabak, M. (2016). Logistic performance evaluation of provinces in Turkey: A GIS-based multi-criteria decision analysis. Transportation Research Part A: Policy and Practice, 94, 323-337. https://doi.org/10.1016/j.tra.2016.09.020
[2] Longaray, A., Ensslin, L., Ensslin, S., Alves, G., Dutra, A., & Munhoz, P. (2018). Using MCDA to evaluate the performance of the logistics process in public hospitals: the case of a Brazilian teaching hospital. International Transactions in Operational Research, 25(1), 133-156. https: //doi.org/10.1111/itor. 12387
[3] Uhde, B., Andreas Hahn, W., Griess, V. C., & Knoke, T. (2015). Hybrid MCDA methods to integrate multiple ecosystem services in forest management planning: a critical review. Environmental management, 56, 373-388. https://doi.org/10.1007/s00267-015-0503-3
[4] Wątróbski, J., & Jankowski, J. (2016). Guideline for MCDA method selection in production management area. New Frontiers in Information and Production Systems Modelling and Analysis: Incentive Mechanisms, Competence Management, Knowledge-based Production, 119-138. https://doi.org/10.1007/978-3-319-23338-3_6
[5] Angelis, A., & Kanavos, P. (2017). Multiple criteria decision analysis (MCDA) for evaluating new medicines in health technology assessment and beyond: the advance value framework. Social Science & Medicine, 188, 137-156. https://doi.org/10.1016/j.socscimed.2017.06.024
[6] Badia, X., Chugani, D., Abad, M. R., Arias, P., Guillén-Navarro, E., Jarque, I., Posada, M., Vitoria, I., & Poveda, J. L. (2019). Development and validation of an MCDA framework for evaluation and decision-making of orphan drugs in Spain. Expert Opinion on Orphan Drugs, 7(7-8), 363372. https://doi.org/10.1080/21678707.2019.1652163
[7] Deshpande, P. C., Skaar, C., Brattebø, H., & Fet, A. M. (2020). Multi-criteria decision analysis (MCDA) method for assessing the sustainability of end-of-life alternatives for waste plastics: A case study of Norway. Science of the total environment, 719, 137353. https://doi.org/10.1016/ j.scitotenv.2020.137353
[8] Puška, A., Stević, Ž., & Pamučar, D. (2022). Evaluation and selection of healthcare waste incinerators using extended sustainability criteria and multi-criteria analysis methods. Environment, Development and Sustainability, 1-31. https://doi.org/10.1007/s10668-021-01902-2
[9] Colapinto, C., Jayaraman, R., Ben Abdelaziz, F., & La Torre, D. (2020). Environmental sustainability and multifaceted development: multi-criteria decision models with applications. Annals of Operations Research, 293(2), 405-432. https://doi.org/10.1007/s10479-019-03403-y
[10] Lahdelma, R., Miettinen, K., & Salminen, P. (2005). Reference point approach for multiple decision makers. European Journal of Operational Research, 164(3), 785-791. https://doi.org/10. 1016/j.ejor.2004.01.030
[11] Hatefi, S., & Torabi, S. A. (2010). A common weight MCDA-DEA approach to construct composite indicators. Ecological Economics, 70(1), 114-120. https://doi.org/10.1016/j.ecolecon.2010. 08.014
[12] Zborowski, M., & Chmielarz, W. (2023). Sensitivity analysis of the criteria weights used in selected MCDA methods in the multi-criteria assessment of banking services in Poland in 2022. 2023 18th Conference on Computer Science and Intelligence Systems (FedCSIS), 1217-1222. https: //doi.org/10.15439/2023F3745
[13] Martin, T. G., Burgman, M. A., Fidler, F., Kuhnert, P. M., Low-Choy, S., McBride, M., & Mengersen, K. (2012). Eliciting expert knowledge in conservation science. Conservation Biology, 26(1), 2938. https://doi.org/10.1111/j.1523-1739.2011.01806.x
[14] Paradowski, B., Shekhovtsov, A., Bączkiewicz, A., Kizielewicz, B., & Sałabun, W. (2021). Similarity Analysis of Methods for Objective Determination of Weights in Multi-Criteria Decision Support Systems. Symmetry, 13(10), 1874. https://doi.org/10.3390/sym13101874
[15] Kizielewicz, B., Paradowski, B., Więckowski, J., & Sałabun, W. (2022). Identification of weights in multi-cteria decision problems based on stochastic optimization. AMCIS 2022 Proceedings, (17). https://aisel.aisnet.org/amcis2O22/sig_odis/sig_odis/17
[16] Yoon, K. P., & Kim, W. K. (2017). The behavioral TOPSIS. Expert Systems with Applications, 89, 266-272. https://doi.org/10.1016/j.eswa.2017.07.045
[17] Kizielewicz, B., Więckowski, J., & Wątrobski, J. (2021). A study of different distance metrics in the TOPSIS method. Intelligent Decision Technologies: Proceedings of the 13th KES-IDT 2021 Conference, 275-284. https://doi.org/10.1007/978-981-16-2765-1_23
[18] Dancelli, L., Manisera, M., & Vezzoli, M. (2013). On two classes of Weighted Rank Correlation measures deriving from the Spearman’s . In Statistical models for data analysis (pp. 107-114). Springer. https://doi.org/10.1007/978-3-319-00032-9_13
[19] Kizielewicz, B., Shekhovtsov, A., & Sałabun, W. (2023). pymcdm-The universal library for solving multi-criteria decision-making problems. SoftwareX, 22, 101368. https://doi.org/10.1016/j. softx.2023.101368
[20] Sałabun, W., & Piegat, A. (2017). Comparative analysis of MCDM methods for the assessment of mortality in patients with acute coronary syndrome. Artificial Intelligence Review, 48, 557571. https://doi.org/10.1007/s10462-016-9511-9
[21] Van Thieu, N., & Mirjalili, S. (2023). MEALPY: An open-source library for latest meta-heuristic algorithms in Python. Journal of Systems Architecture, 139, 102871. https://doi.org/10.1016/j. sysarc.2023.102871