DOI: https://doi.org/10.1126/sciadv.adj4883
PMID: https://pubmed.ncbi.nlm.nih.gov/38295181
تاريخ النشر: 2024-01-31
مراقبة كسر تناظر عكس الزمن في بنية النطاق لمادة الألترمغناطيسية RuO2
الملخص
المغناطيسات البديلة هي فئة ناشئة من المغناطيسات المتوازية. على عكس المغناطيسات الحديدية، فإن التماثلات البلورية المميزة لها تمنع المغنطة، بينما على عكس المغناطيسات المضادة، فإنها تعزز الاستقطاب القوي للدوران في هيكل النطاق. وقد اعتُبر الآلية غير التقليدية المعنية لكسر تماثل عكس الزمن دون مغنطة في الطيف الإلكتروني كعلامة رئيسية للمغناطيسية البديلة، ولكن لم يتم تصورها تجريبيًا حتى الآن. نحن نلاحظ مباشرة كسرًا قويًا لتماثل عكس الزمن في هيكل النطاق للمغناطيس البديل.
أعمال الحكومة. موزعة بموجب ترخيص المشاع الإبداعي – النسبة للمؤلف
ترخيص 4.0 (CC BY).
مقدمة
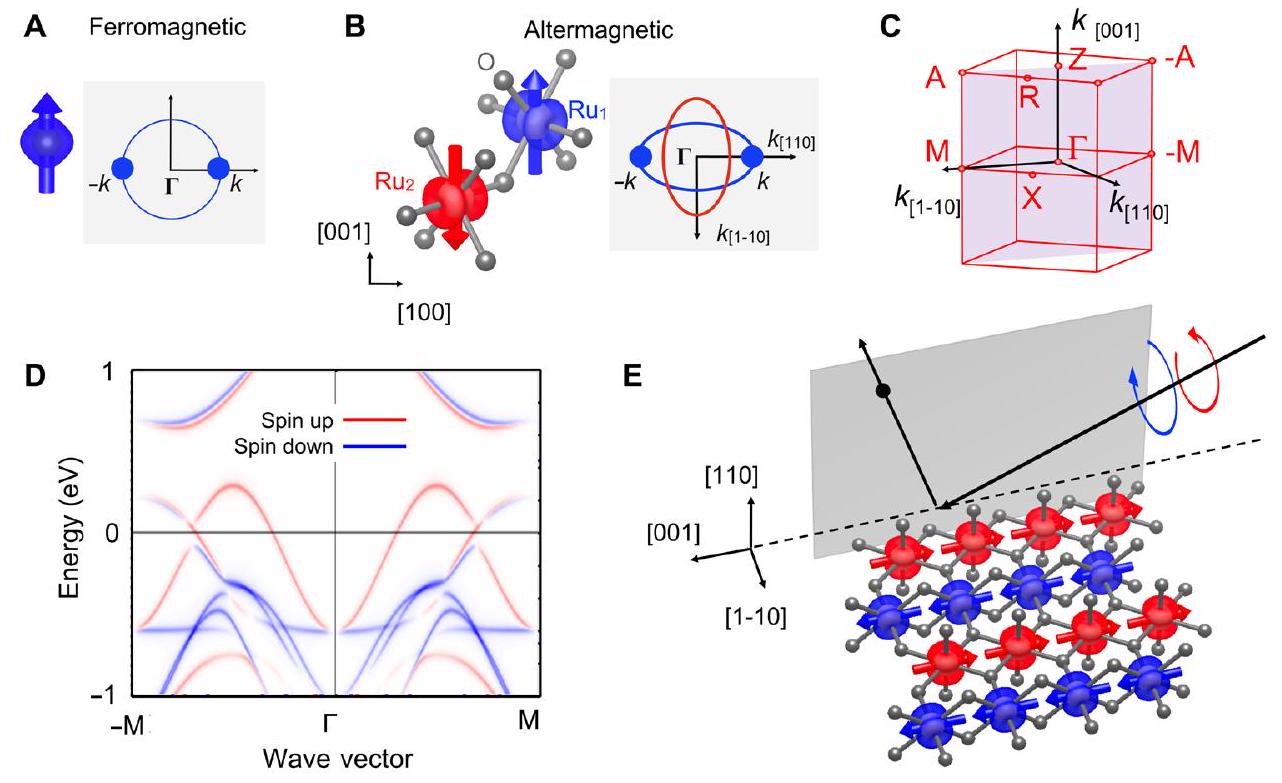
المغناطيسية الشبكية، مع التأكيد على الأصل التبادلي لرفع الكرامر المتعدد الذي تم ملاحظته.
النتائج
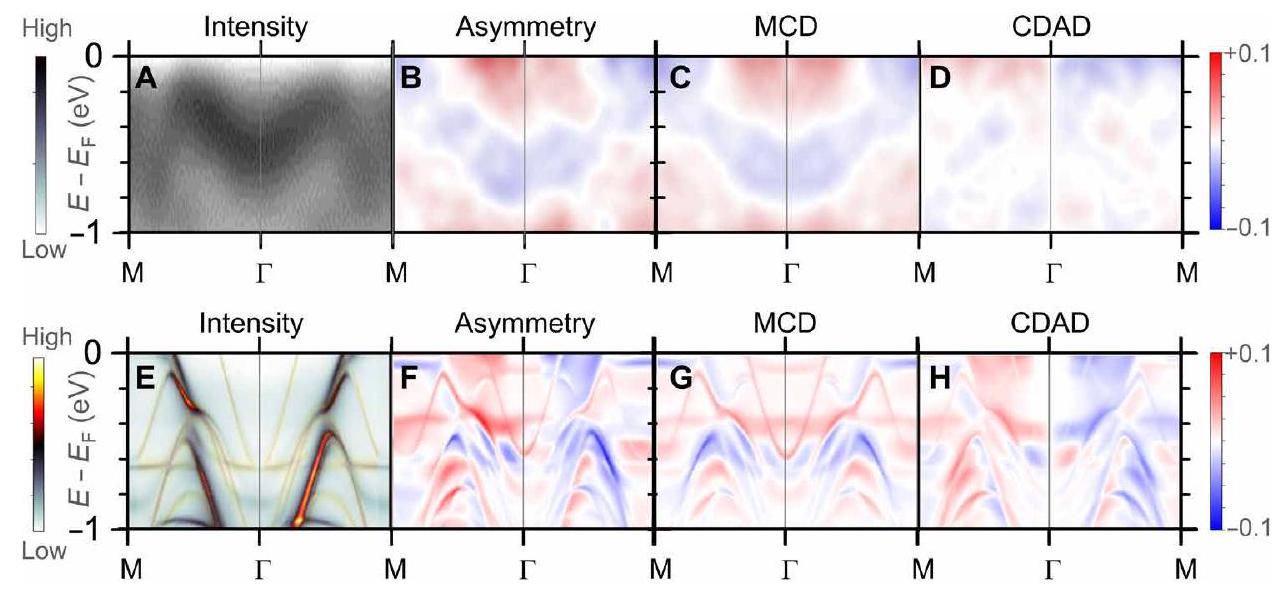
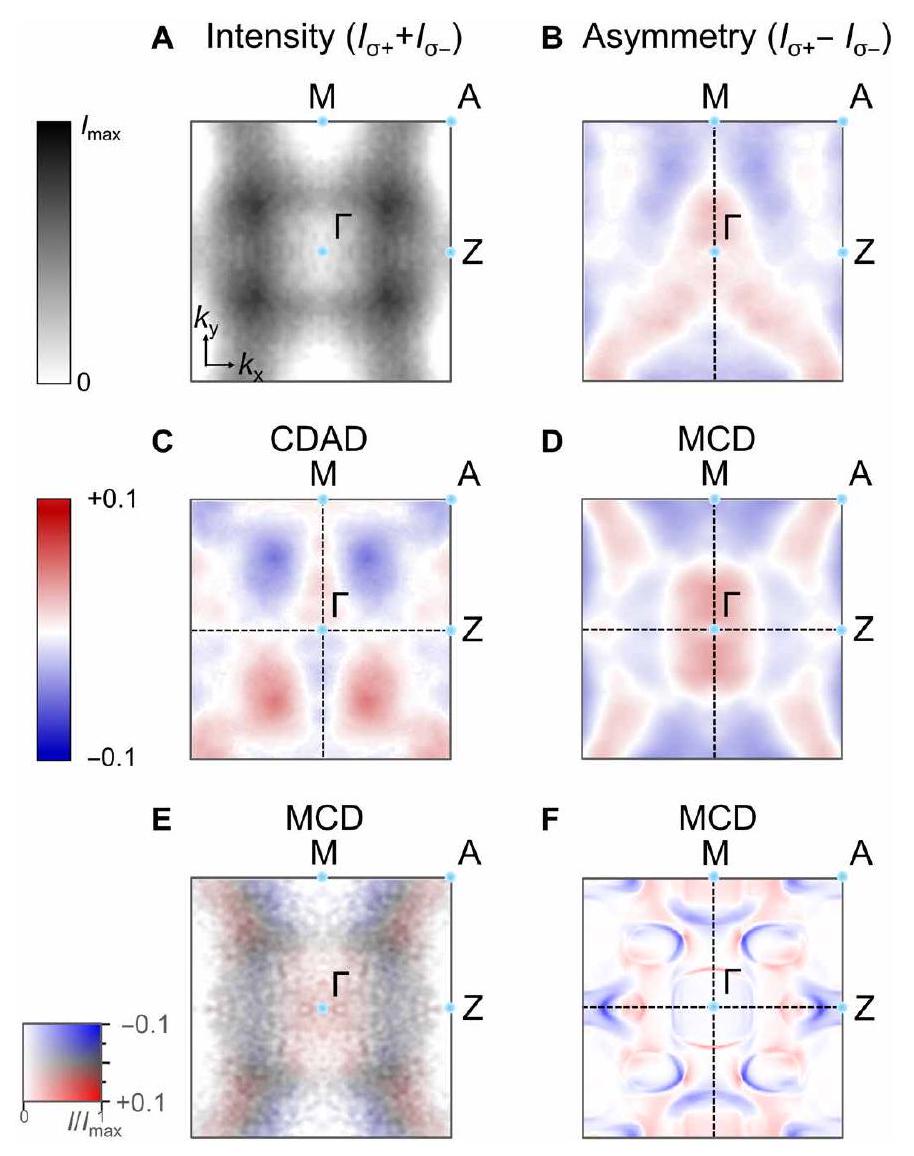
أن طيف MCD ليس خريطة مباشرة لاستقطاب الحالة الأساسية، كما هو موضح في (54)، بسبب تأثيرات الحالة النهائية. تأخذ الحسابات في الاعتبار الحالة النهائية الشبيهة بالإلكترون الحر عند النقطة المقابلة
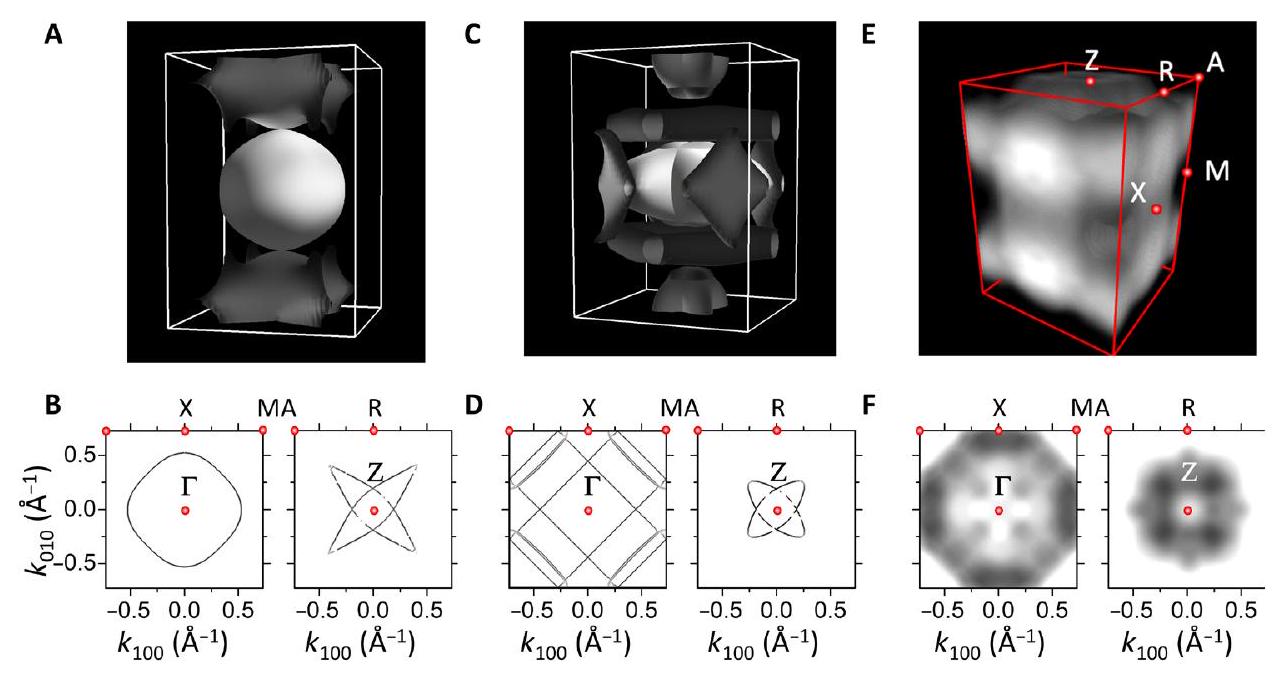
نقاش
المواد والأساليب
المواد التكميلية
يتضمن هذا الملف PDF:
الأشكال S1 إلى S9
المراجع
REFERENCES AND NOTES
- N. Nagaosa, J. Sinova, S. Onoda, A. H. MacDonald, N. P. Ong, Anomalous Hall effect. Rev. Mod. Phys. 82, 1539 (2010).
- Y. Tokura, K. Yasuda, A. Tsukazaki, Magnetic topological insulators. Nat. Rev. Phys. 1, 126-143 (2019).
- L. Šmejkal, A. H. MacDonald, J. Sinova, S. Nakatsuji, T. Jungwirth, Anomalous Hall antiferromagnets. Nat. Rev. Mater. 7, 482-496 (2022).
- C. Chappert, A. Fert, F. N. Van Dau, The emergence of spin electronics in data storage. Nat. Mater. 6, 813-823 (2007).
- D. C. Ralph, M. D. Stiles, Spin transfer torques. J. Magn. Magn. Mater. 320, 1190-1216 (2008).
- S. D. Bader, S. Parkin, Spintronics. Annu. Rev. Condens. Matter Phys. 1, 71-88 (2010).
- S. Bhatti, R. Sbiaa, A. Hirohata, H. Ohno, S. Fukami, S. Piramanayagam, Spintronics based random access memory: A review. Mater. Today 20, 530-548 (2017).
- T. Jungwirth, X. Marti, P. Wadley, J. Wunderlich, Antiferromagnetic spintronics. Nat. Nanotechnol. 11, 231-241 (2016).
- A. Manchon, J. Železný, I. M. Miron, T. Jungwirth, J. Sinova, A. Thiaville, K. Garello, P. Gambardella, Current-induced spin-orbit torques in ferromagnetic and antiferromagnetic systems. Rev. Mod. Phys. 91, 035004 (2019).
- T. Jungwirth, J. Sinova, A. Manchon, X. Marti, J. Wunderlich, C. Felser, The multiple directions of antiferromagnetic spintronics. Nat. Phys. 14, 200-203 (2018).
- V. Baltz, A. Manchon, M. Tsoi, T. Moriyama, T. Ono, Y. Tserkovnyak, Antiferromagnetic spintronics. Rev. Mod. Phys. 90, 015005 (2018).
- A. V. Kimel, M. Li, Writing magnetic memory with ultrashort light pulses. Nat. Rev. Mater. 4, 189-200 (2019).
- L. Šmejkal, J. Sinova, T. Jungwirth, Beyond conventional ferromagnetism and antiferromagnetism: A phase with nonrelativistic spin and crystal rotation symmetry. Phys. Rev. X 12, 031042 (2022).
- L. Šmejkal, J. Sinova, T. Jungwirth, Emerging research landscape of altermagnetism. Phys. Rev. X 12, 040501 (2022).
- H.-J. Elmers, S. V. Chernov, S. W. D’Souza, S. P. Bommanaboyena, S. Y. Bodnar, K. Medjanik, S. Babenkov, O. Fedchenko, D. Vasilyev, S. Y. Agustsson, C. Schlueter, A. Gloskovskii, Y. Matveyev, V. N. Strocov, Y. Skourski, L. Šmejkal, J. Sinova, J. Minár, M. Kläui, G. Schönhense, M. Jourdan, Néel vector induced manipulation of valence states in the collinear antiferromagnet
. ACS Nano 14, 17554-17564 (2020). - I. E. Dzyaloshinkii, J. Exptl. Theoret. Phys. 37, 881-882 (1959).
- T. Moriya, Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 120, 91-98 (1960).
- L. Šmejkal, R. González-Hernández, T. Jungwirth, J. Sinova, Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets. Sci. Adv. 6, eaaz8809 (2020).
- K. Samanta, M. Ležaić, M. Merte, F. Freimuth, S. Blügel, Y. Mokrousov, Crystal Hall and crystal magneto-optical effect in thin films of
. J. Appl. Phys. 127, 213904 (2020). - M. Naka, S. Hayami, H. Kusunose, Y. Yanagi, Y. Motome, H. Seo, Anomalous Hall effect in
-type organic antiferromagnets. Phys. Rev. B 102, 075112 (2020). - S. Hayami, H. Kusunose, Essential role of the anisotropic magnetic dipole in the anomalous Hall effect. Phys. Rev. B 103, L180407 (2021).
- I. I. Mazin, K. Koepernik, M. D. Johannes, R. González-Hernández, L. Šmejkal, Prediction of unconventional magnetism in doped FeSb
. Proc. Natl. Acad. Sci. U.S.A. 118, e2108924118 (2021). - R. D. Gonzalez Betancourt, J. Zubáč, R. Gonzalez-Hernandez, K. Geishendorf, Z. Šobáň, G. Springholz, K. Olejník, L. Šmejkal, J. Sinova, T. Jungwirth, S. T. B. Goennenwein, A. Thomas, H. Reichlová, J. Železný, D. Kriegner, Spontaneous anomalous hall effect arising from an unconventional compensated magnetic phase in a semiconductor. Phys. Rev. Lett. 130, 036702 (2023).
- M. Naka, Y. Motome, H. Seo, Anomalous Hall effect in antiferromagnetic perovskites. Phys. Rev. B 106, 195149 (2022).
- M. Naka, S. Hayami, H. Kusunose, Y. Yanagi, Y. Motome, H. Seo, Spin current generation in organic antiferromagnets. Nat. Commun. 10, 4305 (2019).
- R. González-Hernández, L. Šmejkal, K. Výborný, Y. Yahagi, J. Sinova, T. Jungwirth, J. Železný, Efficient electrical spin splitter based on nonrelativistic collinear antiferromagnetism. Phys. Rev. Lett. 126, 127701 (2021).
- M. Naka, Y. Motome, H. Seo, Perovskite as a spin current generator. Phys. Rev. B 103, 125114 (2021).
- H.-Y. Ma, M. Hu, N. Li, J. Liu, W. Yao, J.-F. Jia, J. Liu, Multifunctional antiferromagnetic materials with giant piezomagnetism and noncollinear spin current. Nat. Commun. 12, 2846 (2021).
- L. Šmejkal, A. B. Hellenes, R. González-Hernández, J. Sinova, T. Jungwirth, Giant and tunneling magnetoresistance in unconventional collinear antiferromagnets with nonrelativistic spin-momentum coupling. Phys. Rev. X 12, 011028 (2022).
- Z. Feng, X. Zhou, L. Šmejkal, L. Wu, Z. Zhu, H. Guo, R. González-Hernández, X. Wang, H. Yan, P. Qin, X. Zhang, H. Wu, H. Chen, Z. Meng, L. Liu, Z. Xia, J. Sinova, T. Jungwirth, Z. Liu, An anomalous Hall effect in altermagnetic ruthenium dioxide. Nat. Electron. 5, 735-743 (2022).
- A. Bose, N. J. Schreiber, R. Jain, D. F. Shao, H. P. Nair, J. Sun, X. S. Zhang, D. A. Muller, E. Y. Tsymbal, D. G. Schlom, D. C. Ralph, Tilted spin current generated by the collinear antiferromagnet ruthenium dioxide. Nat. Electron. 5, 267-274 (2022).
- H. Bai, L. Han, X. Feng, Y. Zhou, R. Su, Q. Wang, L. Liao, W. Zhu, X. Chen, F. Pan, X. L. Fan, C. Song, Observation of spin splitting torque in a collinear antiferromagnet
. Phys. Rev. Lett. 128, 197202 (2022). - S. Karube, T. Tanaka, D. Sugawara, N. Kadoguchi, M. Kohda, J. Nitta, Observation of spin-splitter torque in collinear antiferromagnetic
. Phys. Rev. Lett. 129, 137201 (2022). - A. Hariki, T. Yamaguchi, D. Kriegner, K. W. Edmonds, P. Wadley, S. S. Dhesi, G. Springholz, L. Šmejkal, K. Výborný, T. Jungwirth, J. Kuneš, X-ray magnetic circular dichroism in altermagnetic
-MnTe. arXiv:2305.03588 [cond-mat.mtrl-sci] (2023). - C. M. Schneider, M. S. Hammond, P. Schuster, A. Cebollada, R. Miranda, J. Kirschner, Observation of magnetic circular dichroism in UV photoemission from fcc cobalt films. Phys. Rev. B 44, 12066-12069 (1991).
- J. Bansmann, C. Westphal, M. Getzlaff, F. Fegel, G. Schönhense, Magnetic circular dichroism in valence-band photo-emission from Fe(100). J. Magn. Magn. Mater. 104-107, 1691-1692 (1992).
- J. Stöhr, Y. Wu, B. D. Hermsmeier, M. G. Samant, G. R. Harp, S. Koranda, D. Dunham, B. P. Tonner, Element-specific magnetic microscopy with circularly polarized x-rays. Science 259, 658-661 (1993).
- G. van der Laan, B.T.Thole, Spin polarization and magnetic dichroism in photoemission from core and valence states in localized magnetic systems. II. Emission from open shells. Phys. Rev. B 48, 210-223 (1993).
- J. Braun, The theory of angle-resolved ultraviolet photoemission and its applications to ordered materials. Rep. Prog. Phys. 59, 1267-1338 (1996).
- H. Ebert, J. Schwitalla, Magnetic dichroism in valence-band x-ray photoemission spectroscopy. Phys. Rev. B 55, 3100 (1997).
- J. Henk, T. Scheunemann, S. V. Halilov, R. Feder, Magnetic dichroism and electron spin polarization in photoemission: Analytical results. J. Phys. Condens. Matter 8, 47-65 (1996).
- T. Yokoyama, T. Nakagawa, Y. Takagi, Magnetic circular dichroism for surface and thin film magnetism: Measurement techniques and surface chemical applications. Int. Rev. Phys. Chem. 27, 449-505 (2008).
- K. Hild, J. Maul, G. Schönhense, H. J. Elmers, M. Amft, P. M. Oppeneer, Magnetic circular dichroism in two-photon photoemission. Phys. Rev. Lett. 102, 057207 (2009).
- T. Berlijn, P. Snijders, O. Delaire, H.-D. Zhou, T. Maier, H.-B. Cao, S.-X. Chi, M. Matsuda, Y. Wang, M. Koehler, P. R. C. Kent, H. H. Weitering, Itinerant antiferromagnetism in
. Phys. Rev. Lett. 118, 077201 (2017). - Z. Zhu, J. Strempfer, R. Rao, C. Occhialini, J. Pelliciari, Y. Choi, T. Kawaguchi, H. You, J. Mitchell, Y. Shao-Horn, R. Comin, Anomalous antiferromagnetism in metallic
determined by resonant x-ray scattering. Phys. Rev. Lett. 122, 017202 (2019). - K.-H. Ahn, A. Hariki, K.-W. Lee, J. Kuneš, Antiferromagnetism in
as -wave Pomeranchuk instability. Phys. Rev. B 99, 184432 (2019). - V. Jovic, R. J. Koch, S. K. Panda, H. Berger, P. Bugnon, A. Magrez, K. E. Smith, S. Biermann, C. Jozwiak, A. Bostwick, E. Rotenberg, S. Moser, Dirac nodal lines and flat-band surface state in the functional oxide
. Phys. Rev. B 98, 241101 (2018). - K. Medjanik, O. Fedchenko, S. Chernov, D. Kutnyakhov, M. Ellguth, A. Oelsner, B. Schönhense, T. R. F. Peixoto, P. Lutz, C.-H. Min, F. Reinert, S. Däster, Y. Acremann, J. Viefhaus, W. Wurth, H. J. Elmers, G. Schönhense, Direct 3D mapping of the Fermi surface and Fermi velocity. Nat. Mater. 16, 615-621 (2017).
- C. Westphal, J. Bansmann, M. Getzlaff, G. Schönhense, Circular dichroism in the angular distribution of photoelectrons from oriented CO molecules. Phys. Rev. Lett. 63, 151-154 (1989).
- H. Daimon, T. Nakatani, S. Imada, S. Suga, Circular dichroism from non-chiral and non-magnetic materials observed with display-type spherical mirror analyzer. J. Electron Spectrosc. Relat. Phenom. 76, 55-62 (1995).
- H. Ebert, D. Ködderitzsch, J. Minár, Calculating condensed matter properties using the KKR-Green’s function method—Recent developments and applications.Rep.Prog.Phys. 74, 096501 (2011).
- J. Braun, J. Minár, H. Ebert, Correlation, temperature and disorder: Recent developments in the one-step description of angle-resolved photoemission. Phys. Rep. 740, 1-34 (2018).
- L. Šmejkal, A. Marmodoro, K.-H. Ahn, R. Gonzalez-Hernandez, I. Turek, S. Mankovsky, H. Ebert, S. W. D’Souza, O. Šipr, J. Sinova, T. Jungwirth, Chiral magnons in altermagnetic
. arXiv:2211.13806 [cond-mat.mes-hall] (2022). - M. R. Scholz, J. Sánchez-Barriga, J. Braun, D. Marchenko, A. Varykhalov, M. Lindroos, Y. J. Wang, H. Lin, A. Bansil, J. Minár, H. Ebert, A. Volykhov, L. V. Yashina, O. Rader, Reversal of the circular dichroism in angle-resolved photoemission from
. Phys. Rev. Lett. 110, 216801 (2013). - J. Baruchel, M. Schlenker, B. Barbara,
Antiferromagnetic domains in by neutron topography. J. Magn. Magn. Mater. 15-18, 1510-1512 (1980). - G. Schönhense, Circular dichroism and spin polarization in photoemission from adsorbates and non-magnetic solids. Phys. Scr. 1990, 255-275 (1990).
- G. Derondeau, F. Bisti, M. Kobayashi, J. Braun, H. Ebert, V. A. Rogalev, M. Shi, T. Schmitt, J. Ma, H. Ding, V. N. Strocov, J. Minár, Fermi surface and effective masses in photoemission response of the
superconductor. Sci. Rep. 7, 8787 (2017). - O. Stejskal, M. Veis, J. Hamrle, Band structure analysis of the magneto-optical effect in bcc Fe. Sci. Rep. 11, 21026 (2021).
- H. Ebert, A. Perlov, S. Mankovsky, Incorporation of the rotationally invariant LDA + U scheme into the SPR-KKR formalism: Application to disordered alloys. Solid State Commun. 127, 443-446 (2003).
- P. Lloyd, Wave propagation through an assembly of spheres: II. The density of single-particle eigenstates. Proc. Phys. Soc. 90, 207-216 (1967).
Accepted 29 December 2023
Published 31 January 2024
10.1126/sciadv.adj4883
Institut für Physik, Johannes Gutenberg-Universität Mainz, Staudingerweg 7, D-55128 Mainz, Germany. University of West Bohemia, New Technologies Research Center, Plzen 30100, Czech Republic. Sumy State University, Rymski-Korsakov 2, 40007 Sumy, Ukraine. Linac Coherent Light Source, SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA. Deutsches Elektronen-Synchrotron DESY, 22607 Hamburg, Germany. Ruprecht Haensel Laboratory, Deutsches ElektronenSynchrotron DESY, 22607 Hamburg, Germany. Institut für Experimentalphysik, Universität Hamburg, 22761 Hamburg, Germany. Institut für Experimentelle und Angewandte Physik, Christian-Albrechts-Universität zu Kiel, 24098 Kiel, Germany. Institut für Experimentelle und Angewandte Physik, Christian-Albrechts-Universität zu Kiel, 24098 Kiel, Germany. Universität Kaiserslautern, Department of Physics, 67663 Kaiserslautern, Germany. Institute of Physics Academy of Sciences of the Czech Republic, Cukrovarnick’a 10, Praha 6, Czech Republic. School of Physics and Astronomy, University of Nottingham, NG7 2RD Nottingham, UK.
*Corresponding author. Email: elmers@uni-mainz.de
DOI: https://doi.org/10.1126/sciadv.adj4883
PMID: https://pubmed.ncbi.nlm.nih.gov/38295181
Publication Date: 2024-01-31
Observation of time-reversal symmetry breaking in the band structure of altermagnetic
Abstract
Altermagnets are an emerging elementary class of collinear magnets. Unlike ferromagnets, their distinct crystal symmetries inhibit magnetization while, unlike antiferromagnets, they promote strong spin polarization in the band structure. The corresponding unconventional mechanism of time-reversal symmetry breaking without magnetization in the electronic spectra has been regarded as a primary signature of altermagnetism but has not been experimentally visualized to date. We directly observe strong time-reversal symmetry breaking in the band structure of altermagnetic
Government Works. Distributed under a Creative Commons Attribution
License 4.0 (CC BY).
INTRODUCTION

net magnetization, emphasizing the exchange origin of the altermagnetic lifting of the Kramer’s degeneracy observed.
RESULTS
that the MCD spectra are not a direct map of the ground state polarization, as shown in (54), due to the final state effects. The calculations take into account the free electron-like final state at the corresponding


DISCUSSION
MATERIALS AND METHODS

Supplementary Materials
This PDF file includes:
Figs. S1 to S9
References
REFERENCES AND NOTES
- N. Nagaosa, J. Sinova, S. Onoda, A. H. MacDonald, N. P. Ong, Anomalous Hall effect. Rev. Mod. Phys. 82, 1539 (2010).
- Y. Tokura, K. Yasuda, A. Tsukazaki, Magnetic topological insulators. Nat. Rev. Phys. 1, 126-143 (2019).
- L. Šmejkal, A. H. MacDonald, J. Sinova, S. Nakatsuji, T. Jungwirth, Anomalous Hall antiferromagnets. Nat. Rev. Mater. 7, 482-496 (2022).
- C. Chappert, A. Fert, F. N. Van Dau, The emergence of spin electronics in data storage. Nat. Mater. 6, 813-823 (2007).
- D. C. Ralph, M. D. Stiles, Spin transfer torques. J. Magn. Magn. Mater. 320, 1190-1216 (2008).
- S. D. Bader, S. Parkin, Spintronics. Annu. Rev. Condens. Matter Phys. 1, 71-88 (2010).
- S. Bhatti, R. Sbiaa, A. Hirohata, H. Ohno, S. Fukami, S. Piramanayagam, Spintronics based random access memory: A review. Mater. Today 20, 530-548 (2017).
- T. Jungwirth, X. Marti, P. Wadley, J. Wunderlich, Antiferromagnetic spintronics. Nat. Nanotechnol. 11, 231-241 (2016).
- A. Manchon, J. Železný, I. M. Miron, T. Jungwirth, J. Sinova, A. Thiaville, K. Garello, P. Gambardella, Current-induced spin-orbit torques in ferromagnetic and antiferromagnetic systems. Rev. Mod. Phys. 91, 035004 (2019).
- T. Jungwirth, J. Sinova, A. Manchon, X. Marti, J. Wunderlich, C. Felser, The multiple directions of antiferromagnetic spintronics. Nat. Phys. 14, 200-203 (2018).
- V. Baltz, A. Manchon, M. Tsoi, T. Moriyama, T. Ono, Y. Tserkovnyak, Antiferromagnetic spintronics. Rev. Mod. Phys. 90, 015005 (2018).
- A. V. Kimel, M. Li, Writing magnetic memory with ultrashort light pulses. Nat. Rev. Mater. 4, 189-200 (2019).
- L. Šmejkal, J. Sinova, T. Jungwirth, Beyond conventional ferromagnetism and antiferromagnetism: A phase with nonrelativistic spin and crystal rotation symmetry. Phys. Rev. X 12, 031042 (2022).
- L. Šmejkal, J. Sinova, T. Jungwirth, Emerging research landscape of altermagnetism. Phys. Rev. X 12, 040501 (2022).
- H.-J. Elmers, S. V. Chernov, S. W. D’Souza, S. P. Bommanaboyena, S. Y. Bodnar, K. Medjanik, S. Babenkov, O. Fedchenko, D. Vasilyev, S. Y. Agustsson, C. Schlueter, A. Gloskovskii, Y. Matveyev, V. N. Strocov, Y. Skourski, L. Šmejkal, J. Sinova, J. Minár, M. Kläui, G. Schönhense, M. Jourdan, Néel vector induced manipulation of valence states in the collinear antiferromagnet
. ACS Nano 14, 17554-17564 (2020). - I. E. Dzyaloshinkii, J. Exptl. Theoret. Phys. 37, 881-882 (1959).
- T. Moriya, Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 120, 91-98 (1960).
- L. Šmejkal, R. González-Hernández, T. Jungwirth, J. Sinova, Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets. Sci. Adv. 6, eaaz8809 (2020).
- K. Samanta, M. Ležaić, M. Merte, F. Freimuth, S. Blügel, Y. Mokrousov, Crystal Hall and crystal magneto-optical effect in thin films of
. J. Appl. Phys. 127, 213904 (2020). - M. Naka, S. Hayami, H. Kusunose, Y. Yanagi, Y. Motome, H. Seo, Anomalous Hall effect in
-type organic antiferromagnets. Phys. Rev. B 102, 075112 (2020). - S. Hayami, H. Kusunose, Essential role of the anisotropic magnetic dipole in the anomalous Hall effect. Phys. Rev. B 103, L180407 (2021).
- I. I. Mazin, K. Koepernik, M. D. Johannes, R. González-Hernández, L. Šmejkal, Prediction of unconventional magnetism in doped FeSb
. Proc. Natl. Acad. Sci. U.S.A. 118, e2108924118 (2021). - R. D. Gonzalez Betancourt, J. Zubáč, R. Gonzalez-Hernandez, K. Geishendorf, Z. Šobáň, G. Springholz, K. Olejník, L. Šmejkal, J. Sinova, T. Jungwirth, S. T. B. Goennenwein, A. Thomas, H. Reichlová, J. Železný, D. Kriegner, Spontaneous anomalous hall effect arising from an unconventional compensated magnetic phase in a semiconductor. Phys. Rev. Lett. 130, 036702 (2023).
- M. Naka, Y. Motome, H. Seo, Anomalous Hall effect in antiferromagnetic perovskites. Phys. Rev. B 106, 195149 (2022).
- M. Naka, S. Hayami, H. Kusunose, Y. Yanagi, Y. Motome, H. Seo, Spin current generation in organic antiferromagnets. Nat. Commun. 10, 4305 (2019).
- R. González-Hernández, L. Šmejkal, K. Výborný, Y. Yahagi, J. Sinova, T. Jungwirth, J. Železný, Efficient electrical spin splitter based on nonrelativistic collinear antiferromagnetism. Phys. Rev. Lett. 126, 127701 (2021).
- M. Naka, Y. Motome, H. Seo, Perovskite as a spin current generator. Phys. Rev. B 103, 125114 (2021).
- H.-Y. Ma, M. Hu, N. Li, J. Liu, W. Yao, J.-F. Jia, J. Liu, Multifunctional antiferromagnetic materials with giant piezomagnetism and noncollinear spin current. Nat. Commun. 12, 2846 (2021).
- L. Šmejkal, A. B. Hellenes, R. González-Hernández, J. Sinova, T. Jungwirth, Giant and tunneling magnetoresistance in unconventional collinear antiferromagnets with nonrelativistic spin-momentum coupling. Phys. Rev. X 12, 011028 (2022).
- Z. Feng, X. Zhou, L. Šmejkal, L. Wu, Z. Zhu, H. Guo, R. González-Hernández, X. Wang, H. Yan, P. Qin, X. Zhang, H. Wu, H. Chen, Z. Meng, L. Liu, Z. Xia, J. Sinova, T. Jungwirth, Z. Liu, An anomalous Hall effect in altermagnetic ruthenium dioxide. Nat. Electron. 5, 735-743 (2022).
- A. Bose, N. J. Schreiber, R. Jain, D. F. Shao, H. P. Nair, J. Sun, X. S. Zhang, D. A. Muller, E. Y. Tsymbal, D. G. Schlom, D. C. Ralph, Tilted spin current generated by the collinear antiferromagnet ruthenium dioxide. Nat. Electron. 5, 267-274 (2022).
- H. Bai, L. Han, X. Feng, Y. Zhou, R. Su, Q. Wang, L. Liao, W. Zhu, X. Chen, F. Pan, X. L. Fan, C. Song, Observation of spin splitting torque in a collinear antiferromagnet
. Phys. Rev. Lett. 128, 197202 (2022). - S. Karube, T. Tanaka, D. Sugawara, N. Kadoguchi, M. Kohda, J. Nitta, Observation of spin-splitter torque in collinear antiferromagnetic
. Phys. Rev. Lett. 129, 137201 (2022). - A. Hariki, T. Yamaguchi, D. Kriegner, K. W. Edmonds, P. Wadley, S. S. Dhesi, G. Springholz, L. Šmejkal, K. Výborný, T. Jungwirth, J. Kuneš, X-ray magnetic circular dichroism in altermagnetic
-MnTe. arXiv:2305.03588 [cond-mat.mtrl-sci] (2023). - C. M. Schneider, M. S. Hammond, P. Schuster, A. Cebollada, R. Miranda, J. Kirschner, Observation of magnetic circular dichroism in UV photoemission from fcc cobalt films. Phys. Rev. B 44, 12066-12069 (1991).
- J. Bansmann, C. Westphal, M. Getzlaff, F. Fegel, G. Schönhense, Magnetic circular dichroism in valence-band photo-emission from Fe(100). J. Magn. Magn. Mater. 104-107, 1691-1692 (1992).
- J. Stöhr, Y. Wu, B. D. Hermsmeier, M. G. Samant, G. R. Harp, S. Koranda, D. Dunham, B. P. Tonner, Element-specific magnetic microscopy with circularly polarized x-rays. Science 259, 658-661 (1993).
- G. van der Laan, B.T.Thole, Spin polarization and magnetic dichroism in photoemission from core and valence states in localized magnetic systems. II. Emission from open shells. Phys. Rev. B 48, 210-223 (1993).
- J. Braun, The theory of angle-resolved ultraviolet photoemission and its applications to ordered materials. Rep. Prog. Phys. 59, 1267-1338 (1996).
- H. Ebert, J. Schwitalla, Magnetic dichroism in valence-band x-ray photoemission spectroscopy. Phys. Rev. B 55, 3100 (1997).
- J. Henk, T. Scheunemann, S. V. Halilov, R. Feder, Magnetic dichroism and electron spin polarization in photoemission: Analytical results. J. Phys. Condens. Matter 8, 47-65 (1996).
- T. Yokoyama, T. Nakagawa, Y. Takagi, Magnetic circular dichroism for surface and thin film magnetism: Measurement techniques and surface chemical applications. Int. Rev. Phys. Chem. 27, 449-505 (2008).
- K. Hild, J. Maul, G. Schönhense, H. J. Elmers, M. Amft, P. M. Oppeneer, Magnetic circular dichroism in two-photon photoemission. Phys. Rev. Lett. 102, 057207 (2009).
- T. Berlijn, P. Snijders, O. Delaire, H.-D. Zhou, T. Maier, H.-B. Cao, S.-X. Chi, M. Matsuda, Y. Wang, M. Koehler, P. R. C. Kent, H. H. Weitering, Itinerant antiferromagnetism in
. Phys. Rev. Lett. 118, 077201 (2017). - Z. Zhu, J. Strempfer, R. Rao, C. Occhialini, J. Pelliciari, Y. Choi, T. Kawaguchi, H. You, J. Mitchell, Y. Shao-Horn, R. Comin, Anomalous antiferromagnetism in metallic
determined by resonant x-ray scattering. Phys. Rev. Lett. 122, 017202 (2019). - K.-H. Ahn, A. Hariki, K.-W. Lee, J. Kuneš, Antiferromagnetism in
as -wave Pomeranchuk instability. Phys. Rev. B 99, 184432 (2019). - V. Jovic, R. J. Koch, S. K. Panda, H. Berger, P. Bugnon, A. Magrez, K. E. Smith, S. Biermann, C. Jozwiak, A. Bostwick, E. Rotenberg, S. Moser, Dirac nodal lines and flat-band surface state in the functional oxide
. Phys. Rev. B 98, 241101 (2018). - K. Medjanik, O. Fedchenko, S. Chernov, D. Kutnyakhov, M. Ellguth, A. Oelsner, B. Schönhense, T. R. F. Peixoto, P. Lutz, C.-H. Min, F. Reinert, S. Däster, Y. Acremann, J. Viefhaus, W. Wurth, H. J. Elmers, G. Schönhense, Direct 3D mapping of the Fermi surface and Fermi velocity. Nat. Mater. 16, 615-621 (2017).
- C. Westphal, J. Bansmann, M. Getzlaff, G. Schönhense, Circular dichroism in the angular distribution of photoelectrons from oriented CO molecules. Phys. Rev. Lett. 63, 151-154 (1989).
- H. Daimon, T. Nakatani, S. Imada, S. Suga, Circular dichroism from non-chiral and non-magnetic materials observed with display-type spherical mirror analyzer. J. Electron Spectrosc. Relat. Phenom. 76, 55-62 (1995).
- H. Ebert, D. Ködderitzsch, J. Minár, Calculating condensed matter properties using the KKR-Green’s function method—Recent developments and applications.Rep.Prog.Phys. 74, 096501 (2011).
- J. Braun, J. Minár, H. Ebert, Correlation, temperature and disorder: Recent developments in the one-step description of angle-resolved photoemission. Phys. Rep. 740, 1-34 (2018).
- L. Šmejkal, A. Marmodoro, K.-H. Ahn, R. Gonzalez-Hernandez, I. Turek, S. Mankovsky, H. Ebert, S. W. D’Souza, O. Šipr, J. Sinova, T. Jungwirth, Chiral magnons in altermagnetic
. arXiv:2211.13806 [cond-mat.mes-hall] (2022). - M. R. Scholz, J. Sánchez-Barriga, J. Braun, D. Marchenko, A. Varykhalov, M. Lindroos, Y. J. Wang, H. Lin, A. Bansil, J. Minár, H. Ebert, A. Volykhov, L. V. Yashina, O. Rader, Reversal of the circular dichroism in angle-resolved photoemission from
. Phys. Rev. Lett. 110, 216801 (2013). - J. Baruchel, M. Schlenker, B. Barbara,
Antiferromagnetic domains in by neutron topography. J. Magn. Magn. Mater. 15-18, 1510-1512 (1980). - G. Schönhense, Circular dichroism and spin polarization in photoemission from adsorbates and non-magnetic solids. Phys. Scr. 1990, 255-275 (1990).
- G. Derondeau, F. Bisti, M. Kobayashi, J. Braun, H. Ebert, V. A. Rogalev, M. Shi, T. Schmitt, J. Ma, H. Ding, V. N. Strocov, J. Minár, Fermi surface and effective masses in photoemission response of the
superconductor. Sci. Rep. 7, 8787 (2017). - O. Stejskal, M. Veis, J. Hamrle, Band structure analysis of the magneto-optical effect in bcc Fe. Sci. Rep. 11, 21026 (2021).
- H. Ebert, A. Perlov, S. Mankovsky, Incorporation of the rotationally invariant LDA + U scheme into the SPR-KKR formalism: Application to disordered alloys. Solid State Commun. 127, 443-446 (2003).
- P. Lloyd, Wave propagation through an assembly of spheres: II. The density of single-particle eigenstates. Proc. Phys. Soc. 90, 207-216 (1967).
Accepted 29 December 2023
Published 31 January 2024
10.1126/sciadv.adj4883
Institut für Physik, Johannes Gutenberg-Universität Mainz, Staudingerweg 7, D-55128 Mainz, Germany. University of West Bohemia, New Technologies Research Center, Plzen 30100, Czech Republic. Sumy State University, Rymski-Korsakov 2, 40007 Sumy, Ukraine. Linac Coherent Light Source, SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA. Deutsches Elektronen-Synchrotron DESY, 22607 Hamburg, Germany. Ruprecht Haensel Laboratory, Deutsches ElektronenSynchrotron DESY, 22607 Hamburg, Germany. Institut für Experimentalphysik, Universität Hamburg, 22761 Hamburg, Germany. Institut für Experimentelle und Angewandte Physik, Christian-Albrechts-Universität zu Kiel, 24098 Kiel, Germany. Institut für Experimentelle und Angewandte Physik, Christian-Albrechts-Universität zu Kiel, 24098 Kiel, Germany. Universität Kaiserslautern, Department of Physics, 67663 Kaiserslautern, Germany. Institute of Physics Academy of Sciences of the Czech Republic, Cukrovarnick’a 10, Praha 6, Czech Republic. School of Physics and Astronomy, University of Nottingham, NG7 2RD Nottingham, UK.
*Corresponding author. Email: elmers@uni-mainz.de
