مشغلات تجميع هاماشر لمجموعة فuzzy البيثاغورية وتطبيقها في مشكلة اتخاذ القرار متعددة السمات Hamacher Aggregation Operators for Pythagorean Fuzzy Set and its Application in Multi-Attribute Decision-Making Problem

المجلة: Spectrum of Operational Research.، المجلد: 2، العدد: 1
DOI: https://doi.org/10.31181/sor2120258
تاريخ النشر: 2024-08-24

مشغلات تجميع هاماشر لمجموعة فuzzy البيثاغورية وتطبيقها في مشكلة اتخاذ القرار متعددة السمات

محمد أسيف عمر إشتياق يوانس ك. أرجيروس 1 كلية الرياضيات والإحصاء، جامعة جنوب الوسط، تشانغشا 4100083، الصين2 قسم الرياضيات، جامعة قائد أعظم، إسلام آباد 45320، باكستان3 قسم علوم الحوسبة والرياضيات، جامعة كاميرون، لوتون، أوكلاهوما 73505، الولايات المتحدة الأمريكية

معلومات المقال

تاريخ المقال:

تم الاستلام في 13 مايو 2024
تم استلامه بصيغة معدلة في 29 يوليو 2024
تم القبول في 19 أغسطس 2024
متاح على الإنترنت 24 أغسطس 2024

الكلمات المفتاحية:

مجموعة ضبابية؛ مجموعة ضبابية فيثاغورية؛ معايير هاماشر t؛ عوامل التجميع؛ اتخاذ القرار متعدد المعايير.

الملخص

المجموعة الضبابية البايثاغورية هي توسيع مفيد للمجموعة الضبابية الحدسية للتعامل مع الغموض، الذي يحدث غالبًا في مشاكل الحياة الواقعية. كما أن معيار هاماشر t-norm يحتوي على معايير مهمة ومتوافقة تتضمن معلمة تقدم خيارات متنوعة لصانعي القرار خلال عملية دمج المعلومات، مما يعزز قدرتهم على نمذجة مشاكل اتخاذ القرار بشكل فعال مقارنة بالطرق البديلة. في هذه الدراسة، يتم استخدام مشغلات هاماشر لتقديم عدة مشغلات متوسطة وزنية تفاعلية ضبابية بايثاغورية (PFHIWA)، ومتوسطة مرتبة وزنية تفاعلية ضبابية بايثاغورية (PFHIOWA)، وهندسية وزنية تفاعلية ضبابية بايثاغورية (PFHIWG)، وهندسية مرتبة وزنية تفاعلية ضبابية بايثاغورية (PFHIOWG). يتم فحص خصائص هذه المشغلات بالتفصيل. فائدة استخدام المشغلات التقدمية هي أنها تقدم فهمًا أكبر للسيناريو لصانعي القرار. يتم استخدام المشغلات المقترحة لتفصيل اتخاذ القرار متعدد المعايير (MADM). من خلال عرض تحليل الحساسية، يظهر أن مشغلنا المقترح يتمتع باستقرار عالٍ يتعلق باتخاذ القرار متعدد المعايير (MADM) تحت مجموعة البيانات الضبابية البايثاغورية.

1. المقدمة

اتخاذ القرار (DM) أمر حيوي لحل المشكلات، وتحقيق الأهداف، وتخصيص الموارد بشكل فعال. إنه يسهل الابتكار، وإدارة المخاطر، وحل النزاعات، بينما يمكّن الأفراد والمنظمات من التكيف مع التغيير ودفع التحسين المستمر. كان زاده [1] هو الأول الذي قدم مفهوم مجموعة الضباب (FS)، التي كانت تحتوي فقط على درجة العضوية (MDg). وقد حظيت بمزيد من الاهتمام حيث تتعامل نظرية FS مع الغموض في البيانات. ثم، قام أتاناسوف [2] بتوسيع هذا المفهوم من FS وقدم فكرة مجموعة الضباب الحدسية (IFS) التي كانت تحتوي على درجة عدم العضوية (NMDg) بجانب MDg. هذا يعزز دراسة FS، وبدأ العديد من الباحثين في إيلاء اهتمام لهذا المجال. ومع ذلك، كانت IFS لها بعض القيود، مثل مجموع MDg وNMDg.
كونه بين 0 و 1. للتغلب على هذه المشكلة، قدم ياجر [3] فكرة مجموعة فuzzy البيثاغورية (PyFS).
في PyFS، مجموع مربع MDg و NMDg يتراوح بين 0 و 1، أي، 1 (الشكل 1). عرّف ياجر [4] القواعد التشغيلية وخصائص أخرى لـ PyFS وقارنها مع IFS. اقترح بينغ ويانغ [5] القسمة والطرح لـ PyFS وطوروا طريقة تصنيف للتفوق والتفوق الأدنى لـ PyFS. طور ياجر وأباسوف [6] مشغلات التجميع المتوسطة والهندسية (AOs) بناءً على PyFS. في دراستهم، استخدم تشانغ وشو [7] طريقة TOPSIS على PyFS لحل مشاكل اتخاذ القرار. تم إجراء تحليل ببليومتري لـ PyFS بواسطة لين وآخرون [8]. قدم لي ولو [9] بعض التشابهات الفريدة ومقاييس المسافة لـ PyFS واستخدموها في قضايا تتعلق بالحياة الواقعية. تم تصميم PyFS الدائري بواسطة أولغون وأونفير [10] وأظهروا تطبيقاتهم باستخدام هذه المشغلات في قضايا اتخاذ القرار متعددة الخصائص (MADM). قدم أكرم وآخرون [11] طريقة تحسين جديدة تحت بيئة PyFS. في نفس السياق، قام العديد من الباحثين بعمل قائم على PyFS [12-17].
الشكل 1. مجموعة فuzzy البيثاغورية
من بين ما ذُكر أعلاه، يُلاحظ أن الباحثين المختلفين استخدموا أساليب مختلفة لتعزيز دراساتهم. بشكل عام، كانت قواعد AOs المعتادة تفترض عادةً قواعد جبرية بسيطة. Tnorms ( ) و t-التوافقات ( ) تُستخدم على نطاق واسع في FS وهي مهمة بسبب التعبيرات الجبرية. تم استخدام رقم أينشتاين [18]، ورقم أرخميدس [19]، ورقم فرانك [20] على نطاق واسع في تطوير AOs مختلفة في FS. قدم سرفراز [21] مشغلات متوسط دومي هامي الكروية الضبابية ذات القيم الفترية كأداة قوية لاتخاذ القرار الجماعي باستخدام رقم دومي. عرّف تيشيك ومارينكوفيتش [22] مشغلات التجميع العادية باستخدام مشغلات متوسط بونفيروني. كما أن رقم هاماشر t-Nr [23] له أهمية وتوافق كبير. تتضمن هذه المعايير معلمة تقدم خيارات متنوعة لصانعي القرار خلال عملية دمج المعلومات، مما يعزز قدرتهم على نمذجة مشاكل اتخاذ القرار بشكل فعال مقارنة بالطرق البديلة. طور هوانغ [24] AOs في بيئة رقم هاماشر t-Nr. درس تانغ وآخرون [25] تحليل AOs هاماشر وتأثيرها على مشاكل MADM. تم تقديم AOs اللغوية q -ROFS المستندة إلى رقم هاماشر t-Nr بواسطة ديب وآخرون [26]. كما استخدم غارغ [27] رقم هاماشر T-Nr لتطوير بعض AOs الجديدة واستخدم هذه AOs بواسطة طريقة الانتروبيا لمشكلة MADM. هناك دراسات مفيدة [28-32] لفهم رقم هاماشر t-Nr.
استنادًا إلى العيوب البحثية المعترف بها، نقترح AOs مصممة خصيصًا لـ PyFS. تكشف دراستنا عن AOs المتوسطة الموزونة والهندسية، مستفيدة من عمليات معيار هاماشر. هذه
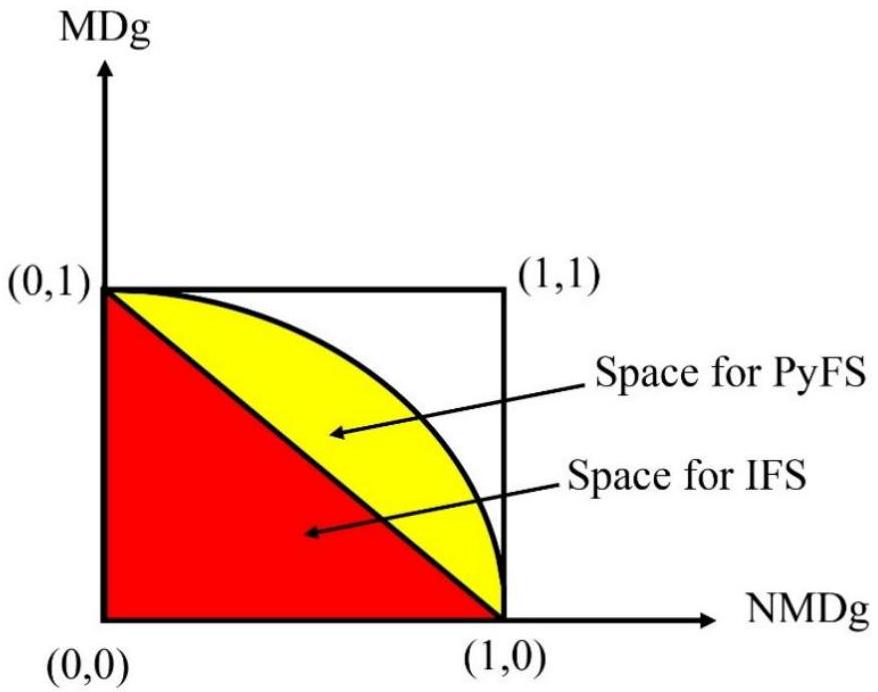
يقدم المشغلون خدماتهم وفقًا للتفضيلات المعبر عنها من خلال PyFS. ومن الجدير بالذكر أن الترتيب النسبي للبدائل يعتمد بشكل كبير على اختيار متجهات الوزن المخصصة لـ PyFSs، مما يبرز أهمية التمييز بين التعيينات المناسبة للأوزان. تسعى هذه المساهمة إلى معالجة الفجوات في منهجيات اتخاذ القرار من خلال تقديم أدوات محسّنة للتعامل مع عدم اليقين والغموض.
نمط الورقة هو كما يلي: في القسم 2، هناك بعض المفاهيم الأساسية والتعريفات. يقدم القسم 3 عمليات محسّنة على هاماشر. تحت بيئة PyFS، يقدم هذا النص متوسط الوزن التفاعلي PFH (PFHIWA)، ومتوسط الوزن المرتب التفاعلي PFH (PFHIOWA)، والهندسة التفاعلية ذات الوزن PFH (PFHIWG) والهندسة المرتبة التفاعلية ذات الوزن PFH (PFHIOWG) على التوالي. تم مناقشة تقنية MADM بإيجاز في القسم 4 لمعالجة المشغلين المقترحين. في القسم 5، أظهرنا تطبيقات المشغلين المقترحين من خلال مثال عملي. تم تخصيص القسمين 6 و 7 لتحليل الحساسية والتحليل المقارن لإظهار استقرار وأهمية مشغلينا. في القسم 8، يقدم استنتاج هذا العمل رؤى حول النتائج المهمة ويقترح اتجاهات مستقبلية لمزيد من البحث.

2. المقدمات

ستتناول هذه القسم بعض التعريفات والقواعد الأساسية التي ستساعد في بناء ورقتنا.
التعريف 1 [2]. IFS T المعرفة في Y هي مجموعة مرتبة مقدمة بواسطة
أين تمثل MDg و NMDg للعنصر y بحيث و لكل y.
التعريف 2 [3]. إن PyFS T المحدد في Y هو ألم مرتب مقدم بواسطة
أين تمثل MDg و NMDg للعنصر y بحيث و لكل y.
التعريف 3 [5]. يتم إعطاء دالة الدرجة SF لأي PyFN بواسطة

عند استخدام SF لاثنين من PyFNs، يتم استخدام دالة الدقة (AF) لمقارنتهما.
التعريف 4. يتم إعطاء AF لأي PyFN بواسطة
التعريف 5 [19]. دالة : [ 0,1 ] يُعرف بـ t-Nr إذا كان يحتفظ بخصائص الأحادية، التبادلية، شروط الحدود، والترابط. على العكس من ذلك، فإن دالة Q المعرفة بواسطة للجميع يُعرف باسم t-CNr.
التعريف 6 [19]. الأرخميدية الدالة G هي دالة مستمرة الذي يفي بالشرط لـ أرخميدس صارم يزداد بشكل صارم .
التعريف 7 [23]. عرّف غارغ عمليات bnorm من خلال اعتبار لنوعين مختلفين من IFN و مثل:
(ط)
(ii)
التعريف 8 [24]. لمجموعة من IFNS اقترح هوانغ AOs، والتي تُعرف كما يلي
و
التعريف 9 [27]. لمجموعة من IFNS اقترح غارغ تحسينات على AOs، والتي تم توضيحها في [24]، والتي تُعرف على أنها
𝕕𝕕𝕕𝕕𝕕𝕕𝕕𝕕
و

3. تحسين القوانين التشغيلية وعوامل التجميع لمجموعة فuzzy البيثاغورية

سنقدم بعض القواعد والقوانين الجديدة التي ستكون مفيدة في دراسة AOs.
تعريف 10. لنفترض و لتكن مجموعة من PyFNs، ثم يمكن تعريف القوانين التشغيلية الجديدة باستخدام معيار هاماشر لهذه الأعداد على النحو التالي:
(ط)
(ii)
(iii)
(iv)
أين و هي الأعداد الحقيقية.
يمكن ملاحظة في التعريف 10 أن عملية الجمع أصبحت أكثر تفاؤلاً من الجمع المحدد في التعريف 7. وبالتالي، فإن السلوك يميل أكثر نحو MD من NMD. لذا، ستكون النتيجة أكثر دقة.

3.1 مشغلات المتوسطات

لمجموعة من مع للجميع وبالاعتماد على القواعد المذكورة أعلاه، سنقدم مشغلات التوسط التفاعلية الموزونة (PFHIWA) والموزونة حسب الطلب (PFHIOWA).
التعريف 11. لنفترض أن Y هو مجموعة PyNFs و PFHIWA: بحيث:
đđđ
أين 𝕕𝕕𝕕𝕕هو متجه الوزن لـ بحيث 𝕕 و 𝕕; ثم، يتم تعريف PFHIWA كعامل متوسط مرجح تفاعلي PFH.
النظرية 1. بالنسبة لـ PyFNs مع القيمة المجمعة باستخدام PFHIWA هي مرة أخرى PyFN وتُعرف على النحو التالي:
برهان: سنثبت النظرية 1 بواسطة الاستقراء الرياضي. لذا، لدينا
عندما لدينا و đ. الآن، بالنسبة لـ PyFNs و لدينا

و

لذا، لدينا
đđ



لذا، المعادلة (4) صحيحة لـ
II. افترض أن المعادلة (4) صحيحة أيضًا لـ
III. الآن، لـ لدينا
đℊℊℊℊℊℊ
لذا، المعادلة (4) تنطبق أيضًا على .
ومن ثم، تم إثبات أن المعادلة (4) صحيحة لجميع الأعداد الصحيحة الموجبة. .
الآن، سنحدد بعض الخصائص لـ PFHIWA.
النظرية 2 (التماثل). إذا كان لكل i إذن .
برهان: لمجموعة من PyFNs و متجه الوزن đبحيث đ و đ 1. افترض لكل i إذن بواسطة مشغل PFHIWA، لدينا
đđđ
النظرية 3 (الحدود). افترض أن هو مشغل PFHIWA، و .
الدليل: بما أن و و ليكن m مشغل PFHIWA. لذا، وفقًا للنظرية 1، لدينا
đđđđđđ
منذ đ. لذا، لدينا
و
لذلك، .
النظرية 4 (التزايدية). لمجموعات من نوعين مختلفين من PyFNs و بحيث للجميع و لكي تكون مشغل PFHIWA، إذن .
الدليل: الدليل هو نفسه كما في الأعلى.
سنقوم بعرض مشغل المتوسط المرجح المرتب حسب PFH (PFHIOWA).
تعريف 12. لنفترض أن Y هو مجموعة PyNFs و PFHIOW A: بحيث:
đđđ
أين كن التباديل بحيث و هو متجه الوزن المعاير لـ .
النظرية 5. بالنسبة لـ PyFNs مع القيمة المجمعة باستخدام PFHIOWA هي مرة أخرى PyFN وتُعرف على النحو التالي:
الخصائص الخاصة بـ PFHIOWA محددة أدناه.
نظرية 6 (التماثل). إذا كان لكل i ثم PFHIOWA .
نظرية 7 (الحدود). لنفترض أن m هو مشغل PFHIOWA، ، و .
النظرية 8 (التزايدية). لمجموعات من نوعين مختلفين من PyFNs و بحيث لكل i و m أن يكونا مشغل PFHIOWA، إذن

3.2 المشغلين الهندسيين

لمجموعة من مع للجميع وبالاعتماد على القواعد المذكورة أعلاه، سنقدم مشغلات هندسية تفاعلية موزونة جديدة (PFHIWG) وموزونة حسب الطلب (PFHIOWG).
التعريف 13. لنفترض أن Y هو مجموعة PyNFs و PFHIWA: بحيث:
أين هو متجه الوزن لـ بحيث و ; ثم، يتم تعريف PFHIWG كعامل هندسي تفاعلي مرجح لـ PFH.
النظرية 9. بالنسبة لـ PyFNs مع القيمة المجمعة باستخدام PFHIWG هي مرة أخرى PyFN وتُعرف على النحو التالي:
برهان: سنثبت النظرية 9 بواسطة الاستقراء الرياضي. لذا، لدينا
عندما لدينا و . الآن، بالنسبة لـ PyFNs و لدينا
ℊ
و
ℊ
لذا، لدينا
لذا، المعادلة (5) صحيحة لـ
II. افترض أن المعادلة (5) صحيحة أيضًا لـ
III. الآن، لـ لدينا
لذا، المعادلة (5) تنطبق أيضًا على .
ومن ثم، تم إثبات أن المعادلة (5) صحيحة لجميع الأعداد الصحيحة الموجبة .
الآن، سنحدد بعض الخصائص لـ PFHIWG.
النظرية 10 (التماثل). إذا كان لكل i ثم PFHIWG .
برهان: لمجموعة من PyFNs و متجه الوزن đبحيث đ و đ 1. افترض للجميع ثم بواسطة مشغل PFHIWG، لدينا
النظرية 11 (الحدية). لنفترض أن m هو مشغل PFHIWG، ، و .
الدليل: بما أن و و كن مشغل PFHIWG. لذا، وفقًا لنظرية 1، لدينا
đđđđđđ
منذ đ. لذا، لدينا
و
لذلك، .
النظرية 12 (التزايدية). لمجموعات من اثنين من PyFNs المختلفين و بحيث للجميع و لكي تكون مشغل PFHIWG، إذن .
الدليل: الدليل هو نفسه كما في الأعلى.
الآن، سنعرض مشغل الهندسة الوزنية المرتبة PFH (PFHIOWG).
التعريف 14. لنفترض أن Y هو مجموعة PyNFs و PFHIOWG: بحيث:
أين كن التباديل بحيث و هو متجه الوزن المعاير لـ .
النظرية 13. بالنسبة لـ PyFNs مع القيمة المجمعة باستخدام PFHIOWG هي مرة أخرى PyFN وتُعرف على النحو التالي:
الخصائص لـ PFHIOWG محددة أدناه.
النظرية 14 (التماثل). إذا كان لكل i إذن .
نظرية 15 (الحدود). لنفترض أن m هو مشغل PFHIOWG، ، و .
النظرية 16 (التزايدية). لمجموعات من نوعين مختلفين من PyFNs و بحيث للجميع و لكي تكون مشغل PFHIOWG، إذن .

4. تقنية اتخاذ القرار متعددة الخصائص

ستعرض هذه القسم طريقة اتخاذ القرار لحل مشكلة MADM في ظل ظروف PyF. في الحياة اليومية، ينطوي اتخاذ القرار على اختيار الخيار الأفضل من مجموعة من الخيارات. عادةً ما يعتمد صانعو القرار على الحدس والخبرة. ومع ذلك، نظرًا لأن مشاكل اتخاذ القرار يمكن أن تكون معقدة، فإن تمثيل المعلومات الضبابية وغير الواضحة بدقة أمر بالغ الأهمية. لالتقاط تفضيلات صانعي القرار، تعتبر علاقات التفضيل أدوات قيمة لترتيب المعايير. لمجموعة من المعايير ، “ يقوم الخبراء بمقارنة كل زوج وبناء علاقات تفضيل.
سنناقش الخطوات المتبعة في تقنية MADM.
الخطوة 1. أولاً، نقوم بإنشاء مصفوفة قرار بيانات PyF. ثم يتم تحويل هذه المصفوفة إلى المصفوفة المعيارية.
الخطوة 2. ثم، باستخدام المشغل المقترح لدينا، يتم تحويل جميع بيانات PyF إلى قيمة واحدة.
الخطوة 3. ابحث عن قيم الدرجات باستخدام SF. إذا كانت قيم الدرجات متساوية، نقوم بحساب الدقة باستخدام AF. لذا، سيكون الترتيب بناءً على قيم الدقة.
الخطوة 4. يتم العثور على الخيار الأفضل وفقًا لترتيب الخيارات.
الخطوة 5. النهاية.
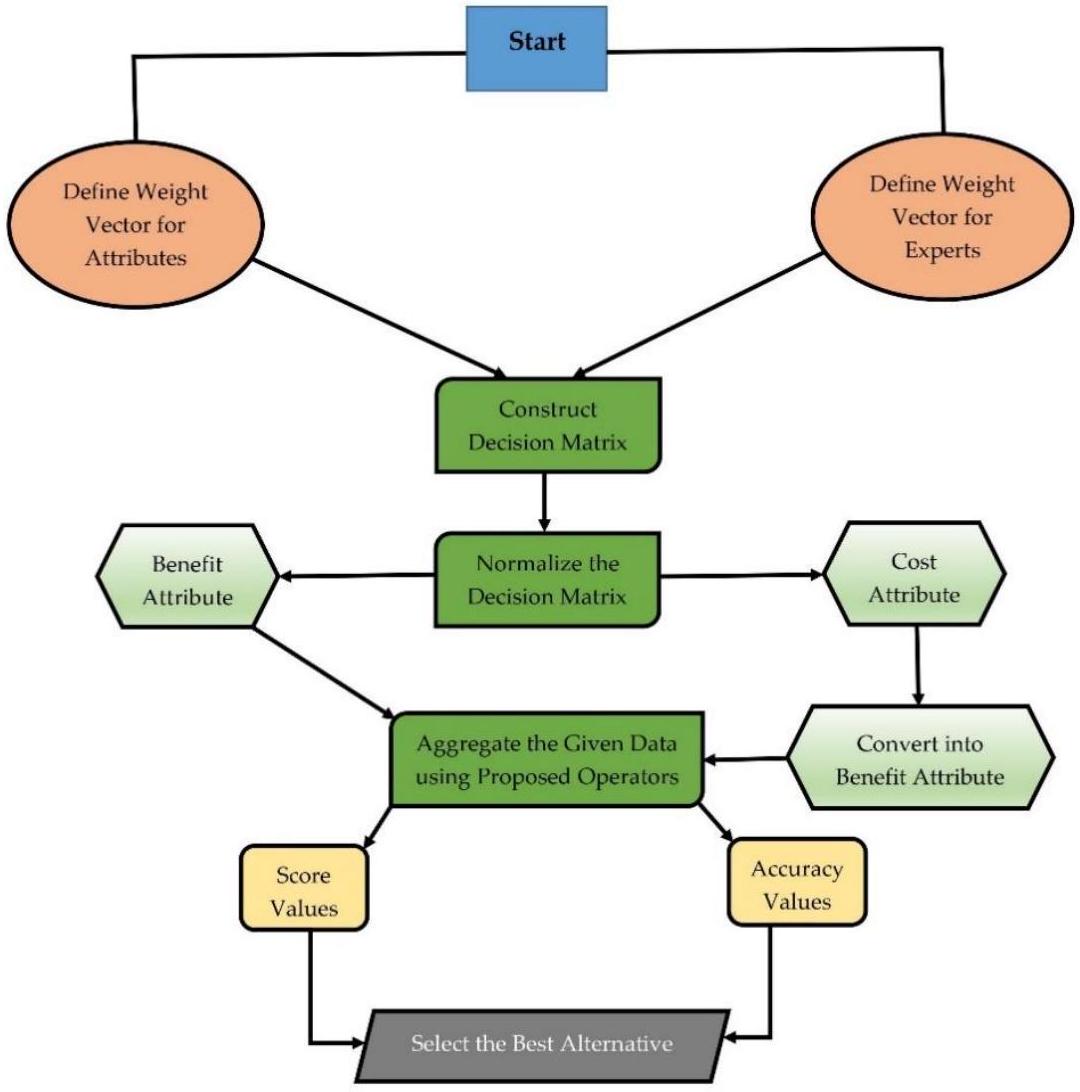
مخطط التدفق لـ MADM موضح في الشكل 2.
الشكل 2. مخطط انسيابي لتقنية MADM

5. مثال عملي

هذا السيناريو يتضمن مؤسسة تقع في المنطقة الصناعية في خواريز، المكسيك، وتحديداً ضمن قطاع الماكيلادوراس، المتخصص في تصنيع التجميع. أطلقت الشركة مشروعاً يهدف إلى خفض التكاليف، حيث تم تحديد التعبئة والتغليف كمنطقة هامة لتحقيق وفورات محتملة. لتحقيق هذا الهدف، تخطط الشركة لتقييم خمسة موردين يقدمون التعبئة والتغليف للمكونات الإلكترونية. تم دعوة اثنين من صانعي القرار للمشاركة في عملية التقييم. تم وضع أربعة معايير (التكلفة، الخدمة، وقت التسليم، والجودة) لتقييم ومقارنة عروض الموردين بشكل شامل لضمان تقييم كامل. لذلك، يتم الإشارة إلى مجموعة الموردين على أنها يحدد صانع القرار أوزان السمات على النحو التالي: سيشمل تقييم المرشحين الأربعة تقييم الغموض باستخدام بيانات PyF عبر السمات الأربعة الموضحة في الجدول 1.
الجدول 1
مصفوفة PyF للموردين
الآن، بعد استخدامنا لـ PFHIWA المقترح على البيانات المعطاة، نحصل على النتائج المدرجة في الجدول 2.
الجدول 2
النتائج حسب PFHIWA
مشغل PFHIWA
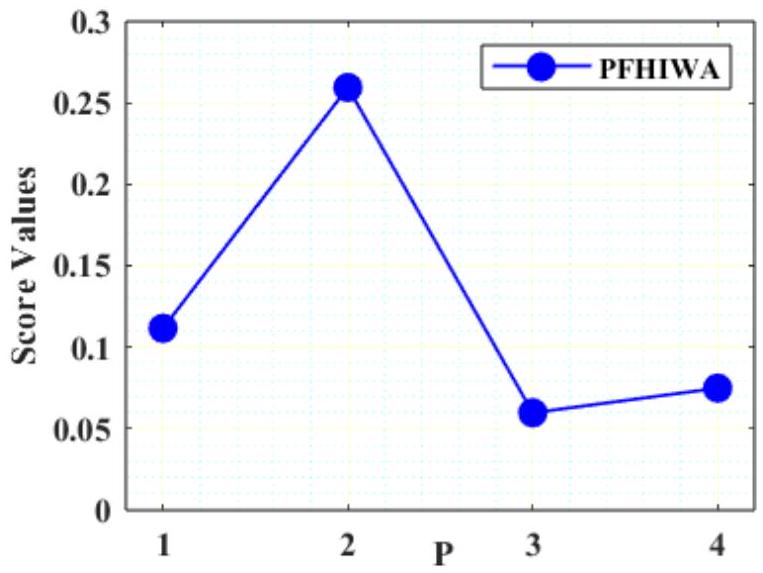
باستخدام المعادلة (1)، سنجد قيمة الدرجة، الجدول 3.
الجدول 3
قيم الدرجات
مشغل PFHIWA
0.1116
0.2594
0.05976
0.07487
لذا، من خلال قيمة النقاط، نحصل على الترتيب كـ . لذا، تم اختيارها كأفضل مورد. كما تظهر النتائج بشكل بياني في الشكل 3.
الشكل 3. قيم الدرجات

6. تحليل الحساسية

تأثير المتغير ) تم فحص عملية إدارة البيانات في الجدول 4 من خلال تطبيق قيم مختلفة من باستخدام الطريقة المقدمة. استنادًا إلى هذه التفضيلات المتنوعة، يمكن لصانعي القرار اختيار الخيار أو الخيارات التي تتوافق بشكل أكبر مع معايير رضاهم. يتم بعد ذلك تقديم الترتيب الشامل للبدائل المعطاة باستخدام المشغل المقترح في الجدول 4 ورسمياً في الشكل 4، مما يعرض النطاق الكامل من التباينات.
الجدول 4
قيم مختلفة من )
تصنيف
٥ 0.07634 0.21902 0.03700 0.05658
10 0.05740 0.19696 0.02045 0.04288
15 0.04949 0.18392 0.01190 0.03574
20 0.03574 0.17516 0.00656 0.03119
٢٥ 0.02950 0.15906 0.00286 0.02809
الشكل 4. قيم مختلفة من .

7. التحليل المقارن

ستقوم هذه القسم بمقارنة تقنياتنا المقترحة مع التقنيات الموجودة. لقد قمنا بمقارنة مشغلينا المقترحين مع IFHWA [24]، IFHWG [29]، IFHIWA، و IFHIWG [27]. يتم مقارنة النتائج لهذه المشغلات ومشغلينا المقترحين في الجدول 5.
الجدول 5
تحليل مقارن
مشغل ب 1 P4 تصنيف
IFHWA 0.3727 0.2767 0.3033 0.2933
IFHWG 0.3393 0.2504 0.3018 0.2476
إفهيوا 0.3536 0.2227 0.2834 0.2639
IFHIWG 0.3530 0.2858 0.3210 0.2806
PFHIWA (مقترح) 0.5946 0.4719 0.5323 0.5137
PFHIWG (مقترح) 0.5941 0.5346 0.5665 0.5297
الشكل 5 يظهر مقارنة بين مشغلاتنا المقترحة والتقنيات الحالية.
الشكل 5. تحليل المقارنة
إذا نظرنا إلى الجدول 5 والشكل 5، فمن الواضح أن مشغلنا المقترح أكثر كفاءة ويظهر نتائج أفضل، لكن الترتيب هو نفسه. لذا، هذا يظهر قوة واستقرار مشغلاتنا المقترحة.

8. الخاتمة

تهدف هذه الورقة إلى تقديم مشغلات تجميع هاماشر بناءً على معيار هاماشر و t-conorm لتجميع معلومات PyF. أولاً، اقترحنا قوانين تشغيل جديدة لـ PFN بناءً على معيار هاماشر و t-conorm. ثم، باستخدام هذه القوانين التشغيلية، نقدم مشغلات PFHIWA و PFHIOWA و PFHIWG و PFHIOWG. بالإضافة إلى ذلك، ناقشنا الخصائص الأساسية لهذه المشغلات. بعد ذلك، قدمنا خوارزمية لحل مشاكل اتخاذ القرار متعددة الخصائص (MADM) في بيئة PyF باستخدام هذه المشغلات. أخيرًا، من خلال مثال عددي، أظهرنا حساسية الطريقة المقترحة. تظهر النتائج أن الطريقة المقترحة تقدم حلاً محسناً مقارنة بالطرق الحالية لترتيب الخيارات. ستوسع الأبحاث المستقبلية هذا العمل لمعالجة تحديات تحسين الأهداف المتعددة في سياقات غير مؤكدة وضبابية مختلفة.

شكر وتقدير

لم يتم تمويل هذا البحث من أي منحة.

تعارض المصالح

يعلن المؤلفون عدم وجود أي تعارض في المصالح.

References

[1] Zadeh, L.A. (1965). Fuzzy sets. Information and control, 8(3), 338-353. https://doi.org/10.1016/S0019-9958(65)90241-X
[2] Atanassov, K.T. (1999). Intuitionistic fuzzy sets (pp. 1-137). Physica-Verlag HD. https://doi.org/10.1007/978-3-7908-1870-3_1
[3] Yager, R. R. (2013). Pythagorean membership grades in multicriteria decision making. IEEE Transactions on fuzzy systems, 22(4), 958-965. https://doi.org/10.1109/TFUZZ.2013.2278989
[4] Yager, R. R. (2013). Pythagorean fuzzy subsets. In 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS) (pp. 57-61). IEEE. https://doi.org/10.1109/IFSA-NAFIPS.2013.6608375
[5] Peng, X., & Yang, Y. (2015). Some results for Pythagorean fuzzy sets. International Journal of Intelligent Systems, 30(11), 1133-1160. https://doi.org/10.1002/int. 21738
[6] Yager, R. R., & Abbasov, A. M. (2013). Pythagorean membership grades, complex numbers, and decision making. International journal of intelligent systems, 28(5), 436-452. https://doi.org/10.1002/int. 21584
[7] Zhang, X., & Xu, Z. (2014). Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. International journal of intelligent systems, 29(12), 1061-1078. https://doi.org/10.1002/int.21676
[8] Lin, M., Chen, Y., & Chen, R. (2021). Bibliometric analysis on Pythagorean fuzzy sets during 2013-2020. International Journal of Intelligent Computing and Cybernetics, 14(2), 104-121. https://doi.org/10.1108/ijicc-06-2020-0067
[9] Li, Z., & Lu, M. (2019). Some novel similarity and distance measures of pythagorean fuzzy sets and their applications. Journal of Intelligent & Fuzzy Systems, 37(2), 1781-1799. https://doi.org/10.3233/JIFS-179241
[10] Olgun, M., & Ünver, M. (2023). Circular Pythagorean fuzzy sets and applications to multi-criteria decision making. Informatica, 34(4), 713-742. https://doi.org/10.15388/23-INFOR529
[11] Akram, M., Zahid, K., & Kahraman, C. (2023). New optimization technique for group decision analysis with complex Pythagorean fuzzy sets. Journal of Intelligent & Fuzzy Systems, 44(3), 3621-3645. https://doi.org/10.3233/JIFS220764
[12] Aldring, J., & Ajay, D. (2023). Multicriteria group decision making based on projection measures on complex Pythagorean fuzzy sets. Granular Computing, 8, 137-155. https://doi.org/10.1007/s41066-022-00321-6
[13] Wu, D. L., Zhu, Z., Ullah, K., Liu, L., Wu, X., & Zhang, X. (2023). Analysis of Hamming and Hausdorff 3D distance measures for complex pythagorean fuzzy sets and their applications in pattern recognition and medical diagnosis. Complex & Intelligent Systems, 9, 4147-4158. https://doi.org/10.1007/s40747-022-00939-8
[14] Chaurasiya, R., & Jain, D. (2023). Hybrid MCDM method on pythagorean fuzzy set and its application. Decision Making: Applications in Management and Engineering, 6(1), 379-398. https://doi.org/10.31181/dmame0306102022c
[15] Al-shami, T. M. (2023). (2, 1)-Fuzzy sets: properties, weighted aggregated operators and their applications to multicriteria decision-making methods. Complex & Intelligent Systems, 9, 1687-1705. https://doi.org/10.1007/s40747-022-00878-4
[16] Alhamzi, G., Javaid, S., Shuaib, U., Razaq, A., Garg, H., & Razzaque, A. (2023). Enhancing interval-valued Pythagorean fuzzy decision-making through Dombi-based aggregation operators. Symmetry, 15(3), 765. https://doi.org/10.3390/sym15030765
[17] Ullah, K., Mahmood, T., Ali, Z., & Jan, N. (2020). On some distance measures of complex Pythagorean fuzzy sets and their applications in pattern recognition. Complex & Intelligent Systems, 6, 15-27. https://doi.org/10.1007/s40747-019-0103-6
[18] Wang, W., & Liu, X. (2012). Intuitionistic fuzzy information aggregation using Einstein operations. IEEE Transactions on Fuzzy Systems, 20(5), 923-938. http://doi.org/10.1109/tfuzz.2012.2189405
[19] Klir, G., & Yuan, B. (1995). Fuzzy sets and fuzzy logic (Vol. 4, pp. 1-12). New Jersey: Prentice hall.
[20] Garg, H. (2016). Novel single-valued neutrosophic aggregated operators under Frank norm operation and its application to decision-making process. International Journal for Uncertainty Quantification, 6(4). http://doi.org/10.1615/Int.J.UncertaintyQuantification. 2016018603
[21] Sarfraz, M. (2024). Application of Interval-valued T-spherical Fuzzy Dombi Hamy Mean Operators in the antiviral mask selection against COVID-19. Journal of Decision Analytics and Intelligent Computing, 4(1), 67-98. https://doi.org/10.31181/jdaic10030042024s
[22] Tešić, D., & Marinković, D. (2023). Application of fermatean fuzzy weight operators and MCDM model DIBR-DIBR II-NWBM-BM for efficiency-based selection of a complex combat system. Journal of Decision Analytics and Intelligent Computing, 3(1), 243-256. https://doi.org/10.31181/10002122023t
[23] Garg, H. (2016). Some series of intuitionistic fuzzy interactive averaging aggregation operators. SpringerPlus, 5(1), 999. https://doi.org/10.1186/s40064-016-2591-9
[24] Huang, J. Y. (2014). Intuitionistic fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. Journal of Intelligent & Fuzzy Systems, 27(1), 505-513. http://doi.org/10.3233/IFS-131019
[25] Tang, X., Fu, C., Xu, D. L., & Yang, S. (2017). Analysis of fuzzy Hamacher aggregation functions for uncertain multiple attribute decision making. Information Sciences, 387, 19-33. https://doi.org/10.1016/j.ins.2016.12.045
[26] Deb, N., Sarkar, A., & Biswas, A. (2022). Linguistic q-rung orthopair fuzzy prioritized aggregation operators based on Hamacher t-norm and t-conorm and their applications to multicriteria group decision making. Archives of Control Sciences, 451-484. http://doi.org/10.24425/acs.2022.141720
[27] Garg, H. (2019). Intuitionistic fuzzy hamacher aggregation operators with entropy weight and their applications to multi-criteria decision-making problems. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 43, 597-613. http://doi.org/10.1007/s40998-018-0167-0
[28] Dong, H., Ali, Z., Mahmood, T., & Liu, P. (2023). Power aggregation operators based on Hamacher t-norm and tconorm for complex intuitionistic fuzzy information and their application in decision-making problems. Journal of Intelligent & Fuzzy Systems, (Preprint), 1-21. https://doi.org/10.3233/JIFS-230323
[29] Liu, P. (2013). Some Hamacher aggregation operators based on the interval-valued intuitionistic fuzzy numbers and their application to group decision making. IEEE Transactions on Fuzzy systems, 22(1), 83-97. http://doi.org/10.1109/TFUZZ.2013.2248736
[30] Gál, L., Lovassy, R., Rudas, I. J., & Kóczy, L. T. (2014). Learning the optimal parameter of the Hamacher t-norm applied for fuzzy-rule-based model extraction. Neural Computing and Applications, 24, 133-142. http://dx.doi.org/10.1007/s00521-013-1499-3
[31] Silambarasan, I., & Sriram, S. (2021). Some operations over intuitionistic fuzzy matrices based on Hamacher t-norm and t-conorm. TWMS Journal of Applied and Engineering Mathematics, 11(2), 541-551.
[32] Zhu, J., & Li, Y. (2018). Hesitant Fuzzy Linguistic Aggregation Operators Based on the Hamacher t-norm and tconorm. Symmetry, 10(6), 189. https://doi.org/10.3390/sym10060189
    • Corresponding author.
    E-mail address: umarishtiaq000@gmail.com

Journal: Spectrum of Operational Research., Volume: 2, Issue: 1
DOI: https://doi.org/10.31181/sor2120258
Publication Date: 2024-08-24

Hamacher Aggregation Operators for Pythagorean Fuzzy Set and its Application in Multi-Attribute Decision-Making Problem

Muhammad Asif , Umar Ishtiaq , Ioannis K. Argyros 1 School of Mathematics and Statistics, Central South University, Changsha 4100083, China2 Department of Mathematics, Quaid-i-Azam University, Islamabad 45320, Pakistan3 Department of Computing and Mathematical Sciences, Cameron University, Lawton, OK 73505, USA

ARTICLE INFO

Article history:

Received 13 May 2024
Received in revised form 29 July 2024
Accepted 19 August 2024
Available online 24 August 2024

Keywords:

Fuzzy set; Pythagorean fuzzy set; Hamacher t-Norms; Aggregation Operators; MADM.

Abstract

Pythagorean fuzzy set is a useful expansion of intuitionistic fuzzy set for dealing with ambiguities, which mostly occur in real-life problems. Hamacher t-norm also has important and compatible norms that incorporate a parameter that offers various options to decision-makers during the information fusion process, thereby enhancing their ability to model decisionmaking problems effectively compared to alternative methods. In this study, Hamacher operators are being used to introduce several Pythagorean fuzzy Hamacher interactive weighted averaging (PFHIWA), Pythagorean fuzzy Hamacher interactive ordered weighted averaging (PFHIOWA), Pythagorean fuzzy Hamacher interactive weighted geometric (PFHIWG), and Pythagorean fuzzy Hamacher interactive ordered weighted geometric (PFHIOWG) operators. The properties of these operators are examined in detail. The benefit of using progressive operators is that they deliver more understanding of the scenario to the decision-makers. Proposed operators are utilized to elaborate multi-attribute decision-making (MADM). By showing the sensitivity analysis, our proposed operator has high stability related to multi-attribute decision-making (MADM) under the Pythagorean fuzzy data set.

1. Introduction

Decision-making (DM) is vital for problem-solving, achieving goals, and allocating resources effectively. It facilitates innovation, risk management, and conflict resolution while empowering individuals and organizations to adapt to change and drive continuous improvement. Zadeh [1] was the first one to introduce the concept of fuzzy set (FS), which only had a membership degree (MDg). It got more attention as FS theory deals with ambiguity in the data. Then, Atanassov [2] extended this concept of FS and gave the idea of intuitionistic FS (IFS) in which there was a non-membership degree (NMDg) alongside MDg. This boosts the study of FS, and many researchers have started paying attention to this area. However, IFS had some restrictions, such as the sum of MDg and NMDg
being between 0 and 1. To overcome this issue, Yager [3] presented the idea of a Pythagorean fuzzy set (PyFS).
In PyFS, the sum of the square of MDg and NMDg is between 0 and 1, i.e., 1 (Figure 1). Yager [4] defined the operational rules and other properties of PyFS and compared them with IFS. Peng and Yang [5] proposed division and subtraction for PyFS and developed a superiority and inferiority ranking method for PyFS. Yager and Abbasov [6] developed the averaging and geometric aggregation operators (AOs) based on PyFS. In their study, Zhang and Xu [7] used the TOPSIS method on PyFS to solve the DM problems. Bibliometric analysis of PyFS was done by Lin et al., [8]. Li and Lu [9] presented some unique similarities and distance measures of PyFS and utilized them in issues related to real life. Circular PyFS was designed by Olgun and Ünver [10] and showed their applications by using these operators in multi-attribute DM (MADM) issues. Akram et al., [11] introduced a new optimization method under the PyFS environment. In the same, many researchers have done work based on PyFS [12-17].
Fig. 1. Pythagorean fuzzy set
From those mentioned above, it is noticed that different researchers used different approaches to strengthen their studies. Overall, the customary AOs usually assumed simple algebraic rules. Tnorms ( ) and t -conorms ( ) are widely used in FS and are important because of algebraic expressions. Einstein Nr [18], Archimedean Nr [19], and Frank Nr [20] have been widely used in developing different AOs in FS. Sarfraz [21] introduces interval-valued T-spherical fuzzy Dombi Hamy mean operators as a powerful tool for group decision-making by using Dombi Nr. Tešić and Marinković [22] defined normalized aggregation operators using Bonferroni Mean operators. Hamacher t-Nr [23] also has important and compatible Nr. These norms incorporate a parameter that offers various options to decision-makers during the information fusion process, thereby enhancing their ability to model decision-making problems effectively compared to alternative methods. Huang [24] developed AOs under the Hamacher t-Nr environment. Tang et al., [25] studied the analysis of Hamacher AOs and their effect on MADM problems. Linguistic q -ROFS AOs based on Hamacher t-Nr were introduced by Deb et al., [26]. Garg [27] also used Hamcher T-Nr to develop some new AOs and used these AOs by entropy method for the MADM issue. There are useful studies [28-32] to understand Hamacher t-Nr.
Building upon recognized research deficiencies, we propose AOs tailored for PyFS. Our study unveils weighted averaging and geometric AOs, leveraging Hamacher norm operations. These
operators cater to preferences articulated through PyFS. Notably, the relative ranking of alternatives hinges significantly on the choice of weight vectors allocated to PyFSs, underscoring the importance of discerning suitable weight assignments. This contribution seeks to address gaps in DM methodologies by offering refined tools for handling uncertainty and ambiguity.
The pattern of the paper is as follows: in Section 2, there are some fundamental concepts and definitions. Section 3 presents improved operations on Hamacher under the PyFS environment and introduces PFH interactive weighted averaging (PFHIWA), PFH interactive ordered weighted averaging (PFHIOWA), PFH interactive weighted geometric (PFHIWG) and PFH interactive ordered weighted geometric (PFHIOWG) operators respectively. The MADM technique has been briefly discussed in Section 4 to tackle our proposed operators. In section 5, we have shown the applications of our proposed operators by a practical example. Sections 6 and 7 are devoted to sensitivity analysis and comparative analysis to show the stability and importance of our operators. In Section 8, the conclusion of this work provides insights into important findings and suggests prospective directions for further research.

2. Preliminaries

This section will discuss some basic definitions and rules that will help construct our paper.
Definition 1 [2]. An IFS T defined in Y is an ordered pain presented by
where represent the MDg and NMDg of the element y such that and for all y .
Definition 2 [3]. A PyFS T defined in Y is an ordered pain presented by
where represent the MDg and NMDg of the element y such that and for all y .
Definition 3 [5]. The score function SF for any PyFN is given by

when SF of two PyFNs, the accuracy function (AF) is used to compare them.
Definition 4. The AF for any PyFN is given by
Definition 5 [19]. A function : [ 0,1 ] is known as t-Nr if it holds the properties of monotonicity, commutativity, boundary conditions, and associativity. On the contrary, a function Q defined by for all is known as t-CNr.
Definition 6 [19]. Archimedean function G is a continuous which satisfies the condition for . A strict Archimedean is strictly increasing .
Definition 7 [23]. Garg defined the bnorm operations by considering for two different IFN and such as:
(i)
(ii)
Definition 8 [24]. For a set of IFNS , Huang proposed AOs, which are defined as below
and
Definition 9 [27]. For a set of IFNS , Garg proposed improved AOs, which was shown in [24], which are defined as
𝕕𝕕𝕕𝕕𝕕𝕕𝕕𝕕
and

3. Improved Operational Laws and Aggregation Operators for Pythagorean Fuzzy Set

We will present some new rules and laws which will be helpful in the study of AOs.
Definition 10. Suppose and be a set of PyFNs, then the new operational laws using the Hamacher norm for these numbers can be defined as:
(i)
(ii)
(iii)
(iv)
where and are the real numbers.
It can be seen in Definition 10 that the sum operation has become more optimistic than the sum defined in Definition 7. Hence, the behavior is more inclined toward the MD than the NMD. So, the result will be more accurate.

3.1 Averaging Operators

For the set of with for all and relying on the above-mentioned rules, we will present new PFH interactive weighted (PFHIWA) and order weighted (PFHIOWA) averaging operators.
Definition 11. Suppose Y be the collection of PyNFs and PFHIWA: , such that:
đđđ
where 𝕕𝕕𝕕𝕕 is the weight vector of such that 𝕕 and 𝕕; then, PFHIWA is defined as the PFH interactive weighted averaging operator.
Theorem 1. For PyFNs with , the aggregated value by using PFHIWA is again a PyFN and is defined as:
Proof: We will prove Theorem 1 by mathematical induction. So, we have
I. When , we have and đ. Now, for PyFNs and , we have

and

So, we have
đđ



So, Eq. (4) is true for
II. Suppose that Eq. (4) is also true for
III. Now, for , we have
đℊℊℊℊℊℊ
So, Eq. (4) also holds for .
Hence, it is proved that the Eq.(4) holds for all positive integer .
Now, we will define some properties for PFHIWA.
Theorem 2 (Idempotency). If for all i then .
Proof: For a set of PyFNs and weight vector đ such that đ and đ 1. Suppose for all i then by PFHIWA operator, we have
đđđ
Theorem 3 (Boundedness). Suppose is the PFHIWA operator, and .
Proof: Since and and m be a PFHIWA operator. So, by Theorem 1, we have
đđđđđđ
Since đ. So, we have
and
Therefore, .
Theorem 4 (Monotonicity). For collections of two different PyFNs and such that for all and to be a PFHIWA operator, then .
Proof: The proof is the same as above.
We will show the PFH-ordered weighted averaging operator (PFHIOWA).
Definition 12. Suppose Y be the collection of PyNFs and PFHIOW A: , such that:
đđđ
Where be the permutation such that and is the normalized weight vector of .
Theorem 5. For PyFNs with , the aggregated value by using PFHIOWA is again a PyFN and is defined as:
Properties for PFHIOWA are defined below.
Theorem 6 (Idempotency). If for all i then PFHIOWA .
Theorem 7 (Boundedness). Suppose m is the PFHIOWA operator, , and .
Theorem 8 (Monotonicity). For collections of two different PyFNs and such that for all i and m to be a PFHIOWA operator, then

3.2 Geometric Operators

For the set of with for all and relying on the above rules, we will present new PFH interactive weighted (PFHIWG) and order weighted (PFHIOWG) geometric operators.
Definition 13. Suppose Y be the collection of PyNFs and PFHIWA: , such that:
where is the weight vector of such that and ; then, PFHIWG is defined as PFH interactive weighted geometric operator.
Theorem 9. For PyFNs with , the aggregated value by using PFHIWG is again a PyFN and is defined as:
Proof: We will prove Theorem 9 by mathematical induction. So, we have
I. When , we have and . Now, for PyFNs and , we have
ℊ
and
ℊ
So, we have
So, Eq. (5) is true for
II. Suppose that Eq. (5) is also true for
III. Now, for , we have
So, Eq. (5) also holds for .
Hence, it is proved that the Eq. (5) holds for all positive integer .
Now, we will define some properties for PFHIWG.
Theorem 10 (Idempotency). If for all i then PFHIWG .
Proof: For a set of PyFNs and weight vector đ such that đ and đ 1. Suppose for all then by PFHIWG operator, we have
Theorem 11 (Boundedness). Suppose m is the PFHIWG operator, , and .
Proof: Since and and be a PFHIWG operator. So, by Theorem 1, we have
đđđđđđ
Since đ. So, we have
and
Therefore, .
Theorem 12 (Monotonicity). For collections of two different PyFNs and such that for all and to be a PFHIWG operator, then .
Proof: The proof is the same as above.
Now, we will show the PFH-ordered weighted geometric operator (PFHIOWG).
Definition 14. Suppose Y be the collection of PyNFs and PFHIOWG: , such that:
Where be the permutation such that and is the normalized weight vector of .
Theorem 13. For PyFNs with , the aggregated value by using PFHIOWG is again a PyFN and is defined as:
Properties for PFHIOWG are defined below.
Theorem 14 (Idempotency). If for all i then .
Theorem 15 (Boundedness). Suppose m is the PFHIOWG operator, , and .
Theorem 16 (Monotonicity). For collections of two different PyFNs and such that for all and to be a PFHIOWG operator, then .

4. Multi-attribute Decision Making Technique

This section will show a DM method for solving the MADM issue under PyF circumstances. In everyday life, DM involves selecting the best option from a set of choices. Typically, decision-makers rely on intuition and expertise. However, because decision-making problems can be complex, accurately representing fuzzy and vague information is crucial. To capture decision makers’ preferences, preference relations are valuable tools for ranking criteria. For a set of criteria , , experts compare each pair and construct preference relations.
We will discuss the steps involved in the MADM technique.
Step 1. First, we construct a PyF data decision matrix. This matrix is then converted into the normalized matrix.
Step 2. Then, using our proposed operator, all the PyF data is converted into a single value.
Step 3. Find the score values by using the SF. If the score values are the same, we find accuracy using the AF . So, the ranking will be based on accuracy values.
Step 4. The best choice is found according to the ranking of the options.
Step 5. End.
The flowchart for the MADM is shown in Figure 2.
Fig. 2. Flowchart for MADM technique

5. Practical Example

This scenario involves an enterprise located in the industrial zone of Juárez, Mexico, specifically within the Maquiladoras sector, specializing in assembly manufacturing. The company has launched a project aimed at cost reduction, identifying packaging as a significant area for potential savings. To achieve this goal, the company plans to evaluate five suppliers providing packaging for electronic components. Two decision-makers have been invited to participate in the evaluation process. Four criteria (cost, service, lead time, and quality) have been established to evaluate and thoroughly compare the suppliers’ offerings to ensure a comprehensive assessment. Therefore, the group of suppliers is denoted as . The decision maker assigns attribute weights as follows: . Evaluating the four candidates will involve assessing ambiguity using PyF data across the four attributes outlined in Table 1.
Table 1
PyF matrix for suppliers
Now, after using our proposed PFHIWA on the given data, we get the results listed in Table 2.
Table 2
Results by PFHIWA
Operator PFHIWA
By using Eq. (1), we will find the score value, Table 3.
Table 3
Score Values
Operator PFHIWA
0.1116
0.2594
0.05976
0.07487
So, by score value, we get the ranking as . So, is selected as the best supplier. Results are also shown graphically in Figure 3.
Fig. 3. Score Values

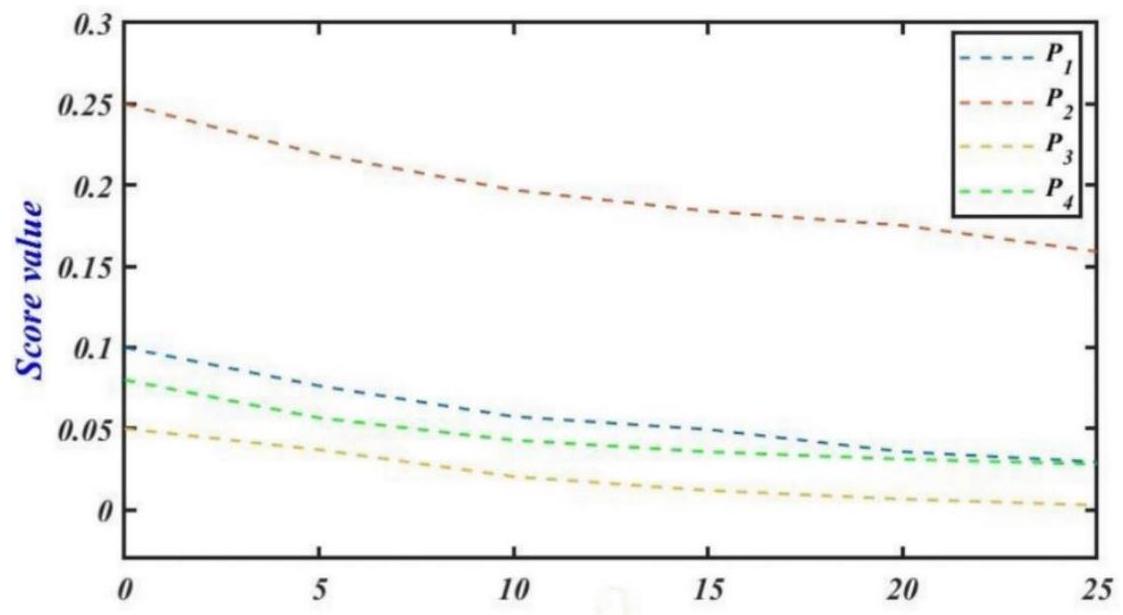
6. Sensitivity Analysis

The influence of the variable ) on the DM process has been examined in Table 4 by applying different values of ) using the provided method. Based on these diverse preferences, decisionmakers can choose the option or options that most closely match their satisfaction criteria. The comprehensive ranking of the given alternatives using our proposed operator is then presented in Table 4 and graphically in Figure 4, showcasing the full range of variations.
Table 4
Different values of )
Ranking
5 0.07634 0.21902 0.03700 0.05658
10 0.05740 0.19696 0.02045 0.04288
15 0.04949 0.18392 0.01190 0.03574
20 0.03574 0.17516 0.00656 0.03119
25 0.02950 0.15906 0.00286 0.02809
Fig. 4. Different values of .

7. Comparative Analysis

This section will compare our proposed techniques with the existing ones. We have compared our proposed operators with IFHWA [24], IFHWG [29], IFHIWA, and IFHIWG [27]. The results for these operators and our proposed operators are compared in Table 5.
Table 5
Comparative Analysis
Operator P 1 P4 Ranking
IFHWA 0.3727 0.2767 0.3033 0.2933
IFHWG 0.3393 0.2504 0.3018 0.2476
IFHIWA 0.3536 0.2227 0.2834 0.2639
IFHIWG 0.3530 0.2858 0.3210 0.2806
PFHIWA (Proposed) 0.5946 0.4719 0.5323 0.5137
PFHIWG (Proposed) 0.5941 0.5346 0.5665 0.5297
Figure 5 shows the comparison of our proposed operators with the existing techniques.
Fig. 5. Comparison Analysis
If we look at Table 5 and Figure 5, then it is clear that our proposed operator is more efficient and shows better results, but the ranking is the same. So, this shows the strength and stability of our proposed operators.

8. Conclusion

This paper aims to introduce Hamacher aggregation operators based on Hamacher t-norm and tconorm for aggregating PyF information. Firstly, we proposed new operational laws of PFN based on Hamacher t-norm and t-conorm. Then, using these operational laws, we introduce the PFHIWA, PFHIOWA, PFHIWG, and PFHIOWG operators. Additionally, we discussed the fundamental properties of these operators. Subsequently, we presented an algorithm for solving Multiple Attribute Decision Making (MADM) problems under a PyF environment using these operators. Finally, through a numerical example, we demonstrated the sensitivity of the proposed method. The results show that the proposed method offers an improved solution compared to existing methods for ranking options. Future research will extend this work to address multi-objective optimization challenges in various uncertain and fuzzy contexts.

Acknowledgment

This research was not funded by any grant.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1] Zadeh, L.A. (1965). Fuzzy sets. Information and control, 8(3), 338-353. https://doi.org/10.1016/S0019-9958(65)90241-X
[2] Atanassov, K.T. (1999). Intuitionistic fuzzy sets (pp. 1-137). Physica-Verlag HD. https://doi.org/10.1007/978-3-7908-1870-3_1
[3] Yager, R. R. (2013). Pythagorean membership grades in multicriteria decision making. IEEE Transactions on fuzzy systems, 22(4), 958-965. https://doi.org/10.1109/TFUZZ.2013.2278989
[4] Yager, R. R. (2013). Pythagorean fuzzy subsets. In 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS) (pp. 57-61). IEEE. https://doi.org/10.1109/IFSA-NAFIPS.2013.6608375
[5] Peng, X., & Yang, Y. (2015). Some results for Pythagorean fuzzy sets. International Journal of Intelligent Systems, 30(11), 1133-1160. https://doi.org/10.1002/int. 21738
[6] Yager, R. R., & Abbasov, A. M. (2013). Pythagorean membership grades, complex numbers, and decision making. International journal of intelligent systems, 28(5), 436-452. https://doi.org/10.1002/int. 21584
[7] Zhang, X., & Xu, Z. (2014). Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. International journal of intelligent systems, 29(12), 1061-1078. https://doi.org/10.1002/int.21676
[8] Lin, M., Chen, Y., & Chen, R. (2021). Bibliometric analysis on Pythagorean fuzzy sets during 2013-2020. International Journal of Intelligent Computing and Cybernetics, 14(2), 104-121. https://doi.org/10.1108/ijicc-06-2020-0067
[9] Li, Z., & Lu, M. (2019). Some novel similarity and distance measures of pythagorean fuzzy sets and their applications. Journal of Intelligent & Fuzzy Systems, 37(2), 1781-1799. https://doi.org/10.3233/JIFS-179241
[10] Olgun, M., & Ünver, M. (2023). Circular Pythagorean fuzzy sets and applications to multi-criteria decision making. Informatica, 34(4), 713-742. https://doi.org/10.15388/23-INFOR529
[11] Akram, M., Zahid, K., & Kahraman, C. (2023). New optimization technique for group decision analysis with complex Pythagorean fuzzy sets. Journal of Intelligent & Fuzzy Systems, 44(3), 3621-3645. https://doi.org/10.3233/JIFS220764
[12] Aldring, J., & Ajay, D. (2023). Multicriteria group decision making based on projection measures on complex Pythagorean fuzzy sets. Granular Computing, 8, 137-155. https://doi.org/10.1007/s41066-022-00321-6
[13] Wu, D. L., Zhu, Z., Ullah, K., Liu, L., Wu, X., & Zhang, X. (2023). Analysis of Hamming and Hausdorff 3D distance measures for complex pythagorean fuzzy sets and their applications in pattern recognition and medical diagnosis. Complex & Intelligent Systems, 9, 4147-4158. https://doi.org/10.1007/s40747-022-00939-8
[14] Chaurasiya, R., & Jain, D. (2023). Hybrid MCDM method on pythagorean fuzzy set and its application. Decision Making: Applications in Management and Engineering, 6(1), 379-398. https://doi.org/10.31181/dmame0306102022c
[15] Al-shami, T. M. (2023). (2, 1)-Fuzzy sets: properties, weighted aggregated operators and their applications to multicriteria decision-making methods. Complex & Intelligent Systems, 9, 1687-1705. https://doi.org/10.1007/s40747-022-00878-4
[16] Alhamzi, G., Javaid, S., Shuaib, U., Razaq, A., Garg, H., & Razzaque, A. (2023). Enhancing interval-valued Pythagorean fuzzy decision-making through Dombi-based aggregation operators. Symmetry, 15(3), 765. https://doi.org/10.3390/sym15030765
[17] Ullah, K., Mahmood, T., Ali, Z., & Jan, N. (2020). On some distance measures of complex Pythagorean fuzzy sets and their applications in pattern recognition. Complex & Intelligent Systems, 6, 15-27. https://doi.org/10.1007/s40747-019-0103-6
[18] Wang, W., & Liu, X. (2012). Intuitionistic fuzzy information aggregation using Einstein operations. IEEE Transactions on Fuzzy Systems, 20(5), 923-938. http://doi.org/10.1109/tfuzz.2012.2189405
[19] Klir, G., & Yuan, B. (1995). Fuzzy sets and fuzzy logic (Vol. 4, pp. 1-12). New Jersey: Prentice hall.
[20] Garg, H. (2016). Novel single-valued neutrosophic aggregated operators under Frank norm operation and its application to decision-making process. International Journal for Uncertainty Quantification, 6(4). http://doi.org/10.1615/Int.J.UncertaintyQuantification. 2016018603
[21] Sarfraz, M. (2024). Application of Interval-valued T-spherical Fuzzy Dombi Hamy Mean Operators in the antiviral mask selection against COVID-19. Journal of Decision Analytics and Intelligent Computing, 4(1), 67-98. https://doi.org/10.31181/jdaic10030042024s
[22] Tešić, D., & Marinković, D. (2023). Application of fermatean fuzzy weight operators and MCDM model DIBR-DIBR II-NWBM-BM for efficiency-based selection of a complex combat system. Journal of Decision Analytics and Intelligent Computing, 3(1), 243-256. https://doi.org/10.31181/10002122023t
[23] Garg, H. (2016). Some series of intuitionistic fuzzy interactive averaging aggregation operators. SpringerPlus, 5(1), 999. https://doi.org/10.1186/s40064-016-2591-9
[24] Huang, J. Y. (2014). Intuitionistic fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. Journal of Intelligent & Fuzzy Systems, 27(1), 505-513. http://doi.org/10.3233/IFS-131019
[25] Tang, X., Fu, C., Xu, D. L., & Yang, S. (2017). Analysis of fuzzy Hamacher aggregation functions for uncertain multiple attribute decision making. Information Sciences, 387, 19-33. https://doi.org/10.1016/j.ins.2016.12.045
[26] Deb, N., Sarkar, A., & Biswas, A. (2022). Linguistic q-rung orthopair fuzzy prioritized aggregation operators based on Hamacher t-norm and t-conorm and their applications to multicriteria group decision making. Archives of Control Sciences, 451-484. http://doi.org/10.24425/acs.2022.141720
[27] Garg, H. (2019). Intuitionistic fuzzy hamacher aggregation operators with entropy weight and their applications to multi-criteria decision-making problems. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 43, 597-613. http://doi.org/10.1007/s40998-018-0167-0
[28] Dong, H., Ali, Z., Mahmood, T., & Liu, P. (2023). Power aggregation operators based on Hamacher t-norm and tconorm for complex intuitionistic fuzzy information and their application in decision-making problems. Journal of Intelligent & Fuzzy Systems, (Preprint), 1-21. https://doi.org/10.3233/JIFS-230323
[29] Liu, P. (2013). Some Hamacher aggregation operators based on the interval-valued intuitionistic fuzzy numbers and their application to group decision making. IEEE Transactions on Fuzzy systems, 22(1), 83-97. http://doi.org/10.1109/TFUZZ.2013.2248736
[30] Gál, L., Lovassy, R., Rudas, I. J., & Kóczy, L. T. (2014). Learning the optimal parameter of the Hamacher t-norm applied for fuzzy-rule-based model extraction. Neural Computing and Applications, 24, 133-142. http://dx.doi.org/10.1007/s00521-013-1499-3
[31] Silambarasan, I., & Sriram, S. (2021). Some operations over intuitionistic fuzzy matrices based on Hamacher t-norm and t-conorm. TWMS Journal of Applied and Engineering Mathematics, 11(2), 541-551.
[32] Zhu, J., & Li, Y. (2018). Hesitant Fuzzy Linguistic Aggregation Operators Based on the Hamacher t-norm and tconorm. Symmetry, 10(6), 189. https://doi.org/10.3390/sym10060189
    • Corresponding author.
    E-mail address: umarishtiaq000@gmail.com