تطوير وتطبيقات توزيع وايبل-وايبل العكسي الهجين الجديد Development and Applications of a New Hybrid Weibull-Inverse Weibull Distribution

المجلة: Modern Journal of Statistics، المجلد: 1، العدد: 1
DOI: https://doi.org/10.64389/mjs.2025.01112
تاريخ النشر: 2025-07-12

مقالة بحثية

تطوير وتطبيقات توزيع وايبل-وايبل العكسي الهجين الجديد

نور الدين أ. نوري كمال نجم عبد الله ، ومظهر أ. خليل مديرية التربية في الأنبار، الأنبار 31002، العراق؛ Nooruldeen.a.noori35508@st.tu.edu.iq أقسام الرياضيات، كلية علوم الحاسوب والرياضيات، جامعة تكريت، تكريت 34001، العراق؛kn230022pcm@st.tu.edu.iq، mun880088@tu.edu.iq*المراسلة: Nooruldeen.a.noori35508@st.tu.edu.iq

معلومات المقال

الكلمات المفتاحية:

توزيع ويبل
تقدير المعلمات
التوزيعات الهجينة
محاكاة مونت كارلو
تحليل البيانات الحقيقية

تصنيف موضوعات الرياضيات:

62F10، 62P10

التواريخ المهمة:

تاريخ الاستلام: 8 يونيو 2025
تمت المراجعة: 8 يوليو 2025
تم القبول: 10 يوليو 2025
عبر الإنترنت: 12 يوليو 2025
حقوق الطبع والنشر © 2025 من قبل المؤلفين. منشور بموجب رخصة المشاع الإبداعي النسب (CC BY).

الملخص

تقدم هذه الدراسة وتطبق نموذجًا إحصائيًا جديدًا يعرف بتوزيع وايبل العكسي الهجين (HWIW)، الذي يجمع بين خصائص توزيعي وايبل والعكسي وايبل لتوفير نموذج أكثر مرونة لتمثيل البيانات الواقعية، خاصة تلك التي تتميز باللامركزية أو القيم المتطرفة. تم اشتقاق الوظائف الأساسية للتوزيع، بالإضافة إلى اشتقاق مقاييس إحصائية أخرى مثل اللحظات، ودالة الكمية، والإنتروبيا. تم تقدير معلمات التوزيع باستخدام ثلاث طرق متميزة، وتم تقييم أدائها من خلال محاكاة مونت كارلو لتقييم أداء ودقة كل تقنية تقدير. تم استخدام النتائج لإظهار أكثر طرق التقدير دقة لعينات مختلفة. تم استخدام النموذج المقترح لاختبار مجموعتين عمليتين من البيانات؛ وأظهرت النتائج أن توزيع HWIW تفوق على ستة توزيعات IW منافسة من حيث مقاييس اختيار النموذج. تؤكد هذه النتائج كفاءة قدرة نموذج HWIW على التقاط هيكل مجموعات البيانات المعقدة وتفتح الطريق لاستخدامه في تطبيقات متعددة، بما في ذلك المجالات الطبية والصناعية والاجتماعية، مع إمكانية توسيعه ليشمل بيانات متعددة الأبعاد أو دمجه مع تقنيات الذكاء الاصطناعي.

1. المقدمة

تلعب توزيع الاحتمالات دورًا أساسيًا في مجال النمذجة الإحصائية وتحليل البيانات. إنها الأداة الرئيسية لفهم السلوك العشوائي المرتبط بمختلف الظواهر العلمية والتطبيقية، من تحليل الموثوقية والتنبؤ إلى تقييم المخاطر والهندسة الإحصائية. من بين التوزيعات الشائعة، يبرز توزيع وايبول لمرونته العالية في تمثيل بيانات الفشل والموثوقية، بينما يتميز توزيع وايبول العكسي بقدرته على تمثيل البيانات التي تتسم بمعدلات فشل غير ثابتة أو سلوك غير متجانس. على الرغم من القوة التمثيلية لكل من هذين التوزيعين بشكل فردي، قد لا يكون استخدام أي منهما بمفرده كافيًا لتمثيل البيانات الواقعية التي تتسم بعدم التماثل، والذيل الثقيل، أو مستويات عالية من التشتت. وغالبًا ما يؤدي ذلك إلى دقة تقدير ضعيفة وملاءمة سيئة للنماذج الإحصائية.
لقد دفعت هذه التحديات الباحثين للبحث عن بدائل إحصائية أكثر مرونة تتجاوز القيود التي تفرضها النماذج التقليدية. ومن هنا نشأت فكرة التوزيعات الهجينة، التي تهدف إلى دمج خصائص توزيع أو أكثر ضمن نموذج إحصائي واحد، مما يمنح النموذج قدرة أكبر على التكيف مع خصائص البيانات المتنوعة. وقد شهدت التطورات الأخيرة في هذا المجال
لقد ساهمت في ظهور منهجية T-X، وهي واحدة من أبرز الطرق المستخدمة لتوليد توزيعات جديدة من خلال تحويل التوزيعات الأساسية باستخدام دوال تحويل مرنة. وقد أدت هذه المنهجية إلى ظهور عدة عائلات جديدة من التوزيعات [1]، مثل عائلة BIIIEE-X [2]، عائلة NOGEE-G [3]، عائلة WEE-X [2]، عائلة OLG [5]، عائلة NGOF-G [6]، عائلة EOIW-G [7]، عائلة GOM-G [8]، HOLGE [9]، و HOE- العائلة [10]، التي أثبتت فعاليتها في تمثيل البيانات غير القياسية ذات الخصائص المتنوعة.
تقدم هذه البحث نموذج توزيع جديد ضمن إطار عائلة HWG، التي تعتمد على تحويل التوزيع الأساسي إلى توزيع أكثر مرونة. تحتوي هذه العائلة على دالة توزيع تراكمي بالشكل [11] :
بينما يأخذ ملف PDF الخاص به الشكل:
أين و تمثل دوال CDF و PDF، المعلمات و حدد شكل عائلة HWG، استنادًا إلى أي توزيع أساسي محدد، بحيث .
على الرغم من أن توزيعات الاحتمالات تُستخدم على نطاق واسع في النمذجة الإحصائية وتحليل البيانات، إلا أن التوزيعات التقليدية غالبًا ما تواجه تحديات في تمثيل البيانات المعقدة بدقة، خاصة تلك التي تكون غير متناظرة أو تحتوي على قيم متطرفة. مع التقدم في الأساليب الإحصائية، هناك حاجة متزايدة لتطوير نماذج أكثر مرونة قادرة على التعامل بفعالية مع مثل هذه البيانات. من بين التوزيعات المستخدمة بشكل شائع، تُعتبر توزيعات ويبل وتوزيع ويبل العكسي مهمة؛ ومع ذلك، عند تطبيقها بشكل فردي، قد لا تُنتج دائمًا نتائج دقيقة أو مرضية بشكل كافٍ. تكشف مراجعة الأدبيات عن نقص في الدراسات التي تدمج هذين التوزيعين في نموذج واحد يستفيد من نقاط القوة في كلاهما.
وبناءً عليه، يتم تقديم توزيع إحصائي جديد في هذا العمل يسمى توزيع HWIW، والذي يتميز بمرونة عالية وقدرة محسّنة على تمثيل البيانات الواقعية. تتضمن هذه الدراسة اشتقاق وفحص الخصائص الإحصائية للتوزيع المقترح وتحديد معاييره من خلال ثلاث تقنيات تقدير متميزة: MLE، LSE، WLSE. ثم يتم تقييم أدائه من خلال تطبيق النموذج على مجموعة بيانات حقيقية ومقارنته بعدة توزيعات أخرى لتقييم دقته وكفاءته.
تم تنظيم هذه الورقة على النحو التالي. في القسم 2، قمنا باشتقاق الوظائف الرئيسية للنموذج المقترح الآخر. تم حساب الخصائص الإحصائية لتوزيع HWIW في القسم 3. تم تقديم مقدرات النموذج المقترح في القسم 4 بواسطة ثلاث طرق مختلفة، وتم استخدام المحاكاة في القسم 5 للتحقق من سلوك هذه الطرق. استخدم القسم 6 مجموعتين عمليتين من البيانات لإظهار تفوق توزيع HWIW في ملاءمتهما. أخيرًا، تم كتابة الملاحظات الختامية للورقة بأكملها في القسم 7.

2. توزيع وايبول الهجين العكسي (HWIW)

نفترض أن التوزيع الأساسي يتبع توزيع IW، حيث يمكن تمثيل دالة الكثافة الاحتمالية ودالة التوزيع التراكمي كما يلي [12]:
أين هي معلمات الشكل لتوزيع IW.
من أجل الحصول على دالة التوزيع التراكمي لتوزيع HWIW، يتم دمج المعادلتين (1.1) و(3) في صيغة موحدة كما يلي:
يمكن التعبير عن دالة الكثافة الاحتمالية لتوزيع HWIW من خلال استبدال المعادلة (2.1) في المعادلتين (2.1) و (4) كالتالي:
توضح الأشكال 1 و 2 دالة الكثافة الاحتمالية (PDF) ودالة التوزيع التراكمي (CDF) لتوزيع HWIW تحت إعدادات معلمات مختلفة. كما هو موضح في الشكل 1، تظهر منحنيات دالة الكثافة الاحتمالية مجموعة واسعة من الأشكال، بما في ذلك الاتجاهات المتناقصة، والقمم الأحادية، والأشكال المنحرفة نحو اليمين، والأشكال المعكوسة على شكل حرف J. تسلط هذه التنوعات الضوء على مرونة التوزيع العالية وقدرته على نمذجة أنواع مختلفة من البيانات، خاصة تلك التي تتميز بسلوك غير متماثل أو ذي ذيول ثقيلة.
الشكل 1: منحنيات PDF لتوزيع HWIW تحت قيم معلمات متغيرة.
تقدم الشكل 2 منحنيات دالة التوزيع التراكمي، التي تبدأ جميعها من الصفر وتقترب بشكل غير نهائي من الواحد، كما هو متوقع. تعكس التغيرات في انحدار المنحنيات قدرة التوزيع على التكيف مع أنماط تراكم الاحتمالات المختلفة. تم إنشاء جميع الرسوم البيانية باستخدام لغة البرمجة R، مما يبرز الصرامة الإحصائية والوضوح البصري للتحليل.
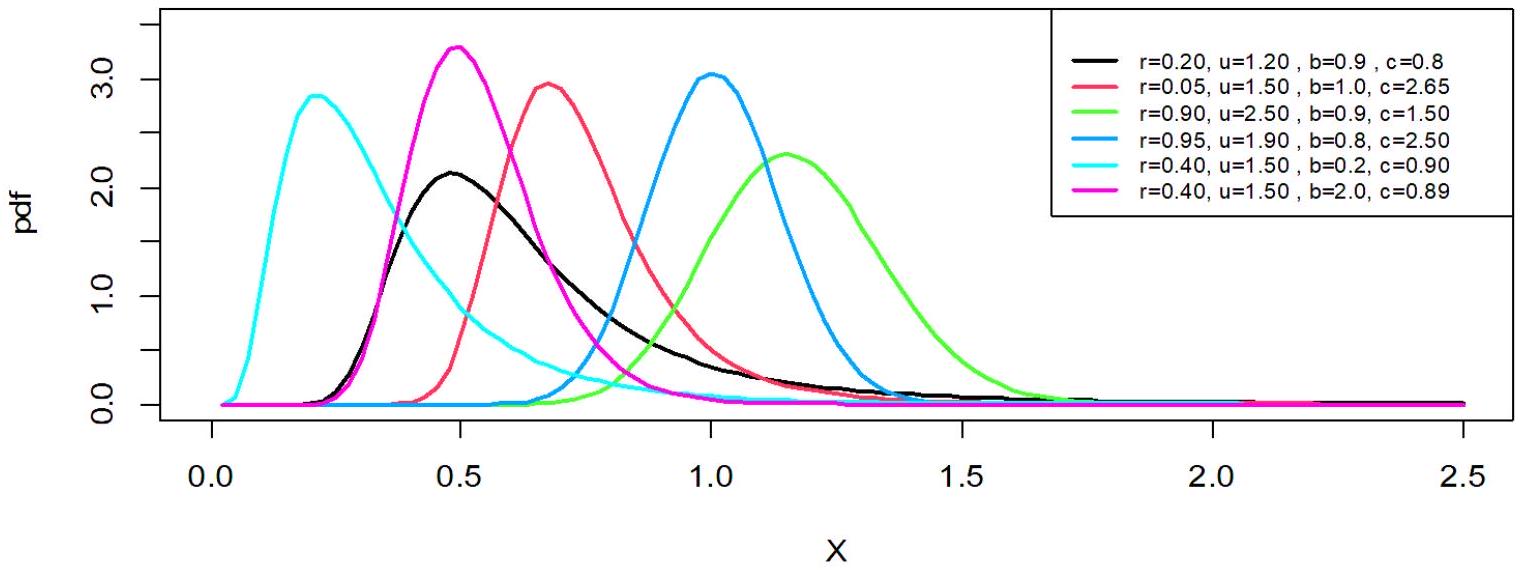
وظيفة البقاء المرتبطة بتوزيع HWIW تُعطى بالتعبير التالي [13] :
تم صياغة دالة الخطر المرتبطة بتوزيع HWIW رياضيًا على النحو التالي [14]:
الشكل 2: منحنيات CDF لتوزيع HWIW تحت قيم معلمات متغيرة.
تُبرز الأشكال 3 و 4 سلوك كل من منحنيات البقاء والخطر لتوزيع HWIW المعطى مع معلمات مختلفة. ) يبرز مرونته في تمثيل أنماط الفشل المختلفة. في الشكل 3، وظائف البقاء تتناقص تدريجياً من 1 كـ تزداد، مع وجود بعض المنحنيات التي تشير إلى فشل مبكر (مثل الأخضر)، بينما تعكس أخرى بقاءً أطول (مثل الأرجواني والأسود).
الشكل 3: رسم منحنى البقاء لتوزيع HWIW.
الشكل 4: رسم منحنى الخطر لتوزيع HWIW.
تُبرز الشكل 4 التنوع في نمط دالة الخطر بعض المنحنيات تظهر نمطًا متناقصًا يشير إلى الشيخوخة، بينما تتبنى منحنيات أخرى شكلًا غير أحادي الاتجاه يبدأ بارتفاع، ثم ينخفض، ثم يرتفع مرة أخرى، مما يشبه شكل حوض الاستحمام المعروف من تحليل الموثوقية.
نظرًا لتعقيد الصيغ الأصلية لدالة التوزيع التراكمي (CDF) ودالة الكثافة الاحتمالية (PDF) في المعادلتين (5) و(6)، قمنا بتبسيطها لتسهيل اشتقاق الأرباح لتوزيع HWIW. تم ذلك من خلال تطبيق توسعات مثل استخدام الأشكال السلسلية للثنائي، والأسية، وتوسيع اللوغاريتم، مما أسفر عن صيغة لدالة التوزيع التراكمي كما يلي:
أين ، و لـ و .
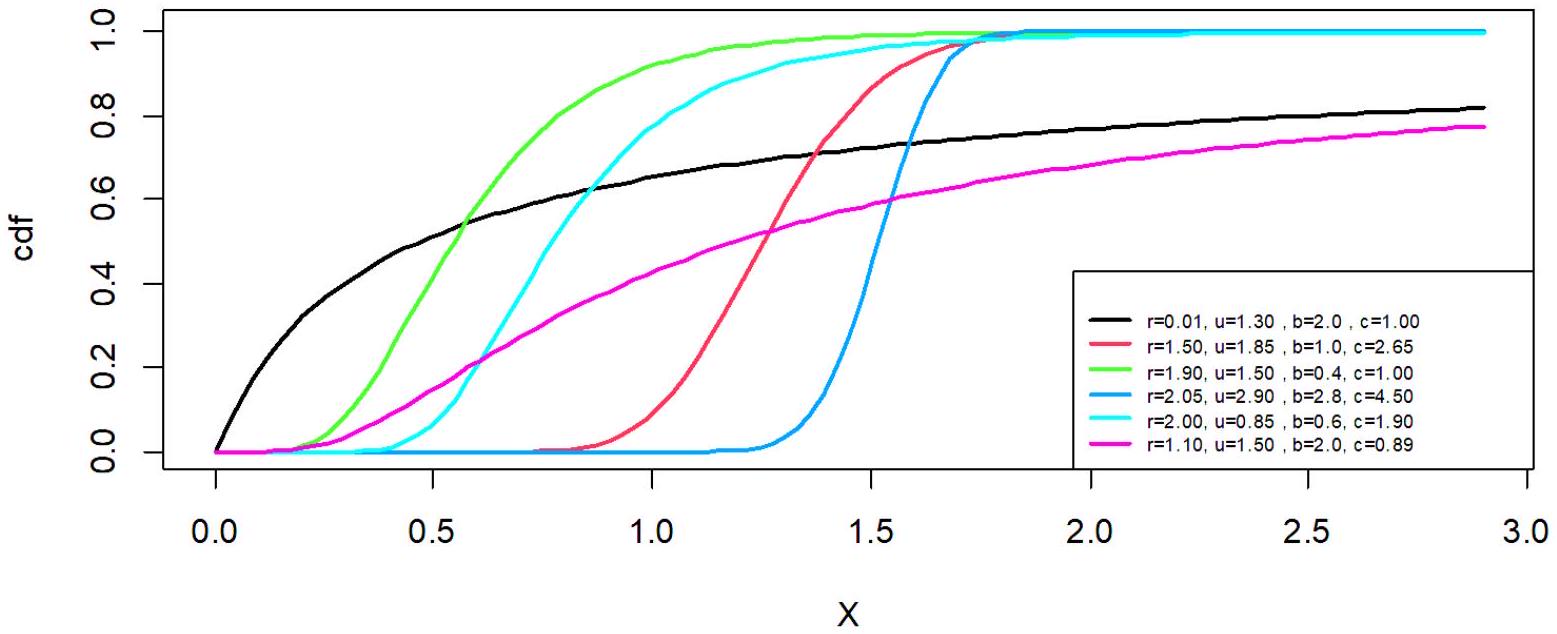
باتباع نفس النهج، يمكن أيضًا تبسيط PDF من خلال التوسع الرياضي، مما يؤدي إلى الصيغة التالية:
أين ، و .
كـ لـ و و لـ و .

3. خصائص توزيع HWIW

3.1 دالة الكمية لتوزيع HWIW

نظرية: إذا يمثل دالة التوزيع التراكمي لتوزيع HWIW، بحيث إذا كانت دالة متزايدة وغير متناقصة، فإن دالة الكوانتيل المقابلة توزيع هذا يُعطى بواسطة:
برهان: دع كن دالة التوزيع التراكمي لتوزيع HWIW
افترض أن ، ثم خذ اللوغاريتم لكلا الجانبين للحصول على: . نقسم كلا الجانبين على ، لذا نحصل على: قم برفع كلا الجانبين إلى القوة للحصول على: نضرب كلا الجانبين من المعادلة في -1 نحصل على: .
لتبسيط التعبير، نقوم بتعريف متغير بديل كما يلي: .
لذلك .
حيث هو الفرع السفلي من دالة لامبرت W [5] إذن: .
الآن، عُد إلى الوراء لإيجاد خذ اللوغاريتم لكلا الجانبين للحصول على: .
قسمة كلا الجانبين على -ب يعطي: خذ ارفع كلا الجانبين إلى القوة للحصول على: .
أخيرًا، باستخدام التعريف الأصلي لـ دالة الكوانتيل هو:
أخيرًا، نحصل على صيغة في المعادلة (3.1).
تم تحديد تمثيل عددي لدالة الكوانتيل للنموذج المقترح في الجدول 1.
الجدول 1: دالة الكوينتيل لتوزيع HWIW.
( )
(0.7,1.3,0.4,0.2) (0.6,1.5,1.4,1) (0.5,1.1,0.9,1.1) (1.2,1,0.8,1.2) (0.7,1.9,0.7,0.5)
0.1 0.0218168 1.906395 1.062304 0.6697021 1.099829
0.2 0.1115255 ٢.٦٢٠٩٣٠ 1.532390 0.8610302 1.868169
0.3 0.3981566 3.348908 2.071615 1.0475163 ٢.٧٦٥٠٩٤
0.4 1.2719911 ٤.١٧٦٧٧٦ 2.766355 1.2531876 ٣.٨٩٠٤٠٠
0.5 ٤.٠٤١٤٥٥٠ 5.189129 ٣.٧٤٤٧٥٦ 1.4990069 5.381479
0.6 13.8737973 6.519626 ٥.٢٦٧٠٤٧ 1.8168022 7.483554
0.7 57.2273272 8.437554 7.985730 2.2706451 10.714995
0.8 ٣٤٧.٧٥٩٦٩٦٥ 11.637871 14.089895 ٣.٠٢٩٦٣٠٥ 16.449317
0.9 ٥٧٤.١٨٩٠١٦٥ 18.902468 ٣٦.٧١٢٧٢١ ٤.٨٠٥٢٣٧١ 30.300980

3.2 دالة العزم لتوزيع HWIW

نظرية: ليكن X متغيرًا عشوائيًا تحكمه توزيع HWIW و يمثل دالة الكثافة الاحتمالية الخاصة به، ثم لحظة من الرتبة توزيع هذا يُعطى بواسطة:
برهان: افترض أن X هي متغير عشوائي مع دالة كثافة الاحتمال هي ثم يتم إعطاء لحظة الرتبة n بالعبارة التالية [15]، [9] :
استبدال المعادلة (2.8) في التعبير السابق يعطي النتيجة التالية
أين ، و .
لـ دع
ثم تبسيط للحصول على النهائي التالي من:
اتباع إجراء مشابه لـ نصل إلى الشكل النهائي
أخيرًا، نحصل على شكل في المعادلة (3.2).
تم اشتقاق اللحظات الأربعة الأولى عن طريق استبدال قيم مختلفة لـ n، كما هو موضح أدناه:
باستخدام هذه النتيجة، نحصل على الانحراف المعياري والتفلطح لتوزيع HWIW بالطريقة التالية:
تظهر الجدول 2 فترات بعض لحظات توزيع HWIW، موضحة كيف تتغير هذه اللحظات مع تغير معلمات التوزيع. كما تسلط الضوء على تأثير المعلمات على اللحظات الأربعة الأولى، مما يساعد في تحليل الخصائص الإحصائية للتوزيع عندما تتغير قيم المعلمات.
الجدول 2: يعرض فترات بعض لحظات توزيع HWIW.
ج انحراف التفرطح
– 1.1 1.596876 ٤.٧٨٦٣٢٦ ٣٧.٦١٦٩١ ١٣٦٣.٢٥٦ ٢.٢٣٦٣١٣ ٣.٥٩٢٣٥٩ ٥٩٫٥٠٧٦٦
1.2 1.50402 ٣.٧٧٢٣٦٤ 19.97024 ٣٣٣.٨٢٠٥ 1.510288 2.725605 ٢٣.٤٥٧٧٢
ج 1.3 1.959321 5.865176 31.84193 157.4864 ٢.٠٢٦٢٣٧ ٢.٢٤١٧٠٢ ٤.٥٧٨٠٥٤
1.4 1.844062 ٤.٨٦٠٠٧١ 20.81439 179.4392 1.459506 1.942673 7.596825
٨ 1.5 2.012762 ٤.٨٦٣٨٥ 14.33673 52.54653 0.812639 1.336533 ٢.٢٢١١٨
1.6 1.916656 ٤.٣١٠٣٩٤ 11.52101 ٣٧.١٦٤٦٦ 0.636824 1.287405 2.000305
60 1.7 1.968528 ٤.٤٦١٨١٦ ١١.٧٦٧٤٨ ٣٦.٥٦٤٧٨ 0.586714 1.248579 1.836706
1.8 1.769355 ٣.٥٤٨٣٨٤ 8.136669 21.553 0.417767 1.217309 1.711774

3.3 دالة توليد اللحظات لتوزيع HWIW

نظرية: دع كن متغيرًا عشوائيًا مع دالة كثافة الاحتمال هي ثم يتم إعطاء MGF لتوزيع HWIW بواسطة:
برهان: لنفترض أن هي متغير عشوائي مع دالة كثافة الاحتمال هي ثم يتم إعطاء MGF بواسطة [16]، [17]:
باستخدام التوسع الأسي للمعادلة أعلاه، نحصل على شكل:
من المعادلة (12)، فإن دالة التوليد العشوائي لتوزيع HWIW لها شكل في المعادلة (3.3).

3.4 دالة اللحظات غير المكتملة لتوزيع HWIW

نظرية: دع كن متغيرًا عشوائيًا تحكمه توزيع HWIW و يمثل دالة الكثافة الاحتمالية الخاصة به، ثم يتم إعطاء دالة اللحظة غير المكتملة لهذه التوزيعة بواسطة:
برهان: افترض هي متغير عشوائي مع دالة كثافة الاحتمال هي ثم دالة اللحظات غير المكتملة المعطاة بالتعبير التالي [18]:
من المعادلة (3.2)، نحصل على:
أين ، و . ل “، دع
عندما وإذا .
اتباع إجراء مشابه لـ نصل إلى الشكل النهائي
ثم فإن دالة اللحظات غير المكتملة لتوزيع HWIW لها شكل في المعادلة (3.4).

3.5 الدالة المميزة لتوزيع HWIW

نظرية: دع كن متغيرًا عشوائيًا تحكمه توزيع HWIW و يمثل دالة الكثافة الاحتمالية الخاصة به، فإن الدالة المميزة لهذه التوزيعة تُعطى بواسطة:
برهان: افترض هي متغير عشوائي مع دالة كثافة الاحتمال هي ثم الدالة المميزة المعطاة بالتعبير التالي [19]:
باستخدام التوسع الأسي للمعادلة أعلاه، نحصل على الشكل:
من المعادلة (3.2)، فإن الدالة المميزة لتوزيع HWIW لها شكل في المعادلة (3.5).

3.6 إنتروبيا ريني لتوزيع NMWIW

نظرية: دع كن متغيرًا عشوائيًا تحكمه توزيع HWIW و يمثل دالة الكثافة الاحتمالية الخاصة به، فإن إنتروبيا ريني لهذه التوزيعة تُعطى بـ:
أين
برهان: افترض هي متغير عشوائي مع دالة كثافة الاحتمال هي ثم تكون إنتروبيا ريني المعطاة بالعبارة التالية [20]:
من المعادلة 10، نحصل على:
استخدام سلسلة ثنائية الحدود
ثم إن إنتروبيا ريني لتوزيع HWIW لها شكل في المعادلة (3.6).

4. التقدير

4.1 تقدير الاحتمالية القصوى (MLE)

يتم تقدير معلمات توزيع HWIW باستخدام طريقة الاحتمال الأقصى (MLE). اعتبر أن المتغير العشوائي يتبع توزيع HWIW. ويتم الإشارة إلى متجه المعاملات بـ دالة الاحتمالية اللوغاريتمية المقابلة لـ يُعبر عنه كـ [21]، [22]:
نحسب لوغاريتم الاحتمالية:

4.2 تقدير المربعات الصغرى

يمكن استخدام طريقة تقدير المربعات الصغرى (LSE) لتقدير معلمة باستخدام الصيغة التالية [23]:

4.3 تقدير المربعات الصغرى الموزونة (WLSE)

يمكن تقدير المعامل باستخدام تقنية WLSE من خلال التعبير التالي [24]:
تُستمد تقديرات المعلمات باستخدام الطرق الثلاث المذكورة أعلاه، من خلال التفاضل الجزئي لدالة الاحتمالية للمعلمات الأربعة ثم تعيين المشتقات تساوي صفر. نظرًا لتعقيد الحلول العددية لهذه المعادلات، تُستخدم تقنيات الحوسبة مثل لغة R للحصول على القيم المطلوبة.

5. المحاكاة

محاكاة مونت كارلو هي تقنية رياضية تعتمد على المتغيرات العشوائية لنمذجة الأنظمة المعقدة وتحليل سلوكها. يتم تطبيقها على نطاق واسع في الإحصاء والاقتصاد والهندسة والعلوم الطبيعية بسبب قدرتها على تقديم تقديرات دقيقة للنماذج التي يصعب أو حتى يستحيل الحصول على حلول لها باستخدام الطرق التحليلية التقليدية. الفكرة الأساسية هي توليد عدد كبير من العينات العشوائية من أجل حساب كميات محددة أو تقدير النتائج الاحتمالية، مما يسهل دراسة الظواهر التي يصعب التنبؤ بها تحليليًا. لتقييم كفاءة ودقة تقدير معلمات توزيع HWIW، تم إجراء محاكاة مونت كارلو باستخدام ثلاث طرق تقدير: MLE، LSE، WLSE. عينات عشوائية من أحجام وحتى تم توليدها، وتم تقييم أداء كل طريقة بالنسبة لثلاثة معايير: MSE، RMSE [25]، [26]، وانحياز تقديرات المعلمات.
تُلخص نتائج المحاكاة في الجدول 3، الذي يُبلغ عن جميع مقاييس الأداء الثلاثة لكل حجم عينة، مما يوفر تقييمًا عمليًا لفعالية تقنيات التقدير.
الجدول 3: نتائج محاكاة مونت كارلو المطبقة على توزيع HWIW.
ن تأسس. أس. بار. MLE لندن سكول أوف إيكونوميكس WLSE
50 معنى 0.66218994 0.7935073 0.7945322
0.94482752 0.90725405 0.87221447
0.8173529 0.9586352 0.9458078
1.6005334 1.3007755 1.3224457
MSE 0.34450955 0.3029998 0.3196053
0.09171262 0.16296775 0.09943654
0.5872540 0.5312079 0.5426379
0.8883328 0.4236644 0.3828196
جذر متوسط مربع الخطأ 0.58694936 0.5504542 0.5653365
0.30284092 0.40369264 0.31533560
0.7663250 0.7288401 0.7366396
0.9425141 0.6508951 0.6187241
تحيز 0.06218994 0.1935073 0.1945322
0.04482752 0.00725405 0.02778553
0.1173529 0.2586352 0.02778553
0.4005334 0.1007755 0.1224457
100 معنى 0.64384318 0.7219438 0.7182429
0.94033751 0.87454167 0.87775399
0.76723431 0.8778392 0.8340620
1.4001384 1.3028549 1.27703038
MSE 0.23499950 0.2124502 0.1981540
0.06256473 0.07460193 0.04674475
0.33109832 0.3405407 0.2714449
0.2971453 0.2258667 0.18424882
جذر متوسط مربع الخطأ 0.48476747 0.4609232 0.4451449
0.25012943 0.27313355 0.21620533
0.57541144 0.5835586 0.5210037
0.5451103 0.4752543 0.42924215
تحيز 0.5451103 0.1219438 0.1182429
0.04033751 0.02545833 0.02224601
0.06723431 0.1778392 0.1340620
0.2001384 0.1028549 0.07703038
150 معنى 0.609999358 0.7218282 0.64903158
0.95149716 0.87361891 0.91132615
0.72423747 0.8539909 0.75548383
1.3746361 1.27230291 0.75548383
MSE 0.180700778 0.2093021 0.16223096
0.05561927 0.05271935 0.04119156
0.25410926 0.2817639 0.20157287
0.2018948 0.13858398 0.1762926
جذر متوسط مربع الخطأ 0.425089141 0.4574955 0.40277904
0.23583739 0.22960694 0.20295704
0.50409251 0.5308143 0.44896867
0.4493271 0.37226869 0.4198721
تحيز 0.009999358 0.1218282 0.04903158
0.05149716 0.02638109 0.01132615
0.02423747 0.1539909 0.05548383
0.1746361 0.07230291 0.1213862
معنى 0.62953303 0.67330833 0.62552888
0.92401550 0.892643858 0.91648996
0.73728692 0.8049638 0.7284962
1.3183908 1.25742869 1.3022389
MSE 0.14542449 0.12782454 0.12441776
0.03766835 0.043226750 0.03072519
0.18643346 0.2099843 0.1550041
0.1322101 0.11526679 0.1274526
٢٠٠ جذر متوسط مربع الخطأ 0.38134563 0.3636071 0.35272902
0.19408336 0.207910437 0.17528603
0.43177941 0.4582404 0.3937056
0.3636071 0.33950963 0.3570051
تحيز 0.02953303 0.07330833 0.02552888
0.02401550 0.007356142 0.01648996
0.03728692 0.1049638 0.0284962
0.1183908 0.05742869 0.1022389
٢٥٠ معنى 0.605497333 0.67616917 0.608383893
0.93281004 0.88124099 0.92341073
0.706005227 0.79824836 0.71403583
1.30557693 1.26590402 1.29949605
MSE 0.109527538 0.12320369 0.108918047
0.03389573 0.03761672 0.03328868
0.136416881 0.17672820 0.14360899
0.09854788 0.10182472 0.10257126
جذر متوسط مربع الخطأ 0.330949450 0.35100383 0.330027342
0.18410793 0.19395029 0.18245186
0.369346559 0.42039054 0.37895777
0.31392336 0.31909986 0.32026748
تحيز 0.005497333 0.07616917 0.008383893
0.03281004 0.01875901 0.02341073
0.006005227 0.09824836 0.01403583
0.10557693 0.06590402 0.09949605
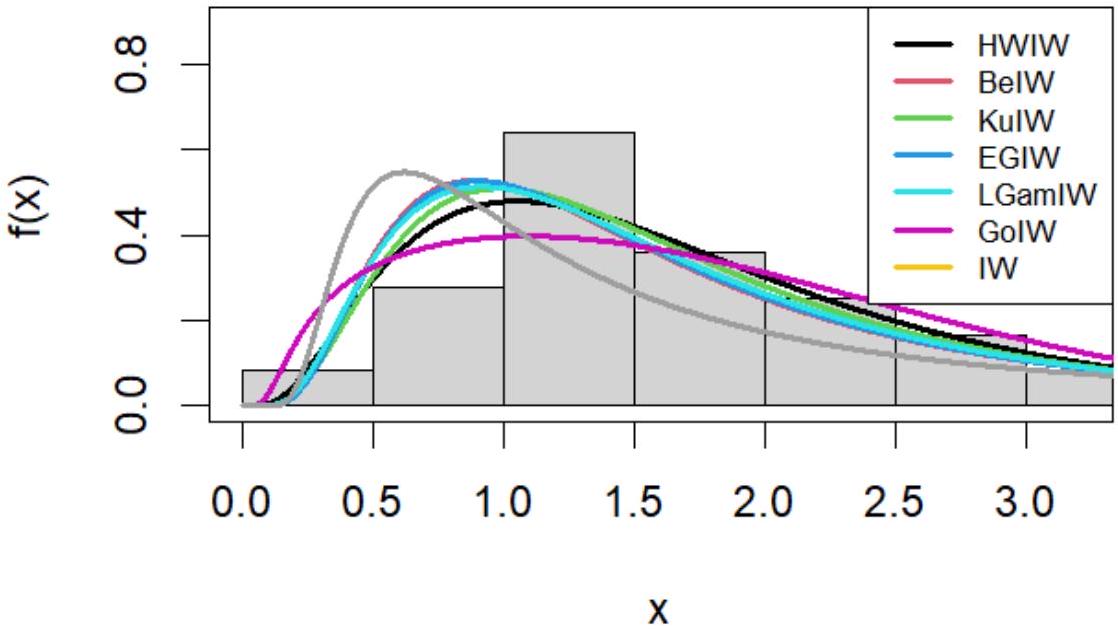
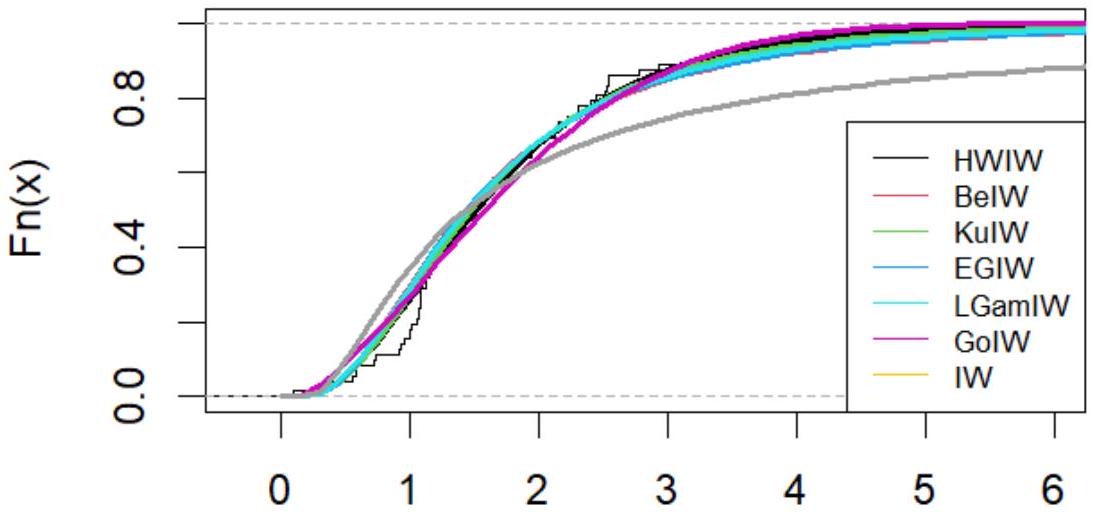
الجدول 3 يعرض نتائج محاكاة مونت كارلو المستخدمة لتقدير معلمات توزيع HWIW من خلال ثلاث تقنيات تقدير متميزة: (MLE، LSE، و WLSE). يُظهر الجدول أن دقة التقدير تتحسن مع زيادة حجم العينة، حيث تتناقص قيم MSE و RMSE تدريجياً من 50 إلى 250 حجم عينة. تُظهر النتائج أن طريقة WLES تحقق أفضل أداء من حيث الدقة لمعظم المعلمات، خاصةً لأحجام العينات الصغيرة والمتوسطة، بينما حافظت طريقة MLE على أدنى قيم انحياز في معظم الحالات، مما يدل على استقرارها وموثوقيتها.
من ناحية أخرى، كانت طريقة LSE ذات أداء ضعيف نسبيًا، خاصة في تقدير المعلمات بدقة في حجم عينة صغير، مع قيم MSE وBias أعلى. تعكس هذه النتائج أهمية اختيار طريقة التقدير المناسبة بناءً على حجم العينة ومتطلبات الدقة الإحصائية.

6. التطبيق

لإظهار قوة وملاءمة التوزيع المقترح في السياقات الواقعية، تلعب المكون العملي دورًا مركزيًا في هذا التقييم. لذلك، توفر هذه القسم تطبيقًا على بيانات حقيقية، مصحوبًا ومقارنًا بستة توزيعات معروفة لتقييم الأداء.
  • بيتا مع توزيع وايبل العكسي الأساسي (BeIW)
  • كوماراسوامي مع توزيع وايبول العكسي الأساسي (KuIW)
  • الويبل المعكوس العام المعزز (EGIW)
  • لوغ-جاما مع توزيع وايبول العكسي الأساسي (LGamIW)
  • غومبيرتس مع وايبول عكسي أساسي (GoIW)
  • ويبل العكسي (IW)
جميع التوزيعات المختارة تنتمي إلى عائلات موسعة أو معدلة من توزيع IW، مما يجعلها منافسين مباشرين لتوزيع HWIW. تعتبر هذه التوزيعات نماذج قوية لتحليل البيانات الإحصائية، ويتميز توزيع HWIW بينها بمرونته وقدرته على تمثيل البيانات بدقة، وهو ما كان الدافع الرئيسي وراء تطويره. تم إجراء هذه المقارنة باستخدام أربعة معايير معلوماتية AIC [27]، CAIC [28]، BIC [29]، وHQIC [30]. كما تم استخدام أربعة مقاييس إحصائية لتقييم الدقة K-S، A، W وp-value.
مجموعة البيانات-1: تتضمن مجموعة البيانات المستخدمة في هذه الدراسة أوقات بقاء 72 خنزير غينيا تم إصابتها بعصيات السل الفتاكة. يتم قياس أوقات البقاء بالأيام. تم إجراء الملاحظة والتقرير الأصلي لهذه المجموعة من البيانات بواسطة بييركيدال [5].
، ، .
يوفر الجدول 4 ملخصًا لمعايير اختيار النموذج المستخدمة لمقارنة التوزيع. بينما يقدم الجدول 5 قيم الاختبارات الإحصائية المقابلة، يعرض الجدول 6 المعلمات المقدرة لكل توزيع قيد الدراسة.
الجدول 4. نتائج المعايير للتوزيعات.
منطقة -لوج إيه آي سي CAIC بيك HQIC
HWIW 95.88984 199.8247 ٢٠٠.٤٢١٧ ٢٠٨.٩٣١٣ ٢٠٣.٤٥٠١
كن ١٠١.٢٩٦ 210.6642 211.2612 ٢١٩.٧٧٠٨ ٢١٤.٢٨٩٥
KuIW 97.89873 203.7986 204.3956 212.9053 ٢٠٧.٤٢٤
إيجي و 100.9368 ٢٠٩.٨٨٢٦ 210.4796 218.9893 ٢١٣.٥٠٨
LGamIW 99.80569 ٢٠٧.٦٢٤٧ ٢٠٨.٢٢١٧ 216.7314 211.2501
GoIW 97.17087 ٢٠٢.٣٤١٨ ٢٠٢.٩٣٨٨ 211.4485 205.9672
آي دبليو ١١٨.١١٧٨ ٢٤٠٫٢٣٥٦ 240.4095 244.7889 242.0483
تظهر الجدول 4 نتائج معايير المقارنة بين التوزيعات، حيث تشير القيم المنخفضة إلى أداء أفضل. أظهرت نتائج التقييم أن توزيع HWIW حقق أدنى القيم عبر جميع المعايير (AIC، BIC، إلخ)، مما يدل على تمثيله المتفوق للبيانات. في المقابل، حقق توزيع IW أعلى القيم، مما يشير إلى ملاءمته الضعيفة مقارنة بالتوزيعات الأخرى.
الجدول 5. قيمة المقاييس الإحصائية.
منطقة W أ K-S قيمة p
HWIW 0.0922143 0.6110752 0.1130676 0.316085
كن 0.1675262 1.155408 0.1438356 0.1016569
KuIW 0.1107239 0.7703783 0.11985 0.2522606
إي جي آي دبليو 0.1608632 1.111592 0.1402135 0.117882
LGamIW 21.91134 ١٤١٫٢٥٨ 0.9999952
GoIW 0.1616563 0.9825052 0.1283847 0.1861575
آي دبليو 0.5284354 3.310617 0.1991304 0.006625223
يوضح الجدول 5 نتائج مقاييس جودة الملاءمة الإحصائية. تشير القيم المنخفضة لـ W و A و K-S إلى ملاءمة أفضل للبيانات، وتعتبر قيم p مؤشراً إضافياً على ذلك. كانت توزيع HWIW هو الأفضل، حيث حقق أدنى القيم عبر جميع المقاييس وأعلى قيمة p (0.316)، مما يدل على ملاءمة قوية للبيانات. بالمقابل، كانت التوزيعات مثل LGamIW و IW ذات أداء ضعيف، مع قيم مرتفعة وقيم p منخفضة جداً، مما يدل على تمثيل ضعيف للبيانات.
الجدول 6. فترة قيمة المقدّر للمعلمات بواسطة تقدير الاحتمالية القصوى.
منطقة
HWIW 1.3782752 3.1107381 0.4686840 0.5414699
كن 0.9168564 5.9240884 ٣.٠٠٧٤٠٥٨ 0.7257823
KuIW 2.0448702 15.6432752 1.9116895 0.5584649
إيجي و 6.5028232 0.9572174 ٣.٠٢١٥٦٧٣ 0.7065691
LGamIW 0.6738629 7.9310308 ٣.٩٧٦٧٦٩٠ 0.7099198
GoIW 0.7349332 ٣.٢٢٤٣٢٩٧ 1.4417615 0.6936903
آي دبليو —- —– 1.061440 1.171994
تظهر الجدول 6 تقديرات المعلمات للتوزيعات باستخدام تقدير الاحتمال الأقصى. أظهرت توزيع HWIW معلمات معتدلة، مما يعكس توازنًا جيدًا في التمثيل. بالمقابل، سجلت توزيعات مثل KuIW وEGIW قيمًا عالية لبعض المعلمات، مما يشير إلى نماذج أكثر تعقيدًا. كان توزيع IW، كونه أبسط من التوزيعات الأخرى، يحتوي على معلمين فقط. تعكس هذه التقديرات مرونة كل توزيع في تمثيل البيانات.
الشكل 5: ملاءمة PDFs HWIW مع مجموعة بيانات المدرج التكراري.
الشكل 6: دوال التوزيع التراكمي التجريبية الملائمة HWIW مع مجموعة البيانات.
تظهر الشكل 5 مدى توافق دالة الكثافة الاحتمالية لتوزيع WHIW مع مجموعة البيانات الأولى. توضح المنحنى الملائم تطابقًا وثيقًا مع البيانات التجريبية، مما يعكس كفاءتها العالية في تمثيل السلوك الفعلي للبيانات بشكل فعال ومرن. يظهر الشكل 6 مقارنة بين دالة التوزيع التراكمي التجريبية ودالة التوزيع التراكمي النظرية المرتبطة بتوزيع HWIW. توضح هذه الشكل توافقًا واضحًا بين المنحنيين، مما يؤكد قدرة التوزيع المقترح على تمثيل الاحتمالية التراكمية للبيانات بدقة، وبالتالي تعكس فعاليته في نمذجة البيانات الحقيقية بشكل موثوق.
مجموعة البيانات-2: أوقات الفشل لـ 50 مكونًا [29]
، ، 6.274، 6.816، 7.896، 7.904، 8.022، 9.337، 10.940، 11.020، 13.880، 14.730، 15.080
الجدول 7. نتائج المعايير للتوزيعات.
منطقة -لوج إيه آي سي CAIC بيك HQIC
HWIW ١٠٢.٥٨٩٧ 213.1842 ٢١٤.٠٧٣١ ٢٢٠.٨٣٢٣ 216.0967
كن ١٠٤.٧٦٢٢ ٢١٧.٥٤٠٤ 218.4292 ٢٢٥.١٨٨٤ 220.4528
KuIW ١٠٤.٤١٠٤ 216.8386 ٢١٧.٧٢٧٥ 224.4867 ٢١٩.٧٥١١
إيجي و ١٠٤.٧٦٧١ ٢١٧.٥٤٣٨ 218.4327 ٢٢٥.١٩١٩ ٢٢٠.٤٥٦٢
LGamIW ١٠٤.٤٦٥١ ٢١٧.٠١٨٦ ٢١٧.٩٠٧٥ ٢٢٤.٦٦٦٧ ٢١٩.٩٣١
GoIW ١٠٤.٥٨٧٣ 217.1846 218.0735 224.8327 ٢٢٠٫٠٩٧١
آي دبليو ١٠٦.٠٩٦٧ 216.1933 216.4486 220.0174 ٢١٧.٦٤٩٥
تظهر الجدول 7 أن توزيع HWIW حقق أدنى القيم عبر جميع مقاييس المعلومات (AIC، BIC، CAIC، وHQIC) مقارنة بالتوزيعات الأخرى، مما يدل على كفاءته العالية في ملاءمة البيانات. في المقابل، حققت التوزيعات مثل BeIW وGoIW وEGIW قيمًا أعلى، مما يعكس أدائها الضعيف مقارنةً بـ HWIW.
الجدول 8. قيمة المقاييس الإحصائية.
منطقة W أ K-S قيمة p
HWIW 0.1719594 1.063281 0.1379881 0.2711381
كن 0.2246938 1.384528 0.1585079 0.1453208
KuIW 0.2160847 1.333744 0.1558378 0.1584046
إي جي آي دبليو 0.224653 1.384445 0.1614739 0.1318197
LGamIW 17.95769 99.77021 0.9818669
GoIW 0.2123711 1.31562 0.1496055 0.1925845
آي دبليو 0.2575837 1.57173 0.16011 0.1378965
تظهر الجدول 8 أن توزيع HWIW كان الأفضل بين التوزيعات المقارنة، حيث سجل أدنى القيم لمقاييس W و A و K-S، بالإضافة إلى أعلى قيمة p، مما يؤكد تمثيله الدقيق للبيانات. بالمقابل، كانت التوزيعات مثل IW و LGamIW ذات أداء ضعيف، مما يدل على عدم ملاءمتها للبيانات.
الجدول 9. فترة قيمة المقدّر للمعلمات بواسطة تقدير الاحتمالية القصوى.
منطقة
HWIW 1.2975383 2.5187226 0.3953556 0.2346634
كن 1.2809056 ٢.١٩٩٧٤٦٣ 1.0261864 0.3948558
KuIW 1.3911669 ٢.٧٤٠٧٦٣٦ 1.0465352 0.3649795
إيجي و 2.1705086 1.0785869 1.1698675 0.4009732
LGamIW 1.2129747 ٢.٩٤٧٢٠٤٩ 1.3521062 0.3473045
GoIW 1.2129747 ٢.٩٤٧٢٠٤٩ 1.3521062 0.3473045
آي دبليو —- —– 0.6040943 0.5912884
تظهر الجدول 9 أن توزيع HWIW قدم تقديرات معلمات أكثر استقرارًا ودقة مقارنة بالتوزيعات الأخرى. ومع ذلك، أظهرت التوزيعات مثل GoIW و BeIW تباينًا كبيرًا في التقديرات، مما يدل على انخفاض موثوقيتها.
الشكل 7: ملاءمة PDFs HWIW مع مجموعة بيانات المدرج التكراري-II.
الشكل 8: دوال التوزيع التراكمي التجريبية الملائمة HWIW مع مجموعة البيانات-II.
تُبرز الشكل 7 مدى تطابق دالة الكثافة الاحتمالية لتوزيع HWIW مع المدرج التكراري للبيانات التجريبية. يُظهر هذا التوزيع بوضوح قدرته على تمثيل الشكل العام للبيانات، خاصة في المناطق المبكرة من التوزيع والانحدار، مما يعكس مرونة HWIW في استيعاب التغيرات والسلوك الفعلي للبيانات. تُظهر الشكل 8 تقاربًا وثيقًا بين دالة التوزيع التراكمي النظرية لتوزيع HWIW والتوزيع التراكمي التجريبي. يدعم هذا التقارب قدرة النموذج على تمثيل السلوك التراكمي للبيانات بدقة، حتى في وجود تباين أو عدم يقين في القيم التجريبية.

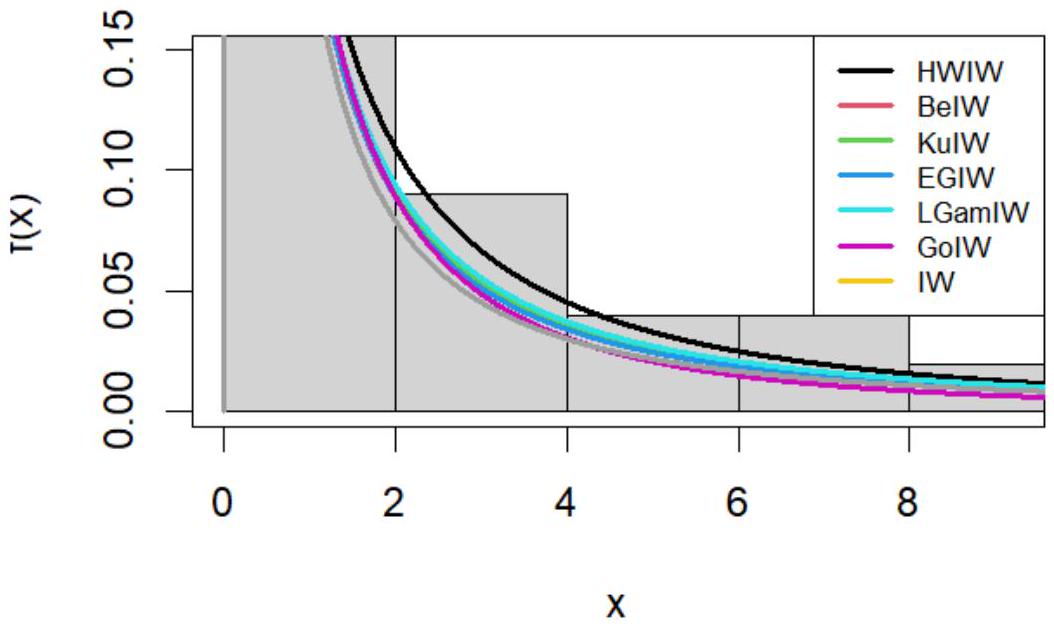
7. الخاتمة

أظهرت توزيع HWIW كفاءة عالية في تمثيل البيانات المعقدة من العالم الحقيقي، متفوقة بوضوح على ستة توزيعات IW الممتدة المنافسة. حقق أقل قيمة لمعيار المعلومات (AIC، CAIC، BIC، HQIC)، وأفضل مؤشرات جودة الملاءمة (W، A، K-S)، وأعلى قيمة للاحتمالية (P-value)، مما يعكس قدراته الدقيقة والفعالة في النمذجة. أكدت النتائج
تتميز توزيع HWIW بقدرتها على التكيف مع البيانات غير المتماثلة والثقيلة الذيل، مما يجعلها مناسبة لتمثيل مجموعة واسعة من مجموعات البيانات الواقعية. كشفت نتائج محاكاة مونت كارلو أن طريقة WLSE كانت الأكثر دقة من حيث MSE و RMSE، خاصة بالنسبة للعينات الصغيرة والمتوسطة الحجم، بينما أظهرت طريقة MLE تحيزًا أقل واستقرارًا أكبر مع زيادة حجم العينة. بالمقابل، أدت طريقة LES أداءً ضعيفًا نسبيًا، مما يبرز أهمية اختيار طريقة التقدير المناسبة بناءً على حجم العينة وأهداف التحليل – WLES للدقة و MLE للاستقرار. يتمتع التوزيع المقترح بخصائص رياضية متقدمة، مثل مرونة دوال الكثافة والتوزيع، وسهولة اشتقاق اللحظات، ودالة الكمية، والإنتروبيا، مما يعزز موثوقيته كأداة تحليلية في الإحصاءات التطبيقية. نظرًا لتفوقه على التوزيعات الأخرى، يعد HWIW نموذجًا واعدًا يمكن توسيعه ليشمل البيانات متعددة الأبعاد أو دمجه مع تقنيات الذكاء الاصطناعي وتعلم الآلة لتحسين التنبؤات في البيئات غير المؤكدة. تفتح هذه النتائج آفاقًا جديدة لاستخدام توزيع HWIW في مجموعة واسعة من التطبيقات الواقعية، بما في ذلك المجالات الطبية والصناعية والاجتماعية، حيث تقدم النماذج التقليدية تحديات في تمثيل التباين والانحراف في البيانات الحقيقية.

مساهمات المؤلفين:

عمل المؤلفون بالتساوي لكتابة ومراجعة المخطوطة.

بيان توافر البيانات:

البيانات التي تدعم نتائج هذه الدراسة متاحة ضمن المقال.

تعارض المصالح:

يعلن المؤلفون عدم وجود أي تضارب في المصالح.

References

[1] Alzaatreh, A., Lee, C., and Famoye, F. (2013). A new method for generating families of continuous distributions. Metron, 71(1), 6379.
[2] Hussain, S., Hassan, M. U., Rashid, M. S., and Ahmed, R. (2023). Families of Extended Exponentiated Generalized Distributions and Applications of Medical Data Using Burr III Extended Exponentiated Weibull Distribution. Mathematics, 14(11), 3090.
[3] Odeyale, A. B., Gulumbe, S. U., Umar, U., and Aremu, K. O. (2023). New Odd Generalized Exponentiated Exponential-G Family of Distributions. UMYU Scientifica, 4(2), 56-64.
[4] Noori, N. A., Khalaf, A. A., and Khaleel, M. A. (2023). A New Generalized Family of Odd Lomax-G Distributions Properties and Applications. Advances in the Theory of Nonlinear Analysis and Its Application, 4(7), 1-16.
[5] Sadiq, I. A., Doguwa, S. I., Yahaya, A., and Garba, J. (2023). New Generalized Odd Fréchet-G (NGOF-G) Family of Distribution with Statistical Properties and Applications. UMYU Scientifica, 3(2), 100-107.
[6] Abdelall, Y. Y., Hassan, A. S., and Almetwally, E. M. (2024). A new extension of the odd inverse Weibull-G family of distributions: Bayesian and non-Bayesian estimation with engineering applications. Computational Journal of Mathematical and Statistical Sciences, 2(3), 359-388.
[7] Ishaq, A. I., Panitanarak, U., Alfred, A. A., Suleiman, A. A., and Daud, H. (2024). The Generalized Odd Maxwell-Kumaraswamy Distribution: Its Properties and Applications. Contemporary Mathematics, 1(1), 711-742.
[8] Noori, N. A., Abdullah, K. N., and Khaleel, M. A. (2025). Data Modelling and Analysis Using Odd Lomax Generalized Exponential Distribution: an Empirical Study and Simulation. Iraqi Statisticians Journal, 1(2), 146-162.
[9] Mahdi, G. A., Khaleel, M. A., Gemeay, A. M., Nagy, M., Mansi, A. H., Hossain, M. M., and Hussam, E. (2024). A new hybrid odd exponential- family: Properties and applications. AIP Advances, 14(4), 1-15.
[10] Noori, N. A., and Khaleel, M. A. (2024). Estimation and Some Statistical Properties of the hybrid Weibull Inverse Burr Type X Distribution with Application to Cancer Patient Data. Iraqi Statisticians Journal, 2(1), 8-29.
[11] Noori, N. A., Khalaf, A. A., and Khaleel, M. A. (2024). A new expansion of the Inverse Weibull Distribution: Properties with Applications. Iraqi Statisticians Journal, 1(1), 52-62.
[12] Noori, N. A. (2023). Exploring the Properties, Simulation, and Applications of the Odd Burr XII Gompertz Distribution. Advances in the Theory of Nonlinear Analysis and Its Application, 4(7), 60-75.
[13] Khalaf, A. A., Khaleel, M. A., and Noori, N. A. (2024). A new expansion of the Inverse Weibull Distribution: Properties with Applications. Iraqi Statisticians Journal, 1(1), 52-62.
[14] Alanaz, M. M., and Algamal, Z. Y. (2023). Neutrosophic exponentiated inverse Rayleigh distribution: Properties and Applications. International Journal of Neutrosophic Science, 21(4), 36-43.
[15] Khalaf, A. A., Ibrahim, M. Q., and Noori, N. A. (2024). [0,1] Truncated Exponentiated Exponential Burr type X Distribution with Applications. Iraqi Journal of Science, 65(8), 4428-4440.
[16] Gómez, H. J., Santoro, K. I., Chamorro, I. B., Venegas, O., Gallardo, D. I., and Gómez, H. W. (2023). A Family of Truncated Positive Distributions. Mathematics, 11(21), 4431.
[17] Muhammad, B., Mohsin, M., and Aslam, M. (2021). Weibull-exponential distribution and its application in monitoring industrial process. Mathematical Problems in Engineering, 2021(1), 1-13.
[18] Al Abbasi, J. N., Resen, I. A., Abdulwahab, A. M., Oguntunde, P. E., Al-Mofleh, H., and Khaleel, M. A. (2023). The right truncated Xgamma-G family of distributions: Statistical properties and applications. AIP Conference Proceedings, 2834(1), 1-15.
[19] Al-Habib, K. H., Khaleel, M. A., and Al-Mofleh, H. (2023). A new family of truncated Nadarajah-Haghighi-G properties with real data applications. Tikrit Journal of Administrative and Economic Sciences, 19(61), 2.
[20] Afify, A. Z., Yousof, H., and Nadarajah, S. (2017). The beta transmuted-H family for lifetime data. Statistics and its Interface, 10(3), 505-520.
[21] Bhatti, F. A., Hamedani, G. G., Korkmaz, M. C., Cordeiro, G. M., Yousof, H. M., and Ahmad, M. (2019). On Burr III Marshal Olkin family: development, properties, characterizations and applications. Journal of Statistical Distributions and Applications, 6(1), 1-21.
[22] Teamah, A.-E. A. M., Elbanna, A. A., and Gemeay, A. M. (2020). Frèchet-Weibull distribution with applications to earthquakes data sets. Pakistan Journal of Statistics, 36(2), 135-147.
[23] Abd El-latif, A. M., Almulhim, F. A., Noori, N. A., Khaleel, M. A., and Alsaedi, B. S. (2025). Properties with application to medical data for new inverse Rayleigh distribution utilizing neutrosophic logic. Journal of Radiation Research and Applied Sciences, 18(2), 101391.
[24] Abed, R. A., Khaleel, M. A., and Noori, N. A. (2025). Modified Weibull-Fréchet Distribution Properties with Application. Iraqi Statisticians Journal, 1(2), 195-216.
[25] Noori, N. A., Ahmed, D. D., and Khaleel, M. A. (2025). Odd Lomax Chen distribution: An Innovative Statistical Tool for Improving Real Data Modeling and Its Practical Applications. Tikrit Journal of Administrative and Economic Sciences, 21(Special Issue, Part 1), 1098-1126.
[26] Noori, N. A., Khaleel, M. A., and Salih, A. M. (2025). Some Expansions to The Weibull Distribution Families with Two Parameters: A Review. Babylonian Journal of Mathematics, 1(1), 61-87.
[27] Noori, N. A., Khaleel, M. A., Khalaf, S. A., and Dutta, S. (2025). Analytical Modeling of Expansion for Odd Lomax Generalized Exponential Distribution in Framework of Neutrosophic Logic: a Theoretical and Applied on Neutrosophic Data. Innovation in Statistics and Probability, 1(1), 47-59.
[28] Habib, K. H., Khaleel, M. A., Al-Mofleh, H., Oguntunde, P. E., and Adeyeye, S. J. (2024). Parameters Estimation for the [0, 1] Truncated Nadarajah Haghighi Rayleigh Distribution. Scientific African, 1(1), e02105.
[29] Khaoula, A., Seddik-Ameur, N., Abd El-Baset, A. A., and Khaleel, M. A. (2022). The Topp-Leone Extended Exponential Distribution: Estimation Methods and Applications. Pakistan Journal of Statistics and Operation Research, 18(4), 817-836
© 2025 by the authors. Disclaimer / Publisher’s Note: The views, opinions, and data presented in all published content are solely those of the individual authors and contributors. They do not necessarily reflect the positions of Sphinx Scientific Press (SSP) or its editorial team. SSP and the editors disclaim any responsibility for harm or damage to individuals or property that may result from the use of any information, methods, instructions, or products mentioned in the content.

Journal: Modern Journal of Statistics, Volume: 1, Issue: 1
DOI: https://doi.org/10.64389/mjs.2025.01112
Publication Date: 2025-07-12

Research article

Development and Applications of a New Hybrid Weibull-Inverse Weibull Distribution

Nooruldeen A. Noori , Kamal Najim Abdullah , and Mundher A. khaleel ¹Anbar Education Directorate, Anbar 31002, Iraq; Nooruldeen.a.noori35508@st.tu.edu.iq Mathematics Departments, College of Computer Science and Mathematics, Tikrit University, Tikrit 34001, Iraq;Kn230022pcm@st.tu.edu.iq, mun880088@tu.edu.iq*Correspondence: Nooruldeen.a.noori35508@st.tu.edu.iq

ARTICLE INFO

Keywords:

Weibull distribution
Parameter estimation
Hybrid distributions
Monte-Carlo simulation
Real data analysis

Mathematics Subject Classification:

62F10, 62P10

Important Dates:

Received: 8 June 2025
Revised: 8 July 2025
Accepted: 10 July 2025
Online: 12 July 2025
Copyright © 2025 by the authors. Published under Creative Commons Attribution (CC BY) license.

Abstract

This study introduces and applies a novel statistical model known as the hybrid Weibull inverse Weibull (HWIW) distribution, which combines the characteristics of the Weibull and inverse Weibull distributions to provide a more flexible model for representing real-world data, especially those characterized by asymmetry or extreme values. The basic functions of the distribution were derived, along with other statistical measures such as moments, the quantile function, and entropy were also derived. The distribution parameters were estimated using three distinct approaches, and their performance was evaluated through a Monte Carlo simulation to assess the performance and precision of each estimation technique. The results were used to show the most accurate estimation method for different samples. The proposed model was utilized to test two practical datasets; the findings demonstrated that the HWIW distribution outperformed six competing IW distributions in terms of model selection metrics. These results confirm the efficiency of the HWIW model’s ability to capture the structure of complex datasets and open the way for its use in multiple applications, including medical, industrial, and social fields, with the potential to be expanded to include multidimensional data or integrated with artificial intelligence techniques.

1. Introduction

Probability distribution plays a fundamental role in the field of statistical modeling and data analysis. They are the primary tool for understanding the random behavior associated with various scientific and applied phenomena, from reliability analysis and forecasting to risk assessment and statistical engineering. Among the common distribution, the Weibull distribution stands out for its high flexibility in representing failure and reliability data, while the inverse Weibull distribution is characterized by its ability to represent data characterized by non-constant failure rates or heterogeneous behavior. Despite the representative power of each of these two distributions individually, using either of them alone may not be sufficient to represent real-world data characterized by asymmetry, heavy tails, or high levels of dispersion. This often leads to poor estimation accuracy and poor fit of statistical models.
This challenge has prompted researchers to search for more flexible statistical alternatives that go beyond the limitations imposed by traditional models. Hence, the idea of hybrid distributions arose, which aims to combine the characteristics of two or more distribution within a single statistical model, giving the model greater adaptability to diverse data characteristics. Recent developments in this field
have contributed to the emergence of the T-X methodology, one of the most prominent methods used to generate new distribution by transforming basic distribution using flexible transformation functions. This methodology has resulted in the emergence of several new distribution families [1], such as BIIIEE-X family [2], NOGEE-G family [3], WEE-X Family[2], OLG family [5], NGOF-G Family [6], EOIW-G Family [7], GOM-G family [8], HOLGE [9], and HOE- family [10], which have proven effective in representing non-standard data with heterogeneous properties.
This research presents a new distribution model within the framework of the HWG family, which relies on transforming basic distribution into more flexible distribution. This family has a CDF of the form [11] :
While its PDF takes the form:
where and represent the CDF and PDF functions, the paramters and characterize the shape of the HWG family, based on any specified base distribution, such that .
Although probability distributions are widely used in statistical modeling and data analysis, traditional distributions often face challenges in accurately representing complex data, especially those that are asymmetric or contain extreme values. With advances in statistical methods, there is a growing need to develop more flexible models capable of effectively handling such data. Among the commonly used distribution, the Weibull and inverse Weibull distribution are important; however, when applied individually, they may not always yield sufficiently accurate or satisfactory results. A review of the literature reveals a lack of studies that integrate these two distributions into a single model that leverages the strengths of both.
Accordingly, a new statistical distribution is presented in this work called the HWIW distribution, characterized by high flexibility and improved capability in representing real-world data. This study includes deriving examining the statistical characteristics of the proposed distribution and determining its parameters through three distinct estimation techniques: MLE, LSE, WLSE. Its performance is then evaluated by applying the model to real dataset and comparing it with several other distributions to assess its accuracy and efficiency.
This paper is organized as follows. In Section 2, we derived other proposed model main functions. The statistical properties of the HWIW distribution were calculated in Section 3. Estimators of the proposed model were presented in Section 4 by three different methods, and the simulation in Section 5 was used to check these methods’ behavior. Section 6 used two practical datasets to show the HWIW distribution superiority for fitting them. Finally, concluding remarks for the whole paper were written in Section 7.

2. The hybrid Weibull inverse Weibull (HWIW) distribution

We assume that the underlying distribution follows the IW distribution, where the PDF and CDF can be represented as follows [12]:
where are shape parameters for IW distribution.
In order the obtain the CDF of the HWIW distribution, Equation (1.1) and (3) are combined into a unified from as follows:
Substituting Equation (2.1) into Equation (2.1) and 4, the PDF of the HWIW distribution can be expresses as:
Figures 1 and 2 illustrate the PDF and CDF of the HWIW distribution under various parameter settings. As depicted in Figure 1, the PDF curves demonstrate a wide variety of shapes, including decreasing trends, unimodal peaks, right-skewed forms, and reverse J-shapes. This diversity highlights the distribution’s high flexibility and its ability to model different types of data, especially those with asymmetric behavior or heavy tails.
Figure 1: PDF curves of the HWIW distribution under varying parameter values.
Figure 2 presents the CDF curves, which all start from zero and asymptotically approach one, as expected. The variation in the steepness of the curves reflects the adaptability of the distribution to different accumulation patterns of probability. All graphs were generated using the R programming language, emphasizing the statistical rigor and visual clarity of the analysis.
The survival function corresponding to the HWIW distribution is given by the following expression [13] :
The hazard function associated with the HWIW distribution is mathematically formulated as follows [14]:
Figure 2: CDF curves of the HWIW distribution under varying parameter values.
Figures 3 and 4 highlight the behavior of both survival and hazard curves for the HWIW distribution given different parameters ( ) highlighting its flexibility in representing various failure patterns. In Figure 3, the survival functions gradually decrease from 1 as increases, with some curves indicating early failure (e.g., green), while others reflect longer survival (e.g., purple and black).
Figure 3: Survival curve plot of the HWIW distribution.
Figure 4: hazard curve plot of the HWIW distribution.
Figure 4 highlights the diversity in the pattern of the hazard function . Some curves exhibit a decreasing pattern indicating aging, while others adopt a non-monotonic shape that begins with a rise, then decreases, then increases, resembling the shape of a bathtub familiar from reliability analysis.
Due to the complexity of the original formulas for the CDF and PDF in Equations (5) and (6), we simplified them to facilitate the derivation of the dividends for the HWIW distribution. This was done by applying expansions such as the utilizing the series forms of binomial, the exponential, and logarithm expansion, resulting in a formula for the CDF as follows:
where , and for and .
Following the same approach, the PDF can also be simplified through mathematical expansion, leading to the following formula:
where , and .
As for and and for and .

3. Properties for HWIW distribution

3.1 Quantile function for HWIW distribution

Theorem: If represents the CDF of the HWIW distribution, such that is an increasing, non-decreasing function, then the corresponding quantile function for this distribution is given by:
Proof: let be the CDF of the HWIW distribution
Assume that , then . Take the log for both sides to get: . We divide both sides by , so we get: . Take raise both sides to strength to get: . Multiply both sides of the equation by -1 we get: .
To simplify the expression, we define a substitution variable as follows: .
So that .
where the is the lower branch of the lambert W function [5] then: .
Now, substitute back to find , take the log for both sides to get: .
Dividing both sides by -b yields: , take raise both sides to strength to get: .
Finally, using the original definition of , the quantile function is:
Finally, we get a form in Equation (3.1).
A numerical representation of our proposed model quantile function is determined in Table 1.
Table 1: Quintile function of HWIW distribution.
( )
(0.7,1.3,0.4,0.2) (0.6,1.5,1.4,1) (0.5,1.1,0.9,1.1) (1.2,1,0.8,1.2) (0.7,1.9,0.7,0.5)
0.1 0.0218168 1.906395 1.062304 0.6697021 1.099829
0.2 0.1115255 2.620930 1.532390 0.8610302 1.868169
0.3 0.3981566 3.348908 2.071615 1.0475163 2.765094
0.4 1.2719911 4.176776 2.766355 1.2531876 3.890400
0.5 4.0414550 5.189129 3.744756 1.4990069 5.381479
0.6 13.8737973 6.519626 5.267047 1.8168022 7.483554
0.7 57.2273272 8.437554 7.985730 2.2706451 10.714995
0.8 347.7596965 11.637871 14.089895 3.0296305 16.449317
0.9 574.1890165 18.902468 36.712721 4.8052371 30.300980

3.2 Moment function for HWIW distribution

Theorem: let X be a random variable governed by HWIW distribution and represents its pdf, then the moment of order for this distribution is given by:
Proof: assume X is a random variable with pdf is , then the moment of order n is then given by the following expression [15], [9] :
substituting Equation (2.8) into the previous expression yields the following result
where , and .
For , let
Then , simplify to obtain the following final from:
Following a similar procedure for , we arrive at the final form
Finally, we get a from in Equation (3.2).
The first four moments are derived by substituting different values of n , as shown below:
Using this result, we obtain the skewness and kurtosis for the HWIW distribution in the following manner:
Table 2 displays the intervals of some moments of the HWIW distribution, illustrating how these moments change as the distribution’s parameters change. It also highlights the effect of the parameters on the first four moments, which helps analyze the distribution’s statistical properties when parameter values vary.
Table 2: displays the intervals of some moments of the HWIW distribution.
C skew kurtosis
– 1.1 1.596876 4.786326 37.61691 1363.256 2.236313 3.592359 59.50766
1.2 1.50402 3.772364 19.97024 333.8205 1.510288 2.725605 23.45772
g 1.3 1.959321 5.865176 31.84193 157.4864 2.026237 2.241702 4.578054
1.4 1.844062 4.860071 20.81439 179.4392 1.459506 1.942673 7.596825
8 1.5 2.012762 4.86385 14.33673 52.54653 0.812639 1.336533 2.22118
1.6 1.916656 4.310394 11.52101 37.16466 0.636824 1.287405 2.000305
60 1.7 1.968528 4.461816 11.76748 36.56478 0.586714 1.248579 1.836706
1.8 1.769355 3.548384 8.136669 21.553 0.417767 1.217309 1.711774

3.3 Moment Generating function for HWIW distribution

Theorem: Let be a random variable with a pdf is , then MGF of the HWIW distribution is given by:
Proof: Let is a random variable with pdf is , then MGF is given by [16], [17]:
Using exponential expansion for above equation, we get a form:
From Equation (12), the MGF for HWIW distribution has a from in Equation (3.3).

3.4 Incomplete Moments function for HWIW distribution

Theorem: Let be a random variable governed by HWIW distribution and represents its pdf then the incomplete moment function for this distribution is given by:
Proof: assume is a random variable with pdf is , then the Incomplete Moments function given by the following expression [18]:
From Equation (3.2), we get:
where , and . For , let
, when and if .
Following a similar procedure for , we arrive at the final form
then the Incomplete Moments function for HWIW distribution has a from in Equation (3.4).

3.5 Characteristic function of HWIW distribution

Theorem: Let be a random variable governed by HWIW distribution and represents its pdf then the Characteristic function for this distribution is given by:
Proof: assume is a random variable with pdf is , then the Characteristic function given by the following expression [19]:
Using exponential expansion for above equation, then we get a form:
From Equation (3.2), the Characteristic function for HWIW distribution has a from in Equation (3.5).

3.6 Rényi entropy for NMWIW distribution

Theorem: Let be a random variable governed by HWIW distribution and represents its pdf then the Rényi entropy for this distribution is given by:
where
Proof: assume is a random variable with pdf is , then the Rényi entropy given by the following expression [20]:
From Equation 10, we get:
Using the Binomial Series
Then the Rényi entropy for HWIW distribution has a from in Equation (3.6).

4. Estimation

4.1 Maximum likelihood estimation (MLE)

The estimation of HWIW distribution parameters is carried out using the MLE. Consider that the random variable follows the HWIW , and the parameter vector is denoted by , the log-likelihood function corresponding to is expressed as [21], [22]:
we compute the log- likelihood:

4.2 Least square estimation

The Least square estimation (LSE) method can be used to estimate a parameter using the following formula [23]:

4.3 Weighted Least square estimation (WLSE)

Parameter can be estimated using the WLSE technique through the following expression [24]:
Parameter estimates are derived using the three methods mentioned above, by partially differentiating the likelihood function for the four parameters and then setting the derivatives equal to zero. Given the complexity of numerical solutions to these equations, computational techniques such as the R language are used to obtain the desired values.

5. Simulation

Monte Carlo simulation is a mathematical technique that relies on random variables to model complex systems and analyze their behavior. It is widely applied in statistics, economics, engineering, and the natural sciences because of its ability to yield accurate estimates for models whose solutions are difficult or even impossible to obtain with traditional analytical methods. The core idea is to generate a large number of random samples in order to compute specific quantities or estimate probabilistic outcomes, thereby facilitating the study of phenomena that are hard to predict analytically. To assess the efficiency and accuracy of estimating the parameters of the HWIW distribution, a Monte Carlo simulation was carried out using the three estimation methods: MLE, LSE, WLSE. Random samples of sizes and up to ere generated, and the performance of each method was evaluated with respect to three criteria MSE, RMSE [25], [26], and Bias of the parameter estimates.
The simulation results are summarized in Table 3, which reports all three performance measures for each sample size, providing a practical evaluation of the effectiveness of the estimation techniques.
Table 3: Results of Monte Carlo simulations applied to the HWIW distribution.
N Est. Ess. Par. MLE LSE WLSE
50 Mean 0.66218994 0.7935073 0.7945322
0.94482752 0.90725405 0.87221447
0.8173529 0.9586352 0.9458078
1.6005334 1.3007755 1.3224457
MSE 0.34450955 0.3029998 0.3196053
0.09171262 0.16296775 0.09943654
0.5872540 0.5312079 0.5426379
0.8883328 0.4236644 0.3828196
RMSE 0.58694936 0.5504542 0.5653365
0.30284092 0.40369264 0.31533560
0.7663250 0.7288401 0.7366396
0.9425141 0.6508951 0.6187241
Bias 0.06218994 0.1935073 0.1945322
0.04482752 0.00725405 0.02778553
0.1173529 0.2586352 0.02778553
0.4005334 0.1007755 0.1224457
100 Mean 0.64384318 0.7219438 0.7182429
0.94033751 0.87454167 0.87775399
0.76723431 0.8778392 0.8340620
1.4001384 1.3028549 1.27703038
MSE 0.23499950 0.2124502 0.1981540
0.06256473 0.07460193 0.04674475
0.33109832 0.3405407 0.2714449
0.2971453 0.2258667 0.18424882
RMSE 0.48476747 0.4609232 0.4451449
0.25012943 0.27313355 0.21620533
0.57541144 0.5835586 0.5210037
0.5451103 0.4752543 0.42924215
Bias 0.5451103 0.1219438 0.1182429
0.04033751 0.02545833 0.02224601
0.06723431 0.1778392 0.1340620
0.2001384 0.1028549 0.07703038
150 Mean 0.609999358 0.7218282 0.64903158
0.95149716 0.87361891 0.91132615
0.72423747 0.8539909 0.75548383
1.3746361 1.27230291 0.75548383
MSE 0.180700778 0.2093021 0.16223096
0.05561927 0.05271935 0.04119156
0.25410926 0.2817639 0.20157287
0.2018948 0.13858398 0.1762926
RMSE 0.425089141 0.4574955 0.40277904
0.23583739 0.22960694 0.20295704
0.50409251 0.5308143 0.44896867
0.4493271 0.37226869 0.4198721
Bias 0.009999358 0.1218282 0.04903158
0.05149716 0.02638109 0.01132615
0.02423747 0.1539909 0.05548383
0.1746361 0.07230291 0.1213862
Mean 0.62953303 0.67330833 0.62552888
0.92401550 0.892643858 0.91648996
0.73728692 0.8049638 0.7284962
1.3183908 1.25742869 1.3022389
MSE 0.14542449 0.12782454 0.12441776
0.03766835 0.043226750 0.03072519
0.18643346 0.2099843 0.1550041
0.1322101 0.11526679 0.1274526
200 RMSE 0.38134563 0.3636071 0.35272902
0.19408336 0.207910437 0.17528603
0.43177941 0.4582404 0.3937056
0.3636071 0.33950963 0.3570051
Bias 0.02953303 0.07330833 0.02552888
0.02401550 0.007356142 0.01648996
0.03728692 0.1049638 0.0284962
0.1183908 0.05742869 0.1022389
250 Mean 0.605497333 0.67616917 0.608383893
0.93281004 0.88124099 0.92341073
0.706005227 0.79824836 0.71403583
1.30557693 1.26590402 1.29949605
MSE 0.109527538 0.12320369 0.108918047
0.03389573 0.03761672 0.03328868
0.136416881 0.17672820 0.14360899
0.09854788 0.10182472 0.10257126
RMSE 0.330949450 0.35100383 0.330027342
0.18410793 0.19395029 0.18245186
0.369346559 0.42039054 0.37895777
0.31392336 0.31909986 0.32026748
Bias 0.005497333 0.07616917 0.008383893
0.03281004 0.01875901 0.02341073
0.006005227 0.09824836 0.01403583
0.10557693 0.06590402 0.09949605
Table 3 Display the outcomes of a Monte Carlo simulation used to estimate the parameters of the HWIW distribution through three distinct estimation techniques: (MLE, LSE, and WLSE). The table shows that the estimation accuracy improves with increasing sample size, with both MSE and RMSE values gradually decreasing from 50 to 250 sample size. The results show that the WLES method performs best in terms of accuracy for most parameters, especially for small and medium sample sizes, while the MLE method maintained the lowest Bias values in most cases, indicating its stability and reliability.
The LSE method, on the other hand, performed relatively poorly, particularly in accurately estimating parameters at small sample size, with higher MSE and Bias values. These results reflect the importance of choosing the appropriate estimation method based on sample size and statistical accuracy requirements.

6. Application

To demonstrate the robustness and applicability of the proposed distribution in real-world contexts, the practical component plays a central role in this evaluation. Therefore, this section provides a real-data application, accompanied by and benchmarked against six established distributions for performance assessment
  • Beta with baseline inverse Weibull (BeIW)
  • Kumaraswamy with baseline inverse Weibull (KuIW)
  • Exponeted generalized with baseline inverse Weibull (EGIW)
  • Log-Gamma with baseline inverse Weibull (LGamIW)
  • Gompertz with baseline inverse Weibull (GoIW)
  • Inverse Wiebull (IW)
All of the selected distribution belongs to extended or modified families of the IW distribution, making them direct competitors of the HWIW distribution. These distributions serve as powerful models for statistical data analysis, and the HWIW distribution stands among them due to its flexibility and ability to accurately represent data, which was the primary motivation behind its development. This comparison was conducted using four informative criteria AIC [27], CAIC [28], BIC [29], and HQIC [30]. Four statistical measures were also used to evaluate accuracy K-S, A, W and p-value.
Data set-1: The dataset used in this study includes the survival times of 72 guinea pigs that were infected with virulent tubercle bacilli. The survival times are measured in days. The original observation and reporting of this dataset were conducted by Bjerkedal [5].
, , .
Table 4 provides a summary of the model selection criteria used to compare the distribution. Table 5 reports the corresponding statistical test values, while Table 6 displays the estimated parameters for each distribution under study.
Table 4. results of the criteria for the distributions.
Dist. -log AIC CAIC BIC HQIC
HWIW 95.88984 199.8247 200.4217 208.9313 203.4501
BeIW 101.296 210.6642 211.2612 219.7708 214.2895
KuIW 97.89873 203.7986 204.3956 212.9053 207.424
EGIW 100.9368 209.8826 210.4796 218.9893 213.508
LGamIW 99.80569 207.6247 208.2217 216.7314 211.2501
GoIW 97.17087 202.3418 202.9388 211.4485 205.9672
IW 118.1178 240.2356 240.4095 244.7889 242.0483
Table 4 shows the results of the comparison criteria between the distributions, with lower values indicating better performance. The evaluation results showed that the HWIW distribution achieved the lowest values across all criteria (AIC, BIC, etc.), demonstrating its superior representation of the data. In contrast, the IW distribution achieved the highest values, indicating its poor fit compared to the other distributions.
Table 5. value of the statistical measures.
Dist. W A K-S p-value
HWIW 0.0922143 0.6110752 0.1130676 0.316085
BeIW 0.1675262 1.155408 0.1438356 0.1016569
KuIW 0.1107239 0.7703783 0.11985 0.2522606
EGIW 0.1608632 1.111592 0.1402135 0.117882
LGamIW 21.91134 141.258 0.9999952
GoIW 0.1616563 0.9825052 0.1283847 0.1861575
IW 0.5284354 3.310617 0.1991304 0.006625223
Table 5 shows the results of the statistical goodness-of-fit measures. Lower values for W , A , and K -S indicate a better fit to the data, and p-values are an additional indicator of this. The HWIW distribution performed best, achieving the lowest values across all measures and the highest p -value ( 0.316 ), indicating a strong fit to the data. In contrast, distributions such as LGamIW and IW performed poorly, with high values and very low p-values, indicating poor representativeness of the data.
Table 6. Estimator value interval for parameters by MLE.
Dist.
HWIW 1.3782752 3.1107381 0.4686840 0.5414699
BeIW 0.9168564 5.9240884 3.0074058 0.7257823
KuIW 2.0448702 15.6432752 1.9116895 0.5584649
EGIW 6.5028232 0.9572174 3.0215673 0.7065691
LGamIW 0.6738629 7.9310308 3.9767690 0.7099198
GoIW 0.7349332 3.2243297 1.4417615 0.6936903
IW —- —– 1.061440 1.171994
Table 6 displays parameter estimates for the distributions using the MLE. The HWIW distribution showed moderate parameters, reflecting a good balance of representativeness. In contrast, distributions such as KuIW and EGIW recorded high values for some parameters, indicating more complex models. The IW distribution, being simpler than the other distributions, contained only two parameters. These estimates reflect the flexibility of each distribution in representing data.
Figure 5: Fitting PDFs HWIW with histogram data set.
Figure 6: Empirical Fitted CDFs HWIW with data set.
Figure 5 displays how well the pdf of the WHIW distribution aligns with the first dataset. The fitted curve demonstrates a close match to the empirical data, effectively capturing its structural characteristics, reflecting the high efficiency of the HWIW distribution in efficiently and flexibly representing the actual behavior of the data.Figure 6 shows a comparison between the empirical CDF and the theoretical cumulative distribution associated with the HWIW distribution. This figure shows a clear fit between the two curves, confirming the proposed distribution’s ability to accurately represent the cumulative probability of the data, thus reflecting its effectiveness in reliably modeling real data.
Data set-2: Failure Times of 50 Components [29]
, , 6.274,6.816, 7.896, 7.904, 8.022, 9.337, 10.940, 11.020, 13.880, 14.730, 15.080
Table 7. results of the criteria for the distributions.
Dist. -log AIC CAIC BIC HQIC
HWIW 102.5897 213.1842 214.0731 220.8323 216.0967
BeIW 104.7622 217.5404 218.4292 225.1884 220.4528
KuIW 104.4104 216.8386 217.7275 224.4867 219.7511
EGIW 104.7671 217.5438 218.4327 225.1919 220.4562
LGamIW 104.4651 217.0186 217.9075 224.6667 219.931
GoIW 104.5873 217.1846 218.0735 224.8327 220.0971
IW 106.0967 216.1933 216.4486 220.0174 217.6495
Table 7 shows that the HWIW distribution achieved the lowest values across all information metrics (AIC, BIC, CAIC, and HQIC) compared to the other distributions, demonstrating its high data-fitting efficiency. In contrast, distributions such as BeIW, GoIW, and EGIW achieved higher values, reflecting their poor performance compared to HWIW.
Table 8. value of the statistical measures.
Dist. W A K-S p-value
HWIW 0.1719594 1.063281 0.1379881 0.2711381
BeIW 0.2246938 1.384528 0.1585079 0.1453208
KuIW 0.2160847 1.333744 0.1558378 0.1584046
EGIW 0.224653 1.384445 0.1614739 0.1318197
LGamIW 17.95769 99.77021 0.9818669
GoIW 0.2123711 1.31562 0.1496055 0.1925845
IW 0.2575837 1.57173 0.16011 0.1378965
Table 8 shows that the HWIW distribution performed best among the compared distributions, recording the lowest values for the W, A, and K-S metrics, along with the highest p-value, confirming its accurate representation of the data. In contrast, distributions such as IW and LGamIW performed poorly, indicating their poor fit to the data.
Table 9. Estimator value interval for parameters by MLE.
Dist.
HWIW 1.2975383 2.5187226 0.3953556 0.2346634
BeIW 1.2809056 2.1997463 1.0261864 0.3948558
KuIW 1.3911669 2.7407636 1.0465352 0.3649795
EGIW 2.1705086 1.0785869 1.1698675 0.4009732
LGamIW 1.2129747 2.9472049 1.3521062 0.3473045
GoIW 1.2129747 2.9472049 1.3521062 0.3473045
IW —- —– 0.6040943 0.5912884
Table 9 shows that the HWIW distribution provided more stable and accurate parameter estimates than the other distributions. However, distributions such as GoIW and BeIW exhibited significant variability in estimates, indicating their low reliability.
Figure 7: Fitting PDFs HWIW with histogram data set-II.
Figure 8: Empirical Fitted CDFs HWIW with data set-II.
Figure 7 highlights the extent to which the PDF of the HWIW distribution matches the histogram of the experimental data. This distribution clearly demonstrates its ability to represent the overall shape of the data, especially in the early regions of the distribution and the slope, reflecting the flexibility of the HWIW in accommodating variations and the actual behavior of the data. Figure 8 shows a close convergence between the theoretical CDF of the HWIW distribution and the experimental cumulative distribution. This convergence supports the model’s ability to accurately represent the cumulative behavior of the data, even in the presence of variability or uncertainty in the experimental values.

7. Conclusion

The HWIW distribution demonstrated high efficiency in representing complex real-world data, clearly outperforming six competing extended IW distributions. It achieved the lowest information criterion value (AIC, CAIC, BIC, HQIC), the best goodness of fit indices (W, A, K-S), and the highest likelihood value (P-value), reflecting its accurate and effective modeling capabilities. The results confirmed
the HWIW distribution’s adaptability to asymmetric and heavy-tailed data, making it well-suited for representing a wide range of realworld datasets. Monte-Carlo simulation results revealed that the WLSE method was the most accurate in terms of MSE and RMSE, particularly for small and medium-size samples, while the MLE method exhibited lower bias and greater stability as sample size increased. In contrast, the LES method performed relatively poorly, underscoring the importance of selecting the appropriate estimation method based on sample size and analysis goals-WLES for accuracy and MLE for stable. The proposed distribution possesses advanced mathematical properties, such as the flexibility of density and distribution functions, and the ease of deriving moments, quantile function, and entropy, enhancing its reliability as an analytical tool in applied statistics. Given its superiority over other distributions, the HWIW is a promising model that can be extended to multidimensional data or combined with artificial intelligence and machine learning techniques to improve predictions in uncertain environments. These results open new avenues for employing the HWIW distribution in a wide range of real-world applications, including medical, industrial, and social fields, where traditional models present challenges in representing variance and skewness in real data.

Authors’ Contributions:

Authors have worked equally to write and review the manuscript.

Data Availability Statement:

The data that supports the findings of this study are available within the article.

Conflicts of Interest:

The authors declare no conflict of interest.

References

[1] Alzaatreh, A., Lee, C., and Famoye, F. (2013). A new method for generating families of continuous distributions. Metron, 71(1), 6379.
[2] Hussain, S., Hassan, M. U., Rashid, M. S., and Ahmed, R. (2023). Families of Extended Exponentiated Generalized Distributions and Applications of Medical Data Using Burr III Extended Exponentiated Weibull Distribution. Mathematics, 14(11), 3090.
[3] Odeyale, A. B., Gulumbe, S. U., Umar, U., and Aremu, K. O. (2023). New Odd Generalized Exponentiated Exponential-G Family of Distributions. UMYU Scientifica, 4(2), 56-64.
[4] Noori, N. A., Khalaf, A. A., and Khaleel, M. A. (2023). A New Generalized Family of Odd Lomax-G Distributions Properties and Applications. Advances in the Theory of Nonlinear Analysis and Its Application, 4(7), 1-16.
[5] Sadiq, I. A., Doguwa, S. I., Yahaya, A., and Garba, J. (2023). New Generalized Odd Fréchet-G (NGOF-G) Family of Distribution with Statistical Properties and Applications. UMYU Scientifica, 3(2), 100-107.
[6] Abdelall, Y. Y., Hassan, A. S., and Almetwally, E. M. (2024). A new extension of the odd inverse Weibull-G family of distributions: Bayesian and non-Bayesian estimation with engineering applications. Computational Journal of Mathematical and Statistical Sciences, 2(3), 359-388.
[7] Ishaq, A. I., Panitanarak, U., Alfred, A. A., Suleiman, A. A., and Daud, H. (2024). The Generalized Odd Maxwell-Kumaraswamy Distribution: Its Properties and Applications. Contemporary Mathematics, 1(1), 711-742.
[8] Noori, N. A., Abdullah, K. N., and Khaleel, M. A. (2025). Data Modelling and Analysis Using Odd Lomax Generalized Exponential Distribution: an Empirical Study and Simulation. Iraqi Statisticians Journal, 1(2), 146-162.
[9] Mahdi, G. A., Khaleel, M. A., Gemeay, A. M., Nagy, M., Mansi, A. H., Hossain, M. M., and Hussam, E. (2024). A new hybrid odd exponential- family: Properties and applications. AIP Advances, 14(4), 1-15.
[10] Noori, N. A., and Khaleel, M. A. (2024). Estimation and Some Statistical Properties of the hybrid Weibull Inverse Burr Type X Distribution with Application to Cancer Patient Data. Iraqi Statisticians Journal, 2(1), 8-29.
[11] Noori, N. A., Khalaf, A. A., and Khaleel, M. A. (2024). A new expansion of the Inverse Weibull Distribution: Properties with Applications. Iraqi Statisticians Journal, 1(1), 52-62.
[12] Noori, N. A. (2023). Exploring the Properties, Simulation, and Applications of the Odd Burr XII Gompertz Distribution. Advances in the Theory of Nonlinear Analysis and Its Application, 4(7), 60-75.
[13] Khalaf, A. A., Khaleel, M. A., and Noori, N. A. (2024). A new expansion of the Inverse Weibull Distribution: Properties with Applications. Iraqi Statisticians Journal, 1(1), 52-62.
[14] Alanaz, M. M., and Algamal, Z. Y. (2023). Neutrosophic exponentiated inverse Rayleigh distribution: Properties and Applications. International Journal of Neutrosophic Science, 21(4), 36-43.
[15] Khalaf, A. A., Ibrahim, M. Q., and Noori, N. A. (2024). [0,1] Truncated Exponentiated Exponential Burr type X Distribution with Applications. Iraqi Journal of Science, 65(8), 4428-4440.
[16] Gómez, H. J., Santoro, K. I., Chamorro, I. B., Venegas, O., Gallardo, D. I., and Gómez, H. W. (2023). A Family of Truncated Positive Distributions. Mathematics, 11(21), 4431.
[17] Muhammad, B., Mohsin, M., and Aslam, M. (2021). Weibull-exponential distribution and its application in monitoring industrial process. Mathematical Problems in Engineering, 2021(1), 1-13.
[18] Al Abbasi, J. N., Resen, I. A., Abdulwahab, A. M., Oguntunde, P. E., Al-Mofleh, H., and Khaleel, M. A. (2023). The right truncated Xgamma-G family of distributions: Statistical properties and applications. AIP Conference Proceedings, 2834(1), 1-15.
[19] Al-Habib, K. H., Khaleel, M. A., and Al-Mofleh, H. (2023). A new family of truncated Nadarajah-Haghighi-G properties with real data applications. Tikrit Journal of Administrative and Economic Sciences, 19(61), 2.
[20] Afify, A. Z., Yousof, H., and Nadarajah, S. (2017). The beta transmuted-H family for lifetime data. Statistics and its Interface, 10(3), 505-520.
[21] Bhatti, F. A., Hamedani, G. G., Korkmaz, M. C., Cordeiro, G. M., Yousof, H. M., and Ahmad, M. (2019). On Burr III Marshal Olkin family: development, properties, characterizations and applications. Journal of Statistical Distributions and Applications, 6(1), 1-21.
[22] Teamah, A.-E. A. M., Elbanna, A. A., and Gemeay, A. M. (2020). Frèchet-Weibull distribution with applications to earthquakes data sets. Pakistan Journal of Statistics, 36(2), 135-147.
[23] Abd El-latif, A. M., Almulhim, F. A., Noori, N. A., Khaleel, M. A., and Alsaedi, B. S. (2025). Properties with application to medical data for new inverse Rayleigh distribution utilizing neutrosophic logic. Journal of Radiation Research and Applied Sciences, 18(2), 101391.
[24] Abed, R. A., Khaleel, M. A., and Noori, N. A. (2025). Modified Weibull-Fréchet Distribution Properties with Application. Iraqi Statisticians Journal, 1(2), 195-216.
[25] Noori, N. A., Ahmed, D. D., and Khaleel, M. A. (2025). Odd Lomax Chen distribution: An Innovative Statistical Tool for Improving Real Data Modeling and Its Practical Applications. Tikrit Journal of Administrative and Economic Sciences, 21(Special Issue, Part 1), 1098-1126.
[26] Noori, N. A., Khaleel, M. A., and Salih, A. M. (2025). Some Expansions to The Weibull Distribution Families with Two Parameters: A Review. Babylonian Journal of Mathematics, 1(1), 61-87.
[27] Noori, N. A., Khaleel, M. A., Khalaf, S. A., and Dutta, S. (2025). Analytical Modeling of Expansion for Odd Lomax Generalized Exponential Distribution in Framework of Neutrosophic Logic: a Theoretical and Applied on Neutrosophic Data. Innovation in Statistics and Probability, 1(1), 47-59.
[28] Habib, K. H., Khaleel, M. A., Al-Mofleh, H., Oguntunde, P. E., and Adeyeye, S. J. (2024). Parameters Estimation for the [0, 1] Truncated Nadarajah Haghighi Rayleigh Distribution. Scientific African, 1(1), e02105.
[29] Khaoula, A., Seddik-Ameur, N., Abd El-Baset, A. A., and Khaleel, M. A. (2022). The Topp-Leone Extended Exponential Distribution: Estimation Methods and Applications. Pakistan Journal of Statistics and Operation Research, 18(4), 817-836
© 2025 by the authors. Disclaimer / Publisher’s Note: The views, opinions, and data presented in all published content are solely those of the individual authors and contributors. They do not necessarily reflect the positions of Sphinx Scientific Press (SSP) or its editorial team. SSP and the editors disclaim any responsibility for harm or damage to individuals or property that may result from the use of any information, methods, instructions, or products mentioned in the content.