الكلمات الرئيسية: النماذج المختلطة، R.

عند تركيب نموذج التأثيرات المختلطة، غالبًا ما يكون من الضروري استخدام تأثير عشوائي متعدد المتغيرات مع مصفوفة تغاير غير قطرية من أجل إدخال مجموعات من المعلمات المرتبطة في النموذج. هذه الطريقة مطلوبة، على سبيل المثال، عند تركيب نماذج المنحدرات العشوائية (بولكر وآخرون 2009؛ أزار، بولين، ديجل، ووالين 2020)، لأخذ في الاعتبار الارتباط بين معاملات المنحدر وعبارات الاعتراض، وعند استخدام التأثيرات العشوائية لإحداث الارتباط في البيانات متعددة المتغيرات (كول وآغريستي 2000؛ بولوك وآخرون 2014، على سبيل المثال). دون فرض هيكل على مصفوفة التغاير، يزداد عدد المعلمات التي تحتاج إلى تقدير بشكل تربيعي مع بعد التأثير العشوائي (على وجه التحديد، يجب تقدير المعلمات لهيكل غير منظم مصفوفة التغاير)، وتصبح التقديرات صعبة بسرعة حيث يصبح أكبر.

على سبيل المثال، في القسم 3.1 نصف دراسة تأثير مزارع الرياح على تجمعات الأسماك، حيث نقوم بعد الأفراد من عدة أنواع في عدة مواقع. نرغب في استخدام تأثيرات عشوائية متعددة المتغيرات لتقدير الارتباط عبر الأنواع. يمكننا القيام بذلك باستخدام نموذج مختلط يتم تركيبه باستخدام حزمة lme4 (Bates، Mächler، Bolker، وWalker 2014) في R (فريق R الأساسي 2024) كما يلي:

R> glmer(abundance ~ Zone + Year + (Species + 0 | ID), family = "poisson",
+ data = windfarm)

أو بشكل مكافئ، باستخدام حزمة glmmTMB (بروكس وآخرون 2017):

R> glmmTMB(abundance ~ Zone + Year + (Species + 0 | ID), family = "poisson",
+ data = windfarm)

نظهر في الملحق أ أنه إذا كان هناك نوعان فقط في مجموعة البيانات، فإن هذا النهج معقول (وهذان السطران من الشيفرة ينتجان إجابات متطابقة، باستثناء خطأ الآلة)، ولكن تبدأ مشاكل التقارب في الظهور عندما يكون هناك ثلاثة أنواع أو أكثر. مجموعة البيانات الكاملة التي نرغب في تحليلها تحتوي على تسعة أنواع، وغالبًا ما تتضمن أنواع مماثلة من البيانات العديد من الأنواع الأخرى، أحيانًا الآلاف (نيكو، هوي، تاسكين، وورتون 2019).
إحدى الطرق الشائعة للتعامل مع الأبعاد العالية هي استخدام نهج منخفض الرتبة، من خلال إجراء افتراضات مبسطة تقلل من أبعاد المشكلة إلى لقد شهدت الأساليب ذات الرتبة المخفضة استخدامًا كبيرًا في المعلوماتية الحيوية (مثل سميث، كوليس، وتومسون 2001؛ بويتنر وآخرون 2015) والإحصاءات المكانية (كريسّي ويوهانسون 2008؛ بانيرجي، جيلفاند، فينلي، وسونغ 2008). تتضمن الطريقة ذات الرتبة المخفضة لتناسب تأثير عشوائي متعدد المتغيرات كتابته كمزيج خطي من المتغيرات الكامنة، التي تُعرف غالبًا بأنها نموذج تحليل العوامل (بارثولوميو، نوت، وموساتكي 2011)؛ في حالة استجابات العائلة الأسية، يُطلق عليها أحيانًا نموذج المتغيرات الكامنة المعمم (GLVM: سكرواندال ورابي-هيسكيث 2004).
تم استخدام نماذج GLVM بشكل متكرر في علم البيئة والعلوم الاجتماعية، وكانت الأمثلة المبكرة نماذج لوجود أو غياب أنواع الأسماك (Walker و Jackson 2011) ونماذج لاختيار الأحزاب المتعددة وتصنيفات البيانات (Skrondal و Rabe-Hesketh 2003). يمكن أن تكون نماذج GLVM صعبة من الناحية التقنية، ولكن هناك عدد من الحلول البرمجية المخصصة. تستخدم حزمة gllamm (Rabe-Hesketh و Skrondal و Pickles 2004) في Stata (StataCorp 2023) تكامل غاوسي التكيف لإزالة المتغيرات الكامنة. استخدمت البرمجيات المبكرة المكتوبة بلغة R، مع وضع علماء البيئة في الاعتبار، سلسلة ماركوف بايزي (Hui 2016؛ Ovaskainen وآخرون 2017). يمكن الحصول على ملاءمات أسرع بكثير باستخدام تقريب لابلاس (Huber و Ronchetti و Victoria-Feser 2004؛ Niku و Warton و Hui و Taskinen 2017) أو تقريب تبايني (Hui و Warton و Ormerod و Haapaniemi و Taskinen 2017) لاحتمالية الهامش، كما هو مطبق في حزمة R gllvm (Niku وآخرون 2019). تم كتابة هذه الأدوات مع نموذج معين في الاعتبار، حيث يتم استخدام تقاطع عشوائي متعدد المتغيرات لفرض الارتباط عبر العديد من الاستجابات، وتستخدم التأثيرات الثابتة لربط المتنبئ الخطي بالمتغيرات المقاسة، على الرغم من وجود بعض التمديدات لتخفيف هذا القيد بطرق مختلفة (Van der Veen و Hui و Hovstad و Solbu و O’Hara 2021؛ Niku و Hui و Taskinen و Warton 2021). ومع ذلك، فإن هذه البرمجيات غير قادرة على التعامل مع مجموعة من تصاميم العينة الشائعة. مثال تم النظر فيه في القسم 3.2 هو عندما يكون التأثير العشوائي المتعدد المتغيرات له متغيرات قد تختلف عبر المجموعات وداخلها.
في هذه الورقة، نضيف وظيفة الرتبة المنخفضة إلى حزمة glmmTMB (بروكس وآخرون 2017) لنماذج التأثيرات المختلطة المرنة التي يمكن أن تشمل مصطلحات تحليل العوامل، للبيانات المتعددة المتغيرات.
آثار عشوائية ذات أبعاد كبيرة. حزمة glmmTMB، المتاحة من شبكة أرشيف R الشاملة (CRAN) فيhttps://CRAN.R-project.org/package=glmmTMBتم بناءه كامتداد لـ lme4 (Bates et al. 2014)، والذي يُستخدم على نطاق واسع في العلوم التطبيقية لمشاكل تتعلق بمجموعة من تصاميم الدراسة، بما في ذلك التصاميم متعددة المستويات وتصاميم القياسات المتكررة. يستخدم حزمة glmmTMB واجهة مشابهة لـ lme4 ولكنها تستفيد من التمايز التلقائي لتقدير أسرع لنماذج التأثيرات المختلطة (Brooks et al. 2017). من خلال إضافة وظيفة تقليل الرتبة إلى glmmTMB، نثري فئة النماذج المختلطة التي يمكن تركيبها لتشمل تأثيرات عشوائية متعددة المتغيرات بأبعاد أكبر بكثير مما كان ممكنًا سابقًا، بحيث يمكننا الآن تركيب تأثيرات عشوائية بأبعاد تصل إلى المئات، أو ربما الآلاف. تشمل هذه الفئة الجديدة من النماذج، على سبيل المثال، GLVMs مع وظيفة لأي من تصاميم الدراسة التي يمكن تحليلها باستخدام lme4، بما في ذلك التصاميم متعددة المستويات أو تصاميم القياسات المتكررة.
يوفر القسم 2 نظرة عامة على نموذج الانحدار الخطي المختلط العام، والامتدادات التحليلية للعوامل للتعامل مع التأثيرات العشوائية المتعددة الأبعاد ذات الأبعاد العالية، ونهج التقدير المستخدم في glmmTMB لتناسب مثل هذه النماذج. نصف استخدام glmmTMB لتناسب التأثيرات العشوائية المتعددة الأبعاد ذات الرتبة المخفضة. نقوم بتحليل مجموعتين مختلفتين من البيانات، من علم البيئة والعلوم الاجتماعية، في القسم 3. يختتم القسم 4 الورقة.

نبدأ بتقديم نموذج مختلط خطي عام ونسخة تحليل العوامل التي نستخدمها للتعامل مع التأثيرات العشوائية المتعددة المتغيرات ذات الأبعاد الكبيرة. ثم نناقش عملية التقدير لهذه النماذج والواجهة لتناسب التأثيرات العشوائية المتعددة المتغيرات ذات الرتبة المخفضة كما هو مطبق في glmmTMB.

دع كن الرد على وحدات الملاحظة في العنقود متجه من المتغيرات الثابتة الأثر ، و متغيرات التأثير العشوائي يمكن أيضًا تسجيله لكل وحدة. بالنسبة لنموذج مختلط خطي عام (GLMM)، مشروطًا على متجه التأثيرات العشوائية، والمتجه الخاص بالمعلمات، (المعرف أدناه)، يُفترض أن تأتي الاستجابات من عائلة التوزيعات الأسية، أين و هي دوال معروفة تعتمد على التوزيع المختار هي معلمات معيارية، و هو معامل التشتت. ثم الاستجابة المتوسطة، المشار إليها بـ يمكن تحديدها كالتالي، تم الانحدار ضد المتغيرات الثابتة والعشوائية

أين . هو متجه ذو أبعاد من معاملات الانحدار المتعلقة بالمتغيرات المرافقة، ، و هو متجه المتغيرات العشوائية المؤثرة. التوزيع غير المشروط للتأثيرات العشوائية، أو أخطاء مستوى العنقود، يُفترض أن يتبع توزيعًا طبيعيًا متعدد المتغيرات بمتوسط صفر ومعامل محدد مصفوفة التباين-التغاير ، أي، مصفوفة التباين-التغاير، ، يتحكم في التباينات والارتباطات بين الوحدات في المجموعات. الخيار الأكثر مرونة لـ هو مصفوفة تباين-تغاير غير منظمة، والتي تتطلب المعلمات. بالنسبة للنماذج التي تحتوي على تأثيرات عشوائية متعددة المتغيرات كبيرة، تصبح هذه المرونة مشكلة.
مع عدد المعلمات في تزداد بشكل تربيعي مع حجم التأثير العشوائي، .
يتضمن نهج المرتبة المخفضة لتناسب تأثير عشوائي متعدد المتغيرات التعبير عنه كدالة خطية لـ المتغيرات الكامنة:

أين هو متجه لـ متغيرات كامنة، كل منها مستقل وذو توزيع طبيعي قياسي، و هو مصفوفة تحميل العوامل. المتغيرات الكامنة لها متوسط صفري وتباين وحدة، دون فقدان العمومية. العناصر العليا المثلثية من تم تعيينها إلى الصفر للمساعدة في تحديد معالم الهوية، دون فقدان العمومية. أخيرًا، نسمح لـ تشير إلى مجموعة كاملة من معلمات النموذج.
بالنظر إلى هذه التعريفات، فإن التأثير العشوائي المتعدد المتغيرات موزع كـ

وهو تقريب من الرتبة المنخفضة لـ ، كما يُرى غالبًا في نماذج التحليل العاملي (بارثولوميو وآخرون 2011؛ نيكو وآخرون 2017). تتيح هذه الطريقة ملاءمة تأثيرات عشوائية متعددة المتغيرات كبيرة، لأن عدد المعلمات المطلوبة في مصفوفة التباين-التغاير لـ الآن الذي (لـ يزداد فقط بشكل خطي مع .

شرطًا على المتغيرات الكامنة، تُفترض أن الاستجابات مستقلة، ومن ثم نظرًا لأن المتغيرات الكامنة غير مرصودة، يتم دمجها، مما يؤدي إلى الاحتمالية اللوغاريتمية الهامشية:

في بعض الحالات يمكن حل هذه المعادلة بشكل صريح والتعبير عنها بشكل مغلق، ولكن بالنسبة للتوزيعات غير الطبيعية، فإنه عادةً لا يوجد لها شكل مغلق. تم اقتراح عدد من طرق التقدير لتقريب الاحتمالية الهامشية بما في ذلك تقريب لابلاس، والتكامل العددي باستخدام التكامل التكيفي (سكروندال ورابي-هيسكيث 2004)، وتكامل مونت كارلو (هوي، تاسكينين، بليجر، فوستر، وورتون 2015) ومؤخراً تقريب التباين (هوي وآخرون 2017).
نركز على تقريب لابلاس لاحتمالية الهامش، والتي تُستخدم على نطاق واسع لنماذج التأثيرات المختلطة العامة (GLMMs) (راودنبوش، يانغ، ويوسف 2000) وكذلك لنماذج التأثيرات العامة المتغيرة (GLVMs) (هوبر وآخرون 2004؛ نيكو وآخرون 2017). من خلال كتابة المعادلة 3 بالشكل ، حيث

يمكننا تطبيق طريقة لابلاس لتقريب التكامل حول وضعه. افتراضاً يعظم ، يتم اشتقاق التقريب من خلال توسيع كسلسلة تايلور من الدرجة الثانية حول الوضع، وفقًا لـ Huber وآخرون (2004)، فإن تقريب لابلاس لدالة اللوغاريتم الهامشي لاحتمالية النموذج العام المحدد في المعادلة 1
يمكن كتابته كـ

أين

و هو الحد الأقصى لـ .
في glmmTMB نقوم بتعظيم تقريب لابلاس للاحتمالية اللوغاريتمية الهامشية المستمدة من حزمة Template Model Builder (TMB) (كريستنسن، نيلسن، بيرغ، سكاوغ، وبل 2015) في R (أو بشكل أكثر دقة، تقليل اللوغاريتم السالب للاحتمالية). يقوم TMB بتقييم تقريب لابلاس ومشتقاته باستخدام التمايز التلقائي. يمكن استخدام أي طريقة تحسين تعتمد على التدرج متاحة في R للقيام بالتعظيم، وبشكل افتراضي يستخدم glmmTMB nlminb(). ثم يستخدم TMB طريقة دلتا المعممة لحساب الانحرافات المعيارية الهامشية للتأثيرات الثابتة والعشوائية (كاس وستيفي 1989).

يتم تحديد هيكل التباين ذو الرتبة المخفضة في glmmTMB باستخدام rr. على سبيل المثال، لنفترض أن x هو مصفوفة من المتنبئات مع الأعمدة، وأننا نريد تطبيق معاملات عشوائية بُعدية تأخذ قيمًا مختلفة لمستويات مختلفة من متغير التجميع group بالنسبة للمتنبئات x. لتحديد أن هذه المعاملات العشوائية مستمدة من توزيع طبيعي متعدد المتغيرات حيث تكون مصفوفة التباين والتغاير ذات رتبة اثنين (أي يمكن كتابتها كتركيبة خطية من متغيرين كامنين مستقلين) نستخدم هيكل التأثير العشوائي rr في الصيغة كما يلي
rr(x | المجموعة، 2)
لذا على سبيل المثال، لنموذج متوسط الاستجابة (y) كدالة لـ x ولتترك معاملات x تتغير عشوائيًا بين المجموعات كدالة لاثنين من المتغيرات الكامنة، تكون الصيغة هي
مجموعة، 2)
العدد الصحيح غير السالب بعد الفاصلة في المعادلة يحدد عدد المتغيرات الكامنة، أو الرتبة، لمصفوفة التباين-التغاير للتأثيرات العشوائية المتعددة، والتي تكون افتراضيًا يمكن اعتبار اختيار عدد المتغيرات الكامنة مشكلة اختيار نموذج (هوي وآخرون 2015). يمكن استخدام أدوات اختيار النموذج بما في ذلك التحقق المتقاطع أو معايير المعلومات لاختيار الرتبة (بارثولوميو وآخرون 2011).
تتمثل إحدى المشكلات في ملاءمة نموذج تحليل العوامل في أن دالة الاحتمالية غالبًا ما تكون متعددة القمم، مما قد يؤدي إلى التقارب نحو حد أقصى محلي. للتغلب على ذلك، نقوم بتضمين طريقة مدفوعة بالبيانات استنادًا إلى عمل نيكو وآخرين (2019) لتهيئة القيم للمعلمات بحيث يبدأ خوارزمية التعظيم بالقرب من الحد الأقصى العالمي. الإعداد الافتراضي في glmmTMB يحدد قيم المعلمات على أنها صفر، أو واحد للمعلمات ذات التأثير الثابت لبعض دوال الربط. للتحكم في الخوارزمية المستخدمة لتهيئة المعلمات، يتم تحديد وسيط start_method، كقائمة تحتوي على مكونات method وانحراف التذبذبتمت إضافته إلى
glmmTMBControl(). تعيين الطريقة = “res” يناسب نموذج خطي عام (GLM) للبيانات للحصول على تقديرات المعلمات الثابتة، والتي تُستخدم بعد ذلك كقيم ابتدائية للمعلمات الثابتة. من النموذج الملائم، يتم حساب المتبقيات للنماذج باستخدام عائلات بواسون، ثنائية الحد السلبية، وثنائية الحد باستخدام الطريقة التي اقترحها دان وسميث (1996)، بينما تُستخدم الدالة الداخلية dev.residuals للعائلات الأخرى. قيم ابتدائية للمتغيرات الكامنة، وأحمال العوامل، يتم الحصول عليها من خلال تطبيق نموذج منخفض الرتبة على المتبقيات من نموذج GLM الملائم. للتحقق من استقرار الحل، نقترح تكرار الملاءمة عدة مرات وإضافة تباين إلى القيم الابتدائية للمتغيرات الكامنة عند استخدام الطريقة “الموارد” عن طريق تعيين انحراف التذبذب أو ما شابه، لتشويش القيم الابتدائية لـ بواسطة متغير عادي بمتوسط صفر وانحراف معياريانحراف التذبذب.
تظهر المزيد من الأمثلة على تنفيذ هيكل rr في القسم 3. يمكن العثور على معلومات حول هيكل التباين والتغاير ذو الرتبة المنخفضة والهياكل الأخرى المتاحة في glmmTMB في الكتيب (“covstruct”، الحزمة = “glmmTMB”).

نقدم تطبيقين لتوضيح استخدام هيكل التباين منخفض الرتبة في glmmTMB. المثال الأول، الذي يستخدم بيانات مزارع الرياح، يناسب نموذج متغيرات كامنة عامة لبيانات الوفرة المتعددة، وهو نوع من البيانات التي غالبًا ما يتم جمعها للدراسات البيئية. المثال الثاني يقدم نموذج المنحدرات العشوائية، مع العديد من المنحدرات العشوائية، المطبق على بيانات من دراسة التقدم في القراءة الدولية (PIRLS).

تم جمع بيانات مزرعة الرياح لمزرعة ليلغوند البحرية قبالة الساحل الجنوبي للسويد، لدراسة آثار مزرعة الرياح على مجتمع الأسماك القاعية (بيرغستروم، سوندكفيست، وبيرغستروم 2013). هذه واحدة من الدراسات الكبيرة القليلة التي تقيم آثار مزارع الرياح البحرية على مدى فترة طويلة من الزمن، وعلى أكثر من نوع واحد من الأسماك. تمثل هذه الدراسة تصميم BACI (قبل-بعد-تحكم-أثر)؛ حيث تم قياس وفرة الأسماك قبل (2003) وبعد البناء (2010)، في منطقة مزرعة الرياح وفي منطقتين مرجعيتين (المنطقة المرجعية الجنوبية والشمالية). حدثت عمليات أخذ العينات في محطات الصيد داخل كل منطقة؛ حيث ظلت المحطات كما هي طوال فترة الدراسة. تم استبعاد المحطات التي لم يتم أخذ عينات منها في كلا الفترتين الزمنيتين. لا تظهر بيانات الوفرة الخام (الشكل 1) تأثيرًا واضحًا لمزرعة الرياح، على الرغم من أن الأنواع Strensnultra و Oxsimpa قد تظهر اختلافات قبل-بعد للمناطق الجنوبية والشمالية على التوالي. نظرًا لأننا مهتمون بتأثير مزارع الرياح، التي تم إنشاؤها بين أوقات أخذ العينات، فإن اهتمامنا ينصب على التفاعل بين المنطقة والسنة.
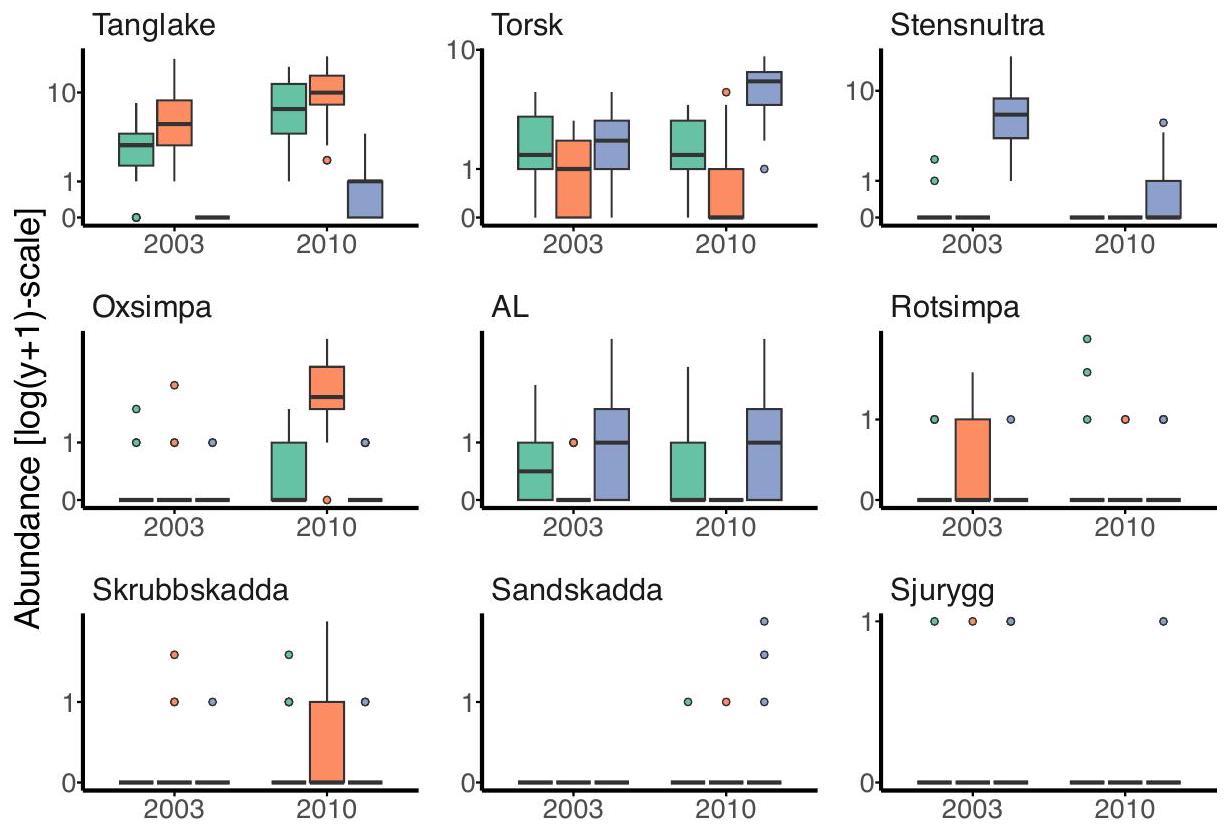
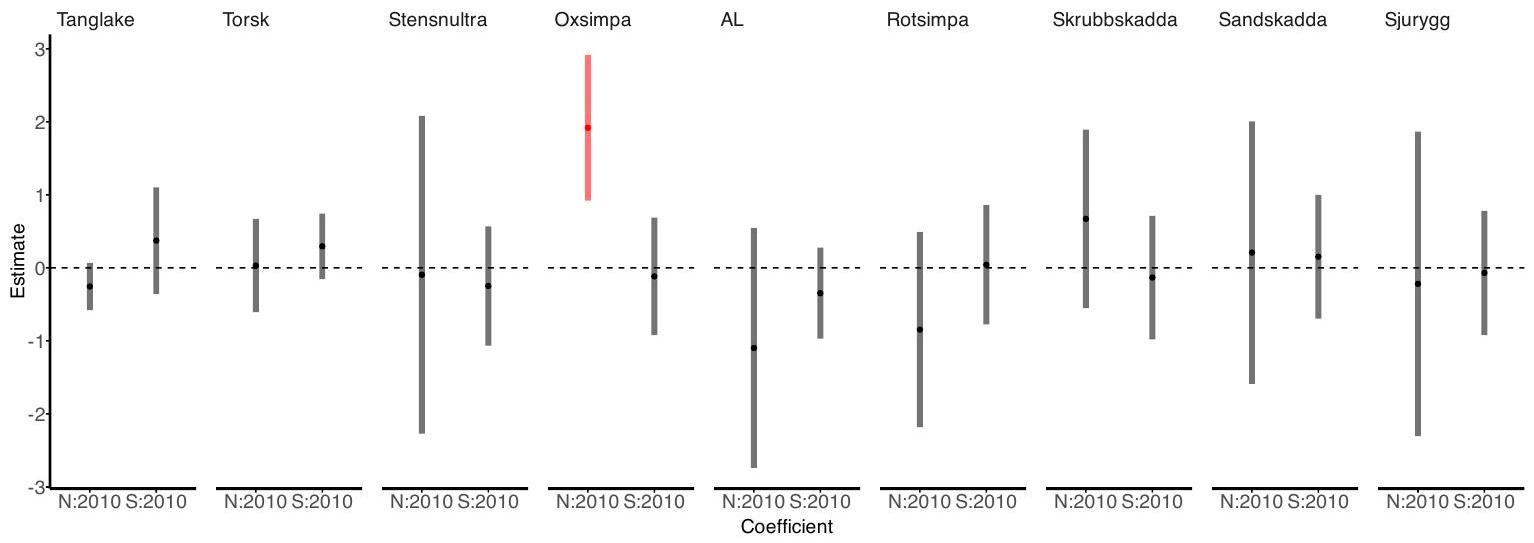
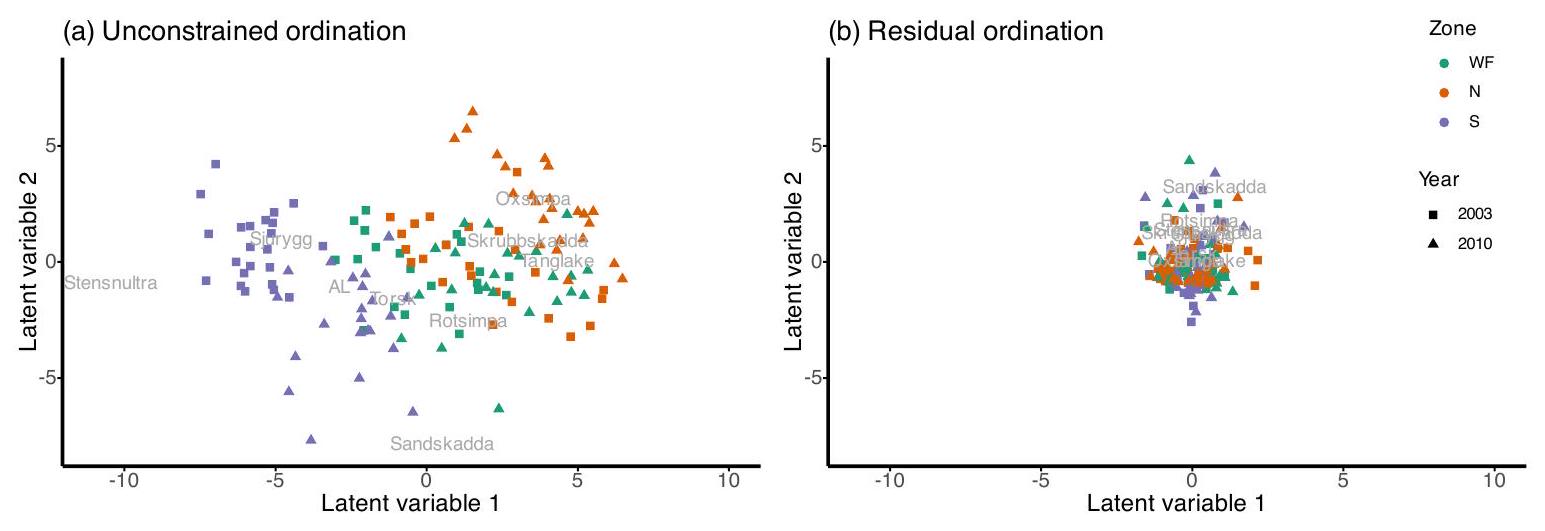
تتطلب التأثيرات العشوائية متعددة المتغيرات حساب الارتباط في استجابات الأنواع داخل عينة – نتوقع وجود ارتباط عبر الأنواع بسبب التفاعلات بين الأنواع، أو الاستجابة لظروف بيئية غير مرصودة (Warton et al. 2015) ونرغب في أن نكون قادرين على تقدير الارتباطات الإيجابية أو السلبية. ليس لدينا أي هيكل مسبق لهذا الارتباط، ولتسع أنواع سنحتاج إلى 45 معلمة لتقدير مصفوفة التباين-التغاير بين الأنواع. وبالتالي، نتوقع عدم استقرار كبير في الملاءمة، خاصة بالنسبة لمصطلحات الارتباط التي تتضمن الأنواع النادرة. بالمقارنة، ستتطلب بنية التغاير ذات الرتبة المخفضة من الرتبة الثانية 17 معلمة فقط.
نحن نضع نماذج للوفرة، كشرط بواسون بمتوسط ، تم رصده عند

عينات، لـ نوع، عند محطات ( ) بحيث:

حيث هي متجهات من المتغيرات البيئية تحدد التقاطع، المنطقة، السنة وتفاعل المنطقة والسنة، و هو متجه من المعاملات الثابتة. نحن ندرج تأثيرًا عشوائيًا متعدد المتغيرات (مع ) على المتغيرات البيئية، للسماح بتغير تأثيرات كل متغير عبر الأنواع. التقاطع العشوائي للمحطة، يهدف إلى حساب أخذ العينات المزدوجة في المحطات، مع جمع البيانات في نقطتين زمنيتين لكل محطة. نفترض أن كل من هذه التأثيرات العشوائية مستقلة عن جميع الآخرين وعن الاستجابة (شرط على ). يتم تحفيز الارتباط بين الأنواع بواسطة التأثير العشوائي ذو الرتبة المخفضة، ، المفترض أن يحقق

حيث هو زوج (البعد ) من المتغيرات الكامنة، والمتجه يحتوي على تحميلات العوامل المقابلة. يمكن بعد ذلك ملاءمة هذا النموذج باستخدام الأمر التالي:

R> glmmTMB(abundance ~ Zone * Year + diag(Zone * Year | Species) +
+ (1 | Station) + rr(Species + 0 | ID, 2), family = "poisson",
+ control = glmmTMBControl(start_method = list(method = "res")),
+ data = windfarm)

تم استبعاد التقاطع من مصطلح التأثير العشوائي ذو الرتبة المخفضة (باستخدام الأنواع + 0 كالمصطلح المتغير) من أجل تسهيل تفسير مصفوفة الارتباط التي تم مناقشتها

بالأسفل. يمكن الحصول على مصفوفة الارتباط المقدرة للتأثير العشوائي ذو الرتبة المخفضة من مخرجات طريقة الملخص، أو باستخدام طريقة VarCorr، بنفس الطريقة التي يتم بها إرجاع القيم المقدرة لأي مصفوفة تباين-تغاير بواسطة

مصفوفة الارتباط المقدرة للتقاطع العشوائي لبيانات مزرعة الرياح، باستخدام نموذج الرتبة الثانية المحدد أعلاه، هي كما يلي:

هذه الارتباطات هي ارتباطات متبقية بين الأنواع لم يتم حسابها بواسطة المتغيرات المشتركة وتأثيرات عشوائية أخرى في النموذج. على سبيل المثال، الارتباط بين الأنواع Oxsimpa و AL هو 0.89 بعد التحكم في المتغيرات الثابتة والعشوائية في النموذج. لاحظ أن هذه الارتباطات على مقياس المتنبئ الخطي (في هذه الحالة مقياس اللوغاريتم)، وأن الارتباط الفعلي الملاحظ في البيانات أضعف بكثير من هذه القيم، بسبب ضوضاء بواسون المقدمة بواسطة المعادلة 4. هيكل الارتباط الهامشي هو مفرد (لـ ) حيث يتم تقريبه من المعادلة 2، حيث هو رتبة مخفضة؛ هذا ليس مشكلة حيث يتم استخدام تقديرات تحميلات العوامل، ، والمتغيرات الكامنة، في التحليل الإضافي. محاولة ملاءمة هذا النموذج باستخدام هيكل تغاير غير منظم تواجه مشاكل في التقارب؛ البيانات ليست ذات جودة كافية لدعم تقدير 45 معلمة تباين منفصلة. لاختبار ما إذا كان بناء مزرعة رياح بحرية له تأثير كبير على وفرة الأسماك، تم إجراء تحليل Bootstrap بارامتري لاختبار تفاعل المنطقة بالسنة في كل من المصطلحات الثابتة والعشوائية (الكود المقدم

في الملحق ب). تم اختيار تحليل Bootstrap بارامتري على الاختبارات التقريبية مثل اختبارات والد واختبارات نسبة الاحتمالات، لأن التوزيعات التقريبية لهذه الاختبارات عادة ما تكون غير معروفة للنماذج المختلطة (Bolker et al. 2009). كانت التفاعلات ذات دلالة (LR )، مما يشير إلى أنه بالنسبة لواحد على الأقل من الأنواع، تغيرت متوسط الوفرة عبر المناطق (بمعنى نسبي) منذ بناء مزرعة الرياح (الشكل 2). بعد التحكم في المتغيرات الأخرى، كانت كثافات Oxsimpa أكبر بوضوح في المنطقة الشمالية مقارنة بمنطقة مزرعة الرياح (أي أن التباين إيجابي بوضوح، Dushoff وKain وBolker 2019)، بينما التباين بين الجنوب ومزرعة الرياح سلبي وقريب من الصفر. judging من الشكل 1، من المحتمل أن يكون لهذا التأثير علاقة أكبر بزيادة Oxsimpa في المنطقة الشمالية، بدلاً من تأثير مزرعة الرياح. لتصور الارتباطات بين الأنواع، يمكن إنتاج مخطط ثنائي الأبعاد من المتغيرات الكامنة المقدرة وتحميلات العوامل (الشكل 3). يظهر مخطط ثنائي الأبعاد غير المقيد (الشكل 3أ)، الذي يرسم المتغيرات الكامنة من نموذج بدون مؤشرات تأثير ثابت، فصلًا في المتغيرات الكامنة حسب المنطقة والسنة، مما يبرز أهمية هذه المتغيرات. إضافة تحميلات العوامل إلى المخطط تظهر لنا كيف تختلف الأنواع عبر المواقع، مع وجود وفرة أعلى لنوع ما تميل إلى أن توجد في المواقع في نفس اتجاه النوع، بالنسبة للأصل. يمكن توقع أن يتم العثور على Oxsimpa بأعداد كبيرة في المنطقة الشمالية في 2010، ويمكن توقع أن يتم العثور على Stensnultra بأعداد كبيرة في المنطقة الجنوبية، خاصة في 2003. الشكل 1 يؤكد كلا هذين النتيجتين. تعطي المواقع النسبية للأنواع أيضًا معلومات عن ارتباطها – لأن Oxsimpa وStensnultra مرتبطتان سلبًا، فإنهما تظهران بعيدتين عن الأصل ولكن على جوانب متقابلة من المخطط، بينما Oxsimpa وSkrubbskadda المرتبطتان إيجابيًا هما جيران في مخطط الترتيب.

بعد ملاءمة النموذج في المعادلة 4، التي تتحكم في تأثيرات المنطقة، السنة، تفاعلهما، والمحطة، تختفي أنماط التجميع حسب المنطقة ووقت أخذ العينات (الشكل 3ب). النقاط تقع أقرب بكثير من بعضها البعض، مع تحميلات أصغر، مما يعكس حقيقة أن إضافة مؤشرات إلى النموذج تقلل بشكل كبير من حجم مصطلحات التباين-التغاير. هذا يؤكد أن الأنماط السائدة التي تم رؤيتها في الترتيب غير المقيد، وبالتالي في مجتمعات الأسماك التي يتم أخذ عينات منها، يمكن تفسيرها من خلال المكان والزمان الذي تم فيه أخذ العينات.

التقدم في دراسة القراءة الدولية (PIRLS) هو مشروع بحث دولي واسع النطاق يقيس مهارات القراءة لدى الأطفال الذين تتراوح أعمارهم بين تسع إلى عشر سنوات (Martin وMullis وHooper 2017). تم إجراء PIRLS كل خمس سنوات منذ عام 2001، بمشاركة 61 دولة في PIRLS 2016. اقترحت الدراسات المنشورة أن المتغيرات المدرسية أكثر أهمية من الخلفية الأسرية في تحديد الإنجاز الأكاديمي في البلدان النامية (Heyneman وLoxley 1982). ومع ذلك، تشير الدراسات الأحدث إلى نتائج متضاربة تظهر أن هذه المتغيرات متشابهة عبر البلدان (Marôco 2021)، مع اقتراح المؤلفين أن هذا التماثل قد يكون بسبب زيادة التعليم الجماعي. لذلك، نحن مهتمون باستكشاف كيف يختلف تأثير المتغيرات المدرسية على درجات القراءة للطلاب حسب البلد.
نقترح أن الطلاب من المدارس ذات الوضع الاقتصادي المتدني (Eco_disad) الذين لديهم مكتبة تحتوي على المزيد من الكتب (Size_lib) لديهم درجات محو أمية أعلى من الطلاب من مدرسة بلا مكتبة، لكن الفرق في درجات محو الأمية سيكون أقل عندما يكون الطلاب من مدارس ذات خلفية اقتصادية أعلى، أي أن هناك تفاعل بين المتغيرين المدرسيين. علاوة على ذلك، نود أن نعرف كيف سيتغير التأثير التفاعلي لهذه المتغيرات على مستوى المدرسة حسب البلد، ومن ثم نريد ملاءمة نموذج منحدرات عشوائية، مع تأثيرات مختلفة لـ Eco_disad:Size_lib لكل بلد. كلا من Eco_disad و Size_lib هما متغيرات فئوية بأربعة مستويات، وبالتالي نحتاج إلى 15 معلمة لوصف تأثيرهما المشترك و15 تأثير عشوائي ذو أبعاد في النموذج. تقدير مصفوفة التباين-التغاير غير الهيكلية سيتطلب 136 معلمة. بالمقابل، بالنسبة لهيكل تغاير منخفض الرتبة من الرتبة الثالثة، يتطلب فقط 42 معلمة – تم استخدام AIC لاختيار الرتبة الثالثة.
نعتبر النموذج لدرجة محو الأمية، , للطالب , في المدرسة والبلد كما يلي:

حيث هي متجهات من المتغيرات المرتبطة بعوامل المدرسة و هو متجه المعاملات الثابتة. يعكس التقاطع العشوائي للمدرسة، تباين درجات محو الأمية المتوسطة بين المدارس. يسمح التقاطع العشوائي والمنحدرات لمتغيرات المدرسة بأن تتغير حسب البلد حيث هي المصفوفة الكاملة لأحمال العوامل، و هو الخطأ المتبقي.
يمكن ملاءمة هذا النموذج في glmmTMB باستخدام الأمر التالي:

R> glmmTMB(Overall ~ Size_lib * Eco_disad + (1 | School) +
+ rr(Size_lib * Eco_disad | Country, d = 3),
+ control = glmmTMBControl(start_method = list(method = "res")),
+ family = gaussian(), data = pirls)

تحتاج خوارزمية البدء لتهيئة المعلمات المحددة في حجة التحكم عند ملاءمة هذا النموذج، وإلا ستظهر مشاكل في التقارب.
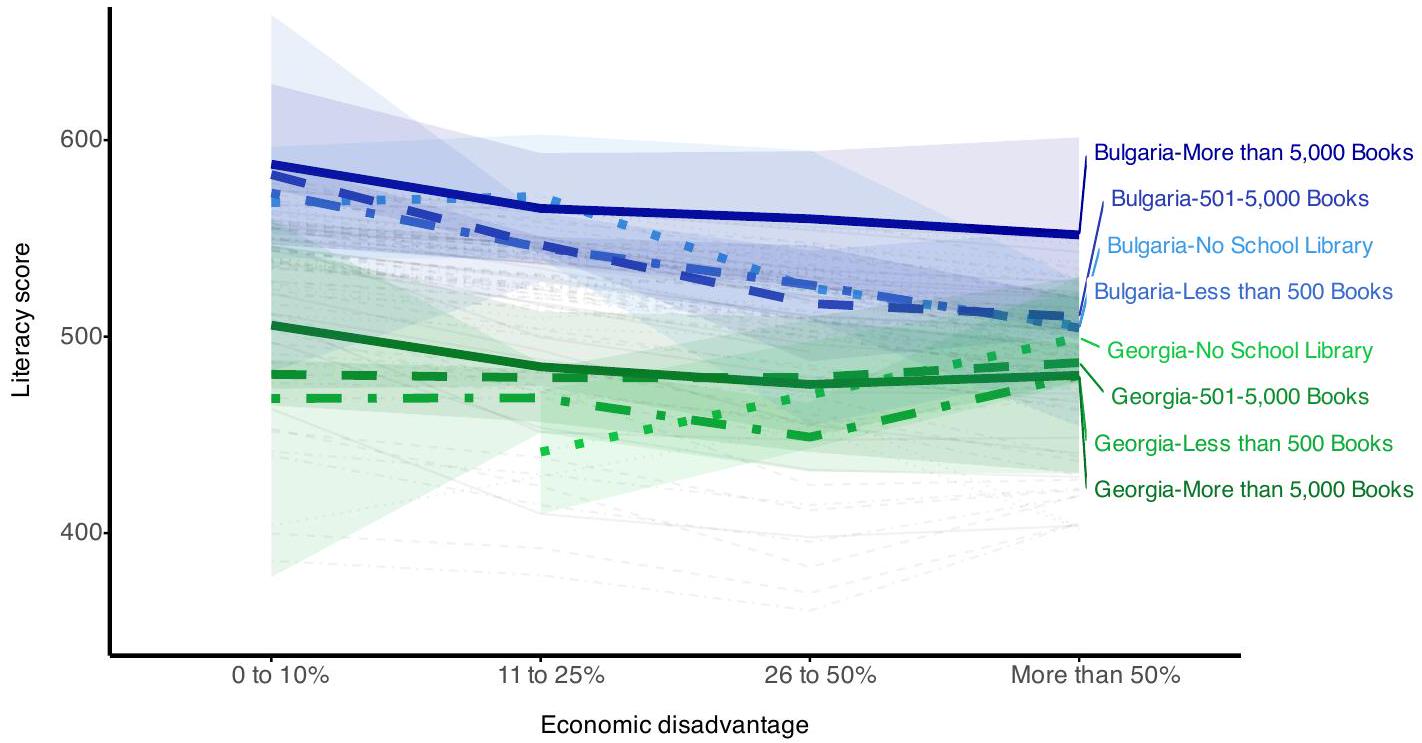
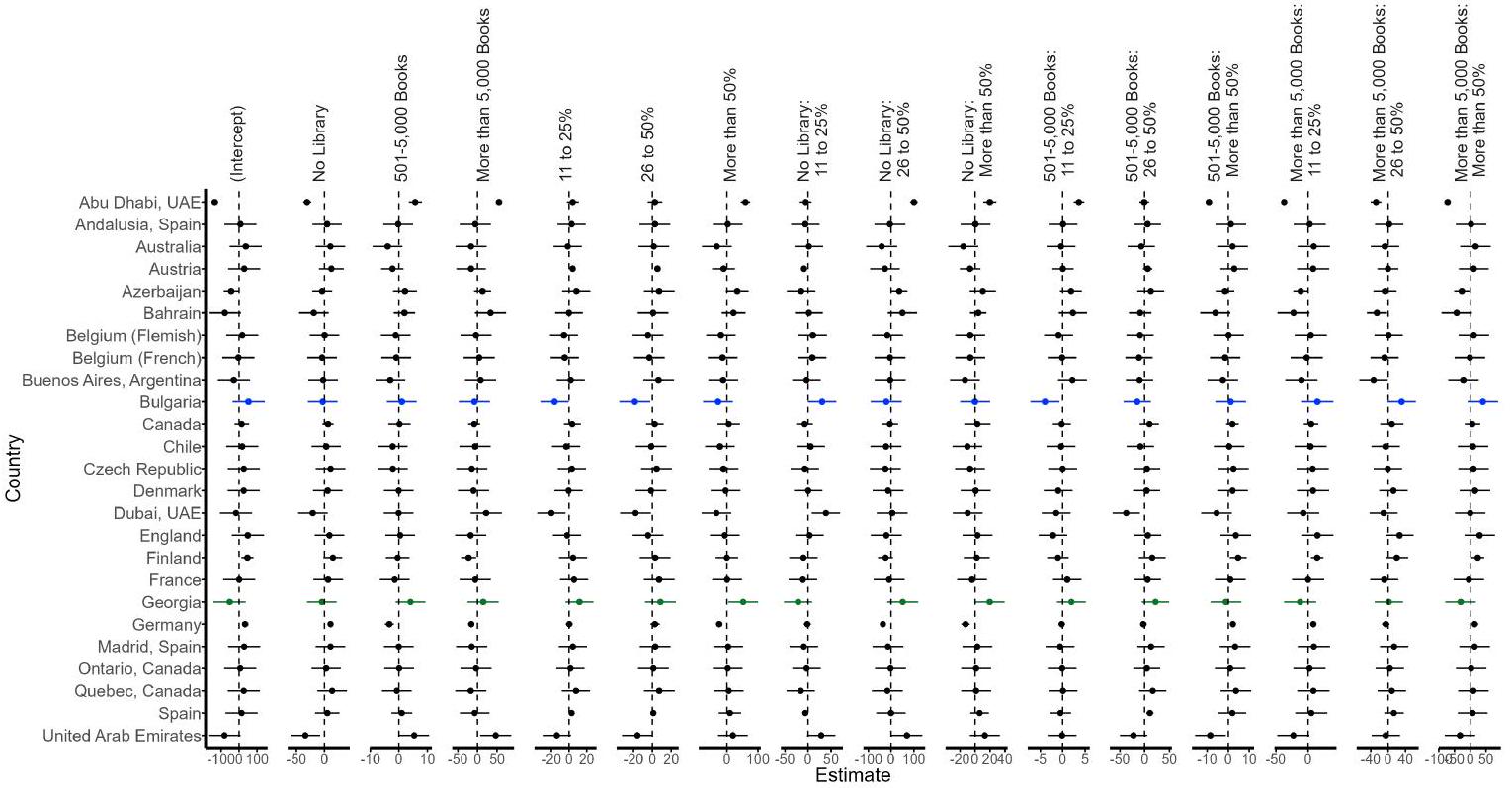
تقديرات التأثيرات العشوائية للمدرسة حسب البلد معقدة (الشكل 7): سنركز على تباين معين بين بلغاريا وجورجيا (النتائج الملونة في الشكل 7). هذه المقارنة مثيرة للاهتمام لأن هذين البلدين يبدو أنهما لديهما أنماط مختلفة من تفاعل المكتبة والحرمان الاقتصادي (الشكل 4). النمط الأكثر وضوحًا الذي يظهر في مخطط التفاعل (الشكل 4) هو أن الطلاب من بلغاريا (الخطوط الزرقاء) لديهم

درجات محو أمية أعلى من الطلاب من جورجيا (الخطوط الخضراء). ومع ذلك، يبدو أن درجات محو أمية الطلاب البلغاريين تنخفض أيضًا مع زيادة الحرمان الاقتصادي؛ علاوة على ذلك، بدا أن معدل الانخفاض أبطأ للمدارس ذات الموارد الأفضل (أي تلك التي تحتوي على المزيد من الكتب). تم ملاحظة هذه الأنماط، المتوقعة من المبادئ الاجتماعية الاقتصادية العامة، عبر العديد من البلدان. تبدو جورجيا غير عادية: كان للحرمان الاقتصادي تأثير ضئيل على درجات محو الأمية، وكانت تأثيرات حجم المكتبة عكس ما كان متوقعًا – بدت المدارس ذات المكتبات الكبيرة لديها درجات محو أمية أعلى من تلك ذات المكتبات الصغيرة عندما كانت المدارس في وضع جيد، لكن حجم المكتبة لم يكن له تأثير كبير على المدارس ذات الحرمان الشديد.

في هذه المقالة، قدمنا هيكل جديد للتباين-التغاير، rr، في glmmTMB، لإضافة وظيفة منخفضة الرتبة إلى النماذج المختلطة. هذه الميزة توسع نطاق النماذج التي يمكن ملاءمتها من خلال كتابة تأثير عشوائي متعدد الأبعاد كبير كتركيب خطي لـ متغيرات كامنة، وهي هيكل أكثر اقتصادية يمكن تقديره بسهولة أكبر عندما تكون أبعاد التأثير العشوائي كبيرة. في القسم 1، ناقشنا الأدوات المتاحة في R، مثل gllvm، التي تناسب أيضًا نماذج المتغيرات الكامنة. تم تطوير هذه الحزم مع تركيز أساسي على النماذج للبيانات البيئية. الميزة الرئيسية لعملنا هي إضافة مصطلح تحليلي للعوامل إلى مجموعة هياكل التأثيرات العشوائية المتاحة بالفعل في glmmTMB، بحيث يمكن الآن ملاءمة نماذج المتغيرات الكامنة العامة لتصاميم دراسات معقدة، باستخدام واجهة مألوفة.

قدمنا تطبيقين لتوضيح استخدام نهج منخفض الرتبة. في كلا المثالين كانت أبعاد التأثير العشوائي معتدلة – 9 و 15 لهذين المثالين – لكن هذا كان بالفعل كبيرًا جدًا ليكون قابلًا للتقدير عمليًا، مما استلزم استخدام نموذج منخفض الرتبة
. النماذج منخفضة الرتبة قادرة على ملاءمة التأثيرات العشوائية ذات الأبعاد الكبيرة جدًا: على سبيل المثال، قام Niku وآخرون (2019) بملاءمة GLVM بأبعاد 985 لمجموعة بيانات ميكروبية. عند ملاءمة النماذج لمجموعات بيانات أكبر، يمكن مواجهة صعوبات؛ على سبيل المثال، في علم البيئة، يكون عدد الأنواع غالبًا كبيرًا مقارنة بعدد العينات. في مثل هذه الحالات، قد يكون من المفيد ملاءمة نموذج عدة مرات مع قيم بدء مختلفة للمعلمات، ويعتبر الملاءمة ذات أعلى قيمة للاحتمالية اللوغاريتمية هي أفضل نموذج ملاءمة.

يساهم النموذج منخفض الرتبة في صندوق أدوات تبسيط النموذج، مما يسمح بتأثير عشوائي أكثر اقتصادية قد يكون ضروريًا لبعض تصاميم الدراسات (Matuschek، Kliegl، Vasishth، Baayen، وBates 2017). حاليًا، تفترض الطرق المتاحة للتبسيط مصفوفة تباين-تغاير قطرية، مع تباينات متجانسة أو غير متجانسة؛ تفترض تماثل مركب؛ أو تفترض شكلًا محددًا من الهيكل (AR(1)، توبيليتز، إلخ). جميع هذه الهياكل متاحة في glmmTMB. بديل آخر للتحكم في التعقيد هو شكل من أشكال الانكماش نحو الصفر على أحمال العوامل كما هو مقترح في إطار بايزي (Bhattacharya وDunson 2011).
خطوة رئيسية في تطبيق تأثير عشوائي منخفض الرتبة هي اختيار الرتبة . يمكن استخدام استراتيجيات مختلفة لاختيار , اعتمادًا على هدف التحليل. في تطبيق مزرعة الرياح، استخدمنا مخطط ثنائي الأبعاد لتصور الارتباطات عبر الأنواع (الشكل 3) ولهذا الغرض كان مناسبًا. في تطبيقنا الثاني، دراسة PIRLS، كان هدفنا هو إجراء استنتاجات حول التأثيرات الثابتة المرتبطة، وتم استخدام النهج منخفض الرتبة لتقدير هذا الارتباط. في هذه الحالة، استخدمنا معايير المعلومات لاختيار قيمة لـ التي أعطتنا ملاءمة جيدة للبيانات. وجدنا أن التقديرات وفترات الثقة لتقديرات التأثير الثابت كانت قوية أمام خيارات مختلفة للرتبة (انظر المواد التكميلية، الشكل 5 والشكل 6). مدى تغير التأثيرات الثابتة مع تغير افتراضات التغاير على التأثيرات العشوائية هو دالة لمدى تغير الهيكل التغايري الملائم فعليًا. تقدم المصطلحات التحليلية للعوامل عوائد متناقصة من حيث التغيرات في مع زيادة ، لذا هناك أكبر قدرة على التغيرات في التفسير عندما يكون صغيرًا (في الممارسة العملية، رأينا تغييرات نوعية مهمة فقط لـ ، كما في الشكل 6).
هيكل الرتبة المنخفضة له نقطة اختلاف مثيرة للاهتمام عن الطرق الأخرى لملاءمة تأثير عشوائي متعدد المتغيرات حيث يسمح بمصفوفة تباين-تغاير مفردة، أو بشكل أكثر دقة، يفترض التفرد. تتطلب الطرق الأخرى لملاءمة التأثيرات العشوائية المرتبطة مصفوفة تباين-تغاير إيجابية محددة وتعيد تحذيرات عند مواجهة (قرب) التفرد، وهي مشكلة تم تجاوزها هنا من خلال افتراض هيكل منخفض الرتبة.
تقدم أمثلتنا لمحات قليلة فقط عن كيفية استخدام هياكل التباين-التغاير منخفضة الرتبة في النمذجة المختلطة، حيث كان من الصعب تقنيًا ملاءمة نماذج بتأثيرات عشوائية ذات أبعاد عالية. بعض المجالات التي نرى فيها استخدامًا محتملاً لهذا النهج تشمل التحليل العاملي مع تصاميم متعددة المستويات أو قياسات متكررة، وتحليل تفاعل الجين مع البيئة (Piepho 1997؛ Smith وآخرون 2001). نرى العديد من التطبيقات المحتملة، ونتطلع إلى رؤية كيف سيتم استخدام هذه الأداة الجديدة في الممارسة العملية.

Asar Ö, Bolin D, Diggle PJ, Wallin J (2020). “Linear Mixed Effects Models for Non-Gaussian Continuous Repeated Measurement Data.” Journal of the Royal Statistical Society C, 69(5), 1015-1065. doi:10.1111/rssc. 12405.

Banerjee S, Gelfand AE, Finley AO, Sang H (2008). “Gaussian Predictive Process Models for Large Spatial Data Sets.” Journal of the Royal Statistical Society B, 70(4), 825-848. doi:10.1111/j.1467-9868.2008.00663.x.

Bartholomew DJ, Knott M, Moustaki I (2011). Latent Variable Models and Factor Analysis: A Unified Approach. John Wiley & Sons.

Bates D, Mächler M, Bolker BM, Walker S (2014). “Fitting Linear Mixed-Effects Models Using lme4.” Journal of Statistical Software, 67(1), 1-48. doi:10.18637/jss.v067.i01.

Bergstrom L, Sundqvist F, Bergstrom U (2013). “Effects of an Offshore Wind Farm on Temporal and Spatial Patterns in the Demersal Fish Community.” Marine Ecology Progress Series, 485, 199-210. doi:10.3354/meps10344.

Bhattacharya A, Dunson DB (2011). “Sparse Bayesian Infinite Factor Models.” Biometrika, 98(2), 291-306. doi:10.1093/biomet/asr013.

Bolker BM, Brooks ME, Clark CJ, Geange SW, Poulsen JR, Stevens MHH, White JSS (2009). “Generalized Linear Mixed Models: A Practical Guide for Ecology and Evolution.” Trends in Ecology & Evolution, 24(3), 127-135. doi:10.1016/j.tree.2008.10.008.

Brooks ME, Kristensen K, Van Benthem KJ, Magnusson A, Berg CW, Nielsen A, Skaug HJ, Mächler M, Bolker BM (2017). “glmmTMB Balances Speed and Flexibility among Packages for Zero-Inflated Generalized Linear Mixed Modeling.” The Journal, 9(2), 378-400. doi:10.32614/rj-2017-066.

Buettner F, Natarajan KN, Casale FP, Proserpio V, Scialdone A, Theis FJ, Teichmann SA, Marioni JC, Stegle O (2015). “Computational Analysis of Cell-to-Cell Heterogeneity in Single-Cell RNA-Sequencing Data Reveals Hidden Subpopulations of Cells.” Nature Biotechnology, 33(2), 155-160. doi:10.1038/nbt. 3102.

Coull BA, Agresti A (2000). “Random Effects Modeling of Multiple Binomial Responses Using the Multivariate Binomial Logit-Normal Distribution.” Biometrics, 56(1), 73-80. doi:10.1111/j.0006-341x.2000.00073.x.

Cressie N, Johannesson G (2008). “Fixed Rank Kriging for Very Large Spatial Data Sets.” Journal of the Royal Statistical Society B, 70(1), 209-226. doi:10.1080/10618600. 1996. 10474708.

Dunn PK, Smyth GK (1996). “Randomized Quantile Residuals.” Journal of Computational and Graphical Statistics, 5(3), 236-244. doi:10.1080/10618600.1996.10474708.

Dushoff J, Kain MP, Bolker BM (2019). “I Can See Clearly Now: Reinterpreting Statistical Significance.” Methods in Ecology and Evolution, 10(6), 756-759. doi:10.1111/ 2041-210x. 13159.

Heyneman SP, Loxley WA (1982). “Influences on Academic Achievement Across High and Low Income Countries: A Re-Analysis of IEA Data.” Sociology of Education, pp. 13-21. doi:10.2307/2112607.

Huber P, Ronchetti E, Victoria-Feser MP (2004). “Estimation of Generalized Linear Latent Variable Models.” Journal of the Royal Statistical Society B, 66(4), 893-908. doi:10. 1111/j.1467-9868.2004.05627.x.

Hui FKC (2016). “Boral – Bayesian Ordination and Regression Analysis of Multivariate Abundance Data in R.” Methods in Ecology and Evolution, 7(6), 744-750. doi:10.1111/ 2041-210x. 12514.

Hui FKC, Taskinen S, Pledger S, Foster SD, Warton DI (2015). “Model-Based Approaches to Unconstrained Ordination.” Methods in Ecology and Evolution, 6(4), 399-411. doi: 10.1111/2041-210x. 12236.

Hui FKC, Warton DI, Ormerod JT, Haapaniemi V, Taskinen S (2017). “Variational Approximations for Generalized Linear Latent Variable Models.” Journal of Computational and Graphical Statistics, 26(1), 35-43. doi:10.1080/10618600.2016.1164708.

Kass RE, Steffey D (1989). “Approximate Bayesian Inference in Conditionally Independent Hierarchical Models (Parametric Empirical Bayes Models).” Journal of the American Statistical Association, 84(407), 717-726. doi:10.1080/01621459.1989.10478825.

Kristensen K, Nielsen A, Berg CW, Skaug H, Bell B (2015). “TMB: Automatic Differentiation and Laplace Approximation.” Journal of Statistical Software, Articles, 70(5), 1-21. doi: 10.18637/jss.v070.i05.

Marôco J (2021). “What Makes a Good Reader? Worldwide Insights from PIRLS 2016.” Reading and Writing, 34(1), 231-272. doi:10.1007/s11145-020-10068-8.

Martin MO, Mullis IVS, Hooper M (2017). “Methods and Procedures in PIRLS 2016.” URL https://timssandpirls.bc.edu/pirls2016/international-database/.

Matuschek H, Kliegl R, Vasishth S, Baayen H, Bates D (2017). “Balancing Type I Error and Power in Linear Mixed Models.” Journal of Memory and Language, 94, 305-315. doi:10.1016/j.jml.2017.01.001.

Niku J, Hui FKC, Taskinen S, Warton DI (2019). “gllvm: Fast Analysis of Multivariate Abundance Data with Generalized Linear Latent Variable Models in R.” Methods in Ecology and Evolution, 10(12), 2173-2182. doi:10.1111/2041-210x. 13303.

Niku J, Hui FKC, Taskinen S, Warton DI (2021). “Analyzing Environmental-Trait Interactions in Ecological Communities with Fourth-Corner Latent Variable Models.” Environmetrics, p. e2683. doi:10.1002/env. 2683.

Niku J, Warton DI, Hui FKC, Taskinen S (2017). “Generalized Linear Latent Variable Models for Multivariate Count and Biomass Data in Ecology.” Journal of Agricultural, Biological and Environmental Statistics, 22(4), 498-522. doi:10.1007/s13253-017-0304-7.

Ovaskainen O, Tikhonov G, Norberg A, Guillaume Blanchet F, Duan L, Dunson D, Roslin T, Abrego N (2017). “How to Make More Out of Community Data? A Conceptual Framework and Its Implementation as Models and Software.” Ecology Letters, 20(5), 561-576. ISSN 1461-0248. doi:10.1111/ele. 12757.

Piepho HP (1997). “Analyzing Genotype-Environment Data by Mixed Models with Multiplicative Terms.” Biometrics, pp. 761-766. doi:10.2307/2533976.

Pollock LJ, Tingley R, Morris WK, Golding N, O’Hara RB, Parris KM, Vesk PA, McCarthy MA (2014). “Understanding Co-Occurrence by Modelling Species Simultaneously with a Joint Species Distribution Model (JSDM).” Methods in Ecology and Evolution, 5(5), 397406. doi:10.1111/2041-210x. 12180.

Rabe-Hesketh S, Skrondal A, Pickles A (2004). “Generalized Multilevel Structural Equation Modeling.” Psychometrika, 69(2), 167-190. doi:10.1007/bf02295939.

Raudenbush SW, Yang ML, Yosef M (2000). “Maximum Likelihood for Generalized Linear Models with Nested Random Effects via High-Order, Multivariate Laplace Approximation.” Journal of Computational and Graphical Statistics, 9(1), 141-157. doi: 10.1080/10618600.2000.10474870.

R Core Team (2024). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.

Skrondal A, Rabe-Hesketh S (2003). “Multilevel Logistic Regression for Polytomous Data and Rankings.” Psychometrika, 68(2), 267-287. doi:10.1007/bf02294801.

Skrondal A, Rabe-Hesketh S (2004). Generalized Latent Variable Modeling: Multilevel, Longitudinal, and Structural Equation Models. Chapman & Hall/CRC.

Smith A, Cullis B, Thompson R (2001). “Analyzing Variety by Environment Data Using Multiplicative Mixed Models and Adjustments for Spatial Field Trend.” Biometrics, 57(4), 1138-1147. doi:10.1111/j.0006-341x.2001.01138.x.

StataCorp (2023). Stata Statistical Software: Release 18. StataCorp LLC, College Station.
Van der Veen B, Hui FKC, Hovstad KA, Solbu EB, O’Hara RB (2021). “Model-Based Ordination for Species with Unequal Niche Widths.” Methods in Ecology and Evolution, 12(7), 1288-1300. doi:10.1111/2041-210x. 13595.

Walker SC, Jackson DA (2011). “Random-Effects Ordination: Describing and Predicting Multivariate Correlations and Co-Occurrences.” Ecological Monographs, 81(4), 635-663. doi:10.1890/11-0886.1.

Warton DI, Blanchet FG, O’Hara RB, Ovaskainen O, Taskinen S, Walker SC, Hui FKC (2015). “So Many Variables: Joint Modeling in Community Ecology.” Trends in Ecology & Evolution, 30(12), 766-779. doi:10.1016/j.tree.2015.09.007.

ملخص النموذج لمثال مزرعة الرياح في القسم 3.1 الملائم باستخدام lme4 هو كما يلي:

R> summary(glmer(abundance ~ Zone + Year + (Species + 0 | ID),
+ family = "poisson", data = wf.ex))
Generalized linear mixed model fit by maximum likelihood (Laplace
        Approximation) ['glmerMod']
    Family: poisson ( log )
Formula: abundance ~ Zone + Year + (Species + 0 | ID)
            Data: wf.ex
            AIC BIC logLik deviance df.resid
        1310.5 1336.1 -648.3 1296.5 277
Scaled residuals:
            Min 1Q Median 3Q Max
-1.38779 -0.67079 0.06129 0.43556 1.58605
Random effects:
    Groups Name Variance Std.Dev. Corr
    ID SpeciesTorsk 0.7603 0.8719
                SpeciesTanglake 0.9839 0.9919-0.74
Number of obs: 284, groups: ID, 142
Fixed effects:

begin{tabular}{lrrrrr} 
& Estimate & Std. Error & z & value & $operatorname{Pr}(>|z|)$ \
(Intercept) & 0.63001 & 0.10942 & 5.758 & $8.52 mathrm{e}-09$ & $* * *$ \
ZoneN & 0.07242 & 0.12807 & 0.565 & 0.57174 & \
ZoneS & -0.57875 & 0.19527 & -2.964 & 0.00304 & $* *$ \
Year2010 & 0.57457 & 0.10360 & 5.546 & $2.92 mathrm{e}-08$ & $* * *$
end{tabular}
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
                (Intr) ZoneN ZoneS
ZoneN -0.343
ZoneS -0.525-0.014
Year2010-0.493 0.057-0.130

ملخص النموذج الملائم باستخدام glmmTMB هو كما يلي:

R> summary(glmmTMB(abundance ~ Zone + Year + (Species + 0 | ID),
+ family = "poisson", data = wf.ex))
    Family: poisson ( log )
Formula: abundance ~ Zone + Year + (Species + 0 | ID)
Data: wf.ex

Random effects:
Conditional model:

begin{tabular}{lllll} 
Groups & Name & Variance & Std.Dev. & Corr \
ID & SpeciesTorsk & 0.7603 & 0.8719 & \
& SpeciesTanglake & 0.9839 & 0.9919 & -0.74
end{tabular}
Number of obs: 284, groups: ID, 142
Conditional model:

begin{tabular}{lrrrrl} 
& Estimate & Std. Error z value & $operatorname{Pr}(>|z|)$ & \
(Intercept) & 0.63000 & 0.10942 & 5.758 & $8.53 e-09$ & $* * *$ \
ZoneN & 0.07243 & 0.12807 & 0.566 & 0.57170 & \
ZoneS & -0.57876 & 0.19528 & -2.964 & 0.00304 & $* *$ \
Year2010 & 0.57457 & 0.10360 & 5.546 & $2.92 e-08$ & $* * *$
end{tabular}
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

إعادة تمثيل بارامترية لاختبار تفاعلات المنطقة والسنة لبيانات مزرعة الرياح. يتم تقدير القيمة من خلال مقارنة إحصائية نسبة الاحتمال الملحوظة بالتوزيع المحاكى لإحصائية الاختبار تحت فرضية العدم. يتم تجاهل تكرارات إعادة التمثيل التي فشلت في التقارب.

R> LRobs <- 2 * logLik(wf.glmm) - 2 * logLik(wf.glmm.null)
R> library("boot")
R> lrt.fun <- function(data) {
+ library("glmmTMB")
+ null <- try(glmmTMB(abundance ~ Zone + Year +
+ diag(Zone + Year|Species) +
+ (1|Station) + rr(Species + 0 | ID, d = 2),
+ family = "poisson", data = data))
+ alt <- try(glmmTMB(abundance ~ Zone * Year + diag(Zone * Year|Species) +
+ (1|Station) + rr(Species + 0 | ID, d = 2),
+ family = "poisson", data = data))
+ LR <- tryCatch({2 * logLik(alt) - 2 * logLik(null)},
+ error = function(e) {NA})
+ return(LR)
+ }
R> sim.abund <- function(data, mle) {
+ library("glmmTMB")
+ out <- data
+ out$abundance <- simulate(mle)$sim_1
+ out
+ }
R> wf.boot <- boot(data = windfarm, ran.gen = sim.abund, lrt.fun,
+ mle = wf.glmm.null, sim = "parametric", R = 1000, parallel = "snow",
+ ncpus = 4)
R> p <- (sum(wf.boot$t[,1] >= LRobs, na.rm = TRUE) + 1)/(1000 + 1)

انظر الشكل 5 والشكل 6.

انظر الشكل 7.

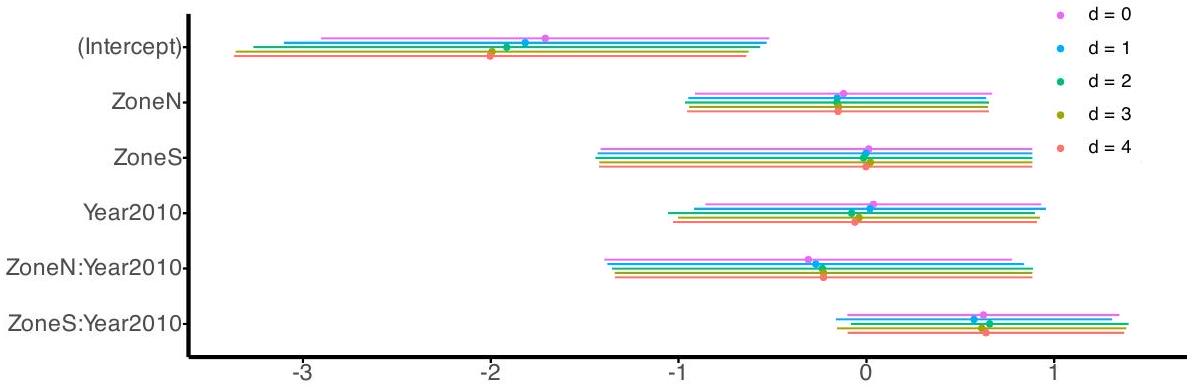
الشكل 7: تقديرات شرطية لمتغيرات المدرسة حسب البلد من التأثير العشوائي ذو الرتبة المخفضة في نموذج PIRLS.

مايف مكغيللي كادي، ديفيد آي. وارتون
جامعة UNSW سيدني
مدرسة الرياضيات والإحصاء ومركز أبحاث التطور والبيئة
NSW 2052، أستراليا
البريد الإلكتروني: m.mcgillycuddy@unsw.edu.au

غوردانا بوبوفيتش
جامعة UNSW سيدني
مركز الإحصائيات، مركز مارك وينرايت التحليلي
NSW 2052، أستراليا

بنجامين م. بولكر
جامعة مكماستر
قسم الرياضيات والإحصاء
1280 الشارع الرئيسي الغربي
هاميلتون، أونتاريو L8S 4K1، كندا

Keywords: mixed models, R.

When fitting a mixed effects model, it is often necessary to use a multivariate random effect with a non-diagonal covariance matrix in order to introduce sets of correlated parameters to a model. This approach is needed, for example, when fitting random-slopes models (Bolker et al. 2009; Asar, Bolin, Diggle, and Wallin 2020), to account for correlation between the slope coefficient(s) and intercept terms, and when using random effects to induce correlation in multivariate data (Coull and Agresti 2000; Pollock et al. 2014, for example). Without imposing structure on the variance-covariance matrix, the number of parameters that need to be estimated increases quadratically with the dimension of the random effect (specifically, parameters need to be estimated for an unstructured covariance matrix), and estimation quickly becomes challenging as gets larger.

For example, in Section 3.1 we describe a study of the effect of wind farms on fish assemblages, where we count individuals of multiple species at several sites. We wish to use multivariate random effect to estimate correlation across species. We can do this using a mixed model fitted using the lme4 package (Bates, Mächler, Bolker, and Walker 2014) in R (R Core Team 2024) as follows:

R> glmer(abundance ~ Zone + Year + (Species + 0 | ID), family = "poisson",
+ data = windfarm)

or equivalently, using the glmmTMB package (Brooks et al. 2017):

R> glmmTMB(abundance ~ Zone + Year + (Species + 0 | ID), family = "poisson",
+ data = windfarm)

We show in Appendix A that if there are only two species in the data set then this approach is reasonable (and these two lines of code produce identical answers, up to machine error), but convergence issues start to be seen when there are three or more species. The complete data set that we wish to analyse has nine species, and similar types of data frequently involve many more species, sometimes thousands (Niku, Hui, Taskinen, and Warton 2019).
One common way to deal with high dimensionality is to use a reduced-rank approach, making simplifying assumptions that reduce the dimension of the problem to . Reduced-rank approaches have seen considerable use in bioinformatics (e.g., Smith, Cullis, and Thompson 2001; Buettner et al. 2015) and spatial statistics (Cressie and Johannesson 2008; Banerjee, Gelfand, Finley, and Sang 2008). A reduced-rank approach to fitting a multivariate random effect involves writing it as a linear combination of latent variables, often referred to as a factor analytical model (Bartholomew, Knott, and Moustaki 2011); in the case of exponential family responses, it is sometimes called a generalized latent variable model (GLVM: Skrondal and Rabe-Hesketh 2004).
GLVMs have been used frequently in ecology and the social sciences, early examples being models of the presence-absence of fish species (Walker and Jackson 2011) and of polytomous party choice and rankings data (Skrondal and Rabe-Hesketh 2003). GLVMs can be technically challenging to fit, but there are a number of dedicated software solutions. The gllamm package (Rabe-Hesketh, Skrondal, and Pickles 2004) in Stata (StataCorp 2023) uses adaptive Gaussian quadrature to integrate out the latent variables. Early software written in R , with ecologists in mind, used Bayesian Markov chain Monte Carlo (Hui 2016; Ovaskainen et al. 2017). Substantially faster fits can be obtained using a Laplace (Huber, Ronchetti, and Victoria-Feser 2004; Niku, Warton, Hui, and Taskinen 2017) or variational approximation (Hui, Warton, Ormerod, Haapaniemi, and Taskinen 2017) to the marginal likelihood, as implemented in the R package gllvm (Niku et al. 2019). These tools were written with a particular model in mind, where a multivariate random intercept is used to induce correlation across many responses, and fixed effects are used to relate the linear predictor to measured variables, although there have been some extensions to relax this constraint in different ways (Van der Veen, Hui, Hovstad, Solbu, and O’Hara 2021; Niku, Hui, Taskinen, and Warton 2021). However, this software is unable to handle a range of common sampling designs. An example considered in Section 3.2 is when the multivariate random effect has covariates that may vary across and within clusters.
In this paper we add reduced-rank functionality to the glmmTMB package (Brooks et al. 2017) for flexible mixed effects models that can include factor analytic terms, for multivariate
random effects of large dimension. The glmmTMB package, available from the Comprehensive R Archive Network (CRAN) at https://CRAN.R-project.org/package=glmmTMB, is built as an extension to lme4 (Bates et al. 2014), widely used in the applied sciences for problems involving a range of study designs, including multi-level and repeated measures designs. The glmmTMB package uses a similar interface to lme4 but exploits automatic differentiation for faster estimation of mixed effects models (Brooks et al. 2017). By adding reduced-rank functionality to glmmTMB, we enrich the class of mixed models that can be fitted to include multivariate random effects with much larger dimension than was previously possible, such that we can now routinely fit random effects of dimension in the hundreds, or perhaps in the thousands. This new class of models includes, for example, GLVMs with functionality for any of the study designs that can be analysed using lme4, including multi-level or repeated measures designs.
Section 2 provides an overview of the generalized linear mixed model, the factor analytic extensions to handle multivariate random effects of high dimension, and the estimation approach used in glmmTMB to fit such models. We describe the usage of glmmTMB to fit reduced-rank multivariate random effects. We analyse two different data sets, from ecology and the social sciences, in Section 3. Section 4 concludes the paper.

We start by introducing a generalized linear mixed model and the factor analytic variant we use to handle multivariate random effects with large dimension. Then we discuss the estimation process for these models and the interface to fit reduced-rank multivariate random effects as implemented in glmmTMB.

Let be the response for observational units in cluster . A vector of fixed effect covariates, , and random effect covariates, , may also be recorded for each unit. For a generalized linear mixed model (GLMM), conditional on the vector of random effects, , and the vector of parameters, (defined below), the responses are assumed to come from the exponential family of distributions, where and are known functions that depend on the chosen distribution are canonical parameters, and is a dispersion parameter. Then the mean response, denoted as , regressed against the fixed and random covariates can be specified as

where . is a -dimensional vector of regression coefficients related to the covariates, , and is the vector of random effect covariates. The unconditional distribution of the random effects, or cluster level errors, , is assumed to follow a multivariate normal distribution with mean zero and a parameterized variance-covariance matrix, , i.e., . The variance-covariance matrix, , controls the variances of and correlations between units in clusters. The most flexible option for is an unstructured variance-covariance matrix, which requires parameters. For models with large multivariate random effects, this flexibility becomes a problem,
with the number of parameters in increasing quadratically with the size of the random effect, .
A reduced-rank approach to fit a multivariate random effect involves expressing it as a linear function of latent variables:

where is a vector of latent variables, each of which is independent and standard normal, and is a matrix of factor loadings. The latent variables have a zero mean and unit variance, without loss of generality. Upper triangular elements of are set to zero to assist with parameter identifiability, without loss of generality. Finally, we let denote the complete set of model parameters.
Given these definitions, the multivariate random effect is distributed as

which is a reduced-rank approximation of , as often seen in factor analytic models (Bartholomew et al. 2011; Niku et al. 2017). This approach makes it possible to fit large multivariate random effects, because the number of parameters required in the variancecovariance matrix of is now , which (for fixed ) increases only linearly with .

Conditional on the latent variables, , responses are assumed to be independent, hence . As the latent variables are not observed, they are integrated out, leading to the marginal log-likelihood:

In some cases this expression can be explicitly solved and expressed in closed form, but for non-normal distributions it does not generally have a closed form. A number of estimation methods have been proposed to approximate the marginal likelihood including Laplace approximation, numerical integration using adaptive quadrature (Skrondal and Rabe-Hesketh 2004), Monte Carlo integration (Hui, Taskinen, Pledger, Foster, and Warton 2015) and more recently variational approximation (Hui et al. 2017).
We focus on the Laplace approximation of the marginal likelihood, which is widely used for GLMMs (Raudenbush, Yang, and Yosef 2000) as well as GLVMs (Huber et al. 2004; Niku et al. 2017). By writing Equation 3 in the form , where

we can apply Laplace’s method for integral approximation around its mode, . Assuming maximizes , the approximation is derived by expanding as a second order Taylor series around the mode, . Following Huber et al. (2004), a Laplace approximation of the marginal log-likelihood function of the GLVM defined in Equation 1
can be written as

where

and is the maximum of .
In glmmTMB we maximize a Laplace approximation of the marginal log-likelihood obtained from the package Template Model Builder (TMB) (Kristensen, Nielsen, Berg, Skaug, and Bell 2015) in R (or more precisely, minimize the negative log-likelihood). TMB evaluates the Laplace approximation and its derivatives using automatic differentiation. Any gradientbased optimization method available in R can be used to do the maximization, by default glmmTMB uses nlminb(). TMB then uses the generalized delta method to calculate marginal standard deviations of fixed and random effects (Kass and Steffey 1989).

A reduced rank covariance structure is specified in glmmTMB using rr. For example, suppose x is a matrix of predictors with columns, and that we want to apply -dimensional random coefficients that take different values for different levels of a grouping variable group to predictors x . To specify that these random coefficients are drawn from a multivariate normal distribution whose variance-covariance matrix has rank two (that is, they can be written as a linear combination of two independent latent variables) we use the rr random effect structure in the formula as follows
rr(x | group, 2)
So for example to model the mean of a response ( y ) as a function of x and let the coefficients of x vary randomly among groups as a function of two latent variables, the formula is
group, 2)
The non-negative integer after the comma in the formula specifies the number of latent variables, or rank, of the variance-covariance matrix of the multivariate random effects, which defaults to . The choice of the number of latent variables can be seen as a model selection problem (Hui et al. 2015). Model selection tools including cross-validation, or information criteria can be used to select the rank (Bartholomew et al. 2011).
One issue with fitting a factor-analytic model is that the likelihood function is often multimodal, which may lead to convergence to a local maximum. To overcome this we include a data-driven method based on the work of Niku et al. (2019) to initialize values for parameters so that the maximizing algorithm starts closer to the global maximum. The default in glmmTMB sets parameter values to zero, or one for fixed-effect parameters for some link functions. To control the algorithm used for initializing parameters a start_method argument, specified as a list with components method and jitter.sd, has been added to
glmmTMBControl(). Setting method = “res” fits a generalized linear model (GLM) to the data to obtain estimates of the fixed parameters, which are then used as starting values of the fixed parameters. From the fitted model, residuals are calculated for models using the Poisson, negative binomial, and binomial families using the method due to Dunn and Smyth (1996), while the internal function dev.residuals is used for other families. Starting values for latent variables, , and factor loadings, , are obtained by applying a reduced-rank model to the residuals from the fitted GLM. To check stability of a solution, we suggest repeating a fit multiple times and adding variation to the starting values of latent variables when method “res” by setting jitter.sd , or similar, to jitter starting values for by a normal variate with mean zero and standard deviation jitter.sd.
More examples of implementing the rr structure are shown in Section 3. Information on the reduced-rank and other available variance-covariance structures in glmmTMB can be found in vignette(“covstruct”, package = “glmmTMB”).

We present two applications to illustrate the use of a reduced-rank covariance structure in glmmTMB. The first example, using wind farm data, fits a generalized latent variable model to multivariate abundance data, a form of data often gathered for ecological studies. The second example presents a random-slopes model, with many random slopes, applied to data from the Progress in International Reading Literacy Study (PIRLS).

The wind farm data were gathered for the Lillgrund offshore wind farm off the southern coast of Sweden, to study the effects of the wind farm on the demersal fish community (Bergstrom, Sundqvist, and Bergstrom 2013). This is one of the few large-scale studies assessing the effects of offshore wind farms over a long period of time, and on more than one individual fish species. This study exemplifies a BACI (before-after-control-impact) design; abundance of fish was measured before (2003) and after construction (2010), in the wind farm zone and in two reference zones (southern and northern reference zones). Sampling occurred at fishing stations within each zone; stations remained the same throughout the study. Stations which were not sampled in both time periods were omitted. The raw abundance data (Figure 1) does not show an obvious windfarm effect, although species Strensnultra and Oxsimpa may show before-after differences for the south and north zones respectively. Because we are interested in the effect of wind farms, which were established between the sampling times, our interest is in the interaction between zone and year.
A multivariate random effect is required to account for correlation in species responses within a sample – we expect correlation across species due to inter-specific interactions, or response to unobserved environmental conditions (Warton et al. 2015) and we wish to be able to estimate positive or negative correlations. We do not have any a priori structure for this correlation, and for nine species we would require 45 parameters to estimate the variance-covariance matrix among species. Thus we would expect considerable instability in the fit, especially for correlation terms involving rarer species. In comparison, a reduced-rank covariance structure of rank two would require only 17 parameters.
We model abundances, , as conditionally Poisson with mean , observed at

samples, for species, at stations ( ) such that:

where are vectors of environmental covariates specifying the intercept, zone, year and the interaction of zone and year, and is a vector of fixed coefficients. We include a multivariate random effect (with ) on the environmental variables, to allow the effects of each covariate to vary across species. The random intercept for station, is intended to account for paired sampling at stations, with data collected at two time points for each station. We assume each of these random effects is independent of all others and of the response (conditional on ). The correlation between species is induced by the reduced-rank random effect, , assumed to satisfy

where is a pair (dimension ) of latent variables, and the vector contains the corresponding factor loadings. This model can then be fitted using the following command:

R> glmmTMB(abundance ~ Zone * Year + diag(Zone * Year | Species) +
+ (1 | Station) + rr(Species + 0 | ID, 2), family = "poisson",
+ control = glmmTMBControl(start_method = list(method = "res")),
+ data = windfarm)

The intercept was excluded from the reduced-rank random effect term (using Species + 0 as the varying term) in order to aid interpretability of the correlation matrix discussed

below. The estimated correlation matrix of the reduced-rank multivariate random effect can be obtained from the output of the summary method, or using the VarCorr method, in the same way that the estimated values for any variance-covariance matrix are returned by

The estimated correlation matrix of the random intercept for the wind farm data, using the rank-two model specified above, is as follows:

These correlations are residual correlations between species not accounted for by the covariates and other random effects in the model. For example, the correlation between species Oxsimpa and AL is 0.89 after controlling for the fixed and random covariates in the model. Note that these correlations are on the linear predictor scale (in this case the log scale), and the actual correlation observed in data is much weaker than these values, because of Poisson noise introduced by Equation 4. The marginal correlation structure is singular (for ) as it is approximated from Equation 2, where is reduced rank; this is not problematic as the estimates of the factor loadings, , and latent variables, , are used in further analysis. Attempting to instead fit this model using an unstructured covariance structure runs into convergence problems; the data are of insufficient quality to support estimation of 45 separate variance parameters. To test if the construction of an offshore wind farm had a significant effect on fish abundance, a parametric bootstrap analysis was conducted to test the Zone by Year interaction in both the fixed and random effect terms (code provided

in Appendix B). A parametric bootstrap analysis was chosen over asymptotic tests such as Wald and likelihood ratio tests, because the asymptotic distributions of these tests are usually unknown for mixed models (Bolker et al. 2009). The interactions were significant (LR ), indicating that for at least one of the species, mean abundance across zones has changed (in a relative sense) since construction of the wind farm (Figure 2). After controlling for other covariates, Oxsimpa densities were clearly larger in the North zone than in the Wind Farm zone (i.e., the contrast is clearly positive, Dushoff, Kain, and Bolker 2019), while the South-Wind Farm contrast is negative and close to zero. Judging from Figure 1, this effect probably has more to do with an increase in Oxsimpa in the North Zone, rather than an effect of wind farms. To visualize the correlations between species, an ordination biplot can be produced from the estimated latent variables and factor loadings (Figure 3). An unconstrained ordination biplot (Figure 3a), plotting the latent variables from a model without and fixed effects predictors, shows a separation in the latent variables by Zone and Year, emphasizing the importance of these variables. Adding factor loadings to the plot shows us how species vary across sites, with higher abundance of a species tending to be found in sites in the same direction as the species, with respect to the origin. Oxsimpa for example could be expected to be found in high numbers in the North Zone in 2010, and Stensnultra could expect to be found in high numbers in the South Zone, especially in 2003. Figure 1 corroborates both of these results. The relative positions of the species also gives information about their correlation – because Oxsimpa and Stensnultra are negatively correlated they appear far from the origin but at opposite sides of the ordination, whereas the positively correlated Oxsimpa and Skrubbskadda are neighbors in the ordination plot.

After fitting the model in Equation 4, which controls for the effects of Zone, Year, their interaction, and Station, the clustering patterns by zone and sampling time disappear (Figure 3b). The points lie much closer together, with smaller loadings, reflecting the fact that adding predictors to the model substantially reduces the magnitude of the variance-covariance terms. This verifies that the prevailing patterns seen in the unconstrained ordination, and hence in the fish communities being sampled, can be explained by where and when samples were taken.

Progress in international reading literacy study (PIRLS) is a large-scale international research project measuring reading literacy in children aged nine to ten years (Martin, Mullis, and Hooper 2017). PIRLS has been conducted every five years since 2001, with 61 countries participating in PIRLS 2016. Published studies have proposed that school variables are more important than family background in determining academic achievement in developing countries (Heyneman and Loxley 1982). However, more recent studies report conflicting results which show that these variables are similar across countries (Marôco 2021), with authors proposing this homogenization may be due to the increase of mass schooling. Therefore, we are interested in exploring how the effect of school variables on literacy scores of students vary by country.
We propose that students from economically disadvantaged schools (Eco_disad) with a library containing more books (Size_lib) have higher literacy scores than students from a school with no library, but the difference in literacy scores will be less when students are from schools of higher economic background i.e., there is an interaction between the two school variables. Further, we would like to know how the interactive effect of these school-level variables will vary by country, hence we want to fit a random slopes model, with different Eco_disad:Size_lib effects for each country. Both Eco_disad and Size_lib are categorical variables with four levels, hence we need 15 parameters to characterize their joint effect and a 15-dimensional random effect in the model. Estimating an unstructured variance-covariance matrix would require 136 parameters. In contrast, for a reduced-rank covariance structure of rank three, only 42 parameters are required – AIC was used to select the rank of three.
We consider the model for literacy score, , for student , in school and country as follows:

where are vectors of covariates relating to school factors and is the vector of fixed coefficients. The random intercept for school, , accounts for heterogeneity of average literacy scores between schools. The random intercept and slopes of school variables allow the school variables to vary by country where is the full matrix of factor loadings, and is the residual error.
This model can be fitted in glmmTMB using the following command:

R> glmmTMB(Overall ~ Size_lib * Eco_disad + (1 | School) +
+ rr(Size_lib * Eco_disad | Country, d = 3),
+ control = glmmTMBControl(start_method = list(method = "res")),
+ family = gaussian(), data = pirls)

The starting algorithm for initializing parameters specified in the control argument is needed when fitting this model, otherwise there will be convergence issues.
The conditional estimates of the school random effects by country are complex (Figure 7): we will focus on a particular contrast between Bulgaria and Georgia (colored results in Figure 7). This comparison is of interest because these two countries appear to have different patterns of library-economic disadvantage interaction (Figure 4). The most obvious pattern shown in the interaction plot (Figure 4) is that students from Bulgaria (blue lines) have

higher literacy scores than students from Georgia (green lines). However, Bulgarian students’ literacy scores also appear to decrease with increasing economic disadvantage; furthermore, the rate of decline appeared to be slower for better resourced-schools (i.e., those with more books). These patterns, expected from general socioeconomic principles, were generally observed across many countries. Georgia appears unusual: economic disadvantage had little overall effect on literacy scores, and the effects of library size were opposite from those expected – schools with large libraries appeared to have higher literacy scores than those with small libraries when schools were well off, but library size made little difference for strongly disadvantaged schools.

In this article, we introduced a new variance-covariance structure, rr, in glmmTMB, to add reduced-rank functionality to mixed models. This feature broadens the scope of models that can be fitted by writing a large dimensional multivariate random effect as a linear combination of latent variables, a more parsimonious structure that can be more readily estimated when the dimension of the random effect is large. In Section 1, we discussed available tools in R , such as gllvm, which also fit latent variable models. These packages were developed with a primary focus on models for ecological data. The key advantage of our work is adding a factor analytic term to the suite of random effects structures already available in glmmTMB, such that generalized latent variable models can now be fitted to complex study designs, using a familiar interface.

We presented two applications to illustrate the use of a reduced-rank approach. In both examples the dimension of the random effect was moderate -9 and 15 for these two examples – but this was already too large to be practically estimable, necessitating the use of a reduced-rank
model. Reduced-rank models are capable of fitting random effects of very large dimension: for example, Niku et al. (2019) fitted a GLVM with a dimension of 985 to a microbial data set. When fitting models to larger data sets, difficulties can be encountered; for example, in ecology the number of species is often large compared to the number of samples. In situations like this, it may be useful to fit a model multiple times with different starting values for the parameters, and the fit with the highest log-likelihood value is considered the best fitting model.

The reduced-rank model contributes to the model-simplification toolbox, allowing for a more parsimonious random effect which may be necessary for some study designs (Matuschek, Kliegl, Vasishth, Baayen, and Bates 2017). Currently, available methods for simplification are assuming a diagonal variance-covariance matrix, with homogeneous or heterogeneous variances; assuming compound symmetry; or assuming some specific form of structure (AR(1), Toeplitz, etc.). All of these structures are available in glmmTMB. Another alternative for controlling complexity is some form of shrinkage towards zero on the factor loadings as proposed in a Bayesian framework (Bhattacharya and Dunson 2011).
A key step in applying a reduced-rank random effect is choosing the rank . Different strategies may be used for choosing , depending on the analysis goal. In the wind farm application, we used a two-dimensional biplot to visualize correlations across species (Figure 3) and for this purpose was appropriate. In our second application, the PIRLS study, our goal was to make inferences about correlated fixed effects, and the reduced rank approach was used to estimate this correlation. In this case we used information criteria to choose a value for that gave us a good fit to the data. We found that estimates and confidence intervals for the fixed effect estimates were robust to different choices of rank (see supplementary material, Figure 5 and Figure 6). The extent to which fixed effects can change as covariance assumptions on random effects change is a function of how much the fitted covariance structure actually changes. Factor analytical terms offer diminishing returns in terms of changes to as increases, so there is greatest capacity for changes in interpretation when is small (in practice we have seen qualitatively important changes only for , as in Figure 6).
The reduced-rank structure has an interesting point of difference from other approaches to fitting a multivariate random effect in that it permits a singular variance-covariance matrix, or more precisely, it assumes singularity. Other methods of fitting correlated random effects require a positive-definite variance-covariance matrix and return warnings when encountering (near-)singularity, an issue circumvented here by assuming a reduced-rank structure.
Our examples give just a few tastes of how reduced rank variance-covariance structures can be used in mixed modelling, where it has previously been technically difficult to fit models with random effects of high dimension. Some example areas where we see potential use for this approach include factor analysis with multi-level designs or repeated measures, and genotype-by-environment interaction analysis (Piepho 1997; Smith et al. 2001). We see a myriad of potential applications, and look forward to seeing how this new tool is used in practice.

Asar Ö, Bolin D, Diggle PJ, Wallin J (2020). “Linear Mixed Effects Models for Non-Gaussian Continuous Repeated Measurement Data.” Journal of the Royal Statistical Society C, 69(5), 1015-1065. doi:10.1111/rssc. 12405.

Banerjee S, Gelfand AE, Finley AO, Sang H (2008). “Gaussian Predictive Process Models for Large Spatial Data Sets.” Journal of the Royal Statistical Society B, 70(4), 825-848. doi:10.1111/j.1467-9868.2008.00663.x.

Bartholomew DJ, Knott M, Moustaki I (2011). Latent Variable Models and Factor Analysis: A Unified Approach. John Wiley & Sons.

Bates D, Mächler M, Bolker BM, Walker S (2014). “Fitting Linear Mixed-Effects Models Using lme4.” Journal of Statistical Software, 67(1), 1-48. doi:10.18637/jss.v067.i01.

Bergstrom L, Sundqvist F, Bergstrom U (2013). “Effects of an Offshore Wind Farm on Temporal and Spatial Patterns in the Demersal Fish Community.” Marine Ecology Progress Series, 485, 199-210. doi:10.3354/meps10344.

Bhattacharya A, Dunson DB (2011). “Sparse Bayesian Infinite Factor Models.” Biometrika, 98(2), 291-306. doi:10.1093/biomet/asr013.

Bolker BM, Brooks ME, Clark CJ, Geange SW, Poulsen JR, Stevens MHH, White JSS (2009). “Generalized Linear Mixed Models: A Practical Guide for Ecology and Evolution.” Trends in Ecology & Evolution, 24(3), 127-135. doi:10.1016/j.tree.2008.10.008.

Brooks ME, Kristensen K, Van Benthem KJ, Magnusson A, Berg CW, Nielsen A, Skaug HJ, Mächler M, Bolker BM (2017). “glmmTMB Balances Speed and Flexibility among Packages for Zero-Inflated Generalized Linear Mixed Modeling.” The Journal, 9(2), 378-400. doi:10.32614/rj-2017-066.

Buettner F, Natarajan KN, Casale FP, Proserpio V, Scialdone A, Theis FJ, Teichmann SA, Marioni JC, Stegle O (2015). “Computational Analysis of Cell-to-Cell Heterogeneity in Single-Cell RNA-Sequencing Data Reveals Hidden Subpopulations of Cells.” Nature Biotechnology, 33(2), 155-160. doi:10.1038/nbt. 3102.

Coull BA, Agresti A (2000). “Random Effects Modeling of Multiple Binomial Responses Using the Multivariate Binomial Logit-Normal Distribution.” Biometrics, 56(1), 73-80. doi:10.1111/j.0006-341x.2000.00073.x.

Cressie N, Johannesson G (2008). “Fixed Rank Kriging for Very Large Spatial Data Sets.” Journal of the Royal Statistical Society B, 70(1), 209-226. doi:10.1080/10618600. 1996. 10474708.

Dunn PK, Smyth GK (1996). “Randomized Quantile Residuals.” Journal of Computational and Graphical Statistics, 5(3), 236-244. doi:10.1080/10618600.1996.10474708.

Dushoff J, Kain MP, Bolker BM (2019). “I Can See Clearly Now: Reinterpreting Statistical Significance.” Methods in Ecology and Evolution, 10(6), 756-759. doi:10.1111/ 2041-210x. 13159.

Heyneman SP, Loxley WA (1982). “Influences on Academic Achievement Across High and Low Income Countries: A Re-Analysis of IEA Data.” Sociology of Education, pp. 13-21. doi:10.2307/2112607.

Huber P, Ronchetti E, Victoria-Feser MP (2004). “Estimation of Generalized Linear Latent Variable Models.” Journal of the Royal Statistical Society B, 66(4), 893-908. doi:10. 1111/j.1467-9868.2004.05627.x.

Hui FKC (2016). “Boral – Bayesian Ordination and Regression Analysis of Multivariate Abundance Data in R.” Methods in Ecology and Evolution, 7(6), 744-750. doi:10.1111/ 2041-210x. 12514.

Hui FKC, Taskinen S, Pledger S, Foster SD, Warton DI (2015). “Model-Based Approaches to Unconstrained Ordination.” Methods in Ecology and Evolution, 6(4), 399-411. doi: 10.1111/2041-210x. 12236.

Hui FKC, Warton DI, Ormerod JT, Haapaniemi V, Taskinen S (2017). “Variational Approximations for Generalized Linear Latent Variable Models.” Journal of Computational and Graphical Statistics, 26(1), 35-43. doi:10.1080/10618600.2016.1164708.

Kass RE, Steffey D (1989). “Approximate Bayesian Inference in Conditionally Independent Hierarchical Models (Parametric Empirical Bayes Models).” Journal of the American Statistical Association, 84(407), 717-726. doi:10.1080/01621459.1989.10478825.

Kristensen K, Nielsen A, Berg CW, Skaug H, Bell B (2015). “TMB: Automatic Differentiation and Laplace Approximation.” Journal of Statistical Software, Articles, 70(5), 1-21. doi: 10.18637/jss.v070.i05.

Marôco J (2021). “What Makes a Good Reader? Worldwide Insights from PIRLS 2016.” Reading and Writing, 34(1), 231-272. doi:10.1007/s11145-020-10068-8.

Martin MO, Mullis IVS, Hooper M (2017). “Methods and Procedures in PIRLS 2016.” URL https://timssandpirls.bc.edu/pirls2016/international-database/.

Matuschek H, Kliegl R, Vasishth S, Baayen H, Bates D (2017). “Balancing Type I Error and Power in Linear Mixed Models.” Journal of Memory and Language, 94, 305-315. doi:10.1016/j.jml.2017.01.001.

Niku J, Hui FKC, Taskinen S, Warton DI (2019). “gllvm: Fast Analysis of Multivariate Abundance Data with Generalized Linear Latent Variable Models in R.” Methods in Ecology and Evolution, 10(12), 2173-2182. doi:10.1111/2041-210x. 13303.

Niku J, Hui FKC, Taskinen S, Warton DI (2021). “Analyzing Environmental-Trait Interactions in Ecological Communities with Fourth-Corner Latent Variable Models.” Environmetrics, p. e2683. doi:10.1002/env. 2683.

Niku J, Warton DI, Hui FKC, Taskinen S (2017). “Generalized Linear Latent Variable Models for Multivariate Count and Biomass Data in Ecology.” Journal of Agricultural, Biological and Environmental Statistics, 22(4), 498-522. doi:10.1007/s13253-017-0304-7.

Ovaskainen O, Tikhonov G, Norberg A, Guillaume Blanchet F, Duan L, Dunson D, Roslin T, Abrego N (2017). “How to Make More Out of Community Data? A Conceptual Framework and Its Implementation as Models and Software.” Ecology Letters, 20(5), 561-576. ISSN 1461-0248. doi:10.1111/ele. 12757.

Piepho HP (1997). “Analyzing Genotype-Environment Data by Mixed Models with Multiplicative Terms.” Biometrics, pp. 761-766. doi:10.2307/2533976.

Pollock LJ, Tingley R, Morris WK, Golding N, O’Hara RB, Parris KM, Vesk PA, McCarthy MA (2014). “Understanding Co-Occurrence by Modelling Species Simultaneously with a Joint Species Distribution Model (JSDM).” Methods in Ecology and Evolution, 5(5), 397406. doi:10.1111/2041-210x. 12180.

Rabe-Hesketh S, Skrondal A, Pickles A (2004). “Generalized Multilevel Structural Equation Modeling.” Psychometrika, 69(2), 167-190. doi:10.1007/bf02295939.

Raudenbush SW, Yang ML, Yosef M (2000). “Maximum Likelihood for Generalized Linear Models with Nested Random Effects via High-Order, Multivariate Laplace Approximation.” Journal of Computational and Graphical Statistics, 9(1), 141-157. doi: 10.1080/10618600.2000.10474870.

R Core Team (2024). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.

Skrondal A, Rabe-Hesketh S (2003). “Multilevel Logistic Regression for Polytomous Data and Rankings.” Psychometrika, 68(2), 267-287. doi:10.1007/bf02294801.

Skrondal A, Rabe-Hesketh S (2004). Generalized Latent Variable Modeling: Multilevel, Longitudinal, and Structural Equation Models. Chapman & Hall/CRC.

Smith A, Cullis B, Thompson R (2001). “Analyzing Variety by Environment Data Using Multiplicative Mixed Models and Adjustments for Spatial Field Trend.” Biometrics, 57(4), 1138-1147. doi:10.1111/j.0006-341x.2001.01138.x.

StataCorp (2023). Stata Statistical Software: Release 18. StataCorp LLC, College Station.
Van der Veen B, Hui FKC, Hovstad KA, Solbu EB, O’Hara RB (2021). “Model-Based Ordination for Species with Unequal Niche Widths.” Methods in Ecology and Evolution, 12(7), 1288-1300. doi:10.1111/2041-210x. 13595.

Walker SC, Jackson DA (2011). “Random-Effects Ordination: Describing and Predicting Multivariate Correlations and Co-Occurrences.” Ecological Monographs, 81(4), 635-663. doi:10.1890/11-0886.1.

Warton DI, Blanchet FG, O’Hara RB, Ovaskainen O, Taskinen S, Walker SC, Hui FKC (2015). “So Many Variables: Joint Modeling in Community Ecology.” Trends in Ecology & Evolution, 30(12), 766-779. doi:10.1016/j.tree.2015.09.007.

Summary of the model for the wind farm example in Section 3.1 fitted using lme4 is as follows:

R> summary(glmer(abundance ~ Zone + Year + (Species + 0 | ID),
+ family = "poisson", data = wf.ex))
Generalized linear mixed model fit by maximum likelihood (Laplace
        Approximation) ['glmerMod']
    Family: poisson ( log )
Formula: abundance ~ Zone + Year + (Species + 0 | ID)
            Data: wf.ex
            AIC BIC logLik deviance df.resid
        1310.5 1336.1 -648.3 1296.5 277
Scaled residuals:
            Min 1Q Median 3Q Max
-1.38779 -0.67079 0.06129 0.43556 1.58605
Random effects:
    Groups Name Variance Std.Dev. Corr
    ID SpeciesTorsk 0.7603 0.8719
                SpeciesTanglake 0.9839 0.9919-0.74
Number of obs: 284, groups: ID, 142
Fixed effects:

begin{tabular}{lrrrrr} 
& Estimate & Std. Error & z & value & $operatorname{Pr}(>|z|)$ \
(Intercept) & 0.63001 & 0.10942 & 5.758 & $8.52 mathrm{e}-09$ & $* * *$ \
ZoneN & 0.07242 & 0.12807 & 0.565 & 0.57174 & \
ZoneS & -0.57875 & 0.19527 & -2.964 & 0.00304 & $* *$ \
Year2010 & 0.57457 & 0.10360 & 5.546 & $2.92 mathrm{e}-08$ & $* * *$
end{tabular}
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
                (Intr) ZoneN ZoneS
ZoneN -0.343
ZoneS -0.525-0.014
Year2010-0.493 0.057-0.130

The summary of the model fitted using glmmTMB is as follows:

R> summary(glmmTMB(abundance ~ Zone + Year + (Species + 0 | ID),
+ family = "poisson", data = wf.ex))
    Family: poisson ( log )
Formula: abundance ~ Zone + Year + (Species + 0 | ID)
Data: wf.ex

Random effects:
Conditional model:

begin{tabular}{lllll} 
Groups & Name & Variance & Std.Dev. & Corr \
ID & SpeciesTorsk & 0.7603 & 0.8719 & \
& SpeciesTanglake & 0.9839 & 0.9919 & -0.74
end{tabular}
Number of obs: 284, groups: ID, 142
Conditional model:

begin{tabular}{lrrrrl} 
& Estimate & Std. Error z value & $operatorname{Pr}(>|z|)$ & \
(Intercept) & 0.63000 & 0.10942 & 5.758 & $8.53 e-09$ & $* * *$ \
ZoneN & 0.07243 & 0.12807 & 0.566 & 0.57170 & \
ZoneS & -0.57876 & 0.19528 & -2.964 & 0.00304 & $* *$ \
Year2010 & 0.57457 & 0.10360 & 5.546 & $2.92 e-08$ & $* * *$
end{tabular}
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

A parametric bootstrap to test the interaction terms of zone and year for the wind farm data. The value is estimated by comparing the observed likelihood ratio statistic to the simulated distribution of the test statistic under the null hypothesis. Bootstrap replications which failed to converge are ignored.

R> LRobs <- 2 * logLik(wf.glmm) - 2 * logLik(wf.glmm.null)
R> library("boot")
R> lrt.fun <- function(data) {
+ library("glmmTMB")
+ null <- try(glmmTMB(abundance ~ Zone + Year +
+ diag(Zone + Year|Species) +
+ (1|Station) + rr(Species + 0 | ID, d = 2),
+ family = "poisson", data = data))
+ alt <- try(glmmTMB(abundance ~ Zone * Year + diag(Zone * Year|Species) +
+ (1|Station) + rr(Species + 0 | ID, d = 2),
+ family = "poisson", data = data))
+ LR <- tryCatch({2 * logLik(alt) - 2 * logLik(null)},
+ error = function(e) {NA})
+ return(LR)
+ }
R> sim.abund <- function(data, mle) {
+ library("glmmTMB")
+ out <- data
+ out$abundance <- simulate(mle)$sim_1
+ out
+ }
R> wf.boot <- boot(data = windfarm, ran.gen = sim.abund, lrt.fun,
+ mle = wf.glmm.null, sim = "parametric", R = 1000, parallel = "snow",
+ ncpus = 4)
R> p <- (sum(wf.boot$t[,1] >= LRobs, na.rm = TRUE) + 1)/(1000 + 1)

See Figure 5 and Figure 6.

See Figure 7.

Figure 7: Conditional estimates of school variables by country from the reduced-rank random effect in the PIRLS model.

Maeve McGillycuddy, David I. Warton
UNSW Sydney
School of Mathematics and Statistics and Evolution & Ecology Research Centre
NSW 2052, Australia
E-mail: m.mcgillycuddy@unsw.edu.au

Gordana Popovic
UNSW Sydney
Stats Central, Mark Wainwright Analytical Centre
NSW 2052, Australia

Benjamin M. Bolker
McMaster University
Department of Mathematics & Statistics
1280 Main Street West
Hamilton, Ontario L8S 4K1, Canada