DOI: https://doi.org/10.1080/00268976.2024.2306881
تاريخ النشر: 2024-02-12
رؤية شبكة التنسور لطرق هارتري متعددة الطبقات ومتعددة التكوين المعتمدة على الزمن
الملخص
طريقة هارتري متعددة الطبقات ومتعددة التكوينات المعتمدة على الزمن (ML-MCTDH) ومجموعة إعادة تنظيم مصفوفة الكثافة (DMRG) هما أداتان قويتان تُستخدمان بشكل رئيسي في مجالات علمية مختلفة. على الرغم من أن كلا الطريقتين تستندان إلى حالات الشبكة التنسورية، إلا أن لغات رياضية مختلفة تمامًا تُستخدم لوصفهما. هذا يحد بشدة من نقل المعرفة وأحيانًا يؤدي إلى إعادة اختراع أفكار معروفة جيدًا في المجال الآخر. هنا، نستعرض نظرية ML-MCTDH وDMRG باستخدام تعبيرات MCTDH ومخططات الشبكة التنسورية. نستنتج معادلات الحركة لـ ML-MCTDH باستخدام المخططات ونقارنها بخوارزميات DMRG المعتمدة على الزمن وغير المعتمدة على الزمن. كما نستعرض تقدمين حديثين مختارين. التقدم الأول يتعلق بتحسين دوال الجسيمات الفردية غير المشغولة في MCTDH، والتي تت correspond إلى إثراء الفضاء الفرعي في DMRG. التقدم الثاني يتعلق بالعثور على هياكل شجرية مثالية وتسليط الضوء على أوجه التشابه والاختلاف في الشبكات التنسورية المستخدمة في نظريات MCTDH وDMRG. نأمل أن يسهم هذا المساهمة في تعزيز تبادل الأفكار بشكل أكثر إنتاجية بين ML-MCTDH وDMRG.
المقدمة
II. الاقتراح متعدد الطبقات ومتعدد التكوينات المعتمد على الزمن هارتري
(2) بالنسبة لـ MCTDH مع مجموعة الأوضاع [103]،
| وصف | رمز | رموز بديلة | ||
| البعد الفيزيائي |
|
|
||
| حالة الأساس الفيزيائية (“البدائية”) |
|
|
||
| البعد الأساسي الفيزيائي |
|
|
||
| عدد الطبقات | ل | |||
| طبقة |
|
|||
| حالة أساس SPF |
|
|
||
| الموضع الأفقي في الطبقة
|
|
|
||
| موضع العقدة/SPF |
|
|
||
| موضع الطبقة والعقدة/SPF |
|
|
||
|
|
||||
| موضع موتر المعامل |
|
|
||
| بعدد العقد/الموتر/الموقع/أبعاد SPF |
|
|
||
| حجم السند/الرتبة/أساس SPF |
|
|
||
| حجم قاعدة SPF العامة |
|
|
||
| الحجم الإجمالي للأساس الذي يمثل SPF |
|
|||
| مؤشر SPF |
|
|
||
| مؤشر SPF المركب |
|
|||
| مؤشر SHF المركب |
|
|||
| موتر SPF/موقع |
|
|
||
| تكوين |
|
|
||
| وظيفة الثقب الواحد (SHF) |
|
|||
| تكوين SHF |
|
|
||
| جهاز عرض SPF |
|
|
||
| جهاز عرض SHF |
|
|||
| مصفوفة كثافة الجسيم الفردي |
|
|||
| مشغل الحقل المتوسط |
|
|||
| مشغل القياس |
|
|
||
| حد هاملتوني أحادي البعد |
|
(3) بالنسبة لـ ML-MCTDH،
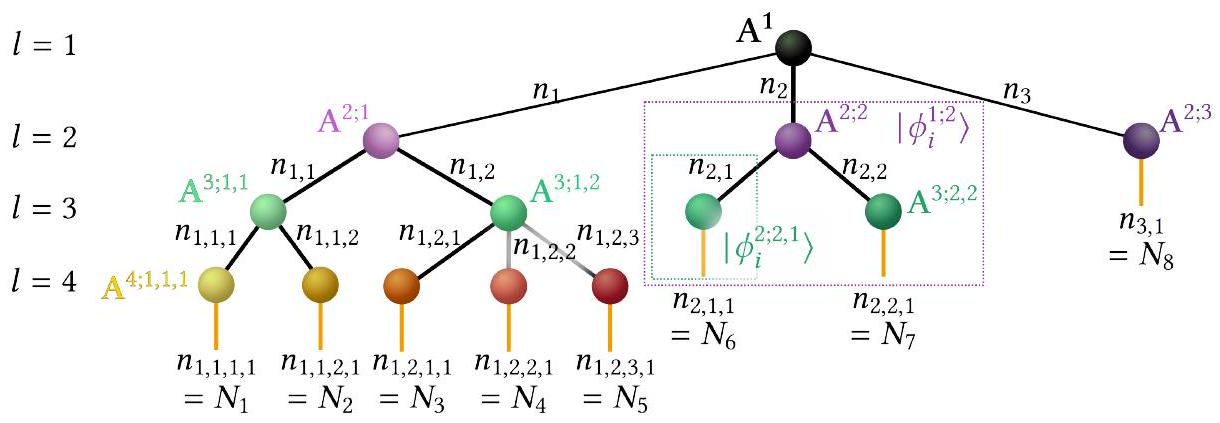
مسلحين بهذه التدوين المبسط، نقدم نظير SPFs، وظائف الثقب الواحد
في لغة DMRG التقليدية [4، 35، 51]، المعادلة (8) تت correspond إلى استخدام DMRG لموقع واحد وتوسيع الحالة من حيث كتلة النظام،
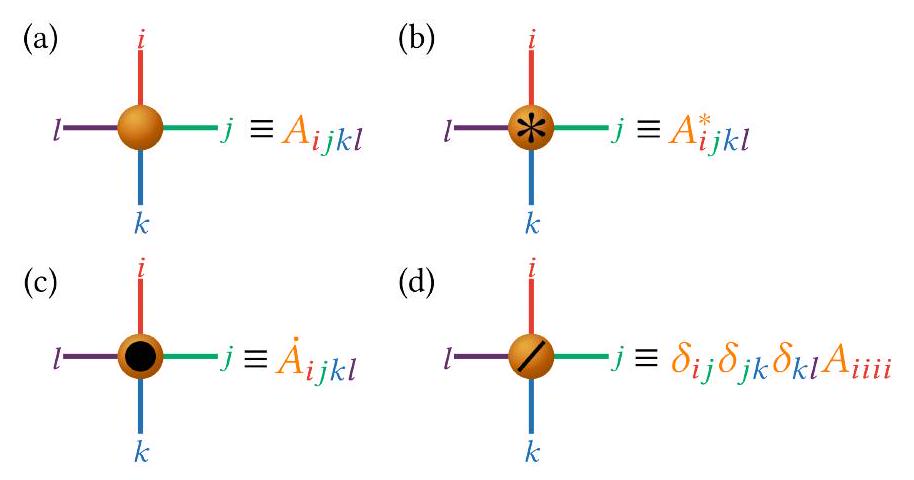

III. مخططات الشبكة التنسورية
الرابع. مخططات الشبكة التنسورية مقارنة بلغة MCTDH
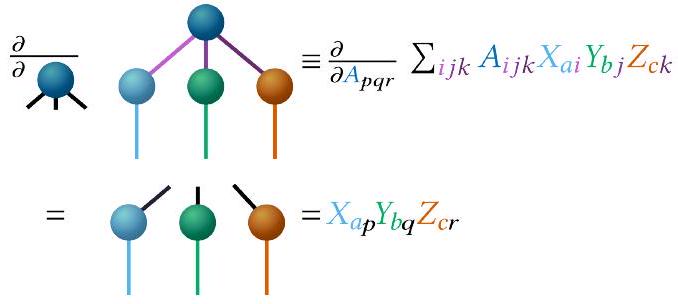
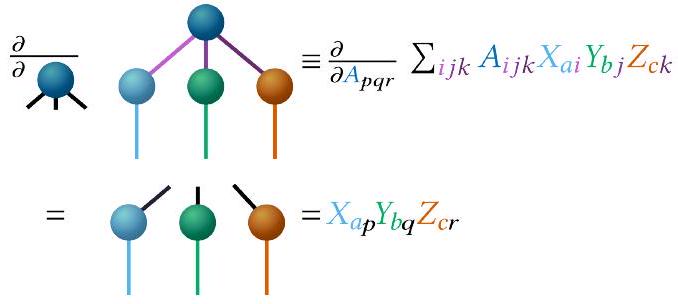
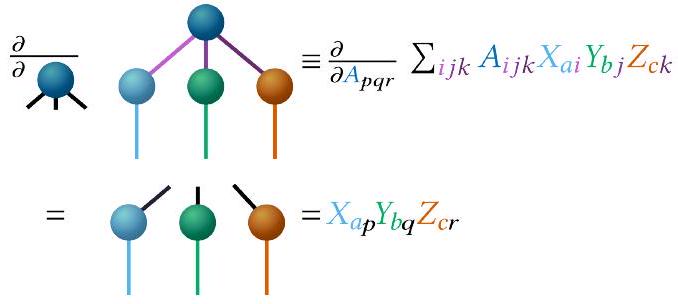


مثال على SHF

يسمح بتعريف تكراري لـ SHFs:
V. معادلات ML-MCTDH والاتصال بالرسوم البيانية

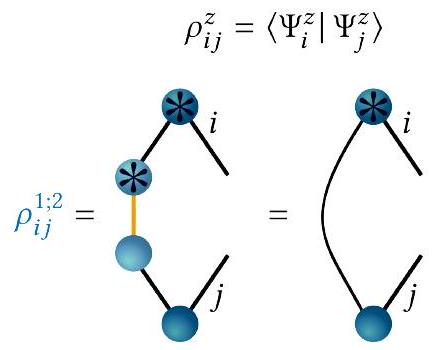
أ. مصفوفات الكثافة والحقول المتوسطة
ب. معادلات الحركة
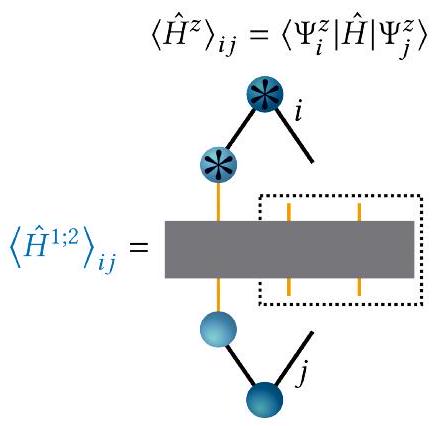
ج. بعض الأشكال الشائعة للهاميلتوني
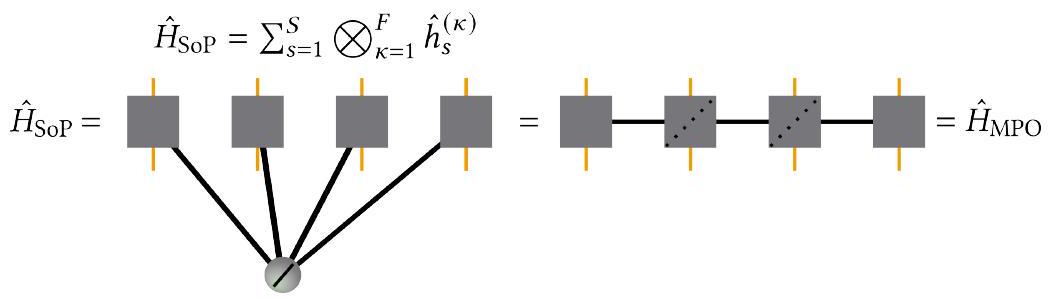

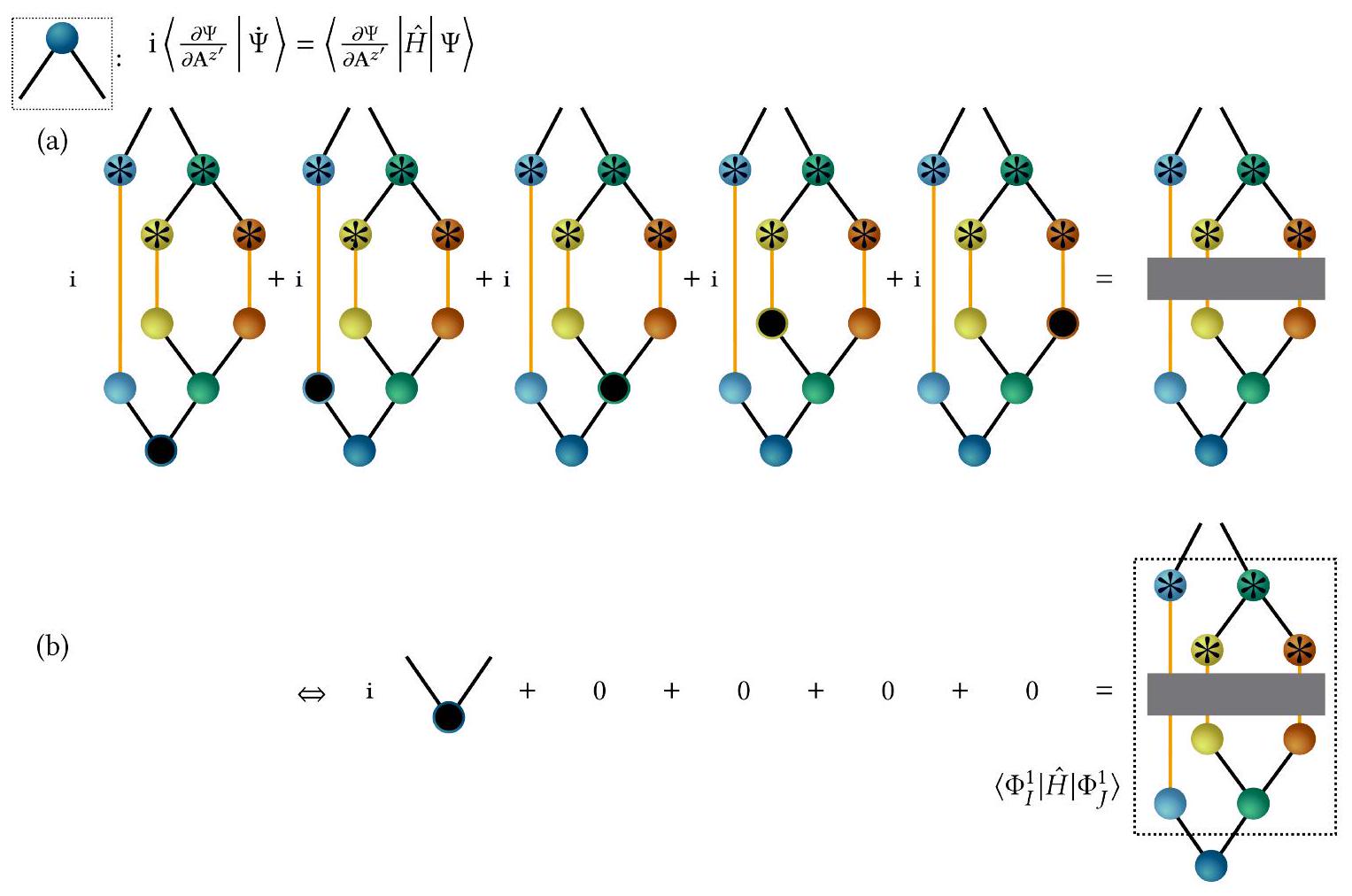
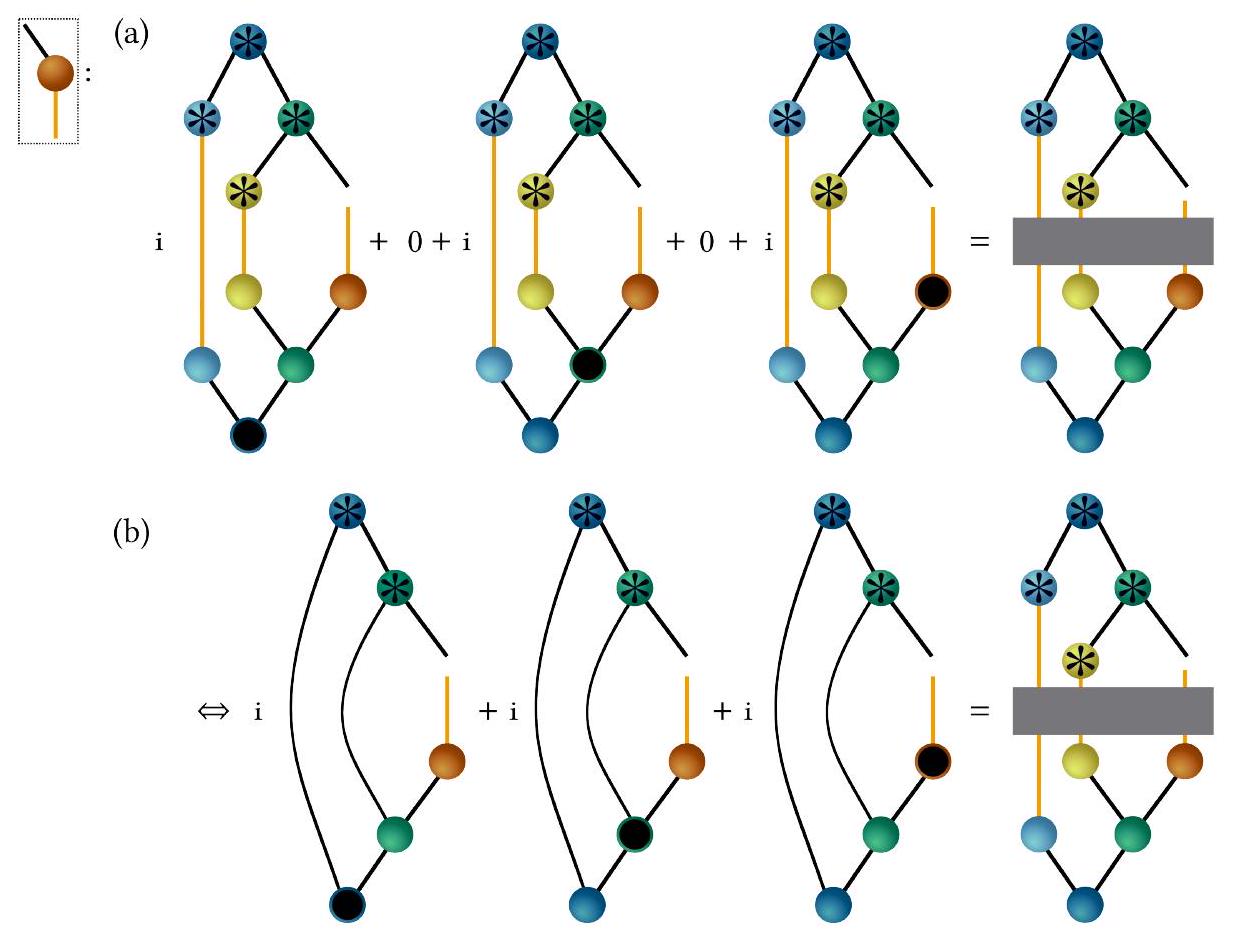
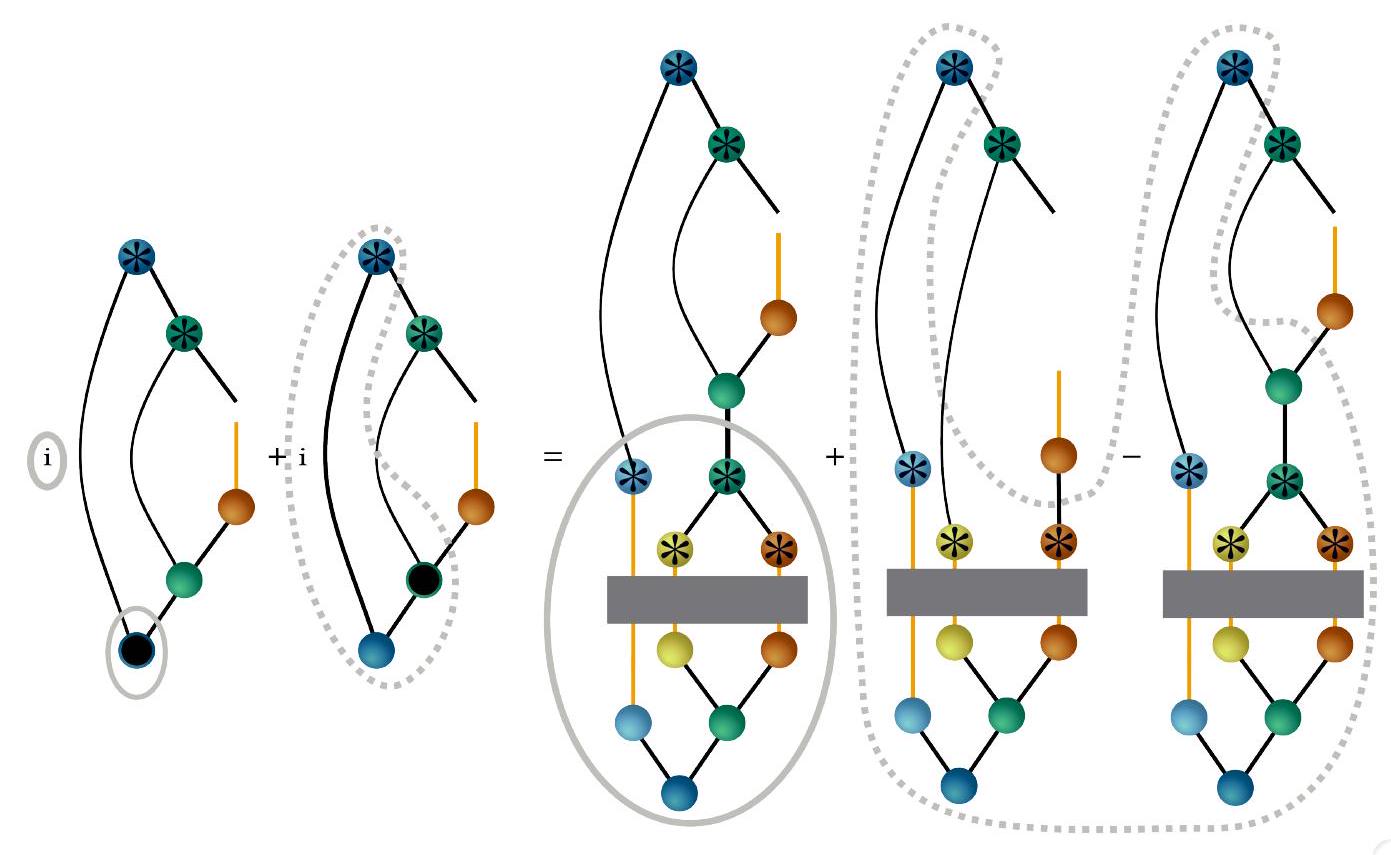
VI. اشتقاق ML-MCTDH باستخدام الرسوم البيانية
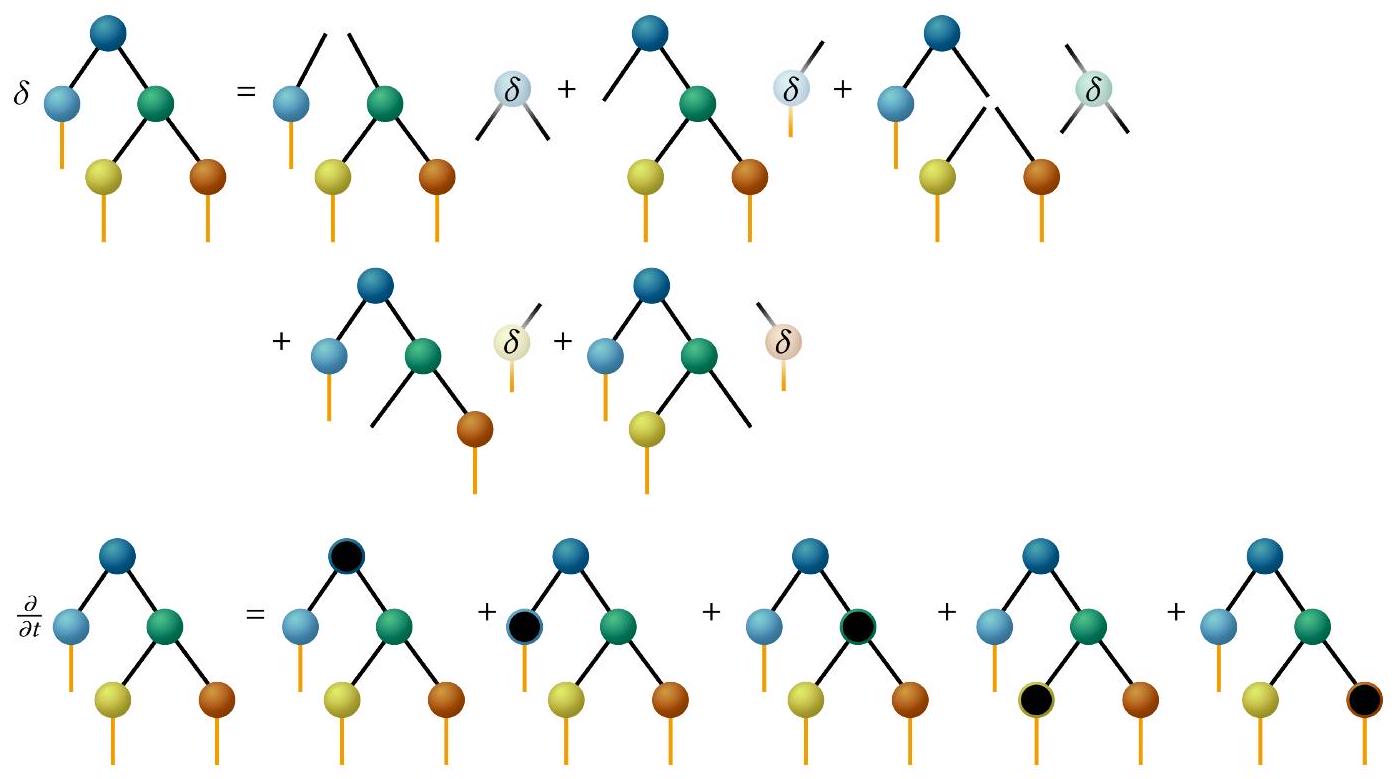
لاشتقاقات معادلات الحركة لكل موتر، نستخدم مرة أخرى TTNS من الشكل 5 كمثال بسيط ولكن نلاحظ أن هذا يمكن تعميمه بسهولة على أي TTNS، بما في ذلك TTNSs ذات طبقات أكثر. التغير من الدرجة الأولى والمشتقة الزمنية لـ
VII. التوحيد: تغيير العقدة الجذرية والتنظيف
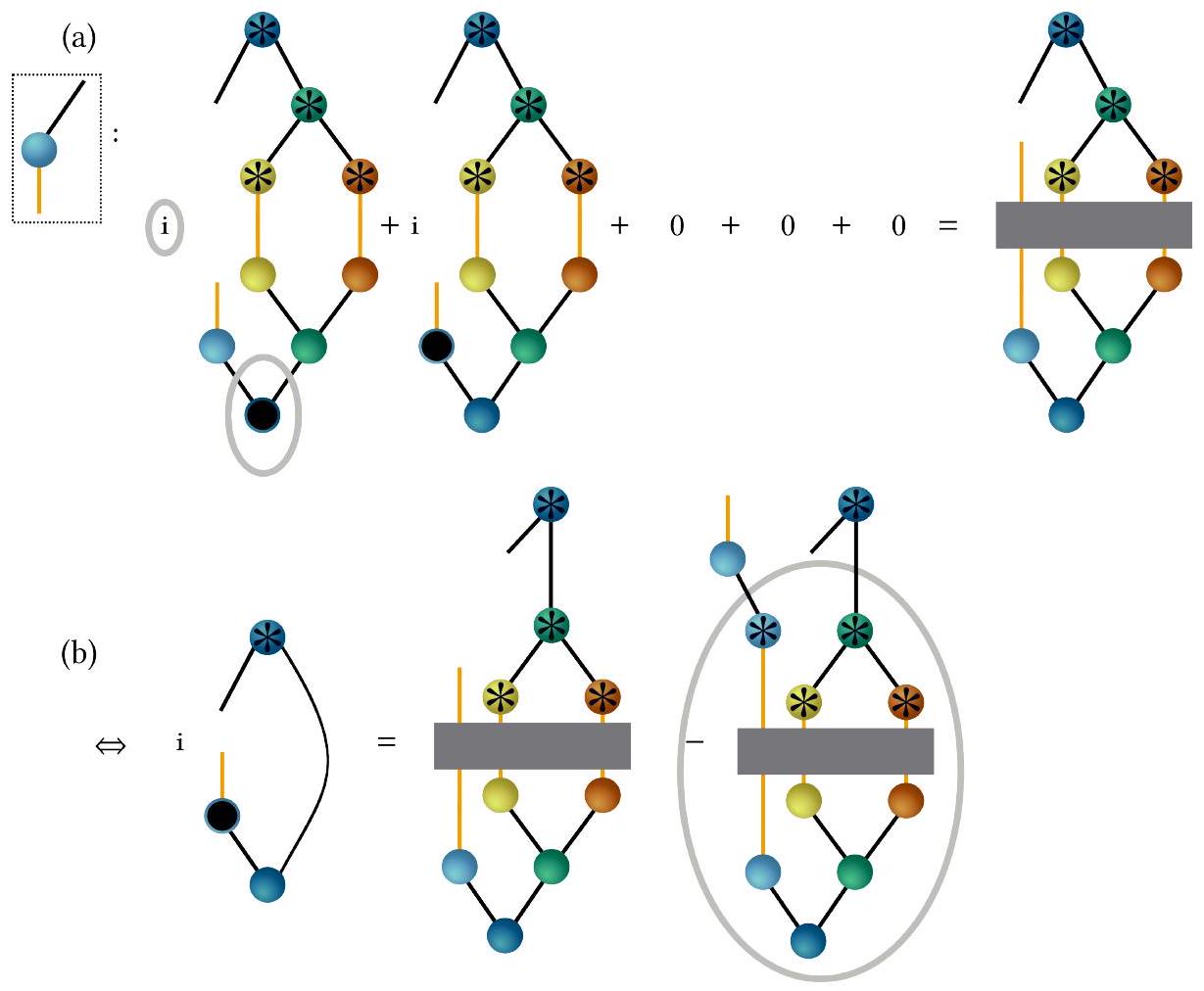

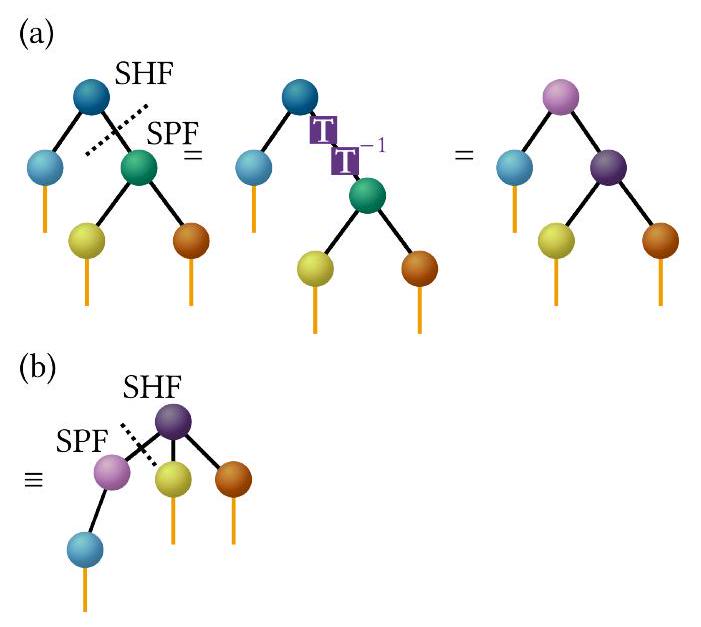
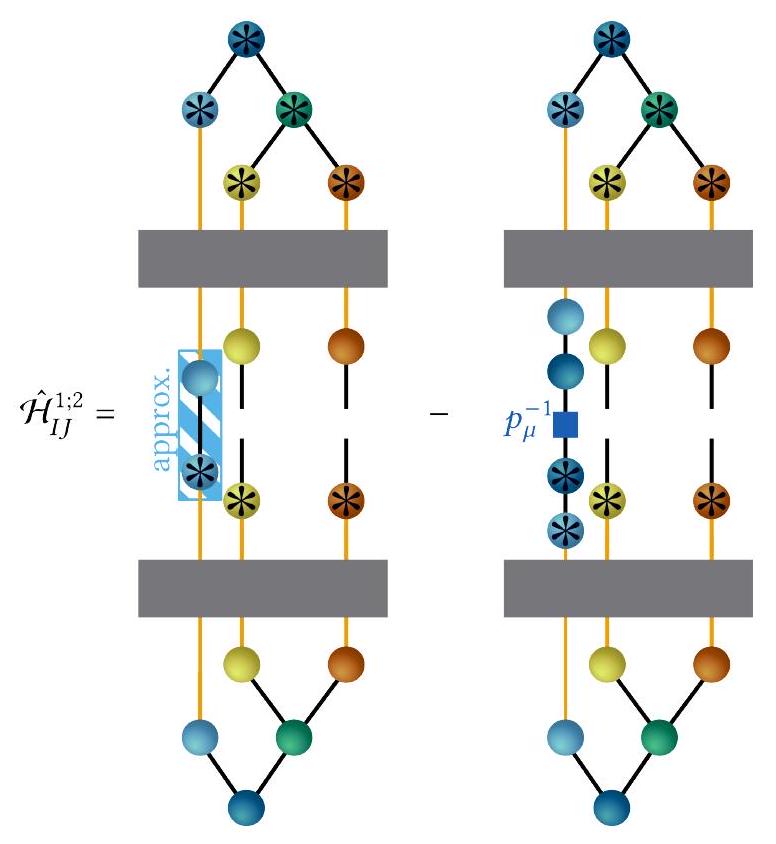
يمكن اختيار T لتعامد وتطبيع SHFs. وهذا يؤدي بعد ذلك إلى SPFs غير المتعامدة التي تم تحويلها بواسطة T. ومع ذلك، نظرًا لأن SPFs يجب أن تكون متعامدة وطبيعية، يمكننا الآن إعادة تفسير المعادلة (34) ببساطة من خلال تبادل معاني SHFs وSPFs المحولة بواسطة T عن طريق تحويل SHFs المتعامدة الآن إلى SPFs والعكس بالعكس. وهذا يؤدي إلى تغيير في هيكل الشجرة. بالإضافة إلى ذلك، إذا تم إجراء التحويل للطبقة الأولى، فإن عقدة الجذر تتغير. وهذا موضح في الشكل 25(b).

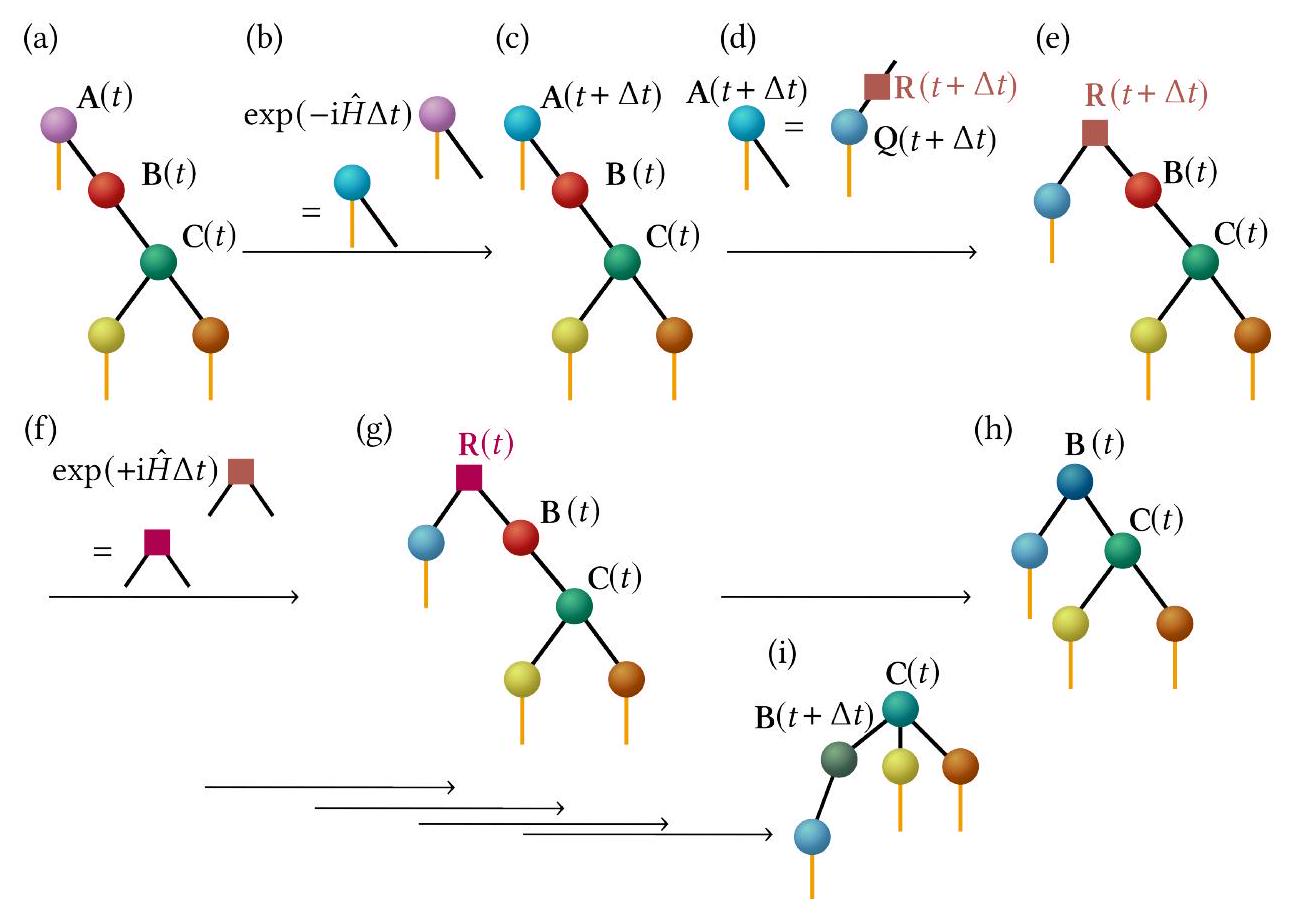
ثامناً. تقريب DMRG المعتمد على الزمن


هنا، قبل رسم الاشتقاق، نشرح أولاً الأفكار الأساسية لـ TDVP-DMRG باستخدام حجج غير دقيقة بعض الشيء. نظرًا لأن TTNS يغير عقدة الجذر الخاصة به أثناء مسح TDVP-DMRG، فإن نظام تسمية ML-MCTDH، الذي يرتبط بعقدة جذر معينة، يصعب استخدامه. بدلاً من ذلك، سنستخدم رموزًا عامة مثل

IX. DMRG غير المعتمد على الزمن
حساب
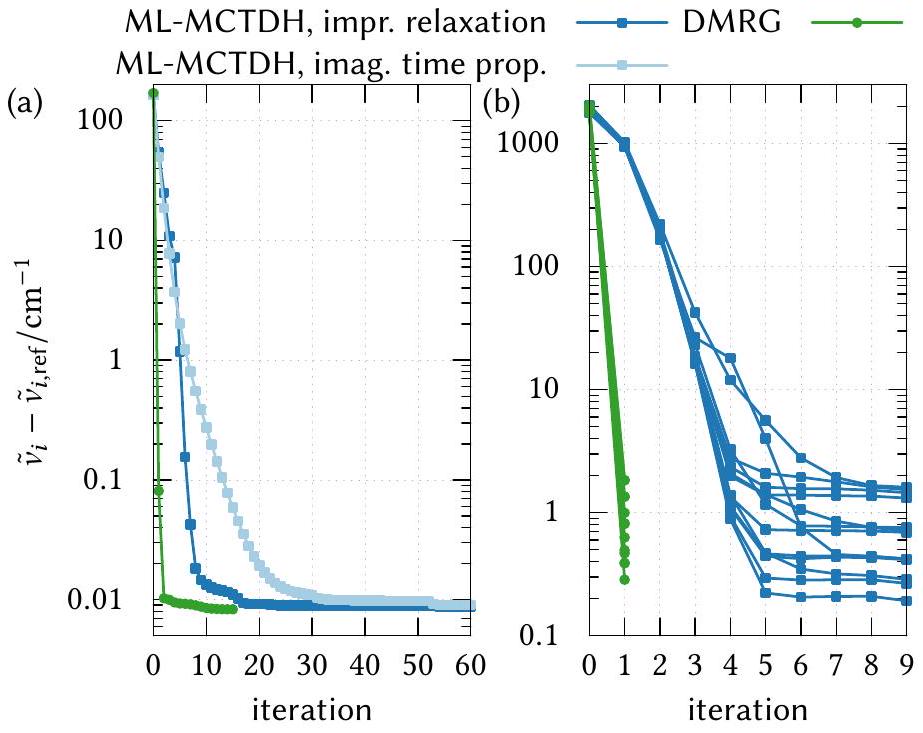
X. نشر SPFs غير المشغولة وإثراء الفضاء الفرعي
A. نشر SPFs غير المشغولة
B. توسيع الفضاء الفرعي: تحسين SPFs غير المشغولة
1. نهج DMRG ذو الموقعين
يمكن أن يتجنب المتغير ذو الموقعين مشاكل التقارب وهو مهم بشكل خاص لـ DMRG المتكيف مع التناظر [35]. قبل أن يتمكن المرء من تقويم العقدة التالية في المسح، يجب فك انكماش التنسور ذو الموقعين باستخدام، على سبيل المثال، SVD. وهذا يسمح بطريقة مباشرة لضبط أبعاد الربط ديناميكيًا (عدد SPFs). من خلال ملاحظة مجموع القيم المفردة المهملة، يحصل المرء على تقدير للخطأ، والذي يمكن استخدامه لتقديرات الطاقة [7، 181، 182]. في الواقع، تم صياغة DMRG القياسي في البداية كخوارزمية ذات موقعين [3] والإصدار ذو الموقع الواحد هو تطوير أكثر حداثة [183]. ومع ذلك، لاحظ أن TDVP-DMRG ذو الموقعين لا يزال يعتمد على TDVP وبالتالي قد لا يتم حل القضايا المحتملة بسبب SPFs غير المشغولة بالكامل. يُعرف DMRG ذو الموقعين أيضًا باسم ALS المعدل [168].
2. نهج لي/فيشر/مانث
3. نهج منديف-تابيا/ماير
4. نهج DMRG ذو الموقع الواحد
5. نهج وايت
6. نهج تباين الطاقة
7. نهج مُدمج BUG
XI. هياكل الشجرة
A. TTNSs أم MPSs؟
ب. هيكل الشجرة الأمثل
اثنا عشر. الاستنتاجات
التي تُستخدم بشكل أكثر نشاطًا في طرق MCTDH هي التقليم (اختيار التكوين) وتمثيلات الشبكة ذات الأساس المختلط. وعلى العكس، فإن المواضيع التي تُستخدم بشكل أكثر نشاطًا في سياق DMRG هي التماثلات، وحسابات الطيف في مجال التردد، والنهج العالمية التي تطبق مباشرة الهاميلتوني على شبكة الموتر. بالنظر إلى هذه الأمثلة، لا يزال هناك مجال كبير لتبادل الأفكار بشكل متبادل. نأمل أن يساعد هذا المقال في تعزيز المزيد من تبادل المعرفة الذي سيساهم في تقدم الموضوع الشامل لحالات شبكة الموتر.
شكر وتقدير
تمويل
[1] هـ. د. ماير، أ. مانث، و ل. س. سيدر باوم، نهج هارتري متعدد التكوينات المعتمد على الزمن، رسائل الكيمياء والفيزياء 165، 73 (1990).
[2] U. Manthe، H.-D. Meyer، و L. S. Cederbaum، ديناميات حزمة الموجات ضمن إطار هارتري متعدد التكوينات: الجوانب العامة والتطبيق على NOCl، J. Chem. Phys. 97، 3199 (1992).
[3] س. ر. وايت، صيغة مصفوفة الكثافة لمجموعات إعادة التعيين الكمية، فيزيكال ريفيو ليترز 69، 2863 (1992).
[4] س. ر. وايت، خوارزميات مصفوفة الكثافة لمجموعات إعادة التدوير الكمومية، فيزي. ريف. ب 48، 10345 (1993).
[5] س. ر. وايت و ر. ل. مارتن،
[6] أ. أ. ميتروشينكوف، ج. فانو، ف. أورطولاني، ر. لينغويري، و ب. بالمييري، الكيمياء الكمومية باستخدام مجموعة إعادة تنظيم مصفوفة الكثافة، مجلة الكيمياء الفيزيائية 115، 6815 (2001).
[7] ج. ك.-ل. تشان و م. هيد-غوردون، حسابات ذات ارتباط عالٍ باستخدام خوارزمية بتكلفة متعددة الحدود: دراسة لمجموعة إعادة تطبيع مصفوفة الكثافة، مجلة الكيمياء الفيزيائية 116، 4462 (2002).
[8] Ö. ليغيزا، ج. رودر، و ب. أ. هيس، دراسة QC-DMRG لتقاطع المنحنى الأيوني-المحايد لـ LiF، فيزيائيات الجزيئات 101، 2019 (2003)، arxiv:condmat/0208187.
[9] ج. زانغيليني، م. كيتزلر، س. فابيان، ت. برافك، وأ. سكرينزي، نهج MCTDHF لديناميات الإلكترونات المتعددة في مجالات الليزر، فيزياء الليزر. 13، 6 (2003).
[10] ت. كاتو و هـ. كونو، نظرية التعددية الزمنية المعتمدة على الزمن لديناميات الإلكترونات في الجزيئات في حقل ليزر مكثف، كيمياء. فيزيكس. رسائل 392، 533 (2004).
[11] م. نيست، ت. كلمروث، و ب. سالفرانك، طريقة هارتري-فوك متعددة التكوينات المعتمدة على الزمن للحسابات الكيميائية الكمومية، مجلة الكيمياء الفيزيائية 122، 124102 (2005).
[12] ج. كايلات، ج. زانغيليني، م. كيتزلر، أ. كوتش، و. كراوزر، و أ. سكرينزي، أنظمة متعددة الإلكترونات المترابطة في مجالات الليزر القوية: نهج هارتري-فوك متعدد التكوينات المعتمد على الزمن، فيزي. ريف. أ 71، 012712 (2005).
[13] ه.-د. ماير، ف. غاتي، و ج. أ. وورث، محررون، الديناميات الكمومية متعددة الأبعاد: نظرية MCTDH وتطبيقاتها، الطبعة الأولى. (وايلي-فيتش، فاينهايم، 2009).
[14] د. هوشتول، ج. م. هينز، وم. بونيتز، طرق متعددة التكوين تعتمد على الزمن لمحاكاة العمليات الضوئية لأشعة الإلكترونات في الذرات ذات الإلكترونات المتعددة، المجلة الأوروبية للفيزياء: الموضوعات الخاصة 223، 177 (2014).
[15] أ. ي. ج. لود، س. ليفيك، ل. ب. مادسن، أ. إ. ستريلتسوف، وأ. إ. ألون، ندوة: طرق هارتري متعددة التكوين تعتمد على الزمن للجسيمات غير القابلة للتمييز، مراجعة الفيزياء الحديثة 92، 011001 (2020).
[16] ت. ج. كولدا و ب. و. بادير، تحليل الموترات وتطبيقاتها، مراجعة SIAM 51، 455 (2009).
[17] ه.-د. ماير و ج. أ. وورث، الديناميات الجزيئية الكمومية: نشر حزم الموجات ومشغلات الكثافة باستخدام طريقة هارتري متعددة التكوينات المعتمدة على الزمن، الحسابات الكيميائية النظرية 109، 251 (2003).
[18] هـ. وانغ و م. ثوس، صياغة متعددة الطبقات لنظرية هارتري متعددة التكوين المعتمدة على الزمن، مجلة الكيمياء الفيزيائية 119، 1289 (2003).
[19] U. Manthe، نهج هارتري متعدد الطبقات ومتعدد التكوينات المعتمد على الزمن للديناميات الكمومية على أسطح الطاقة المحتملة العامة، مجلة الكيمياء الفيزيائية 128، 164116 (2008).
[20] ر. جوليان، ب. بفيوتي، ج. ن. فيلدز، و س. دونياش، طريقة إعادة التسمية عند درجة حرارة صفر للأنظمة الكمومية. I. نموذج إيسينغ في حقل عرضي في بعد واحد، فيزيكال ريفيو B 18، 3568 (1978).
[21] ي.-ي. شي، ل.-م. دوآن، و ج. فيدال، المحاكاة الكلاسيكية لأنظمة الكم ذات الجسم المتعدد باستخدام شبكة موتر شجرية، فيزيكس ريفيو A 74، 022320 (2006).
[22] و. هاكبوش وس. كوهين، مخطط جديد لتمثيل التنسور، مجلة تحليل فورييه والتطبيقات 15، 706 (2009).
[23] و. هاكبوش، فضاءات التنسور وحساب التنسور العددي، الطبعة الثانية، سلسلة سبرينغر في الرياضيات الحاسوبية، المجلد 56 (سبرينغر، شام، سويسرا، 2019).
[24] ل. غراسي ديك، تحليل القيم الفردية الهرمي للموترات، مجلة SIAM لتحليل المصفوفات والتطبيقات 31، 2029 (2010).
[25] ل. غراسي ديك، د. كريسنر، و ج. توبلر، مسح أدبي لتقنيات تقريب التنسور منخفض الرتبة، ميتل شترايفن غام 36، 53 (2013).
[26] س. سزلاي، م. بففر، ف. مورغ، ج. باركزا، ف. فيرسترات، ر. شنايدر، و أ. ليغيزا، طرق حاصل الضرب التنسوري وتحسين التشابك لـ
[27] ج. فيدال، محاكاة فعالة للأنظمة الكمية ذات الجسم الواحد، فيزيكال ريفيو ليترز 93، 040502 (2004).
[28] س. ر. وايت و أ. إ. فيغوين، التطور في الوقت الحقيقي باستخدام مجموعة إعادة تنظيم مصفوفة الكثافة، فيزيكال ريفيو ليترز 93، 076401 (2004).
[29] أ. إ. فيغوين و س. ر. وايت، طرق استهداف خطوة الزمن للديناميات في الوقت الحقيقي باستخدام مجموعة إعادة تشكيل مصفوفة الكثافة، فيزي. ريف. ب 72، 020404 (2005).
[30] س. بايكل، ت. كوهلر، أ. سوبودا، س. ر. مانمانا، أ. شولووك، و ج. هوبغ، طرق تطور الزمن لحالات المنتج المصفوفي، آن. فيز. 411، 167998 (2019).
[31] م. فانس، ب. ناتشرغالي، و ر. ف. ويرنر، حالات مرتبطة نهائيًا على سلاسل سبين الكم، اتصالات. رياضيات. فيزيكس 144، 443 (1992).
[32] س. أستلوند وس. رومر، الحد الديناميكي الحراري لمصفوفة الكثافة المعاد تنظيمها، فيزيكال ريفيو ليترز 75، 3537 (1995).
[33] ج. فيدال، محاكاة كلاسيكية فعالة للحسابات الكمومية المتشابكة قليلاً، فيزيكال ريفيو ليترز 91، 147902 (2003).
[34] ف. فيرسترات وج. إ. سيراك، تمثل حالات المنتج المصفوفي الحالات الأساسية بدقة، فيزيكس ريفيو ب 73، 094423 (2006).
[35] U. Schollwöck، مجموعة إعادة تنظيم مصفوفة الكثافة في عصر حالات منتج المصفوفات، آن. فيز. 326، 96 (2011).
[36] ر. هوبنر، ف. نيبندال، و و. دور، حالات الشبكة التنسيلية المتسلسلة، نيو ج. فيز. 12، 025004 (2010).
[37] V. Murg، F. Verstraete، Ö. Legeza، و R. M. Noack، محاكاة الأنظمة الكمومية المرتبطة بقوة باستخدام شبكات موتر الشجرة، فيزيكال ريفيو B 82، 205105 (2010).
[38] H. J. Changlani، S. Ghosh، C. L. Henley، و A. M. Läuchli، مضاد المغناطيس هايزنبرغ على أشجار كايلي: طيف الطاقة المنخفضة وعدم التوازن في المواقع الزوجية والفردية، فيزيكال ريفيو B 87، 085107 (2013).
[39] م. جيرستر، ب. سيلفي، م. ريتزي، ر. فازيو، ت. كالاركو، و س. مونتانجيرو، شبكة موتر الشجرة غير المقيدة: صورة قياس تكيفية لأداء معزز، فيز. ريف. ب 90، 125154 (2014).
[40] V. Murg، F. Verstraete، R. Schneider، P. R. Nagy، و Ö. Legeza، حالة شبكة موتر الشجرة بترتيب موتر متغير: طريقة متعددة المراجع فعالة للأنظمة المرتبطة بقوة، J. Chem. Theory Comput. 11، 1027 (2015).
[41] ف. فيرسترات وج. إ. سيراك، خوارزميات إعادة التعيين للأنظمة الكمية ذات الجسم المتعدد في بعدين وأبعاد أعلى، arXiv:condmat/0407066 (2004)، arxiv:cond-mat/0407066.
[42] ج. فيدال، إعادة تنظيم التشابك، فيزيكال ريفيو ليترز 99، 220405 (2007).
[43] ج. فيدال، فئة حالات الكوانتم ذات الجسم المتعدد التي يمكن محاكاتها بكفاءة، فيزيكال ريفيو ليترز 101، 110501 (2008).
[44] ف. فيرسترات، م. م. وولف، د. بيريز-غارثيا، وج. إ. سيراك، الحرجية، قانون المساحة، والقوة الحسابية لحالات الأزواج المتشابكة المتوقعة، فيزيكال ريفيو ليترز 96، 220601 (2006).
[45] إتش. جي. تشانغلاني، جي. إم. كيندر، سي. جي. أومريغار، وجي. كيه.-إل. تشان، تقريبات دوال الموجة المرتبطة بقوة باستخدام حالات ناتج المرافقات، فيزيكال ريفيو بي 80، 245116 (2009).
[46] ك. هـ. مارتى، ب. باور، م. رايهر، م. تروير، و ف. فيرسترات، حالات شبكة موتر الرسم البياني الكامل: اقتراح جديد لوظيفة موجية فرميونية للجزيئات، نيو ج. فيز. 12، 103008 (2010).
[47] ج. ك.-ل. تشان، دوال الموجة ذات التشابك المنخفض، وايلي إنتر ديسيبلاين. ريف. كومبيوتر. مول. ساي. 2، 907 (2012).
[48] ر. أورو، مقدمة عملية لشبكات التنسور: حالات المنتج المصفوفي وحالات الزوج المتشابك المتوقعة، آن. فيز. 349، 117 (2014).
[49] ر. هاغشناس، م. ج. أوروك، و ج. ك.-ل. تشان، تحويل حالات الزوج المتشابك المتوقعة إلى شكل قياسي، فيزيكال ريفيو ب 100، 054404 (2019).
[50] م. ب. زالتيل و ف. بولمان، حالات الشبكة التنسورية المتساوية القياس في بعدين، فيزيكال ريفيو ليترز 124، 037201 (2020).
[51] U. Schollwöck، مجموعة إعادة التعيين لمصفوفة الكثافة، مراجعة الفيزياء الحديثة 77، 57 (2005).
[52] ك. أوييدا، ج. جين، ن. شباتا، ي. هيدا، و ت. نيشينو، مبدأ العمل الأقل لمجموعة إعادة تطبيع مصفوفة الكثافة في الزمن الحقيقي، arXiv:0612480 (2006)، arxiv:cond-mat/0612480.
[53] ج. ج. دوراندو، ج. هاكمان، و ج. ك.-ل. تشان، نظرية الاستجابة التحليلية لمجموعة إعادة تنظيم مصفوفة الكثافة، مجلة الكيمياء الفيزيائية 130، 184111 (2009).
[54] ج. هايجيمان، ج. آي. سيراك، ت. ج. أوزبورن، إ. بيزوران، هـ. فيرشيلد، و ف. فيرسترات، مبدأ التباين الزمني للأنظمة الكمومية، فيزيكال ريفيو ليترز 107، 070601 (2011).
[55] ن. ناكاتاني، س. ووتيرز، د. فان نيك، و ج. ك.-ل. تشان، نظرية الاستجابة الخطية لمجموعة إعادة تشكيل مصفوفة الكثافة: خوارزميات فعالة للحالات المثارة المرتبطة بقوة، مجلة الكيمياء الفيزيائية 140، 024108 (2014).
[56] س. ووترز، ن. ناكاتاني، د. فان نيك، و ج. ك.-ل. تشان، نظرية ثولس لحالات المنتج المصفوفي وطرق إعادة تنظيم مصفوفة الكثافة اللاحقة، فيزي. ريف. ب 88، 075122 (2013).
[57] ج. م. كيندر، س. س. رالف، و ج. كين-ليك تشان، تطور الزمن التحليلي، تقريب الطور العشوائي، ودوال غرين لحالات المنتج المصفوفي، في تقدم في الفيزياء الكيميائية، تحرير س. كايس (جون وايلي وأولاده، هوبوكين، نيو جيرسي، الولايات المتحدة الأمريكية، 2014) الطبعة الأولى، الصفحات 179-192.
[58] هـ. وانغ و م. ثوس، الديناميات الكمية الدقيقة عددياً للجسيمات غير القابلة للتمييز: نظرية هارتري متعددة الطبقات متعددة التكوين المعتمدة على الزمن في تمثيل الكوانتization الثاني، مجلة الكيمياء الفيزيائية 131، 024114 (2009).
[59] هـ. ر. لارسون، حساب حالات الاهتزاز الذاتية باستخدام حالات الشبكة التنسورية الشجرية (TTNS)، مجلة الكيمياء الفيزيائية 151، 204102 (2019).
[60] ب. كلوس، د. ر. رايشمان، ور. تيمبيلا، حسابات حالة المنتج المصفوفة متعددة المجموعات تكشف عن إثارات فرانك-كوندون المتنقلة تحت اقتران هولشتاين من النوع القوي، فيزيكال ريفيو ليترز 123، 126601 (2019).
[61] ج. هايجيمان، س. لوبيتش، إ. أوسيليديتس، ب. فانديرايكن، و ف. فيرسترات، توحيد تطور الزمن والتحسين باستخدام حالات المنتج المصفوفي، فيزيكس ريفيو ب 94، 165116 (2016).
[62] إكس. شي، واي. ليو، واي. ياو، يو. شولووك، سي. ليو، و إتش. ما، الديناميات الكمومية لمجموعة إعادة التشكيل لمصفوفة الكثافة المعتمدة على الزمن للأنظمة الكيميائية الواقعية، مجلة الكيمياء الفيزيائية 151، 224101 (2019).
[63] أ. باياردى و م. رايهر، الديناميات الكمومية على نطاق واسع باستخدام حالات المنتج المصفوفي، مجلة نظرية الكيمياء والحساب 15، 3481 (2019).
[64] أ. بايارد، ج. ستاين، ف. باروني، و م. رايهر، تحسين حالات المنتج المصفوفي المثارة بشدة مع تطبيق على الطيف الاهتزازي، مجلة الكيمياء الفيزيائية 150، 094113 (2019).
[65] ي. كوراشيغي، صياغة حالة المنتج المصفوفي لنظرية هارتري متعددة التكوين المعتمدة على الزمن، مجلة الكيمياء الفيزيائية 149، 194114 (2018).
[66] ج. رين، ي. وانغ، و. لي، ت. جيانغ، وز. شواي، مجموعة إعادة الترتيب لمصفوفة الكثافة المعتمدة على الزمن المرتبطة بإمكانات تمثيل النمط n لمعدل الانحلال غير الإشعاعي للحالة المثارة: الشكل والتطبيق على الأزولين، المجلة الصينية لفيزياء الكيمياء 34، 565 (2021).
[67] س. مينا لي، ف. غاتي، د. يوتشينكو، ب.-ن. روي، و هـ.-د. ماير، مقارنة بين طريقة هارتري متعددة الطبقات ومتعددة التكوين المعتمدة على الزمن (ML-MCTDH) ومجموعة إعادة تنظيم مصفوفة الكثافة (DMRG) لخصائص الحالة الأساسية لسلاسل الدوارات الخطية، مجلة الكيمياء الفيزيائية 154، 174106 (2021).
[68] إتش. آر. لارسون، إتش. زهاي، ك. غونست، وجي. ك.-ل. تشان، حالات المنتج المصفوفي مع مواقع كبيرة، مجلة نظرية الكيمياء والحساب 18، 749 (2022).
[69] ي. شو، ز. شيا، إكس. شيا، أ. شولووك، و هـ. ما، مبدأ التباين الزمني التكيفي العشوائي لموقع واحد، JACS Au 2، 335 (2022).
[70] إتش. آر. لارسون، م. شرويدر، ر. بيكمان، ف. بريوك، س. شران، د. ماركس، وأو. فندريل، طيف الأشعة تحت الحمراء المحلّل حسب الحالة للثنائي المائي المؤين: إعادة النظر في قمة ثنائية نقل البروتون المميزة، كيمياء. علوم 13، 11119 (2022).
[71] ن. غلاسر، أ. بايارد، وم. ريهير، إطار مرن قائم على DMRG للحسابات الاهتزازية غير التوافقية، مجلة نظرية الكيمياء والحسابات 10.1021/acs.jctc.3c00902 (2023).
[72] ف. كوهلر، ر. موكيرجي، و ب. شميلشر، استكشاف نماذج الدوران الكمي غير المرتبة باستخدام نهج متعدد الطبقات ومتعدد التكوينات، فيزيكال ريفيو ريسيرش 5، 023135 (2023).
[73] أ. كوتش و ج. لوبيتش، تقريب ديناميكي منخفض الرتبة، مجلة SIAM لتحليل المصفوفات والتطبيقات 29، 434 (2007).
[74] سي. لوبيش، من الديناميكا الجزيئية الكمومية إلى الكلاسيكية: نماذج مختزلة وتحليل عددي، الطبعة الأولى. (الجمعية الرياضية الأوروبية، زيورخ، سويسرا، 2008).
[75] ل. ب. ليندوي، ب. كلوس، و د. ر. رايشمان، تطور الزمن لدوال الموجة ML-MCTDH. I. شروط القياس، دوال الأساس، والانفرادات، مجلة الكيمياء الفيزيائية 155، 174108 (2021).
[76] ت. ويك وأ. مانث، التناظرات في تمثيل دالة الموجة هارتري المعتمدة على الزمن متعددة التكوينات وانتشارها، مجلة الكيمياء الفيزيائية 154، 194108 (2021).
[77] د. غوتليب و س. أ. أورزاغ، التحليل العددي للطرق الطيفية: النظرية والتطبيقات (جمعية الرياضيات الصناعية والتطبيقية، فيلادلفيا، بنسلفانيا، 1987).
[78] ب. أ. م. ديراك، تدوين جديد لميكانيكا الكم، إجراءات الرياضيات. كامب. فلسفة. مجتمع. 35، 416 (1939).
[79] سي. كوهين-تانودجي، ب. ديو، وف. لالو، ميكانيكا الكم، المجلد 1: المفاهيم الأساسية، الأدوات، والتطبيقات، الطبعة الثانية (وايلي-فيتش، فاينهايم، 2019).
[80] د. أ. هاريس، ج. ج. إنجرهولم، و و. د. غوين، حساب عناصر المصفوفة لمشاكل ميكانيكا الكم أحادية البعد وتطبيقها على المذبذبات غير التوافقية، مجلة الكيمياء الفيزيائية 43، 1515 (1965).
[81] أ. س. ديكنسون و ب. ر. سيرتين، حساب عناصر المصفوفة لمشاكل ميكانيكا الكم أحادية البعد، مجلة الكيمياء الفيزيائية 49، 4209 (1968).
[82] ج. ف. ليل، ج. أ. باركر، وج. س. لايت، تمثيلات المتغيرات المنفصلة والنماذج المفاجئة في نظرية التشتت الكمي، رسائل الفيزياء الكيميائية 89، 483 (1982).
[83] ج. سي. لايت وت. كاريغتون جونيور، تمثيلات المتغيرات المنفصلة واستخداماتها، تقدم في الكيمياء الفيزيائية 114، 263 (2000).
[84] د. تانور، مقدمة في ميكانيكا الكم، الطبعة الأولى. (كتب العلوم الجامعية، سوساليتو، كاليفورنيا، 2008).
[85] د. تانور، س. ماخنس، إ. أسيما، و هـ. ر. لارسون، طرق الفضاء الطوري مقابل طرق الفضاء الإحداثي: التوقعات للحسابات الكمومية الكبيرة، في تقدم في الفيزياء الكيميائية، المجلد 163، تحرير ك. ب. ويلي (جون وايلي وأولاده، هوبوكين، نيو جيرسي، الولايات المتحدة الأمريكية، 2018) الصفحات 273-323.
[86] د. باي، طريقة شبكة لاغرانج، تقرير فيزيائي 565، 1 (2015).
[87] ج. ب. بويd، طرق شبيشيف وفورييه الطيفية: الطبعة الثانية المنقحة، الطبعة الثانية، الطبعة المنقحة (منشورات دوفر، مينيولا، نيويورك، 2001).
[88] I. Burghardt، K. Giri، و G. A. Worth، الديناميات الكمومية متعددة الأوضاع باستخدام حزم الموجات الغاوسية: طريقة هارتري متعددة التكوينات المعتمدة على الغاوسية (G-MCTDH) المطبقة على طيف الامتصاص للبيرازين، J. Chem. Phys. 129، 174104 (2008).
[89] س. رومر، م. روكنباور، و I. بورغارت، هارتري المعتمد على الزمن متعدد التكوينات القائم على غاوسي: نهج ذو طبقتين. I. النظرية، ج. كيم. فيز. 138، 064106 (2013).
[90] ب. أ. م. ديراك، ملاحظة حول ظواهر التبادل في ذرة توماس، إجراءات الرياضيات، جمعية كامبريدج الفلسفية 26، 376 (1930).
[91] ج. فرانكل، ميكانيكا الموجات؛ نظرية عامة متقدمة، الطبعة الأولى. (دار نشر جامعة أكسفورد، 1934).
[92] أ. مكلاكلان، حل تبايني لمعادلة شرودنجر المعتمدة على الزمن، فيزياء الجزيئات 8، 39 (1964).
[93] ب. كرامر و م. سارسينو، هندسة المبدأ المتغير الزمني في ميكانيكا الكم، الطبعة الأولى. (سبرينجر، برلين، 1981).
[94] م. هـ. بيك، أ. يكل، ج. أ. وورث، و هـ.-د. ماير، طريقة هارتري متعددة التكوينات المعتمدة على الزمن (MCTDH): خوارزمية فعالة للغاية لنشر حزم الموجات، فيزيكس. ريب. 324، 1 (2000).
[95] U. Manthe، ديناميات حزمة الموجات ونهج هارتري متعدد التكوينات المعتمد على الزمن، مجلة الفيزياء: المادة المكثفة 29، 253001 (2017).
[96] أ. فندريل و هـ.-د. ماير، طريقة هارتري متعددة الطبقات ومتعددة التكوين تعتمد على الزمن: التنفيذ والتطبيقات على هاملتونيان هينون-هيلز وعلى البيرازين، مجلة الكيمياء الفيزيائية 134، 044135 (2011).
[97] هـ. وانغ، نظرية هارتري متعددة الطبقات ومتعددة التكوينات المعتمدة على الزمن، مجلة الفيزياء الكيميائية A 119، 7951 (2015).
[98] سي. لوبيتش، تي. روهفيدر، آر. شنايدر، وبي. فانديرايكن، الاقتراب الديناميكي بواسطة موترات تاكر الهرمية وموترات تدريب التنسور، مجلة SIAM لتحليل المصفوفات والتطبيقات 34، 470 (2013).
[99] سي. لوبيتش وإي. في. أوسيلدس، مُدمج تقسيم الإسقاط للتقريب الديناميكي منخفض الرتبة، BIT الرياضيات العددية 54، 171 (2014).
[100] C. لوبيتش، دمج الزمن في طريقة هارتري المعتمدة على الزمن متعددة التكوينات لديناميات الكم الجزيئي، أبحاث الرياضيات التطبيقية EXpress 2015، 311 (2015).
[101] ب. كلوس، إ. بورغارت، و ج. لوبيش، تنفيذ مُدمج جديد لتقسيم الإسقاط لطريقة هارتري متعددة التكوينات المعتمدة على الزمن، مجلة الكيمياء الفيزيائية 146، 174107 (2017).
[102] سي. لوبيتش، بي. فانديرايكن، و هـ. والاش، دمج الزمن لمتجهات توكر ذات قيود الرتبة، مجلة SIAM للتحليل العددي 56، 1273 (2018).
[103] ج. أ. وورث، هـ.-د. ماير، و ل. س. سيدر باوم، استرخاء نظام مع تقاطع مخروطي مرتبط بحمام: دراسة معيارية لحزمة موجية بُعدها 24 تعالج البيئة بشكل صريح، ج. كيم. فيز. 109، 3518 (1998).
[104] س. سوكيسيان و هـ.-د. ماير، حول تأثير الدوران الأولي على التفاعل. دراسة انتشار حزمة الموجات متعددة التكوينات المعتمدة على الزمن (MCTDH) على H + D2 و D
[105] ج. فوكشل، ب. س. توماس، ج. دين أيل، ي. أوزتورك، ف. ناتينو، هـ.-د. ماير، و ج.-ج. كرويس، التأثيرات الدورانية على ديناميات التفكك لـ
[106] إتش. آر. لارسون ودي. جي. تانور، تقليم ديناميكي لطريقة هارتري متعددة التكوينات المعتمدة على الزمن (DP-MCTDH): نهج فعال للديناميات الكمومية متعددة الأبعاد، مجلة الكيمياء الفيزيائية 147، 044103 (2017).
[107] د. ر. هارتري، و. هارتري، و ب. سويرلز، المجال الذاتي المتسق، بما في ذلك التبادل وتراكب التكوينات، مع بعض النتائج للأكسجين، فلسفة. ترانس. ر. سوس. لندن. سير. رياضيات. فيزي. علوم. 238، 229 (1939).
[108] ج. هينز، MC-SCF. I. طريقة الحقل الذاتي المتسق متعدد التكوينات، ج. كيم. فيز. 59، 6424 (1973).
[109] ج. داس و أ. سي. وال، دوال الموجة هارتري-فوك الممتدة: تكوينات التكافؤ المحسّنة لـ
[110] ب. أ. روس، ب. ر. تايلور، و ب. إ. م. سيغبهان، طريقة SCF لمساحة نشطة كاملة (CASSCF) باستخدام نهج super-CI المعتمد على مصفوفة الكثافة، كيمياء. فيزيكس. 48، 157 (1980).
[111] ت. هيلغاكر، ب. يورغنسن، وج. أولسن، نظرية البنية الإلكترونية الجزيئية، الطبعة الأولى. (وايلي، تشيتشستر؛ نيويورك، 2013).
[112] د. ل. ييجر و ب. يورغنسن، نهج هارتري-فوك متعدد التكوينات المعتمد على الزمن، كيمياء. فيزيكس. رسائل 65، 77 (1979).
[113] ر. موتشيا، الخصائص الثابتة والديناميكية من الدرجة الأولى والثانية بواسطة دوال الموجة التغيرية، المجلة الدولية للكيمياء الكمومية 8، 293 (1974).
[114] إ. دالغارد، نظرية هارتري-فوك متعددة التكوينات المعتمدة على الزمن، مجلة الكيمياء الفيزيائية 72، 816 (1980).
[115] ر. مكوين، بعض الملاحظات حول نظرية هارتري-فوك المعتمدة على الزمن متعددة التكوينات، المجلة الدولية للكيمياء الكمومية 23، 405 (1983).
[116] ل. ب. ليندوي، ب. كلوس، و د. ر. رايشمان، تطور الزمن لدوال الموجة ML-MCTDH. II. تطبيق مُجزئ الفاصل للمشغل، ج. كيم. فيز. 155، 174109 (2021).
[117] أ. ب. كيمبي، حول تطبيق رسومات كليفورد على الكوانتيك الثنائي العادي، محاضر جمعية الرياضيات اللندنية، السلسلة 1-17، 107 (1885).
[118] ب. كليفورد، مقتطف من رسالة إلى السيد سيلفستر من البروفيسور كليفورد من كلية جامعة لندن، المجلة الأمريكية للرياضيات 1، 126 (1878).
[119] ج. ج. سيلفستر، حول تطبيق النظرية الذرية الجديدة على التمثيل البياني للثوابت والمتغيرات المشتركة للكميات الثنائية، مع ثلاثة ملاحق، مجلة الرياضيات الأمريكية 1، 64 (1878)، 2369436.
[120] ج. هـ. كيم، م. س. هـ. أوه، وك. -ي. كيم، تعزيز حساب المتجهات باستخدام التدوين الرسومي، المجلة الأمريكية للفيزياء 89، 200 (2021).
[121] ر. بنروز، تطبيقات الموترات ذات الأبعاد السلبية، في الرياضيات التوافقية وتطبيقاتها: وقائع مؤتمر عُقد في المعهد الرياضي، أكسفورد، من 7-10 يوليو، 1969، تحرير د. ج. أ. ويلش (مطبعة أكاديمية، 1971) الصفحات 221-244.
[122] أ. تشيكوكي، ن. لي، إ. أوسيليديتس، أ.-هـ. فهان، ق. تشاو، و د. ب. مانديك، الشبكات التنسورية لتقليل الأبعاد والتحسين على نطاق واسع: الجزء 1 تحلل التنسورات ذات الرتبة المنخفضة، مؤسسون الاتجاهات® في تعلم الآلة 9، 249 (2016).
[123] ج. سي. بريدجمان و ج. تي. تشاب، التلويح باليد والرقص التفسيري: دورة تمهيدية حول شبكات التنسور، مجلة الفيزياء الرياضيات النظرية 50، 223001 (2017).
[124] أ. أينشتاين، أساس نظرية النسبية العامة، آن. فيز. 354، 769 (1916).
[125] م. هـ. بيك و هـ.-د. ماير، نظام تكامل فعال وموثوق لمعادلات الحركة لطريقة هارتري متعددة التكوين المعتمدة على الزمن (MCTDH)، Z. Für Phys. At. Mol. Clust. 42، 113 (1997).
[126] U. Manthe، تعليق على “تقريب هارتري الزمني متعدد التكوينات القائم على حالات الجسيمات الفردية الطبيعية” [J. Chem. Phys. 99، 4055 (1993)]، J. Chem. Phys. 101، 2652 (1994).
[127] ك. ج. كاي، مشكلة تفرد المصفوفة في طريقة التباين المعتمدة على الزمن، كيمياء. فيزي. 137، 165 (1989).
[128] ل. فانديرستراتن، ج. هاجيمان، و ف. فيرسترات، طرق الفضاء المماس لحالات المنتج المصفوفي الموحد، ملاحظات محاضرات ساي بوست فيزيكس، 7 (2019).
[129] U. Manthe، إعادة النظر في نهج هارتري متعدد التكوينات المعتمد على الزمن، J. Chem. Phys. 142، 244109 (2015).
[130] هـ. وانغ و هـ.-د. ماير، حول تنظيم معادلات الحركة لـ ML-MCTDH، مجلة الكيمياء الفيزيائية 149، 044119 (2018).
[131] U. Manthe و H. Köppel، طريقة جديدة لحساب ديناميات حزمة الموجات: الأسطح المرتبطة بقوة والأساس الأديباتي، J. Chem. Phys. 93، 345 (1990).
[132] م. ج. براملي وت. كارينجتون، طريقة عامة للمتغيرات المنفصلة لحساب مستويات الطاقة الاهتزازية للجزيئات المكونة من ثلاثة وأربعة ذرات، مجلة الكيمياء الفيزيائية 99، 8519 (1993).
[133] إتش. آر. لارسون، ب. هارتكي، و د. ج. تانور، ديناميات الكم الجزيئية الفعالة في فضاء الإحداثيات وفضاء الطور باستخدام قواعد مقطوعة، مجلة الكيمياء الفيزيائية 145، 204108 (2016).
[134] ب. بيرفو، ف. مورغ، ج. إ. سيراك، وف. فيرسترات، تمثيلات مشغلات المنتج المصفوفي، نيو ج. فيز. 12، 025012 (2010).
[135] ج. ك.-ل. تشان، أ. كيسلمان، ن. ناكاتاني، ز. لي، و س. ر. وايت، مشغلات المنتج المصفوفي، حالات المنتج المصفوفي، و
[136] ف. أوتو، وعاء متعدد الطبقات: تمثيل دقيق للإمكانات من أجل ديناميات كمومية عالية الأبعاد بكفاءة، مجلة الكيمياء الفيزيائية 140، 014106 (2014).
[137] ف. أوتو، ي.-س. تشيانغ، و د. بيلايز، دقة تمثيلات الجهد المعتمدة على Potfit وتأثيرها على أداء (ML)MCTDH، كيمياء. فيزيكس. 509، 116 (2018).
[138] ز. لي و ج. ك.-ل. تشان، حالات المنتج المصفوفي المعتمدة على الدوران: أداة متعددة الاستخدامات للأنظمة المرتبطة بقوة، مجلة نظرية الكيمياء والحساب 13، 2681 (2017).
[139] إتش. آر. لارسون، سي. أ. خيمينيز-هويوس، وجي. كيه.-ل. تشان، حالات المنتج المصفوفي الدنيا والتعميمات لوظائف الموجة المتوسطة والمجموعة، مجلة نظرية الكيمياء والحساب 16، 5057 (2020).
[140] ه.-د. ماير، ج. كوتشار، و ل. س. سيدر باوم، هارتري المدور المعتمد على الزمن: التطوير الرسمي، مجلة الرياضيات والفيزياء 29، 1417 (1988).
[141] سي. لوبيتش، آي. في. أوسيلدس، وبي. فانديريكن، دمج الزمن لقطارات التنسور، مجلة SIAM للتحليل العددي 53، 917 (2015).
[142] إ. كيري، ج. لوبيتش، و هـ. والاش، تقريب ديناميكي منخفض الرتبة المنفصل في وجود قيم فردية صغيرة، مجلة SIAM للتحليل العددي 54، 1020 (2016).
[143] م. بونفانتي و I. بورغارت، صياغة فضاء المماس لمعادلات الحركة متعددة التكوين المعتمدة على الزمن هارتري: إعادة النظر في خوارزمية تقسيم المشروع، كيمياء. فيزي. 515، 252 (2018).
[144] أ. كوتش و ج. لوبيش، تقريب الموتر الديناميكي، مجلة SIAM لتحليل المصفوفات والتطبيقات 31، 2360 (2010).
[145] ج. هـ. غولوب و س. ف. ف. لون، حسابات المصفوفات، الطبعة الرابعة (دار جونز هوبكنز الجامعية، بالتيمور، 2013).
[146] ل. ج. دوريو، ف. غاتي، س. يونغ، و هـ.-د. ماير، حساب مستويات الطاقة الاهتزازية والحالات الذاتية للفلوروفورم باستخدام طريقة هارتري متعددة التكوينات المعتمدة على الزمن، مجلة الكيمياء الفيزيائية 129، 224109 (2008).
[147] U. Manthe، حول دمج معادلات الحركة متعددة التكوينات المعتمدة على الزمن هارتري (MCTDH)، كيمياء. فيزيكس. 329، 168 (2006).
[148] ت. ج. بارك وج. س. لايت، تطور الزمن الكمي الأحادي بواسطة تقليل لانكز التكراري، مجلة الكيمياء الفيزيائية 85، 5870 (1986).
[149] ه.-د. ماير و ه. وانغ، حول تنظيم معادلات الحركة MCTDH، مجلة الكيمياء الفيزيائية 148، 124105 (2018).
[150] ن. ليو، م. ب. سولي، و ف. س. باتيستا، طريقة مشغل تقسيم Tensor-Train KSL (TT-SOKSL) لمحاكاة الديناميات الكمومية، مجلة نظرية الكيمياء والحساب 18، 3327 (2022).
[151] ف. أ. ي. ن. شرويدر، د. هـ. ب. توربان، أ. ج. موسر، ن. د. م. هاين، وأ. و. تشين، محاكاة شبكة التنسور للديناميات الكمومية المفتوحة متعددة البيئات عبر التعلم الآلي وإعادة تنظيم التشابك، نات. كوميونيك. 10، 1062 (2019).
[152] ج. سيروتي، س. لوبيتش، و هـ. والاش، دمج الزمن لشبكات التنسور الشجرية، مجلة SIAM للتحليل العددي 59، 289 (2021).
[153] د. باورنفايند و م. آيشهورن، مبدأ التباين المعتمد على الزمن لشبكات التنسور الشجرية، ساي بوست فيزيكس. 8، 024 (2020).
[154] أ. غليس، ج.-و. لي، وج. فون ديلفت، الشكل الرسمي للمشاريع للمساحات المحتفظ بها والم discarded من حالات المنتج المصفوفي، فيزي. ريف. ب 106، 195138 (2022).
[155] ب.-أو. لودين، حول مشكلة عدم التوافق، في التقدم في الكيمياء الكمومية، المجلد 5، تحرير ب.-أو. لودين (دار النشر الأكاديمية، 1970) الصفحات 185-199.
[156] ج. سيروتي و ج. لوبيتش، مُتكامل قوي غير تقليدي للتقريب الديناميكي منخفض الرتبة، BIT الرياضيات العددية 62، 23 (2022).
[157] ر. كوسلوف و هـ. تال-إزر، طريقة استرخاء مباشرة لحساب الدوال الذاتية والقيم الذاتية لمعادلة شرودنجر على شبكة، رسائل الكيمياء والفيزياء 127، 223 (1986).
[158] ه.-د. ماير، ف. ل. كويري، س. ليونارد، وف. غاتي، حساب وتحديد انتقائي لمستويات الاهتزاز باستخدام خوارزمية هارتري متعددة التكوين المعتمدة على الزمن (MCTDH)، كيمياء. فيزيكس. 329، 179 (2006).
[159] إ. ر. دافيدسون، الحساب التكراري لبعض القيم الذاتية الأدنى والمتجهات الذاتية المقابلة لمصفوفات حقيقية متناظرة كبيرة، مجلة الفيزياء الحاسوبية 17، 87 (1975).
[160] ف. كولوت وج. لييفين، طريقة حسابية متعددة التكوينات لحل معادلة شرودنجر الاهتزازية في الجزيئات متعددة الذرات، نظرية الكيمياء. أكتا 89، 227 (1994).
[161] ك. دروكير و س. هاملز-شيفر، اشتقاق تحليلي لوظائف الموجة الاهتزازية لـ MC-SCF لمحاكاة الديناميكا الكمومية لتفاعلات نقل البروتونات المتعددة: التطبيق الأول على سلاسل الماء المؤينة، مجلة الكيمياء الفيزيائية 107، 363 (1997).
[162] س. هايسلبيز و ج. راوهوت، نظرية المجال الذاتي المتعدد التكوين الاهتزازي: التنفيذ وحسابات الاختبار، مجلة الكيمياء الفيزيائية 132، 124102 (2010).
[163] U. Manthe و F. Matzkies، التقطيع التكراري ضمن نهج هارتري متعدد التكوينات المعتمد على الزمن: حساب الحالات المثارة اهتزازياً ومعدلات التفاعل، كيمياء. فيزيكس. رسائل 252، 71 (1996).
[164] ر. وودرازكا وU. مانث، نهج هارتري متعدد التكوينات المعتمد على الزمن لحالات eigen لأنظمة متعددة الآبار، مجلة الكيمياء الفيزيائية 136، 124119 (2012).
[165] U. Manthe، نهج هارتري متعدد التكوينات متوسط الدولة المعتمد على الزمن: حسابات حالة الاهتزاز ومعدل التفاعل، مجلة الكيمياء الفيزيائية 128، 064108 (2008).
[166] ت. هامر وU. مانث، التقطيع التكراري في نهج هارتري متعدد التكوينات المعتمد على متوسط الحالة: انقسامات النفق في الحالة المثارة في المالونالديهيد، J. Chem. Phys. 136، 054105 (2012).
[167] هـ. وانغ، الحساب التكراري لحالات الطاقة الذاتية باستخدام نظرية هارتري متعددة الطبقات ومتعددة التكوين المعتمدة على الزمن، مجلة الفيزياء الكيميائية A 118، 9253 (2014).
[168] س. هولتز، ت. روهفيدر، ور. شنايدر، المخطط الخطي المتناوب لتحسين التنسور في تنسيق تنسور ترين، مجلة SIAM للعلوم الحاسوبية 34، A683 (2012).
[169] جي. كيه.-إل. تشان، لاغرانجيان مجموعة إعادة تنظيم مصفوفة الكثافة، فيزي. كيم. كيم. فيزي. 10، 3454 (2008).
[170] إ. رونكا، ز. لي، س. أ. خيمينيز-هويوس، و ج. ك.-ل. تشان، استهداف الزمن في خوارزميات مجموعة إعادة تشكيل مصفوفة الكثافة الديناميكية المعتمدة على الزمن مع هاملتونيان من النوع أب Initio، مجلة نظرية الكيمياء والحساب 13، 5560 (2017).
[171] ج. أفيلا و ت. كاريغتون، استخدام شبكات التكامل غير المنتجة لحل معادلة شرودنجر الاهتزازية في 12D، مجلة الكيمياء الفيزيائية 134، 054126 (2011).
[172] س. ووترز، و. بولمانز، و. ب. و. آيرز، و. د. فان نيك، CheMPS2: تنفيذ مفتوح المصدر ومتكيف مع الدوران لمجموعة إعادة تنظيم مصفوفة الكثافة في الكيمياء الكمومية من الدرجة الأولى، اتصالات الفيزياء الحاسوبية 185، 1501 (2014).
[173] ج. ج. دوراندو، ج. هاكمان، و ج. ك.-ل. تشان، خوارزميات الحالة المثارة المستهدفة، مجلة الكيمياء الفيزيائية 127، 084109 (2007).
[174] م. راخوبا و إ. أوسيلدس، حساب طيف الاهتزاز للجزيئات باستخدام تحليل مصفوفة التنسور، مجلة الكيمياء الفيزيائية 145، 124101 (2016).
[175] أ. بايارد، أ. ك. كيلمن، و م. ريهير، حالة الإثارة DMRG بسيطة مع FEAST، مجلة نظرية الكيمياء والحساب 18، 415 (2021).
[176] د. مينديف-تابيا، ت. فيرمينو، هـ.-د. ماير، و ف. غاتي، نحو تقارب منهجي لوظائف الموجة النووية متعددة الطبقات (ML) متعددة التكوين المعتمدة على الزمن هارتري: خوارزمية ML-spawning، كيمياء. فيزيكس. 482، 113 (2017).
[177] د. مينديف-تابيا و هـ.-د. ماير، تنظيم معادلات الحركة MCTDH من خلال اختيار مثالي على الفور (أي، توليد) لدوال الجسيمات الفردية غير المشغولة، مجلة الكيمياء الفيزيائية 153، 234114 (2020).
[178] أ. كوتش و ج. لوبيتش، انتظام تقريب هارتري الزمني متعدد التكوينات في الديناميكا الجزيئية الكمومية، ESAIM الرياضيات. نموذج. عدد. تحليل. 41، 315 (2007).
[179] سي. إم. هينز، إس. باوخ، و إم. بونيتز، عدم الاستقرار وعدم الدقة في هارتري-فوك متعدد التكوينات المعتمد على الزمن، سلسلة مؤتمرات الفيزياء 696، 012009 (2016).
[180] ب. كلوس، ي. ب. ليف، و د. رايشمان، مبدأ التباين المعتمد على الزمن في مجالات حالة المنتج المصفوفي: المخاطر والإمكانات، فيزي. ريف. ب 97، 024307 (2018).
[181] أ. ليغيزا، ج. رودر، و ب. أ. هيس، التحكم في دقة طريقة إعادة تشكيل مصفوفة الكثافة: نهج اختيار حالة الكتلة الديناميكية، فيزي. ريف. ب 67، 125114 (2003).
[182] ر. أوليفاريس-أماريا، و. هو، و. ناكاتاني، و. شارما، و. يانغ، و. ج. ك.-ل. تشان، مجموعة إعادة تشكيل مصفوفة الكثافة من البداية في الممارسة، مجلة الكيمياء الفيزيائية 142، 034102 (2015).
[183] س. ر. وايت، خوارزميات مجموعة إعادة تنظيم مصفوفة الكثافة مع موقع مركزي واحد، فيزي. ريف. ب 72، 180403(R) (2005).
[184] أ. ج. دانييت وأ. و. تشين، نهج فعال متكيف مع الروابط للديناميات الكمية المفتوحة عند درجات حرارة نهائية باستخدام مبدأ التباين الزمني المعتمد على موقع واحد لحالات المنتج المصفوفي، فيزي. ريف. ب 104، 214302 (2021).
[185] أ. ديكتور، أ. رودجرز، و د. فينتوري، طرق التنسور القابلة للتكيف مع الرتبة للمعادلات التفاضلية غير الخطية عالية الأبعاد، مجلة الحوسبة العلمية 88، 36 (2021).
[186] أ. إ. ستريلتسوف، أ. إ. ألون، و ل. س. سيدر باوم، دور الحالات المثارة في انقسام تكثيف بوز-أينشتاين المتفاعل المحبوس بواسطة حاجز يعتمد على الزمن، فيزي. ريف. ليت. 99، 030402 (2007).
[187] أ. إ. ألون، أ. إ. ستريلتسوف، و ل. س. سيدر باوم، طريقة هارتري المعتمدة على الزمن متعددة التكوينات للبوزونات: ديناميات العديد من الجسيمات للأنظمة البوزونية، فيزي. ريف. أ 77، 033613 (2008).
[188] ك.س. لي وأ.ر. فيشر، ديناميات العديد من الجسيمات المتفاعلة المختصرة: مبدأ تبايني مع مراقبة الخطأ، المجلة الدولية للفيزياء الحديثة ب 28، 1550021 (2014).
[189] U. Manthe، وظائف الجسيمات الفردية غير المشغولة المحسّنة في نهج هارتري متعدد التكوينات المعتمد على الزمن (متعدد الطبقات)، كيمياء. فيزي. 515، 279 (2018).
[190] ر. مارتينازو و I. بورغارت، خطأ محلي في الزمن في الديناميات الكمومية المتغيرة، فيزيكال ريفيو ليترز 124، 150601 (2020).
[191] ب. كلوس، قيد الإعداد (2023).
[192] م. يانغ و س. ر. وايت، مبدأ التباين المعتمد على الزمن مع فضاء كريلوف الفرعي المساعد، فيزي. ريف. ب 102، 094315 (2020).
[193] سي. هوبغ، آي. بي. مكولوك، يو. شولووك، وف. آ. وولف، خوارزمية DMRG ذات الموقع الواحد الصارمة مع توسيع الفضاء الفرعي، فيزيكال ريفيو بي 91، 155115 (2015).
[194] سي. هوبغ، ج. هاجيمان، ويو. شولووك، تقديرات الخطأ للتقديرات باستخدام حالات المنتج المصفوفي، فيزيكال ريفيو بي 97، 045125 (2018).
[195] ف. زاونر-شتاوبير، ل. فانديرستراتن، م. ت. فيشمان، ف. فيرسترات، و ج. هايغيمان، خوارزميات تحسين متغيرة لحالات المنتج المصفوفي الموحد، فيزيكس ريفيو ب 97، 045145 (2018).
[196] ج.و. لي، أ. غليس، وج. فون ديلفت، مبدأ التباين المعتمد على الزمن مع توسيع الروابط المتحكم فيه لحالات المنتج المصفوفي، arXiv.2208.10972 10.48550/arXiv.2208.10972 (2022).
[197] أ. غليس، ج.-و. لي، وج. فون ديلفت، توسيع الروابط المنضبط للبحث عن الحالة الأساسية لمجموعة إعادة تشكيل مصفوفة الكثافة بتكاليف موقع واحد، فيزي. ريف. ليت. 130، 246402 (2023).
[198] ج. سيروتي، ج. كوش، و س. لوبيتش، مُتكامل قوي متكيف مع الرتبة للتقريب الديناميكي منخفض الرتبة، BIT Numer. Math. 62، 1149 (2022).
[199] ج. سيروتي، ج. كوش، و س. لوبيتش، مُتكامل متوازي قابل للتكيف مع الرتبة للتقريب الديناميكي منخفض الرتبة (2023)، arxiv:2304.05660.
[200] ج. سيروتي، س. لوبيتش، و د. سولز، تكامل الزمن القابل للتكيف مع الرتبة لشبكات التنسور الشجرية، مجلة SIAM للتحليل العددي 61، 194 (2023).
[201] ن. ناكاتاني و ج. ك.-ل. تشان، حالات شبكة موتر الشجرة الفعالة (TTNS) في الكيمياء الكمومية: تعميمات لخوارزمية إعادة تشكيل مصفوفة الكثافة، مجلة الكيمياء الفيزيائية 138، 134113 (2013).
[202] ك. غونست، ف. فيرسترات، س. ووترز، أ. ليغيزا، و د. فان نيك، T3NS: حالات شبكة موتر الشجرة ثلاثية الأرجل، مجلة نظرية الكيمياء والحساب 14، 2026 (2018).
[203] هـ. ر. لارسون، هـ. زهاي، ج. ج. أومريغار، و ج. ك.-ل. تشان، ثنائي الكروم: إنهاء فصل من الكيمياء الكمومية، ج. أم. كيم. سوس. 144، 15932 (2022).
[204] أ. مينزر وأو. ليغيزا، خوارزميات حالة الشبكة التنسورية المتوازية بشكل كبير على الهياكل المعتمدة على وحدات المعالجة المركزية ووحدات معالجة الرسوميات، arXiv.2305.05581 10.48550/arXiv.2305.05581 (2023).
[205] H. Zhai، H. R. Larsson، S. Lee، Z.-H. Cui، T. Zhu، C. Sun، L. Peng، R. Peng، K. Liao، J. Tölle، J. Yang، S. Li، و G. K.-L. Chan، Block2: إطار عمل شامل مفتوح المصدر لتطوير وتطبيق خوارزميات DMRG المتطورة في هيكل الإلكترون وما بعده، J. Chem. Phys. 159، 234801 (2023).
[206] أو. كريستيانسن، صياغة الكوانتization الثانية لديناميات متعددة الأوضاع، مجلة الكيمياء الفيزيائية 120، 2140 (2004).
[207] ن. ك. مادسن، م. ب. هانسن، ج. أ. وورث، و أ. كريستيانسن، القطع المنهجي والتغيري لمساحة التكوين في طريقة هارتري متعددة التكوين المعتمدة على الزمن: تسلسل MCTDH[n]، مجلة الكيمياء الفيزيائية 152، 084101 (2020).
[208] ن. ك. مادسن، م. ب. هانسن، ج. أ. وورث، و أ. كريستيانسن، MR-MCTDH
[209] سي. إيفنهويز، جي. نيمان، ويو. مانث، الديناميات الكمومية لـ
[210] أ. فندريل، ف. غاتي، د. لوفيرغنات، و هـ.-د. ماير، محاكاة ديناميكية كمومية كاملة الأبعاد (15 بعدًا) لثنائي الماء المؤين. I. إعداد هاملتوني وتحليل حالة الاهتزاز الأرضية، ج. كيم. فيز. 127، 184302 (2007).
[211] م. شرويدر، تحويل أسطح الطاقة الكامنة عالية الأبعاد إلى تحليل متعدد الأبعاد قياسي باستخدام طرق مونت كارلو، مجلة الكيمياء الفيزيائية 152، 024108 (2020).
[212] م. شرويدر، ف. غاتي، د. لوفيرنات، هـ.-د. ماير، و أ. فندريل، اقتران البروتون المائي بقشرة الترطيب الأولى، نات كوميون 13، 6170 (2022).
[213] ج. موريز، ب. أ. هيس، و م. رايهر، سلوك التقارب لخوارزمية مجموعة إعادة تشكيل مصفوفة الكثافة لترتيبات المدارات المحسّنة، مجلة الكيمياء الفيزيائية 122، 024107 (2005).
[214] ج. باركزا، أ. ليغيزا، ك. هـ. مارتي، و م. رايهر، تحليل المعلومات الكمية للحالات الإلكترونية لهياكل جزيئية مختلفة، فيزيكال ريفيو A 83، 012508 (2011).
[215] و. لي، ج. رين، هـ. يانغ، وز. شواي، خوارزمية التبديل الفوري لترتيب درجات الحرية في مجموعة إعادة تنسيق مصفوفة الكثافة، مجلة الفيزياء: المادة المكثفة 34، 254003 (2022).
[216] أ. ب. ج. يانسن، تقريب هارتري المعتمد على الزمن متعدد التكوينات استنادًا إلى حالات الجسيمات الفردية الطبيعية، مجلة الكيمياء الفيزيائية 99، 4055 (1993).
[217] ه.-د. ماير، دراسة الديناميات الكمية الجزيئية باستخدام طريقة هارتري متعددة التكوينات المعتمدة على الزمن، وايلي مراجعات متعددة التخصصات في علوم الحوسبة والجزيئات 2، 351 (2012).
[218] م. شرويدر و هـ.-د. ماير، تحويل أسطح الطاقة الكامنة عالية الأبعاد إلى شكل مجموع المنتجات باستخدام طرق مونت كارلو، مجلة الكيمياء الفيزيائية 147، 064105 (2017).
[219] ر. إيليربروك وU. مانث، تمثيل متغيرات منفصلة غير هرمية، مجلة الكيمياء الفيزيائية 156، 134107 (2022).
[220] ر. ويلش وU. مانث، ديناميات التفاعل باستخدام نهج هارتري متعدد الطبقات ومتعدد التكوينات المعتمد على الزمن:
[221] ك. مينغ و هـ.-د. ماير، دراسة متعددة الطبقات متعددة التكوين تعتمد على الزمن الكامل لأطياف الامتصاص فوق البنفسجية لأكسيد الفورمالديهايد، مجلة الكيمياء الفيزيائية 141، 124309 (2014).
[222] ب. هارتكي، التحسين العالمي، WIREs علوم الحوسبة والجزيئات 1، 879 (2011).
[223] م. شرويدر، ف. غاتي، د. لوفيرنات، هـ.-د. ماير، و أ. فندريل، اقتران البروتون المائي مع غلافه الأول من الترطيب [مجموعة بيانات] (2022).
[224] ك. أوكونيشي، هـ. أوييدا، و ت. نيشينو، تقسيم التشابك وشبكات موتر الشجرة، تقدم. النظرية. التجريب. الفيزياء 2023، 023A02 (2023).
[225] ت. هيكيهارا، هـ. أوييدا، ك. أوكونيشي، ك. هارادا، و ت. نيشينو، تحسين الهيكل التلقائي لشبكات موتر الشجرة، فيزيكال ريفيو ريسيرش 5، 013031 (2023).
[226] د. مينديف-تابيا، هـ.-د. ماير، و أ. فندريل، الجمع الأمثل للأوضاع في طريقة هارتري متعددة التكوين المعتمدة على الزمن من خلال الإحصائيات متعددة المتغيرات: تحليل العوامل والتجميع الهرمي، مجلة نظرية الكيمياء والحساب 19، 1144 (2023).
- لارسون [في] ucmerced.e
- لارسون [في] ucmerced.e
DOI: https://doi.org/10.1080/00268976.2024.2306881
Publication Date: 2024-02-12
A tensor network view of multilayer multiconfiguration time-dependent Hartree methods
Abstract
The multilayer multiconfiguration time-dependent Hartree (ML-MCTDH) method and the density matrix renormalization group (DMRG) are powerful workhorses applied mostly in different scientific fields. Although both methods are based on tensor network states, very different mathematical languages are used for describing them. This severely limits knowledge transfer and sometimes leads to re-inventions of ideas well known in the other field. Here, we review ML-MCTDH and DMRG theory using both MCTDH expressions and tensor network diagrams. We derive the ML-MCTDH equations of motions using diagrams and compare them with timedependent and time-independent DMRG algorithms. We further review two selected recent advancements. The first advancement is related to optimizing unoccupied single-particle functions in MCTDH, which corresponds to subspace enrichment in the DMRG. The second advancement is related to finding optimal tree structures and on highlighting similarities and differences of tensor networks used in MCTDH and DMRG theories. We hope that this contribution will foster more fruitful cross-fertilization of ideas between ML-MCTDH and DMRG.
I. INTRODUCTION
II. THE MULTILAYER MULTICONFIGURATION TIME-DEPENDENT HARTREE ANSATZ
(2) For MCTDH with mode combination [103],
| description | symbol | alternative symbols | ||
| physical dimension |
|
|
||
| physical (“primitive”) basis state |
|
|
||
| physical basis dimension |
|
|
||
| number of layers | L | |||
| layer |
|
|||
| SPF basis state |
|
|
||
| horizontal position in layer
|
|
|
||
| node/SPF position |
|
|
||
| layer and node/SPF position |
|
|
||
|
|
||||
| coefficient tensor position |
|
|
||
| node/tensor/site/SPF dimension |
|
|
||
| bond dim./rank/SPF basis size |
|
|
||
| generic SPF basis size |
|
|
||
| total size of basis representing SPF |
|
|||
| SPF index |
|
|
||
| SPF composite index |
|
|||
| SHF composite index |
|
|||
| SPF tensor/site |
|
|
||
| configuration |
|
|
||
| single-hole function (SHF) |
|
|||
| SHF configuration |
|
|
||
| SPF projector |
|
|
||
| SHF projector |
|
|||
| single-particle density matrix |
|
|||
| mean-field operator |
|
|||
| gauge operator |
|
|
||
| one-dimensional Hamiltonian term |
|
(3) For ML-MCTDH,

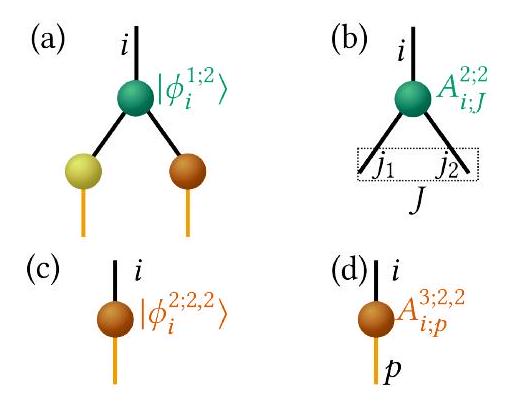
Armed with this simplified notation, we introduce the counterpart of the SPFs, the single-hole functions
In traditional DMRG language [4, 35, 51], Eq. (8), corresponds to using single-site DMRG and expanding the state in terms of a system block,


III. TENSOR NETWORK DIAGRAMS
IV. TENSOR NETWORK DIAGRAMS IN COMPARISON TO MCTDH LANGUAGE
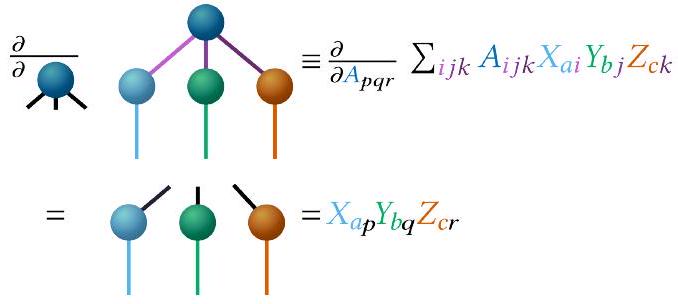
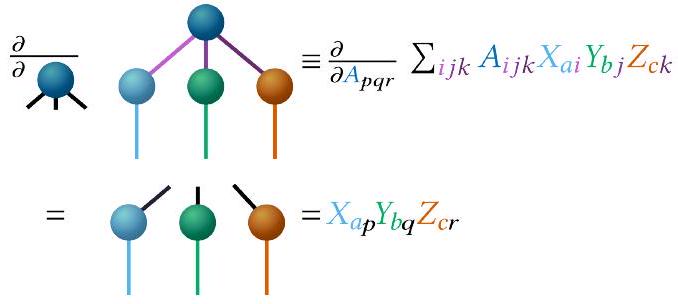
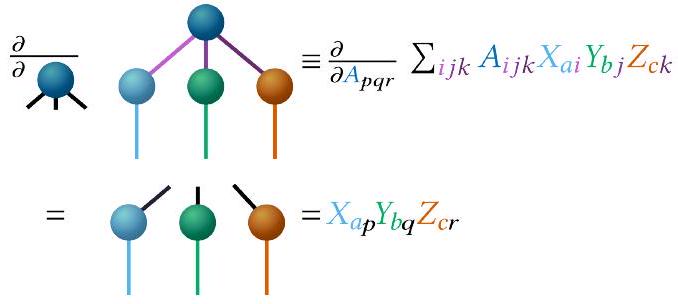




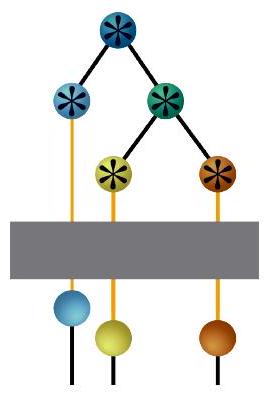
An example of an SHF


allow for a recursive definition of the SHFs:
V. ML-MCTDH EQUATIONS AND CONNECTION TO DIAGRAMS


A. Density matrices and mean fields
B. Equations of motions

C. Some common forms of the Hamiltonian


VI. DERIVATION OF ML-MCTDH USING DIAGRAMS

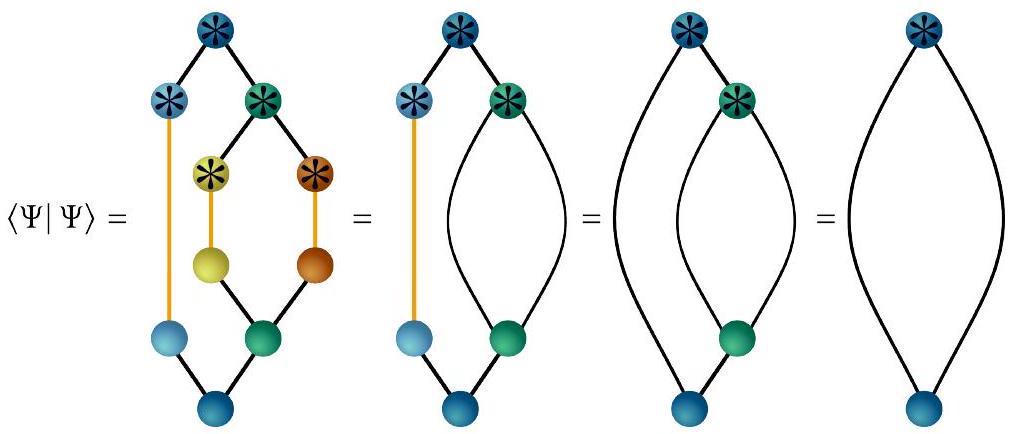
For the derivations of the equations of motions for each tensor, we again use the TTNS from Fig. 5 as a simple example but note that this can be easily generalized to any TTNS, including TTNSs with more layers. The first-order variation and time-derivative of

VII. CANONICALIZATION: CHANGE OF ROOT NODE AND SWEEPS



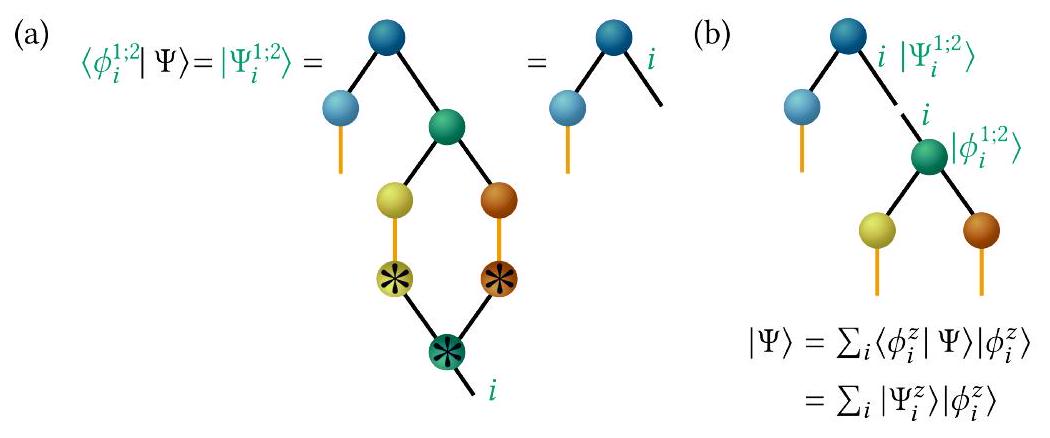
T can be chosen to orthogonalize and normalize the SHFs. This then leads to nonorthogonal T-transformed SPFs. Since SPFs should be orthonormal, however, now we can re-interpret Eq. (34) and just exchange the meanings of the T-transformed SHFs and SPFs by formally turning the now orthonormal SHFs into SPFs and vice versa. This leads to a change of the tree structure. Additionally, if the transformation is done for the first layer, the root node changes. This is shown in Fig. 25(b).


VIII. TIME-DEPENDENT DMRG APPROXIMATION



Here, before sketching the derivation, we first explain the basic ideas of TDVP-DMRG using somewhat hand-waving arguments. Since the TTNS changes its root node during the TDVP-DMRG sweep, the ML-MCTDH labeling scheme, which is tied to a particular rood node, is difficult to use. Instead, we will use generic symbols such as



IX. TIME-INDEPENDENT DMRG
compute the
X. PROPAGATING UNOCCUPIED SPFS AND SUBSPACE ENRICHMENT
A. Propagating unoccupied SPFs
B. Subspace enlargement: Optimizing unoccupied SPFs

1. Two-site DMRG approach
The two-site variant can avoid convergence issues and is particularly important for symmetry-adapted DMRG [35]. Before one can orthogonalize to the next node in the sweep, the two-site tensor needs to be decontracted using, e.g., an SVD. This allows for a straightforward way to dynamically adjust the bond dimension (number of SPFs). By observing the sum of discarded singular values, one obtains an error estimate, which can be used for energy extrapolations [7,181,182]. In fact, standard DMRG initially was formulated as two-site algorithm [3] and the one-site version is a more recent development [183]. Note, however, that two-site TDVP-DMRG still is based on the TDVP and thus possible issues due to unoccupied SPFs may not be fully resolved. Two-site DMRG also is known as modified ALS [168].
2. Lee/Fischer/Manthe approach


3. Mendive-Tapia/Meyer approach
4. One-site DMRG approaches
5. White approach
6. Energy variance approaches
7. BUG integrator approach
XI. TREE STRUCTURES
A. TTNSs or MPSs?
B. Optimal tree structure

XII. CONCLUSIONS
that are more actively used in MCTDH methods are pruning (configuration selection) and mixed basis-grid representations. Vice versa, topics that are more actively used in the context of the DMRG are symmetries, spectra calculations in frequency domain, and global approaches that directly apply the Hamiltonian onto the tensor network. Given these examples, there is still much room for mutual cross-fertilization of ideas. We hope that this article will help to foster more exchange of knowledge that will advance the overarching topic of tensor network states.
ACKNOWLEDGEMENTS
FUNDING
[1] H.-D. Meyer, U. Manthe, and L. S. Cederbaum, The multi-configurational time-dependent Hartree approach, Chem. Phys. Lett. 165, 73 (1990).
[2] U. Manthe, H.-D. Meyer, and L. S. Cederbaum, Wave-packet dynamics within the multiconfiguration Hartree framework: General aspects and application to NOCl, J. Chem. Phys. 97, 3199 (1992).
[3] S. R. White, Density matrix formulation for quantum renormalization groups, Phys. Rev. Lett. 69, 2863 (1992).
[4] S. R. White, Density-matrix algorithms for quantum renormalization groups, Phys. Rev. B 48, 10345 (1993).
[5] S. R. White and R. L. Martin,
[6] A. O. Mitrushenkov, G. Fano, F. Ortolani, R. Linguerri, and P. Palmieri, Quantum chemistry using the density matrix renormalization group, J. Chem. Phys. 115, 6815 (2001).
[7] G. K.-L. Chan and M. Head-Gordon, Highly correlated calculations with a polynomial cost algorithm: A study of the density matrix renormalization group, J. Chem. Phys. 116, 4462 (2002).
[8] Ö. Legeza, J. Röder, and B. A. Hess, QC-DMRG study of the ionic-neutral curve crossing of LiF, Mol. Phys. 101, 2019 (2003), arxiv:condmat/0208187.
[9] J. Zanghellini, M. Kitzler, C. Fabian, T. Brabec, and A. Scrinzi, An MCTDHF Approach to Multielectron Dynamics in Laser Fields, Laser Phys. 13, 6 (2003).
[10] T. Kato and H. Kono, Time-dependent multiconfiguration theory for electronic dynamics of molecules in an intense laser field, Chem. Phys. Lett. 392, 533 (2004).
[11] M. Nest, T. Klamroth, and P. Saalfrank, The multiconfiguration time-dependent Hartree-Fock method for quantum chemical calculations, J. Chem. Phys. 122, 124102 (2005).
[12] J. Caillat, J. Zanghellini, M. Kitzler, O. Koch, W. Kreuzer, and A. Scrinzi, Correlated multielectron systems in strong laser fields: A multiconfiguration time-dependent Hartree-Fock approach, Phys. Rev. A 71, 012712 (2005).
[13] H.-D. Meyer, F. Gatti, and G. A. Worth, eds., Multidimensional Quantum Dynamics: MCTDH Theory and Applications, 1st ed. (Wiley-VCH, Weinheim, 2009).
[14] D. Hochstuhl, C. M. Hinz, and M. Bonitz, Time-dependent multiconfiguration methods for the numerical simulation of photoionization processes of many-electron atoms, Eur. Phys. J. Spec. Top. 223, 177 (2014).
[15] A. U. J. Lode, C. Lévêque, L. B. Madsen, A. I. Streltsov, and O. E. Alon, Colloquium: Multiconfigurational time-dependent Hartree approaches for indistinguishable particles, Rev. Mod. Phys. 92, 011001 (2020).
[16] T. G. Kolda and B. W. Bader, Tensor Decompositions and Applications, SIAM Rev. 51, 455 (2009).
[17] H.-D. Meyer and G. A. Worth, Quantum molecular dynamics: Propagating wavepackets and density operators using the multiconfiguration time-dependent Hartree method, Theor. Chem. Acc. 109, 251 (2003).
[18] H. Wang and M. Thoss, Multilayer formulation of the multiconfiguration time-dependent Hartree theory, J. Chem. Phys. 119, 1289 (2003).
[19] U. Manthe, A multilayer multiconfigurational time-dependent Hartree approach for quantum dynamics on general potential energy surfaces, J. Chem. Phys. 128, 164116 (2008).
[20] R. Jullien, P. Pfeuty, J. N. Fields, and S. Doniach, Zero-temperature renormalization method for quantum systems. I. Ising model in a transverse field in one dimension, Phys. Rev. B 18, 3568 (1978).
[21] Y.-Y. Shi, L.-M. Duan, and G. Vidal, Classical simulation of quantum many-body systems with a tree tensor network, Phys. Rev. A 74, 022320 (2006).
[22] W. Hackbusch and S. Kühn, A New Scheme for the Tensor Representation, J. Fourier Anal. Appl. 15, 706 (2009).
[23] W. Hackbusch, Tensor Spaces and Numerical Tensor Calculus, 2nd ed., Springer Series in Computational Mathematics, Vol. 56 (Springer, Cham, Switzerland, 2019).
[24] L. Grasedyck, Hierarchical Singular Value Decomposition of Tensors, SIAM J. Matrix Anal. Appl. 31, 2029 (2010).
[25] L. Grasedyck, D. Kressner, and C. Tobler, A literature survey of low-rank tensor approximation techniques, GAMM-Mitteilungen 36, 53 (2013).
[26] S. Szalay, M. Pfeffer, V. Murg, G. Barcza, F. Verstraete, R. Schneider, and Ö. Legeza, Tensor product methods and entanglement optimization for
[27] G. Vidal, Efficient Simulation of One-Dimensional Quantum Many-Body Systems, Phys. Rev. Lett. 93, 040502 (2004).
[28] S. R. White and A. E. Feiguin, Real-Time Evolution Using the Density Matrix Renormalization Group, Phys. Rev. Lett. 93, 076401 (2004).
[29] A. E. Feiguin and S. R. White, Time-step targeting methods for real-time dynamics using the density matrix renormalization group, Phys. Rev. B 72, 020404 (2005).
[30] S. Paeckel, T. Köhler, A. Swoboda, S. R. Manmana, U. Schollwöck, and C. Hubig, Time-evolution methods for matrix-product states, Ann. Phys. 411, 167998 (2019).
[31] M. Fannes, B. Nachtergaele, and R. F. Werner, Finitely correlated states on quantum spin chains, Commun. Math. Phys. 144, 443 (1992).
[32] S. Östlund and S. Rommer, Thermodynamic Limit of Density Matrix Renormalization, Phys. Rev. Lett. 75, 3537 (1995).
[33] G. Vidal, Efficient Classical Simulation of Slightly Entangled Quantum Computations, Phys. Rev. Lett. 91, 147902 (2003).
[34] F. Verstraete and J. I. Cirac, Matrix product states represent ground states faithfully, Phys. Rev. B 73, 094423 (2006).
[35] U. Schollwöck, The density-matrix renormalization group in the age of matrix product states, Ann. Phys. 326, 96 (2011).
[36] R. Hübener, V. Nebendahl, and W. Dür, Concatenated tensor network states, New J. Phys. 12, 025004 (2010).
[37] V. Murg, F. Verstraete, Ö. Legeza, and R. M. Noack, Simulating strongly correlated quantum systems with tree tensor networks, Phys. Rev. B 82, 205105 (2010).
[38] H. J. Changlani, S. Ghosh, C. L. Henley, and A. M. Läuchli, Heisenberg antiferromagnet on Cayley trees: Low-energy spectrum and even/odd site imbalance, Phys. Rev. B 87, 085107 (2013).
[39] M. Gerster, P. Silvi, M. Rizzi, R. Fazio, T. Calarco, and S. Montangero, Unconstrained tree tensor network: An adaptive gauge picture for enhanced performance, Phys. Rev. B 90, 125154 (2014).
[40] V. Murg, F. Verstraete, R. Schneider, P. R. Nagy, and Ö. Legeza, Tree Tensor Network State with Variable Tensor Order: An Efficient Multireference Method for Strongly Correlated Systems, J. Chem. Theory Comput. 11, 1027 (2015).
[41] F. Verstraete and J. I. Cirac, Renormalization algorithms for Quantum-Many Body Systems in two and higher dimensions, arXiv:condmat/0407066 (2004), arxiv:cond-mat/0407066.
[42] G. Vidal, Entanglement Renormalization, Phys. Rev. Lett. 99, 220405 (2007).
[43] G. Vidal, Class of Quantum Many-Body States That Can Be Efficiently Simulated, Phys. Rev. Lett. 101, 110501 (2008).
[44] F. Verstraete, M. M. Wolf, D. Perez-Garcia, and J. I. Cirac, Criticality, the Area Law, and the Computational Power of Projected Entangled Pair States, Phys. Rev. Lett. 96, 220601 (2006).
[45] H. J. Changlani, J. M. Kinder, C. J. Umrigar, and G. K.-L. Chan, Approximating strongly correlated wave functions with correlator product states, Phys. Rev. B 80, 245116 (2009).
[46] K. H. Marti, B. Bauer, M. Reiher, M. Troyer, and F. Verstraete, Complete-graph tensor network states: A new fermionic wave function ansatz for molecules, New J. Phys. 12, 103008 (2010).
[47] G. K.-L. Chan, Low entanglement wavefunctions, Wiley Interdiscip. Rev. Comput. Mol. Sci. 2, 907 (2012).
[48] R. Orús, A practical introduction to tensor networks: Matrix product states and projected entangled pair states, Ann. Phys. 349, 117 (2014).
[49] R. Haghshenas, M. J. O’Rourke, and G. K.-L. Chan, Conversion of projected entangled pair states into a canonical form, Phys. Rev. B 100, 054404 (2019).
[50] M. P. Zaletel and F. Pollmann, Isometric Tensor Network States in Two Dimensions, Phys. Rev. Lett. 124, 037201 (2020).
[51] U. Schollwöck, The density-matrix renormalization group, Rev. Mod. Phys. 77, 57 (2005).
[52] K. Ueda, C. Jin, N. Shibata, Y. Hieida, and T. Nishino, Least Action Principle for the Real-Time Density Matrix Renormalization Group, arXiv:0612480 (2006), arxiv:cond-mat/0612480.
[53] J. J. Dorando, J. Hachmann, and G. K.-L. Chan, Analytic response theory for the density matrix renormalization group, J. Chem. Phys. 130, 184111 (2009).
[54] J. Haegeman, J. I. Cirac, T. J. Osborne, I. Pižorn, H. Verschelde, and F. Verstraete, Time-Dependent Variational Principle for Quantum Lattices, Phys. Rev. Lett. 107, 070601 (2011).
[55] N. Nakatani, S. Wouters, D. Van Neck, and G. K.-L. Chan, Linear response theory for the density matrix renormalization group: Efficient algorithms for strongly correlated excited states, J. Chem. Phys. 140, 024108 (2014).
[56] S. Wouters, N. Nakatani, D. Van Neck, and G. K.-L. Chan, Thouless theorem for matrix product states and subsequent post density matrix renormalization group methods, Phys. Rev. B 88, 075122 (2013).
[57] J. M. Kinder, C. C. Ralph, and G. Kin-Lic Chan, Analytic Time Evolution, Random Phase Approximation, and Green Functions for Matrix Product States, in Advances in Chemical Physics, edited by S. Kais (John Wiley & Sons, Inc., Hoboken, NJ, USA, 2014) 1st ed., pp. 179-192.
[58] H. Wang and M. Thoss, Numerically exact quantum dynamics for indistinguishable particles: The multilayer multiconfiguration time-dependent Hartree theory in second quantization representation, J. Chem. Phys. 131, 024114 (2009).
[59] H. R. Larsson, Computing vibrational eigenstates with tree tensor network states (TTNS), J. Chem. Phys. 151, 204102 (2019).
[60] B. Kloss, D. R. Reichman, and R. Tempelaar, Multiset Matrix Product State Calculations Reveal Mobile Franck-Condon Excitations Under Strong Holstein-Type Coupling, Phys. Rev. Lett. 123, 126601 (2019).
[61] J. Haegeman, C. Lubich, I. Oseledets, B. Vandereycken, and F. Verstraete, Unifying time evolution and optimization with matrix product states, Phys. Rev. B 94, 165116 (2016).
[62] X. Xie, Y. Liu, Y. Yao, U. Schollwöck, C. Liu, and H. Ma, Time-dependent density matrix renormalization group quantum dynamics for realistic chemical systems, J. Chem. Phys. 151, 224101 (2019).
[63] A. Baiardi and M. Reiher, Large-Scale Quantum Dynamics with Matrix Product States, J. Chem. Theory Comput. 15, 3481 (2019).
[64] A. Baiardi, C. J. Stein, V. Barone, and M. Reiher, Optimization of highly excited matrix product states with an application to vibrational spectroscopy, J. Chem. Phys. 150, 094113 (2019).
[65] Y. Kurashige, Matrix product state formulation of the multiconfiguration time-dependent Hartree theory, J. Chem. Phys. 149, 194114 (2018).
[66] J. Ren, Y. Wang, W. Li, T. Jiang, and Z. Shuai, Time-dependent density matrix renormalization group coupled with n-mode representation potentials for the excited state radiationless decay rate: Formalism and application to azulene, Chin. J. Chem. Phys. 34, 565 (2021).
[67] S. Mainali, F. Gatti, D. Iouchtchenko, P.-N. Roy, and H.-D. Meyer, Comparison of the multi-layer multi-configuration time-dependent Hartree (ML-MCTDH) method and the density matrix renormalization group (DMRG) for ground state properties of linear rotor chains, J. Chem. Phys. 154, 174106 (2021).
[68] H. R. Larsson, H. Zhai, K. Gunst, and G. K.-L. Chan, Matrix Product States with Large Sites, J. Chem. Theory Comput. 18, 749 (2022).
[69] Y. Xu, Z. Xie, X. Xie, U. Schollwöck, and H. Ma, Stochastic Adaptive Single-Site Time-Dependent Variational Principle, JACS Au 2, 335 (2022).
[70] H. R. Larsson, M. Schröder, R. Beckmann, F. Brieuc, C. Schran, D. Marx, and O. Vendrell, State-resolved infrared spectrum of the protonated water dimer: Revisiting the characteristic proton transfer doublet peak, Chem. Sci. 13, 11119 (2022).
[71] N. Glaser, A. Baiardi, and M. Reiher, Flexible DMRG-Based Framework for Anharmonic Vibrational Calculations, J. Chem. Theory Comput. 10.1021/acs.jctc.3c00902 (2023).
[72] F. Köhler, R. Mukherjee, and P. Schmelcher, Exploring disordered quantum spin models with a multilayer multiconfigurational approach, Phys. Rev. Res. 5, 023135 (2023).
[73] O. Koch and C. Lubich, Dynamical Low-Rank Approximation, SIAM J. Matrix Anal. & Appl. 29, 434 (2007).
[74] C. Lubich, From Quantum to Classical Molecular Dynamics: Reduced Models and Numerical Analysis, 1st ed. (European Mathematical Society, Zürich, Switzerland, 2008).
[75] L. P. Lindoy, B. Kloss, and D. R. Reichman, Time evolution of ML-MCTDH wavefunctions. I. Gauge conditions, basis functions, and singularities, J. Chem. Phys. 155, 174108 (2021).
[76] T. Weike and U. Manthe, Symmetries in the multi-configurational time-dependent Hartree wavefunction representation and propagation, J. Chem. Phys. 154, 194108 (2021).
[77] D. Gottlieb and S. A. Orszag, Numerical Analysis of Spectral Methods: Theory and Applications (Society for Industrial and Applied Mathematics, Philadelphia, Pa, 1987).
[78] P. A. M. Dirac, A new notation for quantum mechanics, Math. Proc. Camb. Philos. Soc. 35, 416 (1939).
[79] C. Cohen-Tannoudji, B. Diu, and F. Laloë, Quantum Mechanics, Volume 1: Basic Concepts, Tools, and Applications, 2nd ed. (Wiley-VCH, Weinheim, 2019).
[80] D. O. Harris, G. G. Engerholm, and W. D. Gwinn, Calculation of Matrix Elements for One-Dimensional Quantum-Mechanical Problems and the Application to Anharmonic Oscillators, J. Chem. Phys. 43, 1515 (1965).
[81] A. S. Dickinson and P. R. Certain, Calculation of Matrix Elements for One-Dimensional Quantum-Mechanical Problems, J. Chem. Phys. 49, 4209 (1968).
[82] J. V. Lill, G. A. Parker, and J. C. Light, Discrete variable representations and sudden models in quantum scattering theory, Chemical Physics Letters 89, 483 (1982).
[83] J. C. Light and T. Carrington Jr, Discrete-variable representations and their utilization, Adv. Chem. Phys. 114, 263 (2000).
[84] D. Tannor, Introduction to Quantum Mechanics, 1st ed. (University Science Books, Sausalito, Calif, 2008).
[85] D. Tannor, S. Machnes, E. Assémat, and H. R. Larsson, Phase-Space Versus Coordinate-Space Methods: Prognosis for Large Quantum Calculations, in Advances in Chemical Physics, Vol. 163, edited by K. B. Whaley (John Wiley & Sons, Inc., Hoboken, NJ, USA, 2018) pp. 273-323.
[86] D. Baye, The Lagrange-mesh method, Phys. Rep. 565, 1 (2015).
[87] J. P. Boyd, Chebyshev and Fourier Spectral Methods: Second Revised Edition, second edition, revised ed. (Dover Publications, Mineola, N.Y, 2001).
[88] I. Burghardt, K. Giri, and G. A. Worth, Multimode quantum dynamics using Gaussian wavepackets: The Gaussian-based multiconfiguration time-dependent Hartree (G-MCTDH) method applied to the absorption spectrum of pyrazine, J. Chem. Phys. 129, 174104 (2008).
[89] S. Römer, M. Ruckenbauer, and I. Burghardt, Gaussian-based multiconfiguration time-dependent Hartree: A two-layer approach. I. Theory, J. Chem. Phys. 138, 064106 (2013).
[90] P. A. M. Dirac, Note on Exchange Phenomena in the Thomas Atom, Math. Proc. Camb. Philos. Soc. 26, 376 (1930).
[91] J. Frenkel, Wave Mechanics; Advanced General Theory, 1st ed. (Oxford Univ. Press, 1934).
[92] A. McLachlan, A variational solution of the time-dependent Schrodinger equation, Mol. Phys. 8, 39 (1964).
[93] P. Kramer and M. Saraceno, Geometry of the Time-Dependent Variational Principle in Quantum Mechanics, 1st ed. (Springer, Berlin, 1981).
[94] M. H. Beck, A. Jäckle, G. A. Worth, and H.-D. Meyer, The multiconfiguration time-dependent Hartree (MCTDH) method: A highly efficient algorithm for propagating wavepackets, Phys. Rep. 324, 1 (2000).
[95] U. Manthe, Wavepacket dynamics and the multi-configurational time-dependent Hartree approach, J. Phys. Condens. Matter 29, 253001 (2017).
[96] O. Vendrell and H.-D. Meyer, Multilayer multiconfiguration time-dependent Hartree method: Implementation and applications to a Henon-Heiles Hamiltonian and to pyrazine, J. Chem. Phys. 134, 044135 (2011).
[97] H. Wang, Multilayer Multiconfiguration Time-Dependent Hartree Theory, J. Phys. Chem. A 119, 7951 (2015).
[98] C. Lubich, T. Rohwedder, R. Schneider, and B. Vandereycken, Dynamical Approximation by Hierarchical Tucker and Tensor-Train Tensors, SIAM J. Matrix Anal. Appl. 34, 470 (2013).
[99] C. Lubich and I. V. Oseledets, A projector-splitting integrator for dynamical low-rank approximation, BIT Numer. Math. 54, 171 (2014).
[100] C. Lubich, Time Integration in the Multiconfiguration Time-Dependent Hartree Method of Molecular Quantum Dynamics, Appl. Math. Res. EXpress 2015, 311 (2015).
[101] B. Kloss, I. Burghardt, and C. Lubich, Implementation of a novel projector-splitting integrator for the multi-configurational timedependent Hartree approach, J. Chem. Phys. 146, 174107 (2017).
[102] C. Lubich, B. Vandereycken, and H. Walach, Time Integration of Rank-Constrained Tucker Tensors, SIAM J. Numer. Anal. 56, 1273 (2018).
[103] G. A. Worth, H.-D. Meyer, and L. S. Cederbaum, Relaxation of a system with a conical intersection coupled to a bath: A benchmark 24-dimensional wave packet study treating the environment explicitly, J. Chem. Phys. 109, 3518 (1998).
[104] S. Sukiasyan and H.-D. Meyer, On the Effect of Initial Rotation on Reactivity. A Multi-Configuration Time-Dependent Hartree (MCTDH) Wave Packet Propagation Study on the H + D 2 and D
[105] G. Füchsel, P. S. Thomas, J. den Uyl, Y. Öztürk, F. Nattino, H.-D. Meyer, and G.-J. Kroes, Rotational effects on the dissociation dynamics of
[106] H. R. Larsson and D. J. Tannor, Dynamical pruning of the multiconfiguration time-dependent Hartree (DP-MCTDH) method: An efficient approach for multidimensional quantum dynamics, J. Chem. Phys. 147, 044103 (2017).
[107] D. R. Hartree, W. Hartree, and B. Swirles, Self-consistent field, including exchange and superposition of configurations, with some results for oxygen, Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 238, 229 (1939).
[108] J. Hinze, MC-SCF. I. The multi-configuration self-consistent-field method, J. Chem. Phys. 59, 6424 (1973).
[109] G. Das and A. C. Wahl, Extended Hartree-Fock Wavefunctions: Optimized Valence Configurations for
[110] B. O. Roos, P. R. Taylor, and P. E. M. Siegbahn, A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach, Chem. Phys. 48, 157 (1980).
[111] T. Helgaker, P. Jorgensen, and J. Olsen, Molecular Electronic-Structure Theory, 1st ed. (Wiley, Chichester ; New York, 2013).
[112] D. L. Yeager and P. Jørgensen, A multiconfigurational time-dependent Hartree-Fock approach, Chem. Phys. Lett. 65, 77 (1979).
[113] R. Moccia, Static and dynamic first- and second-order properties by variational wave functions, Int. J. Quantum Chem. 8, 293 (1974).
[114] E. Dalgaard, Time-dependent multiconfigurational Hartree-Fock theory, J. Chem. Phys. 72, 816 (1980).
[115] R. McWeeny, Some remarks on multiconfiguration time-dependent Hartree-Fock theory, Int. J. Quantum Chem. 23, 405 (1983).
[116] L. P. Lindoy, B. Kloss, and D. R. Reichman, Time evolution of ML-MCTDH wavefunctions. II. Application of the projector splitting integrator, J. Chem. Phys. 155, 174109 (2021).
[117] A. B. Kempe, On the Application of Clifford’s Graphs to Ordinary Binary Quantics, Proc. Lond. Math. Soc. s1-17, 107 (1885).
[118] P. Clifford, Extract of a Letter to Mr. Sylvester from Prof. Clifford of University College, London, Am. J. Math. 1, 126 (1878).
[119] J. J. Sylvester, On an Application of the New Atomic Theory to the Graphical Representation of the Invariants and Covariants of Binary Quantics, with Three Appendices, Am. J. Math. 1, 64 (1878), 2369436.
[120] J.-H. Kim, M. S. H. Oh, and K.-Y. Kim, Boosting vector calculus with the graphical notation, Am. J. Phys. 89, 200 (2021).
[121] R. Penrose, Applications of negative dimensional tensors, in Combinatorial Mathematics and Its Applications: Proceedings of a Conference Held at the Mathematical Institute, Oxford, from 7-10 7uly, 1969, edited by D. J. A. Welsh (Academic Press, 1971) pp. 221-244.
[122] A. Cichocki, N. Lee, I. Oseledets, A.-H. Phan, Q. Zhao, and D. P. Mandic, Tensor Networks for Dimensionality Reduction and Large-scale Optimization: Part 1 Low-Rank Tensor Decompositions, Found. Trends® Mach. Learn. 9, 249 (2016).
[123] J. C. Bridgeman and C. T. Chubb, Hand-waving and interpretive dance: An introductory course on tensor networks, J. Phys. Math. Theor. 50, 223001 (2017).
[124] A. Einstein, Die Grundlage der allgemeinen Relativitätstheorie, Ann. Phys. 354, 769 (1916).
[125] M. H. Beck and H.-D. Meyer, An efficient and robust integration scheme for the equations of motion of the multiconfiguration time-dependent Hartree (MCTDH) method, Z. Für Phys. At. Mol. Clust. 42, 113 (1997).
[126] U. Manthe, Comment on “A multiconfiguration time-dependent Hartree approximation based on natural single-particle states” [J. Chem. Phys. 99, 4055 (1993)], J. Chem. Phys. 101, 2652 (1994).
[127] K. G. Kay, The matrix singularity problem in the time-dependent variational method, Chem. Phys. 137, 165 (1989).
[128] L. Vanderstraeten, J. Haegeman, and F. Verstraete, Tangent-space methods for uniform matrix product states, SciPost Phys. Lect. Notes , 7 (2019).
[129] U. Manthe, The multi-configurational time-dependent Hartree approach revisited, J. Chem. Phys. 142, 244109 (2015).
[130] H. Wang and H.-D. Meyer, On regularizing the ML-MCTDH equations of motion, J. Chem. Phys. 149, 044119 (2018).
[131] U. Manthe and H. Köppel, New method for calculating wave packet dynamics: Strongly coupled surfaces and the adiabatic basis, J. Chem. Phys. 93, 345 (1990).
[132] M. J. Bramley and T. Carrington, A general discrete variable method to calculate vibrational energy levels of three- and four-atom molecules, J. Chem. Phys. 99, 8519 (1993).
[133] H. R. Larsson, B. Hartke, and D. J. Tannor, Efficient molecular quantum dynamics in coordinate and phase space using pruned bases, J. Chem. Phys. 145, 204108 (2016).
[134] B. Pirvu, V. Murg, J. I. Cirac, and F. Verstraete, Matrix product operator representations, New J. Phys. 12, 025012 (2010).
[135] G. K.-L. Chan, A. Keselman, N. Nakatani, Z. Li, and S. R. White, Matrix product operators, matrix product states, and
[136] F. Otto, Multi-layer Potfit: An accurate potential representation for efficient high-dimensional quantum dynamics, J. Chem. Phys. 140, 014106 (2014).
[137] F. Otto, Y.-C. Chiang, and D. Peláez, Accuracy of Potfit-based potential representations and its impact on the performance of (ML)MCTDH, Chem. Phys. 509, 116 (2018).
[138] Z. Li and G. K.-L. Chan, Spin-Projected Matrix Product States: Versatile Tool for Strongly Correlated Systems, J. Chem. Theory Comput. 13, 2681 (2017).
[139] H. R. Larsson, C. A. Jiménez-Hoyos, and G. K.-L. Chan, Minimal Matrix Product States and Generalizations of Mean-Field and Geminal Wave Functions, J. Chem. Theory Comput. 16, 5057 (2020).
[140] H.-D. Meyer, J. Kučar, and L. S. Cederbaum, Time-dependent rotated Hartree: Formal development, J. Math. Phys. 29, 1417(1988).
[141] C. Lubich, I. V. Oseledets, and B. Vandereycken, Time Integration of Tensor Trains, SIAM J. Numer. Anal. 53, 917 (2015).
[142] E. Kieri, C. Lubich, and H. Walach, Discretized Dynamical Low-Rank Approximation in the Presence of Small Singular Values, SIAM J. Numer. Anal. 54, 1020 (2016).
[143] M. Bonfanti and I. Burghardt, Tangent space formulation of the Multi-Configuration Time-Dependent Hartree equations of motion: The projector-splitting algorithm revisited, Chem. Phys. 515, 252 (2018).
[144] O. Koch and C. Lubich, Dynamical Tensor Approximation, SIAM J. Matrix Anal. & Appl. 31, 2360 (2010).
[145] G. H. Golub and C. F. V. Loan, Matrix Computations, fourth edition ed. (Johns Hopkins University Press, Baltimore, 2013).
[146] L. J. Doriol, F. Gatti, C. Iung, and H.-D. Meyer, Computation of vibrational energy levels and eigenstates of fluoroform using the multiconfiguration time-dependent Hartree method, J. Chem. Phys. 129, 224109 (2008).
[147] U. Manthe, On the integration of the multi-configurational time-dependent Hartree (MCTDH) equations of motion, Chem. Phys. 329, 168 (2006).
[148] T. J. Park and J. C. Light, Unitary quantum time evolution by iterative Lanczos reduction, J. Chem. Phys. 85, 5870 (1986).
[149] H.-D. Meyer and H. Wang, On regularizing the MCTDH equations of motion, J. Chem. Phys. 148, 124105 (2018).
[150] N. Lyu, M. B. Soley, and V. S. Batista, Tensor-Train Split-Operator KSL (TT-SOKSL) Method for Quantum Dynamics Simulations, J. Chem. Theory Comput. 18, 3327 (2022).
[151] F. A. Y. N. Schröder, D. H. P. Turban, A. J. Musser, N. D. M. Hine, and A. W. Chin, Tensor network simulation of multi-environmental open quantum dynamics via machine learning and entanglement renormalisation, Nat. Commun. 10, 1062 (2019).
[152] G. Ceruti, C. Lubich, and H. Walach, Time Integration of Tree Tensor Networks, SIAM J. Numer. Anal. 59, 289 (2021).
[153] D. Bauernfeind and M. Aichhorn, Time dependent variational principle for tree Tensor Networks, SciPost Phys. 8, 024 (2020).
[154] A. Gleis, J.-W. Li, and J. Von Delft, Projector formalism for kept and discarded spaces of matrix product states, Phys. Rev. B 106, 195138 (2022).
[155] P.-O. Löwdin, On the Nonorthogonality Problem, in Advances in Quantum Chemistry, Vol. 5, edited by P.-O. Löwdin (Academic Press, 1970) pp. 185-199.
[156] G. Ceruti and C. Lubich, An unconventional robust integrator for dynamical low-rank approximation, BIT Numer. Math. 62, 23 (2022).
[157] R. Kosloff and H. Tal-Ezer, A direct relaxation method for calculating eigenfunctions and eigenvalues of the Schrödinger equation on a grid, Chem. Phys. Lett. 127, 223 (1986).
[158] H.-D. Meyer, F. L. Quéré, C. Léonard, and F. Gatti, Calculation and selective population of vibrational levels with the Multiconfiguration Time-Dependent Hartree (MCTDH) algorithm, Chem. Phys. 329, 179 (2006).
[159] E. R. Davidson, The iterative calculation of a few of the lowest eigenvalues and corresponding eigenvectors of large real-symmetric matrices, J. Comput. Phys. 17, 87 (1975).
[160] F. Culot and J. Liévin, A multiconfigurational SCF computational method for the resolution of the vibrational Schrödinger equation in polyatomic molecules, Theor. Chim. Acta 89, 227 (1994).
[161] K. Drukker and S. Hammes-Schiffer, An analytical derivation of MC-SCF vibrational wave functions for the quantum dynamical simulation of multiple proton transfer reactions: Initial application to protonated water chains, J. Chem. Phys. 107, 363 (1997).
[162] S. Heislbetz and G. Rauhut, Vibrational multiconfiguration self-consistent field theory: Implementation and test calculations, J. Chem. Phys. 132, 124102 (2010).
[163] U. Manthe and F. Matzkies, Iterative diagonalization within the multi-configurational time-dependent Hartree approach: Calculation of vibrationally excited states and reaction rates, Chem. Phys. Lett. 252, 71 (1996).
[164] R. Wodraszka and U. Manthe, A multi-configurational time-dependent Hartree approach to the eigenstates of multi-well systems, J. Chem. Phys. 136, 124119 (2012).
[165] U. Manthe, The state averaged multiconfigurational time-dependent Hartree approach: Vibrational state and reaction rate calculations, J. Chem. Phys. 128, 064108 (2008).
[166] T. Hammer and U. Manthe, Iterative diagonalization in the state-averaged multi-configurational time-dependent Hartree approach: Excited state tunneling splittings in malonaldehyde, J. Chem. Phys. 136, 054105 (2012).
[167] H. Wang, Iterative Calculation of Energy Eigenstates Employing the Multilayer Multiconfiguration Time-Dependent Hartree Theory, J. Phys. Chem. A 118, 9253 (2014).
[168] S. Holtz, T. Rohwedder, and R. Schneider, The Alternating Linear Scheme for Tensor Optimization in the Tensor Train Format, SIAM J. Sci. Comput. 34, A683 (2012).
[169] G. K.-L. Chan, Density matrix renormalisation group Lagrangians, Phys. Chem. Chem. Phys. 10, 3454 (2008).
[170] E. Ronca, Z. Li, C. A. Jimenez-Hoyos, and G. K.-L. Chan, Time-Step Targeting Time-Dependent and Dynamical Density Matrix Renormalization Group Algorithms with ab Initio Hamiltonians, J. Chem. Theory Comput. 13, 5560 (2017).
[171] G. Avila and T. Carrington, Using nonproduct quadrature grids to solve the vibrational Schrödinger equation in 12D, J. Chem. Phys. 134, 054126 (2011).
[172] S. Wouters, W. Poelmans, P. W. Ayers, and D. Van Neck, CheMPS2: A free open-source spin-adapted implementation of the density matrix renormalization group for ab initio quantum chemistry, Comput. Phys. Commun. 185, 1501 (2014).
[173] J. J. Dorando, J. Hachmann, and G. K.-L. Chan, Targeted excited state algorithms, J. Chem. Phys. 127, 084109 (2007).
[174] M. Rakhuba and I. Oseledets, Calculating vibrational spectra of molecules using tensor train decomposition, J. Chem. Phys. 145, 124101 (2016).
[175] A. Baiardi, A. K. Kelemen, and M. Reiher, Excited-State DMRG Made Simple with FEAST, J. Chem. Theory Comput. 18, 415 (2021).
[176] D. Mendive-Tapia, T. Firmino, H.-D. Meyer, and F. Gatti, Towards a systematic convergence of Multi-Layer (ML) Multi-Configuration Time-Dependent Hartree nuclear wavefunctions: The ML-spawning algorithm, Chem. Phys. 482, 113 (2017).
[177] D. Mendive-Tapia and H.-D. Meyer, Regularizing the MCTDH equations of motion through an optimal choice on-the-fly (i.e., spawning) of unoccupied single-particle functions, J. Chem. Phys. 153, 234114 (2020).
[178] O. Koch and C. Lubich, Regularity of the multi-configuration time-dependent Hartree approximation in quantum molecular dynamics, ESAIM Math. Model. Numer. Anal. 41, 315 (2007).
[179] C. M. Hinz, S. Bauch, and M. Bonitz, Instabilities and inaccuracies of multi-configuration time-dependent Hartree-Fock, J. Phys. Conf. Ser. 696, 012009 (2016).
[180] B. Kloss, Y. B. Lev, and D. Reichman, Time-dependent variational principle in matrix-product state manifolds: Pitfalls and potential, Phys. Rev. B 97, 024307 (2018).
[181] Ö. Legeza, J. Röder, and B. A. Hess, Controlling the accuracy of the density-matrix renormalization-group method: The dynamical block state selection approach, Phys. Rev. B 67, 125114 (2003).
[182] R. Olivares-Amaya, W. Hu, N. Nakatani, S. Sharma, J. Yang, and G. K.-L. Chan, The ab-initio density matrix renormalization group in practice, J. Chem. Phys. 142, 034102 (2015).
[183] S. R. White, Density matrix renormalization group algorithms with a single center site, Phys. Rev. B 72, 180403(R) (2005).
[184] A. J. Dunnett and A. W. Chin, Efficient bond-adaptive approach for finite-temperature open quantum dynamics using the one-site time-dependent variational principle for matrix product states, Phys. Rev. B 104, 214302 (2021).
[185] A. Dektor, A. Rodgers, and D. Venturi, Rank-Adaptive Tensor Methods for High-Dimensional Nonlinear PDEs, J. Sci. Comput. 88, 36 (2021).
[186] A. I. Streltsov, O. E. Alon, and L. S. Cederbaum, Role of Excited States in the Splitting of a Trapped Interacting Bose-Einstein Condensate by a Time-Dependent Barrier, Phys. Rev. Lett. 99, 030402 (2007).
[187] O. E. Alon, A. I. Streltsov, and L. S. Cederbaum, Multiconfigurational time-dependent Hartree method for bosons: Many-body dynamics of bosonic systems, Phys. Rev. A 77, 033613 (2008).
[188] K.-S. Lee and U. R. Fischer, Truncated many-body dynamics of interacting bosons: A variational principle with error monitoring, Int. J. Mod. Phys. B 28, 1550021 (2014).
[189] U. Manthe, Optimized unoccupied single-particle functions in the (multi-layer) multi-configurational time-dependent Hartree approach, Chem. Phys. 515, 279 (2018).
[190] R. Martinazzo and I. Burghardt, Local-in-Time Error in Variational Quantum Dynamics, Phys. Rev. Lett. 124, 150601 (2020).
[191] B. Kloss, in preparation (2023).
[192] M. Yang and S. R. White, Time-dependent variational principle with ancillary Krylov subspace, Phys. Rev. B 102, 094315 (2020).
[193] C. Hubig, I. P. McCulloch, U. Schollwöck, and F. A. Wolf, Strictly single-site DMRG algorithm with subspace expansion, Phys. Rev. B 91, 155115 (2015).
[194] C. Hubig, J. Haegeman, and U. Schollwöck, Error estimates for extrapolations with matrix-product states, Phys. Rev. B 97, 045125 (2018).
[195] V. Zauner-Stauber, L. Vanderstraeten, M. T. Fishman, F. Verstraete, and J. Haegeman, Variational optimization algorithms for uniform matrix product states, Phys. Rev. B 97, 045145 (2018).
[196] J.-W. Li, A. Gleis, and J. von Delft, Time-dependent variational principle with controlled bond expansion for matrix product states, arXiv.2208.10972 10.48550/arXiv.2208.10972 (2022).
[197] A. Gleis, J.-W. Li, and J. von Delft, Controlled Bond Expansion for Density Matrix Renormalization Group Ground State Search at Single-Site Costs, Phys. Rev. Lett. 130, 246402 (2023).
[198] G. Ceruti, J. Kusch, and C. Lubich, A rank-adaptive robust integrator for dynamical low-rank approximation, BIT Numer. Math. 62, 1149 (2022).
[199] G. Ceruti, J. Kusch, and C. Lubich, A parallel rank-adaptive integrator for dynamical low-rank approximation (2023), arxiv:2304.05660.
[200] G. Ceruti, C. Lubich, and D. Sulz, Rank-Adaptive Time Integration of Tree Tensor Networks, SIAM J. Numer. Anal. 61, 194 (2023).
[201] N. Nakatani and G. K.-L. Chan, Efficient tree tensor network states (TTNS) for quantum chemistry: Generalizations of the density matrix renormalization group algorithm, J. Chem. Phys. 138, 134113 (2013).
[202] K. Gunst, F. Verstraete, S. Wouters, Ö. Legeza, and D. Van Neck, T3NS: Three-Legged Tree Tensor Network States, J. Chem. Theory Comput. 14, 2026 (2018).
[203] H. R. Larsson, H. Zhai, C. J. Umrigar, and G. K.-L. Chan, The Chromium Dimer: Closing a Chapter of Quantum Chemistry, J. Am. Chem. Soc. 144, 15932 (2022).
[204] A. Menczer and Ö. Legeza, Massively Parallel Tensor Network State Algorithms on Hybrid CPU-GPU Based Architectures, arXiv.2305.05581 10.48550/arXiv.2305.05581 (2023).
[205] H. Zhai, H. R. Larsson, S. Lee, Z.-H. Cui, T. Zhu, C. Sun, L. Peng, R. Peng, K. Liao, J. Tölle, J. Yang, S. Li, and G. K.-L. Chan, Block2: A comprehensive open source framework to develop and apply state-of-the-art DMRG algorithms in electronic structure and beyond, J. Chem. Phys. 159, 234801 (2023).
[206] O. Christiansen, A second quantization formulation of multimode dynamics, J. Chem. Phys. 120, 2140 (2004).
[207] N. K. Madsen, M. B. Hansen, G. A. Worth, and O. Christiansen, Systematic and variational truncation of the configuration space in the multiconfiguration time-dependent Hartree method: The MCTDH[n] hierarchy, J. Chem. Phys. 152, 084101 (2020).
[208] N. K. Madsen, M. B. Hansen, G. A. Worth, and O. Christiansen, MR-MCTDH[
[209] C. Evenhuis, G. Nyman, and U. Manthe, Quantum dynamics of the
[210] O. Vendrell, F. Gatti, D. Lauvergnat, and H.-D. Meyer, Full-dimensional (15-dimensional) quantum-dynamical simulation of the protonated water dimer. I. Hamiltonian setup and analysis of the ground vibrational state, J. Chem. Phys. 127, 184302(2007).
[211] M. Schröder, Transforming high-dimensional potential energy surfaces into a canonical polyadic decomposition using Monte Carlo methods, J. Chem. Phys. 152, 024108 (2020).
[212] M. Schröder, F. Gatti, D. Lauvergnat, H.-D. Meyer, and O. Vendrell, The coupling of the hydrated proton to its first solvation shell, Nat Commun 13, 6170 (2022).
[213] G. Moritz, B. A. Hess, and M. Reiher, Convergence behavior of the density-matrix renormalization group algorithm for optimized orbital orderings, J. Chem. Phys. 122, 024107 (2005).
[214] G. Barcza, Ö. Legeza, K. H. Marti, and M. Reiher, Quantum-information analysis of electronic states of different molecular structures, Phys. Rev. A 83, 012508 (2011).
[215] W. Li, J. Ren, H. Yang, and Z. Shuai, On the fly swapping algorithm for ordering of degrees of freedom in density matrix renormalization group, J. Phys.: Condens. Matter 34, 254003 (2022).
[216] A. P. J. Jansen, A multiconfiguration time-dependent Hartree approximation based on natural single-particle states, J. Chem. Phys. 99, 4055 (1993).
[217] H.-D. Meyer, Studying molecular quantum dynamics with the multiconfiguration time-dependent Hartree method, Wiley Interdiscip. Rev. Comput. Mol. Sci. 2, 351 (2012).
[218] M. Schröder and H.-D. Meyer, Transforming high-dimensional potential energy surfaces into sum-of-products form using Monte Carlo methods, J. Chem. Phys. 147, 064105 (2017).
[219] R. Ellerbrock and U. Manthe, A non-hierarchical correlation discrete variable representation, J. Chem. Phys. 156, 134107 (2022).
[220] R. Welsch and U. Manthe, Reaction dynamics with the multi-layer multi-configurational time-dependent Hartree approach:
[221] Q. Meng and H.-D. Meyer, A full-dimensional multilayer multiconfiguration time-dependent Hartree study on the ultraviolet absorption spectrum of formaldehyde oxide, J. Chem. Phys. 141, 124309 (2014).
[222] B. Hartke, Global optimization, WIREs Comput Mol Sci 1, 879 (2011).
[223] M. Schröder, F. Gatti, D. Lauvergnat, H.-D. Meyer, and O. Vendrell, The coupling of the hydrated proton to its first solvation shell [Data set] (2022).
[224] K. Okunishi, H. Ueda, and T. Nishino, Entanglement bipartitioning and tree tensor networks, Prog. Theor. Exp. Phys. 2023, 023A02 (2023).
[225] T. Hikihara, H. Ueda, K. Okunishi, K. Harada, and T. Nishino, Automatic structural optimization of tree tensor networks, Phys. Rev. Res. 5, 013031 (2023).
[226] D. Mendive-Tapia, H.-D. Meyer, and O. Vendrell, Optimal Mode Combination in the Multiconfiguration Time-Dependent Hartree Method through Multivariate Statistics: Factor Analysis and Hierarchical Clustering, J. Chem. Theory Comput. 19, 1144 (2023).
- larsson [at] ucmerced.e
- larsson [at] ucmerced.e
