القيمة المضافة لتعلم الآلة في الاستدلال السببي: أدلة من دراسات تمت مراجعتها
الملخص
ملخص: الأدبيات الاقتصادية القياسية الجديدة والسريعة النمو تحقق تقدمًا في مشكلة استخدام أساليب التعلم الآلي لأسئلة الاستدلال السببي. ومع ذلك، لم تبدأ الأدبيات الاقتصادية التجريبية بعد في استغلال نقاط القوة لهذه الأساليب الحديثة بشكل كامل. نحن نعيد النظر في الدراسات التجريبية المؤثرة باستخدام أساليب التعلم الآلي السببي بهدف ربط النظرية الاقتصادية القياسية حول هذه الأساليب مع الاقتصاد التجريبي. نركز على التعلم الآلي المزدوج، والغابة السببية، وأساليب التعلم الآلي العامة، في سياق كل من تأثيرات المعالجة المتوسطة والمتنوعة. نوضح تنفيذ هذه الأساليب في مجموعة متنوعة من السياقات ونبرز الصلة والقيمة المضافة مقارنة بالأساليب التقليدية المستخدمة في الدراسات الأصلية.
1. المقدمة
2. تأثيرات العلاج المتوسطة
2.1. تأثير الضرائب على الشركات على الاستثمار وريادة الأعمال
2.1.2. تحليل DML. نعيد النظر في الفحص النهائي للمتانة في الورقة، والذي يتضمن جميع مجموعات المتغيرات الأربعة في نفس الوقت، باستخدام نموذج DML الجزئي الخطي. تقدم الجدول 1 النتائج. تعرض الأعمدة (1) إلى (7) تقديرات DML للنقطة لتأثير الضرائب على الشركات على الاستثمار وريادة الأعمال، باستخدام طرق ML مختلفة لتقدير دوال الإزعاج. يتم وصف مزيد من التفاصيل حول كيفية الحصول على تقديرات DML، والأساليب المستخدمة، ومعلمات الضبط في القسم S2.1 من الملحق الإلكتروني.
| (1) لاسو | (2) شجرة السجل | (3) تعزيز | (4) غابة | (5) الشبكة العصبية. | (6) مجموعة | (7) الأفضل | (8) OLS | |
| اللوحة أ: الاستثمار 2003-2005 | ||||||||
| معدل الضريبة على الشركات القانوني | -0.081 (0.083) | -0.056 (0.075) | -0.065 (0.076) | -0.077 (0.084) | -0.056 (0.103) | -0.074 (0.09) | -0.068 (0.089) | -0.064 (0.098) |
| معدل الضريبة الفعّالة للسنة الأولى | -0.122 (0.092) | -0.133 (0.089) | -0.156 (0.087) | -0.142 (0.093) | -0.137 (0.101) | -0.134 (0.091) | -0.138 (0.091) | -0.117 (0.106) |
| معدل الضريبة الفعّالة لمدة خمس سنوات | -0.178 (0.096) | -0.179 (0.095) | -0.199 (0.091) | -0.204 (0.094) | -0.218 (0.101) | -0.195 (0.099) | -0.203 (0.101) | -0.189 (0.118) |
| ملاحظات | 61 | 61 | 61 | 61 | 61 | 61 | 61 | 61 |
| اللوحة ب: الاستثمار الأجنبي المباشر 2003-2005 | ||||||||
| معدل الضريبة على الشركات القانوني | -0.136 (0.085) | -0.167 (0.088) | -0.142 (0.09) | -0.131 (0.091) | -0.078 (0.09) | -0.123 (0.092) | -0.112 (0.092) | -0.030 (0.066) |
| معدل الضريبة الفعّالة للسنة الأولى | -0.172 (0.091) | -0.203 (0.084) | -0.188 (0.085) | -0.169 (0.079) | -0.154 (0.084) | -0.168 (0.088) | -0.16 (0.085) | -0.1 (0.071) |
| معدل الضريبة الفعّالة لمدة خمس سنوات | -0.162 (0.093) | -0.183 (0.076) | -0.169 (0.076) | -0.177 (0.08) | -0.164 (0.09) | -0.17 (0.086) | -0.15 (0.084) | -0.095 (0.081) |
| ملاحظات | 61 | 61 | 61 | 61 | 61 | 61 | 61 | 61 |
| اللوحة ج: كثافة الأعمال | ||||||||
| معدل الضريبة على الشركات القانوني | -0.054 (0.063) | -0.088 (0.072) | -0.063 (0.066) | -0.06 (0.063) | -0.031 (0.077) | -0.054 (0.067) | -0.042 (0.069) | -0.034 (0.083) |
| معدل الضريبة الفعّالة للسنة الأولى | -0.105 (0.074) | -0.158 (0.087) | -0.123 (0.073) | -0.115 (0.07) | -0.091 (0.083) | -0.099 (0.074) | -0.102 (0.076) | -0.068 (0.092) |
| معدل الضريبة الفعّالة لمدة خمس سنوات | -0.093 (0.075) | -0.14 (0.085) | -0.11 (0.072) | -0.104 (0.068) | -0.087 (0.086) | -0.107 (0.076) | -0.098 (0.075) | -0.070 (0.103) |
| ملاحظات | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 |
| اللوحة د: معدل الدخول المتوسط 2000-2004 | ||||||||
| معدل الضريبة على الشركات القانوني | -0.128 (0.067) | -0.15 (0.066) | -0.141 (0.066) | -0.133 (0.065) | -0.079 (0.081) | -0.12 (0.071) | -0.113 (0.071) | -0.029 (0.086) |
| معدل الضريبة الفعّالة للسنة الأولى | -0.107 (0.075) | -0.136 (0.066) | -0.14 (0.069) | -0.115 (0.066) | -0.109 (0.082) | -0.116 (0.074) | -0.112 (0.072) | -0.083 (0.094) |
| معدل الضريبة الفعّالة لمدة خمس سنوات | -0.156 (0.076) | -0.146 (0.072) | -0.155 (0.072) | -0.15 (0.07) | -0.175 (0.087) | -0.155 (0.075) | -0.152 (0.077) | -0.133 (0.103) |
| ملاحظات | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 |
| المتغيرات الخام | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
الأخطاء المعيارية أقل في معظم الانحدارات. بالإضافة إلى ذلك، فإن النتائج ذات دلالة إحصائية، على الأقل عند
تحليل معاملات اللاسو التي لم يتم تقليصها إلى الصفر والبحث عن غير الخطية بينها. كمثال، نعرض في الشكل S3.1 في الملحق الإلكتروني، الأكثر صلة من بين الحدود غير الخطية التي اختارها اللاسو، لأحد انحدارات DML المبلغ عنها في الجدول 1.
2.2. تأثير التعريفات الجمركية الموجهة نحو المهارات على النمو
2.2.2. تحليل DML. نعيد النظر في الانحدارات على مستوى الدول والصناعات المبلغ عنها في نون وتريفيلر (2010a، الجدول 4 [الأعمدة 1 و 2 و 4]، الجدول 5 [الأعمدة 1 و 2 و 4]، الجدول 6 [الأعمدة 1 و 3 و 7]). يتم الإبلاغ عن مزيد من التفاصيل حول كيفية الحصول على تقديرات DML وقيم معلمات الضبط في القسم S2.2 من الملحق الإلكتروني.
| (1) لاسو | (2) شجرة السجل | (3) تعزيز | (4) غابة | (5) الشبكة العصبية | (6) مجموعة | (7) الأفضل | (8) OLS | |
| اللوحة أ: ارتباط تعرفة المهارات | ||||||||
| ارتباط تعرفة المهارات | 0.019 (0.010) | 0.016 (0.012) | 0.016 (0.011) | 0.016 (0.011) | 0.013 (0.015) | 0.019 (0.012) | 0.016 (0.011) | 0.035 (0.010) |
| اللوحة ب: فرق التعرفة (حد القطع المنخفض) | ||||||||
| فرق التعرفة (حد أدنى منخفض) | 0.010 (0.005) | 0.008 (0.005) | 0.009 (0.005) | 0.008 (0.006) | 0.006 (0.008) | 0.008 (0.006) | 0.008 (0.006) | 0.016 (0.006) |
| اللوحة ج: فرق التعرفة (حد القطع العالي) | ||||||||
| فرق التعرفة (حد القطع العالي) | 0.009 (0.005) | 0.006 (0.005) | 0.007 (0.005) | 0.008 (0.005) | 0.013 (0.008) | 0.009 (0.005) | 0.008 (0.005) | 0.02 (0.004) |
| ملاحظات | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 |
| المتغيرات الخام | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 |
3. آثار العلاج غير المتجانسة
3.1. تأثير قناة فوكس نيوز على حصة التصويت الجمهوري
3.1.2. تحليل الغابة السببية. نقوم بإجراء تحليل التأثيرات المتغايرة باستخدام طريقة الغابة السببية. إن استكشاف التأثيرات المتغايرة مهم لهذه الدراسة، لفهم ما إذا كانت هناك خصائص للمدن أو المناطق تعمل كعوامل معدلة للتأثير. بينما تكون التأثيرات المتوسطة مفيدة لفهم تأثير قناة فوكس نيوز على العينة الكاملة، غالبًا ما تكون التأثيرات العلاجية غير متجانسة. من الممكن أن يكون تأثير قناة فوكس نيوز مركّزًا في بعض المناطق فقط. يمكن أن يساعد فهم خصائص المناطق التي شهدت أقوى وأضعف الاستجابات في تسليط الضوء على الآليات. الهدف من هذا التمرين هو مزدوج. أولاً، نتبنى وجهة نظر محايدة بشأن طبيعة التغاير، ونحقق فيما إذا كانت هناك خصائص للمدن أو المناطق تعمل كعوامل معدلة للتأثير العلاجي. ثانيًا، نفحص ما إذا كان تحليل التأثيرات المتغايرة من الورقة الأصلية يتطابق مع النتائج من طرق التعلم الآلي السببي.
| (1) متغيرات المناطق | (2) قوي العنقود | |
| أثر فوكس نيوز (ATE) | 0.0065 (0.0016) | 0.0065 (.0026) |
| تأثير فوكس نيوز فوق المتوسط | 0.011 (0.0023) | 0.0078 (0.0028) |
| تأثير فوكس نيوز دون المتوسط | -0.0028 (0.0022) | 0.0034 (0.0042) |
| فترة الثقة 95% للاختلاف | (0.00759, 0.01985) | ( – 0.00545, 0.01437) |
| ملاحظات | ٩٢٥٦ | ٩٢٥٦ |
تُقدم العادية التقريبية للغابة السببية في الحالات التي يكون فيها عدد المتغيرات التفسيرية منخفضًا نسبيًا، وتكون المتغيرات مستمرة. لتجاوز هذه المشكلة، نقوم بإجراء اختبار للمتانة باستخدام النهج الذي نفذه أثيري وواجر (2019)، حيث نقوم بتدريب غابة عشوائية أولية على جميع المتغيرات التفسيرية، وبعد ذلك نقوم بتشغيل غابة عشوائية نهائية على عدد مخفض من الميزات. يتم مناقشة النتائج في القسم S2.3 من الملحق الإلكتروني وهي مشابهة جدًا لتلك المقدمة في هذا القسم.
| (1) كات تحت الوسيط | (2) كات فوق الوسيط | (3)
|
||||||
| اللوحة أ: متغيرات المنطقة | ||||||||
| معدل التوظيف، الفرق بين 2000 و 1990 | 0.00929 (0.00243) | 0.0005 (0.00204) | 0.00562 | |||||
| شارك شهادة الثانوية العامة 2000 | 0.00806 (0.00222) | -0.00032 (0.00216) | 0.00676 | |||||
| ال décile 10 في عدد قنوات الكابل المتاحة | 0.00872 (0.00191) | -0.00456 (0.00262) |
|
|||||
|
|
|||||||
| شارك شهادة الثانوية العامة 2000 | 0.0085 (0.00301) | -0.0015 (0.00425) | 0.05492 | |||||
| ال décile 10 في عدد قنوات الكابل المتاحة | 0.0086 (0.00284) | -0.00524 (0.00513) | 0.01823 | |||||
تلتقط التأثيرات الخاصة بالمنطقة بشكل مناسب. يوفر غابة الأسباب القابلة للتجمع طريقة أكثر مرونة لالتقاط التأثيرات الخاصة بالمنطقة، وقد تكون أكثر ملاءمة في هذه الحالة.
3.2. تأثير تدريب المعلمين على أداء الطلاب
3.2.2. تحليل ML العام. نحن نوسع تحليل HTE الذي تم إجراؤه في الورقة الأصلية، من خلال تنفيذ طريقة التعلم الآلي العامة التي طورها تشيرنوزوكوف، ديميرير وآخرون (2018). إن استكشاف آثار العلاج غير المتجانسة له أهمية خاصة لهذه التدخل، لأن تقدير صغير وغير ذي دلالة للـ ATE قد يخفي تباينًا كبيرًا. هدفنا هو التعمق في تحليل آثار العلاج غير المتجانسة. أولاً، نحقق فيما إذا كان هناك تباين كبير في آثار العلاج؛ ثانياً، نقوم بتحليل ما إذا كانت طرق التعلم الآلي السببية، من خلال تنفيذ بحث منهجي عن التباين عبر عدد كبير من المتغيرات، يمكن أن تقدم رؤى إضافية حول خصائص أولئك الذين استفادوا من البرنامج وأولئك الذين لم يستفيدوا، مقارنة بالطرق التقليدية المستخدمة في الورقة الأصلية.
| (1) أكلت (
|
(2) هيت (
|
|
| تقدير | 0.002 | 0.651 |
| فترة الثقة 90% | ( – 0.068, 0.072) | (0.312, 0.990) |
|
|
1.000 | 0.0003 |
| ملاحظات | ١٠٠٠٦ | ١٠٠٠٦ |
عدد المتغيرات على مستوى الطلاب، بالإضافة إلى المتغيرات التي تشير إلى سلوك المعلمين في الفصل، والتي تم تقييمها من قبل الطلاب في البداية.
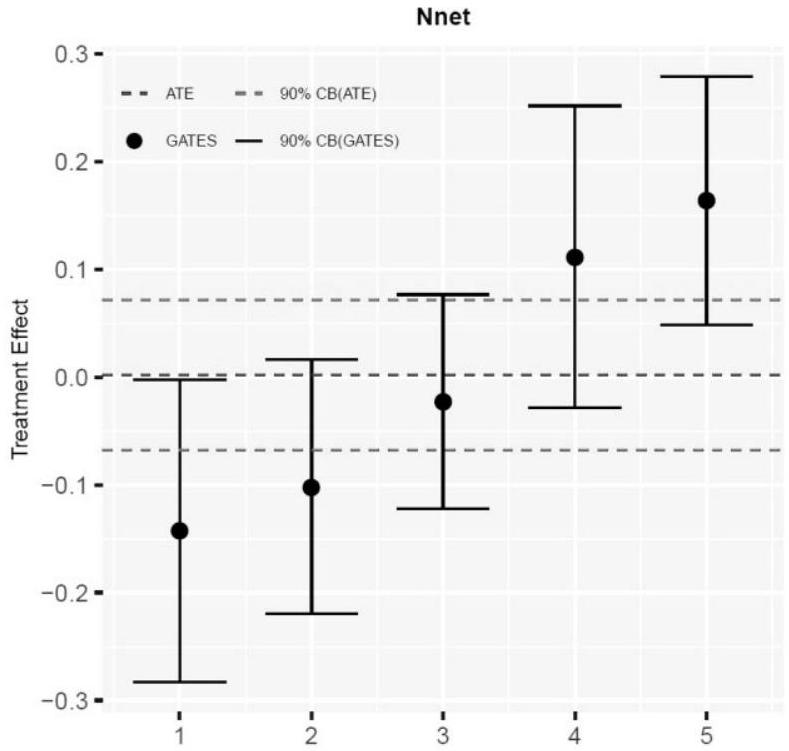
ملاحظة: تم الحصول على التقديرات باستخدام الشبكة العصبية لإنتاج المتنبئ البديل
| (1) 20% الأكثر تأثراً | (2) 20% الأقل تأثراً |
|
|||
| درجة بكاليوس في التعليم | 0.039 (0.019، 0.059) | 0.800 (0.780، 0.820) | 0.000 | ||
| ساعات تدريب المعلمين | 2.447 (2.399، 2.494) | 1.684 (1.636، 1.731) | 0.000 | ||
| تصنيف المعلمين | 0.666 (0.635، 0.697) | 0.405 (0.374، 0.437) | 0.000 | ||
| عمر الطالب | 14.18 (14.11، 14.25) | ١٣.٧٣ (١٣.٦٥، ١٣.٨٠) | 0.000 | ||
| خبرة المعلم (بالسنوات) | 16.18 (15.60، 16.76) | ١٣.١٦ (١٢.٥٨، ١٣.٧٤) | 0.000 | ||
| طالبة | 0.417 (0.385، 0.449) | 0.555 (0.523، 0.587) | 0.000 | ||
| عمر المعلم | ٣٧.٥١ (٣٧.٠٢، ٣٨.٠٠) | ٣٥.٠١ (٣٤.٥٢، ٣٥.٥٠) | 0.000 | ||
| درجة الطالب في الرياضيات عند البداية | -0.029 ( – 0.088, 0.031) | 0.169 (0.110، 0.229) | 0.005 | ||
| قلق الرياضيات الأساسي لدى الطلاب | 0.298 (0.236، 0.360) | -0.219 ( – 0.281, -0.157) | 0.000 | ||
| حجم الفصل | ٥٢.٨٧ (٥١.٨٢، ٥٣.٩٣) | ٦٤.٣٧ (٦٣.٣٢، ٦٥.٤٣) | 0.000 |
التدريب الذي تلقاه المعلم قبل التدخل، والذي لم يُعتبر محددًا للاختلاف في الورقة الأصلية، هو أعلى في المجموعة الأكثر تأثرًا مقارنة بالمجموعة الأقل تأثرًا.
4. الخاتمة
(أ) تعتبر طرق التعلم الآلي السببي مفيدة في البيئات التي تحتوي على العديد من المتغيرات المربكة المحتملة بالنسبة لحجم العينة. من خلال أمثلتنا المعاد النظر فيها، نوضح أهمية أخذ جميع المتغيرات المربكة المحتملة في الاعتبار دفعة واحدة، سواء بشكل خطي أو غير خطي. نعيد النظر في أكثر فحوصات القوة اكتمالاً لدجانكوف وآخرين (2010أ) ونون وتريفيلر (2010أ)، مع الأخذ في الاعتبار جميع المتغيرات المربكة المحتملة بشكل خطي وغير خطي، وهو ما لن يكون ممكنًا مع الطرق التقليدية. علاوة على ذلك، تشير نتائجنا من دراسة مونت كارلو إلى أنه مع زيادة عدد المتغيرات المستخدمة في التقدير بالنسبة لحجم العينة، تزداد الفوائد من استخدام DML مقارنةً بـ OLS.
(ب) تعتبر طرق التعلم الآلي السببي أكثر ملاءمة من الطرق التقليدية لالتقاط تأثير المتغيرات المشتركة بشكل مرن. نظرًا لأن الشكل الوظيفي الحقيقي غير معروف، فإن التقدير المرن يمكن أن يساعدنا في التقاط تأثير العوامل المربكة بشكل أفضل. على سبيل المثال، عند إعادة النظر في نتائج
(ج) نوصي أيضًا باستخدام طرق التعلم الآلي السببي في الحالات التي لا يمتلك فيها الباحث الكثير من الإرشادات من النظرية حول المتغيرات التي يجب تضمينها. وذلك لأن هذه الطرق تنفذ اختيار نموذج منهجي، بدلاً من اختيار مواصفة عشوائية، كما نناقش عند إعادة النظر في نتائج جانكوف وآخرون (2010أ). هذه الحجة مهمة أيضًا عند إجراء تحليل الحساسية وفحوصات المتانة، كما يتضح من نتائجنا عند إعادة النظر في نون وتريفيلر (2010أ).
(د) أخيرًا، إذا كان الباحث مهتمًا بتنوع التأثيرات، يمكن أن تضمن طرق التعلم الآلي السببية عدم تفويت التنوع ذي الصلة وعوامله، أو اكتشافه بشكل خاطئ بسبب مشكلات اختبار الفرضيات المتعددة. على سبيل المثال، يكشف تحليلنا لتنوع التأثيرات في الأوراق البحثية لديللا فيغنا وكابلان (2007أ) ولويالكا وآخرين (2019أ) عن عوامل محتملة للتنوع لم يتم أخذها في الاعتبار في التحليلات الأصلية، التي تعتمد على الطرق التقليدية. علاوة على ذلك، يمكن استخدام طرق التعلم الآلي السببية لكشف التنوع بعد الحدث، دون أن تكون ملزمة لاستكشاف تنوع التأثيرات فقط للمجموعات الفرعية المحددة في خطة التحليل المسبق.
شكر وتقدير
REFERENCES
Athey, S. and G. W. Imbens (2017). The state of applied econometrics: Causality and policy evaluation. Journal of Economic Perspectives 31(2), 3-32.
Athey, S. and G. W. Imbens (2019). Machine learning methods that economists should know about. Annual Review of Economics 11, 685-725.
Athey, S., J. Tibshirani and S. Wager (2019). Generalized random forests. Annals of Statistics 47, 1148-78.
Athey, S. and S. Wager (2019). Estimating treatment effects with causal forests: An application. Observational Studies 5, 37-51.
Bertrand, M., B. Crépon, A. Marguerie and P. Premand (2017). Contemporaneous and post-program impacts of a public works program: Evidence from Côte d’Ivoire. Working paper, University of Chicago, IL.
Chernozhukov, V., D. Chetverikov, M. Demirer, E. Duflo, C. Hansen and W. Newey (2017). Double/debiased/neyman machine learning of treatment effects. American Economic Review 107(5), 261-5.
Chernozhukov, V., D. Chetverikov, M. Demirer, E. Duflo, C. Hansen, W. Newey and J. Robins (2018). Double/debiased machine learning for treatment and structural parameters. Econometrics Journal 21, C1-68.
Chernozhukov, V., M. Demirer, E. Duflo and I. Fernandez-Val (2018). Generic machine learning inference on heterogenous treatment effects in randomized experiments. Working Paper 24678, National Bureau of Economic Research, Cambridge, MA.
Colangelo, K. and Y.-Y. Lee (2020). Double debiased machine learning nonparametric inference with continuous treatments. arXiv: Econometrics 2004.03036.
Davis, J. M. and S. B. Heller (2017). Using causal forests to predict treatment heterogeneity: An application to summer jobs. American Economic Review 107(5), 546-50.
Davis, J. M. and S. B. Heller (2020). Rethinking the benefits of youth employment programs: The heterogeneous effects of summer jobs. Review of Economics and Statistics 102, 664-77.
DellaVigna, S. and E. Kaplan (2007a). The Fox News effect: Media bias and voting. Quarterly Journal of Economics 122, 1187-234.
DellaVigna, S. and E. Kaplan (2007b). The Fox News effect: Media bias and voting [data]. Quarterly Journal of Economics. Data available at. https://eml.berkeley.edu/
Deryugina, T., G. Heutel, N. H. Miller, D. Molitor. and J. Reif (2019). The mortality and medical costs of air pollution: Evidence from changes in wind direction. American Economic Review 109(12), 4178-219.
Djankov, S., T. Ganser, C. McLiesh, R. Ramalho and A. Shleifer (2010a). The effect of corporate taxes on investment and entrepreneurship. American Economic Journal: Macroeconomics 2, 31-64.
Djankov, S., T. Ganser, C. McLiesh, R. Ramalho and A. Shleifer (2010b). The effect of corporate taxes on investment and entrepreneurship [data]. American Economic Journal: Macroeconomics. Data deposited at ICPSR, https://www.openicpsr.org/openicpsr/project/114179/version/V1/view.
Fair, R. C. (1978). The effect of economic events on votes for president. Review of Economics and Statistics 60, 159-73.
Farrell, M. H., T. Liang and S. Misra (2021). Deep neural networks for estimation and inference. Econometrica 89, 181-213.
Grossman, G. M. and E. Helpman (1991). Innovation and Growth in the Global Economy. Cambridge, MA: MIT Press.
Hill, J. L. (2011). Bayesian nonparametric modeling for causal inference. Journal of Computational and Graphical Statistics 20, 217-40.
Imai, K. and M. Ratkovic (2013). Estimating treatment effect heterogeneity in randomized program evaluation. Annals of Applied Statistics 7, 443-70.
Imbens, G. W. and D. B. Rubin (2015). Causal Inference in Statistics, Social, and Biomedical Sciences. New York: Cambridge University Press.
Knaus, M. C., M. Lechner and A. Strittmatter (2022). Heterogeneous employment effects of job search programmes: A machine learning approach. Journal of Human Resources 57, 597-636.
Kramer, G. H. (1971). Short-term fluctuations in us voting behavior, 1896-1964. American Political Science Review 65, 131-43.
Lewis-Beck, M. S. and M. Stegmaier (2000). Economic determinants of electoral outcomes. Annual Review of Political Science 3, 183-219.
List, J. A., A. M. Shaikh and Y. Xu (2019). Multiple hypothesis testing in experimental economics. Experimental Economics 22, 773-93.
Loyalka, P., A. Popova, G. Li and Z. Shi (2019a). Does teacher training actually work? Evidence from a large-scale randomized evaluation of a national teacher training program. American Economic Journal: Applied Economics 11, 128-54.
Loyalka, P., A. Popova, G. Li and Z. Shi (2019b). Does teacher training actually work? Evidence from a large-scale randomized evaluation of a national teacher training program [data]. American Economic Journal: Applied Economics. Data deposited at ICPSR, https://www.openicpsr.org/openicpsr/project/11 6356/version/V1/view.
Nunn, N. and D. Trefler (2010a). The structure of tariffs and long-term growth. American Economic Journal: Macroeconomics 2, 158-94.
Nunn, N. and D. Trefler (2010b). The structure of tariffs and long-term growth [data]. American Economic Journal: Macroeconomics. Data deposited at ICPSR, https://www.openicpsr.org/openicpsr/project/1141 83/version/V1/view.
Oprescu, M., V. Syrgkanis and Z. S. Wu (2019). Orthogonal random forest for causal inference. Proceedings of the 36th International Conference on Machine Learning PMLR 97, 4932-41.
Pissarides, C. A. (1980). British government popularity and economic performance. Economic Journal 90, 569-81.
Semenova, V., M. Goldman, V. Chernozhukov and M. Taddy (2018). Orthogonal machine learning for demand estimation: High dimensional causal inference in dynamic panels. arXiv: Machine Learning 1712.09988.
Su, X., C.-L. Tsai, H. Wang, D. M. Nickerson and B. Li (2009). Subgroup analysis via recursive partitioning. Journal of Machine Learning Research 10, 141-58.
Van der Laan, M. J. and S. Rose (2011). Targeted Learning: Causal Inference for Observational and Experimental Data. New York: Springer Science and Business Media.
Wager, S. and S. Athey (2018). Estimation and inference of heterogeneous treatment effects using random forests. Journal of the American Statistical Association 113, 1228-42.
Zeileis, A., T. Hothorn and K. Hornik (2008). Model-based recursive partitioning. Journal of Computational and Graphical Statistics 17, 492-514.
معلومات داعمة
حزمة النسخ المتماثل
شارك في تحرير هذا المخطوط فيكتور تشيرنوجوكوف.
- © المؤلف(ون) 2024. نُشر بواسطة مطبعة جامعة أكسفورد نيابة عن الجمعية الاقتصادية الملكية. هذه مقالة مفتوحة الوصول موزعة بموجب شروط ترخيص المشاع الإبداعي للنسب (“https://creativecommons.org/licenses/by/4.0/الذي يسمح بإعادة الاستخدام والتوزيع والاستنساخ غير المقيد في أي وسيلة، بشرط أن يتم الاقتباس من العمل الأصلي بشكل صحيح.
أحد الأسباب الأساسية هو أنه، على سبيل المثال، تعديلات الانحدار عالية الأبعاد مثل لاسو، ريدج، الشبكة المرنة، وما إلى ذلك، تقلل من التأثيرات المقدرة بشكل متعمد، وتجاهل هذه الانكماشات سيؤدي إلى تقديرات متحيزة لتأثير العلاج. من المهم أن نلاحظ هنا أن فكرة تقدير تأثيرات العلاج دون إجراء افتراضات بارامترية حول الطريقة التي تدخل بها المتغيرات المشتركة في المعادلة قد تم النظر فيها بالفعل في أدبيات الاقتصاد القياسي شبه البارامتري. انظر الورقة الاستعراضية لإمبنس وولدرج (2009) وإمبنس وروبين (2015). ومع ذلك، في الممارسة العملية، فإن هذه الطرق شبه البارامترية القائمة على النواة تنهار بسرعة إذا كان عليها التعامل مع أكثر من عدد قليل من المتغيرات المشتركة. لاحظ أن طريقة الغابة السببية التي قدمها واغر وأثي (2018) لم تُطور للإعدادات ذات الأبعاد العالية جدًا؛ ومع ذلك، فإن الطريقة العامة للتعلم الآلي التي قدمها تشيرنوزوكوف، ديميرير وآخرون (2018) يمكن أن تتعامل مع عدد كبير من المتغيرات.
بينما تم اقتراح حلول لتصحيح مشكلة اختبار الفرضيات المتعددة (على سبيل المثال، ليست وآخرون، 2019)، عندما يكون عدد المتغيرات التفسيرية كبيرًا، فإن قدرة هذه الأساليب على اكتشاف التباين تكون منخفضة (أثي وإيمبنس، 2017).
مسألة ذات صلة هي الاختيار المتأخر للتأثيرات المتغايرة الهامة. لتجنب هذه المشكلة، يُطلب من الباحثين في التجارب العشوائية المضبوطة تحديد التأثيرات المتغايرة التي يهتمون بالبحث فيها قبل التجربة، لتفادي البحث عن التأثيرات الهامة والإبلاغ عنها فقط. ومع ذلك، فإن هذا يحد من قدرة الباحث على اكتشاف التغاير ذي الصلة غير المتوقع. تضمن طرق التعلم الآلي السببي عدم تفويت التغاير ذي الصلة مع توفير فترات ثقة صحيحة. بالإضافة إلى ذلك، في الدراسات الرصدية، حيث لا تُعتبر خطط التحليل المسبق ممارسة شائعة، يمكن أن تكون طرق التعلم الآلي السببي مفيدة بشكل خاص. لتحليلنا، نستخدم بيانات النسخ المقدم من المؤلفين جانكوف وآخرون (2010ب) ونون وتريفلر (2010ب).
تشمل المجموعة الأولى من الضوابط تدابير للضرائب الأخرى؛ تشمل المجموعة الثانية تدابير لعدد المدفوعات الضريبية الأخرى التي تم القيام بها ولتجنب الضرائب؛ تشمل المجموعة الثالثة تدابير للمؤسسات؛ تشمل المجموعة الرابعة تدابير التضخم. يتضمن القسم S2.1 من الملحق الإلكتروني مزيدًا من التفاصيل حول الانحدارات المقدرة في جانكوف وآخرون (2010a) ويصف المتغيرات الضابطة. من المهم أن نلاحظ هنا أننا لا نستنتج باستخدام معاملات اللasso، ولكننا نقوم بتحليل حجم المعاملات كمقياس لأهمية المتغيرات التفسيرية في التنبؤ بالنتيجة ومتغيرات العلاج.
ترد تفاصيل إضافية حول تحليل معاملات اللasso في القسم S2.1 من الملحق الإلكتروني.
انظر القسم S1.2 في الملحق الإلكتروني لوصف طريقة الغابة السببية. نحن نعتبر الغابة السببية، وليس الطريقة العامة التي طورها تشيرنوزوكوف، ديميرير وآخرون (2018)، حيث تتطلب الأخيرة متغير علاج ثنائي.
الجدول S3.2 في الملحق الإلكتروني يظهر النتائج باستخدام القيم الافتراضية للمعلمات (التي تم الإبلاغ عنها في ملاحظات الجدول). نظرًا لصغر حجم العينة، لا يمكننا ضبط المعلمات باستخدام التحقق المتقاطع؛ وبالتالي، نقوم بإجراء تحليل الحساسية من خلال تغيير قيم المعلمات. النتائج، المتاحة عند الطلب، تتماشى مع تلك المبلغ عنها في الجدول S3.2 في الملحق الإلكتروني. الفترة الزمنية الأولية هي 1972 لـ 21 دولة، 1980-1983 لـ 30 دولة و1985-1987 لـ 12 دولة. الفترة النهائية هي 2000 لمعظم الدول، باستثناء ثلاث منها، حيث تنتهي البيانات في 1996. انظر نون وتريفلر (2010a، الجدول 1) للحصول على قائمة بالدول المشمولة والفترات الزمنية المعنية.
تُوصف التفاصيل الإضافية حول الانحدارات المقدرة بواسطة نون وتريفيلر (2010أ) وحول متغيرات التحكم في القسم S2.2 من الملحق الإلكتروني. كما في التطبيق الأول، فإن قيم معلمات الضبط المستخدمة هي القيم الافتراضية، وقد تم الإبلاغ عنها في ملاحظات الجدول S3.5 في الملحق الإلكتروني. النتائج التي تأخذ في الاعتبار قيمًا مختلفة للمعلمات تتماشى مع تلك المبلغ عنها ومتاحة عند الطلب. لتحليلنا، نستخدم بيانات النسخ المقدم من المؤلفين ديلا فيغنا وكابلان (2007ب) ولويالكا وآخرون (2019ب).
تُوصف التفاصيل الإضافية حول الانحدارات والمتغيرات الضابطة في ديللا فيغنا وكابلان (2007a) في القسم S2.3 من الملحق الإلكتروني.
تم الإبلاغ عن النتائج في ديللا فيغنا وكابلان (2007a، الجدول 6 من الورقة الأصلية). لتعزيز تحليلنا، نقوم بتنفيذ اختبار إضافي للتباين العام، مستلهم من طريقة أفضل متنبئ خطي في تشيرنوجوكوف، ديميرير وآخرون (2018). النتائج، المبلغ عنها في الجدول S3.6 والمناقشة في القسم S2.3 من الملحق الإلكتروني، تتماشى مع تلك التي تم الحصول عليها من الاختبار في الجدول 3. وجد أثيري وويجر (2019) نتيجة مشابهة في تطبيقهما، عند مقارنة الغابة السببية بدون تجميع مع النسخة المقاومة للتجميع.
انظر القسم S2.3 من الملحق الإلكتروني للحصول على تفاصيل حول كيفية بناء هذا المقياس. القيمة المتوسطة لل décile العاشر في عدد قنوات الكابل هي صفر؛ وبالتالي، فإن المدن التي تكون قيمة هذه المتغير أعلى من المتوسط تت correspond إلى المدن التي تقع في décile الأعلى من حيث عدد قنوات الكابل المتاحة.
وجد ديللا فيغنا وكابلان (2007أ) نتائج مختلطة للمناطق الجمهورية في مواصفات مختلفة. كما يظهر لوياكا وآخرون (2019أ) نتائج مماثلة عند تقدير تأثير التدخل في منتصف الدراسة أو نهايتها، نركز على متغيرات النتائج المقاسة في نهاية الدراسة.
يصف القسم S2.4 من الملحق الإلكتروني الانحدارات والمتغيرات الضابطة. تُوصف هذه المتغيرات الإضافية في القسم S2.4 من الملحق الإلكتروني. في دراسة لوياكا وآخرون (2019a)، يتم تضمين القيمة الأساسية لمتغير النتيجة كعنصر تحكم. وبالتالي، فإن الخصائص الأساسية الموصوفة أعلاه غير مدرجة في جميع الانحدارات في التحليل الأصلي. ومع ذلك، نعتبر هذه الخصائص كعوامل محتملة للتباين؛ لذلك، نقوم بتضمين القيم الأساسية لجميع المتغيرات المتاحة في تحليل التباين لدينا.
تتم مناقشة مزيد من التفاصيل حول أفضل مقاييس BLP وأفضل مقاييس GATES والمعلمات المستخدمة في هذه التحليل في القسم S2.4 من الملحق الإلكتروني. عند النظر في برنامج التنمية المهنية مع المتابعة، يجد المؤلفون تأثيرًا سلبيًا كبيرًا على درجات الطلاب الذين تخصص معلموهم في الرياضيات مقارنةً بدرجات أولئك الذين لم يتخصص معلموهم في ذلك. المتغير الذي يشير إلى ساعات تدريب المعلمين قبل التدخل هو متغير فئوي، يعتمد على الثلثيات للمتغير المستمر. نظرًا لأن المتغير المستمر غير مدرج في مجموعة بيانات النسخ الأصلية، فإننا نستخدم في تحليلنا هذا المتغير الفئوي، الذي يأخذ القيم من 1 إلى 3، حيث 3 هو الثلث الأعلى في عدد ساعات التدريب.
The value added of machine learning to causal inference: evidence from revisited studies
Abstract
Summary: A new and rapidly growing econometric literature is making advances in the problem of using machine learning methods for causal inference questions. Yet, the empirical economics literature has not started to fully exploit the strengths of these modern methods. We revisit influential empirical studies with causal machine learning methods aiming to connect the econometric theory on these methods with empirical economics. We focus on the double machine learning, causal forest, and generic machine learning methods, in the context of both average and heterogeneous treatment effects. We illustrate the implementation of these methods in a variety of settings and highlight the relevance and value added relative to traditional methods used in the original studies.
1. INTRODUCTION
2. AVERAGE TREATMENT EFFECTS
2.1. The Effect of corporate taxes on investment and entrepreneurship
2.1.2. DML analysis. We revisit the final robustness check of the paper, which includes all four sets of covariates at the same time, using the DML partially linear model. Table 1 presents the results. Columns (1) to (7) display the DML point estimates for the effect of corporate taxes on investment and entrepreneurship, using different ML methods to estimate the nuisance functions. Further details on how the DML estimates are obtained, the methods used, and the tuning parameters are described in Section S2.1 of the Online Appendix.
| (1) Lasso | (2) Reg. Tree | (3) Boosting | (4) Forest | (5) Neural Net. | (6) Ensemble | (7) Best | (8) OLS | |
| Panel A: Investment 2003-2005 | ||||||||
| Statutory corporate tax rate | -0.081 (0.083) | -0.056 (0.075) | -0.065 (0.076) | -0.077 (0.084) | -0.056 (0.103) | -0.074 (0.09) | -0.068 (0.089) | -0.064 (0.098) |
| First-year effective tax rate | -0.122 (0.092) | -0.133 (0.089) | -0.156 (0.087) | -0.142 (0.093) | -0.137 (0.101) | -0.134 (0.091) | -0.138 (0.091) | -0.117 (0.106) |
| Five-year effective tax rate | -0.178 (0.096) | -0.179 (0.095) | -0.199 (0.091) | -0.204 (0.094) | -0.218 (0.101) | -0.195 (0.099) | -0.203 (0.101) | -0.189 (0.118) |
| Observations | 61 | 61 | 61 | 61 | 61 | 61 | 61 | 61 |
| Panel B: FDI 2003-2005 | ||||||||
| Statutory corporate tax rate | -0.136 (0.085) | -0.167 (0.088) | -0.142 (0.09) | -0.131 (0.091) | -0.078 (0.09) | -0.123 (0.092) | -0.112 (0.092) | -0.030 (0.066) |
| First-year effective tax rate | -0.172 (0.091) | -0.203 (0.084) | -0.188 (0.085) | -0.169 (0.079) | -0.154 (0.084) | -0.168 (0.088) | -0.16 (0.085) | -0.1 (0.071) |
| Five-year effective tax rate | -0.162 (0.093) | -0.183 (0.076) | -0.169 (0.076) | -0.177 (0.08) | -0.164 (0.09) | -0.17 (0.086) | -0.15 (0.084) | -0.095 (0.081) |
| Observations | 61 | 61 | 61 | 61 | 61 | 61 | 61 | 61 |
| Panel C: Business density | ||||||||
| Statutory corporate tax rate | -0.054 (0.063) | -0.088 (0.072) | -0.063 (0.066) | -0.06 (0.063) | -0.031 (0.077) | -0.054 (0.067) | -0.042 (0.069) | -0.034 (0.083) |
| First-year effective tax rate | -0.105 (0.074) | -0.158 (0.087) | -0.123 (0.073) | -0.115 (0.07) | -0.091 (0.083) | -0.099 (0.074) | -0.102 (0.076) | -0.068 (0.092) |
| Five-year effective tax rate | -0.093 (0.075) | -0.14 (0.085) | -0.11 (0.072) | -0.104 (0.068) | -0.087 (0.086) | -0.107 (0.076) | -0.098 (0.075) | -0.070 (0.103) |
| Observations | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 |
| Panel D: Average entry rate 2000-2004 | ||||||||
| Statutory corporate tax rate | -0.128 (0.067) | -0.15 (0.066) | -0.141 (0.066) | -0.133 (0.065) | -0.079 (0.081) | -0.12 (0.071) | -0.113 (0.071) | -0.029 (0.086) |
| First-year effective tax rate | -0.107 (0.075) | -0.136 (0.066) | -0.14 (0.069) | -0.115 (0.066) | -0.109 (0.082) | -0.116 (0.074) | -0.112 (0.072) | -0.083 (0.094) |
| Five-year effective tax rate | -0.156 (0.076) | -0.146 (0.072) | -0.155 (0.072) | -0.15 (0.07) | -0.175 (0.087) | -0.155 (0.075) | -0.152 (0.077) | -0.133 (0.103) |
| Observations | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 |
| Raw covariates | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
standard errors are lower in most regressions. Additionally, the results are statistically significant, at least at the
analysing the lasso coefficients that are not shrunk to zero and looking for nonlinearities among these. As an example, we show in Figure S3.1 in the Online Appendix, the most relevant among the nonlinear terms selected by the lasso, for one of the DML regressions reported in Table 1.
2.2. The effect of skill-biased tariffs on growth
2.2.2. DML analysis. We revisit the country and industry-level regressions reported in Nunn and Trefler (2010a, tbl. 4 [cols. 1, 2, and 4], tbl. 5 [cols. 1, 2, and 4], tbl. 6 [cols. 1, 3, and 7]). Further details on how the DML estimates are obtained and on the tuning parameter values are reported in Section S2.2 of the Online Appendix.
| (1) Lasso | (2) Reg. Tree | (3) Boosting | (4) Forest | (5) Neural Net | (6) Ensemble | (7) Best | (8) OLS | |
| Panel A: Skill tariff correlation | ||||||||
| Skill tariff correlation | 0.019 (0.010) | 0.016 (0.012) | 0.016 (0.011) | 0.016 (0.011) | 0.013 (0.015) | 0.019 (0.012) | 0.016 (0.011) | 0.035 (0.010) |
| Panel B: Tariff differential (low cut-off) | ||||||||
| Tariff differential (low cut-off) | 0.010 (0.005) | 0.008 (0.005) | 0.009 (0.005) | 0.008 (0.006) | 0.006 (0.008) | 0.008 (0.006) | 0.008 (0.006) | 0.016 (0.006) |
| Panel C: Tariff differential (high cut-off) | ||||||||
| Tariff differential (high cut-off) | 0.009 (0.005) | 0.006 (0.005) | 0.007 (0.005) | 0.008 (0.005) | 0.013 (0.008) | 0.009 (0.005) | 0.008 (0.005) | 0.02 (0.004) |
| Observations | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 |
| Raw covariates | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 17 |
3. HETEROGENEOUS TREATMENT EFFECTS
3.1. The effect of Fox News on the republican vote share
3.1.2. Causal forest analysis. We perform the HTE analysis using the causal forest method. Exploring heterogeneous effects is important for this study, in order to understand whether there are town or district characteristics that act as effect modifiers. While the average effects are informative for the impact of Fox News on the whole sample, it is often the case that treatment effects are not homogeneous. It is possible that the effect of Fox News was concentrated in some areas only. Understanding better the characteristics of the areas which saw the strongest and weakest responses can shed light on the mechanisms. The aim of this exercise is two-fold. First, we take an agnostic view about the nature of heterogeneity, and we investigate whether there are town or district characteristics which are treatment effect modifiers. Second, we examine whether the HTE analysis from the original paper matches the results from the causal ML methods.
| (1) District dummies | (2) Cluster-robust | |
| Fox News effect (ATE) | 0.0065 (0.0016) | 0.0065 (.0026) |
| Fox News effect above median | 0.011 (0.0023) | 0.0078 (0.0028) |
| Fox News effect below median | -0.0028 (0.0022) | 0.0034 (0.0042) |
| 95% Confidence interval for the difference | (0.00759, 0.01985) | ( – 0.00545, 0.01437) |
| Observations | 9,256 | 9,256 |
asymptotic normality for the causal forest is provided for cases where the number of covariates is relatively low, and the covariates are continuous. To circumvent this issue, we perform a robustness check using the approach implemented by Athey and Wager (2019), where we train a preliminary random forest on all covariates, after which we run a final random forest on a reduced number of features. The results are discussed in Section S2.3 of the Online Appendix and are very similar to those presented in this section.
| (1) CATE below median | (2) CATE above median | (3)
|
||||||
| Panel A: District dummies | ||||||||
| Employment rate, diff. btw. 2000 and 1990 | 0.00929 (0.00243) | 0.0005 (0.00204) | 0.00562 | |||||
| Share high school degree 2000 | 0.00806 (0.00222) | -0.00032 (0.00216) | 0.00676 | |||||
| Decile 10 in no. cable channels available | 0.00872 (0.00191) | -0.00456 (0.00262) |
|
|||||
|
|
|||||||
| Share high school degree 2000 | 0.0085 (0.00301) | -0.0015 (0.00425) | 0.05492 | |||||
| Decile 10 in no. cable channels available | 0.0086 (0.00284) | -0.00524 (0.00513) | 0.01823 | |||||
appropriately capture the district-specific effects. The cluster-robust causal forest offers a more flexible way to capture district-specific effects, and may be more suitable in this case.
3.2. The effect of teacher training on student performance
3.2.2. Generic ML analysis. We extend the analysis of HTE conducted in the original paper, by implementing the generic machine learning method developed by Chernozhukov, Demirer et al. (2018). Exploring heterogeneous treatment effects is particularly relevant for this intervention, because a small and insignificant estimate for the ATE could hide significant heterogeneity. Our aim is to dig deeper into the analysis of heterogeneous treatment effects. First, we investigate whether there is significant heterogeneity in treatment effects; second, we analyse whether causal machine learning methods, by implementing a systematic search for heterogeneity across a large number of covariates, can offer additional insights about the characteristics of those who benefited from the programme and those who did not, compared to the traditional methods used in the original paper.
| (1) ATE (
|
(2) HET (
|
|
| Estimate | 0.002 | 0.651 |
| 90% Confidence interval | ( – 0.068, 0.072) | (0.312, 0.990) |
|
|
1.000 | 0.0003 |
| Observations | 10,006 | 10,006 |
number of student-level variables, plus variables indicating teachers behaviour in the classroom, evaluated by students at baseline.
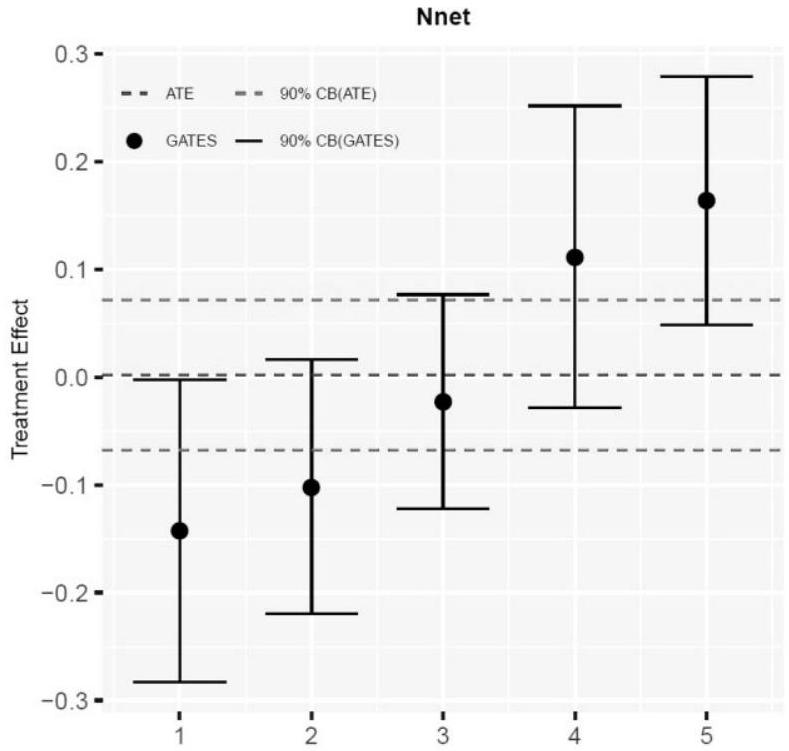
Note: The estimates are obtained using neural network to produce the proxy predictor
| (1) 20% most affected | (2) 20% least affected |
|
|||
| Teacher college degree | 0.039 (0.019, 0.059) | 0.800 (0.780, 0.820) | 0.000 | ||
| Teacher training hours | 2.447 (2.399, 2.494) | 1.684 (1.636, 1.731) | 0.000 | ||
| Teacher ranking | 0.666 (0.635, 0.697) | 0.405 (0.374, 0.437) | 0.000 | ||
| Student age | 14.18 (14.11, 14.25) | 13.73 (13.65, 13.80) | 0.000 | ||
| Teacher experience (years) | 16.18 (15.60, 16.76) | 13.16 (12.58, 13.74) | 0.000 | ||
| Student female | 0.417 (0.385, 0.449) | 0.555 (0.523, 0.587) | 0.000 | ||
| Teacher age | 37.51 (37.02, 38.00) | 35.01 (34.52, 35.50) | 0.000 | ||
| Student math score at baseline | -0.029 ( – 0.088, 0.031) | 0.169 (0.110, 0.229) | 0.005 | ||
| Student baseline math anxiety | 0.298 (0.236, 0.360) | -0.219 ( – 0.281, -0.157) | 0.000 | ||
| Class size | 52.87 (51.82, 53.93) | 64.37 (63.32, 65.43) | 0.000 |
training that the teacher received prior to the intervention, which is not found to be a determinant of heterogeneity in the original paper, is higher in the most affected group compared to the least affected group.
4. CONCLUSION
(a) Causal ML methods are useful in settings with many potential confounders relative to the sample size. With our revisited examples, we show the importance of taking into account all potentially relevant confounders at once, both linearly and nonlinearly. We revisit the most complete robustness checks of Djankov et al. (2010a) and Nunn and Trefler (2010a), considering all potential confounders linearly and nonlinearly, which would not be possible with traditional methods. Furthermore, our results from the Monte Carlo study suggest that, as the number of covariates used in the estimation increases relative to the sample size, the gains from using DML over OLS increase.
(b) Causal ML methods are more suitable than traditional methods to flexibly capture the effect of covariates. As the true functional form is unknown, with flexible estimation we can better capture the effect of confounders. For instance, when revisiting the results of
(c) We further recommend using causal ML methods in settings where the researcher does not have a lot of guidance from theory on which covariates should be included. This is because they implement a systematic model selection, rather than choosing an ad hoc specification, as we discuss when revisiting the results of Djankov et al. (2010a). This argument is also important when performing sensitivity analysis and robustness checks, as highlighted by our results when revisiting Nunn and Trefler (2010a).
(d) Finally, if the researcher is interested in HTE, causal machine learning methods can ensure that relevant heterogeneity and its determinants are not missed, or falsely discovered due to multiple hypothesis testing issues. For example, our analysis of the HTEs of the papers by DellaVigna and Kaplan (2007a) and Loyalka et al. (2019a) reveals potential determinants of heterogeneity that were not considered in the original analyses, which rely on traditional methods. Moreover, causal ML methods can be used to uncover heterogeneity ex post, without being bound to explore HTE only for the specific subgroups indicated in the pre-analysis plan.
ACKNOWLEDGEMENTS
REFERENCES
Athey, S. and G. W. Imbens (2017). The state of applied econometrics: Causality and policy evaluation. Journal of Economic Perspectives 31(2), 3-32.
Athey, S. and G. W. Imbens (2019). Machine learning methods that economists should know about. Annual Review of Economics 11, 685-725.
Athey, S., J. Tibshirani and S. Wager (2019). Generalized random forests. Annals of Statistics 47, 1148-78.
Athey, S. and S. Wager (2019). Estimating treatment effects with causal forests: An application. Observational Studies 5, 37-51.
Bertrand, M., B. Crépon, A. Marguerie and P. Premand (2017). Contemporaneous and post-program impacts of a public works program: Evidence from Côte d’Ivoire. Working paper, University of Chicago, IL.
Chernozhukov, V., D. Chetverikov, M. Demirer, E. Duflo, C. Hansen and W. Newey (2017). Double/debiased/neyman machine learning of treatment effects. American Economic Review 107(5), 261-5.
Chernozhukov, V., D. Chetverikov, M. Demirer, E. Duflo, C. Hansen, W. Newey and J. Robins (2018). Double/debiased machine learning for treatment and structural parameters. Econometrics Journal 21, C1-68.
Chernozhukov, V., M. Demirer, E. Duflo and I. Fernandez-Val (2018). Generic machine learning inference on heterogenous treatment effects in randomized experiments. Working Paper 24678, National Bureau of Economic Research, Cambridge, MA.
Colangelo, K. and Y.-Y. Lee (2020). Double debiased machine learning nonparametric inference with continuous treatments. arXiv: Econometrics 2004.03036.
Davis, J. M. and S. B. Heller (2017). Using causal forests to predict treatment heterogeneity: An application to summer jobs. American Economic Review 107(5), 546-50.
Davis, J. M. and S. B. Heller (2020). Rethinking the benefits of youth employment programs: The heterogeneous effects of summer jobs. Review of Economics and Statistics 102, 664-77.
DellaVigna, S. and E. Kaplan (2007a). The Fox News effect: Media bias and voting. Quarterly Journal of Economics 122, 1187-234.
DellaVigna, S. and E. Kaplan (2007b). The Fox News effect: Media bias and voting [data]. Quarterly Journal of Economics. Data available at. https://eml.berkeley.edu/
Deryugina, T., G. Heutel, N. H. Miller, D. Molitor. and J. Reif (2019). The mortality and medical costs of air pollution: Evidence from changes in wind direction. American Economic Review 109(12), 4178-219.
Djankov, S., T. Ganser, C. McLiesh, R. Ramalho and A. Shleifer (2010a). The effect of corporate taxes on investment and entrepreneurship. American Economic Journal: Macroeconomics 2, 31-64.
Djankov, S., T. Ganser, C. McLiesh, R. Ramalho and A. Shleifer (2010b). The effect of corporate taxes on investment and entrepreneurship [data]. American Economic Journal: Macroeconomics. Data deposited at ICPSR, https://www.openicpsr.org/openicpsr/project/114179/version/V1/view.
Fair, R. C. (1978). The effect of economic events on votes for president. Review of Economics and Statistics 60, 159-73.
Farrell, M. H., T. Liang and S. Misra (2021). Deep neural networks for estimation and inference. Econometrica 89, 181-213.
Grossman, G. M. and E. Helpman (1991). Innovation and Growth in the Global Economy. Cambridge, MA: MIT Press.
Hill, J. L. (2011). Bayesian nonparametric modeling for causal inference. Journal of Computational and Graphical Statistics 20, 217-40.
Imai, K. and M. Ratkovic (2013). Estimating treatment effect heterogeneity in randomized program evaluation. Annals of Applied Statistics 7, 443-70.
Imbens, G. W. and D. B. Rubin (2015). Causal Inference in Statistics, Social, and Biomedical Sciences. New York: Cambridge University Press.
Knaus, M. C., M. Lechner and A. Strittmatter (2022). Heterogeneous employment effects of job search programmes: A machine learning approach. Journal of Human Resources 57, 597-636.
Kramer, G. H. (1971). Short-term fluctuations in us voting behavior, 1896-1964. American Political Science Review 65, 131-43.
Lewis-Beck, M. S. and M. Stegmaier (2000). Economic determinants of electoral outcomes. Annual Review of Political Science 3, 183-219.
List, J. A., A. M. Shaikh and Y. Xu (2019). Multiple hypothesis testing in experimental economics. Experimental Economics 22, 773-93.
Loyalka, P., A. Popova, G. Li and Z. Shi (2019a). Does teacher training actually work? Evidence from a large-scale randomized evaluation of a national teacher training program. American Economic Journal: Applied Economics 11, 128-54.
Loyalka, P., A. Popova, G. Li and Z. Shi (2019b). Does teacher training actually work? Evidence from a large-scale randomized evaluation of a national teacher training program [data]. American Economic Journal: Applied Economics. Data deposited at ICPSR, https://www.openicpsr.org/openicpsr/project/11 6356/version/V1/view.
Nunn, N. and D. Trefler (2010a). The structure of tariffs and long-term growth. American Economic Journal: Macroeconomics 2, 158-94.
Nunn, N. and D. Trefler (2010b). The structure of tariffs and long-term growth [data]. American Economic Journal: Macroeconomics. Data deposited at ICPSR, https://www.openicpsr.org/openicpsr/project/1141 83/version/V1/view.
Oprescu, M., V. Syrgkanis and Z. S. Wu (2019). Orthogonal random forest for causal inference. Proceedings of the 36th International Conference on Machine Learning PMLR 97, 4932-41.
Pissarides, C. A. (1980). British government popularity and economic performance. Economic Journal 90, 569-81.
Semenova, V., M. Goldman, V. Chernozhukov and M. Taddy (2018). Orthogonal machine learning for demand estimation: High dimensional causal inference in dynamic panels. arXiv: Machine Learning 1712.09988.
Su, X., C.-L. Tsai, H. Wang, D. M. Nickerson and B. Li (2009). Subgroup analysis via recursive partitioning. Journal of Machine Learning Research 10, 141-58.
Van der Laan, M. J. and S. Rose (2011). Targeted Learning: Causal Inference for Observational and Experimental Data. New York: Springer Science and Business Media.
Wager, S. and S. Athey (2018). Estimation and inference of heterogeneous treatment effects using random forests. Journal of the American Statistical Association 113, 1228-42.
Zeileis, A., T. Hothorn and K. Hornik (2008). Model-based recursive partitioning. Journal of Computational and Graphical Statistics 17, 492-514.
SUPPORTING INFORMATION
Replication Package
Co-editor Victor Chernozhukov handled this manuscript.
- © The Author(s) 2024. Published by Oxford University Press on behalf of Royal Economic Society. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted reuse, distribution, and reproduction in any medium, provided the original work is properly cited.
One of the underlying reasons is that, for instance, high dimensional regression adjustments such as lasso, ridge, elastic net, etc., shrink the estimated effects by construction, and ignoring this shrinkage will lead to biased treatment effect estimates. It is important to note here that the idea of estimating treatment effects without making parametric assumptions about the way in which the covariates enter the equation has already been considered in the semi-parametric econometrics literature. See the review paper of Imbens and Wooldridge (2009) and Imbens and Rubin (2015). However, in practice, these semi-parametric kernel methods quickly break down if they have to deal with more than a few covariates. Note that the causal forest method by Wager and Athey (2018) is not developed for very high dimensional settings; however, the generic machine learning method of Chernozhukov, Demirer et al. (2018) can handle a large number of covariates.
While solutions have been proposed to correct for the issue of multiple hypothesis testing (for example, List et al., 2019), when the number of covariates is large, the power of these approaches to detect heterogeneity is low (Athey and Imbens, 2017).
A related issue is the ex post selection of significant heterogeneous effects. To avoid this problem, in randomized control trials researchers are often required to specify before the experiment which heterogeneous effects they are interested to look into, in order to avoid searching for, and only reporting, significant effects. However, this limits the ability of the researcher to find unexpected relevant heterogeneity. Causal ML methods ensure that relevant heterogeneity is not missed while also providing valid confidence intervals. In addition, in observational studies, where pre-analysis plans are not common practice, causal ML methods can be particularly useful. For our analysis, we use the replication data provided by the authors Djankov et al. (2010b) and Nunn and Trefler (2010b).
The first set of controls includes measures of other taxes; the second set includes measures for the number of other tax payments made and for tax evasion; the third set includes measures for institutions; the fourth set includes measures of inflation. Section S2.1 of the Online Appendix includes more details on the regressions estimated in Djankov et al. (2010a) and describes the control variables. It is important to note here that we do not make inference using the lasso coefficients, but we analyse the magnitude of the coefficients as a measure of the covariates’ importance for predicting the outcome and the treatment variables.
Further details about the lasso coefficients analysis are reported in Section S2.1 of the Online Appendix.
See Section S1.2 in the Online Appendix for a description of the causal forest method. We consider the causal forest, and not the generic method developed by Chernozhukov, Demirer et al. (2018), as the latter requires a binary treatment variable.
Table S3.2 in the Online Appendix shows the results using default values of the parameters (which are reported in the notes of the table). Due to the small sample size, we are unable to tune the parameters with cross-validation; thus, we perform sensitivity analysis varying the parameter values. The results, available on request, are consistent with those reported in Table S3.2 in the Online Appendix. The initial time period is 1972 for 21 countries, 1980-1983 for 30 countries and 1985-1987 for twelve countries. The end period is 2000 for most countries, except for three of them, for which data ends in 1996. See Nunn and Trefler (2010a, tbl. 1) for a list of the countries included and the respective time periods.
Further details on the regressions estimated by Nunn and Trefler (2010a) and on the control variables are described in Section S2.2 of the Online Appendix. As in the first application, the values of the tuning parameters used are the default values, and they are reported in the notes of Table S3.5 in the Online Appendix. Results considering different values for the parameters are consistent with those reported and are available on request. For our analysis, we use the replication data provided by the authors DellaVigna and Kaplan (2007b) and Loyalka et al. (2019b).
Further details on the regressions and on the control variables in DellaVigna and Kaplan (2007a) are described in Section S2.3 of the Online Appendix.
The findings are reported in DellaVigna and Kaplan (2007a, tbl. 6 of the original paper). To supplement our analysis, we implement an additional test for overall heterogeneity, inspired by the best linear predictor method in Chernozhukov, Demirer et al. (2018). The results, reported in Table S3.6 and discussed in Section S2.3 of the Online Appendix, are in line with those obtained from the test in Table 3. Athey and Wager (2019) find a similar result in their application, when comparing the causal forest without clustering with the cluster-robust version.
See Section S2.3 of the Online Appendix for details on how this measure is constructed. The median value for the 10th decile in number of cable channels is zero; hence, towns with value of this variable above median correspond to towns that are in the top decile in terms of number of cable channels available.
DellaVigna and Kaplan (2007a) found mixed results for Republican districts in different specifications. As Loyalka et al. (2019a) show similar results when estimating the impact of the intervention at midline or endline, we focus on the outcome variables measured at endline.
Section S2.4 of the Online Appendix describes the regressions and the control variables. These additional variables are described in Section S2.4 of the Online Appendix. In Loyalka et al. (2019a), the baseline value of the outcome variable is included as a control. Hence, the baseline characteristics described above are not included in all regressions in the original analysis. However, we consider these characteristics as potential drivers of heterogeneity; therefore, we include the baseline values of all available variables in our heterogeneity analysis.
Further details on the Best BLP and Best GATES measures and on the tuning parameters used in this analysis are discussed in Section S2.4 of the Online Appendix. When considering the PD plus follow-up, the authors find a significant negative effect on the scores of students whose teachers majored in math relative to the scores of those whose teachers did not. The variable indicating teacher training hours previous to the intervention is a categorical variable, based on the terciles of the continuous variable. As the continuous variable is not included in the replication data set of the original paper, for our analysis we use this categorical variable, which takes values 1 to 3 , where 3 is the top tercile in the number of training hours.
