التصنيف: الرياضيات (Mathematics)

تطوير وتطبيقات توزيع وايبل-وايبل العكسي الهجين الجديد Development and Applications of a New Hybrid Weibull-Inverse Weibull Distribution

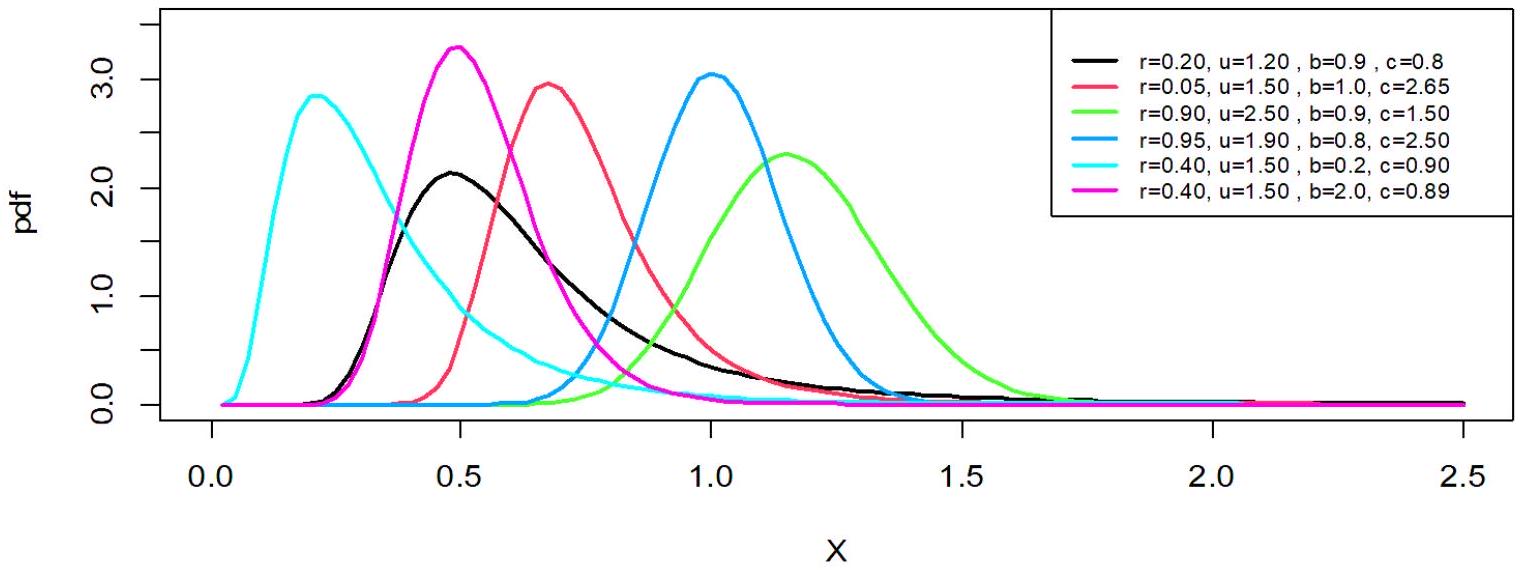
تقدم هذه الدراسة وتطبق نموذجًا إحصائيًا جديدًا يعرف بتوزيع وايبل العكسي الهجين (HWIW)، الذي يجمع بين خصائص توزيعي وايبل والعكسي وايبل لتوفير نموذج أكثر مرونة لتمثيل البيانات الواقعية، خاصة تلك التي تتميز باللامركزية أو القيم المتطرفة. تم اشتقاق الوظائف الأساسية للتوزيع، بالإضافة إلى اشتقاق مقاييس إحصائية أخرى مثل اللحظات، ودالة الكمية، والإنتروبيا. تم تقدير معلمات…
مقدرات ليو المعدلة الجديدة للتعامل مع التعدد الخطي في نموذج الانحدار بيتا: المحاكاة والتطبيقات New Modified Liu Estimators to Handle the Multicollinearity in the Beta Regression Model: Simulation and Applications

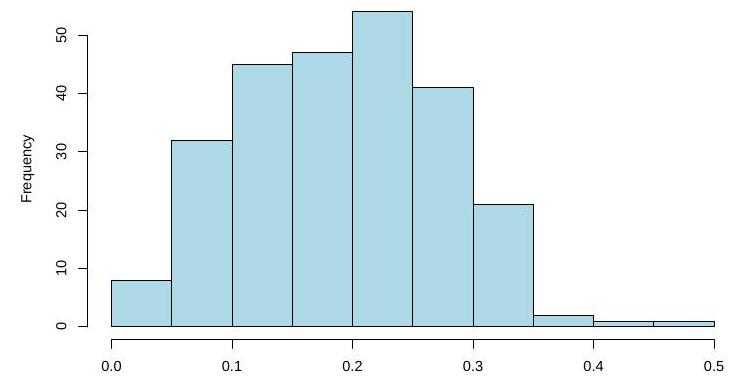
نموذج الانحدار بيتا (BRM) يُستخدم على نطاق واسع لتحليل المتغيرات المستجيبة المحدودة، مثل النسب والنسب المئوية. ومع ذلك، عندما يوجد تعدد خطي بين المتغيرات التفسيرية، يصبح مقدر الاحتمالية القصوى التقليدي (MLE) غير مستقر وغير فعال. لمعالجة هذه المشكلة، نقترح مقدرات ليو المعدلة الجديدة لـ BRM، المصممة لتعزيز دقة التقدير في وجود تعدد خطي مرتفع بين…
استغلال التفرد المخفي على سطح كرة بوانكاريه Exploiting hidden singularity on the surface of the Poincaré sphere

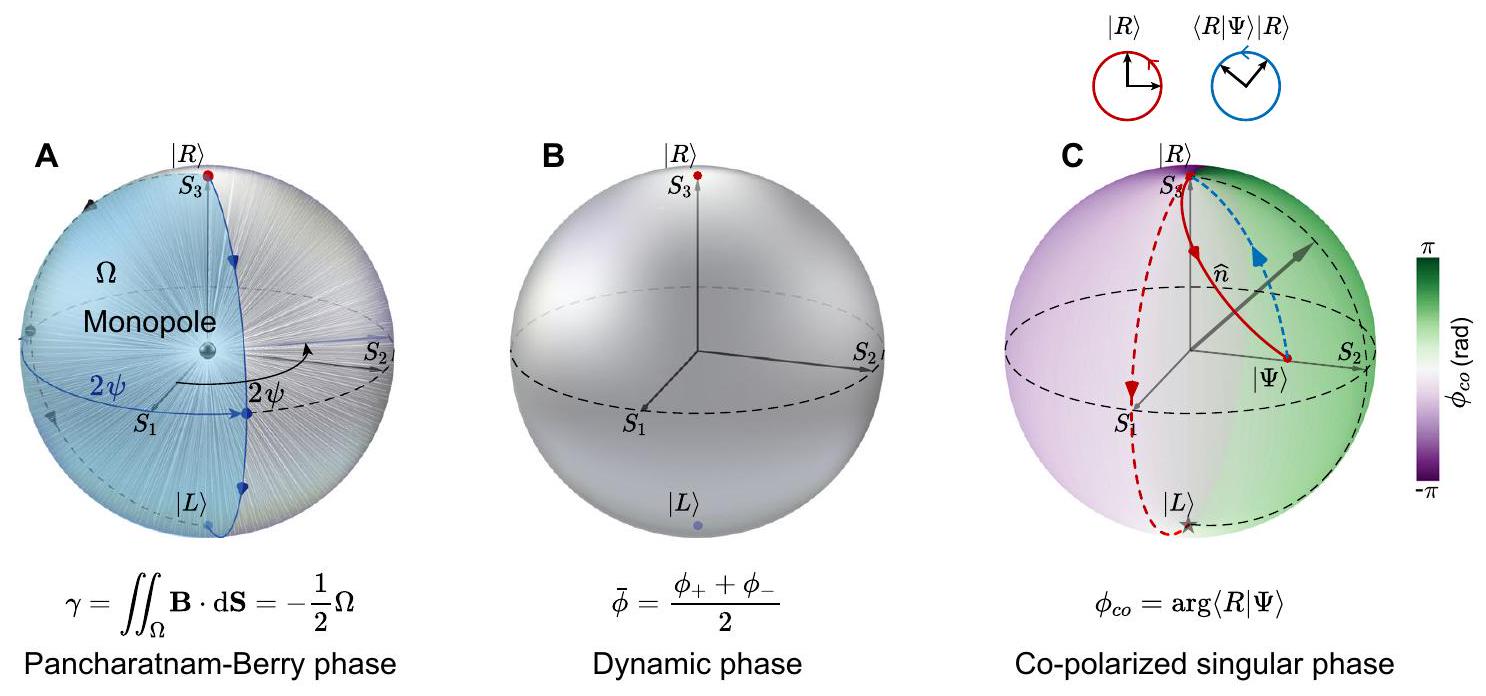
تظهر المرحلة الكلاسيكية بانشاراتنام-بيري، وهي نوع من المرحلة الهندسية، بشكل خالص من تعديل حالة الاستقطاب لشعاع الضوء. نظرًا لاعتمادها على تغييرات الاستقطاب، لا يمكن استخدامها بشكل فعال في تشكيل واجهة الموجة في الأنظمة التي تتطلب الحفاظ على حالة استقطاب ثابتة (متزامنة). هنا، نقدم آلية جديدة لتعديل الطور محمية طوبولوجيًا قادرة على تحقيق التماثل المعاكس الكامل.…
نموذج رياضي لمرض الجلد المتكتل باستخدام مشتق كابوتو من الرتبة الكسرية عبر تقنية النقطة الثابتة Mathematical model of the lumpy skin disease using Caputo fractional-order derivative via invariant point technique

$نموذج رياضي لمرض الجلد المتكتل باستخدام مشتق كابوتو من الرتبة الكسرية عبر تقنية النقطة الثابتة Mathematical model of the lumpy skin disease using Caputo fractional-order derivative via invariant point technique$

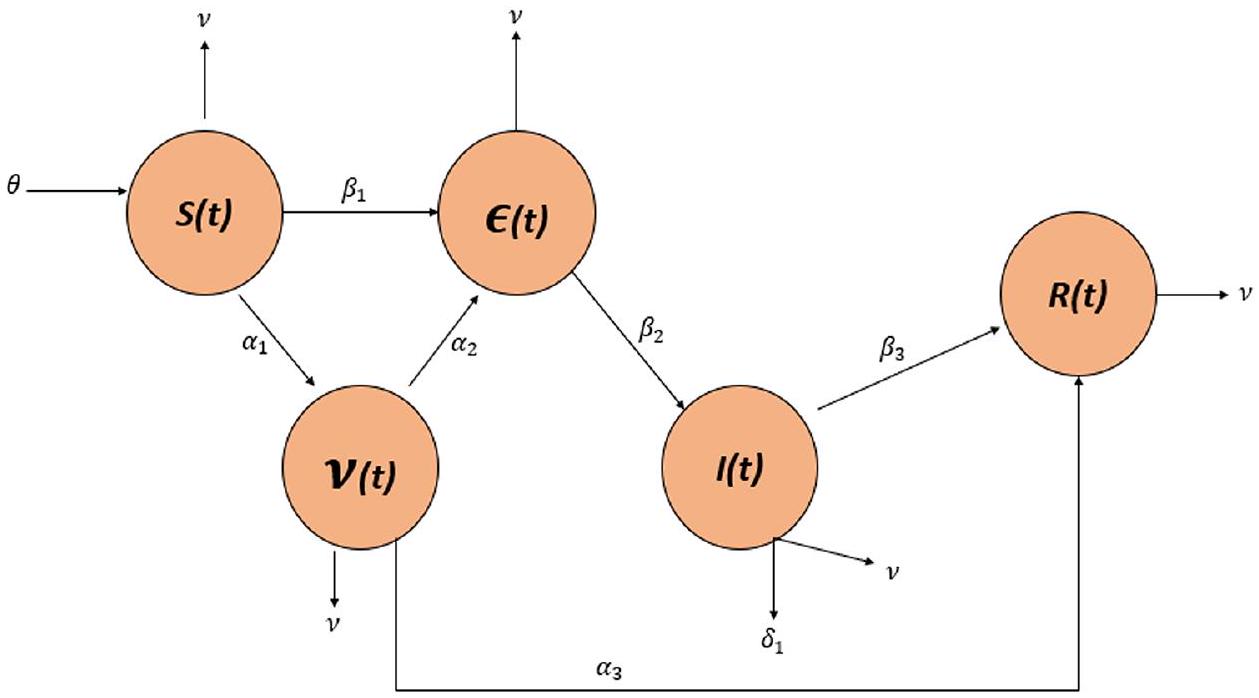
الهدف من هذه الورقة هو دراسة النموذج الكسرى لمرض الجلد المتكتل، بهدف تعزيز فهمنا لهذا المرض. على وجه التحديد، نستخدم المشتق الكسرى كابوتو-فابريزيو (CFF) الذي تم تقديمه مؤخرًا لتحليل نموذج مرض الجلد المتكتل بالتفصيل. لدراسة حلول النموذج بشكل شامل، نستخدم نهج بيكارد-لينديلوف لتقييم وجودها وتفردها. علاوة على ذلك، نستخدم تقنيات عددية، وتحديدًا المشتق CFF مع…
تعديل العوامل المربكة في الدراسات الرصدية التي تحقق في عوامل الخطر المتعددة: دراسة منهجية Confounder adjustment in observational studies investigating multiple risk factors: a methodological study

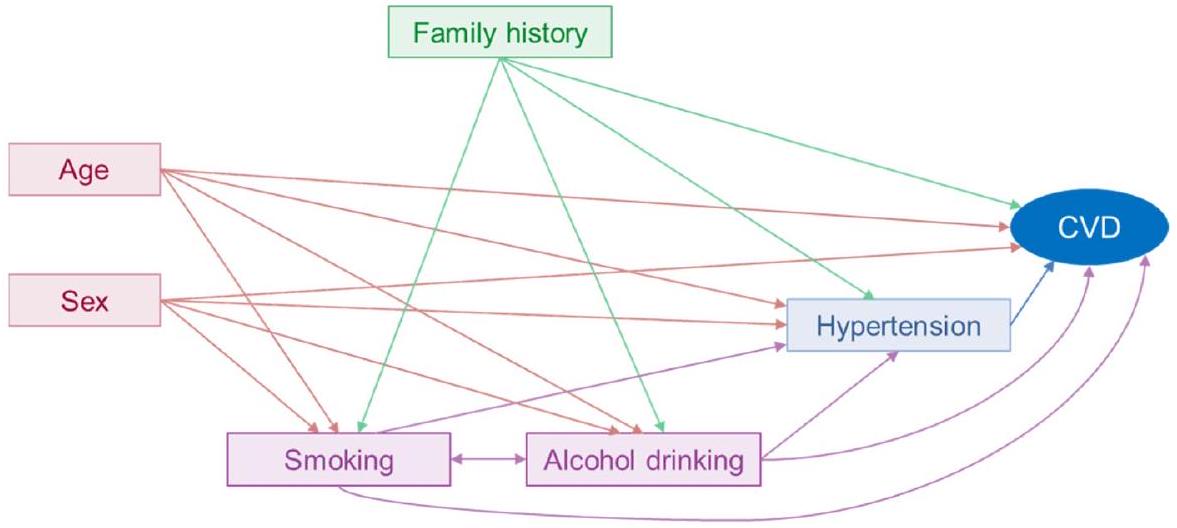
الخلفية: يعد تعديل العوامل المربكة أمرًا حاسمًا لاستنتاجات سببية دقيقة في الدراسات الرصدية. ومع ذلك، غالبًا ما يتم تجاهل ملاءمة الأساليب لتعديل العوامل المربكة في الدراسات التي تحقق في عوامل خطر متعددة، حيث لا تكون العوامل مرتبطة ببعضها البعض ببساطة. تهدف هذه الدراسة إلى تلخيص الأساليب المستخدمة لتعديل العوامل المربكة والقضايا ذات الصلة في الدراسات…
نهج التجميع الطيفي لمعادلة كورتويغ-دي فريس-بورجرز ذات الكسر الزمني عبر متعددات حدود تشيبيشيف من النوع الأول A Spectral Collocation Approach for Time-Fractional Korteweg-de Vries-Burgers Equation via First-Kind Chebyshev Polynomials

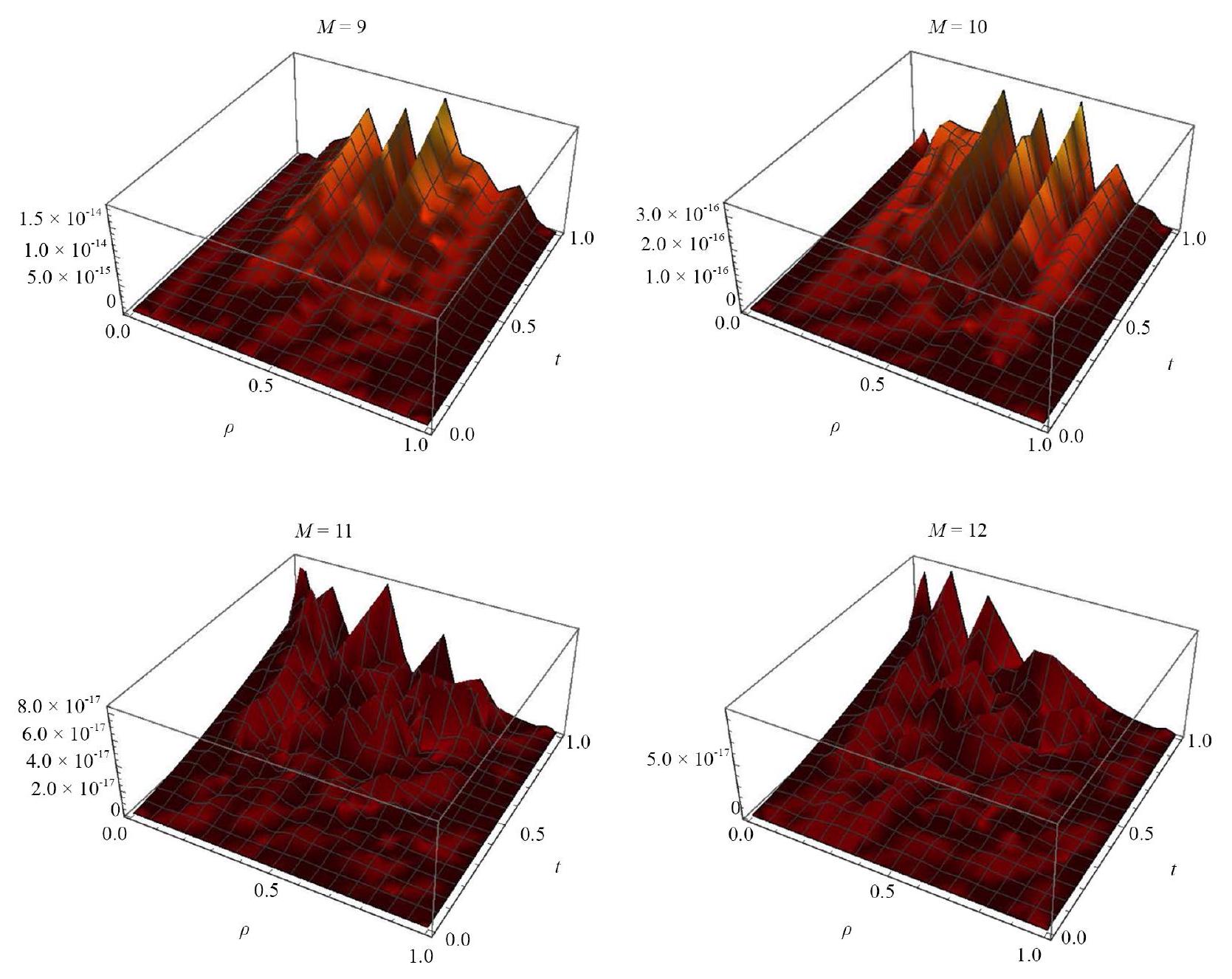
تم حل مشكلة كورتويغ-دي فريس-برجرز ذات الكسر الزمني (TFKdVB) عددياً في هذه الدراسة. يستخدم النهج طريقة التراص لمتعددات شبيشيف من النوع الأول المنقولة (SFKCPs). من خلال استخدام صيغة كابوتو لتقريب المشتقات ذات الكسر الزمني وفرض شروط الحدود، نصل إلى حل طيفي. تم تقديم أمثلة عددية لتوضيح دقة وفعالية النهج المقترح.
طريقة تشيبيشيف بيتروف-غاليركين للمعادلات التكاملية التفاضلية غير الخطية ذات النواة ذات التفرد المعتدل Chebyshev Petrov–Galerkin method for nonlinear time-fractional integro-differential equations with a mildly singular kernel

$طريقة تشيبيشيف بيتروف-غاليركين للمعادلات التكاملية التفاضلية غير الخطية ذات النواة ذات التفرد المعتدل Chebyshev Petrov–Galerkin method for nonlinear time-fractional integro-differential equations with a mildly singular kernel$

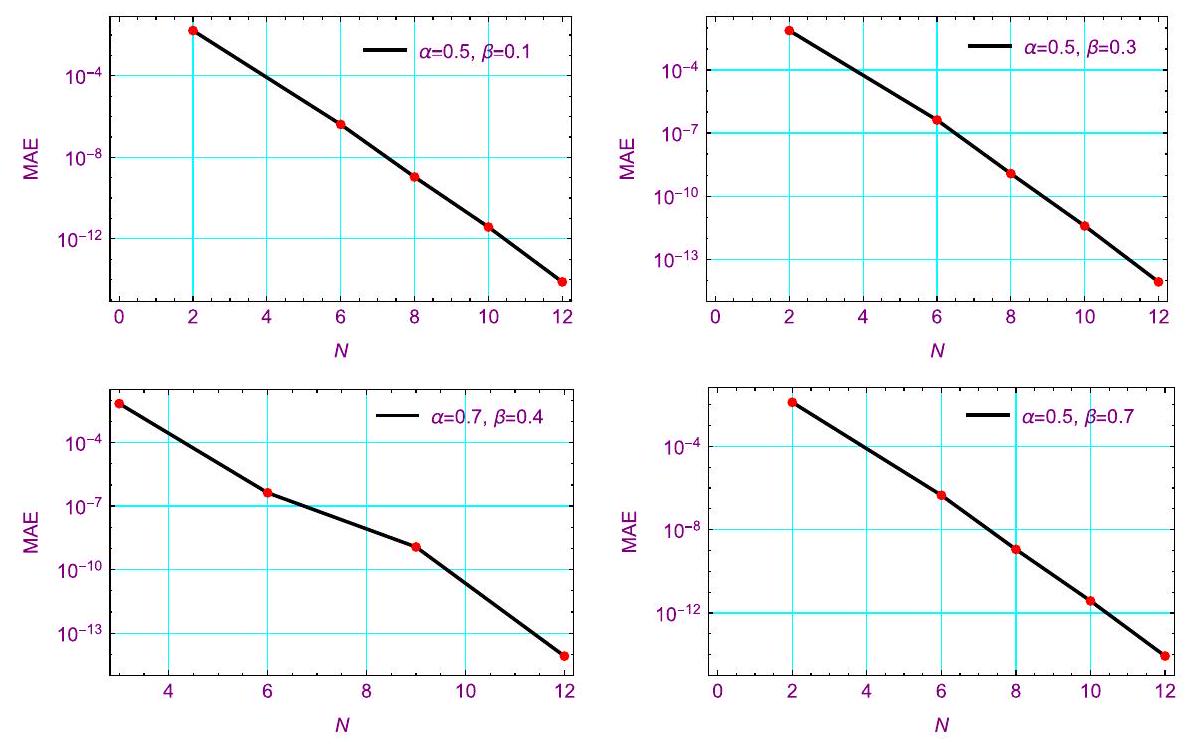
في هذه الورقة، يتم تقديم نهج جديد للمعادلات الجزئية التكاملية غير الخطية ذات الفواصل الزمنية مع نوى ضعيفة التفرد (TFPIDE). تنتج الطريقة المقترحة حلاً طيفياً شبه تحليلي باستخدام كثيرات حدود تشيبيشيف من النوع الأول المنقولة (SCP1K) كدوال أساسية. لتلبية متطلبات البداية والحدود المتجانسة، يجب اختيار مجموعة مناسبة من الدوال الأساسية. ثم يتم العثور على معاملات…
إطار طيفي باستخدام متعددات الحدود الشيفية المعدلة من النوع الثالث للحلول العددية لمعادلات التلغراف الهايبرولية ذات البعد الواحد والبعدين Spectral framework using modified shifted Chebyshev polynomials of the third-kind for numerical solutions of one- and two-dimensional hyperbolic telegraph equations

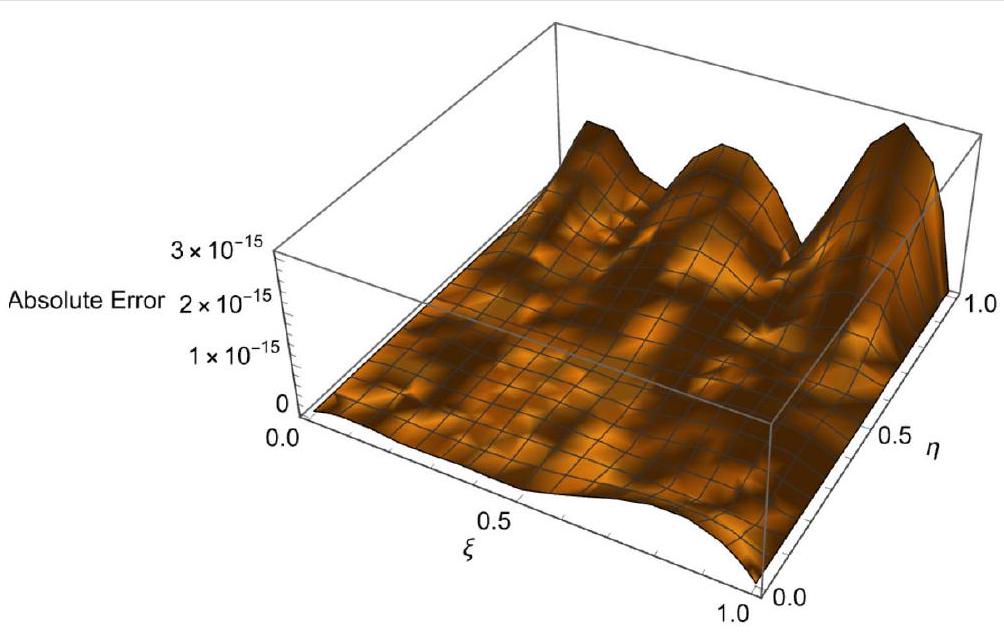
تناقش هذه الدراسة نهجًا عدديًا لحل معادلة التلغراف الهايبروليكية في بعدين وواحد. يعتمد هذا النهج على تطبيق طريقة غاليركين. نستخدم تركيبات مناسبة من متعددات الشيفر الثالث المعدلة المنقولة (3KMSCPs) كدوال أساسية لتحويل المعادلات التفاضلية الجزئية الحاكمة إلى مجموعة من المعادلات الجبرية. من خلال تقنيات غاليركين الطيفية، نثبت خطأ التقارب لإظهار أن خوارزمينا أكثر فعالية وكفاءة.…
أنماط الشكل الخارجي لجمجمة البيسون الأوروبي (Bison bonasus) Morphological patterns of the European bison (Bison bonasus) skull

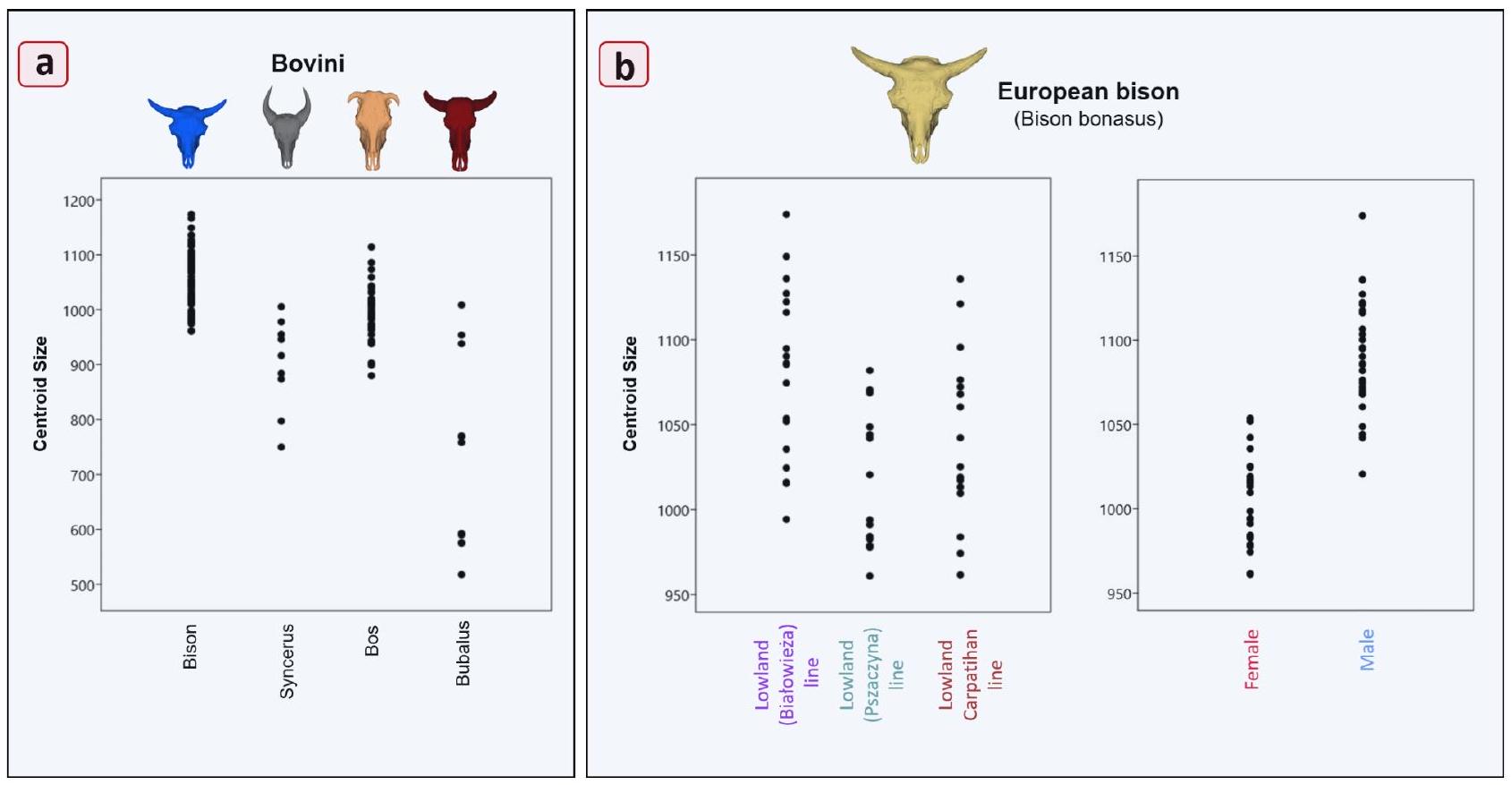
هدفت هذه الدراسة إلى التحقيق في تأثير العوامل البيئية، والاختيار الجنسي، والتنوع الجيني على شكل الجمجمة من خلال فحص بنية جمجمة البيسون الأوروبي، وهو نوع مهدد بالانقراض، ومقارنته بأنواع أخرى من البقريات. كانت جمجمة البيسون الأوروبي أكبر بكثير من جمجمة الأنواع الأخرى من قبيلة Bovini، وكشفت النتائج عن اختلافات شكلية كبيرة في شكل الجمجمة مقارنة…
توافق بشكل مقتصد مع تأثيرات عشوائية متعددة المتغيرات الكبيرة في glmmTMB Parsimoniously Fitting Large Multivariate Random Effects in glmmTMB

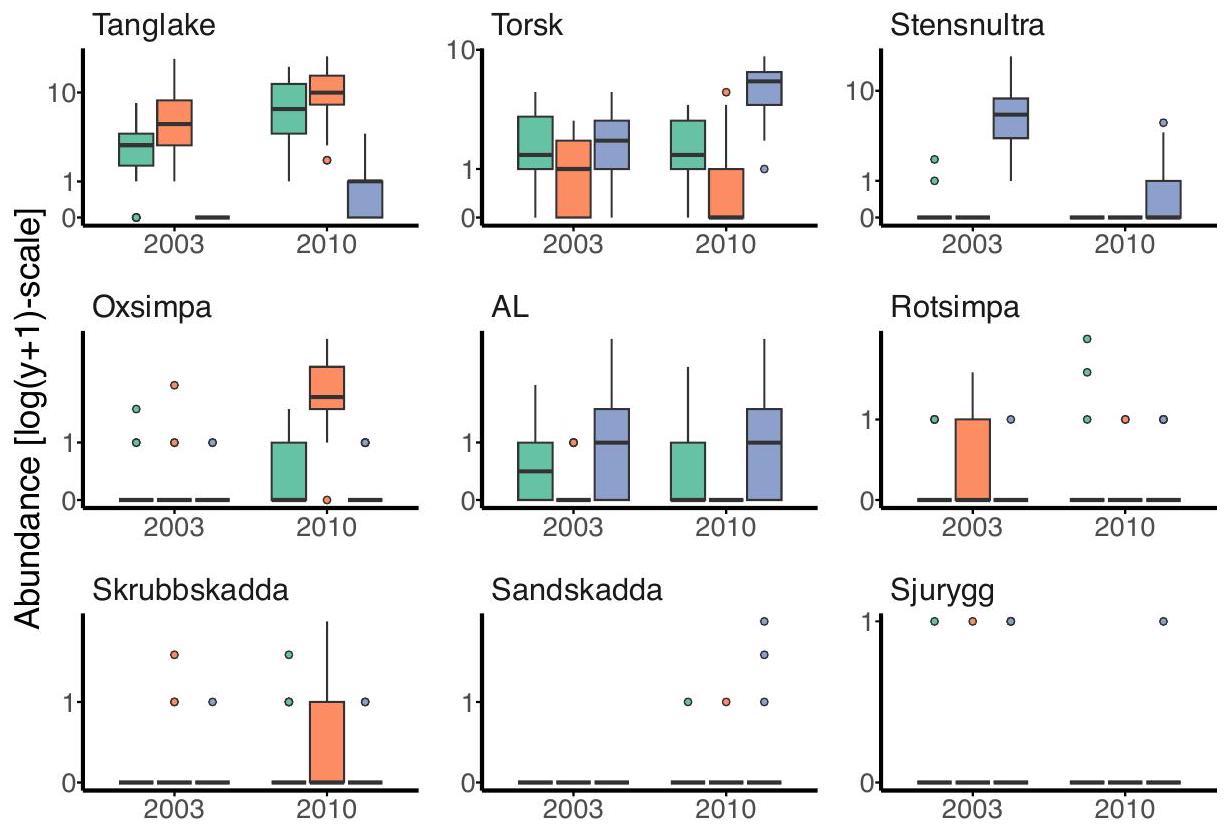
آثار عشوائية متعددة المتغيرات مع مصفوفات التباين-التغاير غير الهيكلية ذات الأبعاد الكبيرة، يمكن أن يكون تحديًا كبيرًا في التقدير. في هذه الورقة، نقدم تنفيذًا جديدًا لنهج منخفض الرتبة لتناسب التأثيرات العشوائية متعددة الأبعاد الكبيرة من خلال كتابتها كمزيج خطي من المتغيرات الكامنة. من خلال إضافة وظيفة منخفضة الرتبة إلى حزمة glmmTMB، نقوم بتحسين النماذج المختلطة…