التصنيف: النمذجة والمحاكاة (Modeling and Simulation)

نموذج رياضي لمرض الجلد المتكتل باستخدام مشتق كابوتو من الرتبة الكسرية عبر تقنية النقطة الثابتة Mathematical model of the lumpy skin disease using Caputo fractional-order derivative via invariant point technique

$نموذج رياضي لمرض الجلد المتكتل باستخدام مشتق كابوتو من الرتبة الكسرية عبر تقنية النقطة الثابتة Mathematical model of the lumpy skin disease using Caputo fractional-order derivative via invariant point technique$

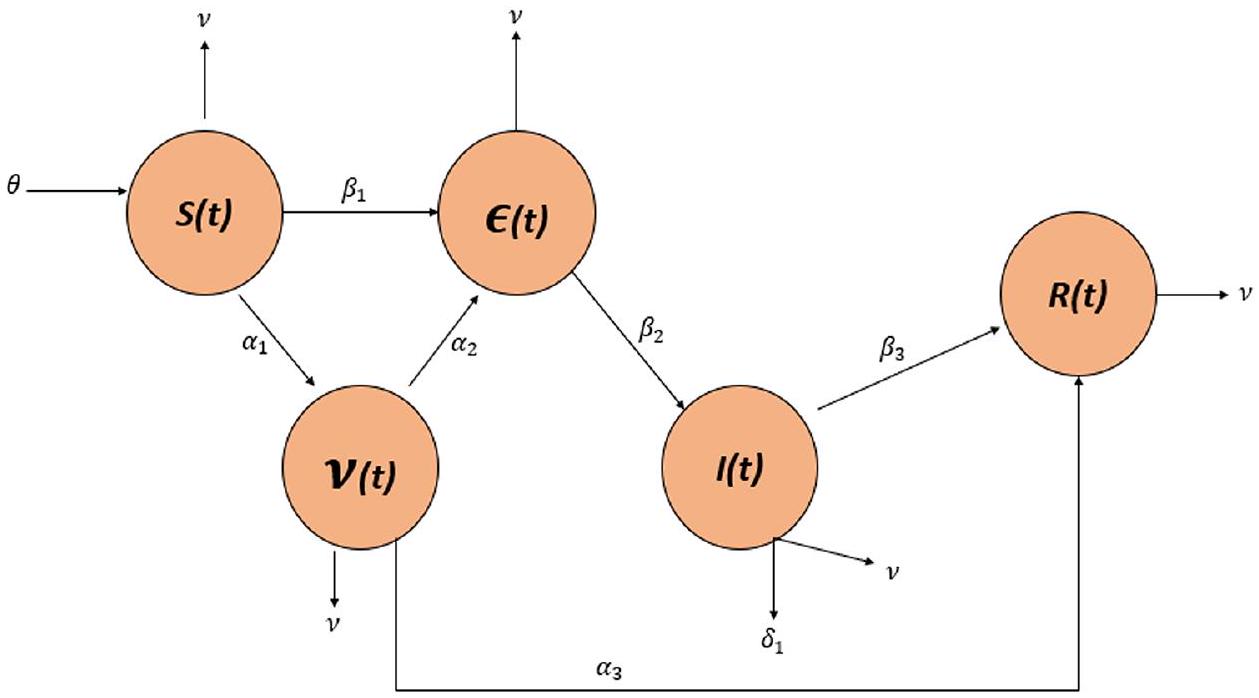
الهدف من هذه الورقة هو دراسة النموذج الكسرى لمرض الجلد المتكتل، بهدف تعزيز فهمنا لهذا المرض. على وجه التحديد، نستخدم المشتق الكسرى كابوتو-فابريزيو (CFF) الذي تم تقديمه مؤخرًا لتحليل نموذج مرض الجلد المتكتل بالتفصيل. لدراسة حلول النموذج بشكل شامل، نستخدم نهج بيكارد-لينديلوف لتقييم وجودها وتفردها. علاوة على ذلك، نستخدم تقنيات عددية، وتحديدًا المشتق CFF مع…
نهج التجميع الطيفي لمعادلة كورتويغ-دي فريس-بورجرز ذات الكسر الزمني عبر متعددات حدود تشيبيشيف من النوع الأول A Spectral Collocation Approach for Time-Fractional Korteweg-de Vries-Burgers Equation via First-Kind Chebyshev Polynomials

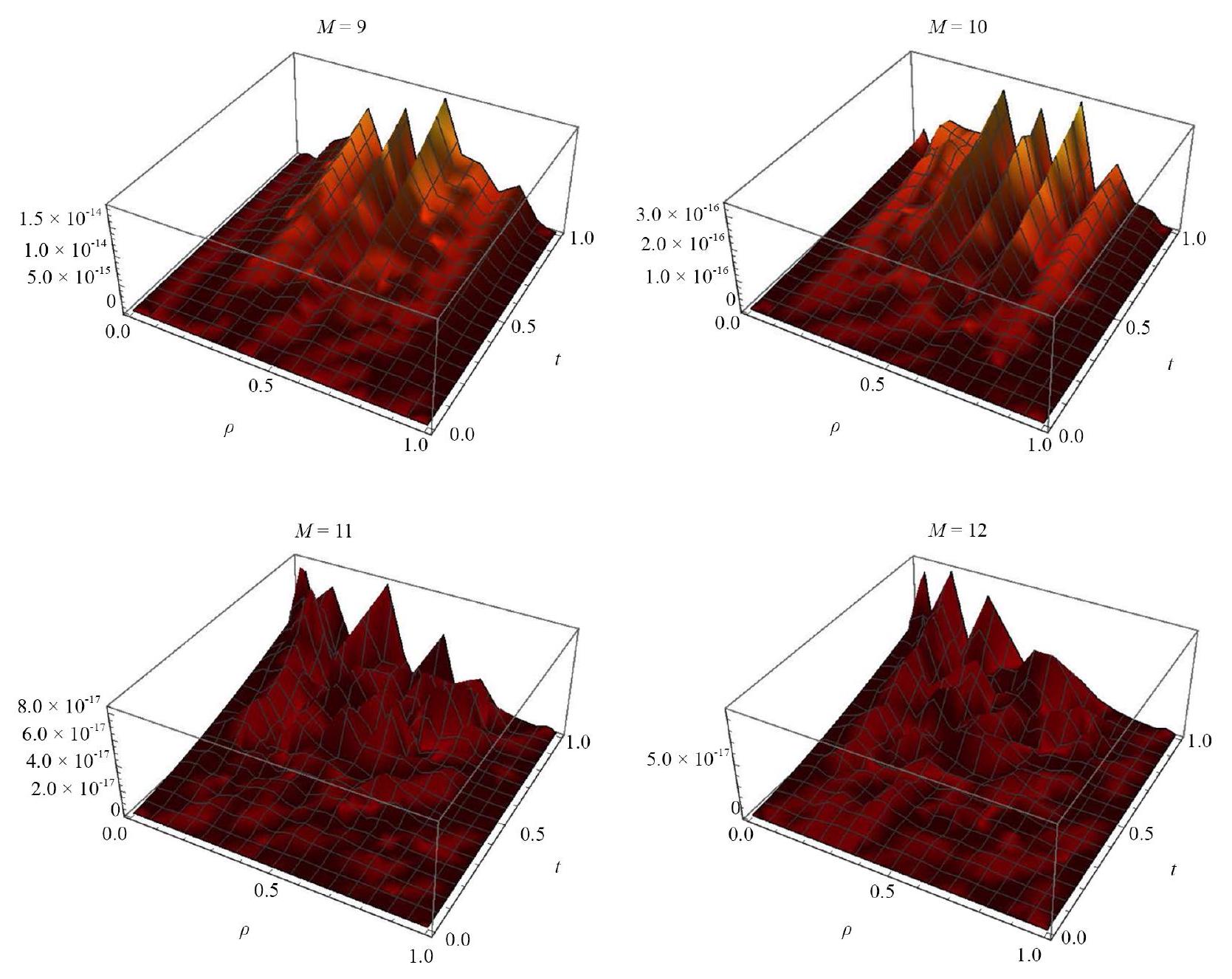
تم حل مشكلة كورتويغ-دي فريس-برجرز ذات الكسر الزمني (TFKdVB) عددياً في هذه الدراسة. يستخدم النهج طريقة التراص لمتعددات شبيشيف من النوع الأول المنقولة (SFKCPs). من خلال استخدام صيغة كابوتو لتقريب المشتقات ذات الكسر الزمني وفرض شروط الحدود، نصل إلى حل طيفي. تم تقديم أمثلة عددية لتوضيح دقة وفعالية النهج المقترح.
طريقة تشيبيشيف بيتروف-غاليركين للمعادلات التكاملية التفاضلية غير الخطية ذات النواة ذات التفرد المعتدل Chebyshev Petrov–Galerkin method for nonlinear time-fractional integro-differential equations with a mildly singular kernel

$طريقة تشيبيشيف بيتروف-غاليركين للمعادلات التكاملية التفاضلية غير الخطية ذات النواة ذات التفرد المعتدل Chebyshev Petrov–Galerkin method for nonlinear time-fractional integro-differential equations with a mildly singular kernel$

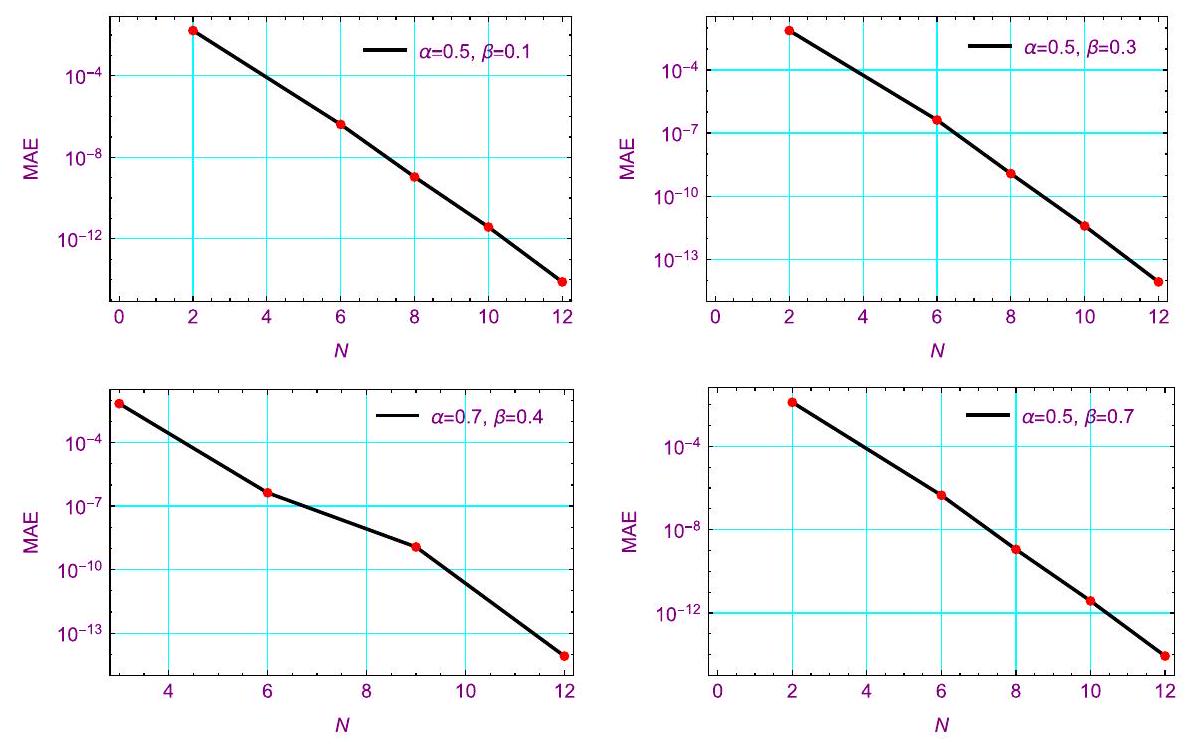
في هذه الورقة، يتم تقديم نهج جديد للمعادلات الجزئية التكاملية غير الخطية ذات الفواصل الزمنية مع نوى ضعيفة التفرد (TFPIDE). تنتج الطريقة المقترحة حلاً طيفياً شبه تحليلي باستخدام كثيرات حدود تشيبيشيف من النوع الأول المنقولة (SCP1K) كدوال أساسية. لتلبية متطلبات البداية والحدود المتجانسة، يجب اختيار مجموعة مناسبة من الدوال الأساسية. ثم يتم العثور على معاملات…
تطور الورم وتفاعلات البيئة الدقيقة في الفضاء ثنائي وثلاثي الأبعاد Tumour evolution and microenvironment interactions in 2D and 3D space

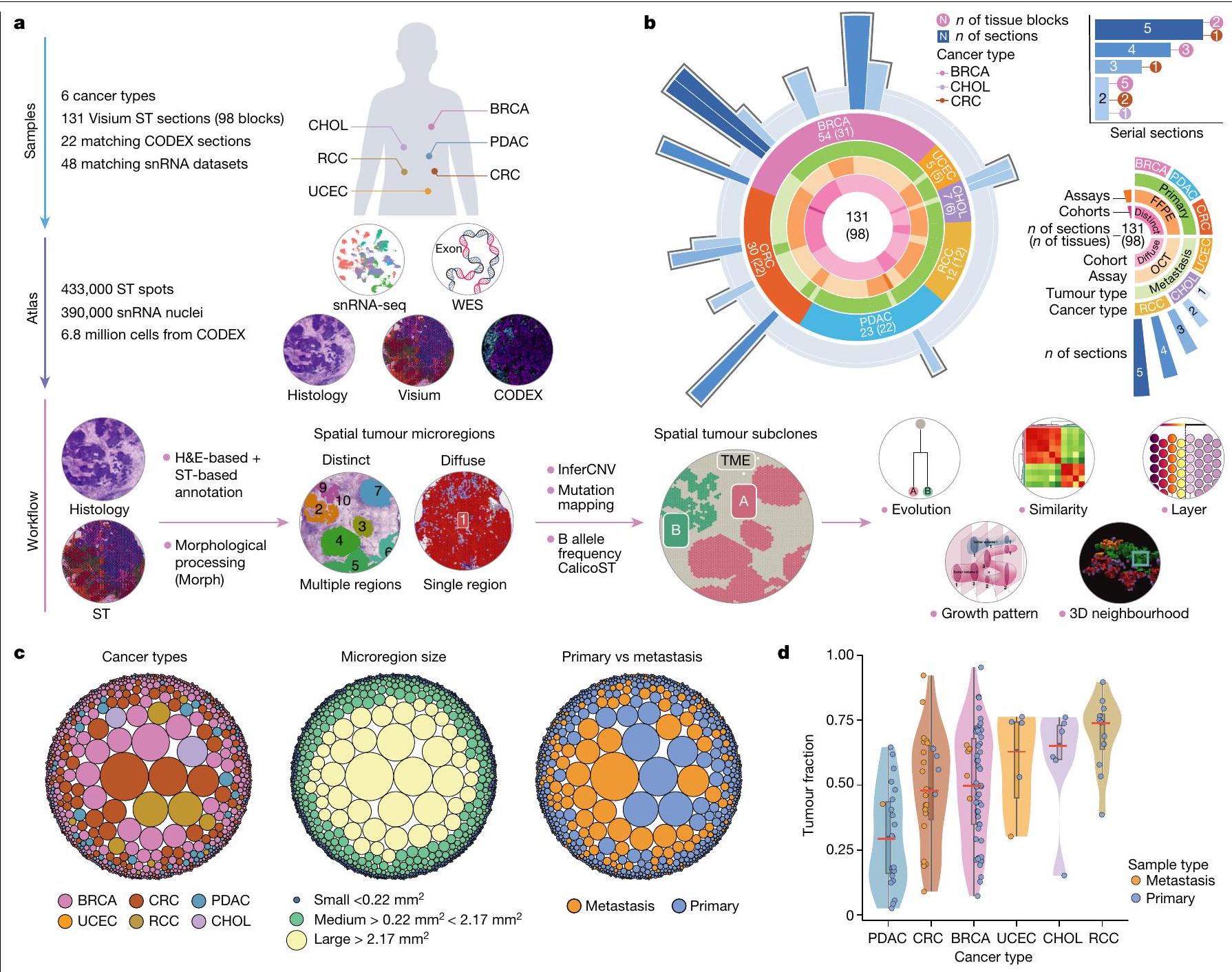
لدراسة التفاعلات المكانية بين خلايا السرطان وغير السرطان , قمنا هنا بفحص مجموعة من 131 مقطع ورمي من 78 حالة عبر 6 أنواع من السرطان باستخدام تقنية النسخ الجيني المكاني (ST). تم دمج ذلك مع 48 عينة من تسلسل RNA أحادي النواة المتطابقة و22 عينة من الكشف المشترك بواسطة الفهرسة (CODEX). لوصف هياكل الورم والموائل،…
آثار حركة البشر على ديناميات انتقال 18 فيروسًا تنفسيًا في المدينة خلال سنوات ما قبل وما بعد جائحة كوفيد-19 Impacts of human mobility on the citywide transmission dynamics of 18 respiratory viruses in pre- and post-COVID-19 pandemic years

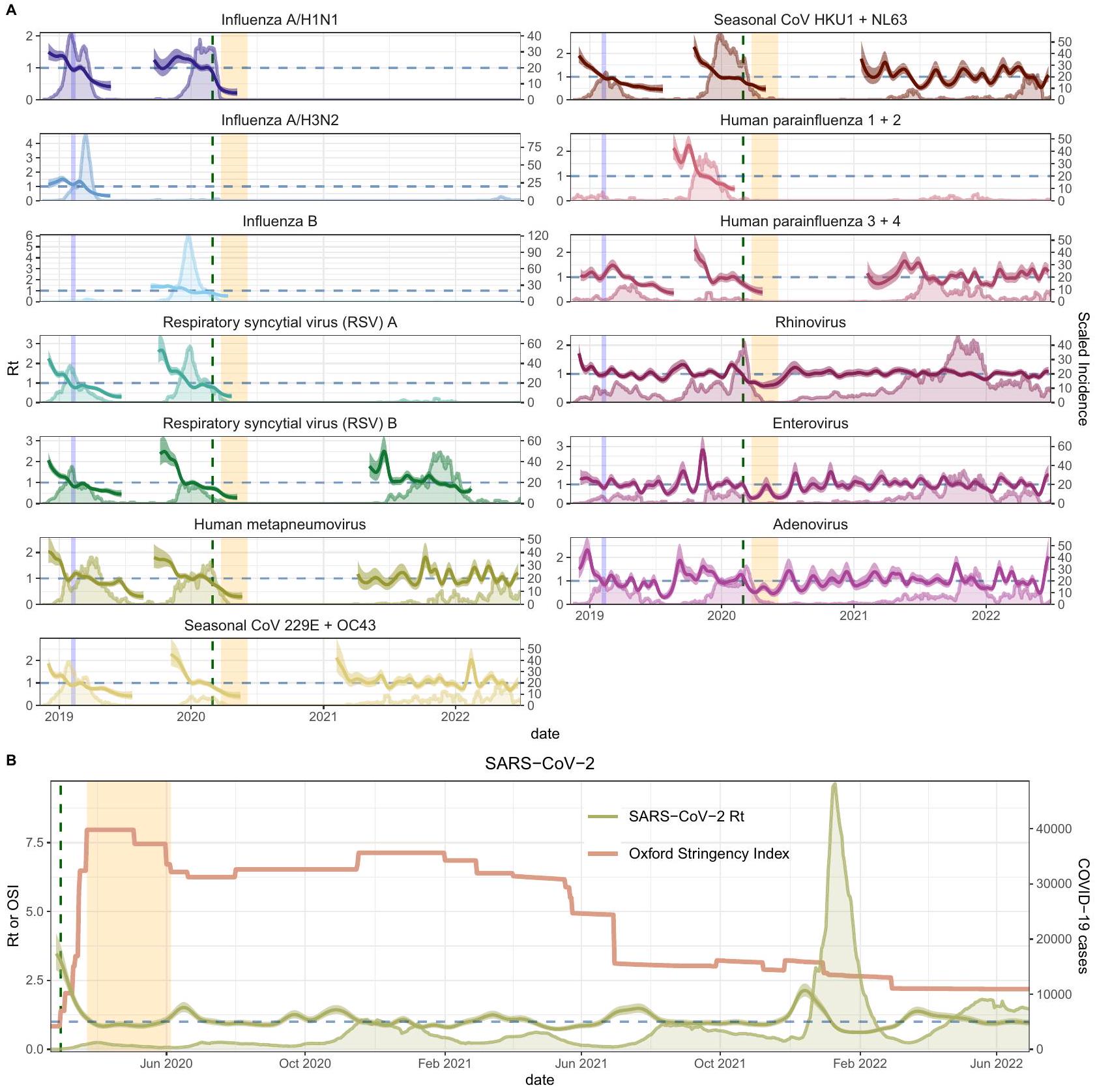
لقد استخدمت العديد من الدراسات بيانات موقع الأجهزة المحمولة لنمذجة ديناميات فيروس SARS-CoV-2، ومع ذلك فإن العلاقات بين سلوك التنقل والفيروسات التنفسية المستوطنة أقل فهمًا. درسنا تأثيرات تنقل السكان على انتقال 17 فيروسًا مستوطنًا وSARS-CoV-2 في سياتل على مدى فترة 4 سنوات، من 2018 إلى 2022. قبل عام 2020، كانت الزيارات إلى المدارس ورياض الأطفال،…
الحدود الثابتة زمنياً في فئة من نماذج الكيمياء الحيوية الجاذبة–الطاردة غير الخطية المحلية وغير المحلية مع اللوجستيات Uniform-in-time boundedness in a class of local and nonlocal nonlinear attraction–repulsion chemotaxis models with logistics

الملخص. يتم دراسة نموذج الجذب-النفور غير الخطي بالكامل وكيمياء الحركة ذات التدفق الصفري كما يلي:
التشريح المنهجي لبيئات الخلايا المفردة بين الأورام الطبيعية عبر ألف ورم من 30 نوعًا من السرطان Systematic dissection of tumor-normal single-cell ecosystems across a thousand tumors of 30 cancer types

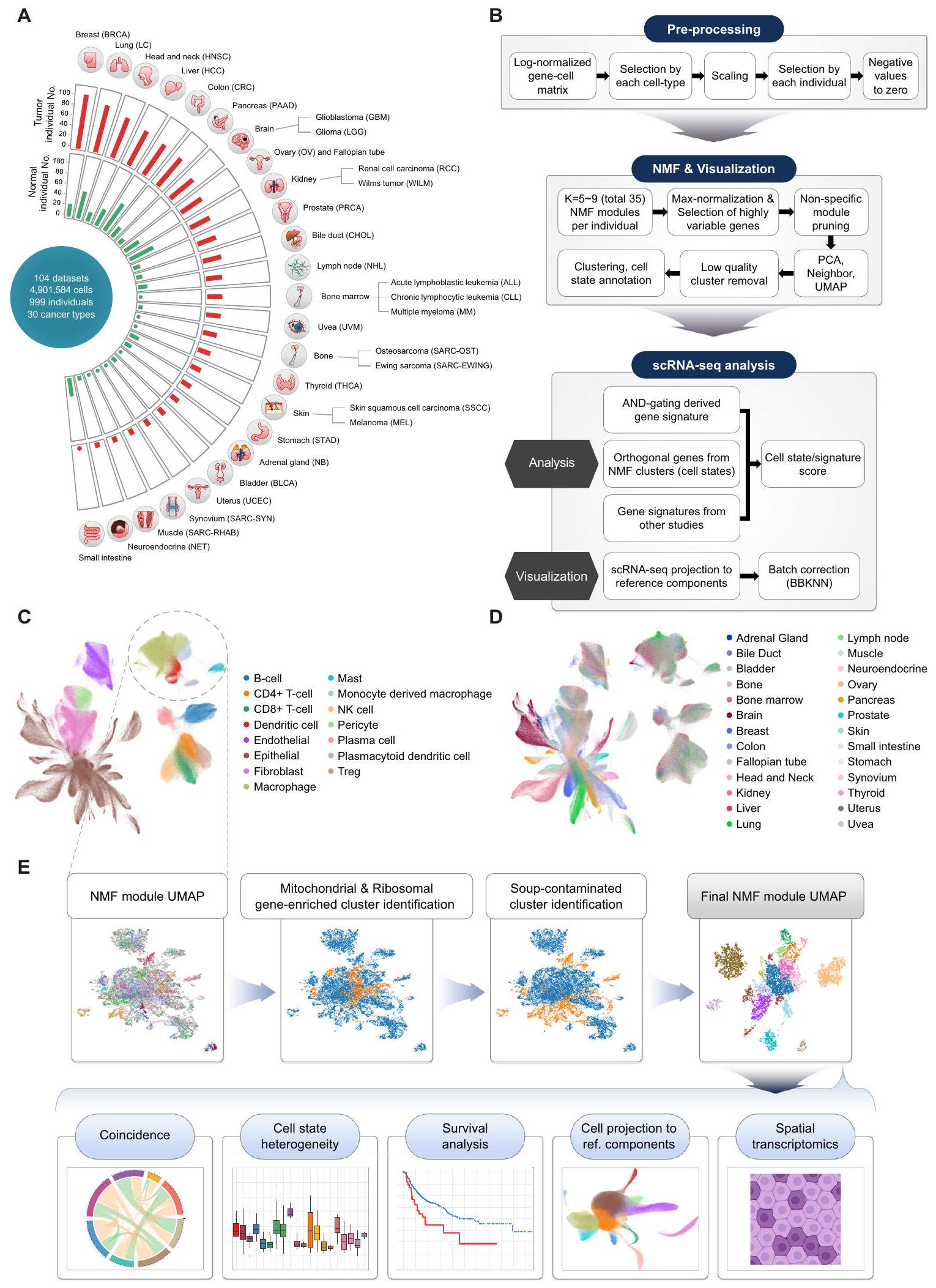
تعقيد بيئة الورم الدقيقة يطرح تحديات كبيرة في علاج السرطان. هنا، للتحقيق بشكل شامل في النظم البيئية للورم والطبيعي، نقوم بإجراء تحليل تكاملي لـ 4.9 مليون ترانسكريبتوم أحادي الخلية من 1070 عينة ورمية و493 عينة طبيعية، بالاشتراك مع 137 ترانسكريبتوم مكاني شامل للسرطان، و8887 من TCGA، و1261 ورم معالج بمثبطات نقاط التفتيش. نحن نحدد مجموعة…
التغيرات الزمنية في 24 مرضًا معديًا قابلًا للإبلاغ في الصين قبل وأثناء جائحة COVID-19 Temporal shifts in 24 notifiable infectious diseases in China before and during the COVID-19 pandemic

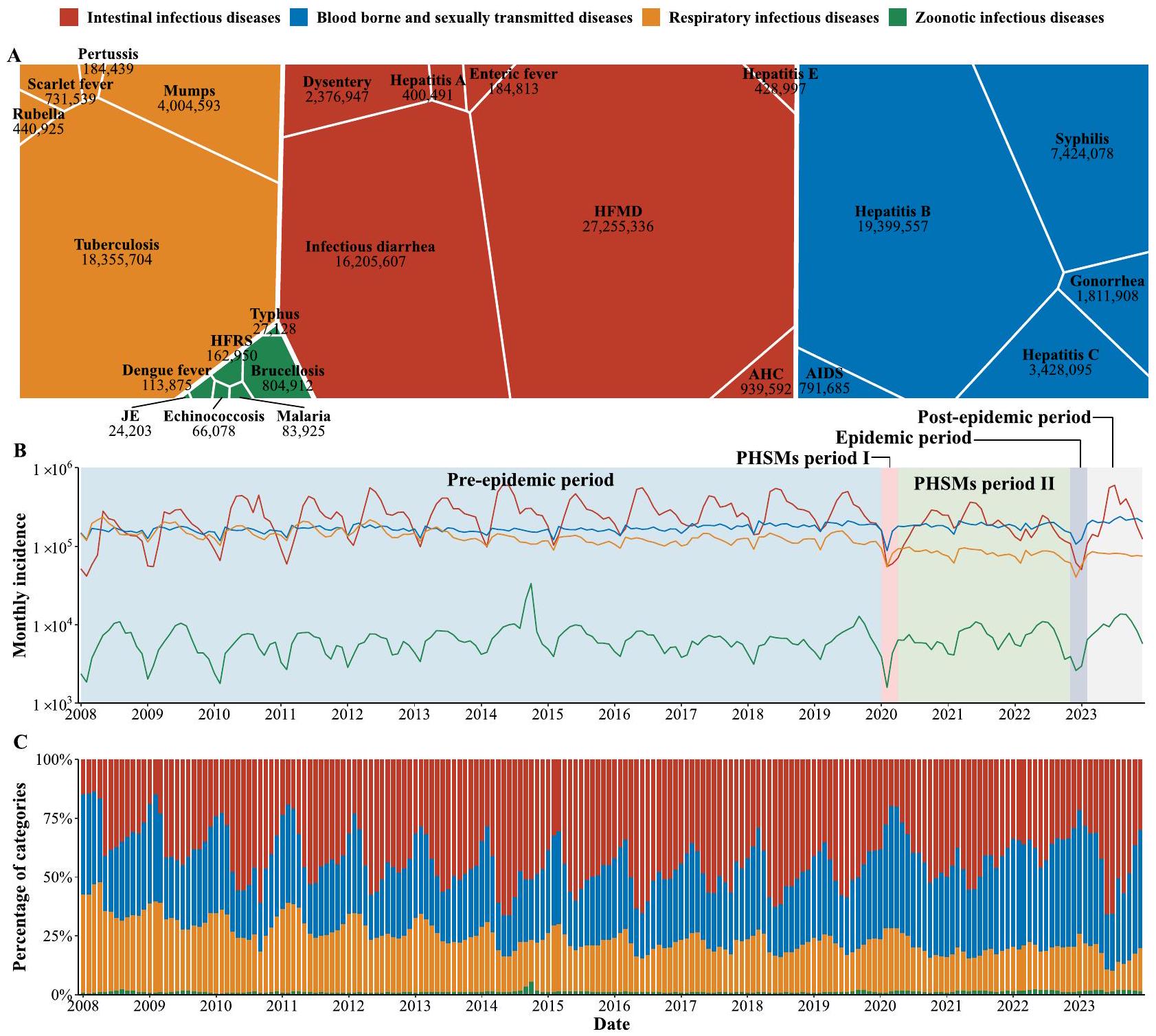
جائحة مرض فيروس كورونا 2019 (COVID-19)، جنبًا إلى جنب مع تنفيذ تدابير الصحة العامة والاجتماعية (PHSMs)، أعادت تشكيل ديناميات انتقال الأمراض المعدية بشكل ملحوظ. قمنا بتحليل تأثير PHSMs على 24 مرضًا معديًا قابلًا للإبلاغ (NIDs) في البر الرئيسي الصيني، باستخدام نماذج السلاسل الزمنية للتنبؤ باتجاهات الانتقال بدون PHSMs أو جائحة. كشفت نتائجنا عن أنماط موسمية…
نتائج الوجود والقابلية للتحكم في معادلات فولتيرا-فريدولم التكاملية التفاضلية الكسرية المحايدة Existence and controllability results for neutral fractional Volterra-Fredholm integro-differential equations

تتناول هذه الورقة البحثية التحقيق في معادلة فولتيرا-فريدولم التكاملية التفاضلية المعززة بمشتقات كابوتو الكسرية الخاضعة لظروف ترتيب محددة. تؤسس الدراسة بشكل صارم وجود الحلول من خلال تطبيق نظرية نقطة الثبات لشودر. علاوة على ذلك، تشمل المعادلات التكاملية التفاضلية المحايدة لفولتيرا-فريدولم، مما يوسع من قابلية تطبيق النتائج. بالإضافة إلى ذلك، تستكشف الورقة مفهوم القابلية للتحكم في…
ديناميات نموذج البحيرات الملوثة عبر مشغلات كسرية-فراكتالية باستخدام خوارزميتين عدديتين مختلفتين Dynamics of a model of polluted lakes via fractal–fractional operators with two different numerical algorithms

$ديناميات نموذج البحيرات الملوثة عبر مشغلات كسرية-فراكتالية باستخدام خوارزميتين عدديتين مختلفتين Dynamics of a model of polluted lakes via fractal–fractional operators with two different numerical algorithms$

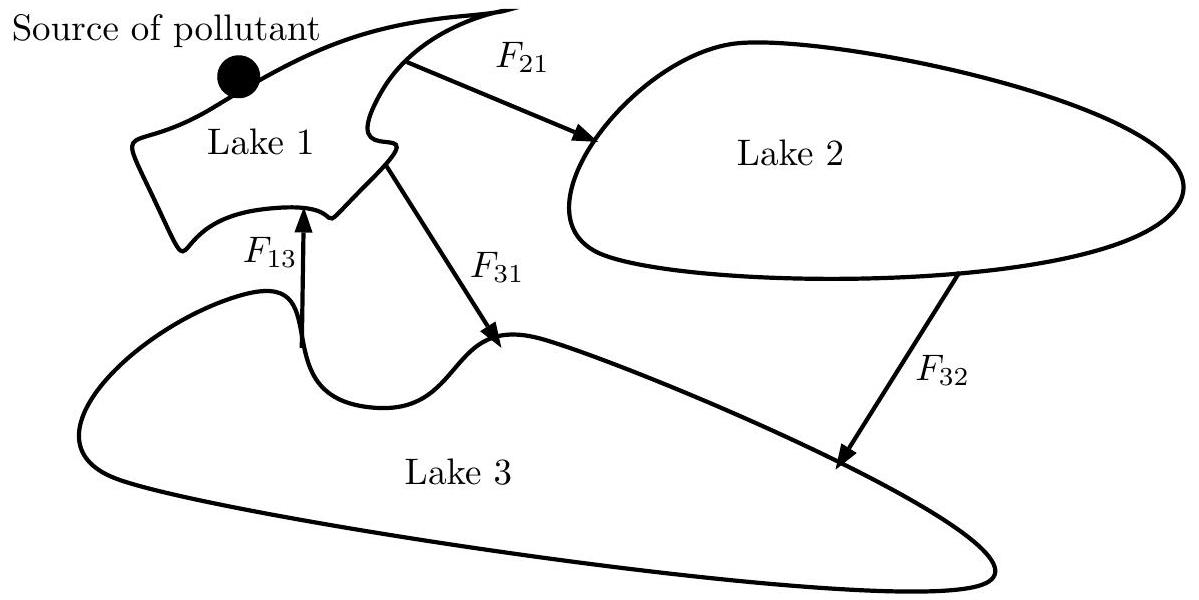
نستخدم نوى من نوع ميتاج-ليفلر لحل نظام من المعادلات التفاضلية الكسرية باستخدام مشغلات كسرية-فراغية (FF) ذات ترتيب كسرية وفراغية. باستخدام مفهوم المشتقات FF ذات الذاكرة غير المتناهية وغير المحلية، يتم دراسة نموذج لثلاثة بحيرات ملوثة مع مصدر واحد للتلوث. تُستخدم خصائص التحويل غير المتناقص والمضغوط لإثبات وجود حل لنموذج FF لنظام البحيرات الملوثة. لهذا الغرض،…